
VESTIBULARES RECENTES POR ASSUNTO
Gravitação Universal – 2017, 2016 e 2015
LEIS DE KEPLER
01- (FATEC – SP – 017)

O Sistema de Coordenadas Geográficas é definido por linhas imaginárias, que têm como objetivo localizar qualquer ponto sobre a superfície terrestre.
No Planeta Marte, um sistema semelhante ao descrito.
(A) pode ser utilizado, uma vez que esse planeta é o maior do sistema solar e o que possui a maior massa.
(B) pode ser utilizado, pois esse planeta possui formato aproximadamente esférico, assim como a Terra.
(C) não pode ser utilizado, por causa da existência de um intenso campo gravitacional ao seu redor.
(D) não pode ser utilizado, já que sua composição atmosférica é diferente da composição encontrada na Terra.
(E) não pode ser utilizado, haja vista que esse sistema só pode ser aplicado em um planeta que apresente hidrosfera semelhante à terrestre.
02-(FATEC – SP –017)

Considere que essa viagem da Terra a Marte tem duração de 210 dias terrestres. Sabe-se que um ano marciano equivale a 687 dias terrestres. Uma expedição a Marte sairá da Terra daqui a exatos seis anos terrestres.
O total de anos marcianos para que essa expedição chegue a Marte é, aproximadamente, igual a
(A) 1,5.
(B) 2,0.
(C) 2,5.
(D) 3,0.
(E) 3,5.
03-(FGV-SP-017)

Johannes Kepler (1571-1630) foi um cientista dedicado ao estudo do sistema solar.

Uma das suas leis enuncia que as órbitas dos planetas, em torno do Sol, são elípticas, com o Sol situado em um dos focos dessas elipses.
Uma das consequências dessa lei resulta na variação
(A) do módulo da aceleração da gravidade na superfície dos planetas.
(B) da quantidade de matéria gasosa presente na atmosfera dos planetas.
(C) da duração do dia e da noite em cada planeta.
(D) da duração do ano de cada planeta.
(E) da velocidade orbital de cada planeta em torno do Sol.
04- (IFMG-MG-2017)

As leis de Kepler trouxeram uma nova compreensão para a mecânica celeste. Elas possibilitaram analisar as trajetórias, períodos e distâncias de corpos celestes. De acordo com as Leis de Kepler, é CORRETO afirmar que o:
A) módulo da velocidade de um planeta em órbita elíptica é constante.
B) Sol se situa em um dos focos da trajetória elíptica descrita por um planeta.
C) período de translação e a massa de um planeta se relacionam através de uma proporção direta.
D) período de rotação de um planeta, em torno de seu eixo, e seu o período de translação em torno do Sol são diretamente proporcionais.
05- (UNCISAL-AL-017)

Na noite do dia 14 de novembro de 2016 aconteceu o chamado fenômeno da Super Lua.

A informação transmitida por muitos dos veículos de comunicação era de que, naquela noite, “a lua cheia aumentaria de tamanho”.
Essa afirmativa não é cientificamente correta, visto que a Lua em simantém seu tamanho natural. Qual a explicação mais correta para o fenômeno?
A) O aumento visual no tamanho da Lua ocorre pelo aumento de seu brilhogerado quando nosso satélite se encontra na fase de lua cheia.
B) A Terra se encontra no ponto mais próximo do Sol, o que aproxima mais a Lua da Terra devido ao aumento dos efeitos gravitacionais do Sol.
C) No perigeu da órbita lunar, a coluna de ar entre a Terra e a Lua diminui; assim, a atmosfera proporciona um efeito de ampliação visual por refração.
D) As forças de maré são mais intensas durante o período de Lua cheia proporcionando, assim, uma maior aproximação desse astro em relação à Terra.
E) A trajetória lunar não é circular, de forma que ao atingir o ponto mais próximo da Terra temos apenas um aumento aparente devido à proximidade.
06- (FUVEST-SP-016)

Quando a Lua está em quarto crescente ou quarto minguante, o triângulo formado pela Terra, pelo Sol e pela Lua é retângulo, com a Lua no vértice do ângulo reto.
O astrônomo grego Aristarco, do século III a.C., usou este fato para obter um valor aproximado da razão entre as distâncias da Terra à Lua, dL, e da Terra ao Sol, dS.

É possível estimar a medida do ângulo α,relativo ao vérticeda Terra,nessas duas fases, a partir da observação de que o tempo t1 , decorrido de uma lua quarto crescente a uma lua quarto minguante, é um pouco maior do que o tempo t2,decorrido de uma lua quarto minguante a uma lua quarto
crescente.
Supondo que a Lua descreva em torno da Terra um movimento circular uniforme, tomando t1 = 14,9 dias e t2 = 14,8 dias, conclui-se que a razão dL/dS seria aproximadamente dada por
![]()
07- (FAMERP-SP-015)

Atualmente, a Lua afasta-se da Terra a uma razão média aproximada de 4 cm/ano. Considerando

as Leis de Kepler, é correto concluir que o período de
(A) rotação da Lua não se altera.
(B) rotação da Lua está diminuindo.
(C) translação da Lua ao redor da Terra não se altera.
(D) translação da Lua ao redor da Terra está aumentando.
(E) translação da Lua ao redor da Terra está diminuindo.
08- (UNICAMP-SP-015)

A primeira lei de Kepler demonstrou que os planetas se movem em órbitas elípticas e não circulares.
A segunda lei mostrou que os planetas não se movem a uma velocidade constante.
(Adaptado Marvin Perry, Civilização Ocidental: uma história concisa. São Paulo: Martins Fontes, 1999, p. 289.)

É correto afirmar que as leis de Kepler
a) confirmaram as teorias definidas por Copérnico e são exemplos domodelo científico que passou a vigorar a partir da Alta Idade Média.
b) confirmaram as teorias defendidas por Ptolomeu e permitiram a produção das cartas náuticas usadas no período do descobrimento da América.
c) são a base do modelo planetário geocêntrico e se tornaram as premissas cientificas que vigoram até hoje.
d) forneceram subsídios para demonstrar o modelo planetário heliocêntrico e criticar as posições
defendidas pela Igreja naquela época.
O texto a seguir refere-se às questões de números 09 e 10.
Em seu livro O pequeno príncipe, Antoine de Saint-Exupéry imaginou haver vida em certo planeta

ideal.
Tal planeta teria dimensões curiosas e grandezas gravitacionais inimagináveis na prática. Pesquisas científicas, entretanto, continuam sendo realizadas e não se descarta a possibilidade de haver mais planetas no sistema solar, além dos já conhecidos.
Imagine um hipotético planeta, distante do Sol 10 vezes mais longe do que a Terra se encontra desse astro, com massa 4 vezes maior que a terrestre e raio superficial igual à metade do raio da Terra. Considere a aceleração da gravidade na superfície da Terra expressa por g.
09-(FGV-SP-015)

Esse planeta completaria uma volta em torno do Sol em um tempo, expresso em anos terrestres,

mais próximo de
![]()
10-(FGV-SP-015)

Em seu livro O pequeno príncipe, Antoine de Saint-Exupéry imaginou haver vida em certo planeta

ideal.
Tal planeta teria dimensões curiosas e grandezas gravitacionais inimagináveis na prática.
Pesquisas científicas, entretanto, continuam sendo realizadas e não se descarta a possibilidade de haver mais planetas no sistema solar, além dos já conhecidos.
Imagine um hipotético planeta, distante do Sol 10 vezes mais longe do que a Terra se encontra desse astro, com massa 4 vezes maior que a terrestre e raio superficial igual à metade do raio da Terra.
Considere a aceleração da gravidade na superfície da Terra expressa por g.
Um objeto, de massa m, a uma altura h acima do solo desse planeta, com h muito menor do que o raio superficial do planeta teria uma energia potencial dada por m·g·h multiplicada pelo fator
![]()
11-(UFLA-MG-015)

Sobre a trajetória elíptica realizada pela Terra em torno do Sol, ilustrado na figura abaixo, é CORRETO afirmar:

(A) O sistema mostrado na figura representa o modelo heliocêntrico.
(B) O sistema mostrado na figura representa o modelo geocêntrico.
(C) O período de evolução da Terra em torno do Sol é de aproximadamente 24 horas.
(D) O período de evolução da Terra em torno do Sol é de aproximadamente 28 dias.
12-(UFJF-MG-015)

Muitas teorias sobre o Sistema Solar se sucederam, até que, no século XVI, o polonês Nicolau

Copérnico apresentou uma versão revolucionária. Para Copérnico, o Sol, e não a Terra era o centro do sistema.
Atualmente, o modelo aceito para o Sistema Solar é, basicamente, o de Copérnico, feitas as correções propostas pelo alemão Johannes Keppler e por cientistas subsequentes.
Sobre Gravitação e as Leis de Kepler, considere as afirmativas, a seguir, verdadeiras (V) ou falsas (F).
I) ( ) Adotando-se o Sol como referencial, todos os planetas movem-se descrevendo órbitas elípticas, tendo o Sol como um dos focos da elipse.
II) ( ) O vetor posição do centro de massa de um planeta do Sistema Solar, em relação ao centro de massa do Sol, varre áreas iguais em intervalos de tempo iguais, não importando a posição do planeta em sua órbita.
III) ( ) O vetor posição do centro de massa de um planeta do Sistema Solar, em relação ao centro de massa do Sol, varre áreas proporcionais em intervalos de tempo iguais, não importando a posição do planeta em sua órbita.
IV) ( ) Para qualquer planeta do Sistema Solar, o quociente do cubo do raio médio da órbita pelo quadrado do período de revolução em torno do Sol é constante.
Assinale a alternativa CORRETA.
a) Todas as afirmativas são verdadeiras.
b) Apenas as afirmativas I, II e III são verdadeiras.
c) Apenas as afirmativas I, II e IV são verdadeiras.
d) Apenas as afirmativas II, III e IV são verdadeiras.
e) Apenas as afirmativas I e II são verdadeiras.
LEI DA ATRAÇÃO UNIVERSAL
01- (UEFS-BA-017)

A figura mostra como a força gravitacional entre dois corpos de massas M1 e M2 varia com a

distância entre seus centros de massas.
Baseado nas informações contidas no diagrama é correto afirmar que arazão F1/F2 é dada por
![]()
02- (CEFET-MG-015)

A figura seguinte mostra dois corpos 1 e 2 idênticos, em repouso, completamente imersos em recipientes com o mesmo líquido, próximos àsuperfície da Terra e da Lua, respectivamente.

Se T1 e T2 são as tensões nos fios, P1 e P2 os pesos dos corpos e F1 e F2as forças de empuxo que agem sobre esses corpos, então é correto afirmar que
![]()
ACELERAÇÂO GRAVITACIONAL
01- (UEMG-MG-015)

No poema O que se afasta, o eu-poético de Sísifodesce a montanhaafirma, por comparação, que as coisas perdem seu peso e gravidade, percepção que está relacionada ao envelhecimento do homem:
“De repente você começa a se despedir
das pessoas, paisagens e objetos
como se um trem
— fosse se afastando (…)”.
Aproveitando o ensejo literário, imagine um objeto próximo à superfície da Terra e uma situação

hipotética, porém sem abrir mão de seus importantes conhecimentos de Física. Supondo a possibilidade de haver alteração no raio e/ou na massa da Terra, assinale a opção que traz uma hipótese que justificaria a diminuição do peso desse objeto, que se mantém próximo à superfície do Planeta:
A) diminuição do raio da Terra e manutenção de sua massa.
B) aumento da massa da Terra e manutenção de seu raio.
C) aumento do raio da Terra e diminuição de sua massa, na mesma proporção.
D) diminuição do raio da Terra e aumento de sua massa, na mesma proporção.
02- (ESCS-DF-015) RL RLU2/R= 4,2 J Sendo a densidade da água 1g/cm3= 103kg/m3 =
 QUESTÃO
10
QUESTÃO
10
O volume e a massa do planeta Marte são menores que os da Terra. Lá, a pressão atmosférica é muito pequena, da ordem de 0,007 atm, e a temperatura pode variar de – 12 oC a 62 oC.
A tabela a seguir apresenta alguns parâmetros de Marte e da Terra, considerando-se que as orbitas desses planetas sejam circulares.

Tendo como referencia as informações acima, assinale a opção correta.
A. A gravidade em Marte e duas vezes maior que na Terra.
B. Caso exista água em Marte, ela ferverá a uma temperatura menor que na Terra.
C. Se, na Terra, um corpo tem massa de 70 kg, então, em Marte, ele terá massa menor.
D. O ano em Marte é menor que o ano na Terra.
03- (Medicina – USCS-SP-016)

Em julho deste ano, a nave americana New Horizons passou bem perto dasuperfície de Plutão, colhendo dados importantes sobre esse planeta-anão.
Agora se sabe que Plutão possui 5 satélites naturais orbitando ao seu redor. Caronte, o maior deles,

possui massa aproximadamente igual à décima parte da de Plutão, tendo o diâmetro superficial igual à metade do diâmetro superficial de Plutão.Com base nesses dados, a relação correta entre as intensidades dos campos gravitacionais na superfície de Caronte e na de Plutão (gC /gP ) é
(A) 5/4 (B) 1/5 (C) 2/5 (D) 5/6 (E) 3/5
04- (MACKENZIE-SP-2017)


Quando o astronauta Neil Armstrong desceu do módulo lunar e pisou na Lua, em 20 de julho de 1969, a sua massa total, incluindo seu corpo, trajes especiais e equipamento de sobrevivência eram de aproximadamente300 kg.
O campo gravitacional lunar é, aproximadamente, 1/6 do campo gravitacional terrestre.
Se a aceleração da gravidade na Terra é aproximadamente 10,0 m/s2, podemos afirmar que
a) a massa total de Armstrong na Lua é de 300 kg e seu peso é 500 N.
b) a massa total de Armstrong na Terra é de 50,0 kg e seu peso é 3000 N.
c) a massa total de Armstrong na Terra é de 300 kg e seu peso é 500 N.
d) a massa total de Armstrong na Lua é de 50,0 kg e seu peso é 3000 N.
e) o peso de Armstrong na Lua e na Terra são iguais.
05- (FAMERP-SP-017)

A figura representa um satélite artificial girando ao redor da Terra em movimento circular e uniforme com período de rotação de 140 minutos.

O gráfico representa como varia o módulo da aceleração da gravidade terrestre para pontos situados até uma distância 2R do centro da Terra, onde R = 6 400 km é o raio da Terra.
Considere a Terra perfeitamente esférica e as informações contidas na figura e no gráfico.
a) Calcule o menor intervalo de tempo, em minutos, para que o satélite se movimente da posição A para a posição B.
b) Determine o módulo da aceleração da gravidade terrestre, em m/s2, na posição em que se encontra o satélite.
VELOCIDADES EM ÓRBITAS CIRCULARES
01- (PUC-RJ-016)

Dois pequenos satélites de mesma massa descrevem órbitas circulares em torno de um planeta, tal que o raio da órbita de um é quatro vezes menor que o do outro. O satélite mais distante tem um período de 28 dias. Qual é o período, em dias, do satélite mais próximo?
(A) 3,5
(B) 7,0
(C) 14
(D) 56
(E) 112
02-(UFSC-SC-016)

Quer
subir de elevador até
o espaço? Apesar de esta ideia já ter surgido há mais
de 100 anos,
um avanço em nanotecnologia pode significar que iremos de elevador
até o espaço com um cabo feito de diamante ou de carbono. A empresa
japonesa de construção Obayashi investiga a viabilidade de um
elevador espacial, visando a uma estação espacial ligada ao equador
por um cabo de 96000 quilômetros feito de nanotecnologia de carbono,
conforme a figura abaixo. A estação espacial orbitaria a Terra
numa posição
geoestacionária e
carros robóticos com motores magnéticos levariam sete dias para
alcançar a estação espacial, transportando carga e pessoas até o
espaço por uma fração dos custos atuais.
Considerando que, fisicamente, seja possível a implementação desse elevador espacial, é CORRETO afirmar que:
01. a estação espacial japonesa deve possuir movimento circular ao redor da Terra com velocidade linear igual à velocidade linear de rotação da superfície da Terra.
02. as pessoas que visitarem a estação espacial poderão flutuar no seu interior porque lá não haverá atração gravitacional.
04. a velocidade angular da estação espacial deve ser igual à velocidade angular de rotação da Terra.
08. um carro robótico terá, no trajeto da Terra até a estação espacial, vetor velocidade constante.
16. o período do movimento da estação espacial ao redor da Terra deve ser igual ao período de rotação diária da Terra.
32. a força de atração gravitacional da Terra será a força centrífuga, responsável por manter a estação espacial em órbita.
64. o valor da aceleração da gravidade (g) na posição da estação espacial terá um módulo menor que seu valor na superfície da Terra.
03-(FUVEST-SP-015)

A notícia “Satélite brasileiro cai na Terra após lançamento falhar”, veiculada pelo jornal O Estado de S. Paulo de 10/12/2013, relata que o satélite CBERS-3, desenvolvido em parceria entre Brasil e

China, foi lançado no espaço a uma altitude de 720 km (menor do que a planejada) e com uma velocidade abaixo da necessária para colocá-lo em órbita em torno da Terra. Para que o satélite pudesse ser colocado em órbita circular na altitude de 720 km, o módulo de sua velocidade (com direção tangente à órbita) deveria ser de, aproximadamente,
![]()
Resoluções
Gravitação Universal – 2017, 2016 e 2015
LEIS DE KEPLER
01-

Marte não é o maior planeta do sistema solar, nem o de maior massa. Ambos os títulos são de Júpiter que possui 2,5 vezes a massa de todos outros somados.
O fato de o campo gravitacional ser intenso não influencia nesse tipo de coordenada, e mesmo que influenciasse Marte tem um campo gravitacional da ordem de 3,711 m/s². Enquanto que o da Terra é de 9,807 m/s².
A composição atmosférica também não influencia nas coordenadas, porém a composição atmosférica de Marte realmente é bem diferente da Terra, sendo mais rarefeita e com uma porcentagem muito grande de CO2.
A hidrosfera tampouco influencia nas coordenadas.
Sendo assim a alternativa correta é a B, como podemos observar na imagem o formato da Terra e de Marte é parecido, sendo assim o sistema de coordenadas efetivo para ambos.
02- Vamos começar pelo tempo total da viagem:
Tempo total = 365*6 (dias para saírem da Terra) + 210 (dias equivalentes ao percurso)
Tempo total = 2400 dias terrestres
Para calcularmos em anos marcianos, precisamos fazer uma proporção:
1 ano marciano -> 687 dias terrestres
x anos marcianos -> 2400 dias terrestres
Multiplicando em cruz:
2400.1 = 687.x
Isolando o x:
x
= ![]()
x = 3,4934
O resultado mais próximo é o da letra E.
03-
Se você não domina a teoria ela está a seguir:
Segunda lei de Kepler (lei das áreas)
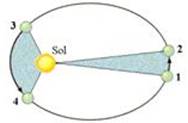
“ O segmento de reta imaginário que une o centro do Sol ao centro do planeta varre áreas iguais em períodos de tempo iguais”
A figura abaixo representa um planeta em órbita elíptica ao redor do Sol.

V12 > V34
Essa constante K depende do planeta e recebe o nome de velocidade areolar (velocidade escalar orbital)..
Observação
importante: Observe
que, quando A1 =
A2 ![]() ∆t1 = ∆t2, ou
seja, para o arco
maior (1,2), ser
percorrido no mesmo
intervalo de tempo que o arco menor (3,4), a velocidade
em (1,2) (mais
perto do Sol, periélio) deve
ser maior que a velocidade em (3,4) (mais
afastado do Sol, afélio).
∆t1 = ∆t2, ou
seja, para o arco
maior (1,2), ser
percorrido no mesmo
intervalo de tempo que o arco menor (3,4), a velocidade
em (1,2) (mais
perto do Sol, periélio) deve
ser maior que a velocidade em (3,4) (mais
afastado do Sol, afélio).
Então, V12 > V34.

Portanto os planetas aceleram do afélio para o periélio e retardam do periélio para o afélio.
Ainda, de acordo com essa lei, se as órbitas forem circulares a velocidade de translação será constante e se a órbita do planeta tiver raio R e seu período de translação for T, sua velocidade areolar (velocidade escalar orbital) será constante e dada por: K = V = A/∆t = πR2 /T.
R- E
04- De acordo com a primeira lei de Kepler as órbitas são elípticas ao redor do sol, sendo que o sol está localizado em um dos focos. Alternativa B.
No caso de A, a velocidade do planeta aumenta quando o corpo se aproxima do sol.
No caso de C e D, o período de translação só depende da distância entre o planeta e o sol.
05- A trajetória da Lua ao redor da Terra não é circular, é elíptica.
Quando o dia em que ocorre uma Lua Cheia coincide com o dia em que ela passa pelo perigeu (mais próxima da Terra) ela pode se apresentar até cerca de 30% mais brilhante que uma Lua Cheia no

apogeu (mais afastada da Terra).
Nesse caso, ela aparenta ter um aumento de 14% em relação ao seu tamanho real.
Essa Lua
Cheia mais próxima da Terra é
chamada de Super
Lua.
R-
E
06- O tempo total T para a Lua efetuar uma volta completa ao redor da Terra(“varrer” um ângulo de 360o) vale T = t1 + t2 = 14,9 + 14,8 = 29,7 dias. (I)
O tempo t2 = 14,8 dias que é aquele decorrido de uma lua quarto minguante a uma lua quarto
crescentee que é o mesmo que a Lua demora para “varrer” um ângulo 2α.(II)
Como, pelo enunciado você deve supor que o movimento é uniforme você pode utilizar uma regra de três com (I) e (II):


07- Terceira lei de Kepler (lei dos períodos)
“ Os quadrados dos períodos T de revolução dos planetas (tempo que demora para efetuar uma volta completa em torno do Sol) são proporcionais aos cubos das suas distâncias médias R ao Sol”
T2/R3=constante=K’
O mesmo é válido para Terra-Lua. Se a distância média R da Lua à Terra aumenta, e ela é proporcional ao período de translação da Lua ao redor da Terra, este período também deve aumentar.
R- D
08- a) confirmaram as teorias definidas por Copérnico e são exemplos domodelo científico que passou a vigorar a partir da Alta Idade Média.
a)
Falsa ![]() foi
por volta do século XVI (e
não na Alta idade média (do século V ao século X) que, Nicolau
Copérnico (1473-1543)
apresentou ummodeloheliocêntrico,
em que o Sol
estava no centro do
universo,
e osplanetas
descreviam órbitas circulares ao seu redor.
foi
por volta do século XVI (e
não na Alta idade média (do século V ao século X) que, Nicolau
Copérnico (1473-1543)
apresentou ummodeloheliocêntrico,
em que o Sol
estava no centro do
universo,
e osplanetas
descreviam órbitas circulares ao seu redor.
b) confirmaram as teorias defendidas por Ptolomeu e permitiram a produção das cartas náuticas usadas no período do descobrimento da América.
b)
Falsa ![]() Ptolomeu apresentou
e desenvolveu argumentos a favor dateoria
geocêntrica na qual o universo os planetas, o Sol e a Lua giravam em
torno da Terra.
Ptolomeu apresentou
e desenvolveu argumentos a favor dateoria
geocêntrica na qual o universo os planetas, o Sol e a Lua giravam em
torno da Terra.

c) são a base do modelo planetário geocêntrico e se tornaram as premissas cientificas que vigoram até hoje.
c)
Falsa ![]() as leis
de Kepler não são a base do modelo
geocêntrico proposto por Pttolomeu (veja b acima).
as leis
de Kepler não são a base do modelo
geocêntrico proposto por Pttolomeu (veja b acima).
d) forneceram subsídios para demonstrar o modelo planetário heliocêntrico e criticar as posições
defendidas pela Igreja naquela época.
d)
Correta ![]() as leis
de Kepler confirmaram o sistema heliocêntrico
defendido
por Nicolau Copérnico e contrariaram
a teoria do geocentrismo
defendida pela igreja.
as leis
de Kepler confirmaram o sistema heliocêntrico
defendido
por Nicolau Copérnico e contrariaram
a teoria do geocentrismo
defendida pela igreja.
R- D
09-

10-
Cálculo da aceleração da gravidade na superfície do planeta.
A Terra (ou qualquer outro planeta) origina ao seu redor um campo gravitacional de maneira que qualquer corpo de massa m, quando colocado no interior desse campo fica sujeito àuma força de atração gravitacional Fg=GMm/r2, sendo, G a constante de gravitação universal, Ma massa da Terra ou do planeta e r a distância do centro da Terra ou docentro do planeta até o corpo de massa m.

Mas, esta força que age sobre o corpo ou satélite corresponde ao seupróprio peso, tal que, P=mg.
Portanto — Fg=P — GMm/r2=mg — g=GM/r2



11-
Heliocentrismo é
a teoria a respeito do sistema cosmológico, segundo a qual a Terra
e os demais planetas giram em torno do Sol.
Nicolau
Copérnico, um polonês que viveu entre 1453 – 1543,
é considerado o fundador da astronomia moderna e pai do
heliocentrismo.
R- A
12- A seguir, a teoria:
Primeira lei de Kepler (lei das órbitas)
“As órbitas que os planetas descrevem ao redor do Sol são elípticas, com o Sol ocupando um dos focos da elipse”.



Numa elipse (figura acima), para qualquer posição do ponto P a soma das distâncias FP com PF’ é sempre a mesma.
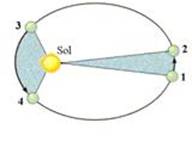
Segunda lei de Kepler (lei das áreas)
“ O segmento de reta imaginário que une o centro do Sol ao centro do planeta descreve áreas iguais em intervalos de tempo iguais”

Sejam:
A1 — área entre 1,2 e o Sol
A2 — área entre 3, 4 e o Sol
∆t1 — tempo que o planeta demora para ir de 1 a 2
∆t2 — tempo que o planeta demora para ir de 3 a 4
Então:
A1/∆t1~A2/∆t2 = constante = K
Terceira lei de Kepler (lei dos períodos)
“ Os quadrados dos períodos T de revolução dos planetas (tempo que demora para efetuar uma volta completa em torno do Sol) são proporcionais aos cubos das suas distâncias médias R ao Sol”
T2/R3 = constante = K’

O raio médio R da órbita de um planeta corresponde à média aritmética entre a distância do Sol ao afélio e a distância do Sol ao periélio. Observe que esse valor é o mesmo que a medida do semi-eixo maior da elipse, que na figura acima seria a.
R- C
LEI DA ATRAÇÃO UNIVERSAL
01-

02-

Observando as figuras abaixo você verificará que, tanto na Terra quanto na Lua, os corpos estão em repouso (equilíbrio estático) e a força resultante sobre eles deve ser nula.

ACELERAÇÃO GRAVITACIONAL
01- Sendo o peso P = mg e a massa do objeto a mesma, o peso diminuiria se a aceleração da gravidade g diminuísse, sendo g fornecida por g = GM/r2 onde:
g —valor da aceleração da gravidade à uma distância r do centro do planeta (m/s2 ou N/kg)
G — constante de gravitação universal (6,67.10-11 Nm2/kg2)
M — massa do planeta (kg)
r —distância do centro do planeta ao centro do corpo (m)
Observe na expressão g = GM/r2 que, para que g e consequentemente o peso diminua, você deve aumentar o raio r da Terra (inversamente proporcional a r2) e diminuir a massa M da Terra (diretamente proporcional a M).
R – C
02-
A.
Falsa ![]() gT =GMT/RT2 =
G.6.1024/(150.106)2 =
6.1024
G/22500.1012 =
6.1024
G/2,25.1016
gT =GMT/RT2 =
G.6.1024/(150.106)2 =
6.1024
G/22500.1012 =
6.1024
G/2,25.1016
![]() gT =
2,7 .108
G.gM = GMM/RM2 = G.6,5.1023/(230.106)2=
G.6,5.1023/52900.1012 =
G.6,5.1023/5,29.1016
gT =
2,7 .108
G.gM = GMM/RM2 = G.6,5.1023/(230.106)2=
G.6,5.1023/52900.1012 =
G.6,5.1023/5,29.1016 ![]() gM =
1,23.107
G.
gM =
1,23.107
G.
Observe que gM < gT.
B.
Correta ![]() quanto menor
a pressão atmosférica no planeta, menor será a temperatura de
ebulição da
água nele. Como
a pressão atmosférica em Marte (PM =
0,00 atm) é menor que a da Terra (1 atm), em
Marte a água ferverá a uma temperatura menor que na Terra..
quanto menor
a pressão atmosférica no planeta, menor será a temperatura de
ebulição da
água nele. Como
a pressão atmosférica em Marte (PM =
0,00 atm) é menor que a da Terra (1 atm), em
Marte a água ferverá a uma temperatura menor que na Terra..
C.
Falsa ![]() a massa de
um corpo é uma grandeza
invariável independente
do lugar ou do planeta onde
ele esteja.
a massa de
um corpo é uma grandeza
invariável independente
do lugar ou do planeta onde
ele esteja.
D.
Falsa ![]() Na expressão da
terceira lei de Kepler, T2/R3 =
K = constante,
observamos que à
medida que R aumenta,
T também aumenta, o
que significa que quanto mais
afastado o planeta estiver do Sol maior
será seu ano (tempo
que demora para dar um volta completa ao redor do Sol). Como Marte
está mais
afastado do
Sol (RM = 230.106 km)
que a Terra (RT= 150.106 km), seu
ano será maior que o da Terra.
Na expressão da
terceira lei de Kepler, T2/R3 =
K = constante,
observamos que à
medida que R aumenta,
T também aumenta, o
que significa que quanto mais
afastado o planeta estiver do Sol maior
será seu ano (tempo
que demora para dar um volta completa ao redor do Sol). Como Marte
está mais
afastado do
Sol (RM = 230.106 km)
que a Terra (RT= 150.106 km), seu
ano será maior que o da Terra.
R- B
03- A Terra (ou qualquer outro planeta) origina ao seu redor um campo gravitacional de maneira que qualquer corpo de massa m, quando colocado no interior desse campo fica sujeito à uma força de atração gravitacional, dirigida para o centro da Terra e de intensidade
FG=GMm/r2, sendo G a constante de gravitação universal, M a massa da Terra ou do planeta e r a distância do centro da Terra ou do planeta ao centro do corpo. Essas forças que o corpo de massa m troca com o centro do planeta de massa M constituem par ação e reação.






04-
Se você não domina a teoria, leia o breve resumo a seguir:
A massa (m) de um corpo é a medida de sua inércia (resistência de um corpo em ter seu movimento acelerado ou retardado), sendo um valor numérico atribuído acada corpo comparando-o com outro tomado como padrão.
É uma grandeza escalar, positiva e invariável para cada corpo não dependendo do lugar onde ele se encontra.
Assim, a massa de um corpo é sempre a mesma em qualquer ponto da Terra, do espaço ou de

qualquer planeta.



No caso do exercício, a massa do astronauta, incluindo seu corpo, trajes especiais e equipamento de sobrevivência eram de aproximadamente 300 kg (na Terra, na Lua ou em qualquer outro planeta).
Peso
total do astronauta na Lua onde gLua = gTerra/6 = 10/6 m/s2 ![]() P
= m.g = 300.
P
= m.g = 300.![]()
![]() P
= 500 N.
P
= 500 N.
R- A
05- O menor intervalo de tempo, em minutos, para que o satélite se movimente da posição A para a posição B, ocorre quando o satélite se move no sentido anti-horário varrendo o ângulo de 108o.
Pelo enunciado, o período do satélite (tempo que ele demora para efetuar uma volta completa em torno da Terra e percorrer um arco de 360o) é de 140 min, então para percorrer 108o basta utilizar uma regra de três:

b) O raio
da órbita do satélite (Ro) é medido
em relação ao centro da Terra, ou
seja Ro =
RT + 2560 ![]() Ro =
6400 + 2650
Ro =
6400 + 2650 ![]() Ro =
8960 km.
Ro =
8960 km.
Assim,
o satélite
dista do centro da Terra em função
ao raio da Terra R
de![]() Ro =
Ro = ![]() =
1,4R.
=
1,4R.
Veja no gráfico a correspondência entre essa distância (Ro =1,4R) e g:

R– g = 5m/s2
VELOCIDADES EM ÓRBITAS CIRCULARES
01- Vamos analisar esse exercício estudando a fórmula de velocidade orbital:
![]()
Aonde: V é a velocidade orbital.
G
é a constante de gravitação universal ![]() 6,67.
6,67.![]() N.m²/kg²
N.m²/kg²
M é a massa do objeto que está ao centro da órbita.
r é o raio dessa órbita.
Agora
precisamos decompor essa velocidade: ![]()
![]()
Como
é um movimento circular o ![]() vai
ser o comprimento do círculo (2πr) e o
vai
ser o comprimento do círculo (2πr) e o ![]() vai
ser o período (T).
vai
ser o período (T).
Substituindo:
![]()
Substituindo na primeira fórmula, já elevando todos os componentes ao quadrado:
![]()
Como precisamos analisar o raio em relação ao período, vamos isolar o T, primeiro elevando ambos os lados por -1.
![]()
Multiplicando
ambos lados por ![]() :
:
![]()
Ao fazer a raiz quadrada da equação, podemos notar que a relação entre T e r é:
![]()
Se
o raio é 4 vezes menor, o período é ![]() =
8 vezes menor,
diretamente proporcional, ou seja, o
período menor é de 28/8 = 3,5. A
alternativa correta é a A.
=
8 vezes menor,
diretamente proporcional, ou seja, o
período menor é de 28/8 = 3,5. A
alternativa correta é a A.
02-
Falso ![]() A
estação espacial deve ter velocidade
angular igual à velocidade angular da Terra,
pois no caso da velocidade
linear (
A
estação espacial deve ter velocidade
angular igual à velocidade angular da Terra,
pois no caso da velocidade
linear (![]() ),
elavaria com
a distância,
como a estação espacial está em uma altura
maiorque
a da Terra, sua velocidade seria
maior, com isso a estação perderiasua
posição geoestacionária, por terem velocidades
diferentes.
Diferente da velocidade angular
(
),
elavaria com
a distância,
como a estação espacial está em uma altura
maiorque
a da Terra, sua velocidade seria
maior, com isso a estação perderiasua
posição geoestacionária, por terem velocidades
diferentes.
Diferente da velocidade angular
(![]() ),
que por não depender
da distância,
manteria essa posição
geoestacionária,
por manter sempre
a posição
relativa com
a Terra.
),
que por não depender
da distância,
manteria essa posição
geoestacionária,
por manter sempre
a posição
relativa com
a Terra.
02 ![]() Falso
Falso ![]() Ainda haveria
atração gravitacional,
que perderia
forçasconforme
a estação ganhasse altitude.
Porém, devido à aceleração
de subida da
estação, uma força
contrária pressionaria
essas pessoas contra o chão, similar ao
que acontece nos elevadores comuns.
Ainda haveria
atração gravitacional,
que perderia
forçasconforme
a estação ganhasse altitude.
Porém, devido à aceleração
de subida da
estação, uma força
contrária pressionaria
essas pessoas contra o chão, similar ao
que acontece nos elevadores comuns.
04 ![]() Verdadeiro
Verdadeiro ![]() Como
já estudado no caso (01).
Como
já estudado no caso (01).
08 ![]() Falsa
Falsa ![]() varia
intensidade, direção e sentido.
varia
intensidade, direção e sentido.
16 ![]() Verdadeiro
Verdadeiro ![]() Pois
no caso da velocidade angular
(
Pois
no caso da velocidade angular
(![]() ),
para manter
a
velocidade da Terra e da estação igual, o período deve
ser o mesmo,
já que o ângulo
percorrido entre
os dois é sempre igual e
de valor 360°.
),
para manter
a
velocidade da Terra e da estação igual, o período deve
ser o mesmo,
já que o ângulo
percorrido entre
os dois é sempre igual e
de valor 360°.
32 ![]() Falso
Falso ![]() A
força de atração
gravitacional da Terra não
será a centrífuga, que exerce uma força para
fora do
movimento circular, e sim acentrípeta,
que exerce uma força para
dentro do
movimento circular, ou seja, em direção a Terra, sendo similar à
força gravitacional.
A
força de atração
gravitacional da Terra não
será a centrífuga, que exerce uma força para
fora do
movimento circular, e sim acentrípeta,
que exerce uma força para
dentro do
movimento circular, ou seja, em direção a Terra, sendo similar à
força gravitacional.
64 ![]() Verdadeiro
Verdadeiro ![]() A
força gravitacional (
A
força gravitacional (![]() ) varia
conforme adistância entre
as duas massas, com isso, ao aumentar
a altitude,
a distância aumenta e
a força gravitacional diminui, por
serem inversamente proporcionais.
) varia
conforme adistância entre
as duas massas, com isso, ao aumentar
a altitude,
a distância aumenta e
a força gravitacional diminui, por
serem inversamente proporcionais.
03- Na órbita circular da figura abaixo, M é a massa da Terra, m a massa do satélite, V a velocidade de



GRAVITAÇÃO
2014 e 2013
Gravitação
01-(FUVEST-SP-014)

Há um ponto no segmento de reta unindo o Sol à Terra, denominado “Ponto de Lagrange L1”. Um
satélite artificial colocado nesse ponto, em órbita ao redor do Sol, permanecerá sempre na mesma posição relativa entre o Sol e a Terra. Nessa situação, ilustrada na figura abaixo, a velocidade angular orbital WA do

orbital WA do satélite em torno do Sol será igual à da Terra, WT.
Para essa condição, determine
a) WT em função da constante gravitacional G, da massa MS do Sol e da distância R entre a Terra e o Sol;
b) o valor de WA em rad/s;
c)a expressão do módulo Fr da força gravitacional resultante que age sobre o satélite, em função de G, MS, MT, m, R e d, sendo MT e m, respectivamente, as massas da Terra e do satélite e d a distância entre a Terra e o satélite.

02-(FUVEST-SP-014)

Uma estação espacial foi projetada com formato cilíndrico, de raio R igual a100m, como ilustra a figura.

Para simular o efeito gravitacional e permitir que as pessoas caminhem na parte interna da casca cilíndrica, a estação gira em torno de seu eixo, com velocidade angular constante Z. As pessoas terão sensação de peso, como se estivessem na Terra, se a velocidade Z for de, aproximadamente, Dado: aceleração gravitacional na superfície da Terra – g=10m/s2)
a) 0,1rad/s b) 0,3rad/s c) 1rad/s d) 3rad/s e) 10rad/s
03-(UNESP-SP-014)

Saturno é o sexto planeta a partir do Sol e o segundo maior, em tamanho, do sistema solar. Hoje, são conhecidos mais de sessenta satélites naturais de Saturno, sendo que o maior deles, Titã, está a uma distância média de 1 200 000 km de Saturno e tem um período de translação de, aproximadamente, 16 dias terrestres ao redor do planeta.

Tétis é outro dos maiores satélites de Saturno e está a uma distância média de Saturno de 300 000 km.
Considere:

O período aproximado de translação de Tétis ao redor de Saturno, em dias terrestres, é
(A) 4. (B) 2. (C) 6. (D) 8. (E) 10.
04-(UNICAMP-SP-014)

“As denúncias de violação de telefonemas e transmissão de dados de empresas e cidadãos brasileiros serviram para reforçar a tese das Forças Armadas da necessidade de o Brasil dispor de

seu próprio satélite geoestacionário de comunicação militar” (O Estado de São Paulo, 15/07/2013). Uma órbita geoestacionária é caracterizada por estar no plano equatorial terrestre, sendo que o satélite que a executa está sempre acima do mesmo ponto no equador da superfície terrestre. Considere que a órbita geoestacionária tem um raio r=42000km.
a) Calcule a aceleração centrípeta de um satélite em órbita circular geoestacionária.
b) A energia mecânica de um satélite de massa m em órbita circular em torno da terra é dada por
E= - GMm/2r, em que r é o raio da órbita, M=6.1024 kg é a massa da Terra e G=6,7.10-11 Nm2/kg2.
O raio de órbita de satélites comuns de observação (não geoestacionários) é tipicamente de 7000 km.
Calcule a energia adicional necessária para colocar um satélite de 200 kg de massa em uma órbita
geoestacionária, em comparação a colocá-lo em uma órbita comum de observação.
05-(PUC-MG-014)

Proprietários de antenas parabólicas de televisão estão acostumados a direcionar suas antenas para determinado ponto no céu a fim de que possam receber o sinal das emissoras. Ao se ajustar a orientação de uma antena, apenas se está apontando-a na direção de um satélite retransmissor.
É CORRETO afirmar:
a) Os satélites estão em repouso em relação à Terra.
b) Os satélites transmissores giram com velocidade angular maior que a da Terra.
c) O raio da órbita destes satélites é menor que o raio da Terra.
d) A velocidade linear dos satélites é menor que a da superfície da Terra.
06-(PUC-RJ-014)

Um satélite de transmissão de dados é posicionado estrategicamente sobre a cidade do Rio de

Janeiro a uma altitude de 20.000 km. Sabendo que este satélite é geoestacionário, i.e., fica parado
em relação a uma localização geográfica no Rio de Janeiro, calcule o período da órbita deste satélite, em horas, em torno do eixo da terra.
(A) 0 (B) 6 (C) 12 (D) 24 (E) 365
07-(UDESC-SC-014)

Um satélite está em uma órbita circular em torno de um planeta de massa M e raio R a uma altitude H. Assinale a alternativa que representa a velocidade escalar adicional que o satélite precisa adquirir para escapar completamente do planeta.

08-(UEFS-BA-014)

O raio médio da órbita do planeta Marte é cerca de quatro vezes o raio médio da órbita do
planeta Mercúrio, no seu movimento de translação em torno do Sol.
Considerando-se o período de translação de Mercúrio quatro vezes menor do que um ano
na Terra, o período de translação de Marte em torno do Sol, estimado em anos terrestres,
é de, aproximadamente,
A) 2,5 B) 2,0 C) 1,5 D) 0,6 E) 0,3
Leis de Kepler
28-(UFPE-PE-013)

Um planeta realiza uma órbita elíptica com uma estrela em um dos focos. Em dois meses, o segmento de reta que liga a

estrela ao planeta varre uma área A no plano da órbita do planeta. Em 32 meses tal segmento varre uma área igual a αA. Qual o valor de α?
29-(UDESC-SC-013)

Analise as proposições sobre o planeta Mercúrio, com base nas três leis de Kepler.

I. A órbita de Mercúrio é circular, com o Sol localizado no centro da circunferência.
II. A magnitude da velocidade de translação de Mercúrio varia ao longo de sua trajetória.
III. A magnitude da velocidade de translação de Mercúrio é constante em toda a sua trajetória.
IV. O período de translação de Mercúrio independe do raio de sua órbita circular.
Assinale a alternativa correta.
A. ( ) Somente a afirmativa III é verdadeira.
B. ( ) Somente as afirmativas I e III são verdadeiras.
C. ( ) Somente a afirmativa II é verdadeira.
D. ( ) Somente as afirmativa II e IV são verdadeiras.
E. ( ) Somente as afirmativas I e IV são verdadeiras.
30-(UFV-MG-013)

A figura abaixo ilustra a órbita elíptica de um planeta em torno do Sol, sendo X e Y as áreas descritas por uma linha imaginária que liga o planeta ao Sol.

Sabendo-se que, de acordo com a 2ª Lei de Kepler (Lei das Áreas), a linha que une o Sol ao planeta descreve áreas iguais em tempos iguais, é CORRETO afirmar que a velocidade escalar média do planeta entre os pontos 3 e 4 da figura é:
a) menor que sua velocidade escalar média entre os pontos 1 e 2, quaisquer que sejam as áreas X e Y.
b) menor que sua velocidade escalar média entre os pontos 1 e 2, se forem iguais as áreas X e Y.
c) igual a sua velocidade escalar média entre os pontos 1 e 2, quaisquer que sejam as áreas X e Y.
d) igual a sua velocidade escalar média entre os pontos 1 e 2, se forem iguais as áreas X e Y.
Lei da Gravitação Universal
16-(ENEM-MEC-012)

A característica que permite identificar um planeta no céu é o seu movimento relativo às estrelas fixas. Se observarmos a posição de um planeta por vários dias, verificaremos que sua posição em relação às estrelas fixas se modifica regularmente. A figura destaca o movimento de Marte observado em intervalos de 10 dias, registrado da Terra.

Qual a causa da forma da trajetória do planeta Marte registrada na figura?
a) A maior velocidade orbital da Terra faz com que, em certas épocas, ela ultrapasse Marte.
b) A presença de outras estrelas faz com que sua trajetória seja desviada por meio da atração gravitacional.
c) A órbita de Marte, em torno do Sol, possui uma forma elíptica mais acentuada que a dos demais planetas.
d) A atração gravitacional entre a Terra e Marte faz com que este planeta apresente uma órbita irregular em torno do Sol.
e) A proximidade de Marte com Júpiter, em algumas épocas do ano, faz com que a atração gravitacional de Júpiter interfira em seu movimento.
SATÉLITES EM ÓRBITAS CIRCULARES
18-(ESCOLA NAVAL-012-013)

Dois pequenos satélites A e B, idênticos, descrevem órbitas circulares ao redor da Terra. A

velocidade orbital do satélite A vale VA=2.103m/s. Sabendo que os raios orbitais dos satélites são relacionados por RB/RA=1.102, a velocidade orbital do satélite B, em m/s, vale
a) 2.103 b) 1.103 c) 4.102 d) 2.102 e) 1.102
19-(PUC-RJ-013)

A Lua leva 28 dias para dar uma volta completa ao redor da Terra. Aproximando a órbita como

circular, sua distância ao centro da Terra é de cerca de 380 mil quilômetros. A velocidade aproximada da Lua, em km/s, é:
(A) 13 (B) 0,16 (C) 59 (D) 24 (E) 1,0
20-(UFPR-PR-013)

Dois satélites, denominados de SA e SB, estão orbitando um planeta P. Os dois satélites são esféricos e possuem tamanhos e massas iguais. O satélite SB possui uma órbita perfeitamente circular e o satélite SA uma órbita elíptica, satélite SA uma órbita elíptica conforme mostra a figura. Em relação ao movimento desses dois satélites, ao longo de suas respectivas órbitas, considere as seguintes afirmativas:
1. Os módulos da força gravitacional entre o satélite SA e o planeta P e entre o satélite SB e o planeta P são constantes.
2. A energia potencial gravitacional entre o satélite SA e o satélite SB é variável.
3. A energia cinética e a velocidade angular são constantes para ambos os satélites.
Assinale a alternativa correta.
a) Somente a afirmativa 1 é verdadeira.
b) Somente a afirmativa 2 é verdadeira.
c) Somente a afirmativa 3 é verdadeira.
d) Somente as afirmativas 1 e 2 são verdadeiras.
e) Somente as afirmativas 2 e 3 são verdadeiras.
21-(UEL-PR-013)

A posição média de um satélite geoestacionário em relação à superfície terrestre se mantém devido à

a) sua velocidade angular ser igual à velocidade angular da superfície terrestre.
b) sua velocidade tangencial ser igual à velocidade tangencial da superfície terrestre.
c) sua aceleração centrípeta ser proporcional ao cubo da velocidade tangencial do satélite.
d) força gravitacional terrestre ser igual à velocidade angular do satélite.
e) força gravitacional terrestre ser nula no espaço, local em que a atmosfera é rarefeita.
Aceleração da gravidade
18-(PUC-PR-013)

O planeta Y possui a mesma densidade “d” que a Terra, porém seu raio é três vezes maior.

Considere os planetas esféricos e desconsidere o efeito de rotação dos planetas. Sabendo que a aceleração da gravidade na Terra vale g, a gravidade do planeta Y (gy) valerá:
Dado: V=(4/3) π.R³
A) g/27 B) g/9 C) 9g D) g E) 3g
19-(UFRGS-RS-013)

Em 6 de agosto de 2012, o jipe “Curiosity “ pousou em Marte. Em um dos mais espetaculares empreendimentos da era espacial, o veículo foi colocado na superfície do planeta vermelho com muita precisão. Diferentemente das missões anteriores, nesta, depois da usual descida balística na atmosfera do planeta e da diminuição da velocidade provocada por um enorme para quedas, o veículo de quase 900 kg de massa, a partir de 20 m de altura, foi suave e lentamente baixado até o solo, suspenso por três cabos, por um tipo de guindaste voador estabilizado no ar por meio de 4 pares de foguetes direcionais. A ilustração abaixo representa o evento.

O cabo ondulado que aparece na figura serve apenas para comunicação e transmissão de energia entre os módulos.
Considerando as seguintes razões: massa da Terra/massa de Marte ~ 10 e raio médio da Terra/raio médio de Marte ~ 2, a comparação com descida similar, realizada na superfície terrestre, resulta que a razão correta entre a tensão em cada cabo de suspensão do jipe em Marte e na Terra TM/TT é, aproximadamente, de
(A) 0,1. (B) 0,2. (C) 0,4. (D) 2,5. (E) 5,0.
RESOLUÇÕES
2013 - 2014
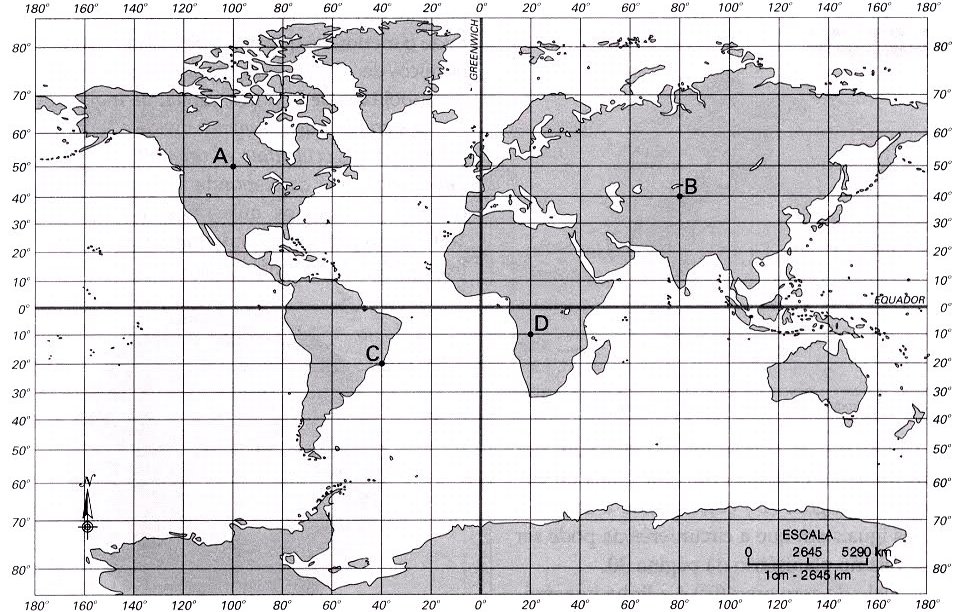
01- a) O “Note e adote” afirma que você pode considerar as órbitas como sendo circulares e, assim, a Terra executa um movimento circular uniforme (MCU) em torno do Sol com velocidade angular WT constante --- então, a força gravitacional FG que o Sol de massa MS aplica sobre a Terra de massa MT será a força resultante centrípeta Fc que é responsável por manter a Terra em órbita circular ao redor do Sol --- FG = Fc
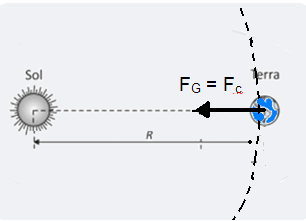

b)
A velocidade
angular orbital WA do
satélite pedida é a mesma que a da Terra
WT já
que ambos, satélite e Terra giram alinhados ao redor do Sol
“varrendo” a mesma área no mesmo tempo --- WA=WT=2![]() /T,
onde T é
o período de rotação da Terra em torno do Sol e pelo “Note e
adote” T=1
ano=3,14.107s ---
WA=2x3,14/3,14.107 --- WA=2.10-7 rad/s.
/T,
onde T é
o período de rotação da Terra em torno do Sol e pelo “Note e
adote” T=1
ano=3,14.107s ---
WA=2x3,14/3,14.107 --- WA=2.10-7 rad/s.
02- Gravidade
artificial - Na Terra estamos acostumados com a “sensação se
peso” e que quando estamos apoiados ela (sensação
de peso)
ocorre devido à força de reação
normal ![]() do
apoio sobre nosso corpo.
do
apoio sobre nosso corpo.

Estando
em equilíbrio ![]() e
e ![]() possuem
a mesma intensidade, ou seja, N=P ---
N=m.g--- como a massa m é
sempre constante, se variarmos a “gravidade” g,
estaremos variando essa “sensação
de peso”.
possuem
a mesma intensidade, ou seja, N=P ---
N=m.g--- como a massa m é
sempre constante, se variarmos a “gravidade” g,
estaremos variando essa “sensação
de peso”.
Essa “sensação de peso” pode ser obtida fazendo a estação espacial, que deve ter a forma de um cilindro oco, efetuar movimento contínuo de rotação com velocidade angular W.
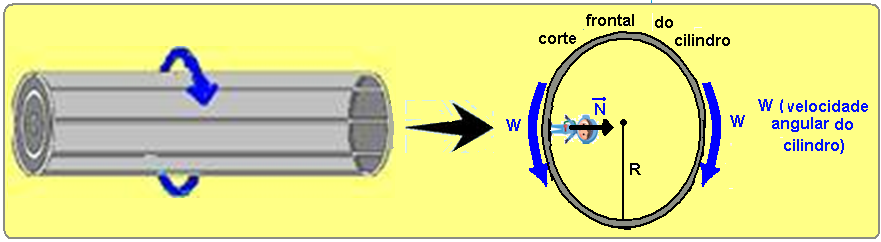
Essa simulação
da “gravidade”
ocorre, pois todo corpo em movimento circular tende a se afastar do
centro e, no caso, “colando”
nas paredes internas do cilindro--- o“peso
aparente” do astronauta é
percebido pela reação
normal ![]() das
paredes da nave sobre ele, que é a própria força resultante
centrípeta Fc=m.V2/R,
que deve ser igual ao peso
do astronauta na Terra onde
g==10m/s2 ---
portanto, para que as pessoas tenham a sensação
de peso,
como se estivessem
na Terra a
condição é ---N=P com
N=mW2R
e P=mg --- no caso do exercício são dados --- R=100m ---
g=10m/s2 ---
portanto, N=P --- mW2R=mg
--- W2.100=10
--- W=√(10/100) --- W=√(0,1)≈0,316 rad/s --- R-
B
das
paredes da nave sobre ele, que é a própria força resultante
centrípeta Fc=m.V2/R,
que deve ser igual ao peso
do astronauta na Terra onde
g==10m/s2 ---
portanto, para que as pessoas tenham a sensação
de peso,
como se estivessem
na Terra a
condição é ---N=P com
N=mW2R
e P=mg --- no caso do exercício são dados --- R=100m ---
g=10m/s2 ---
portanto, N=P --- mW2R=mg
--- W2.100=10
--- W=√(10/100) --- W=√(0,1)≈0,316 rad/s --- R-
B
03- Titã está a uma distância média de 1 200 000 km de Saturno e tem um período de translação de, aproximadamente, 16 dias terrestres ao redor do planeta:
TTitã=16d e rTitã=1 200 000km=12.105km.
Tétis é outro dos maiores satélites de Saturno e está a uma distância média de Saturno de 300 000 km e pede-se seu período de translação ao redor de Saturno:
TTétis=? --- rTétis=300 000km=3.105km.
Aplicando a terceira lei de Kepler:

R- B
04-

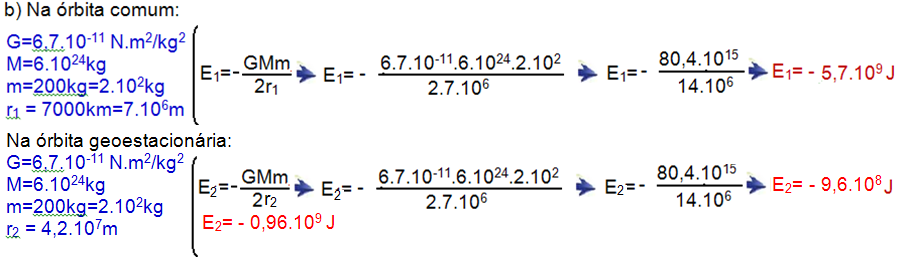
Energia
adicional ![]() Ea=
- 0,96.109 –
( - 5,7.109)
Ea=
- 0,96.109 –
( - 5,7.109) ![]() Ea=
4,74.109 J
Ea=
4,74.109 J
05- Satélites geoestacionários ou geosincrônicos (sincronizados com o movimento de rotação da Terra) --- A maioria dos satélites de telecomunicações são satélites geoestacionários pois se encontram parados em relação a um ponto fixo sobre a Terra.

Seu período é o mesmo que o da Terra (24h), o raio de sua órbita é de, aproximadamente 36000km, tem a mesma velocidade angular (W) que a Terra e se encontram em órbitas sobre a linha do equador.
R- A
06- Satélites geoestacionários ou geosincrônicos(sincronizados com o movimento de rotação da Terra) --- A maioria dos satélites de telecomunicações são satélites geoestacionários pois se encontram parados em relação a um ponto fixo sobre a Terra.

Seu período é o mesmo que o da Terra (24h), o raio de sua órbita é de, aproximadamente 36000km, tem a mesma velocidade angular (W) que a Terra e se encontram em órbitas sobre a linha do equador.
Acima da altura aproximada de 36000km o período do satélite aumenta e abaixo desse valor, diminui.
R- D
07- Se você não domina o conteúdo, leia atentamente a teoria a seguir: Para colocar um objeto em órbita ao redor da Terra, como fazemos com os satélites artificiais, a partir de sua superfície da Terra, devemos lançá-lo com uma velocidade mínima, que denominamos velocidade de escape Ve).
Essa velocidade mínima (Ve) deve ser a velocidade necessária para que um objeto, sem propulsão própria, saia da superfície da Terra e chegue no infinito com velocidade zero.
Assim, considerando:
G --- constante gravitacional
M --- massa da Terra
M --- massa do objeto a ser lançado com velocidade Ve e que vai escapar do campo gravitacional
r=R --- Distância entre o centro do planeta (Terra) e o ponto no qual a velocidade de escape está sendo calculada (superfície da Terra)
Energia mecânica na superfície da Terra de raio R
Energia potencial gravitacional --- Ep=-GMm/r --- Ep=-GMm/R --- Energia cinética --- Ec=mVe2/2
EMT=Ec+Ep --- EMT=mVe2/2 – GMm/R
Energia mecânica no infinito
Energia
potencial gravitacional --- Ep=-GMm/![]() ---
Ep=0
--- Energia cinética --- Ec=m02/2
--- Ec=0
---
---
Ep=0
--- Energia cinética --- Ec=m02/2
--- Ec=0
---
Energia mecânica --- EM¥=0 --- pelo princípio da conservação da energia mecânica --- EMT=EM¥
mVe2/2 – GMm/R=0 --- Ve=√(2GM/R)

Substituindo os valores de G, M, e R que conhecemos, obtemos:
Ve=11,3km/s que é a velocidade com que um corpo, sem propulsão própria deve sair da superfície da Terra para “libertar-se” de seu campo gravitacional.
Como a velocidade de um corpo em órbita é dada por V=√(GM/R) e a velocidade de escape por Ve=√(2GM/R), a velocidade de escape na altura R é √2 vezes maior que a velocidade em órbita circular na mesma altura.
Assim, velocidade escalar adicional que o satélite precisa adquirir para escapar completamente do planeta.
deve valer --- Ve=√2. √(2GM/(R + H) - √(2GM/(R + H) --- R- D
08- RMa=4RMe --- TMe=TT/4 --- Terceira lei de Kepler --- TMa2/RMa3 = TMa2/RMe3 --- TMa2/(4RMe)3 =
(TT/4)2/RMe3 --- TMa2/64RMe3 = TT 2 /16RMe3 --- TMa2/64 = TT 2 /16 --- 4TMa2 = 64TT2 --- TMa2= 4Tt2 ---
TMa=2TT.
R- B
Leis de Kepler
28- Segunda lei de Kepler (lei das áreas)
“ O segmento de reta imaginário que une o centro do Sol ao centro do planeta descreve áreas proporcionais aos tempos
gastos para percorre-las”
Sendo as áreas proporcionais --- regra de três --- A – 2 meses --- αA – 32 meses --- 2.αA=32.A --- α=16;
29- I. Falsa --- a primeira lei de Kepler afirma que as órbitas são elípticas com o Sol ocupando um dos focos da elipse.
II. Verdadeira --- Segunda lei de Kepler (lei das áreas) --- “ O segmento de reta imaginário que une o centro do Sol ao centro do planeta descreve áreas proporcionais aos tempos gastos para percorrê-las”
Sejam:
A1--- área entre 1,2 e o Sol --- A2--- área entre 3, 4 e o Sol --- ∆t1--- tempo que o planeta demora para ir de 1 a 2 ---∆t2--- tempo que o planeta demora para ir de 3 a 4 --- então:
A1∆t1 ~A2/∆t2=constante=K --- essa constante K depende do planeta e recebe o nome de velocidade areolar
Observe na expressão acima que quando A1=A2, ∆t1= ∆t1, ou seja, para o arco maior 34, ser percorrido no mesmo
intervalo de tempo que o arco menor12, a velocidade em 3,4 (mais perto do Sol - periélio) deve ser maior que a velocidade em 1,2 (mais afastado do Sol – afélio).
Portanto os planetas aceleram do afélio para o periélio e retardam do periélio para o afélio.
III. Falsa --- veja (II).
IV. Falsa --- a órbita de Mercúrio não é circular, é elíptica.
R- C.
30- Leia atentamente a teoria a seguir:
“ O segmento de reta imaginário que une o centro do Sol ao centro do planeta descreve áreas proporcionais aos tempos gastos para percorrê-las”
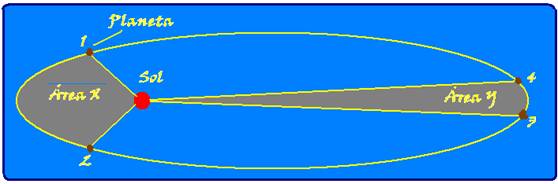
Sejam:
Ax--- área entre 1,2 e o Sol --- Ay --- área entre 3, 4 e o Sol --- ∆tx--- tempo que o planeta demora para ir de 1 a 2 ---
∆tx --- tempo que o planeta demora para ir de 3 a 4 --- pela lei das áreas de Kepler --- Ax/∆tx ~ Ay/∆ty --- essa constante K depende do planeta e recebe o nome de velocidade areolar.
Observe na expressão acima que, quando Ax=Ay, ∆tx=∆ty, ou seja, para o arco maior 34, ser percorrido no mesmo intervalo de tempo que o arco menor12, a velocidade em 3,4 (mais perto do Sol - periélio) deve ser maior que a velocidade em 1,2 (mais afastado do Sol – afélio).
Portanto os planetas aceleram do afélio para o periélio e retardam do periélio para o afélio. Ainda, de acordo com essa lei, se as órbitas forem circulares a velocidade de translação será constante e se a órbita do planeta tiver raio R e seu período de translação for T, sua velocidade areolar (constante K) será dada por: K=A/∆t =πR2/T.
R- B.
Lei da Gravitação Universal
16- Considere
um planeta de massa m em órbita aproximadamente circular ao redor do
Sol de massa M --- a força gravitacional entre o planeta
e Sol tem intensidade FG=GMm/r2,
sendo G a constante de gravitação universal e R a distância
entre os centros do Sol e do planeta --- a intensidade da
força resultante centrípeta sobre o planeta vale Fc=mV2/R,
sendo V a velocidade escalar (de translação) do planeta em torno do
Sol --- sobre o planeta essas duas forças são iguais
--- FG =
FC
--- GMm/R2 mV2/R
--- V=√(G.M/R) --- observe por essa expressão
que, quanto mais afastado o planeta estiver do Sol, menor será sua
velocidade orbital e que essa velocidade não depende da massa m do
planeta --- assim, a velocidade orbital de translação
da Terra é maior que a de Marte --- esse é o motivo da
trajetória em forma de laço, que você pode entender observando
atentamente a figura abaixo.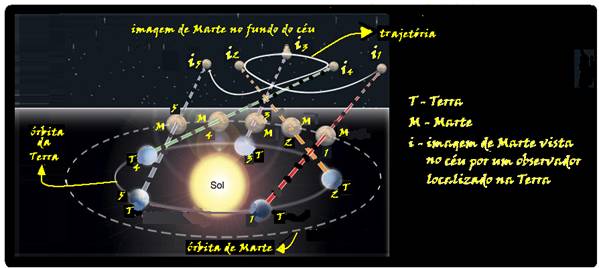
R- A.
SATÉLITES EM ÓRBITAS CIRCULARES
18- A
velocidade orbital de um satélite ao redor de um planeta (no caso, a
Terra) é fornecida por --- V=√(GM/r) ---
G-constante gravitacional, M - massa da Terra e r - raio da órbita
--- são dados ---
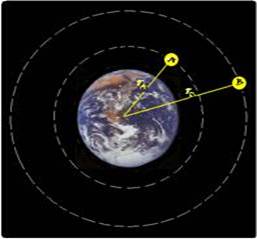
VA=2.103m/s --- RB/RA=102 --- satélite A --- VA=√(GM/rA) --- 2.103=√(GM/rA) (I) --- satélite B --- VB=√(GM/rB) --- VB=√(GM/102rA) (II).
(I)/(II) --- 2.103/VB=√(GM/rA)/√(GM/102rA) --- 2.103/VB={√(GM)/√rA}x{√(102rA)/√(GM) --- 2.103/VB=10√rA/√rA --- 10VB=2.103 --- VB=2.102m/s --- R- D.
19- Dados --- R=380 000km --- T=28diasx24hx3600s=2 419 200s --- π=3 --- V=2πR/T=2X3X380 000km/2 419 200s --- V=0,94km/s --- R- E.
20- 1. Falsa --- A intensidade da força gravitacional entre cada satélite e o planeta P é dada por --- Fg=GMS.MP/R2 --- observe nessa expressão que para o satélite SA o raio da órbita é variável, assim a intensidade da força gravitacional entre o satélite SA e o planeta P também é variável.
2. Verdadeira --- Por meio de cálculos que fogem ao nível do ensino médio podemos demonstrar que a energia potencial gravitacional de um satélite em relação ao outro, adotando-se o referencial no infinito, é dada por:
Ep=-GMm/r --- observe que essa energia potencial gravitacional é função da distância r entre os dois satélites, que é variável.
3. Falsa --- essa afirmativa é válida para o satélite B mas para o satélite B é falsa, pois em órbitas elípticas ele acelera do afélio para o periélio variando sua velocidade o que implica numa variação da energia cinética e da velocidade angular.
R- B.
21- Satélites geoestacionários ou geosincrônicos (sincronizados com o movimento de rotação da Terra) --- a maioria dos satélites de telecomunicações são satélites geoestacionários pois se encontram parados em relação a um ponto fixo

sobre a Terra --- seu período é o mesmo que o da Terra (24h), o raio de sua órbita é de, aproximadamente 36000km, tem a mesma velocidade angular (W) que a Terra e se encontram em órbitas sobre a linha do equador.
Acima da altura aproximada de 36000km o período do satélite aumenta e abaixo desse valor, diminui.
R- A.
Aceleração da gravidade
18- Pelo enunciado eles possuem a mesma densidade --- dT=dY --- dT=mT/VT=mT/(4/3)πRT3 --- dY=mY/VY=mY/(4/3)πRY3 --- dY= mY/(4/3)π(3RT)3 --- dY=mY/36πRT3 --- dT=dY --- mT/(4/3)πRT3= mY/(4/3)36πRT3 --- mY=27mT --- aceleração da gravidade na superfície da Terra --- g=GmT/RT2 --- aceleração da gravidade na superfície de Y --- gY=GmY/RY2=G.27mT/(3RT)2 --- gY=27GmT/9RT2 --- gY=3.GmT/RT2 --- gY=3g --- R- E.
19- O peso do jipe na Terra --- PT=m.gT --- a massa do jipe é a mesma na Terra e em Marte --- peso do jipe em Marte --- PM=m.gM --- como, pelo enunciado, o veículo foi suave e lentamente baixado até o solo, ele se encontra em equilíbrio dinâmico e a força resultante sobre ele é nula --- assim, a tração T nos cabos é igual ao peso, tanto na Terra como em Marte --- PT=TT=m.gT e PM=TM=m.gM --- a aceleração da gravidade na superfície de um planeta é fornecida por --- g=G.M/R2 --- G é uma constante, M a massa do planeta e R o raio médio do planeta --- TT=m.gT=
m.GMT/RT2=mG.10MM/(2RM)2 --- TT=2,5mGMM/RM (I) --- TM=m.gM=m GMM/RM (II) --- (II)/(I) --- TM/TT=
(mGMM/RM)x (RM/2,5GMM) --- TM/TT=1/2,5=0,4 --- R- C.
|
|