Estática

ESTÁTICA – 2017 – 2016 - 2015

Estática de um ponto material


01-(FMJ-SP-017)

Considere um objeto, cuja massa não varia, se deslocando em uma trajetória retilínea com velocidade constante. É correto afirmar que necessariamente

(A) a resultante das forças sobre esse objeto tem direção perpendicular à da velocidade.

(B) a resultante das forças sobre esse objeto é igual a seu peso.

(C) a resultante das forças sobre esse objeto tem direção e sentido iguais aos da velocidade.

(D) a resultante das forças sobre esse objeto é nula.

(E) não há forças agindo sobre esse objeto.


02-(FAMERP-SP-017)


03-(UERJ-RJ/017)

No esquema, está representado um bloco de massa igual a 100 kg em equilíbrio estático.

Determine, em newtons, a tração no fio ideal AB.



04-(ACAFE-SC-017)

Um homem queria derrubar uma árvore que estava inclinada e oferecia perigo de cair em cima de sua casa. Para isso, com a ajuda de um amigo, preparou um sistema de roldanas preso a outra árvore para segurar a árvore que seria derrubada, a fim de puxá-la para o lado oposto de sua suposta queda, conforme figura.

Sabendo que para segurar a árvore em sua posição o homem fez uma força de 1000 N sobre a corda, a força aplicada pela corda na árvore que seria derrubada é:

a) 2000 N

b) 1000 N

c) 500 N

d) 4000 N



Estática de um ponto material 2017 – 2016 – 2015

Resoluções


01- Nesse caso o objeto tem uma velocidade constante, logo sua aceleração é 0. Como sua aceleração é 0, a força resultante também só pode ser 0, com isso a alternativa correta é a D.

Vamos analisar as outras, também:

A velocidade tem sempre a mesma direção e sentido da força resultante, pois ela é uma consequência da aceleração que vai ser exercida por essa força.

Se a resultante fosse igual ao peso, o objeto estaria em queda livre.

A alternativa C pode causar confusão, porque realmente ela é verdadeira, mas no caso aonde há uma força resultante.

Sempre há forças agindo, porém a soma delas vai ser igual a 0.

R – D


02- Peso do conjunto A  PA = 4mg  peso do conjunto B  PB = 2mg.

Chamando a distância entre cada marca consecutiva de d e de Y a distância de P até onde se deve colocar o peso PB você obterá o esquema da figura abaixo:

Adotando o ponto P como polo 0 (eixo de rotação) e o sentido horário de rotação como positivo e anti horário como negativo, vamos calcular o momento de cada força em relação ao polo.

MPA = – F.dPA P = – PA.2d  MPA = – 4mg2d  MPA = – 8mgd  (sinal negativo, pois tende a girar no sentido anti horário)

MT = T.0  MT = 0

MPB = + F.dPPB = + PB .Y  MPB = + 2mgY  (sinal positivo, pois tende a girar no sentido horário)

A condição de equilíbrio de rotação é que a soma dos momentos de cada força em relação ao polo deve ser nula  MPA + MT + MPB = 0  – 8mgd + 0 + 2mgY = 0  Y =   Y = 4

R- C


03-

Figura 2  TCBh = TCB.cos30o = TCB)/2  TCBv = TCB.sen30o =TCB/2.

Figura 3  equilíbrio na vertical  TCBv = P  TCB/2 = mg = 100.10 TCB/2 = 1000  TCB = 2000N.

Figura 3  equilíbrio na horizontal  TCBh = TAB  TCB)/2 = TAB  )/2 = TAB 

TAB = 1000


04- Vamos analisar as polias:

No caso do exercício nós temos duas polias móveis e uma força de 1000 N, então só precisamos dobrar duas vezes a força inicial, sendo assim a força aplicada é de 4000 N. Alternativa D.



ESTÁTICA – 2017 – 2016 - 2015

Estática de um corpo extenso


01- (UNESP-SP-017)

Três cubos laranja idênticos e três cubos azuis idênticos estão equilibrados em duas balanças de pratos, também idênticas, conforme indicam as figuras.

A massa de um cubo laranja supera a de um cubo azul em exato

(A) 1,3 kg.

(B) 1,5 kg.

(C) 1,2 kg.

(D) 1,4 kg.

(E) 1,6 kg.


02-(EsPCEx- AMAN – SP- RJ – 2016/17)

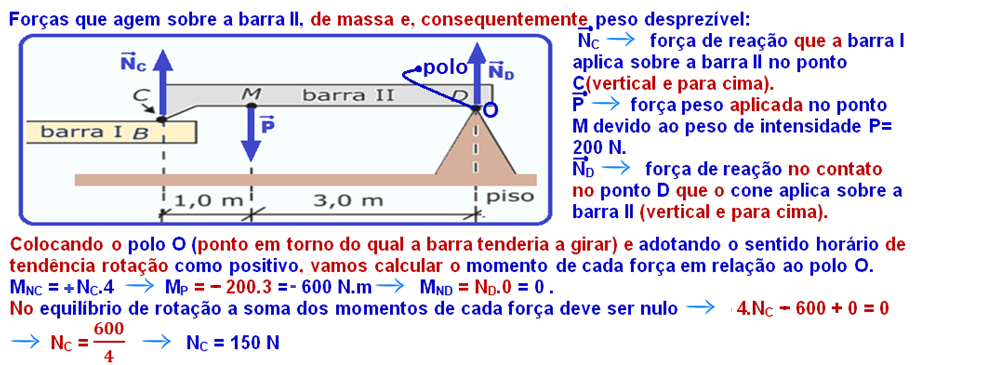
O desenho abaixo representa um sistema composto por duas barras rígidas I e II, homogêneas e de massas desprezíveis na posição horizontal, dentro de uma sala. O sistema está em equilíbrio estático.

No ponto M da barra II, é colocado um peso de 200 N suspenso por um cabo de massa desprezível.

A barra I está apoiada no ponto N no vértice de um cone fixo no piso.

O ponto A da barra I toca o vértice de um cone fixo no teto.

O ponto B da barra I toca o ponto C, na extremidade da barra II.

O ponto D, localizado na outra extremidade da barra II, está apoiado no vértice de um cone fixo no piso.

Os módulos das forças de contato sobre a barra I, nos pontos A e N, são respectivamente:


03-(AFA – 016/017)



04-(UFES – ES – 017)



05-(ACAFE-SC-017)

Para cortar galhos de árvores um jardineiro usa uma tesoura de podar, como mostra a figura 1. Porém, alguns galhos ficam na copa das árvores e como ele não queria subir nas mesmas, resolveu improvisar, acoplando à tesoura cabos maiores, conforme figura 2.

Assim, assinale a alternativa correta que completa as lacunas da frase a seguir.

Utilizando a tesoura da ________ o rapaz teria que fazer uma força ________ a força aplicada na tesoura da ______ para produzir o mesmo torque.

a) figura 2 – menor do que – figura 1

b) figura 2 – maior do que – figura 1

c) figura 1 – menor do que – figura 2

d) figura 1 – igual – figura 2




06-(PUC-GO-017)

Nos fragmentos do Texto 3 “Tentava acompanhar os passos de meu pai. […] dizer-lhe que parasse.” Temos referência a movimento e a repouso.

O movimento de um corpo pode ser de translação e/ou rotação.

Para que um corpo permaneça em repouso, é necessário que esteja em equilíbrio de translação e rotação.

Considere uma gangorra construída com uma tábua rígida, homogênea, demassa igual a 10 kg, com espessura e largura desprezíveis em relação aseu comprimento, que é de 8 m.

A tábua pode girar em torno de um eixo de rotação colocado perpendicularmente ao seu comprimento, a 4 m de cada uma das extremidades.

Duas pessoas, uma de massa m1 = 85 kg e outra de massa m2 = 40 kg,estão sentadas em cada uma das extremidades da tábua.

Para que a tábua fique em equilíbrio horizontal, uma terceira pessoa é colocada entre o eixo de rotação e a pessoa mais leve, a uma distância de 1,5 m desse eixo.

A massa da terceira pessoa é de (assinale a resposta correta):



07-(ENEM-MEC-015)

08-(Medicina – USCS-SP-016)

Um cilindro de 600 g de massa e 200 cm3 de volume é totalmente imerso em água, de densidade 1,0 g/cm3 = 103 kg/m3, e suspenso por um fio ideal atado a uma das extremidades de uma barra rígida de peso desprezível.

A barra é apoiada em um ponto O, distante 30 cm da extremidade em que se encontra suspenso o cilindro e distante 10 cm da outra extremidade em que há uma esfera de peso Pe , mantendo o sistema em equilíbrio. A figura ilustra a situação descrita.

Considerando a aceleração da gravidade igual a 10 m/s2, a intensidade do peso Pe , em N, deve ser igual a


Estática de um ponto material 2017 – 2016 - 2015

Resoluções






01-Denominando de ml a massa de cada cubo laranja e de ma a massa de cada cubo azul e, estando as balanças em equilíbrio, você terá:

Balança da esquerda2ma + ml = 2 (I)

Balança da direita ma + 3 = 2ml (II)

Isolando ma em (II) e substituindo em (I) ma = 2ml – 3 2(2ml – 3) + ml = 2  4ml – 6 + ml = 2 5ml = 8 ml= 8/5 = 1,6 kg.

2ma + 1,6 =2  ma = 0,4/2 ma = 0,2 kg.

Assim, a massa de um cubo laranja supera a de um cubo azul em ml – ma= 1,6 – 0,2 = 1,4 kg.

R- D

02-

No equilíbrio de translação, para que ocorra equilíbrio na vertical a resultante das forças deve ser nula, ou seja, NA + NB = NN  75 + 150 = NN  NN = 225 N

R- D

03-

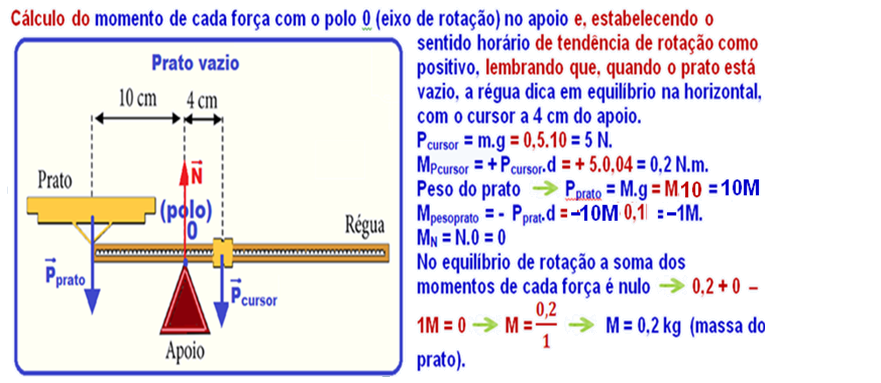
04- A) Colocando o polo (eixo de rotação) no ponto O, e estabelecendo o sentido de tendência de rotação em torno de O como positivo para o horário e negativo para o anti

horário, vamos calcular o momento (torque) de cada força em relação a O, sendo dP e dm as distâncias entre o ponto de aplicação das forças O até as forças FP e Fm:

MP = P.d = P.0 = 0

MFP = + FP.dP

MFm = – Fm.dm

A condição de equilíbrio de rotação é de que a soma dos momentos (torques) de cada força seja nula

 0 + FP.dP – Fm.dm = 0  FP.dP = Fm.dm  Fm = FP.dP/dm.

B) O momento (torque) exercido pelo prego sobre o martelo (e vice versa) é fornecido e tem intensidade MP = FP.dP = 30 Nm com dm = 0,2 m, que substituidos em Fm = FP.dP/dm fornrcem  Fm =   Fm = 150 N.

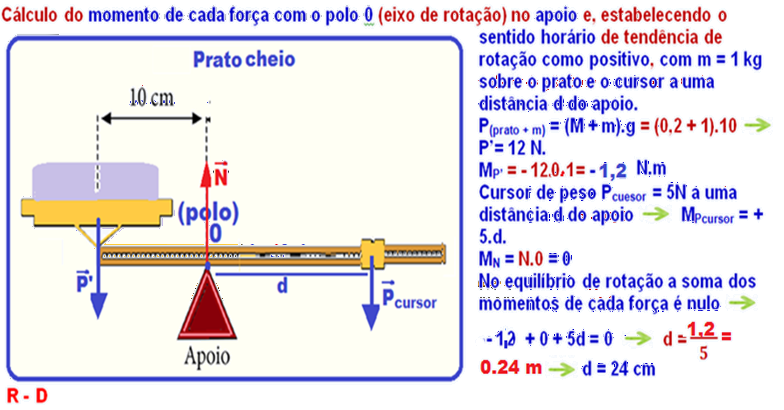
C) Aquí o peso de intensidade P participa e sua distância ao polo é d, e astrês forças que influem na rotação tem intensidades P, Fp e Fm, cujosmomentos (torques) em relação à O, estabelecendo o sentido de tendência de rotação em torno de O como positivo para o horário e negativo para o anti horário, serão:

MP = – P.d

MFm = – Fm.dm = - Fm.20d = – 20dFm

MFP = + FP.dP = + FP.4d = + 4dFP

No equilíbrio de rotação a soma desses momentos deve ser nula  - P.d – 20dFm + 4dFP = 0  20Fm = P – 4FP  Fm = (P – 4FP/20 =  – 



05- Para esse exercício precisamos analisar a fórmula do momento (ou torque):

M = F.d.sen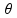

Sendo:

M é o momento ou torque

F é a força exercida

d é a distância entre a força e aonde ela é executada

 é o ângulo entre a força e aonde ela está sendo executada

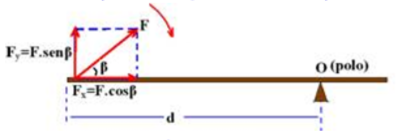
Ao mantermos o momento e o ângulo constantes, como o jardineiro aumentou a distância ao prolongar o cabo, a força, consequentemente, será menor. Alternativa a correta.



06- Calculando o momento de cada força com o polo (eixo de rotação) na posição indicada e estabelecendo o sentido horário de rotação como positivo e anti- horário como negativo:

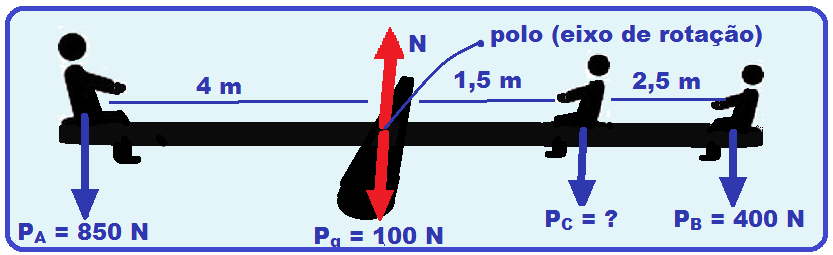
MPA = – 850.4 = – 3400 N.m  MPG = MN = 0  MPC = + Pc.1,5  MPB = + 400.4 = + 1600 N.m.

No equilíbrio de rotação a soma dos momentos de cada força deve ser nulo  - 3400 + 0 + 1,5PC +

1600 = 0  1,5PC = 1800  PC =  = 1200 N.

PC = mC.g  1200 = mC.10  mC = 120 kg.

R- D



07- Se você não domina a teoria, veja as informações a seguir:

Momento (ou torque) de uma força

O sinal do momento da força pode ser negativo ou positivo e, por convenção, vamos adotar osentido horário de rotação em torno de O como positivo e anti-horário como negativo.

Condições de equilíbrio de um corpo extenso

São duas as condições para que um corpo extenso rígido esteja em equilíbrio:

1a  Equilíbrio de translação    A resultante do sistema de forças deve ser nula.

2a  Equilíbrio de rotação    A soma algébrica dos momentos das forças que agem sobre o sistema, em relação à qualquer ponto (polo O),deve ser nula.

Resolvendo o sistema composto pelas duas equações acima você chega à resolução do exercício.

No caso do exercício, vamos colocar as forças que agem sobre a barra de intensidades:

Parroz (peso do arroz) Pbarrapeso da barra (no meio da barra, pois ela é homogênea)  N (reação normal que o apoio aplica na barra)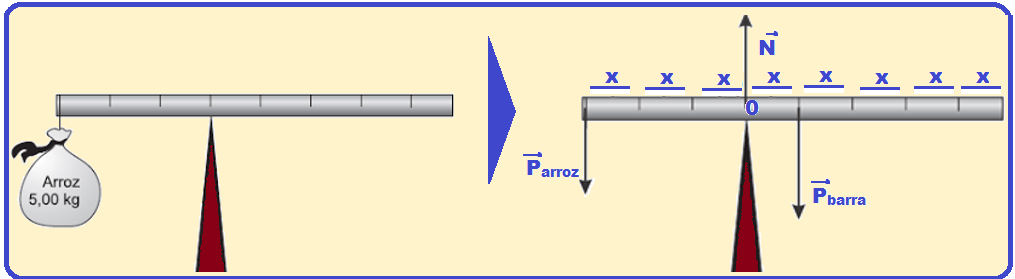

Momento de cada força em relação ao polo 0:

Mbarra = + Pbarra.1x  MN = N.0 = 0 Marroz = – Parroz.3x.


Condição de equilíbrio de rotação a soma dos momentos de cada força, em relação ao ponto O, deve ser nula:
Pbarra.1x + 0 – Parroz.3x = 0  mbarra.g= 3.marroz.g marroz = 5,00 kg (veja desenho) 
mbarra.g = marroz.g.3 mbarra = 3.5,00  mbarra = 15,00 kg.  
R- E



08-

Momento ou torque de uma força

O sinal do momento da força pode ser negativo ou positivo e, por convenção, vamos adotar o sentido horário de rotação em torno de O como positivo e anti-horário como negativo.

São duas as condições para que um corpo extenso rígido esteja em equilíbrio:

1a  Equilíbrio de translação    A resultante do sistema de forças deve ser nula.

2a  Equilíbrio de rotação    A soma algébrica dos momentos das forças que agem sobre o sistema, em relação ao ponto de apoio (pólo O),deve ser nula.

ESTÁTICA – 2014 - 2013

Estática de um ponto material

01-(UNEMAT-MT-014)

Com a Copa do Mundo de 2014, diversas obras estão sendo realizadas, tais como construção de novos estádios de futebol, novos terminais de transporte público, entre outras. Neste período, é comum se ver trabalhadores sobre vigas e pilares nas construções.

Considerando uma construção simples, constituída de uma viga na horizontal apoiada nas suas

extremidades em duas colunas verticais, denominadas de A e B e supondo que um trabalhador se encontra a 1 (um) metro do ponto A e que a viga possua 3 metros de comprimento, assinale a alternativa correta:

(A) A carga imposta pela viga às colunas é igual.

(B) A carga imposta pela viga na coluna A é o dobro da carga imposta pela viga na coluna B.

(C) A carga imposta pela viga na coluna B é o dobro da carga imposta pela viga na coluna A.

(D) Não é possível efetuar qualquer relação de carga, pois não foi dado o valor da massa do homem.

(E) Se o homem continuar movimentando no sentido de B, a carga nesta coluna reduzirá.


02-(MACKENZIE-SP-014)

Na figura abaixo, a mola M, os fios e a polia possuem inércia desprezível e o coeficiente de atrito

estático entre o bloco B, de massa 2,80 kg, e o plano inclinado é μ = 0,50. O sistema ilustrado se encontra em equilíbrio e representa o instante em que o bloco B está na iminência de entrar em movimento descendente.

Sabendo-se que a constante elástica da mola é k = 350 N/m, nesse instante, a distensão da mola M, em relação ao seu comprimento natural é de

03-(UNISINOS-RS-014)

A importância do atrito

Este anúncio, da Standard Motor Oil (1932), mostra um exemplo de como o atrito pode ser positivo: “O atrito, nos freios, salva até a vi­da humana. Mas, no motor, é fatal”. A ilustra­ção vem acompanhada da explicação: “Bem controlado, o atrito é muito útil. Os freios do carro seriam inúteis sem ele. É o atrito dos freios nos tambores dos pneus na estrada que freia o carro. Mas, se o atrito é um elemento de segurança nos freios, é também elemento de destruição do motor: pode reduzi-lo rapida­mente a uma massa inerte”.

Um aluno coloca um corpo sobre um plano inclinado que forma um ângulo θ = 30º com a horizontal, e o corpo permanece em repouso.

Neste caso, o coeficiente de atrito estático mínimo entre o corpo e a superfície inclinada é de


04-(UEFS-BA-014)

A figura é uma representação da vista de cima da secção transversal do tronco de uma árvore e das

forças aplicadas no tronco através de uma corda tensionada.

Nessas condições, a intensidade da força resultante aplicada no tronco da árvore é determinada pela

Relação


05-(UFLA-MG-014)

Considere uma prateleira, em repouso, de massa m=2 kg, que está dependurada horizontalmente na parede por meio de um cabo, de massa desprezível, como mostra a figura. O cabo está fixo em um dos extremos na parede e, no outro extremo, está fixo no meio da prateleira. Considere: g = 10 m/s2; cos60o=1/2.

A tensão do cabo é:

06-(UFLA-MG-014)

Um lustre formado por três esferas de vidro é dependurado no teto, como mostrado na figura. As massas

das esferas são 300 g, 200 g e 100 g, respectivamente. Determine a tensão em cada uma das cordas, de massa desprezível.

(A) T1 = 6 N, T2 = 3 N e T3 = 1 N

(B) T1 = 1 N, T2 = 6 N e T3 = 3 N

(C) T1 = 3 N, T2 = 1 N e T3 = 6 N (

D) T1 = 1 N, T2 = 3 N e T3 = 6 N

07-(UFLA-MG-014)

Duas crianças estão sobre uma gangorra de massa desprezível. A criança da direita (II) é duas vezes mais pesada do que a criança da esquerda (I). A figura abaixo que representa uma situação de equilíbrio é:


08-(UFRGS-RS-014)

Na figura abaixo, blocos idênticos estão suspensos por cordas idênticas em três situações distintas, (1), (2) e (3).

Assinale a alternativa que apresenta as situações na ordem crescente de probabilidade de

rompimento das cordas. (O sinal de igualdade abaixo indica situações com a mesma probabilidade de rompimento.)

(A) (3), (2), (1).

(B) (3), (2) = (1).

(C) (1), (2), (3).

(D) (1) = (2), (3).

(E) (1) = (2) = (3).


09-(UFRR-RR-014)

O uso da física nos esportes é comum e vem crescendo de ano para ano. Vamos considerar que um atleta de alto rendimento usou uma tira de borracha atada ao seu abdômen, conseguindo alongar a tira de borracha segundo a tabela:

Considerando que a tira elástica obedece a lei de Hooke e possui constante elástica igual a 60,0N/m, assinale a opção a qual corresponde a força exercida pelo atleta na tira, no dia de menor rendimento:

10-(UFSC-SC-014)

Símbolo de beleza e elegância, os sapatos de salto alto são usados e desejados por mulheres de

todas as idades. Todavia, o seu uso excessivo pode trazer sérios riscos à saúde, associados a alterações de variáveis físicas importantes para o caminhar, como lesões, lordose (curvatura acentuada da coluna para dentro) e deformidades nos pés, por exemplo. Na figura acima, são apresentados dois modelos (A e B) bastante comuns de sapatos de salto alto, ambos número 34.

Assinale a(s) proposição(ões) CORRETA(S).

01. O sapato A permite maior estabilidade no caminhar que o sapato B.

02. Com o uso do sapato de salto alto, o centro de gravidade do corpo é deslocado para a frente em relação a sua posição normal (sem o sapato de salto).

04. O sapato B permite uma distribuição mais homogênea do peso do corpo, nas partes da frente e de trás do pé, que o sapato A.

08. Caminhar com sapato de salto alto pode ser comparado a caminhar descendo um plano inclinado.

16. A pressão sobre o solo em uma caminhada com o sapato A é maior que com o sapato B, para

uma mesma pessoa.


11-(UFV-MG-014)

Um bloco de massa m repousa sobre um plano inclinado de um ângulo θ. Uma corda inextensível passando por uma roldana sem atrito conecta esse bloco a outro bloco de massa M, conforme ilustrado na figura.

As massas da corda e da roldana são desprezíveis. Seja μe o coeficiente de atrito estático e μc o coeficiente de atrito cinético entre o bloco e o plano. A alternativa que apresenta CORRETAMENTE o valor da massa M para que o bloco de massa m desça o plano com velocidade constante é:


12-(UnB-014)

A figura abaixo mostra um indivíduo em repouso, na vertical e apoiado em uma parede.

Considerando que não haja atrito apenas entre o indivíduo e a parede, desenhe as forças que atuam no indivíduo.


Estática de um ponto material

 

38-(MACKENZIE-SP-013)

Em uma experiência de laboratório, um estudante utilizou os dados do gráfico da figura 1, que se referiam à intensidade da força aplicada a uma mola helicoidal, em função de sua deformação (F=kx). Com esses dados e uma montagem semelhante à da figura 2, determinou a massa (m) do corpo suspenso.

Considerando que as massas da mola e dos fios (inextensíveis) são desprezíveis, que  g=10m/s2 e que, na posição de equilíbrio, a mola está deformada de 6,4 cm, a massa (m) do corpo suspenso é

a) 12 kg                  b) 8,0 kg                    c) 4,0 kg                        d) 3,2 kg                         e) 2,0 kg

 

Corpo extenso – centro de massa e tipos de equilíbrio

 

21-(UNIMONTES-MG-013)

 

Um conjunto de molas sustenta o peso de um carro. Com 2 pessoas de 60kg em seu interior, o carro abaixa 2cm. Com 4

Com 4 pessoas de 70kg, o carro vai abaixar, aproximadamente: g=10m/s2.

A) 3,0cm.                     B) 3,5cm.                           C) 4,0cm.                          D) 4,7cm.

 

22-(UFV-MG-013)

As três figuras abaixo apresentam um mesmo bloco de peso de módulo P suspenso por roldana(s). As roldanas e as

cordas ilustradas têm massas desprezíveis e o equilíbrio estático é mantido, em cada caso, por um homem que exerce uma força de módulo F na extremidade livre da corda.

Com base nas observações das duas primeiras situações de equilíbrio, é CORRETO afirmar que, na terceira situação, o módulo da força F exercida pelo homem é:

a) P                                 b) P/2                                      c) P/3                                   d) P/4

 

Estática de um corpo extenso – máquinas simples

66-(UFV-MG-013)

“Dê-me uma alavanca e um ponto de apoio que levantarei o mundo”. Essa célebre frase proferida pelo filósofo grego Arquimedes sintetiza bem a importância das alavancas, base do funcionamento de inúmeros utensílios, máquinas, e até mesmo de membros de nosso corpo.

A figura abaixo ilustra uma alavanca, chamada interfixa devido ao fato de o ponto de apoio O se encontrar entre o ponto B, de aplicação da força potente , e o ponto A, de aplicação da força resistente . Sabe-se que, na situação de equilíbrio rotacional, o produto do módulo da força potente pela distância BO é igual ao produto do módulo da força resistente pela distância .

Um exemplo típico desse tipo de alavanca é o alicate de cortar fio, ilustrado abaixo.

Sendo F o módulo da força potente aplicada ao longo da direção assinalada, o correspondente módulo da força resistente do fio ao corte será:

a) 2F                          b) 4F                                  c) F/4                                 d) F/2

67-(ENEM-MEC-012)

O mecanismo que permite articular uma porta (de um móvel ou de acesso) é a dobradiça. Normalmente, são necessárias

duas ou mais dobradiças para que a porta seja fixada no móvel ou no portal, permanecendo em equilíbrio e podendo ser articulada com facilidade.

No plano, o diagrama vetorial das forças que as dobradiças exercem na porta está representado em

 

 

68-(PUC-RJ-013)

Deseja-se construir um móbile simples, com fios de sustentação, hastes e pesinhos de chumbo. Os fios e as hastes têm peso desprezível. A configuração está demonstrada na figura abaixo.

O pesinho de chumbo quadrado tem massa 30 g, e os pesinhos triangulares têm massa 10 g.

Para que a haste maior possa ficar horizontal, qual deve  ser a distância horizontal x, em centímetros?

(A) 45                      (B) 15                   (C) 20                            (D) 10                     (E) 30

 

69-(ESPCEX-013)

Uma barra homogênea de peso igual a 50 N está em repouso na horizontal. Ela está apoiada em seus extremos nos pontos A e B, que estão distanciados de 2 m. Uma esfera Q de peso 80 N é colocada sobre a barra, a uma distância de 40 cm do ponto A, conforme representado no desenho abaixo:

A intensidade da força de reação do apoio sobre a barra no ponto B é de

a)  32 N             b)  41 N               c)  75 N                 d)  82 N                 e)  130 N

 

70-(UERJ-RJ-013)

Um homem de massa igual a 80 kg está em repouso e em equilíbrio sobre uma prancha rígida de 2,0 m de

comprimento, cuja massa é muito menor que a do homem.

A prancha está posicionada horizontalmente sobre dois apoios, A e B, em suas extremidades, e o homem está a 0,2 m da extremidade apoiada em A.

A intensidade da força, em newtons, que a prancha exerce sobre o apoio A equivale a (adote g=10m/s2):

(A) 200                             (B) 360                                (C) 400                                     (D) 720 

71-(ESCOLA NAVAL-012-013)

A viga inclinada de 60o mostrada na figura repousa sobre dois apoios A e D. Nos pontos C e E, dois

blocos de massa 8,00kg estão pendurados por meio de um fio ideal. Uma força de F=30N traciona um fio ideal preso à viga no ponto B. Desprezando o peso da viga e o atrito no apoio D, a reação normal que o apoio D exerce na viga, em newtons, é igual a
a) 30,0                           b) 50,0                          c) 70,0                     d) 90,0                    e) 110

Estática – 2013 – 2014

RESOLUÇÕES

01- Equilíbrio na vertical --- NA + NB = P.

Equilíbrio de rotação --- a soma dos momentos de cada força em relação ao polo (colocado em A)

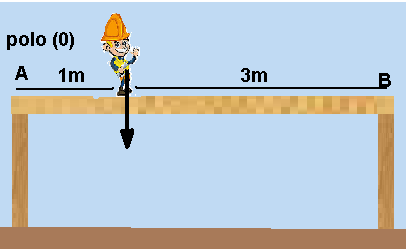
deve ser nula.

MNA=NA.0=0 --- MP= + P.1= p --- MNB= - NB.3= - 3NB --- 0 + P – 3NB = 0 --- NB = P/3 (I).

NA + NB = 3 --- NA + P/3 = P --- NA=P – P/3= (3P – P)/3 NA=2.(P/3) (II).

Comparando (I) com (II) --- NA = 2 NB.

R- B

02- A componente do peso (Pp) paralela ao plano inclinado, responsável pela descida do bloco, é fornecida por Pp=PsenӨ=m.g.senӨ=2,8,10,0,8 --- Pp=22,4N --- intensidade da força de atrito estático máxima (iminência de movimento) é dada por Fat=μN=μPcosӨ=μmgcosӨ --- Fat=0,5x2,8x10x0,6 --- Fat=8,4N ---

a intensidade da força elástica (Fe) é fornecida por Fe=K.x, onde x é de quanto a mola está distendida ---

Fe=350.x --- essas forças estão colocadas na figura abaixo --- como, pelo enunciado, o sistema se

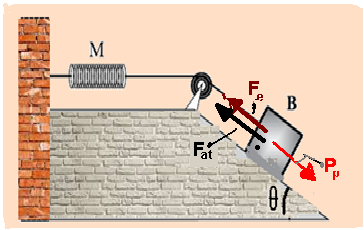
encontra em equilíbrio, a força resultante sobre o bloco é nula (FR=0) e, assim Pp = Fel + Fat --- 22,4 = 350 + 8,4 --- 350.x = 14 --- x=14/350 --- x=0,04m=4,0cm --- R- E

03- Teoria: Plano inclinado com atrito 

As forças que agem sobre um corpo apoiado sobre um plano inclinado são seu peso, vertical e para baixo e a força normal , perpendicular à superfície de contato entre o bloco e o plano.

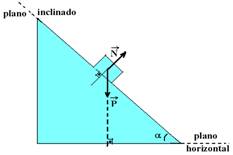
α é o ângulo de inclinação do plano. Como  e  não tem a mesma direção, vamos decompor o peso  em duas parcelas:

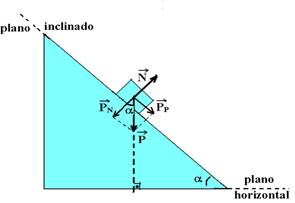
  parcela do peso paralela à superfície do plano inclinado (responsável pela tentativa de descida do bloco).

 parcela do peso perpendicular à superfície do plano inclinado (força que comprime o bloco contra o plano)

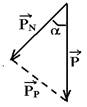
sen α =cateto oposto/hipotenusa  ---  sen α =PP/P  ---  PP=P.senα

cos α =cateto adjacente/hipotenusa  ---  cos α =PN/P  ---  PN=P.cosα

 

As duas forças acima substituem o peso e podemos tirá-lo:

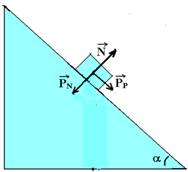
A componente normal do peso  anula a reação normal do apoio , assim temos:

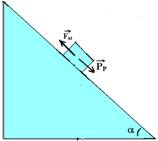
A força de atrito é sempre contrária ao movimento ou à sua tendência e é fornecida por Fat=μN  ---  PN=N  ---  Fat=μPN  --- Fat=μPcosa  ---  Fat=μmgcosα

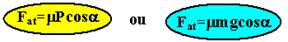
Se o bloco estiver em equilíbrio (estático ou dinâmico), a força resultante sobre ele seria nula e, nesse caso, PP=Fat .

Para se determinar o coeficiente de atrito estático (Fate) de um corpo, que é o valor máximo do coeficiente de atrito, devemos colocar esse corpo sobre um plano inclinado e ir aumentando o ângulo até que ele esteja na iminência de movimento e medir esse ângulo.

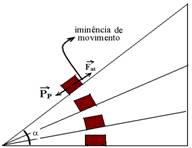
Na iminência de movimento PP=Fate  ---  Psenα=μePcosα  ---  μe=sena/cosα  ---  μe=tgα

N0 caso do exercício --- μe=tgα=tg30o = √3/3

R- D

04- Veja a figura abaixo onde foi calculada a soma vetorial pela regra do paralelogramo --- aplicando

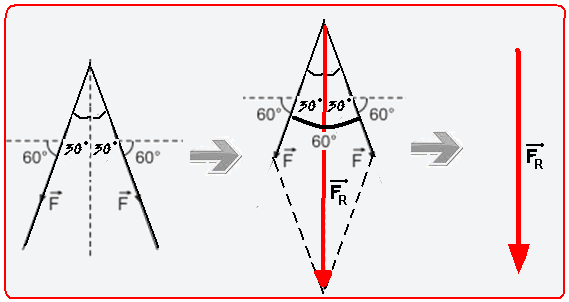
a lei dos cossenos --- FR2 = F2 + F2 + 2.F.F.cos60o=2F2 + 2F2.(1/2) --- FR=√(3F2) --- FR=√(3) .F

R- E

05- Na primeira figura estão colocadas as forças e, considerando a prateleira de densidade homogênea o peso e todas as outras forças estão aplicadas no centro (meio) da prateleira e essas forças são:

Peso  --- vertical, para baixo e de intensidade P=mg=2.10 --- P=20N

Tensão (tração)  no cabo aplicada na prateleira pela parede

Normal  --- aplicada pela parede na prateira (horizontal e para a direita)

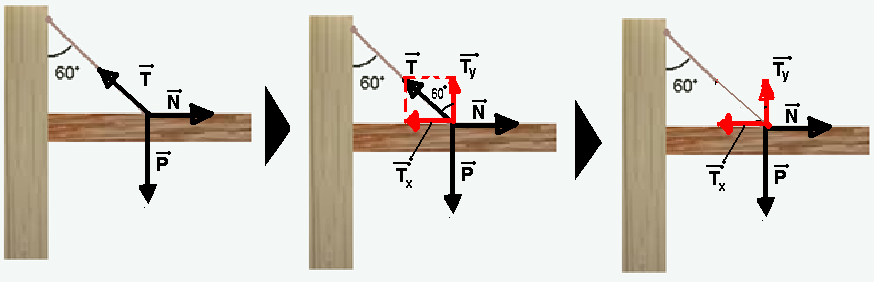
Na segunda figura a tração  foi decomposta em duas parcelas de intensidades Ty=Tcos60o=0,5T e Tx=Tsen60o=(√3/2)T.

Na terceira figura, como o sistema está em equilíbrio, na vertical, Ty=P --- 0,5T=20 --- T=40N.

R- D

Obs: Se fosse pedido a reação normal  aplicada pela parede na prateira você teria que na horizontal também existe equilíbrio e N=Fy=(√3/2)T=(√3/2).40 --- N=20√3N

06- Peso de cada esfera --- P1=m1g=0,3.10 --- P1=3N --- P2=m2g=0,2.10 --- P2=2N --- P3=m3g=0,1.10 --- P3=1N

Observe na figura todas as forças que agem sobre cada esfera e, como cada uma está em equilíbrio a força resultante sobre cada uma será nula, então você terá:

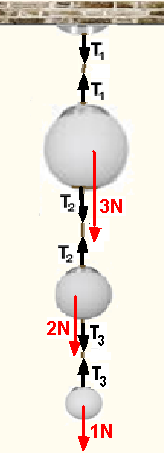
Esfera 3 --- T3=1N --- esfera 2 --- T3 + 2 = T2 --- 1 + 2=T2 --- T2=3N --- esfera 1 --- T1 = T2 + 3 ---

T1=3 + 3 --- T1=6N

R- A

07- Se o peso da criança (II) é duas vezes maior que o da criança (I), a criança (II), para que haja equilíbrio, deve estar a uma distância duas vezes menor que a criança (I) do apoio.

R- C

08- Veja teoria a seguir:

Se você pendurar um quadro na parede por meio de dois fios, quanto menor for o ângulo formado com o teto, ou o suporte, maior será a força de tração (tensão) no fio.

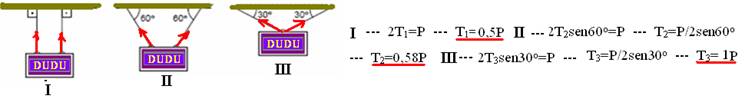
R- A

09-Lei de Hooke --- Fe=kx --- k=60N/m e no dia de menor rendimento x=0,8m --- Fe=60.0,8=48N.

R- E

10-

O1. Correta --- possui maior área de contato com o solo oferecendo mais estabilidade para caminhar.

02. Correta --- o salto alto desloca o peso e consequentemente o centro de gravidade. Veja figura

abaixo.

04. Falsa --- veja 02.

08. Correta --- com salto o peso é deslocado para a frente e sem salto, num plano inclinado o peso

também é deslocado para a frente.

16. Falsa --- pressão=força (no caso, o peso)/área de contato com o solo) --- P=P/S --- observe que a pressão P é inversamente proporcional à área de contato --- com o sapato B, S é menor, e a pressão sobre o solo é maior.

Soma (01 + 02 + 08)= 11

11- Como os blocos se movem com velocidade constante, estão em MRU e a intensidade da força resultante sobre cada um deles é nula.

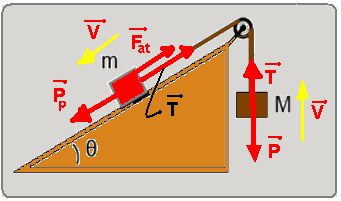
Bloco de massa M --- T=P -- T=Mg (I)

Bloco de massa m --- Pp = T + Fat --- mgsenθ = T + μcmgcosθ --- T=mgsenθ - μcmgcosθ (II)

(I) = (II) --- Mg = mgsenθ - μcmgcosθ --- M= msenθ - μcmcosθ

R-B

12- Observe as figuras abaixo onde as forças são:

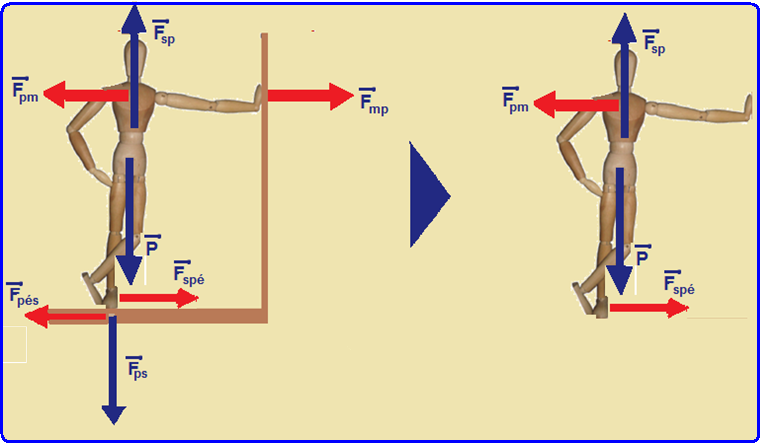
 – força que a mão aplica aplica na parede e  – força com que a parede reage na mão e consequentemente na pessoa.

 – peso da pessoa cuja reação está no centro da Terra.

 – força que a pessoa aplica no solo e  - força com que o solo reage sobre a pessoa (essa força é denominada de força normal )

 – força com que o pé empurra o solo e  força com que o solo reage sobre o pé (essas forças são as força de atrito trocadas entre o pé e o solo).

Na figura da direita estão colocadas apenas as forças que agem sobre o indivíduo e que se anulam na vertical e na horizontal, pois o indivíduo encontra-se em repouso (força resultante nula).

Estática de um ponto material

 

38- Determinando  o valor da constante elástica k da mola pela figura 1  ---  quando x=4,0cm=4.10-2m, F=20N  ---  Fe=kx  ---  20=k.4.10-2  ---  k=5.102 N/m  ---  força aplicada pela mola quando o sistema está em equilíbrio e a mola deformada de x=6,4cm=6,4.10-2m  ---  F=kx=5.102.6,4.10-2=32N  ---  observe a seqüência das figuras abaixo onde

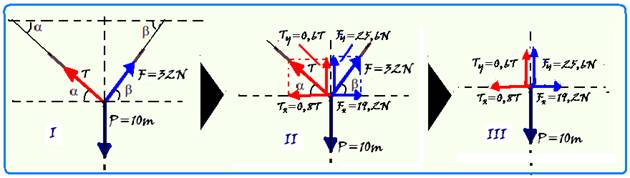
foram colocadas todas as forças no ponto de interseção dos fios (I)  ---  em (II) foram decompostas as forças inclinadas  ---  Tx=Tcosα=0,8T  ---  Ty=Tsenα=0,6T  ---  Fx=Fcosβ=32.0,6=19,2N  ---  Fy=Fsenβ=32.0,8=25,6N  ---  em (III) estão colocadas apenas as forças que agem nas direções horizontal e vertical  ---  estando o sistema em equilíbrio essas forças se anulam em cada direção  ---  na horizontal  ---  0,8T=19,2  ---  T=24N  ---  na vertical  ---  0,6T + 25,6 = 10m  --- 

0,6.24 + 25,6 = 10m  ---  14,4 + 25,6 = 10m  ---  m=40/10=4kg  ---  R- C.

 

Corpo extenso – centro de massa e tipos de equilíbrio

 

 21- Com duas pessoas no carro a deformação do sistema de molas é x=2cm=2.10-2m e  a força que deformadora é o peso das duas pessoas  ---  P=2mg=2.60.10=12.102N  ---  esse peso corresponde à força elástica  ---  FeP=kx  --- 

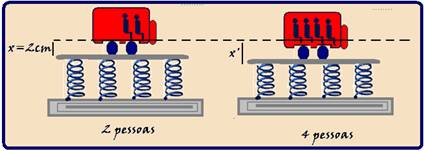
12.102=k.2.10-2  ---  k=6.104N/m (constante elástica do sistema de molas que é constante independente da força deformadora)  ---  com  4 pessoas a deformação é x’ e o peso é P’=4mg=4.70.10=28.102N  ---   P’=kx’  ---  28.102=6.104x’  ---  x’=4,66.10-2m=4,66cm  ---  R- D.

 

22- Leia a teoria abaixo:

Associação de polias ou roldanas

a) Uma polia fixa e outra móvel

A polia de cima, fixa, não interfere no valor da força aplicada pela pessoa, serve apenas para sua comodidade, levantando o bloco ao puxar o fio para baixo.

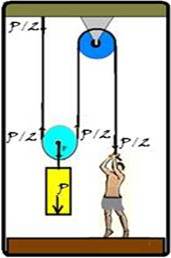
A polia de baixo, móvel, reduz à metade a força aplicada pela pessoa (metade do peso do bloco). Lembre-se de que, se a pessoa puxar o fio de uma distancia d, o bloco subirá d/2.

 b) Uma polia fixa e várias polias móveis (talha exponencial)

Na figura abaixo, onde temos 3 polias móveis e uma fixa, o bloco de peso P é mantido em equilíbrio pela pessoa. Observe que

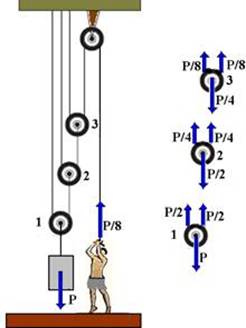
a força que a pessoas aplica tem intensidade 8 vezes menor que o peso do bloco e que cada polia móvel reduz pela metade a força aplicada nela. Esse tipo de associação é chamado de talha exponencial e a força exercida pela pessoa, se tivermos n polias móveis, corresponde a 2n do peso do bloco com n=1,2,3... .

Assim, se o bloco da figura acima tiver peso de 80N, a pessoa deve fazer uma força de apenas 10N para mantê-lo em equilíbrio, mas, se ele puxar a corda de 1m, o bloco subirá apenas 0,125m (8 vezes menor).

Observe na figura do exercício que existem duas polias móveis  ---  F=P/22=P/4  ---  R- D.

 

Estática de um corpo extenso – máquinas simples

 

66- Trata-se de uma alavanca interfixa – o apoio está entre a força potente e a força resistente  ---  observe a alavanca

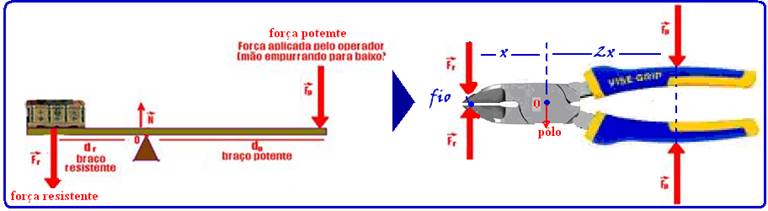
 interfixa acima  ---  havendo equilíbrio, a soma dos momentos das forças em relação ao apoio deve ser nula  ---  Fo.2x=Fr.x­  ­---  Fr/Fo=2x/x­  ---  Fr=2Fp  ---  observe que quanto maior for o braço potente, maior será a vantagem mecânica, ou seja, maior será a força transmitida  ---  R- A.

67- O exercício quer o diagrama das forças que as dobradiças aplicam na porta:

Na horizontal: ao girar, a porta traciona  (puxa) para a direita a dobradiça superior e esta, pelo princípio da ação e reação reage na porta com uma força de mesma intensidade, mesma direção, mas sentido contrário, tracionando-a (puxando-a) para a esquerda com uma força   ---  analogamente ao girar, a porta comprime  (empurra) para a esquerda a dobradiça superior e esta, pelo princípio da ação e reação reage na porta com uma força de mesma intensidade, mesma direção mas sentido contrário, comprimindo-a (empurrando-a) para a direita com uma força . 

Na vertical, devido ao seu peso, a porta aplica em cada dobradiça uma força puxando-as para baixo e, elas reagem sobre a porta com forças  e , verticais e para cima.

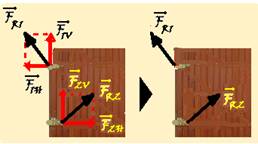
A soma vetorial dessas forças, fornece as forças resultantes  e que cada dobradiça exerce sobre a porta (figura)  R- D.

68- Peso do chumbo quadrado  ---  P=m.g=0,030x10=0,3N  ---  peso dos triângulos de chumbo  ---  P=m.9=0,010x10=0,1N  ---  colocando as forças na haste maior e considerando o ponto O como pólo (figura)  ---  equilíbrio de rotação  ---  a soma dos momentos de cada força em relação ao pólo O deve ser nula  ---  M0,3N= - F,d = -

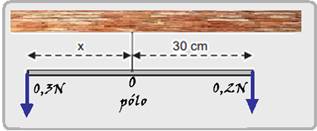
0,3.x  ---  M0,2N = + F.d=+0,2.30 =6N.cm  ---  M0,3N + M0,2N=0  ---  - 0,3x + 6=0  ---  x=6/0,3  ---  x=20cm  ---    R- C.

69- Se você chamar as reações em A e B de NA e NB, a reação de contato da esfera Q na barra de PQ, e considerar o 

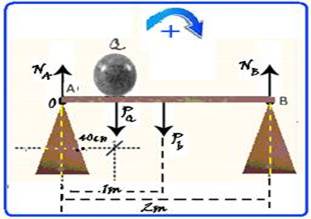
peso da barra (Pb) atuando no centro geométrico da mesma, aplicando a condições de equilíbrio de rotação: somatório de momentos em relação ao ponto A (pólo) igual a zero, você terá  ---   MNA=NA.d=0  ---  MpQ=+PQ.d=+80.0,4=32N.m  ---  MPb=+Pb.d  --- MPb=50.1=50N.m  ---  MNB=- NB.d=-NB.2  --- 0 + 32 + 50 - 2NB = 0  ---  NB=82/2  ---  NB=41N  ---  R- B.  

70- Peso do homem  ---  PH=m.g=80.10=800N  ---  cálculo do momento de cada força colocando o polo (eixo

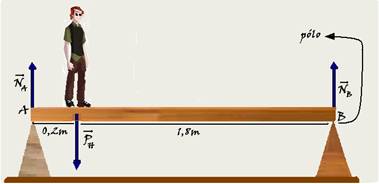
de rotação) em B  ---  NNA=NA.dAB=2NA  ---  MPH= - PH.dHB= - 800.1,8= - 1440N.m  ---  MNB=NB.d=NB.0=0  ---  equilíbrio de rotação  ---  a soma dos momentos de cada força em relação ao pólo é nula  ---  2NA – 1440 + 0 = 0  ---  NA=1440/2  ---  NA=720 N  ---  R- D.

71- Projetando as forças e as distâncias nas direções perpendiculares à viga  ---  em (I), forças  ---  cos60o=F/80  ---  1/2 =

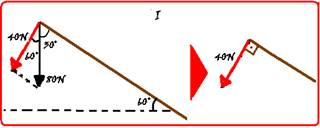
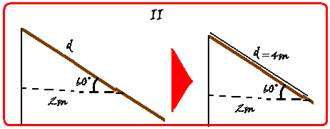
F/80  ---  2F=80  ---  F=40N  ---  em (II), distâncias  ---  cos60o=2/d  ---  1/2 = 2/d  ---  d=4m  ---  veja na figura (III) como fica o esquema pronto para você calcular o momento de cada força com o pólo em A  ---  MPE= - 40.16= - 640

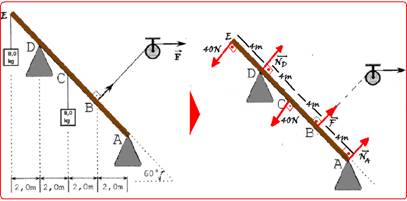
 N.m  ---  MNB= + NDx12  ---  MPC= - 40.8= - 320N  ---  MF= + 30.4  ---  MNA=NA.0=0  ---  a soma dos momentos de cada força deve ser nula  ---  -640 +12ND – 320 +120 + 0=0  ---  12ND=840  ---  ND=70N  ---  R- C.