Vestibulares Recentes

Eletrodinâmica - 2017 – 2016 - 2015

Corrente elétrica

01-UNICAMP-SP-017)

Tecnologias móveis como celulares e tablets têm tempo de autonomia limitado pela carga armazenada em suas baterias.

O gráfico abaixo apresenta, de forma simplificada, a corrente de recarga de uma célula de bateria de

íon de lítio, em função do tempo.

Considere uma célula de bateria inicialmente descarregada e que é carregada seguindo essa curva de corrente.

A sua carga no final da recarga é de

02-(FMJ-SP-017)

O gráfico representa, de forma simplificada, a intensidade da corrente elétrica, em função do tempo, resultante do fluxo de íons de sódio através da membrana de um axônio gigante de lula, obtido em um experimento.

(www.sisne.org. Adaptado.)

Considerando o valor da carga elétrica de cada íon igual a 1,6.10-19 C, a quantidade de íons de sódio que atravessaram a membrana entre os instantes 0 s e 4,0.10-3 s foi de

(A) 2,5 × 10³.

(B) 5,0 × 10³.

(C) 7,5 × 10⁴.

(D) 2,5 × 10⁵.

(E) 5,0 × 10⁵.

03-(FUVEST-SP-017)

a) zero e zero.

b) zero e – 5,0.10-12 C.

c) – 2,5.10-12 C e – 2,5.10-12 C.

d) – 2,5.10-12 C e + 2,5.10-12 C.

e) + 5,0.10-12 C e zero.

04-(UEL-PR-015)

Desde a elaboração dos modelos atômicos por Dalton, Thomson, Rutherford e Bohr, cientistas como Murray Gell-Man (EUA) e Georg Zweig (Alemanha) têm desvendado os segredos subatômicos

da matéria.

Assinale a alternativa que apresenta, corretamente, as subpartículas que constituem as partículas atômicas conforme os modelos de Gell-Man e Georg Zweig.

Resistores – Primeira lei de Ohm – Potência elétrica em um resistor

05-(UERJ-RJ-016)

06-(Faculdade Israelita de Ciências da Saúde Albert Einstein – SP – 016)

A descoberta se inscreve no “espírito Alfred Nobel” de fazer invenções que geram grandes benefícios à humanidade, afirmou o comitê do Nobel no instituto Karolinska, em Estocolmo, na Suécia.

No entanto, para obter a luz branca, era necessário ter a componente azul. A importância vem do fato que era impossível obter lâmpadas com luz branca sem o uso do azul.

Para fazer qualquer coisa, você precisa de três cores primárias (vermelho, verde e azul).

Vermelho era mais fácil por causa do arsenieto de gálio que já estava disponível, mas ninguémsabia como fazer o azul, disse Nakamura em entrevista em 2009.

Empolgado com a divulgação da notícia do prêmio Nobel de Física de 2014, o SrPiril Lampo resolve desembolsar R$ 60,00 e substituir a lâmpada incandescente de sua casa, cuja potência é de 100 W e cujo custo de aquisição foi de R$ 5,00, por uma lâmpada de tecnologia LED, de 9 W, que tem o mesmo fluxo luminoso da lâmpada a ser substituída.

07-(Medicina – USCS-SP-016)

A potência nominal de consumo de um aparelho de diagnóstico por imagem de certo hospital é de 2500 W.

Sabe-se que ele opera com rendimento de 90%, trabalhando durante 5 min de cada vez e 12 vezes a cada dia, durante 20 dias úteis por mês.

Se o kWh custa R$ 0,90, a despesa mensal de energia elétrica devido ao uso desse aparelho é de

08-(MACKENZIE-SP-2017)

Muitos aparelhos elétricos são acionados por controle remoto.

O manual do usuário desses aparelhos informa que para mantê-lo em estado de prontidão (stand-by), isto é, acioná-lo por controle remoto, é necessária uma potência de 20 W.

A energia consumida por esse aparelho em um dia é, aproximadamente,

a) 1,3.10⁶ J

b) 1,7.10⁶ J

c) 1,9.10⁶ J

d) 2,1.10⁶ J

e) 2,3.10⁶ J

09-(FGV-SP-017)

A usina hidrelétrica de Itaipu, empresa binacional, localizada na fronteira do Brasil com o Paraguai, tem uma potência instalada de 14 000 MW gerada por 20 unidades de 700 MW cada.

Essa potência é distribuída por 12 linhas de transmissão que operam sob tensão de 500 kV cada.

A energia produzida é levada até as cidades por cabos condutores de corrente elétrica, sustentados por altas torres que podem ser vistas quando se viaja pelas estradas.

A intensidade da corrente elétrica através desses cabos é, em kA, mais próxima de

10-(FUVEST-SP-017)

Na bateria de um telefone celular e em seu carregador, estão registradas as seguintes especificações:

Com a bateria sendo carregada em uma rede de 127 V, a potência máxima que o carregador pode fornecer e a carga máxima que pode ser armazenada na bateria são, respectivamente, próximas de

11-(PUC-MG-015)

Um chuveiro elétrico foi projetado para funcionar corretamente quando ligado em 220 V

Se ele for ligado a uma rede elétrica de 110 V, é CORRETO afirmar que:

a) sua resistência elétrica irá reduzir pela metade fazendo com que ele aqueça menos a água.

b) a resistência do chuveiro irá se reduzir pela metade e sua potência não será modificada.

c) a resistência do chuveiro irá dobrar de valor, já que a voltagem de 110 V é a metade da voltagem de 220 V para a qual ele foi projetado.

d) sua resistência elétrica não muda de valor e sua potência ficará quatro vezes menor.

12-(UEMG-MG-015)

“Nos anúncios da tevê

Somos lindos, sorridentes,

Cabelos longos e radiosos…”

(Sísifo desce a montanha)

Affonso chegou em casa, acendeu uma lâmpada, cuja potência é de 60 W,e, em seguida, ligou a

televisão, cuja potência é de 90 W. A lâmpada e a televisão ficaram ligadas por uma (1) hora.

Com relação ao consumo de energia elétrica e à tensão elétrica nesse intervalo de tempo, é CORRETO afirmar que

A) o consumo da lâmpada é maior, mas a tensão nos dois aparelhos é a mesma.

B) tanto o consumo quanto a tensão na televisão são maiores.

C) tanto o consumo quanto a tensão na lâmpada são maiores.

D) o consumo na televisão é maior, mas a tensão nos dois aparelhos é a mesma.

Segunda lei de Ohm (Resistividade)

13-(CEDERJ-RJ-015)

As extremidades de um pedaço de fio de comprimento L são conectadas aos terminais de uma bateria ideal. Verifica-se que a corrente elétrica a qual percorre o fio é, nesse caso, i₁. O pedaço

original é substituído por outro, do mesmo fio, porém com o dobro do comprimento. Após a substituição, verifica-se que, sob a mesma voltagem, a corrente que o percorre é i₂. Assinale

a alternativa que descreve a relação entre as correntes i₁ e i₂.

14-(UFRGS-RS-015)

No circuito esquematizado abaixo, R₁ e R₂ são resistores com a mesma resistividade ρ.

R₁ tem comprimento 2L e seção transversal A, e R₂ tem comprimento L e seção transversal 2A.

Nessa situação, a corrente elétrica que percorre o circuito é

(A) 2AV/(5 ρ L).

(B) 2AV/(3 ρ L).

(C) AV/( ρ L).

(D) 3AV/(2ρ L).

(E) 5AV/(2 ρ L).

Resistor equivalente nas associações série, paralelo e mista

15-(UNIFESP-SP-016)

Um fio metálico homogêneo tem comprimento L e área de secção transversal constante.

Com base no circuito representado na figura 2, calcule:

a) a resistência equivalente, em Ω.

b) a potência total dissipada, em W.

16-(ENEM-MEC-016)

Por apresentar significativa resistividade elétrica, o grafite pode ser utilizado para simular resistores elétricos em circuitos desenhados no papel, com o uso de lápis e lapiseiras.

Dependendo da espessura e do comprimento das linhas desenhadas, é possível determinar a resistência elétrica de cada traçado produzido.

No esquema foram utilizados três tipos de lápis diferentes (2H, HB e 6B)para efetuar três traçados

distintos.

Munida dessas informações, um estudante pegou uma folha de papel e fez o desenho de um sorvete de casquinha utilizando-se desses traçados.

Os valores encontrados nesse experimento, para as resistências elétricas (R), medidas com o auxílio de um ohmímetro ligado nas extremidades das resistências, são mostrados na figura.

Verificou-se que os resistores obedeciam a Lei de Ohm.

Na sequência, conectou o ohmímetro nos terminais A e B do desenho e, em seguida, conectou-o nos terminais B e C, anotando as leituras R_AB e R_BC, respectivamente.

Ao estabelecer a razão R_AB / R_BC qual resultado o estudante obteve?

17-(Faculdade Israelita de Ciências da Saúde Albert Einstein – SP – 016)

Por decisão da Assembleia Geral da Unesco, realizada em dezembro de 2013, a luz e as tecnologias nela baseadas serão celebradas ao longo de2015, que passará a ser referido simplesmente como Ano Internacional da Luz. O trabalho de Albert Einstein sobre o efeito fotoelétrico (1905) foi fundamental para a ciência e a tecnologia desenvolvidas a partir de 1950, incluindo a fotônica, tida como a tecnologia do século 21.

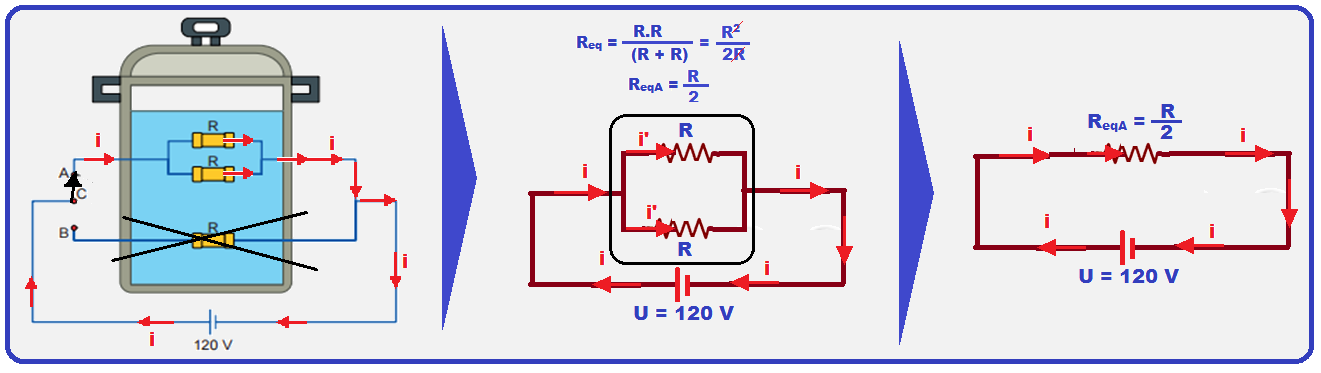
Com o intuito de homenagear o célebre cientista, um eletricista elabora um inusitado aquecedor conforme mostra a figura abaixo.

Esse aquecedor será submetido a uma tensão elétrica de 120V, entre seus terminais A e B, e será utilizado, totalmente imerso, para aquecer a água que enche completamente um aquário de dimensões 30cm x 50cmx 80cm.

Desprezando qualquer tipo de perda, supondo constante a potência do aquecedor e considerando que a distribuição de calor para a água se dê de maneira uniforme, determine após quantas horas de funcionamento, aproximadamente, ele será capaz de provocar uma variação de temperatura de 36°F na água desse aquário

Adote:
Pressão atmosférica = 1 atm

Densidade da água = 1 g/cm3

Calor específico da água = 1g.cm^-3 .^oC^-1

Resistência do resistor = 1 Ω

18-(UNIFESO-RJ-015)

No circuito esquematizado na figura, o gerador tem uma resistência interna desprezível, os

quatro resistores têm a mesma resistência R e o amperímetro (ideal) indica 5 A. Se a chave C estivesse fechada, o amperímetro estaria indicando

Características das associação série e associação paralela

19-(ENEM-MEC-015)

20-(UNICAMP-SP-016)

Muitos dispositivos de aquecimento usados em nosso cotidiano usamresistores elétricos como fonte de calor.

Um exemplo é o chuveiro elétrico, em que é possível escolher entre diferentes opções de potências

usadas no aquecimento da água, por exemplo, morno (M), quente (Q) e muito quente (MQ).

Considere um chuveiro que usa a associação de três resistores, iguais entre si, para oferecer

essas três opções de temperatura.

A escolha é feita por uma chave que liga a rede elétrica entre o ponto indicado pela letra N e um outro ponto indicado por M, Q ou MQ, de acordo com a opção de temperatura desejada. O esquema que representa corretamente o circuito equivalente do chuveiro é

21-(FAMERP-SP-017)

Uma lâmpada incandescente, de especificações técnicas 40 V – 25 W estabelecidas pelo fabricante queima se for submetida a tensões acima da especificada.

Conforme a figura, essa lâmpada será instalada em um soquete ligado em série com o resistor R e com outros resistores que serão conectados entre os pontos A e B, formando um circuito que Considerando que os fios e as conexões utilizados nesse circuito tenham resistências desprezíveis:

a) determine a quantidade de carga elétrica, em coulombs, que atravessará a lâmpada se ela permanecer acesa, de acordo com suas especificações, durante 20 minutos.

b) indique o número máximo de resistores iguais, de 320 Ω cada um, que podem ser ligados em paralelo entre A e B, sem que a lâmpada queime.

22-(ENEM-MEC-016)

23-(UERJ-RJ-015)

No esquema abaixo, está representada a instalação de uma torneira elétrica.

De acordo com as informações do fabricante, a resistência interna r da torneira corresponde a 200 Ω. A corrente que deve percorrer o circuito da torneira é de 127 mA.

Determine o valor da resistência R que deve ser ligada em série à torneira para que esta possa

funcionar de acordo com a especificação do fabricante, quando ligada a uma tomada de 127 V.

Calcule, em watts, a potência dissipada por essa torneira.

Cálculo de correntes, tensões e potências em associações mistas

24-(EsPCEx- AMAN – SP- RJ – 2016/17)

Um aluno irá montar um circuito elétrico com duas lâmpadas incandescentes, L₁ e L₂, de resistências elétricas constantes, que têm as seguintes especificações técnicas fornecidas pelo fabricante, impressas nas lâmpadas:

Além das duas lâmpadas, ele também usará um gerador ideal de tensão elétrica contínua de 60 V, um resistor ôhmico de 30 Ω e fios condutores elétricos ideais.

Utilizando todo material acima descrito, a configuração da montagem do circuito elétrico, para que as lâmpadas funcionem corretamente com os valores especificados pelo fabricante das lâmpadas será:

25-(Medicina – USCS-SP-017)

26-(UNIFESP-SP-017)

A figura representa o esquema de uma panela elétrica, na qual existe uma chave seletora C que pode ser ligada em dois pontos, A e B, que definem qual circuito será utilizado para dissipar, por efeito joule, a energia térmica necessária para o funcionamento da panela.

Uma pessoa deseja utilizar essa panela para elevar a temperatura de quatro litros de água de 20 ºC para 80 ºC.

Considerando que o calor específico da água seja 4.10³ J/(kg⋅ºC), que a densidade da água seja 1 kg/L, que toda a energia térmica dissipada pelos resistores seja absorvida pela água e, ainda, que a água não perca calor durante o processo, calcule:

Geradores, receptores e associação de geradores e de receptores

27-(EsPCEx-AMAN-SP-RJ)

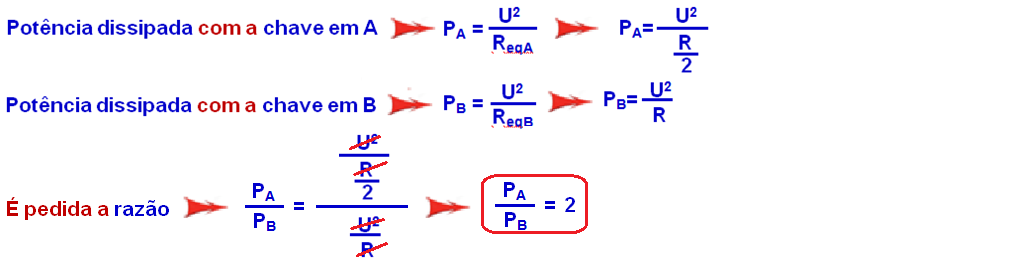
Em um circuito elétrico, representado no desenho abaixo, o valor da força eletromotriz (fem)

do gerador ideal é E=1,5 V, e os valores das resistências dos resistores ôhmicos são

R1=R4=0,3 Ω , R2=R3=0,6 Ω e R5=0,15 Ω . As leituras no voltímetro V e no amperímetro A, ambos

ideais, são, respectivamente,

[A] 0,375 V e 2,50 A

[B] 0,750 V e 1,00 A

[C] 0,375 V e 1,25 A

[D] 0,750 V e 1,25 A

[E] 0,750 V e 2,50 A

28-(EsPCEx- AMAN – SP- RJ – 2016/17)

O desenho ao lado representa um circuito elétrico composto por resistores ôhmicos, um gerador ideal e um receptor ideal. A potência elétrica dissipada no resistor de 4 Ω do circuito é:

a) 0,16 W.

b) 0,20 W.

c) 0,40 W.

d) 0,72 W.

e) 0,80 W.

29-(PUC-RJ-016)

Um estudante arma um circuito elétrico simples a partir de uma bateria de 15 V e três resistores idênticos de 10 kΩ. Com um amperímetro, ele mede uma corrente de 1,0 mA que passa em um dos resistores. Qual é a resistência equivalente do circuito, em kΩ?

(A) 3,3

(B) 5,0

(C) 10

(D) 15

(E) 30

30-(UEM-PR-015)

Considere um circuito elétrico composto de dois ramos paralelos, A e B, que é alimentado por uma bateria de 10 V ligada em paralelo com o circuito.

O ramo A é constituído por três resistores ligados em série, enquanto o ramo B é constituído por

dois resistores ligados em paralelo. Considere que todos os resistores do circuito são

ôhmicos e possuem resistência elétrica de 10 Ω.

Com base nessas informações, assinale o que for correto.

01) Os resistores equivalentes nos dois ramos do circuito possuem, respectivamente, resistência elétrica de 30 Ω e de 5 Ω.

02) A corrente elétrica que flui no ramo A é de 2 A.

04) A potência dissipada no ramo B é de 20 W.

08) A potência dissipada e a corrente elétrica no ramo B são maiores que as observadas no ramo A.

16) A diferença de potencial entre os terminais do segundo resistor do ramo A é de aproximadamente 3,3 V

Geradores

31-(UFPR-PR-015)

A função principal de geradores elétricos é transformar em energia elétrica algum outro tipo de energia.

No caso de geradores elementares de corrente contínua, cujo circuito equivalente está mostrado abaixo, onde r é a resistência interna do gerador e ε sua força eletromotriz, o comportamento característico é descrito pela conhecida equação do gerador, que fornece a diferença de potencial ΔV em seus terminais A e B em função da corrente i fornecida por ele. Um dado gerador tem a curva característica mostrada no gráfico abaixo.

A partir do circuito e do gráfico apresentados, assinale aalternativa correta para a potência dissipada internamente na fonte quando esta fornece uma corrente de 2,0 mA.

Aparelhos de medição elétrica (amperímetros e voltímetros)

32-(COLÉGIO NAVAL-015)

Considere que um determinado estudante utilizando resistores disponíveis, no laboratório de sua escola, montou os circuitos mostrados abaixo:

Querendo fazer algumas medidas elétricas, usou um voltímetro (V) para medir a tensão e um amperímetro (A) para medir a intensidade da corrente elétrica.

Considerando todos os elementos envolvidos como sendo ideais, osvalores medidos pelo voltímetro (situação 1) e pelo amperímetro (situação 2) foram, respectivamente:

(A) 2V e 1,2A

(B) 4V e 1,2 A

C) 2V e 2,4 A

(D) 4V e 2,4A (

E) 6V e 1,2 A

33-(FUVEST-SP-016)

34-(FAMERP-SP-017)

A figura representa o esquema de ligação dos faróis de um automóvel à bateria do veículo.

O circuito é constituído por: duas lâmpadas de 12 V – 60 W cada uma; uma chave de acionamento e um fusível de proteção, ambos de resistências desprezíveis; e fios de ligação e conectores, também ideais.

Se os dois faróis estiverem acesos, das opções indicadas nas alternativas, aquela que corresponde à menor amperagem do fusível capaz de proteger esse circuito é

(A) 15 A.

(B) 12 A.

(C) 6 A.

(D) 4 A.

(E) 9 A.

35-(COLÉGIO NAVAL-015)

Considere que um determinado estudante utilizando resistores disponíveis, no laboratório de sua escola, montou os circuitos mostrados abaixo:

Querendo fazer algumas medidas elétricas, usou um voltímetro (V) para medir a tensão e um amperímetro (A) para medir a intensidade da corrente elétrica.

Considerando todos os elementos envolvidos como sendo ideais, os valores medidos pelo voltímetro (situação 1) e pelo amperímetro (situação 2) foram, respectivamente:

(A) 2V e 1,2A

(B) 4V e 1,2ª

C) 2V e 2,4A

(D) 4V e 2,4A

(E) 6V e 1,2A

Resolução Comentada

Eletrodinâmica - 2017 – 2016 – 2015.

01-

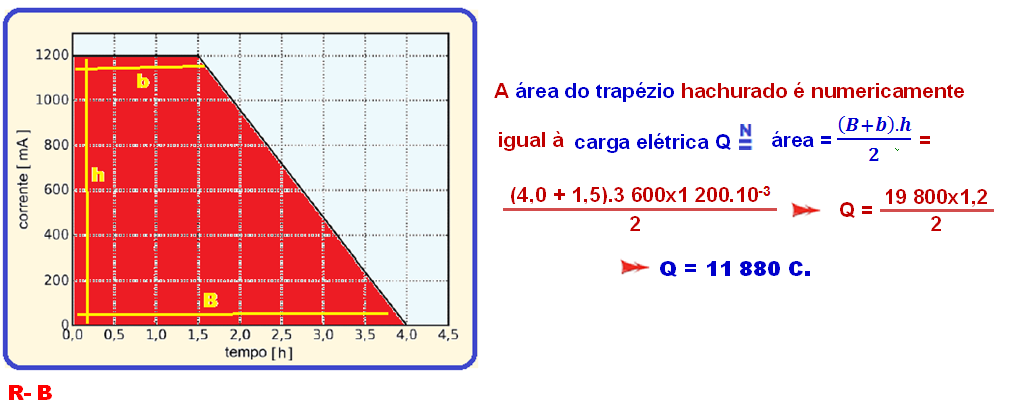
02-

Assim como no cálculo de ΔS em um gráfico V x Δt, nossa carga também pode ser calculada pela área do gráfico, pois como a variação da distância é a multiplicação entre tempo e velocidade, a carga é a multiplicação entre intensidade da corrente e o tempo, logo:

Não podemos esquecer dos coeficientes que multiplicam as unidades, na hora de substituir:

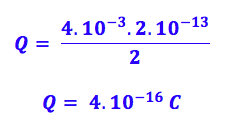
Agora que temos a carga, podemos fazer uma regra de três e achar quantidade de íons:

1 íon -> 1,6.10^-19 C

x íons -> 4.10^-16 C

Multiplicando em cruz:

Isolando o x:

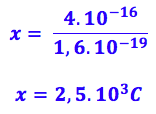
R – A

03-

Como, pelo enunciado, X estava eletrizada com carga de 5,0.10-12 C ela transferiu toda sua carga para Y, ficando X neutra (carga zero).

Acontece que todo corpo ligado à Terra fica totalmente descarregado transferindo integralmente toda sua carga (5,0.10^-12 C) para a Terra. Assim Y também ficará neutro com carga zero.

Portanto, no final desse processo, as cargas elétricas totais dos objetos X e Y serão, respectivamente, zero e zero.

R- A

04- Os físicos, Murray Gell-Mann e George Zweig desenvolveram, independentemente, um modelo para classificar as Partículas Elementares. Segundo esse modelo (hoje conhecido como Modelo dosQuarks), os hádrons (bárions, mésons e outras partículas subatômicas)formavam os quarks, que por sua vez eram componentes dos prótons e nêutrons.

R- A

05- Veja a expressão abaixo que relaciona potência elétrica (Po) com energia elétrica (W):

Usa-se também como unidade de medida o kWh onde a potência deve estar em kW = 1000W e o tempo em horas (h).

Lembrando que , o ano tem 365 dias e que são 10 painéis que funcionam durante 6 horas por dia, temos:

Por dia e por cada painel,

Por dia (10 painéis)

No ano, com 365 dias, temos, por fim

Como o exercício pede em kWh

06-

Diferença diária d = (0,21 – 0,0189) d = C$ 0,1911 descontando dos C$ 60,00 os 5,00 que ele pagou pela lâmpada incandescente, sobram C$ 55,00, que divididos pela diferença diária de C$0,1011 fornecem 55/0,1911= 287,8 ≈ 288 dias consecutivos.

R- B

07-

R- B

08-

Potência = = W = Po.∆t = 20x24hx3600s Po = 1 728 000 = 1,728.106 J.

R- B

09-

R- B

10- Para calcular a potência máxima de saída que o carregador pode fornecer você deve utilizar a tensão de saída U = 5 V e a corrente de saída i = 1,3 A, fornecidas nas especificações utilizando a expressão P = i.U = 1,3.5 = 6,5 W.

A carga máxima armazenada na bateria também é fornecida pelasespecificações da bateria Q = 1650 mAh que, transformado em coulomb (C) fornece Q = 1650.10-3..3600s Q = 5940 C.

R- D

11- Observe na expressão P=U2/R que, sendo a resistência elétrica R constante, a potência é diretamente proporcional ao quadrado da voltagem U. Assim, se ele for ligado a uma voltagem duas vezes menor (220 V para 110 V), a potência ficará 22 = 4 vezes menor.

R- D

12- P = W/∆t— lâmpada — 60 = Wl/3600 — Wl = 216 000 J

P = W/∆t— televisão — 90 = Wt/3600 — Wt = 324 000 J

A televisão consome mais energia elétrica, mas a tensão em cada aparelho é a mesma, pois estão associados em paralelo.

R- D

13- Veja abaixo a expressão matemática da segunda lei de Ohm:

A resistência elétrica R é diretamente proporcional ao comprimento l do fio e à resistividade ρ (característica do material que constitui o fio) e inversamente proporcional à área se seção reta transversal (S) “grossura do fio”.

Assim, se você dobrar o comprimento do fio estará dobrando o valor da resistência elétrica R do mesmo.

R₁ = R e R₂ = 2R

Corrente i₁ no fio de comprimento L submetido à voltagem U — R₁ = U/i₁ — i₁ = U/R. (I)

Corrente i₂ no fio de comprimento 2L submetido à voltagem U — R₂ = U/i₂— i₂ = U/2R. (II)

Comparando (I) com (II) — i₁ =2i₂.

R- A

14- Segunda lei de Ohm R = ρL/A.

Resistor 1 R₁ = ρ2L/A resistor 2 R₂ = ρL/2A.

Resistor equivalente Req = R₁ + R₂ = ρ2L/A + ρL/2A = 5ρL/2A.

Req = V/i i = V/Req = V/5ρL/2A i = 2AV/5ρL.

R- A

15-

a) a resistência equivalente, em Ω.

Observe a sequência abaixo para o cálculo da resistência equivalente Req no circuito da figura 2, onde os três resistores estão em paralelo:

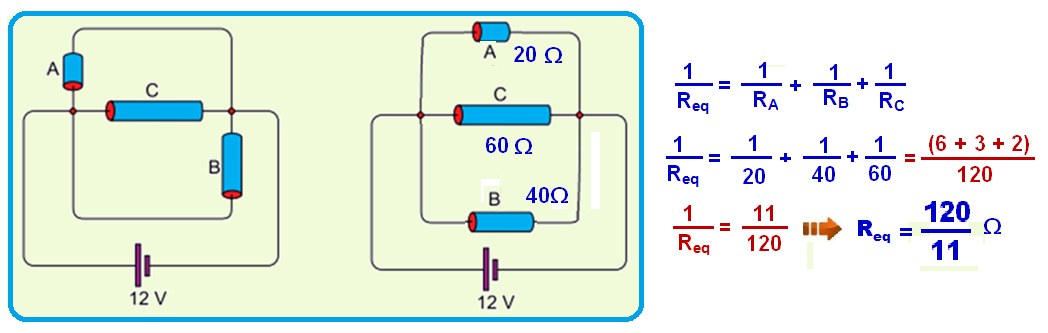
b) a potência total dissipada, em W.

Você pode calcular a potência total dissipada utilizando a resistência equivalente que está submetida à uma tensão de U = 12 V.

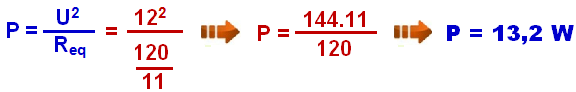
16-
Com o ohmímetro conectado entre A e B você deve calcular a resistência do resistor equivalente R_AB entre esses dois pontos.

Assim, o circuito ficará conforme a figura (1), onde os dois resistores de 10 kΩ estão em série podendo ser substituidos por um único resistor de(10 kΩ + 10 kΩ) = 20 kΩ.

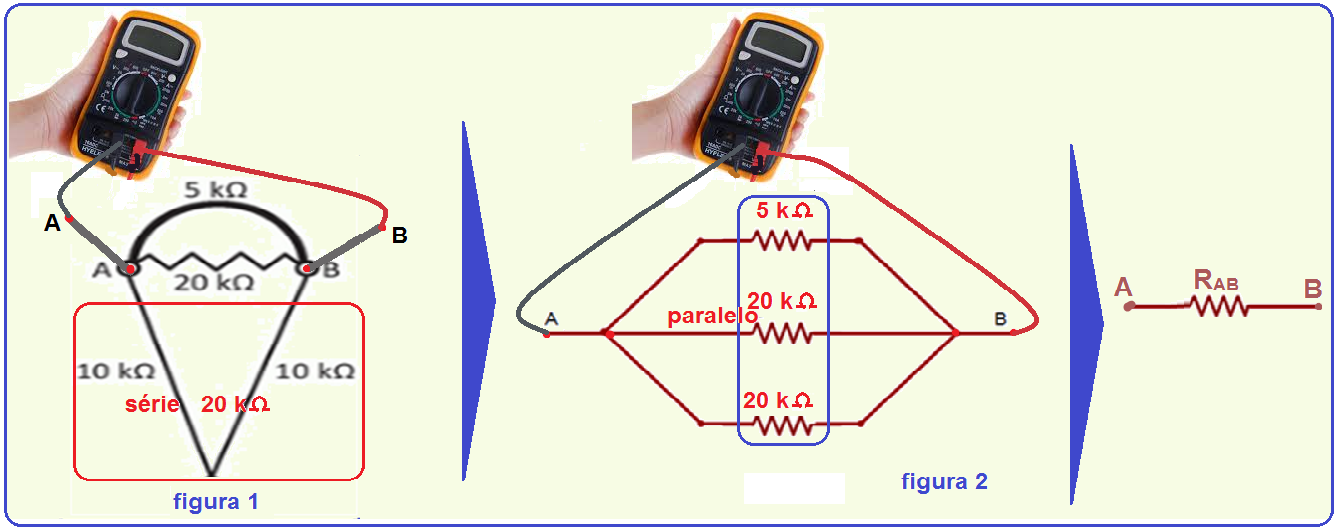
Com o ohmímetro conectado entre B e C você deve calcular a resistência do resistor equivalente R_BC entre esses dois pontos.

Observe na sequência abaixo o cálculo da resistência entre B e C, R_BC .

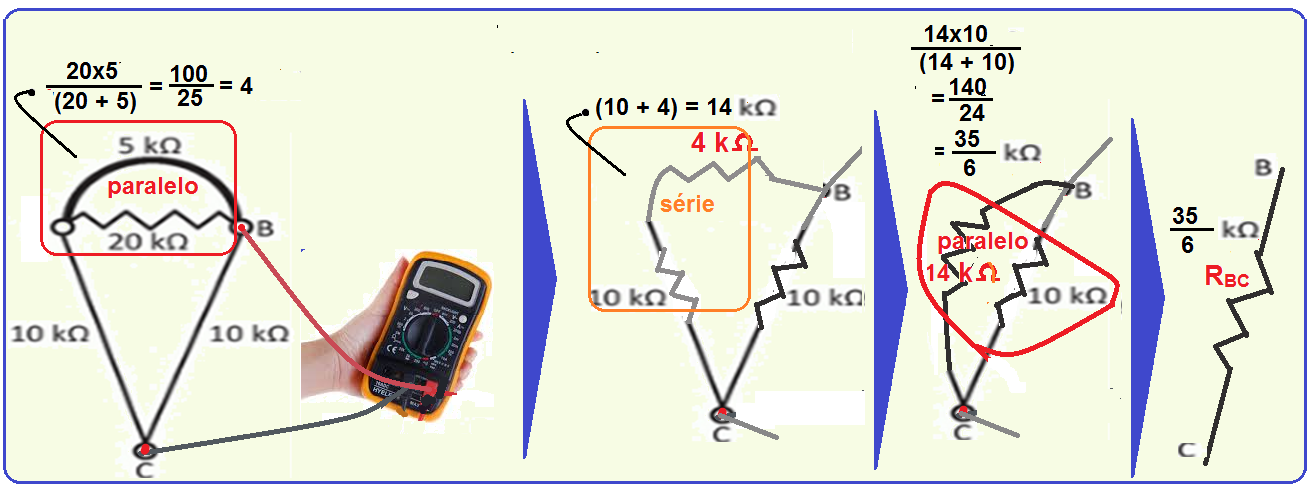
17- Calculando a resistência do resistor equivalente entre os pontos A e B da figura que mostra os trechos pelos quais não circula corrente elétrica (circuito em aberto):

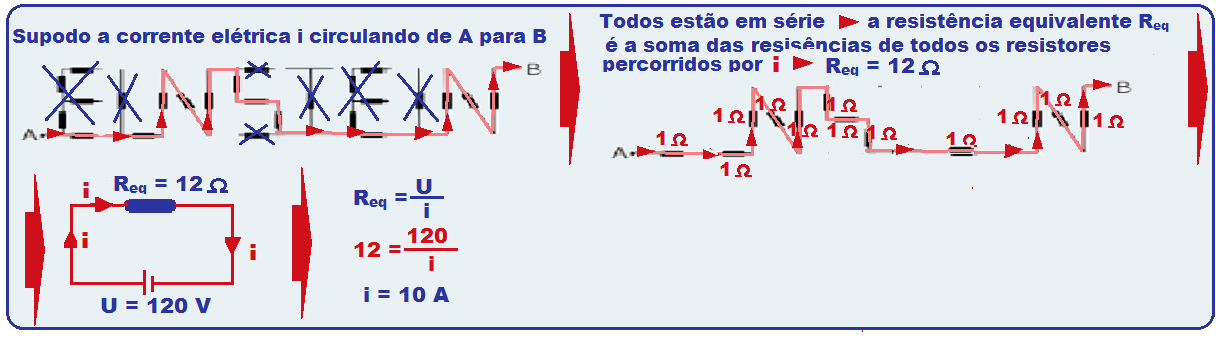
Então, a intensidade de corrente elétrica que irá aquecer a água do aquário é de i = 10 A.

Agora vamos calcular a quantidade de energia térmica (calor)W que irá aquecer a massa de água do aquáriom = 120000 g, de calor específico c= 1g.cm-3.oC-1 de modo que sofra uma variação de temperatura ∆Ɵ = 36oF = 20oC.

18- Cálculo da resistência equivalente e da fem do gerador com a chave C aberta:

Essa fem ε = 15R é constante, pois o gerador é o mesmo:

A sequência de figuras abaixo mostra o cálculo da resistência do resistor equivalente com a chave C fechada e retirando o amperímetro ideal (resistência interna nula):

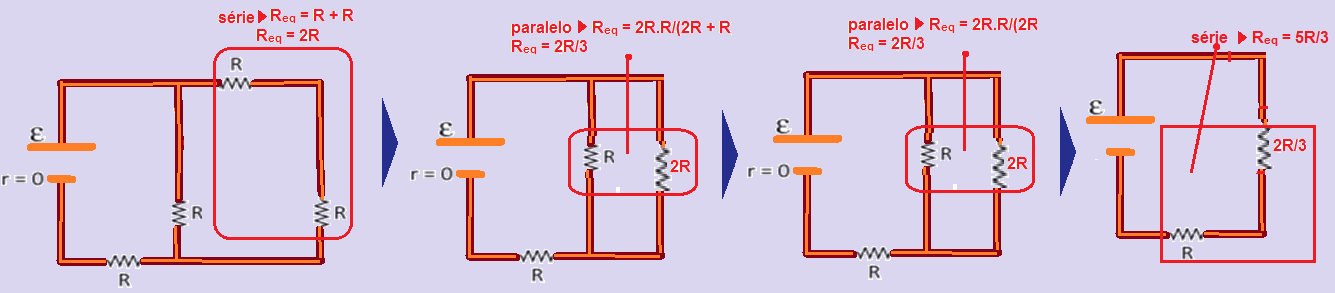
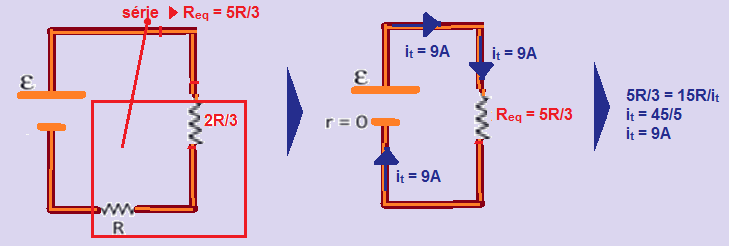
Observe atentamente na figura abaixo que a corrente elétrica indicada pelo amperímetro é i_A = 3 A.

R- E

19- Para que as tomadas, como pede o enunciado estejam submetidas à mesma diferença de potencial (ddp), tensão ou voltagem U, essas duas tomadas devem estar ligadas em paralelo já que nesse tipo de associação a tensão é a mesma que a tensão nominal da rede elétrica (U).

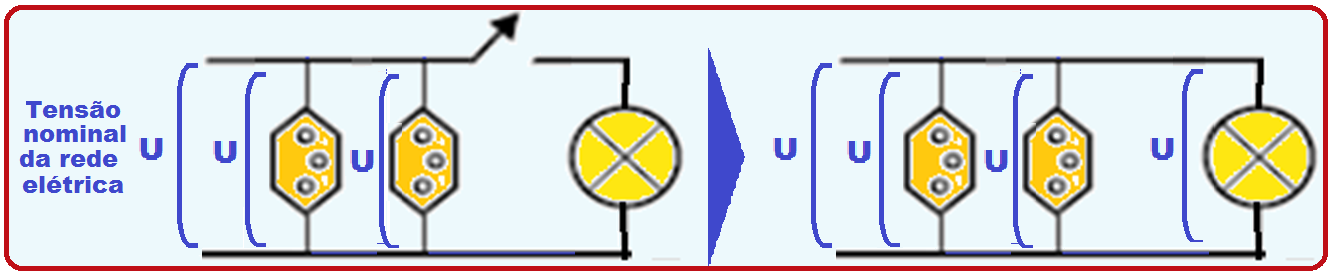
Mas, o interruptor deve estar ligado em série com a lâmpada e, quandofechado ele acende a lâmpada que fica em paralelo com as tomadas e, portanto, submetida à tensão nominal (U) da rede que as tomadas.

Desligando o interruptor, desliga-se a lâmpada, sem alterar a ligação paralelo das tomadas com a rede, que continuam sujeitas à mesma ddp nominal U, da rede.

R- E

20- No chuveiro elétrico, podemos alterar a resistência elétrica equivalente através da variação do comprimento do resistor.

R- A

21- a) Cálculo da intensidade de corrente elétrica i utilizando os valores nominais fornecidos: P = 25 W e U = 40 V P = i.U 25 = i.40 i = = 0,625 A.

A carga elétrica ∆Q no intervalo de tempo ∆t = 20 minx60 = 1200 s pode ser determinada por i = 0,625 = .

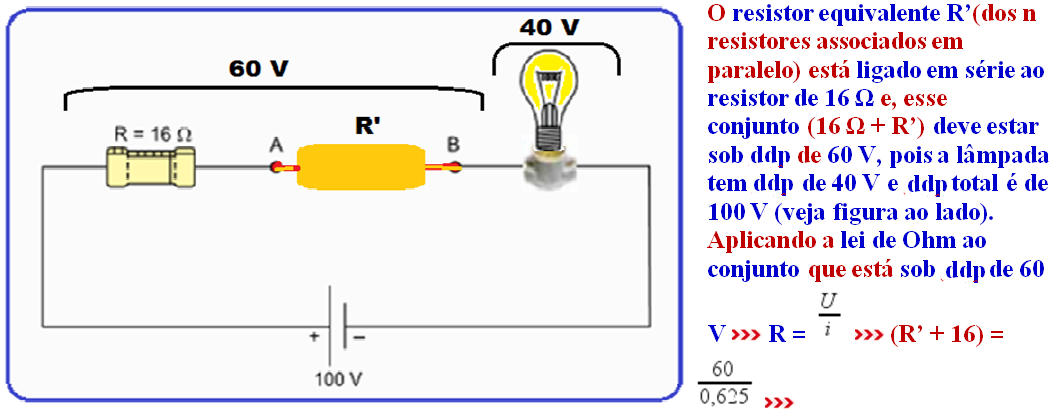R’ + 16 = 96 R’ = 80 Ω.

Então, você deve associar em paralelo n resistores de 320Ω de maneira a obter um único resistor de 80 Ω n = n = 4.

22- Trata-se de uma associação de resistores (lâmpadas) associados em paralelo e, cujas características são fornecidas a seguir:

Características da associação paralelo

Os resistores são associados pelos seus terminais, ou seja, todos saem de um mesmo ponto e todos chegam a um mesmo ponto.

A diferença de potencial (tensão) U de toda a associação (entre A e B) é a mesma para todos os resistores

A corrente total i é a soma das correntes parciais,ou seja, i = i1 + i2 + i3.

No caso do exercício:

Observe que a intensidade de corrente i_A (corrente total) que sai do polo positivo da bateria deve ser a mesma que i_E que chega ao polo negativo da mesma bateria.

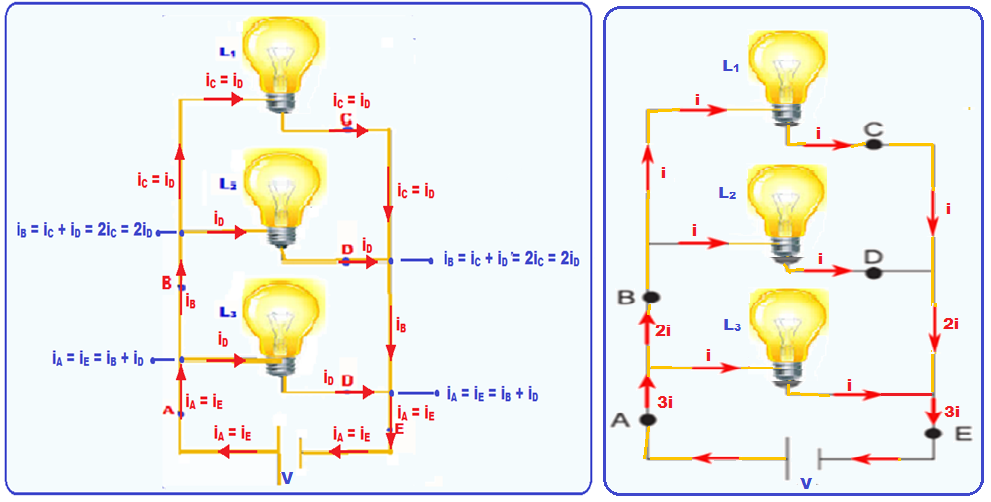
Como, pelo enunciado, as lâmpadas são idênticas elas possuem a mesma resistência e, consequentemente são percorridas pela mesma corrente elétrica, ou seja, i_C = i_D.

R- A

23-

24-

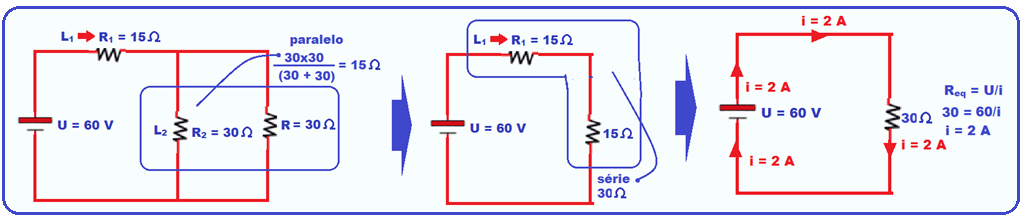
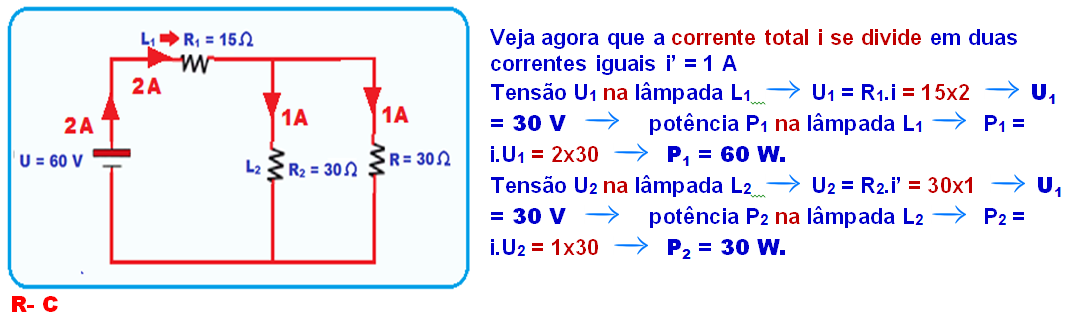
Observe que a alternativa correta é a C, cuja análise é feita a seguir:

Na sequência abaixo é fornecido o cálculo da corrente elétrica total i.

25-

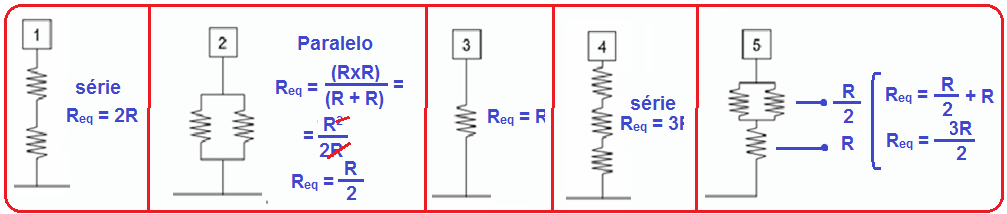
Observe que o circuito de número 2 possui menor resistência elétrica equivalente, portanto será percorrido por maior corrente elétrica.

R – A

26- a) Cálculo da resistência equivalente ReqA quando a chave está ligada no ponto A e a corrente

elétrica passando apenas pelos dois resistores que estão em paralelo.

b) Se a densidade da água é d = 1 kg/L, isso significa que o volume de 1 L de água possui massa de m = 1 kg.

Assim, o volume de 4L de água equivale à massa de m = 4 kg.

Da equação fundamental da calorimetria Q = m.c.∆θ = 4.1.(80 – 20) = 4.60 Q = W = 240 kcal.

Com a chave em A PA = = = PA = 400 W.

PA = 2.40 = R = R = 18 Ω

27- Sendo o voltímetro ideal ele possui resistência interna infinita (isolante), por ele não circula corrente elétrica, então você pode retirá-lo do circuito, que fica conforme a figura abaixo:

Na sequência a seguir está sendo calculada a resistência elétrica do resistor equivalente:

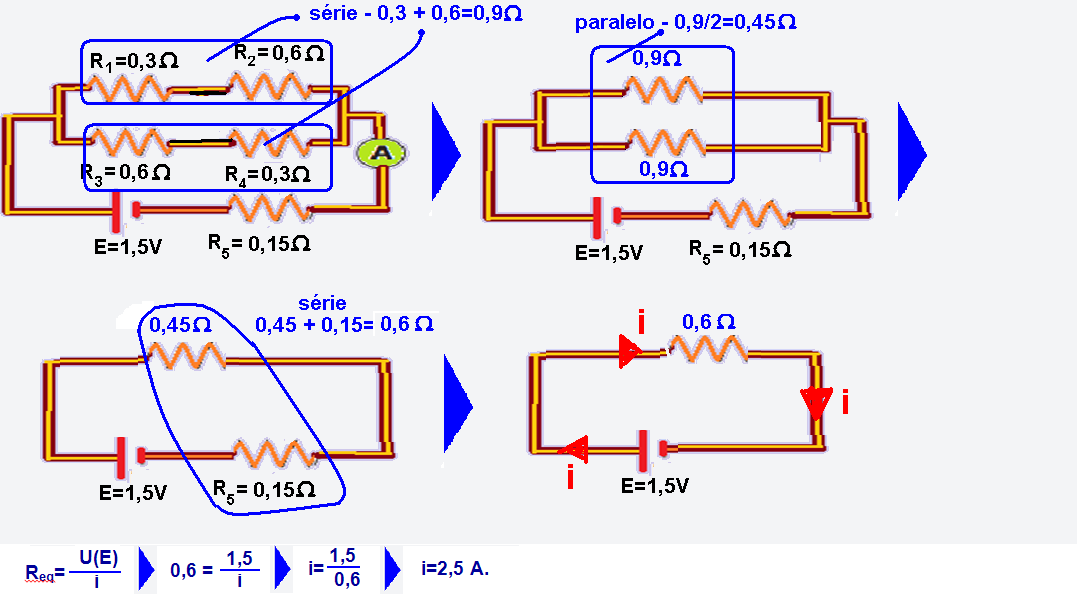
Veja na figura abaixo que a corrente elétrica que circula peloamperímetro (indicação do mesmo) é de 2,5A e veja também as correntes que circulam por cada resistor:

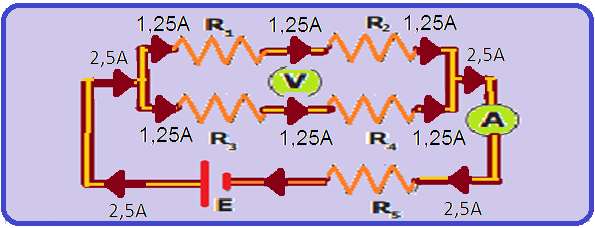
A diferença de potencial (tensão, voltagem) entre A e B é fornecida porUAB=R.i=0,3.1,25=0,375V.

A diferença de potencial (tensão, voltagem) entre A e C é fornecida por U_AC= R.i = 0,6.1,25 = 0,75V.

U_AB = V_A – V_B --- V_A – V_B = 0,375V --- U_AC = V_A –V_C--- VA – VC = 0,75V.

UAC – UAB = 0,75 – 0,375 = 0,375V --- (V_A – VC) – (V_A – VB) = 0,375 = VA – VC– VA + VB --- V_B – V_C = 0,375V.

Observe na figura que o voltímetro está inserido entre os pontos B e C então ele indicará a ddp entre esses dois pontos, ou seja, indicará U_BC= 0,375V.

R- A

28- Observe que o dispositivo de 8V (maior valor) é o gerador (a corrente sai de seu polo positivo) e o de 6 V é o receptor (a corrente sai de seu polo negativo) U = 8 – 6 = 2V.

Os resistores estão associados em série Req = 3 + 3 + 4 = 10 Ω.

Req = 10 = i = 0,2 A (corrente em cada resistor) P4Ω = R.i2 = 4.(0,2)2 = 4.0,04

P4Ω = 0,16 W.

R- A

29- Vamos começar o exercício analisando o valor de corrente dado no enunciado, através da fórmula da resistência:

Aonde: R é a resistência elétrica = 10kΩ.

U é a tensão da corrente (ddp).

i é a corrente elétrica = 1 mA.

Isolando o U:

Substituindo:

Resolvendo:

U = 10 V

Esse resultado é importante para nos mostrar que os outros dois resistores não podem estar em série, visto que se estivessem cada um teria uma tensão de 10 V, somados teriam uma tensão geral de 30 V, maior que a do enunciado. Como os resistores não podem estar em sérieeles só podem estar em paralelo. Formando um circuito exemplificado na imagem abaixo:

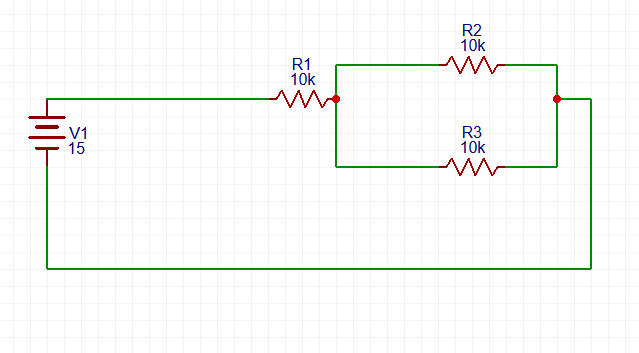
A resistência total vai ser a soma do resistor R1 com a soma da resistência em série dos outros dois resistores, vamos calcular essa resistência em série pela fórmula abaixo:

Substituindo os valores:

Calculando:

Simplificando:

Elevando ambos os lados por -1:

R = Ω

Somando com o outro resistor para achar a resistência total:

R = + 10.10³

R = Ω

R- D

30- 01) Os resistores equivalentes nos dois ramos do circuito possuem, respectivamente, resistência elétrica de 30 Ω e de 5 Ω.

01. Correta ramo A série Req = 10 + 10 + 10 = 30 Ω ramo B paralelo Req = 10.10/(10 + 10) = 100/20 Req = 5 Ω.

02) A corrente elétrica que flui no ramo A é de 2 A.

02. Falsa Req = U/i 30/7 = 10/i i = 2,33 A iA = 10/30 = 0,33 A iB = 10/5 = 2 A.

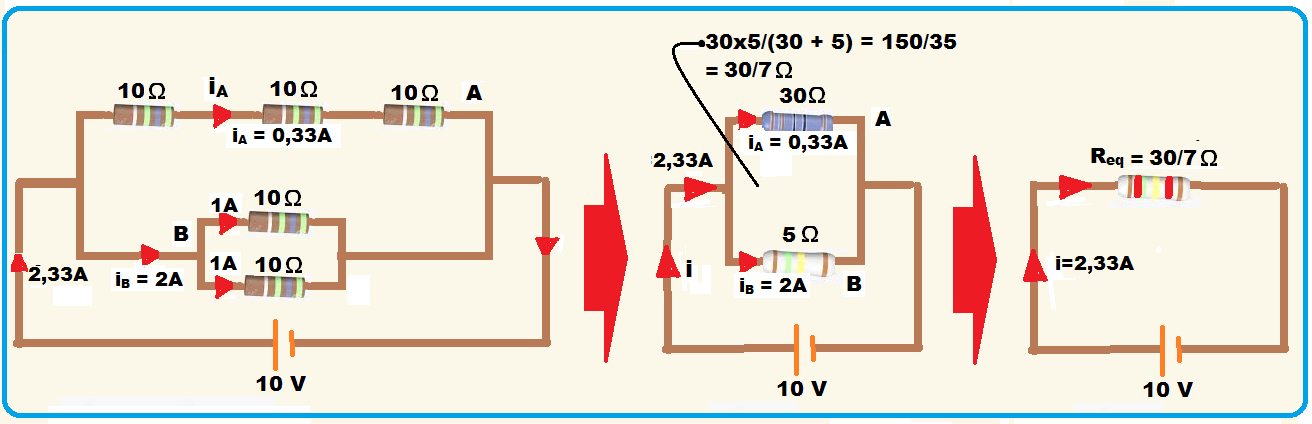
Veja acima que iA = 0,33 A.

04) A potência dissipada no ramo B é de 20 W.

04. Correta P = R.iB2 = 5.22 = 20 W.

08) A potência dissipada e a corrente elétrica no ramo B são maiores que as observadas no ramo A.

08. Correta de 04, PB = 20W PA = R.iA2 = 30.0,33 = 9,9 W.

16) A diferença de potencial entre os terminais do segundo resistor do ramo A é de aproximadamente 3,3 V

16. Correta R = U/iA 10 = U/0,33 U = 3,3 V.

R- (01 + 04 + 08 + 16) = 29

31-

Veja um resumo da teoria a seguir:

Curva característica do gerador – é representada por um gráfico que relaciona a intensidade de corrente elétrica i no gerador com a diferença de potencial (tensão) U em seus terminais.

Se i=0, ou seja, se o gerador estiver em circuito aberto, tem-se:

Se U=0, ou seja, se o gerador estiver em curto circuito, tem-se:

Os pares de valores U=E e icc=E/r determinam dois pontos no gráfico Uxi, que unidos

por um segmento de reta (função do primeiro grau) fornece acurva característica de um gerador.

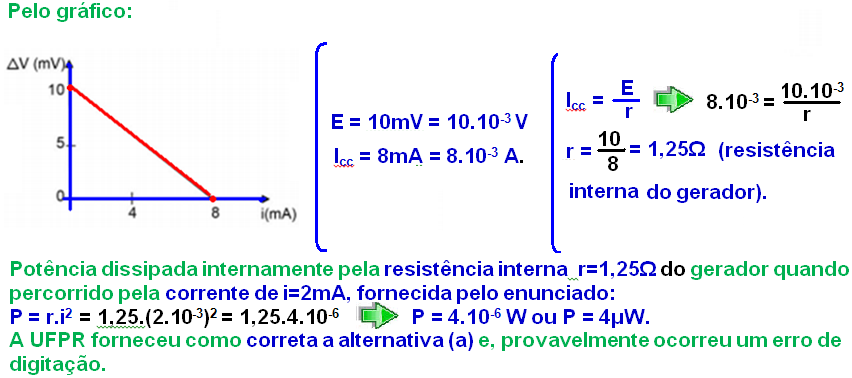
32- Na situação 1, como o voltímetro é ideal, possui resistência interna infinita, isolante), você pode retirá-lo e calcular a resistência equivalente conforme a sequência abaixo:

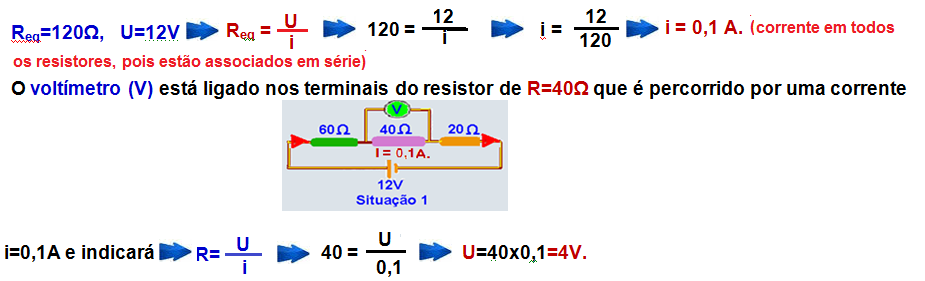
Na situação 2 o amperímetro está ligado em série e, como ele é ideal(resistência interna nula) você pode curto-circuitá-lo e calcular a resistência equivalente conforme a sequência abaixo:

Req=U / i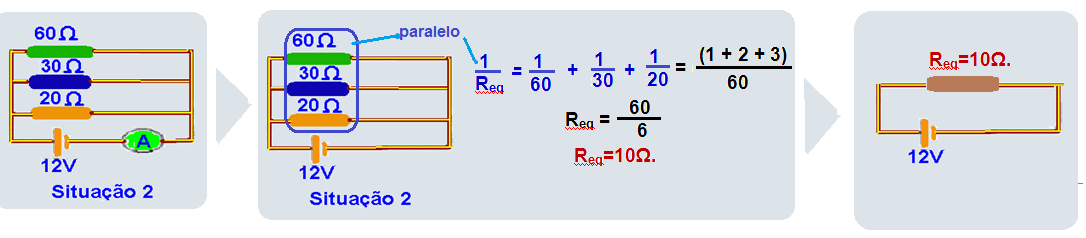

R- B

33- Refazendo simbolicamente o circuito:

Sendo os aparelhos de medida ideais você pode “curto-circuitar” o amperímetro,retirar o voltímetro e calcular a resistência equivalente na seqüência abaixo:

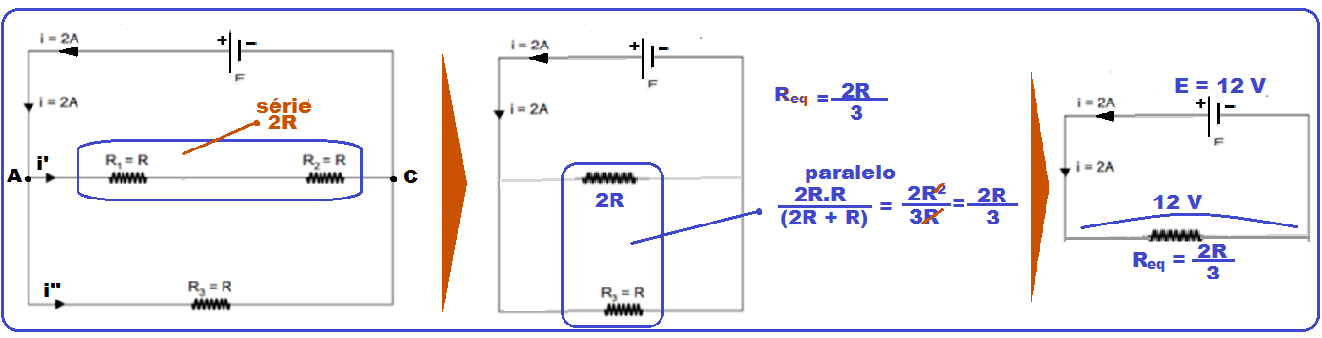
34- Observe que as duas lâmpadas acesas de mesma potência P = 60 W e sob tensão de U = 12 V estão associadas em paralelo e, ambas também em paralelo com a bateria de U = 12 V o que é óbvio, pois a tensão U é a mesma.

Assim, usando os valores nominais fornecidos a corrente elétrica i em cada lâmpada será a mesma e fornecida por P = i.U 60 = i.12 i = 5 A.

Veja na figura abaixo que a corrente que passa pelo fusível deve valer if = 2.i = 2.5 if = 10 A.

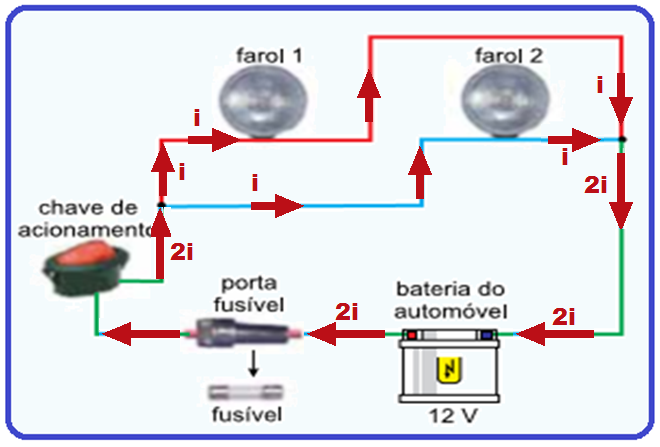
Das alternativas, aquela cujo fusível apresenta menor amperagem(intensidade de corrente elétrica)

capaz de proteger esse circuito é o de 12 A.

R- B

35-
Na situação 1, como o voltímetro é ideal, possui resistência interna infinita, isolante), você pode retirá-lo e calcular a resistência equivalente conforme a sequência abaixo:

Na situação 2 o amperímetro está ligado em série e, como ele é ideal(resistência interna nula) você pode curto-circuitá-lo e calcular aresistência equivalente conforme a sequência abaixo:

Req=U / i

R- B

Vestibulares Recentes

Eletrodinâmica - 2014 – 2013

01-(UNISINOS-RS-014)

Uma lâmpada de lanterna apresenta as seguintes especificações: 12V – 24W.

Ao aplicar-se 6V à lâmpada, a corrente elétrica que nela circula é de .................. A, e a potência que dissipa é de .................. W.

As lacunas são corretamente preenchidas, respectivamente, por

02-(UNIFESP-SP-014)

Para compor sua decoração de Natal, um comerciante decide construir uma estrela para pendurar na fachada de sua loja. Para isso, utilizará um material que, quando percorrido por corrente elétrica, brilhe emitindo luz colorida. Ele tem à sua disposição barras de diferentes cores desse material, cada uma com resistência elétrica constante R = 20 Ω.

Utilizando dez dessas barras, ele montou uma estrela e conectou os pontos A e B a um gerador ideal de força eletromotriz constante e igual a 120 V.

Considerando desprezíveis as resistências elétricas dos fios utilizados e das conexões feitas, calcule:

a) a resistência equivalente, em ohms, da estrela.

b) a potência elétrica, em watts, dissipada em conjunto pelas pontas de cores laranja (CAD), azul (DEF) e vermelha (FBG) da estrela, quando ela se encontrar acesa.

03-(UNESP-SP-014)

O circuito representado na figura é utilizado para obter diferentes intensidades luminosas com a mesma lâmpada L.

A chave Ch pode ser ligada ao ponto A ou ao ponto B do circuito. Quando ligada em B, a lâmpada L dissipa uma potência de 60 W e o amperímetro ideal indica uma corrente elétrica de intensidade 2 A.

Considerando que o gerador tenha força eletromotriz constante E = 100 V e resistência interna desprezível, que os resistores e a lâmpada tenham resistências constantes e que os fios de ligação e as conexões sejam ideais, calcule o valor da resistência R_L da lâmpada, em ohms, e a energia dissipada pelo circuito, em joules, se ele permanecer ligado durante dois minutos com a chave na posição A.

04-(ACAFE-SC-014)

Em uma situação cotidiana, uma pessoa liga duas lâmpadas incandescentes em paralelo em uma rede de 220V. As lâmpadas apresentam certa intensidade luminosa (brilho), sendo que a lâmpada

2 tem um filamento de mesmo material, mesmo comprimento, mas é mais grosso que o filamento

da lâmpada 1.

Nessas condições, a alternativa correta é:

A) Desligando a lâmpada L₁, a lâmpada L₂ diminui o seu brilho.

B) A lâmpada L₁ brilha mais que a lâmpada L₂.

C) As lâmpadas L₁ e L₂ tem o mesmo brilho.

D) A lâmpada L₂ brilha mais que a lâmpada L₁.

05-(UNESP-SP-014)

Para compor a decoração de um ambiente, duas lâmpadas idênticas, L₁ e L₂, com valores nominais (100 V – 100 W), devem ser ligadas em paralelo a uma fonte de tensão constante de 200 V. Deseja-se que L₁ brilhe com uma potência de 100 W e que L₂ brilhe com uma potência de 64 W. Para

que as lâmpadas não queimem, dois resistores ôhmicos, R₁e R₂, com valores convenientes, são ligados em série comas respectivas lâmpadas, conforme o esquema representadona figura.

Considerando todos os fios utilizados na ligação como ideais e que as lâmpadas estejam acesas e brilhando com as potências desejadas, é correto afirmar que os valores das resistências de R₁ e R₂, em ohms, são, respectivamente, iguais a

(A) 200 e 100.

(B) 200 e 150.

(C) 100 e 150.

(D) 100 e 300.

(E) 100 e 200.

06-(AFA-014)

Dispõe-se de duas pilhas idênticas de f.e.m ε e resistência interna r constante e de um reostato, cuja resistência elétrica R varia de zero até 6 r. Essas pilhas podem ser associadas em série ou em paralelo, conforme ilustram as figuras I e II, respectivamente.

O gráfico que melhor representa a potência P dissipada pelo reostato, para cada uma das associações, em função da resistência R é

07-(UFSCAR-SP-014)

Um professor pede a seus alunos que tabelem as leituras do voltímetro e do amperímetro associados aos circuitos 1, 2 e 3, quando esses circuitos são conectados, um de cada vez, aos terminais A e B de um gerador ideal. Os resistores utilizados têm igual valor ôhmico.

Após a série de leituras, os alunos construíram a seguinte tabela:

A partir da análise da tabela, os alunos puderam concluir acertadamente que, em circuitos série, à medida que se aumenta o número de resistores associados, a resistência equivalente da associação _________ , a diferença de potencial entre os extremos de um mesmo resistor ____________ e a intensidade de corrente elétrica no circuito___________ .

Assinale a alternativa que preenche, correta e respectivamente, as lacunas do texto.

(A) diminui – diminui – diminui

(B) diminui – aumenta – aumenta

(C) aumenta – aumenta – aumenta

(D) aumenta – aumenta – diminui

(E) aumenta – diminui – diminui

08-(UERJ-RJ-014)

Cinco resistores de mesma resistência R estão conectados à bateria ideal E de um automóvel,

conforme mostra o esquema:

Inicialmente, a bateria fornece ao circuito uma potência P_i. Ao estabelecer um curto-circuito

entre os pontos M e N, a potência fornecida é igual a P_f.

A razão é Pf/Pi é dada por:

09-(FUVEST-SP-014)

A curva característica de uma lâmpada do tipo led (diodo emissor de luz) é mostrada no gráfico. Essa lâmpada e um resistor de resistência R estão ligados em série a uma bateria de 4,5 V,

como representado na figura ao lado do gráfico. Nessa condição, a tensão na lâmpada é 2,5 V.

a) Qual é o valor da corrente i_R no resistor?

b) Determine o valor da resistência R.

c) A bateria de 4,5 V é substituída por outra de 3 V, que fornece 60 mW de potência ao circuito, sem

que sejam trocados a lâmpada e o resistor. Nessas condições, qual é a potência P_R dissipada no

resistor?

10-(FUVEST-SP-014)

Dois fios metálicos, F₁e F₂, cilíndricos, do mesmo material de resistividade ρ, de seções transversais de áreas, respectivamente, A₁e A₂=2A₁, têm comprimento L e são emendados, como ilustra a figura abaixo.

O sistema formado pelos fios é conectado a uma bateria de tensão V.

Nessas condições, a diferença de potencial V₁, entre as extremidades de F₁, e V₂, entre as de F₂, são tais que

11-(UNESP-SP-014)

Dois resistores ôhmicos, R₁ e R₂, podem ser associados em série ou em paralelo. A resistência equivalente quando são associados em série é R_Se quando são associados em paralelo é R_p.

No gráfico, a curva S representa a variação da diferença de potencial elétrico entre os extremos da associação dos dois resistores em série, em função da intensidade de corrente elétrica que atravessa a associação de resistência equivalente R_S , e a curva P representa a variação da diferença de potencial elétrico entre os extremos da associação dos dois resistores em paralelo R_p, em função da intensidade da corrente elétrica que atravessa a associação de resistência equivalente R_p.

Considere a associação seguinte, constituída por dois resistores R₁ e dois resistores R₂.

De acordo com as informações e desprezando a resistência elétrica dos fios de ligação, calcule a resistência equivalente da associação representada na figura e os valores de R₁ e R₂ , ambos em ohms.

12-(UNICAMP-SP-014)

No fenômeno de “Magnetoimpedância gigante”, a resistência elétrica de determinado material pelo qual circula uma corrente alternada de frequência f varia com a aplicação de um campo magnético H. O

gráfico da figura 1 mostra a resistência elétrica de determinado fio de resistividade elétrica ρ=64,8.10^-8 Ωm

em função da frequência f da corrente elétrica alternada que circula por esse fio, para diferentes valores de H .

a) Como podemos ver na figura 1, o valor da resistência elétrica do fio para f =0Hz é R=1,5Ω. Calcule

o comprimento L desse fio, cuja área de seção transversal vale A=1,296 10^-8 m².

b) Para altas frequências, a corrente elétrica alternada não está uniformemente distribuída na seção reta do fio, mas sim confinada em uma região próxima a sua superfície. Esta região é determinada pelo comprimento de penetração, que é dado por =k√(ρ/μ_r.f), em que ρ é a resistividade do fio, f é a frequência da corrente elétrica alternada, μ_r é a permeabilidade magnética relativa do fio e k=500√(mHz/Ω).

Sabendo que μ_r varia com o campo magnético aplicado H , como mostra a figura 2, e que, para o

particular valor de f=8MHz temos R≈4Ω, calcule o valor de para essa situação.

13-(CEDERJ-RJ-014)

O circuito mostra três elementos resistivos de resistências R₁, R₂ e R₃ ligados a uma fonte de tensão

V por fios condutores de resistência desprezível. Os valores das diferenças de potencial entre os terminais desses resistores e das correntes elétricas que fluem através deles são, respectivamente, V₁ = 8,0V e I₁ = 4,0A, V₂ = 4,0V e I₂ = 2,0A, V₃ = 4,0V e I₃ = 2,0A.

Assinale a alternativa que descreve corretamente a comparação entre as resistências R₁, R₂ e R₃ e entre as potências dissipadas, respectivamente, pelo resistor R₁ (potência P₁) e pelo conjunto formado por R₂ e R₃ (potência P₂₃).

14-(UERJ-RJ-014)

No circuito, uma bateria B está conectada a três resistores de resistências R₁, R₂ e R₃:

Sabe-se que R₂ = R₃=2R₁.

A relação entre as potências P₁, P₂ e P₃, respectivamente associadas a R₁. R₂ e R₃, pode ser expressa como:

(A) P₁= P₂= P₃

(B) 2P₁= P₂= P₃

(C) 4P₁= P₂= P₃

(D) P₁= 2P₂= 2P₃

15-(MACKENZIE-SP-014)

No circuito desenhado abaixo, a intensidade de corrente elétrica contínua que passa pelo resistor de 50 Ω é

de 80 mA. A força eletromotriz ε do gerador ideal é igual a

16-(MACKENZIE-SP-014)

Duas pilhas elétricas de resistências internas nulas, associadas em série, “alimentam” a lâmpada

incandescente ilustrada na figura ao abaixo.

O amperímetro ideal A indica a intensidade de corrente elétrica 0,50 A, quando o voltímetro V, também ideal, indica a d.d.p. de 3,00 V. Sabendo-se que a potência dissipada por efeito Joule no filamento da lâmpada corresponde a 1/4 do valor nominal, indicado pelo fabricante, pode-se afirmar que os valores máximos nominais, de potência e tensão elétrica especificados na lâmpada (potência — d.d.p.), são

a) 1,50 W — 3,00 V

b) 3,00 W — 3,00 V

c) 3,00 W — 6,00 V

d) 6,00 W — 6,00 V

e) 6,00 W — 3,00 V

Corrente elétrica

37-(UNICAMP-SP-013)

Um carro elétrico é uma alternativa aos veículos com motor a combustão interna. Qual é a autonomia

de um carro elétrico que se desloca a 60km/h, se a corrente elétrica empregada nesta velocidade é igual a 50A e a carga máxima armazenada em suas baterias é q = 75Ah?

a) 40,0km. b) 62,5km. c) 90,0km. d) 160,0km

38-(ENEM-MEC-012)

Para ligar ou desligar uma mesma lâmpada a partir de dois interruptores, conectam-se os interruptores para que a mudança de posição de um deles faça ligar ou desligar a lâmpada, não importando qual a posição do outro.

Esta ligação é conhecida como interruptores paralelos. Este interruptor é uma chave de duas posições constituída por um polo e dois terminais, conforme mostrado nas figuras de um mesmo interruptor.

Na Posição I a chave conecta o polo ao terminal superior, e na Posição II a chave o conecta ao terminal inferior

O circuito que cumpre a finalidade de funcionamento descrita no texto é:

Potência elétrica – Energia elétrica

51-(FGV-RJ-013)

Um grupo de estudantes, em aula de laboratório de Física, mergulhou o resistor de um aquecedor elétrico, ligado a uma fonte de tensão de 120 V, em um recipiente, termicamente isolado, contendo água. Mediram a temperatura da água em função do tempo e verificaram que, em 2 minutos, a temperatura variou de 20°C a 80°C. A partir dos resultados obtidos, construíram o gráfico apresentado na figura abaixo, da quantidade de calor Q, em calorias, fornecida à água em função do instante t, a partir do mergulho do resistor na água, em minutos. Dados: 1cal=4J e c_água=1cal/g^oC

Os valores da resistência elétrica do aquecedor e da massa de água aquecida são, respectivamente, iguais a:

A. 72 Ω e 400 g

B. 18 Ω e 400 g

C. 72 Ω e 200 g

D. 18 Ω e 200 g

E. 750 m Ω e 16,7 g

52-(PUC-MG-013)

A geração de energia elétrica através da luz se dá pelo uso de células fotossensíveis, chamadas de

células solares fotovoltaicas. As células fotovoltaicas em geral são constituídas de materiais semicondutores, com características cristalinas e depositadas sobre sílica. Essas células, agrupadas em módulos ou painéis, compõem os painéis solares fotovoltaicos. A quantidade de energia gerada por um painel solar é limitada pela sua potência, ou seja, um painel de 145 W, com seis horas úteis de sol, gera aproximadamente 810 Watts por dia.

Fonte http://www.sunlab.com.br/Energia_solar_Sunlab.htm

Assinale o número de horas em que o painel acima consegue manter acesa uma lâmpada fluorescente de 9 Watts.

a) 9 h b) 18 h c) 58 h d) 90 h

53-(UNICAMP-SP-013)

Na reciclagem de embalagens de alumínio, usam-se apenas 5% da energia despendida na sua

fabricação a partir do minério de bauxita. No entanto, não se deve esquecer a enorme quantidade de energia envolvida nessa fabricação (3,6.10⁶ joules por latinha), além do fato de que a bauxita contém (em média) 55% de óxido de alumínio (alumina) e 45% de resíduos sólidos.

a) Considerando que em 2010 o Brasil produziu 32.10⁶ toneladas de alumínio metálico a partir da bauxita, calcule quantas toneladas de resíduos sólidos foram geradas nesse período por essa atividade.

b) Calcule o número de banhos que poderiam ser tomados com a energia necessária para produzir apenas uma latinha de alumínio, estimando em 10 minutos o tempo de duração do banho, em um chuveiro cuja potência é de 3.000 W. Dado: W = J s^-1.

54-(ENEM-MEC-012)

A eficiência das lâmpadas pode ser comparada utilizando a razão, considerada linear, entre a quantidade de luz produzida e o consumo. A quantidade de luz é medida pelo fluxo luminoso, cuja unidade é o lúmen(Im).

O consumo está relacionado à potência elétrica da lâmpada que é medida em watt(W). Por exemplo, uma lâmpada incandescente de 40 W emite cerca de 600 Im, enquanto uma lâmpada fluorescente de 40 W emite cerca de 3000 Im.

Disponível em: http://tecnologia.terra.com.br.Acesso em :29 fev.2012(adaptado)

A eficiência de uma lâmpada incandescente de 40 W é
a) maior que a de uma lâmpada fluorescente de 8W,
b) maior que a de uma lâmpada fluorescente de 40 W, que produz menor quantidade de luz.
c) menor que a de uma lâmpada fluorescente de 8 W,que produz a mesma quantidade de luz.
d) menor que a de uma lâmpada fluorescente de 40 W, pois maior quantidade de energia.
e) igual a de uma lâmpada fluorescente de 40 W, que consome a mesma quantidade de energia.

Resistores – Primeira lei de Ohm – Potência elétrica em um resistor

47-(UEAP-AP-013)

Marque a opção em que o gráfico representa a Lei de Ohm.

48-(UFPA-PA-013)

No rio Amazonas, um pescador inexperiente tenta capturar um poraquê segurando a cabeça do peixe

com uma mão e a cauda com a outra. O poraquê é um peixe elétrico, capaz de gerar, entre a cabeça e a cauda, uma diferença de potencial de até 1500 V. Para esta diferença de potencial, a resistência elétrica do corpo humano, medida entre as duas mãos, é de aproximadamente 1000 Ω. Em geral, 500 mA de corrente contínua, passando pelo tórax de uma pessoa, são suficientes para provocar fibrilação ventricular e morte por parada cardiorrespiratória. Usando os valores mencionados acima, calculamos que a corrente que passa pelo tórax do pescador, com relação à corrente suficiente para provocar fibrilação ventricular, é:

49-(UFRN-RN-013)

Conhecido como um dos equipamentos que mais consome energia em uma residência, o chuveiro elétrico está presente na maioria dos lares brasileiros. Um chuveiro elétrico simples é composto por uma câmara, na qual existem dois resistores de dimensões diferentes, como mostrado na figura abaixo. Existe ainda uma chave seletora que

pode ser ligada na posição VERÃO ou na posição INVERNO.

Considere uma residência que consome em média 200 kWh por mês, na qual está instalado um chuveiro cujas especificações do fabricante são: 3.600/4.800W, 220 V.

A) Em que posição da figura acima, X ou Y, deve ser ligada a chave seletora do chuveiro para que ele opere no modo INVERNO (4.800 W)? Justifique sua resposta.

B) Determine o consumo de energia pelo chuveiro operando no modo INVERNO, durante um banho cuja duração é de 10 minutos.

C) Considerando que esse chuveiro está instalado em uma residência na qual moram quatro pessoas e que cada um toma um banho diário com duração de 10 minutos, qual seria o percentual de economia em quilowatts na conta de energia da família, se eles resolvessem deixar de usar o chuveiro elétrico? Justifique sua resposta.

50-(PUC-MG-013)

O principal componente de um chuveiro elétrico é a sua resistência elétrica. Quando ela estraga, o

equipamento deixa de aquecer a água. Sobre a capacidade do chuveiro de aquecer a água e sua resistência elétrica, é CORRETO afirmar:

a) Se a resistência do chuveiro for trocada por outra de maior valor, ele irá aquecer mais a água, fornecendo mais calor a ela.

b) Quando fechamos um pouco a torneira, aumentamos a potência do chuveiro e a água sai com temperatura mais elevada.

c) Quando abrimos mais a torneira, diminuímos a potência do chuveiro fazendo com que a água saia com temperatura mais baixa.

d) Se diminuímos a resistência elétrica do chuveiro, aumentamos sua potência fazendo com que a água saia com uma maior temperatura.

51-(PUC-RS-013)

O gráfico a seguir mostra o comportamento da corrente elétrica em função da diferença de potencial entre os extremos de um fio condutor.

Analisando os dados mostrados no gráfico, conclui-se que a resistência elétrica e a potência dissipada nesse condutor quando percorrido por uma corrente elétrica de 1,50A são, respectivamente,

A) 60Ω, 60W

B) 60Ω, 80W

C) 40Ω, 90W

D) 40Ω ,120W

E) 20Ω, 150W

52-(PUC-PR-013)

O fusível é um componente projetado com o intuito de proteger circuitos elétricos, seja em um carro, em uma residência ou até mesmo em grandes indústrias.

Porém seu uso vem sendo substituído por outro componente, o disjuntor, já que este raramente

precisa ser trocado, bastando apenas ser religado em caso de problemas. Com base nessas informações e em seus conhecimentos a respeito desses acessórios dos circuitos elétricos, é CORRETO afirmar:

A) O fusível não conduz corrente elétrica, ao contrário do disjuntor.

B) Somente o disjuntor é condutor, por isso vem substituindo os fusíveis.

C) Os fusíveis atuam como elementos de proteção ao circuito elétrico, porém não podem evitar possíveis incêndios.

D) Tanto o fusível quanto o disjuntor são condutores que têm como função evitar as correntes elétricas excessivas.

E) Em condições normais de funcionamento, isto é, quando a corrente ultrapassa o valor máximo admitido, a temperatura atingida pelo fusível é inferior ao seu ponto de fusão.

Segunda lei de Ohm (Resistividade)

33-(UNCISAl-AL-013)

Sabendo que uma corrente elétrica maior que 200 mA pode ser fatal a um ser humano se mantida por um intervalo de tempo da ordem de alguns ciclos cardíacos, calcule o valor da corrente elétrica estabelecida se uma diferença de

potencial elétrico de 270 V for aplicada entre as duas mãos de um adulto por um intervalo de tempo de 120 s e

determine se esta corrente é suficiente para matá-lo.

Considere que a menor distância percorrida pela corrente elétrica entre as duas mãos é 1,5 m, a resistividade elétrica

média do corpo humano é 1,8 Ωm, o trajeto da corrente apresenta secção circular de área 30 cm² e a frequência

cardíaca é igual a 80 ciclos cardíacos por minuto.

A) 133,3 A; não é suficiente.

B) 3000 A; é suficiente.

C) 300 mA; não é suficiente.

D) 600 mA; é suficiente.

E) 300 mA; é suficiente.

34-(URCA-CE-013)

Visando a copa do mundo de 2014, cabos de aço com 2,0 cm² de seção reta e 300 km de

comprimento são utilizados para concluir a reforma e ampliação do pátio de aeronaves do terminal de passageiros do aeroporto Pinto Martins, em Fortaleza.

Podemos então afirmar que a resistência elétrica de cada um desses cabos, em ohm, é igual a?

DADO: ρ_aço = 1,8.10^-9Ω.m

a) 2,4 b) 2,5 c) 2,6 d) 2,7 e) 2,8

Resistor equivalente nas associações série, paralelo e mista – curto circuito

49-(UERN-RN-PSV-013)

Na figura estão representadas duas associações de resistores.

Considere que, aplicando-se uma tensão de 60 V nos seus terminais, a diferença entre as correntes totais que as percorrem seja igual a 9 A. Sendo assim, o valor de R e igual a

A) 2 Ω. B) 5 Ω. C) 8 Ω. D) 10 Ω.

50-(FGV-RJ-013)

Quando duas resistências elétricas de valores R₁ e R₂ são dispostas em paralelo (figura abaixo), o valor da resistência equivalente às duas primeiras é dado por R=R₁.R₂/(R₁ + R₂)

A figura a seguir mostra duas semirretas AX e BY perpendiculares à reta r. Na primeira foi marcado o ponto A', de forma que AA’=R₁ , e na segunda foi marcado o ponto B', de forma que BB’=R₂perpendicular a r. cortaram-se em P e foi traçado o segmento PP’ . As retas A’B e AB’

Mostre que PP' é igual ao valor da resistência R.

Características de associação série e associação paralela

60-(UERN-RN-PSV-013)

Na figura estão representadas duas associações de resistores.

Considere que, aplicando-se uma tensão de 60 V nos seus terminais, a diferença entre as correntes totais que as percorrem seja igual a 9 A. Sendo assim, o valor de R e igual a

A) 2 Ω. B) 5 Ω. C) 8 Ω. D) 10 Ω.

61-(URCA-CE-013)

Uma sala e iluminada por um circuito de lâmpadas incandescentes em paralelo. Considere os dados abaixo:

− a corrente elétrica eficaz limite do fusível que protege esse circuito e igual a 10 A;

− a tensão eficaz disponível é de 120 V;

− sob essa tensão, cada lâmpada consome uma potencia de 60 W.

O numero máximo de lâmpadas que podem ser mantidas acesas corresponde a:

a) 10 b) 15 c) 20 d) 25 e) 30

62-(UNESP-SP-013)

Determinada massa de água deve ser aquecida com o calor dissipado por uma associação de resistores ligada nos pontos A e B do esquema mostrado na figura.

Para isso, dois resistores ôhmicos de mesma resistência R podem ser associados e ligados aos pontos A e B. Uma ddp constante U, criada por um gerador ideal entre os pontos A e B, é a mesma para ambas as associações dos resistores, em série ou em paralelo.

Considere que todo calor dissipado pelos resistores seja absorvido pela água e que, se os resistores forem associados em série, o aquecimento pretendido será conseguido em 1 minuto.

Dessa forma, se for utilizada a associação em paralelo, o mesmo aquecimento será conseguido num intervalo de tempo, em segundos, igual a

(A) 30. (B) 20. (C) 10. (D) 45. (E) 15.

63-(UNESP-SP-013)

Em um jogo de perguntas e respostas, em que cada jogador deve responder quatro perguntas (P₁, P₂, P₃ e P₄), os acertos de cada participante são indicados por um painel luminoso constituído por quatro lâmpadas coloridas. Se uma pergunta for respondida corretamente, a lâmpada associada a ela acende. Se for respondida de forma errada, a lâmpada permanece apagada. A figura abaixo representa, de forma esquemática, o circuito que controla o painel. Se uma pergunta é respondida corretamente, a chave numerada associada a ela é fechada, e a lâmpada correspondente acende no painel, indicando o acerto. Se as quatro perguntas forem respondidas erradamente, a chave C será fechada no final, e o jogador totalizará zero pontos.

Cada lâmpada tem resistência elétrica constante de 60 Ω e, junto com as chaves, estão conectadas ao ramo AB do circuito, mostrado na figura, onde estão ligados um resistor ôhmico de resistência R = 20 Ω, um gerador ideal de f.e.m. E = 120 V e um amperímetro A de resistência desprezível, que monitora a corrente no circuito. Todas as chaves e fios de ligação têm resistências desprezíveis.

Calcule as indicações do amperímetro quando um participante for eliminado com zero acertos, e quando um participante errar apenas a P₂

64-(MACKENZIE-SP-013)

Nesta época de Natal, muitas pessoas utilizam conjuntos de pequenas lâmpadas incandescentes, popularmente conhecidos por pisca-piscas, para adornarem ambientes. Um dos modelos utilizados por certa pessoa possui 4 séries de

25 lâmpadas cada uma, que são associadas em paralelo entre si, conforme esquema abaixo:

Considerando-se que os valores nominais do fabricante, da potência total e da tensão elétrica entre os terminais A e B do pisca-pisca, são, respectivamente, 22 W e 220 V, a resistência elétrica de cada lâmpada é

a) 88 W b) 176 W c) 352 W d) 460 W e) 528 W

65-(UNIFESP-SP-013)

Observe a charge.

Em uma única tomada de tensão nominal de 110 V, estão ligados, por meio de um adaptador, dois abajures (com lâmpadas incandescentes com indicações comerciais de 40 W – 110 V), um rádio-relógio (com potência nominal de 20 W em 110 V) e um computador, com consumo de 120 W em 110 V. Todos os aparelhos elétricos estão em pleno funcionamento.

a) Utilizando a representação das resistências ôhmicas equivalentes de cada aparelho elétrico como R_L para cada abajur, R_R para o rádio-relógio e R_C para o computador, esboce o circuito elétrico que esquematiza a ligação desses 4 aparelhos elétricos na tomada (adaptador) e, a partir dos dados da potência consumida por cada aparelho, calcule a corrente total no circuito, supondo que todos os cabos de ligação e o adaptador são ideais.

b) Considerando que o valor aproximado a ser pago pelo consumo de 1,0 kWh é R$ 0,30 e que os aparelhos permaneçam ligados em média 4 horas por dia durante os 30 dias do mês, calcule o valor a ser pago, no final de um mês de consumo, devido a estes aparelhos elétricos.

Cálculo de correntes, tensões e potências em associações mistas

42-(UFPE-PE-013)

A figura mostra um circuito elétrico onde se aplica uma ddp de entrada e se mede uma ddp de saída. Calcule qual deve

ser a razão R₁/R₂, para que a ddp de saída seja um décimo da ddp de entrada.

43-(ESPCEX-013)

Quatro lâmpadas ôhmicas idênticas A, B, C e D foram associadas e, em seguida, a associação é ligada a um gerador de energia elétrica ideal. Em um dado instante, a lâmpada A queima, interrompendo o circuito no trecho em que ela se encontra. As lâmpadas B, C e D permanecem acesas, porém o brilho da lâmpada B aumenta e o brilho das lâmpadas C e D diminui. Com base nesses dados, a alternativa que indica a associação formada por essas lâmpadas é:

44-FUVEST-SP-013)

No circuito da figura ao lado, a diferença de potencial, em módulo, entre os pontos A e B é de

a) 5 V. b) 4 V. c) 3 V. d) 1 V. e) 0 V.

Geradores - associação de geradores

48-(Católica Santa Catarina –SC-013)

O circuito a seguir é composto de um gerador (ε = 12V e r = 1 Ω) e mais três resistores (R₁ = 7 Ω, R₂ = 3 Ω e R₃ = 6 Ω).

Qual é o valor da diferença de potencial nos polos desse gerador?

A) 12 volts. B) 8,4 volts. C) 10,8 volts. D) 15 volts. E) 11,2 volts.

49-(CEFET-MG-013)

Uma bateria cujas especificações são 1,2 V e 1.200 mAh, após ser completamente carregada, é ligada

a um motor de força contraeletromotriz de 1,0 V e resistência interna 0,20 Ω.

Considerando-se que essa bateria desenvolva toda sua potência nominal, o tempo, em horas, que ela consegue manter o motor em funcionamento, é

a) 0,50. b) 0,60. c) 1,2. d) 2,0. e) 2,4

50-(UFRN-RN-013)

Em uma situação em que a bateria de um carro está descarregada e, portanto, não é possível dar a partida no motor, geralmente uma bateria carregada é ligada à bateria do carro para fazê-lo funcionar.

As figuras I e II abaixo representam duas alternativas para interligar as duas baterias através de fios condutores.

A figura que representa a ligação correta é a

A) II, cuja ligação é do tipo em série.

B) II, cuja ligação é do tipo em paralelo.

C) I, cuja ligação é do tipo em série.

D) I, cuja ligação é do tipo em paralelo.

51-(FUVEST-SP-013)

Em uma aula de laboratório, os alunos determinaram a força eletromotriz ε e a resistência interna r de uma bateria. Para realizar a tarefa, montaram o circuito representado na figura abaixo e, utilizando o voltímetro, mediram a diferença de

potencial V para diferentes valores da resistência R do reostato. A partir dos resultados obtidos, calcularam a corrente I no reostato e construíram a tabela apresentada na página de respostas.

a) Complete a tabela, na página de respostas, com os valores da corrente I.

b) Utilizando os eixos da página de respostas, faça o gráfico de V em função de I.

c) Determine a força eletromotriz ε e a resistência interna r da bateria.

Circuitos com geradores – exercícios

29-(PUC-RJ-013)

Um determinado circuito é composto de uma bateria de 12,0 V e mais quatro resistores, dispostos como mostra a figura.

a) Determine a corrente elétrica no ponto A indicado na figura.

b) Determine a diferença de potencial entre os pontos B e C apresentados na figura.

30-(PUC-RJ-013)

No circuito mostrado na figura, a diferença de potencial entre os pontos B e A vale, em Volts:

(A) 3,0 (B) 1,0 (C) 2,0 (D) 4,5 (E) 0,75

31-(MACKENZIE-SP-013)

Um professor solicitou a um aluno que calculasse o valor da resistência elétrica do resistor R representado ao lado, de maneira que a potência dissipada pelo resistor de 4 Ω fosse 36 W.

O estudante acertou a questão, pois sua resposta foi

a) 2 Ω b) 4 Ω c) 6 Ω d) 10 Ω e) 16 Ω

Receptores e associação de geradores e de receptores – (lei de Pouillet)

30-(UniFOA-RJ-013)

Os receptores elétricos são muito comuns no nosso dia a dia. Provavelmente você, que está lendo

esse artigo, deve ter alguns deles na sua residência. Definem-se receptores elétricos como qualquer

dispositivo que transforma energia elétrica em energia não elétrica que não seja exclusivamente em

energia térmica, pois os dispositivos que transformam e energia elétrica totalmente em energia térmica são definidos como resistores.

(http://educacao.uol.com.br/disciplinas/fisica/receptores-eletricos-ventiladores-liquidificadorese-batedeiras.htm)

A ddp nos terminais de um grande ventilador de teto instalado em um hospital, varia com a corrente

conforme o gráfico abaixo.

A resistência interna e a fcem desse receptor elétrico são, respectivamente:

a) 1 Ω e 37V b) 2 Ω e 37V c) 1 Ω e 40V d) 3 Ω e 37V e) 3 Ω e 40V

31-(UFES-ES-013)

O circuito indicado ao lado é composto de uma bateria não ideal e de uma carga resistiva (lâmpada L).

O gráfico representa a curva característica tensão U versus corrente I que a bateria fornece a diferentes cargas.

Considere que a bateria esteja operando com uma particular lâmpada, à qual fornece a particular corrente I = 6,0 A . Determine

A) a força eletromotriz da bateria;

B) a resistência interna da bateria;

C) a resistência dessa particular lâmpada;

D) a potência elétrica dissipada por essa lâmpada e o rendimento (eficiência) da bateria nessa situação de

operação.

Aparelhos de medição elétrica (amperímetros, voltímetros, ponte de Wheatstone)

36-(UFGD-MS-013)

A figura a seguir corresponde a um painel composto por cinco lâmpadas idênticas.

Supondo que o interruptor as conecte a uma bateria de 9 V, qual das lâmpadas não irá acender?

(A) I. (B) II. (C) III. (D) IV. (E) V.

37-(UEMA-MA-013)

Um estudante de Física, para verificar se um determinado condutor é ôhmico, usou uma fonte de tensão C.C. variável, um voltímetro, um amperímetro e fios de ligação. Ao ligar o circuito para diferentes tensões, obteve os pares de valores, (U(v), i(A)), (U₁=1,50, i₁=0,04), (U₂=3,00, i₂=0,08), (U₃=4,50, i₃=0,13), (U₄=6,00, i₄=0,16), (U₅=7,50, i₅=0,21), (U₆=9,00, i₆=0,25) e (U₇=12,00, i₇=0,32).

Nessas condições, pode-se concluir, em relação aos três aparelhos, que

A) o amperímetro foi ligado em paralelo com o condutor, e o voltímetro foi ligado em série com a fonte. O condutor não é ôhmico.

B) o voltímetro foi ligado em série com o condutor, e o amperímetro foi ligado em paralelo com a fonte. O condutor não é ôhmico.

C) o voltímetro foi ligado em paralelo com o condutor, e o amperímetro foi ligado em série com a fonte. O condutor é ôhmico.

D) o voltímetro foi ligado em paralelo com o condutor, e o amperímetro foi ligado em série com a fonte. O condutor não é ôhmico.

E) o amperímetro foi ligado em paralelo com o condutor, e o voltímetro foi ligado em série com a fonte. O condutor é ôhmico

38-(ESPCEX-013)

O amperímetro é um instrumento utilizado para a medida de intensidade de corrente elétrica em um circuito

constituído por geradores, receptores, resistores, etc. A maneira correta de conectar um amperímetro a um trecho do circuito no qual queremos determinar a intensidade da corrente é

a) em série

b) em paralelo

c) na perpendicular

d) em equivalente

e) mista

Capacitores - condensadores

52-(UERN-RN-PSV-013)

O capacitor equivalente de uma associação em série, constituída por 3 capacitores iguais, tem capacitância 2 pF.

Utilizando-se 2 destes capacitores para montar uma associação em paralelo, a mesma apresentará uma capacitância de

A) 3 pF. B) 6 pF. C) 12 pF. D) 18 pF.

53-(UFT-TO-013)

Determinar, respectivamente, a capacitância equivalente entre os terminais A e B e, também, a

energia acumulada entre esses terminais quando o circuito está submetido a uma diferença de potencial constante de 500 V.

(A) 100 μF; 50 J

(B) 65 μF; 8,125 J

(C) 50 μF; 8,125 J

(D) 200 μF; 60 J

(E) 80 μF; 20 J

54-(UniFOA-RJ-013)

O que realmente salva vidas em casos de parada cardiorrespiratória é o choque elétrico no coração (desfibrilação), o que pode ser feito por meio de um desfibrilador externo automático, sendo que nem

todos os casos de parada cardiorrespiratória têm indicação de choque elétrico.

(www.cardiologiasemfronteiras.com.br/2011/07/como-usar-o-desfibrilador-externo.html)

Um aparelho moderno de desfibrilação possui um circuito análogo ao descrito na figura abaixo.

Encontre a carga armazenada nesse desfibrilador sabendo que a tensão sobre a qual será ligado será de 110V entre A e B e os capacitâncias são determinadas por: C₁=20μF; C₂=30μF; C₃=10μF; C₄=40μF; C₅=50μF e C₆=60μF.

a) 210μC b) 4.200μC c) 16,2μC d) 12μC e) 38μC

Resoluções Vestibulares Recentes

Eletrodinâmica – 2014 - 2013

01- Cálculo da resistência elétrica R da lâmpada pelas especificações --- P=U²/R --- 24=12²/R ---

R=144/24 --- R=6Ω.

Sendo essa R=6 Ω constante, quando a lâmpada estiver sob ddp (tensão) de 6V a corrente i que circula por ela será --- R=U/i --- 6=6/i --- i=1 A.

Potência elétrica dissipada pela lâmpada quando sob ddp de U=6V --- P=R.i² = 6.1² --- P=6W.

R- A

02- a) Observe na figura fornecida que a resistência equivalente R_eq está entre os pontos A e B:

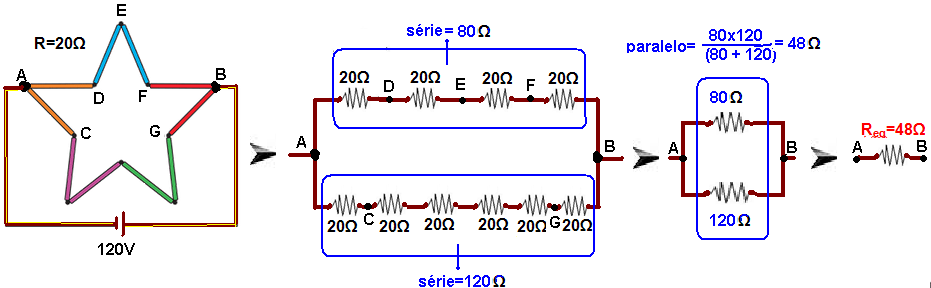
R_eq=48Ω

b) Como os ramos superior e inferior estão associados em paralelo a tensão U=120V é a mesma em cada um --- sendo a resistência R=20Ω de cada barra (resistor) a mesma, a tensão em cada resistor do ramo superior vale U_s=120/4=30V e em cada resistor do ramo inferior vale U_i=120/6=20V

A potência elétrica dissipada em cada resistor (barra) do ramo superior vale P_s=U_s²/R=30²/20=45W e em cada resistor do ramo inferior vale P_i=U_i²/R=20²/20=20W

Cores laranja; uma no ramo superior (45W) e outra no inferior (20W) --- P_l=45 + 20 --- P_l=65W

Cores azul; duas no ramo superior (2x45W=90W) --- P_a=90W

Cores vermelha; uma no ramo superior (45W) e outra no inferior (20W) --- P_v=45 + 20 --- P_v=65W

03- Colocando a chave na posição B você terá o circuito da figura abaixo cuja sequência nos

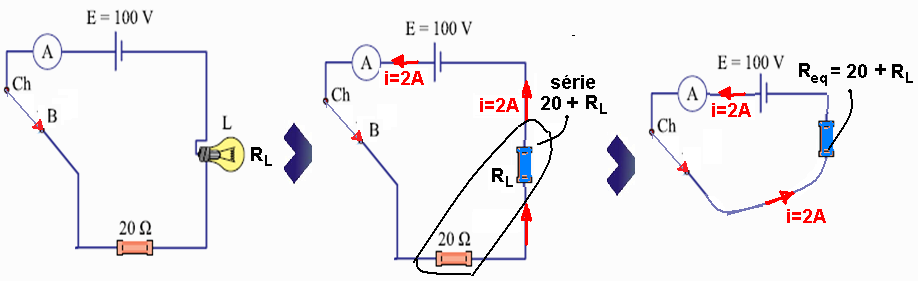
fornece o resistor equivalente R_eq=20 + R_L --- R_eq=U(E)/i --- 20 + R_L=100/2 --- 20 + R_L=50 --- R_L=30Ω.

Veja que o enunciado afirma que, com a chave em B onde i=2A, a potência elétrica dissipada pela lâmpada é de P_d=60W, o que nos forneceria uma resistência de --- P=R_L.i² --- 60=R_L.2² --- R_L=15Ω.

Como o exercício afirma que a resistência da lâmpada é constante, essa potência fornecida de 60W é incompatível e vamos ignorá-la na continuação do exercício e considerar a resistência da lâmpada como seno R_L=30Ω.

Colocando agora a chave em A, a nova resistência equivalente será R_eq=45 + 20 + 30=95Ω (figura).

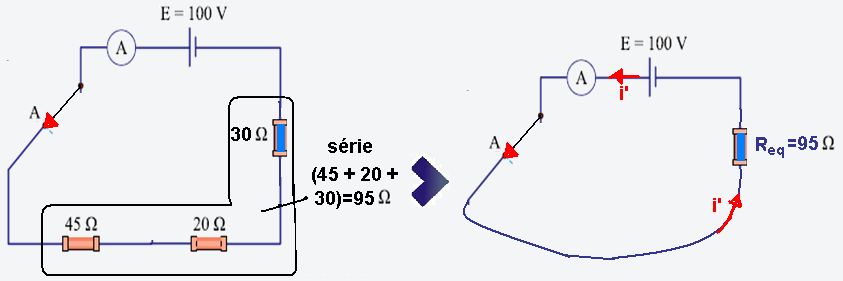
R_eq=E/i’ --- 95=100/i’ --- i’=100/95≈1A --- potência dissipada pelo circuito --- P=R_eq.i²=95.1²=95W.

Energia elétrica dissipada pelo circuito durante Δt=2min=2.60=120s --- W=P.Δt=95.120 ---

W=11400J=1,1.10⁴J.

04- A) Falsa --- desligando-se L₁, L₂ manterá seu brilho já que será percorrida pela mesma corrente que antes pois, como estão em paralelo a tensão U é a mesma antes e depois de desligar L₁ e a potencia de L₂ também será a mesma já que P₂=U²/R e R também é a mesma.

B) Falsa --- pela segunda lei de Ohm R=ρℓ/S e, sendo o material (ρ) o mesmo e o comprimento (ℓ) do filamento o mesmo, a lâmpada 2 que é mais grossa (maior S), possuirá menor resistência elétrica R e, consequentemente será pecorrida por maior corrente elétrica brilhando mais

C) Falsa --- os filamentos possuem resistências elétricas diferentes possuindo diferentes brilhos.

D- Correta --- veja (B)

R- D

05- Usando os valores nominais de cada lâmpada idênticas você pode calcular o valor da resistência elétrica de cada uma pela expressão P=U²/R --- 100=100²/R --- R=100Ω.

Observe na figura abaixo que a lâmpada L₁ de resistência R=100 Ω, é percorrida por i₁, e pelo enunciado sob potência de 100W, tal que --- P₁=R.i₁² --- 100=100. i₁² --- i₁=1 A (corrente por L₁ quando sob potência de 100W).

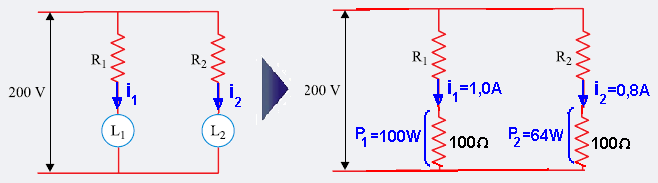
Observe na figura acima que a lâmpada L₂ de resistência R=100 Ω, é percorrida por i₂, e pelo enunciado sob potência de 64W, tal que --- P₂=R.i₂² --- 64=100. i₁² --- i₂=0,8A. (corrente por L₂ quando sob potência de 64W)

No trecho série R₁ e L₁ (R=100 Ω), percorridos por i₁=1 A e sob ddp de U=200V (paralelos à fonte) você terá:

R_eq=(R₁ + 100) --- U=200V e i₁=1 A --- R_eq=U/i₁ --- R₁ + 100 = 200/1 --- R₁=100 Ω.

No trecho série R₂ e L₂ (R=100 Ω), percorridos por i₁=0,8 A e sob ddp de U=200V (paralelos à fonte) você terá:

R_eq=(R₂ + 100) --- U=200V e i₂=0,8 A --- R_eq=U/i₂ --- R₂ + 100 = 200/0,8 --- R₂ + 100 = 250 ---

R₂=150 Ω.

Se R₁ = 100 Ω, L₁ dissipará uma potência de 100W e se R₂ = 150 Ω, L₂ dissipará uma potência de 64W,

conforme pedido no enunciado.

R- C

06- Você deve se lembrar de que a potência elétrica máxima que um gerador (no caso associação de geradores) fornece ao circuito externo (no caso, reostato R) ocorre quando a resistência externa R é igual à resistência interna r da associação de geradores, ou seja, quando R=r_equivalente --- na associação série --- r_equ=r + r=2r --- R=2r --- na associação paralelo --- r_eq=(r.r)/(r + r)=r/2 --- r_eq=r/2 --- R=r/2 --- veja na figura abaixo que a resposta corresponde à alternativa C:

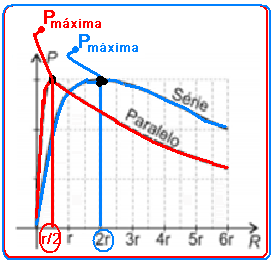
R- C

07- Associação série

Todos os resistores são ligados um em seguida ao outro.

A resistência equivalente (R_eq) é igual à soma das resistências parciais --- no circuito 1 R_eq=R; no 2, R_eq=2R e no 3 R_eq=3R --- a resistência equivalente da associação aumenta.

A tensão (diferença de potencial) U, constante, nos terminais da associação (entre A e B) é igual à soma das tensões em cada resistor, ou seja, no circuito 1 U₁=U/1; no 2 U₂=U/2 e no 3 U₃=U/3 --- a diferença de potencial nos extremos de um mesmo resistor diminui.

Pela lei de Ohm, como R_eq=U/i, a corrente elétrica i é inversamente proporcional à resistência equivalente R_eq, 0u seja, a medida que você acrescenta resistores, R_eq aumenta e, consequentemente i diminui.

R- E --- Observação: Você poderia chegar à mesma conclusão observando a tabela fornecida e lembrando que, no caso, o voltímetro marca a ddp em cada resistor e o amperímetro a corrente total no circuito.

08- Cálculo da resistência equivalente R_eqi antes de estabelecer o curto circuito:

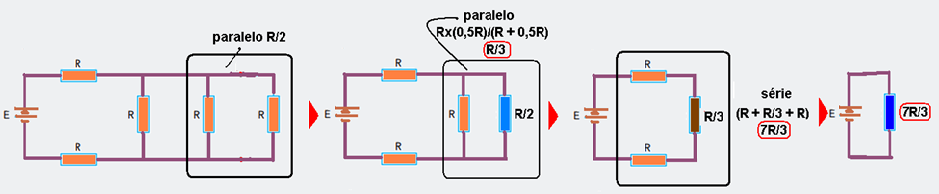
R_eqi=7R/3 --- P_i=U²/R_eqi=E²/R_eqi=E²/(7R/3) --- P_i=3E²/7R (I)

Cálculo da resistência equivalente R_eqf depois de estabelecer o curto circuito:

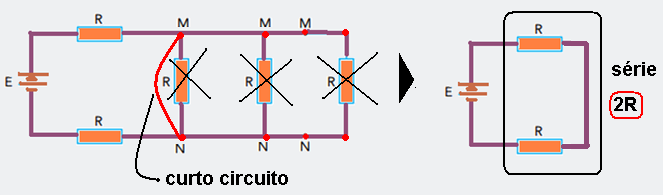
R_eqf=2R --- P_f=E²/R_eqf --- P_f=E²/2R (II)

(II)/(I) --- P_f/P_i=(E²/2R)x(7R/3E²)=7/6

R- D

09- a) Observe no circuito que o resistor R e a lâmpada tipo led estão associados em série e uma das características da associação série é que a corrente elétrica que circula em cada aparelho é a mesma, ou seja, i_ℓ = i_R --- o enunciado fornece que a tensão (ddp) na lâmpada led é U_ℓ=2,5V e, pelo gráfico, você

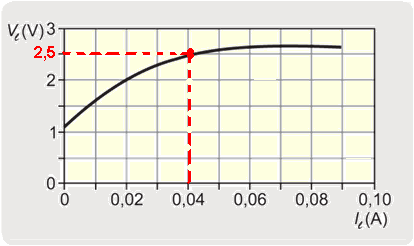
observa que i_ℓ=0,04 A --- assim, i_ℓ = i_R=0,04 A

b) Outra característica da associação série é que a tensão total (da bateria U=4,5V) é a soma das tensões

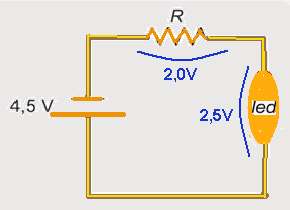
de cada elemento do circuito série --- assim, U = U_ℓ + U_R --- 4,5 = 2,5 + U_R --- U_R=2,0V --- R=U_R/i_R ---

R=2/0,04 --- R=50Ω

c) Corrente elétrica total i no circuito, agora com U=3V e R=50Ω pode ser determinada por P=i.U, onde P é fornecida P=60mW=60.10^-3W --- 60.10^-3 = i.3 --- i=60.10^-3/3 --- i=20.10^-3A --- essa corrente é a mesma que flui pelo resistor R=50Ω (característica da associação série) --- em R --- P=R.i²=50.(20.10^-3)² 50.400.10^-6 --- P=20000.10^-6 =20.10^-3 --- P=20mW

10- Segunda lei de Ohm: Através de pesquisa, Ohm descobriu que a resistência elétrica de um condutor, mantida a temperatura constante, é diretamente proporcional ao comprimento L do fio, é inversamente proporcional à área de seção reta transversal S e depende do material que constitui o corpo (essa dependência do valor da resistência em relação ao material que constitui o resistor, chama-se resistividade do material e representa-se pela letra grega ρ “rô”).

Matematicamente:

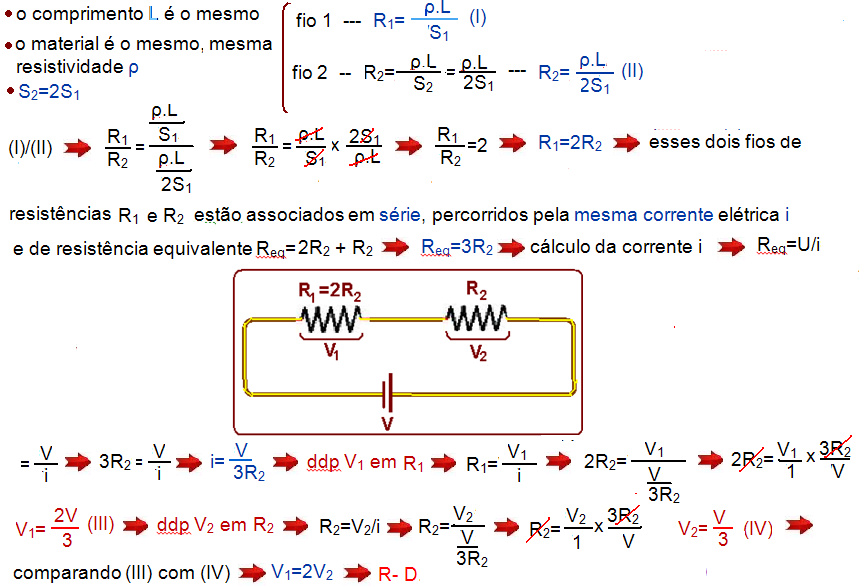
11- Da curva S do gráfico você pode calcular a resistência equivalente da associação série R_S e da curva P do gráfico você pode calcular a resistência equivalente da associação série R_p: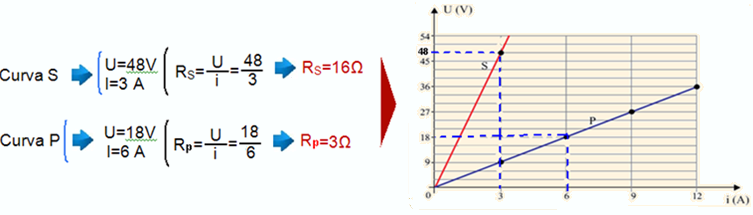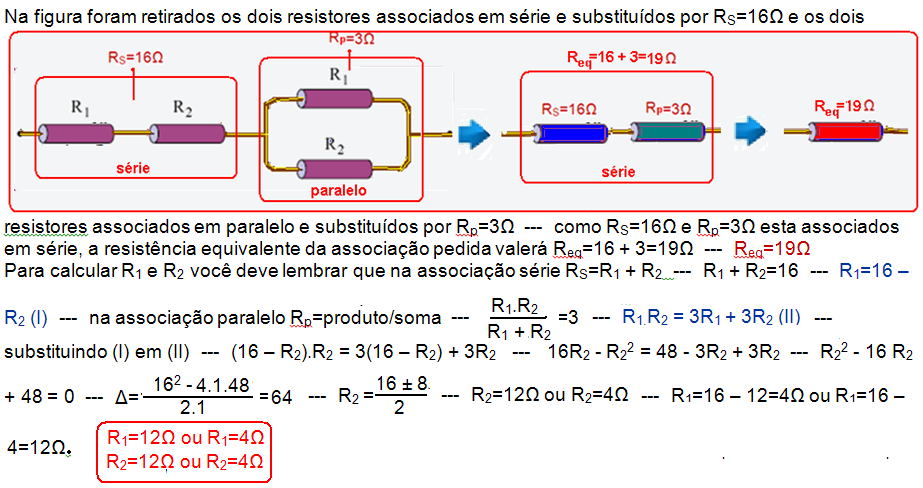

12-

b) Inicialmente você deve determinar, utilizando o gráfico1, a intensidade do campo magnético H, sendo

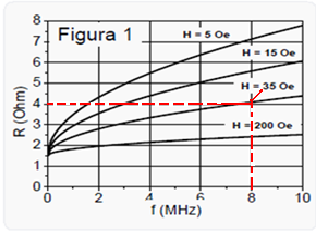
fornecido f=8MHz=8.10⁶Hz e R≈4Ω --- pelo gráfico --- H=35Oe --- em seguida, com esse valor

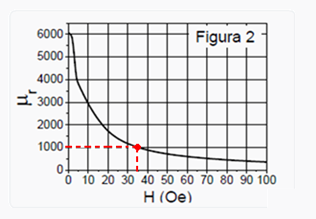
13- 04- Cálculo das resistências --- R₁=V₁/i₁=8/2=2Ω --- R₂=V₂/i₂=4/2=2Ω --- R₃=V₃/i₃=4/2=2Ω --- R₁=R₂=R₃.

Cálculo das potências --- P₁=i₁.V₁=4.8=32W --- P₂=i₂.V₂=2.4=8W --- P₃=i₃.V₃=2.4=8W --- P₁> P₂₃

R- D

14- Veja no circuito abaixo:

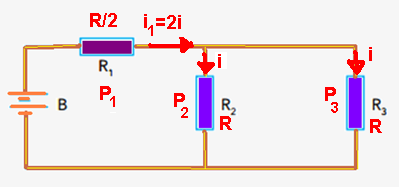
Relação entre P₂ e P₃:

Como R₂=R₃=R e, como eles estão em paralelo estão submetidos à mesma ddp (tensão) U eles são percorridos pela mesma corrente elétrica i₂=i₃=i --- P₂=R₂.i₂²=R.i² --- P₃=R₃.i₃²=R.i² --- portanto P₂=P₃.

Potência em R₁:

Pelo enunciado R₁=R₂/2=R₃/2=R/2 --- i₁=i₂ + i₃=i + i=2i --- P₁=R₁.i₁²=(R/2).(2i)²=(R/2)x4i² --- P₁=

2Ri² --- mas, Ri²=P₂=P₃ --- P₁= 2P₂= 2P₃

R- D

15-

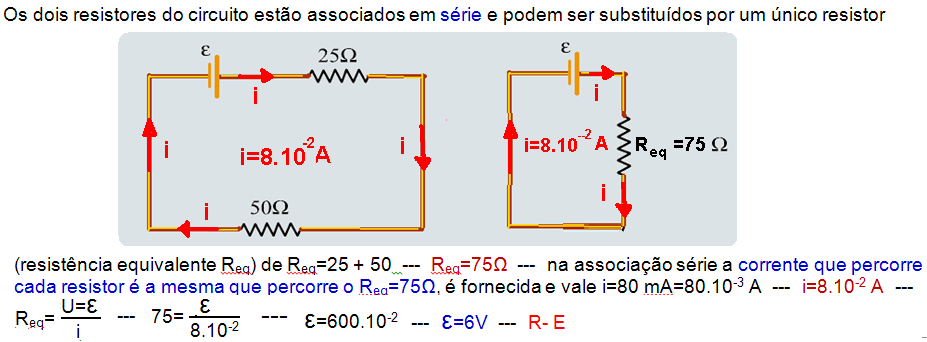
16- O voltímetro ideal (resistência interna infinita), associado corretamente (em paralelo às pilhas e à lâmpada) indica a ddp Ufornecida pelas duas pilhas à lâmpada que é fornecida --- U=3,00V --- o

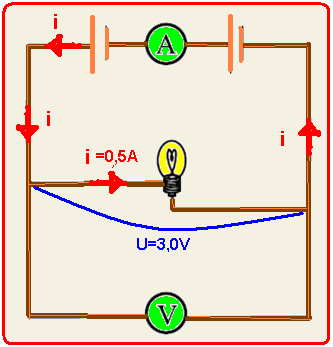
amperímetro ideal (resistência interna nula) indica a corrente elétrica i que circula pela lâmpada, também fornecida --- i=0,50 A

--- cálculo da potência P da lâmpada, que não é o valor nominal, nas condições do exercício --- P=i.U=0,50x3,00 --- P=1,50W --- o enunciado afirma, sabe-se que a potência dissipada por efeito Joule no filamento da lâmpada corresponde a 1/4 do valor nominal P_n, indicado pelo fabricante, ou seja, P=P_n/4 ---

P_n=4P=4x1,50 --- P_n=6,0W --- pela expressão P_n=U_n²/R você observa que, sendo a resistência R da lâmpada a mesma, a potência nominal P_n é diretamente proporcional ao quadrado da tensão (ddp) nominal U_n, ou seja, como a potência foi quadruplicada, a tensão deve ser dobrada, (2)²=4 para manter a igualdade --- Un=2.3,00 --- U_n=6,0V

R- D

Corrente elétrica

37- Intervalo de tempo durante o qual a bateria está descarregando, até acabar, ou seja descarregar sua carga máxima que é de q=75 A.h --- i=q/∆t --- 75A.h = 50A/∆t --- ∆t=75A.h/50A --- ∆t=1,5h --- supondo a velocidade de V=60km/h constante --- V=∆S/∆t --- 60=∆S/1,5 --- ∆S=90,0km/h --- R- C.

38- Deve funcionar assim, se um deles mantém a lâmpada acesa, o outro, quando acionado, deve apagá-la e vice versa, mantendo sempre o circuito fechado. Analise atentamente cada alternativa:

a) Falsa --- tem apenas um fio ligado à rede elétrica externa o que impedirá a lâmpada de acender, não fechando o circuito, qualquer que seja a posição das chaves.

b) Falsa --- a lâmpada está apagada --- se você mudar a chave da esquerda ela continuará apagada --- se você mudar a chave da direita ela continuará apagada --- se você mudar as duas chaves, provocará um curto-circuito.

c) Falsa --- a lâmpada está apagada --- se você mudar a chaves da direita ou da esquerda ela continuará apagada.

d) Falsa --- a lâmpada só acenderá com as duas chaves na posição superior --- se você mudar uma delas, a outra não acenderá a lâmpada.

e) Correta --- esse é o único caso em que você consegue acender ou apagar a lâmpada invertendo apenas uma das

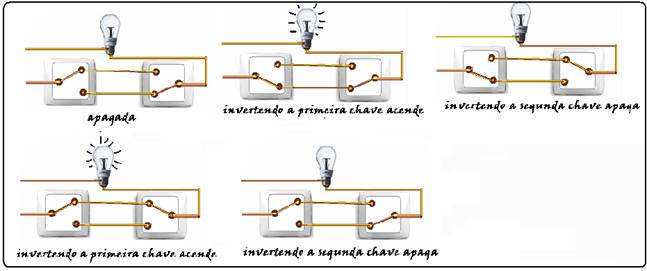
chaves, não importando a posição da outra.

R- E.

Potência elétrica – Energia elétrica

51- Em ∆t=2min=120s, a água recebeu Q=24000cal de energia térmica, que, em joules vale --- regra de três --- 1cal – 4J --- 24000cal – W (J) --- W=24000x4 --- W=96000J --- Potência elétrica do aquecedor --- P=W/∆t=96000/120 --- P=800W --- P=U²/R --- 800=120²/R --- R=14400/800 --- R=18Ω --- pelo enunciado, em ∆t=2min=120s, a temperatura da água variou de 20°C a 80°C --- ∆θ=(80 – 20)=60^oC --- equação fundamental da calorimetria --- Q=m.c.∆θ --- 24000=m.1.60 --- m=400g --- R- B.

52- Painel --- Pp=Wp/24h --- 810=Wp/24h --- Wp=19440Wh (energia fornecida pelo painel em 1 dia) --- energia dissipada pela lâmpada em 1 dia --- Pl=Wl/24.∆t --- 9=Wl/24.∆t --- Wl=216.∆t (W) --- Wp = Wl --- 19440 = 216∆t --- ∆t=90h --- R- D.

53- a) Pelo enunciado observe que, para cada 100g de bauxita você tem 55g de óxido de alumínio (Al₂O₃) e 45g de resíduos --- massa molar do óxido de alumínio (Al₂O₃) --- 2x(27) + 3x(16)=102g.mol^-1 --- massa de alumínio que compõe o óxido de alumínio (alumina) --- Al₂=2x(27)= 54g.mol^-1 --- regra de três --- 102g de Al₂O₃ – 54g de Al --- 55g de Al₂O₃ – x --- x=55x54/102 --- x=29,12g de alumínio em 100g de bauxita --- cálculo da massa de resíduos --- regra de três --- 29,12g de Al – 45g de resíduos --- 32.10⁶t de Al – y --- y=45x32.10⁶/29,12 --- y=49,45t.10⁶≈

4,9.10⁷t de resíduos.

b) Dados --- tempo de duração do banho --- ∆t=10mim=10.60=600s --- potência elétrica do chuveiro --- P=3000W --- P=energia(W)/ ∆t --- 3000=W/600 --- W=18.10⁵J (energia dissipada num banho de 10min) --- pelos dados, 1 latinha 3,6.10⁶J --- regra de três --- 1 latinha – 3,6.10⁶J --- n latinhas – 18.10⁶J --- n=3,6.10⁵/18.10⁶=0,2.10 --- n=2 banhos.

54- Pelo enunciado, a eficiência ε é fornecida pela razão entre a quantidade de luz produzida Q e a energia elétrica W consumida --- ε =Q/W (I) --- potência=energia/tempo de utilização --- P=W/∆t --- W=P.∆t (II) --- substituindo (II) em (I) --- ε =Q/P.∆t --- para a lâmpada incandescente de 40W --- ε’=600lm/40∆t --- o intervalo de tempo ∆t é o mesmo para cada alternativa.

a) Falsa --- lâmpada fluorescente de 8W --- se uma lâmpada fluorescente de 40W emite Q=3000lm, uma de 8W emitirá 5 vezes menos, ou seja, Q=3000/5=600lm --- ε=600lm/8∆t --- observe que ε > ε’.

b) Falsa --- lâmpada fluorescente de 40W --- ε=3000lm/40∆t --- observe que ε > ε’.

c) Verdadeira --- lâmpada fluorescente de 8W --- ε=600lm/8∆t --- ε’ < ε e mesmo Q=600lm.

d) Falsa --- veja (b).

e) Falsa --- veja (B).

R- C.

Resistores – Primeira lei de Ohm – Potência elétrica em um resistor

47- Resistência elétrica de um resistor – representa a medida da dificuldade imposta à movimentação das cargas elétrica que o atravessam (corrente elétrica), e é definida como a razão entre a diferença de potencial (U) nos terminais do resistor e a intensidade da corrente elétrica ( i ) que o atravessa:

A expressão acima é conhecida como Lei de Ohm

Um ohm (1Ω) é o valor da resistência elétrica entre dois pontos P e Q de um condutor quando, sob diferença de potencial de 1 volt

(1V) é percorrido por uma corrente elétrica constante de 1 ampère (1A).

Representação simbólica:

Primeira lei de Ohm – Se a resistência elétrica de um resistor for constante, a diferença de potencial aplicada nos seus extremos é diretamente proporcional à intensidade da corrente elétrica, ou seja,U₁/i₁=U₂/i₂= . . . =U/i=constante. Nesse caso eles são chamados de resistores (ou condutores) ôhmicos e, como a relação R=U/i é uma função do primeiro grau o gráfico U x i tem o aspecto do gráfico da esquerda da figura abaixo:

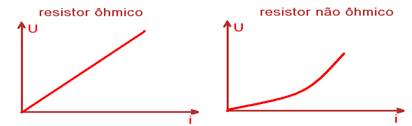
Qualquer gráfico U x i diferente do gráfico da esquerda da figura acima não representa um resistor ôhmico, como por exemplo, o gráfico da direita.

R- A.

48- Corrente que provoca fibrilação ventricular passando pelo tórax --- iv=500mA=500.10-3=0,5 A --- corrente provocada pelo poraquê de U=1500Vquando o pescador o segura com uma mão na cabeça e outra na cauda e que passa pelo seu tórax de R=1000Ω --- R=U/i --- 1000=1500/i --- i=1500/1000 --- i=1,5 A --- relação entre essas correntes --- i/iv=1,5/0,5 --- i=3iv --- R- E.

49- A) Na posição INVERNO o chuveiro deve dissipar a maior potência (4800W) --- como a ddp (tensão) U é constante, pela expressão P=U²/R você observa que a potência P é inversamente proporcional à resistência elétrica R e,

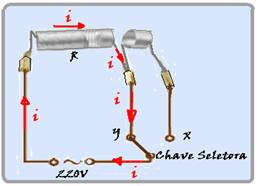
assim para uma maior potência corresponde uma menor resistência elétrica, o que ocorre quando a chave seletora estiver ligada na posição Y.

B) Na posição INVERNO a potência deve ser P=4800W --- ∆t=10min=10/60=1/6h --- P=W/∆t --- 4800=W/(1/6) --- W=0,8kWh.

C) Uma pessoa num dia --- P=0,8kWh --- 4 pessoas num dia --- P=3,2kWh --- 4 pessoas num mês --- P=3,2x30 = 96kWh --- como a residência consome num mês 200kWh, sem os banhos a economia será de W’=200 – 96=104kWh.

50- Num chuveiro elétrico, normalmente de tensão 220V (mantida constante), as posições inverno (quente), verão (morna) correspondem à diferentes potências. Quando você muda o cursor do chuveiro, por exemplo, do verão para

o inverno, você está diminuindo a resistência elétrica no interior do chuveiro e, consequentemente aumentando a potência, fazendo-o aquecer mais, claro que mantendo a vazão constante. O oposto ocorre quando você muda o cursor do chuveiro do inverno para o verão. Isso acontece porque, para a mesma tensão, a potência é inversamente proporcional à resistência, pois, P=U²/R, com U constante.

R- D.

51- O condutor possui resistência ôhmica, pois o gráfico é uma reta inclinada a partir da origem e a ddp U é diretamente proporcional a i de modo que R seja constante --- R= U/i= 20/0,5 = 40/1 = 60/1,5 = 80/2=40Ω --- P=R.i2=40.(1,5)2 P=40.2,25 --- P=90W --- R- C.

52- O funcionamento do fusível baseia-se no princípio segundo o qual uma corrente que passa por um condutor gera calor proporcional ao quadrado de sua intensidade --- quando a corrente atinge a intensidade máxima tolerável, o calor gerado não se dissipa com rapidez suficiente, derretendo um componente e interrompendo o circuito.

Disjuntores --- modernamente, nos circuitos elétricos de residências, edifícios e indústrias, em vez de fusíveis, utilizam-se dispositivos baseados no efeito magnético da corrente denominados disjuntores --- em essência, o disjuntor é uma chave magnética que se desliga automaticamente quando a intensidade da corrente no condutor supera certo valor --- tem sobre o fusível a vantagem de não precisar ser trocado --- uma vez resolvido o problema que provocou o desligamento, basta religá-lo para que a circulação da corrente se restabeleça --- R- D.

Segunda lei de Ohm (Resistividade)

33- U=270V -- l=1,5m --- ρ=1,8Ωm --- S=30cm²=30.10^-4=3.10^-3m³ --- R=ρ.l/S=1,8.1,5/3.10^-3 --- R=900Ω --- R=U/i --- 900=270/i --- i=270/900=0,3 A=300mA --- a corrente elétrica fatal é de 200mA --- R- E.

34- Segunda lei de Ohm --- R=ρℓ/S=1,8.10-9.3.105/2.10-4=1,8.1,5.10o --- R=2,7Ω --- R- D.

Resistor equivalente nas associações série, paralelo e mista – curto circuito

49- Série --- R_eq=2R --- R_eq=U/i₁ --- 2R=U/i₁ --- i₁=U/2R --- paralelo --- R_eq=R/2 --- R/2=U/i₂ --- i₂=2U/R --- i₂ – i₁ = 9 --- 2U/R – U/2R=9 --- 3U/2R=9 --- 3.60/2R=9 --- R=10Ω --- R- D.

50- Pelo enunciado A’A=R₁ e B’B=R₂ --- denominando AP’ de m e P’B de n e observando que os

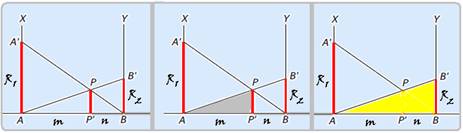
triângulos nas figuras são semelhantes --- P’P/R₂=m/(m + n) (I) --- os dois triângulos hachurados

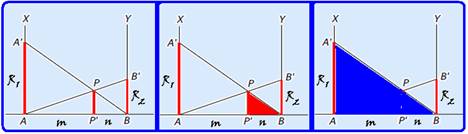
nas figuras a seguir também hachurados são semelhantes --- P’P/R₁=n/(m + n) (II) --- (I) + (II) --- P’P/R₂ + P’P/R₁ = m/(m + n) + n/(m + n)=(m + n)/(m + n)=1 --- P’P/R₂ + P’P/R₁=1 --- P’P.R₁ + P’P.R₂=R₁.R₂ --- P’P=R₁.R₂/(R₁ + R₂).

Características de associação série e associação paralela

60- Série --- R_eq=2R --- R_eq=U/i₁ --- 2R=U/i₁ --- i₁=U/2R --- paralelo --- R_eq=R/2 --- R/2=U/i₂ --- i₂=2U/R --- i₂ – i₁ = 9 --- 2U/R – U/2R=9 --- 3U/2R=9 --- 3.60/2R=9 --- R=10Ω --- R- D.

61- Como as lâmpadas estão associadas em paralelo, a tensão U é a mesma para cada lâmpada e vale U=120V --- potência de cada lâmpada P=60W --- corrente i em cada lâmpada --- P=i.U --- 60=i.120 --- i=0,5 A --- a corrente limite do fusível (corrente total de entrada) deve ser de it=10 A --- essa corrente é dividida em n lâmpadas cada uma com 0,5 A --- it=n.i --- 10=n.0,5 --- n=20 lâmpadas --- R- C.

62- O mesmo aquecimento corresponde à mesma quantidade de energia, assim, Wparalelo=Wsérie --- P=W/∆t --- W=P.∆t --- Wp = Ws --- Pp.∆tp = Ps.∆ts --- P=U2/R (U constante, dado do exercício) --- (U2/Rp).∆tp = (U2/Rs),∆ts --- ∆tp/Rp=∆ts/Rs --- associação paralelo Req=Rp=R/2 --- associação série Req=Rs=2R --- ∆tp/(R/2) = ∆ts/2R --- ∆tp = ∆ts/4 --- ∆ts=1min=60s --- ∆tp=60/4=15s --- R- E.

63- Pelo enunciado, se o acerto é zero, somente a chave C é fechada e o circuito fica conforme a

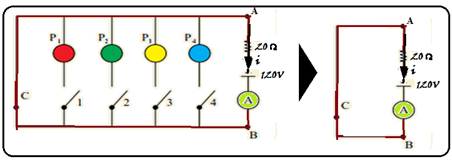
figura --- o amperímetro indica a corrente no circuito de valor --- R=U/i --- 20=120/i --- i=6 A --- se o participante errar apenas P₂, não passará corrente por ela e a corrente circulará apenas nas lâmpadas P₁, P₃ e P₄, com a chave C aberta

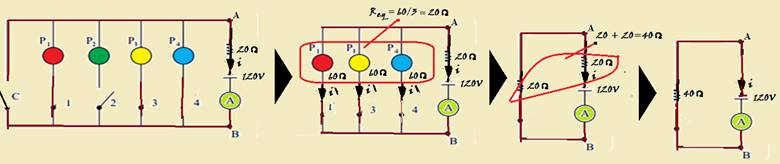
--- veja a sequência indicada na figura acima onde a resistência equivalente vale R_eq=40Ω --- R_eq=U/i --- 40=120/i --- i=3 A.

64- Cálculo da resistência equivalente para as 25 lâmpadas, cada uma com resistência R associadas em série (i é a mesma e a resistência equivalente é a soma da resistência de todas as lâmpadas em série) --- R_eqs=25R --- na associação em paralelo que fornece a resistência equivalente total (R_eqtotal), você tem 4 resistência de 25R associadas em paralelo --- 1/R_eqtotal= 1/25R + 1/25R + 1/25R + 1/25R=4/25R --- R_eqtotal=25R/4 (I) --- cálculo da resistência equivalente total pelos valores nominais fornecidos (potência elétrica e tensão totais) --- P=U²/R_eqtotal --- 22 = 220²/R_eqtotal --- R_eqtotal=48400/22 --- R_eqtotal=2200Ω (II) --- igualando (I) com (II) --- 25R/4 = 2200 --- R=8800/25=352Ω ---

R- C.

65- a) Estando esses aparelhos funcionando normalmente, todos eles estão submetidos à mesma ddp (tensão) que é de U-110V e, para que isso ocorra, todos esses aparelhos devem estar associados em paralelo.

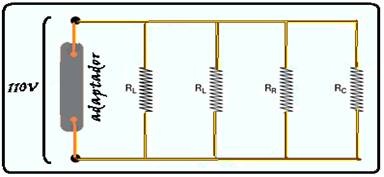
Como todos os aparelhos estão funcionando dentro das especificações comerciais, a potência total dissipada é a soma da potência de cada um desses aparelhos --- P_total=40 + 40 + 20 + 120=220W --- P_total=i_total..U --- 220= i_total.110 ---

i_total=2 A.

b) Tempo de funcionamento --- ∆t=30diasx4h=120h --- P_total=W/∆t --- 220W=W/120h --- W=26400W=26,4kWh --- custo --- C$=26,4x0,30=7,92 --- C$=7,92 reais.

Cálculo de correntes, tensões e potências em associações mistas

42- Um voltímetro ideal (resistência interna infinita) inserido na entrada indicaria --- V_entrada=R_eq.i=(R₁ + R₂).i --- um

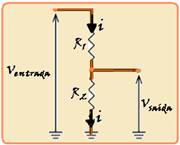
voltímetro ideal (resistência interna infinita) inserido na saída indicaria --- V_saída=R_eq.i=R₂.i --- pelo enunciado V_saída=

V_entrada/10 --- R₂.i = (R₁ + R₂).i/10 --- 10R₂=R₁+ R₂ --- 9R₂=R₁ --- R₁/R₂=9.

43-

R- C.

44- Observe que entre os pontos P (de potencial +5V) e A você tem o resistor de 4kΩ em circuito aberto e que, nesse trecho não passa corrente --- assim, o potencial no ponto A é o mesmo que no ponto P e vale +5V --- observe também que os dois resistores de 2kΩ estão em paralelo e devem ser substituídos por um único de R_eq=produto/soma=(2x2)/(2 + 2) --- R_eq=1kΩ --- haverá passagem de corrente elétrica apenas nos trechos PBQ (veja

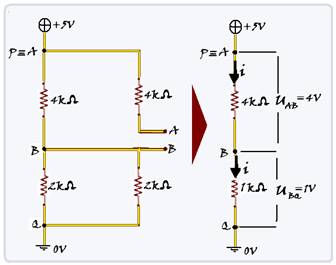
figura) e nele os resistores de 4kΩ e 1kΩ estão em série, sobrando apenas um resistor de R=4 + 1=5kΩ submetido a uma ddp de U=(5 – 0)=5V --- R=U/i --- 5.10³ = 5/i --- i=5/5.10³ --- i=1.10^-3 A ou i=1m A --- entre A e B --- R_AB=U_AB/i --- 4.10³=U_AB/10^-3 --- U_AB=4.10³.10^-3 --- U_AB=4V --- entre B e Q --- R_BQ=U_BQ/i --- 1.10³=U_BQ/10^-3 --- U_BQ=1.10³.10^-3 --- U_BQ=1V --- R- B.

Geradores - associação de geradores

48- Observe na sequência abaixo o cálculo do resistor equivalente de resistência R_eq=10Ω e da

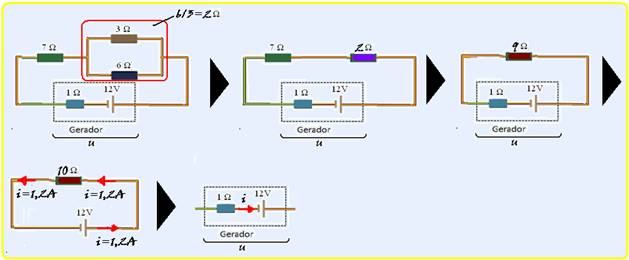
corrente total i --- R_eq=ε /i --- 10=12/i --- i=1,2 A --- cálculo da diferença de potencial U nos terminais do gerador de resistência interna r=1Ω --- Usando a equação do gerador --- U= ε – r.i=12 – 1.1,2 --- U=10,8V --- R- C.

49- Corrente i no motor de equação U=E’ + r’.i --- 1,2=1,0 + 0,2i --- i=1 A --- tempo que ele demora

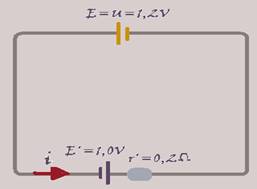
para dissipar a carga Q=1200mAh=1,2Ah fornecida pelo motor --- i=Q/t --- 1A = 1,2Ah/∆t --- ∆t=1,2h --- R- C.

50- A ligação em paralelo obtida quando se liga entre si todos os pólos positivos dos geradores (o terminal da união é o de mais alta tensão do circuito) e todos os pólos negativos (o terminal de união é o de mais baixa tensão do circuito). Nesse tipo de associação convém que todos os geradores tenham a mesma força eletromotriz E, para que não dissipem parte da energia que fornecem ao circuito externo.

Características desse tipo de associação:

A intensidade de corrente elétrica se subdivide entre os geradores

A força eletromotriz da associação é igual àquela de cada um dos geradores --- E_eq=E

Observe que, quando você liga as duas baterias do exercício em paralelo (figura I) a tensão do sistema é a mesma que a da bateria carregada --- R- D.

51- a) Utilizando a primeira lei de Ohm (R=V/i) você pode completar a tabela --- quando V=1,10V e R=4,40Ω --- 4,40 = 1,10/i --- i=0,25 A --- quando V=0,96V e R=1,60Ω --- 1,60 =0,96/i --- i=0,60 A.

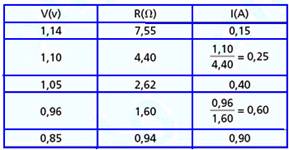
b) Construindo o gráfico a partir dos valores da tabela:

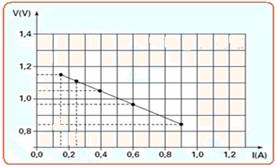
c) Você pode obter a força eletromotriz do gerador, prolongando a reta representativa até tocar o eixo das tensões ---

este ponto fornece a força eletromotriz ε que no caso é aproximadamente de ε≈1,20V --- a resistência interna r pode ser determinada pela equação do gerador --- V = E – r.i --- quando, por exemplo V=0,96V, i=0,6 A --- 0,96 = 1,2 – r.0,6 --- r≈0,4Ω.

Circuitos com geradores

29- a) Observe na seqüência abaixo o cálculo da resistência do resistor equivalente (R_eq) ---

R_eq=U/i --- 4,5.10³=12/i --- i=12/4,5.10³ --- i=2,7.10^-3A=2,7mA.

b) Observe na figura abaixo os valores das correntes devidamente distribuídas --- entre os pontos B

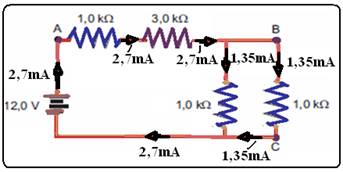
e C, R=1kΩ e i=1,35.10^-3 A --- R=U/i --- 1.10³=U/1,35.10^-3 --- U=1,35.10^-3.10³ --- U=1,35V.

30- Observe na sequência abaixo o cálculo da resistência do resistor equivalente --- R_eq=U/i ---

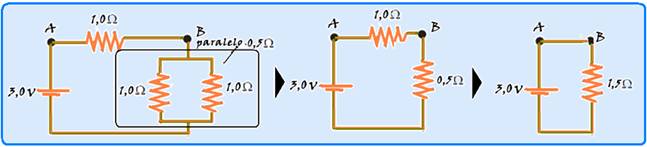
1,5=3/i --- i=2A ---entre os pontos A e B flui uma corrente i=2A na resistência de R=1Ω --- R=U_AB/i --- U_AB=1.2=2V --- R- C.

31- Cálculo da corrente elétrica i que percorre o resistor de 4Ω quando dissipa uma potência de 36W --- P=R.i² --- 36=4.i² --- i=3A --- observe que a resistência equivalente (R_eq) é percorrida pela corrente i=3A quando submetida à ddp (tensão) de U=24V --- R_eq=U/i=24/3=8Ω --- observe na

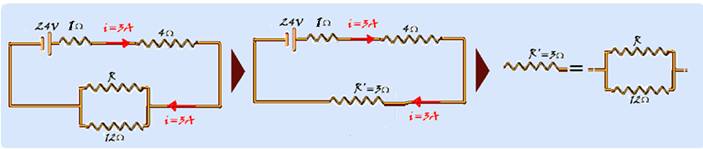
sequência abaixo que, como R_eq=8Ω, a resistência R’ (que corresponde a R associado em paralelo com 12Ω) deve valer R’=8 - (1 + 4) =3Ω --- 3=produto/soma=12R/(12 + R) --- 3=12R/(12 + R) --- 36 + 3R=12R --- 9R=36 --- R=4Ω --- R- B.

Receptores e associação de geradores e de receptores

30- Equação do receptor --- U=E’ + r.i --- pelo gráfico --- quando U=45V, i=8 A --- 45=E’ + r.8 (I) --- quando U=40V, i=3 A --- 40=E’ + r.3 (II) --- multiplicando (II) por (-1) e somando com (I) --- 5=5r --- r=1Ω --- subst. Em (I) --- 45=E’ + 1.8 --- E’=37V --- R- A.

31- A) A tensão U que a bateria de fem E e resistência interna r fornece ao circuito externoé dada pela equação do gerador --- U=E – r.i --- do gráfico --- quando U=10V, i=4 A --- 10=E – r.4 (I) --- quando U=8V, i=8 A --- 8=E – r.8 (II) --- resolvendo (I) com (II) --- E=12V e r=0,5Ω.

B) Calculado em (A) --- r=0,5Ω.

C) Para essa particular lâmpada a corrente I=6,0A --- U=12 – 0,5.6=12 – 3=9V --- R=9/6=1,5Ω.

D) Potência dessa particular lâmpada de R=1,5Ω e I=6 A --- P=R.I²=1,5.36 --- P=54W --- o rendimento do gerador (bateria) é fornecido por η=P_útil/P_total=Ui/Ei=9/12=0,0,75 --- η=75%

Aparelhos de medição elétrica (amperímetros, voltímetros, ponte de Wheatstone)

36- Se você não domina a teoria, leia as informações a seguir:

Ponte de Wheatstone – trata-se de uma associação de três resistores fixos e um variável (reostato), como representado na figura.

Serve, dentre outras coisas, para determinar a resistência de um resistor. Conhecendo, por exemplo, R₁, R₂ e R₄, pode-se determinar R₃, da seguinte maneira:

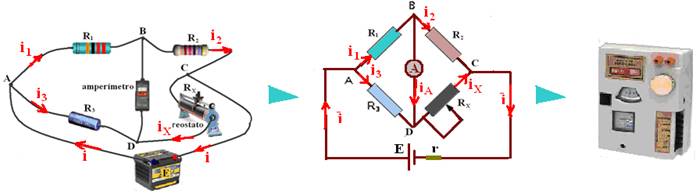
Liga-se entre B e D um amperímetro muito sensível (galvanômetro)

Varia-se o reostato (resistência variável) R_X até que a intensidade i_A de corrente no amperímetro se torne nula (i_A=0). Nessa situação, diz-se que a ponte está em equilíbrio. Sendo nula a corrente no amperímetro, não existe diferença de potencial entre os pontos B e D.

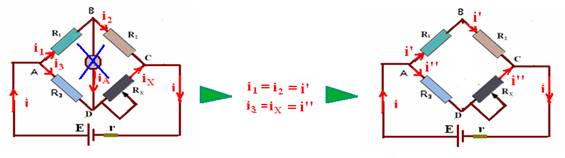
U_AB=U_AD --- R₁.i₁=R₃.i₃ (I) --- U_BC=U_CD --- R₂.i₂=R_X.i_X (II) --- Dividindo membro a membro (I) por (II) --- (R₁.i₁)/(R₂.i₂)=(R₃.i₃)/(R_X.i_X) --- R₁.i’)/(R₂.i’)=(R₃.i’’)/(R_X.i’’) --- R₁/R₂=R₃/R_X --- R₂.R₃=R₁.R_X

Observe no circuito fornecido que, como as lâmpadas são idêntica, possuem a mesma resistência R --- R_I.R_V=R_II.R_IV --- assim, trata-se de uma ponte de Wheatstone em equilíbrio e pela lâmpada de resistência R_III não passa corrente elétrica --- R- C.

37- Os aparelhos estão ligados corretamente --- o amperímetro em série e o voltímetro em paralelo --- considerando os aparelhos ideais, se o amperímetro estivesse ligado em paralelo você teria um curto circuito e, se o voltímetro estivesse ligado em série não passaria corrente pelo condutor --- o resistor não é ôhmico, pois R=U/i não é constante para todas as medidas --- R- D.

38- Se você quer medir a intensidade da corrente, por exemplo, em uma lâmpada, você deve inserir o amperímetro no trecho onde ela está, pois ele “lê” a corrente que passa através dele --- assim o amperímetro deve ser associado em série no trecho onde você deseja medir a corrente --- R- A.

Capacitores - condensadores

52- Série --- 1/Ceq=1/C + 1/C + 1/C --- 2p=C/3 --- C=6p --- paralelo --- Ceq=6p + 6p=12pF ---

R- C.

53- Na seqüência abaixo, em (I) foi calculada a capacitância equivalente de cada linha (associadas em série) e calculadas por 1/C_eq=1/C + 1/C + 1/C + 1/C, cujos valores estão fornecidos em (II) --- em (II) eles estão associados em paralelo

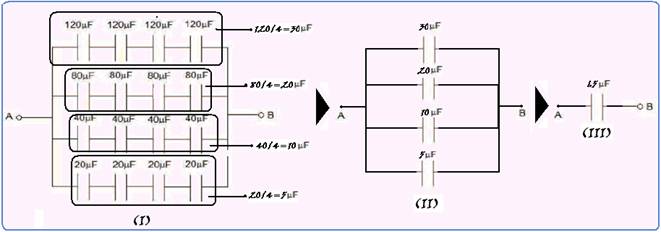
(C_eq=30 + 20 + 10 + 5=65 μF) --- C_eq= 65 μF --- a energia elétrica acumulada entre os terminais é fornecida por --- W=C_eq.U²/2=65.10^-6.500²/2=8125000.10-6J --- W=8,125J --- R- B.

54- Observe na seqüência a seguir o cálculo do capacitor equivalente (C_eq) --- C₁ e C₂ estão em

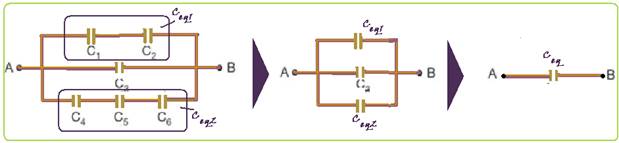
série --- C_eq1=20.30/(20 + 30) --- C_eq1=600/50=12μF --- C₄, C₅ e C₆ estão em série --- 1/C_eq2=1/40 + 1/50 + 1/60=(15 + 12 + 10)/600 --- C_eq2=600/37=16,2μF --- C_eq1, C₂ e C_eq2 estão em paralelo --- C_eq=12 + 16,2 + 10= 38,2μF --- C_eq=Q/U --- 38,2.10^-6=Q/110 --- Q=4202μC --- R- B.