DINÂMICA

Exercícios-Vestibulares Recentes por assunto

2017-2016 e 2015

APLICAÇÕES DAS TRÊS LEIS DE NEWTON

01-(FMJ-SP-017)

Considere um objeto, cuja massa não varia, se deslocando em uma trajetória retilínea com velocidade constante. É correto afirmar que necessariamente

(A) a resultante das forças sobre esse objeto tem direção perpendicular à da velocidade.

(B) a resultante das forças sobre esse objeto é igual a seu peso.

(C) a resultante das forças sobre esse objeto tem direção e sentido iguais aos da velocidade.

(D) a resultante das forças sobre esse objeto é nula.

(E) não há forças agindo sobre esse objeto.

02-(UNESP-SP-017)

Na linha de produção de uma fábrica, uma esteira rolante movimenta-se no sentido indicado na figura 1, e com velocidade constante, transportando caixas de um setor a outro.

Para fazer uma inspeção, um funcionário detém uma das caixas, mantendo-a parada diante de si por alguns segundos, mas ainda apoiada na esteira que continua rolando, conforme a figura 2.

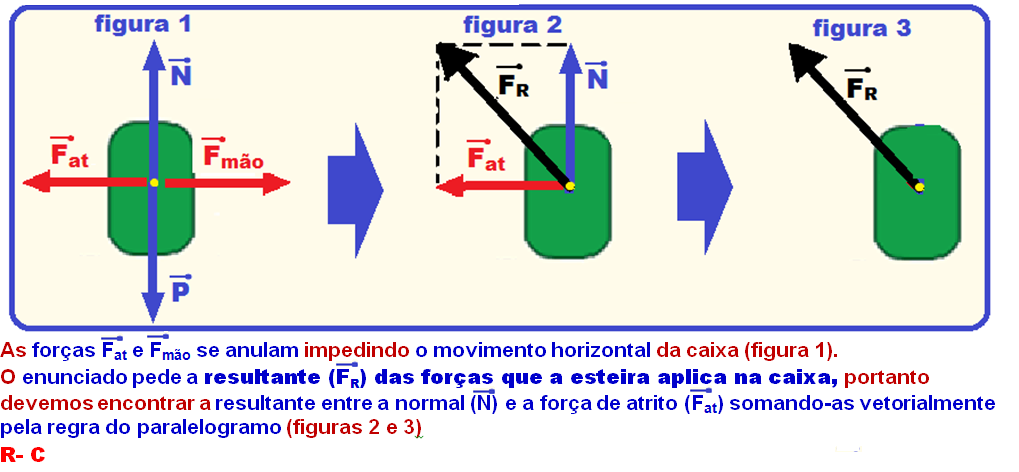
No intervalo de tempo em que a esteira continua rolando com velocidade constante e a caixa é mantida parada em relação ao funcionário (figura 2), a resultante das forças aplicadas pela esteira sobre a caixa está corretamente representada na alternativa

03-(UNESP-SP-017)

Três cubos laranjas idênticos e três cubos azuis idênticos estão equilibrados em duas balanças de pratos, também idênticas, conforme indicam as figuras.

A massa de um cubo laranja supera a de um cubo azul em exato

(A) 1,3 kg.

(B) 1,5 kg.

(C) 1,2 kg.

(D) 1,4 kg.

(E) 1,6 kg.

04-(Medicina – USCS-SP-017)

05-(FAMERP-SP-017)

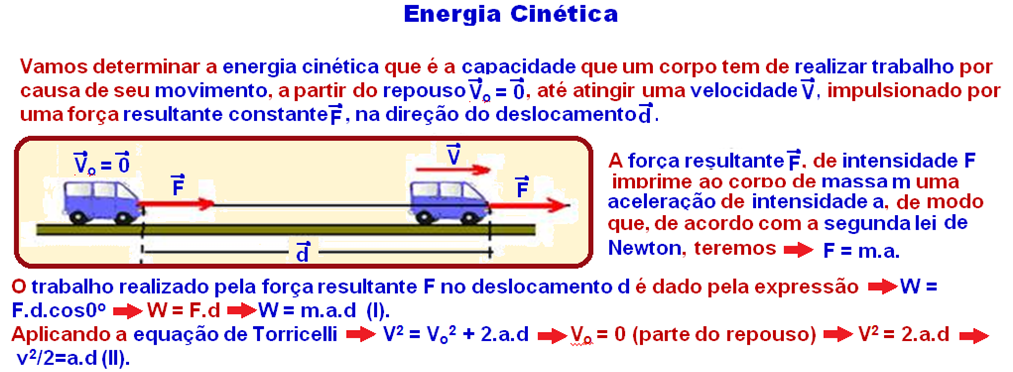
Um corpo de massa 8 kg movimenta-se em trajetória retilínea sobre um plano horizontal e sua posição (s) e sua velocidade escalar (v) variam emfunção do tempo (t), conforme os gráficos.

a) Determine a posição x, em metros, desse corpo no instante t = 10 s.

b) Calcule o módulo da resultante das forças, em newtons, que atuam sobre o corpo no intervalo de tempo entre t = 6 s e t = 12 s.

06-(UERJ-RJ-017)

Um reboque de 16 toneladas é puxado por um caminhão através de um cabo de aço.

Sabe-se que a aceleração do conjunto caminhão-reboque corresponde a 200 cm/s2, e que a massa do cabo de aço é desprezível em relação às massas do caminhão e do reboque.

Estime, em newtons, a tração no cabo de aço.

07-(UECE-CE-017)

08-(UECE-CE-017)

09-(UNESP-SP)

Algumas embalagens trazem, impressas em sua superfície externa,informações sobre a quantidade máxima de caixas iguais a ela que podem ser empilhadas, semque haja risco de danificar a embalagem ou os produtos contidos na primeira caixa da pilha, de baixo para cima.

10-(PUC-MG-015)

Após certo tempo de queda, a velocidade de um paraquedista torna-se constante.

Nessas condições é CORRETO afirmar:

a) A aceleração do paraquedista é igual à aceleração da gravidade.

b) O peso do paraquedista fica nulo.

c) A aceleração do paraquedista é nula fazendo com que ele flutue no ar.

d) Ele vai percorrer distâncias iguais no mesmo intervalo do tempo.

FORÇA ELÁSTICA

01-(FAMERP-SP-015)

Uma mola helicoidal de massa desprezível e comprimento 20 cm é presa de modo que seu eixo longitudinal fique na direção vertical. Quando se prende na mola um objeto de massa 100 g, ela se deforma até que seu comprimento atinja 25 cm.

Considere a aceleração da gravidade igual a 10 m/s².

a) Calcule a constante elástica da mola, em N/m.

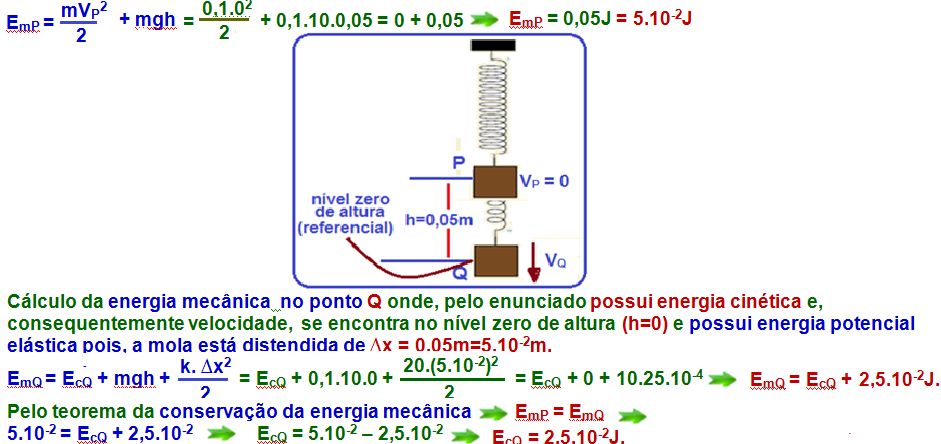
b) Suponha que o objeto seja elevado até a altura em que o comprimento da mola volta a ser 20 cm e, em seguida, solto a partir do repouso. Determine a energia cinética do objeto, em joules, no instante em que passa pelo ponto em que o comprimento da mola é de 25 cm. Despreze qualquer perda de energia mecânica.

02-(AFA – 016/017)

03-(UECE-CE-017)

Considere duas associações de dois pares de molas, todas iguais, um par em série e outro em

paralelo.

Os coeficientes elásticos das molas equivalentes nas duas associações são

A) ksérie > kparalelo > 0

B) kparalelo > ksérie > 0

C) kparalelo = ksérie > 0

D) kparalelo = ksérie = 0

04-(FUVEST-SP-015)

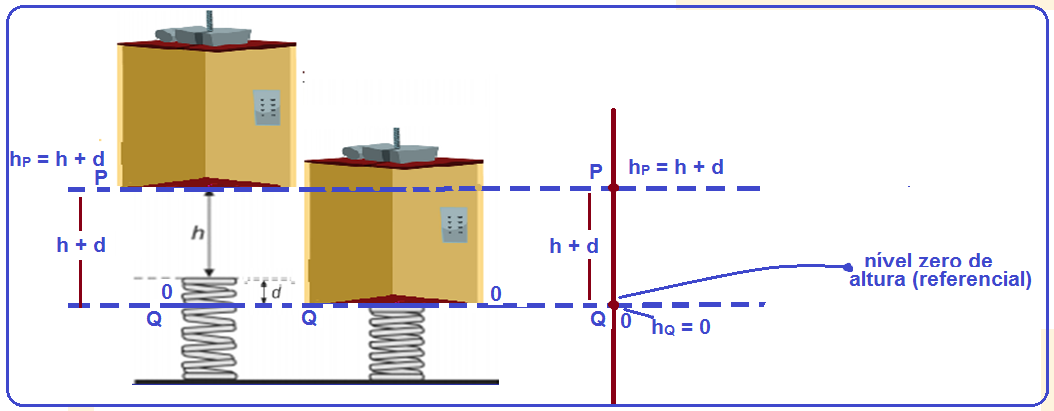
No desenvolvimento do sistema amortecedor de queda de um elevador de massa m, o engenheiro projetista impõe que a mola deve se contrair de um valor máximo d, quando o elevador cai, a partir

do repouso, de uma altura h, como ilustrado na figura abaixo.

Para que a exigência do projetista seja satisfeita, a mola a ser empregada deve ter constante elástica

dada por

05-(UNICAMP-SP-016)

O trabalho realizado pela fibra sobre a massa, ao se contrair 10%, erguendo a massa até uma nova posição de repouso, é

06-(UECE-CE-017)

Se fossem desprezados todos os atritos e retirados os amortecedores, um automóvel parado em uma via horizontal poderia ser tratado como um sistema massa mola.

Suponha que a massa suspensa seja de 1.000 kg e que a mola equivalente ao conjunto que o sustenta tenha coeficiente elástico k.

Como há ação também da gravidade, é correto afirmar que, se o carro oscilar verticalmente, a frequência de oscilação.

A) não depende da gravidade e é função apenas do coeficiente elástico k.

B) é função do produto da massa do carro pela gravidade.

C) não depende da gravidade e é função da razão entre k e a massa do carro.

D) depende somente do coeficiente elástico k .

PÊNDULOS SIMPLES

01-(FUVEST-SP-016)

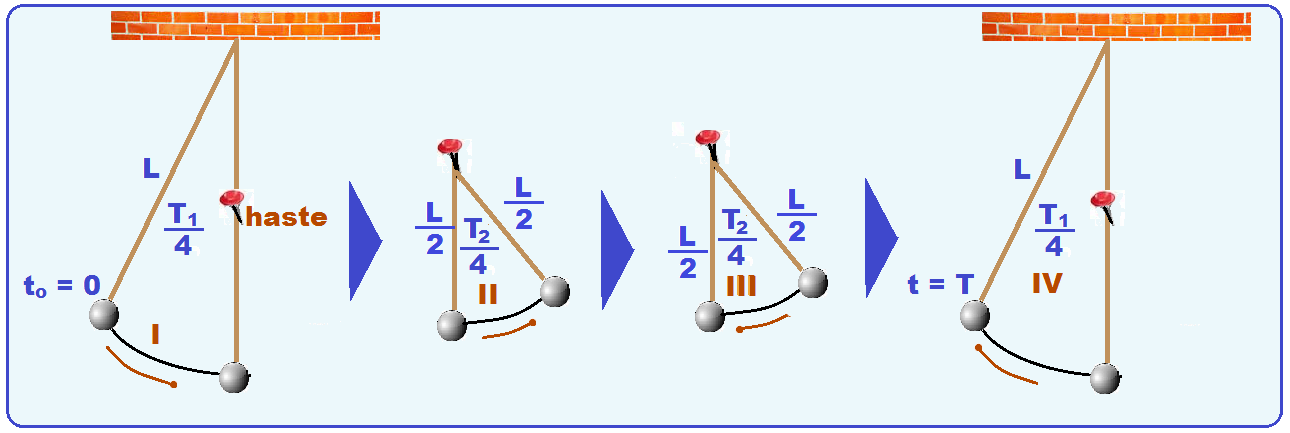
Um pêndulo simples, constituído por um fio de comprimento L e uma pequena esfera, é colocado em oscilação.

Uma haste horizontal rígida é inserida perpendicularmente ao plano de oscilação desse pêndulo, interceptando o movimento do fio na metade do seu comprimento, quando ele está na direção vertical. A partir desse momento, o período do movimento da esfera é dado por

02-(ENEM-MEC-2014)

Christiaan Huygens, em 1656, criou o relógio de pêndulo. Nesse dispositivo, a pontualidade

baseia-se na regularidade das pequenas oscilações do pêndulo. Paramanter a precisão desse relógio, diversos problemas foram contornados. Por exemplo, a haste passou por ajustes até que, no início do século XX, houve uma inovação, que foi sua fabricação usando uma liga metálica que se comporta regularmente em um largo intervalo de temperaturas.
YODER, J. G. Unrolling Time: Christiaan Huygens and the mathematization of nature. Cambridge: Cambridge University P ress, 2004 (adaptado).
Desprezando a presença de forças dissipativas e considerando a aceleração da gravidade constante, para que esse tipo de relógio realize corretamente a contagem do tempo, é necessário que o(a)

a) comprimento da haste seja mantido constante.

b) a massa do corpo suspenso pela haste seja pequena.

c) da haste possua alta condutividade térmica.

d) amplitude da oscilação seja constante a qualquer temperatura.

e) energia potencial gravitacional do corpo suspenso se mantenha constante.

PLANO INCLINADO

01-(MACKENZIE-SP-2017)

02- (Faculdade de Tecnologia Termomecânica – SP)

Um menino de 30 kg, inicialmente em repouso e a 4 m do solo, inicia um movimento de descida de A para B, como mostra a figura.

(http://3.bp.blogspot.com)

Ele chega a B, ao nível do solo, com uma velocidade de 6,0 m/s. Considerando a aceleração da gravidade igual a 10 m/s², a energia mecânica dissipada pelo atrito, no movimento apresentado pela figura, é de

(A) 540 J.

(B) 580 J.

(C) 620 J.

(D) 660 J.

(E) 740 J.

03- (AFA – 016/017)

04-(FAMERP-SP-015)

Uma esquiadora de massa 80 kg, incluindo todo o equipamento, desce com velocidade constante por uma rampa plana e inclinada que forma com a horizontal umângulo θ, em um local em que a aceleração da gravidade vale 10 m/s2.

Considere que existe resistência do ar, que o coeficiente de atrito dinâmico entre os esquis e a neve é igual a 0,10 e que sen θ = 0,6 e cos θ = 0,8.

a) Na figura inserida no campo de Resolução e Resposta, represente as forças que atuam no conjunto esquiadora mais equipamento.

b) Calcule o valor da força de resistência do ar, em newtons, que age sobre o conjunto durante o movimento.

05-(MACKENZIE-SP-2017)

POLIAS E ROLDANAS

01-(ENEM-MEC-016)

Uma invenção que significou um grande avanço tecnológico na Antiguidade, a polia composta ou a associação de polias, é atribuída a Arquimedes (287 a.C. a 212 a.C.).

O aparato consiste em associar uma serie de polias moveis a uma polia fixa.

A figura exemplifica um arranjo possível para esse aparato.

É relatado que Arquimedes teria demonstrado para o rei Hierão um outro arranjo desse aparato, movendo sozinho, sobre areias da praia, um navio repleto de passageiros e cargas, algo que seria impossível sem a participação de muitos homens.

Suponha que a massa do navio era de 3000 kg, que o coeficiente de atrito estático entre navio e a areia era 0,8 e que Arquimedes tenha puxado o navio com uma força , paralela à direção do movimento e de modulo igual a 400 N.

Considere os fios e as polias ideias, a aceleração da gravidade igual a 10 m/s² e que a superfície da

Praia é perfeitamente horizontal.

O número mínimo de polias móveis usadas, nessa situação, por Arquimedes foi

02- (CEDERJ-RJ-2017)

Por meio de um sistema de roldanas, um trabalhador desce, a uma aceleração constante de 2,0m/s², um engradado contendo duas caixas. Considerando que a aceleração da gravidade no local é igual a 10 m/s², que a caixa superior pesa 300N e a caixa inferior, 500N, calcule o módulo da força que: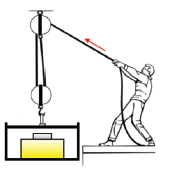

a) a caixa inferior exerce sobre a caixa superior;

b) o piso do engradado exerce sobre a caixa inferior.

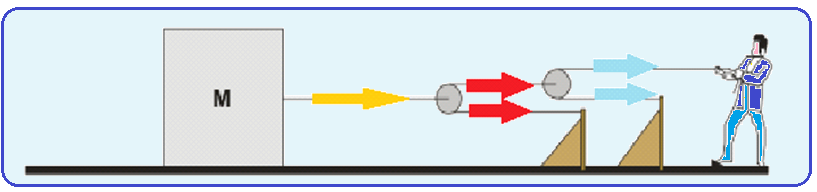
03-(UFSC-SC-016)

Um professor de Física realiza um experimento sobre dinâmica para mostrar aos seus alunos. Ele puxa um bloco de 400 kg a partir do repouso, aplicando sobre a corda uma força constante de 350 N, como mostra a figura abaixo.

O sistema é constituído por fios inextensíveis e duas roldanas, todos demassa desprezível.

Existe atrito entre a superfície horizontal e o bloco. Os coeficientes de atrito estático e de atrito cinético são 0,30 e 0,25, respectivamente.

Com base no que foi exposto, é CORRETO afirmar que:

01. a força de tração no fio ligado ao bloco é de 1400 N.

02. o bloco adquire uma aceleração de 2,0 m/s².

04. apenas três forças atuam sobre o bloco: o peso, a força de atrito e a tração.

08. a força resultante sobre o bloco é de 400 N.

16. a força mínima que o professor deve aplicar sobre a corda para movimentar o bloco é de 290 N.

FORÇAS NO MCU

01-(FAMERP-SP-017)

Em uma exibição de acrobacias aéreas, um avião pilotado por uma pessoa de 80 kg faz manobras e deixa no ar um rastro de fumaça indicando sua trajetória.

Na figura, está representado um looping circular de raio 50 m contido em um plano vertical, descrito por esse avião.

Adotando g = 10 m/s2 e considerando que ao passar pelo ponto A, ponto mais alto da trajetória circular, a velocidade do avião é de 180 km/h, a intensidade da força exercida pelo assento sobre o piloto, nesse ponto, é igual a (A) 3 000 N.

(B) 2 800 N.

(C) 3 200 N.

(D) 2 600 N.

(E) 2 400 N.

02-(AFA – 016/017)

03- (UEMG-MG-017)

TRABALHO E ENERGIA

01-(ENEM-MEC-016)

02-(FUVEST-SP-017)

03-(FMJ-SP-017)

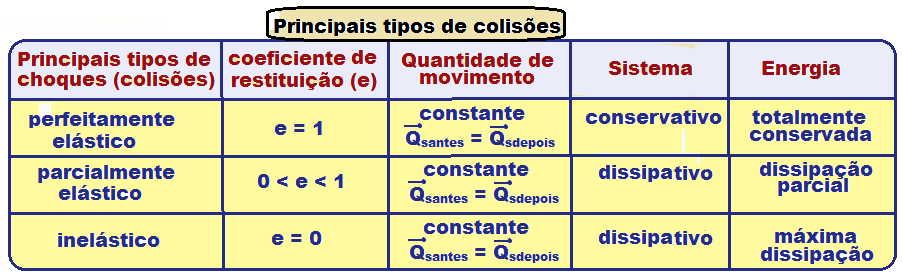
O bate-bate é um brinquedo composto por duas esferas de material rígido presas a dois fios e a um anel. O objetivo do brinquedo consiste em fazer as esferas girarem em sentidos opostos e se chocarem continuamente em cima e embaixo.

Suponha que as esferas tenham a mesma massa e que suas velocidades escalares sejam iguais antes e depois de cada choque. Durante os choques, no sistema constituído pelas duas esferas, ocorre

(A) perda de energia cinética e ganho de quantidade de movimento.

(B) perda de energia cinética e conservação da quantidade de movimento.

(C) conservação da energia cinética e perda da quantidade de movimento.

(D) ganho de energia cinética e perda da quantidade de movimento.

(E) conservação de energia cinética e conservação da quantidade de movimento.

04-(UNIFESP-SP-017)

Em um teste realizado na investigação de um crime, um projétil de massa 20 g é disparado horizontalmente contra um saco de areia apoiado, emrepouso, sobre um carrinho que, também em repouso, está apoiado sobre uma superfície horizontal na qual pode mover-se livre de atrito.

O projétil atravessa o saco perpendicularmente aos eixos das rodas do carrinho, e sai com velocidade menor que a inicial, enquanto o sistema formado pelo saco de areia e pelo carrinho, que totaliza 100 kg, sai do repouso com velocidade de módulo v.

O gráfico representa a variação da velocidade escalar do projétil, vP, em função do tempo, nesse teste.

Calcule:

a) o módulo da velocidade v, em m/s, adquirida pelo sistema formado pelo saco de areia e pelo carrinho imediatamente após o saco ter sido atravessado pelo projétil.

b) o trabalho, em joules, realizado pela resultante das forças que atuaram sobre o projétil no intervalo de tempo em que ele atravessou o saco de areia.

05-(UNICAMP-SP-017)

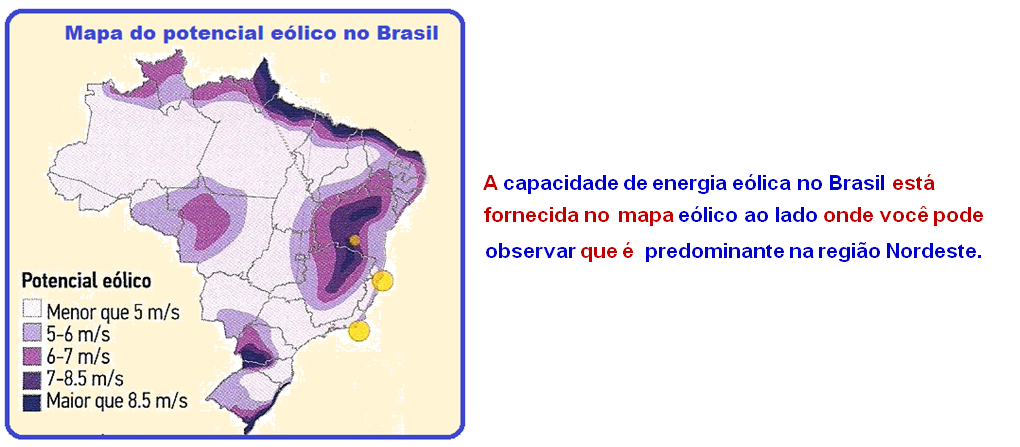
Denomina-se energia eólica a energia cinética contida no vento.

Seu aproveitamento ocorre por meio da conversão da energia cinética de translação em energia cinética de rotação e, com o emprego de turbinas eólicas, também denominadas aerogeradores, é gerada energia elétrica.

Indique a região em questão e qual seria a quantidade de energia elétrica produzida, se houvesse a redução da velocidade do vento pela metade.

a) Região Sul; 3.900 MWh.

b) Região Nordeste; 1.950 MWh.

c) Região Nordeste; 3.900 MWh.

d) Região Sul; 1.950 MWh.

06-(FMABC-SP-017)

07-(COLÉGIO NAVAL – 2016/17)

08- (UEMG-MG-017)

Uma pessoa arrasta uma caixa sobre uma superfície sem atrito de duas maneiras distintas, conforme mostram as figuras (a) e (b).

Nas duas situações, o módulo da força exercida pela pessoa é igual e semantém constante ao longo de um mesmo deslocamento.

Considerando a força , é correto afirmar que

a) o trabalho realizado em (a) é igual ao trabalho realizado em (b).

b) o trabalho realizado em (a) é maior do que o trabalho realizado em (b).

c) o trabalho realizado em (a) é menor do que o trabalho realizado em (b).

d) não se pode comparar os trabalhos, porque não se conhece o valor da força.

09-(UERJ-RJ-016)

Atualmente, o navio mais rápido do mundo pode navegar em velocidade superior a 100 km/h.

Em uma de suas viagens, transporta umacarga de 1000 passageiros e 150 carros.

Admita, além da massa do navio, de 450000 kg, os seguintes valores médios mpara as demais massas: mpassageiro = 70 kg e mcarro = 1000 kg.

Estime, em MJ, a energia cinética do conjunto, no instante em que o navio se desloca com velocidade igual a 108 km/h.

10-(FUVEST-SP-015)

A figura abaixo mostra o gráfico da energia potencial gravitacional U de uma esfera em uma pista, em função da componente horizontal x da posição da esfera na pista.

se Em = Ec + Ep = constante, então no ponto x = x1 onde a cinética é nula a potencial será máxima e a mecânica valerá Em1 =0 + E — Em1 = E.

A esfera é colocada em repouso na pista, na posição de abscissa x = x1,tendo energia mecânica E < 0. A partir dessa condição, sua energia cinética tem valor

a) máximo igual a |Uo|.

b) igual a |E| quando x = x3.

c) mínimo quando x = x2.

d) máximo quando x = x3.

e) máximo quando x = x2.

DINÂMICA IMPULSIVA

01-(ENEM-MEC-016)

O trilho de ar é um dispositivo utilizado em laboratórios de física para analisar movimentos em que corpos de prova (carrinhos) podem se mover com atrito desprezível.

A figura ilustra um trilho horizontal com dois carrinhos (1 e 2) em que serealiza um experimento para obter a massa do carrinho 2.

No instante em que o carrinho1, de massa 150,0 g,passa a se mover comvelocidade escalar constante, o carrinho 2 está em repouso.

No momento em que o carrinho 1 se choca com o carrinho 2,ambospassam a se movimentar juntos com velocidade escalar constante.

Os sensores eletrônicos distribuídos ao longo do trilho determinam as posições e registram os instantes associados à passagem de cada carrinho, gerando os dados do quadro.

Com base nos dados experimentais, o valor da massa do carrinho 2 é igual a

02-(PUC-SP-017)

A figura mostra uma colisão envolvendo um trem de carga e uma camionete.

Segundo testemunhas, o condutor da camionete teria ignorado o sinal sonoro e avançou a cancela da passagem de nível.

Após a colisão contra a lateral do veículo, o carro foi arrastado pelo trem por cerca de 300 metros. Supondo a massa total do trem de 120 toneladas e a da camionete de 3 toneladas, podemos afirmar que, no momento da colisão, a intensidade da força que

(A) o trem aplicou na camionete foi 40 vezes maior do que a intensidade da força que a camionete aplicou no trem e a colisão foi parcialmente elástica.

(B) o trem aplicou na camionete foi 40 vezes maior do que a intensidade da força que a camionete aplicou no trem e a colisão foi inelástica.

(C) a camionete aplicou no trem foi igual à intensidade da força que o trem aplicou na camionete e a colisão foi parcialmente elástica.

(D) a camionete aplicou no trem foi igual à intensidade da força que o trem aplicou na camionete e a colisão foi inelástica.

03-(UNICAMP-SP-016)

Beisebol é um esporte que envolve o arremesso, com a mão, de uma bola de 140 g de massa na direção de outro jogador que irá rebatê-la com um taco sólido.

Considere que, em um arremesso, o módulo da velocidade da bola chegou a 162 km/h,

imediatamente após deixar a mão do arremessador.

Sabendo que o tempo de contato entre a bola e a mão do jogador foi de 0,07 s, o módulo da força

média aplicada na bola foi de

04-(UERJ-RJ-016)

Observe ográfico, que indica aforça exercidapor uma máquina em função do tempo.

Admitindo que não há perdas no sistema, estime, em N.s, a impulsão fornecida pela máquina no intervalo entre 5 e 105 segundos.

05-(UDESC-SC-016)

Em uma colisão elástica frontal (em uma dimensão) entre duas partículas de massas m1 e m2, a partícula 2 estava em repouso antes da colisão. Analise as proposições em relação à colisão.

I. A quantidade de movimento e a energia cinética do sistema se conservam.

II. Se as massas são iguais, a magnitude da velocidade adquirida pela partícula 2, após a colisão, é igual à magnitude da velocidade da partícula 1, antes da colisão.

III. Se m1 é maior que m2, a magnitude da velocidade adquirida pela partícula 2, após a colisão, será maior que a magnitude da velocidade da partícula 1, antes da colisão.

IV. Se m1 é menor que m2, o vetor velocidade da partícula 1, após a colisão, é igual ao vetor velocidade que ela tinha antes da colisão.

Assinale a alternativa correta:

A. ( ) Somente as afirmativas I e III são verdadeiras.

B. ( ) Somente as afirmativas I, III e IV são verdadeiras.

C. ( ) Somente as afirmativas I, II e III são verdadeiras.

D. ( ) Somente a afirmativa II é verdadeira.

E. ( ) Somente a afirmativa IV é verdadeira.

06-(ENEM-MEC-2014)

O pêndulo de Newton pode ser constituído por cinco pêndulos idênticossuspensos em um mesmo suporte. Em um dado instante, as esferas de três pêndulos são deslocadas para a esquerda e liberadas, deslocando-se para a direita e colidindo elasticamente com as outras duas esferas, que inicialmente estavam paradas.

O movimento dos pêndulos após a primeira colisão está representado em :

07-(UNESP-SP-015)

O gol da conquista do tetracampeonato pela Alemanha na Copa do Mundo de 2014 foi feito pelo jogador Götze. Nessa jogada, ele recebeu um cruzamento, matou a bola no peito, amortecendo-a, e chutou de esquerdapara fazer o gol. Considere que, imediatamente antes de tocar o jogador, a bola tinha velocidade de módulo V1 = 8 m/s em uma direção perpendicular ao seu peito e que, imediatamente depois de tocaro jogador, sua velocidade manteve-se perpendicular ao peito do jogador,porém com módulo V2 = 0,6 m/se em sentido contrário.

Admita que, nessa jogada, a bola ficou em contato com o peito do jogador por 0,2 s e que, nesse intervalo de tempo, a intensidade da força resultante (FR ), que atuou sobre ela, variou em função do tempo, conforme o gráfico.

Considerando a massa da bola igual a 0,4 kg, é correto afirmar que, nessa jogada, o módulo da força resultante máxima que atuou sobre a bola, indicada no gráfico por Fmáx , é igual, em newtons, a

08-(FMABC-SP-015)

Uma bola de futebol de massa m é abandonada verticalmente e atinge a cabeça de um jogador com velocidade de módulo vvertical. Instintivamente, o jogador cabeceia a bola lançando-a na direção horizontal com velocidade de módulo v horizontal.

Determine o módulo do impulso da força resultante que a cabeça do jogador aplica na bola devido ao cabeceio.

09-(UERJ-RJ-015)

Admita uma colisão frontal totalmente inelástica entre um objeto que se move com velocidade

inicial vo e outro objeto inicialmente em repouso, ambos com mesma massa.

Nessa situação, a velocidade com a qual os dois objetos se movem após a colisão equivale a:

10-(UERJ-RJ-015)

Um esquiador, com 70 kg de massa, colide elasticamente contra uma árvore a uma velocidade de

72 km/h.

Calcule, em unidades do SI, o momento linear e a energia cinética do esquiador no instante da colisão.

MOVIMENTO HARMÔNICO SIMPLES

01- (AFA – 015/016)

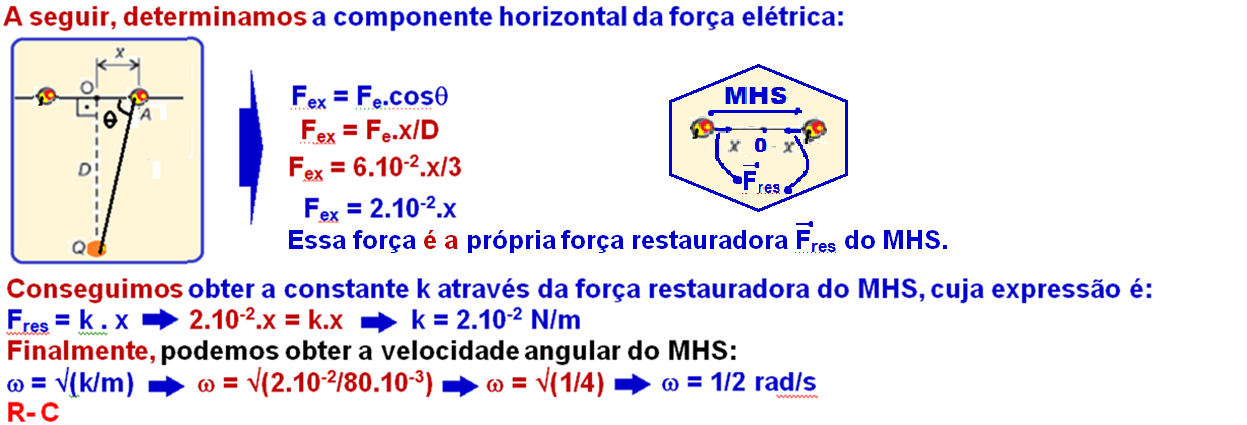
A figura abaixo mostra uma pequena esfera vazada E, com carga elétrica q = + 2,0.10-5 C e massa 80 g, perpassada por um eixo retilíneo situado num plano horizontal e distante D = 3m de uma carga puntiforme fixa Q = -3,0.10-6 C.

Se a esfera for abandonada, em repouso, no ponto A, a uma distância x,muito próxima da posição de equilíbrio 0, tal que x/D << 1 a esfera passará a oscilar de MHS, em torno de 0, cuja pulsação é, em rad/s, igual a

02-(FMABC-SP-016)

Um oscilador massa-mola ideal é montado, conforme indica a figura.

03-(UFSC-SC-016)

Pedro, Tiago, João e Felipe resolveram comprar um carro do ano 2000, mas se esqueceram de verificar os registros sobre as revisões periódicas. A fim de evitar problemas físicos devido ao excesso de oscilação do carro durante viagens longas, decidem analisar a qualidade dos amortecedores. Eles modelam o carro, na situação em que estão os quatro como passageiros, como um único corpo sobre uma mola ideal, realizando um MHS. Então, eles fazem três medidas, obtendo os seguintes valores:

a) 1000 kg para a massa do carro;

b) 250 kg para a soma de suas massas;

c) 5,0 cm para a compressão da mola quando os quatro estavam dentro do carro parado.

Sobre o MHS e com base no exposto acima, é CORRETO afirmar que:

01. a frequência e o período do MHS realizado dependem daamplitude.

02. a frequência de oscilação do carro com os passageiros é de Hz:

04. a energia cinética é máxima na posição de equilíbrio.

08. a constante elástica da mola é 25 x 104 N/m.

16. o período de oscilação do carro vazio é de 1,0 s.

Resoluções-Vestibulares Recentes por assunto

2017, 2016 e 2015

APLICAÇÕES DAS TRÊS LEIS DE NEWTON

01-Nesse caso o objeto tem uma velocidade constante, logo sua aceleração é 0. Como sua aceleração é 0, a força resultante também só pode ser 0, com isso a alternativa correta é a D.

Vamos analisar as outras, também:

A velocidade tem sempre a mesma direção e sentido da força resultante, pois ela é uma consequência da aceleração que vai ser exercida por essa força.

Se a resultante fosse igual ao peso, o objeto estaria em queda livre.

A alternativa C pode causar confusão, porque realmente ela é verdadeira, mas no caso aonde há uma força resultante.

Sempre há forças agindo, porém a soma delas vai ser igual a 0.

R – D

02-

03-Denominando de ml a massa de cada cubo laranja e de ma a massa de cada cubo azul e, estando as balanças em equilíbrio, você terá:

Balança da esquerda2ma + ml = 2 (I)

Balança da direita ma + 3 = 2ml (II)

Isolando ma em (II) e substituindo em (I) ma = 2ml – 3 2(2ml – 3) + ml = 2 4ml – 6 + ml = 2 5ml = 8 ml= 8/5 = 1,6 kg.

2ma + 1,6 =2 ma = 0,4/2 ma = 0,2 kg.

Assim, a massa de um cubo laranja supera a de um cubo azul em ml – ma= 1,6 – 0,2 = 1,4 kg.

R- D

04-

05-a) Em todo gráfico Vxt o deslocamento do corpo é numericamente igual á área, nesse caso, entre os instantes 0 e 10 s que é a área de um trapézio:

Mas, o enunciado não pede o deslocamento entre 0s e 10s, mas sim aposição no instante t = 10 s

e, pelo gráfico Sxt você observa que ele partiu da origem So = 0, entãoquando t = 10s o espaço S será = S – So 26 = S – 0 S = 26 m.

b) Observe no gráfico da velocidade que, entre 5s e 10 s o gráfico é uma mesma reta inclinada o que significa que nesse intervalo de tempo a aceleração tem o mesmo módulo que pode ser calculado por a = = a = - em módulo a = 0,8 m/s2.

Pelo Princípio Fundamental da Dinâmica ou Segunda lei de Newton FR= m.a = 8.0,8

FR = 6,4 N.

06- Dados: massa do reboque m = 16.103 kg aceleração do reboque a = 200 cm/s² = 200.10^-2 m/s² a = 2 m/s².

07-No início, quando ele sobe acelerando, a força exercida pelo cabo na cabine tem intensidade maior que a do peso, pois a força resultante é para cima FI > P.

No final, antes da parada, ele está freando e desacelerando com a força resultante sendo para cima até se tornar nula quando FF = P (ele para)

R- B

08-

09-

R- C

10-Se a velocidade de queda é constante, ele deverá percorrer distâncias iguais em intervalos de tempo iguais.

R- D

FORÇA ELÁSTICA

01-a) Observe na figura abaixo que, depois que o objeto foi preso à mola que estava em seu comprimento natural de 20cm, ela foi deformada com seu comprimento passando para 25cm e

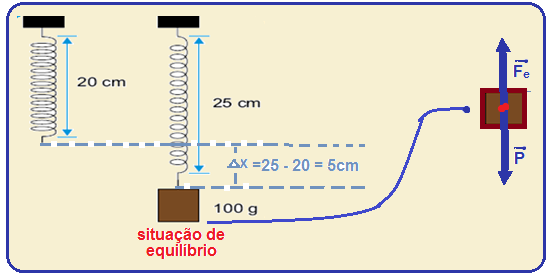
sofrendo uma deformação de ∆x = 5cm = 0,05m, quando atingiu a situação de equilíbrio.

Na situação de equilíbrio, as forças que agem sobre o objeto são, seu peso (vertical e para baixo) e a força elástica (vertical e para cima), que sustenta o objeto, que está em equilíbrio, mas não em repouso (força resultante sobre ele é nula).

b) Cálculo da energia mecânica no ponto P onde, pelo enunciado partiu do repouso VP = 0 e se encontra na altura de h=0,05m em relação ao ponto Q tomado como referencial. Nesse ponto, a mola está em sua posição natural e não existe energia potencial elástica armazenada.

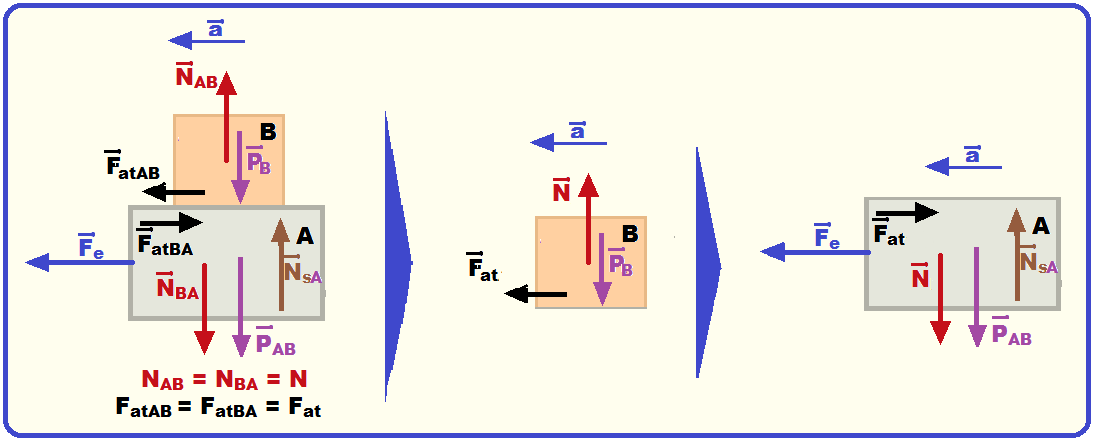
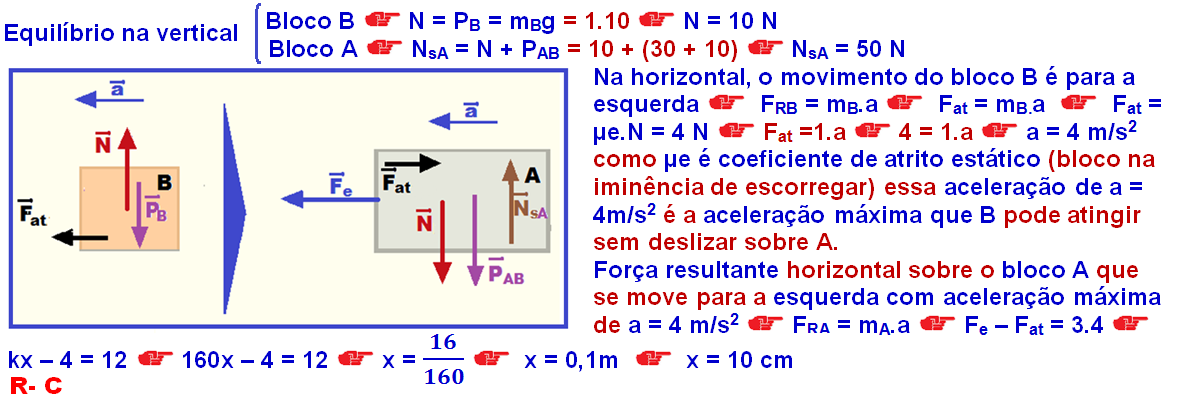
02- Forças que agem sobre cada bloco supondo que a mola está sendo esticada e, quando solta, se moverá para a esquerda:

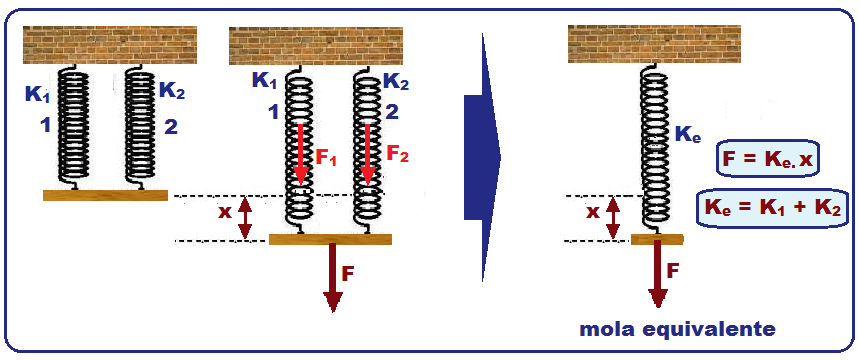
03-Veja as características das associações série e paralelo de molas abaixo:

Associação em paralelo

Nesse caso a deformação x sofrida por cada uma das molas é a mesma.

Associação em série

Nesse caso as molas 1 e 2 estão sujeitas à mesma força F e sofrem deformações diferentes x1 e x2.

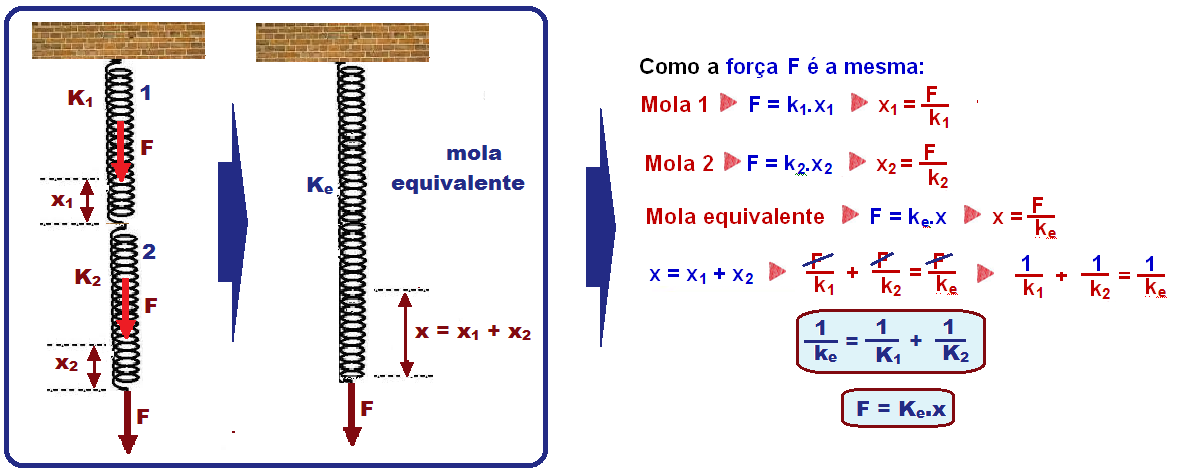
Observe que a constante elástica (coeficiente elástico) da associação paralelo é maior do que a da série.

R- B

04-

05-Podemos descrever a situação conforme o esquema abaixo:

R- C

06-A expressão da frequência de oscilação de um sistema massa mola é (se você não domina a teoria, a demonstração está em fisicaevestibular.com.br – mecânica – dinâmica – MHS – sistema massa-mola).

R- C

PÊNDULOS SIMPLES

01-

Pêndulo Simples

Pêndulo Simples consta de uma massa m, presa na extremidade inferior de um fio ideal, fixada verticalmente na sua extremidade superior (figura) .

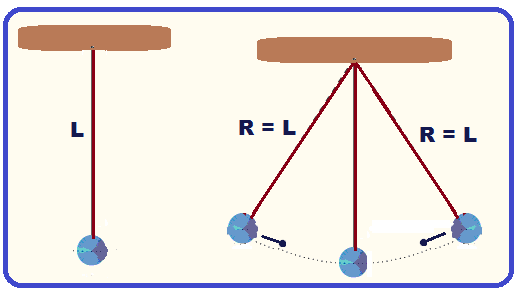
Se o pêndulo simples oscilar, com oscilações de pequena abertura (no máximo 15o), ele descreve um movimento circular de raio R=L, sendo L o comprimento do fio.

Seu período (T), que é o tempo que ele demora para efetuar um “vai e vem” completo é fornecido pela expressão:

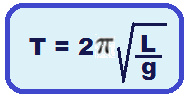
onde g é a aceleração da gravidade local.

Observe na figura abaixo a sequência da situação descrita desde to = 0 até a esfera efetuar uma oscilação completa com período T.

R- E

02-Pêndulo Simples: consta de uma massa m, presa na extremidade inferior de um fio ideal, fixada verticalmente na sua extremidade superior(figura)

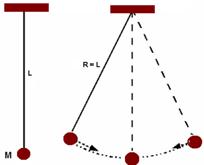
Se o pêndulo simples oscilar, com oscilações de pequena abertura (no máximo 15o), ele descreve um movimento circular de raio R=L, sendo L o comprimento do fio.

Seu período (T), que é o tempo que ele demora para efetuar um “vai e vem” completo é fornecido pela expressão:

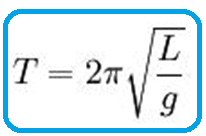
onde g é a aceleração da gravidade local.

Observe que:

* a massa pendular m não influi no período T do movimento influindo apenas o comprimento L do pêndulo, e a aceleração da gravidade local.Assim, dois pêndulos de mesmo comprimento L, mas de massas diferentes M e m, apresentam o mesmo período T.

* O período de um pêndulo simples independe da amplitude, ou seja, daaltura em que m é abandonada, assim, os pêndulos da figura abaixo, tanto na situação 1 como na 2, demoram o mesmo tempo para ir de A até B, de B até C, de C até B e de B até A.

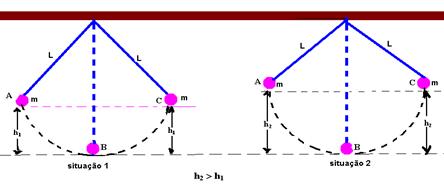
R- A

PLANO INCLINADO

01-

As duas esferas possuem a mesma massa e são abandonadas do repouso da mesma altura h.

A esfera A cai em queda livre sujeita apenas ao seu peso de intensidade P = m.g que é a força resultante sobre ele de modo que FR = m.aA FR = P m.aA = m.g aA = g (I)

R- E

02-

03-

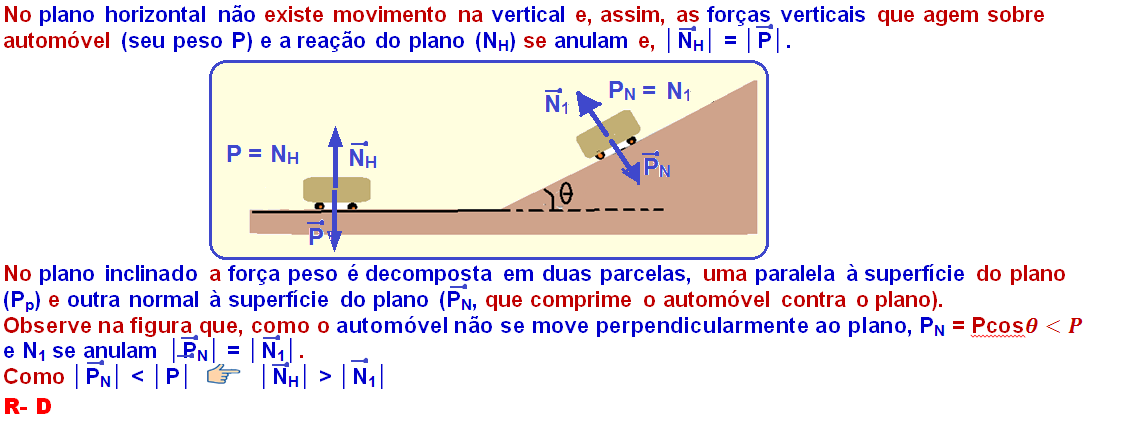
Plano inclinado com atrito

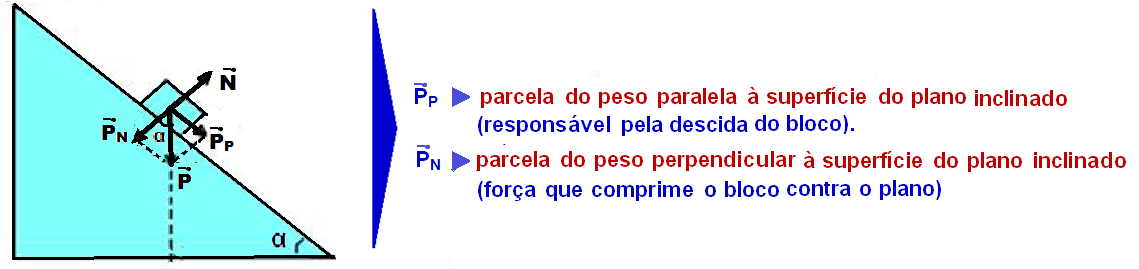
Cálculo da intensidade de PP e PN utilizando o triângulo retângulo da figura abaixo:

No caso do exercício no trecho BC existe atrito com o Fat valendo Fat = mgcos30o.= .mg Fat = .

No trecho com atrito sen30o = h2/BC = h2/BC BC = 2h2

Energia dissipada pelo atrito no trecho BC WFat = Fat.BC.cos30o = .2h2 WFat = .h2.

Energia mecânica no ponto A EmA = EcA + EpA = mVA2/2 + mg(h1 + h2) = 0 + mg(h1 + h2) EmA =mg.(h1 + h2).

Energia mecânica no ponto C onde, pelo enunciado, chega com velocidade nula EmC = mVC2/2 + mgh = m.02/2 + mg.0 EmC = 0.

Pelo teorema da conservação da energia mecânica EmA = WFat + EmC mg.(h1 + h2) = .h2 + 0 (h1 + h2)/h2 = h1/h2 + 1 = h1/h2 = – 1 = (3-2)/2 h1/h2 =

R- A

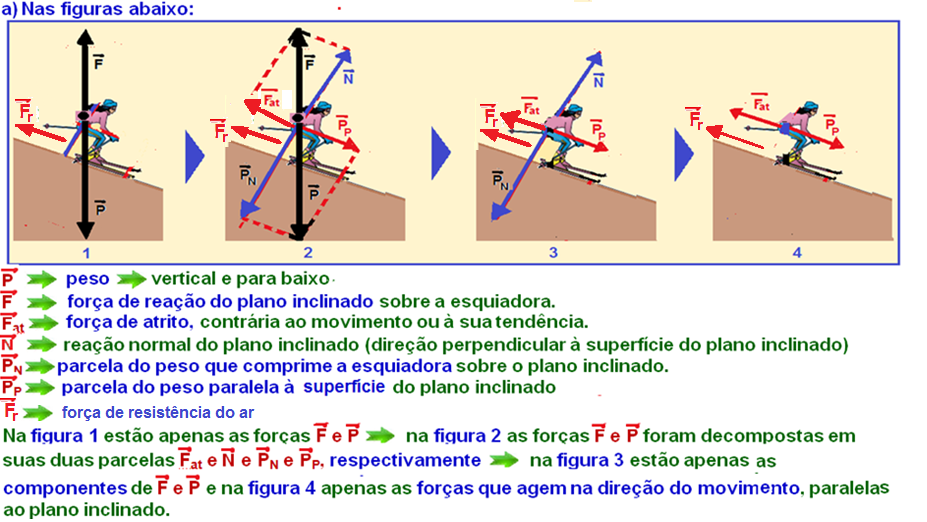
05-

POLIAS E ROLDANAS

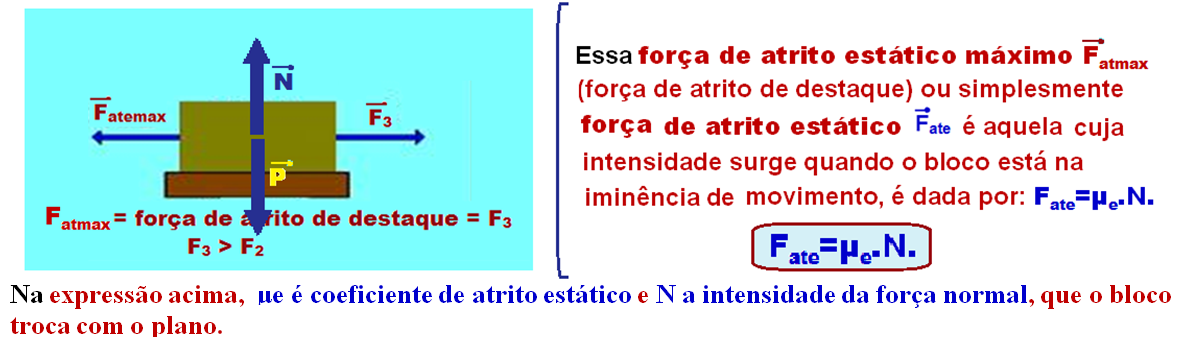
01-Cálculo da intensidade da forçanecessária para deixar o navio na iminência do escorregamento que deve ser maior que o módulo da força de atrito estático máxima

No caso do exercício, sendo a praia horizontal N = PFate = e.N = e.P = e.mg = 0,8x3000x10

Fate = 24000 N.

A intensidade da força de tração que puxa o navio tem que ser maior que 24000 N T > 24000 N.

Analise a teoria abaixo com uma polia fixa e várias polias móveis (talha exponencial):

02-

Vamos analisar as forças desse exercício:

A seta vermelha representa a força resultante, a azul representa a força que a caixa inferior exerce na superior (precisamos descobrir o valor) e averde a força que a superior exerce na inferior. A força resultante deve ser igual à soma das outras forças, então:

Onde:

FR é a força resultante (vermelho)

FI é a força da inferior (azul)

FS é a força do superior (verde)

Como as forças estão em direções opostas, precisamos que uma seja negativa, para facilitar vamos escolher FI, porque ela está em direção oposta em relação à resultante, então:

Isolando FI:

Nesse caso FS é apenas a força peso da caixa superior, nós já temos ela no enunciado (300 N). A força resultante é:

Aonde:

FR é a força resultante

m é a massa

a é aceleração

No entanto nós não sabemos a massa do bloco superior, podemosdescobrir utilizando a força peso:

Aonde:

P é o peso

m é a massa

g é a aceleração da gravidade

Isolando a massa:

Substituindo:

Substituindo na equação da força resultante, a massa é apenas do bloco superior, porque estudamos as reações que acontecem apenas nele:

Agora que temos tudo, podemos substituir para chegarmos ao resultado:

(resposta da a)

Essa é a resposta para o exercício a.

Para o b nós teremos que fazer exatamente as mesmas contas, mas dessa vez o peso será a soma de ambas as caixas e força é a que o piso exerce na caixa inferior:

A relação entre as forças ainda pode ser escrita dessa forma, porém o peso que antes era apenas 300, agora é 300 + 500 = 800 N.

Calculando a massa da caixa inferior:

Substituindo:

Sendo assim a resultante fica:

Substituindo:

(resposta da b)

03-

01 Verdadeiro pelo fato de o sistema ser constituído por duas roldanas acontece o seguinte equilíbrio de forças:

Onde as setas de mesma cor têm a mesma intensidade.

A seta azul representa a força exercida pelo professor (350N). Por ser umaroldana e pelas propriedades de ação e reação uma outra força igual e de mesma direção é aplicada no outro fio.

A soma dessas duas forças resulta na força representada pela seta vermelha, que terá intensidade de 350 + 350 = 700N.

O mesmo raciocínio é válido para se calcular a força representada pela seta amarela, só que nesse caso com forças de 700N, ou seja, 700 + 700 = 1400N.

A seta vermelha é a força normal, que nesse caso tem mesma intensidade da força peso, já que possuem sentidos opostos e não existem outras forças agindo verticalmente no bloco:

N = P N = 4000N.

A seta amarela é a tração, calculada no (01), logo tem intensidade de F=1400N.

A seta verde representa a força de atrito, nesse caso estudaremos o movimento, portanto deveremos considerar o coeficiente de atrito cinético (μc = 0,25). A força de atrito cinético (Fc) pode ser calculada por Fc = N.μc Fc = 4000.0,25 Fc = 1000N.

Essa força terá sentido para a direita, pois a soma das forças exercidas horizontalmente no lado direito do corpo terão maior intensidade que as do esquerdo. A intensidade dessa força pode ser calculada por Fr = F – Fc Fr = 1400 – 1000 Fr = 400 N.

04 Falso Como estudado no item anterior (02), existe uma outra força além das citadas, a força normal, que surge do contato entre o corpo e o chão.

08 Verdadeiro Também demonstrado no item (02), a força resultante é de 400N.

16 Falso Nesse caso vamos estudar o objeto antes do movimento, com isso utilizaremos o coeficiente de atrito estático (μe), a força exercida para que o bloco se movimente deve ser maior que a força de atrito estático (Fe), calculada a seguir Fe = N.μe Fe = 4000.0.3

Fe = 1200 N.

FORÇAS NO MCU

01-Veja a teoria abaixo que está relacionada com o exercício onde o avião (ou o piloto) comportam-se como a moto e a normal que a moto troca com o piso do globo pela força que o avião troca com o ar.

Globo da morte

Suponha um motociclista de massa total m (massa dele + massa da moto) descrevendo voltas segundo um plano vertical, com velocidade escalar constante no interior de uma esfera metálica oca de raio R “globo da morte”.

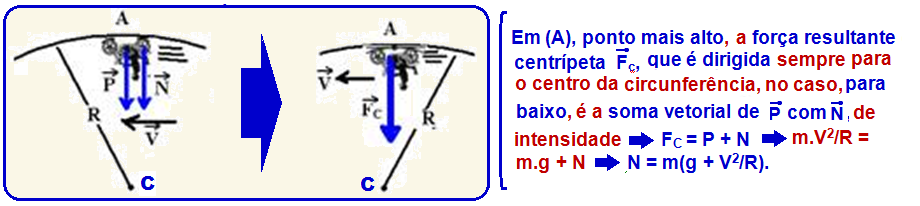
02-Quando a corda atinge a tensão máxima no ponto A (figura), a ela se rompe e a partícula com velocidade VA sai pela tangente e executa um lançamento horizontal com velocidade VA, com trajetória parabólica até atingir o solo percorrendo a distância horizontal 4R e vertical 2R.

Decompõe-se o movimento horizontal em duas parcelas:

Segundo o eixo Y trata-se de um movimento uniformemente variado com velocidade inicial Voy = 0, ou seja, é uma queda livre com o corpo abandonado da origem, sujeito

apenas à aceleração da gravidade, de intensidade g, direção vertical e sentido para baixo.

Equações:

S = So + Vo.t + at2/2 Y= 0 + 0.t + gt2/2 Y = g.t2/2

Vy = Voy + a.t Vy= 0 + g.t Vy = g.t

Na vertical, a partícula em queda livre, sai do ponto A com Vo = 0 e percorre a distância vertical Y =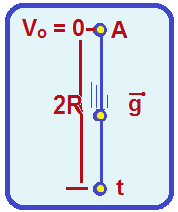

2R até chegar ao solo e demora um tempo t, tal que Y = g.t2/2 2R = g. t2 = t = 2

(tempo de queda na vertical que é o mesmo tempo que apartícula demora para percorrer a distância d = 4R na horizontal)

Segundo o eixo X trata-se de um movimento horizontal uniforme comvelocidade constante de intensidade VA , que é a velocidade de lançamento S = So + V.t X= 0 + VA.t X = VA.t.

O tempo t que ela demora para percorrer x = 4R na horizontal é o mesmo que demorou na queda livre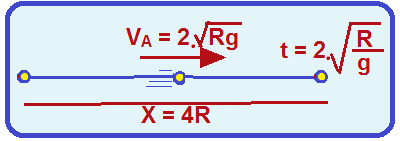

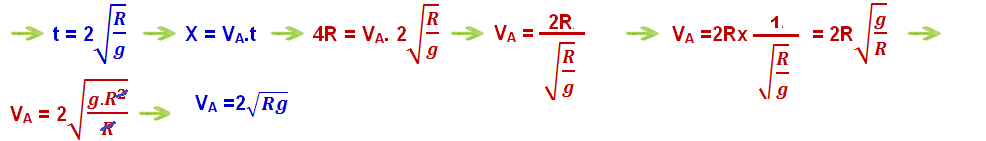
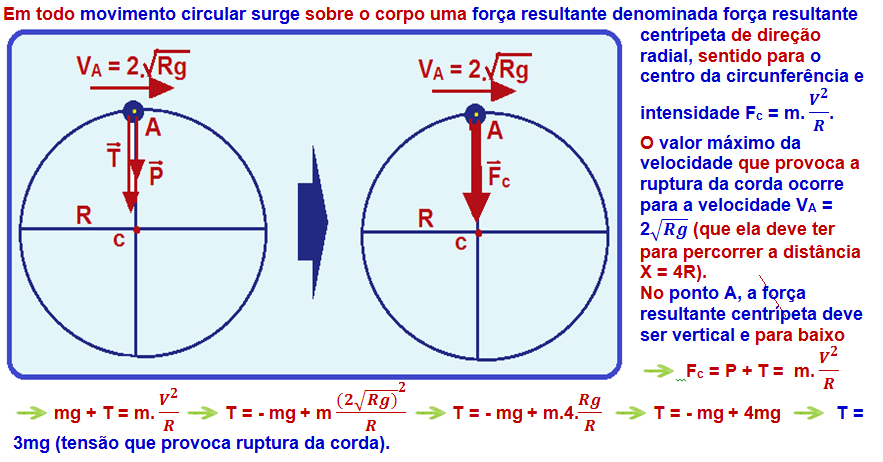R – C

03-

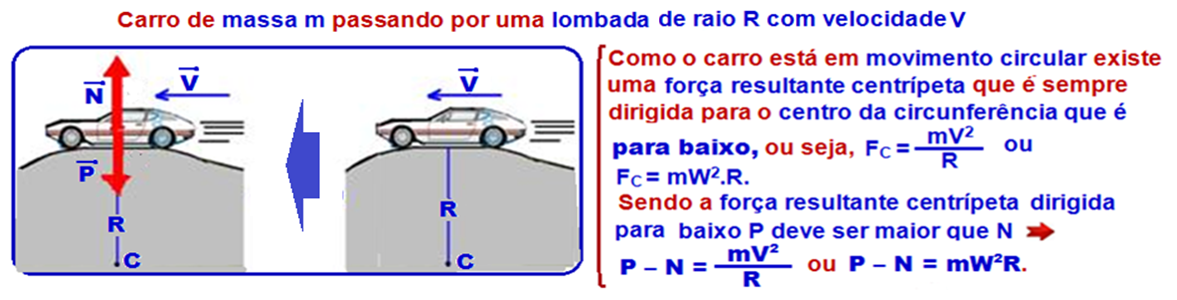
P – N = como a força exercida pela pista sobre o carro tem intensidade N tal que - N = – P N = Mg – .

R- B

TRABALHO E ENERGIA

01-

Cálculo da potência teórica (Pt) de cada usina (unidade geradora) que leva em conta a altura (h) da massa m de água represada pela barragem, a gravidade local (g = 10 m/s2) e a densidade da água (da= 1 000 kg/m3) Pt = W (energia potencial gravitacional armazenada pela massa m de água na

Sendo a vazão nominal da água de Z = 690 m3/s = Volume/intervalo de tempo (1 s) Z = V/∆t

690 = V/1 V = 690 m3 (volume de água que cai em cada 1s).

dágua = 1000 = m =69.104 kg (massa de água).

Energia potencial gravitacional liberada por m = 69.104 kg de água numaaltura de h = 118,4 m num local onde g = 10 m/s2 W = m.g.h= 69.104.10.118,4 = 8169,6.105 = 816,96.106 J.

Potência teórica (Pt) de cada usina (unidade geradora) Pt = =Pt =816,96.106 W

Pt = 816,96 MW (potência teórica).

Potência não aproveitada em cada unidade geradora de Itaipu = potência teórica – potência instalada

Pperdida= 816,96MW – 700MW Pperdida = 116,96 MW
R – C

02-

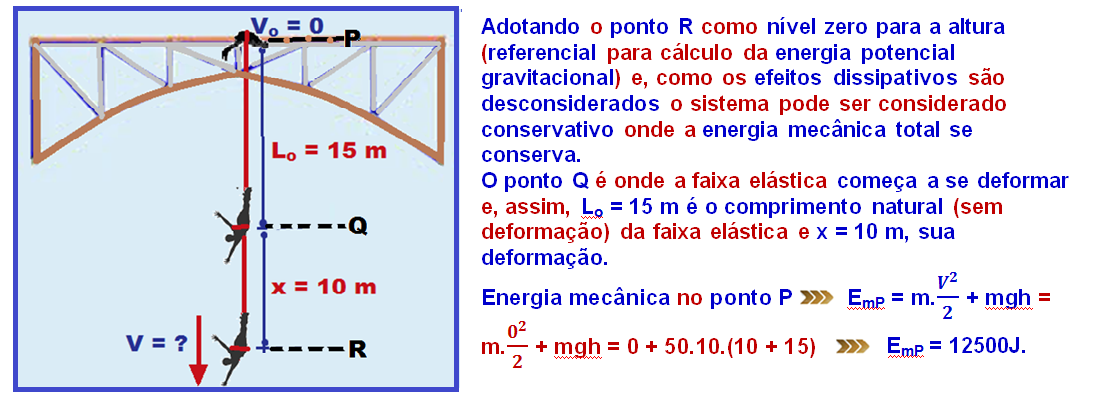
Energia mecânica no ponto R onde a mola está deformada de x = 10 m, h= 0 e o corpo tem velocidade V EmR = m. + mgh + k. EmR = 50. + 50.10.0 + 250. EmR = 25.V2 + 0 + 125.100 EmR = 25.V2+12500.

Sistema conservativo EmP = EmR 12500 = 25.V2 +12500 25V2 = 0 V = 0 e este é o ponto onde a deformação da mola é máxima.

R – A

03-Como em qualquer choque a quantidade de movimento é conservada, já podemos excluir algumas alternativas. Agora só falta resolvermos o problema da energia cinética, o texto deixa bem claro que as velocidades não mudam, antes e depois do choque, como a massa também se mantém, podemos concluir que a energia cinética não muda, portanto, a alternativa E é a correta.

R – E

04-a) Considerando o sistema “projétil, saco de areia e carrinho” isolado de forças externasvocê pode aplicar o teorema da conservação da quantidade de movimento.

Qsa = Qsd 10 = 1,6 + 100 V V = V = 8,4.10-2 m/s

Teorema da energia cinética:

“ O trabalho da resultante de todas as forças que agem sobre um corpo é igual à variação da energia cinética sofrida pelo corpo “

WFR = ∆Ec = Ecd – Eca = mp.(Vpd)²/2 – mp.(Vpa)²/2 WFR = 20.10^-3 .80²/ 2 – 20.10^-3 .500²/ 2 = 64 – 2500 WFR = – 2435 J (o sinal negativo significa que a energia cinética do projétil foi dissipada).

05-Pelo enunciado o aproveitamento da energia eólica ocorre por meio da conversão da energia cinética (Ec) de translação em energia cinética de rotação.

A análise das turbinas eólicas é complexa porque envolve aerodinâmica e mecânica dos fluidos.

Contudo, os conceitos básicos podem ser obtidos a partir de simplificações na análise.

A energia contida no vento horizontal é basicamente sua energia cinética, uma vez que não há variação de pressão, variação de altitude, e, pelo enunciado, a densidade do ar permanece constante o que implica que amassa de ar m que atravessa os permanece constante.

A energia cinética é uma grandeza escalar, não tem direção nem sentido,apenas intensidade, fornecida pela expressão:.

R- B

06-

Propriedade do gráfico forçaxdeslocamento

Em todo gráfico da força F em função do deslocamento d, o trabalho realizado pela força F é numericamente igual à área compreendida entre a reta representativa (linha cheia) e o eixo do deslocamento.

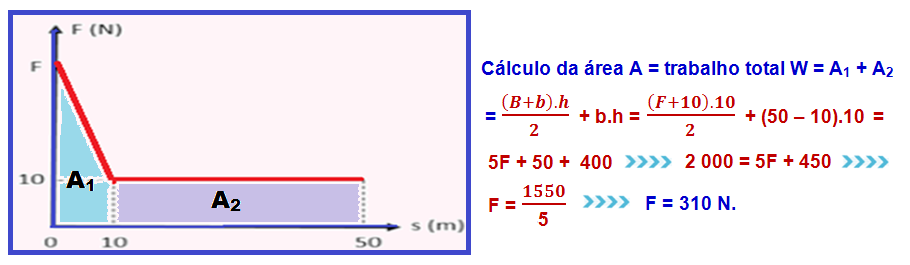
Se, ao final desse deslocamento de d= 50 m a intensidade dessa força F (suposta resultante) fosse mantida constante (F = 310 N), o trabalho realizado por ela seria W = F.d = 310.50

W = 15 500 J.

Supondo que essa força F seja a força resultante você pode aplicar o teorema do Trabalho como variação da energia cinética:

WF = Ecf – Eci = Ecf – mVo²/2 = mV²/2 – m0²/2 = Ecf – 0 Ecf = 15 500 J.

R- C

07-

08- Observe na figura a que a força é decomposta em duas parcelas e e que a parcela responsável pela realização do trabalho no deslocamento é Fx tal que Fx < F.

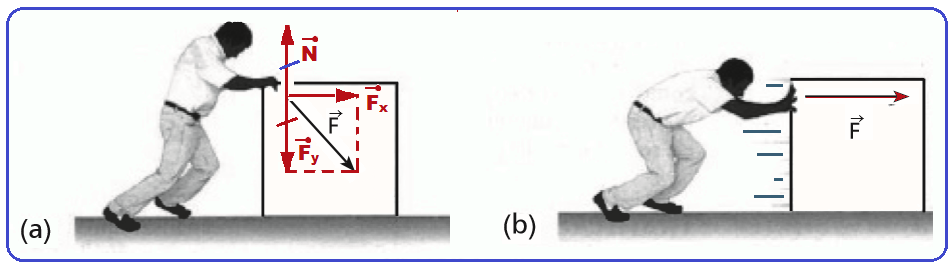
Em b a força que age no deslocamento é .

Como o trabalho em a vale Wa =Fx.d e em b vale, Wb = F.d Wa < Wb.

R- C

09-

Essa é a expressão da energia cinética de um corpo de massa m no instante em que ele possuivelocidade de

intensidade V

No caso do exercício:

Massa do navio mnavio = 450.000 kg massa das pessoas mpessoas = 1000×70 = 70.000 kg

Massa dos carros mcarros = 150×1000 = 150.000 kg.

Massa total do sistema = 450000 + 70000 + 150000 =

670.000 kg.
301,5 MJ

10- O enunciado afirma que a esfera está em repouso na posição x = x1 o que implica que, nessa posição, sua energia cinética é nula (Ec = mV2/2 = m.02/2=0).

Sendo os efeitos dissipativos desprezíveis você pode aplicar o Princípio da Conservação da energia Mecânica em que, para qualquer posição da trajetória, a energia mecânica (Em) é constante, ou seja, a soma das energias cinética (Ec) e potencial gravitacional (Ep) em cada ponto fornece sempre o mesmo valor.

Assim, se Em = Ec + Ep = constante, então no ponto x = x1 onde a cinética é nula a potencial será máxima.

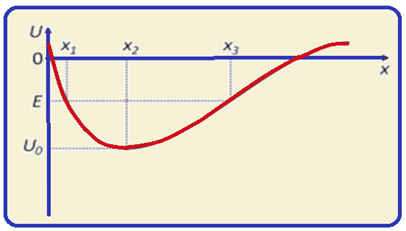
Da mesma maneira, se Em = Ec + Ep = constante, então no ponto x = x2onde a energia potencial gravitacional é mínima (veja gráfico) e de valor Uo, a cinética será máxima.

R- E

DINÂMICA IMPULSIVA

01-Cálculo das velocidades dos carrinhos 1 e 2 de massas m1 = 150 g e m2 pedida, antes do choque, registrados nos instantes O e 1 s fornecidos no quadro:

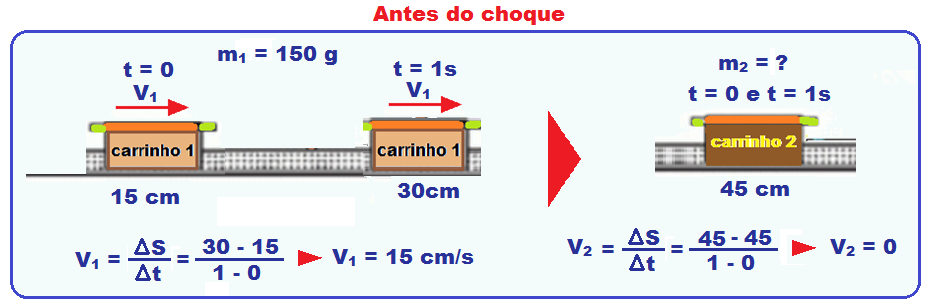
Após o choque, pelo enunciado eles se movem unidos (choque inelástico) com massa (M = 150 +m2), com a mesma velocidade V’ fornecida no quadro nos instantes 8s e 11 s:

Aplicando o teorema da conservação da quantidade de movimento:

Quantidade de movimento do sistema antes do choque Qsa = m1.V1 + m2.V2 = 150.15 + m2.0

Qsa = 2250 + 0 Qsa = 2250 g.cm/s.

Quantidade de movimento do sistema depois do choque Qsd = M.V’ = (150 + m2).5 = 750 + 5m2 Qsd = 750 + 5m2.

Qsa = Qsd 2250 = 750 + 5m2 m2 = 1500/5 m2 = 300 g.

R- C

02-As forças trocadas entre o trem e a camionete obedecem ao princípio da ação e reação, ou seja, tem sempre a mesma intensidade, mesma direção, mas sentidos contrários.

Choque inelástico

Neste tipo de choque a dissipação de energia é máxima, o coeficiente de restituição é nulo, e, após o choque, os corpos obrigatoriamente se juntam e se movem unidos com a mesma velocidade. Lembre-se de que em qualquer tipo de choque a quantidade de movimento sempre se conserva.

R- D

03-

04-Definimos impulso da força no intervalo de tempo ∆t como sendo a grandeza vetorial:

Como ∆t é uma grandeza escalar positiva, o impulso I tem sempre a mesma direção e mesmo sentido que a força e, com as características abaixo:

Observe no gráfico que, no intervalo de tempo entre 5 s e 105 s, a força de mantém constante em 100N, assim, em um intervalo de tempo de Δt =105 – 5 = 100 s, aplicando a fórmula do impulso, em modulo, temos I = F.Δt = 100.100 I = 10.000 N.s = 104 N.s.

OBS: repare que o exercício pede somente a intensidade do impulso, mesmo ela sendo uma grandeza VETORIAL (possui intensidade, direção e sentido).

05- I. Correta Quando temos uma colisão perfeitamente elástica significa que o sistema é conservativo, isto é, a quantidade de movimento e a energia cinética permanecem constantes.

IV. Errada Analogamente a afirmação III, como m1 < m2 V’2 < V’1,porém, V’1 será menor que V1.

R- C

06- Sendo a colisão elástica a energia total (cinética do sistema constituído pelas 5 esferas) é a mesma antes e depois do choque e ocoeficiente de restituição vale e=1. Como em todo em tipo de choque, aquantidade de movimento do sistema também se conserva.

Se você chamar de m a massa de cada esfera e de V sua respectiva velocidade, o módulo da quantidade de movimento do sistema antes do choque (com as 3 esferas se movendo para a direita) é Qsa = mV + mV = mV = 3mV.

Assim, o módulo da quantidade de movimento do sistema depois do choque deve ser também Qsd =

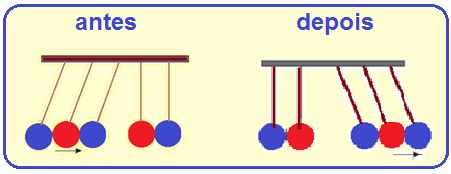
3mV é a única alternativa que satisfaz é a C.

R- C.

07-

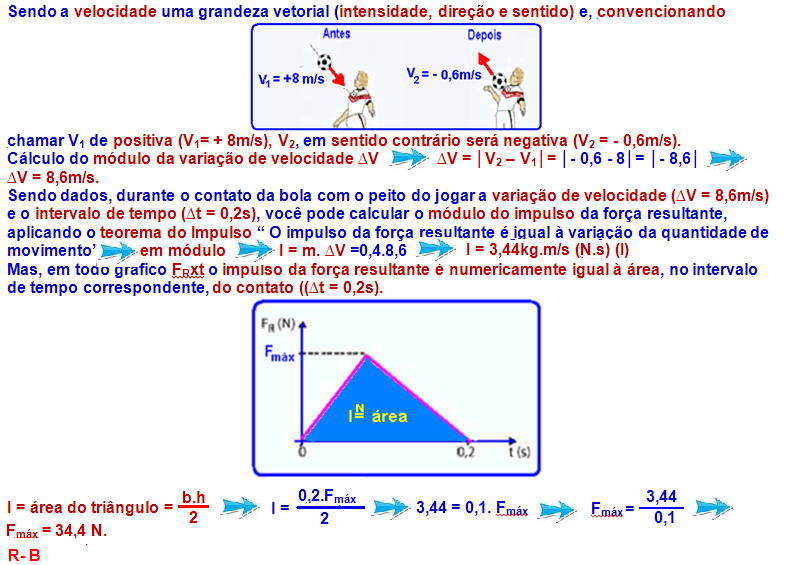
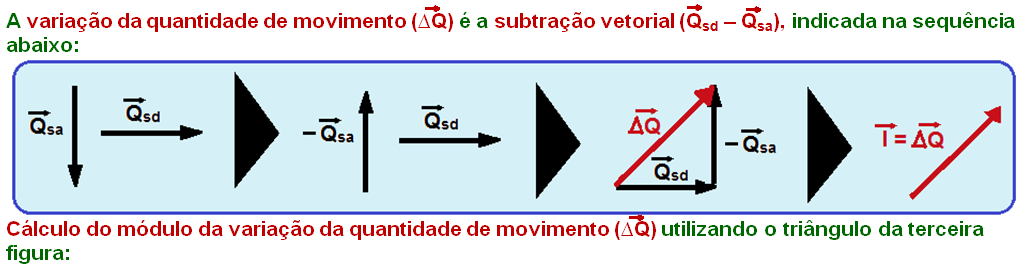
08-Supondo a cabeça do jogador parada (obstáculo fixo), o módulo quantidade de movimento da bola antes do choque, quando incide verticalmente com velocidade de módulo Vvertical será:

Qsa = mVvertical, com direção vertical e sentido para baixo.

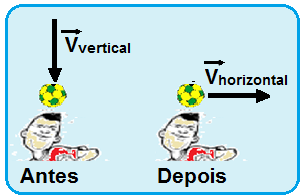
Supondo a cabeça do jogador parada (obstáculo fixo), o módulo da quantidade de movimento da bola depois do choque, quando retorna horizontalmente com velocidade de módulo Vhorizontal será:

Qsd = mVhorizontal, com direção horizontal e sentido para a direita.

09-

10-

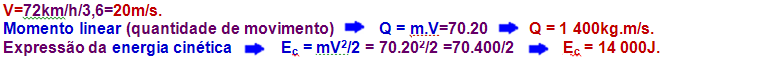
MOVIMENTO HARMÔNICO SIMPLES

01-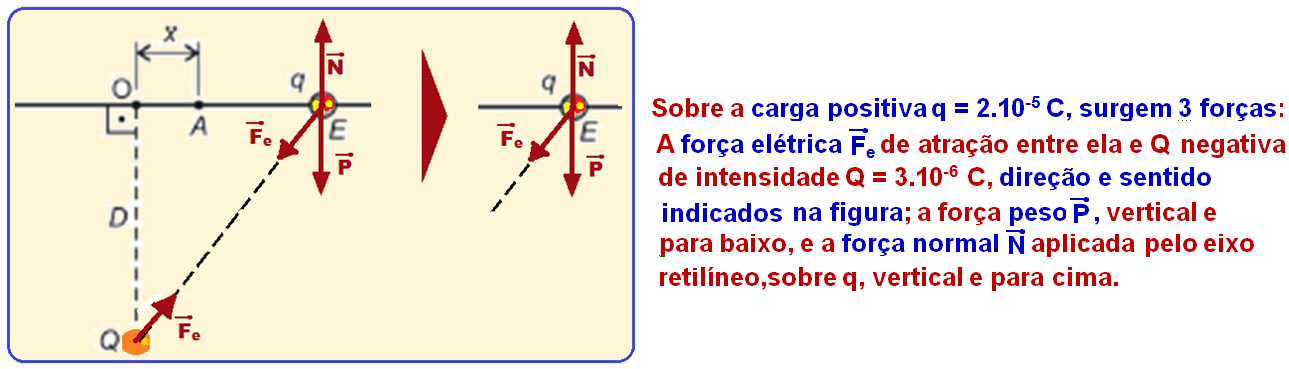

02-O período T (tempo que o oscilador massa-mola demora para efetuar uma oscilação “vai e vem” completa) é fornecido por:

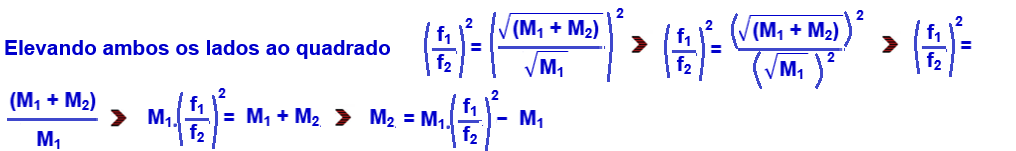
R- B

03-

01 Falso O período e a frequência dependem apenas do número de ciclos e do intervalo de tempo.

02 Verdadeiro A frequência no MHS pode ser calculada como:

Onde T é o período, m a massa desejada e k a constante elástica.Para calcularmos a frequência, precisamos elevar toda a equação por -1, pois a frequência é o inverso do período, nesse caso apenas vamos inverter as frações.

Colocando os valores:

Transformando 25.104 em 2500.102:

Saindo da raiz:

Simplificando:

Exercícios-Vestibulares Recentes por assunto

2014 e 2013

As três leis de Newton

01-(FMJ-SP-014)

Um avião, de massa m, está decolando inclinado de um ângulo αcom a horizontal, com velocidade

constante e aceleração da gravidade local igual a g. Para continuar subindo nessas condições,a força resultante sobre o avião deverá ter intensidade igual a

(A) m.g.senα. (B) m.g.tgα. (C) m.g.cosα. (D) zero. (E) m.g.

02-(IFPE-PE-014)

Um bloco desliza sobre um piso horizontal liso (sem atrito) com velocidade de 20 m/s quando atinge

uma região áspera muito extensa, cujo coeficiente de atrito cinético vale μ = 0,4 (ver figura).

A distância percorrida pelo bloco sobre o piso com atrito, até ele parar, vale em metros: (Adote g = 10 m/s²)

a) 10 b) 20 c) 30 d) 40 e) 50

03-(FATEC-SP-014)

Os aviões voam porque o perfil aerodinâmico de suas asas faz com que o ar que passa por cima e por baixo delas ocasione uma diferença de pressão que gera o empuxo.

Esta força de empuxo é que permite ao avião se sustentar no ar. Logo, para que o avião voe, as hélices ou turbinas do avião é que empurram o ar para trás, e o ar reage impulsionando a aeronave para a frente. Desta forma, podemos dizer que o avião se sustenta no ar sob a ação de 4 forças:

- a motora ou propulsão;

- de resistência do ar ou arrasto;

- a peso;

- a de empuxo ou sustentação.

Caso um avião voe em velocidade constante e permaneça à mesma altitude, é correto afirmar que a somatória das

(A) forças verticais é nula e a das horizontais, não nula.

(B) forças horizontais é nula e a das verticais, não nula.

(C) forças horizontais e verticais é nula.

(D) forças positivas é nula.

(E) forças negativas é nula

04-(UERJ-RJ-014)

A imagem abaixo ilustra uma bola de ferro após ser disparada por um canhão antigo.

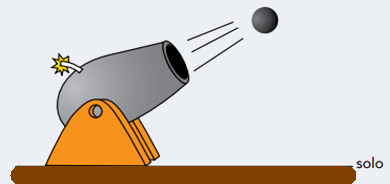
Desprezando-se a resistência do ar, o esquema que melhor representa as forças que atuam sobre a bola de ferro é:

05-(EsPCEx-SP-014)

Um portão maciço e homogêneo de 1,60m de largura e 1,80m de comprimento, pesando 800N está fixado em um muro por meio das dobradiças "A", situada a 0,10m abaixo do topo do portão, e "B", situada a 0,10 m de sua parte inferior. A distância entre as dobradiças é de 1,60m conforme o desenho abaixo.

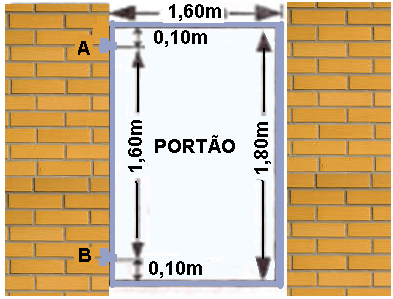
Elas têm peso e dimensões desprezíveis, e cada dobradiça suporta uma força cujo módulo da componente vertical é metade do peso do portão.

Considerando que o portão está em equilíbrio, e que o seu centro de gravidade está localizado em seu centro geométrico, o módulo da componente horizontal da força em cada dobradiça "A" e "B" vale, respectivamente:

a) 130 N e 135 N b) 135 N e 135 N c) 400 N e 400 N d) 450 N e 450 N e) 600 N e 65ON

06-(UERJ-RJ-014)

O corpo de um aspirador de pó tem massa igual a 2,0 kg. Ao utilizá-lo, durante um dado intervalo de tempo, uma pessoa faz um esforço sobre o tubo 1 que resulta em uma força de intensidade constante igual a 4,0 N aplicada ao corpo do aspirador. A direção dessa força é paralela ao tubo 2, cuja inclinação em relação ao solo é igual a 60º, e puxa o corpo do aspirador para perto da pessoa.

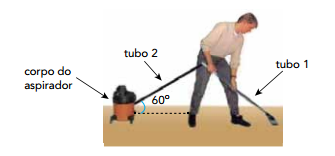
Considere sen 60º = 0,87, cos 60º = 0,5 e também que o corpo do aspirador se move sem atrito.

Durante esse intervalo de tempo, a aceleração do corpo do aspirador, em m/s², equivale a:

(A) 0,5 (B) 1,0 (C) 1,5 (D) 2,0

07-(UNESP-SP-013)

O bungeejumpé um esporte radical no qual uma pessoa salta no ar amarrada pelos tornozelos ou pela cintura a uma corda elástica.

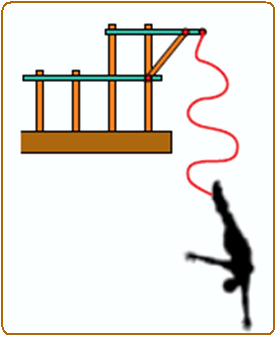
Considere que a corda elástica tenha comprimento natural (não deformada) de 10 m. Depois de saltar, no instante em que a pessoa passa pela posição A, a corda está totalmente na vertical e com seu comprimento natural. A partir daí, a corda é alongada, isto é, tem seu comprimento crescente até que a pessoa atinja a posição B, onde para instantaneamente, com a corda deformada ao máximo.

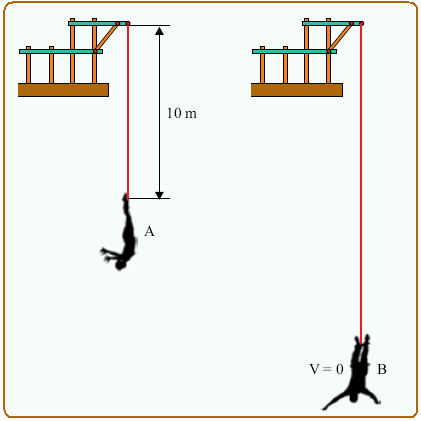
Desprezando a resistência do ar, é correto afirmar que, enquanto a pessoa está descendo pela primeira vez depois de saltar, ela

(A) atinge sua máxima velocidade escalar quando passa pela posição A.

(B) desenvolve um movimento retardado desde a posição A até a posição B.

(C) movimenta-se entre A e B com aceleração, em módulo, igual à da gravidade local.

(D) tem aceleração nula na posição B.

(E) atinge sua máxima velocidade escalar numa posição entre A e B

08-(UNESP-SP-014)

Ao tentar arrastar um móvel de 120 kg sobre uma superfície plana e horizontal, Dona Elvira percebeu que, mesmo exercendo sua máxima força sobre ele, não conseguiria movê-lo, devido à força de atrito entre o móvel e a superfície do solo.

Chamou, então, Dona Dolores, para ajudá-la. Empurrando juntas, elas conseguiram arrastar o móvel

em linha reta, com aceleração escalar constante de módulo 0,2 m/s².

Sabendo que as forças aplicadas pelas duas senhoras tinham a mesma direção e o mesmo sentido do movimento do móvel, que Dona Elvira aplicou uma força de módulo igual ao dobro da aplicada por Dona Dolores e que durante o movimento atuou sobre o móvel uma força de atrito de intensidade constante e igual a 240 N, é correto afirmar que o módulo da força aplicada por Dona Elvira, em newtons, foi igual a

(A) 340. (B) 60. (C) 256. (D) 176. (E) 120.

09-(ACAFE-SC-014)

O tratamento de tração é a aplicação de uma força de tração sobre uma parte do corpo. A tração

ainda é usada principalmente como uma prescrição em curto prazo até que outras modalidades,

como a fixação externa ou interna, sejam possíveis. Isso reduz o risco da síndrome do desuso.

Seja um paciente de massa 50 kg submetido a um tratamento de tração como na figura abaixo, que

está deitado em uma cama onde o coeficiente de atrito entre a mesma e o paciente é μ=0,26.

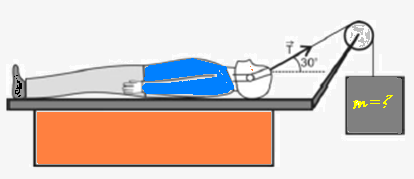
Sabendo-se que o ângulo entre a força de tração e a horizontal é 30^o, a alternativa correta que

apresenta a máxima massa, em kg, que deve ser utilizada para produzir tal força de tração sem que

o paciente se desloque em cima da cama é:

A) 25 B) 13 C) 10 D) 50

10-(CEDERJ-RJ-014)

Um pequeno bloco de madeira é lançado com velocidade inicial sobre uma superfície horizontal,

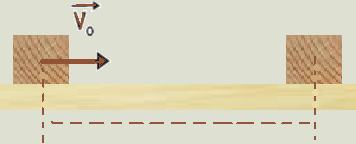
conforme ilustra a figura. O bloco desliza sobre esta superfície, parando depois de percorrer uma determinada distância sob ação de uma força de atrito constante

11-(CEFET-MG-014)

Uma caixa, inicialmente em repouso, sobre uma superfície horizontal e plana, é puxada por um operário que aplica uma força variando linearmente com o tempo. Sabendo-se que há atrito entre a caixa e a superfície, e que a rugosidade entre as áreas em contato é sempre a mesma, a força de atrito, no decorrer do tempo, está corretamente representada pelo gráfico

12-(MACKENZIE-SP-014)

Ao montar o experimento abaixo no laboratório de Física, observa-se que o bloco A, de massa 3 kg,

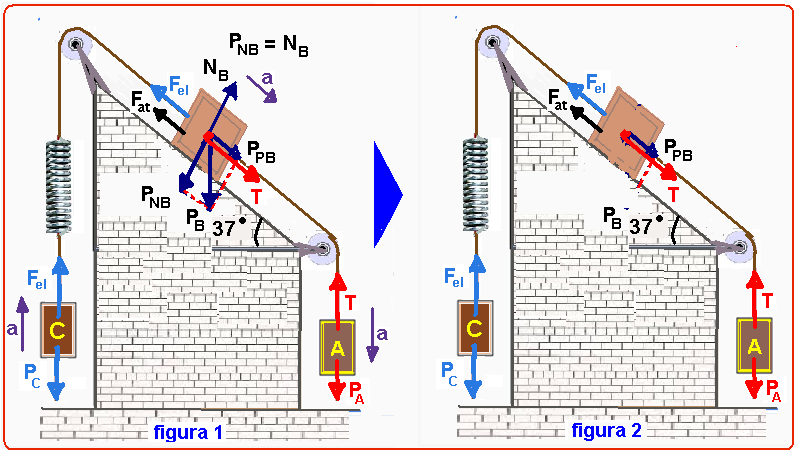
cai com aceleração de 2,4 m/s², e que a mola ideal, de constante elástica 1240 N/m, que suspende o bloco C, está distendida de 2 cm. O coeficiente de atrito entre o bloco B e o plano inclinado é 0,4. Um aluno determina acertadamente a massa do bloco B como sendo

a) 1,0 kg b) 2,0 kg c) 2,5 kg d) 4,0 kg e) 5,0 kg

13-(PUC-MG-014)

Um pequeno bloco desce um plano inclinado com velocidade constante. Sobre essa situação, é CORRETO

afirmar:

a) A força resultante que age sobre o bloco é nula.

b) A força de atrito entre o bloco e a superfície do plano é desprezível.

c) O peso do bloco interfere na velocidade com que ele desce pelo plano inclinado.

d) Na realidade é impossível que um bloco desça um plano inclinado com velocidade constante devido à aceleração da gravidade.

Forças no MCU

01-(UNESP-SP-014)

Em um show de patinação no gelo, duas garotas de massas iguais giram em movimento circular uniforme em torno de uma haste vertical fixa, perpendicular ao plano horizontal.

Duas fitas, F₁ e F₂, inextensíveis, de massas desprezíveis e mantidas na horizontal, ligam uma garota à outra, e uma delas à haste. Enquanto as garotas patinam, as fitas, a haste e os centros de massa das garotas mantêm-se num mesmo plano perpendicular ao piso plano e horizontal.

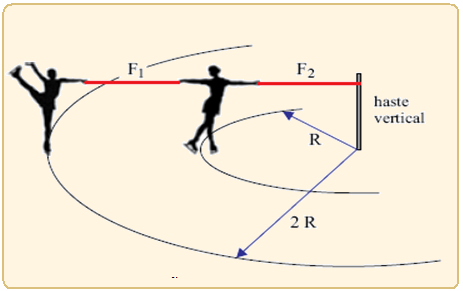
Considerando as informações indicadas na figura, que o módulo da força de tração na fita F₁ é igual a 120 N e desprezando o atrito e a resistência do ar, é correto afirmar que o módulo da força de tração, em newtons, na fita F₂ é igual a

(A) 120. (B) 240. (C) 60. (D) 210. (E) 180.

02-(FUVEST-SP-014)

Para passar de uma margem a outra de um rio, uma pessoa se pendura na extremidade de um cipó

esticado, formando um ângulo de 30°com a vertical, e inicia, com velocidade nula, um movimento pendular. Do outro lado do rio, a pessoa se solta do cipó no instante em que sua velocidade fica novamente igual a zero. Imediatamente antes de se soltar, sua aceleração tem

a) valor nulo.

b) direção que forma um ângulo de 30°com a vertical e módulo 9 m/s².

c) direção que forma um ângulo de 30°com a vertical e módulo 5m/s².

d) direção que forma um ângulo de 60°com a vertical e módulo 9m/s².

e) direção que forma um ângulo de 60°com a vertical e módulo 5m/s².

03-(AFA-014)

Um motociclista, pilotando sua motocicleta, move-se com velocidade constante durante a realização do looping da figura abaixo.

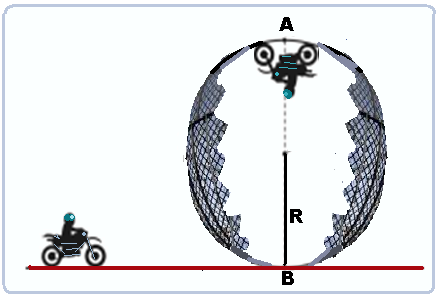
Quando está passando pelo ponto mais alto dessa trajetóriacircular, o motociclista lança, para trás, um objeto de massa desprezível, comparada à massa de todo o conjunto motocicleta-motociclista. Dessa forma, o objeto cai, em relação à superfície da Terra, como se tivesse sido abandonado em A, percorrendo uma trajetória retilínea até B. Ao passar, após esse lançamento, em B, o motociclista consegue recuperar o objeto imediatamente antes dele tocar o solo.

Desprezando a resistência do ar e as dimensões do conjunto motocicleta-motociclista, e considerando π² = 10, a razão entre a normal (N), que age sobre a motocicleta no instante em que passa no ponto A, e o peso (P) do conjunto

motocicleta-motociclista, (N/P), será igual a

a) 0,5 b) 1,0 c) 1,5 d) 3,5

04-(CEDERJ-RJ-014)

Um pêndulo é constituído por um pequeno corpo de massa m preso a um fio inextensível, de comprimento d e de massa desprezível. Esse pêndulo oscila em um plano vertical em torno do ponto P ao qual o fio está preso. As posições I e II especificam, respectivamente, os pontos mais alto e

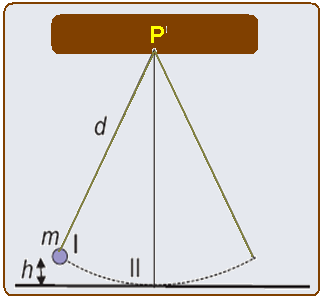
mais baixo da trajetória do pequeno corpo. Sabendo que a altura máxima que o corpo atinge em relação ao ponto II é h, calcule (em função de m, d, h e do valor g da aceleração da gravidade):

a) a velocidade do corpo ao passar pelo ponto II. Sugestão: Utilize a conservação da energia mecânica;

b) a tensão T no fio do pêndulo ao passar pelo ponto II.

Trabalho- Energia

01-(UFSCAR-SP-014)

Para realizar uma reforma na laje de um edifício, uma empreiteira instalou um pequeno guindaste a uma

altura de 15 m do chão. Ao descer uma carga de entulho, o guindaste necessita de 60 s e emprega

uma potência de 900 W, fazendo com que a velocidade de descida seja constante. Sabendo que a aceleração da gravidade é 10 m/s² e supondo que toda a potência seja empregada para realizar o movimento da carga, a massa de entulho, em kg, é

(A) 120. (B) 180. (C) 300. (D) 360. (E) 540.

02-(UERJ-RJ-014)

Em um experimento, são produzidos feixes de átomos de hidrogênio, de hélio, de prata e de

chumbo. Estes átomos deslocam-se paralelamente com velocidades de mesma magnitude.

Suas energias cinéticas valem, respectivamente, E_H, E_He, E_Ag e E_Pb.

A relação entre essas energias é dada por:

A) E_He > E_H > E _Pb > E_Ag B) E _Ag > E_Pb > E_H > E_He

C) E_H > E_He > E _Ag > E_Pb D) E_Pb > E_Ag > E_He > E_H

03-(UNICAMP-SP-014)

Andar de bondinho no complexo do Pão de Açúcar no Rio de Janeiro é um dos passeios aéreos urbanos mais famosos do mundo. Marca registrada da cidade, o Morro do Pão de Açúcar é constituído de um único

bloco de granito, despido de vegetação em sua quase totalidade e tem mais de 600 milhões de anos.

A altura do Morro da Urca é de 220 m e a altura do Pão de Açúcar é de cerca de 400 m, ambas em relação

ao solo. A variação da energia potencial gravitacional do bondinho com passageiros de massa total M = 5000 kg, no segundo trecho do passeio, é (Use g = 10 m/s²)

a) 9.10⁶J. b) 11.10⁶ J c) 20.10⁶ J d) 31.10⁶ J

04-(UNICAMP-SP-014)

O ar atmosférico oferece uma resistência significativa ao movimento dos automóveis. Suponha que

um determinado automóvel movido a gasolina, trafegando em linha reta a uma velocidade constante de

V=72km/h com relação ao ar, seja submetido a uma força de atrito de F_ar= 380 N.

Em uma viagem de uma hora, aproximadamente quantos litros de gasolina serão consumidos somente para “vencer” o atrito imposto pelo ar?

Dados: calor de combustão da gasolina: 35 MJ/ℓ . Rendimento do motor a gasolina: 30%.

05-(FUVEST-SP-014)

Em uma competição de salto em distância, um atletade70kgtem, imediatamente antes do salto, uma

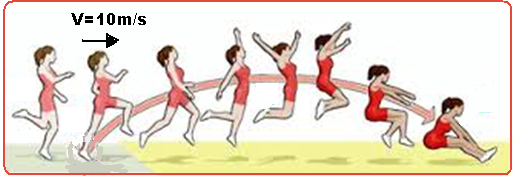
velocidade na direção horizontal de módulo10m/s. Aosaltar, o atleta usa seus músculos para empurrar o chão na direção vertical, produzindo uma energia de 500J, sendo 70% desse valornaformadeenergia cinética.Imediatamenteapósseseparardochão,omódulodavelocidadedoatleta é maispróximode

a) 10,0m/s b) 10,5m/s c) 12,2m/s d) 13,2m/s e) 13,8m/s

06-(FGV-SP-014)

Com a velocidade crescendo de modo constante, em função do tempo, é correto afirmar que a

distância entre os dois radares é de

(A) 450 m. (B) 675 m. (C) 925 m. (D) 1,075 km. (E) 1,350 km.

07-(FGV-SP-014)

O trabalho realizado pela resultante das forças agentes sobre o automóvel foi, em joules, mais próximo de

(A) 1,5·10⁴. (B) 5,2·10⁴. (C) 7,5·10⁴. (D) 1,7·10⁵. (E) 3,2·10⁵.

08-(AFA-014)

Um bloco, de massa 2 kg, desliza sobre um plano inclinado, conforme a figura 1. O gráfico v x t, figura 2, representa a

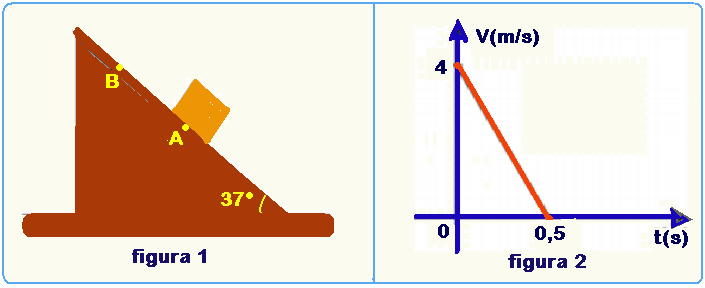
velocidade desse bloco em função do tempo, durante sua subida, desde o ponto A até o ponto B.

Considere a existência de atrito entre o bloco e o plano inclinado e despreze quaisquer outras formas de resistência

ao movimento. Sabendo que o bloco retorna ao ponto A, a velocidade com que ele passa por esse ponto, na descida,

em m/s, vale

a) 4 b) 2√2 c) 2 d) √3

09-(ACAFE-SC-014)

Sem proteção adequada, uma queda com skate pode causar sérias lesões, dependendo da velocidade que ocorre a queda. Um menino em repouso no seu skate encontra-se no ponto mais alto

de uma rampa e começa a descer, chegando ao ponto mais baixo com velocidade de módulo 2,0 m/s.

Em seguida, o menino se lança para baixo com o mesmo skate desse ponto mais alto com uma velocidade inicial de módulo 1,5 m/s.

Sabendo que, em ambas as situações, após iniciado o movimento, o menino não toca mais os pés no solo, a alternativa correta que indica o módulo da velocidade, em m/s, com que o menino no skate chega ao ponto mais baixo na segunda situação,

é:

A) 0,5 B) 3,5 C) 2,1 D) 1,2

10-(IFMT-MT-014)

Um corpo de 2 kg é jogado de baixo para cima, a partir da base de um plano inclinado de 8 m de

comprimento. Ele para exatamente no ponto mais alto do plano e, em seguida, retorna à base. Considerando g = 10 m/s2² e sabendo que o ângulo que o plano forma com a horizontal é de 30°, assinale o trabalho do peso do corpo em Joule (J), na subida e na descida respectivamente. Dados: cos30° = 0,866 e sen30º= 0,500.

a) - 40 e 40 b) 40 e – 40 c) - 80 e 80 d) -160 e 160 e) 160 e 160

Dinâmica Impulsiva

01-(FMJ-SP-014)

Suponha dois corpos celestes viajando no espaço sideral. Suasmassas são M_A e M_B. Em relação a um referencial inercial, o primeiro se desloca a uma velocidade v_A e o segundo a uma velocidadev_B,

perpendicular a v_A. Considere que ocorra uma colisão totalmente inelástica entre eles. A quantidade de movimento do sistema, logo após a colisão, será expressa por

02-(EsPCEx-SP-014)

Um bloco de massa M=180g está sobre uma superfície horizontal sem atrito, e prende-se à

extremidade de uma mola ideal de massa desprezível e constante elástica igual a 2.10³ N/m. A outra

extremidade da mola está presa a um suporte fixo, conforme mostra o desenho.

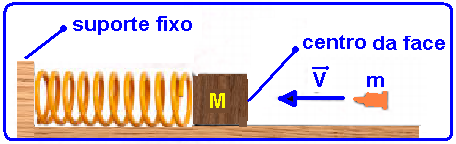
Inicialmente o bloco se encontra em repouso e a mola no seu comprimento natural, isto é, sem deformação.

Um projétil de massa m=20g é disparado horizontalmente contra o bloco, que é de fácil penetração.

Ele atinge o bloco no centro de sua face, com velocidade de v=200m/s. Devido ao choque, o projétil

aloja-se no interior do bloco. Desprezando a resistência do ar, a compressão máxima da mola é de:

a) 10,0 cm b) 12,0 cm c) 15,0 cm d) 20,0 cm e) 30,0 cm

03-(FGV-SP-014)

Na loja de um supermercado, uma cliente lança seu carrinho com compras, de massa total 30 kg, em

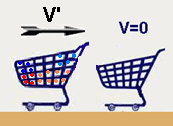
outro carrinho vazio, parado e de massa 20 kg. Ocorre o engate entre ambos e, como consequência do engate, o conjunto dos carrinhos percorre 6,0 m em 4,0 s, perdendo velocidade de modo uniforme até parar. O sistema de carrinhos é considerado isolado durante o engate. A velocidade do carrinho com compras imediatamente antes do engate era, em m/s, de

(A) 5,0. (B) 5,5. (C) 6,0. (D) 6,5. (E) 7,0.

04-(UNICAMP-SP-014)

Existem inúmeros tipos de extintores de incêndio que devem ser utilizados de acordo com a classe do

fogo a se extinguir. No caso de incêndio envolvendo líquidos inflamáveis, classe B, os extintores à base

de pó químico ou de dióxido de carbono (CO₂) são recomendados, enquanto extintores de água devem ser evitados, pois podem espalhar o fogo.

Suponha que um extintor de CO₂ completamente carregado, isolado e inicialmente em repouso, lance um jato de CO₂ de massa m=50 g com velocidade v=20 m/s . Estime a massa total do extintor M_ext e calcule a sua velocidade de recuoprovocada pelo lançamento do gás.

Despreze a variação da massa total do cilindro decorrente do lançamento do jato.

05-(UPF-RS-014)

Em uma mesa de sinuca, uma bola é lançada frontalmente contra outra bola em repouso. Após a

colisão, a bola incidente para e a bola alvo (bola atingida) passa a se mover na mesma direção do movimento da bola incidente. Supondo que as bolas tenham massas idênticas, que o choque seja elástico e que a velocidade da bola incidente seja de 2 m/s, qual será, em m/s, a velocidade inicial da bola alvo após a colisão?

a) 0,5 b) 1 c) 2 d) 4 e) 8

06-(UNESP-SP-014)

Um garoto de 50 kg está parado dentro de um barco de 150 kg nas proximidades da plataforma de um ancoradouro. Nessa situação, o barco flutua em repouso, conforme a figura 1. Em um determinado instante, o garoto salta para o ancoradouro, de modo que, quando abandona o barco, a componente horizontal de sua velocidade tem módulo igual a 0,9 m/s em relação

às águas paradas, de acordo com a figura 2.

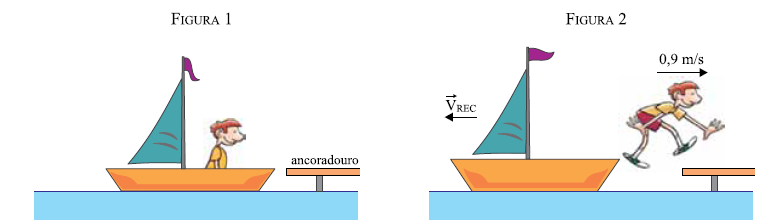
Sabendo que a densidade da água é igual a 10³ kg/m³, adotando g = 10 m/s² e desprezando a resistência da água ao movimento do barco, calcule o volume de água, em m³, que a parte submersa do barco desloca quando o garoto está em repouso dentro dele, antes de saltar para o ancoradouro, e o módulo da velocidade horizontal de recuo (Vrec) do barco em relação às águas, em m/s,

imediatamente depois que o garoto salta para sair dele.

07-(FUVEST-SP-014)

Um núcleo de polônio-204(²⁰⁴P_o), em repouso, transmuta-se em um núcleo de chumbo-200(²⁰⁰P_b), emitindo

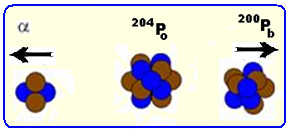
uma partícula alfa(α) com energia cinética E_α.

Nesta reação, a energia cinética do núcleo de chumbo é igual a

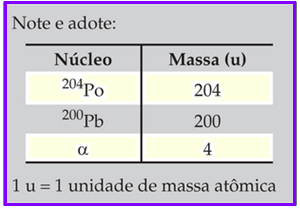
08-(UNIFESP-SP-014)

Uma empresa de demolição utiliza um guindaste, extremamente massivo, que se mantém em repouso e em equilíbrio estável no solo durante todo o processo. Ao braço superior fixo da treliça do guindaste, ponto O, prende-se um cabo, de massa desprezível e inextensível, de 10 m de comprimento. A outra extremidade do cabo é presa a uma bola de 300 kg que parte do repouso, com o cabo esticado, do ponto A.

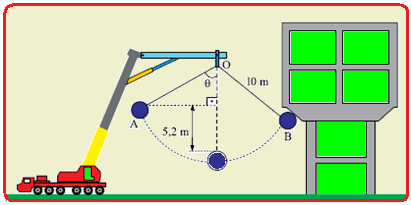
Sabe-se que a trajetória da bola, contida em um plano vertical, do ponto A até o ponto B, é um arco de circunferência com centro no ponto O; que o módulo da velocidade da bola no ponto B, imediatamente antes de atingir a estrutura do prédio, é de 2 m/s; que o choque frontal da bola com o prédio dura 0,02 s; e que depois desse intervalo de tempo a bola para instantaneamente. Desprezando a resistência do ar e adotando g = 10 m/s², calcule, em newtons:

a) o módulo da força resultante média que atua na bola no intervalo de tempo de duração do choque.

b) o módulo da força de tração no cabo no instante em que a bola é abandonada do repouso no ponto A.

09-(UNIFESP-SP-014)

Em uma bancada horizontal da linha de produção de uma indústria, um amortecedor fixo na bancada tem a função de reduzir a zero a velocidade de uma caixa, para que um trabalhador possa pegá-la. Esse amortecedor contém uma mola horizontal de constante elástica K = 180 N/m e um pino acoplado a ela tendo esse conjunto massa desprezível.

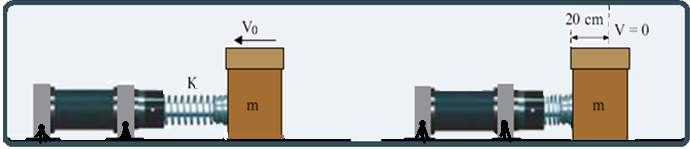
A caixa tem massa m = 3 kg e escorrega em linha reta sobre a bancada, quando toca o pino do amortecedor com velocidade V_o.

Sabendo que o coeficiente de atrito entre as superfícies da caixa e da bancada é 0,4, que a compressão máxima sofrida pela mola quando a caixa para é de 20 cm e adotando g = 10 m/s², calcule:

a) o trabalho, em joules, realizado pela força de atrito que atua sobre a caixa desde o instante em que ela toca o amortecedor até o instante em que ela para.

b) o módulo da velocidade V_o da caixa, em m/s, no instante em que ela toca o amortecedor.

10-(UEL-PR-014)

Analise as figuras a seguir.

Uma partícula 1 com massa M, inicialmente em repouso, que está a uma altura de h = 1, 25 m, desliza sem atrito por uma calha, como esquematizado na Figura 1. Essa partícula colide elasticamente com

a partícula 2 com massa m, inicialmente em repouso. Após a colisão, a velocidade horizontal final da partícula 1 é V_1f = 4,5 m/s.

Utilizando a aceleração da gravidade g = 10 m/s², calcule

a) a velocidade horizontal da partícula 1 antes da colisão.

b) a velocidade horizontal da partícula 2 após a colisão e a altura máxima que ela atinge.

Primeira lei de Newton

29-(UDESC-SC-013)

Considere o movimento de um objeto sujeito à ação de várias forças, de modo que a resultante delas seja nula em todos os instantes.

Analise as proposições em relação à informação acima.

I. Se o objeto estiver inicialmente em movimento, ele não poderá atingir o repouso em algum instante de tempo posterior ao inicial.

II. Se o objeto estiver inicialmente em movimento, ele poderá atingir o repouso em algum instante de tempo posterior ao inicial.

III. Se o objeto estiver inicialmente em repouso, ele poderá entrar em movimento em algum instante de tempo posterior ao inicial.

Assinale a alternativa correta.

A. ( ) Somente a afirmativa III é verdadeira. B. ( ) Somente a afirmativa II é verdadeira.

C. ( ) Somente a afirmativa I é verdadeira. D. ( ) Somente as afirmativas II e III são verdadeiras.

E. ( ) Somente as afirmativas I e III são verdadeiras.

30-(UFRN-RN-013)

Um dos esportes olímpicos mais tradicionais é o salto ornamental em piscina. Nele, o atleta salta do alto de um trampolim visando executar uma trajetória parabólica até atingir a água. Aliado a esse movimento, ele tem de executar outros movimentos, pontuados pelos juízes, como o de encolher momentaneamente braços e pernas de modo que, além da trajetória parabólica de seu centro de massa, ele passe também a girar seu corpo em torno do seu centro de massa. No final do salto, ele estica novamente os braços e as pernas visando cair de cabeça na água. Essa

sequência de movimentos está representada na figura abaixo.

Comparando o movimento inicial feito pelo atleta com braços e pernas estendidos ao movimento realizado com esses membros dobrados junto ao tronco, a lei de conservação do momento angular permite afirmar que

A) há uma diminuição do momento de inércia do atleta e, portanto, uma diminuição na sua velocidade de rotação.

B) há uma diminuição do momento de inércia do atleta e, portanto, um aumento na sua velocidade de rotação.

C) há um aumento do momento de inércia do atleta e, portanto, um aumento na sua velocidade de rotação.

D) há um aumento do momento de inércia do atleta e, portanto, uma diminuição na sua velocidade de rotação.

31-(PUC-MG-013)

FORÇA ESTRANHA

Com a Terra girando a quase 1700 km/h no equador, seria de se esperar que todos ficássemos enjoados, certo? Errado. Não é a velocidade que nos afeta, é a aceleração, como qualquer piloto de corridas pode confirmar. O giro “vagaroso”

da Terra produz uma aceleração 100 vezes menor do que a experimentada num carrossel de um parque de diversões. Ainda assim, a rotação da Terra pode se fazer notar por seus habitantes, por meio do fenômeno chamado Força de Coriolis, que ganhou esse nome em homenagem ao físico e matemático Gaspard-Gustave Coriolis. Coriolis determinou que qualquer coisa que se mova em conjunto com um objeto em rotação vai perceber a realidade como se tivesse sido retirada do seu curso natural por uma força vinda sabe-se-lá de onde.

Por exemplo, uma pessoa num carrossel girando que tente jogar uma bola numa cesta fixa do outro lado do carrossel, vai achar que a bola sempre é desviada do alvo por alguma “força estranha”. Essa tal “força estranha” não existe de fato.

Qualquer um que olhe a cena de fora do carrossel vai perceber que o fenômeno é simplesmente o resultado do movimento da cesta, que se moveu em sua rotação enquanto a bola está no ar. Mas, para os que estão no carrossel, a força é bem real. Por isso, ela precisa ser levada em conta quando calculamos os percursos de objetos tão distintos como mísseis e furacões.

Adaptado do texto Robert Matthews. Revista Conhecer – Nº 33, março de 2012.

(PUC-MG-013)

Considerando-se a velocidade de rotação da Terra informada no texto, uma pessoa na superfície não sente o efeito:

a) porque a velocidade relativa é praticamente zero, devido à inércia.

b) porque a força centrípeta é igual à força centrífuga.

c) porque não há força centrípeta.

d) devido à força da gravidade.

Segunda lei de Newton

34-(CEDERJ-RJ-013)

Uma caixa é arrastada em trajetória retilínea sobre a superfície horizontal de uma mesa, puxada por um fio (F) paralelo à superfície. Existe atrito () entre a mesa e a caixa. A figura a seguir ilustra a situação.

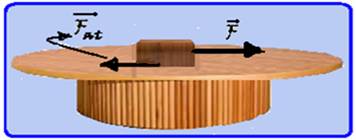
Quando o arrasto se dá a uma velocidade constante, o valor da tensão no fio é de 1N, não importando qual é o valor da velocidade. Quando o arrasto se dá com aceleração constante, a tensão no fio cresce linearmente com a aceleração. O gráfico abaixo mostra esse comportamento.

a) Justifique , com base nessas informações, porque o valor da força de atrito entre a caixa e a superfície da mesa é de 1N.

b) Qual a massa da caixa?

35-(UEPG-PR-013)

Analisando a ação do sistema de forças que age no corpo, conforme figura abaixo, assinale o que for correto.

01) A resultante das forças sobre o eixo X será conhecida por R_x=F₁cosα – μN – F₂senβ.

02) A resultante de todo o sistema é conhecida pela soma dos vetores R_x e R_y.

04) Se a resultante do sistema for igual a zero, então o corpo está em repouso absoluto.

08) A resultante das forças sobre o eixo Y será conhecida por R_y=F₁cosα + F₂cosβ - P.

16) A força de atrito mostrada na figura está fora do eixo X e não pode ser computada como força atuante no sistema.

Terceira lei de Newton

20-(UEG-GO-013)

No reino animal, existem seres que têm a capacidade de realizar diferentes tipos de vôos. O vôo pode ser dividido em

três grupos: o paraquedismo, o planeio e o voo propulsionado. Com relação aos tipos de voo, considera-se o seguinte:

a) no animal planador, a facilidade do voo depende da forma e da dimensão das asas, sendo o movimento no ar ascendente e sem realização de trabalho.

b) no paraquedismo, a força de resistência do ar no animal equilibra-se com o seu peso, fazendo-o cair com velocidade constante.

c) nos voos propulsionados, os animais exercem a movimentação de seus músculos para impulsionarem o deslocamento vertical.

d) o paraquedismo e o planeio baseiam-se em princípios físicos iguais, pois as forças de resistência e peso são um par de ação e reação.

Exercícios sobre conceitos das três leis de Newton

57-(UENP-PR-013)

Um automóvel de massa 1200kg se desloca sobre uma rodovia com velocidade de 108 km/h, quando avista uma

fiscalização policial e aciona os freios até parar. Sabendo-se que a distância percorrida nesse intervalo de tempo em que os freios foram acionados é de 200m, calcule o módulo da aceleração e o módulo do trabalho realizado pelos freios do veículo.

a) 1,00 m/s²; 5,9.10⁵J b) 2,25 m/s²; 5,4.10⁵J c) 2,50 m/s²; 2,8.10⁵J d) 2,25 m/s²; 3,7.10⁵J

e) 1,00 m/s²; zero

58-(UCS-RS-013)

Na luta de sumô, em que dois lutadores se enfrentam dentro de uma área circular, para vencer é necessário, utilizando o

corpo e os braços, empurrar o oponente para fora do círculo. Suponha que dois oponentes, de 200 kg cada, colidam exatamente no centro do círculo e que um dos lutadores consiga aplicar uma força de 1.000 N permanentemente sobre o outro, o qual, por sua vez, aplica uma força de 950 N permanentemente sobre o primeiro. Ambas as forças têm direção paralela ao chão e sentidos opostos. Se o círculo possui 2,0 m de raio, quanto tempo aproximadamente levará para a luta acabar? Para fins de simplificação, ignore o volume do corpo dos lutadores, e considere que, no momento exato da colisão, eles ficam em breve repouso.

a) 0,5 s b) 1,0 s c) 2,0 s d) 3,0 s e) 4,0 s

Tipos de força

39-(FATEC-SP-013)

Um carro em um veículo do tipo “cegonha” (que transporta vários carros) tem cada uma de suas rodas travada por uma cinta, cujos extremos estão presos sobre a plataforma em que se apóia o carro. A cinta abraça parcialmente o pneu, e a regulagem de sua tensão garante a segurança para o transporte, já que aumenta a intensidade da força de contato entre cada pneu e a plataforma.

Se o ângulo formado entre a plataforma e a cinta, de ambos os lados do pneu, é de 60^o, admitindo que cada extremo da cinta se encontre sob uma tração de intensidade T, o acréscimo da força de contato de intensidade F entre cada pneu e a plataforma, devido ao uso desse dispositivo, é dado por

(A) F=T/2 (B) F=(√3/2)T (C) F=T (D) F=√3.T (E) F=4(√3/3).T

40-(ENEM-MEC-012)

O mecanismo que permite articular uma porta (de um móvel ou de acesso) é a dobradiça. Normalmente, são necessárias

duas ou mais dobradiças para que a porta seja fixada no móvel ou no portal, permanecendo em equilíbrio e podendo ser articulada com facilidade.

No plano, o diagrama vetorial das forças que as dobradiças exercem na porta está representado em

Peso e massa

33-(PUC-RJ-013)

Um objeto de 3,10 kg é liberado por um astronauta, a partir do repouso, e cai em direção à superfície do planeta

Marte. Calcule a força peso em Newtons atuando sobre o objeto, expressando o resultado com o número de algarismos significativos apropriado.

Considere a aceleração da gravidade g_Marte= 3,69 m/s²

(A) 31,0 (B) 11,439 (C) 11,44 (D) 11,4 (E) 6,79

34-(UNIMONTES-MG-013)

Um conjunto de molas sustenta o peso de um carro. Com 2 pessoas de 60kg em seu interior, o carro abaixa 2cm. Com 4

pessoas de 70kg, o carro vai abaixar, aproximadamente: g=10m/s^2.

A) 3,0cm. B) 3,5cm. C) 4,0cm. D) 4,7cm.

Leis de Newton do MUV

48-(UEL-PR-013)

Considere a ﬁgura a seguir.

Despreze qualquer tipo de atrito.

a) O móvel de massa M = 1200 kg é uniformemente acelerado (com aceleração a) a partir do repouso em t = 0 segundos, atingindo B, em t = 10 segundos, com a velocidade de 108 km/h.

Calcule a força resultante que atua no móvel de A até B.

b) No ponto B, a aceleração a do móvel deixa de existir.

Calcule a distância BC percorrida pelo móvel, sabendo-se que ele alcança C no instante t = 15 segundos.

Considerando g = 10 m/s², determine a energia mecânica total do móvel em C.

Apresente os cálculos realizados na resolução deste item

Plano inclinado sem atrito

25-(FMABC-SP-013)

Considere um escorregador radical constituído de uma mega rampa de 31,25m de altura e que forma com o plano

horizontal 30^o. Para escorregar, a partir do repouso, as pessoas devem vestir roupas especialmente desenvolvidas com materiais revolucionários que reduzem o atrito com a plataforma da rampa e com o ar a valores desprezíveis. Qual o intervalo de tempo gasto para as pessoas escorregarem do topo até a base da rampa?

Adote para o módulo da aceleração da gravidade o valor de 10m/s².

(A) 5,0s (B) 4,0s (C) 3,5s (D) 3,0s (E) 2,5s

26-(UERJ-RJ-013)

Uma pequena caixa é lançada em direção ao solo, sobre um plano inclinado, com velocidade igual a 3,0 m/s. A altura do ponto de lançamento da caixa, em relação ao solo, é igual a 0,8 m (adote g=10m/s²)

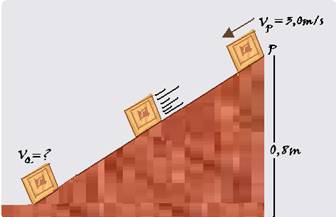
Considerando que a caixa desliza sem atrito, estime a sua velocidade ao atingir o solo.

27-(PUC-GO-013)

Nos versos “A hirta cena de uma difícil fórmula/ ganhadora na velocidade da grafia/ Sem estuprar o tempo/ invento mandingas com a caneta/ de fazer inveja a qualquer Ferrari/ faço curvas com as letras/ manobro perigosas ideias sem capacete”, aparecem as palavras velocidade e tempo. Acrescentando a estas os conceitos de aceleração e de peso de um corpo, analise as afirmativas abaixo:

I- Quando uma bola em repouso está pendurada por uma corda vertical, a tensão na corda é mg. Se a bola é colocada a se mover formando um círculo na horizontal de tal forma que a corda descreve um cone, a tensão na corda é superior a mg.

II- Se um bloco desce um plano inclinado, sem atrito, nele a força normal (a força perpendicular ao plano) é inferior a mg.

III- Duas pedras, uma de massa maior que a outra, em queda livre (resistência do ar nula), têm a mesma aceleração. A razão pela qual a pedra de maior massa não apresenta uma maior aceleração é a de que a proporção da força pela massa é a mesma.

De acordo com os itens analisados, marque a alternativa que contenha apenas proposição(ões) correta(s):

A ( ) I B ( ) I e II C ( ) I, II e III D ( ) III

Lei de Hooke

28-(UNIMONTES-MG-013)

Um conjunto de molas sustenta o peso de um carro. Com 2 pessoas de 60kg em seu interior, o carro abaixa 2cm. Com 4

pessoas de 70kg, o carro vai abaixar, aproximadamente: g=10m/s^2.

A) 3,0cm. B) 3,5cm. C) 4,0cm. D) 4,7cm.

29-(MACKENZIE-SP-013)

Em uma experiência de laboratório, um estudante utilizou os dados do gráfico da figura 1, que se referiam à intensidade da força aplicada a uma mola helicoidal, em função de sua deformação (F=kx). Com esses dados e uma montagem

semelhante à da figura 2, determinou a massa (m) do corpo suspenso.

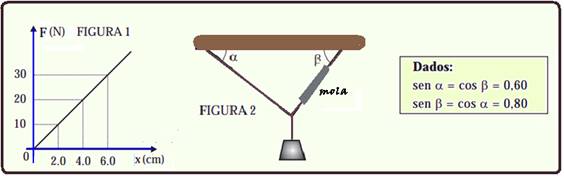
Considerando que as massas da mola e dos fios (inextensíveis) são desprezíveis, que g=10m/s² e que, na posição de equilíbrio, a mola está deformada de 6,4 cm, a massa (m) do corpo suspenso é

a) 12 kg b) 8,0 kg c) 4,0 kg d) 3,2 kg e) 2,0 kg

Movimento Harmônico Simples (MHS)

20-(UNICENTRO-PR-013)

Uma mola se encontra sobre um plano horizontal sem atrito. Um alongamento de 10 cm é obtido com uma força de 10 N.

Adicionamos uma massa de 0,25 kg à mola e produziu-se um alongamento de 20 cm. Abandonamos o sistema. Nestas condições, assinale a alternativa correta.

(A) A constante da força da mola será 1,0.103 N/m.

(B) O período será de 31s.

(C) A velocidade máxima será de 4,0 m/s.

(D) A aceleração máxima será de 8,0 m/s2.

(E) A energia mecânica total do sistema será 20,0 J.

21-(ESCOLA NAVAL-012-013)

Um bloco de massa m=1,00kg executa, preso a uma mola de constante k=100N/m, um MHS de amplitude A cm ao longo do plano inclinado mostrado na figura. Não há atrito em qualquer parte do sistema. Na posição de altura máxima,

a mola está comprimida e exerce sobre o bloco uma força elástica de módulo igual a 3,00N. A velocidade do bloco, em m/s, ao passar pela posição de equilíbrio é

a) 1,10 b) 0,800 c) 0,500 d) 0,300 e) 0,200

15-(AFA-013)

Num local onde a aceleração da gravidade é constante, um corpo de massa m, com dimensões desprezíveis, é posto a

oscilar, unido a uma mola ideal de constante elástica k, em um plano fixo e inclinado de um ângulo θ, como mostra a

figura abaixo.

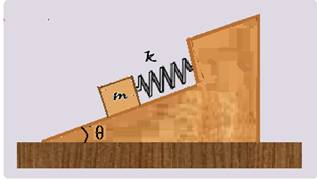
Nessas condições, o sistema massa-mola executa um movimento harmônico simples de período T.

Colocando-se o mesmo sistema massa-mola para oscilar na vertical, também em movimento harmônico simples, o seu

novo período passa a ser T’.

Nessas condições, a razão T’/T é

a) 1/senθ b) senθ c) 1/2 d) 1

16-(ESPCEX-013)

Uma mola ideal está suspensa verticalmente, presa a um ponto fixo no teto de uma sala, por uma de suas extremidades. Um corpo de massa 80 g é preso à extremidade livre da mola e verifica-se que a mola desloca-se para uma nova posição de equilíbrio. O corpo é puxado verticalmente para baixo e abandonado de modo que o sistema

massa-mola passa a executar um movimento harmônico simples. Desprezando s forças dissipativas, sabendo que a constante elástica da mola vale 0,5 N/m e considerando π = 3,14, o período do

movimento executado pelo corpo é de

a) 1,256 s b) 2,512 s c) 6,369 s d) 7,850 s e) 15,700 s

Força de resistência no ar

36-(UNICAMP-SP-013)

Em agosto de 2012, a NASA anunciou o pouso da sonda Curiosity na superfície de Marte. A sonda, de massa m=1000

kg , entrou na atmosfera marciana a uma velocidade v_o=6000 m/s .

a) A sonda atingiu o repouso, na superfície de Marte, 7 minutos após a sua entrada na atmosfera. Calcule o módulo da força resultante média de desaceleração da sonda durante sua descida.

b) Considere que, após a entrada na atmosfera a uma altitude h_o=125 km, a força de atrito reduziu a velocidade da sonda para v= 4000 m/s quando a altitude atingiu h=100 km. A partir da variação da energia mecânica, calcule o trabalho realizado pela força de atrito neste trecho. Considere a aceleração da gravidade de Marte, neste trecho, constante e igual a g_Marte=4 m/s².

37-(UNICAMP-SP-013)

As nuvens são formadas por gotículas de água que são facilmente arrastadas pelo vento. Em determinadas situações,

várias gotículas se juntam para formar uma gota maior, que cai, produzindo a chuva. De forma simplificada, a queda da gota ocorre quando a força gravitacional que age sobre ela fica maior que a força do vento ascendente. A densidade da água é ρ_água=1,0.10³kg/m³.

a) O módulo da força, que é vertical e para cima, que certo vento aplica sobre uma gota esférica de raio r pode ser aproximado por F_vento=b.r, com b=1,6.10^-3N/m. Calcule o raio mínimo da gota para que ela comece a cair.

b) O volume de chuva e a velocidade com que as gotas atingem o solo são fatores importantes na erosão.

O volume é usualmente expresso pelo índice pluviométrico, que corresponde à altura do nível da água da chuva acumulada em um recipiente aberto e disposto horizontalmente. Calcule o impulso transferido pelas gotas da chuva para cada metro quadrado de solo horizontal, se a velocidade média das gotas ao chegar ao solo é de 2,5 m/s e o índice pluviométrico é igual a 20 mm. Considere a colisão como perfeitamente inelástica.

Força de atrito

66-(UCS-RS-013)

Numa festa junina, uma das brincadeiras mais tradicionais é a escalada de um poste de madeira, vertical e besuntado de graxa, conhecido como pau de sebo. Numa dessas ocasiões, o único

candidato que conseguiu escalar o pau de sebo possuía 60 kg. Em certo momento da escalada, ele parou para descansar. Porém, a fim de não escorregar de volta ao chão, ele precisou aplicar no poste um abraço, com os braços e pernas, utilizando uma força total, perpendicular ao poste, de 800N, de forma ininterrupta, pois percebeu que, se aplicasse uma força um pouco menor, escorregaria. Qual foi o coeficiente de atrito estático entre o candidato e a superfície do pau de sebo? Ignore detalhes do contato entre o candidato e o pau de sebo e considere a aceleração da gravidade como 10 m/s².

a) 0,048 b) 0,48 c) 0,75 d) 1,04 e) 1,33

67-(PUC-RJ-013)

Sobre uma superfície sem atrito, há um bloco de massa m₁= 4,0 kg sobre o qual está apoiado um bloco menor de massa m₂= 1,0 kg. Uma corda puxa o bloco menor com uma força horizontal F de módulo 10 N, como mostrado na figura abaixo, e observa-se que nesta situação os dois blocos movem-se juntos.

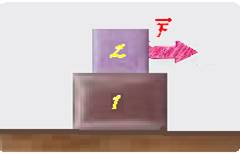
A força de atrito existente entre as superfícies dos blocos vale em Newtons:

(A) 10 (B) 2,0 (C) 40 (D) 13 (E) 8,0

68-(UNESP-SP-2013)

Um garçom deve levar um copo com água apoiado em uma bandeja plana e mantida na horizontal, sem deixar que o copo escorregue em relação à bandeja e sem que a água transborde do copo. O copo, com massa total de 0,4 kg, parte do repouso e descreve um movimento retilíneo e acelerado em relação ao solo, em um plano horizontal e com aceleração constante.

Em um intervalo de tempo de 0,8 s, o garçom move o copo por uma distância de 1,6 m. Desprezando a resistência do ar, o módulo da força de atrito devido à interação com a bandeja, em newtons, que atua sobre o copo nesse intervalo de tempo é igual a

(A) 2. (B) 3. (C) 5. (D) 1. (E) 4

69-(MACKENZIE-SP-013)

Um aluno observa em certo instante um bloco com velocidade de 5 m/s sobre uma superfície plana e horizontal.

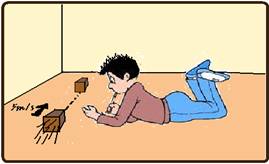
Esse bloco desliza sobre essa superfície e pára após percorrer 5 m. Sendo g=10m/s², o coeficiente de atrito cinético entre o bloco e a superfície é

a) 0,75 b) 0,60 c) 0,45 d) 0,37 e) 0,25

70-(ENEM-MEC-012)

Os freios ABS são uma importante medida de segurança no trânsito, os quais funcionam para impedir o travamento das rodas do carro quando o sistema de freios é acionado, liberando as rodas quando estão no limiar do deslizamento. Quando as rodas travam, a força de frenagem é governada pelo atrito cinético.

As representações esquemáticas da força de atrito f_at entre os pneus e a pista, em função da pressão p aplicada no pedal de freio, para carros sem ABS e com ABS, respectivamente, são

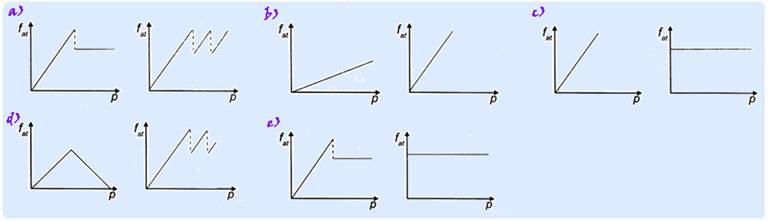
Plano inclinado com atrito

32-(PUC-PR-013)

Um bloco de 10 kg encontra-se em repouso sobre um plano inclinado, conforme figura a seguir. Sabe-se que os coeficientes de atrito estático e dinâmico entre o corpo e a superfície são, respectivamente, 0,75 e 0,70. Para esse plano também considere senθ = 0,6 e cos θ = 0,8.

A partir do exposto, pode-se marcar como CORRETA qual das alternativas a seguir? (Adote g = 10 m/s²)

A) O corpo desce acelerado. O módulo da aceleração é de 6 m/s².

B) Faltam dados para calcular a situação em que o corpo se encontra.

C) O corpo desce em movimento uniforme. As forças que atuam no corpo se anulam.

D) A força de atrito torna-se superior à intensidade do componente tangencial ao plano da forçaPeso. Sendo assim, mesmo que muito lentamente, o corpo irá subir o plano.

E) O corpo permanece em repouso. A situação será de iminência de movimento.

33-(MACKENZIE-SP-013)

Certo menino encontra-se sentado sobre uma prancha plana e desce por uma rampa inclinada, conforme ilustração.

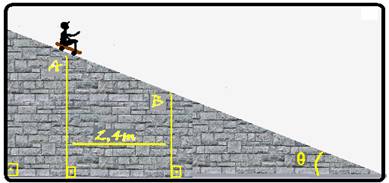
O coeficiente de atrito cinético entre a prancha e a rampa é μ_c=0,25, cosθ=0,8, senθ=0,6 e g=10m/s². Sabe-se que o conjunto, menino e prancha, possui massa de 50 kg e que ao passar pelo ponto A, sua velocidade era 1,0 m/s. A variação de quantidade de movimento sofrida por esse conjunto entre os pontos A e B foi

a) 100 N.s b) 200 N.s c) 300 N.s d) 400 N.s e) 500 N.s

Forças no movimento circular

49-(UNESP-SP-013)

A figura representa, de forma simplificada, o autódromo de Tarumã, localizado na cidade de Viamão, na Grande Porto Alegre. Em um evento comemorativo, três veículos de diferentes categorias do automobilismo, um kart (K), um fórmula 1 (F) e um stock-car (S), passam por diferentes curvas do circuito, com velocidades escalares iguais e constantes.

As tabelas 1 e 2 indicam, respectivamente e de forma comparativa, as massas de cada veículo e os raios de curvatura das curvas representadas na figura, nas posições onde se encontram os veículos.

Sendo F_K, F_F e F_S os módulos das forças resultantes centrípetas que atuam em cada um dos veículos nas posições em que eles se encontram na figura, é correto afirmar que

(A) F_S < F_K < F_F. (B) F_K < F_S < F_F. (C) F_K < F_F < F_S. (D) F_F < F_S < F_K. (E) F_S < F_F < F_K

50-(FUVEST-SP-013)

O pêndulo de um relógio é constituído por uma haste rígida com um disco de metal preso em uma de suas extremidades. O disco oscila entre as posições A e C, enquanto a outra extremidade da haste permanece imóvel no ponto P. A figura abaixo ilustra o sistema.

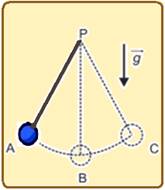
A força resultante que atua no disco quando ele passa por B, com a haste na direção vertical, é

a) nula. b) vertical, com sentido para cima. c) vertical, com sentido para baixo.

d) horizontal, com sentido para a direita. e) horizontal, com sentido para a esquerda.

Trabalho

48-(UCS-RS-013)

Uma moça comprou um par de brincos, de 50 gramas cada um, e os usou durante o período em que

esteve num aniversário. Considerando que o evento aconteceu em lugar plano e que, portanto, os deslocamentos da moça ocorreram sempre em direções paralelas ao chão, qual foi o trabalho realizado pela força peso dos brincos, durante o tempo em que a moça esteve no aniversário?

a) 0,05 J b) 0,025 J c) 1,00 J d) 0,1 J e) zero

49-(UEL-PR-013)

Suponha que o conjunto formado pelo satélite e pelo foguete lançador possua massa de 1,0.10³ toneladas e seja impulsionado por uma força propulsora de aproximadamente 5,0.10⁷N, sendo o sentido de lançamento desse foguete perpendicular ao solo.

Desconsiderando a resistência do ar e a perda de massa devido à queima de combustível, assinale a alternativa que apresenta, corretamente, o trabalho realizado, em joules, pela força resultante aplicada ao conjunto nos primeiros 2,0 km de sua decolagem. Considere a aceleração da gravidade g = 10, 0 m/s² em todo o percurso descrito.

a) 4,0.10⁷ J b) 8,0.10⁷ J c) 4,0.10¹⁰ J -- d) 8,0.10¹⁰ J e) 10,0.10¹⁰J

Potência

51-(UniFOA-RJ-013)

Um ciclista que fará uma prova de "bike indoor" nas olimpíadas do Rio de Janeiro, em 2016, está sujeito a um rigoroso

treino de preparação. Seu treinador importou dos Estados Unidos uma bicicleta eletrônica estática que faz uma análise completa do atleta em preparação. Considerando que o ciclista tenha uma massa de 70kg e parta do repouso, qual a potência necessária que desenvolverá para atingir a velocidade de 72km/h em 2 minutos?

a) 117W b) 10.080W c) 181.440W d) 1.512W e) 14.000W

52-(UFSC-SC-013)

Em Santa Catarina, existe uma das maiores torres de queda livre do mundo, com 100 m de altura. A viagem começa com uma subida de 40 s com velocidade considerada constante, em uma das quatro gôndolas de 500 kg, impulsionadas por motores de 90 kW. Após alguns instantes de suspense, os passageiros caem em queda livre, alcançando a velocidade máxima de 122,4 km/h, quando os freios magnéticos são acionados. Em um tempo de 8,4 s depois de iniciar a descida, os passageiros estão de volta na base da torre em total segurança. Considere a gôndola carregada com uma carga de 240 kg.

Disponível em: <http://www.cbmr.com.br/index.php/parques/20-pqatracoes/275-bigtower>. Acesso em: 5 set. 2012.

Com base nas informações acima, assinale a(s) proposição(ões) CORRETA(S).

01. A potência média desenvolvida pela força aplicada pelo motor durante a subida de uma gôndola carregada é de

18500 W.

02.O módulo da força média sobre a gôndola carregada durante a frenagem na descida é de 5032 N.

04. O tempo total de queda livre é de aproximadamente 4,47 s.

08. A distância percorrida pela gôndola carregada durante a queda livre é de 57,8 m.

16. A aceleração da gôndola carregada durante todo o percurso é igual a g.

Energia

26-(UFRN-RN-013)

O Sol irradia energia para o espaço sideral. Essa energia tem origem na sua autocontração gravitacional. Nesse

processo, os íons de hidrogênio (prótons) contidos no seu interior adquirem velocidades muito altas, o que os leva a atingirem temperaturas da ordem de milhões de graus.

Com isso, têm início reações exotérmicas de fusão nuclear, nas quais núcleos de hidrogênio são fundidos, gerando núcleos de H_e (Hélio) e propiciando a produção da radiação, que é emitida para o espaço. Parte dessa radiação atinge a Terra e é a principal fonte de toda a energia que utilizamos.

Nesse contexto, a sequência de formas de energias que culmina com a emissão da radiação solar que atinge a terra é

27-(UNICAMP-SP-013)

Alguns tênis esportivos modernos possuem um sensor na sola que permite o monitoramento do desempenho do usuário

durante as corridas. O monitoramento pode ser feito através de relógios ou telefones celulares que recebem as informações do sensor durante os exercícios. Considere um atleta de massa m=70 kg que usa um tênis com sensor durante uma série de três corridas.

a) O gráfico 1) abaixo mostra a distância percorrida pelo atleta e a duração em horas das três corridas realizadas em velocidades constantes distintas. Considere que, para essa série de corridas, o consumo de energia do corredor pode ser aproximado por E=C_MET.m.t, onde m é a massa do corredor, t é a duração da corrida e C_MET é uma constante que depende da velocidade do corredor e é expressa em unidade de (kJ/kg.h).

Usando o gráfico 2) abaixo, que expressa C_MET em função da velocidade do corredor, calcule a quantidade de energia que o atleta gastou na terceira corrida.

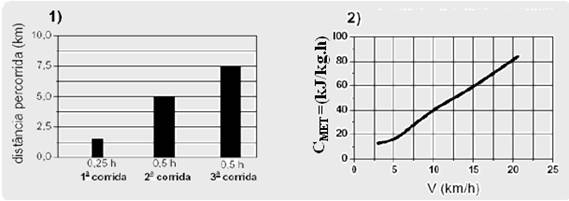
b) O sensor detecta o contato da sola do tênis com o solo pela variação da pressão. Estime a área de contato entre o tênis e o solo e calcule a pressão aplicada no solo quando o atleta está em repouso e apoiado sobre um único pé.

Tipos de energia – Trabalho

39-(ENEM-MEC-012)

Os carrinhos de brinquedo podem ser de vários tipos. Dentre eles, há os movidos à corda, em que uma mola em seu

interior é comprimida quando a criança puxa o carrinho para trás. Ao ser solto, o carrinho entra em movimento enquanto a mola volta à sua forma inicial.

O processo de conversão de energia que ocorre no carrinho descrito também é verificado em

a) um dínamo. b) um freio de automóvel. c) um motor a combustão. d) uma usina hidrelétrica.
e) uma atiradeira (estilingue)

Energia mecânica

72-(PUC-RS-013)

Num salto em altura com vara, um atleta atinge a velocidade de 11m/s imediatamente antes de fincar a vara no chão

para subir. Considerando que o atleta consiga converter 80% da sua energia cinética em energia potencial gravitacional e que a aceleração da gravidade no local seja 10m/s², a altura máxima que o seu centro de massa pode atingir é, em metros, aproximadamente,

A) 6,2 B) 6,0 C) 5,6 D) 5,2 E) 4,8

73-(PUC-RJ-013)

Na figura abaixo, o bloco 1, de massa m₁=1,0 kg, havendo partido do repouso, alcançou uma velocidade de 10 m/s após descer uma distância d no plano inclinado de 30^o. Ele então colide com o bloco 2, inicialmente em repouso, de massa m₂= 3,0 kg. O bloco 2 adquire uma velocidade de 4,0 m/s após a colisão e segue a trajetória semicircular mostrada, cujo raio é de 0,6 m. Em todo o percurso, não há atrito entre a superfície e os blocos. Considere g = 10 m/s².

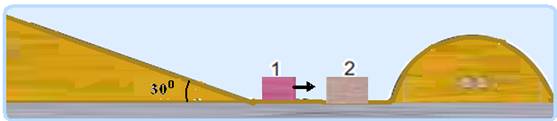
a) Ao longo da trajetória no plano inclinado, faça o diagrama de corpo livre do bloco 1 e encontre o módulo da força normal sobre ele.

b) Determine a distância d percorrida pelo bloco 1 ao longo da rampa.

c) Determine a velocidade do bloco 1 após colidir com o bloco 2.

d) Ache o módulo da força normal sobre o bloco 2 no ponto mais alto da trajetória semicircular.

74-(PUC-SP-013)

Um canhão é fixado sobre uma plataforma retangular de madeira, constituindo um conjunto que se

encontra inicialmente em repouso apoiado sobre um terreno plano e horizontal. Num dia de demonstração para os recrutas é disparado um projétil de massa m com velocidade horizontal v. Após o disparo constata-se que o conjunto (canhão + plataforma de madeira) sofre um recuo horizontal d em relação à sua posição inicial. Considerando que o conjunto tem uma massa M (M>>m) e adotando para o módulo da aceleração da gravidade o valor g, podemos afirmar que o coeficiente de atrito cinético (μ) entre a superfície inferior da plataforma de madeira e o solo pode ser obtido através da expressão:

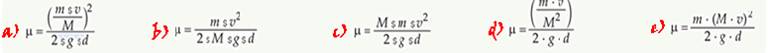
75-(UNESP-SP-013)

Um brinquedo é constituído por dois carrinhos idênticos, A e B, de massas iguais a 3 kg e por uma mola de massa desprezível, comprimida entre eles e presa apenas ao carrinho A. Um pequeno dispositivo, também de massa desprezível, controla um gatilho que, quando acionado, permite que a mola se distenda.

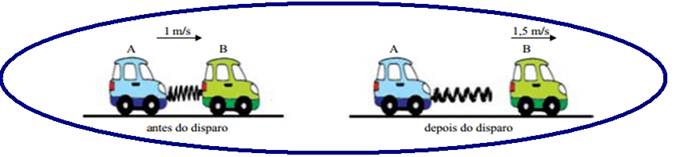
Antes de o gatilho ser acionado, os carrinhos e a mola moviam-se juntos, sobre uma superfície plana horizontal sem atrito, com energia mecânica de 3,75 J e velocidade de 1 m/s, em relação à superfície. Após o disparo do gatilho, e no instante em que a mola está totalmente distendida, o carrinho B perde contato com ela e sua velocidade passa a ser de 1,5 m/s, também em relação a essa mesma superfície.

Nas condições descritas, calcule a energia potencial elástica inicialmente armazenada na mola antes de o gatilho ser disparado e a velocidade do carrinho A, em relação à superfície, assim que B perde contato com a mola, depois de o gatilho ser disparado

76-(FUVEST-SP-013)

Uma das hipóteses para explicar a extinção dos dinossauros, ocorrida há cerca de 60 milhões de anos, foi a colisão de

um grande meteoro com a Terra. Estimativas indicam que o meteoro tinha massa igual a 10¹⁶ kg e velocidade de 30 km/s, imediatamente antes da colisão. Supondo que esse meteoro estivesse se aproximando da Terra, numa direção radial em relação à órbita desse planeta em torno do Sol, para uma colisão frontal, determine

a) a quantidade de movimento P_i do meteoro imediatamente antes da colisão;

b) a energia cinética E_c do meteoro imediatamente antes da colisão;

c) a componente radial da velocidade da Terra, V_r, pouco depois da colisão;

d) a energia E_d, em megatons, dissipada na colisão.

Impulso e quantidade de movimento

39-(PUC-SP-013)

Um canhão é fixado sobre uma plataforma retangular de madeira, constituindo um conjunto que se

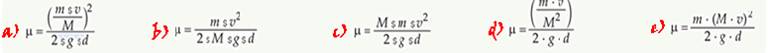
40-(MACKENZIE-SP-013)

Em uma competição de tênis, a raquete do jogador é atingida por uma bola de massa 60 g, com velocidade horizontal

de 40 m/s. A bola é rebatida na mesma direção e sentido contrário com velocidade de 30 m/s. Se o tempo de contato

da bola com a raquete é de 0,01 s, a intensidade da força aplicada pela raquete à bola é

a) 60 N b) 120 N c) 240 N d) 420 N e) 640 N

41-(UNICAMP-SP-013)

Muitos carros possuem um sistema de segurança para os passageiros chamado airbag. Este sistema consiste em uma

bolsa de plástico que é rapidamente inflada quando o carro sofre desaceleração brusca, interpondo-se entre o passageiro e o painel do veículo. Em uma colisão, a função do airbag é

a) aumentar o intervalo de tempo de colisão entre o passageiro e o carro, reduzindo assim a força recebida pelo passageiro.

b) aumentar a variação de momento linear do passageiro durante a colisão, reduzindo assim a força recebida pelo passageiro.

c) diminuir o intervalo de tempo de colisão entre o passageiro e o carro, reduzindo assim a força recebida pelo passageiro.

d) diminuir o impulso recebido pelo passageiro devido ao choque, reduzindo assim a força recebida pelo passageiro

42-(FUVEST-SP-013)

Um fóton, com quantidade de movimento na direção e sentido do eixo x, colide com um elétron em repouso.

Depois da colisão, o elétron passa a se mover com quantidade de movimento p_e, no plano xy, como ilustra a figura abaixo.

Dos vetores p_f abaixo, o único que poderia representar a direção e sentido da quantidade de movimento do fóton, após

a colisão, é

43-(UNESP-SP-013)

Colisões mecânicas

49-(FUVEST-SP-013)

Compare as colisões de uma bola de vôlei e de uma bola de golfe com o tórax de uma pessoa, parada e em pé. A bola

de vôlei, com massa de 270 g, tem velocidade de 30 m/s quando atinge a pessoa, e a de golfe, com 45 g, tem velocidade de 60 m/s ao atingir a mesma pessoa, nas mesmas condições. Considere ambas as colisões totalmente inelásticas. É correto apenas o que se afirma em:

a) Antes das colisões, a quantidade de movimento da bola de golfe é maior que a da bola de vôlei.

b) Antes das colisões, a energia cinética da bola de golfe é maior que a da bola de vôlei.

c) Após as colisões, a velocidade da bola de golfe é maior que a da bola de vôlei.

d) Durante as colisões, a força média exercida pela bola de golfe sobre o tórax da pessoa é maior que a exercida pela bola de vôlei.

e) Durante as colisões, a pressão média exercida pela bola de golfe sobre o tórax da pessoa é maior que a exercida pela bola de vôlei.

50-(UNESP-SP-013)

Em um jogo de sinuca, a bola A é lançada com velocidade de módulo constante e igual a 2 m/s em uma direção paralela às tabelas (laterais) maiores da mesa, conforme representado na figura 1. Ela choca-se de forma perfeitamente elástica com a bola B, inicialmente em repouso, e, após a colisão, elas se movem em direções distintas, conforme a figura

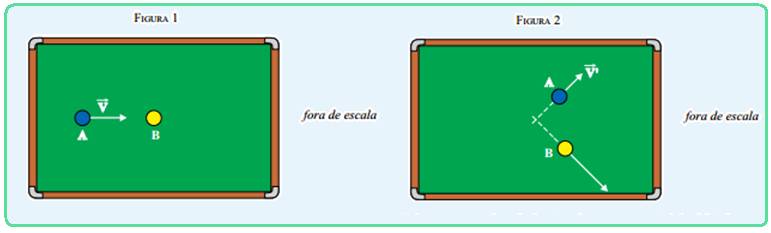2. Sabe-se que as duas bolas são de mesmo material e idênticas em massa e volume. A bola A tem, imediatamente depois da colisão, velocidade de módulo igual a 1 m/s. Desprezando os atritos e sendo E_B’ a energia cinética da bola B imediatamente depois da colisão e E_A a energia cinética da bola A antes da colisão, a razão

E'_B/E_A é igual a

(A) 1/2 (B) 4/5 (C) 3/4 (D) 1/5 (E) 2/3

51-(PUC-MG-013)

Uma bola de borracha é solta de uma altura de 5 m e cai livremente, chocando-se diversas vezes com um piso rígido.

Observa-se que, após cada colisão, a bola sobe e atinge uma altura que corresponde a 80% da altura anterior. Após a terceira colisão, com o piso rígido, a bola atinge uma altura aproximadamente, em metros, de:

a) 4,0 b) 3,2 c) 2,5 d) 1,0

52-(PUC-MG-013)

Considerando-se, por exemplo, a primeira colisão da questão de número 51, é CORRETO afirmar:

a) A velocidade com que a bola atinge o solo é igual à velocidade com que ela abandona o solo.

b) A velocidade com que a bola se solta do solo é 80% da velocidade com que ela atinge o solo.

c) A velocidade com que a bola se solta do solo é menor que 80% da velocidade com que ela atinge o solo, já que a energia cinética depende da velocidade ao quadrado.

d) A velocidade com que a bola se solta do solo é maior que 80% da velocidade com que ela atinge o solo, já que a energia cinética depende da velocidade ao quadrado.

53-(UNIMONTES-MG-013)

Duas bolas de gude, com massas m₁ e m₂, sendo m₁ = 3 m₂, movimentam-se ao longo de uma mesma reta, mas em

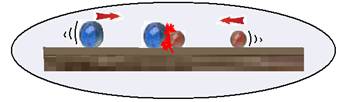
sentidos contrários. Num determinado instante, elas colidem. A colisão dura um intervalo de tempo muito curto. Durante esse intervalo, a bola 1 fica sujeita a uma aceleração de módulo igual a 3m/s². Nesse mesmo intervalo de tempo, o módulo da aceleração a que fica sujeita a bola 2 é igual a (considere g=10m/s²)

A) 3m/s² B) 9m/s² C) 18m/s² D) 27m/s

RESOLUÇÕES – 2014 - 2013

As três leis de Newton

01- Se ele está com velocidade constante, independente da inclinação, ele está em MRU na vertical e na horizontale, pelo princípio da inércia, a resultante das forças que agem sobre ele é nula (equilíbrio dinâmico) --- R- D

02- A força resultante sobre o bloco na direção do movimento é a força de atrito F_at=μN=μP= μmg= 0,4.m.10 --- F_at=4m --- segunda lei de Newton --- F_R=F_at=ma --- 4m=ma --- a=4m/s² --- Torricelli --- V²=V_o² + 2.a.d --- 0² = 20² + 2.(-4)d --- d=400/8 ---d=50m.

R- E

03- Como ele se move com velocidade constante na mesma altitude, na horizontal ele está em equilíbrio dinâmico (MRU) e, assim a força resultante na horizontal é nula (as forças horizontais se anulam).

Como ele permanece na mesma altitude (não sobe nem desce) a força resultante na vertical é nula (as forças verticais se anulam).

R- C

04- Desprezando-se a resistência do ar, qualquer corpo que estiver no espaço após lançamento

verical, lançamento oblíquo,queda livre, etc, terá como força resultante a força peso que tem sempre direção vertival e sentido para baixo.

R- A

05- Na vertical: Como cada dobradiça sustenta o peso do portão P=800N (vertical e para baixo) e cada uma suporta metade desse peso, cada dobradiça receberá uma força vertical e para cima de P’=800/2

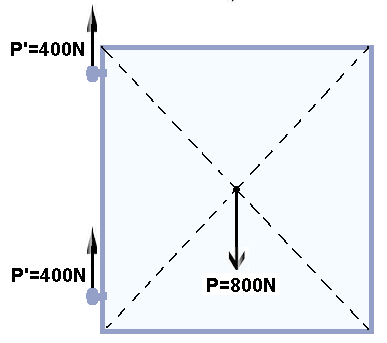
--- P’=400N (figura acima). Assim, na vertical o portão está em equilíbrio, pois 2P’=P.

Na horizontal: na dobradiça superior deve surgir uma força horizontal e para a esquerda impedindo que o portão gire no sentido horário e na inferior uma força horizontal e para a direita

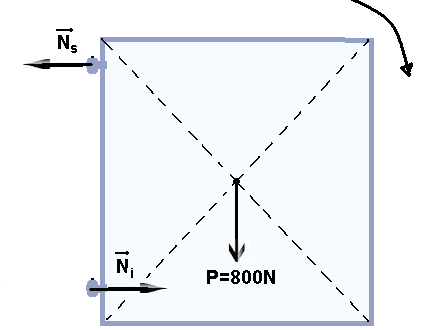
também impedindo que ele gire no sentido horário (figura acima).

Colocando o polo 0 (eixo de rotação) na dobradiça inferior vamos calcular o momento de cada força em relação a 0, estabelecendo o sentido horário de rotação como positivo:

M_Ns= - N_s.d= - N_s.1,6 --- M_NS= - 1,6N_s

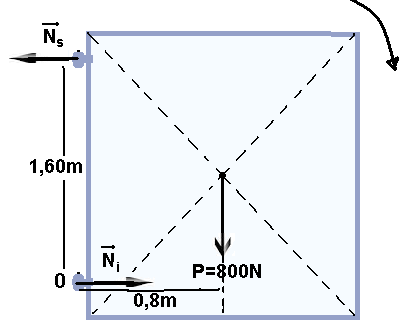
M_P= + P.d= + 800.0,8 --- M_P= + 640 N.m

M_ni= N_i.d=N_i.0 --- M_Ni=0

No equilíbrio de rotação a soma dos momentos de cada força deve ser nula:

- 1,6N_s + 640 = 0 --- N_s=640/1,6 --- N_s=400N --- como na horizontal as forças devem se anular para que haja equilíbrio, N_s=N_i=400N.

R- C

06- Observe na sequência da figura abaixo que a força aplicada no tubo 1 tem direção paralela a do tubo 2 formando também um ângulo de 60^o com a horizontal e, como não existe atrito essa força

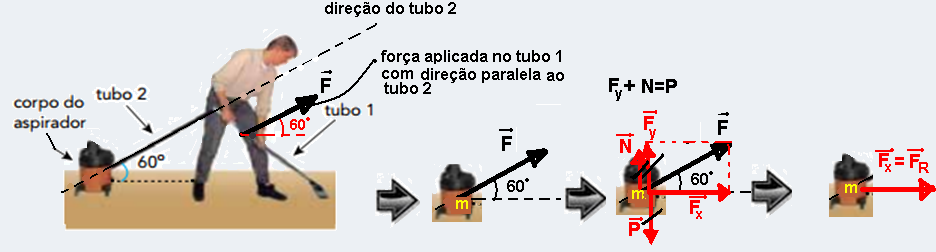
é transmitida até ao aspirador formando um ângulo de 60^o com a horizontal.

Essa força foi decomposta em duas parcelas F_x=Fcos60^o=4.0,5=2N e em . Como o aspirador não se move na vertical a força peso anula as forças e a normal . Assim, a única força responsável pelo movimento do aspirador é F_x=2N que é a força resultante sobre o mesmo.

Aplicando a segunda lei de Newton F_R=F_x=ma --- 2=2.a --- a=1m/s²

R- B

07-

Observe a análise de cada trecho:

Resumindo:

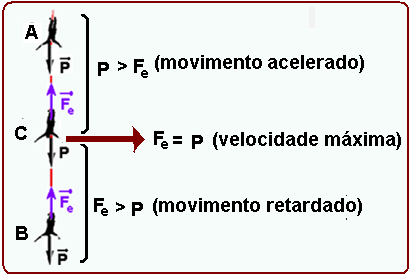
R- E

08- Pelo enunciado --- F_E=2F_D --- durante o movimento com aceleração de a=0,2m/s² a força de atrito F_at =240N e é constante.

Aplicando a segunda lei de Newton --- F_R=ma --- F_D + F_E – F_at = ma --- F_D + 2F_D – F_at = ma ---

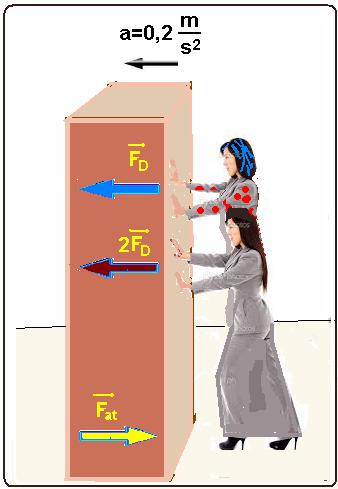
3F_D – F_at =ma --- 3F_D – 240 = 120.0,2 --- F_D = (24 + 240)/3 --- F_D=88N.

F_E=2F_D=2.88=176N.

R- D

09- Peso do paciente --- P=m.g=50.10=500N --- parcela horizontal da tração --- T_x=Tcos30^o=T√3/2 --- T_x=0,87T.

Observe na figura que ele não deve se deslocar horizontalmente então a força de atrito deve anular a parcela horizontal da tração --- F_at=μN=μP=0,26.500 --- F_at=130N --- F_at = T_x --- 130 = 0,87T --- T=

130/0,87 --- T=148,5N.

Até T=149,5N e m=14,95kg ele não se desloca e assim, a massa máxima deve ser de m=13kg.

R- B

10- A força resultante na direção do movimento é a força de atrito, constante, contrária ao mesmo que produz uma aceleração de retardamento também constante de intensidade F_R=F_at=ma --- V=V_o - at --- função de primeiro grau (reta decrescente), velocidade diminuindo até parar, quando V=0.

R- B

11- Se você não domina a teoria, ela está detalhada a seguir:

Força de atrito estático () e força de atrito dinâmico().

Considere um bloco de massa m sujeito a uma força externa de intensidade variável

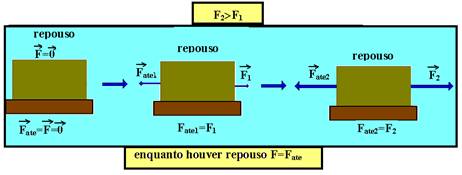
Quando o corpo estiver em repouso e não houver força externa, F_at=0. Com o corpo permanecendo em repouso, aumentando F, a intensidade da força de atrito estático também aumenta (figuras acima), até que o corpo fique na iminência de movimento (figura abaixo).

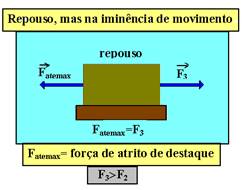
Quando o corpo está na iminência de movimento a intensidade da força de atrito estático é máxima. Uma força de intensidade maior que F₃ faz com que o corpo entre em movimento e, a partir daí a força de atrito é dinâmica ou cinética.

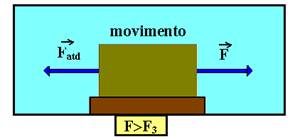
Depois que o bloco entra em movimento a força de atrito é denominada força de atrito dinâmica, e é sempre a mesma, independente da velocidade A intensidade da força de atrito dinâmica é ligeiramente menor que a intensidade da força de atrito estática máxima.

Suponha, nos exemplos acima, que se F₁ tiver intensidade de 3N, F_at1 também terá intensidade de 3N e o corpo continua em repouso.. Se F₂=5N, F_at2=5N e o corpo continua em repouso. Se F₃=7N, a máxima intensidade de atrito estático, que corresponde à iminência de movimento, é dada por:

F_ate=m_e.N

Onde, F_ate é força de atrito estático máximo ou simplesmente força de atrito estático, m_eé coeficiente de atrito estático e N a intensidade da força normal, que o bloco troca com o plano.

Portanto o bloco só entrará em movimento com qualquer força que seja maior que 7N. Assim, se aplicarmos por exemplo, 8N o bloco entrará em movimento e agora a força de atrito será dinâmica e dada por:

F_atd=m_d.N

Onde, F_atd é força de atrito dinâmico, m_d é coeficiente de atrito dinâmico e N a intensidade da força normal, que o bloco troca com o plano.

Verifica-se experimentalmente que F_ate>F_atd e que m_e>m_d.

O gráfico abaixo representa todo o processo explicado acima.

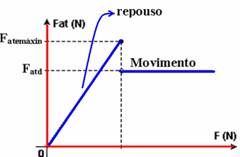
R- B

12- Na figura 1 foram colocados os módulos de todas as forças que agem sobre cada bloco --- P_A. P_B e P_C que correspondem aos pesos de cada bloco --- F_el – força elástica aplicada pela mola sobre os blocos C e B --- Fat - força de atrito sobre o bloco B, contrária ao movimento --- T – força de tração trocada entre os blocos A e B --- P_NB – parcela do peso perpendicular ao plano inclinado que o comprime contra o mesmo --- P_PB – parcela do peso paralela ao plano responsável pela descida do bloco --- a – aceleração de cada bloco no sentido horário --- na figura 2 foram colocadas apenas as forças que agem na direção do movimento de cada bloco:

P_pB=Psen37^o=mgsen37^o=m_B.10.0,6=6m_B.

F_at=μ.N_B= μP_NB= μm_B.10.cos37^o=0,4.m_B.10.0,8=3,2m_B.

F_el=k.x=1240.0,02=24,8.

F_R=m_b.a --- T + P_pB – (F_el + F_at) = m_B.a --- 22,8 + 6m_B – 24,8 – 3,2m_B = m_B.2,4 --- 6m_B – 5,6m_B = 2 --- m_B=2/0,4 --- m_B=5kg.

R- E.

13- Princípio da Inércia (Primeira Lei de Newton)

“Todo corpo que esteja em repouso ou em movimento retilíneo e uniforme (movendo-se em trajetória reta com velocidade vetorial constante), tende a continuar nestes estados se a força resultante que age sobre ele for nula”.

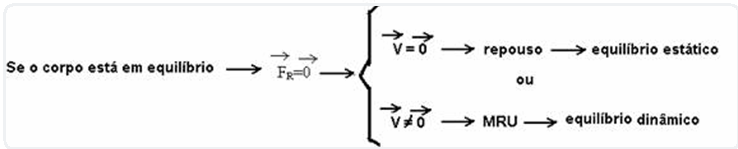
R- A

Forças no MCU

01- Cada garota encontra-se em movimento circular uniforme com a mesma velocidade angular (W), pois “varrem” o mesmo ângulo no mesmo tempo --- em todo movimento circular surge sempre uma força resultante denominada força resultante centrípeta com as seguintes características:

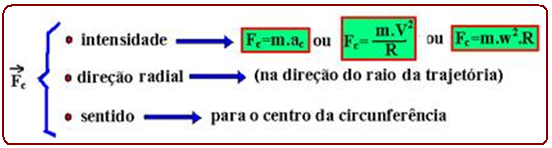
Essa força resultante centrípeta sobre a garota 1 tem intensidade F_c1=T₁=m.W².2R --- T₁=2mW²R (I) e

sobre a garota 2 --- F_c2=T₂ – T₁=mW²R --- T₂ – T₁= mW²R (II) --- veja figuras abaixo:

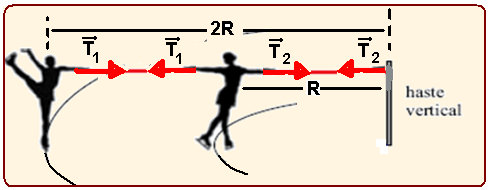
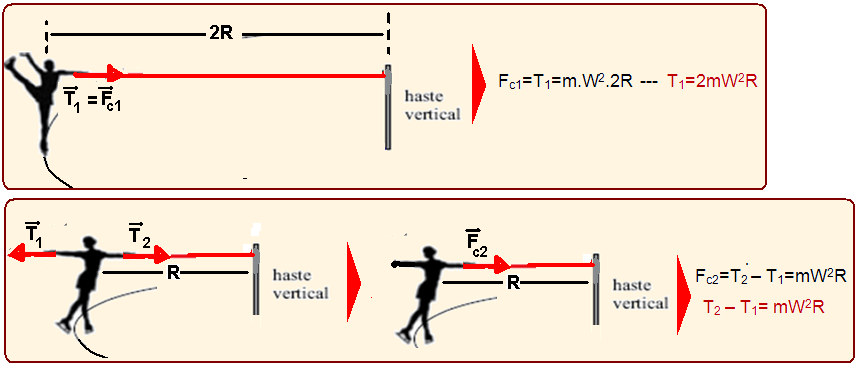
substituindo (I) em (II) --- T₂ – 2mW²R = mW²R --- T₂=3mW²R e T₁=2mW²R (I) --- dados --- T₁=120N ---120=2mw²R ---mw²R=120/20=60 --- T₂=3.60 --- T₂=180N --- R- E.

02- Na direção radial--- o exercício afirma quea pessoa se solta do cipó no instante em que sua velocidade fica novamente igual a zero, ponto S da figura --- se nesse ponto a velocidade é nula V_S=0, nele a força resultante centrípeta também é nula, pois F_CS=m.(V_S)²/2=m.0²/2=0 --- F_CS=0 --- então a aceleração

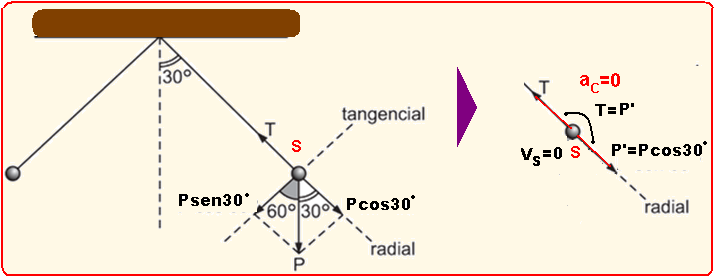
centrípeta em S será também nula, pois F_C=m.a_C=0 --- a_C=0 e isso ocorre porque a tensão T anula a componente oposta do peso P’=Pcos30^o

Na direção tangencial--- a força resultanteF_R sobre o corpo em S (responsável pelo movimento na

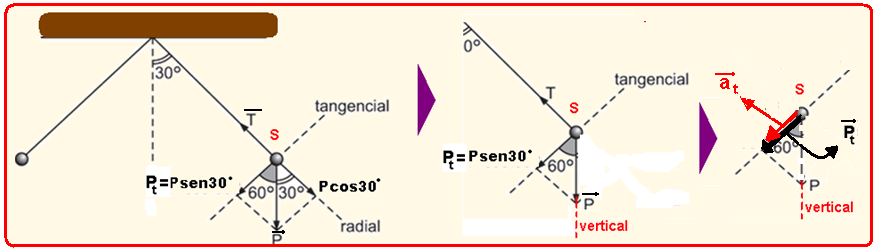
direçãoperpendicular ao cipó) é a parcela tangencial do peso P_t=Psen30^o --- F_R=ma --- F_R=P_t ---

ma=mgsen30 --- a=gsen30^o=10.(1/2) --- a_t=5m/s²--- essa aceleração é a tangencial e forma um ângulo de 60^o com a vertical ---R- E

03- Para ir de A até B o motociclista percorre meio arco de circunferência de raio R, ou seja, percorre ΔS=2πR/2--- ΔS=πR --- sua menor velocidade média será V=ΔS/Δt, onde Δt é o intervalo de tempo que ele demora para percorrer ΔS --- V=πR/Δt--- note que essa é velocidade média e, portanto, é a mesma em A e em B --- Δt=πR/V (I) --- sendo o objeto abandonado (V_o=0) em A ele cai em queda livre com aceleração igual à da gravidade g, percorrendo a distância vertical 2R=ΔS --- equação horária do espaço de uma queda livre --- ΔS=V_o.Δt + g.(Δt)²/2 --- 2R=0 + g.(Δt)²/2 (II) --- observe que o tempo que o objeto demora para chegar em B em queda livre, é o mesmo que o motociclista demorou também para chegar em B e, assim, você pode substituir (I) em (II) --- 2R=g.(πR/V)²/2 --- 4R=g.(πR/V)² --- 4R=g.π².R²/V² --- 4=g.π².R/V² --- 4V²=g.π².R --- V²= g.π².R/4 (III) --- mas, no ponto A as forças que agem sobre o motociclista são seu peso P (vertical e para baixo) e a força normal N que ele troca com a superfície superior do globo

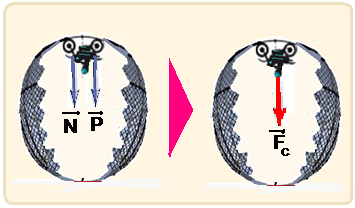
(também vertical e para baixo)--- em todo movimento circular existe sempre uma força resultante centrípeta dirigida para o centro da circunferência, de intensidade F_c=m.V²/R --- no ponto A F_c=P + N --- mV²/R=N + P (IV) --- substituindo (III) em (IV) --- m.(g.π².R/4)/R=N + P --- m. g.π²/4=N + P --- mg=P --- P.π²/4=N + P --- π²=10 ---

10P/4=N + P --- 2,5P=N + P --- 2,5P – P=N --- 1,5P=N --- N/P=1,5.

04- a) Energia mecânica no ponto I --- E_mI=mgh + mV²/2= mgh + m0²/2 --- E_mI=mgh

Energia mecânica no ponto II --- E_mII= mgh + mV²/2= mg0 + mV²/2 --- E_mII=mV²/2

Pelo teorema da conservação da energia mecânica --- E_mI=E_mII --- mgh=mV²/2 --- V=√(2gh)

b) No ponto II as forças que agem sobre o corpo são seu peso (vertical e para baixo) e força de tração no fio (vertical e para cima) --- em todo corpo em movimento circular surge uma força

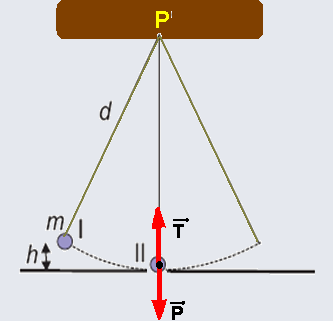
resultante centrípeta de direção radial, dirigida para o centro da circunferência (no caso, para cima) e de intensidade F_c=mV²/R=mV²/d --- mas, F_c=T – P --- mV²/d = T – mg --- m.(√(2gh)²/d = T – mg ---

m.2gh/d = T – mg --- T=mg + 2mgh/d --- T=mg(1 + 2h/d)

Trabalho- Energia

01- Como o entulho de massa m está descendo com velocidade constante ele está em MR( (equilíbrio dinâmico) e a força resultante sobre ele deve ser nula e, para que isso ocorra, a intensidade da força

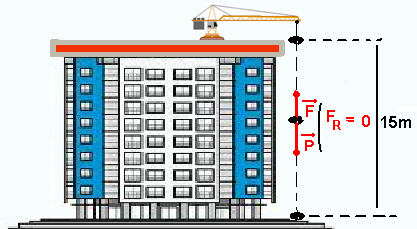
aplicada pelo guindaste deve ser igual ao peso do entulho --- F=P=mg=m.10 --- P=F=10m.

Cálculo do trabalho realizado pela força F=P --- W=F.d.cosα=10m.15.cos0^o--- W=150.m.

R- D

02- Pela tabela periódica, você tem que as massas dos isótopos do chumbo (Pb), da prata (Ag), do hélio (He) e do hidrogênio (H), são respectivamente: 207,2, 107,8, 4,002 e 1,008.
Assim, m_Pb > m_Ag > m_He > m_HPela expressão da energia cinética E_c=mV²/2 você verifica que, sendo a velocidade a mesma para os 4 feixes de átomos, aenergia cinética é diretamente proporcional à massa. Assim, a relação pedida é: E_Pb > E_Ag > E_He > E_H

R- D

03- A energia armazenada por um corpo de massa m devido ao fato de ele se encontrar a certa altura h recebe o nome de energia potencial gravitacional (E_p), de expressão matemática:

onde:

E_p --- energia potencial gravitacional – no SI, medida em joules (J)

m --- massa – no SI, medida em quilograma (kg)

g --- aceleração da gravidade local – no SI, medida em m/s² ou N/kg

O segundo trecho do passeio corresponde à ida do bondinho de massa m=5000kg do Morro da Urca (h_U=220m) ao Pão de Açúcar (h_P=400m) --- energia potencial gravitacional do bondinho no Morro da

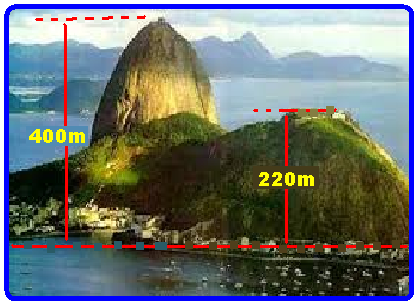
Urca,em relação ao solo --- E_pU=m.g.h_U=5000x10x220=11000000=11.10⁶ J --- --- energia potencial gravitacional do bondinho no Pão de Açúcar, em relação ao solo --- E_pP= m.g.h_P=5000x10x400=

20000000=20.10⁶ J --- variação de energia potencial gravitacional pedida --- ΔE_p=20.10⁶ – 11.10⁶=

9.10⁶ J --- R- A

04- Cálculo do trabalho da força de atrito (F_at), contrária ao deslocamento, e de intensidade fornecida F_at=380N num deslocamento de ΔS=d=72km=72.10³m --- W_Fat=F_at.d.cos180^o=380.72.10³.(-1) ---

W_Fat= - 27 360.10³ J= - 2,736.10⁷J --- em módulo --- |W_Fat|= 2,736.10⁷J (energia dissipada devido ao atrito com o ar)

05- No instante do salto o atleta tem duas velocidades, uma horizontal de intensidade V_h=10m/s e outra, vertical de intensidade V_vque produz uma energia cinética de E_c=70% de uma energia de E=500J, ou seja, produz uma E_c vertical de E_Cv=(70/100)x500=0,7x500 --- E_Cv=350J --- essa energia cinética origina uma velocidade vertical de E_Cv=mV_v²/2 --- 350=70.V_v²/2 --- 70V_v²=2x350 --- V_v²=700/70 --- V_v=√(10) m/s ---

então, no instante do salto você tem duas velocidades --- uma horizontal de intensidade fornecida V_h=10m/s e outra vertical de intensidade V_v=√(10)m/s --- a velocidade pedida, velocidade resultante, no momento do salto corresponde à soma vetorial dessas duas velocidades --- aplicando Pitágoras --- V_R²=V_h² + V_v²= 10² + (√10)²=100 + 10--- V_R=√(110)≈10,488m/s --- R- B

06-

R- E

07- Força resultante sobre o automóvel pela segunda lei de Newton --- F_R=m.a=1500x(1/12) --- F_R=125N

trabalho da força resultante no deslocamento de d=1350m --- W=F_R.d=125x1350 --- W=168 750J W=1,678.10⁵J --- R- D

08- Trata-se de um sistema dissipativo que surge quando o trabalho é realizado por forças dissipativas(força de atrito, força de resistência do ar, etc.) no qual, parte da energia mecânica do sistema é dissipada nas formas de energia térmica, sonora, etc. Assim a energia mecânica do sistema, diminui e, nesse caso, o trabalho das forças não conservativas W (força de atrito, força de resistência do ar, etc.) é igual à energia total dissipada, ou seja, é igual à variação da energia mecânica ---E_{mecanicafinal} – E_{mecanicainicial}=W_{forçasdissipativas}.

Inicialmente você pode calcular a distância ∆S percorrida pelo bloco entre os pontos A e B pela área do gráfico Vxt fornecido (figura 2) --- área do triângulo=AB=∆S=b.h/2=0,5x4/2=1m --- cálculo da altura h entre os pontos A e B

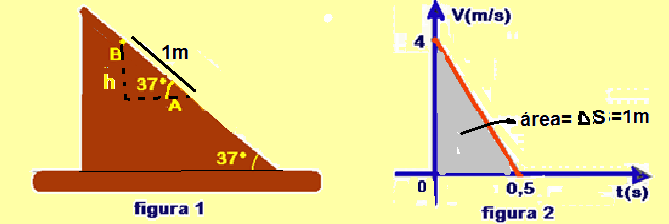
(figura 1) --- sen37^o=cateto oposto/hipotenusa --- 0,6=h/1 --- h=0,6m --- para a subida --- W_{forçasdissipativas=}E_{mecanicafinal} – E_{mecanicainicial} --- W_fat=E_mA – E_mB --- veja pelo gráfico da figura 2 que a velocidade inicial em A é 4m/s e a em B é zero --- E_mA=mgh_A + mV_A²/2=2.10.0 + 2.4²/2=0 + 16 --- E_mA=16J --- E_mB=mgh_B + mV_B²/2=2.10.0,6 + 2.0²/2 --- E_mB=12J --- W_fat=16 – 12=4J --- esse trabalho é o mesmo tanto para a subida quanto para a descida --- para a descida --- ---W_{forçasdissipativas=} E_{mecanicafinal} – E_{mecanicainicial} --- W_fat=E_mB – E_mA --- veja pelo gráfico da figura 2 que a velocidade inicial em A é 4m/s e a em B é zero --- E_mA=mgh_A + mV_A²/2=2.10.0 + 2.V_A²/2 --- E_mA=V_A²E_mB=mgh_B + mV_B²/2=2.10.0,6 + 2.0²/2 --- E_mB=12J --- W_fat=16 – 12=4J --- esse trabalho é o mesmo tanto para a subida quanto para a descida --- para a descida --- W_fat=E_mB – E_mA --- 4=12 – V_A² --- V_A=√8=2√2m/s.

09- Energia mecânica no ponto A de onde o menino parte do repouso --- E_mA=m.g.h --- energia mecânica no ponto B de onde chega com V_B=2m/s --- E_mB=mV_B²/2=m.4/2 --- E_mB=2m --- E_mA = E_mB

mgh = 2m --- h=2/g=2/10 --- h=0,2m.

Agora ele sai do ponto A com velocidade de V_A=1,5m/s --- E_mA=mV_A²/2 + mgh=m.1,5²/2 + m.10.0,2 --- E_mA= 1,125m + 2m ---E_mA=2,125m --- E_mB=mV_B²/2 --- E_mA =E_mB--- 2,125m = mV_B²/2 --- V_B=√4,25 --- V_B=2.06m/s.

R- C

10- O trabalho da força peso é negativo na subida, positivo na descida e nulo num deslocamento horizontal e fornecido por W=P.h ou W=m.g.h.

O trabalho da força peso entre dois pontos A e B, não depende da trajetória, mas apenas da altura

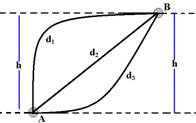
(h) vertical entre A e B e é fornecido por W_BA=+P.h na descida e por W_AB= -P.h na subida por qualquer trajetória (d₁, d₂ ou d₃).

No caso do exercício a altura h vale --- sen30^o=h/8 --- h=8.0,5=4m --- módulo do trabalho do peso --- W=P.h=20.4=80J.

R- C

Dinâmica Impulsiva

01-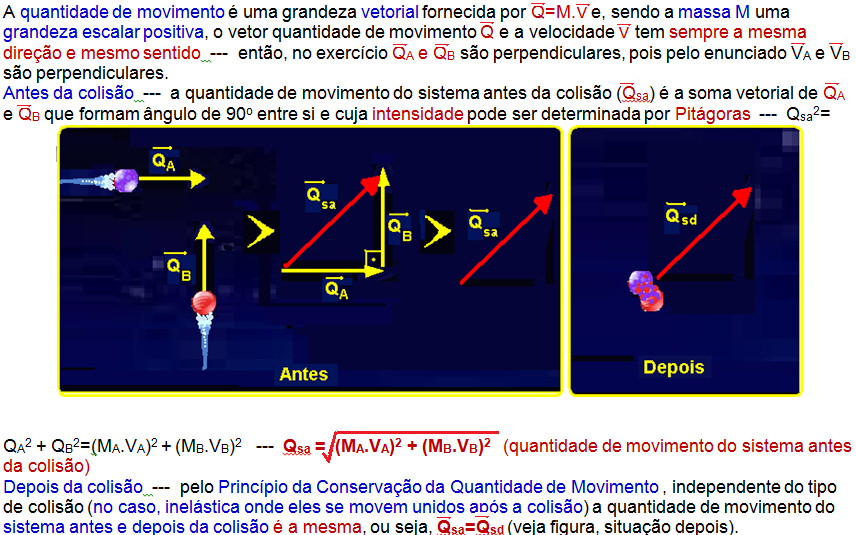

R- B

02- Cálculo da velocidade V com que o sistema bloco + projétil inicia a compressão da mola pela conservação da quantidade de movimento.

Choque entre o projétil e o bloco:

M=180g=0,18kg --- m=20g=0,02kg --- V_p=200m/s --- V=?

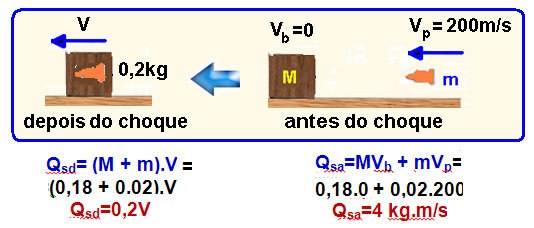
Pelo princípio da conservação da quantidade de movimento --- Q_sa = Q_sd.

4 = 0,2V --- V=4/0,2 --- V=20m/s (velocidade com que o sistema (projétil + bloco) começa a comprimir a mola.

Agora vamos utilizar o teorema da conservação da energia mecânica no sistema (bloco-projétil) de massa M_s=(0,18 + 0,02)=0,2kg em duas situações:

* Energia mecânica de M_s imediatamente antes de começar a comprimir a mola onde a energia potencial elástica é nula (mola descomprimida) só possuindo energia cinética --- E_mi=M_sV²/2= 0,2.(20)²/2 --- E_mi=40J.

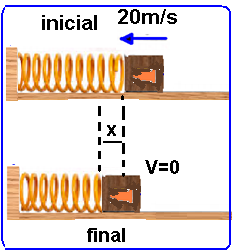
* Energia mecânica de M_s após a mola estar comprimida de x e M_s parado (V_s=0) onde a energia cinética é nula e o sistema só possui energia potencial elástica --- E_mf=kx²/2=2.10³x²/2 --- E_mf=10³x².

Sendo o sistema conservativo --- E_mi = E_mf --- 40 = 10³x² --- x²=40/10³=4.10^-2 --- x²=0,04 --- x=0,2m

X=20cm.

R- D

03- Depois de unidos, o carrinho com compras de massa 30kg e o vazio de massa 20kg se movem

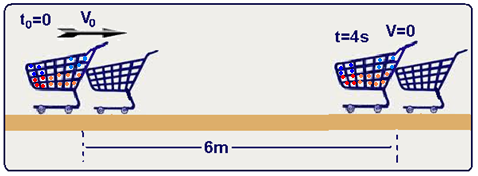
engatados, com massa total m=50kg, e com sua velocidade passando de V_o para V=0 (para), percorrendo ΔS=6m em t=4s.

Cálculo da velocidade V_o do conjunto:

Pelo enunciado, antes do acoplamento o carrinho de massa 30kg e velocidade V’ se move em direção ao carrinho de massa 20kg que estava parado e, imediatamente após o acoplamento ambos, de massa 50kg se movem unidos com velocidade V_o=3m/s. Aplicando o princípio da conservação da quantidade de movimento:

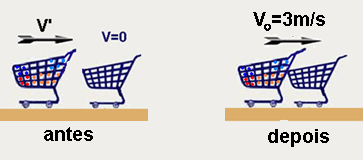
Antes --- Q_sa=30V’ + 20.0 --- Q_sa=30V’

Depois --- Q_sd=(30 + 20).3 --- Q_sd=150kgm/s

Q_sa = Q_sd --- 30V’ = 150 --- V’=5m/s

R- A

04- Como a massa M_ext do extintor não foi fornecida você deve avaliar uma massa que esteja dentro de um intervalo razoável, por exemplo, M_ext=20kg --- você pode utilizar a conservação da quantidade de movimento para avaliar a velocidade pedida já que o extintor (sistema) está isolado --- antes de lançar o jato de CO₂, o sistema está em repouso (V_antes=0) --- depois que foi lançado a massa m=50g=0,05kg com velocidade de V_CO2=20m/s, o extintor de massa M_ext=20kg recua com velocidade V_ext tal que:

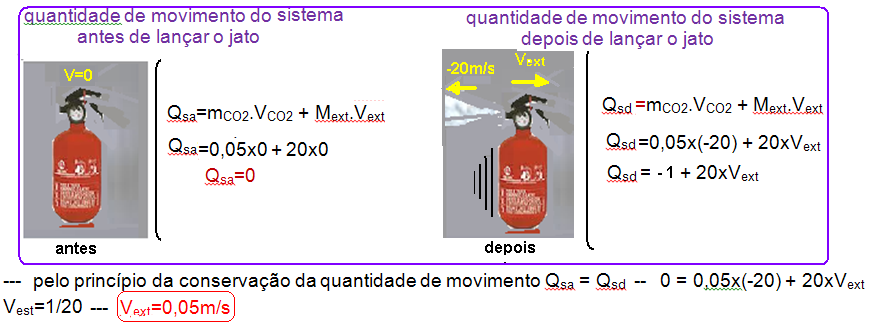
05- Em todo choque elástico (perfeitamente elástico) se os corpos possuirem a mesma massa eles trocam suas velocidades.

Após o choque a bola incidente para e a bola alvo segue com velocidade de 2m/s.

R- C

06- Estando o garoto em repouso dentro do barco, o sistema está em equilíbrio estático na vertical e a força resultante sobre ele é nula.

Forças verticais que agem sobre sistema (garoto mais barco) de massa m_s=50 + 150=200kg:

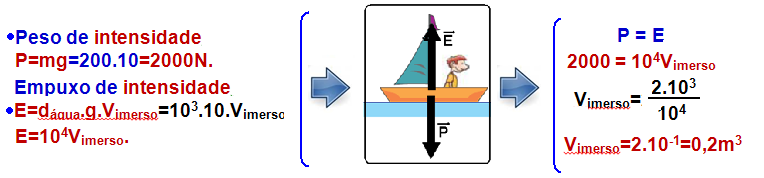
Agora você vai trabalhar na horizontal, utilizando o princípio da conservação da quantidade de movimento do sistema garoto-barco:

Antes do salto:

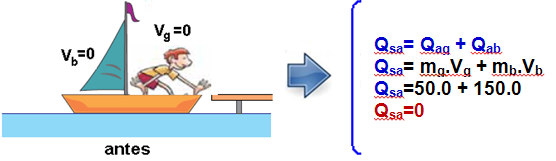
Depois do salto:

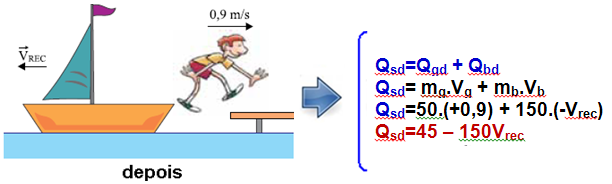
Pelo princípio da conservação da quantidade de movimento:

Q_sa = Q_sd --- 0 = 45 – 150V_rec --- V_rec=45/150 --- V_rec=0,3m/s

07- Inicialmente você tem o núcleo de polônio inicialmente em repouso (V_Po=0) e, assim a quantidade de

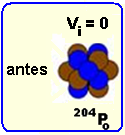
movimento inicial é nula pois, Q_i=mV_po=204u.0 --- Q_i=0 --- depois o núcleo de polônio se transforma em

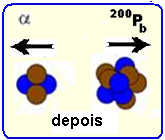
um núcleo de chumbo com velocidade de módulo V_Pb e em uma partícula alfa com velocidade de módulo V_α --- a quantidade de movimento do sistema depois da transmutação será --- Q_d=m_Pb.V_Pb + m_α.V_α=200u.V_P

+ 4u.V_α--- pelo Princípio da Conservação da quantidade de movimento --- Q_i=Q_d --- 0 = 200u.V_P + 4u.V_α

4u.V_α = - 200uV_Pb --- V_α = - 50 V_Pb--- energia cinética do núcleo de chumbo --- E_Pb=m_Pb.V²_Pb/2 --- E_Pb=200u.V²_Pb/2 (I) --- energia cinética da partícula alfa --- E_α=m_α.V²_α/2 --- E_α=4u.(-50V_Pb)²/2 = 4ux 2500. V²_Pb/2--- E_α=10000u.V²_Pb/2 (II) --- (I)/(II) --- E_Pb/E_α=(200u.V²_Pb/2)/(10000u.V²_Pb/2) --- E_Pb/E_α =

(200u.V²_Pb/2)x(2/10000u.V²_Pb) --- E_Pb/E_α =200/10000=1/50 --- E_Pb=E_α/50 --- R- C

08- a) Teorema do Impulso: "O impulso da força resultante de um sistema de forças que age sobre um corpo é igual à variação da quantidade de movimento do corpo"

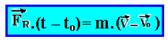
Pelo enunciado, o módulo da velocidade da bola de massa m=300kg no ponto B, imediatamente antes de atingir a estrutura do prédio é de V_o=2m/s, o choque dura Δt=0,02s e após esse intervalo de tempo a bola para instantaneamente V=0 --- aplicando o teorema do impulso:

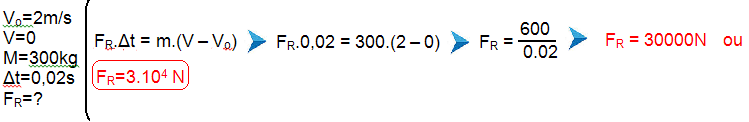
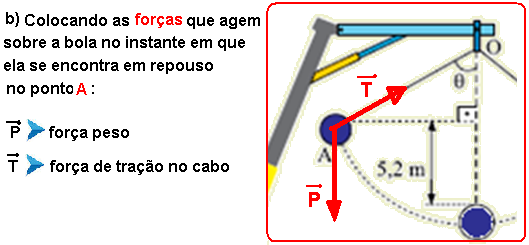
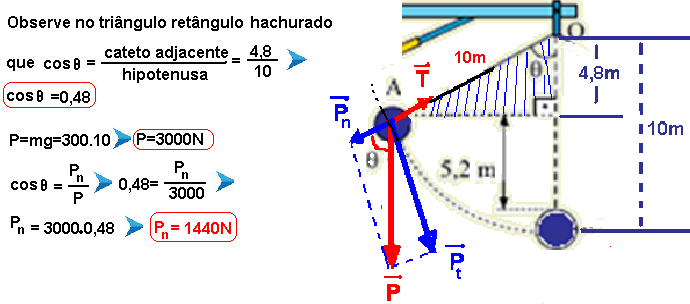
Se o enunciado afirma que no ponto A a velocidade da bola é nula, ele está afirmando que a força resultante centrípeta nesse ponto também é nula, pois F_c=mV²/R=m.0²/R=0 --- para que isso ocorra, a intensidade da componente normal (radial) do peso P_n=1440N deve anular a força de tração no fio que é pedida, ou seja, F_n=T=1440N --- observação: É a componente tangencial do peso P_t=Psenθ que faz a bola descer.

09- a) Observe que, nesse deslocamento de d=20cm=0,2m fornecido o exercício pede o trabalho da força de atrito de intensidade F_at=μN=μP=μmg=0,4.3.10 --- F_at=12N

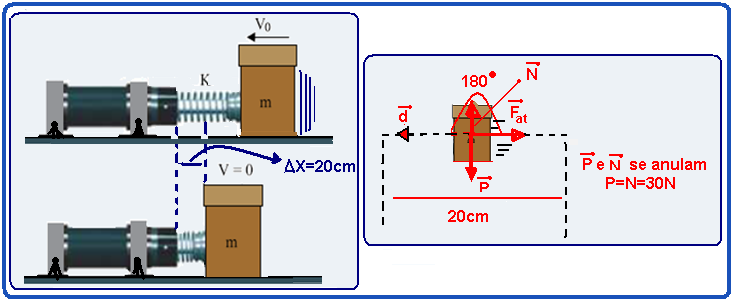
O trabalho da força de atrito W_Fat, onde F_at=12N, no deslocamento de d=0,2m e α=180^o é fornecido por

W_Fat=F_at.d.cosα=12.0,2.cos180^o=1,4x(-1) --- W_Fat= - 2,4J

10- a) Cálculo da velocidade V_1i com que a partícula de massa M que partiu de P com velocidade V_p=0 e chega em que Q no início da pista horizontal, pela conservação da energia mecânica (figura 1):

Energia mecânica em P --- E_mP = MV²/2+ Mgh=M.0²/2+ M.10.1,25 --- E_mP = 12,5M.

Energia mecânica em Q --- E_mQ = MV_1i²/2+ Mgh= MV_1i²/2+ M.10.0 --- E_mQ = MV_1i²/2

E_mP= E_mQ --- 12,5M = MV_1i²/2--- V_1i=√25 --- V_1i=5m/s --- como não existe atrito é com essa velocidade com que ela chega até a partícula 2 imediatamente antes da colisão.

b) Observe na figura abaixo a situação antes da colisão e depois da colisão onde será calculada a quantidade de movimento do sistema antes e depois da colisão.

Antes --- Q_sa=M.5 + m.0 --- Q_sa=5M --- depois --- Q_sd=M.4,5 + m.V_2f --- Q_sd=4,5M + V_2fm.

Q_sa = Q_sd --- 5M = 4,5M + V_2fm --- 0,5M = V_2fm --- V_2f=0,5M/m.

Sendo a colisão elástica o coeficiente de restituição e é igual a 1 --- e=módulo da velocidade relativa depois/módulo da velocidade relativa antes --- 1 = V_2f – 4,5/5 – 0 --- 5 = V_2f – 4,5 --- V_2f = 9,5m/s.

Com essa velocidade inicial de V_i=9,5m/s a partícula m atinge a altura máxima em S onde V_S=0 ---

Energia mecânica em R --- E_mR=m.(9,5)²/2 + m.10.0 --- E_mR=45,125m (I). --- energia mecânica em S --- E_mS=m.0²/2+ m.10.h_max --- E_mS=10mh_máx. (II).

Igualando (I) com (II) --- 45,125m = 10mh_máx --- h_máx=4,5125m

Primeira lei de Newton

29- Princípio da Inércia (Primeira Lei de Newton)

“Todo corpo que esteja em repouso ou em movimento retilíneo e uniforme (movendo-se em trajetória reta com velocidade vetorial constante), tende a continuar nestes estados se a força resultante que age sobre ele for nula”.

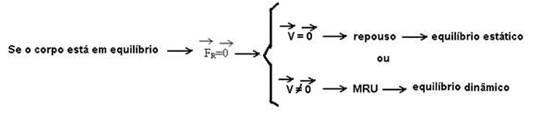
Quando a força resultante sobre ele for nula, se ele estiver em repouso, tende a continuar em repouso e se estiver em movimento com velocidade tenderá a se mover em linha reta com velocidade .

R- C.

30 - O momento de inércia refere-se a uma resistência à mudança no movimento rotacional de um corpo --- é evidente que quanto mais próximo o centro massa do corpo estiver do eixo de rotação, menor será o momento de inércia, e quanto mais afastada a massa estiver do eixo de rotação, maior será seu momento de inércia --- R- B.

31- Isso ocorre porque você está na atmosfera que, por sua vez, por inércia, está acompanhando a Terra --- isso se deve ao fato de existir uma força que atrai todos os corpos em direção ao centro da Terra chamada força gravitacional ou força peso --- R- D.

Segunda lei de Newton

34- - a) Quando a caixa é arrastada com velocidade constante, pelo princípio da inércia a força resultante sobre ela é nula (equilíbrio dinâmico) --- nesse caso, a intensidade da força aplicada pelo fio deve anular a força de atrito --- F = F_at --- F=1N.

b) Quando a intensidade da força aplicada pelo fio é maior que F=1N, a caixa entra em movimento acelerado, mas a força de atrito continua sendo de F_at=1N, pois, dentro de certos limites, independe da velocidade que, no caso, vai aumentando --- pelo gráfico, a força (F) de tração no fio é proporcional à aceleração (a) --- quando, por exemplo, a aceleração for de 15m/s², a força será de 4N --- a força resultante sobre a caixa vale --- F_E=F – F_at=4 – 1=3N ---

Princípio fundamental da Dinâmica --- F_R=m.a --- 3=m.15 --- m=0,2 kg.

35- Na figura abaixo as forças foram projetadas na vertical e na horizontal --- F_1x=F₁cosα ---

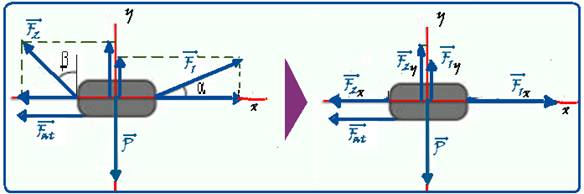
F_1y=F₁senα --- F_2x=F₂senβ --- F_2y=F₂cosβ.

01. Correta --- supondo que o corpo se mova para a direita --- R_x=F_1x – F_2x – F_at --- R_x=F₁cosα – F₂senβ – μN.

02. Correta --- .

04. Falsa --- se a resultante do sistema for nula, o poderá estar em repouso(equilíbrio estático ou em movimento retilíneo e uniforme (princípio da inércia).

08. Falsa --- se ele estiver subindo --- R_y=F_1y + F_2y – P --- R_y=F₁senα + F₂cosβ – P.

16. Falsa --- como existe força de atrito, ele deve atuar no sistema.

R- (01 + 02)=03.

Terceira lei de Newton

20- Entre os animais que desenvolveram o tipo de vôo pára-quedismo está o sapo voador de Bornéu, Rhacophorus dulitensis --- o pára-quedas é formado através de membranas presentes nas patas --- quando os animais descem das árvores, age uma força aerodinâmica paralela a direção do ar que passa por eles --- essa força pode ser chamada de

força de resistência --- o animal atinge uma velocidade constante quando esta força total contrabalancear o seu peso.

O animal planador se desloca no ar em movimento descendente, sem realizar trabalho --- sua trajetória é retilínea --- como animal planador podemos citar o esquilo voador (Glaucomys volans) --- possui geralmente uma pele que se

--- possui geralmente uma pele que se estende das patas dianteiras até as traseiras, denominada patágio.

Vôos propulsionados --- é o tipo de vôo realizado por grande parte dos animais que voam e é resultado da movimentação de músculos --- devido a existência da força de arrastamento, um animal não consegue planar horizontalmente por muito tempo, devido a perda de velocidade --- para voar horizontalmente com velocidade constante,uma força de impulso deve ser fornecida com direção igual, sentido contrário e mesma intensidade que a

força de arrastamento --- essa potência é fornecida pelos músculos que impulsionam e movimentam as asas.

R- B.

Exercícios sobre conceitos das três leis de Newton

57- - Dados --- m=1200kg --- Vo=108/3,6=30m/s --- V=0 (pára) --- ∆S=200m --- cálculo da aceleração de retardamento pela equação de Torricelli --- V2 = Vo2 – 2.a.∆S --- 02 = 302 – 2.a.200 --- a=900/400=2.25m/s2 --- força resultante durante a frenagem --- FR=m.a=1200.2,25 --- FR=2700N --- essa força é a força de atrito que está segurando o carro --- Fat=2700N --- trabalho da força de atrito (realizado pelos freios) --- WFat=Fat.d.cos180o=2700.200.(-1) --- WFat= - 540000J=5,4.105 J --- R- B.

58- A intensidade da força resultante sobre os dois lutadores juntos, de massa M=200 + 200=400kg é de F_R=1000 – 950=950N --- cálculo da aceleração --- F_R=M.a --- 50=400.a --- a=0,125m/s² ---

como eles se encontram no centro do círculo, para sair do mesmo eles devem percorrer R=∆S=2m --- ∆S=V_ot + a.t²/2 --- 2=0.t + 1,25.t²/2 ---

t²=4/0,125 --- t=√32 --- t≈5,6s --- R- E.

Tipos de força

39- Colocando as forças que agem sobre cada cinta, que correspondem ao acréscimo da força de contato entre a plataforma e o pneu, que no caso é a força (T) que traciona ou tensiona o fio em cada

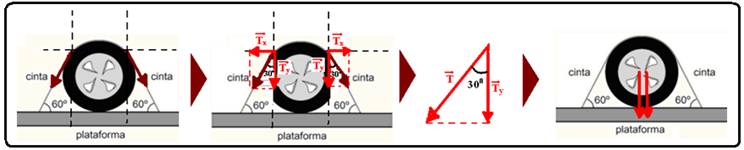
lado do pneu --- decompondo essas forças na horizontal e na vertical (observe a seqüência da figura) --- T_x=T.sen30^o=0,5.T --- T_y=T.cos30^o=(√3/2).T --- observe que, na horizontal as componentes (T_x) se anulam --- na vertical sobram, para baixo as duas forças T_y que pressionam a plataforma para baixo e que, somadas, fornecem --- F = 2T_y=2x(√3/2)T --- F =√3.T --- R- D.

40- O exercício quer o diagrama das forças que as dobradiças aplicam na porta:

Na horizontal: ao girar, a porta traciona (puxa) para a direita a dobradiça superior e esta, pelo princípio da ação e reação reage na porta com uma força de mesma intensidade, mesma direção, mas sentido contrário, tracionando-a (puxando-a) para a esquerda com uma força --- analogamente ao girar, a porta comprime (empurra) para a esquerda a dobradiça superior e esta, pelo princípio da ação e reação reage na porta com uma força de mesma intensidade, mesma direção mas sentido contrário, comprimindo-a (empurrando-a) para a direita com uma força _.

Na vertical, devido ao seu peso, a porta aplica em cada dobradiça uma força puxando-as para baixo e, elas reagem sobre a porta com forças e , verticais e para cima.

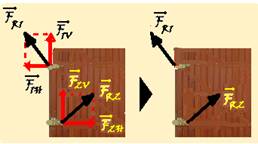
A soma vetorial dessas forças, fornece as forças resultantes e que cada dobradiça exerce sobre a porta (figura) R- D.

Peso e massa

33- O peso do corpo em Marte é o produto de sua massa que é a mesma em qualquer lugar ou planeta pela aceleração da gravidade na superfície do planeta Marte --- P=m.g=3,10x3,69=11,439N --- com três algarismos significativos ---

P=11,4N --- R- D.

34- Com duas pessoas no carro a deformação do sistema de molas é x=2cm=2.10^-2m e a força que deformadora é o peso das duas pessoas --- P=2mg=2.60.10=12.10²N --- esse peso corresponde à força elástica --- F_eP=kx ---

12.10²=k.2.10^-2 --- k=6.10⁴N/m (constante elástica do sistema de molas que é constante independente da força deformadora) --- com 4 pessoas a deformação é x’ e o peso é P’=4mg=4.70.10=28.10²N --- P’=kx’ --- 28.10²=6.10⁴x’ --- x’=4,66.10^-2m=4,66cm --- R- D.

Leis de Newton do MUV

48- a) Cálculo da aceleração do móvel no trecho AB --- V_B = V_A + a.t --- 30 = 0 + a.10 --- a=3m/s² --- como não

tem atrito a força resultante vale F_R=m.a=1200.3 --- F_R=3600N ou F_R=3,6.10³N.

b) Parcela do peso na direção do movimento que diminui a velocidade do móvel durante a subida e que é a força resultante sobre ele --- P_p=Psen30^o=m,g.sen30^o=1200.10.1/2 --- P_p=6000N --- aceleração de subida --- F_R=P_p=

m.a --- 6000=1200.a --- a=5m/s² (retardamento) --- ∆S=V_o.t + a.t²/2 --- o tempo de subida é t=(15 – 10)=5s ---

∆S=30.5 + (-5).5²/2 --- ∆S=87,5m.

No trecho BC a única força que age sobre ele, na direção do movimento é a parcela do peso (P_p=P.sen30^o) e, como não existe atrito, o sistema é conservativo --- assim, a energia mecânica total do móvel em B (somente a cinética) é

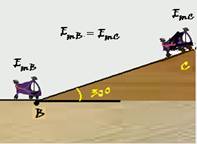
igual à energia mecânica total do móvel em C --- E_mC=E_mB= mV_B²/2=1200.30²/2 --- E_mC=540000J ou E_m

Plano inclinado sem atrito

25- Sendo o atrito com a plataforma da rampa desprezado a única força responsável pela descida das pessoas é a

parcela do peso paralela à superfície da plataforma, que é igual à força resultante --- P_p=Psen30^o=m.g.1/2=m.10/2 --- P_p=

5m (I) --- F_R=m.a (II) --- (I)=(II) --- P_p=F_R --- 5m = ma --- a=5m/s² (aceleração de descida das pessoas) --- cálculo da distância percorrida ∆S pela rampa --- sen30^o=31,25/∆S --- 0,5=31,25/∆S --- ∆S=62,5m --- ∆S=V_ot +

At²/2--- pelo enunciado, partiu do repouso V_o=0 --- 62,5=0.t + 5t²/2 --- t²=125/5 --- t=√25 --- t=5s --- R- A.

26- Sendo o atrito desprezado, o sistema é conservativo --- usando o teorema da conservação da energia mecânica --- energia mecânica em P --- EmP = mVP2/2 + m.g.h = m.32/2 + m.10.0,8 --- EmP = 12,5m --- Energia mecânica em Q --- EmQ = mVQ2/2 + m.g.h = m.VQ2/2 + m.10.0 --- EmQ=mVQ2/2 --- EmP = EmQ --- 12,5m = mVQ2/2 --- VQ=√(25) --- VQ=5,0 m/s.

27- I. Verdadeira --- em (I) ela está em repouso, equilíbrio estático e F_R=0 o que implica que T=P=mg --- em (II) ela

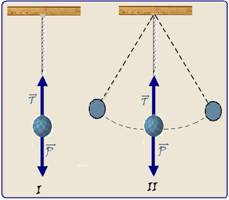
está em movimento circular surgindo sobre ela uma força resultante centrípeta (dirigida para o centro da circunferência) e de intensidade F_c=mV²/R, com F_c=T – P --- T=P + mV²/R --- observe, nesse caso, que T>P.

II. Verdadeira --- As forças que agem sobre um corpo apoiado sobre um plano inclinado são seu peso, vertical e para baixo e a força normal , perpendicular à superfície de contato entre o bloco e o plano.

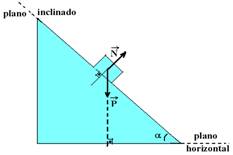
Α é o ângulo de inclinação do plano. Como e não tem a mesma direção, vamos decompor o peso em duas parcelas:

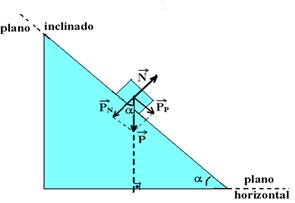
parcela do peso paralela à superfície do plano inclinado (responsável pela tentativa de descida do bloco).

parcela do peso perpendicular à superfície do plano inclinado (força que comprime o bloco contra o plano)

Observe que P_n é menor que o peso, pois é parcela do mesmo.

III. Verdadeira --- se a resistência do ar é nula, a aceleração de queda é a da gravidade g, que é constante, pois elas chegam juntas ao solo, quando largadas de mesma altura --- P=mg --- g=P/m=constante.

R- C.

Lei de Hooke

28- Com duas pessoas no carro a deformação do sistema de molas é x=2cm=2.10^-2m e a força que deformadora é o peso das duas pessoas --- P=2mg=2.60.10=12.10²N --- esse peso corresponde à força elástica --- F_eP=kx ---

29- Determinando o valor da constante elástica k da mola pela figura 1 --- quando x=4,0cm=4.10^-2m, F=20N --- F_e=kx --- 20=k.4.10^-2--- k=5.10²N/m --- força aplicada pela mola quando o sistema está em equilíbrio e a mola deformada de x=6,4cm=6,4.10^-2m --- F=kx=5.10².6,4.10^-2=32N --- observe a seqüência das figuras abaixo onde

foram colocadas todas as forças no ponto de interseção dos fios (I) --- em (II) foram decompostas as forças inclinadas --- T_x=Tcosα=0,8T --- T_y=Tsenα=0,6T --- F_x=Fcosβ=32.0,6=19,2N --- F_y=Fsenβ=32.0,8=25,6N --- em (III) estão colocadas apenas as forças que agem nas direções horizontal e vertical --- estando o sistema em equilíbrio essas forças se anulam em cada direção --- na horizontal --- 0,8T=19,2 --- T=24N --- na vertical --- 0,6T + 25,6 = 10m ---

0,6.24 + 25,6 = 10m --- 14,4 + 25,6 = 10m --- m=40/10=4kg --- R- C.

Movimento Harmônico Simples (MHS)

Dinâmica do MHS – Sistema massa-mola

20- A. Falsa --- F_e=kx --- 10=k.0,1 --- k=100n/m --- k=10²N/m.

B. Falsa --- o período de oscilação do sistema massa-mola vale --- T=2π√(m/k)=2π√(0,25/10²) --- T=2π√(25.10^-4) --- T=2π.5.10^-2 --- T≈30.10^-2s.

C. Correta --- a amplitude A vale A=20cm=2.10^-1m --- energia mecânica nos extremos --- E_me=k.A²/2=10².(2.10^-

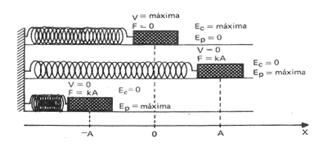
¹)²/2 --- E_me=10².10^-2.4/2 --- E_me=2J --- a velocidade é máxima no ponto médio onde a energia cinética é máxima --- teorema da conservação da energia mecânica --- E_me=E_c --- 2=m.V²/2 --- 2=0,25.V²/2 --- V=16 --- V_max=4m/s.

D. Falsa --- F=ma --- F=kx --- m.a=kx --- 0,25.a=10².2.10^-1 --- a=20/0,25 --- a=80m/s².

R- C.

21- Na situação inicial (ponto I), de altura máxima, a força elástica vale F_e=3N --- F_e=kx --- 3=100.x --- x=0,03m --- nesse ponto, a mola está comprimida de x=0,03m ao em relação à sua posição natural --- na posição de equilíbrio (ponto O) a força resultante é nula e P_p=mgsen30^o=F_E=kd --- 1.10.1/2 = 100.d --- d=0,05m --- nesse ponto a mola está esticada de d=0,05m em relação à sua posição natural --- sendo a amplitude A a distância entre a posição natural (ponto O) e a compressão máxima (pontoI), então A=0,03 + 0,05=0,08m --- desprezados os atritos, a força elástica e a

força peso são forças conservativas, então o sistema é conservativo e a energia mecânica do sistema é constante --- colocando o nível de altura zero na posição de equilíbrio (ponto O) onde a mola está na posição natural (não deformada), a energia mecânica aí é só a cinética, pois a potencial gravitacional é nula (h’=0) e a potencial elástica também é nula (mola na posição natural, sem deformação) --- E_mO=mv²/2 --- cálculo da altura no ponto I (veja figura) --- sen30^o=h/0,08 --- 0,5=h/0.08 --- h=0,04m --- no ponto I a energia mecânica é a potencial elástica armazenada na mola (E_pe=kA²/2) somada com a potencial gravitacional (E_pg=mgh) --- E_mI=kA^2/2 + mgh=100.(0,08)²/2

+ 1.10.0,04 --- E_pI= 0,32 + 0,4=0,36J --- E_mI=E_mO --- 0,36=mv²/2--- 0,36=1.v²/2 --- V=√(0,64) --- v=0,8m/s --- R- B.

Função horária da elongação

15- O período de um sistema massa-mola efetuando um MHS é fornecido por T=2π√m/k --- observe que se o sistema massa-mola estiver oscilando num plano inclinado, na horizontal ou na vertical, se a massa (m) do corpo e a constante elástica da mola (k) forem as mesmas, o que é o caso, o período de oscilação T será também o mesmo --- R- D.

16- O período T desse MHS é fornecido pela expressão abaixo --- substituindo m=0,08kg, k=0,5 N/m e π = 3,14 na

expressão T=2π√(m/k) --- T=2.3,14.√0,08/0,5)=6,28.√(0,16) --- T=6,28.0,4=2,512s --- R- B.

Força de resistência no ar

36- a) São dados --- V_o=6000m/s --- V=0 --- t_o=0 --- t=7min=7.60=420s --- cálculo da aceleração de

retardamento --- a=(V – V_o)/(t – t_o)=(0 – 6000)/(420 – 0) --- a=-14,3s --- F_R=m.a=1000.(- 14,3)= - 14300N --- em módulo ---

F_R=1,43.10⁴N.

b) Pelos dados ela entrou na atmosfera marciana com V_o=6000m/s em uma altitude de ho=125km=125.10³m e na altura

h=100km=100.10³m ela teve velocidade de V=4000m/s --- Teorema da Energia Mecânica --- Em todo sistema dissipativo, o trabalho das forças não conservativas (força de atrito, força de resistência do ar, etc.) é igual à energia total dissipada, ou seja, é igual à variação da energia mecânica – E_mfinal – E_minicial=W_{forças
dissipativas} --- a força dissipativa

nesse caso é a força de atrito F_at --- W_fat=E_m – E_mo --- E_m=mV²/2 + mgh=10³.(4.10³)²/2 + 10³.10.100.10³=9.10⁹J ---

E_mo=mV_o²/2 + mgh_o=10³.(6.10³)²/2 + 10³.10.125.10³=19,25.10⁹J ---W_fat= - 10,25.10⁹ --- W_fat≈ - 1,0.10¹⁰J.

37- a) Pelo enunciado a intensidade da força vertical e para cima que o vento exerce sobre a gota vale F_vento=b.r com b=1,6.10^-3N/m --- ρ_água=m/V --- volume da gota considerada esférica de raio r --- V=(4/3).π.r³ --- ρ_água=m/(4/3).π.r³ --- m=ρ_água.π.r³=10³.3.(4/3)r³ --- m=4.10³.r³ --- na iminência de começar a cair, o peso da gota

(vertical e para baixo) deve ser igual à força aplicada pelo vento (vertical e para cima) --- P=F_vento --- m.g = b.r --- 4.10³.r³.10 = 1,6.10^-3.r --- r²= 1,6.10^-3/4.10⁴=0,4.10^-7 --- r=√(4.10^-8) --- r=2.10^-4m=0,2mm --- esse deve ser o raio da gota quando ela está na iminência de cair --- para que ela caia você deve ter --- r > 0,2mm.

b) Cálculo da massa dessa água que ocupa um volume V de água contida numa área de S=1m² e altura h=20mm=

20.10^-3m=2.10^-2m --- V=S.h=1.2.10^-2=2.10^-2m³ --- ρ_água=m/V --- 10³=m/2.10^-2 --- m=20kg (é essa massa de água que ao se chocar com o solo provoca nele um impulso vertical e para baixo) --- I=m.∆V --- como o choque é inelástico, a variação de velocidade da água com o solo foi de ∆V=2,5m/s --- I=20.2,5 --- I=50N.s, impulso sobre o solo, vertical e para baixo.

Força de atrito

66- Força que ele aplica no pau de sebo comprimindo-o e trocando com ele uma força perpendicular ao poste de F=800N --- pelo princípio da ação e reação o poste aplica nele uma força de mesma intensidade (N=800N), mesma direção mas sentido contrário --- na vertical, existe sobre ele duas forças --- seu peso vertical e para baixo e uma

força de atrito, vertical e para cima que o impede de cair, anulando o peso --- P=m.g=60.10 --- P=600N --- N=800N ---F_at=μN=

μ.800 --- F_at=800μ --- F_at=P --- 800μ=600 μ=600/800 --- μ=0,75 --- R- C.

67- Considerando os dois blocos como um único de massa M=(4 + 1)=5kg e sob ação da força de F=10N eles se movem com a mesma aceleração de F=Ma --- 10=5.a --- a=2m/s² (aceleração de cada bloco) --- sobre o bloco 2 agem as forças de intensidades F=10N (horizontal e para a direita) e a força de atrito F_at (horizontal e para a esquerda)

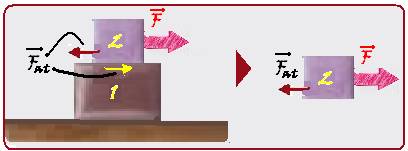
--- força resultante sobre o bloco 2 --- F_R=F – F_at=10 - F_at --- F_R=m₂.a --- 10 – F_at=1.2 --- F_at=8N --- R- E.

68- Dados --- m=0,4kg --- t=0,8s --- ∆S=1,6m --- V_o=0 --- calculo da aceleração do garçom, copo e bandeja --- ∆S=V_ot + at²/2 --- 1,6=0.0,8 + a.(0,8)²/2 --- a=1,6/0,32 --- a=5m/s² --- o copo de massa m=0,4kg que se move com a=5m/s² fica sob ação de uma força resultante --- F_R=ma=0,4.5=2N --- observe na figura abaixo onde foram colocadas

todas as forças que agem sobre o copo que essa força de 2N é a força de atrito que obriga o copo a acompanhar a bandeja e o garçom --- FR=Fat=2N --- R- A.

69- Dados --- Vo=5m/s --- V=0 --- ∆S=5m --- cálculo da aceleração a do bloco utilizando a equação de Torricelli --- V2 = Vo2 + 2.a. ∆S --- 02 = 52 + 2.a.5 --- a = - 2,5m/s2 (negativo, está retardando) --- módulo da força resultante sobre o bloco de massa m --- FR = m.a --- FR=2,5m --- mas, a única força sobre o bloco na direção do movimento é a força de atrito que o retém até parar --- Fat=μ.N= μ.P= μ.mg=10μm --- portanto, a força de atrito é a própria força resultante --- Fat = FR --- 10μm = 2,5m --- μ=0,25 --- R- E.

70- I. Comportamento das forças de atrito que agem em um carro sem o mecanismo ABS:

Considere um bloco de massa m sujeito a uma força externa de intensidade variável

Quando o corpo estiver em repouso e não houver força externa, F_at=0 --- com o corpo permanecendo em repouso, aumentando a intensidade de, a intensidade da força de atrito estático () também aumenta (figuras acima), até que o corpo fique na iminência de movimento (figura abaixo).

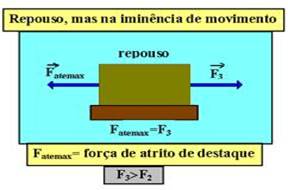
Quando o corpo está na iminência de movimento a intensidade da força de atrito estático é máxima --- uma força de intensidade maior que faz com que o corpo entre em movimento e, a partir daí a força de atrito é denominada dinâmica ou cinética.

Depois que o bloco entra em movimento a força de atrito é denominada força de atrito dinâmica, e é sempre a mesma, independente da velocidade. A intensidade da força de atrito dinâmica é ligeiramente menor que a intensidade da força de atrito estática máxima.

O gráfico abaixo representa todo o processo explicado acima.

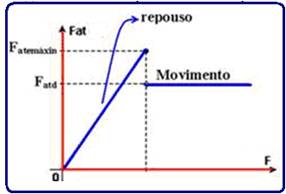
II. Comportamento das forças de atrito que agem em um carro com o mecanismo ABS:

Os freios antitravamento (ABS, anti-lock braking system) ajudam a parar melhor --- eles previnem o

travamento das rodas e proporcionam uma distância de frenagem mais curta em superfícies escorregadias, evitando o descontrole do veículo --- ele mantém as rodas sempre na iminência de deslizar, aproveitando melhor o atrito estático máximo, que é maior que o atrito cinético (de deslizamento) --- quando a força aplicada pelos freios através da pressão aplicada no pedal chega aumentada até as rodas, estando elas na iminência de movimento (força de atrito de destaque), o sistema ABS libera instantaneamente a roda impedindo seu travamento e mantendo assim a força de atrito máxima (força de atrito de destaque) que é superior à força de atrito cinética ou dinâmica que surgiria, caso ele deslizasse --- o

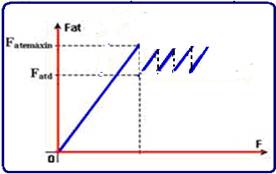
processo é repetido instantânea e sucessivamente conforme o gráfico acima --- R- A.

Plano inclinado com atrito

32- Cálculo da intensidade da força de atrito estático (iminência de movimento) --- F_ate=μ_e.N.cosθ= μ_e.P.cosθ=0,75.100.0,8 --- F_ate=60N --- cálculo da intensidade da parcela do peso paralela ao plano inclinado que tende a puxar o bloco sobre o plano inclinado --- P_p=Psenθ=100.0,6=60N --- observe que a força resultante sobre o

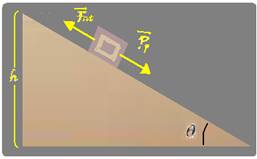
bloco é nula e, como ele estava em repouso, por inércia ele tende a continuar em repouso, mas está na iminência de movimento) --- R- E.

33- -As forças que agem sobre um corpo apoiado sobre um plano inclinado são seu peso, vertical e para baixo e a força normal , perpendicular à superfície de contato entre o bloco e o plano.

α é o ângulo de inclinação do plano. Como e não tem a mesma direção, vamos decompor o peso em duas parcelas:

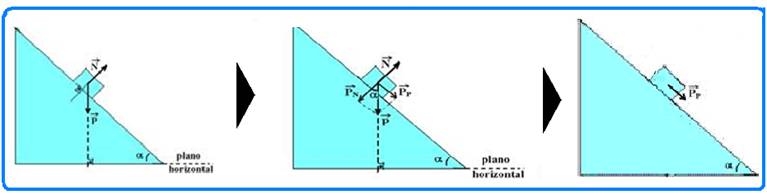
parcela do peso paralela à superfície do plano inclinado (responsável pela tentativa de descida do bloco).

parcela do peso perpendicular à superfície do plano inclinado (força que comprime o bloco contra o plano)

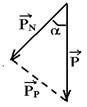
sena=cateto oposto/hipotenusa --- sena=PP/P --- PP=P.sena

cosa=cateto adjacente/hipotenusa --- cosa=PN/P --- PN=P.cosa (segunda figura acima)

A componente normal do peso anula a reação normal do apoio , assim temos (terceira figura acima).

Havendo atrito:

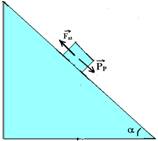
A força de atrito é sempre contrária ao movimento ou à sua tendência e é fornecida por F_at=mμN --- P_N=N --- F_at=mP_N --- F_at=μPcosα --- F_at=μmgcosα

Resolvendo o exercício --- F_R=m.a --- P_p – F_at =m.a --- mgsenθ – μmgcosθ = ma --- 10.0,6 –

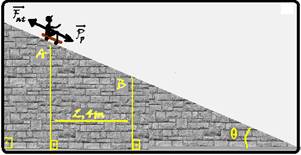
0,25.10.0,8 = a --- a=6 – 2 --- a=4,0m/s² --- deslocamento ∆S entre A e B (veja figura abaixo) ---

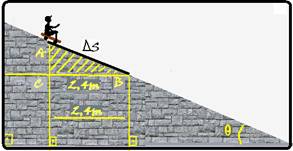
cosθ=cateto adjacente/hipotenusa --- 0,8 = BC/AB --- 0,8=2,4/∆S --- ∆S=3m --- para calcular a velocidade em B (V_B) você pode usar a equação de Torricelli --- V_B² = V_A² + 2.a.∆S --- V_B² = 1² + 2.4.3 --- V_B=5m/s --- variação da quantidade de movimento entre A e B --- ∆Q = Q_B – Q_A=mV_B – mV_A=50.5 – 50.1 --- ∆Q=200N.s --- R- B.

Forças no movimento circular

49- Expressão da intensidade da força resultante centrípeta --- F_c=mV²/R --- kart --- F_K=M.V²/2R=0,5MV²/R --- fórmula 1 --- F_F=3M.V²/R=3MV²/R --- stock-car --- F_S=6M.V²/3R=2MV²/R --- assim, F_F > F_S > F_K --- R- B.

50- Em todo movimento circular existe sempre uma força resultante dirigida para o centro da circunferência denominada força resultante centrípeta (

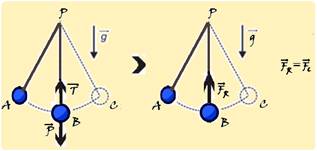
() de intensidade F_c=mV²/R --- no ponto B essa força tem direção vertical e sentido para cima e de intensidade T – P =mV²/R --- R- B.

Trabalho

48- Observe que durante todo os deslocamentos da moça num lugar plano, o ângulo que a força

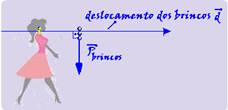
peso dos brincos forma com o deslocamento (na nossa figura, horizontal) é sempre de 90^o --- W_peso=P.d.cos90^o=p.d.0=0 --- R- E.

49- Como não existe atrito com o ar a intensidade da força resultante (F_R) sobre o conjunto (satélite-foguete) é igual à intensidade da força propulsora F_p) menos a intensidade da força peso (P) --- intensidade da força peso ---

P=m.g=1.10⁶.10=10⁷N --- F_R=F_p – P --- F_R = 5.10⁷– 1.10⁷=4.10⁷N --- trabalho da força resultante --- W_FR=

F_R.d.cos0^o=4.10⁷.2.10³.1 --- W_FR=8.10¹⁰ J --- R- D.

Potência

51- Dados --- m=70kg --- V_o=0 --- V=72km/h/3,6=20m/s --- ∆t=2min=2.60=120s --- cálculo do trabalho pela variação de energia cinética --- W=E_c – E_co=mV²/2 – mV_o²/2=70.20²/2 – 70.0²/2 --- W=14000J --- P=W/∆t --- P=14000/120 --- P=116,66W --- R- A.

52- 01. Correta --- pelo enunciado a massa total que sobe é a massa da gôndola (500kg) somada com sua carga (240kg) --- peso --- P=M.g=(500 + 240),g=740.10 --- P=7400N (peso de uma gôndola carregada) --- a gôndola sobe com velocidade constante uma altura ∆S=100m em ∆t=40s e sua velocidade média V_m será --- V_m= ∆S/∆t=100/40 --- V_m=2,5m/s --- a subida é um MRU, então a força resultante sobre a gôndola durante a subida é nula o que implica que

a intensidade da força média aplicada pelo motor equilibra a força peso --- F_m=P=7400N --- F_m=7400N --- o trabalho da força média aplicada pelo motor na subida vale W=F_m.d,cos0^o=F_m.d.1 --- W=F_m.d --- potencia média --- P_o=W/∆t --- P_o=F_m.d//∆t --- d//∆t=V_m --- P_o=F_m,V_m=7400.2,5 --- P_o=18500W.

02. Correta --- tempo que demora, em queda livre (a=g) para , a partir do repouso (V_o=0), atingir velocidade de V=122,4/3,6 --- V=122,4/3,6 =34m/s --- V = V_o + g.t --- 34=0 + 10t --- t=3,4s --- cálculo da aceleração de retardamento a quando, descendo na vertical, com a velocidade passando de V_o=122,4/3,6=34m/s até parar, quando V=0 em ∆t=8,4 – 3,4=5s --- V=V_o - a.t --- 0 = 34 – a.5 --- a=34/5 --- a=6,8m/s² --- força desaceleradora média --- F_R= m.a=740.6,8 --- F_R=5032N.

04. Falsa --- é de 3,4s (veja 02).

08. Correta --- a queda livre demorou t=3,4s, com a=g=10m/s² e V_o=0 --- ∆S=V_ot + at²/2=0.3,4 + 10.(3,4)²/2= 0 + 10.11,56/2=10.5,78 --- ∆S=57,8m.

16. Falsa --- é g apenas na queda livre e não durante todo o percurso.

R- (01 + 02 + 08)=11.

Energia

26- Autocontração gravitacional (potencial gravitacional) --- nesse processo, os íons de hidrogênio (prótons) contidos no seu interior adquirem velocidades muito altas (energia cinética) --- o que os leva a atingirem temperaturas da ordem de milhões de graus (energia térmica) --- com isso, têm início reações exotérmicas de fusão nuclear, nas quais núcleos de hidrogênio são fundidos, gerando núcleos de He (Hélio) e propiciando a produção da radiação (energia de massa) --- parte dessa radiação atinge a Terra (sob forma de radiação eletromagnética) e é a principal fonte de toda a energia que utilizamos --- R- D.

27- a) Massa do atleta --- m=70kg --- como pedido no exercício, pelo gráfico 1, a terceira corrida demorou ∆t=t=0,5h num percurso de ∆S=7,5km --- V=∆S/∆t=7,5/0,5 --- V=15km/h --- pra essa velocidade V=15km/h, você verifica no gráfico 2 que C_MET=60kJ/kg.h --- usando a expressão fornecida pelo enunciado do exercício --- E=C_MET.m.t=60.70.

0,5 --- E=2100kJ.

b) Avaliando a área da sola de um tênis como um retângulo de 35cm=0,35m de comprimento e 9cm=0,09m de largura

--- S=0,35x0,09=30,5.10^-4≈3.10^-5m² --- pressão (P_r)=força(no caso, peso P)/área (S) --- P=mg=70.10=700N --- P_r=

P/S=700/3.10^-5 --- P_r≈2,3.10⁴N/m² (Pa).

Tipos de energia – Trabalho

39- Da mesma maneira que uma atiradeira (estilingue) transforma energia potencial elástica em energia cinética devido à uma distensão da borracha (elástico) o carrinho mencionado também transforma energia potencial elástica em energia cinética devido à compressão da mola --- R- E.

Energia mecânica

72- Colocando o referencial na altura em que se encontra seu centro de massa, no início, quando ele finca a vara no chão para subir ele só possui energia cinética --- E_c=mV²/2=m.11²/2 --- E_c=60,5m ---

pelo enunciado, na altura Máxima, 80% de sua energia cinética é convertida em energia potencial gravitacional --- E_pg=0,8xE_c=0,8x60,5m=48,4m --- R_pg=m.g.h=48,4m --- m.10.h=48,4m --- h=4,84m --- R- E.

73- a) As forças que agem sobre um corpo apoiado sobre um plano inclinado são seu peso, vertical e para baixo e a força normal , perpendicular à superfície de contato entre o bloco e o plano (figura abaixo).

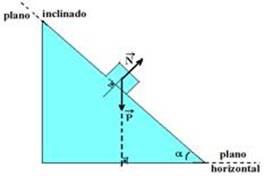
α é o ângulo de inclinação do plano. Como e não tem a mesma direção, vamos decompor o peso em duas parcelas:

parcela do peso paralela à superfície do plano inclinado (responsável pela tentativa de descida do bloco).

parcela do peso perpendicular à superfície do plano inclinado (força que comprime o bloco contra o plano)

senα=cateto oposto/hipotenusa --- senα=P_p/P --- P_p=P.sena

cosα=cateto adjacente/hipotenusa --- cosα=P_N/P --- P_N=P.cosa

As duas forças acima substituem o peso e podemos tirá-lo:

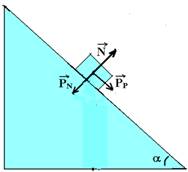
A componente normal do peso anula a reação normal do apoio , assim temos:

Como não existe atrito, o bloco desce com aceleração de intensidade a, tal que F_R=m.a --- P_p=m.a --- mgsenα=ma --- a=gsenα.

Como o bloco está em equilíbrio na direção perpendicular à superfície do plano inclinado --- N=P_N=Pcos30^o=10.√3/2 --- N≈5.1,7≈8,5N.

b) Veja em (a) que ele desce com aceleração a=gsen30⁰=10.1/2 --- a=5m/s² --- aplicando Torricelli --- V²=V_o² +

2.a.∆S --- 10²=0² + 2.5.d --- d=100/10 --- d=10m.

c) Como não existe atrito o bloco 1 atinge o bloco 2 com velocidade de V₁=10m/s --- antes do choque --- V₁=10m/s --- V₂=0 --- quantidade de movimento do sistema antes do choque --- Q_sa=m₁V₁ + m₂V₂=1.10 + 3.0 --- Q_sa=10kg.

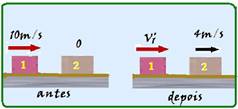
m/s --- depois do choque --- V’₁=? --- V₂=4m/s --- quantidade de movimento do sistema depois do choque --- Q_sd=m₁V’₁ + m₂V₂=1.V₁’ + 3.4 --- Q_sd= V₁’ + 12 --- pelo princípio da conservação da quantidade de movimento ---

Q_sa=Q_sd --- 10 = V₁’ + 12 --- V₁’= - 2m/s (o sinal negativo significa que o bloco 1 retornou após o choque).

d) Cálculo da energia mecânica do bloco 2 no ponto A de altura zero e onde V=4m/s --- E_mA=mV²/2 + mgh=3.4²/2 +

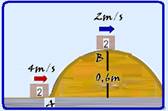
0 --- E_mA=24J --- E_mB=mV_B²2 + m.g.R=3.V_B²/2 + 3.10.0,6 --- V_B=√4=2m/s --- no ponto mais alto B, a força resultante sobre o bloco é a centrípeta, vertical e dirigida para o centro da circunferência (baixo), de intensidade ---

F_c=mV_B²/R --- P – N = 3.2²/0,6 --- 30 – N = 20 --- N=10N.

74- Utilizando o teorema da conservação da quantidade de movimento do sistema --- antes do disparo --- Q_antes=(M + m)V=(M + m).0 --- Q_antes=0 --- depois do disparo --- o canhão de massa M se move para a direita com velocidade

V e o projétil de massa m para a com velocidade ( - v) --- Q_depois=MV – mv --- Q_antes = Q_depois --- 0 = MV –mv ---

V=mv/M --- após o disparo o canhão de massa M se desloca para a direita com velocidade inicial V_i=mv/M até parar V_f=0, percorrendo uma distância d --- a energia dissipada pela variação de energia cinética (∆E_c) do canhão é igual à

energia dissipada pela força de atrito (W_fat) --- ∆E_c = W_fat --- MV_f²/2 – MV_i²2 = F_at.d.cos180^o --- M.0²/2 – M(mv/M)²/2 = F_at.d.(-1) --- 0 – M.(m²v²/M²)/2 = - μNd --- N=P=Mg --- M.m².v²/2M² = μMgd --- μMgd = m²v²/2M --- μ = m²v²/2M²gd --- μ = (mv/M)²/2gd --- R- A.

75- A energia mecânica antes do disparo que vale Ema=3,75J e é a soma das energia cinética Ec=mV2/2 com a potencial elástica armazenada na mola (Epel) --- Ema = Ec + Epel --- 3,75=mV2/2 + Epel --- 3,75 = (3 + 3).12/2 + Epel --- Epel=0,75J --- agora você deve utilizar o teorema da conservação da quantidade de movimento --- antes do disparo do gatilho --- Qsa=mA.VA + mB.VB=3.1 + 3.1=3kgm/s --- depois do disparo do gatilho --- Qsd=mAVA + mBVB=3VA + 3.1,5=3VA + 4,5 --- Qsa = Qsd --- 3=3VA + 4,5 --- VA=1,5/3=0,5m/s.

76- a) Dados --- m_m=10¹⁶kg --- V_m=30km/s=30.10³=3.10⁴m/s --- quantidade de movimento inicial do meteoro --- P_i=m_m.V_m=10¹⁶.3.10⁴=3.10²⁰kg.m/s

b) Definição de energia cinética --- E_ci = m_m.V_m²/2=10¹⁶.(3.10⁴)²/2 --- E_ci=10¹⁶.9.10⁸/2 --- E_ci=4,5.10²⁴ J.

c) Utilizando o princípio da conservação da quantidade de movimento do sistema (Terra-meteoro) antes e depois do fenômeno (colisão) --- antes da colisão --- P_i = P_mi + P_Ti=m_m.V_m + m_T.V_T --- mas, V_T=0 (antes da colisão, a Terra não se move na direção perpendicular à sua trajetória, veja figura) --- P_i=10¹⁶.3.10⁴ + 6.10²⁴.0 --- P_i=3.10²⁰ + 0 ---

--- P_i=3.10²⁰kg.m/s --- depois da colisão --- trata-se de uma colisão inelástica (Terra e meteoro se movem juntos, com a mesma velocidade V) --- P_f = P_mf + P_Tf=m_m.V + m_T.V=(m_m + m_T),V --- como a massa do meteoro é insignificante em relação à massa da Terra, você pode considerar (m_m + m_T)≈m_T --- P_f=m_T.V=6.10²⁴V --- pelo princípio da conservação da quantidade de movimento --- P_i = P_f --- 3.10²⁰=6.10²⁴V --- V=3.10²⁰/6.10²⁴ ---

V=5,0.10^-5m/s (velocidade ‘Terra + meteoro” , no nosso exemplo para a direita, imediatamente após a colisão).

c) Cálculo da energia cinética final do sistema (Terra + meteoro) --- E_cf=m_{(m
+ T)}.V²/2=m_T.V²/2=6.10²⁴.(5.10^-5)²/2 ---

E_cf=7,5.10¹⁵J --- essa energia cinética final do sistema (7,5.10¹⁵J) é muito menor do que a energia cinética inicial do meteoro (4,5.10²⁴J) --- assim, a energia dissipada no choque é praticamente igual à energia cinética inicial do meteoro --- E_d=4,5.10²⁴J --- regra de três --- 1 megaton – 4.10¹⁵J --- E_d – 4,4.10²⁴J --- E_d=4,4.10²⁴/4.10¹⁵ ---

E_d=1,125.10⁹ megatons.

Impulso e quantidade de movimento

39- Utilizando o teorema da conservação da quantidade de movimento do sistema --- antes do disparo --- Q_antes=(M + m)V=(M + m).0 --- Q_antes=0 --- depois do disparo --- o canhão de massa M se move para a direita com velocidade

V e o projétil de massa m para a com velocidade ( - v) --- Q_depois=MV – mv --- Q_antes = Q_depois --- 0 = MV –mv ---

40- Teorema do Impulso: “ O impulso da força resultante de um sistema de forças que age sobre um corpo é igual à variação da quantidade de movimento do corpo”

Se uma bola de massa m incide perpendicularmente numa parede com velocidade de módulo V e retorna na mesma direção, mas em sentido contrário com velocidade de mesmo módulo, teremos:

F.∆t = m.V_f – m.V_i --- F.∆t = m.(+V) – m.(-V) --- F ∆t = m.V – (- m.V) --- F.∆t = mV + mV --- F ∆t = 2mV

No caso do exercício --- V_antes=V_a=-40m/s --- V_depois=V_d=+30m/s --- F.∆t = m.V_d – m.V_a --- F.∆t = m.(+30) – m.(-

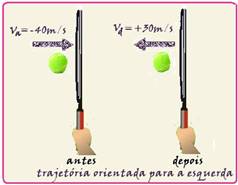
40) --- F.∆t = 30m + 40m --- F.10^-2=70x6.10^-2 --- F=420,10^-2/10^-2 --- F=420N --- R-D.

41- Teorema do Impulso:“ O impulso da força resultante de um sistema de forças que age sobre um corpo é igual à variação da quantidade de movimento do corpo”

Muitos automóveis dispõe de um eficiente sistema de proteção para o motorista, que consiste de uma bolsa inflável de ar (air-bag) --- essa bolsa é automaticamente inflada quando o automóvel sofre uma desaceleração súbita, de modo que a cabeça e o tórax do motorista, em vez de colidirem com o volante, colidem com a bolsa.

Veja pela expressão F.∆t=m.∆V, que m e ∆V são constantes (mesmo motorista e mesma variação de velocidade) e assim, teremos --- F. ∆t=constante, portanto se você aumentar o intervalo de tempo do choque, estará diminuindo a intensidade da força máxima que o motorista troca com o volante.

Assim, a bolsa aumenta o intervalo de tempo da desaceleração da cabeça do motorista, diminuindo, portanto, a força máxima que atua sobre a cabeça e o tórax --- R- A.

42- Como o sistema é isolado, a quantidade de movimento do sistema antes da colisão () deve ser igual à quantidade de movimento do sistema depois da colisão () --- a quantidade de movimento

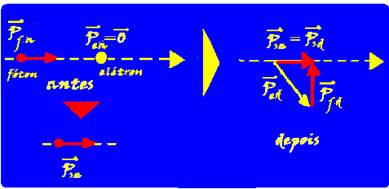
do sistema antes da colisão tem direção horizontal e sentido para a direita, sendo a do próprio fóton, pois a do elétron é nula (figura) --- a quantidade de movimento do sistema depois da colisão também deve ter direção horizontal e sentido para a direita, pois = --- então a soma vetorial de com deve fornecer = (veja figura) --- R- A.

43- A energia mecânica antes do disparo que vale Ema=3,75J e é a soma das energia cinética Ec=mV2/2 com a potencial elástica armazenada na mola (Epel) --- Ema = Ec + Epel --- 3,75=mV2/2 + Epel --- 3,75 = (3 + 3).12/2 + Epel --- Epel=0,75J --- agora você deve utilizar o teorema da conservação da quantidade de movimento --- antes do disparo do gatilho --- Qsa=mA.VA + mB.VB=3.1 + 3.1=3kgm/s --- depois do disparo do gatilho --- Qsd=mAVA + mBVB=3VA + 3.1,5=3VA + 4,5 --- Qsa = Qsd --- 3=3VA + 4,5 --- VA=1,5/3=0,5m/s.

Colisões mecânicas

49- 01- a) Falsa --- quantidade de movimento (Q)=massa (m)xvelocidade (V) --- bola de vôlei --- Q_V=m_V.V_V=(0,27).(30) --- Q_V=8,1kg.m/s --- bola de golfe --- Q_G=m_G.V_G=(0,045).(60) --- Q_G=2,7kg.m/s ---

Q_G < Q_V.

b) Falsa --- E_c=m.V²/2 --- bola de vôlei --- E_cV=m_V.V_V²/2=(0,27).(30)²2 --- E_cV=121,5J --- bola de golfe --- E_cG=m_G.V_G²/2=(0,045).(60)²/2 --- E_cG=81J --- E_cG < E_cV.

c) Falsa --- em todo choque inelástico o coeficiente de restituição é nulo o que implica que, os corpos após o choque, possuem a mesma velocidade e, como a massa da pessoa é bem maior que a das bolas, cada uma delas terá velocidade final nula --- V_fV=0 e V_fG=0.

d) Falsa --- "O impulso da força resultante de um sistema de forças que age sobre um corpo é igual à variação da quantidade de movimento do corpo"

∆t_V= 2∆t_G --- m_V=0,27kg --- m_G=0,045kg --- V_G=60m/s --- V_V=30m/s --- F_G. ∆t_G=0,045x60=2,7 (I) --- F_V.2∆t_G=0,27x30=8,1 (II) --- (I)/(II) --- F_G.∆t_G/2F_V.∆t_G=2,7/8,1 --- F_G/2F_V=1/3 --- F_G=2F_V/3 --- F_G < F_V.

e) Correta --- Pressão=força/área --- P=F/S --- P_G=F_G/S_G=2F_V/3 (I) --- S_V=10S_G --- P_V=F_V/S_V=F_V/10S_G (II) ---

(I)/(II) --- P_G/P_V=2F_V/3S_Gx10S_G/F_V --- P_G/P_V=(20/3)P_V --- P_G > P_V.

R- E.

50- Sendo a colisão perfeitamente elástica, a energia mecânica (no caso, cinética) do sistema, antes

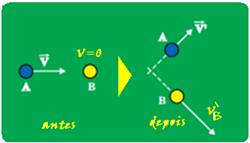
e depois da colisão é a mesma --- antes --- E_ca=m.2²/2 + m.0²/2 --- E_ca=2m --- depois --- E_cd=mV’²/2 + mV_B’²/2=m.1²/2 + mV_B’²/2 --- E_cd=0,5m + mV_B’²/2 --- E_ca = E_cd --- 2m = 0,5m + mV_B’²/2 --- V_B’²=3 --- razão pedida --- E_B^’=mV_B’²/2=m.3/2 (I) --- E_A=m.4/2=2m (II) --- (I)/(II) --- E'_B/E_A = (3m/2)/2m=(3m/2)x(1/2m) --- E'_B/E_A=3/4 --- R- C.

51- Após o primeiro choque --- h₁=0,8x5=4,0m --- após 0 segundo choque --- h₂=0,8x4,0=3,2m --- após o terceiro choque --- h₃=0,8x3,2=2,56m --- R- C.

52- No primeiro choque ela chega ao solo com --- E_mi=mgh=E_mf=mV²/2 --- m.10.5=mV²/2 --- v=10m/s --- 80%de 10m/s=8m/s --- aos o primeiro choque ela se solta do solo com --- E_mi=mV²/2=E_mf=mgh=m.10.4 --- V=√80=8,9ms --- R- D.

53- Intensidade da força sobre a bola 1 --- F₁=3m₂.a₁=3m₂.3=9m₂ --- intensidade da força sobre a bola 2 --- F₂=m₂.a₂ --- mas, pelo princípio da ação e reação essas forças tem a mesma intensidade --- F₁=F₂ --- 9m₂=m₂.a₂== a₂=9m/s²

R- B.