Trabalho de uma Força

Em Física, o trabalho mede a quantidade de energia que fornecemos ou retiramos de um corpo quando, devido a uma força ele efetua um deslocamento.

Então, necessitamos de energia para mover um carro (combustão de gasolina, álcool, gás, etc),

deslocar um trólebus (energia elétrica), movimentar um carrinho de supermercado (energia física com esforço do corpo humano) e realizar um trabalho.

Assim, o trabalho corresponde a uma medida da energia transferida pela aplicação de uma força no decorrer de um deslocamento.

O símbolo do trabalho é na maioria das vezes a letra W (work, em inglês) ou a letra (táu, letra grega).

Trabalho de uma força constante

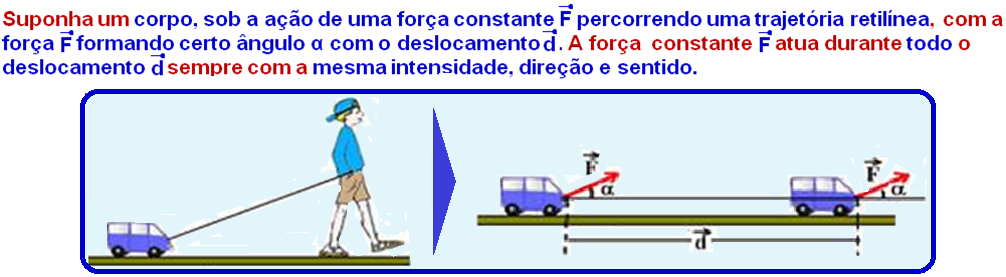
Assim, definimos trabalho W como sendo o produto da intensidade da força pelo deslocamento e pelo cosseno do ângulo α, ou seja:

onde a grandeza escalar (energia não tem direção nem sentido) trabalho W realizado pela força F representa a variação de energia do corpo, nesse deslocamento d. Na figura acima, essa energia é fornecida ao carrinho pelo menino.

A unidade de trabalho ou de qualquer outro tipo de energia no sistema internacional de unidades (SI) é o joule, de símbolo (J).

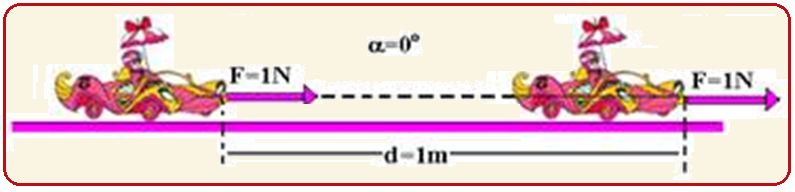
Na figura acima F = 1N d = 1m cos0^o= 1 W = F.d.cosα W = 1N.1m.1 W = 1N.m W = 1 J.

Um joule (J) é o trabalho realizado (energia transferida) quando uma força de 1N age sobre um corpo deslocando-o de 1m, com a força tendo a mesma direção e o mesmo sentido do deslocamento.

Sendo as intensidades de e de números positivos, a única grandeza da expressão W = F.d.cosα que pode ter o sinal variável é o fator cosα (entre +1 e -1), variando assim o sinal do trabalho.

Assim, podemos selecionar três casos:

Trabalho motor ou ativo

Trabalho resistente ou passivo

Trabalho nulo

Como o trabalho é uma grandeza escalar, se várias forças agirem sobre o corpo num mesmo deslocamento de A para B (d_AB), o trabalho da força resultante (W_FR) pode ser calculado pela soma algébrica do trabalho de cada força que age sobre o corpo isoladamente.

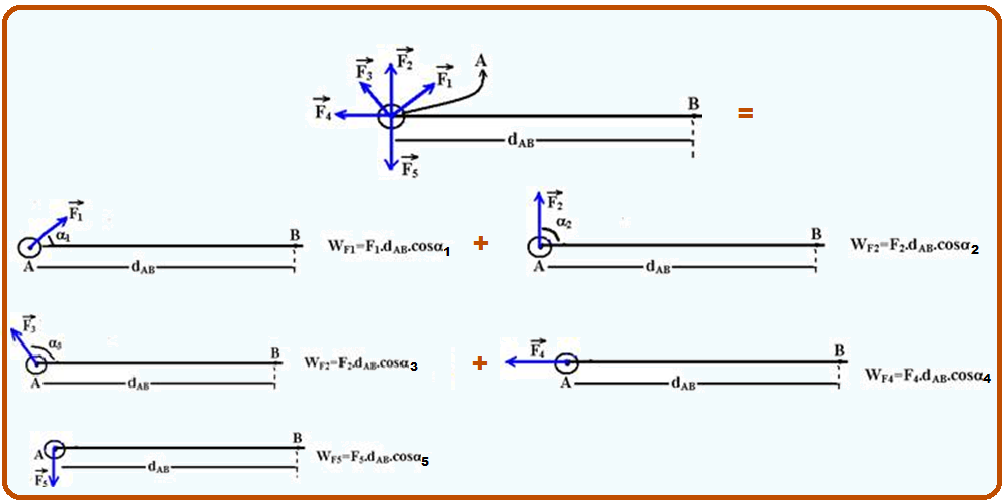
Assim, o trabalho realizado pela força resultante pode ser calculado pela soma algébrica W_FR= W_F1 + W_F2 + W_F3 + W_F4 + W_F5 ou por W_FR= F_R.d_AB.cosθ onde F_R é a intensidade da soma vetorial e θ é o ângulo entre a força resultante e o deslocamento.

O trabalho será nulo quando:

O que você deve saber, informações e dicas

O trabalho W é o produto da intensidade da força pelo deslocamento e pelo cosseno do ângulo α, ou seja:

Trabalho motor ou ativo

Trabalho resistente ou passivo

Trabalho nulo

Se o trabalho da força resultante for positivo, ele é motor e o corpo está acelerando; se for negativo, é resistente e o corpo está freando e se for nulo, o corpo está em MRU.

O trabalho sempre é realizado num deslocamento , compreendido entre dois pontos.

O trabalho é sempre de uma força aplicada num corpo por um agente externo que lhe fornece ou retira energia.

Sendo o trabalho o produto das intensidades de e de pelo cosseno do ângulo, que são grandezas escalares, ele é uma grandeza escalar (tem apenas intensidade, não tendo direção nem sentido).

Trabalho da força de atrito:

Trabalho de uma força variável

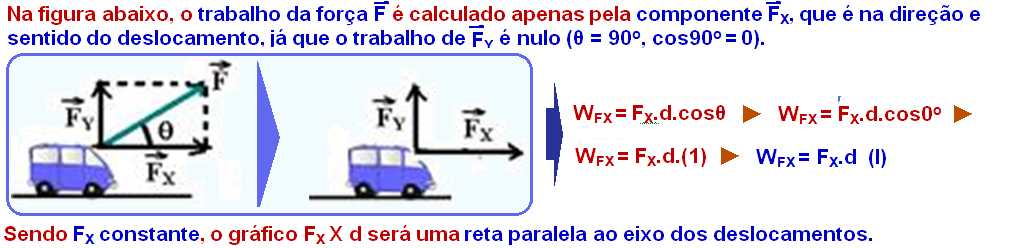
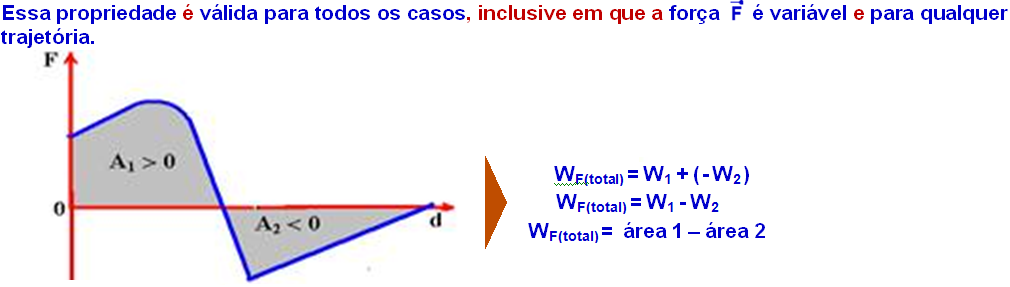
Assim, em todo gráfico da força F em função do deslocamento d, o trabalho realizado pela força F é numericamente igual à área compreendida entre a reta representativa (linha cheia) e o eixo do deslocamento.

Trabalho da Força Peso

Um corpo de peso e massa m efetua um deslocamento vertical d = h, entre dois pontos A e B. Vamos calcular o trabalho da força peso nesse deslocamento quando:

a) O corpo se desloca de A para B, ou seja, está descendo e α = 0^o:

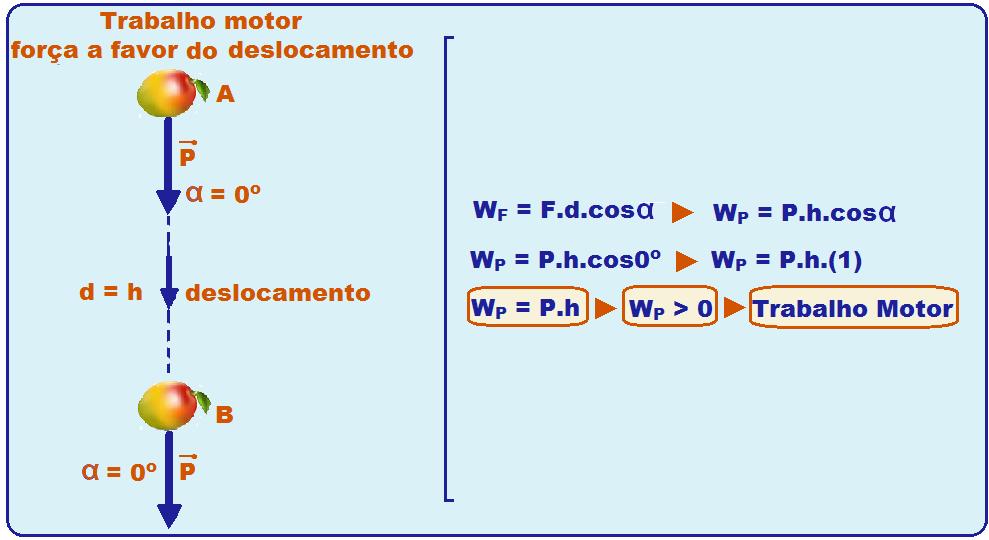
b) O corpo se desloca de B para A, ou seja, está subindo com α = 180^o.

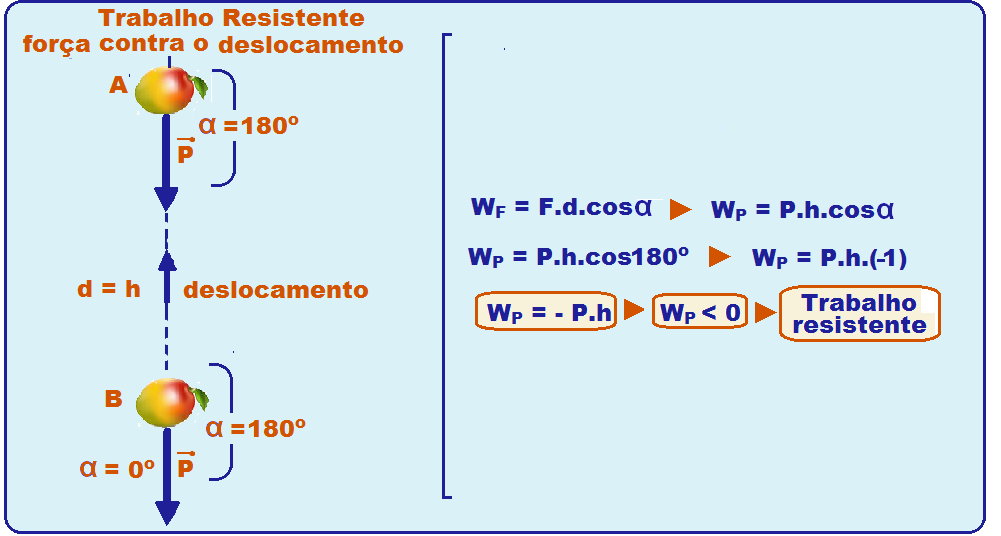
O trabalho da força peso é positivo na descida, negativo na subida e nulo num deslocamento horizontal.

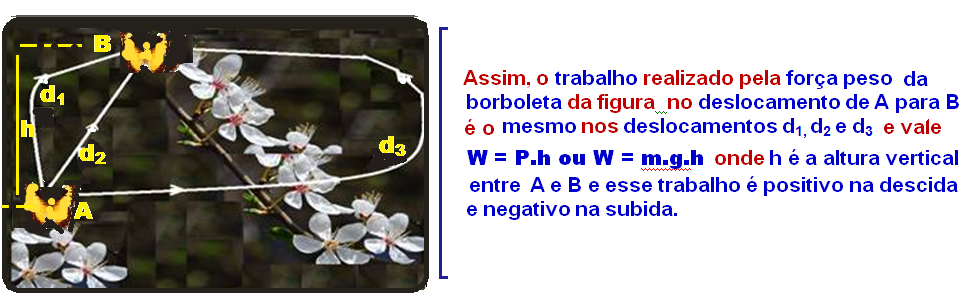
Vamos provar que o trabalho da força peso não depende da trajetória percorrida pelo corpo. Considere o ponto material de massa m da figura abaixo se deslocando sob ação da força peso:

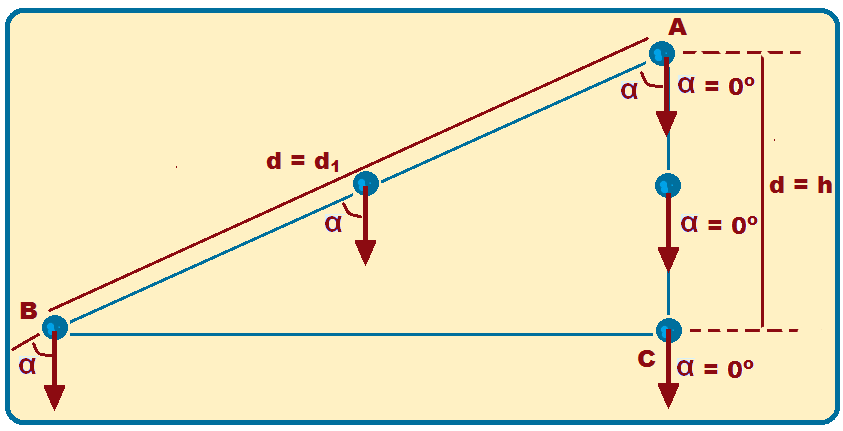
Cálculo do trabalho realizado pela força peso, de A para B, efetuando o deslocamento d = d₁

W_AB= P.d₁.cosa α (I) no triângulo ABC cosα = h/d₁ (II) substituindo II em I W_AB= P.d₁.h/d₁ W_AB= P.h ou W_AB= m.g.h trabalho realizado pela força peso para levar o ponto material no deslocamento de A até B.

Cálculo do trabalho realizado pela força peso, de A até C, efetuando o deslocamento d = h.

W_AC=P.h.cos0^o W_AC= P.h.(1) W_AC= P.h ou W_AC= m.g.h trabalho realizado pela força peso para levar o ponto material de A até C.

Observe que W_AB= W_AC, ou seja, o trabalho realizado pela força peso não depende da trajetória percorrida pelo ponto material.

Trabalho da força elástica

Considere uma mola ideal sofrendo uma deformação quando sujeita a uma força que pode ser o peso ( ) de um corpo pendurado ou uma força externa () qualquer.

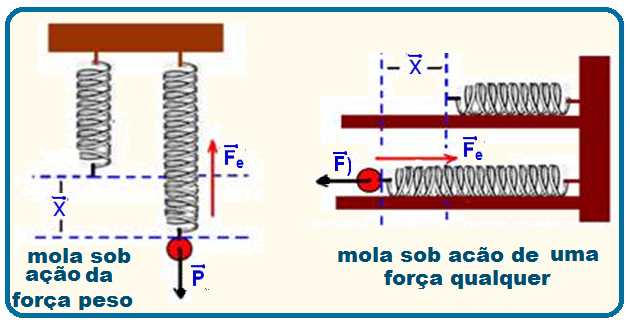
Em qualquer um dos dois casos surge sobre a mola uma força elástica (), de sentido contrário ao deslocamento, e que tende a fazer com que a mola retorne à posição normal (inicial).

Comprova-se experimentalmente que essa força elástica (), tem intensidade diretamente proporcional à deformação () da mola, ou seja, que:

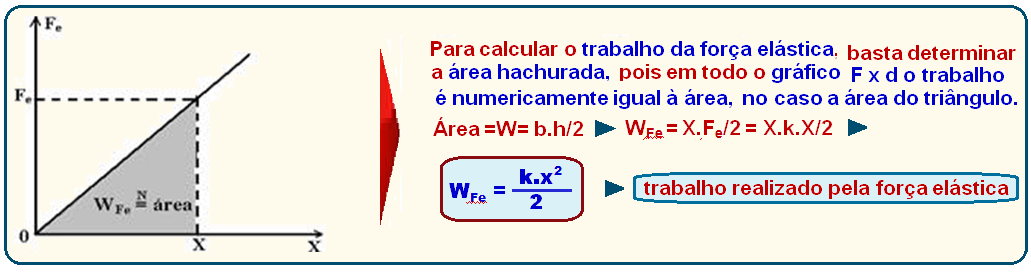
Na expressão acima, k é a constante elástica da mola. Como F_e é diretamente proporcional a X, o gráfico F_e3 x X será uma reta oblíqua.

O trabalho da força elástica será resistente (negativo) se a deformação X for forçada, ou seja, uma força externa estará alongando (esticando) ou comprimindo a mola e, nesse caso, o trabalho da força externa terá em cada ponto a mesma intensidade (módulo) que o trabalho da força elástica, mas que será positivo.

O trabalho da força elástica será motor (positivo), se não existir força externa, com a mola tendendo naturalmente à voltar à posição inicial (de equilíbrio).

O trabalho da força elástica, assim com o trabalho da força peso independe da trajetória e, por isso a força peso e força elástica são chamadas de forças conservativas.

Assim, em relação à posição de equilíbrio de uma mola, o trabalho realizado para comprimi-la por uma distância X é igual ao trabalho para distendê-la da mesma distância X.

Exercícios de vestibulares com resolução comentada sobre

Trabalho de diversos tipos de forças

01-(UFB) Um carrinho de massa 10kg encontra-se sobre um plano horizontal sob ação da força indicada na figura. O coeficiente de atrito entre o carrinho e o plano é 0,2. Determine o trabalho realizado por cada uma das forças que agem sobre o corpo, num deslocamento de 5m, quando ele se mover: (g=10m/s²).

a) Com velocidade constante.

b) Com aceleração de 3m/s².

02-(PUC-MG) Não realiza trabalho:

a) a força de resistência do ar

b) a força peso de um corpo em queda livre

c) a força centrípeta em um movimento circular uniforme

d) a força de atrito durante a frenagem de um veículo

e) a tensão no cabo que mantém um elevador em movimento uniforme.

03-(PUC-BA) A força de módulo 30N atua sobre um objeto formando um ângulo constante de 60^o com a direção do deslocamento do objeto. Dados: sen 60^o=√3/2, cos 60^o=1/2. Se d=10m, o trabalho realizado pela força , em joules, é igual a:

a) 300 b) 150√3 c) 150 d) 125 e) 100

04-(UCS-RS) Sobre um bloco atuam as forças indicadas na figura às quais o deslocam 2m ao longo do plano horizontal. A intensidade da força é F=100N.

Analise as afirmações:

I – O trabalho realizado pela força de atrito é positivo.

II – O trabalho realizado pela força vale 200J.

III- O trabalho realizado pela força peso é diferente de zero

IV - O trabalho realizado pela força normal é nulo.

Quais estão corretas?

a) apenas I e II

b) apenas I e III

c) apenas II e III

d) apenas II e IV

e) apenas III e IV

05-(PUC-MG) Considere um corpo sendo arrastado, com velocidade constante, sobre uma superfície horizontal onde o atrito não é desprezível. Considere as afirmações I, II e III a respeito da situação descrita.

I. O trabalho da força de atrito é nulo.

II. O trabalho da força peso é nulo.

III. A força que arrasta o corpo é nula.

A afirmação está INCORRETA em:

06-(Ufpe) Um carrinho com massa 1,0 kg, lançado sobre uma superfície plana com velocidade inicial de 8,0 m/s, se move em linha reta, até parar. O trabalho total realizado pela força de atrito sobre o objeto é, em J:

07-(UFB) Uma força horizontal , constante, de intensidade de 20N, é aplicada a um carrinho de madeira de massa igual a 2Kg, que, sob a ação dessa força, desloca-se sobre o tampo de uma mesa. Admitindo-se que o coeficiente de atrito cinético entre

o bloco e o tampo da mesa seja igual a 0,2, determine o trabalho realizado pela força resultante que atua ao longo da distância horizontal de 5m. (g=10m/s²)

08-(Uerj-RJ) Observe as situações a seguir, nas quais um homem desloca uma caixa ao longo de um trajeto AB de 2,5 m.

As forças F₁ e F₂ exercidas pelo homem nas duas situações, têm o mesmo módulo igual a 0,4 N e os ângulos entre suas direções e os respectivos deslocamentos medem q e 2q.

Se k é o trabalho realizado, em joules, por F₁, o trabalho realizado por F₂ corresponde a:

a) 2 k

b) k/2

c) (k² + 1)/2

d) 2k² - 1

09-(UFMG-MG) Um bloco movimenta-se sobre uma superfície horizontal, da esquerda para a direita, sob ação das forças mostradas na figura.

Pode-se afirmar que:

a) apenas as forças e realizam trabalho.

B) apenas a força realiza trabalho.

c) apenas a força realiza trabalho

d) apenas as forças e realizam trabalho

e) todas as forças realizam trabalho

10-(UFRN) Um bloco é arrastado sobre um plano horizontal, com o qual possui coeficiente de atrito m, sofrendo um deslocamento horizontal de módulo d. Sendo N a intensidade da força de reação normal da superfície sobre o bloco, o trabalho da força de atrito, nesse deslocamento, é:

a) -μN b) -μNd c) nulo d) μN e) μNd

11-(UNESP-SP) Um jovem exercita-se em uma academia andando e movimentando uma esteira rolante horizontal, sem motor.

Um dia, de acordo com o medidor da esteira, ele andou 40 minutos com velocidade constante de 7,2km/h e consumiu 300 quilocalorias.

a) Qual a distância percorrida pelo jovem? Qual o deslocamento do jovem?

Em um esquema gráfico, represente a esteira, o jovem e a força que ele exerce sobre a esteira para movimentá-la. Admitindo que o consumo de energia assinalado pela esteira é o trabalho realizado pelo jovem para movimentá-la, determine o módulo dessa força, suposta constante. Adote 1cal=4J.

12-(UFES) A força desloca o bloco da figura ao longo da reta AB. A componente de que executa trabalho é:

A componente de que executa trabalho é:

a) Ftgθ b) Fsenθ c) Fcosθ d) F(senθ + cosθ) e) F

13-(UFF-RJ) Uma força puxa um bloco de peso e atua segundo uma direção que forma com a horizontal um ângulo q. Esse bloco se desloca ao longo de uma superfície horizontal percorrendo uma distância x, conforme figura.

A força normal exercida pela superfície sobre o bloco e o trabalho realizado por essa força ao longo da distância x valem, respectivamente:

a) P; P_x

b) P; zero

c) P – Fsenθ; zero

d) P + Fsenθ; (P + Fsenθ).x

e) P - Fsenθ; (P - Fsenθ).x

Trabalho de uma força variável

14-(UNIFESP-SP) A figura representa o gráfico do módulo F de uma força que atua sobre um corpo em função do seu deslocamento x. Sabe-se que a força atua sempre na mesma direção e sentido do deslocamento.

Pode-se afirmar que o trabalho dessa força no trecho representado pelo gráfico é, em joules,

15-(Ufpel-RS) Um corpo de massa m se move ao longo do eixo x sob a ação de uma força, cujo módulo é representado no gráfico a seguir, em função do módulo do deslocamento. Tanto a força quanto o deslocamento x possuem a mesma direção e o mesmo sentido.

A partir da análise do gráfico, pode-se afirmar que o trabalho realizado pela força ao deslocar o corpo desde a origem até a posição x' é

16-(Ufpr-PR) Um engenheiro mecânico projetou um pistão que se move na direção horizontal dentro de uma cavidade cilíndrica. Ele verificou que a força horizontal F, a qual é aplicada ao pistão por um agente externo, pode ser relacionada à sua posição horizontal x por meio do gráfico abaixo. Para ambos os eixos do gráfico, valores positivos indicam o sentido para a direita, enquanto valores negativos indicam o sentido para a esquerda. Sabe-se que a massa do pistão vale 1,5 kg e que ele está inicialmente em repouso. Com relação ao gráfico, considere as seguintes afirmativas:

1. O trabalho realizado pela força sobre o pistão entre x = 0 e x = 1 cm vale 7,5 .10^-2J

2. A aceleração do pistão entre x = 1 cm e x = 2 cm é constante e vale 10 m/s².

3. Entre x = 4 cm e x = 5 cm, o pistão se move com velocidade constante.

4. O trabalho total realizado pela força sobre o pistão entre x = 0 e x = 7 cm é nulo.

a) Somente as afirmativas 1 e 2 são verdadeiras.

b) Somente as afirmativas 1 e 3 são verdadeiras.

c) Somente a afirmativa 3 é verdadeira.

d) Somente as afirmativas 2 e 4 são verdadeiras.

e) Somente as afirmativas 1, 2 e 3 são verdadeiras.

17- (UFSCAR-SP) Um bloco de 10kg movimenta-se em linha reta sobre uma mesa lisa em posição horizontal, sob ação de uma força variável que atua na mesma direção do movimento, conforme o gráfico abaixo.

O trabalho realizado pela força quando o bloco da origem até o ponto x=6m é:

18-(UEL-PR) Um corpo desloca-se em linha reta sob a ação de uma única força paralela à trajetória. No gráfico representa-se a intensidade (F) da força em função da distância percorrida pelo corpo (d).

Durante os 12m de percurso indicados no gráfico, qual foi o trabalho realizado pela força que atua sobre o corpo?

Trabalho da força peso

19-(PUC-RJ) Durante a aula de educação física, ao realizar um exercício, um aluno levanta verticalmente um peso com sua mão, mantendo, durante o movimento, a velocidade constante.

Pode-se afirmar que o trabalho realizado pelo aluno é:

a) positivo, pois a força exercida pelo aluno atua na mesma direção e sentido oposto ao do movimento do peso.

b) positivo, pois a força exercida pelo aluno atua na mesma direção e sentido do movimento do peso.

c) zero, uma vez que o movimento tem velocidade constante.

d) negativo, pois a força exercida pelo aluno atua na mesma direção e sentido oposto ao do movimento do peso.

e) negativo, pois a força exercida pelo aluno atua na mesma direção e sentido do movimento do peso.

20-(FUVEST-SP) Quando uma pessoa de 70kg sobe 2m numa esca, ele realiza um trabalho cuja ordem de grandeza é: (g=10m/s²)

21-(UNICAMP-SP) “ Era uma vez um povo que morava numa montanha onde havia muitas quedas d’água. O trabalho era árduo e o grão era moído em pilões (figura da direita). (---) Um dia, quando um jovem suava ao pilão, seus olhos bateram na queda d’água onde se banhava diariamente. (---) Conhecia a força da água, mais poderosa que o braço de muitos homens. (---) Uma faísca lhe iluminou a mente: não seria possível domesticá-la, ligando-a ao pilão?” Rubem Alves, Filosofia da Ciência: introdução ao jogo e suas regras. São Paulo, Brasiliense, 1987.)

Essa história ilustra a invenção do pilão d’água ( monjolo - figura da esquerda).

Podemos comparar o trabalho realizado por esse monjolo de massa igual a 30kg com o trabalho realizado por um pilão manual de massa igual a 5kg. Nessa comparação desconsidere as perdas e considere g=10m/s².

a) Um trabalhador ergue o pilão manual e deixa-o cair de uma altura de 60cm. Qual o trabalho realizado em cada batida?

b) O monjolo cai sobre grãos de uma altura de 2m. O pilão manual é batido a cada 2s, e o monjolo, a cada 4s. Quantas pessoas seriam necessárias para realizar com o pilão manual o mesmo trabalho que o monjolo, no mesmo intervalo de tempo?

22-(UNIRIO-RJ) Três corpos idênticos de massa M deslocam-se entre dois níveis como mostra a figura. A caindo livremente; B deslizando ao longo de um tobogã e C descendo uma rampa, sendo, em todos os movimentos, desprezíveis as forças dissipativas.

Com relação ao módulo do trabalho (W) realizado pela força peso dos corpos, pode-se afirmar que:

a) W_C > W_B > W_A

b) W_C = W_B > W_A

c) W_C > W_B = W_A

d) W_C = W_B = W_A

e) W_C < W_B > W_A

23-(UFRN-RN) Oscarito e Ankito, operários de construção civil, recebem a tarefade erguer, cada um deles, um balde cheio de concreto, desde o solo até o topo de dois edifícios de mesma altura, conforme ilustra a figura abaixo. Ambos os baldes têm a mesma massa.

Oscarito usa um sistema com uma polia fixa e outra móvel e Ankito um sistema com apenas uma polia fixa. Considere que o atrito, as massas das polias e as massas das cordas são desprezíveis e que cada balde sobe com velocidade constante.

Nessas condições, para erguer seu balde, o trabalho realizado pela força exercida por Oscarito é:

a) menor do que o trabalho que a força exercida por Ankito realiza, e a força mínima que ele que ele exerce é menor que a força mínima que Ankito exerce.

b) igual ao trabalho que a força exercida por Ankito realiza, e a força mínima que ele que ele exerce é maior que a força mínima que Ankito exerce.

c) menor do que o trabalho que a força exercida por Ankito realiza, e a força mínima que ele que ele exerce é maior que a força mínima que Ankito exerce.

d) igual ao trabalho que a força exercida por Ankito realiza, e a força mínima que ele que ele exerce é menor que a força mínima que Ankito exerce.

24-(Uerj-RJ) Um produto vendido no supermercado é recebido em caixas de papelão contendo 16 embalagens de volume igual a 1.312,5 cm³ cada.

As massas de cada embalagem, do seu conteúdo e da caixa de papelão são, respectivamente, 10 g, 1.000 g e 100 g.

O produto é entregue por um caminhão, cuja carroceria está a 1,5 m de altura em relação ao chão, e descarregado com o auxílio de uma empilhadeira.

a) Calcule a densidade do produto, sabendo que, em cada embalagem, 62,5 cm³ estão vazios.

b) Considere o descarregamento de uma única caixa que se encontra sobre o piso da carroceria. Determine o módulo do trabalho realizado pela força que a base da empilhadeira faz sobre essa caixa. Considere g=10m/s²

25-(UFPE) Um bloco de pedra, de 4,0 toneladas, desce um plano inclinado a partir do repouso, deslizando sobre rolos de madeira.

Sabendo-se que o bloco percorre 12 m em 4,0 s, calcule o trabalho, em kJ, realizado sobre o bloco pela força peso e pela resultante no intervalo de tempo considerado. (g=10m/s²)

26-(UFMS) A figura mostra três possíveis maneiras de erguer um corpo de massa M a uma altura h.

Em (I), ela é erguida diretamente; em (II), é arrastada sobre um plano inclinado de 30°, com atrito desprezível e, em (III), através de um arranjo de duas roldanas, uma fixa e outra móvel.

Admitindo que o corpo suba com velocidade constante, assinale a(s) alternativa(s) correta(s).

(01) O módulo da força exercida pela pessoa, na situação (III), é a metade do módulo da força exercida na situação (I).

(02) O módulo da força exercida pela pessoa, na situação (II), é igual ao da força exercida na situação (III).

(04) Os trabalhos realizados pela pessoa, nas três situações, são iguais.

(08) Na situação (III), o trabalho realizado pela pessoa é metade do trabalho realizado pela pessoa na situação (I).

27-(UFF-RJ) Um homem de massa 70kg sobe uma escada, do ponto A ao ponto B, e depois desce, do ponto B ao ponto C, conforme indica a figura.

O trabalho realizado pelo peso do homem desde o ponto A até o ponto C foi de: (g=10m/s²).

a) 5,6.10³J

b) 1,4.10³ J

c) 5,6.10² J

d) 1,4.10²J

e) zero

Trabalho da força elástica

28-(Ufsm-RS) O gráfico representa a elongação de uma mola, em função da tensão exercida sobre ela.

O trabalho da tensão para distender a mola de 0 a 2 m é, em J,

29-(UFB) Considere um sistema constituído por uma mola e um pequeno carrinho. Uma pessoa estica vagarosamente (com velocidade constante) o sistema, a partir do comprimento inicial (sem deformação) no ponto A, passando pelo ponto B até chegar ao ponto C, quando é abandonado e naturalmente retorna ao ponto A. A constante elástica da mola é k=20N/m e as abscissas dos pontos A, B e C, localizados sobre uma reta horizontal orientada para a esquerda estão representadas na figura abaixo.

Pede-se:

a) O comprimento natural da mola (sem deformação).

b) Esquematize o gráfico do módulo de em função da deformação .

c) Calcule o trabalho realizado no deslocamento de B para C pela força elástica e pela força externa aplicada pela pessoa.

30-(UFLavras-MG) Em uma estação ferroviária existe uma mola destinada a parar sem dano o movimento de locomotivas.

Admitindo-se que a locomotiva a ser parada tem velocidade de 7,2km/h, massa de 7,0.10⁴kg, e a mola sofre uma deformação de 1m, qual deve ser a constante elástica da mola e o módulo do trabalho realizado pela força exercida por ela para parar a locomotiva?

31-(CPS-SP) A pesca é um dos lazeres mais procurados. Apetrechos e equipamentos utilizados devem ser da melhor qualidade. O fio para pesca é um exemplo. Ele deve resistir à força que o peixe faz para tentar permanecer na água e também ao peso do peixe.

Supondo que o peixe seja retirado, perpendicularmente em relação à superfície da água, com uma força constante, o trabalho

a) será resistente, considerando apenas a força peso do peixe.

b) da força resultante será resistente, pois o peixe será retirado da água.

c) será indiferente, pois a força, sendo constante, implicará em aceleração igual a zero.

d) poderá ser resistente em relação à força que o pescador aplicará para erguer o peixe.

e) de qualquer força aplicada no peixe será nulo, pois força e deslocamento são perpendiculares entre si.

32-(UNICAMP-SP) A produção de fogo tem sido uma necessidade humana há milhares de anos. O

homem primitivo provavelmente obtinha fogo através da produção de calor por atrito. Mais recentemente, faíscas elétricas geradoras de combustão são produzidas através do chamado efeito piezelétrico.

a) A obtenção de fogo por atrito depende do calor liberado pela ação da força de atrito entre duas superfícies, calor que aumenta a temperatura de um material até o ponto em que ocorre a combustão. Considere que uma superfície se desloca 2,0 cm em relação à outra, exercendo uma força normal de 3,0 N. Se o coeficiente de atrito cinético entre as superfícies vale μ_c = 0,60, qual é o trabalho da força de atrito?

b) Num acendedor moderno, um cristal de quartzo é pressionado por uma ponta acionada por molas. Entre as duas faces do cristal surge então uma tensão elétrica, cuja dependência em função da pressão é dada pelo gráfico abaixo. Se a tensão necessária para a ignição é de 20 kV e a ponta atua numa área de 0,25 mm², qual a força exercida pela ponta sobre o cristal?

33-(UFMS-MS) O condutor de um veículo, em uma pista plana e retilínea, aguarda em repouso o sinal abrir em um semáforo A. No mesmo instante em que o sinal abre, ele coloca o veículo em movimento até outro semáforo B, que está na esquina

seguinte. Como o semáforo B está fechado, então o condutor diminui a velocidade do veículo até atingir o repouso ao chegar no semáforo B, e assim permanece por mais um tempo aguardando o sinal verde para continuar seu trajeto. A linha contínua, da figura a seguir, representa o gráfico da velocidade do veículo em função do tempo, desde o instante em que o semáforo A abriu até o instante em que o semáforo B também abriu, o que totaliza um intervalo de 30 segundos. Analise o percurso no intervalo de tempo de 0 a 30 s e, com fundamentos na mecânica, assinale a(s) proposição(ões) correta(s).

01) O módulo da força resultante que acelerou o veículo, entre 0 e 4 s, é igual à metade do módulo da força resultante que freou o veículo, entre 7 s e 9 s.

02) O veículo percorreu uma distância igual a 75 m, entre 0 e 30 s.

04) O trabalho total realizado sobre o veículo no percurso não é nulo.

08) A distância percorrida pelo veículo, entre 0 e 4 s, é igual à distância percorrida pelo veículo entre 7 s e 9 s.

16) Se os semáforos estivessem calibrados para uma “onda verde”, o veículo percorreria o percurso com velocidade constante e igual a 45 km/h em 6 s.

34-(FGV-SP) Contando que ao término da prova os vestibulandos da GV estivessem loucos por um docinho, o vendedor de

churros levou seu carrinho até o local de saída dos candidatos. Para chegar lá, percorreu 800 m, metade sobre solo horizontal e a outra metade em uma ladeira de inclinação constante, sempre aplicando sobre o carrinho uma força de intensidade 30 N, paralela ao plano da superfície sobre a qual se deslocava e na direção do movimento. Levando em conta o esforço aplicado pelo vendedor sobre o carrinho, considerando todo o traslado, pode-se dizer que,

a) na primeira metade do trajeto, o trabalho exercido foi de 12 kJ, enquanto que, na segunda metade, o trabalho foi maior.

b) na primeira metade do trajeto, o trabalho exercido foi de 52 kJ, enquanto que, na segunda metade, o trabalho foi menor.

c) na primeira metade do trajeto, o trabalho exercido foi nulo, assumindo, na segunda metade, o valor de 12 kJ.

d) tanto na primeira metade do trajeto como na segunda metade, o trabalho foi de mesma intensidade, totalizando 24 kJ.

e) o trabalho total foi nulo, porque o carrinho parte de um estado de repouso e termina o movimento na mesma condição.

35-(PUC-RJ) O Cristo Redentor, localizado no Corcovado, encontra-se a 710 m do nível no mar e pesa 1.140 ton.

Considerando-se g = 10 m/s², é correto afirmar que o trabalho total realizado para levar todo o material que compõe a estátua até o topo do Corcovado foi de, no mínimo:

a) 114.000 kJ

b) 505.875 kJ

c) 1.010.750 kJ

d) 2.023.500 kJ

e) 8.094.000 kJ

36-(UERJ-RJ) Um objeto é deslocado em um plano sob a ação de uma força de intensidade igual a 5 N, percorrendo em linha

reta uma distância igual a 2 m. Considere a medida do ângulo entre a força e o deslocamento do objeto igual a 15º, e T o trabalho realizado por essa força. Uma expressão que pode ser utilizada para o cálculo desse trabalho, em joules, é T= 5 x 2 x senθ .

Nessa expressão, θ equivale, em graus, a:

37-(UECE-CE) Em um corredor horizontal, um estudante puxa uma mochila de rodinhas de 6 kg pela

haste, que faz 60^o com o chão. A força aplicada pelo estudante é a mesma necessária para levantar um peso de 1,5 kg, com velocidade constante. Considerando a aceleração da gravidade igual a 10 m/s2, o trabalho, em Joule, realizado para puxar a mochila por uma distância de 30 m é

a) Zero.

b) 225,0.

c) 389,7.

d) 900,0.

38-(UERJ-RJ) Um homem arrasta uma cadeira sobre um piso plano, percorrendo em linha reta uma distância de 1 m.

Durante todo o percurso, a força que ele exerce sobre a cadeira possui intensidade igual a 4 N e direção de 60° em relação ao piso. O gráfico que melhor representa o trabalho T, realizado por essa força ao longo de todo o deslocamento d, está indicado em:

39-(UFV-MG) Analise as afirmativas a seguir:

I. O trabalho total realizado sobre um bloco em um deslocamento não nulo, quando atua sobre ele uma força resultante não nula, não pode ser igual a zero.

II. Um bloco, ao ser puxado por uma corda, exercerá uma força contrária na corda, de acordo com a 3ª lei de Newton. Então, o trabalho realizado pela força que a corda faz no corpo é necessariamente igual a zero.

III. Sempre que o trabalho realizado pela força resultante em um bloco é nulo, sua energia cinética se mantém constante.

Está CORRETO o que se afirma em:

a) I, apenas.

b) II, apenas.

c) III, apenas.

d) I, II e III.

40-(FGV-RJ) No ano de 2008, a usina hidrelétrica de Itaipu produziu 94.684.781 MWh (megawatts-hora) de energia.

Se o poder calorífico do petróleo é igual a 0,45 x 10⁸ J/kg, a massa de petróleo necessária para fornecer uma quantidade de energia igual à produzida por Itaipu em 2008 é, aproximadamente, igual a: (Dados: 1 W = 1J/s; 1 MW = 10⁶ W e 1tonelada=10³kg)

a) 2 mil toneladas.

b) 45 mil toneladas.

c) 450 mil toneladas.

d) 7,5 milhões de toneladas.

e) 95 milhões de toneladas.

41-(ENEM-MEC) Deseja-se instalar uma estação de geração de energia elétrica em um município localizado no interior de um pequeno vale cercado de altas montanhas de difícil acesso. A cidade é cruzada por um rio, que é fonte de água para consumo,

irrigação das lavouras de subsistência e pesca. Na região, que possui pequena extensão territorial, a incidência solar é alta o ano todo. A estação em questão irá abastecer apenas o município apresentado.

Qual forma de obtenção de energia, entre as apresentadas, é a mais indicada para ser implantada nesse município de modo a causar o menor impacto ambiental?

a) Termelétrica, pois é possível utilizar a água do rio no sistema de refrigeração.

b) Eólica, pois a geografia do local é própria para a captação desse tipo de energia.

c) Nuclear, pois o modo de resfriamento de seus sistemas não afetaria a população.

d) Fotovoltaica, pois é possível aproveitar a energia solar que chega à superfície do local.

e) Hidrelétrica, pois o rio que corta o município é suficiente para abastecer a usina construída.

42-(UDESC-SC) Na figura há uma representação esquemática de um circuito composto por uma

bateria de 12 Volts, fios e uma lâmpada incandescente. Analise o circuito e assinale a alternativa que contém, respectivamente, um reservatório de energia, um transformador de energia e um modo de transferência de energia.

a) bateria, calor, luz

b) ambiente, lâmpada, trabalho elétrico

c) lâmpada, bateria, calor

d) bateria, trabalho elétrico, lâmpada

e) bateria, trabalho elétrico, fios

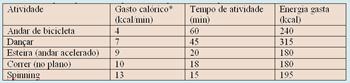
43-(CPS) Uma das dúvidas mais frequentes das pessoas sobre atividade física é o gasto calórico dos exercícios. Quem deseja emagrecer quer saber exatamente quanto gasta em determinada atividade e quanto consome em determinada refeição. Este cálculo depende de muitos fatores. O gasto calórico dos exercícios varia de pessoa para pessoa, dependendo do metabolismo de cada uma delas (da genética e do biotipo), do tempo e da intensidade do exercício. Assim, o gasto calórico, numa atividade específica, difere entre uma pessoa de 90 kg e uma de 50 kg.

A tabela a seguir mostra o gasto calórico aproximado de algumas atividades:

(Valéria Alvin Igayara de Souza Disponível em: http://cyberdiet.terra.com.br/gasto-calorico-dos-exercicios-3-1-2-326.html Acesso em: 27.08.2010. Adaptado)

Se uma pessoa de 60 kg comer uma fatia de pizza de mozzarella (muçarela) que tem 304 quilocalorias, se arrepender e desejar queimá-las, deverá de acordo com essa tabela, em princípio,

a) dançar por cerca de 45 minutos.

b) fazer spinning por cerca de 15 minutos.

c) andar de bicicleta por cerca de 60 minutos.

d) correr em terreno plano por cerca de 18 minutos.

e) andar acelerado na esteira por cerca de 20 minutos.

44-(UPE-PE) Um corpo de massa m desliza sobre o plano horizontal, sem atrito ao longo do eixo AB, sob a ação de duas forças F₁ e F₂, de acordo com a figura a seguir.

A força F₁ é constante, tem módulo igual a 10 N e forma com a vertical um ângulo θ= 30^o.

A força F₂ varia de acordo com o gráfico a seguir:

Dado; sen30^o=cos60^o=1/2

O trabalho realizado pelas forças F₁ e F₂, para que o corpo sofra um deslocamento de 0 a 4m, vale, em joules:

A) 20

B) 47

C) 27

D) 50

E) 40

45-(UERJ-RJ)

Uma pessoa empurrou um carro por uma distância de 26 m, aplicando uma força F de mesma direção e sentido do deslocamento desse

carro. O gráfico abaixo representa a variação da intensidade de F, em newtons, em função do deslocamento d, em metros.

Desprezando o atrito, o trabalho total, em joules, realizado por F, equivale a:

46-(UNESP-SP)

Uma pessoa, com 80 kg de massa, gasta para realizar determinada atividade física a mesma quantidade de energia que gastaria se subisse diversos degraus de uma escada, equivalente a uma distância de 450 m na vertical, com velocidade constante, num local

onde g = 10 m/s².A tabela a seguir mostra a quantidade de energia, em joules, contida em porções de massas iguais de alguns

alimentos. Considerando que o rendimento mecânico do corpo humano seja da ordem de 25%, ou seja, que um quarto da energia química ingerida na forma de alimentos seja utilizada para realizar um trabalho mecânico externo por meio da contração e expansão de músculos, para repor exatamente a quantidade de energia gasta por essa pessoa em sua atividade física, ela deverá ingerir 4 porções de

(A) castanha de caju.

(B) batata frita.

(C) chocolate.

(D) pizza de mussarela.

(E) espaguete.

47-(UNICAMP-SP)

As eclusas permitem que as embarcações façam a transposição dos desníveis causados pelas barragens. Além de ser

uma monumental obra de engenharia hidráulica, a eclusa tem um funcionamento simples e econômico. Ela nada mais é do que um elevador de águas que serve para subir e descer as embarcações. A eclusa de Barra Bonita, no rio Tietê, tem um desnível de aproximadamente 25 m.

Qual é o aumento da energia potencial gravitacional quando uma embarcação de massa m = 1,2.10⁴ kg é elevada na eclusa?

Resolução comentada dos exercícios de vestibulares sobre

Trabalho de diversos tipos de forças

01- a) Colocando todas as forças que agem sobre o carrinho

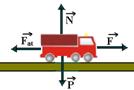
Cálculo da intensidade da força de atrito --- F_at=m.N=m.P=m.m.g --- F_at=0,2.10.10 --- F_at=20N

Se o carrinho está com velocidade constante, a força resultante sobre ele é nula e F=F_at --- F=20N

Trabalho de cada força:

W_F=F.d.cosα --- W_F=20.5.cos0^o --- W_F=100.(1) --- W_F=100J (positivo, motor)

W_Fat=F_at.d.cos α --- W_Fat=20.5.cos 180^o --- W_Fat=100.(-1) --- W_Fat= -100J (negativo, resistente)

W_N=W_P=P.d.cos α α =P.d.cos90^o=P.d.0=0 --- W_N=W_P=0(perpendiculares ao deslocamento)

O trabalho da força resultante é nulo, pois F_R=0.

b) F_at=20N --- a=3m/s² --- F=m.a --- F=10.3 --- F=30N

Trabalho de cada força:

W_F=F.d.cos α --- W_F=30.5.cos0^o --- W_F=150.(1) --- W_F=150J (positivo, motor)

W_Fat=F_at.d.cos α --- W_Fat=20.5.cos 180^o --- W_Fat=100.(-1) --- W_Fat= -100J (negativo, resistente)

W_N=W_P=P.d.cos α =P.d.cos90^o=P.d.0=0 --- W_N=W_P=0 (perpendiculares ao deslocamento)

Trabalho da força resultante --- W_FR=150 – 100 + 0 + 0 --- W_FR=50J ou W_FR=F_R.d.cosa=(30 - 20).5.cos0^o --- W_FR=50.(1) --- W_FR=50J

02- O trabalho realizado pela força resultante centrípeta é sempre nulo, pois ela é sempre perpendicular à velocidade (que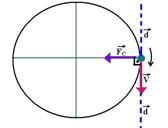

é sempre tangente em cada ponto da circunferência) e consequentemente ao deslocamento . R- C

03- W=F.d.cos α --- W=30.10.1/2 --- W=150J R- C

04- W_F=F.d.cos0^o --- W_F=100.2.(1) --- W_F=200J e o trabalho da força de atrito é negativo (a=180^o).

R- D

05- I- O trabalho da força de atrito não é nulo, é negativo – incorreta II- É nulo sim (a=90^o) – correta III- Não é nula, é igual ao F_at, pois está com velocidade constante e F_R=0 – incorreta R- B

06- Como ele não está sendo impulsionado, puxado ou empurrado, a força resultante sobre ele é a própria força de atrito.

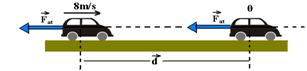
F_R=F_at=m.a --- V²=V_O² + 2.a.d --- 0²=8² - 2.a.d --- a.d= - 32 --- F_at=m.a --- W_Fat=F_at.d.cos0^o=m.a.d.(1) --- W_Fat=1.(-32).1

W_Fat=-32J R- D

07- F_at=m,N=m.P=0,2.2.10 --- F_at=4N --- F_R=F – F_at=20 – 4 --- F_R=16N --- W_FR=F_R.d.cos0^o=16.5.(1) --- W_FR=80J

08- Força F₁ --- W_F1=F_1..d.cosθ --- W_F1=0,4.2,5.cosθ --- W_F1=cosθ=k --- Força F_2
---W_F2=F₂.d.cos2θ --- W_F2=0,4.2,5.cos2θ --- W_F2=cos2θ --- cos2θ =cos²θ - sen²θ --- cos2θ=k² – (1 – cos²θ) --- cos2θ = k² – 1 + k² --- cos2q = 2k² – 1 --- W_F2=cos2q=2k² – 1 R-D

09- R- D (veja teoria)

10- F_at=mN --- W_Fat=F_at.d.cos180^o --- W_Fat=-mNd R- B

11- a) Distância percorrida DS --- V=DS/Dt --- 2=DS/2.400 --- DS=4.800m essa seria a distâcia que ele percorreria se estivesse andando numa estrada reta, plana e horizontal.

O deslocamento que é uma grandeza vetorial é nulo em relação a um referencial (qualquer ponto) fixo no solo.

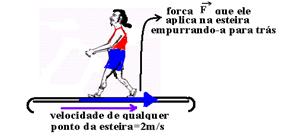
Consumo de calorias em joules --- 1 cal – 4J --- 300.000cal – xJ --- x=4X300.000 --- x=1,2.10⁶J --- esse consumo de calorias é o próprio trabalho --- W=F.DS.cos0^o --- 1,2.10⁶=F.4.400.(1) --- F=250N

12- Observe nas figuras abaixo que podemos decompor em e , sendo que quem realmente realiza trabalho é F_X=Fcosα,

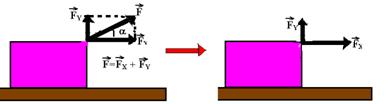
pois é a parcela de que efetivamente influi no deslocamento, tendo a direção e o sentido dele. Já a parcela que é perpendicular ao deslocamento não realiza trabalho, pois não influi no deslocamento.

13- Decompondo a força em e em --- F_X=Fcosθ --- F_Y=Fsenθ --- equilíbrio na vertical --- F + N = P --- N=P - F_Y

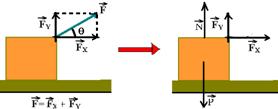
N = P - Fsenθ --- e W_N=0 (θ=90^o) R- C

14- W=b.h/2 --- W=1.10/2 --- W=5J R- C 15- W=b.h/2 --- W=x’.F’/2 --- R- A

16-1- W=b.h/2=1.10^-2.15/2 --- W=7,5.10^-2J verdadeira 2- F é constante e vale F=15N --- F=ma --- 15=1,5.a --- a=10m/s²

Verdadeira 3- correta, se F=0 ele está em equilíbrio dinâmico (MRU) 4- W=1.10^-2.15/2 + 1.10^-2.15 + 2.10^-2.15/2 –

2.10^-2.12/2 --- W=25,5.10^-2J Falsa --- R- E

17- W=1.2/2 + 1.2 + 1.2/2 – 2.2/2 + 0 --- W=2J

18- W=(12 + 4).10/2 + 12.5 --- W=140J R-C

19- R- B (veja teoria)

20- W=m.g.h=70.10.2 --- W=1.400J --- ordem de grandeza --- 1,4.10³ J --- 1,4 está abaixo de 5 e se transforma em 1 ---

W=1.10³ J R- C

21- a) peso do pilão manual --- P=m.g=5.10=50N --- W=P.h=50.0,6 --- W=30J

b) peso do monjolo --- P=m.g=30.10=300N --- trabalho em uma queda --- W=P.h=300.2 --- W=600J

Considerando esse intervalo de tempo como 1s --- manual- W=15J --- monjolo – W=150J

Regra de três --- 15J – 1 pessoa --- 150J – n pessoas --- n=10 pessoas

22- R- D (veja teoria)

23- O trabalho realizado (energia transferida) para elevar o mesmo balde a uma mesma altura com velocidade constante é o mesmo para Oscarito e Ankito, mas a força mínima exercida por Oscarito é menor, já que o deslocamento é maior (no caso, a polia móvel dobra o deslocamento e reduz a força à metade) --- R- D

24- a) densidade do produto=massa do produto/volume do produto --- d=1.000/(1.312,5 – 62,5) --- d=0,8g/cm³

b) massa total de cada caixa – m=10 + 1.000 + 100=1.110g=1,11kg --- peso de cada caixa – P=m.g=1,11.10 --- P=11,1N

W=P.h --- W=11,1.1,5 --- W=16,65J

25- Trabalho do peso

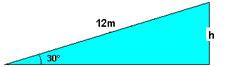
sen30^o=h/12 --- 1/2=h/12 --- h=6m --- W_P=P.h=m.g.h=4.10^3..10.6 --- W_P=240kJ

Trabalho da resultante --- ∆S=d=V_o.t + a.t²/2 --- 12=0.4 + a.16/2 --- a=1,5m/s² --- F_R=m.a=4.10³.1,5 ---

F_R=6.10³N --- W_FR=F_R.d.cos0^o=6.10³.12.(1) --- W_FR=72kJ

26-01- Correta – a polia da direita (móvel) divide a força aplicada pela metade

02- Correta – como a velocidade é constante o corpo está em equilíbrio --- fig. I --- F=P --- fig. 2 --- F=Psen30^o=P/2

04- Correta – O trabalho da força peso independe da trajetória

08- Falsa – vide 04

Soma das corretas 07

27- De A para B --- W_AB= -m.g.h=- 70.10.0,3 --- W_AB= - 2.10 J --- De B para C --- W_BC=+m.g.h=+70.10.0,5 --- W_BC= 350 J

W_total= - 2.10 + 3.50 --- W_total= 1.40 J ou W_total= 1,4.10² J

ou W_AC=m.g.(h_BC – h_AB)=70.10.(0,5 – 0,3) --- W_AC=1,4.10²J R- D

28- O trabalho realizado é numericamente igual à área --- W=b.h/2=2.100/2 --- W=100 J R- B

29- a) 8cm

b) A- F_e=k.X=20.0 --- F_eA=0 --- F_eB=20.0,08 --- Fe_B=1,6N --- F_eC=20.0,16 --- F_eC=3,2N

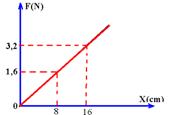
c) Como a força é variável --- W_Fe=área do trapézio=(B + b).h/2=(3,2 + 1,6).(8.10^-2)/2 --- W_Fe= - 0,192 J (negativo, forçado, F_e é contrário ao deslocamento)

W_F tem o mesmo valor, mas é positivo (a favor do deslocamento) --- W_F=0,192 J.

30- V_o=7,2/3,6=2m/s -- V=0 -- DS=X=1m --- Torricelli --- V²=V_o² + 2.(-a).X --- 0 = 4 +2.a --- a=2m/s² --- F_R=F_e=m.a --- F_e=7,0.10⁴.2 --- F_e=14.10⁴N --- F_e=k.x --- 14.10⁴=k.1 --- k=14.10⁴N/m --- W_Fe=k.X²/2=14.10⁴.1²/2 --- W_Fe=7.10⁴J

31- Sobre o peixe agem duas forças --- força de tração (que o pescador aplica para erguer o peixe, vertical e para cima) e o peso do peixe (vertical e para baixo) --- como o deslocamento é para cima e o peso do peixe é para baixo, eles possuem sentidos contrários e o trabalho da força peso é resistente (contrário ao deslocamento) --- R- A

32- a) O trabalho da força de atrito é dado por --- W = F_at.d.cos180° --- W = m.N.d.(-1) --- W = - 0,60.3.2.10^-2 --- W = - 3,6.10^-2 J

b) Pela leitura do gráfico dado temos que na tensão de 20 kV = 2.104 V tem-se uma pressão de 2.10⁸ N/m² --- pressão =força/área

Força = pressão.área --- Força = 2.10⁸.0,25.10^-6 --- F= 50 N

33- (01) Correta --- entre 0 e 4s --- a=(V – V_o)/(t – t_o)=(45 – 0)/(4 – 0) --- a_I=11,25km/s² --- entre 7s e 9s --- a=(V – V_o)/(t – t_o)=(0 – 45)/(9 – 7) --- a_II=22,5km/s² --- como a massa é a mesma (mesmo carro) e F_R=ma --- F_RI=m.11,25 --- F_RII=m.22,5 ---

F_RII=2F_RI.

(02) Correta --- no gráfico v ´ t a distância percorrida é obtida pela “área” entre a linha do gráfico e o eixo do tempo --- área do trapézio --- ΔS=(B + b).h/2=(9 + 3)/2.(45/3,6) --- ΔS=75m.
(04) Errada --- o trabalho total (entenda-se: trabalho da resultante) é igual à variação da energia cinética --- como a velocidade final é igual à inicial, ambas nulas, o trabalho total é nulo.

(08) Errada --- no gráfico, a “área” do triângulo de 0 a 4 s é o dobro da “área” do triângulo de 7 a 9 s --- portanto, a distância percorrida de 0 a 4 s é o dobro da distância percorrida de 7 a 9 s.

(16) Correta --- D = v Dt --- 75=(45/3,6).Δt --- Dt = 6s.

R- (01+ 02 + 16)= 19

34- Dados --- F = 30 N --- DS = 800 m --- o trabalho (W) de uma força constante é dado pela expressão --- W_F=F.d.cosα --- sendo a força paralela ao deslocamento --- a = 0°, cos a = 1 --- W_F=30.(800) = 24.000 J = 24 kJ --- R- D

35- Dados --- m = 1.140 ton = 1,14 ´ 10⁶ kg --- h = 710 m --- g = 10 m/s² --- W_F=m g h = (1,14.10⁶) (10) (710) = 8,094.10⁹ J = 8.094.000.10³ J --- W_F=8.094.000 kJ --- R- E

36- Dados --- F = 5 N --- d = 2 m --- a = 15° --- o enunciado nos permite construir a figura abaixo:

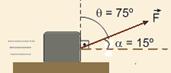
O trabalho de uma força é dado pelo trabalho de sua componente paralela ao deslocamento --- T = F d cos a.

Porém, a e q são complementares --- sen q = cos a --- T = F d cos a = F d sen q --- substituindo os valores dados ---

T = 5.2.sen 75° --- assim, q = 75°. --- R- D

37- Dados --- m₁ = 6 kg --- m₂ = 1,5 kg --- g = 10 m/s² --- DS = 30 m --- a = 60° --- se a força é a necessária para levantar o corpo de massa m₂ com velocidade constante, então a intensidade dessa força é --- F = P₂ = m₂ g = 15 N --- trabalho realizado (W) para arrastar a mochila --- W = F.DS.cos 60° = (15).(30).(0,5) --- W = 225 J --- R- B

38- O trabalho de força constante é calculado pela expressão --- T = F d cos a --- ela mostra que o trabalho (T) de força constante é diretamente proporcional ao deslocamento (d) --- portanto, o gráfico T = f (d) é uma reta que passa pela origem --- para os valores fornecidos --- T = 4 (1) cos 60° = 4 (0,5) --- T = 2 J --- R- D

R- D

39- Analisemos cada uma das afirmações:

(I) Errada --- W=F_R.d.cosα --- se α=90^o --- cos90^o=0 --- W=0

(II) Errada --- A 3ª lei de Newton afirma também que essas forças agem em corpos diferentes, portanto não se equilibram.

(III) Correta --- É exatamente o que afirma o teorema da energia cinética: “o trabalho da resultante das forças que agem num corpo é igual à variação de sua energia cinética.” Portanto, se o trabalho é nulo, a energia cinética se mantém constante.

R- C

40- Dados --- E = 94.684.781 MWh @ 9,5 ´ 10⁷ MWh = 9,5 ´ 10¹³ Wh --- L = 0,45 ´ 10⁸ J/kg --- transformando essa quantidade de energia em joules --- E = 9,5 ´ 10¹³ Wh = (9,5 ´ 10¹³ W) ´(3,6 ´ 10³ s) = 3,4 ´ 10¹⁷ J --- para o petróleo --- E = m L --- m =E/L=3,4x10¹⁷/0,45x10⁸ = 7,5 ´ 10⁹ kg = 7,5 ´ 10⁶ toneladas --- m = 7,5 milhões de toneladas --- R- D

41- O enunciado exige menor impacto ambiental. Já que a incidência solar na região é alta, a melhor forma para obtenção de energia é a fotovoltaica --- R- D

42- Reservatório de energia --- bateria e meio ambiente;

Transformador de energia --- bateria e lâmpada;

Modo de transferência de energia --- realizando trabalho elétrico sobre os elétrons-livres no interior do fio condutor

R- B

43- A tabela mostra a energia gasta em cada uma das atividades, dentro do tempo especificado em cada uma das proposições, destacando aquela que mais se aproxima do gasto de 304 quilocalorias.

R- A

44- A parcela de F₁ que influi no deslocamento horizontal vale F₁’=F₁cos (90^o – 30^o) --- F₁’=10.1/2=5N --- para que o trabalho seja fornecido pela área, no eixo vertical a força deve ser a força resultante, cujos valores são fornecidos no gráfico abaixo ---

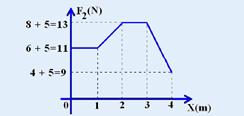
O trabalho total realizado pela força resultante é numericamente igual à soma das áreas --- W=(1.11) + ((13 + 11).1/2 + ((1.13) + (13 + 9).1/2 --- W_FR=47J --- R- B

45-O trabalho da força resultante com ela atuando na mesma direção e sentido do deslocamento é numericamente igual à área entre a reta representativa e o eixo do deslocamento --- W=área do triângulo=b.h/2=26.12/2 --- W=156J --- R- D

46-O trabalho realizado pela força peso da pessoa ao subir as escadas independe da trajetória e é, numericamente igual à variação

de sua energia potencial gravitacional --- W=∆E_p=m.g.∆h=80.10.450 --- W=360 000J=360kJ --- são ingeridas 4 porções e o rendimento de cada uma é 25% (1/4), logo, a energia química de uma porção é convertida em trabalho --- W=360kJ --- R- E

47- Considerando o nível da jusante (parte mais baixa da água) nulo, o da montante (parte mais elevada da água) será

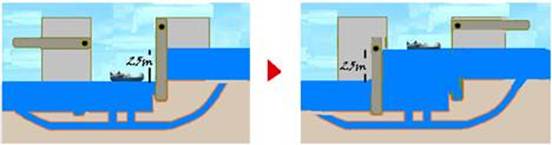
de 25m --- ∆E_pg=m.g.∆h=1,2.10⁴.10.(25 – 0) --- ∆E_pg=300.10⁴J=3,0.10⁶J --- R- D