Tipos de transformações gasosas

O estado de qualquer gás é caracterizado pelos valores de três grandezas que são o volume (V), a pressão (P) e a temperatura (T).

São muito comuns as transformações em que ocorrem duas das variáveis de estado, mantendo-se uma constante. Pode-se ter, então:

Transformação isotérmica

Nela, durante todo o processo termodinâmico de um gás ideal, a temperatura permanece constante (isso=igual; thermos = temperatura).

O cientista Robert Boyle comprovou que, quando a temperatura é constante, a pressão (P) exercida por certa massa gasosa é inversamente proporcional ao volume (V) por ela ocupado, ou P.V = constante, ou ainda, P_o.V_o = P.V.  

P_o e V_o representam a pressão e o volume num estado de equilíbrio inicial.

P e V representam a pressão e o volume num estado de equilíbrio final.

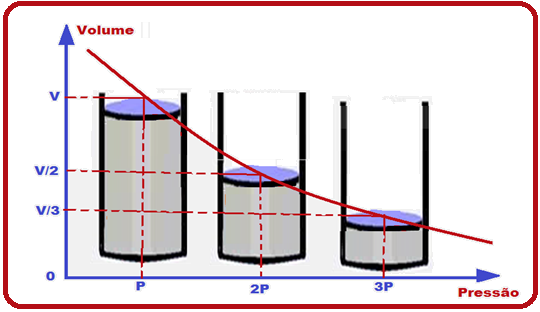
Isotermas

Sendo P.V = constante = k P = e, se V tende a zero, P cresce indefinidamente e se V cresce indefinidamente P tende a zero.

Se você representar graficamente P x V você obterá uma curva de nome isoterma que é um ramo de uma hipérbole eqüilátera.

Cada ponto da curva (isoterma) A tem a mesma temperatura (T_A); cada ponto da curva (isoterma) B tem a mesma temperatura (T_B) e cada ponto da curva (isoterma) C tem a mesma temperatura (T_C).

Observe que T_C > T_B > T_A, pois o produto P_AV_A > P_BV_B > P_CV_C e, assim quanto mais afastada dos eixos maior será o valor da temperatura da hipérbole representativa.

Transformação isocórica, isométrica ou isovolumétrica

Nessa transformação o volume é mantido constante (isso=igual; coros=volume).

Os físicos Jacques Charles e Gay-Lussac descobriram experimentalmente que, numa transformação isocórica, a pressão (P) é diretamente proporcional à temperatura absoluta (T), ou seja:

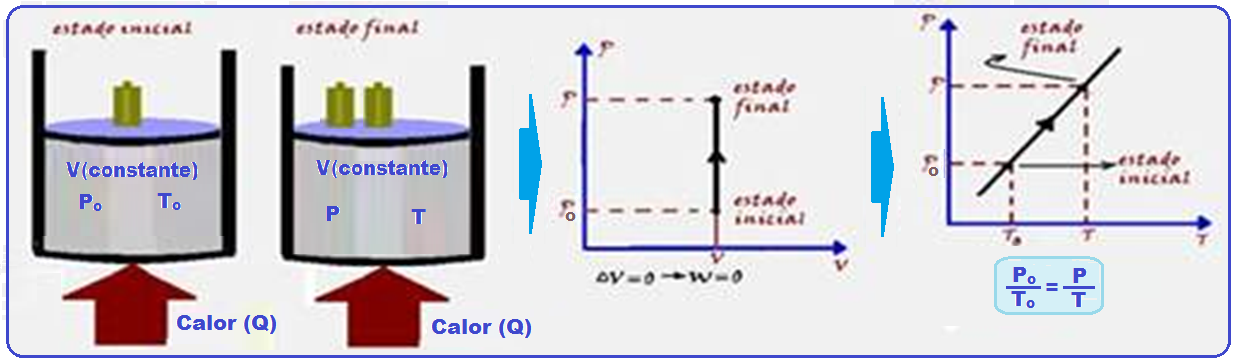
A expressão acima só é válida se considerarmos a temperatura absoluta, isto é, na escala kelvin.

Se a temperatura for medida em graus Celsius, isso não se aplica.

Na expressão P /T_o = P/T, conhecida como lei de Charles, P_o e T_o representam a pressão e a temperatura absoluta do gás no estado inicial: P e T representam, respectivamente, a pressão e a temperatura absoluta do gás no estado final. 

Observe o gráfico abaixo onde você vê representada a lei de Charles (transformação isovolumétrica) que representa a pressão (P) e a temperatura T, medida em graus kelvin (K) para 3 gases 1, 2 e 3.

Como a temperatura de um gás perfeito diminui à medida que a pressão também diminui, então deveria existir uma temperatura muito baixa na qual a pressão seria

nula, obtida pelo prolongamento dos gráficos acima onde as retas representativas de cada gás convergem para um único ponto: -273,15^oC = 0 K, no qual a pressão exercida pelos gases torna-se nula.

Na realidade, esse fenômeno não acontece, pois é impossível se anular a pressão exercida por um gás, pois, com um resfriamento suficiente, todos eles se liquefazem ou se solidificam.

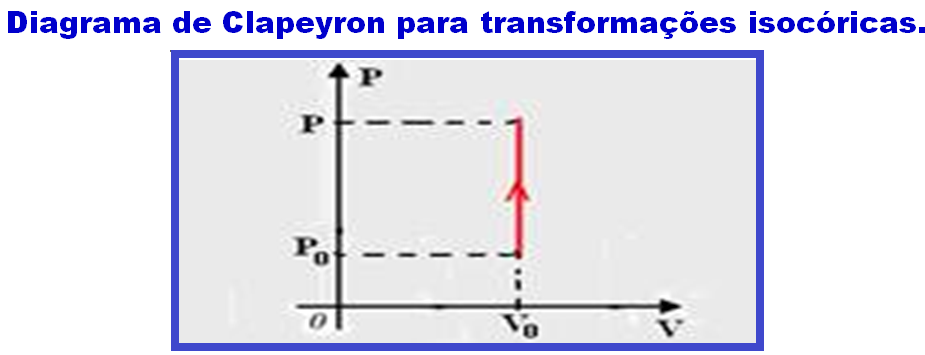
Transformação isobárica

 Ocorre à pressão constante (isso=igual; baros=pressão).

 O físico Jacques Charles observou que, para uma certa massa de gás perfeito, mantida apressão constante, o volume é diretamente proporcional à temperatura absoluta,ou seja:

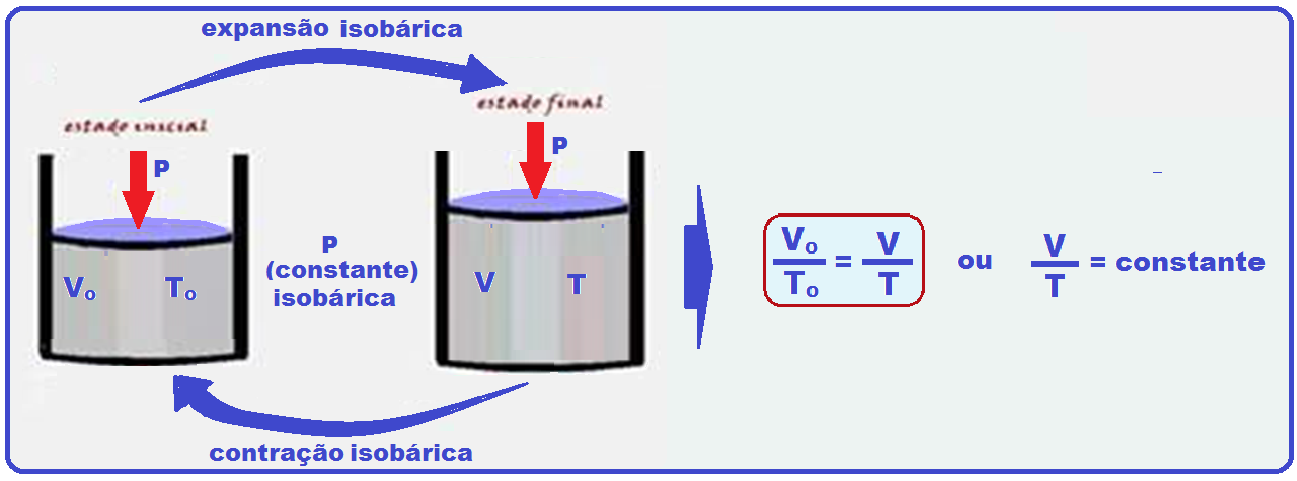
 A relação acima é denominada lei de Charles e Gay-Lussac para transformações isobáricas  e cujo gráfico V x T stá representado abaixo:

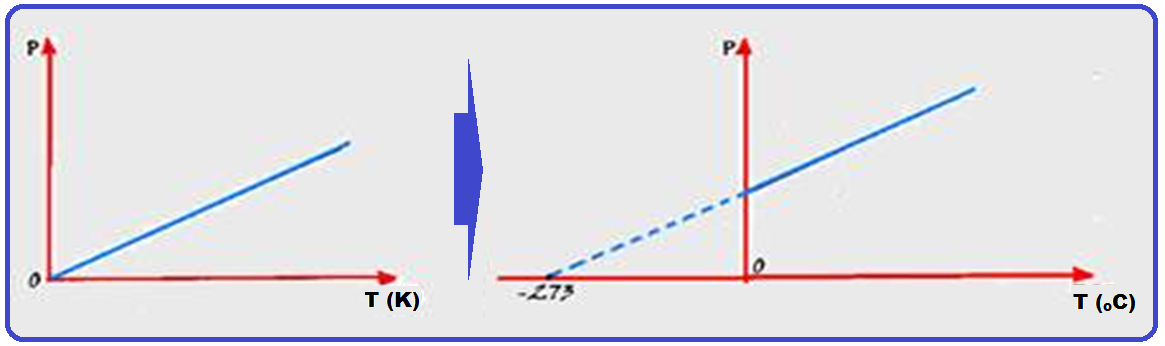
Diagrama de Clapeyron para transformações isobáricas

Equação de Clapeyron

As três leis anteriores mostram como um gás perfeito se comporta quando mantemos uma variável constante e variamos as outras duas.

A equação de Clapeyron ou equação de um gás ideal corresponde a uma síntese dessas três leis, que relacionam entre si pressão, temperatura e volume.
Numa transformação isotérmica, pressão e volume são inversamente proporcionais e em uma transformação isométrica, isocórica ou isovolumétrica, pressão e temperatura são diretamente proporcionais.

Pelas informações acima você pode concluir que a pressão é diretamente proporcional à temperatura e inversamente proporcional ao volume.
Acontece que o número de moléculas (número de mols) influencia na pressão exercida pelo gás, ou seja, a pressão também depende diretamente da massa do gás (número de moléculas nele contidas).

Considerando esses resultados, Paul Emile Clapeyron estabeleceu uma relação entre as variáveis de estado com a seguinte expressão matemática:

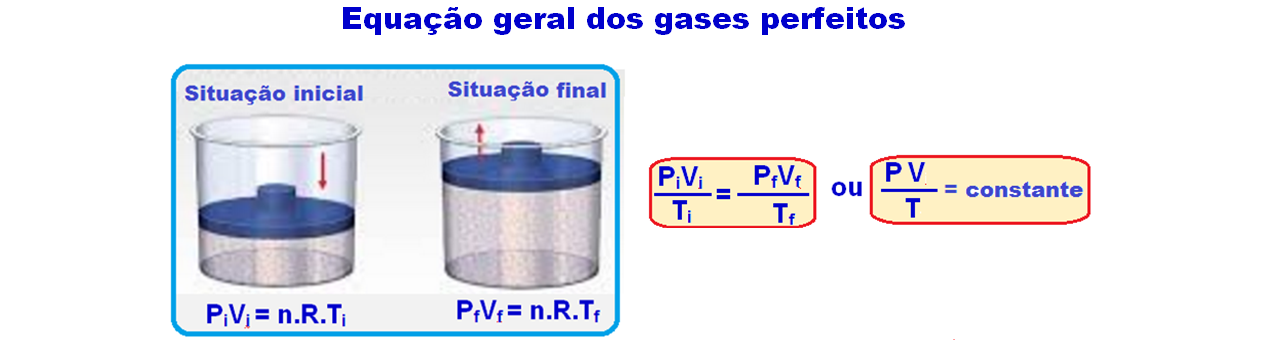
Equação geral dos gases perfeitos

À equação acima se dá o nome de lei geral dos gases perfeitos e você deve utiliza-la quando houver variação de pressão, volume e temperatura simultaneamente, mantendo-se constante a massa.

O que você deve saber, informações e dicas

Transformação Isotérmica

Isotermas

Transformação isocórica, isométrica ou isovolumétrica

Transformação Isobárica

Equação de Clapeyron ou Equação de um gás ideal

Nas lições iniciais de um curso de mergulho com equipamento autônomo – cilindro de ar

comprimido – os alunos são instruídos a voltarem lentamente à superfície, sem prender sua respiração em hipótese alguma, a fim de permitir que ocorra a gradativa descompressão (diminuição da pressão).

O aprisionamento do ar nos pulmões pode ser fatal para o mergulhador durante a subida, pois, nesse caso, a transformação sofrida pelo ar nos pulmões é isotérmica, com aumento do volume do ar.

Como o volume do cilindro que contém o gás se dilata muito pouco com a temperatura, pode-se dizer que se trata de uma transformação gasosa isométrica ou isovolumétrica (volume constante). Como o carro fica exposto ao sol, a temperatura do gás aumenta e conseqüentemente a pressão exercida pelo gás também aumenta, pois P/T = constante e P é diretamente proporcional a T, cujo

gráfico PXT está representado acima.

Um balão de aniversário, cheio de gás Hélio, solta-se da mão de uma criança, subindo até grandes

altitudes e, devido a redução da pressão, seu volume aumenta.

Mistura de gases

Considere dois recipientes rígidos, de volumes V_A e V_B contendo, respectivamente, gases A e B. Esses recipientes estão conectados entre si por um tubo fino munido de torneira que está fechada. Abre-se então a torneira colocando os

dois recipientes em comunicação, com os gases se misturando.

Após a mistura, suas partículas terão o mesmo grau de agitação, portanto a mesma temperatura.

Considerando n o número de mols da mistura, n_A o número de mols do gás A e n_B o número de mols do gás B, pode-se escrever    n = n_A + n_B    Clapeyron  PV = nRT    n = PV/RT, que,

Se P_A for a pressão do no recipiente A antes da mistura e P_B a pressão no recipiente B antes da mistura, tem-se P = P_A + P_B, onde P é a pressão total exercida pela mistura.

Veja um exercício interessante:

Quando abrimos uma geladeira com boa vedação e voltamos a fechá-la, é difícil abri-la novamente em seguida.

a) Como podemos explicar esse fenômeno com base no comportamento termodinâmico dos gases?

b) Considere uma geladeira com volume interno de 1.000 L, temperatura interna -5°C e área da porta 2m². Num dia cuja temperatura ambiente é 25°C, abrimos a porta da geladeira e a fechamos. Supondo que todo o ar frio no interior da geladeira seja substituído por ar à temperatura ambiente, qual será a força média necessária para abrir a porta depois

de restabelecido o equilíbrio termodinâmico no interior da geladeira?

(Dado: 1 atm ≈ 10⁵ N/m²).

Resolução:

a) Se a porta do freezer fica aberta por algum tempo, parte do ar de seu interior é substituído pelo ar mais quente do exterior.

Depois que você fecha a porta da geladeira, a temperatura interna do ar em seu interior irá diminuir e como se trata de uma isovolumétrica, a pressão também diminui (P/T = constante) fazendo com

b) Se a pressão externa é maior que a interna, como Pressão = Força/Área da porta, a força externa terá intensidade maior que a força interna e a intensidade da força resultante será F_R = F_ext – F_int.

A transformação é isovolumétrica (volume constante)   P₁/T₁ = P₂/T₂    1,0.10⁵x1.000 = P₂/(25 + 273)    P₂ = P_int = 0,9.10⁵N/m² (P_a)   ΔP = F_R/S    (1,0.10⁵ – 0,9.10⁵) = F_R/2    F_R = 0,2.10⁵N  F_R=2,0.10⁴ N.

Resolução de exercícios de vestibulares sobre

Tipos de transformações gasosas

02-(PUC-RS) De acordo com a Lei de Robert Boyle (1660), para proporcionar um aumento na pressão de uma determinada amostra gasosa numa transformação isotérmica, é necessário:

a) aumentar o seu volume.                      

b) diminuir a sua massa.                         

c) aumentar a sua temperatura.

d) diminuir o seu volume.                 

e) aumentar a sua massa

03-(UEBA-BA) Um balão-propaganda cheio de gás hélio, ao nível do mar, ocupa um volume de 250 L.

Seu volume após lançamento, numa altitude de 3000 m será: (obs.: admitindo-se que a temperatura tenha se mantido constante)

a) menor, pois a pressão externa aumenta com a altitude.                  

b) maior, pois a pressão externa diminui com a altitude.

c) permanecerá constante, pois a pressão não varia com a altitude.       

d) permanecerá constante, pois a temperatura se manteve constante.           

e) maior, pois a pressão externa aumenta com a altitude.

04-(PUC-BA) Duas amostras de igual massa de um mesmo gás foram submetidas ao seguinte teste, à temperatura constante:

os dados obtidos para a pressão e volume das amostras comprovam a lei de:

a) Boyle                     

b) Gay-Lussac                       

c) Avogadro                    

d) Proust                      

e) Lavoisier

05- (PUC-MG) A figura ao lado representa um gás contido em um cilindro cuja parte superior é vedada por um êmbolo que pode deslizar, sem atrito, para cima e para baixo, ao longo das paredes do cilindro.

Sobre o êmbolo está um objeto de massa constante. Se esse sistema for aquecido lentamente, a transformação a que ele será submetido é:

a) adiabática                         

b) isobárica                       

c) isotérmica                        

d) isocórica                         

e) isostática

06-(MACKENZIE-SP) Se a pressão de um gás confinado é duplicada a temperatura constante, a grandeza do gás que duplicará será:

a) a massa                 

b) a massa específica                 

c) o volume                    

d) o peso                   

e) a energia cinética

07- (UFAC-AC)  Considere o gráfico a seguir:

O gráfico acima representa um comportamento típico de um gás submetido à lei de Boyle – Mariotte (P.V=K). Com relação à curva, pode-se afirmar que:

a) É uma isocórica e o valor de K é igual a 2,0                                       

b) É uma isoterma e o valor de K é igual a 12,0  

c) É uma isocórica e o valor de K é igual a 12,0                                     

d) É uma isoterma e o valor de K é igual a 2,0

e) É uma isobárica e o valor de K é igual a 2,0

08-(CESGRANRIO-RJ) Você brincou de encher, com ar, um balão de gás, na beira da praia, até um volume de 1 L e o fechou.

Em seguida, subiu uma encosta próxima carregando o balão, até uma altitude de 900m, onde a pressão atmosférica é 10% menor que a pressão ao nível do mar. Considerando que a temperatura na praia e na encosta seja mesma, o volume de ar no balão após a subida, será de:

09-(UFRJ-RJ) Um balão, contendo um gás ideal, é usado para levantar cargas subaquáticas. A uma certa profundidade, o gás nele

 contido está em equilíbrio térmico com a água a uma temperatura absoluta T_o e a uma pressão P_o. Quando o balão sai da água, depois de levantar a carga, o gás nele contido entra em equilíbrio térmico com o ambiente a uma temperatura absoluta T e a uma pressão P.

Supondo que o gás no interior do balão seja ideal e sabendo que P_o/P = 3/2 e T_o/T = 0,93, calcule a razão V_o/V entre o volume V_o do gás quando o balão está submerso e o volume V do mesmo gás quando o balão está fora d'água.

10-(UNIFESP-SP) A figura ilustra duas transformações de um gás ideal contido num cilindro de paredes adiabáticas. Em I, através de uma base diatérmica (que permite a passagem do calor), o gás recebe calor e faz o êmbolo, também construído de material adiabático, subir livremente, aumentando seu volume de V_o a V, atingindo a temperatura T. Nesse estado, a fonte quente é retirada e substituída por um reservatório térmico à mesma temperatura T do gás. Em seguida, na transformação II, colocam-se grãos de areia sobre o êmbolo, lentamente, para que o gás possa manter-se em equilíbrio térmico com o reservatório. Nessas condições, o êmbolo baixa até que o gás volte a ocupar o mesmo volume V_o do início.

Considere desprezíveis as variações da pressão atmosférica. O diagrama pV, que melhor representa essas duas transformações, é o da figura:

11-(PUC-MG) Um balão de aniversário, cheio de gás Hélio, solta-se da mão de uma criança, subindo até grandes altitudes.

Durante a subida, é CORRETO afirmar:

a) O volume do balão diminui.                                              

b) A pressão do gás no interior do balão aumenta. 

c) O volume do balão aumenta.                                             

d) O volume do balão permanece constante. 

12-(UEPG-GO)  A respeito do funcionamento da panela de pressão, assinale o que for correto.

01) De acordo com a lei dos gases, as variáveis envolvidas no processo são pressão, volume e temperatura. 

02) O aumento da pressão no interior da panela afeta o ponto de ebulição da água. 

04) A quantidade de calor doado ao sistema deve ser constante, para evitar que a panela venha a explodir. 

08) O tempo de cozimento dos alimentos dentro de uma panela de pressão é menor porque eles ficam submetidos a temperaturas superiores a 100 °C. 

13-(UFSC-SC) Como funciona a panela de pressão?

Dona Maria, uma exímia cozinheira, ficou intrigada ao sair de uma das aulas de Ciências sobre o funcionamento da panela de

pressão, a qual utiliza diariamente em sua casa. Na primeira pesquisa efetuada em um site na Internet, ela encontrou o seguinte fragmento:

"A panela de pressão foi inventada pelo físico francês Denis Papin, que publicou em 1861 uma descrição do equipamento, denominando-o digestor. Numa reunião de cientistas da Royal Society, Papin demonstrou que o seu invento era capaz de reduzir ossos a gelatina comestível."

            Disponível em:  <http://br.geocities.com/saladefisica7/funciona/panela.htm>. Acesso em: 22 out. 2007

Alunos do ensino médio, no intuito de ajudar Dona Maria, enviaram os gráficos (I), (II), (III) e (IV) que representam o comportamento da temperatura de ebulição da água (T_e) em função da pressão máxima de vapor de água (P_max) no interior de quatro panelas de pressão (a, b, c e d), com pressões máximas diferentes P_a, P_b, P_c e  P_d, respectivamente.

Escolha o gráfico que melhor representa o comportamento da temperatura de ebulição da água (Te) em função da pressão máxima do vapor de água (P_max), indique-o na sua resposta, faça uma análise matemática da relação entre as variáveis referidas, explicando o princípio de funcionamento da panela de pressão. 

14-(UFMG) Gabriela segura um balão com gás hélio durante uma viagem do Rio de Janeiro até o pico das Agulhas Negras.

No Rio de Janeiro, o volume do balão era V_o, e o gás estava à pressão p_o e à temperatura T_o, medida em kelvin. Ao chegar ao pico, porém, Gabriela observa que o volume do balão passa a ser 6/5 V_o e a temperatura do gás, 9/10 T_o. 
Com base nessas informações, é correto afirmar que, no pico das Agulhas Negras, a pressão do gás, no interior do balão, é:

15- (FMTM-MG) Nas lições iniciais de um curso de mergulho com equipamento autônomo –

cilindro de ar comprimido – os alunos são instruídos a voltarem lentamente à superfície, sem prender sua respiração em hipótese alguma, a fim de permitir que ocorra a gradativa descompressão. O aprisionamento do ar nos pulmões pode ser fatal para o mergulhador durante a subida, pois, nesse caso, a transformação sofrida pelo ar nos pulmões é

a) isobárica, com redução do volume do ar.                         

b) isobárica, com aumento da temperatura do ar.

c) isotérmica, com aumento da pressão do ar.                      

d) isotérmica, com aumento do volume do ar.

e) isovolumétrica, com diminuição da pressão do ar

16-(UNIFESP-SP) A figura reproduz o esquema da montagem feita por Robert Boyle para estabelecer a lei dos gases para transformações isotérmicas. Boyle colocou no tubo certa quantidade de mercúrio, até aprisionar um determinado volume de ar no ramo fechado, e igualou os níveis dos dois ramos. Em seguida, passou a acrescentar mais mercúrio no ramo aberto e a medir, no outro ramo, o volume do ar aprisionado (em unidades arbitrárias) e a correspondente pressão pelo desnível da coluna de mercúrio, em polegadas de mercúrio. Na tabela, estão alguns dos dados por ele obtidos, de acordo com a sua publicação "New Experiments Physico-Mechanicall, Touching the Spring of Air, and its Effects", de 1662.(http://chemed.chem.purdue.edu/gench m/history/)

a) Todos os resultados obtidos por Boyle, com uma pequena aproximação, confirmaram a sua lei. Que resultados foram esses? Justifique.

b) De acordo com os dados da tabela, qual a pressão, em pascal, do ar aprisionado no tubo para o volume de 24 unidades arbitrárias?

Utilize para este cálculo:

pressão atmosférica p_o = 1,0 × 10⁵ pascal; densidade do mercúrio d(Hg) = 14 × 10³kg/m³; g=10m/s²

17-(UFAM-AM)  Analise as seguintes afirmativas a respeito dos tipos de transformações ou mudanças de estado de um gás.

I. em uma transformação isocórica o volume do gás permanece constante.

II. em uma transformação isobárica a pressão do gás permanece constante.

III. em uma transformação isotérmica a temperatura do gás permanece constante.

IV. em uma transformação adiabática variam o volume, a pressão e a temperatura.

Com a relação as quatro afirmativas acima, podemos dizer que:

a) só I e III são verdadeiras.         

b) só II e III são verdadeiras.           

c) I, II, III e IV são verdadeiras.        

d) só I é verdadeira.

e) todas são falsas.

18-(UFMG-MG) Regina estaciona seu carro, movido a gás natural, ao Sol. Considere que o gás no

reservatório do carro se comporta como um gás ideal. Assinale a alternativa cujo gráfico melhor representa a pressão em função da temperatura do gás na situação descrita.

19-(UNIFENAS-MG) Um mol de um gás ideal é submetido a uma transformação de estado cíclico, como mostra o gráfico a seguir:

Pode-se afirmar que as transformações A, B e C, são, respectivamente:

a) isovolumétrica, isotérmica, isovolumétrica                                     

b) isobárica, isotérmica, isovolumétrica

c) isovolumétrica, isotérmica, isobárica                                         

d) isotérmica, isobárica, isovolumétrica

e) isovolumétrica, isobárica, isotérmica

 20-(FUVEST-SP) Uma bola de futebol impermeável e murcha é colocada sob uma campânula, num ambiente hermeticamente

fechado. A seguir, extrai-se lentamente o ar da campânula até que a bola acabe por readquirir sua forma esférica. Ao longo do processo, a temperatura é mantida constante. Ao final do processo, tratando-se o ar como um gás perfeito, podemos afirmar que:

a) a pressão do ar dentro da bola diminuiu.                          

b) a pressão do ar dentro da bola aumentou.

c) a pressão do ar dentro da bola não mudou.                     

d) a densidade do ar dentro da bola aumentou.

21- (FGV-SP) Na Coréia do Sul, a caça submarina é uma profissão feminina por tradição. As

Haenyeos são "mulheres-peixe" que ganham dinheiro mergulhando atrás de frutos do mar e crustáceos. O trabalho é realizado com equipamentos precários o que não impede a enorme resistência dessas senhoras que conseguem submergir por dois minutos e descer até 20 metros abaixo da superfície.

            ("Revista dos Curiosos", 2003)

Supondo que o ar contido nos pulmões de uma dessas mergulhadoras não sofresse variação significativa de temperatura e se comportasse como um gás ideal, e levando em conta que a

pressão exercida por uma coluna de água de 10m de altura equivale aproximadamente a 1atm, a relação entre o volume do ar contido nos pulmões, durante um desses mergulhos de 20m de profundidade, e o volume que esse ar ocuparia ao nível do mar, se a estrutura óssea e muscular do tórax não oferecesse resistência, corresponderia, aproximadamente, a

Dado: pressão na superfície da água = 1 atm

22-(CESGRANRIO-RJ) Antes da largada e "na volta de apresentação" de um Grande Prêmio de Fórmula 1, os pneus são pré-aquecidos para melhorar o desempenho do carro. Supondo desprezível variação do volume do pneu durante a prova, qual dos gráficos a seguir representa a variação da pressão do ar no interior do pneu em função da variação de temperatura absoluta atingida pelo pneu na reta de chegada?

23-(UFRN-RN) O departamento de Física da UFRN possui um laboratório de pesquisa em criogenia, ciência que estuda a produção e manutenção de temperaturas muito baixas, contribuindo para o entendimento das propriedades físicas e químicas de sistemas nessas temperaturas pouco comuns. Nesse laboratório, uma máquina retira o gás nitrogênio do ar e o liquefaz a uma temperatura de 77,0 kelvin (K), que corresponde a -196 graus celsius (°C). Nessa temperatura o nitrogênio é usado cotidianamente pelos departamentos de Física, Química e Biologia da UFRN, como também por pecuaristas no congelamento de sêmen para reprodução animal.

O nitrogênio líquido, em virtude de suas características, necessita ser manuseado adequadamente, pois pessoas não habilitadas poderão sofrer acidentes e serem vítimas de explosões. Imagine uma pessoa desavisada transportando, num dia quente de verão, uma porção de nitrogênio líquido numa garrafa plástica fechada. Como o nitrogênio líquido tende a entrar em equilíbrio térmico com o ambiente, mudará de estado físico, transformando-se em um gás. A tendência desse gás é se expandir, podendo provocar uma explosão.

Admita que

I) o nitrogênio rapidamente se transforma em gás ideal, ou seja, obedece à equação PV = nRT. Em que R é a constante universal dos gases e P, V, T, n são, respectivamente: a pressão, o volume, a temperatura e o número de moles do gás;

II) a pressão interna e a temperatura iniciais desse gás são, respectivamente, 2,0.10⁵pascal (P_a) e 78,0 K;

III) a garrafa utilizada pode suportar uma pressão máxima de 4,0.10⁵ P_a e o volume dessa garrafa não varia até que a explosão ocorra.

Diante dessas considerações, é correto dizer que a temperatura limite (do gás nitrogênio) que a garrafa suporta sem explodir é

24-(ITA-SP) A pressão total do ar no interior de um pneu era de 2,30 atm, quando a temperatura do pneu era de 27^oC. Depois de ter rodado um certo tempo com este pneu, mediu-se novamente sua pressão e verificou-se que este agora era de 2,53 atm. Supondo variação de volume desprezível do pneu, determine sua nova temperatura. 

25-(UNIFESP-SP) Você já deve ter notado como é difícil abrir a porta de um freezer logo após tê-la fechado, sendo necessário aguardar alguns segundos para abri-la novamente. Considere um freezer vertical cuja porta tenha 0,60 m de largura por 1,0 m de

 altura, volume interno de 150 L e que esteja a uma temperatura interna de - 18ºC, num dia em que a

temperatura externa seja de 27ºC temperatura interna de  e a pressão, 1,0 x 10⁵ N/m².
a) Com base em conceitos físicos, explique a razão de ser difícil abrir a porta do freezer logo após tê-la fechado e por que é necessário aguardar alguns instantes para conseguir abri-la novamente.
b) Suponha que você tenha aberto a porta do freezer por tempo suficiente para que todo o ar frio do seu interior fosse substituído por ar a 27ºC e que, fechando a porta do freezer, quisesse abri-la novamente logo em seguida. Considere que, nesse curtíssimo intervalo de tempo, a temperatura média do ar no interior do -3ºC. Determine a intensidade da força resultante sobre a porta do freezer.

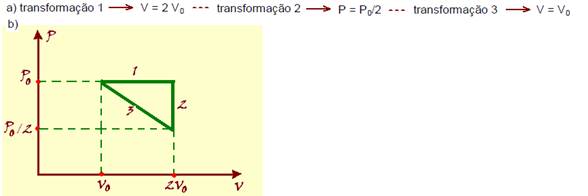
26-(FUVEST-SP) Certa massa de gás ideal, inicialmente à pressão P_o, volume V_o e temperatura T_o, é submetida à seguinte seqüência de transformações:

1. É aquecida à pressão constante até que a temperatura atinja o valor 2T_o.

2. É resfriada a volume constante até que a temperatura atinja o valor inicial T_o.

3. É comprimida à temperatura constante até que atinja a pressão inicial P_o.

a) Calcule os valores da pressão, temperatura e volume final de cada transformação.

b) Represente as transformações num diagrama pressão x volume.

27-(UFRN-RN) Um mergulhador que faz manutenção numa plataforma de exploração de petróleo está a uma profundidade de 15 m quando uma pequena bolha de ar, de volume V_i, é liberada e sobe até a superfície, onde a pressão é a pressão atmosférica (1,0 atm). Para efeito deste problema, considere que: a temperatura dentro da bolha permanece constante enquanto esta existir; a

pressão aumenta cerca de 1,0 atm a cada 10 m de profundidade; o ar da bolha é um gás ideal e obedece à relação PV/T= constante, em que P, V e T são respectivamente, a pressão, o volume e a

temperatura do ar dentro da bolha. Na situação apresentada, o volume da bolha quando ela estiver prestes a chegar à superfície será aproximadamente:

28-(UFLA-MG)

Quando abrimos uma geladeira com boa vedação e voltamos a fechá-la, é difícil abri-la novamente em seguida.

a) Como podemos explicar esse fenômeno com base no comportamento termodinâmico dos gases?

b) Considere uma geladeira com volume interno de 1.000 L, temperatura interna -5°C e área da porta 2m². Num dia cuja temperatura ambiente é 25°C, abrimos a porta da geladeira e a fechamos. Supondo que todo o ar frio no interior da geladeira seja substituído por ar à temperatura ambiente.

Qual será a força média necessária para abrir a porta depois de restabelecido o equilíbrio termodinâmico no interior da geladeira?

(Dado: 1 atm ≈ 10⁵ N/m²).

29-(UFA-MG) Nos manuais de automóveis, na seção que trata da calibragem dos pneus, junto à pressão recomendada, encontramos a seguinte instrução: “os pneus devem ser calibrados enquanto frios”. Qual o motivo da recomendação?

a) Se calibrarmos os pneus quentes com a pressão recomendada, ao esfriarem a pressão cairá a valores mais baixos que o recomendado.

b) Se calibrarmos os pneus quentes com ar à temperatura ambiente, podemos provocar rachaduras nas rodas.

c) Se calibrarmos os pneus ainda quentes, podemos levar a vazamentos de ar, porque a borracha estará dilatada.

d) Se calibrarmos os pneus quentes com a pressão recomendada, quando os pneus esfriarem a pressão ficará muito acima da recomendada, por causa da contração da borracha.

e) Se calibrarmos os pneus a frio, gastaremos menos ar para enchê-los.

31-(UFPB-PB) Antes de iniciar uma viagem, um motorista cuidadoso calibra os pneus de seu carro, que estão à temperatura

ambiente de 27°C, com uma pressão de 30 lb/pol². Ao final da viagem, para determinar a temperatura dos pneus, o motorista mede a pressão dos mesmos e descobre que esta aumentou para 32 lb/pol². Se o volume dos pneus permanece inalterado e se o gás no interior é ideal, o motorista determinou a temperatura dos pneus como sendo:

32-(FUVEST) O gasômetro G, utilizado para o armazenamento de ar, é um recipiente cilíndrico, metálico, com paredes laterais de pequena espessura. G é fechado na sua parte superior, aberto na inferior que permanece imersa em água e pode se mover na direção vertical. G contém ar, inicialmente à temperatura de 300K e o nível da água no seu interior se encontra 2,0m abaixo do nível externo da água. Nessas condições, a tampa de G está 9,0m acima do nível externo da água como mostra a figura a seguir.

Aquecendo-se o gás, o sistema se estabiliza numa nova altura de equilíbrio, com a tampa superior a uma altura H, em relação ao nível externo da água, e com a temperatura do gás a 360K. Supondo que o ar se comporte como um gás ideal, a nova altura H será, aproximadamente, igual a:

33-(UFRJ-RJ) Um recipiente de volume interno total igual a V₀ está dividido em dois compartimentos estanques por meio de uma parede fina que pode se mover sem atrito na direção horizontal, como indica a figura a seguir.

A parede é diatérmica, isto é, permeável ao calor. O compartimento da direita contém dois moles de um gás ideal, enquanto o da esquerda contém um mol de um outro gás, também ideal.

Sabendo que os gases estão em equilíbrio térmico entre si e que a parede se encontra em repouso, calcule o volume de cada gás em função de V_o.

34-(FUVEST-SP) Em algumas situações de resgate, bombeiros utilizam cilindros de ar comprimido

para garantir condições normais de respiração em ambientes com gases tóxicos. Esses cilindros, cujas características estão indicadas e seguir, alimentam máscaras que se acoplam ao nariz. Quando acionados, os cilindros fornecem para a respiração, a cada minuto, cerca de 40 litros de ar, a pressão atmosférica e temperatura ambiente. Nesse caso, a duração do ar de um desses cilindros seria de aproximadamente:

A temperatura durante todo o processo permanece constante.

a) 20 minutos.                   

b) 30 minutos.                       

c) 45 minutos.                  

d) 60 minutos.                       

e) 90 minutos. 

35-(Inatel-MG) Um recipiente cilíndrico tem seu volume V dividido em duas partes por uma membrana rígida.

Em uma das partes tem-se gás ideal à pressão P e temperatura T. Admita que essa parte tenha 1/3 do volume do cilindro. Na outra parte fez-se o vácuo. As paredes do cilindro não permitem que o gás troque calor com o meio externo. A membrana é removida sem que haja troca de calor. Depois que o gás entra em equilíbrio, a pressão e temperatura são, respectivamente:

36-(FUVEST-SP) A figura mostra uma bomba de encher pneu de bicicleta. Quando o êmbolo está todo puxado, a uma distância de 30cm da base, a pressão dentro da bomba é igual à pressão atmosférica normal. A área da seção transversal do pistão da bomba é de 24cm². Um ciclista quer encher ainda mais o pneu da bicicleta que tem volume de 2,4 litros e já está com uma pressão interna de 3atm. Ele empurra o êmbolo da bomba até o final de seu curso. Suponha que o volume do pneu permaneça constante, que o processo possa ser considerado isotérmico e que o volume do tubo que liga a bomba ao pneu seja desprezível. A pressão final do pneu será, então, de aproximadamente:

a) 1,0 atm                      

b) 3,0 atm                       

c) 3,3 atm                          

d) 3,9 atm                        

e) 4,0 atm

37-(UFRGS-RS) Na figura abaixo estão representados dois balões de vidro, A e B, com capacidades  de 3 litros e de 1 litro, respectivamente. Os balões estão conectados entre si  por um tubo fino munido da torneira T, que se encontra fechada. O balão A contém hidrogênio à pressão de 1,6 atmosferas. O balão B foi completamente esvaziado. Abre-se, então, a torneira T, pondo os balões em comunicação, e faz-se também  com que a temperatura dos balões e do gás retorne ao seu valor inicial, (considere 1 atm igual a 10⁵N/m²).

Qual é, em N/m², o valor aproximado  da pressão a que fica submetido o hidrogênio?

38-(Unifor-CE) Dois recipientes rígidos de mesmo volume contém gases perfeitos às pressões de 5,0 atm e 18,0 atm, na mesma temperatura. Os dois recipientes estão ligados por um tubo provido de torneira que, inicialmente, está fechada. Abrindo-se a torneira, os gases se misturam sem reagir, e a temperatura diminui. Aguardando-se algum tempo para que a temperatura volte ao valor inicial, a pressão comum nos dois botijões, em atm, é:

a) 10,0                    b) 11,5                         c) 13,0                        d) 23,0                          e) 26,0

39-(UNICAMP-SP) As baleias são mamíferos aquáticos dotados de um sistema respiratório altamente eficiente que dispensa um acúmulo muito elevado de ar nos pulmões, o que prejudicaria sua capacidade de submergir. A massa de certa baleia é de 1,50 × 10⁵ kg e o seu volume, quando os pulmões estão vazios, é igual a 1,35 × 10² m³ .

a) Calcule o volume máximo da baleia após encher os pulmões de ar, acima do qual a baleia não conseguiria submergir sem esforço. Despreze o peso do ar nos pulmões e considere a densidade da água do mar igual a 1,0 × 10³ kg/m³.

b) Qual é a variação percentual do volume da baleia ao encher os pulmões de ar até atingir o volume máximo calculado no item a? Considere que inicialmente os pulmões estavam vazios.

c) Suponha que uma baleia encha rapidamente seus pulmões em um local onde o ar se encontra inicialmente a uma temperatura de 7 ^°C e a uma pressão de 1,0 atm (1,0 × 10⁵N/m²). Calcule a pressão do ar no interior dos pulmões da baleia, após atingir o equilíbrio térmico com o corpo do animal, que está a 37 ^°C. Despreze qualquer variação da temperatura do ar no seu caminho até os pulmões e considere o ar um gás ideal.

 40-(FUVEST-SP) Um cilindro com comprimento de 1,5m, cuja base inferior é constituída por um bom condutor de calor, permanece semi-imerso em um grande tanque industrial, ao nível do mar, podendo ser utilizado como termômetro. Para isso, dentro do cilindro, há um pistão, de massa desprezível e isolante térmico, que pode mover-se sem atrito.

Inicialmente, com o ar e o líquido do tanque à temperatura ambiente de 27ºC, o cilindro está aberto e o pistão encontra-se na posição indicada na figura 1. O cilindro é, então fechado e, a seguir, o líquido do tanque é aquecido, fazendo com que o pistão atinja uma nova posição, indicada na figura 2.

Supondo que a temperatura da câmara superior A permaneça sempre igual a 27ºC, determine:

a) A pressão final P₁, em Pa, na câmara superior A.

b) A temperatura final T₁ do líquido no tanque, em ºC ou em K.

41-(FUVEST-SP) Um grande cilindro, com ar inicialmente à pressão P₁ e temperatura ambiente (T₁ = 300 K), quando aquecido, pode provocar a elevação de uma plataforma A, que funciona como um pistão, até uma posição mais alta. Tal processo exemplifica a transformação de calor em trabalho, que ocorre nas máquinas térmicas, à pressão constante. Em uma dessas situações, o ar contido em um cilindro, cuja área da base S é igual a 0,16 m², sustenta uma plataforma de massa M_A =160 kg a uma altura H₁ = 4,0 m do chão (situação I). Ao ser aquecido, a partir da queima de um combustível, o ar passa a uma temperatura T₂, expandindo-se e empurrando a plataforma até uma nova altura H₂ = 6,0 m (situação II). Para verificar em que medida esse é um processo eficiente, estime:

a) A pressão P₁ do ar dentro do cilindro, em pascals, durante a operação.

b) A temperatura T₂ do ar no cilindro, em kelvins, na situação II.

c) A eficiência do processo, indicada pela razão R = ∆Ep/Q, onde ∆Ep é a variação da energia potencial da plataforma, quando ela se desloca da altura H₁ para a altura H₂, e Q, a quantidade de calor recebida pelo ar do cilindro durante o aquecime

NOTE E ADOTE:

PV = nRT; P(atmosférica) = P₀ = 1,0x10⁵ Pa; 1 Pa = 1 N/m²  ---  Calor específico do ar a pressão constante Cp ≈ 1,0 × 10³ J/(kg.K)  ---  Densidade do ar a 300 K ≈ 1,1 kg/m³

42-(MACKENZIE-SP)  Uma massa de certo gás ideal está confinada em um reservatório, cuja dilatação térmica é desprezível no intervalo de temperatura considerado. Esse reservatório possui na parte superior, um êmbolo que pode se deslocar livremente, conforme ilustra a figura. Observando-se o gráfico a seguir, destaca-se que, no estado A, o volume ocupado pelo gás é V e a sua pressão é P. Em seguida, esse gás passa por duas transformações sucessivas e "chega" ao estado C, com temperatura e pressão, respectivamente iguais a:

a) 450 K e 3P/2            

 b) 450 K e 4P/3                

c) 600 K e 3P/2     

d) 600 K e 4P/3             e) 600 K e 5P/3 

43-(UFOP-MG) Considere o gráfico a seguir, que descreve o comportamento da pressão e do volume de certa massa de gás ideal.

Com relação às transformações mostradas acima, podemos afirmar que:

a) a transformação BC é isobárica.                                                          

b) a transformação AB é isotérmica.

c) há uma mudança drástica do volume na transformação BC.              

d) a temperatura no ponto A é maior que no ponto C.

44-(UDESC-SC) Um motorista, antes de iniciar sua viagem, calibrou os pneus de seu carro, deixando-os a uma pressão

manométrica de 150,0x10³ Pa. No momento da calibração a temperatura ambiente e dos pneus era de 27,0 ^°C. Quando chegou ao destino de sua viagem, o motorista percebeu que a pressão manométrica do ar (gás) nos pneus aumentara para 160,0x10³ Pa. Considere o ar dentro dos pneus como sendo um gás ideal. Dada a constante de Boltzmann 1,38 × 10^-23 J/K.

a) Ao chegar ao destino, qual a temperatura do gás nos pneus, sabendo que eles expandiram, aumentando seu volume interno em 5%.

b) Considerando as condições iniciais da viagem e que os pneus suportem, no máximo, uma variação de volume de 8%, calcule a pressão do gás no interior dos pneus nessa condição limite. Sabe-se ainda que a temperatura do gás dentro dos pneus, na condição limite, atinge aproximadamente 360 K.

 45-(FUVEST-SP) Em um freezer, muitas vezes, é difícil repetir a abertura da porta, pouco tempo após ter sido fechado, devido à diminuição da pressão interna. Essa diminuição ocorre porque o ar que entra, à temperatura ambiente, é rapidamente resfriado até

a temperatura de operação, em torno de - 18 ^°C. Considerando um freezer doméstico, de 280 l, bem vedado, em um ambiente a 27 ^°C e pressão atmosférica P₀, a pressão interna poderia atingir o valor mínimo de:

Considere que todo o ar no interior do freezer, no instante em que a porta é fechada, está à temperatura do ambiente.

a) 35% de P₀                 

b) 50% de P₀                      

c) 67% de P₀                   

d) 85% de P₀                    

e) 95% de P₀ 

46-(FGV-SP) Para garantir a dosagem precisa, um medicamento pediátrico é acompanhado de uma seringa. Depois de destampado o frasco de vidro que contém o remédio, a seringa é nele encaixada com seu êmbolo completamente recolhido. Em seguida, o frasco é posicionado de cabeça para baixo e o remédio é então sugado para o interior da seringa, enquanto o êmbolo é puxado para baixo. Como consequência da retirada do líquido, o ar que já se encontrava dentro do frasco, expande-se isotermicamente, preenchendo o volume antes ocupado pelo remédio.

Ao retirar-se uma dose de 40 mL de líquido do frasco, que continha um volume ocupado pelo ar de 100 mL, o êmbolo encontra certa resistência, devido ao fato de a pressão no interior do frasco ter se tornado, aproximadamente, em Pa,

Dados: Pressão atmosférica = 1,0x10⁵ Pa  ---  Suponha que o ar dentro do frasco se comporte como um gás ideal  ---  Considere desprezível o atrito entre o êmbolo e a parede interna da seringa.

a) 57 000.                          

b) 68 000.                            

c) 71 000.                            

d) 83 000.                           

e) 94 000.

47-(PUC-RJ)  Seja um mol de um gás ideal a uma temperatura de 400 K e à pressão atmosférica p_o. Esse gás passa por uma expansão isobárica até dobrar seu volume. Em seguida, esse gás passa por uma compressão isotérmica até voltar a seu volume original. Qual a pressão ao final dos dois processos?

a)   0,5 p_o                    b)    1,0 p_o                    c)    2,0 p_o                      d)    5,0 p_o                      e)  10,0 p_o 

 48-(UFAL-AL) Um gás ideal possui, inicialmente, volume V_o e encontra-se sob uma pressão p_o. O gás passa por uma transformação isotérmica, ao final da qual o seu volume torna-se igual a V₀/2. Em seguida, o gás passa por uma transformação isobárica, após a qual seu volume é 2V₀. Denotando a temperatura absoluta inicial do gás por T₀, a sua temperatura absoluta ao final das duas transformações é igual a:

49-(FUVEST-SP) Um balão de ar quente é constituído de um envelope (parte inflável), cesta para três passageiros, queimador e tanque de gás. A massa total do balão, com três passageiros e com o envelope vazio, é de 400 kg. O envelope totalmente inflado tem um volume de 1500m³.

a) Que massa de ar M₁ caberia no interior do envelope, se totalmente inflado, com pressão igual à pressão atmosférica local (P_atm) e temperatura T=27 ^oC?

b) Qual a massa total de ar M₂, no interior do envelope, após este ser totalmente inflado com ar quente a uma temperatura de 127^oC e pressão P_atm?

c) Qual a aceleração do balão, com os passageiros, ao ser lançado nas condições dadas no item b) quando a temperatura externa é T=27 ^oC ?

NOTE E ADOTE:

Densidade do ar a 27 ^oC e à pressão atmosférica local = 1,2 kg/m³.

Aceleração da gravidade na Terra, g = 10 m/s².

Considere todas as operações realizadas ao nível do mar.

Despreze o empuxo acarretado pelas partes sólidas do balão.

T (K) = T (^oC) + 273

Indique a resolução da questão. Não é suficiente apenas escrever as respostas.

50-(UERJ-RJ) A bola utilizada em uma partida de futebol é uma esfera de diâmetro interno igual a 20 cm.

Quando cheia, a bola apresenta, em seu interior, ar sob pressão de 1,0 atm e temperatura de 27 ºC.

Considere π= 3, R = 0,080 atm.L.mol^-1.k^-1 e, para o ar, comportamento de gás ideal e massa molar igual a 30 g.mol^-1.

No interior da bola cheia, a massa de ar, em gramas, corresponde a:

51-(UNESP-SP)

Os desodorantes do tipo aerossol contêm em sua formulação solventes e propelentes inflamáveis. Por essa razão, as embalagens utilizadas para a comercialização do produto fornecem no rótulo algumas instruções, tais como:

• Não expor a embalagem ao sol.

• Não usar próximo a chamas.

• Não descartar em incinerador.

Uma lata desse tipo de desodorante foi lançada em um incinerador a 25 ºC e 1 atm. Quando a temperatura do sistema

atingiu 621 ºC, a lata explodiu. Considere que não houve deformação durante o aquecimento. No momento da explosão a pressão no interior da lata era

(A) 1,0 atm.                

(B) 2,5 atm.                      

(C) 3,0 atm.                    

(D) 24,8 atm.                   

(E) 30,0 atm.

Resolução comentada dos exercícios de vestibulares sobre

Tipos de transformações gasosas

01- R- D  ---  veja teoria

02- Isotérmica  ---  P.V=constante  ---  P é inversa a V  ---  R- D

03- R- B  ---  veja teoria

04- R- A  ---  veja teoria

05- Observe que a pressão sobre o êmbolo é constante, pressão atmosférica que é constante  mais a pressão devido ao peso, que também é constante. Assim trata-se de uma transformação isobárica onde o gás se expande com aumento de temperatura  ---  R- B

06- Trata-se de uma transformação isotérmica  ---  P.V=constante  --- inversamente proporcionais  ---  se você dobra a pressão, o volume cai pela metade  ---  massa específica  ---  μ=m/V  ---  μ e V são inversamente proporcionais  ---  se V cai pela metade, a massa específica μ duplicará  ---  R- B

07- Trata-se de uma transformação isotérmica  ---  P.V=K  ---   (V=1, P=2)  ---  2.1=K  ---  R- D  

08- Isotérmica  ---  P_o.V_o=P.V  ---  P_o.1=0,9P_o.V  ---  V=1/0,9  ---  V=1,111  ---  R- D

09- P_o.V_o/T_o=P.V/T  ---  (3P/2).V_o/0,93.T=P.V/T  ---  3V_o/1,86=V/1  ---  V_o/V=1,86/3  --- V_o/V=0,62

10- Observe que a primeira transformação o gás recebe calor e sua temperatura e volume aumentam sob pressão constante (pressão atmosférica + pressão devido ao peso do êmbolo), portanto trata-se de uma transformação à pressão constante (isobárica)  ---  na segunda transformação o gás está em equilíbrio térmico com o ambiente tendo a mesma temperatura que ele (isotérmica)  ---R- A

11- Devido à redução da pressão externa o volume do balão aumenta para que ocorra redução da pressão interna  ---  R- C

12- R- (1 + 2 + 8) = 11 

13- Como a temperatura de ebulição é crescente, com o aumento de pressão máxima o único diagrama que representa isto é o II. 

14- P_o.V_o/T_o=P.V/T  ---  P_oV_o/T_o=P.(6/5)V_o/(9/10)T_o  ---  P_o.V_o/T_o=(P.6V_o)/5 x 10/(9T_o)  ---  P_o=60P/45  ---  P=3/4P_o  ---  R- B

15- A transformação é isotérmica com diminuição da pressão e aumento de volume  ---  R- D

16-  a) Observe na última coluna que o produto  PxV é praticamente constante (Lei de Boyle para transformações isotérmicas)

b) Supondo que cada 8 unidades tenha 0,5cm  ---  regra de três  ---  8u - 0,5m  ---  24u – h  ---  h=1,5m  ---  P=P_o + dgh=1,0.10⁵ + 14.10³.10.1,5  ---  P=3,1.10⁵N/m²(Pa)

17- R- C  ---  veja teoria

18- Como o volume do cilindro que contém o gás se dilata muito pouco com a temperatura, pode-se dizer que se trata de uma transformação gasosa isométrica ou isovolumétrica (volume constante)  ---  como o carro fica exposto ao sol, a temperatura do gás aumenta e consequentemente a pressão exercida pelo gás também aumenta, pois P/T=constante e P é diretamente proporcional a T  ---  R- D

19- R- C  ---  veja teoria

20- À temperatura constante (isotérmica), se a pressão diminui, no caso a externa, o volume aumenta, pois PV=constante  ---  se a bola aumenta o volume, a pressão interna da bola diminui para igualar a pressão externa que também diminuiu  ---  R- A

21- Pressão na profundidade de 20m=2atm (devido à coluna de água) + 1atm (pressão atmosférica na superfície da água)  ---  P=3atm  ---  isotérmica  ---  P.V=K  ---    P_o.V_o=P.V  ---  1.V_o=3.V  ---  V=V_o/3  ---  V=0,333V_o  ---  R- A

22- Como a variação de volume dos pneus é desprezível, trata-se de uma isométrica, onde P/T=constante, sendo P diretamente proporcional a T  ---  R- C

23-  Até a explosão o volume do recipiente permanece constante (isométrica)  ---  P_i/T_i=P_f/T_f  ---  2,0.10⁵/78=4,0.10⁵/T_f  ---  T_f=156K  ---  R- B

24- Isovolumétrica  ---  P_o/T_o=P/T  ---  2,3/(27 + 273)=2,53/T  ---  2,3T=759  ---  T=330K=330 – 273  ---  T=57^oC

25- a) Se a porta do freezer fica aberta por algum tempo, parte do ar de seu interior é substituído pelo ar mais quente do exterior. Depois que você fecha a porta da geladeira, a temperatura interna do ar em seu interior irá diminuir e como se trata de uma isovolumétrica, a pressão também diminui (P/T=constante) fazendo com que a pressão externa fique maior que a interna, dificultando a abertura da porta. Mas, após alguns instantes, entra ar pelo sistema de vedação da geladeira, diminuindo a diferença entre as pressões externa e interna, facilitando, então, a abertura da porta.

b) Isovolumétrica  ---  P_oint/T_o=P_int/T  ---  1,0.10⁵/(27 + 273)=P_int/(-3 + 273)  ---  P_int=0,9.10⁵ N/m² (P_a)  ---  a diferença entre as pressões interna e externa sobre a porta da geladeira (ΔP) é igual à força resultante externa sobre a área da porta  ---  ΔP=F/S  --- 

(1,0.10⁵ – 0,9.10⁵)=F/(0,6x1)  ---  0,1.10⁵=F/0,6  ---  F=6,0.10³N

26-

27- Pressão à profundidade de 15m  ---  P=P_o + P_{água a 15m}=1,0 + 1,5  ---  P=2,5 atm  ---  trata-se de uma isotérmica (temperatura permanece constante dentro da bolha)  ---  P_o.V_o=P_i.V_i  ---  1.V_o=2,5V_i  ---  V_o=2,5V_i  ---  R- D

28- a) Se a porta do freezer fica aberta por algum tempo, parte do ar de seu interior é substituído pelo ar mais quente do exterior. Depois que você fecha a porta da geladeira, a temperatura interna do ar em seu interior irá diminuir e como se trata de uma isovolumétrica, a pressão também diminui (P/T=constante) fazendo com que a pressão externa fique maior que a interna,

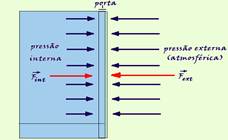
 dificultando a abertura da porta. Mas, após alguns instantes, entra ar pelo sistema de vedação da geladeira, diminuindo a diferença entre as pressões externa e interna, facilitando, então, a abertura da porta.

b) Se a pressão externa é maior que a interna, como Pressão=Força/Área da porta, a força externa terá intensidade maior que a força interna e a intensidade da força resultante será F_R=F_ext – F_int  ---  a transformação é isovolumétrica (volume constante)  --- 

P₁/T₁=P₂/T₂  ---  1,0.10⁵x1.000=P₂/(25 + 273)  ---  P₂=P_int=0,9.10⁵N/m² (P_a)  --- ΔP=F_R/S  ---  (1,0.10⁵ – 0,9.10⁵)=F_R/2  ---  F_R=0,2.10⁵N  ---  F_R=2,0.10⁴N

29- R- A  ---  veja teoria

30- Isobárica  ---  _.V /T=constante  ---  V é diretamente proporcional a T  ---  R- B

31- Isovolumétrica  ---  P_o/T_o=P/T  ---  30/(27 + 273)=32/T  ---  30/300=T/32  ---  T=320K  ---  T=320 – 273  ---  T=47^oC  ---  

R- D

32- Trata-se de uma transformação isobárica, pois a pressão exercida pelo ar no interior do cilindro é igual à pressão externa (atmosférica) exercida sobre a superfície livre da água  ---  observe que o nível da água externa e internamente continuará sendo

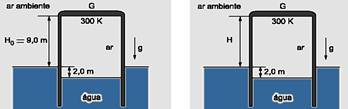
 de 2m, pois o sistema está em equilíbrio e o empuxo é o mesmo (o peso do ar não varia)  ---  volume inicial do ar  ---  V_i=S.h=S.(2 + 9)  ---  V_i=11.S (S é a área de seção transversal do cilindro)  ---  volume final do ar  ---  V=S.(H + 2)  ---  isobárica  ---  V_o/T_o=V/T  ---  11.S/300=(H + 2).S/360  ---  H=11,2m  ---  R- D

33- Utilizando a equação de estado dos gases ideais, temos: p₁V₁ = n₁RT₁ e p₂V₂ = n₂RT₂e, portanto,  . Como a parede é diatérmica e os gases estão em equilíbrio térmico, T₁ = T₂; como a parede pode mover-se sem atrito na horizontal e está em repouso, p₁ = p₂. Portanto,  . Mas   , logo, V₂ = 2 V₁. Substituindo esse resultado em V₁ + V₂ = V_o, obtemos 3V₁ = V_o, ou seja, V₁ = V_o/3 e, consequentemente,V₂ = 2V_o/3.  

34- Isotérmica  ---  P_o.V_o=P.V  ---  200.9=1.V  ---  V=1.800 ℓ   ---  40ℓ - 1min  ---  1.800 ℓ - t min  ---  t=1.800/40=45min  ---

 R- C

35- Como não há trocas de calor com o meio externo, a temperatura continua sendo T  ---  pressão final  ---  P_i.V_i=P_f.V_f  ---  P.(1/3)V=P_f.V  ---  P_f=P/3  ---  R- B

36- antes de comprimir a bomba você tem n₁ mol de ar no interior da bomba e n₂ no interior do pneu  ---  depois que o êmbolo desceu você terá no interior do pneu n mol tal que n=n₁ + n₂  ---  PV/RT=P₁V₁/RT₁ + P₂V₂/RT₂  ---  o processo é isotérmico  ---  PV=P₁V₁ + P₂V₂  ---  P₁=1 atm  ---  P₂=3atm  ---  V_{1 (interior da bomba)}=S.h=24cm².30cm  ---  V₁=720cm³  ---  V₁=0,72L  ---  P.2,4=1.0,72 + 3.2,4  ---  P=3,3 atm  ---  R- C

37- P_oV_o/T_o=P.V/T  ---  T=T_o (do enunciado)  ---  1,6.10⁵.3=P.4  ---  P=1,2.10⁵ Nm²

38- P₁V₁/T₁ + P₂V₂/T₂= P_fV_f/T_f  ---  P₁V₁ + P₂V₂= P_fV_f  ---  P₁V₁ + P₂V₂= P_f(V₁ + V₂)  ---  P_f=(P₁ + P₂)/2  ---  (5,0 + 18,0)/2  ---  P_f=11,5 atm  ---  R- B

39-

40- a) Situação antes - cilindro fechado  ---  situação depois – êmbolo já deslocado

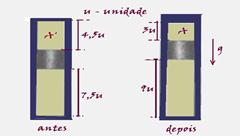
Antes  ---  P_A’=P_atm=1,0.10⁵N/m²  ---  V_A’­=4,5 unidades  ---  T_A’=27^oC=300K

Depois  ---  P_A=?  ---  V_A=3 unidades  ---  T_A=27^oC=300K

Isotérmica  ---  P_A’.V_APA_.VA  ---  1.10⁵.4,5=P_A.3  ---  P_A=1,5.10⁵N/m²

b) Parte inferior do cilindro

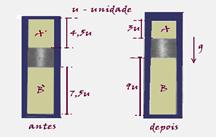
P_B’.V_B’/T_B’=P_B.V_B/T_B  ---  1.10⁵.7,5/300=1,5.10⁵.9/T_B  ---  T_B=540K ou 267^oC

41- a) P₁ = F/S + P_atmosférica = m.g/S + 10⁵ = 160x10/0,16 + 10⁵  = 10.000 + 10⁵ = 10⁴+ 10⁵ = 0,1.10⁵ + 10⁵   ---  P₁= 1,1.10⁵ Pa

b) Pela lei geral dos gases  ---  (p.V/T) = constante  ---  (P₁.V₁/T₁) = (P₂.V₂/T₂) e como V = H.S pode-se ainda escrever  ---   (P₁.V₁/T₁) = (P₂.V₂/T₂)  ---  (P₁.S.H₁/T₁) = (P₂.S.H₂/T₂)  ---  (P₁.H₁/T₁) = (P₂.H₂/T₂), mas o processo ocorre sob pressão constante e logo P₁ = P₂ então (H₁/T₁) = (H₂/T₂)  ---  a partir dos dados disponíveis  ---  (H₁/T₁) = (H₂/T₂)  --- (4/300) = (6/T₂)  --- T₂ = 1800/4  ---  T₂ = 450 K

c) Para o cálculo da eficiência do processo R será necessário determinar a variação de energia potencial gravitacional da plataforma, DE_P = m.g.DH e a quantidade de calor no processo Q que é dada por Q = m.c.DT  ---  DE_P = m.g.DH = 160.10.(6 – 4) = 3200 J  ---  para o cálculo da quantidade de calor é necessário conhecer a massa de ar no cilindro. ---   como a densidade do ar a 300 K foi fornecida pode-se fazer  ---  d = m/V  ---  m = d.V = 1,1.0,16.4  ---  d= 0,704 kg  ---  Q = m.c.DT = 0,704.10³.(450 – 300) ---  Q=105.600 J  ---   eficiência  ---   R = 3.200/105.600  ---  R= 0,03 = 3%

42- A lei geral dos gases afirma que P.V/T é constante  ---  entre o estado A e B o volume é constante e logo P/T = constante  --- 

(P/T)_A = (P/T)_B  ---  P/300 = 2P/T  ---  1/300 = 2/T  ---  T = 600 K  ---  entre o estado B e C a temperatura é constante e logo P.V = constante  ---  (P.V)_B = (P.V)_C  ---  2P.V = P_C.(3V/2)  --- 4P/3 = P_C  ---  R- D

43- a) Falsa- é isovolumétrica  ---  b) Correta- todos os pontos da curva AB tem a mesma temperatura  ---  c) Falsa – o volume é constante  ---  d) Falsa  ---  mais afastada, T₂>T₁  ---  R- B

44- a) p.V/T = constante --- 150.10³.V/300 = 160.10³.1,05.V/T --- (1/2)= 160.1,05./T  T = 168.2 = 336 K  ---  T = 63°C

b) p.V/T = constante --- 150.10³.V/300 = p.1,08.V/360 --- (10³/2)= 1,08.p/360 ---  p = 167.10³ Pa  ---  p = 1,67.10⁵ Pa

45- Isovolumétrica  ---  P_o/T_o=P/T  ---  P_o/(27 + 273)=P/(273 – 18)  ---  P=(255/300)P_o  ---  P=0,85P_o  ---  P=85% da pressão inicial  --- 

R- D 

46- Isotérmica  ---  P_o.V_o=P.V  ---  1.10⁵.100=P.140  ---  P=0,71.10⁵ Pa  ---  P=71.000Pa  ---  R- C

47- R- C

48- Estado inicial  ---   p = p₀  ---   V = V₀  ---   T = T₀  ---  1ª transformação  ---   isotérmica  ---   T₁ = T₀ e V₁ = V_o/2  ---  P₁V₁/T₁=P_oV_o/T_o  ---  P₁.(V_o/2)/T_o=P_oV_o/T_o  ---  P₁/2=P_o  ---  P₁=2P_o  ---  2ª transformação  ---  Isobárica: p₂ = p₁  ---   V₂ = 2 V₀  --- P₁V₁/T₁=P₂V₂/T₂  ---  (P₁.2V_o)/T_o=(P₁.V_o/2)/2T_o  ---  2/T₂=1/2T_o  ---  T₂=4T_o  ---  R- E

49-

50- Dados  ---  D = 20 cm  ---  R = 10 cm = 1 dm  ---  p = 1 atm  ---  T = 27 °C = 300 K  ---  M = 30 g/mol  ---  R = 0,08 atm·L/mol·K  ---  π = 3  ---  volume da bola  ---  V=(4πR³)/3=(4.3.1³)/3  ---  V=4dm³  ---  V=4L  ---  equação de Clapeyron  --- 

pV=(m/M).R.T  ---  m=(M.p.V)/RT=30.1.4/0,08.300=120/24  ---  m=5g  ---  R- B

51-

  Como o enunciado afirma que, durante o aquecimento não houve deformação da lata – Vi=Vf=V  ---  dados: Pi=1atm  ---   Ti=25oC=298K  ---  Vi=V  ---  Pf=?  ---  Tf=621oC=894K  ---  Vf=V  ---  trata-se de uma transformação isovolumétrica (isocórica, isométrica)  ---  Pi.V/Ti = Pf.V/Tf  ---  1.V/298 = Pf.V/894  ---  Pf=894/298  ---  Pf=3 atm  ---  R- C