
Dilatometria
Dilatação linear, superficial, volumétrica e dilatação dos líquidos
Dilatometria

Efeitos da dilatação sobre corpos sólidos

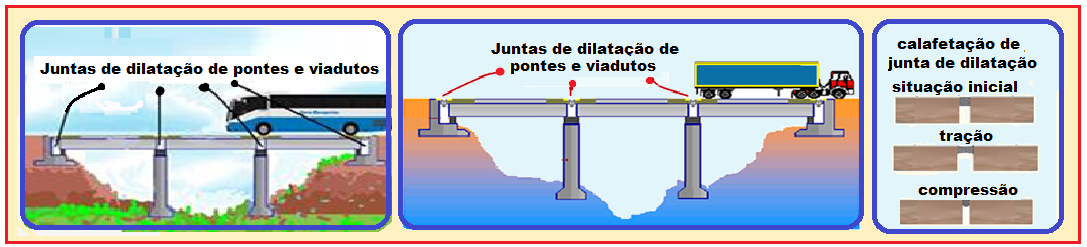

Dilatação linear dos sólidos
Trata-se da dilatação de uma das dimensões de um corpo, como por exemplo, seu comprimento. Considere uma haste metálica de comprimento Lo e à temperatura to.
Quando aquecida terá comprimento L a uma temperatura t.
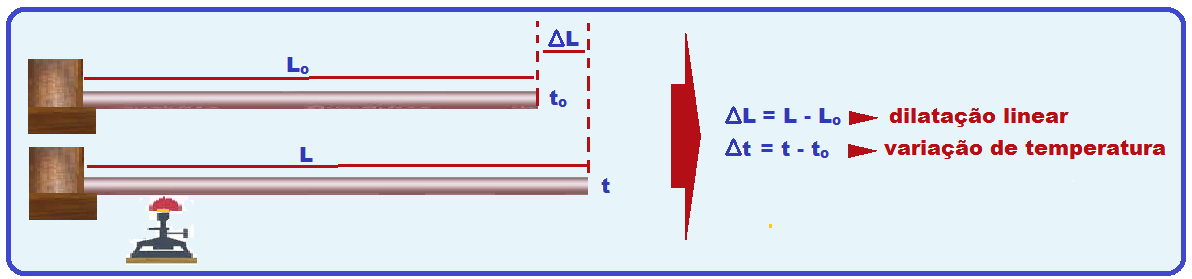
Características da dilatação linear
A dilatação linear ΔL é diretamente proporcional à variação de temperatura Δt.
A dilatação linear ΔL é diretamente proporcional ao comprimento inicial Lo.
A dilatação linear ΔL depende do material de que é constituído o corpo.
Matematicamente:

Sendo:
ΔL
![]() dilatação
linear (de
quanto dilatou o comprimento ou uma dimensão)
dilatação
linear (de
quanto dilatou o comprimento ou uma dimensão)
α
![]() coeficiente
de dilatação linear médio,
característica do material que constitui a barra.
coeficiente
de dilatação linear médio,
característica do material que constitui a barra.
Lo
![]() comprimento
inicial
comprimento
inicial
L
![]() comprimento
final
comprimento
final
Δt
![]() intervalo
de temperatura
intervalo
de temperatura
Unidades do coeficiente de dilatação linear α
Isolando
α
na equação
ΔL = Lo.α.Δt
![]() α
=
α
=
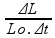
![]() como Lo e
ΔL devem ter a mesma unidade,
elas se
cancelam
como Lo e
ΔL devem ter a mesma unidade,
elas se
cancelam
![]() então a unidade
em que se exprime o coeficiente de dilatação linear é o
então a unidade
em que se exprime o coeficiente de dilatação linear é o
![]()
Observe que o coeficiente de dilatação linear representa a dilatação de um corpo de comprimento unitário, quando sua temperatura varia de um grau.
Gráfico do comprimento L em função da temperatura θ

Aplicações práticas de dilatação linear
![]()
Lâminas bimetálicas
Quando você solda duas barras de materiais diferentes você obtém uma lâmina bimetálica e, se você as submeter à mesma variação de temperatura, o sistema vai curvar-se para o lado da barra de menor coeficiente de dilatação, quando aquecida e para o lado da barra de maior coeficiente de dilatação, quando resfriada.
Observe nas figuras abaixo uma lâmina bimetálica constituída de alumínio (αaluminio=22.10-6 oC-1) e invar (liga de ferro e níquel – αinvar=1,0 .10-6 oC-1) e observe como a lâmina se inclina quando a temperatura aumenta ou diminui.

As lâminas bimetálicas são muito utilizadas nos relés térmicos (termostatos – dispositivos que
desligam automaticamente um circuito quando a temperatura atinge determinado valor) para controlar a temperatura de um dado ambiente, nas geladeiras, freezers, ferro elétrico automático, aparelhos de ar condicionado, fornos de fogões elétricos, etc.
Quando a temperatura do ambiente superar certo limite, o termostato deve desligar o aquecedor fazendo sua lâmina bimetálica envergar, abrindo os contatos, e desligando o aparelho da rede elétrica.
Quando
a temperatura
cair abaixo de certo limite,
o aquecedor
deve ser novamente ligado com a
lâmpada curvando-se em sentido oposto e fecha os contatos.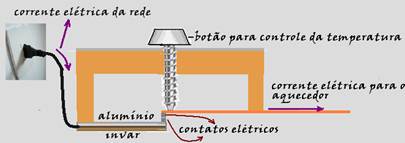
Esse mesmo processo é utilizado na prevenção de incêndio por motivo de sobrecarga elétrica, desligando o circuito quando a temperatura atingir certos limites.
![]()
Nos ferros elétricos automáticos, a temperatura de funcionamento, que é previamente regulada por um parafuso, é controlada por um termostato constituído de duas lâminas bimetálicas de igual composição.
Os dois metais que formam cada uma das lâminas têm coeficientes de dilatação αI (o mais interno) e αII o mais externo). As duas lâminas estão encurvadas e dispostas em contato elétrico, uma no interior da outra, como indicam as figuras.
A
corrente,
suposta contínua, entra pelo ponto 1 e sai pelo ponto 2,
conforme a figura 1, aquecendo
a resistência. 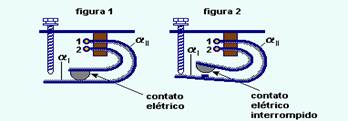
À medida que a temperatura aumenta, as lâminas vão se encurvando, devido à dilatação dos metais, sem interromper o contato.
Quando a temperatura desejada é alcançada, uma das lâminas é detida pelo parafuso, enquanto a outra continua encurvando-se, interrompendo o contato entre elas, conforme a figura 2.
Observe que as lâminas estão se encurvando para dentro, então α2 > α1 e, quanto mais baixo estiver o contato (mais apertado o parafuso), menor será a dilatação das lâminas e consequentemente menor será a temperatura.
![]()
Lâmpada Pisca-pisca
Quando você liga a lâmpada, a corrente elétrica flui da lâmina bimetálica para o filamento no qual

ela está em contato, que, por sua vez flui para todos os outros, tornando-os incandescentes e acendendo a lâmpada.
Quando a lâmina bimetálica ficar suficientemente quente ela se encurvará, interrompendo a corrente elétrica e apagando a lâmpada.
Em seguida ela se resfria e se curva, restabelecendo o contato e acendendo novamente a lâmpada.
E assim por diante.
![]()
Termômetro de lâmina bimetálica

Constituído por duas lâminas bimetálicas com metais diferentes, e soldadas uma com a outra, conforme a figura.
Sendo os metais diferentes, quando aquecidos eles sofrem diferentes dilatações, provocando um encurvamento diferente da lâmina para cada variação de temperatura.
São muito usados no controle de temperaturas de fornos, saunas, etc.
Dilatação superficial dos sólidos
Um corpo sólido sofre dilatação superficial quando sofre aumento em duas de suas dimensões.
Considere uma placa metálica de comprimento Co, largura Lo e espessura desprezível, que se encontra a uma temperatura to.
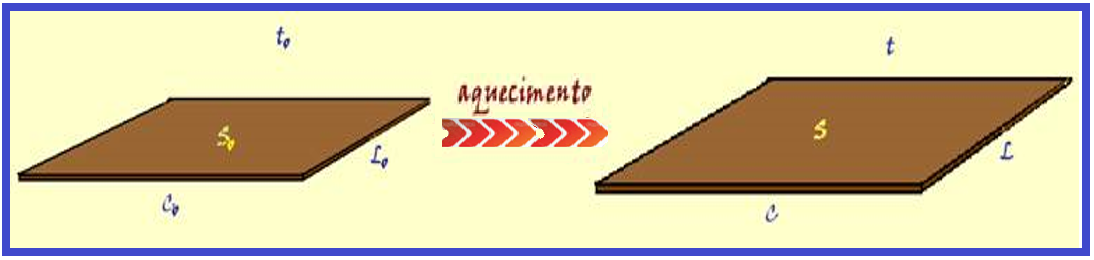
A área de sua superfície antes do aquecimento será So = Co.Lo e após o aquecimento será S = C.L.
Todas as leis válidas para a dilatação linear são também válidas para a dilatação superficial, ou seja:
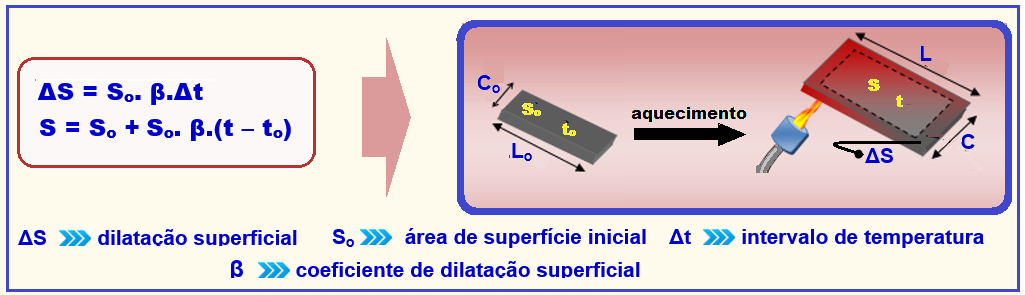
Na expressão acima, a letra grega β (beta) é uma grandeza constante, característica do material, denominada coeficiente de dilatação superficial médio.
Dilatação volumétrica ou cúbica dos sólidos
A dilatação volumétrica ou cúbica ocorre quando, devido a uma elevação de temperatura, um corpo
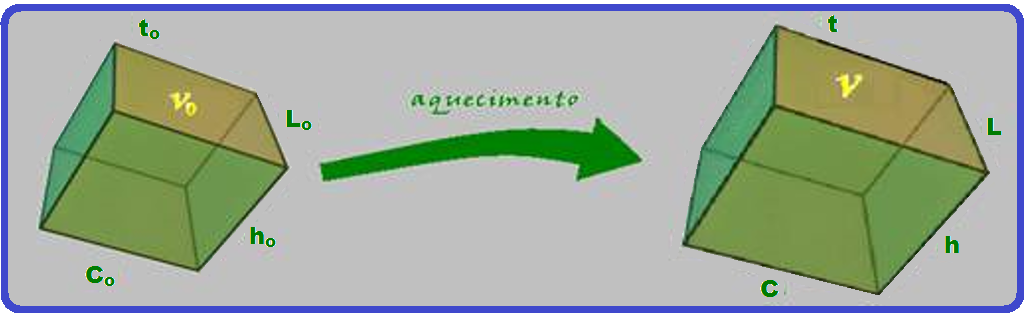
sofre um aumento em suas três dimensões (volume).
Todas as leis válidas para as dilatações linear e superficial são também válidas para a dilatação volumétrica, ou seja:
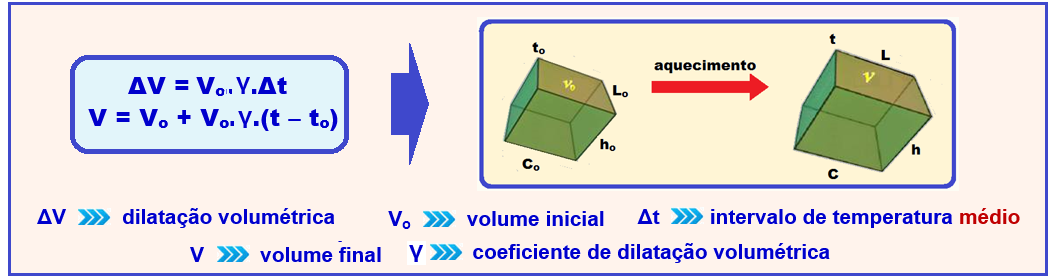
Relação entre os coeficientes de dilatação linear, superficial e volumétrica.

Dilatação dos líquidos
Os líquidos são amorfos, ou seja, não possuem forma própria, adquirindo o formato do recipiente

onde estão contidos.
Por esse motivo sofrem apenas dilatação volumétrica.
Dilatação aparente dos líquidos
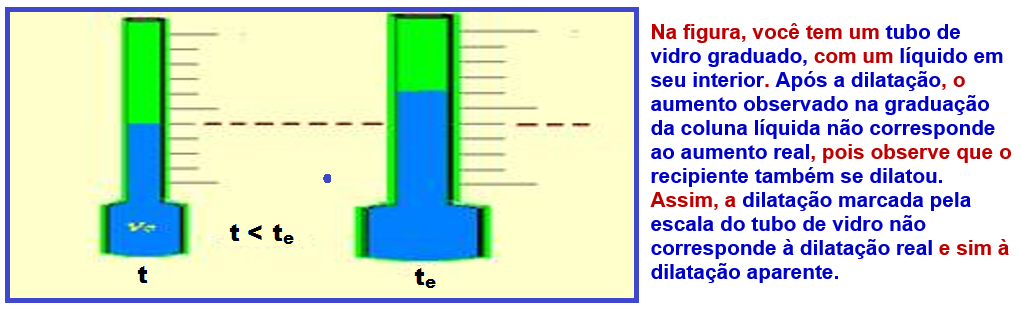
Dilatação real ou absoluta
Nela, leva-se em conta apenas a dilatação do líquido, sem considerar a dilatação do recipiente.
Pode-se verificar que um mesmo líquido, em diferentes frascos, possui um só coeficiente de dilatação absoluta ou real, característico desse líquido.
Porém, tem vários coeficientes de dilatação aparente, dependendo da natureza dos frascos que a encerram.
Dilatação do frasco
Lembre-se de que o frasco se comporta como se fosse maciço e constituído do mesmo material das paredes do recipiente.
Assim, o coeficiente de dilatação que se deve usar é o coeficiente de dilação do material de que é feito o frasco.
Equações que envolvem a dilatação dos líquidos
Observe atentamente as explicações a seguir:
O frasco da figura abaixo contém um “ladrão” com o líquido preenchendo o recipiente até seu nível (figura I).
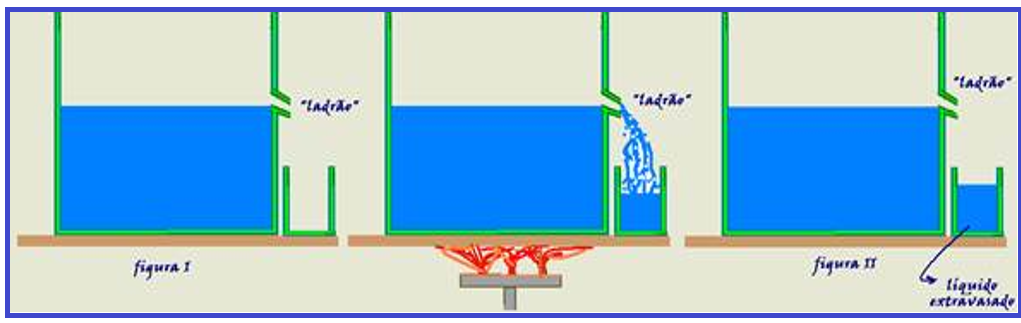
Após o conjunto ser aquecido de Δt, como normalmente os líquidos se dilatam mais que os sólidos, parte do líquido extravasa pelo “ladrão” (figura II).
Esse volume de líquido extravasado corresponde à dilatação aparente do líquido (ΔVap), de volume inicial Vo e coeficiente de dilatação volumétrica aparente (γap) e não à dilatação real do líquido, já que o frasco também se dilata.
Se você conhecer a dilatação do frasco (ΔVf) que corresponde à quanto seu volume aumentou, poderá determinar a dilatação real sofrida pelo líquido.
Exemplo numérico:
Se
o
volume do frasco que contém o líquido (até o nível do “ladrão),
aumentar, por exemplo, de 1 cm3 (ΔVf)
= 1 cm3 e,
se o volume
de líquido extravasado for de 3 cm3 (ΔVap
=
3 cm3),
você
pode obter a dilatação
real do líquido (ΔVR),
pois, ΔVR =
ΔVap +
ΔVf
![]() ΔVR
=
3 + 1 = 4 cm3.
ΔVR
=
3 + 1 = 4 cm3.
Equações:
![]() Dilatação
real do líquido
Dilatação
real do líquido
![]() ΔVR
=
Vo.γlíquido.Δt
ΔVR
=
Vo.γlíquido.Δt
![]() (Vo
(Vo
![]() volume inicial do líquido)
volume inicial do líquido)
 Dilatação
aparente (volume de líquido extravasado)
Dilatação
aparente (volume de líquido extravasado)
![]() ΔVap
=
Vo.γap.Δt
ΔVap
=
Vo.γap.Δt
![]() (Vo
(Vo
![]() volume inicial do líquido)
volume inicial do líquido)
![]() Dilatação
do frasco (recipiente)
Dilatação
do frasco (recipiente) ![]() ΔVf
=
Vo.γfrasco.Δt
ΔVf
=
Vo.γfrasco.Δt
![]() (Vo
(Vo
![]() volume inicial do líquido)
volume inicial do líquido)
![]() ΔVR =
ΔVap +
ΔVf
(veja
exemplo numérico acima)
ΔVR =
ΔVap +
ΔVf
(veja
exemplo numérico acima)
![]() γR
=
γap +
γfrasco
( R
é o coeficiente de dilatação volumétrica real do líquido ap
é o coeficiente de dilatação volumétrica aparente e frasco
é o coeficiente de dilatação volumétrica do frasco).
γR
=
γap +
γfrasco
( R
é o coeficiente de dilatação volumétrica real do líquido ap
é o coeficiente de dilatação volumétrica aparente e frasco
é o coeficiente de dilatação volumétrica do frasco).
Analise alguns exercícios resolvidos sobre dilatação dos líquidos


Um frasco de capacidade para 10 litros está completamente cheio de glicerina e encontra-se à temperatura de 10ºC.
Aquecendo-se o frasco com a glicerina até atingir 90ºC, observa-se que 352 mL de glicerina transborda do frasco.
Sabendo-se que o coeficiente de dilatação volumétrica da glicerina é
5,0.10-4 ºC-1, calcule o coeficiente de dilatação linear do frasco é ºC-1.
São
dados: Vo
= 10 L (do
frasco e da glicerina)
![]() to
= 10 oC
to
= 10 oC
![]() t
= 90 oC
t
= 90 oC
![]() ΔVap
=
352 mL = 352.
ΔVap
=
352 mL = 352.
10-3
L
![]() γglicerina
=
5,0.10-4
oC-1.
γglicerina
=
5,0.10-4
oC-1.
O
volume
de glicerina que extravasou corresponde à dilatação aparente
![]() ΔVap
=
Vo.
γap.Δt
ΔVap
=
Vo.
γap.Δt
![]()
352.10-3
=
10.γap.(90
– 10)
![]() γap
=
γap
=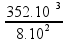
![]() γap
=
44.10-5 oC-1.
γap
=
44.10-5 oC-1.
γglicerina
=
γap+
γf
![]() 5,0.10-4
=
44.10-5 +
γf
5,0.10-4
=
44.10-5 +
γf ![]() γf
=
5,0.10-4 –
4,4.10-4
γf
=
5,0.10-4 –
4,4.10-4
![]() γf
=
6,0.10-5 oC-1
(coeficiente de dilatação volumétrica do frasco).
γf
=
6,0.10-5 oC-1
(coeficiente de dilatação volumétrica do frasco).
Acontece que o exercício quer o coeficiente de dilatação linear do frasco αf = γf/3
αf
=
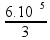
![]() αf
=
2,0.10-5 oC-1 .
αf
=
2,0.10-5 oC-1 .


A
dilatação
aparente corresponde ao
aumento
na indicação da escala
![]() ΔVap
=
525
– 500 =
25 cm3
ΔVap
=
525
– 500 =
25 cm3
![]() ΔVap
=
Vo.γap.Δt
ΔVap
=
Vo.γap.Δt
![]() 25 = 500.γap.50
25 = 500.γap.50
![]() γ
p=
γ
p=
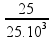
![]() γap
=
10-3 oC-1.
γap
=
10-3 oC-1.
γlíq
=
γV +
γap
![]() γlíq
=
0,001 + 0,00001
γlíq
=
0,001 + 0,00001
![]() γlíq
=
0,00101 oC-1.
γlíq
=
0,00101 oC-1.
![]()
Um
recipiente
de vidro tem capacidade de 100cm3 a
10oC
e contém, a essa temperatura, 99cm3 de
um certo líquido de coeficiente de dilatação cúbica γ =
2.10-4 oC-1.
A que temperatura o recipiente estará
completamente
cheio de líquido?
(Considere o coeficiente de dilatação cúbica do vidro como sendo
10-5 oC-1).
Quando
o recipiente estiver
completamente cheio de líquido,
eles (recipiente e líquido) deverão
ter o mesmo volume
![]() ΔVvidro
=
ΔVlíquido
ΔVvidro
=
ΔVlíquido
![]() 100(1 + 10-5
(t – 10) = 99.(1 + 2.10-4).(t
– 10)
100(1 + 10-5
(t – 10) = 99.(1 + 2.10-4).(t
– 10)
![]()
t
= 19,6.10-2
/18,6.10-3
![]() t
≈ 10,5
oC.
t
≈ 10,5
oC.
![]()
Um
recipiente
de vidro encontra-se
completamente
cheio de
um líquido
a 0 ºC.
Quando o
conjunto
é aquecido até 80 ºC, o volume do líquido que transborda
corresponde a 4% do volume
que
o líquido possuía a 0 ºC. Sabendo
que o coeficiente
de dilatação volumétrica do vidro
é igual
a 27.10-6
ºC-1,
determine o coeficiente
de dilatação real do líquido.
Vo
= volume
inicial do recipiente =
volume inicial do líquido a 0oC.
Dilatação
do vidro com Vo
= volume inicial do líquido
![]() V
= Vo.(1+γ.(t
– to)
V
= Vo.(1+γ.(t
– to)
![]() V = Vo.(1+.27.10-5
.80)
V = Vo.(1+.27.10-5
.80)
![]() V
= 1,00216.Vo
(volume
final do recipiente).
V
= 1,00216.Vo
(volume
final do recipiente).
O
líquido se dilatou V’ que é o volume do recipiente V + o volume
de líquido derramado que é de 4% de Vo.
V’
= V + 0,04Vo
![]() Dilatação
do líquido
Dilatação
do líquido
![]() V'
= Vo.(1+γ'.Δt)
onde
γ'
é o coeficiente
de dilatação aparente do
líquido.
V'
= Vo.(1+γ'.Δt)
onde
γ'
é o coeficiente
de dilatação aparente do
líquido.
V'
= V + 0,04Vo
![]() V'
= (1,00216Vo)
+ 0,04Vo
V'
= (1,00216Vo)
+ 0,04Vo
![]() V' = 1,04216Vo
V' = 1,04216Vo
V'
= Vo.(1+γ'.Δt)
![]() 1,04216Vo
=
Vo(1+γ'.80)
1,04216Vo
=
Vo(1+γ'.80)
![]() 1,04216
= 1 + 80γ'
1,04216
= 1 + 80γ'
![]()
80γ'=0,04216
![]() γ’
= 5,27.10-4
ºC-1.
γ’
= 5,27.10-4
ºC-1.
O que você deve saber, orientações e dicas
![]()

Sendo:
ΔL
![]() dilatação
linear (de
quanto dilatou o comprimento ou uma dimensão)
dilatação
linear (de
quanto dilatou o comprimento ou uma dimensão)
α
![]() coeficiente
de dilatação linear médio,
característica do material que constitui a barra.
coeficiente
de dilatação linear médio,
característica do material que constitui a barra.
Lo
![]() comprimento
inicial
comprimento
inicial
L
![]() comprimento
final
comprimento
final
Δt
![]() intervalo
de temperatura
intervalo
de temperatura
![]()

![]()
Se
as armações
metálicas das figuras forem de mesmo material, homogêneas e de
secção transversal constante e
se sofrerem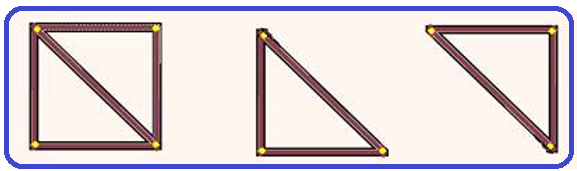
a mesma variação de temperatura (por exemplo, sendo aquecidas), elas não se deformarão, os pontos de contato não trocarão forças entre si, elas manterão o formato inicial, mas com dimensões maiores e, todos os ângulos internos permanecerão os mesmos.
Observe que seus comprimentos não se dilatam por igual, a hipotenusa se dilata mais que os catetos.
![]()
Lâminas bimetálicas
Quando você solda duas barras de materiais diferentes você obtém uma lâmina bimetálica e, se você as submeter à mesma variação de temperatura, o sistema vai curvar-se para o lado da barra de menor coeficiente de dilatação, quando aquecida e para o lado da barra de maior coeficiente de dilatação, quando resfriada.
Observe nas figuras abaixo uma lâmina bimetálica constituída de alumínio (αaluminio = 22.10-6 oC-1) e

invar (liga de ferro e níquel, αinvar = 1,0 .10-6 oC-1) e observe como a lâmina se inclina quando a temperatura aumenta ou diminui.
![]()
Utilidades das lâminas bimetálicas
As lâminas bimetálicas são muito utilizadas nos relés térmicos (termostatos, que são dispositivos que desligam automaticamente um circuito quando a temperatura atinge determinado valor) para controlar a temperatura de um dado ambiente, nas geladeiras, freezers, ferro elétrico automático, aparelhos de ar condicionado, fornos de fogões elétricos, etc.
Quando a temperatura do ambiente superar certo limite, o termostato deve desligar o aquecedor fazendo sua lâmina bimetálica envergar abrindo os contatos, e desligando o aparelho da rede elétrica.
Quando
a temperatura
cair abaixo de certo limite,
o aquecedor
deve ser novamente ligado com
a lâmpada
curvando-se em sentido oposto e fecha os contatos.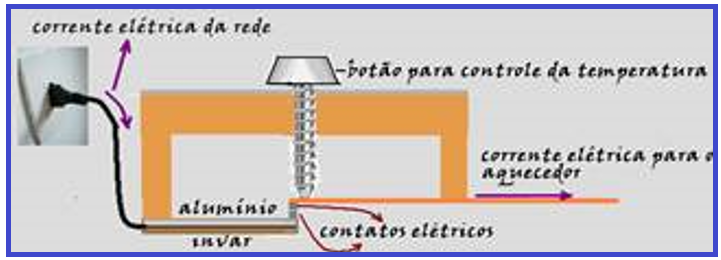
Esse mesmo processo é utilizado na prevenção de incêndio por motivo de sobrecarga elétrica, desligando o circuito quando a temperatura atingir certos limites.
![]()

![]()

![]()
Pêndulo simples
Trata-se de corpo de massa m suspenso por um fio inextensível e de massa desprezível.
Quando
afastado
de sua posição de equilíbrio e solto,
o pêndulo oscilará
em um plano vertical sob
à ação da gravidade
g;
o movimento é periódico
e oscilatório e o seu período (tempo
que ele demora para efetuar um “vai
e vem” completo)
é fornecido por T=2π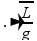
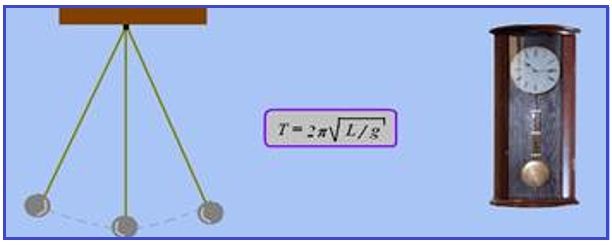
O Pêndulo Simples, através da equação acima, também fornece um método para medições do valor da aceleração da gravidade g num dado local, medindo-se o comprimento do fio L e o período de oscilação T, substituindo esses dois dados na equação acima você acha o valor da aceleração da gravidade g nesse local.
Observe que o período T, é independente da massa m do corpo suspenso (não aparece na fórmula).
![]()
![]()
Veja a resolução desse exercício:
A
figura mostra
uma ponte apoiada sobre
dois
pilares feitos de materiais diferentes.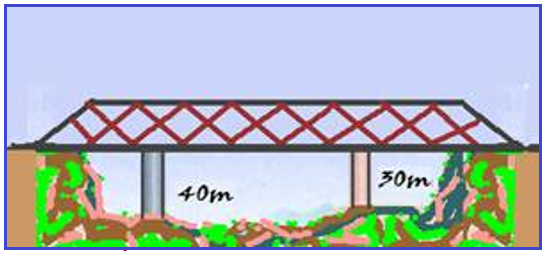
Como se vê, o pilar mais longo, de comprimento L1 = 40 m, possui coeficiente de dilatação linear α = 18. 10-6 °C-1.
O pilar mais curto tem comprimento L2 = 30 m. Para que a ponte permaneça sempre na horizontal, determine o coeficiente linear do material do segundo pilar.
Para
que a ponte
permaneça sempre na horizontal,
os dois
pilares devem sofrer a mesma dilatação para a mesma variação de
temperatura
![]() ΔL1=
ΔL2
ΔL1=
ΔL2
![]() L01.α1.Δt
= L02.α2.Δt
L01.α1.Δt
= L02.α2.Δt
![]() 40.18.10-6
=
30.α2
40.18.10-6
=
30.α2
![]() α2
=
24.10-6 oC-1.
α2
=
24.10-6 oC-1.
![]()

![]()
Se uma placa metálica com orifício for aquecida, verifica-se que o orifício aumenta, como se fosse

constituído pelo material da placa, pois tudo se passa como se o furo tivesse um coeficiente de dilatação superficial igual àquele da substância da placa.
![]()
Se
você despejar
água fervente num copo de vidro,
ele pode se quebrar,
pois a dilatação
não é uniforme,
a parte
interna se dilata mais que a externa.
O mesmo poderia ocorrer se você despejasse água gelada num copo quente e, nesse caso a parte interna se contrai mais que a externa.
Se
você
despejar água fervente num copo de vidro até a metade, ele
pode quebrar
mais facilmente do
que quando cheio
completamente, porque
a temperatura
dele muda uniformemente,
o que causa
a quebra do copo é o fato de que a parte de baixo fique mais quente
e se dilate mais do que a de cima, podendo provocar a ruptura.
![]()
Observe
também que se
você tiver dois copos de diferentes coeficientes de dilatação,
o de menor
coeficiente apresenta maior
dificuldade de se quebrar quando aquecido, pois se dilata menos.
![]()

![]()

![]()
Se
as duas
esferas da figura abaixo forem idênticas
(mesmas dimensões e mesmo material) e sofrerem a
mesma variação de temperatura,
elas sofrem a mesma
dilatação volumétrica.

Corpos ocos se dilatam como se fossem maciços e sua dilatação é calculada utilizando o coeficiente de dilatação volumétrica do material que constitui sua superfície.
O mesmo acontece se ele tiver um furo, e se a esfera com o furo for aquecida, verifica-se que o furo aumenta, como se fosse como se fosse constituído pelo material da esfera.
Assim, o furo se comporta como tivesse o mesmo coeficiente de dilatação volumétrica que o da substância que constitui a esfera.
![]()
Equações utilizadas na dilatação de líquidos
![]() Dilatação
real do líquido
Dilatação
real do líquido
![]() ΔVR
=
Vo.γlíquido.Δt
ΔVR
=
Vo.γlíquido.Δt
![]() (Vo
(Vo
![]() volume inicial do líquido)
volume inicial do líquido)
![]() Dilatação
aparente (volume de líquido extravasado)
Dilatação
aparente (volume de líquido extravasado)
![]() ΔVap
=
Vo.γap.Δt
ΔVap
=
Vo.γap.Δt
![]() (Vo
(Vo
![]() volume inicial do líquido)
volume inicial do líquido)
![]() Dilatação
do frasco (recipiente)
Dilatação
do frasco (recipiente) ![]() ΔVf
=
Vo.γfrasco.Δt
ΔVf
=
Vo.γfrasco.Δt
![]() (Vo
(Vo
![]() volume inicial do líquido)
volume inicial do líquido)
![]() ΔVR =
ΔVap +
ΔVf
(veja
exemplo numérico acima)
ΔVR =
ΔVap +
ΔVf
(veja
exemplo numérico acima)
![]() γR
=
γap +
γfrasco
( R
é o coeficiente de dilatação volumétrica real do líquido ap
é o coeficiente de dilatação volumétrica aparente e frasco
é o coeficiente de dilatação volumétrica do frasco).
γR
=
γap +
γfrasco
( R
é o coeficiente de dilatação volumétrica real do líquido ap
é o coeficiente de dilatação volumétrica aparente e frasco
é o coeficiente de dilatação volumétrica do frasco).
![]()
O coeficiente de dilatação aparente depende da natureza do líquido e do material que constitui o recipiente que o contém.
Exercícios de vestibulares com resolução comentada sobre
Dilatação linear, superficial, volumétrica e dilatação dos líquidos
01-(Uema) Um arame de aço, dobrado conforme a figura, está engastado no teto, no ponto A. Aumentando a sua temperatura de maneira homogênea, a extremidade B terá um deslocamento que será mais bem representado
por qual dos vetores?

02-(UNESP-SP)
A lâmina bimetálica da figura abaixo é feita de cobre (α=
1,4.10-5 ºC-1)
e de alumínio ((α = 2,4.10-5 ºC-1).
Uma das partes não pode deslizar sobre a outra e o sistema está
engastado numa parede.
Se na temperatura ambiente (27 ºC) ela é horizontal, a afirmativa correta sobre o comportamento da lâmina ((α é o coeficiente de dilatação linear) é:
a) Sempre se curva para baixo quando muda a temperatura.
b)
Sempre se curva para cima quando muda a temperatura.
c) Curva-se
para baixo se θ > 27 ºC e para cima de θ < 27 ºC.
d)
Curva-se para cima se θ > 27 ºC e para baixo se θ < 27
ºC.
e) Somente se curva se θ > 27 ºC.
03-(FGV-SP)
Um
serralheiro monta, com o mesmo tipo de vergalhão de ferro, a armação
esquematizada.
A barra transversal que liga os pontos A e B não exerce forças sobre esses pontos. Se a temperatura da armação for aumentada, a barra transversal
a) continua não exercendo forças sobre os pontos A e B.
b) empurrará os pontos A e B, pois ficará √2 vezes maior que o novo tamanho que deveria assumir.
c) empurrará os pontos A e B, pois ficará LoαΔt vezes maior que o novo tamanho que deveria assumir.
d) tracionará os pontos A e B, pois ficará √2 vezes menor que o novo tamanho que deveria assumir.
e) tracionará os pontos A e B, pois ficará LoαΔt vezes menor que o novo tamanho que deveria assumir.
04-(UFAL) O fato de barras de ferro contidas em uma viga de concreto não provocarem
rachaduras no concreto explica-se pela semelhança que existe entre os valores do
a) calor específico desses materiais.
b) calor de fusão desses materiais.
c) coeficiente de condutividade térmica desses materiais.
d) coeficiente de dilatação linear desses materiais.
e) coeficiente de atrito desses materiais.
05-(UFRJ-RJ)
Um
quadrado foi montado com três hastes de alumínio (αAl =
24. 10-6 C-1)
e uma haste de aço (αaço =
12. 10-6 C-1),
e todas inicialmente à mesma temperatura.
O sistema é, então, submetido a um processo de aquecimento, de forma que a variação de temperatura é a mesma em todas as hastes.
Podemos afirmar que, ao final do processo de aquecimento, a figura formada pelas hastes estará mais próxima de um:
a) quadrado.
b) retângulo.
c) losango.
d) trapézio retângulo.
e) trapézio isósceles.
06- (UFF-RJ)
Nos
ferros elétricos automáticos, a temperatura de funcionamento, que é
previamente regulada por um parafuso, é controlada por um termostato
constituído de duas lâminas bimetálicas de igual composição. Os
dois metais que formam cada uma das lâminas têm coeficientes de
dilatação α1 -
o mais interno - α2.
As duas lâminas estão encurvadas e dispostas em contato elétrico,
uma no interior da outra, como indicam as figuras a seguir.
A corrente, suposta contínua, entra pelo ponto 1 e sai pelo ponto 2, conforme a figura 1, aquecendo a resistência. À medida que a temperatura aumenta, as lâminas vão se encurvando, devido à dilatação dos metais, sem interromper o contato. Quando a temperatura desejada é alcançada, uma das lâminas é detida pelo parafuso, enquanto a outra continua encurvando-se, interrompendo o contato entre elas, conforme a figura 2.
Com relação à temperatura do ferro regulada pelo parafuso e aos coeficientes de dilatação dos metais das lâminas, é correto afirmar que, quanto mais apertado o parafuso:
a) menor será a temperatura de funcionamento e α1 > α2
b) maior será a temperatura de funcionamento e α1 < α2
c) maior será a temperatura de funcionamento e α1 > α2
d) menor será a temperatura de funcionamento e α1 < α2
e) menor será a temperatura de funcionamento e α1 = α2
07-(UECE-CE)
Três
barras retas de chumbo são interligadas de modo a formarem um
triângulo isósceles de base 8cm e altura 10cm.
Elevando a temperatura do sistema:
a) a base e os lados se dilatam igualmente
b) os ângulos se mantém
c) a área se conserva
d) o ângulo do vértice varia mais que os ângulos da base.
08-(Olimpíada Paulista de Física) É muito comum acontecer de, quando copos iguais são empilhados, colocando-se um dentro do outro, dois deles ficarem emperrados, tornando-se difícil separá-los. Considerando o efeito da dilatação térmica, pode-se afirmar que é possível retirar um copo de dentro do outro se:
a)
os copos emperrados forem mergulhados em água bem quente.
b) no
copo interno for despejada água quente e o copo externo for
mergulhado em água bem fria.
c) os copos emperrados forem
mergulhados em água bem fria.
d) no copo interno for despejada
água fria e o copo externo for mergulhado em água bem quente.
e)
não é possível separar os dois copos emperrados considerando o
efeito de dilatação térmica.
09-(UFF-RJ)
A
figura representa um dispositivo, que possui uma lâmina bimetálica
enrolada em forma de espiral, utilizado para acusar superaquecimento.
Um ponteiro está acoplado à espiral cuja extremidade interna é fixa. A lâmina é constituída por dois metais, fortemente ligados, com coeficientes de dilatação linear distintos, α1 e α2, indicados, respectivamente, pelas regiões azul e vermelha da espiral.
Assinale a opção que expressa corretamente o funcionamento do dispositivo quando a temperatura aumenta.
a) independentemente da relação entre α1 e α2, a espiral sempre se fecha e o ponteiro gira no sentido horário.
b) com α1 < α2, a espiral se fecha e o ponteiro gira no sentido horário.
c) com α1 > α2, a espiral se abre e o ponteiro gira no sentido horário.
d) com α1 < α2, a espiral se abre e o ponteiro gira no sentido horário.
e) com α1 > α2, a espiral se fecha e o ponteiro gira no sentido horário.
10-(FUNREI-MG)
A
figura mostra uma ponte apoiada sobre dois pilares feitos de
materiais diferentes.
Como se vê, o pilar mais longo, de comprimento L1 = 40 m, possui coeficiente de dilatação linear α = 18. 10-6°C-1.O pilar mais curto tem comprimento L2 = 30 m. Para que a ponte permaneça sempre na horizontal, determine o coeficiente linear do material do segundo pilar.
11-(PUC-RJ)
A imprensa tem noticiado as temperaturas anormalmente altas que vêm
ocorrendo no atual verão, no hemisférionorte. Assinale a opção
que indica a dilatação (em cm) que um trilho de 100 m sofreria
devido a uma variação de temperatura igual a 20 °C, sabendo que o
coeficiente linear de dilatação térmica do trilho vale α =
1,2.10-5 por
grau Celsius.
a) 3,6
b) 2,4
c) 1,2
d) 1,2.10-3
e) 2,4.10-3
12-(UEL-PR)
O
coeficiente de dilatação linear do aço é 1,1.10-5 ºC.
Os trilhos de uma via férrea têm 12m cada um na
temperatura de 0ºC. Sabendo-se que a temperatura máxima na região
onde se encontra a estrada é 40ºC, o espaçamento mínimo
entre dois trilhos consecutivos deve ser, aproximadamente, de:
a) 0,40 cm
b) 0,44 cm
c) 0,46 cm
d) 0,48 cm
e) 0,53 cm
13-(MACKENZIE) Ao se aquecer de 1,0ºC uma haste metálica de 1,0m, o seu comprimento aumenta de 2,0.10-2mm. O aumento do comprimento de outra haste do mesmo metal, de medida inicial 80cm, quando a aquecemos de 20ºC, é:
![]()
14-(UNESP-SP)
A dilatação térmica dos sólidos é um fenômeno importante em
diversas aplicações de engenharia, como construções de pontes,
prédios e estradas de ferro. Considere o caso dos trilhos de trem
serem de aço, cujo coeficiente de dilatação é α = 11 .
10-6 °C-1.
Se a 10°C o comprimento de um trilho é de 30m, de quanto aumentaria
o seu comprimento se a temperatura aumentasse para 40°C?
a) 11 .
10-4 m 
b) 33 . 10-4 m
c) 99 . 10-4 m
d) 132 . 10-4 m
e)
165 . 10-4 m
15-(UFPE-PE)
- O gráfico abaixo representa a variação, em milímetros, do
comprimento de uma barra

metálica, de tamanho inicial igual a 1,000m, aquecida em um forno industrial.
Qual é o valor do coeficiente de dilatação térmica linear do material de que é feita a barra, em unidades de 10-6 ºC-1.
16-(UFRRJ-RJ) Um cilindro de aço, que se encontra em um ambiente cuja temperatura é de 30°C,

tem como medida de seu diâmetro 10,00 cm. Levado para outro ambiente cuja temperatura é de 2,7 °C, ele sofre uma contração térmica.
Considere: coeficiente de dilatação linear do aço α = 11.10-6(°C-1)
Calcule o diâmetro final do cilindro.
17-(UFRS-RS) Uma barra de aço e uma barra de vidro têm o mesmo comprimento à temperatura de 0 °C, mas, a 100 °C, seus comprimentos diferem de 0,1 cm. (Considere os coeficientes de dilatação linear do aço e do vidro iguais a 12.10-6 °C¢ e 8. 10-6 °C¢, respectivamente.)
Qual é o comprimento das duas barras à temperatura de 0 °C?
![]()
18-(UFU-MG) O gráfico a seguir representa o comprimento L, em função da temperatura θ, de dois fios metálicos finos A e B.
Com
base nessas informações, é correto afirmar que
a) os coeficientes de dilatação lineares dos fios A e B são iguais.
b) o coeficiente de dilatação linear do fio B é maior que o do fio A.
c) o coeficiente de dilatação linear do fio A é maior que o do fio B.
d) os comprimentos dos dois fios em š = 0 são diferentes.
19-(UNESP-SP)
Duas
lâminas metálicas, a primeira de latão e a segunda de aço, de
mesmo comprimento à temperatura ambiente, são soldadas rigidamente
uma à outra, formando uma lâmina bimetálica, conforme a figura a
seguir.
O coeficiente de dilatação térmica linear do latão é maior que o do aço. A lâmina bimetálica é aquecida a uma temperatura acima da ambiente e depois resfriada até uma temperatura abaixo da ambiente. A figura que melhor representa as formas assumidas pela lâmina bimetálica, quando aquecida (forma à esquerda) e quando resfriada (forma à direita), é

20-(UFPR-PR)
Um
cientista está à procura de um material que tenha um coeficiente de
dilatação alto. O objetivo dele é produzir vigas desse material
para utilizá-las como suportes para os telhados das casas. Assim,
nos dias muito quentes, as vigas dilatar-se-iam bastante, elevando o
telhado e permitindo uma certa circulação de ar pela casa,
refrescando o ambiente. Nos dias frios, as vigas encolheriam e o
telhado abaixaria, não permitindo a circulação de ar. Após
algumas experiências, ele obteve um composto com o qual fez uma
barra. Em seguida, o cientista mediu o comprimento L da barra em
função da temperatura T e obteve o gráfico a seguir:

Analisando o gráfico, é correto afirmar que o coeficiente de dilatação linear do material produzido pelo cientista vale:
a) α = 2 . 10-5 °C-1.
b) α = 3 . 10-3 °C-1.
c) α = 4 . 10-4 °C-1.
d) α = 5 . 10-5 °C-1.
e) α = 6 . 10-4 °C-1.
21-(UFPE-PE) A figura mostra um balanço AB suspenso por fios, presos ao teto.
Os
fios têm coeficientes de dilatação linear αA =
1,5 x 10-5 K-1 e
αB =
2,0 x 10-5 K-1,
e comprimentos LA e
LB,
respectivamente, na temperatura To.
Considere LB =
72 cm e determine o comprimento LA,
em cm, para que o balanço permaneça sempre na horizontal (paralelo
ao solo), em qualquer temperatura.
22-(UFSC-SC) Um aluno de ensino médio está projetando um experimento sobre a dilatação dos sólidos. Ele utiliza um rebite de material A e uma placa de material B, de coeficientes de dilatação térmica, respectivamente, iguais a αA e αB. A placa contém um orifício em seu centro, conforme indicado na figura. O raio RA do rebite é menor que o raio RB do orifício e ambos os corpos se encontram em equilíbrio térmico com o meio.

Assinale a(s) proposição(ões) CORRETA(S).
(01) Se αA > αB a folga irá aumentar se ambos forem igualmente resfriados.
(02) Se αA > αB a folga ficará inalterada se ambos forem igualmente aquecidos.
(04) Se αA < αB e aquecermos apenas o rebite, a folga aumentará.
(08) Se αA = αB a folga ficará inalterada se ambos forem igualmente aquecidos.
(16) Se αA = αB e aquecermos somente a placa, a folga aumentará.
(32) Se αA > αB a folga aumentará se apenas a placa for aquecida.
23-(UFRS-RS)
Assinale
a alternativa que preenche corretamente as lacunas do texto a seguir,
na ordem em que aparecem.
A figura que segue representa um anel de alumínio homogêneo, de raio interno Ra e raio externo Rb, que se encontra à temperatura ambiente.
Se o anel for aquecido até a temperatura de 200 °C, o raio Ra .......... e o raio Rb .......... .
a) aumentará - aumentará
b) aumentará - permanecerá constante
c) permanecerá constante - aumentará
d) diminuirá - aumentará
e) diminuirá - permanecerá constante
24-(UFRJ-RJ)
Um
incêndio ocorreu no lado direito de um dos andares intermediários
de um edifício construído com estrutura metálica, como ilustra a
figura 1. Em conseqüência do incêndio, que ficou restrito ao lado
direito, o edifício sofreu uma deformação, como ilustra a figura
2.
Com base em conhecimentos de termologia, explique por que o edifício entorta para a esquerda e não para a direita.
25-(UFC-CE)
Duas
barras, A e B, construídas de materiais diferentes, são aquecidas
de 0 a 100 °C. 
Com base na figura a seguir, a qual fornece informações sobre as dilatações lineares sofridas pelas barras, determine:
a) os coeficientes de dilatação linear das barras A e B.
b) a razão entre os coeficientes de dilatação linear das barras A e B.
26-(UFMG-MG) Uma lâmina bimetálica é constituída de duas placas de materiais diferentes, M1 e M2, presas uma a outra.
Essa lâmina pode ser utilizada como interruptor térmico para ligar ou desligar um circuito elétrico, como representado, esquematicamente na figura I.

Quando a temperatura das placas aumenta, elas dilatam-se e a lâmina curva-se, fechando o circuito elétrico, como mostrado na figura II. Esta tabela mostra o coeficiente de dilatação linear α de diferentes materiais:

Considere que o material M1 é cobre e o outro, M2, deve ser escolhido entre os listados nessa tabela. Para que o circuito seja ligado com o menor aumento de temperatura, o material da lâmina M2 deve ser o
![]()
27-
(UFRN-RN)
Uma
prensa mecânica passou tanto tempo fora de uso que seu parafuso
central, constituído de alumínio, emperrou na região de contato
com o suporte de ferro, conforme mostrado nas figuras 1 e 2.
Chamado para desemperrar o parafuso, um mecânico, após verificar, numa tabela, os coeficientes de dilatação volumétrica do alumínio e do ferro, resolveu o problema.

a) Para desemperrar o parafuso considerando os coeficientes de dilatação do Al e do Fe, o mecânico esfriou ou aqueceu o conjunto? Justifique sua resposta.
b) Supondo que, inicialmente, os diâmetros do parafuso e do furo do suporte eram iguais, determine a razão entre as variações dos seus diâmetros após uma variação de temperatura igual a 100°C.
28-(PUC-SP)
A
tampa de zinco de um frasco de vidro agarrou no gargalo de rosca
externa e não foi possível soltá-la. 
Sendo os coeficientes de dilatação linear do zinco e do vidro, respectivamente, iguais a 30.10-6 ºC-1 e 8,5.10-6ºC-1, como proceder?
Justifique sua resposta. Temos à disposição um caldeirão com água quente e outro com água gelada.
29-(UEL-PR)
O volume de um bloco metálico sofre um aumento de 0,60% quando sua
temperatura varia de 200ºC. O coeficiente de dilatação
de dilatação linear médio desse metal, em ºC-1,vale:
a) 1,0.10-5
b) 3,0.10-5
c) 1,0.10-6
d) 3,0.10-4
e) 3,0.10-3
30-(MACKENZIE-SP) A massa específica de um sólido é 10,00g . cm-3 a 100°C e 10,03g . cm-3 a 32ºF. O coeficiente de dilatação linear do sólido é igual a:
a) 5,0 . 10-6 °C-1
b) 10 . 10-6 °C-1
c) 15 . 10-6 °C-1
d) 20 . 10-6 °C-1
e) 30 . 10-6 °C-1
31-(UFRJ-RJ)

Gui Pádua, um brasileiro de 28 anos, quer bater o recorde mundial de tempo em queda livre, o período entre o salto em si e a abertura do pára-quedas. A marca pertence, desde 1960, ao americano Joseph Kittinger, que "despencou" durante quatro minutos e 32 segundos.
A façanha do brasileiro só será possível graças a uma roupa especial, que deixa o sujeito parecido com um morcego e faz com que a descida seja em diagonal. Com isso, Pádua deverá cair com velocidade bem menor que Kittinger, 220 km/h, em média. O salto será feito de um avião Hércules da Aeronáutica posicionado a 12 km de altura em relação ao solo, onde a temperatura é de - 55 °C. Ele vai abrir o pára-quedas quando faltar 1 minuto para chegar ao chão, 5 minutos depois de ter saltado.
Revista Época, 11 ago. 2003 (adaptado).
Considere as informações apresentadas na reportagem acima e imagine que, no mesmo instante em que Gui Pádua saltar do avião, seja solta em queda livre, junto com ele, uma chapa de metal de 500 cm2 de área, que cairá sobre uma elevação de 955m de altura em relação ao solo (despreze a resistência do ar e considere a aceleração da gravidade g = 10,0 m/s2).
a) Qual será a diferença entre o tempo que a chapa levará para atingir a elevação e o tempo de queda de Gui Pádua, desde o momento do salto até o instante de abertura de seu pára-quedas?
b) Considere que a placa, quando lançada, esteja a mesma temperatura externa do avião (-55 °C) e que o coeficiente de dilatação linear do metal que a constitui seja igual a 2,4 x 10-5 °C-1. Sendo a temperatura local de 40 °C, qual a dilatação por ela sofrida ao atingir a elevação?
32-(UNESP-SP) Uma placa circular metálica apresenta um orifício, também circular, concêntrico. Se ao ser aquecida uniformemente

a placa circular metálica tem sua parte externa aumentada em 4%, a circunfereência do orifício concêntrico irá:
a) aumentar em 8%
b) aumentar em 4%
c) diminuir em 4%
d) diminuir em 8%
e) diminuir em 16%
33-(UFRR) O coeficiente de dilatação dos metais é da ordem de 10-5 oC-1. Uma chapa metálica tem um orifício circular. A chapa é aquecida de 25ºC para 50oC. Como consequência do aquecimento, o diâmetro do orifício:
a) reduz-se à metade
b) dobra
c) não se altera
d) aumenta um pouco
e) diminui um pouco
34-(UFPB)
Se
o diâmetro de uma moeda aumenta 0,2% quando sua temperatura é
elevada em 100oC,
os aumentos percentuais na espessura, na área e no volume serão
respectivamente:
a) 0,1%, 0,2%, 0,2%
b) 0,2%, 0,2%, 0,2%
c) 0,2%, 0,4%, 0,5%
d) 0,2%, 0,4%, 0,6%
e) 0,3%, 0,4%, 0,8%
35-(UNESP-SP) A figura mostra uma lâmina bi metálica de comprimento Lo na temperatura Toque deve tocar o contato C quando aquecida. A lâmina é feita dos metais I e II, cujas variações relativas de comprimento ΔL/Lo em função da variação de temperatura ΔT=T – Toencontram-se no gráfico.

Determine:
a) o coeficiente de dilatação dos metais I e II;
b) qual dos metais deve ser utilizado na parte superior da lâmina para que o dispositivo funcione como desejado? Justifique sua resposta.
36-(UEMS-MS) Uma certa quantidade de chá fervente é despejada em um recipiente de vidro.

O recipiente quebra-se provavelmente devido a:
a) O coeficiente de dilatação do recipiente é muito elevado
b) O recipiente permite que o calor se propague com facilidade
c) Dilatação não uniforme do corpo do recipiente
d) Pontos de fusão do recipiente e de ebulição do chá são semelhantes
e) Temperatura do ambiente externo ao copo.
37-(UNIC-MT) Uma chapa de alumínio tem um furo central de 100cm de raio, estando numa temperatura de 12oC.

Sabendo-se que αal=22.10-6 oC-1, a nova área do furo quando a chapa for aquecida até 122oC será:
![]()
38-(UDESC) A tabela a seguir apresenta os valores dos coeficientes de dilatação linear de alguns materiais.
 Com
base nessa tabela, resolva as questões a seguir:
Com
base nessa tabela, resolva as questões a seguir:
a) Em uma região, onde é normal ocorrerem grandes variações de temperatura, foi construída uma passarela de aço. À temperatura
de 15 °C o comprimento da passarela é igual a 50 m. Qual a variação de comprimento dela, num dia em que a temperatura passa de 15 °C para 45 °C?
b) Uma carreta que transporta combustível foi carregada com 20 mil litros de gasolina em uma cidade do Sudeste do Brasil, num dia em que a temperatura era igual a 35 °C (mesma temperatura da gasolina). Qual a perda de volume, por efeito de contração térmica, que essa carga apresenta quando descarregada no Sul do Brasil, a uma temperatura de 10 °C?
c) Placas quadradas de concreto, com largura igual a 1,0 m, são utilizadas na construção de uma calçada para pedestres. Sabendo-se que essas chapas ficarão sujeitas a variações de temperatura que podem chegar a 50 °C, calcule a dimensão mínima das juntas de dilatação que devem ser deixadas entre uma placa de concreto e outra.
39-(UFG-GO) Por medida de economia e conservação da qualidade de alguns alimentos, um supermercado instalou um sistema de refrigeração que funciona da seguinte forma: ao atingir uma temperatura superior Ts, ele é ligado e, ao ser reduzida para uma temperatura inferior Ti, é desligado. Esse sistema, composto por um tudo cilíndrico fechado de área Aoacoplado a um bulbo em sua parte inferior, é preenchido com mercúrio e tem dois contatos metálicos separados por uma distância h, conforme a figura.

Desprezando a dilatação térmica do recipiente, calcule a temperatura Ts quando o sistema é ligado.
Dados: Ti = 12 °C --- Ao = 1,0 ´ 10-7 m2 --- Vo = 1,0 ´ 10-5 m3 --- h = 6,0 cm --- aHg= 40 ´ 10-6 °C-1
40-(UFB)
Dois
recipientes de mesmo volume A e B possuem coeficientes de dilatação
γA e
γB,
tal que γA >
γB.
Ambos contém a mesma quantidade de um mesmo líquido.
a) Se o nível do líquido é o mesmo nos dois recipientes, para uma mesma elevação de temperatura, em qual deles o nível final será maior?
b) O que aconteceria com o nível do líquido nos dois recipientes se o coeficiente de dilação dos dois fosse o mesmo?
41-(UFLA-MG)
Um bulbo de vidro conectado a um tubo fino, com coeficiente de
dilatação desprezível, contendo certa massa de água na fase
líquida, é mostrado a seguir em três situações de temperatura.
Na primeira, o sistema está a 4 ºC; na segunda, a 1 ºC e, na
terceira, a 10 ºC. Conforme a temperatura, a água ocupa uma certa
porção do tubo.
Tal fenômeno é explicado:
a)
pelo aumento de volume da água de 0 ºC a 4 ºC, seguido da
diminuição do volume a partir de 4 ºC.
b) pela diminuição da
densidade da água de 0 ºC a 4 ºC, seguido do aumento da densidade
a partir de 4 ºC.
c) pelo aumento do volume da água a partir de
0 ºC.
d) pelo aumento da densidade da água de 0 ºC a 4 ºC,
seguido da diminuição da densidade a partir de 4 ºC.
e) pela
diminuição do volume da água a partir de 0 ºC.
42-(UFRS-RS)
Em
certo instante, um termômetro de mercúrio com paredes de vidro, que
se encontra à temperatura ambiente, é imerso em um vaso que contém
água a 100 °C.
Observa-se
que, no início, o nível da coluna de mercúrio cai um pouco e,
depois, se eleva muito acima do nível inicial. Qual das alternativas
apresenta uma explicação correta para esse fato?
a) A dilatação
do vidro das paredes do termômetro se inicia antes da dilatação do
mercúrio.
b) O coeficiente de dilatação volumétrica do vidro
das paredes do termômetro é maior que o do mercúrio.
c) A
tensão superficial do mercúrio aumenta em razão do aumento da
temperatura.
d) A temperatura ambiente, o mercúrio apresenta um
coeficiente de dilatação volumétrica negativo, tal corno a água
entre 0 °C e 4 °C.
e) O calor específico do vidro das paredes
do termômetro é menor que o do mercúrio.
43-(UFPEL-RS)
A
água, substância fundamental para a vida no Planeta, apresenta uma
grande quantidade de comportamentos anômalos.
Suponha que um
recipiente, feito com um determinado material hipotético, se
encontre completamente cheio de água a 4°C.
De
acordo com o gráfico e seus conhecimentos, é correto afirmar que
a)
apenas a diminuição de temperatura fará com que a água
transborde.
b) tanto o aumento da temperatura quanto sua
diminuição não provocarão o transbordamento da água.
c)
qualquer variação de temperatura fará com que a água
transborde.
d) a água transbordará apenas para temperaturas
negativas.
e) a água não transbordará com um aumento de
temperatura, somente se o calor específico da substância for menor
que o da água.
44-(UESB-BA)
Um
tanque cheio de gasolina de um automóvel, quando exposto ao sol por
algum tempo, derrama uma certa
quantidade desse combustível. Desse fato, conclui-se que:
a)
só a gasolina se dilatou.
b) a quantidade de gasolina derramada
representa sua dilatação real.
c) a quantidade de gasolina
derramada representa sua dilatação aparente.
d) o tanque dilatou
mais que a gasolina.
e) a dilatação aparente da gasolina é
igual à dilatação do tanque.
45-(PUC-MG)
Uma
esfera de aço, oca, foi construída de tal forma que, quando
completamente mergulhada em óleo diesel à temperatura de 25oC,
permanece em equilíbrio, sem afundar nem emergir. Suponha agora que
a temperatura do sistema, formada
pela bola e pelo óleo diesel, seja lentamente alterada, de forma que seja sempre mantido o equilíbrio térmico. Sabe-se que o coeficiente de dilatação linear do aço é αaço = 11.10-6 oC-1e que o coeficiente de dilatação volumétrica do óleo diesel é αóleo=9,5.10-4 oC-1. Sobre essa situação, é INCORRETO afirmar que:
a) antes da variação da temperatura, a razão entre a massa e o volume da esfera é igual à densidade do óleo diesel.
b) se houver elevação da temperatura, a esfera tenderá a flutuar.
c) se houver elevação da temperatura, tanto o óleo diesel quanto a esfera sofrerão dilatação.
d) caso haja diminuição da temperatura do sistema, a razão entre a massa e o volume da esfera se tornará menor do que a densidade do óleo diesel.
e) se houver diminuição da temperatura do sistema, tanto o óleo diesel quanto a esfera diminuirão de volume.
46-(PUC-MG)
Um
recipiente de vidro está completamente cheio de um determinado
líquido. O conjunto é aquecido fazendo com que transborde um pouco
desse líquido. A quantidade de líquido transbordado representa a
dilatação:
a) do líquido, apenas. 
b) do líquido menos a dilatação do recipiente.
c)
do recipiente, apenas.
d) do recipiente mais a dilatação do
líquido
47-(UFMS-MS) Um motorista retira o carro da garagem, que está a 15oC, passa pelo posto de gasolina e enche o tanque. Em seguida, deixa o carro estacionado ao sol. Após um certo tempo, ao voltar ao carro, verifica que a temperatura do carro é 40oC e que vazou uma certa quantidade de gasolina do tanque. É correto afirmar que:
01. o volume do tanque de combustível do carro diminuiu.
02. a gasolina sofreu dilatação
04. a gasolina e o tanque sofreram dilatação
08. o volume de gasolina que vazou é igual à variação de volume da gasolina.
16. a dilatação real da gasolina foi menor do que a dilatação do tanque.
Dê como resposta a soma dos números associados às afirmações corretas.
48-(UFSCAR-SP) Com motores mais potentes, caminhões com duas carretas têm se tornado muito comuns nas estradas brasileiras.
O caminhão esquematizado a seguir acelera uniformemente com aceleração de valor a. Nessas condições,
- o motor do cavalo aplica sobre o conjunto uma força constante de intensidade F;
- a interação entre as partes unidas pelos engates 1 e 2 têm intensidades respectivamente iguais a f1 e f2;
- as massas do cavalo, da carreta número 1 e da carreta número 2 são, nessa ordem, m, m1e m2;
- a resistência do ar ao movimento da carreta pode ser considerada desprezível.

Antes de iniciar o transporte de combustíveis, os dois tanques inicialmente vazios se encontravam à temperatura de 15 °C, bem como os líquidos que neles seriam derramados. No primeiro tanque, foram despejados 15 000 L de gasolina e, no segundo, 20 000 L de álcool. Durante o transporte, a forte insolação fez com que a temperatura no interior dos tanques chegasse a 30 °C.
Dados: GASOLINA: coeficiente de dilatação volumétrica: 9,6.10-4 °C-1 --- ÁLCOOL: densidade: 0,8 g/cm3 - calor específico: 0,6 cal/(g .°C)
Considerando desde o momento do carregamento até o momento da chegada ao destino, determine:
a) a variação do volume de gasolina.
b) a quantidade de calor capaz de elevar a temperatura do álcool até 30 °C.
49-(UNESP-SP) É largamente difundida a ideia de que a possível elevação do nível dos oceanos ocorreria devido ao derretimento



das grandes geleiras, como consequência do aquecimento global.
No entanto, deveríamos considerar outra hipótese, que poderia também contribuir para a elevação do nível dos oceanos. Trata-se da expansão térmica da água devido ao aumento da temperatura. Para se obter uma estimativa desse efeito, considere que o coeficiente de expansão volumétrica da água salgada à temperatura de 20 °C seja 2,0.10-4 °C-1. Colocando água do mar em um tanque cilíndrico, com a parte superior aberta, e considerando que a variação de temperatura seja 4 °C, qual seria a elevação do nível da água se o nível inicial no tanque era de 20 m? Considere que o tanque não tenha sofrido qualquer tipo de expansão.
50-(UFPR-PR) Uma
taça de alumínio de 120 cm3 contém
119 cm3 de
glicerina a 21°C. Considere o coeficiente de dilatação linear do
alumínio como sendo de 2,3.10-4 K-1 e
o coeficiente de dilatação volumétrico da glicerina de
5,1.10-4 K-1.
Se a temperatura do sistema taça-glicerina for aumentada para 39°C, a glicerina transbordará ou não? Em caso afirmativo, determine o volume transbordado; em caso negativo, determine o volume de glicerina que ainda caberia no interior da taça.
51-(UFPEL-RS) Os
postos de gasolina, são normalmente abastecidos por um
caminhão-tanque. Nessa ação cotidiana, muitas situações
interessantes podem ser observadas.
Um caminhão-tanque, cuja capacidade é de 40.000 litros de gasolina, foi carregado completamente, num dia em que a temperatura ambiente era de 30°C. No instante em que chegou para abastecer o posto de gasolina, a temperatura ambiente era de 10°C, devido a uma frente fria, e o motorista observou que o tanque não estava completamente cheio.
Sabendo que o coeficiente de dilatação da gasolina é 1,1.10-3 °C-1 e considerando desprezível a dilatação do tanque, é correto afirmar que o volume do ar, em litros, que o motorista encontrou no tanque do caminhão foi de
a) 40.880. b) 8.800. c) 31.200. d) 4.088. e) 880.
52-(ENEM-MEC)
De
maneira geral, se a temperatura de um líquido comum aumenta, ele
sofre dilatação. O mesmo não ocorre com a água, se ela estiver a
uma temperatura próxima a de seu ponto de congelamento. O gráfico
mostra como o volume específico (inverso da densidade) da água
varia em função da temperatura, com uma aproximação na região
entre 0ºC e 10ºC, ou seja, nas proximidades do ponto de
congelamento da água.
A partir do gráfico, é correto concluir que o volume ocupado por certa massa de água
a) diminui em menos de 3% ao se resfriar de 100ºC a 0ºC. b) aumenta em mais de 0,4% ao se resfriar de 4ºC a 0ºC.
c) diminui em menos de 0,04% ao se aquecer de 0ºC a 4ºC. d) aumenta em mais de 4% ao se aquecer de 4ºC a 9ºC.
e) aumenta em menos de 3% ao se aquecer de 0ºC a 100ºC.
53-(UNESP-SP) Um recipiente de vidro tem capacidade de 100cm3 a 10oC e contém, a essa temperatura, 99cm3 de um certo líquido de coeficiente de dilatação cúbica γ=2.10-4 oC-1. A que temperatura o recipiente estará completamente cheio de líquido?

(Considere o coeficiente de dilatação cúbica do vidro como sendo 10-5 oC-1.
54-(UFU-MG)
Um
frasco de capacidade para 10 litros está completamente cheio de
glicerina e encontra-se à temperatura de 10ºC.
Aquecendo-se o frasco com a glicerina até atingir 90ºC, observa-se que 352 ml de glicerina transborda do frasco. Sabendo-se que o coeficiente de dilatação volumétrica da glicerina é 5,0 x 10-4 ºC-1, o coeficiente de dilatação linear do frasco é, em ºC-1.
a) 6,0 x 10-5
b) 2,0 x 10-5
c) 4,4 x 10-4
d) 1,5 x 10-4
e) 3,0 x 10-4
55-(UNICAMP-SP)
Um
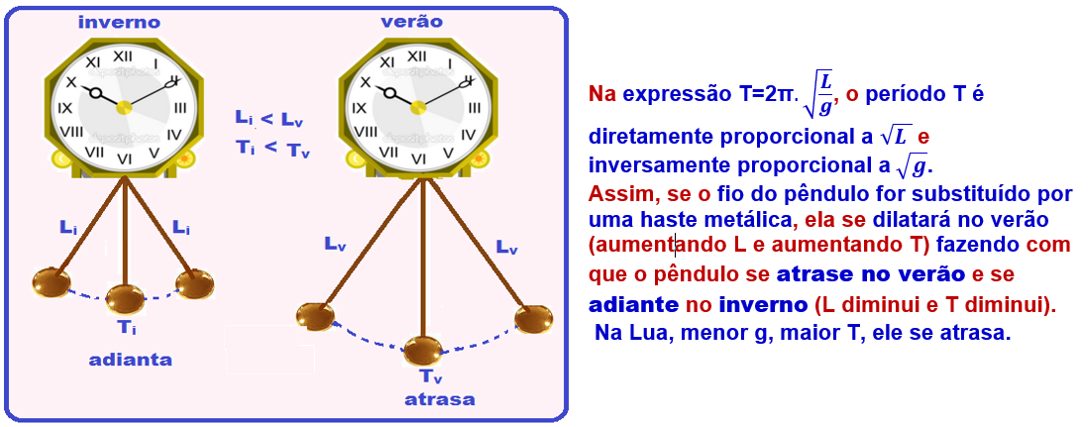
antigo relógio de pêndulo é calibrado no frio inverno gaucho.
Considere que o período desse relógio é dado por:
Onde L é o comprimento do pêndulo e g a aceleração da gravidade, pergunta-se:
a) Este relógio atrasará ou adiantará quando transportado para o quente verão nordestino?
b) Se o relógio for transportado do nordeste para a superfície da Lua, nas mesmas condições de temperatura, ele atrasará ou adiantará?
Justifique suas respostas.
56-(UEG-GO) Um relógio de pêndulo é usado em uma determinada região onde há consideráveis variações de temperatura entre o verão e o inverno. Considerando que o coeficiente de dilatação linear do pêndulo é α, responda às seguintes perguntas:
a) Um relógio de pêndulo se adianta no verão e se atrasa no inverno? Justifique.
b) Qual a relação matemática entre os períodos de oscilação do pêndulo no verão e no inverno em função da variação de temperatura e do coeficiente de dilatação linear (α)?
57-(UFRS-RS)
Um
líquido é aquecido de 0oC
a 50oC,
verificando-se na escala do frasco que o volume passa de 500cm3 a
525cm3.
Sendo o coeficiente de dilatação volumétrica do vidro γV=1,0.10-5 oC-1, determine o coeficiente de dilatação do líquido.
58-(UERJ-RJ) A figura abaixo representa um retângulo formado por quatro hastes fixas.

Considere as seguintes informações sobre esse retângulo:
• sua área é de 75 cm2 à temperatura de 20 ºC;
• a razão entre os comprimentos ℓ0A e ℓ0B é igual a 3;
• as hastes de comprimento ℓ0A são constituídas de um mesmo material, e as hastes de comprimento ℓ0B de outro;
• a relação entre os coeficientes de dilatação desses dois materiais equivale a 9.
Admitindo que o retângulo se transforma em um quadrado à temperatura de 320 ºC, calcule, em ºC-1, o valor do coeficiente de dilatação linear do material que constitui as hastes menores.
59-(UFBA-BA) Houve apenas um jogo do basquetebol de alta tecnologia. A ideia, que parecia promissora e que exigiu enormes investimentos, foi logo bandonada. Superatletas foram criados utilizando técnicas de melhoramentos genéticos em células embrionárias dos melhores jogadores e jogadoras de todos os tempos. A bola, confeccionada com um material isolante térmico de altíssima qualidade, era uma esfera perfeita. Os aros das cestas, círculos perfeitos, foram feitos de uma liga metálica, resultado de longa pesquisa de novos materiais. O ginásio de esportes foi reformulado para o evento, com um sistema de climatização ambiental para assegurar que a temperatura se mantivesse constante em 20°C.
A
plateia, era majoritariamente composta por torcedores do time local,
entre os quais foram reconhecidos cientistas premiados e
representantes de empresas de alta tecnologia.
O jogo estava nos cinco minutos finais e empatado. Aconteceu, então, um grande movimento na plateia. De um lado, os torcedores pedem alimentos e bebidas quentes e iluminam a cesta com lanternas infravermelhas. Do outro, da cesta do time local, todos querem sorvetes e bebidas geladas. Usou-se de todos os meios possíveis, inclusive alterando o sistema de climatização, para aquecer a região em torno da cesta do time visitante e esfriar a do time local. Dois torcedores, representantes da tecnociência, colocados atrás das cestas conversavam ao telefone: – Aqui está 19°C e aí? – Aqui está 21°C, vencemos! Terminado o jogo, o técnico do time visitante desabafou: — Sujaram um bom jogo e mataram uma boa ideia.
Explique, qualitativa e quantitativamente, por que os dois torcedores tinham certeza de ter vencido e comente as opiniões do técnico visitante, considerando que o diâmetro da bola e dos aros são iguais, respectivamente, a 230,0mm e a 230,1mm e que o coeficiente de dilatação linear dos aros é 4,8´10-4 ºC-1.
60-(UDESC-SC) A
tabela abaixo apresenta uma relação de substâncias e os seus
respectivos valores de coeficiente de dilatação linear e
condutividade térmica, ambos medidos à temperatura de 20 °C.
Assinale a alternativa correta, tomando como base as informações acima.
a) Barras do mesmo comprimento dos metais listados na tabela sofrerão dilatações iguais, quando submetidas a uma variação de temperatura de 20 °C.
b) A condutividade térmica das substâncias permanece constante, independentemente da temperatura em que estas se encontram.
c) Substâncias que possuem maior condutividade térmica também apresentam maiores coeficientes de dilatação.
d) Dentre as substâncias listadas na tabela, o cobre é a melhor opção para fazer isolamentos térmicos.
e) Duas chapas de dimensões iguais, uma de alumínio e outra de concreto, são submetidas à mesma variação de temperatura. Constata-se então que a variação de dilatação superficial da chapa de alumínio é duas vezes maior que a da chapa de concreto.
61-(UFRGS)
Dois
cubos metálicos com dimensões idênticas, um de ouro (A), outro de
chumbo (B), estão sobre uma placa aquecedora, inicialmente em
temperatura ambiente.
A tabela a seguir apresenta algumas das propriedades térmicas desses dois materiais.
Assinale a alternativa que preenche corretamente as lacunas do texto a seguir, na ordem em que aparecem.
No topo de cada cubo é colocada uma cabeça de fósforo que fica em contato direto com o cubo. Os dois cubos são aquecidos a uma temperatura final levemente superior à de ignição do fósforo.
Com base nos dados da tabela, conclui-se que o fósforo acenderá primeiro no cubo ________ e que a aresta do cubo A será _________ do cubo B no estado de equilíbrio térmico.
a) A - menor que a
b) A - maior que a
c) B - maior que a
d) B - menor que a
e) A - igual à
62-(UFRN-RN) A figura 1, abaixo, mostra o esquema de um termostato que utiliza uma lâmina bi metálica composta por dois metais diferentes – ferro e cobre – soldados um sobre o outro. Quando uma corrente elétrica aquece a lâmina acima de uma determinada temperatura, os metais sofrem deformações, que os encurvam, desfazendo o contato do termostato e interrompendo a corrente elétrica, conforme mostra a figura 2.

A partir dessas informações, é correto afirmar que a lâmina bi metálica encurva-se para cima devido ao fato de
a) o coeficiente de dilatação térmica do cobre ser maior que o do ferro.
b) o coeficiente de dilatação térmica do cobre ser menor que o do ferro.
c) a condutividade térmica do cobre ser maior que a do ferro.
d) a condutividade térmica do cobre ser menor que a do ferro.
63-(MACKENZIE-SP) Uma chapa metálica de área 1 m2, ao sofrer certo aquecimento, dilata de 0,36 mm2. Com a mesma variação de temperatura, um cubo de mesmo material, com volume inicial de 1 dm3, dilatará
a) 0,72 mm3
b) 0,54 mm3
c) 0,36 mm3
d) 0,27 mm3
e) 0,18 mm3
64-(ITA-SP)
Um
quadro quadrado de lado ℓ e massa m, feito de um material de
coeficiente de dilatação superficial β, e pendurado no pino O por
uma corda inextensível, de massa desprezível, com as extremidades
fixadas no meio das arestas laterais do quadro, conforme a figura. A
força de tração máxima que a corda pode suportar é F. A seguir,
o quadro e submetido a uma variação de temperatura ΔT, dilatando.
Considerando desprezível a variação no comprimento da corda devida
à dilatação, podemos afirmar que o comprimento mínimo da corda
para que o quadro possa ser pendurado com segurança é dado por 

65-(UFG-GO)
Deseja-se acoplar um eixo cilíndrico a uma roda com um orifício
circular. Entretanto, como a área da seção transversal do eixo é
2,0 % maior que a do orifício, decide-se resfriar o eixo e aquecer a
roda. O eixo e a roda estão inicialmente à temperatura de 30 °C.
Resfriando-se o eixo para -20 °C, calcule o acréscimo mínimo
de temperatura da roda para que seja possível fazer o acoplamento. O
eixo e a roda são de alumínio, que tem coeficiente de dilatação
superficial de 5,0´10-5 °C-1.
Dados: b = 5´10-5 °C-1; DTeixo = -50 °C; área inicial do orifício = Ao; área inicial da secção do eixo = 1,02 Ao.
66-(UFG-GO) Têm-se atribuído o avanço dos oceanos sobre a costa terrestre ao aquecimento global. Um modelo para estimar a contribuição da dilatação térmica é considerar apenas a dilatação superficial da água dos oceanos, onde toda a superfície terrestre está agrupada numa calota de área igual a 25% da superfície do planeta e o restante é ocupada pelos oceanos, conforme ilustra a figura.

De acordo com o exposto, calcule a variação de temperatura dos oceanos responsável por um avanço médio de L = 6,4 m sobre superfície terrestre.
Dados: b = 5´10–5 °C–1; DTeixo = -50 °C; área inicial do orifício = A0; área inicial da secção do eixo = 1,02 A0.
67-(UFC-CE) Um
triângulo retângulo isósceles é montado com arames de materiais
distintos, de 
modo que nos catetos o material possui coeficiente de dilatação térmica linear A√2º C-1, enquanto na hipotenusa o material possui coeficiente de dilatação térmica linear A /√2º C-1. Determine a variação de temperatura para que o triângulo torne-se equilátero.
68-(MACKENZIE-SP)

A
20ºC, o comprimento de uma haste A é 99% do comprimento de outra
haste B, à mesma temperatura. Os materiais das hastes
A e B têm alto ponto de fusão e coeficientes de dilatação linear respectivamente iguais a αA= 10.10-5 ºC-1 e αB = 9,1.10-5 ºC-1. A temperatura em que as hastes terão o mesmo comprimento será
![]()
69-(FGV-SP)

Na
Terra, o período de oscilação de um pêndulo, isto é, o tempo que
ele demanda para completar um ciclo completo, corresponde, com boa
aproximação, à raiz quadrada do quádruplo do comprimento do
pêndulo. O pêndulo de um carrilhão, ao oscilar, bate o segundo e é
constituído por uma fina haste de aço de massa desprezível, unida
a um grande disco de bronze, que guarda em seu centro o centro de
massa do conjunto haste-disco. Suponha que a 20ºC, o centro de massa
do conjunto esteja a 1 metro do eixo de oscilação, condição que
faz o mecanismo funcionar com exatidão na medida do tempo.
Considerando que o coeficiente de dilatação linear do aço é 10.10-6 ºC-1 e supondo que o centro de massa da haste-disco se mantenha sempre no centro do disco se a temperatura do conjunto haste-disco subir 10ºC, a medida do tempo, correspondente a meio ciclo de oscilação do pêndulo, se tornará
a) √1,0001 s, fazendo com que o relógio adiante.
b) √2,0002 s, fazendo com que o relógio adiante.
c) √1,0001 s, fazendo com que o relógio atrase.
d) √2,0002 s, fazendo com que o relógio atrase.
e) √3,0003 s, fazendo com que o relógio atrase.
70-(UNIMONTES-MG)

Uma barra de comprimento L = 50 m, feita de um material X, sofre variação de temperatura de 20°C, e seu comprimento varia em 0,02%. Considere duas barras do mesmo material X e de mesmo comprimento L, posicionadas, uma em frente à outra, separadas por uma distância d = 1 cm (veja a figura). Admitindo-se que cada barra cresça de forma homogênea, determine a variação de

temperatura necessária para que a distância d, entre elas, se anule.
71-(UEPG-PR)

Dilatação térmica é o fenômeno pelo qual variam as dimensões geométricas de um corpo quando este experimenta uma variação de temperatura. Sobre esse fenômeno físico, assinale o que for correto.
01) Em geral, as dimensões de um corpo aumentam quando a temperatura aumenta.
02) Um corpo oco se dilata como se fosse maciço.
04) A tensão térmica explica por que um recipiente de vidro grosso comum quebra quando é colocada água em ebulição em seu interior.
08) A dilatação térmica de um corpo é inversamente proporcional ao coeficiente de dilatação térmica do material que o constitui.
16) Dilatação aparente corresponde à dilatação observada em um líquido contido em um recipiente.
72-(UEPG-PR)

Considere uma garrafa de vidro totalmente cheia com água, hermeticamente fechada, submetida a alterações de temperatura.
Nesse
contexto, assinale o que for correto.
01) Diminuindo a temperatura do sistema, desde que a água permaneça líquida, o volume da água diminui em relação ao volume da garrafa, criando um espaço vazio no seu interior.
02) Se a variação de temperatura for de 15 ºC para – 5 ºC a garrafa não se romperá.
04) Sendo o coeficiente de dilatação da água menor que o coeficiente de dilatação do vidro, a dilatação observada na água não é real.
08) Aquecido o sistema, o volume interno da garrafa aumenta, enquanto que o volume de água permanece o mesmo.
As questões 73 e 74 são baseadas no texto a seguir:

Willen Gravesand( 1688-1742). fisico holandês, foi professor de matemática, de astronomia e de física. Sendo


reconhecido dentre as suas contribuições científicas pelo famoso anel de Gravesand, experimento que se constitui de
Fonte: http//comcienciafisicaorg/oteiros/ calor/anel-de-gravesande
uma esfera metálica, suspensa ou presa por uma haste e um anel metálico, conforme ilustrado acima.
73-(UEPB-PB)

Verifica-se na figura acima que inicialmente, não é possível passar a esfera através do anel de metal. Porém, após aquecer o anel de metal, a esfera passa facilmente. A alternativa que explica corretamente esse fenômeno é:
a) O aumento de temperatura, causado pela chama da vela no anel de metal, aumenta a agitação térmica das partículas do metal, o que provoca um aumento do diâmetro do anel, facilitando a passagem da esfera.
b) O calor fornecido pela vela ao anel metálico faz com que o tamanho da esfera diminua, quando cm contato com o anel, facilitando a passagem da esfera.
c) O calor fornecido pela esfera ao anel metálico provoca uma redução no nível de agitação térmica das partículas do metal, o que provoca um aumento do diâmetro do anel, facilitando a passagem da esfera.
d) O aumento de temperatura no anel de metal causado pela chama da vela aumenta a agitação térmica das partículas do metal, o que provoca uma redução do diâmetro do anel, facilitando a passagem da esfera.
e) Não é possível acontecer tal fenômeno, uma vez que, após o anel ser aquecido, haverá uma diminuição do mesmo, impedindo a passagem da esfera de metal.
74-(UEPB-PB)

O
experimento do anel de Gravesand pode ser usado para comprovar a
dilatação volumétrica de um sólido. Considerando que, em outro
artefato experimental, uma esfera metálica tinha, a 10°C. um raio
de 5,0 cm, que a esfera
foi feita com aço de coeficiente de dilatação linear a 1,5. 10-3 °C e adotando π=3, a dilatação volumétrica sofrida pela esfera, se sua temperatura for elevada para 110 °C’, é:
a) l,13 cm3
b)1,00 cm3
c) 500,00cm3
d) 9,00cm3
e) 2,25cm3
75-(UNIOESTE-PR)

O
funcionário de uma ferrovia precisa instalar um segmento de trilho
para recompor uma linha férrea. O comprimento sem trilho é de 25,00
m. O funcionário sabe que a temperatura no local da instalação
varia de 10oC,
no inverno, a 40 oC,
no verão. O coeficiente de dilatação térmica do aço, material do
qual o trilho e fabricado, é igual a 14 .10-6
oC-1.
Se a manutenção ocorrer no inverno, qual dos valores listados
abaixo aproxima-se mais do máximo comprimento que o
funcionário deve cortar o trilho para encaixar no espaço a ser preenchido?
A. 25,00 m.
B. 24,90 m.
C. 25,01 m.
D. 24,99 m.
E. 24,95 m.
76-(UDESC-SC)

Em
um dia típico de verão utiliza-se uma régua metálica para medir o
comprimento de um lápis. 
Após medir esse comprimento, coloca-
se a régua metálica no congelador a uma temperatura de -10oC e esperam-se cerca de 15 min para, novamente, medir o comprimento do mesmo lápis. O comprimento medido nesta situação, com relação ao medido anteriormente, será:
a.( ) maior, porque a régua sofreu uma contração.
b.( ) menor, porque a régua sofreu uma dilatação.
c.( ) maior, porque a régua se expandiu.
d.( ) menor, porque a régua se contraiu.
e.( ) o mesmo, porque o comprimento do lápis não se alterou.
77-(UENP-PR)

As
duas ilustrações a seguir estão relacionadas com a dilatação
térmica dos sólidos, sendo que a figura da esquerda mostra água
quente sendo derramada em um pote de vidro fechado com tampa de
metal; e a outra mostra o aquecimento de uma porca em um
parafuso. Ambas as ilustrações têm o objetivo de mostrar o
desprendimento da tampa e da porca. Sobre esse assunto, analise as
afirmativas abaixo.
I. O desprendimento só é possível porque o coeficiente de dilatação da tampa é menor do que o coeficiente do vidro.
II. Tanto a tampa quanto a porca devem ter coeficientes de dilatação maiores do que os coeficientes do vidro e do parafuso, respectivamente.
III. Se a água despejada no pote fosse gelada, a tampa iria ficar mais firmemente encaixada.
IV. Para desatarraxar, a distância entre os átomos da porca deverá ser maior do que a distância entre os átomos do parafuso.
Está(ão) correta(s) apenas a(s) afirmativa(s):
a) I e III
b) I, III e IV
c) II
d) II e IV
e) II , III e IV
Resolução comentada dos exercícios de vestibulares sobre
dilatação linear, superficial e volumétrica dos sólidos e dilatação dos líquidos.
01- Como A está fixo, as dimensões do sistema devem aumentar, pois está sendo aquecido e o ponto B deve afastar-se de A (veja a figura)
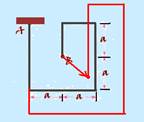
R- B
02- Quando a temperatura aumenta (θ > 27 ºC) o alumínio se dilata mais e ela se curva para cima e quando a temperatura diminui (θ < 27 ºC) o alumínio se dilata menos e ela se curva para baixo ---
R- D
03- Sendo a barra de mesmo material (mesmo coeficiente de dilatação) e como sofre a mesma variação de temperatura, todos os seus pontos sofrerão a mesma dilatação e ela não será deformada --- R- A
04- R- D --- veja teoria
05- A dilatação do alumínio é o dobro da dilatação do aço --- veja figura
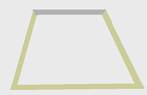
R- E
06- Observe que as lâminas estão se encurvando para dentro, então α2 > α1 e, quanto mais baixo estiver o contato (mais apertado o parafuso), menor será a dilatação das lâminas e consequentemente menor será a temperatura --- R- D
07- R- B --- veja teoria
08- Água fria contrai o interno e água quente dilata o externo --- R- D
09- Sendo α1 (azul) maior que α2 (vermelho), com o aquecimento, a lâmina azul se dilata mais que a vermelha e a espiral se fecha (contrai) fazendo o ponteiro girar no sentido horário --- R- E
10- Para que a ponte permaneça sempre na horizontal, os dois pilares devem sofrer a mesma dilatação para a mesma variação de temperatura --- ΔL1= ΔL2 --- L01.α1.Δt= L02.α2.Δt --- 40.18.10-6=30.α2 --- α2=24.10-6 oC-1.
11- ΔL=Lo.α.Δt=100.1,2.10-5.20 --- ΔL=2,4.10-2m=2,4 cm --- R- B
12- ΔL=Lo.α.Δt=12.1,1.10-5.40 = 528.10-5=52.800.10-5 --- ΔL=0,528 cm --- R- E
13- cálculo do coeficiente de dilatação da haste --- ΔL=Lo.α.Δt --- 2.10-2=103.α.1 --- α=2.10-5oC-1 --- ΔL=Lo.α.Δt=
800.2.10-5.20 === ΔL=32.000.10-5=0,32mm --- R- B
14- ΔL
= Lo .
α . Δθ --- ΔL = 30 . (11 . 10-6)
. (40 – 10) = 99 . 10-4 m
---
R- C
15- ΔL=Lo.α.Δt --- 15=1.000.α.(500 – 0) --- R- α=30.10-6 oC-1
16- ΔL=Lo.α.Δt --- ΔL=10.11.10-6(2,7 – 30) --- ΔL=110.10-6.(-27,3) --- ΔL= - 0,00303 --- L=10,00 – 0,00303 --- L=9,99697cm
17- aço de 0oC a 100oC --- Laço=Lo(1 + α.Δt)=Lo + Lo.12.10-6.100) --- Laço=1,0012Lo --- vidro de 0oC a 100oC --- Lvidro=Lo(1 + α.Δt)=Lo + Lo.8.10-6.100) --- Laço=1,0008Lo --- Laço – Lvidro=0,1 --- 1,0012Lo – 1,0008Lo=0,1 --- Lo=0,1/0.0004 = 0,25.103=250 cm --- R- D
18- A reta A tem maior inclinação --- R- C
19- Como o coeficiente de dilatação linear do latão é maior que o do aço, o latão se dilata mais quando aquecido e se contrai mais
quando resfriado --- R- C
20- α=ΔL/LoΔt=0,24/2.200 ---α=0,24/400 --- α=0,0006 oC-1 --- R- E
21- Para que o balanço permaneça sempre na horizontal, independente da temperatura, eles devem, para qualquer variação de temperatura, sofrer sempre a mesma dilatação ΔL --- ΔLA=ΔLB --- LA.1,5.10-5.Δt=72.2.10-5.Δt --- LA=144.10-5/1,5.10-5 ---
LA=96cm
22- Quanto maior o coeficiente de dilatação mais o corpo se dilata quando aquecido e mais se contrais quando resfriado.
(01) A se dilata mais que B --- Correta
(02) Falsa --- veja (01)
(04) A folga diminuirá --- Falsa
(08) Possuem diferentes Lo --- Falsa
(16) Apenas a placa se dilatará --- Correta
(32) Apenas a placa se dilatará --- Correta
R- (01 + 16 + 32)=49
23- R- A --- veja teoria
24- Como um metal se dilata quando se aquece a estrutura metálica do lado direito do prédio passa a ter um comprimento maior do que a estrutura metálica em seu lado esquerdo devido ao aquecimento provocado pelo incêndio que ocorreu no lado direito. Para que a altura do prédio medida em seu lado direito fique maior do que a medida pelo lado esquerdo, o prédio entortará necessariamente para o lado esquerdo, como indicado na figura 2.
25- a) αA=ΔLA/LoAΔtA=0,0022/1,0022.100 -- αA=22.10-6 oC-1 --- αB=ΔLB/BΔtA=0,0011/1,0011.100 --- αB=11.10-6oC-1
b) αA/αB=22.10-6/11.10-6 --- αA/αB=2
26- Para que o circuito seja ligado com menor aumento de temperatura você deve escolher o que se dilata muito mais que o cobre, que no caso é o alumínio --- R- B
27- a) Esfriou o conjunto, o alumínio tem maior coeficiente de dilatação e se contrai mais que o ferro.
b) ΔLAl=Lo.αAl.Δt --- ΔLFe=Lo.αFe.Δt --- ΔLAl/ ΔLFe=24.10-6/11.10-6≈2,2 --- R- 2,2
28- Deve-se mergulhar a tampa do frasco na água quente. O zinco irá dilatar mais que o vidro, soltando-se do gargalo.
29- ΔV=0,006Vo --- ΔV=Vo.γ.Δt --- 0,006Vo=Vo.γ.200 --- γ=3.10-5 oC-1 --- α/1=γ/3 --- α/1=3.10-5/3 --- α=1,0.10-5 oC-1 ---
R- A
30- a massa é a mesma para qualquer temperatura --- d=m/V --- volume inicial --- 10=m/Vo --- Vo=m/10 --- volume final --- 32oF=0oC --- 10,03=m/V --- V=m/10,03 ---32oF=0oC --- V=Vo.(1 + γ(t – to)) --- m/10,03=(m/10).(1 + γ(0 – 100) --- 1/10.03=1/10 – 100γ/10 --- 1003γ=0,03 --- γ=2,99.10-5=3.10-5 oC-1 --- α/1=γ/3 ---α/1=3.10-5/3 --- α=1,0.10-5 oC-1 --- R- B
31- a) Tempo que a chapa demora para atingir a elevação --- ΔS=Vot + gt2/2 --- 11.045=0.t + 10.t2/2 --- t=√2.209 --- t=47s --- até abrir o pára-quedas ele demorou 5 minutos=5.60=300s --- Δt=300 – 47=253s --- Δt=253s
b) ΔS=So.β.Δt=500.4,8.10-5.(40 - -55) --- ΔS=2,28cm2
32- O orifício se dilata na mesma proporção que a chapa, ou seja, de 4% --- R- B
33- Δl=Lo.α.Δt=Lo.10-5.25 --- ΔL=25.10-5Lo --- R- D
34- Δd=0,02do --- Δd=do.α.Δt --- 0,02.do=do.α.100 --- α=2.10-5 oC-1
espessura --- ΔL=LoαΔt --- ΔL/Lo=αΔt=2.10-5.100 --- ΔL/Lo=2.10-3=0,2%
área --- ΔS=So.β.Δt --- ΔS/So=2αΔt=2.2.10-5.100 --- ΔS/So=4.10-3=0,4%
volume --- ΔV=Vo.γ.Δt --- ΔV/Vo=γ.Δt =3.2.10-5.100 --- ΔV/Vo=6.10-3=0,6%
R- D
35- a)
ΔL=Lo.α.ΔT
--- α = ΔL/(Lo.ΔT)
--- metal I --- αI=300.10-6/30
--- αI=1,0.10-5oC-1
--- metal II --- αII=600.10-6/30
--- αII=2,0.10-5 oC-1
b) A lâmina II deve estar na parte superior que deve se dilatar mais para que o dispositivo se encurve para baixo, pois ela tem maior coeficiente de dilatação.
36- R- C
37- ΔL=Lo.α.ΔT=2.22.10-6.110=484.10-5m --- R=1 + 0,00484=1,00484m --- S=πR2=3,1416.(1,00484)2 --- S=3,172 m2
R-D
38- a)
DL = a.L0.DT ![]() DL
= 11.10-6.50.(45 – 15) = 16500.10-6 = 0,0165 m = 1,65 cm
DL
= 11.10-6.50.(45 – 15) = 16500.10-6 = 0,0165 m = 1,65 cm
b)
ΔV = g.V0.DT ![]() DV
= 9,6.10-4.20000.(10-35) = - 4800000.10-4 = - 480 litros
DV
= 9,6.10-4.20000.(10-35) = - 4800000.10-4 = - 480 litros
c)
ΔL = a.L0.DT ![]() DL
= 12.10-6.1.50 = 600.10-6 = 0,0006 m = 0,06 cm = 0,6 mm
DL
= 12.10-6.1.50 = 600.10-6 = 0,0006 m = 0,06 cm = 0,6 mm
39- ΔV = Vo (γHg) DT --- DV = Vo (3αHg) DT --- ΔT=ΔV/3αHg.Vo=Ao.h/3αHgVo --- ΔT=10-7.6.10-2/(3.40.
10-6.10-5)=6.10-9/120.10-11 --- ΔT=5oC --- ΔT=Tf – Ti --- 5=Tf – 12 --- Tf=17oC
40- a) O recipiente B porque se dilata menos.
b) O nível do líquido continuaria sendo o mesmo nos dois recipientes.
41- Sendo a densidade inversamente proporcionsal ao volume --- R- D
42- R- A
43- Observe no gráfico que, se você diminuir a temperatura do sistema, o volume do recipiente fica menor que o da água e ela transborda e que se você aumentar a temperatura do sistema, o volume da água fica maior qie o do recipiente, e ela transborda --- R- C
44- R- C --- veja teoria
45- a) Correta --- elas possuem a mesma densidade --- estão em equilíbrio estático --- o peso da esfera é igual ao empuxo.
b) Correta --- sofrem dilatação volumétrica e a esfera se dilata mais que o óleo, deslocando mais líquido eaumentando o empuxo.
c) Correta
d) Falsa --- a esfera se contrai mais que o óleo diesel, seu volume diminui mais e sua sensidade aumenta ficando maior que a do óleo diesel.
e) Correta
R- D
46- ΔLlíquido= ΔLaparente(tyransbordado) + ΔLfrasco --- ΔLaparente(tyransbordado)= ΔLlíquido – ΔLrecipiente --- R- B
47- 01. Falso --- como a temperatura aumentou o volume do tanque também aumentou
02. Correto --- a temperatura aumentou
04. Correta
08. Falsa --- o tanque também se dilatou
16. Falsa --- foi maior, pois parte da gasolina vazou
R- (02 + 04)=06
48- a) ΔVgas=Vo.γgas.Δt=15.000.9,6.10-4.(30 – 15) --- ΔVgas=216 L
b) d=0,8g/cm3=0,8.103g/L --- d=m/V --- 0,8.103=m/20.000 --- m=16.105g --- Q=m.c.Δt=16.105.0,6.15 --- Q= 1,44.108 cal
49- ∆V = γ .Vo.∆T --- ∆V = 2.10-4.(S.20).4 --- S.∆h = 160.S.10-4 --- ∆h = 16.10-3m = 1,6 cm --- ∆h=1,6cm
50- ∆Vtaça = γ .Vo.∆T=120.2,3.10-4.18=0,49cm3 --- Val=120,49cm3 --- ∆Vglic = γ .Vo.∆T=5,1.
10-4.119.18=1,092cm3 ---
Vglic=120,092cm3 --- a glicerina não transbordará pois a taça passará a ter um volume de 120,49 centímetros cúbicos, enquanto que o volume total da glicerina passará a ser de 120,092 centímetros cúbicos. Esta diferença 120,49 - 120,092 = 0,398 centímetros cúbicos é quanto ainda se poderia preencher de glicerina, na temperatura final.
51- ∆V = γ .Vo.∆T=4.104.1,1.10-3.20 --- ΔV=880L --- R- E
52- Analisando o gráfico, notamos que o volume específico diminui de 0 °C até 4°C, aumentando a partir dessa temperatura.
Aproximando os valores lidos no gráfico, constatamos uma redução de 1,00015 cm3/g para 1,00000 cm3/g de 0 °C a 4 °C, ou seja, de 0,00015 cm3/g. Isso representa uma redução percentual de 0,015%, o que é menos que 0,04 % --- R- C
53- Quando o recipiente estiver completamente cheio de líquido, eles deverão ter o mesmo volume --- ΔVV= ΔVL --- 100(1 + 10-5(t – 10) = 99.(1 + 2.10-4)(t – 10) --- t=19,6.10-2/18,6.10-3 --- t≈10,5oC
54- O volume de glicerina que extravasou corresponde à dilatação aparente --- ΔVap=Vo.γap.Δt --- 352.10-3=10.γap.(90 – 10) ---
γap=352.10-3/8.102 --- γap=44.10-5 oC-1 --- γg= γap+ γf --- 5,0.10-4=44.10-5 + γf --- γf=5,0.10-4 – 4,4.10-4 --- γf=6,0.10-5 oC-1 ---
αf=6.10-5/3 --- αf=2,0.10-5 oC-1 --- R- B
55- 
56-
![]()
b) T=2π√(L/g) --- L=Lo.α.Δt --- T=2π√( Lo.α.Δt/g)
57- ΔVap=Vo. γap.Δt --- 25=500.γap.50 --- γap=25/25.103 --- γap=10-3 oC-1 --- γlíq= γV = γap --- γlíq=0,001 + 0,00001 ---
γlíq=0,00101 oC-1
58- Cálculo de ℓ0A e de ℓ0B --- ℓ0A. ℓ0B=75 --- 3ℓ0B. ℓ0B=75 --- ℓ0B=5cm e ℓ0A=15cm ---
Após o aquecimento, os comprimentos finais das hastes são iguais, pois a figura transforma-se em um quadrado --- ℓA= ℓB ---
ℓ= ℓ0(1 + αΔt) --- 15.(1 + αAΔt) = 5.(1 + αBΔt) --- a relação entre os coeficientes de dilatação das hastes equivale a 9 e a variação da temperatura a 300 (320º – 20º) --- logo --- 15.(1 + 300.αB/9) = 5.(1 + 300αB) --- 15 + 500αB=5 + 155αB ---
αB=
1,0.10-2 oC-1
59- A expressão matemática que fornece o diâmetro do aro após aquecido ou resfriado vale --- d = do(1+a.ΔT) --- ao aquecer de 1ºC o aro da rede no lado do time visitante eles provocaram uma dilatação em seu diâmetro modificando-o para --- d = 230,1(1+4,8.10-4.(21–20)) = 230,21mm --- o que facilita a marcação de pontos pelo time local, já que o diâmetro do aro foi aumentado.
Por outro lado ao resfriar o aro da cesta em seu lado eles provocaram uma contração deste, reduzindo-o para --- d = 230,1(1+4,8.10-4.(19 – 20)) = 229,99mm --- assim, o time visitante não conseguirá marcar pontos, uma vez que o aro tem diâmetro menor do que o da bola.
As atitudes dos torcedores facilitaram as realizações de pontos para o time local e impossibilitaram a marcação de pontos pelo time adversário.
O técnico do time visitante está reclamando dessas atitudes dos anfitriões em utilizar conhecimentos científicos para fraudar o resultado da partida.
60- Observe que o valor do coeficiente de dilatação do alumínio é o dobro do coeficiente de dilatação do concreto e, como elas tem as mesmas dimensões iniciais e sofrem a mesma variação de temperatura, a chapa de alumínio se dilata dias vezes mais do que a de concreto --- R- E
61- O fósforo acenderá primeiro no cubo que atingir a temperatura final de ignição mais rapidamente, ou seja, aquele que possuir maior condutividade térmica. Neste caso é o cubo feito de ouro, o cubo A. Quanto ao tamanho da aresta do cubo ela dilatará conforme seu coeficiente de dilatação, que é maior no chumbo. Assim a aresta do cubo A será menor que a do cubo B --- R- A
62- O cobre deve se dilatar mais e deve ter maior coeficiente de dilatação --- R- A
63- Dados: Ao = 1 m2 = 106 mm2; DA = 0,36 mm2 e Vo = 1 dm3 = 10-6 mm3 --- DA = Ao.2 a DT --- 0,36 = 10-6 2 a DT ---
DT = 0,36/2.10-6=0,18/10-6 --- DV = Vo3aDT --- ΔV=10-6.3.0,18/10-6 --- DV= 0,54 mm3 --- R- B
64- Veja o esquema abaixo:
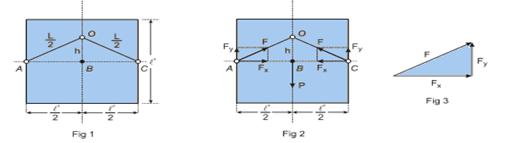
Nas figuras acima --- ℓ: lado inicial do quadrado --- ℓ’: lado do quadrado depois do aquecimento --- L: comprimento da corda --- h: distância OB --- na Fig 1, no triângulo ABO, aplicando o teorema de Pitágoras --- h2 + ℓ’2/4= ℓ2/4 --- h2= ℓ2/4 - ℓ’2/4 --- h=1/2.√ (ℓ2 - ℓ’2) (I) --- na Fig 2, como o quadro está em equilíbrio, a resultante das forças é nula --- assim --- 2 Fy = P --- 2 Fy = m g --- FY=mg/2 (II) --- o triângulo ABO da Fig 1 é semelhante ao triângulo das forças na Fig 3 --- então --- Fy/h=F/ ℓ/2 --- substituindo nessa expressão as equações (I) e (II)
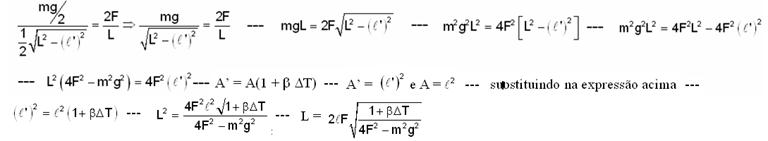
R- E
65- A expressão da dilatação superficial é: A = Ao (1+ b DT). Como As áreas finais terão que ser iguais --- Aeixo = Aorif Þ 1,02 Ao [(1 + 5´10-5) (-50)] = Ao (1 + 5´10-5) DT --- 1,02 – 2,55´10-3 = 1 + 5´10-5 DT --- ΔT=0.02 – 2,55.10-3.5.10-6 --- ΔT=349oC
66- Dados:
R = 6.400 km = 6,4´106 m;
L = 6,4 m; b = ![]() °C-1;
Aagua =
75%ATerra =
°C-1;
Aagua =
75%ATerra = ![]() .
.
Da
figura dada: sen q
= ![]() Þ
r = R sen q
Þ
r = R sen q
O comprimento da base da área de avanço do oceano (DA) é b = 2 p r e a altura é L. Assim:
DA = (2 p r) L = (2 p R sen q) L. Mas:
DA = Aagua b DT. Igualando essas duas expressões:
(2 p R sen q) L
= ![]() b DT.
fazendo os cancelamentos e isolando DT, vem:
b DT.
fazendo os cancelamentos e isolando DT, vem:
DT
= ![]() .
Substituindo os valores dados, temos:
.
Substituindo os valores dados, temos:
DT
= 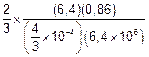 Þ
DT =
Þ
DT = ![]() .
.
DT = 4,3 ´ 10–3 °C.
67- acat =
A![]() °C–1 e ahip =
°C–1 e ahip = ![]() °C–1.
--- como
o triângulo, no início, é retângulo e isósceles, os catetos
possuem inicialmente o mesmo comprimento, L0 --- o
comprimento da hipotenusa, a,
é calculado pelo teorema de Pitágoras ---
°C–1.
--- como
o triângulo, no início, é retângulo e isósceles, os catetos
possuem inicialmente o mesmo comprimento, L0 --- o
comprimento da hipotenusa, a,
é calculado pelo teorema de Pitágoras ---
a2 = ![]() Þ
a =
Þ
a = ![]() . (I)
--- para que o triângulo se torne equilátero, de lado L,
temos --- a(1 + ahip DT)
= L0(1
+ acat DT)
--- substituindo os dados e a expressão (I),
vem ---
. (I)
--- para que o triângulo se torne equilátero, de lado L,
temos --- a(1 + ahip DT)
= L0(1
+ acat DT)
--- substituindo os dados e a expressão (I),
vem --- ![]()
![]() =
L0 (1
+ A
=
L0 (1
+ A ![]() DT)
Þ
DT)
Þ ![]() +
A DT
= 1 + A
+
A DT
= 1 + A![]() DT
--- (
DT
--- (![]() –
1) A DT
=
–
1) A DT
= ![]() –
1 --- DT
=
–
1 --- DT
= ![]() °C–1
°C–1
68- ℓoA=0,99ℓoB --- ℓA=ℓoA(1 + αA.∆t) --- ℓA=0,99ℓoB(1 + αA.∆t) --- ℓB=ℓoB(1 + αB.∆t) --- quando o comprimento for o mesmo
![]()
--- ℓA = ℓB --- 0,99ℓoB(1 + αA.∆t) = ℓB=ℓoB(1 + αB.∆t) --- 0,99ℓoB(1 + 10.10-5.∆t) = ℓB=ℓoB(1 + 9,1.10-5.∆t) --- ∆t=1.250oC ---
∆t=t – to --- 1.250=t – 20 --- t=1.270oC --- R- C
69- Novo comprimento ℓ do pêndulo quando a temperatura subir de 10oC --- ℓ = ℓo (1 + α(t – to) --- ℓ = 10(1 + 10.10-6.10 ---
ℓ=1,0001m --- cálculo do período T que pelo enunciado vale T= √(4ℓ) --- T= √(4.1,0001) --- T= 2.√1,0001 s --- para meio ciclo de oscilação o período será T=√1,0001 s --- se, para cada meia oscilação o período aumenta de T=√1,0001 s, o relógio irá atrasar --- R- C
70- Cálculo do coeficiente de dilatação linear do material --- Lo=50m --- L=50 + 50x0.02/100 --- L=50,01m --- ∆L= L – Lo=L0α∆θ --- 0,01=50.α.20 --- α=10-2/103 --- α=10-5 oC-1 --- o espaço (d) entre as barras é preenchido pelas duas metades das dilatações (∆L) de cada barra --- d=2. ∆L/2=2.(0,01)/2 --- d=0,01=10-2cm --- ∆L=d=Loα∆θ --- 10-2=50.10-5.∆θ ---
∆θ=10-2/50x10-5=1.000/50 --- ∆θ=20 oC
71- Todas estão corretas, com exceção da 08 que está errada pois, pela expressão ∆V=Vo.λ.∆θ você observa que o coeficiente de dilatação térmica (λ) é diretamente proporcional à dilatação (∆V) --- R- (01 + 02 + 04 + 16) = 23
72- 01. Correta --- embora esse “espaço vazio” deva, depois de algum tempo, ser preenchido com vapor d’água que se formará devido à baixa pressão.
02. Falsa --- à temperatura de –5 °C, a água será congelada, aumentará de volume, estourando a garrafa.
04. Correta --- essa dilatação observada é chamada de dilatação aparente --- a dilatação real é soma da dilatação aparente com a dilatação da garrafa.
08. Falsa --- tanto a água como a garrafa aumentam de volume.
R- (01 + 04) = 05
73- R- A.
74- Dilatometria - Estuda a dilatação dos corpos - Quando a temperatura de um sólido aumenta, surge um aumento da amplitude das vibrações atômicas e da distância média entre os átomos e moléculas que o constituem e então eles se
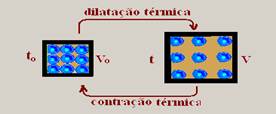
dilatam. Se a temperatura diminui, ocorre o fenômeno inverso, ou seja, eles se contraem.
16- Relação entre os coeficientes de dilação linear (α), superficial (β) e volumétrica (γ) --- α/1 = β/2 = γ/3 --- 1,5.10-3/1 =γ/3 --- γ = 4,5.10-3 oC-1 --- volume inicial da esfera --- Vo=(4/3).π.R3=(4/3).3.(5)3 --- Vo=500=5.102cm3 --- ∆V=Vo. γ.∆θ=5.102.4,5.10-3.(110 – 10) --- ∆V=225cm3 --- R- E.
75- Quando a temperatura do trilho passar de 10oC para 40oC um comprimento de trilho de lo=25m sofrerá uma dilatação linear de --- ∆L=Lo.α.(θ – θo)=25.14.10-6.(40 – 10)=10500.10-6 --- ∆L=0,01m --- o máximo comprimento do trilho a ser colocado deve ser --- L=25,00 – 0,01=24,99m --- R- D.
76- Depois que a régua foi resfriada ela se contraiu e o espaço entre cada unidade diminuiu fazendo com que a medida do mesmo lápis

aumente --- R- A
77- Para qualquer tipo de dilatação no caso volumétrica, quanto maior o coeficiente de dilatação, maior será o volume dilatado, pois ∆V=Vo.γ.∆θ sendo γ o coeficiente de dilatação:
I. Falsa --- a tampa deve se dilatar mais, ou seja, possuir maior coeficiente de dilatação.
II. Correta --- ambos devem se dilatar mais para se desprenderem.
III. Correta --- como a tampa possui maior coeficiente de dilatação ela se dilata mais pra aumento de temperatura ou se contrai mais para diminuição de temperatura.
IV. Correta --- quanto maior a distância entre os átomos maior será a facilidade para se dilatar ou contrair com a variação de temperatura. --- R- E