Introdução à Teoria da Relatividade

Breve Histórico

Albert Einstein (1879-1955), pelos seus feitos científicos que inovaram radicalmente os caminhos

tecnológicos da humanidade, colaborou de forma extraordinária para o desenvolvimento da ciência, para a qualidade de vida  de todos os habitantes do planeta Terra, alterando a visão dos cientistas nas áreas da física das partículas, astronomia, astrofísica, cosmologia, filosofia e outros

conceitos relacionados ao universo, quando, aos 26 anos de idade, em 1905, encaminhou para os Anais da Física um artigo que revolucionaria os conceitos tradicionais de espaço e tempo “ A Teoria Especial da Relatividade”.  

Posteriormente, em 1916 ele publica a Teoria Geral da Relatividade e no ano seguinte um artigo que serviu de base para o raio laser referente à emissão estimulada da luz e um segundo artigo que é a base da cosmologia atual sobre a estrutura do Universo.

Conceito de referencial inercial

Considere um vagão em movimento retilíneo uniforme (MRU) e uma bola colocada sobre uma mesa, ambas no interior do vagão.

A primeira lei de Newton “Princípio da Inércia” afirma que qualquer corpo em repouso ou em movimento retilíneo uniforme tende a manter esses estados, desde que nenhuma força atue sobre ele (força resultante sobre ele nula). 

Nesse caso, um referencial no interior do vagão é inercial, pois em relação a ele as leis da física (no caso, princípio da inércia) são válidos, já que a bola em relação a esse referencial estará em repouso (primeira figura).

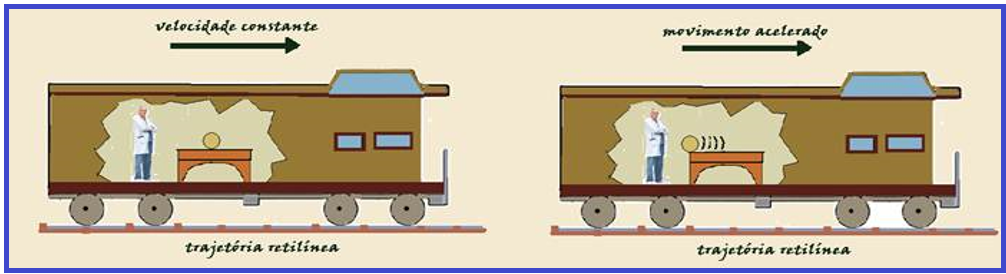
Se o vagão for freado, acelerado ou efetuar uma curva (segunda figura), a bola será deslocada sobre a mesa, saindo da sua posição de equilíbrio e sobre ela não surgiu nenhuma força de interação, ou seja, nenhuma força externa agiu empurrando ou puxando a bola.

Assim, nesse caso, o princípio da inércia não é válido para esse referencial que também está colocado no interior do vagão e ele não é um referencial inercial é um referencial não inercial. Portanto, num referencial não inercial, os corpos estão sujeitos a pseudo-forças (forças de inércia) que, em princípio, não podem ser atribuídas a qualquer agente direto.

Um referencial é denominado referencial inercial se nele a primeira lei de Newton (ou qualquer outra lei física) é válida.

Referenciais inercais são referenciais que se movem, uns em relação aos outros, com velocidade constante.

Conceito de Postulado

Um postulado na Teoria Física tem o mesmo papel que um axioma tem na Matemática.

É uma afirmação fundamental que não pode ser demonstrado logicamente.

Em Física, o postulado, é o resultado da generalização dos fatos experimentais.  

Postulados da Relatividade Especial

A teoria da relatividade especial é construída a partir do postulado do princípio da relatividade de Einstein e do postulado da velocidade da luz:

Primeiro Postulado

“As leis da física devem ser exatamente as mesmas se descritas por observadores em diferentes referenciais inerciais. Não existe um referencial inercial privilegiado (referencial absoluto)”.

Esse postulado afirma que não existe sistema de referência inercial preferencial no estudo de qualquer fenômeno físico.

Assim, o princípio da relatividade da mecânica clássica generaliza-se para todos os processos físicos da Natureza, ou seja, tanto as leis da Mecânica como as leis do Eletromagnetismo devem ter a mesma forma em qualquer referencial.

Então, por exemplo, observadores em referenciais inerciais diferentes medem a mesma aceleração para o movimento de uma partícula.

Segundo Postulado

 Postulado da velocidade da luz: “A velocidade da luz no vácuo tem o mesmo valor em todas as direções e em todos os referenciais inerciais ( a velocidade da luz é independente da velocidade da fonte)”.

Esta é a velocidade máxima com que qualquer tipo de informação pode ser transmitida. 

A velocidade da luz não depende nem da velocidade do emissor (fonte emissora da luz), nem da velocidade do receptor (observador) do sinal luminoso.

 Veja um exemplo: Suponha que, no futuro, uma base avançada seja construída em Marte. Suponha, também, que uma nave espacial está viajando em direção a Terra, com velocidade constante igual à metade da velocidade da luz. Quando essa nave passa por Marte, dois sinais de rádio são emitidos em direção à Terra, um pela base e outro pela nave. Ambos são refletidos pela Terra e, posteriormente, detectados na base em Marte. Sejam t_b e t_n os intervalos de tempo total de viagem dos sinais emitidos, respectivamente, pela base e pela nave, desde a emissão até a detecção de cada um deles pela base em Marte.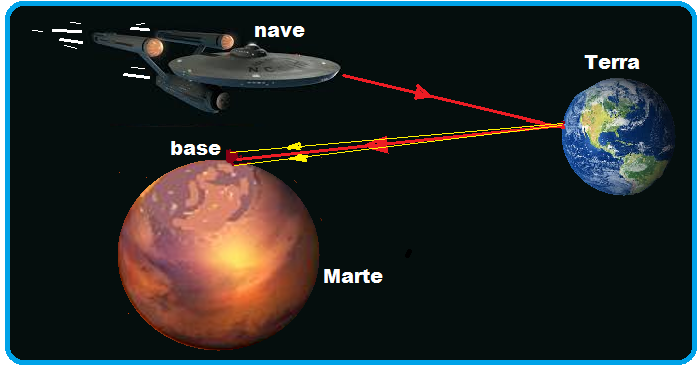

Como a velocidade da luz (onda eletromagnética) é 3.10⁸ m/s e independe do referencial, não importando de a fonte emissora estar em repouso ou em movimento, essa velocidade será sempre a mesma e os tempos t_b e t_n serão iguais.

A velocidade da luz no vácuo é a velocidade máxima possível de transmissão de interação na Natureza e seu valor é c=3,0.10⁸m/s. Ela não depende do sistema de referência inercial adotado. Observe que, se V = c = ΔS/Δt é constante para qualquer observador (referencial) então espaço (ΔS) e tempo (Δt) podem assumir valores diferentes dependendo do observador (referencial), pois o quociente ΔS/Δt é constante.

Dilatação do tempo

Ao discutir o conceito de tempo, Einstein mostrou que a simultaneidade (fatos que ocorrem em diferentes locais e ao mesmo tempo) é algo relativo.

Assim, o que é simultâneo para um observador poderá não ser simultâneo para outro observador que se move em relação ao primeiro.

Em outras palavras, a única razão pela qual todos nós sentimos espaço e tempo da mesma forma deve-se ao fato de todos nós estarmos nos movendo a uma mesma velocidade, uns em relação aos outros.

Contudo, quando os observadores se locomovem a velocidades extremamente diferentes,

o tempo entre eles não será mais simultâneo, mas diferente para cada um deles.

Einstein mostrou que a maneira como a mecânica clássica de Newton abordava alguns conceitos não era válida para algumas situações.

Explicando a dilatação do tempo com um exemplo simples muito utilizado.

Considere um vagão em movimento retilíneo e uniforme com velocidade constante de intensidade V em relação a um observador (O_s) no solo. No interior do vagão existe um sistema de

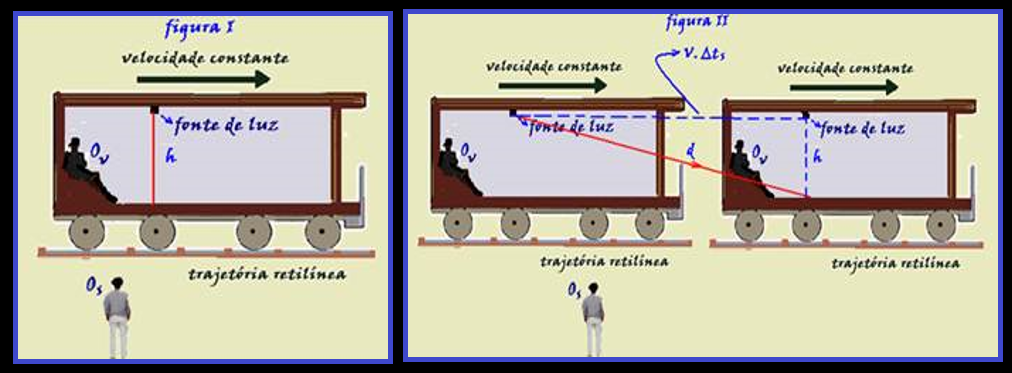
referência inercial, observador O_v. Um raio de luz saindo do teto do vagão atinge o chão, percorrendo em relação ao vagão (ao observador O_v, dentro da vagão, figura I) uma distância h com velocidade da luz c num intervalo de tempo Δt_v, tal que,  V = c = h/Δt_v    h = c.Δt_v.

Com o vagão em movimento (velocidade constante V), em relação ao observador O_s no solo, a luz percorre uma distância d (figura II), maior que a observada por O_v, sendo d = V.Δt_s    aplicando-se Pitágoras no triângulo retângulo da figura II    d² = h² + (V.Δt_s)², onde V é a velocidade do vagão e c a velocidade da luz    observe que d = c.Δt_s e que h = c.Δt_v    c².Δt_s² = c².Δt_v² + V².Δt_s²    c².Δt_s² – V².Δt_s² = c².Δt_v²     Δt_v² = Δt_s².( c² – V²)/c²    Δt_s = Δt_v/√1 – V²/c²     o intervalo de tempo medido quando o observador está em repouso (Δt_v) no interior do vagão é denominado intervalo de tempo próprio (Δt_p) e o intervalo de tempo medido pelo observador que está em repouso em relação ao solo e fora do vagão que está em movimento será denominado de (Δt).

Preste muita atenção no formulário abaixo

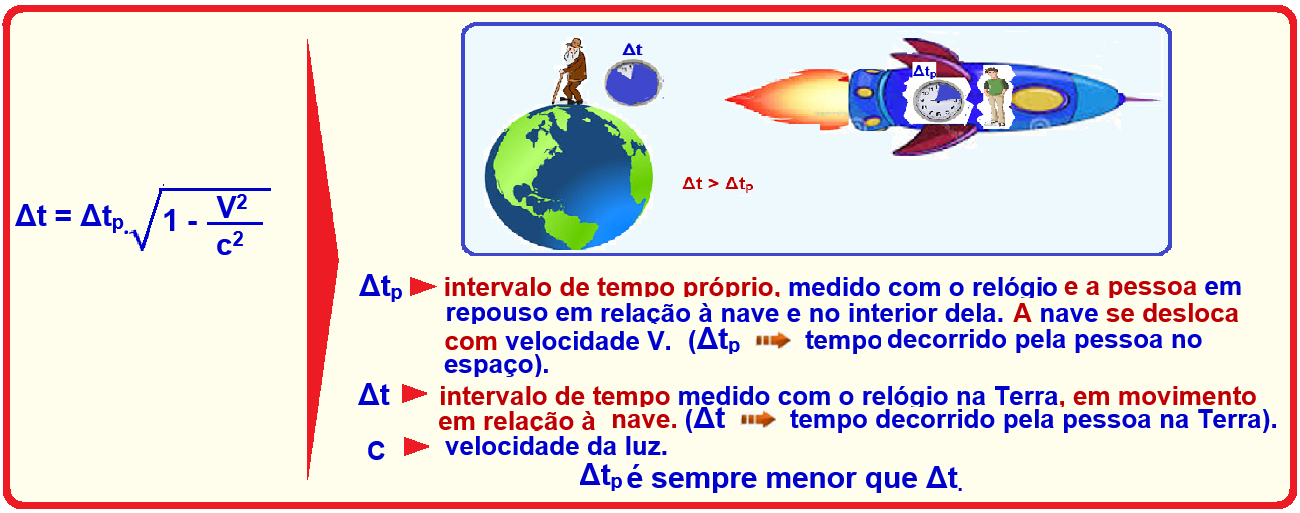
Observe na equação acima que:

 Considerando a velocidade V com que o vagão se move muito pequena em relação à velocidade da luz (3,0.10⁸ m/s), a razão V²/c² ficará extremamente pequena e a expressão √1 – V²/c² tenderá a 1 fazendo com que Δt = Δt_p. 

Assim, para velocidades comparáveis ao nosso dia a dia os efeitos da teoria da relatividade são insignificantes.

 Por outro lado, se a velocidade V do vagão for se aproximando da velocidade da luz c, Δt vai ficando cada vez maior que Δt_p e os efeitos relativísticos vão ficando cada vez maiores.

Veja um exercício exemplo:

A nave Enterprise viaja de Netuno a Plutão a uma velocidade constante v = 0,5c, onde c é a

velocidade da luz no vácuo. No referencial da espaçonave, o tempo transcorrido entre a partida de Netuno e a chegada à Plutão 2,5h = 150 min. Qual o tempo transcorrido medido no referencial de Netuno?

Resolução:

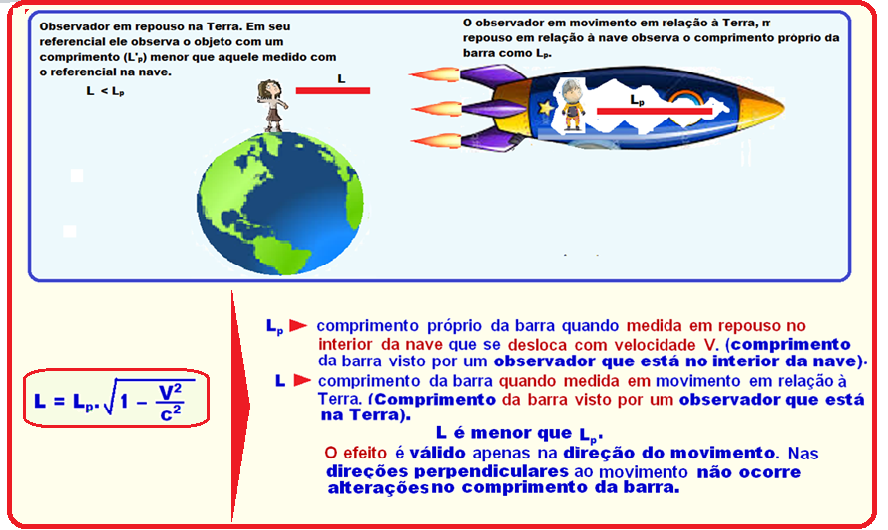
Contração do espaço (do comprimento)

Considere um vagão em movimento retilíneo e uniforme com velocidade constante de intensidade V em relação a um observador (O_s) no solo.

No interior do vagão existe um sistema de referência inercial, observador O_v.

Coloque uma barra de comprimento L_p em relação a O_v no interior do vagão, orientada na direção do movimento.

Devido à dilatação do tempo, essa barra terá comprimento L em relação a O_s, depois que o vagão se deslocou durante um intervalo de tempo Δt    V = L_p/Δt_p    Δt_p = L_p/V    V = L/Δt    Δt = L/V  Δt= Δt_p/(√1 – V²/c²)    Δt/Δt_p = √1 – V²/c²    (L/V)/(L_p/V) = √1 – V²/c²    L/L_p = √1 – V²/c²   

L=L_p. √1 – V²/c².

Preste muita atenção no formulário abaixo

Observe na equação acima que:

o efeito é sentido apenas na direção do movimento.

 As dimensões de um objeto são máximas quando medidas em repouso em relação ao observador.

Quando o objeto se move com velocidade V, em relação ao observador, o resultado da medida de sua dimensão paralela a direção do movimento é menor do que o valor obtido quando em repouso.

  As dimensões do objeto, perpendiculares a direção do movimento, não são afetadas.

  No cotidiano, valor da velocidade V é desprezível em relação à velocidade da luz c e, nesse caso, a razão V²/c² é muito pequena, tendendo a zero e pode ser desprezada.

 Assim, L = L_p. √1 – V²/c²    L = L_p. √1 – 0    L = L_p    que está de acordo com a mecânica  de Newton (clássica).

  Com velocidade da luz, ou velocidades próximas a ela, você pode percorrer uma distância d num intervalo de tempo menor, devido à contração de seu comprimento.

Assim, é possível atravessarmos o diâmetro da Via Láctea, uma distância de aproximadamente 100 anos-luz (equivalente a 10¹⁸m), em um intervalo de tempo bem menor que 100 anos.

Isso pode ser explicado pelo fenômeno de contração do comprimento, como visto pelo viajante, ou ainda pelo fenômeno de dilatação temporal, como observado por quem está em repouso em relação à galáxia.

Veja um exercício exemplo:

Massa Relativística

A massa é a medida da inércia de um corpo. Assim, à medida que a velocidade de um corpo aumenta sua inércia também aumenta e quando a velocidade do corpo tende à velocidade da luz (a maior possível), sua inércia  e consequentemente sua massa tende ao infinito.

Portanto, além do espaço e do tempo, na teoria da velocidade a massa também varia e essa variação é fornecida pela expressão:

Veja um exercício exemplo:

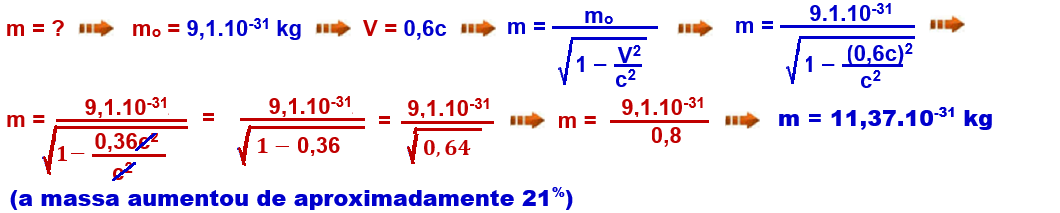
Quando um elétron de massa m = 9,1.10^-31 kg é acelerado até atingir 60% da velocidade da luz (V = 0,6c), o que acontecerá com sua massa(m) em relação à sua massa em repouso (m_o)?

Resolução:

Energia Relativística

Como, na teoria da relatividade, a massa relativística está associada com a velocidade, essa relação faz com que a teoria relativística implique também com a energia.

Albert Einstein, Prêmio Nobel de Física, publicou, em 1905, cinco estudos em que definiu a natureza da luz, revolucionou os conceitos de tempo e espaço e formulou a mais conhecida das equações

E = mc².

Segundo a Teoria da Relatividade Especial, formulada por Einstein, essa relação E = mc² expressa a possibilidade de a massa de um corpo ser convertida em energia e vice-versa.

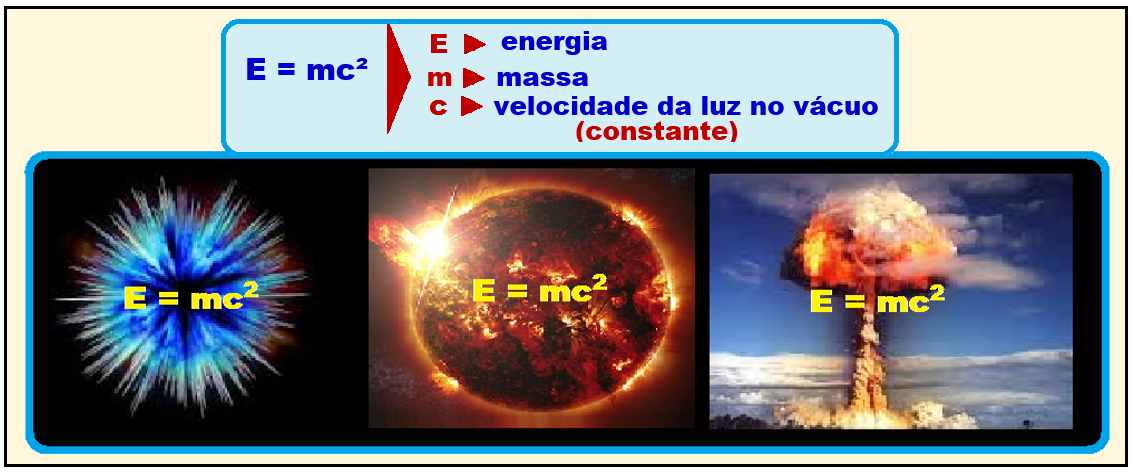
E também é chamada energia própria do corpo.

A energia do repouso é fornecida por E_o =m_o.c², onde m_o é a massa do repouso.

A energia cinética relativística do corpo corresponde à diferença entre a energia própria (E) e a energia do repouso (E_o)    E_c = E – E_o    E_c = mc² – m_oc²    E_c = (m – m_o).c.

Na expressão E_c = (m – m_o).c, como c é constante, se a energia cinética E_c diminuir ou aumentar ocorrerá uma correspondente diminuição ou aumento de massa do corpo. 

Veja um exercício exemplo:

Em 1905 Albert Einstein publica a Teoria da Relatividade, com a qual o conceito de energia ganha um novo significado e esta grandeza passa a ser expressa pela famosa equação de Einstein, que estabeleceu definitivamente a equivalência entre a massa e a energia.

Tal equivalência é talvez o resultado mais revolucionário da teoria da relatividade.

Ela simplesmente nos diz que massa pode ser convertida em energia e vice-versa.

Sabendo-se que a velocidade da luz no vácuo 3 . 10⁸ m/s, determine a energia contida em uma massa de 1 grão de feijão, de aproximadamente 0,2 g.

Relação entre velocidades relativas relativísticas

A velocidade relativa (V_R) para dois corpos deslocando-se em sentidos opostos, com velocidades próximas à da luz de módulos u e v em relação a um referencial inercial é fornecida pela fórmula de Einstein ao lado.

Esta expressão é a fórmula de soma de velocidades no caso relativístico. Observe que:

Para velocidades pequenas em relação à velocidade da luz, o termo u.V/c² tende a zero, e a equação se resume a já esperada fórmula clássica  V_R = u + V.

 Essa fórmula não permite que a velocidade relativa entre dois corpos supere a velocidade da luz. 

Veja um exercício exemplo:

Considere duas naves espaciais, N₁ e N₂ que viajam em sentidos contrários, isto é, opostos, com velocidades de 50% e 70%, respectivamente, da velocidade da luz. Calcule a velocidade relativa de uma nave em relação à outra.

Resolução:

V_R = (N₁ + N₂)/[1 +( N₁.N₂/c²)] V_R = (0,5c + 0,7c)/[1 +( 0,5c.0,7c/c²)] = 1,2c/ (1 + 0,35c²/c²)

V_R = 1,2c/1,35 V_R ≈ 0,9c.

Observação: Se você utilizar a fórmula da Física Clássica você obterá V_R = 0,5c + 0,7c = 1,2c, valor impossível já que a velocidade da luz no vácuo não pode ser maior que c.

Selecionei alguns exercícios interessantes para que você possa conferir as resoluções:

01-(UNESP-SP) Instituído pela Organização das Nações Unidas, 2005 foi o Ano Mundial da Física, em que se comemorou o centenário dos trabalhos revolucionários publicados por Albert Einstein, o mais importante  cientista do século XX (segundo a revista norte americana Time).

Na Teoria da Relatividade Especial, de Einstein, objetos que se movem com velocidade V em relação a um referencial inercial tem o tempo dilatado por um fator λ, para um observador em repouso nesse referencial.

A tabela mostra valores de λ para diversos módulos da velocidade V, representados em múltiplos  da velocidade da luz, c (ou 3,0.10⁸ms).

Segundo esse modelo, pede-se:

a) qual a velocidade, em m/s, que deve ser atingida pelo objeto para que a dilatação do tempo seja de apenas 0,5%?

Comente como esse resultado explica por que as pessoas não percebem os efeitos da dilatação do tempo no seu dia-a-dia.

b) se para o objeto passaram-se 10 minutos, quantos minutos se passaram para um observador no referencial inercial que vê o objeto se movimentando à velocidade de 0,600c?

Resolução:

a) O intervalo de tempo que sofre maior dilatação na expressão Δt = Δt_p/√1 – V²/c² é Δt e ele se dilata de 0,5% desse valor Δt = Δt_p + (0,5/100).Δt_p  Δt = 1,005.Δt_p  1,005 de aumento corresponde ao fator λ Δt = λ.Δt_p.

Procurando na tabela    quando λ = 1,005    v = 0,100c    v = 0,100.3,0.10⁸ v = 3,0.10⁷m/s.

Observe que as velocidades no nosso cotidiano são insignificantes em relação a 3.10⁷ = 30.000.000m/s.

b) quando v = 0,600c    λ = 1,250c  Δt = λ.Δt_p = 1,250.10min    Δt = 12,5 min.       

02-(UFC-CE)

A figura ao lado mostra uma nave espacial em forma de cubo que se move no referencial S, ao longo

do eixo x, com velocidade v = 0,8c (c é a velocidade da luz no vácuo).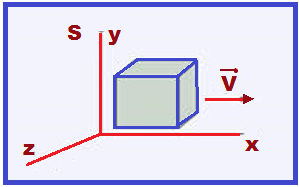

O volume da nave, medido por um astronauta em repouso dentro dela,

é V_o.

Calcule o volume da nave medido por um observador em repouso no referencial S.

Resolução:

Se d for a aresta da nave, medida pelo astronauta, o volume medido pelo astronauta vale V_o =

d.d.d V_o = d³.

O observador em repouso no referencial S observará uma contração da aresta da nave apenas na direção do eixo x, onde ela se move.

Assim, a nova aresta d’ valerá   d’ = d.√(1 – V²/c²)   d’ = d.√(1 – 0,64c²/c²)    d’ = 0,6d.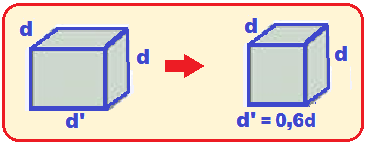

O observador em repouso no referencial S verá o novo volume da nave fornecido por V = d.d.d’

V = d.d.0,6d    V = 0,6.d.d.d   V = 0,6d³ = 0,6V_o.

03-(UPE) Um trem de comprimento igual a 100 m viaja a uma velocidade de 0,8 c, onde c é a velocidade da luz, quando atravessa um túnel de comprimento igual a 70 m.

Quando visto por um observador parado ao lado dos trilhos, é CORRETO afirmar que o trem

a) não chega a ficar totalmente dentro do túnel, restando um espaço de 12 m fora do túnel.

b) fica totalmente dentro do túnel e sobra um espaço de 10 m.

c) fica totalmente dentro do túnel e sobra um espaço de 15 m.

d) não chega a ficar totalmente dentro do túnel, restando um espaço de 5 m fora do túnel.

e) fica totalmente dentro do túnel e não resta nenhum espaço.

Resolução:

L_o = 100m    V = 0,8c    L =70m    para um observador em repouso externo ao trem, o  comprimento do trem será   L=L_o.√(1 – V²/c²)    L=100. √1 – (0,8c)²/c²    L=100.06  L=60m.

Como o comprimento do trem se reduz a 60m, para o observador parado ao lado dos trilhos, o trem

ficará totalmente no interior do túnel de 70m sobrando (70 – 60) = 10m.

R- B

04-(UFG-GO) Antipartículas, raras na natureza, possuem carga elétrica oposta à de suas partículas

correspondentes.

Se encontrássemos uma fonte de antipartículas, poderíamos produzir uma grande quantidade de energia, permitindo que elas se aniquilassem com suas partículas. Dessa forma, calcule:

a) a quantidade de energia que seria liberada se 2,0 gramas de antimatéria fossem aniquiladas com 2,0 gramas de sua matéria (considere a velocidade da luz igual a 3,0.10⁸m/s);

b) por quanto tempo essa energia abasteceria uma cidade com um milhão de habitantes,

considerando que uma pessoa consome, em média, 100 kWh por mês.

Resolução:

a) Massas aniquiladas m = (2g + 2g) = 4g = 4.10^-3kg  fórmula de Einstein da equivalência entre massa e energia   E = m.c² = 4.10^-3.(3.10⁸)²    E = 3,6.10¹⁴J.

b) Energia consumida pela cidade de um milhão de habitantes (10⁶ habitantes) com potência de P =

100x10³ W E = n.P.Δt = 10⁶x100x10³x3600 = 36.10¹³ = 3,6.10¹⁴ J

R: 1 mês

O que você deve saber, informações e dicas

 Postulados da Relatividade Especial 

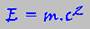
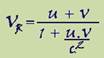
Velocidade relativa (V_R) para dois corpos deslocando-se em sentidos opostos, com velocidades de módulo u e v em relação a um referencial inercial.

A energia cinética relativística de um corpo corresponde à diferença entre a energia própria (E) e a energia do repouso (E_o)    E_c=E – E_o    E_c=mc² – m_oc²    E_c=(m – m_o).c.

Como c é constante, se E_c diminuir ou aumentar ocorrerá uma correspondente diminuição ou aumento de massa do corpo. 

Pela teoria da Relatividade Geral de Einstein, quando raios de luz provenientes de um corpo estelar, como estrelas ou galáxias, passam muito próximos de um objeto estelar de grande densidade de massa, esses raios de luz são desviados para um ponto de encontro oposto ao lado em que os raios incidem no objeto.

Esse encurvamento de um raio de luz em sentido oposto ao do corpo é explicado pelo mesmo modo que um índice de refração variável encurva a luz em uma

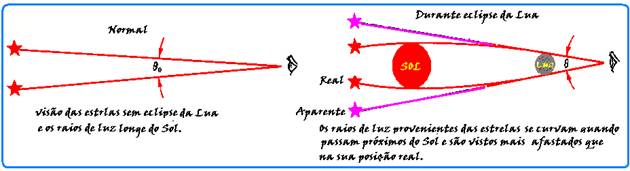
 Miragem.

 Assim, por exemplo, um grupo de galáxias de grande massa também provoca uma forte curvatura no espaço-tempo, fazendo com que todos os raios luminosos que atravessem a região sejam curvados, formando uma verdadeira lente cósmica.

Paradoxo dos gêmeos

 Paradoxo, no exemplo abaixo, pode ser definido como aparente falta de lógica.

O paradoxo dos gêmeos foi um experimento mental proposto para demonstrar a teoria da dilatação do tempo, atualmente já comprovada experimentalmente.

Considere dois irmãos gêmeos, sendo que o irmão gêmeo A fica na Terra, enquanto o outro, o gêmeo B, utilizando uma espaçonave, faz uma viagem espacial na qual viaja próximo a velocidade da luz.

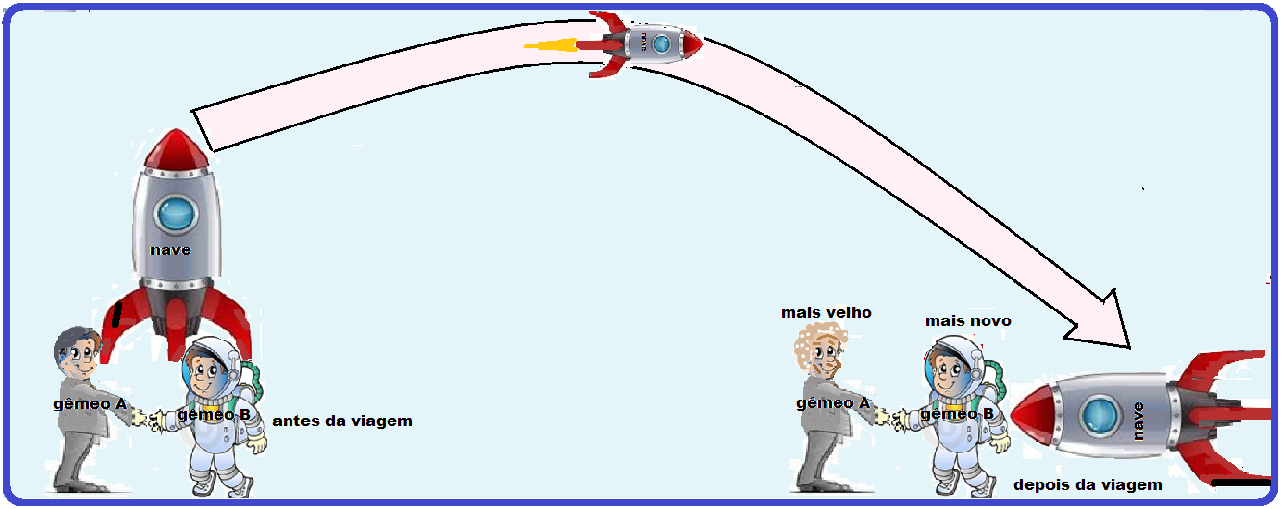
Por causa do movimento do gêmeo B (o que viaja próximo a velocidade da luz) seu tempo passa mais devagar dentro da espaçonave, conforme é visto pelo irmão, gêmeo A, que ficou na Terra.

Quando o gêmeo B retornar para a Terra verificará que seu irmão, o gêmeo A, está mais velho.

O efeito vale para qualquer pessoa.

Se você quiser se aprofundar mais no assunto da Teoria da Relatividade seria aconselhável conferir as resoluções dos exercícios que seleciomei, de números 03, 07,08,15, 17, 18, 26, 30, 36 e 48.

Exercícios de vestibulares com resoluções comentadas sobre

Teoria da Relatividade

01-(UEG-GO) Antes mesmo de ter uma idéia mais correta do que é a luz, o homem percebeu que ela era capaz de percorrer muito depressa enormes distâncias. Tão depressa que levou Aristóteles - famoso pensador grego que viveu no século IV a.C. e cujas

obras influenciaram todo o mundo ocidental até a Renascença - a admitir que a velocidade da luz seria infinita.

            GUIMARÃES, L. A.; BOA, M. F. "Termologia e óptica". São Paulo: Harbra, 1997. p. 177

Hoje sabe-se que a luz tem velocidade de aproximadamente 300.000 km/s, que é uma velocidade muito grande, porém finita. A teoria moderna que admite a velocidade da luz constante em qualquer referencial e, portanto, torna elásticas as dimensões do espaço e do tempo é:

a) a teoria da relatividade.              

b) a teoria da dualidade onda - partícula.                     

c) a teoria atômica de Bohr.

d) o princípio de Heisenberg.             

e) a lei da entropia.

02-(CFT-CE) Em 2005, Ano Mundial da Física, comemora-se o centenário da Teoria da Relatividade de Albert Einstein. Entre outras conseqüências esta teoria poria fim à idéia do éter, meio material necessário, semelhantemente ao som, através do qual a luz

se propagava. O jargão popular "tudo é relativo" certamente não se deve a ele, pois seus postulados estão fundamentados em algo absoluto: a velocidade da luz no vácuo – 300.000 km/s.

Hoje sabe-se que:

I. O som propaga-se no vácuo.

II. A luz propaga-se no vácuo.

III. A velocidade da luz no vácuo é a velocidade limite do universo.

É (são) verdadeira(s):

03-(UFMG-MG) Observe esta figura:

Paulo Sérgio, viajando em sua nave, aproxima-se de uma plataforma espacial, com velocidade de 0,7 c, em que c é a velocidade da luz.

Para se comunicar com Paulo Sérgio, Priscila, que está na plataforma, envia um pulso luminoso em direção à nave. Com base nessas informações, é correto afirmar que a velocidade do pulso medida por Paulo Sérgio é de:

a) 0,7 c.                          

b) 1,0 c.                              

c) 0,3 c.                                

d) 1,7 c.

04-(UFMG-MG) Suponha que, no futuro, uma base avançada seja construída em Marte. Suponha, também, que uma nave espacial está viajando em direção a Terra, com velocidade constante igual à metade da velocidade da luz. Quando essa nave passa por

Marte, dois sinais de rádio são emitidos em direção à Terra - um pela base e outro pela nave. Ambos são refletidos pela Terra e, posteriormente, detectados na base em Marte. Sejam t_B e tn os intervalos de tempo total de viagem dos sinais emitidos, respectivamente, pela base e pela nave, desde a emissão até a detecção de cada um deles pela base em Marte.

Considerando-se essas informações, é CORRETO afirmar que:

05-(UEL-PR) A teoria da Relatividade Restrita, proposta por Albert Einstein (1879 – 1955) em 1905, é revolucionária porque mudou as idéias sobre o espaço e o tempo, mas em perfeito acordo com os resultados experimentais. Ela é aplicada, entretanto, somente a referenciais inerciais. Em 1915, Einstein propôs a Teoria Geral da Relatividade, válida não só para referenciais inerciais, mas também para referenciais não-inerciais.

 Sobre os referenciais inerciais, considere as seguintes afirmativas:

 I. São referenciais que se movem, uns em relação aos outros, com velocidade constante.

 II. São referenciais que se movem, uns em relação aos outros, com velocidade variável.

 III. Observadores em referenciais inerciais diferentes medem a mesma aceleração para o movimento de uma partícula.

 Assinale a alternativa correta:

 a) Apenas a afirmativa I é verdadeira.                                          

b) Apenas a afirmativas II é verdadeira.

c) As afirmativas I e II são verdadeiras.                                       

d) As afirmativas II e III são verdadeiras.

e) As afirmativas I e III são verdadeiras.

06-(UFRN-RN) A teoria da Relatividade Especial prediz que existem situações nas quais dois eventos que acontecem em instantes diferentes, para um observador em um dado referencial inercial, podem acontecer no mesmo instante, para outro

observador que está em outro referencial inercial. Ou seja, a noção de simultaneidade é relativa e não absoluta.

A relatividade da simultaneidade é conseqüência do fato de que:

a) a teoria da Relatividade Especial só é válida para velocidades pequenas em comparação com a velocidade da luz.

b) a velocidade de propagação da luz no vácuo depende do sistema de referência inercial em relação ao qual ela é medida.

c) a teoria da Relatividade Especial não é valida para sistemas de referência inerciais.

d) a velocidade de propagação da luz no vácuo não depende do sistema de referência inercial em relação ao qual ela é medida.

07-(UFRN) Nos dias atuais, há um sistema de navegação de alta precisão que depende de satélites artificiais em órbita em torno da Terra. Para que não haja erros significativos nas posições fornecidas por esses satélites, é necessário corrigir relativisticamente o intervalo de tempo medido pelo relógio a bordo de cada um desses satélites. A Teoria da Relatividade Especial prevê que, se não for feito esse tipo de correção, um relógio a bordo não marcará o mesmo intervalo de tempo que outro relógio em repouso na superfície da Terra, mesmo sabendo-se que ambos os relógios estão sempre em perfeitas condições de funcionamento e foram sincronizados antes do o satélite se lançado.

 Se não for feita a correção relativística para o tempo medido pelo relógio de bordo:

 a) ele se adiantará em relação as relógio em Terra enquanto ele for acelerado em relação à Terra.

b) ele ficará cada vez mais adiantado em relação ao relógio em Terra.

c) ele atrasará em relação ao relógio em Terra durante metade de sua órbita e se adiantará durante a metade da outra órbita.

d) ele ficará cada vez mais atrasado em relação ao relógio em Terra.

08-(UFPE-PE) Um astronauta é colocado a bordo de uma espaçonave e enviado para uma estação espacial a uma velocidade constante v = 0,8 c, onde c é a velocidade da luz no vácuo. No referencial da espaçonave, o tempo transcorrido entre o lançamento e a chegada na estação espacial foi de 12 meses. Qual o tempo transcorrido no referencial da Terra, em meses?

09-(UNESP-SP) Instituído pela Organização das Nações Unidas, 2005 foi o Ano Mundial da Física, em que se comemorou o centenário dos trabalhos revolucionários publicados por Albert Einstein, o mais importante  cientista do século XX (segundo a revista norte americana Time). Na Teoria da Relatividade Especial, de Einstein, objetos que se movem com velocidade V em relação a um referencial inercial tem o tempo dilatado por um fator λ, para um observador em repouso nesse referencial. A tabela mostra valores de λ para diversos módulos da velocidade V, representados em múltiplos  da velocidade da luz, c (ou 3,0.10⁸ms).

Segundo esse modelo, pede-se:

a) qual a velocidade, em m/s, que deve ser atingida pelo objeto para que a dilatação do tempo seja de apenas 0,5%? Comente como esse resultado explica por que as pessoas não percebem os efeitos da dilatação do tempo no seu dia-a-dia.

b) se para o objeto passaram-se 10 minutos, quantos minutos se passaram para um observador no referencial inercial que vê o objeto se movimentando à velocidade de 0,600c?

10-(UFRN) André está parado em relação a um referencial inercial, e Regina está parada em relação a outro referencial inercial, que se move com velocidade (vetorial) constante em relação ao primeiro. O módulo dessa velocidade é v.
André e Regina vão medir o intervalo de tempo entre dois eventos que ocorrem no local onde esta se encontra. (Por exemplo, o intervalo de tempo transcorrido entre o instante em que um pulso de luz é emitido por uma lanterna na mão de Regina e o instante em que esse pulso volta à lanterna, após ser refletido por um espelho.)
A teoria da relatividade restrita nos diz que, nesse caso, o intervalo de tempo medido por André (Δt_André) está relacionado ao intervalo de tempo medido por Regina (Δt_Regina) através da expressão: Δt_André = λ.Δt_Regina. Nessa relação, a letra gama (λ) denota o fator de Lorentz. O gráfico abaixo representa a relação entre λ e v/c, na qual c é a velocidade da luz no vácuo.

Imagine que, realizadas as medidas e comparados os resultados, fosse constatado que Δt_André = 2Δt_Regina.
Usando essas informações, é possível estimar-se que, para se obter esse resultado, a velocidade v teria de ser aproximadamente
a) 50% da velocidade da luz no vácuo.                                             

b) 87% da velocidade da luz no vácuo.
c) 105% da velocidade da luz no vácuo.                                            

d) 20% da velocidade da luz no vácuo.

11-(UEPB-PB) A relatividade proposta por Galileu e Newton na Física Clássica é reinterpretada pela Teoria da Relatividade Restrita, proposta por Albert Einstein (1879-1955) em 1905, que é revolucionária porque mudou as idéias sobre o espaço e o tempo, uma vez que a anterior era aplicada somente a referenciais inerciais. Em 1915, Einstein propôs a Teoria Geral da Relatividade válida para todos os referenciais (inerciais e não inerciais).  

Ainda acerca do assunto tratado no texto, resolva a seguinte situação-problema: Considere uma situação “fictícia”, que se configura como uma exemplificação da relatividade do tempo.

Um grupo de astronautas decide viajar numa nave espacial, ficando em missão durante seis anos, medidos no relógio da nave.

Quando retornam a Terra, verifica-se que aqui se passaram alguns anos.

Considerando que c é a velocidade da luz no vácuo e que a velocidade média da nave é 0,8c, é correto afirmar que, ao retornarem a Terra, se passaram:

a) 20 anos                  

b) 10 anos                     

c)      30 anos                      

d) 12 anos                                 

e)     6 anos

12-(UFMG)

Suponha que uma nave se afasta de um planeta com velocidade v = 0,2c, onde c = 3.10⁸ m/s é a velocidade da luz no vácuo. Em um determinado momento, a nave envia um sinal de rádio para comunicar-se com o planeta. Determine a velocidade do sinal medida por um observador na nave e a medida por um observador no planeta. Explique seu raciocínio.

13-(UFOP-MG) Na figura são representadas duas naves N₁ e N₂ viajando em sentido contrário com

velocidade 12.000 m/s e 10.000 m/s, respectivamente. Medidas da velocidade da luz emitida pelo farol da nave N₂ e realizadas nas naves N₁ e N₂, respectivamente, dão estes valores:

a) 300.022.000 m/s e 300.000.000 m/s.                                            

b) 300.000.000 m/s e 300.000.000 m/s. 
c) 300.012.000 m/s e 299.990.000 m/s.                                            

d) 300.022.000 m/s e 299.990.000 m/s.

14-(UFRJ-RJ) O conceito de éter surgiu na Grécia antiga, significando uma espécie de fluido sutil e rarefeito que preenchia o espaço e envolvia a Terra. Esse conceito evoluiu para representar um referencial privilegiado, a partir do qual se poderia descrever toda a Física, inclusive seria o meio material no qual se propagariam as ondas eletromagnéticas (a luz). No entanto, as experiências de Michaelson-Morley, realizadas em 1887, mostraram a inconsistência desse conceito, uma vez que seus resultados implicavam que ou a Terra estava sempre estacionária em relação ao éter ou a noção de que o éter representava um sistema de referência absoluto era errônea, devendo, portanto, ser rejeitada.

As inconsistências do conceito de éter levaram Einstein a elaborar a teoria de que a velocidade da luz

a) é constante para qualquer observador e dependente de qualquer movimento da fonte ou do observador.

b) é constante para qualquer observador e independente de qualquer movimento da fonte ou do observador.

c) é constante e dependente do observador, porém independente de qualquer movimento relativo da fonte.

d) é constante e independente do observador, porém dependente de qualquer movimento relativo da fonte.

15-(UFG-GO) Segundo a Teoria da Relatividade Restrita de Albert Einstein, o tempo transcorre de maneira diferente para observadores com velocidades diferentes. Isso significa que, para um

observador em um referencial fixo, transcorre um intervalo de tempo  entre dois eventos, enquanto para um observador em um referencial que viaja com uma velocidade constante v, em relação ao referencial anterior, o intervalo de tempo entre os mesmos eventos será . Os dois intervalos de tempo estão relacionados por

que representa uma dilatação temporal. Nesta expressão, c é a velocidade da luz no vácuo. Com esta teoria surge o paradoxo dos gêmeos: para o piloto de uma espaçonave que realizou uma viagem espacial, com uma velocidade constante de 0,8c, transcorreram 18 anos até o seu retorno à Terra.

Para o gêmeo que ficou na Terra, calcule quanto tempo durou a viagem do seu irmão, o piloto.

16-(UNIMAT-MT) Com o advento da Teoria da Relatividade de Einstein, alguns conceitos básicos da física newtoniana, entre eles, o espaço e o tempo, tiveram de ser revistos. Qual a diferença substancial desses conceitos para as duas teorias?

17-(UFRN) Bastante envolvida com seus estudos para a prova do vestibular, Silvia selecionou o seguinte texto sobre Teoria da Relatividade para mostrar a sua colega Tereza: A luz da Teoria da Relatividade Especial, as medidas de comprimento, massa e tempo não são absolutas quando realizadas por observadores em referenciais inerciais diferentes. Conceitos inovadores como massa relativística, contração de Lorentz e dilatação temporal desafiam o senso comum. Um resultado dessa teoria e que as dimensões de um objeto são máximas quando medidas em repouso em relação ao observador.

Quando o objeto se move com velocidade V, em relação ao observador, o resultado da medida de sua dimensão paralela a direção do movimento e menor do que o valor obtido quando em repouso. As suas dimensões perpendiculares a direção do movimento, no entanto, não são afetadas. Depois de ler esse texto para Tereza, Silvia pegou um cubo de lado L_o que estava sobre a mesa e fez a seguinte questão para ela:

Como seria a forma desse cubo se ele estivesse se movendo, com velocidade relativística constante, conforme direção indicada na figura abaixo?

A resposta correta de Tereza a essa pergunta foi:

18-(UFRGR-RS) Assinale a alternativa que preenche corretamente as lacunas do texto a seguir, na ordem em que aparecem.

De acordo com a relatividade restrita, é ___________ atravessarmos o diâmetro da Via Láctea, uma distância de aproximadamente 100 anos-luz (equivalente a 10¹⁸m), em um intervalo de tempo bem menor que 100 anos. Isso pode ser explicado pelo fenômeno de ___________ do comprimento, como visto pelo viajante, ou ainda pelo fenômeno de ___________ temporal, como observado por quem está em repouso em relação à galáxia.

a) impossível - contração – dilatação        

b) possível - dilatação – contração              

c) possível - contração - dilatação

d) impossível - dilatação – contração        

e) impossível - contração – contração

19-(UNISINOS-RS) Segundo a Teoria da Relatividade de Einstein, uma pessoa que viaja a uma velocidade próxima à da luz, vista por outra considerada em repouso.

I – envelhecerá menos rapidamente.

II – terá um tamanho menor.

III – terá uma massa maior.

Das afirmativas acima,

a) apenas a I é correta           

b) apenas a II é correta           

c) apenas I e II são corretas            

d) apenas I e III são corretas

e) I, II e III são corretas.

20-(UFC-CE)

A figura a seguir mostra uma nave espacial em forma de cubo que se move no referencial S, ao longo do eixo x, com velocidade v = 0,8c (c é a velocidade da luz no vácuo). O volume da nave, medido por um astronauta em repouso dentro dela,

é V_o.

Calcule o volume da nave medido por um observador em repouso no referencial S.

21-(UNIFOR-CE) Albert Einstein revolucionou o modo de pensar o espaço e o tempo ao lançar, no início do século XX, as bases da Teoria da Relatividade.

Analise as seguintes afirmações:

I. A Mecânica Clássica não impõe limite para o valor da velocidade que uma partícula pode adquirir, pois enquanto durar a ação de uma força sobre ela haverá aceleração e sua velocidade poderá aumentar indefinidamente.

II. Corpos em movimento, com velocidades próximas à da luz, sofrem contrações em suas três dimensões em relação às que possuem quando em repouso.

III. A velocidade de um objeto, em relação a qualquer referencial, não pode superar a velocidade da luz no vácuo.

É correto o que se afirma SOMENTE em

22-(UNIFOR-CE) Sobre a Teoria da Relatividade são feitas as afirmações abaixo.

I. Corpos em movimento sofrem contração na direção desse movimento em relação ao tamanho que possuem quando medidos em repouso.

II. Um relógio em movimento funciona mais lentamente que o relógio em repouso, para um observador em repouso.

III. A velocidade de qualquer objeto em relação a qualquer referencial não pode ser maior que a velocidade da luz no vácuo.

Está correto o que se afirma em

a) III, somente.          

b) I e II, somente.          

c) I e III, somente.          

d) II e III, somente.          

e) I, II e III.

23-(UEMS-MS) Com base na Teoria da Relatividade de Albert Einstein, publicada em 1905, analise as afirmações:

I. O tempo dilata, isto é, um mesmo evento pode transcorrer em intervalos de tempo diferentes quando medido por dois observadores, um em repouso e o outro em movimento retilíneo uniforme em relação ao primeiro.

II. O comprimento contrai, isto é, um mesmo corpo pode ter comprimentos diferentes quando medido por dois observadores, um em repouso e o outro em movimento retilíneo uniforme em relação ao primeiro.

III. A velocidade da luz no vácuo tem seu valor aproximado de 300.000 km/s, independente do referencial.

Qual(is) está(ão) correta(s):

a) I e II estão corretas     

b) I e III estão corretas     

c) II e III estão corretas     

d) todas estão corretas     

e) nenhuma está correta

24-(UPE) Um trem de comprimento igual a 100 m viaja a uma velocidade de 0,8 c, onde c é a velocidade da luz, quando atravessa um túnel de comprimento igual a 70 m.

Quando visto por um observador parado ao lado dos trilhos, é CORRETO afirmar que o trem

a) não chega a ficar totalmente dentro do túnel, restando um espaço de 12 m fora do túnel.

b) fica totalmente dentro do túnel e sobra um espaço de 10 m.

c) fica totalmente dentro do túnel e sobra um espaço de 15 m.

d) não chega a ficar totalmente dentro do túnel, restando um espaço de 5 m fora do túnel.

e) fica totalmente dentro do túnel e não resta nenhum espaço.

25-(UFSE) A teoria da relatividade de Einstein formaliza adequadamente a mecânica para os corpos que viajam a velocidadesmuito altas, evidenciando as limitações da Mecânica Newtoniana.

De acordo com essa teoria, analise as informações:

 00) A velocidade limite para qualquer corpo é a velocidade da luz no vácuo, aproximadamente, 3,0. 108 m/s.

 11) O tempo pode passar de maneira diferente para observadores a diferentes velocidades.

 22) As dimensões de um objeto são sempre as mesmas, quer ele esteja em repouso, que em movimento.

 33) A massa de um elétron viajando à metade da velocidade da luz é maior que a do elétron em repouso.

 44) A célebre equação E= mc² pode explicar a energia que o sol emite quando parte da sua massa se converte em energia.

26-(UFL-MG-MG) Quando aceleramos um elétron até que ele atinja uma velocidade v = 0,5c, em que c é a velocidade da luz, o

 que acontece com a massa?

a) Aumenta, em relação à sua massa de repouso, por um fator λ=1/√0,75

b) Aumenta, em relação à sua massa de repouso, por um fator λ=1/√0,5

c) Diminui, em relação à sua massa de repouso, por um fator λ=√0,75

d) Diminui, em relação à sua massa de repouso por um fator λ=√0,5

e) Não sofre nenhuma alteração

27-(UFRN) Sendo a velocidade de propagação da luz igual a 3. 10⁸ m/s, a ordem de grandeza da energia de repouso de 1 g de matéria, em J é:

 a) 10⁸                               

b) 10⁹                                        

c) 10¹³                                        

d) 10¹⁴                           

e) 10¹⁵                                                                               

28-(UFPRL-RS) Considere as afirmativas a seguir.

I. O tempo transcorre da mesma maneira em qualquer referencial inercial, independente da sua velocidade.

II. O comprimento dos corpos diminui na direção do movimento.

III. Quando a velocidade de um corpo tende à velocidade da luz (c), sua massa tende ao infinito.

De acordo com seus conhecimentos sobre Física Moderna e as informações dadas, está(ão) correta(s) a(s) afirmativa(s)

29-(UFSC-SC) A Física moderna é o estudo da Física desenvolvido no final do século XIX e início do século XX. Em particular, é o estudo da Mecânica Quântica e da Teoria da Relatividade Restrita.

Assinale a(s) proposição(ões) CORRETA(S) em relação às contribuições da Física moderna.

(01) Demonstra limitações da Física Newtoniana na escala microscópica.

(02) Nega totalmente as aplicações das leis de Newton.

(04) Explica o efeito fotoelétrico e o laser.

(08) Afirma que as leis da Física são as mesmas em todos os referenciais inerciais.

(16) Comprova que a velocidade da luz é diferente para quaisquer observadores em referenciais inerciais.

(32) Demonstra que a massa de um corpo independe de sua velocidade.

30-(UNIFOR-CE)   Uma partícula, cuja massa de repouso é M, é acelerada a partir do repouso até atingir 60% da velocidade de propagação da luz no vácuo.

Na situação final, a massa da partícula será igual a

31-(UNIOESTE-PR) Uma excelente ilustração da virtude da ciência fundamental e prova da utilidade de teorias antes consideradas exóticas é a aplicação da Teoria da Relatividade de Einstein ao Sistema de Posicionamento Global, conhecido pelas

iniciais GPS (Global Positioning System). Sem as correções introduzidas pela teoria da relatividade na medição do tempo, não seria possível definir com precisão a localização dos aviões, barcos ou automóveis que dispõem de um receptor GPS.

Com relação à Teoria da Relatividade Especial ou Restrita assinale a alternativa INCORRETA:

a) A relatividade da noção de simultaneidade deriva do fato de que a velocidade da luz no vácuo independe do sistema referencial inercial em relação ao qual ela é medida.

b) A velocidade da luz no vácuo tem o mesmo valor c em todos os referenciais inerciais, independentemente da velocidade do observador ou da velocidade da fonte que a emite. Nenhuma partícula pode se mover com uma velocidade maior do que a da luz no vácuo.

c) As leis da Física são as mesmas para todos os observadores situados em diferentes referenciais.

d) O comprimento próprio de um corpo é definido como a distância no espaço entre os pontos extremos do corpo, medida por um observador em repouso em relação ao corpo. O comprimento próprio do corpo é máximo, quando medido em repouso em relação ao observador.

e) A energia de um corpo (E) e seu equivalente em massa (m) estão matematicamente relacionados pela equação E=m.c², onde c é a velocidade da luz no vácuo. Isto significa que, ao aquecer uma esfera de ferro de 1,0 kg, inicialmente à temperatura de 10,0 ºC e alcançando a temperatura de 90,0 ºC, obtém-se um aumento da massa da esfera.

 32-(UFL-MG) Quando aceleramos um elétron até que ele atinja uma velocidade v = 0,5c, em que c é a velocidade da luz, o que

 acontece com a massa?

a) Aumenta, em relação à sua massa de repouso, por um fator λ=1/√0,75

b) Aumenta, em relação à sua massa de repouso, por um fator λ=1/√0,5 

c) Diminui, em relação à sua massa de repouso, por um fator  

d) Diminui, em relação à sua massa de repouso por um fator  

e) não sofre nenhuma alteração relação ao qual ela é medida.

33-(UEG-GO) Observe a seguinte sequência de figuras:

 Na sequência indicada, estão representadas várias imagens do logo do Núcleo de Seleção da Universidade Estadual de Goiás, cada uma viajando com uma fração da velocidade da luz (c). O fenômeno físico exposto nessa sequência de figuras é explicado

a) pela ilusão de ótica com lentes.            

b) pela lei de proporções múltiplas.                 

c) pelo efeito Compton da translação. 

d) pela teoria da relatividade especial. 

34-(UFV-MG) A figura a seguir mostra um vagão aberto que se move com velocidade de módulo V em relação a um sistema de referência fixo no solo. Dentro do vagão existe uma lâmpada que emite luz uniformemente em todas as direções. Em relação ao vagão, o módulo da velocidade de propagação da luz é c. Para uma pessoa parada em relação ao solo, na frente do vagão, o módulo da velocidade de propagação da luz emitida pela fonte será:

35-(FUVEST-SP) Segundo uma obra de ficção, o Centro Europeu de Pesquisas Nucleares, CERN, teria recentemente produzido vários gramas de antimatéria. Sabe-se que, na reação de antimatéria com igual quantidade de matéria normal, a massa total m é transformada em energia E, de acordo com a equação E = mc², onde c e a velocidade da luz no vácuo.

a) Com base nessas informações, quantos joules de energia seriam produzidos pela reação 1 g de antimatéria com 1 g de matéria?

b) Supondo que a reação matéria-antimatéria ocorra numa fração de segundo (explosão), a quantas

“Little Boy” (a bomba nuclear lançada em Hiroshima, em 6 de agosto de 1945) corresponde a energia produzida nas condições do item a)?

c) Se a reação matéria-antimatéria pudesse ser controlada e a energia produzida na situação descrita

em a) fosse totalmente convertida em energia elétrica, por quantos meses essa energia poderia suprir as necessidades de uma pequena cidade que utiliza, em média, 9 MW de potência elétrica?

36-(UFC-CE) Em relação a um sistema de referência em repouso, dois elétrons movem-se em sentidos opostos, ao longo da mesma reta, com velocidades de módulos iguais a c/2. Determine a velocidade relativa de aproximação entre os elétrons. Em seguida, assinale a alternativa que apresenta corretamente essa velocidade.

a) c/2                       

b) 3c/4                           

c) 3c/5                        

d) 4c/5                           

e) c  

37-(UNICAMP-SP) O GPS (Global Positioning System) consiste em um conjunto de satélites que orbitam a Terra, cada um deles carregando a bordo um relógio atômico. A Teoria da Relatividade Geral prevê que, por conta da gravidade, os relógios

atômicos do GPS adiantam com relação a relógios similares na Terra. Enquanto na Terra transcorre o tempo de um dia (t_Terra = 1,0 dia =  86.400 s ), no satélite o tempo transcorrido é t_satélite = t_Terra + Δt , maior que um dia, e a diferença de tempo Δt tem que ser corrigida. A diferença de tempo causada pela gravidade é dada por (Δt/t_Terra) = (ΔU/mc²), sendo ΔU a diferença de energia potencial gravitacional de uma massa m entre a altitude considerada e a superfície da Terra, e c = 3,0.10⁸ m/s, a velocidade da luz no vácuo.

a) Para o satélite podemos escrever ΔU = mgR_T (1-R_T/r) , sendo r ≈ 4R_T o raio da órbita, R_T= 6,4.10⁶ m o raio da Terra e g a aceleração da gravidade na superfície terrestre. Quanto tempo o relógio do satélite adianta em t_Terra = 1,0 dia em razão do efeito gravitacional?

b) Relógios atômicos em fase de desenvolvimento serão capazes de medir o tempo com precisão maior que uma parte em 10¹⁶, ou seja, terão erro menor que 10^-16 s a cada segundo. Qual é a altura h que produziria uma diferença de tempo Δt = 10^-16 s a cada T_Terra= 1,0 s? Essa altura é a menor diferença de altitude que poderia ser percebida comparando medidas de tempo desses relógios. Use, nesse caso, a energia potencial gravitacional de um corpo na vizinhança da superfície terrestre.

38-(UFES-ES) Os mésons mu ou múons são partículas instáveis com tempo médio de vida de 2 μs. Os múons são produzidos na alta atmosfera, milhares de km acima do nível do mar. A velocidade típica desses múons é de 0,998c (c = 300.000 km/s é a velocidade da luz no vácuo).

a) Em uma abordagem não relativista, calcule a distância média percorrida pelos múons.

b) Em uma abordagem relativista, sabendo que o fator de Lorentz é λ=1/√(1 – 0,998²)=15, calcule a distância média percorrida pelos múons do ponto de vista de um observador em repouso na Terra.

c) Do ponto de vista do múon, explique, usando novamente uma abordagem relativista, como muitos múons podem atingir o nível do mar, apesar de isso ser impossível em uma abordagem não relativista.

39-(UFG-GO) Antipartículas, raras na natureza, possuem carga elétrica oposta à de suas partículas correspondentes. Se encontrássemos uma fonte de antipartículas, poderíamos produzir uma grande quantidade de energia, permitindo que elas se

 aniquilassem com suas partículas. Dessa forma, calcule:

a) a quantidade de energia que seria liberada se 2,0 gramas de antimatéria fossem aniquiladas com 2,0 gramas de sua matéria (considere a velocidade da luz igual a 3,0.10⁸m/s);

b) por quanto tempo essa energia abasteceria uma cidade com um milhão de habitantes, considerando que uma pessoa consome, em média, 100 kWh por mês.

 40-(UNIMONTES-MG)  Em 1905, Albert Einstein propôs uma teoria física do espaço e do tempo denominada Teoria da Relatividade Especial (ou Restrita), que permitiu a conciliação entre a Mecânica de Newton e o Eletromagnetismo de Maxwell. A teoria de Einstein apresenta conceitos de tempo e espaço muito diferente daqueles da Mecânica de Newton e prevê efeitos muito interessantes, como a contração do espaço e a dilatação do tempo. Quando dois eventos (acontecimentos de curta duração) possuem as mesmas coordenadas espaciais, a distância espacial entre eles é nula e, nesse caso, o intervalo de tempo entre eles é denominado intervalo de tempo próprio, representado por Dt_o. O intervalo de tempo, Dt, em um referencial em que os eventos ocorrem em pontos distintos, é maior que o intervalo de tempo próprio. Esse efeito é denominado dilatação do tempo. Para exemplificar, vamos considerar dois observadores, um na Terra (em

repouso em relação ao solo) e outro numa nave espacial que se move com velocidade de módulo u em relação à Terra, ambos observando uma lâmpada piscar. O observador na Terra mediria o intervalo de tempo próprio, Dt_o, entre duas piscadas, e o da nave, um intervalo Δt, em princípio, diferente. A relação entre os dois intervalos de tempo é dada pela expressão

em que c é o módulo da velocidade da luz (c = 3.10⁸ m/s).

Analisando a expressão que relaciona os dois intervalos, se u aumenta, aproximando-se de c, é CORRETO afirmar que

a) Δt e Δt_o se aproximam de zero.              

b) Δt se aproxima de Δt_o.                

c) Δt fica muito pequeno em relação a Δt_o.

d) Δt aumenta em relação a Δt_o.

41-(UFCG-PB) Um carro viajando com velocidade constante comparável à da luz possui uma fonte de luz no seu interior a igual distância dos detectores 1 e 2 localizados em suas extremidades como mostra a figura.

Num dado instante a fonte emite um pulso de luz. Os observadores inerciais A e B, encontram-se no carro e na superfície da Terra, respectivamente. De acordo com a Teoria Especial da Relatividade, pode-se afirmar, EXCETO, que

a) para o observador A, a luz chega simultaneamente aos detectores.

b) para o observador B, a luz não chega simultaneamente aos detectores.

c) para o observador B, a luz chega primeiro ao detector 1.

d) a simultaneidade é um conceito relativo, depende do observador.

e) tanto para o observador A quanto para o observador B, a luz sempre chegará simultaneamente aos detectores.

42-(UEG-GO) Qual das afirmações a seguir é correta para a teoria da relatividade de Einstein?

a) No vácuo, a velocidade da luz depende do movimento da fonte de luz e tem igual valor em todas as direções.

b) Elétrons são expulsos de uma superfície quando ocorre a incidência de uma radiação eletromagnética (luz).

c) Em determinados fenômenos, a luz apresenta natureza de partícula e, em outros, natureza ondulatória.

d) Na natureza, não podem ocorrer interações de velocidades superiores à velocidade da luz c.

43-(UEPB-PB) Através da relação E_c = Δm.c², fica claro que existe uma equivalência entre a variação de massa de um corpo e a energia cinética que ele ganha ou perde. Sendo assim, é correto afirmar que:

a) independente de ocorrer uma mudança na energia de um corpo, sua massa permanece a mesma.

b) quando a energia cinética de um corpo diminui, há um correspondente acréscimo de massa deste corpo.

c) quando um corpo adquire energia cinética sua massa não sofre um acréscimo.

d) quando um corpo adquire energia cinética sua massa sofre uma diminuição.

e) quando a energia cinética de um corpo diminui, há uma correspondente diminuição de massa deste corpo.

44-(UEPB-PB) Adotando-se que a velocidade da luz no vácuo vale 3.10⁸ m/s, a energia contida em uma massa de 1 grama

vale:

a) 9.10¹³ J                        

b) 4,5.10¹³ J                         

c) 9.10¹⁶ J                          

d) 4,5.10¹⁶ J                            

e) 4,5.10¹⁹ J

45-(UFBA-BA) 

A produção de energia no Sol, que possibilitou a vida na Terra, é, em grande parte, relacionada às reações nucleares que transformam quatro prótons em um núcleo de hélio, 4He++. Nessas reações, uma parte da massa é transformada em energia.

Calcule, usando a equação de Einstein, a quantidade de energia liberada nessas reações, considerando a velocidade da luz 3,0.108 m/s e as massas do próton e do núcleo de hélio iguais a 1,673.10^-27 kg e 6,645.10^-27 kg, respectivamente.

46-(UFES-ES)

Uma partícula, em repouso, decai espontaneamente em duas outras partículas que se movem em direções opostas. A primeira dessas duas partículas tem massa de repouso m e velocidade de módulo 0,8c ( é a velocidade da luz no vácuo), enquanto a segunda tem velocidade de módulo 0,6c . Calcule, em função de m, a massa de repouso da segunda partícula e a da partícula original.

a) em uma abordagem não relativista;                                           

b) em uma abordagem relativista

47-(UFSC-SC)

Com base nos tópicos de Física Moderna, assinale a(s) proposição(ões) CORRETA(S).

01. Corpo negro ideal é todo corpo capaz de absorver toda a radiação que nele incide. Quando um corpo negro é aquecido, ele é uma fonte ideal de radiação térmica.

02. O efeito fotoelétrico só ocorre se a frequência da luz incidente sobre o metal for superior a um valor mínimo e a emissão de cargas elétricas deste material independe da intensidade da radiação incidente.

 04. A Teoria da Relatividade Especial, proposta por Einstein, está baseada em dois postulados, sendo que um deles é enunciado da seguinte forma: “As leis da Física são as mesmas em todos os referenciais inerciais. Ou seja, não existe nenhum sistema de referência inercial preferencial”.

08. A apresentação do trabalho do físico Maxwell sobre a quantização da energia é considerada hoje como o marco oficial da fundação da Física Moderna.

16. A Teoria da Relatividade Restrita tem como consequência a contração espacial e a dilatação temporal.

32. O fenômeno da radiação do corpo negro é explicado pela Física Clássica e pela Moderna como sendo uma distribuição contínua de energia de um sistema.

64. O comportamento dualístico de uma onda-partícula é descrito e aceito pela Física Clássica, sendo mais aprofundado e explicado pela Física Quântica.

48-(UFRN-RN)

Estudantes interessados em analisar a natureza dual da luz preparavam uma apresentação para uma Feira de Ciências com três

experimentos,  conforme mostrados nas Figuras abaixo.

1º experimento 2º experimento 3º experimento

 o 1º experimento mostra a difração da luz ao passar por uma fenda estreita;

 o  2º experimento mostra o efeito fotoelétrico caracterizado pela geração de corrente elétrica a partir da incidência de luz sobre uma célula fotoelétrica;  e

 o  3º experimento mostra o efeito da polarização da luz ao fazê-la incidir sobre  filtros polarizadores.

A partir desses experimentos , é correto afirmar que

A) o efeito fotoelétrico e a polarização evidenciam a natureza ondulatória da luz, enquanto a difração evidencia a natureza corpuscular da luz.

B) a polarização e a difração evidenciam a natureza corpuscular da luz, enquanto  o efeito fotoelétrico evidencia a natureza ondulatória da luz.

C) a difração e a polarização evidenciam a natureza ondulatória da luz, enquanto o efeito fotoelétrico evidencia a natureza corpuscular da luz.

D) o efeito fotoelétrico e a difração evidenciam a natureza ondulatória da luz, enquanto a polarização evidencia a natureza corpuscular da luz

Resolução comentada dos exercícios de vestibulares sobre

Teoria da Relatividade

01- R- A  ---  veja teoria

02- R- D

03- A velocidade da luz é constante independente da velocidade da fonte emissora  ---  R- B

04- A velocidade da luz (ondas eletromagnéticas) é de 3.10⁸m/s independentemente de a fonte emissora estar em repouso ou em movimento  ---  R- D

05- I. Correta  ---  veja teoria

III. Correta  ---  O primeiro postulado afirma que não existe sistema de referência inercial preferencial no estudo de qualquer fenômeno físico.

R- E

06- R- D  ---  veja teoria  

07- R- D  ---  veja teoria

08- Δt=Δt_p/√1 – V²/c²  ---  lembre-se de que na Terra o intervalo de tempo é sempre maior e que Δt é sempre maior que Δt_p  ---  Δt_p=12meses  ---  Δt=12/√1 – (0,8c)²/c²  ---  Δt=12/√1 – (0,64c²/c²  ---  Δt=12/√0,36  ---  Δt=20 meses.

09- a) O intervalo de tempo que sofre maior dilatação na expressão Δt=Δt_p/√1 – V²/c² é Δt e ele se dilata Δt= Δt_p + 0,5/100.Δt_p  --- Δt=1,005.Δt_p  --- Δt=λ.Δt_p   ---  procurando na tabela  ---  quando λ=1,005  ---  v=0,100c  ---  v=0,100.3,0.10⁸  ---  v=3,0.10⁷m/s  ---  observe que as velocidades no nosso cotidiano são insignificantes em relação a 3.10⁷=30.000.000m/s.

b) quando v=0,600c  ---  λ= 1,250c  --- Δt=λ.Δt_p=1,250.10min  ---  Δt=12,5 min       

10- O intervalo de tempo que sofre maior dilatação na expressão Δt=Δt_p/√1 – V²/c² é Δt_André e ele se dilata Δt_André=2Δt_Regina  ---  Δt_André=Δt_Regina/√1 – V²/c²  --- 2Δt_Regina=Δt_Regina/√1 – V²/c²  ---  2=1/√1 – V²/c²  ---  √1 – V²/c²=1/2  ---  1 – V²/c²=1/4  ---  1 – 1/4=  V²/c²  ---  4V²=3c²  ---  V=√3/4.c  ---  V=0,87c  ---  R- B

11- Eles irão retornar mais velhos, ou seja, Δt é maior que Δt_p  ---  Δt= Δt_p/√(1 – V²/c²)  ---  Δt= 6/√(1 – (0,8)²/c²)  ---  Δt= Δt_p/√(1 – 0,64c²/c²)  ---  Δt= 6/0,6  ---  Δt= 10 anos  ---  R- B