MOVIMENTO UNIFORMEMENTE VARIADO

Formulário com as equações do MUV

Exercícios de vestibulares com resoluções comentadas sobre

Movimento Uniformemente Variado (MUV)

01-(UNESP-SP)

O motorista de um veículo A é obrigado a frear bruscamente quando avista um veículo B à sua frente, locomovendo-se no mesmo sentido, com uma velocidade constante menor que a do veículo A.

Ao final da desaceleração, o veículo A atinge a mesma velocidade que B, e passa também a se locomover com velocidade constante.

O movimento, a partir do início da frenagem, é descrito pelo gráfico da figura.

Considerando que a distância que separava ambos os veículos no início da frenagem era de 32 m, ao final dela a distância entre ambos é de

02-(ACAFE-SC)

Para garantir a segurança no trânsito, deve-se reduzir a velocidade de um veículo em dias de chuva, senão vejamos:

um veículo em uma pista reta, asfaltada e seca, movendo-se com velocidade de módulo 36 km/h (10 m/s) é freado e desloca-se 5,0 m até parar.

Nas mesmas circunstâncias, só que com a pista molhada sob chuva, necessita de 1,0 m a mais para parar. 

Considerando a mesma situação (pista seca e molhada) e agora a velocidade do veículo de módulo 108 km/h (30 m/s), a alternativa correta que indica a distância a mais para parar, em metros, com a pista molhada em relação a pista seca é:

03-(UEPA-PA)

No Pará, o perigo relacionado às altas velocidades no trânsito tem aumentado os  riscos de

acidentes, principalmente em Belém.

Considerando que a "distância de freagem" é a distância que o carro percorre desde o momento que os freios são acionados até parar e que o modelo matemático que expressa essa relação é dado por  D = K . V², onde  D representa a distância de freagem em metros, K é uma constante e  V  é a velocidade em Km/h.

Assim, um automóvel que tem seus freios acionados estando a uma velocidade de 80 Km/h ainda percorre 44 metros até parar. A distância de  freagem de um automóvel que tem seus freios acionados, estando a uma velocidade de 160 Km/h é:

a) 2 vezes a distância de freagem se estivesse a 80 Km/h.         

b) 3 vezes a distância de freagem se estivesse a 80 Km/h.

c) 4 vezes a distância de freagem se estivesse a 80 Km/h.         

d) 5 vezes a distância de freagem se estivesse a 80 Km/h.

e) 6 vezes a distância de freagem se estivesse a 80 Km/h.

04-(UNICAMP-SP)

O radar é um dos dispositivos mais usados para coibir o excesso de velocidade nas vias de trânsito. O seu princípio de

funcionamento é baseado no efeito Doppler das ondas eletromagnéticas refletidas pelo carro em movimento.

Considere que a velocidade medida por um radar foi V = 72 km/h para um carro que se aproximava do aparelho.

Quando um carro não se move diretamente na direção do radar, é preciso fazer uma correção da velocidade medida pelo aparelho V_m para obter a velocidade real do veículo V_r.

Essa correção pode ser calculada a partir da fórmula V_m = V_r.cosα, em que α é o ângulo formado entre a direção de tráfego da rua e o segmento de reta que liga o radar ao ponto da via que ele mira. Suponha que o radar tenha sido instalado a uma distância de 50 m do centro da faixa na qual o carro trafegava, e tenha detectado a velocidade do carro quando este estava a 130 m de distância, como mostra a figura.

Se o radar detectou que o carro trafegava a 72 km/h, sua velocidade real era igual a

a) 66,5 km/h

b) 36,3 km/h.                                  

c) 78 km/h.                                   

d) 144/3 km/h

05-(MACKENZIE-SP) 

Dois automóveis A e B se movimentam sobre uma mesma trajetória retilínea, com suas velocidades variando com o tempo de acordo com o gráfico a seguir.

06-(Olimpíada Brasileira de Física)

Uma partícula executa um movimento retilíneo uniformemente variado.

Num dado instante a partícula tem velocidade 50m/s e aceleração negativa de módulo 0,2m/s². Quanto tempo decorre até a partícula alcançar a mesma velocidade em sentido contrário?

07-(UFES-ES)

Um predador, partindo do repouso, alcança sua velocidade máxima de 54 km/h em 4 s e mantém essa velocidade durante 10 s.

Se não alcançar sua presa nesses 14 s, o predador desiste da caçada.

A presa, partindo do repouso, alcança sua velocidade máxima, que é 4/5 da velocidade máxima do predador, em 5 s e consegue mantê-la por mais tempo que o predador.

Suponha-se que as acelerações são constantes, que o início do ataque e da fuga são simultâneos e que predador e presa partem do repouso.

Para o predador obter sucesso em sua caçada, a distância inicial máxima entre ele e a presa é de:

a) 21 m                    

b) 30 m                       

c) 42 m                     

d) 72 m                      

e) 80 m

08-(UEG-GO)

Dois veículos de corrida, deslocando-se no mesmo sentido, A e B, passam em um determinado ponto de uma auto estrada com velocidade V_A = 72 km/h e V_B = 54 km/h e acelerações a_A = 4,0 m/s² e a_B = 6,0 m/s², respectivamente.

a) Depois de percorrer uma distância de 150m, qual é a velocidade dos dois veículos?

b) Após os 150m, cada um dos veículos segue por um caminho diferente.

O veículo A atinge uma curva na estrada e vira 90^o à esquerda, enquanto o outro veículo segue por uma direção que faz um ângulo de 60^o em relação à direção inicial.

Qual será a distância entre os dois veículos depois de passar 10s em que ambos estavam na posição inicial?

09-(FUVEST-SP)

A velocidade máxima permitida em uma auto-estrada é de 110 km/h (aproximadamente 30 m/s) e um carro, nessa velocidade, leva 6s para parar completamente.

Diante de um posto rodoviário, os veículos devem trafegar no máximo a 36 km/h (10 m/s).

Assim, para que carros em velocidade máxima consigam obedecer ao limite permitido, ao passar em frente do posto, a placa referente à redução de velocidade deverá ser colocada antes do posto, a uma distância, pelo menos, de

10-(UNESP-SP)

Um corpo parte do repouso em movimento uniformemente acelerado.

Sua posição em função do tempo é registrada em uma fita a cada segundo, a partir do primeiro ponto à esquerda, que corresponde ao instante do início do movimento.

A fita que melhor representa esse movimento é:

11-(UNICAMP-SP)

Um automóvel trafega com velocidade constante de 12 m/s por uma avenida e se aproxima de um cruzamento onde há um semáforo com fiscalização eletrônica.

Quando o automóvel se encontra a uma distância de 30 m do cruzamento, o sinal muda de verde para amarelo.

 O motorista deve decidir entre parar o carro antes de chegar ao cruzamento ou acelerar o carro e passar pelo cruzamento antes do sinal mudar para vermelho.

Este sinal permanece amarelo por 2,2 s.

O tempo de reação do motorista (tempo decorrido entre o momento em que o motorista vê a mudança de sinal e o momento em que realiza alguma ação) é 0,5 s.

a) Determine a mínima aceleração constante que o carro deve ter para parar antes de atingir o cruzamento e não ser multado.

b) Calcule a menor aceleração constante que o carro deve ter para passar pelo cruzamento sem ser multado. Aproxime (1,7)²  para 3.

12-(PUC-RJ)

Um atleta corre a uma certa velocidade constante em linha reta e ultrapassa um carro que está sendo acelerado (a = 2,0 m/s²) do repouso na mesma direção e sentido.

O instante de tempo t = 0 é o tempo inicial de aceleração do carro e também o instante de tempo em que o atleta passa pelo carro.

O atleta consegue se manter à frente do carro por 3,0 s. Qual é a velocidade do atleta?

a) 1,0 m/s                  

b) 3,0 m/s                      

c) 7,0 m/s                     

d) 9,0 m/s                     

e) 11,0 m/s

 13-(FGV-SP)

O engavetamento é um tipo comum de acidente que ocorre quando motoristas deliberadamente mantêm uma curta distância do carro que se encontra à sua frente e este último repentinamente diminui sua velocidade.

Em um trecho retilíneo de uma estrada, um automóvel e o caminhão, que o segue, trafegam no mesmo sentido e na mesma faixa de trânsito, desenvolvendo, ambos, velocidade de 108 km/h.

Num dado momento, os motoristas vêem um cavalo entrando na pista.

Assustados, pisam simultaneamente nos freios de seus veículos aplicando, respectivamente, acelerações de intensidades 3 m/s² e 2 m/s².

Supondo desacelerações constantes, a distância inicial mínima de separação entre o pára-choque do carro (traseiro) e o do caminhão (dianteiro), suficiente para que os veículos parem, sem que ocorra uma colisão, é, em m, de

14-(UNICAMP-SP) 

A Copa do Mundo é o segundo maior evento desportivo do mundo, ficando atrás apenas dos Jogos Olímpicos.

Uma das regras do futebol que gera polêmica com certa frequência é a do impedimento.

Para que o atacante A não esteja em impedimento, deve haver ao menos dois jogadores adversários a sua frente, G e Z, no exato instante em que o jogador L lança a bola para A (ver figura). Considere que somente os jogadores G e Z estejam à frente de A e que somente A e Z se deslocam nas situações descritas a seguir.

a) Suponha que a distância entre A e Z seja de 12 m.

Se A parte do repouso em direção ao gol com aceleração de 3,0 m/s² e Z também parte do repouso com a mesma aceleração no sentido oposto, quanto tempo o jogador L tem para lançar a bola depois da partida de A antes que A encontre Z?

b) O árbitro demora 0,1 s entre o momento em que vê o lançamento de L e o momento em que determina as posições dos jogadores A e Z.

Considere agora que A e Z movem-se a velocidades constantes de 6,0 m/s, como indica a figura. Qual é a distância mínima entre A e Z no momento do lançamento para que o árbitro decida de forma inequívoca que A não está impedido?

15-(UNICAMP-SP)

A figura abaixo representa parte do mapa de uma cidade, no qual estão identificadas a catedral, a prefeitura e a câmara dos vereadores.

Observe que o quadriculado não representa os quarteirões da cidade, servindo apenas para a localização dos pontos e retas no plano cartesiano.

Nessa cidade, a Avenida Brasil é formada pelos pontos equidistantes da catedral e da prefeitura, enquanto a

Avenida Juscelino Kubitschek (não mostrada no mapa) é formada pelos pontos equidistantes da prefeitura e da câmara de vereadores.

Sabendo que a distância real entre a catedral e a prefeitura é de 500 m, podemos concluir que a distância real, em linha reta, entre a catedral e a câmara de vereadores é de

16-(UEPA-PA)

Uma das causas de acidentes de trânsito é a imprudência de certos motoristas, que realizam manobras arriscadas ou inapropriadas.

Por exemplo, em uma manobra realizada em um trecho retilíneo de uma rodovia, o motorista de um

automóvel de passeio de comprimento igual a 3 m resolveu ultrapassar, de uma só vez, uma fileira de veículos medindo 17 m de comprimento.

Para realizar a manobra, o automóvel, que se deslocava inicialmente a 90 km/h, acelerou uniformemente, ultrapassando a fileira de veículos em um intervalo de tempo de 4 s.

Supondo que a fileira tenha se mantido em movimento retilíneo uniforme, a uma velocidade de 90 km/h, afirma-se que a velocidade do automóvel, no instante em que a sua traseira ultrapassou completamente a fileira de veículos, era, em m/s, igual a:

17-(UFC-CE)

Um trem, após parar em uma estação, sofre uma aceleração, de acordo com o gráfico da figura a seguir, até parar novamente na próxima estação.

 Assinale a alternativa que apresenta os valores corretos de t_f, o tempo de viagem entre as duas estações, e da distância entre as estações.

a) 80 s, 1600 m         

b) 65 s, 1600 m         

c) 80 s, 1500 m         

d) 65 s, 1500 m         

e) 90 s, 1500 m

18-(UERJ-RJ)

Numa operação de salvamento marítimo, foi lançado um foguete sinalizador que permaneceu aceso durante toda sua trajetória. Considere que a altura h, em metros, alcançada por este foguete, em relação ao nível do mar, é descrita por h = 10 + 5t – t², em que t é o tempo, em segundos, após seu lançamento.

A luz emitida pelo foguete é útil apenas a partir de 14 m acima do nível do mar.

O intervalo de tempo, em segundos, no qual o foguete emite luz útil é igual a:

a) 3                       

b) 4                           

c) 5                           

d) 6                         

e) 7

19-(UNIOESTE-PR)

Um comboio ferroviário é composto por uma locomotiva e vários vagões.

Tanto a locomotiva como os vagões possuem 24 m de comprimento cada um.

A locomotiva demora 4,0 s para passar diante de um observador parado próximo aos trilhos e o primeiro vagão demora 2,0 s para passar diante do mesmo observador.

Supondo a aceleração constante, assinale a alternativa CORRETA.

A. A aceleração do comboio é igual a 0,50 m.s^-2.

B. A velocidade da locomotiva, quando começa a passar diante do observador, é igual a 4,0 m.s^-1.

C. O segundo vagão demora 1,0 s para passar diante do observador.

D. Quando o primeiro vagão começa a passar diante do observador, a velocidade do comboio é igual a 36 km.h^-1.

E. Quando o segundo vagão começa a passar diante do observador, a velocidade do comboio é igual a 54 km.h^-1.

20-(UEL-PR)

Em uma prova de atletismo, um corredor, que participa da prova de 100 m rasos, parte do repouso, corre com aceleração constante nos primeiros 50 m e depois mantém a velocidade constante até o final da prova.

Sabendo que a prova foi completada em 10 s, calcule o valor da aceleração, da velocidade atingida

pelo atleta no final da primeira metade da prova e dos intervalos de tempo de cada percurso.

Apresente os cálculos.

Resolução comentada dos exercícios de vestibulares das questões de Física sobre

Movimento Uniformemente Variado (MUV)

01- Quando t=0 a distância entre eles é de 32m  ---  até t=4s, quando terminou a desaceleração o veículo A se deslocou   ---  ΔS_A=área do trapézio=(30 + 15).4/2   ---  ΔS_A=90m  ---  no mesmo intervalo de tempo o veículo B se deslocou  ---  ΔS_B=área do retângulo=4.15=60m  ---  a distância entre eles antes era de   ---  ΔS_a=32m (dado do exercício)  ---  depois, ΔS_d=(90 – 60)=30m  ---  a distância entre eles no final da frenagem será de d=32 – 30=2m  ---  R- B. 

02- Primeira situação  ---  cálculo da aceleração do carro com a pista seca  ---  V²=Vo² + 2.a.∆S  ---  0² = 10² + 2.a.5  ---  a=-10ms2  ---  cálculo da aceleração do carro com a pista molhada  ---  V²=Vo² + 2.a.∆S  ---  0² = 10² + 2.a.6  ---  a=-100/12=-25/3 ms²  ---  segunda situação  ---  cálculo da distância percorrida com a pista seca  ---  V²=Vo² + 2.a.∆S  ---  0² = 30² + 2.(-10). ∆S  ---  ∆S =45m  ---  cálculo da distância percorrida com a pista molhada  ---  V²=Vo²+ 2.a.∆S  ---  0² = 30² + 2.(-25/3).∆S  ---  ∆S=54m  ---  distância percorrida a mais até parar  ---  d=54 – 45=9m  ---  R- D.

03- Observe na expressão D=K.V², onde K é constante e, nela você observa que a velocidade V é diretamente proporcional ao quadrado da velocidade  ---  assim, se a velocidade dobra passando de 80kmh para 160kmh, a distância percorrida pelo carro até parar fica 2²=4 vezes maior  ---  R- C.

04-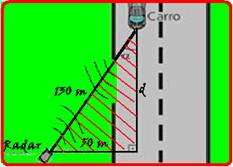  

Observe no esquema abaixo no triângulo hachurado que  ---  130²=50² + d²  ---  d²=14400  ---  d=120  ---  cosα=cateto adjacente/hipotenusa=120/130  ---  72=V_r.120/130  ---  V_r=78km/h  ---  R- C.

05-  Calculando o espaço percorrido entre 0 e 10s pela área  ---  móvel A  ---  ΔS_A=(B + b).h/2=(45 + 30).10/2  ---  ΔS_A=375m (deslocou 375m no sentido positivo da trajetória)  ---  móvel B  ---  ΔS_B=(-10 – 30).10/2  ---  ΔS_B=-200m (deslocou 200m no sentido negativo da trajetória)  ---  d=375 + 200  ---  d=575m  ---  cálculo da aceleração escalar de cada móvel   ---  a_A=∆V_A/∆t  ---  a_A=(45 – 30)/(10 – 0)  ---  a_A=1,5m/s²  ---  a_B=(-30 – (-10)/(10 – 0)  ---  a_B= -2m/s²  --- S_A=So_A + 30t + 0,75t²  ---  S_B=So_B – 10t – t²  ---  supondo S_oA=0 e fazendo t=10s no encontro onde você iguala as equações  ---  30(10) + 0,75(10)² = S_oB – 10(10) – (10)²  ---  375 = So_B – 200  ---  So_B = 575 m, que é a distância inicial entre os móveis, pois supusemos o móvel A partindo da origem.

R- A

06- Ela vai (ida) pára e volta  ---  se, na ida ela tem velocidade de 50m/s, na volta deverá ter velocidade de -50m/s  ---   

na ida, V_o=50m/s e V=0, ela demorou  --- V=V_o + at  ---  0=50 – 0,2t  ---  t=250s (na ida)  ---  na volta  ---  V_o=0 e V=-50m/s  ---  V=Vo + at  ---  -50=0 -0,2t  ---  t=250s (na volta)  ---  t_pedido=t_ida + t_volta  ---  t_pedido=250 + 250=500s  ---t=500s  ---  R- A.

07- Cálculo da distância percorrida pelo predador  ---  entre 0 e 4s  ---  acelerado com a=(54/3,6 – 0)/(4 – 0)=3,75m/s²  ---  ΔS₁=V_o.t + at²/2=0.4 +3,75.16/2  ---  ΔS₁=90m  ---  entre 4s e 10s é um MU com V=15ms  ---  V= ΔS/Δt  ---  15= ΔS₂/6  ---  ΔS₂=90m  --- ΔS_predador=90 + 90  ---  ΔS_predador=180m  ---  cálculo da distância percorrida pela presa  ---  entre 0 e 5s  ---  acelerado com a=(12 – 0)/(5 – 0)=2,4m/s²  ---  ΔS₁=Vot + at²/2=0.5 +2,4.25/2  ---  ΔS₁=30m  ---  entre 5s e 10=14s é um MU com V=12ms  ---  V= ΔS/Δt  ---  12= ΔS₂/9  ---  ΔS₂=108m  --- ΔS_presa=30 + 108  ---  ΔS_presa=138m  ---  portanto para o predador obter sucesso, a distância inicial máxima entre ele e a presa deverá ser de  ---  d=180 – 138  ---  d=42m  ---  R- C.

08- a) Equação de Torricelli  ---  V²=V_o² + 2.a.∆S  ---  veículo A  ---  V_A²=20² + 2.4.150  ---  V_A=40m/s  ---  veículo B  ---  V_B²=15² + 2.6.150  ---  V_B=45m/s.  

b) Cálculo do tempo que cada móvel demora para percorrer os 150m  ---   ∆S_A=V_oA.t + a_A.t²/2  ---  150=40t + 4t²/2  --- 

t₁=-15s (anulado) e t_A=5s  ---  ∆S_B=V_oB.t + a_B.t²/2  ---  150=45t + 6t²/2  ---  t₁=-30s (anulado) e t_B=5s  --- após as curvas os dois veículos se moveram durante 5s  ---  nesses t=5s o móvel A percorreu   S_A=S_oA + V_oA.t + a_A.t²/2=0 + 40.5 + 4.25/2=250m  ---  S_A=300m  ---  S_B=S_oB + V_oB.t + a_B.t²/2=0 + 45.5 + 6.25/2=m  ---  S_A=300m  ---  observe na figura que a projeção de S_B=300m sobre a horizontal fornece S’_B=S_B.cos60^o=300.0,5=150m  ---  agora, aplicando Pitágoras você calcula a distância d pedida  ---  d²=250² + 150²=62500 + 22500=85000  ---  d=291,54m.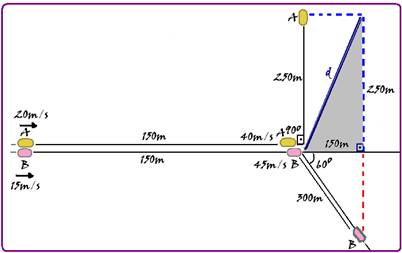

09- Cálculo da aceleração  ---  V=V_o + at  ---  0=30 + a.6  ---  a=-5m/s²  ---  com essa aceleração sua velocidade deve ser reduzida de V_o=30m/s para V=10m/s em  ---  30=10 – 5t  ---  t=4s e, nesse tempo ele deve percorrer ΔS= V_o.t + at²/2=30.4 – 5.16/2=80m ou com Torricelli  ---  V²=Vo² + 2a ΔS  ---  100=900 – 2.5. ΔS  ---  ΔS=80m  ---  R- C.

10- S_o=0  ---  V_o=0  ---  S=S_o + V_o.t + at²/2  ---  s=a.t²/2  ---  como a é constante, S é diretamente proporcional a t², ou seja, aumenta proporcionalmente com o quadrado do tempo  ---  R- C.

11-  a) Até começar a frear ele deve demorar   ---  t=2,2 – 0,5  ---  t=1,7s  para sua velocidade passar de V_o=12m/s até V=0  ---  V= V_o + a.t  ---  0=12 + a.1,7  ---  a= -7,1m/s².

b) Até começar a frear ele percorreu ΔS₁ com velocidade constante de V=12m/s durante t=0,5s  ---  V= ΔS₁/ Δt  ---  12= ΔS₁/0,5  ---  ΔS₁=6m  ---  para passar pelo cruzamento sem ser multado ele deve percorrer ΔS=30 – 6=24m em t=2,2 – 0,5=1,7s  ---  ΔS=V_o.t + a.t²/2  ---  24=12.1,7 + a.(1,7)²/2  ---  24=20,4 + a.3/2  ---  a=2,4m/s^2.

12- 

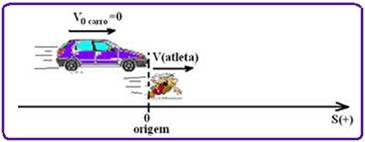
Baseado na figura abaixo deduz-se a equação de cada móvel  ---  carro  --- MUV  ---  S_c=So + V_ot + at²/2= 0 + 0 +2t²/2  ---  S_c=t²  ---  e do atleta  ---  MU    ---  S_at=S_o + V.t  ---  S_at= 0 + V.t  ---  S_at=V.t  ---  se o atleta se mantém na frente do carro por t=3s  ---  S_at = S_c, quando t=3s  ---  V.t=t²  ---  V.3 = 3²  ---  V=3m/s  ---  R- B.

13-  A velocidade inicial V_o é a mesma para os dois veículos V_o=108km/h/3,6=30m/s  ---  deduzindo as

equações de   cada móvel de acordo com o esquema  ---  V=V’=V_o=30m/s  ---  equação de um ponto no pára-choque dianteiro do caminhão  --- S_caminhão=S_o + V_o.t + at²/2=0 + 30.t - 2.t²/2  ---  S_caminhão=30t - 1t²  ---  equação de um ponto do pára-choque traseiro do carro  ---  S_carro= S_o + V_o.t + at²/2= d + 30t - 3t²/2  --- S_carro=d + 30t -1,5t²  ---  o tempo que demorou para parar o caminhão (V=0) vale  ---  V_caminhão=V_o – 2t  ---  0=30 – 2t  ---  t_caminhão=15s  ---  até parar o caminhão percorre  ---  S_caminhão=30t - 1t²=30.15 – 1.(15)²=450 – 225  ---  S_caminhão=225m  ---  tempo que o carro demora para parar  ---  V_carro=V_o – at  ---  0=30 – 3t  ---  t=10s  ---  distância que o carro percorre até parar  ---  S_carro=d + 30t -1,5t²=d + 30.10 – 1,5.100  ---  S_carro=d + 150  --- no encontro  ---  S_carro = S_caminhão  ---  d + 150=225  ---  d=75m  ---  R- B.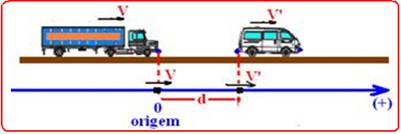

14-  a) Como A e Z se deslocam em sentidos opostos, o módulo da aceleração relativa entre eles é a = 6 m/s²  ---  como

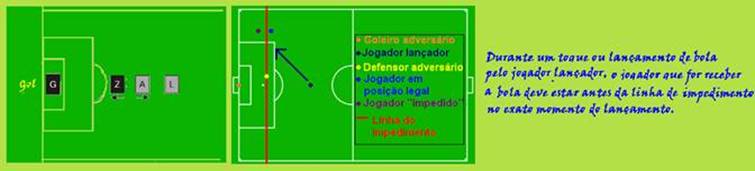 suas acelerações tem mesmo módulo, cada jogador percorre até o encontro metade da distância que os separa, ou seja, d= 6 m, distância que percorre em  ---  S= S_o + V_o.t + a.t²/2  ---  d=0 + 0 =at²/2  ---  6=3t²/2  --- t=2s.

b) Cada jogador tem velocidade constante de 6 m/s, em sentidos opostos  ---  no intervalo de 0,1 s, o deslocamento de cada um é ∆S = v.∆t = 6 (0,1) = 0,6 m  ---  ∆S=6m,  portanto, no momento do lançamento, a distância mínima (dmin) entre eles tem que ser  ---  d_min= 2.(0,6)  ---  d_min= 1,2 m  ---  você também poderia utilizar a velocidade relativa que, em sentidos contrários é a soma das velocidades de cada um  ---  Vr=6 + 6=12  ---  Vr=12m/s  ---  d=Vr.Δt=12.(0,1)  --- d=1,2m.

15- 

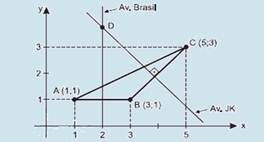
Observe a figura abaixo  ---  a catedral se encontra no ponto A(1;1), a prefeitura no ponto B (3;1) e a câmara de vereadores  no ponto C (5;3)  ---  observe que AB=2 e AC2=(5 – 1)² + (3 – 1)²  ---  AC=2√5  ---  como AB=500m  ---  AC=500√5m    R- A.

16- Observe na figura abaixo que entre o início da ultrapassagem e o final da mesma um ponto P

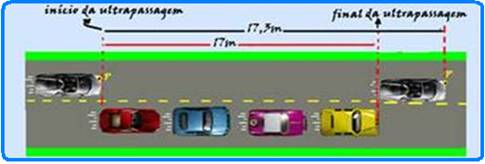
fixo, por exemplo, no farol do carro que está ultrapassando, percorreu ∆S=17 + 3=17,3m  ---  observe também que tanto os carros da fileira como o que está ultrapassando possuem a mesma velocidade, então a velocidade relativa entre eles é nula e, você pode considerar nesse estudo que inicialmente todos estavam em repouso  ---  assim, o ponto P com velocidade inicial V_o=0 inicia seu movimento para ultrapassar uma distância fixa de ∆S=17,3m, com aceleração a, demorando t=4s para isso  ---  ∆S=V_o.t + a.t²/2=  ---  17,3 = 0.4 + a.4²/2  ---  a=17,3/8=2,16m/s²  ---  cálculo da velocidade no final da ultrapassagem  ---  V=V_o + a.t=0 + 2,16.4  ---  V=8,65m/s  ---  essa é a velocidade supondo os carros parados mas, na realidade, eles têm velocidade de 90km/h=25m/s  ---  V_real=25 + 8,65=33,65m/s. 

R- C.

17-  Entre 0 e 10s  ---  V_o=0  ---  V=V_o + at=0 + 1.10=10m/s  ---  entre 10s e 20s  ---  V_o=10m/s  ---  V=V_o + at=10 + 2.10=30m/s  ---  entre 20s e 50s  ---  a aceleração é nula e a velocidade constante de 30m/s  ---  entre 50s e t ele freia e pára com sua velocidade variando de 30m/s para 0  ---  V=V_o + at  ---  0=30 -1.t ---  t=30s  ---  t_f=50 + 30=80s

Construindo o gráfico Vxt, cuja área entre a reta representativa e o eixo t fornece o deslocamento (no

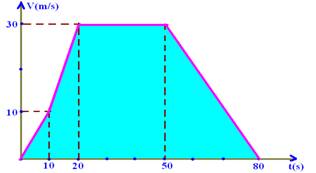
caso, distância)entre as duas estações  ---  ΔS_total=soma das áreas=10.10/2 + (30 + 10).10/2 + 30.30 + 30.30/2  --- ΔS_total=1.600m  ---  R- A

18- 

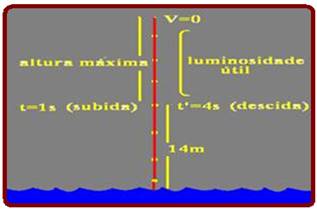
Cálculo dos instantes em que ele passa pela altura de 14m, ou seja, S=14m  ---  S=10 + 5t – t²  ---  14=10 +5t – t²  --- 

t² – 5t + 4=0 ---  t=1s (subida e t’=4s (descida)  ---  ele estará acima de 14m (luminosidade útil) entre os instantes 1s e 4s  ---  Δt=4 – 1=3s   ---   R- A.

19-Se você fixar um ponto P no início da locomotiva , quando P começar a passar diante do observador (marco inicial 0), você terá velocidade inicial V_o e t_o=0, e quando a locomotiva terminar de passar pelo observador P estará a 24m de 0 no instante t=4s (figura I).

Pelo enunciado, quando o primeiro vagão terminar de passar pelo observador o ponto P estará a 48m de 0 e o instante será t=4 + 2 = 6s (figura II)

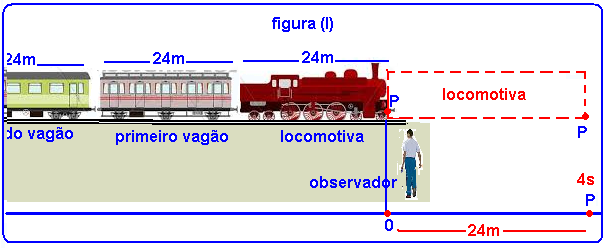
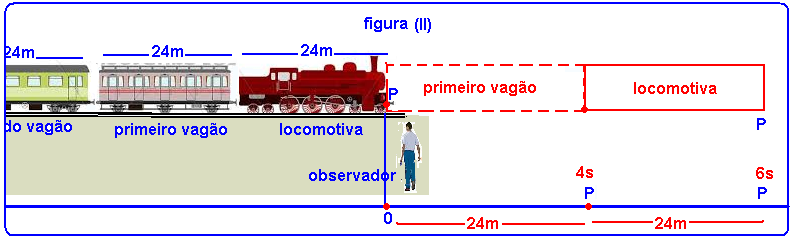
Na figura I, quando t=4s o ponto P, com velocidade inicial V_o e aceleração a, percorreu ΔS=24m ---

ΔS= V_ot + at²/2 --- 24 = v_o.4 + a.4²/2 --- 24 = 4V_o + 8a --- 6 = V_o + 2a --- V_o= 6 – 2a (1).

Na figura II, quando t=6s o ponto P, com velocidade inicial V_o e aceleração a, percorreu ΔS=48m ---

ΔS= V_ot + at²/2 --- 48 = V_o.6 + a.6²/2 --- 48 = 6V_o + 18a --- 8 = V_o + 3a (2).

(1) em (2) --- 8=6 – 2a + 3a --- a=2m/s² (aceleração da composição).

V­_o= 6 – 2.2 --- V_o=2m/s (velocidade inicial do ponto P).

Quando o primeiro vagão começa a passar diante do observador o ponto P está na posição 24m e o instante é t=4s --- V=V_o + at=2 + 2.4=10m/sx3,6=36km/h.

R- D

20- Nos primeiros 50m ele partiu do repouso V_o=0, acelerou com aceleração a e terminou os 50m com velocidade V₁: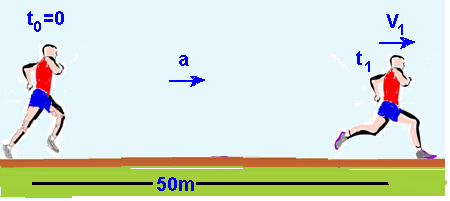

ΔS=V_ot + at²/2 --- 50=0.t₁ + a.t₁²/2 --- 100=at₁² --- t₁=10/√a (I).

V=V_o + at --- V₁ = 0 + a.t₁ --- V₁ = a. 10/√a --- V₁.√a = 10a --- V₁².a = 100a² --- v₁² = 100√a ---

√a = V₁/10 (II).

(II) em (I) --- t₁ = 10/V₁/10 --- t₁=100/V₁ (III).

Os últimos 50m ele percorre com velocidade constante de valor V₁ num intervalo de tempo t₂:

V= ΔS/Δt --- V₁=50/t₂ --- t₂=50/V₁.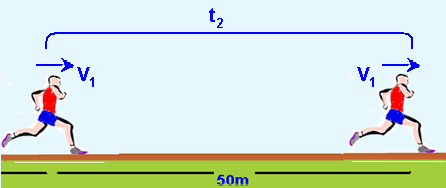

Como ele demorou 10s para efetuar todo o percurso você terá que t₁ + t₂ = 10 --- (III) + (IV) = 10 --- 100/V₁ + 50/V₁ = 10 --- 150 = 10V₁ --- V₁=15m/s.

A aceleração a é calculada substituindo V₁=15m/s em (II) --- √a = V₁/10 --- √a = 15/10=1,5 --- a=1,5² --- a=2,25m/s².

Tempo t₁ --- substituindo V₁=15ms em (III) --- t₁=100/15 --- t₁=6,7s --- tempo t₂ --- t₁ + t₂=10 ---

6,7 + t₂ = 10 --- t₂=3,33s.