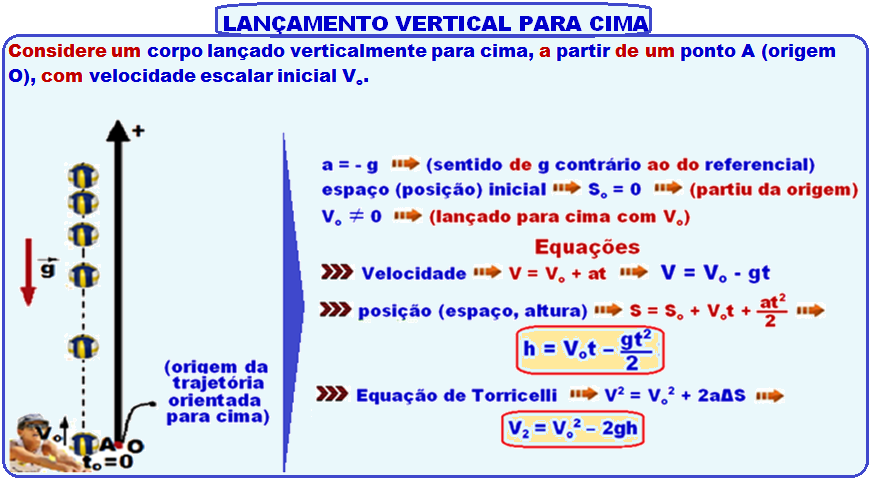
MOVIMENTOS VERTICAIS

FORMULÁRIO

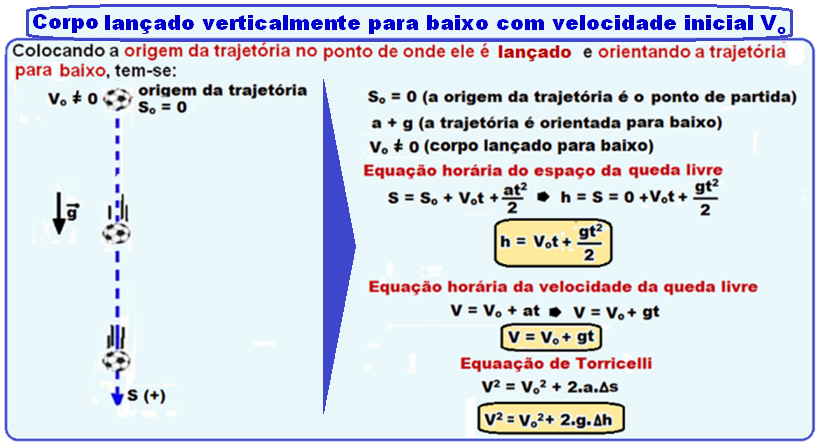
Exercícios de vestibulares com resoluções comentadas sobre

Movimentos Verticais

01-(CEFET-CE)

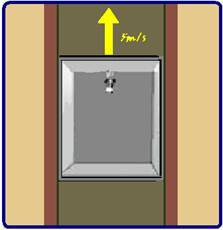
Um elevador de bagagens sobe com velocidade constante de 5m/s.

Uma lâmpada se desprende do teto do elevador e cai livremente até o piso do mesmo.

A aceleração local da gravidade é de 10m/s².

O tempo de queda da lâmpada é de 0,5s.

Determine a altura aproximada do elevador.

02-(UNICAMP-SP)

Um malabarista de circo deseja ter três bolas no ar em todos os instantes.

Ele arremessa uma bola a cada 0,40s (considere g= 10m/s²).
a) Quanto tempo cada bola fica no ar?

b) Com que velocidade inicial deve o malabarista atirar cada bola para cima?
c) A que altura se elevará cada bola acima de suas mãos?

03-(FUVEST-SP)

Duas bolinhas são lançadas verticalmente para cima, a partir de uma mesma altura, com a mesma velocidade inicial de 15m/s, mas num intervalo de tempo de de 0,5s entre os lançamentos.

Despreze a resistência do ar e considere g = 10m/s².

a) Faça, num mesmo sistema de eixos, o gráfico da velocidade em função do tempo para as duas bolinhas.

b) Qual o instante e a altura em que as duas bolinhas coincidem?

04-(UNIFESP-SP)

Em uma manhã de calmaria, um Veículo Lançador de Satélite (VLS) é lançado verticalmente do solo e, após um período desaceleração, ao atingir a altura de 100 m, sua velocidade linear é constante e de módulo igual a 20,0 m/s.

Alguns segundos após atingir essa altura, um de seus conjuntos de instrumentos desprende-se e move-se livremente sob ação da força gravitacional.

A figura fornece o gráfico da velocidade vertical, em m/s, do conjunto de instrumentos desprendido

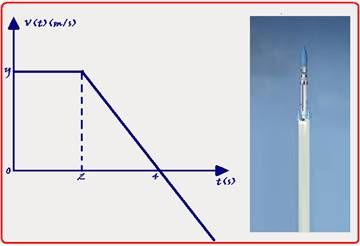
como função do tempo, em segundos, medido no intervalo entre o momento em que ele atinge a altura de 100 m até o instante em que, ao retornar, toca o solo.

a) Determine a ordenada y do gráfico no instante t = 0 s e a altura em que o conjunto de instrumentos se desprende do VLS.

b) Calcule, através dos dados fornecidos pelo gráfico, a aceleração gravitacional do local e, considerando √2 ­=1,4, determine o instante no qual o conjunto de instrumentos toca o solo ao retornar.

05-(FGV-SP)

Frequentemente, quando estamos por passar sob um viaduto, observamos uma placa orientando o motorista para que comunique à polícia qualquer atitude suspeita em cima do viaduto.

O alerta serve para deixar o motorista atento a um tipo de assalto que tem se tornado comum e que segue um procedimento bastante elaborado.

Contando que o motorista passe em determinado trecho da estrada com velocidade constante, um assaltante, sobre o viaduto, aguarda a passagem do pára-brisa do carro por uma referência previamente marcada na estrada.

Nesse momento, abandona em queda livre uma pedra que cai enquanto o carro se move para debaixo do viaduto. A pedra atinge o vidro do carro quebrando-o e forçando o motorista a parar no acostamento mais à frente, onde outro assaltante aguarda para realizar o furto.

Suponha que, em um desses assaltos, a pedra caia por 7,2 m antes de atingir o pára-brisa de um carro.

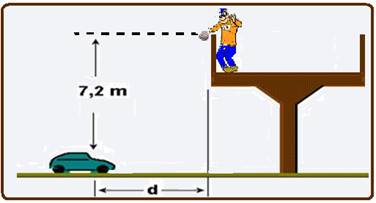
Nessas condições, desprezando-se a resistência do ar e considerando a aceleração da gravidade 10 m/s², a distância d da marca de referência, relativamente à trajetória vertical que a pedra realizará em sua queda, para um trecho de estrada onde os carros se movem com velocidade constante de 120 km/h, está a

06-(UERJ-RJ)

Um corpo em queda livre percorre certa distância vertical em 2s; logo, a distância percorrida em 6s será:

a) dupla.               

b) tripla                  

c) seis vezes maior.          

d) nove vezes maior.          

e) doze vezes maior.

07-(UNIFESP-SP)

Três bolinhas idênticas, são lançadas na vertical, lado a lado e em sequência, a partir do solo horizontal, com a mesma velocidade inicial, de módulo igual a 15 m/s para cima.

Um segundo após o lançamento da primeira, a segunda bolinha é  lançada.

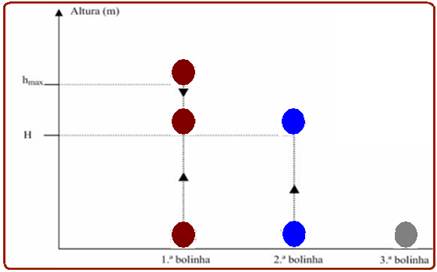
A terceira bolinha é lançada no instante em que a primeira, ao retornar, toca o solo.

Considerando  g = 10m/s² e que os efeitos da resistência do ar ao movimento podem ser desprezados, determine

a) a altura máxima (h_máx) atingida pela primeira bolinha e o instante de lançamento da  terceira bolinha.    

b) o instante e a altura H, indicada na figura, em que a primeira e a segunda bolinha se cruzam.

08-(FUVEST-SP) 

Numa filmagem, no exato instante em que um caminhão passa por uma marca no chão, um dublê se larga de um viaduto para cair dentro de sua caçamba.

A velocidade v do caminhão é constante e o dublê inicia sua queda a partir do repouso, de uma altura de 5 m da caçamba, que tem 6 m de comprimento.

A velocidade ideal do caminhão é aquela em que o dublê cai bem no centro da caçamba, mas a velocidade real v do caminhão poderá ser diferente e ele cairá mais à frente ou mais atrás do centro da caçamba.

Para que o dublê caia dentro da caçamba, v pode diferir da velocidade ideal, em módulo, no máximo:

09-(UNICAMP-SP)

Uma torneira, situada a uma altura de 1 m acima do solo, pinga lentamente à razão de 3 gotas por minuto.

(a) Com que velocidade uma gota atinge o solo ?

b) Que intervalo de tempo separa as batidas de duas gotas consecutivas no solo ? Considere, para simplificar, g = 10 m/s².

10-(PUC-SP)

Um projétil é atirado verticalmente, de baixo para cima, com velocidade v_o = 25 m/s. Uma pessoa

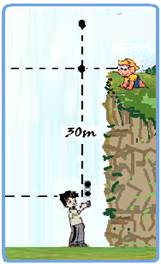
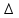situada a 30m de altura vê passar na subida e, após um intervalo de tempo t, o vê voltar. Desprezando a resistência do ar e supondo a aceleração local da gravidade de 10 m/s², o tempo t decorrido entre as duas observações foi de: (g = 10m/s²).

11-(UFMT-MT)

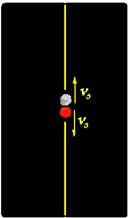
Dois projéteis iguais são atirados da mesma posição ( 40 m acima do solo ), verticalmente, em sentidos opostos e com a mesma velocidade.

Em 2 s o primeiro projétil atinge o solo.

Depois de quanto tempo da chegada do primeiro o segundo atingirá o solo? ( Despreze qualquer tipo de atrito e considere g = 10 m/s².)

12-(ITA-SP)

Um corpo cai, em queda livre, de uma altura tal que durante o último segundo de queda ele percorre 1/4 da altura total.

Calcular o tempo de queda, supondo nula a velocidade inicial do corpo.

a) t=1/(2 - √3) s         

b) t=2/(2 + √3) s         

c) t=2/(2 - √3) s         

d) t=3/(2 - √3) s          

e) t=4/(3 - √3) s

13-(ITA-SP)

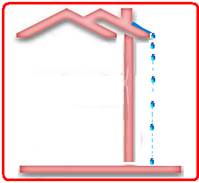
De um telhado caem gotas de chuva separadas por intervalos de tempo iguais entre si.

No momento em que a 5º gota se desprende, a primeira toca o solo.

Qual a distância que separa as duas últimas gotas consecutivas (4° e 5°), nesse instante, se a altura do telhado é de 20m? g = 10m/s².

14-(AFA-SP)

Um corpo é abandonado do topo de um precipício.

O ruído produzido pela queda do corpo ao atingir o chão é ouvido 10s após o seu abandono.

Considerando a velocidade do som no ar igual a 340m/s, pode se afirmar que a altura do precipício, em metros é aproximadamente
a) 200                            

b) 288                           

c) 391                             

d) 423                         

e) 522

15-(FISICAEVESTIBULAR)

Um elevador está descendo com velocidade constante de 5m/s. Quando o elevador está a uma altura de 10m do solo,

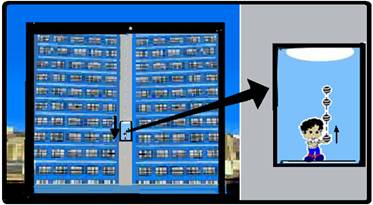
um menino em seu interior joga uma bola verticalmente para cima, com velocidade inicial de 12m/s em relação ao elevador. Considere g = 10m/s².

a) Qual a altura atingida pela bola em relação ao solo?

b) Determine a altura do elevador sabendo que ela equivale à metade da altura máxima atingida pela bola, dentro do elevador, se ele não tivesse teto.

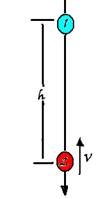
16-(AFA-SP)

Um corpo é abandonado do repouso de uma altura h acima do solo.

No mesmo instante outro é lançado para cima, a partir do solo, segundo a mesma vertical com velocidade v.

Sabendo que os corpos se encontram na metade da altura da descida do primeiro, pode-se afirmar que h vale

Resolução comentada dos exercícios de vestibulares sobre

Movimentos Verticais

01- 

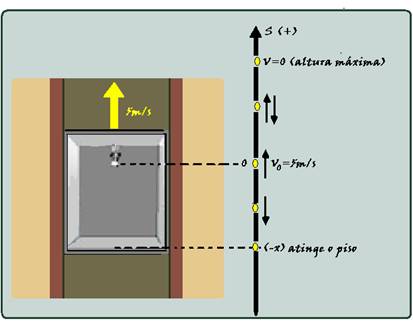
No instante em que a lâmpada se desprende do teto do elevador ela está sendo lançada para cima com velocidade de V_o=5m/s e o tempo de subida e descida até chegar ao piso, na posição (–x), foi t=0,5s  ---  (veja figura abaixo)  ---  S=V_o.t – gt²/2  ---  -x=5.0,5 – 5.(0,5)²  ---  x= - 1,25m  ---  altura do elevador = 1,25m.

02- a) Como são três bolas, cada uma fica no ar t= 3.0,4  ---  t=1,2s.
b) Como cada bola fica no ar 1,2s e o tempo de subida é igual ao tempo de descida, ela demora t=0,6s para atingir a altura máxima,  onde V=0  ---  V=V_o – gt  ---  0=V_o – 10.0,6  ---  V_o=6m/s.

c) Cada bola atinge a altura máxima no instante t=0,6s  ---  S=V_o.t – gt²/2=6.0,6 – 5.(0,6)²  ---  S=1,8m.

03- a) Bolinha P que saiu antes com V_o=15m/s  ---  tempo que demora para atingir a altura máxima, ou seja, quando V=0  ---  V= V_o – gt  ---  0=15 – 10t  ---  t=1,5s (tempo de subida e tempo de descida, ou seja, o tempo de permanência no ar é de 3,0s)  ---  se ela parte com velocidade de 15ms ela retorna ao ponto de partida com velocidade de -15m/s (veja gráfico abaixo).

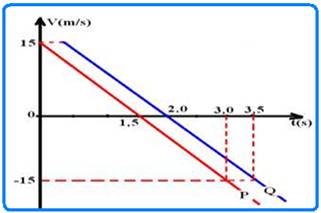
A bolinha Q repete os mesmos movimentos de Q, mas depois de 0,5s (veja gráfico acima)

b) Como P partiu 0,5s antes  ---  t_P – t_Q=0,5  ---  t_P=t_Q + 0,5  ---   equação da Q  ---  S_Q=15t_Q -10t_Q²/2  ---  equação da P  ---  S_P=15t_P -10t_P²/2  ---  S_P=15(t_Q + 0,5) - 5(t_Q + 0,5)²=15t_Q + 7,5 – 5(t_Q2 + 2.t_Q.0,5 + 0,25)=15t_Q + 7,5 – 5t_Q² - 5t_Q – 1,25  ---  S_P=10t_Q – 5t_Q² + 6,25  ---  no encontro S_Q=S_P  ---  15t_Q – 5t_Q²=-5t_Q² + 10t_Q + 6,25  ---  t_Q=6,25/5  ---  t_Q=1,25s (instante do encontro após a partida de Q) e  t_P=(1,25 + 0,5)=1,75s (instante do encontro após a partida de P)  ---  substituindo t_Q=1,25s em S_Q=15t_Q – 5t_Q²=15.1,25 – 5.(1,25)²  ---  S_Q=11m.

04- a) Pelo enunciado o VLS acelera verticalmente até atingir a altura de 100m e, a partir desse instante (t=0), ele se move por alguns segundos com velocidade constante de 20m/s até que um dos conjuntos de instrumentos se desprende, o que ocorre, pelo gráfico, quando t=2s  ---  observando o gráfico você pode concluir que quando t=0 ele atinge a velocidade de 20m/s  ---  portanto a ordenada y vale y=V=20m/s  ---  entre 0 e 2s ele subiu com velocidade constante de 20ms  --- V=∆S/∆t  ---  20=∆S/2  ---  ∆S=h’=40m  ---  como, desde o solo até atingir a velocidade de 20m/s ele já havia subido h=100m, a altura total alcançada foi de h_total=100 + 40=140m  ---  h=140m.

b) No instante em que o conjunto de instrumentos se desprende ele possui a mesma velocidade para cima que o VLS e que é de 20m/s  ---  assim, o movimento do conjunto de instrumentos é como um lançamento vertical para cima com velocidade inicial V_o=20m/s  ---  agora o conjunto está subindo e sua velocidade está variando de V_o=20m/s  (quando t=2s) para V=0 (quando t=4s), veja gráfico  ---  a=g=∆V/∆t=(V – V_o)/(t – t_o)=(0 – 20)/(4 – 2)  ---  g= - 10m/s²  ---  colocando a origem no ponto de lançamento, quando o conjunto de instrumentos atinge o solo ele está na posição S= - 140m  ---  S= S_o + V_o.t + g.t²/2  ---  -140 =0 + 20t -10.t²/2  ---  t² – 4t – 28=0  ---  ∆=16 + 112=128  --- 

t= (4 ± 11,31)/2  ---  t≈7,6s  ---  o tempo pedido vale t=2 + 7,6  ---  t≈9,6s.

05- Tempo que a pedra demora para cair  ---  queda livre da altura de h=7,2m  ---  S=gt²/2  ---  7,2=5t²  ---  t=1,2s  ---  nesse tempo o carro com velocidade constante de 120km/h=33,4m/s o carro se deslocou  ---  V=ΔS/Δt  ---  33,4= ΔS/1,2  ---  ΔS=40,08m.  

R- C.

06- Observe que o tempo de queda é 6/2=3 vezes maior e,que na expressão h=gt²/2 a altura é diretamente proporcional ao quadrado do tempo  ---  assim, a resposta será 3²=9 vezes maior  ---  R-D.

07- a) Trata-se de um lançamento vertical para cima com velocidade inicial V_o=15m/s e a=-g=-10m/s²  ---  na altura máxima V=0  ---  V = V_o– gt  ---  0=15 – 10t  ---  t=1,5s (tempo que demora para subir que é o mesmo que demora para descer)  ---  tempo de permanência no ar  --- t=3s  ---  na altura máxima t=1,5s  ---  S=S_o + V_ot + at²/2  --- 

h_máx=0 + 15.1,5 – 10.1,5²/2=22,5 – 11,25  ---  h_máx=11,25m.

b) Equação da primeira bolinha que é lançada no instante t₁ com V_o=15m/s da origem  --- h₁=0 + 15t₁ – 10t₁²/2  --- 

h₁=15t₁ – 5₁²   ---  quando a segunda bola foi lançada já fazia 1s que a segunda estava no ar  ---  t₁ - t₂=1  ---  t₂=t₁ – 1  ---  equação da bola 2  ---  h₂=0 + 15t₂ – 5t₂²=15(t₁ – 1) – 5.(t₁ – 1)²/2  ---  h₂=-20 + 25t₁ – 5t₁²   ---  no instante em que se cruzam possuem a mesma altura  ---  h₁=h₂  ---  15t₁ – 5t₁² = -20 + 25t₁ -5t₁²  ---  10t₁ – 20 = 0  ---  t₁=2s (instante do encontro)  ---  substituindo t₁=2s em qualquer uma das duas equações, por exemplo na primeira, você obtém  ---  h₁=h₂=H=15.2 – 5.2²=30 – 10  ---  H=10m.

08- Observe a figura abaixo onde L é a distância horizontal entre a marca no chão e o dublê no instante do salto  ---  cálculo do tempo de queda do dublê que cai da altura h=5m  ---  h=gt²/2  ---  5=10t²/2  ---   t²=1  ---  t=1s  ---  a velocidade ideal ocorre quando ele cai no meio da caçamba ∆S=(L + 3) nesse tempo de ∆t=1s  --- V_i=ΔS/Δt=(L + 3)/1  ---  V_i=(L + 3)  ---  a velocidade mínima do caminhão ocorre quando em ∆t=1s ele cai no início da caçamba ∆S=L  ---  V_min= ΔS/Δt=L/1  ---  V_min=L  ---  a velocidade máxima do caminhão ocorre quando em ∆t=1s ele cai no final da caçamba ∆S=(L + 6) ---  V_max= ΔS/Δt=(L + 6)/1  ---  V_max=L + 6  ---  diferenças  --- V₁=V_i – V_min= (L + 3) – L  ---  V₁=3m/s  ---  V₂= V_max  - V_i=(L + 6) – (L + 3)  ---  V₂=3m/s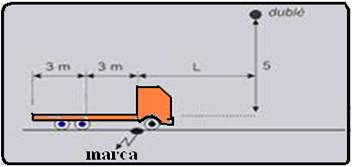

R- B.

09- a) Velocidade com que cada gota chega no solo  ---  equação de Torricelli  ---  V²=Vo² + 2.g.h=0² + 2.10.1  ---  V=√20  ---  V=4,47m/s.

b) Como o tempo de queda é o mesmo, o intervalo de tempo entre as batidas de duas gotas consecutivas é o mesmo intervalo de tempo compreendido entre as saídas de duas gotas consecutivas da torneira  ---  se saem 3 gotas em cada 1min=60s, tem-se que, entre a 1^a e a 2^adecorreram (20s); entre a 2^a e a 3^a (20s) e entre a 3^a e a 4^a (20s) e assim, a partir do instante em que uma bate no solo, depois de 20s chega a outra ao solo  ---  R- 20s.

10- Trata-se de um lançamento vertical para cima de equação S=S_o + V_ot + at²/2  ---  cálculo do tempo t nos instantes em que o projétil passa pela posição S=30m  ---  30=25t – 10t²/2  ---  t² – 5t + 6=0  ---  resolvendo essa equação você obtém dois instantes  ---   t₁=2s (passa pela posição 30m na subida) e t₂=3s (passa pela posição 30m na descida)  --- 

o tempo Dt decorrido entre as duas observações foi de  ---   Dt=3 – 2=1s  ---  R- B.

11- Colocando a origem no ponto de lançamento e orientando a trajetória para cima  ---  equação do corpo lançado verticalmente para baixo com velocidade V_o  ---  S=S_o + V_ot + at²/2  ---  S=h₁  ---  V_o e a

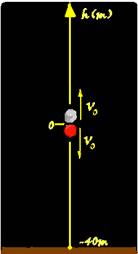
são negativas (contrárias à orientação da trajetória)  ---  h₁=0 –V_o.t – gt²/2  ---  quando ele chega ao solo h₁=-40m e t=2s  ---  -40=-V_o.2 – 10.2²/2  ---  V_o=10m/s  ---  equação do corpo lançado verticalmente para cima com V_o=10m/s (positiva, a favor da trajetória) e a=-g (contrária à orientação da trajetória)  ---  h₂=0 + V_ot – gt²/2  ---  ela sobe, desce e quando chega ao solo está na posição h₂=-40m  ---  -40=10t – 5t²  ---  5t² -10t -40=0  ---  resolvendo essa equação você obtém dois instantes  --- 

t₁=-1s (negativo, não convém) e t₂=4s (tempo com que o segundo projétil chega ao solo)  ---  como o primeiro chega ao solo após 2s e o segundo após 4s, a diferença de tempo pedida é de t=2s.

12- Observe a figura onde foi colocada a origem no ponto de partida quando V_o=0 e orientando a trajetória para baixo  ---  observe na figura que, no final do último segundo o instante é t e no segundo anterior é  t₁=t – 1  ---     no instante t₁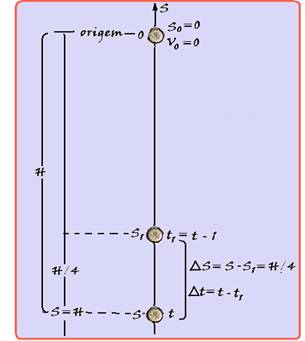 

---  S=S_o + V_o.t₁ + a.t₁²/2  ---  S₁=0 + 0 + g.t₁²/2  ---  S₁=g.t₁²/2  ---  no instante t  ---  S₂=g.t²/2  ---  ∆S=H/4=S₂ – S₁  --- 

H/4=g.t²/2 – g.t₁²/2=g/2 (t² – t₁²)  ---  H/2=g( t² – t₁²)  ---  H/2=g.(t – t₁).(t + t₁)= g.[t – (t – 1)]. [t + (t – 1)]  ---  H/2=g.(t – t +1).(t + t -1)  ---  H/2=g.(t + t – 1)=(2t – 1)  ---  H/2=g.(2t – 1)  ---  H=2g(2t – 1)  ---  H=4gt- 2g  ---  4gt=H + 2g  ---

t=(H + 2g)/4g (I)  ---  no instante t  ---  S₂=H=g.t²/2 (II)  ---  (II) em (I)  ---  t=[(g.t²/2) + 2g]/4g  ---  t=[(gt² + 4g)/2]4g  ---  t=(gt² + 4g)/8g=(t² + 4)/8  ---  8t=t² + 4  ---  t² – 8t + 4 = 0  ---  resolvendo  ---  t₁=4 + 2√3 s e t₂=4 - 2√3 (negativo, não satisfaz)  ---  t=(4 + 2√3)s  ---  t=2(2 + √3)x(2 - √3)/(2 - 2√3)  ---  t=2[2² – (√3)²]/(2 - √3)  ---  t=2.(4 – 3)/(2 - √3)  ---  t=2/( 2 - √3)  ---  R- C.

13- 

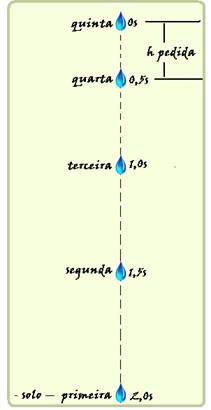
Cálculo do tempo que a gota demora para chegar ao solo e percorrer h=20m  ---  S=S_o + V_ot + gt²/2  ---  20=0 + 0t + 10t²/2  ---  20=5t²  ---  t=√4  ---  t=2s  ---  como esse é o tempo que cada gota demora para chegar ao solo, dividindo-o por 4 você obterá o intervalo de tempo em que cada gota se desprende do telhado (observe a figura)  ---  quando a quinta gota está saindo a quarta gota já estava se deslocando durante t=0,5s, fornecendo a distância pedida (entre a 4^a e a 5^a gotas) pela expressão h=gt²/2=10.(0,5)²2  ---  h=1,25m.

14- Seja t o tempo que a pedra demora para descer e t₁ o tempo que o som demora para subir  ---  t + t₁=10  ---  t₁=10 – t  ---  o corpo está em queda livre  ---  S=S_o + V_o.t  _a.t²/2  ---  h=0 + 0 + 10.t²/2  ---  h=5t² (I)  ---  o som sobe com velocidade constante de V=340m/s demorando t₁=10 – t  ---  V=∆S/∆t  ---  340=h/(10 – t)  ---  h=340.(10 – t) (II)  ---  igualando (I) com (II)  ---  5t² = 340(10 – t)  ---  5t² + 340t – 3400=0  ---  t² + 68t – 680=0  ---  ∆=4624 + 2720=7344  ---  √∆≈85,7  ---  t₁= -68 +85,7/2 =8,85s  ---  t₂=negativo, não satisfaz  ---  t=8,85s (tempo que a pedra demora para descer ---   substituindo t=8,85s em h=5t²=5.(8,85)²=391,6125m  ---  R- C.

15- a) Para um observador fixo no solo a bola estará subindo com velocidade relativa de VR=12 – 5=7m/s  ---  colocando a origem do sistema de referência nas mãos do menino e orientando a trajetória para cima você terá  ---  S=So + Vo.t + a.t²/2  ---  h= 0 + 7t – gt²/2  ---  h = 7t – 5t²  ---  na altura máxima V=0  ---  V=Vo + at  ---  0=7 – 10t  ---  t=0,7s (tempo que demora para atingir a altura máxima)  ---  este tempo, substituído em h=7t – 5t2 fornece a altura  máxima  atingida pela bola  ---   h_máx=7.(0,7) – 5.(0,7)²=4,9 – 2,45=2,45m  ---  h_máx=10 + 2,45  ---  h_máx=12,45m (altura máxima atingida pela bola em relação a um observado no solo) ou ainda  ---  durante os t=0,7s o elevador desce V=∆S/∆t  ---  5=h/0,7  ---  h=3,5m  ---  nesse mesmo intervalo de tempo a bola sobe até atingir a altura máxima, durante t=0,7s, de h’=0 + 12.0,7 – 10.(0,7)²/2=8,4 – 2,45=5,95m  ---  assim, em t=0,7s o elevador desce 3,5m e a bola sobe 5,95m  ---  h_máx=5,95 – 3,5=2,45m  ---  h_máx=2,45m.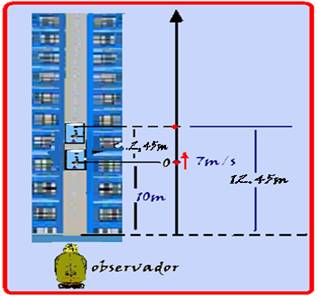

b) Para um observador dentro do elevador que se move em MRU com velocidade (equilíbrio dinâmico) a bola estará subindo sendo lançada verticalmente para cima com V_o=12m/s  ---  equação de Torricelli  ---  V²=V_o² + 2.a.∆S  ---  na altura máxima V=0  ---  0² = 12² – 2.10.h_máx  ---  h_máx=144/20=7,2m  ---  altura do elevador h_e=7,2/2=3,6m  ---  h_e=3,6m.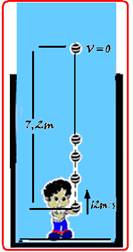 

Observação: Veja que, para o observador dentro do elevador a bola demorou V=V_o + at  ---  0=12 – 10t  ---  t=1,2s  (para subir)  ---  para o observador fora do elevador, para percorrer h=5,95m, ela deve demorar, com V_o=7m/s  ---  5,95=7t – 5t⁵  ---  5t² -7t +5,95=0  ---  ∆=144 – 119=25  ---  √∆=5  ---  t₁=(7 – 5)/10=- 0,2s (negativo, desprezado)  ---  t₂=(7 + 5)/10  ---  t₂=1,2s (para subir)  ---  observe que o tempo de subida  é o mesmo tanto para o observador fora do elevador como para o observador dentro do elevador, como deveria ocorrer.

16- Primeiro corpo abandonado V_o=0  ---  colocando a origem da trajetória nesse ponto e orientando-a para baixo (g=+10m/s²), sua equação fica  ---  S=S_o + V_ot + at²/2  ---  h₁=0 + 0.t + 10t²/2  ---  h₁=5t²  ---  0 corpo 2 é lançado verticalmente para cima da posição h abaixo da origem 0 com velocidade (-V, contrária à orientação da trajetória)) e sua equação fica  ---  h₂=h + (-V).t + 10t²/2  ---  h₂=h – Vt + 5t²  ---  como, pelo enunciado, eles se encontram na altura h₁=h₂=h/2, a equação horária do corpo 1 fica  ---  h/2=5t²  ---  t=√(h/10)  ---  substituindo esse tempo na equação do corpo 2, onde h₂=h/2, você terá  ---  h/2=h – Vt + 5t²  ---  h/2 – h= - Vt + 5t²  ---  -h/2= - Vt + 5t²  ---  10t² – 2Vt +h=0  ---  10.√(h/10) – 2V√(h/10) + h=0  ---  h – 2V√(h/10) + h=0  ---  h=V.√(h/10)  ---  h² = V².h/10  ---  h=V²/10=V²/g  ---

R- B.