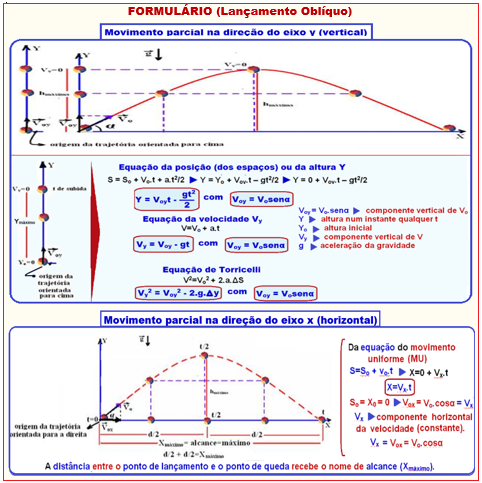
LANÇAMENTO OBLÍQUO E LANÇAMENTO HORIZONTAL

Exercícios de vestibulares com resoluções comentadas sobre

Lançamento Oblíquo e Lançamento Horizontal

01-(CEFET-CE)

Um caminhão se desloca em movimento retilíneo e horizontal, com velocidade constante de 20m/s. Sobre sua carroceria, está um canhão, postado para tiros verticais, conforme indica a figura.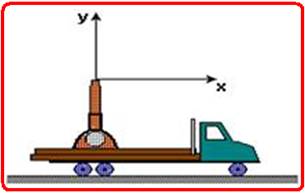

A origem do sistema de coordenadas coincide com a boca do canhão e, no instante t = 0, ele dispara um projétil, com velocidade de 80m/s. Despreze a resistência do ar e considere g = 10 m/s².

Determine o deslocamento horizontal do projétil, até ele retornar à altura de lançamento, em relação:

a) ao caminhão;

b) ao solo.

02-(UFF-RJ)

Após um ataque frustrado do time adversário, o goleiro se prepara para lançar a bola e armar um contra ataque.

Para dificultar a recuperação da defesa adversária, a bola deve chegar aos pés de um atacante no menor tempo possível.

O goleiro vai chutar a bola, imprimindo sempre a mesma velocidade, e deve controlar apenas o ângulo de lançamento.

A figura mostra as duas trajetórias possíveis da bola num certo momento da partida.

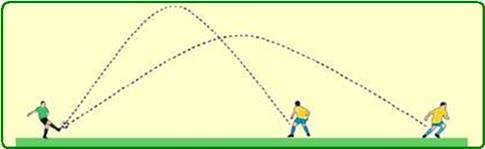
Assinale a alternativa que expressa se é possível ou não determinar qual destes dois jogadores receberia bola no menor tempo. Despreze o efeito da resistência do ar.

(A) Sim, é possível, e o jogador mais próximo receberia a bola no menor tempo.

(B) Sim, é possível, e o jogador mais distante receberia a bola no menor tempo.

(C) Os dois jogadores receberiam a bola em tempos iguais.

(D) Não, pois é necessário conhecer os valores da velocidade inicial e dos ângulos de lançamento.

(E) Não, pois é necessário conhecer o valor da velocidade inicial.

(UERJ-RJ)

Este enunciado refere-se às questões de números 03 e 04.

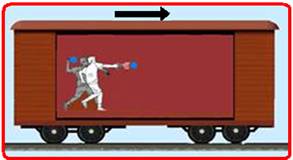
Um trem em alta velocidade desloca-se ao longo de um trecho retilíneo a uma velocidade constante de 108 km/h.

Um passageiro em repouso arremessa horizontalmente ao piso do vagão, de uma altura de 1 m, na mesma direção e sentido do deslocamento do trem, uma bola de borracha que atinge esse piso a uma distância de 5 m do ponto de arremesso.

03-(UERJ-RJ)

Se a bola fosse arremessada na mesma direção, mas em sentido oposto ao do deslocamento do trem, a distância, em metros, entre o ponto em que a bola atinge o piso e o ponto de arremesso seria igual a:

( 04-(UERJ-RJ)

O intervalo de tempo, em segundos, que a bola leva para atingir o piso é cerca de:

 05-(UFC-CE)

Uma partícula pontual é lançada de um plano inclinado conforme esquematizado na figura a seguir. O plano tem um ângulo de inclinação θ em relação à horizontal, e a partícula é lançada, com velocidade de módulo v, numa direção que forma um ângulo de inclinação α em relação ao plano inclinado.

Despreze qualquer efeito da resistência do ar.

Considere que a aceleração da gravidade local é constante (módulo igual a g, direção vertical, sentido para baixo).  

a) Considerando o eixo x na horizontal, o eixo y na vertical e a origem do sistema de coordenadas cartesianas no ponto de lançamento, determine as equações horárias das coordenadas da partícula, assumindo que o tempo é contado a partir do instante de lançamento.

b) Determine a equação da trajetória da partícula no sistema de coordenadas definido no item (a).

06-(UNICAMP-SP)

Uma bola de tênis rebatida numa das extremidades da quadra descreve a trajetória representada na figura a seguir, atingindo o chão na outra extremidade da quadra.

O comprimento da quadra é de 24 m.

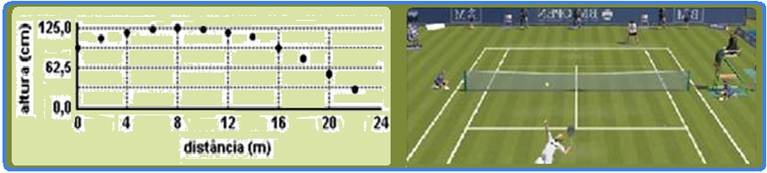
a) Calcule o tempo de vôo da bola, antes de atingir o chão. Desconsidere a resistência do ar nesse caso.

b) Qual é a velocidade horizontal da bola no caso acima?

07-(CEFET-CE)

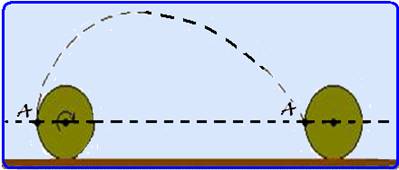
Uma roda de raio R rola uniformemente, sem escorregar, ao longo de uma superfície horizontal.

Do ponto A da roda se desprende uma gota de barro, como mostra a figurar.

Com que velocidade v deve se deslocar a roda, se a gota, depois de lançada ao espaço, volta a cair sobre o mesmo ponto da roda após efetuar uma volta? Considere desprezível a resistência do ar.

08-(PUC-SP)

O esquema apresenta uma correia que transporta minério, lançando-o no recipiente R.

A velocidade da correia é constante. Para que todo o minério caia dentro do recipiente, a velocidade v da correia, dada em m/s, deve satisfazer a desigualdade: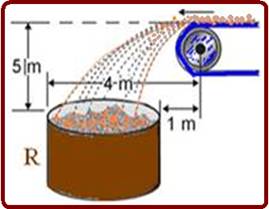

a) 2 < v < 3              

 b) 2 < v < 5                    

c) 1 < v < 3                   

d) 1 < v < 4                   

e) 1 < v < 5

09-(UERJ-RJ) 

Um avião, em trajetória retilínea paralela à superfície horizontal do solo, sobrevoa uma região com

velocidade constante igual a 360 km/h.

Três pequenas caixas são largadas, com velocidade inicial nula, de um compartimento na base do avião, uma a uma, a intervalos regulares iguais a 1 segundo.

Desprezando-se os efeitos do ar no movimento de queda das caixas, determine as distâncias entre os respectivos pontos de impacto das caixas no solo.

10-(FISICA E VESTIBULAR)

Se, com um arco e flecha, você mirar a flecha diretamente para o alvo fixo (figura 1), a flecha atingirá o ponto visado?

Por outro lado, se você mirar a flecha diretamente para uma maçã em queda livre (figura 2), a flecha a atingirá?

Justifique.

11-(UFJF-MG)

Durante uma partida de futebol, um jogador, percebendo que o goleiro do time adversário está longe do gol, resolve tentar um chute de longa distância (vide figura).

O jogador se encontra a 40 m do goleiro.

O vetor velocidade inicial da bola tem módulo V_o= 26 m/s e faz um ângulo de 25° com a horizontal, como mostra a figura a seguir.

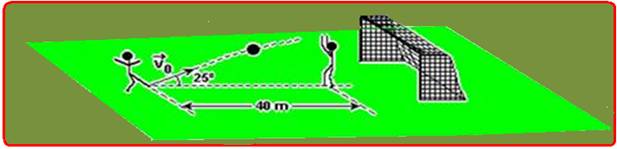
Desprezando a resistência do ar, considerando a bola pontual e usando cos 25° = 0,91, sen 25° = 0,42 e g=10m/s²:

a) Faça o diagrama de forças sobre a bola num ponto qualquer da trajetória durante o seu vôo, após ter sido chutada. Identifique a(s) força(s).

b) Saltando com os braços esticados, o goleiro pode atingir a altura de 3,0 m. Ele consegue tocar a bola quando ela passa sobre ele? Justifique.

c) Se a bola passar pelo goleiro, ela atravessará a linha de gol a uma altura de 1,5 m do chão.

A que distância o jogador se encontrava da linha de gol, quando chutou a bola? (Nota: a linha de gol está atrás do goleiro).

12-(PUC-SP)

Dois amigos, Berstáquio e Protásio, distam de 25,5m.

Berstáquio lança obliquamente uma bola para Protásio que, partindo do repouso, desloca-se ao encontro da bola para segurá-la.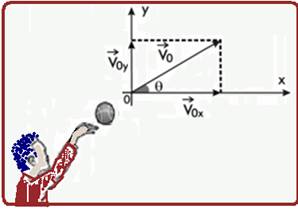

No instante do lançamento, a direção da bola lançada por Berstáquio formava um ângulo θ com a horizontal, o que permitiu que ela  alcançasse, em relação ao ponto de lançamento, a  altura máxima de 11,25m e uma velocidade de 8m/s  nessa posição.

Desprezando o atrito da bola com o ar e adotando g = 10m/s², podemos afirmar que a aceleração de Protásio, suposta constante, para que ele consiga pegar a bola no mesmo nível do lançamento

deve ser de

13-(FUVEST-SP) Um motociclista de MotoCross, move-se com velocidade V = 10 m/s, sobre uma superfície plana, até atingir uma rampa (em A), inclinada de 45^o com a horizontal, como indicado na figura.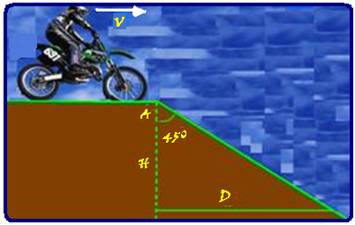

A trajetória do motociclista deverá atingir novamente a rampa a uma distância horizontal D (D=H), do ponto A, aproximadamente igual a: (g=10m/s²)

a) 20m              

b) 15m                

c) 10m                

d) 7,5m                

e) 5m

14-(Olimpíada Brasileira de Física)

Dois rapazes brincam de tênis na praia.

Um deles dá uma raquetada na bola a 2,45 m de altura e esta sai horizontalmente com velocidade de 72 km/h.

Qual deve ser a velocidade mínima do outro rapaz, situado inicialmente 20,3 m à frente do primeiro, para que consiga aparar a bola antes que ela bata na areia? (Adote g = 10 m/s²).

15-(FISICAEVESTIBULAR)

Um projétil 1 se move em linha reta, a 1125m do solo, com velocidade horizontal V =1080 km/h

No solo existe um projétil 2 que é disparado com velocidade de 540 km/h, exatamente quando o projétil 1 está passando sobre ele na mesma vertical. Despreze a resistência do ar, as dimensões dos dois projéteis e considere g = 10 m/s².

a) Calcule o ângulo com que deve ser lançado o projétil 2 com o solo para que atinja o projétil 1.

b) Localize o ponto do impacto entre os dois projéteis num plano de coordenadas cartesianas com a origem no ponto de lançamento do projétil 2.

16-(UFMG-MG)

Um cano de irrigação, enterrado no solo, ejeta água a uma taxa de 15 litros por minuto com uma velocidade de 10 m/s.

A saída do cano é apontada para cima fazendo um ângulo de 30° com o solo, como mostra a figura. Despreze a resistência do ar e considere g = 10 m/s², sen 30° = 0,50 e cos 30° = 0,87.

Calcule quantos litros de água estarão no ar na situação em que o jato d’água é contínuo do cano ao solo.

17-(UFG-GO)

Os quatro blocos, representados na figura com suas respectivas massas, são abandonados em um plano inclinado que não apresenta atrito e termina voltado para a direção horizontal.

Os blocos, ao deixarem a plataforma, descrevem trajetórias parabólicas em queda livre e alcançam o solo, formando, da esquerda para a direita, a seqüência:

a) m; 5m; 2m; 3m           

b) m; 2m; 3m; 5m           

c) 3m; 2m; 5m; m         

d) 3m; 5m; m; 2m        

e) 5m; 3m; 2m; m

18-(PFB)

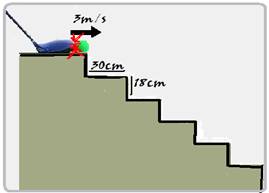
Uma bola de golfe é jogada do alto de uma escada com velocidade horizontal de 3m/s.

Cada degrau tem 30cm de comprimento (profundidade, passo)) e 18 cm de altura (espelho).

Despreze a resistência do ar, considere g = 10 m/s² e determine que degrau a bola tocará primeiro.

19-(PUC-RJ)

Em um campeonato recente de vôo de precisão, os pilotos de avião deveriam "atirar" um saco de areia dentro de um alvo localizado no solo.

Supondo que o avião voe horizontalmente a 500 m de altitude com uma velocidade de 144 km/h e que o saco é deixado cair do avião, ou seja, no instante do "tiro" a componente vertical do vetor velocidade é zero, podemos afirmar que: (Considere a aceleração da gravidade g = 10 m/s² e despreze a resistência do ar)

a) o saco deve ser lançado quando o avião se encontra a 100 m do alvo;

b) o saco deve ser lançado quando o avião se encontra a 200 m do alvo;

c) o saco deve ser lançado quando o avião se encontra a 300 m do alvo;

d) o saco deve ser lançado quando o avião se encontra a 400 m do alvo;

e) o saco deve ser lançado quando o avião se encontra a 500 m do alvo.

20-(UFAM-AM)

Uma bola de futebol com 450 g de massa, inicialmente em repouso, é chutada obliquamente para cima com velocidade inicial de 20m/s. A bola atinge altura máxima de 10m e atinge uma parede vertical 2s após o chute.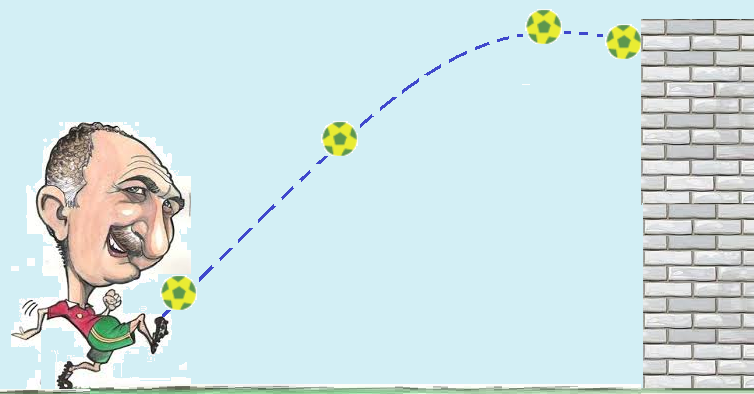 

Desprezando a resistência do ar,

podemos afirmar que a distância do ponto de lançamento da bola até a parede é aproximadamente igual a:

a) 40m 

b) 28m 

c) 20m 

d) 10m 

e) 14m

21-(UPF-RS)

Considere um vagão deslocando-se em uma trajetória retilínea com velocidade constante e igual a 5 m/s.

Um observador, A,dentro dele, lança uma pedra verticalmente para cima.

Um outro observador, B, do lado de fora do vagão e em repouso em relação à Terra, observa o vagão passar.

Sendo V_A e V_B , respectivamente, as velocidades da pedra no ponto mais alto de sua trajetória em relação a cada observador, pode-se concluir que:

a) V_A = 0 e V_B = 0

b) V_A = 0 e V_B = 5 m/s

c) V_A = 5 m/s e V_B = 0

d) V_A = 5 m/s e V_B = 5m/s

e) V_A = 0 e V_B = 10 m/s

22-(UEFS-BA)

Um goleiro chuta uma bola, que se encontra parada no gramado, para um jogador situado a 57,0m da

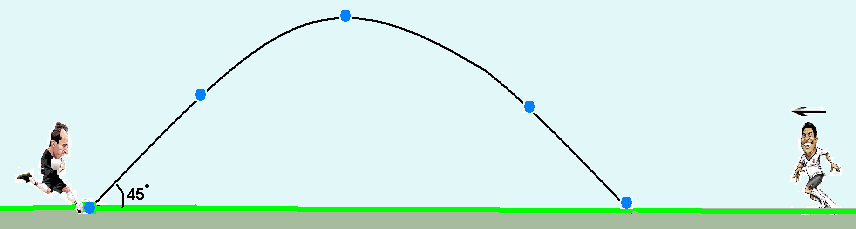
posição do goleiro. 

A bola é lançada com velocidade de 20,0m/s, fazendo um ângulo de 45° com o plano horizontal.

Desprezando-se a resistência do ar, considerando-se o módulo da aceleração da gravidade local igual a 10,0m/s² e sabendo-se que sen45° = cos45° = √2/2, o módulo da velocidade do jogador para alcançar a bola, no instante em que ela toca o gramado, em m/s, deve ser de, aproximadamente,

A) 4,0 B) 5,0 C) 6,0 D) 7,0 E) 8,0

Resolução comentada dos exercícios de vestibulares sobre

Lançamento Oblíquo e Lançamento Horizontal

01- a) Como a resistência do ar é desprezada, a velocidade horizontal inicial do projétil é constante e, em cada instante, a mesma do caminhão  ---  assim, se ele partiu de um ponto P da carroceria do caminhão, retornará ao mesmo ponto P e o deslocamento horizontal em relação ao caminhão será zero.

b) V_ox=20m/s  ---  V_o=80m/s  ---  V_o²=V_ox² + V_oy²  ---  6.400=400 + V _oy²  ---  V _oy=77.5m/s  ---  tempo de subida  ---  V_y = V _oy – g.t_s  ---  0=77,5 – 10t_s  ---  t_s=7,75s  ---  tempo que demora para subir e descer e se deslocar X na horizontal  ---  t=2.7.75  ---  t=15,5s  ---  deslocamento máximo horizontal  ---  X=V_ox.t=20,15,5  ---  X=310m.

02- O tempo de subida é igual ao tempo de descida o que ocorre quando V_y=0  ---  V_y=V_oy – g.t  ---  0=V_osenθ – g.t  ---  t=V_osenθ/g  ---  tempo no ar  ---  t_total=2t=2V_osenθ/g  ---  sendo 2V_o e g constantes, o tempo de permanência no ar depende apenas do ângulo θ com a horizontal  ---  quanto menor θ, menor será senθ e, consequentemente menor t_total, o que ocorre com o jogador que está mais distante  ---  R- B.

03- Para um observador no interior do trem que se desloca em movimento retilíneo e uniforme (equilíbrio dinâmico), o alcance de um objeto lançado horizontalmente só depende da intensidade da velocidade do objeto  ---  assim, caso a bola fosse arremessada em sentido oposto ao do deslocamento do trem, a distância entre o ponto de arremesso e o ponto de impacto também seria igual a 5 m  ---  não haveria diferença, pois a queda só é influenciada por g  ---  logo, seria 5m ao contrário da origem  ---  R- B.

04- O tempo de queda é calculado exclusivamente pelo movimento vertical (queda livre da altura de 1m com a=g=10m/s²  ---  h=gt²/2  ---  1=10t2/2  ---  t=√0,2  ---  t=0,447s  ---  R- C.

05- 

a) Observe a figura abaixo, onde você deve decompor V em suas componentes vertical V_y e horizontal V_x  ---  V_x=Vcosβ  ---  V_x=Vcos(α + θ)  ---  V_y=Vsenβ  ---  V_y=Vsen(α + θ)  ---  equação horária segundo a horizontal X  ---  X=V_ox.t=V_x.t  ---  X=V.cos (α + θ).t  ---  Y=V_yt – gt²/2  --- Y=Vsen (α + θ).t – gt²/2.

b) Isolando t em X=Vcos(α + θ)t  ---  t=X/Vcos(α + θ) que, substituída em Y=Vsen(α + θ)t – gt²/2  ---  Y=Vsen(α + θ).X/Vcos(α + θ) – g(X/Vcos(α + θ))²/2  ---  Y=tg(α + θ) – g.X²/2V²cos²(α + θ).

06- a) Do gráfico  ---  distância vertical que percorre  até atingir a altura máxima onde V_y=0  ---  ΔS=[125 – (62,5 – 62,5/2)]=125 – 93,75=31,25cm  ---  ΔS=0,3125m  ---  na altura máxima V_y=0  ---  Torricelli  ---  V­_y² = V_oy² + 2.a.ΔS  ---  0²=V_oy² – 2x10x0,3125  ---  V_oy=2,5m/s  ---  função horária vertical  ---  Y=Y_o + V_oy.t – gt²/2  ---  quando chega ao solo Y=0  ---  0=0,9375 + 2,5t – 5t²  ---  5t2 – 2,5t – 0,9375=0  ---  √Δ=5  --- t=(2,5 ±5)/10  ---  t=0,75s.

b) Na horizontal  ---  quando X=24m  ---  t=0,75s  ---  X=V_ox.t  ---  24=V_ox.0,75  --- V_ox=32m/s.

a) Do gráfico  ---  distância vertical que percorre  até atingir a altura máxima onde V_y=0  ---  ΔS=[125 – (62,5 – 62,5/2)]=125 – 93,75=31,25cm  ---  ΔS=0,3125m  ---  na altura máxima V_y=0  ---  Torricelli  ---  V­_y² = V_oy² + 2.a.ΔS  ---  0²=V_oy² – 2x10x0,3125  ---  V_oy=2,5m/s  ---  função horária vertical  ---  Y=Y_o + V_oy.t – gt²/2  ---  quando chega ao solo Y=0  ---  0=0,9375 + 2,5t – 5t²  ---  5t2 – 2,5t – 0,9375=0  ---  √Δ=5  --- t=(2,5 ±5)/10  ---  t=0,75s.

b) Na horizontal  ---  quando X=24m  ---  t=0,75s  ---  X=V_ox.t  ---  24=V_ox.0,75  --- V_ox=32m/s.

07- O tempo que a gota de barro permanece no ar é o mesmo tempo que a roda demora para efetuar uma volta completa, ou seja, percorrer ΔS=2πR com velocidade constante V, que é a velocidade de translação e de rotação da roda (não derrapa) e que também é a velocidade de lançamento da gota de barro  ---  V= ΔS/Δt  ---  V=2πR/t  ---  t=2πR/V  ---  a gota de barro atinge a altura máxima h_máx na metade desse tempo, quando sua velocidade vertical V_y se anula (V_y=0)  ---  V_y=V_oy – gt  ---  0=V – g(πR/V)  --- V²=πRg  ---  V=√(πRg).

08- Cálculo do tempo de queda vertical do minério  ---  Y=gt²/2  ---  5=5t²  ---  t=1s (é sempre o mesmo, depende apenas da altura vertical)  ---  velocidade mínima (limite inferior de R)  ---  X=V.t  ---  1=V.1  ---  V=1ms  ---  limite posterior (velocidade máxima)  ---  X=V’.t  ---  4=V’.1  ---  V’=4ms  --- R- D.

09- Por inércia as três caixas continuaram em movimento com a mesma velocidade horizontal do avião de 360 km/h  ---  desta forma os impactos no solo ocorrerão sobre a mesma linha reta, separadas pela distância percorrida pelo avião durante aquele 1 s entre os lançamentos das caixas  ---   velocidade de 360 km/h corresponde a 100 m/s (100m a cada 1s) e desta forma a distância entre os pontos de impacto será de 100 m.  

10- Primeiro caso  ---  não, pois enquanto o alvo permanece imóvel, o projétil (flecha), durante todo seu movimento estará caindo, sujeito à aceleração da gravidade e chegará ao alvo numa posição abaixo daquela em que ele mirou.

Segundo caso  ---  sim, porque enquanto a maçã está caindo sujeita à aceleração da gravidade, o projétil (flecha) também estará caindo na mesma proporção sujeita à mesma aceleração (da gravidade), atingindo o a maçã.

11- a) A única força que age sobre a bola (a resistência do ar é desprezada) durante todo o movimento é a força peso, vertical e para baixo.

b) Cálculo do tempo que a bola demora  a chegar até o goleiro percorrendo X=40m com velocidade horizontal constante e de valor V_ox=V_ocos25^o=26.0,91  ---  V_ox=23,66m/s  ---  X=V_ox.t  ---  40=23,66.t  ---  t=1,69s  ---  cálculo da altura, na direção vertical, que a bola estará ao chegar ao goleiro nesse instante (t=1,69s)  ---  Y=V_oy.t – gt²/2  ---  Y=Vo.sen25^o.t –gt²/2  ---  Y=26.0,42.1,69 – 10.(1,69)²/2  ---  Y=18,45 – 14,28  ---  Y=4,17m  ---  esse valor é maior que 3m e assim, o goleiro não consegue tocar a bola.

c) Cálculo do tempo que a bola demora para chegar à altura vertical de 1,5m  ---  Y=V_o.sen25^o.t – gt²/2  ---  1,5=26x0,42t – 5t²  ---  5t² - 10,92t + 1,5=0  ---  Δ=119,25 – 30=89,25  ---  √Δ=9,5  ---  t=(10,92 ±9,5)/2.5  ---  considera-se o tempo maior que ocorre quando a bola já está descendo  ---  t=2,042s  ---  nesse instante a distância horizontal da linha de gol será de X=V_ocos25^o.t  ---  X=26.0,91.2,042  ---  X=48,3m.

12- Trata-se de um lançamento oblíquo, representado na figura, onde foram colocados os respectivos dados fornecidos  

no enunciado  ---  cálculo de V_oy  --- na altura máxima (H=11,25m) a velocidade vertical V_y é nula (V_y=0)  ---  equação de Torricelli  --- V_y² = V_oy² + 2.(-g).H  ---  0² = V_oy² – 2.10.11,25  ---  V_oy=√(225)  ---  V_0y=15m/s  ---  tempo de subida  ---V_y = V_oy – gt  ---  0=15 – 10t  ---  t=1,5s  ---  para que Protásio consiga alcançar a bola no mesmo nível do lançamento, ele deve alcança-la no ponto C, onde, desde que partiu, ela demora t=1,5 (metade do percurso horizontal) + 1,5s (outra metade do percurso horizontal)  ---  t=3s  ---  cálculo do alcance horizontal x lembrando que,  ---  Vox é constante e durante todo o movimento horizontal tem intensidade  V_ox=8m/s  ---  x=V_ox.t=8.3=24m  ---  aceleração de Protásio  ---  até alcançar a bola ele percorreu ∆S no mesmo tempo que a bola permaceu no ar, ou seja, t=3s  ---  ∆S=25,5 – 24 =1,5m  ---∆S= V_ot + at²/2  ---  como ele partiu do repouso, V_o=0  ---  1,5=0 + a.3²/2  ---  a=1,5/4,5  ---  a=1/3m/s²  ---  R- B

13- tg45^o=cateto oposto/cateto adjacente=D/H  ---  1=D/H  ---  D=H  --- na vertical  ---   queda livre  ---  H=gt²/2  ---  H=5t²  ---  na horizontal  ---  X=Vt  ---  X=D=H=10t  ---  10t=5t²  ---  t=2s  ---  D=H=10.2=20m  ---  R- A.

14- Cálculo do tempo na vertical que a bola demora e percorrer h=2,45m para chegar ao solo  ---  queda livre  ---  h=gt²/2  ---  2,45=10t²/2  ---  t²=0,49  ---  t=0,7s  ---  esse tempo é o mesmo com que a bola percorre a distância horizontal  x com velocidade horizontal constante V=72km/h=20m/s até alcançar o solo  ---  V=x/t  ---  20=x/0,7  ---  x=14m  ---  observe na figura que, nesse mesmo tempo t=0,7s, o rapaz que está 2,3m à frente do primeiro deve percorrer s’=20,3 – 14=6,3m com velocidade V de maneira que chegue na bola no instante em que  ela vai bater na areia  ---  V=s’/t=6,3/0,7=9m/s  ---  com qualquer velocidade acima de 9m/s o rapaz vai chegar na bola antes que ela bata na areia.

15- a) O projétil 2 deve ser lançado com a mesma velocidade horizontal que a do projétil 1 para que possa acompanhá-lo horizontalmente, ou seja, V_ox=1080/3,6=300m/s  ---  cálculo da velocidade vertical V_oy com que o projétil 2  é lançado verticalmente para cima  ---  na altura máxima V_y=0  ---  V_y² = V_oy² – 2.g.h  ---  0² = V_oy² – 2.10.1125  ---  V_oy=√22500  ---  V_oy=150m/s  ---  cálculo da velocidade V_o com que o projétil 2 é lançado  ---  Torricelli  ---  V_y² = V_ox² + V_oy²  ---

V_y² = 300² + 150²  ---V_y=335,4m/s  ---  V_oy=V_o.senθ  ---  150=335,4. senθ  ---  senθ≈0,45  ---  θ=arc sen=0,45  ---

θ ≈ 27^o.

b)

Cálculo do tempo de subida do projétil 2  ---  na altura máxima V_y=0  ---  V_y=V_oy – gt  ---  0=150 – 10t  ---  t=15s  ---  esse tempo é o mesmo que o projétil 1 se moveu na horizontal com velocidade constante V_x=300m/s  --- X=V_x.t  ---

x=300.15=4500m  ---  x=4500m  ---  na vertical a altura vale sempre  y=1125m.

16- Cálculo do tempo de subida da água que, ao atingir a altura máxima possui V_y=0  ---  V_y=V_oy.sen30^o – g.t  ---  0=10.0,5 – 10.t  ---  t=0,5s  ---  o intervalo de tempo decorrido desde quando a água sai do cano até o instante em que retorna ao solo é dado por  ---  t’=0,5 (subida) + 0,5 (descida)=1s  ---  regra de três  ---  15 litros – 60s  ---  V litros – 1s  ---  60V=15  ---  V=15/60  ---  V=0,25 litros.

17- A ordem de chegada ao solo, independente das massas , depende da altura de queda  ---  menor altura, menos tempo de queda  ---  R- C.

18- Observe nas figuras abaixo a determinação da equação da reta  ---  tgθ=18/30=0,6  ---  tgθ=y/x 

0,6=y/x  ---  y=0,6x equação do movimento (parábola)  ---  na horizontal  ---  x=V_ox.t  ---  x=v.t  ---  x=3t  ---  t=x/3 (I)  ---  na vertical é uma queda livre  ---  y=g.t²/2  ---  y=10.t²/2  ---  y=5t² (II)  ---  (I) em (II)  ---  y=5.x²/9  ---  na interseção da reta com a

parábola está o local onde a a bola tocará primeiro  ---  igualando suas equações  ---  0,4x = 5.x²/9  ---  x=0 e  ---  x=1,08m  ---  a distância percorrida na horizontal pela bola é 1,08m e, como cada degrau tem 0,3m de comprimento a bola cairá na horizontal d=1,08/0,3=3,6  ---  assim ele tocará primeiro no 4^o degrau.

Observação: se o comprimento e a altura de cada degrau tivessem as mesmas dimensões, o ângulo seria de 45^o, tgθ=1 e a equação da reta seria y=x.

19- V_o=144km/h=144/3,6  ---  V_o=40m/s  --- tempo que o saco demora para chegar ao solo na direção vertical  ---  Y=gt²/2  ---  500=5t²  ---  t=10s  ---  nesse instante o alvo deve estar a uma distância horizontal de X=V_ot=40.10  ---  X=400m  ---  R- D.

20- Cálculo de V_oy quando a bola atinge a altura máxima h_max=10m, onde V_y=0 utilizando a equação de Torricelli --- V_y² = V_oy² – 2.g.h_máx --- 0² = V_oy² – 2.10.10 --- V_oy = √(200) m/s.

Cálculo de V_ox com V_o fornecida e igual a 20m/s --- V_o² = V_ox² + V_oy² --- 20² = V_ox² + {√(200)}² ---

V_ox=√(200) m/s.

Na horizontal o movimento é uniforme com V_ox=√(200)m/s (constante) e a bola demora 2s para atingir a parede ---x=V_oxt=√(200).t=14.2 --- x≈28m.

R- B

21- O observador A, dentro do vagão observa a trajetória da pedra como um laçamento vertical para

cima e, no ponto mais alto da trajetória a velocidade da pedra é zero, pois, nesse instante ela para e em seguida começa a retornar (figura1).

O observador B do lado de fora do vagão e em repouso em relação à Terra, observa o vagão passar e vê a trajetória da bola como um arco de parábola (lançamento oblíquo) e, no ponto mais alto da trajetória a velocidade vertical é nula mas a horizontal é constante e vale V=5m/s (figura 2).

R- B

22-Trata-se de um lançamento obliquo com ângulo de 45^o com a horizontal e velocidade de V=20m/s.

Tempo que a bola demora para subir e descer na vertical com V_oy=20.√2/2=10√2m/s e quando chega novamente ao solo V_y= - 10√2m/s --- -10√2 = 10√2 – gt --- -20√2 = -10t --- t=2√2s

Esse tempo t=2√2s é o mesmo tempo que a bola demora para percorrer a distância horizontal x com velocidade constanteV_ox=V_ocos45^o=20. √2=10√2m/s --- V_ox=x/t --- 10√2=x/2√2 --- x=40m.

Nesse mesmo tempo t=2√2s o jogador deve percorrer d=57 – 40=17m com velocidade V tal que ---V=d/t=17/2√2=17/2.1,4=17/2,8 --- V=6,07m.

R- C