
Físicaevestibular.com.br
RACIOCÍNIO LÓGICO
HIDROSTÁTICA
Como esse conteúdo envolve muita teoria, em caso de dúvidas você pode encontrá-la em
fisicaevestibular.com.br – Mecânica – Hidrostática)
01-(UEPA-PA)

O peixe-gota ("Psychrolutes marcidus"), uma espécie do Pacífico que lembra um senhor velho e
amargurado,
foi eleito o animal
mais feio do mundo em
um concurso organizado na Grã-Bretanha.
O peixe-gota é capaz de suportar uma pressão máxima de 121 vezes a pressão atmosférica.
Nessas condições, a profundidade máxima em que vive este peixe, em metros, é igual a:
Dados: Pressão atmosférica = 105 N/m2; Densidade da água = 103 kg/m3; Aceleração da gravidade = 10 m/s2.
![]()
02-(UEPA-PA)

As balsas estão entre os veículos mais utilizados para transporte nos rios da Amazônia, pois

apresentam espessuras relativamente pequenas, o que lhes permite navegar em rios com trechos
de pouca profundidade.
Considere um modelo simplificado de balsa, cujo casco tem a forma de
um paralelepípedo de dimensões 30 m X 10 m X 2 m, e suponha que essa balsa esteja navegando em

um trecho de rio de 1,8 m de profundidade.
Admitindo que essa balsa tenha uma massa de 150 t e que a distância mínima de segurança do fundo do casco para o leito do rio seja de 1 m, afirma-se que a sua capacidade máxima de carga para poder navegar sem problemas nesse trecho de rio, em t, é igual a:
Dado: Aceleração da gravidade = 10 m/s2; Densidade da água = 103 kg/m3.
![]()
03-(UFPA-PA)

Uma criança brinca com um balde de água, um barquinho e uma âncora de metal.
Na situação
“A”,
a criança
coloca
o barquinho flutuando na água.

Na situação “B”, coloca o barquinho flutuando com a âncora dentro do barquinho.
Na situação “C”, joga a âncora no fundo do balde e o barquinho flutuando na superfície da água. Denotemos por NA, NB e NC, as alturas da superfície da água do balde nas situações “A”, “B” e “C” respectivamente. Use a lei de Arquimedes para determinar qual das seguintes alternativas é a correta.
(A) NA > NB > NC
(B) NC > NB > NA
(C) NB > NC > NA
(D) NA > NC > NB
(E) NC > NB > NA
04-(UFRGS-RS)

Na figura abaixo, estão representados três blocos (A, B e C) de mesmas dimensões, que estão em equilíbrio mecânico na água.

Os blocos A e B têm, respectivamente, 3/4 e 1/4 de seus volumes acima da superfície, enquanto o bloco C está totalmente submerso.
Considerando que o bloco C tem peso P, os pesos de A e B são, respectivamente,
![]()
05-(ACAFE-SC)

Buscando aumentar a resistência dos músculos de um paciente, um fisioterapeuta elaborou um
exercício de hidroginástica com o auxilio de uma bola.
O exercício consistia na atividade de baixar uma bola de raio r metros e massa 0,4 kg até que sua base ficasse a uma profundidade de h metros da superfície da água.
Após a realização do exercício algumas vezes, o fisioterapeuta observou que quando o paciente abandonava a bola daquela profundidade ela subia certa altura acima da superfície da água.
Decidiu, então, com o auxilio do gráfico abaixo, que despreza a força de resistência da água e mostra o aumento da velocidade da bola enquanto está totalmente submersa, investigar o movimento da bola, e fez algumas suposições a respeito desse movimento.
Desprezando
a resistência
do ar, considerando que a bola sobe em linha reta e utilizando o
gráfico,
verifique quais das suposições levantadas pelo fisioterapeuta estão corretas. (considere a posição zero na profundidade máxima)
l. O módulo do empuxo é maior que o módulo do peso enquanto a bola estiver toda submersa.
ll. A medida que a bola sobe de 0 até 0,50m o empuxo sobre ela diminui até que se iguala
numericamente ao peso.
Ill. De acordo com o gráfico, após o abandono da bola na profundidade indicada, até imediatamente
antes de tocar a superfície da água, a bola sofre um empuxo superior a 15 N.
lV. O empuxo sobre a bola na profundidade de 0,66m é o dobro do empuxo sobre a bola na
profundidade de 0,25m.
V. Quando a bola começa a sair da água, o empuxo que a água exerce sobre ela diminui até que se
anula, quando ela está totalmente fora da água, porém, nesse intervalo de tempo sua velocidade
aumenta para depois começar a diminuir.
Todas as afirmações corretas estão em:
![]()
06-(UECE-CE)

Considere um cubo imerso em água, conforme a figura a seguir.

No ponto destacado de uma das faces desse cubo, há uma força devido à pressão hidrostática exercida pela água. Assinale o vetor que melhor representa essa força.
![]()
07-(UECE-CE)

Três
sólidos, um
cubo,
um cilindro
e uma esfera, têm
massas
iguais e distribuídas
homogeneamente ao longo de seus volumes. Os sólidos flutuam parcialmente submersos em um
mesmo líquido. A relação entre os volumes submersos de cada objeto é
A) Δcub > Δcil > Δesf .
B) Δcub = Δcil > Δesf .
C) Δcub > Δcil = Δesf .
D) Δcub = Δcil = Δesf .
08-(UPE-PE)


Um bloco de volume V = 0,25 m3 e massa 0,05 kg está preso a um fio ideal e completamente imerso em um líquido de densidade ρ = 400 kg/m3 contido em uma caixa selada, conforme ilustra a figura.
Sabendo-se que a tensão no fio nessa situação é igual a 89,5 N, determine o módulo da reação normal da superfície superior da caixa sobre o bloco.
a) 0,0 N
b) 89,0 N
c) 910,0 N
d) 910,5 N
e) 1000,0 N
09-(PUC-SP)


Uma esfera oca de alumínio tem massa de 50g e volume de 30cm3.
O volume da parte vazia é de 10cm3. Pede-se:
a) a densidade da esfera
b) a massa específica do alumínio
10-(CEFET-MG)

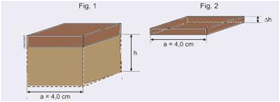
A figura 1 representa quatro barras metálicas maciças de mesmo volume.
Essas barras foram fundidas e, parcelas iguais de suas massas, usadas na construção de novas barras maciças A, B, C, D, mais finas e de diâmetros idênticos, mostradas na figura 2.

Os metais 1, 2, 3 e 4 foram usados, respectivamente, na fabricação das barras
a) C, A, B, D. b) C, B, A, D. c) B, D, C, A. d) A, D, B, C.
11-(ENEM-MEC)

Pelas
normas
vigentes, o litro do álcool hidratado que
abastece os veículos deve
ser constituído
de 96% de álcool puro e 4% de água(em volume).
As densidades desses componentes são dados a seguir.
Água = 1000 g/L álcool = 800g/L
Um técnico de um órgão de defesa do consumidor inspecionou cinco postos suspeitos de venderem álcool hidratado fora das normas.
Colheu, então uma amostra do produto de cada posto e mediu a densidade de cada uma delas.
Obteve os seguintes reusltados:

A partir desses dados, o técnico pôde concluir que estavam com o combustível adequado somente os postos
![]()
12- (UNIFOR-CE)

Um corpo sólido, de massa 90 g e volume 100 cm3, encontra-se no fundo de um recipiente de um líquido de densidade 0,60 g/cm3.

Misturando-se um outro líquido de densidade 1,5g/cm3, o corpo começa a flutuar quando a densidade da mistura, em g/cm3, for superior a:
![]()
13-(UNICAMP-SP)

O avião estabeleceu um novo paradigma nos meios de transporte.
Em 1906, Alberto Santos-Dumont realizou em Paris um vôo histórico com o 14 Bis.

A massa desse avião, incluindo o piloto, era de 300kg, e a área total das duas asas era de aproximadamente 50m2.
A
força
de sustentação
de um avião, dirigida
verticalmente
de baixo para cima, resulta
da diferença
de
pressão
entre a parte inferior e a parte superior das asas.
O gráfico representa, de forma simplificada, o módulo da força de sustentação aplicada ao 14 Bis em função do tempo, durante a parte inicial do vôo.
a) Em que instante a aeronave decola, ou seja, perde contato com o chão?
b) Qual é a diferença de pressão entre a parte inferior e a parte superior das asas, ΔP = P(inf) – P(sup) , no instante t = 20s? (g = 10 ms2)
14-(UFPR-PR)

Quatro cubos metálicos homogêneos e iguais, de aresta 10-1m, acham-se dispostos sobre um plano.
Sabe-se que a pressão aplicada pelo conjunto sobre um plano é 103 N/m2. Adotando g = 10 m/s2, calcule a densidade dos cubos.
15-(UFRJ-RJ)

Uma ventosa comercial é constituída por uma câmara rígida que fica totalmente vedada em contato com uma placa, mantendo o ar em seu interior a uma pressão Pint = 0,95x105 N/m2.
A placa está suspensa na horizontal pela ventosa e ambas estão no ambiente à pressão atmosférica usual, Patm = 1,00x105 N/m2, como indicado nas figuras a seguir.
A área de contato A entre o ar dentro da câmara e a placa é de 0,10 m2. A parede da câmara tem

espessura desprezível, o peso da placa é 40N e o sistema está em repouso.
Calcule o módulo da força vertical de contato entre a placa e as paredes da câmara da ventosa.
16-(FUVEST-SP)

Água e etanol misturam-se completamente, em quaisquer proporções.
Observa-se que o volume final da mistura é menor do que a soma dos volumes de etanol e de água empregados para prepará-la.

O gráfico acima mostra como a densidade varia em função da porcentagem de etanol (em volume) empregado para preparar a mistura (densidades medidas a 20oC).
Se 50 mL de etanol forem misturados a 50 mL de água, a 20oC, o volume da mistura resultante, a essa mesma temperatura, será de, aproximadamente,
![]()
17-(UFMG-MG)

Um
reservatório
de água é constituído de duas partes cilíndricas, interligadas,
como mostrado na figura.
A área da seção reta do cilindro inferior é maior que a do cilindro superior.
Inicialmente, esse reservatório está vazio.
Em certo instante, começa-se a enchê-lo com água, mantendo-se uma vazão constante.
Assinale a alternativa cujo gráfico MELHOR representa a pressão, no fundo do reservatório, em função do tempo, desde o instante em que se começa a enchê-lo até o instante em que ele começa a transbordar.

18-(UNESP-SP)

Para que se administre medicamento via endovenosa, o frasco deve ser colocado a uma certa altura acima do ponto de aplicação no paciente.
O frasco fica suspenso em um suporte vertical com pontos de fixação de altura variável e se conecta ao paciente por um cateter, por onde desce o medicamento.
A
pressão
na superfície livre é a pressão atmosférica; no
ponto
de aplicação no paciente, a
pressão
deve
ter um valor
maior do que a atmosférica. 
Considere que dois medicamentos diferentes precisam ser administrados.
O frasco do primeiro foi colocado em uma posição tal que a superfície livre do líquido encontra-se a uma altura h do ponto de aplicação.
Para aplicação do segundo medicamento, de massa específica 1,2 vezes maior que a do anterior, a altura de fixação do frasco deve ser outra. Tomando h como referência, para a aplicação do segundo medicamento deve - se
a) diminuir a altura de h/5.
b) diminuir a altura de h/6.
c) aumentar a altura de h/5.
d) aumentar a altura de 2h/5.
e) aumentar a altura de h/6.
19-(UFAL-AL)

Uma
torneira
aberta derrama água à vazão constante de 100 mL por segundo numa
caixa
d’água cúbica de volume 1 m3,
inicialmente vazia. 
Após algum tempo, a torneira é fechada, e a pressão medida no fundo da caixa, devido à água derramada, é igual a 103 Pa.
Considere a densidade da água e a aceleração da gravidade respectivamente iguais a 1 kg/L e 10 m/s2.
Durante quanto tempo, em segundos, a torneira permaneceu aberta?
a) 10o
b) 101
c) 102
d) 103
e) 104
20-(ENEM-MEC)

Um tipo de vaso sanitário que vem substituindo as válvulas de descarga está esquematizado na figura.
Ao acionar a alavanca, toda a água do tanque é escoada e aumenta o nível no vaso, até cobrir o sifão. De acordo com o Teorema de Stevin, quanto maior a profundidade, maior a pressão. Assim, a água desce levando os rejeitos até o sistema de esgoto.

A válvula da caixa da descarga se fecha e ocorre o seu enchimento.
Em relação às válvulas de descarga, esse tipo de sistema proporciona maior economia de água.
A característica de funcionamento que garante essa economia é devida
A) à altura do sifão de água.
B) ao volume do tanque de água.
C) à altura do nível de água no vaso.
D) ao diâmetro do distribuidor de água.
E) à eficiência da válvula de enchimento do tanque.
21-(UEG-GO) Uma maneira de observar a pressão exercida por uma "coluna de líquido" é efetuar orifícios numa garrafa plástica de dois litros (como as de refrigerante) e enchê-las de água.
A
seguir, são apresentadas
três situações experimentais bem simples.
Tendo em vista as informações apresentadas, é INCORRETO afirmar:
a) Na situação (I), com a garrafa tampada, a água não escoará, enquanto com a garrafa aberta a água jorrará pelo orifício.
b) Na situação (II), com a boca da garrafa totalmente tampada, a água não escoará pelos orifícios, porém, retirando-se a tampa, a água jorrará pelos dois orifícios.
c) Na situação (III), com a garrafa aberta, a água jorrará com menor velocidade pelo orifício superior do que pelo orifício inferior.
d) Na situação (III), tampando-se a boca da garrafa, a água jorrará apenas pelo orifício superior.
22-(UFRJ-RJ) Aristóteles acreditava que a natureza tinha horror ao vácuo.
Assim, segundo Aristóteles, num tubo como o da figura, onde se produzisse o vácuo pela elevação de um êmbolo, a água subiria até preencher totalmente o espaço vazio.
Séculos mais tarde, ao construir os chafarizes de Florença,os florentinos descobriram que a água

recusava-se a subir, por sucção mais do que 10 metros.
Perplexos, os construtores pediram a Galileu que explicasse esse fenômeno.
Após brincar dizendo que talvez a Natureza não abominasse mais o vácuo acima de 10 metros, Galileu sugeriu que Torricelli e Viviani, então seus alunos, obtivessem a explicação; como sabemos, eles conseguiram.
Com os conhecimentos de hoje, explique porque a água recusou-se a subir mais que 10 metros.
23-(UNESP-SP) Uma pessoa, com o objetivo de medir a pressão interna de um botijão de gás contendo butano, conecta à válvula do botijão um manômetro em forma de U, contendo mercúrio.
Ao
abrir
o registro R, a
pressão
do gás provoca um desnível de mercúrio no
tubo, como ilustrado na figura. Considere a pressão
atmosférica dada por 105 Pa,
o desnível h = 104 cm de Hg e a secção do tubo 2 cm2.
Adotando a massa específica do mercúrio igual a 13,6 g/cm3 e g = 10 m/s2, calcule
a) a pressão do gás, em pascal.
b) a força que o gás aplica na superfície do mercúrio em A.
(Advertência: este experimento é perigoso. Não tente realizá-lo.)
24-(FUVEST-SP) Um tanque industrial, cilíndrico, com altura total Ho = 6,0m, contém em seu interior água até uma altura ho, a uma temperatura de 27°C (300 K).
O tanque possui um pequeno orifício A e, portanto, está à pressão atmosférica Po, como esquematizado em I.
No
procedimento
seguinte, o
orifício
é fechado, sendo
o tanque
invertido e aquecido até 87°C (360 K).
Quando o orifício é reaberto, e mantida a temperatura do tanque, parte da água escoa, até que as pressões no orifício se equilibrem, restando no interior do tanque uma altura h1 = 2,0 m de água, como em II.
Determine
a) a pressão P1, em N/m2, no interior do tanque, na situação II.
b) a altura inicial ho da água no tanque, em metros, na situação I.

25-(CPS-SP) No início do século XX, a indústria e o comércio da cidade de São Paulo possibilitaram uma qualidade de vida melhor para seus habitantes.
Um dos hábitos saudáveis, ligados à higienização bucal, foi a utilização de tubos de pasta dental e as respectivas escovas de dente.
Considerando
um tubo
contendo pasta dental de densidade homogênea, uma
pessoa resolve apertá-lo.

A pressão exercida sobre a pasta, dentro do tubo, será:
a) maior no fundo do tubo, se apertar no fundo.
b) menor no fundo do tubo, se apertar perto do bico de saída.
c) maior no meio do tubo, se apertar no meio.
d) menor no fundo do tubo, se apertar no meio.
e) igual em todos os pontos, qualquer que seja o local apertado.
26-(MACKENZIE-SP)

O diagrama da figura mostra o principio do sistema hidráulico do freio de um automóvel.
Quando uma força de 50N é exercida no pedal, qual a força aplicada pelo êmbolo de 80mm² de área?
a) 100N
b) 200N
c) 300N
d) 400N
e) 500N
27-(UFRN-RN)

Do ponto de vista da Física, o sistema de freios dos carros atuais é formado por uma alavanca e por uma prensa hidráulica.
Enquanto a alavanca tem a capacidade de ampliação da força aplicada por um fator igual à razão direta de seus braços, a prensa hidráulica amplia a força da alavanca na razão direta de suas áreas. Finalmente, a força resultante aciona os freios, conforme mostrado na figura, fazendo o
veículo
parar.
Considere que a alavanca tem braço maior, L, igual a 40cm e braço menor , l, igual a 10cm, e a prensa hidráulica apresenta êmbolos com área maior, A, oito vezes maior que a área menor, a. Levando em consideração as características descritas acima, tal sistema de freios é capaz de fazer a força exercida no pedal dos freios, pelo motorista, aumentar
![]()
28-(FUVEST-SP) Um recipiente cilíndrico vazio flutua em um tanque de água com parte de seu volume submerso, como na figura (fig. 1).
O recipiente possui marcas graduadas igualmente espaçadas, paredes laterais de volume desprezível e um fundo grosso e pesado.
Quando o recipiente começa a ser preenchido, lentamente, com água, a altura máxima que a água pode atingir em seu interior, sem que ele afunde totalmente, é melhor representada por

29-(UFSM-RS)
A
posição
dos peixes ósseos e
seu equilíbrio
na água são
mantidos, fundamentalmente,
pela
bexiga
natatória que eles possuem.
Regulando a quantidade de gás nesse órgão, o peixe se situa mais ou menos elevado no meio aquático.
"Para _______________ a profundidade, os peixes ______________ a bexiga natatória e, com isso, _______________ a sua densidade."
Selecione a alternativa que preenche corretamente as lacunas.
a) aumentar - desinflam – aumentam
b) aumentar - inflam – diminuem
c) diminuir - inflam - aumentam
d) diminuir - desinflam – diminuem
e) aumentar - desinflam – diminuem
30-(UFSM-RS) Na Figura (I), um recipiente com água está sobre uma balança que marca um certo valor P para o peso do conjunto (água + recipiente).
Coloca-se uma esfera de chumbo imersa na água do recipiente suspensa por um fio ideal, como mostra a Figura (II). Assinale a(s) alternativa(s) correta(s).
(01)
Na
situação da Figura
(II), a
balança marca um peso P mais o peso da esfera de chumbo.
(02) Na situação da Figura (II), a balança marca um peso igual a P.
(04) Na situação da Figura (II), a balança marca um peso P mais o peso da água deslocada pela esfera de chumbo.
(08) Na situação da Figura (II), a balança marca um peso igual a P mais o peso da esfera de chumbo menos a tensão do fio.
(16) Na situação da figura (II), a balança marca um peso igual a P menos a tensão do fio.
31-(UFPE-PE)

Um bloco homogêneo e impermeável, de densidade d = 0,25 g/cm3, está em repouso, imerso em um tanque completamente cheio de água e vedado, como mostrado na figura.
Calcule a razão entre os módulos da força que o bloco exerce na tampa superior do tanque e do peso do bloco.
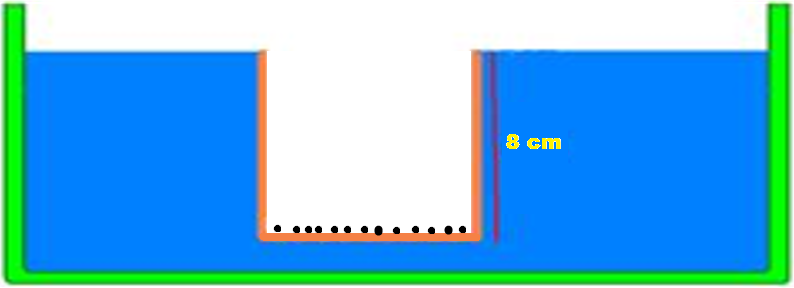
32-(UNESP-SP) A figura representa um recipiente cilindrico vazio flutuando na água, em repouso. A área da base desse cilindro é 80cm2.

a) Qual a massa desse recipiente?
b) Suponha que uma estudante coloque, um a um, chumbinhos de pesca iguais, de 12g cada um, dentro desse recipiente, mantendo sua base sempre horizontal. Qual o número máximo de chumbinhos que podem ser colocados nesse recipiente sem que ele afunde?
c) Ultimamente, têm sido detectados fortes indícios de que já houve água no estado líquido em Marte.
Se essa experiência fosse feita em Marte, seus resultados mudariam? Justifique. Suponha que a densidade e o estado físico da água permaneçam inalterados. (Dados: dágua = 1.000kg/m3; gTerra = 10 m/s2 e gMarte = 3,7 m/s2)
33-(UFRJ-RJ) Realizando um experimento caseiro sobre hidrostática para seus alunos, um professor pôs, sobre uma balança, um recipiente graduado contendo água e um pequeno barco de brinquedo, que nela flutuava em repouso, sem nenhuma quantidade de água em seu interior.
Nessa
situação, a turma
constatou que a balança indicava uma massa M1 e
que a altura
da água no recipiente era h1.

Em dado instante, um aluno mexeu inadvertidamente no barco. O barco encheu de água, foi para o fundo do recipiente e lá permaneceu em repouso.
Nessa nova situação, a balança indicou uma massa M2 e a medição da altura da água foi h2.
a) Indique se M1 é maior, menor ou igual a M2. Justifique sua resposta.
b) Indique se h1 é maior, menor ou igual a h2. Justifique sua resposta.
34-(ITA-SP)
Um
cubo
maciço homogêneo com 4,0 cm de aresta flutua
na água
tranquila de uma pequena lagoa, de
modo a manter
70% da área total da sua superfície em contato com a água,
conforme
mostra a figura.
A seguir, uma pequena rã se acomoda no centro da face superior do cubo e este se afunda mais 0,50 cm na água.
Assinale a opção com os valores aproximados da densidade do cubo e da massa da rã, respectivamente.
a) 0,20 g/cm3 e 6,4 g
b) 0,70 g/cm3 e 6,4 g
c) 0,70 g/cm3 e 8,0 g
d) 0,80 g/cm3 e 6,4 g
35-(UFG-GO)

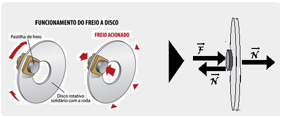
Os carros modernos utilizam freios a disco em todas as rodas, e o acionamento é feito por um

sistema hidráulico fechado, que é acionado quando o motorista pisa no pedal de freio.
Neste sistema, ao mover o pistão, as pastilhas de freio entram em contato com o disco nos dois lados.
Considere que um carro de 500 kg, viajando a uma velocidade de 20 m/s, precisa parar imediatamente.
O motorista o faz sem deslizamento dos pneus, dentro de uma distância de 20 m. Considerando-se o exposto, calcule:
a) A força média com que cada pistão pressiona o disco de freio. Use 0,8 como o coeficiente de atrito entre a pastilha e o disco.
b) A pressão do óleo que empurra o pistão. Use o diâmetro de 4 cm para esse pistão.
36-(UFJF-MG)

Os
pneus
dianteiros
de um automóvel
foram calibrados com 30 lb/pol² (21.104N/m²)
e os pneus traseiros com 32 lb/pol² (22.104N/m²).
A área de contato dos pneus com o solo é cerca de 110 cm² em cada um deles.
Sabe-se que a pressão indicada pelo calibrador é a diferença entre a pressão interna e a pressão atmosférica.
a) É possível estimar o peso de um automóvel conhecendo a pressão dos pneus e a área de contato dos mesmos com o solo? Justifique por quê.
b) Calcule o peso aproximado do automóvel do exemplo citado.
Resoluções comentadas dos exercícios de vestibulares sobre
Hidrostática
01-

Aplicando o teorema de Stevin --- pressão hidrostática devido apenas à altura da coluna de água --- P=dágua.g.h --- Pmáx=120Patm --- 120.Patm= dágua.g.h --- 120.105 = 103.10.h --- h=120.105/104 --- h=1200m.
R- C
02- Cálculo da altura h da parte imersa com a balsa de massa m=150000kg sem carga --- o empuxo E, força vertical e para cima corresponde ao peso do volume de líquido deslocado, no caso, o volume de um paralelepípedo de comprimento 30m, largura 10m e altura h --- E=dágua.g.Vimerso --- E=103.10. (30.10.h) --- E=300.104h.
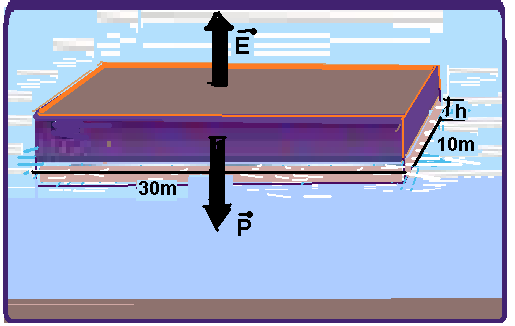
Peso da balsa sem carga --- P=mg=150.103.10 --- P=150.104N.
Estando a balsa em equilíbrio vertical, flutuando, o peso deve anular o empuxo --- P = E --- 150.104 = 300.104h --- h=150/300 ---h=0,5m (altura da balsa imersa com ela descarregada).
Observe atentamente na figura que, quando a carga de peso P’ for colocada, a balsa deve afundar
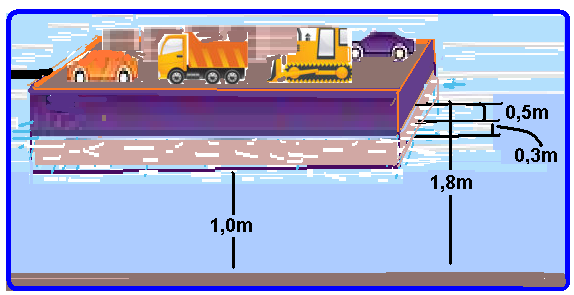
mais 0,3m, pois distância mínima de segurança do fundo do casco para o leito do rio deve ser de 1m.
Assim, o volume de água deslocado por essa carga corresponde ao de um paralelepípedo de comprimento 30m, largura 10m e altura h’=0,3m --- V’=30.10.0,3=90m3 e o empuxo produzido será:
E’=dágua.V.g=103.90.10 --- E’=90.104N.
Esse empuxo é igual ao peso da carga colocada sobre a balsa P’=90.104N.
R- D
03- O empuxo (força vertical e para cima) é igual ao peso do volume de líquido deslocado e assim, quanto maior o pesomaior será o volume de líquido deslocado e consequentemente, maior será a altura da superfície da água do balde.
Maior peso B (barco + âncora dentro, deslocam maior volume de água) --- menor peso A (barco sem
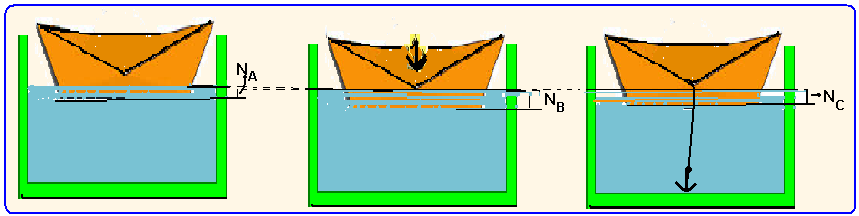
âncora, desloca menor volume de água) --- intermediário C (volume deslocado somente pelo barco ) + volume deslocado somente pela âncora).
R- C
04- Bloco C totalmente imerso Vimerso=Vcorpo e em equilíbrio mecânico --- Ec = Pc=P --- dágua.vimerso.g =P (I).
Bloco A 1/4 imerso e em equilíbrio mecânico --- EA= PA --- dágua.Vimerso.g = dágua.(1/4)V.g=PA --- compare com (I) --- P/4 = PA.
Bloco B 3/4 imerso e em equilíbrio mecânico --- EA= PA --- dágua.Vimerso.g = dágua.(3/4)V.g=PA --- compare com (I) --- 3P/4 = PA.
R- B.
05- I. Correta --- veja pelo gráfico que, enquanto totalmente submersa ela sobe com aceleração constante e sujeita a umaforça resultante para cima sendo que, nesse caso, o módulo do empuxo
(força
vertical e para cima) deve ser maior que o módulo do
peso (força vertical e para baixo).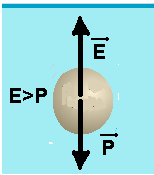
II. Falsa --- de 0 a 0,5m a bola está totalmente imersa e o empuxo de intensidade E=dágua.Vbola.g é constante, pois todas as grandezas (dágua.Vbola.g) são constantes.
III. Correta --- enquanto totalmente imersa a bola, que partiu do repouso Vo=0 e, após subir h=0,5m atingiu V=7m/s até chegar à superfície, subindo com aceleração de valor --- equação de Torricelli --- V2 = Vo2 + 2.a.h --- 72 = 02 + 2.a.0,5 --- a=49m/s2.
Como ela sobe o módulo do empuxo é maior que o módulo do peso --- FR=m.a --- E – P = m.a ---
E – mg = m.a --- E – 0,4.10 = 0,4.49 --- E= 19,6 + 4 --- E=23,6N.
IV. Falsa --- veja (II)
V. Correta --- a medida que a bola vai saindo da água o empuxo (peso do volume de líquido deslocado) vai diminuindo até que, quando ela está totalmente fora da água, não desloca mais água e o empuxo é nulo.
A respeito das velocidades veja figuras abaixo:
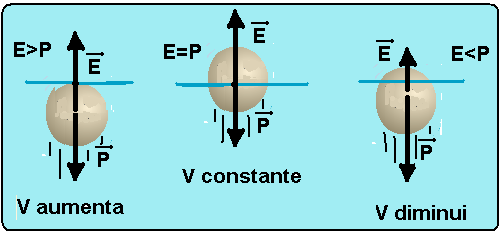
R- C
06- Pressão
(P) é uma grandeza física obtida pelo quociente entre a
intensidade da força (![]() )
e a área (S) em que a força se distribui. Observe
na figura abaixo que a força (
)
e a área (S) em que a força se distribui. Observe
na figura abaixo que a força (![]() )
que produz a pressão sobre a área S é perpendicular à mesma.
)
que produz a pressão sobre a área S é perpendicular à mesma.
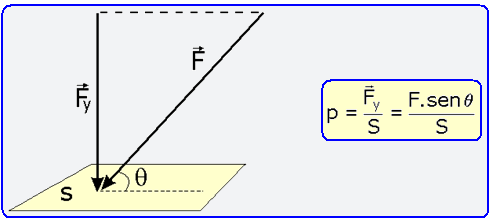
No caso do exercício a força é a hidrostática, devida à pressão hidrostática e também é
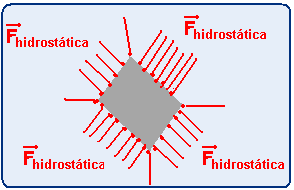
perpendicular à área da superfície em cada ponto.
R- A.
07- Peso de cada corpo --- Pc=dc.vcg=mcg --- Empuxo de cada corpo --- E=dL.Vi.g --- como estão flutuando estão em equilíbrio e P = E --- mc.g = dL.Vi.g --- Vi=mc/dL --- como a massa do corpo é a mesma e o líquido é o mesmo (mesma dL) o volume imerso é o mesmo para os três sólidos.
R- D
08- Peso do bloco --- P=mg=0,05.10 --- P=0,5N.
Força de tensão no fio --- fornecida T=89,5N.
Empuxo --- E=ρ.V.g=400.0,25.10 --- E=1000N.
Na figura abaixo estão colocadas todas as forças que agem sobre o bloco que, como está em
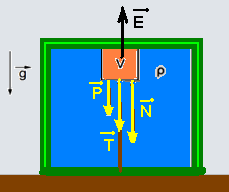
equilíbrio a força resultante sobre ele deve ser nula e, para que isso ocorra --- E = P + T + N ---
1000 = 89,5 + 0,5 + N --- N=910N.
R- C
08- Em cada litro de álcool hidratado têm-se --- 0,96L de álcool (96%) e 0,04L de água (4%) --- massa de álcool --- dálcool=málcool/Válcool --- 800g/L=málcool/0,96L --- málcool=768g --- massa de água --- dágua=mágua/Vágua --- 1.000g/L=mágua/0,04L --- mágua=40g --- dmistura=(málcool +mágua)/Vmistura=(768 + 40)/1 --- dmistura=808g/L --- R- E
09- a) a densidade da esfera leva em conta o volume total --- d=m/v=50/30 --- d=1,7g/cm3
b) a massa específica leva em conta apenas a parte de volume que contém alumínio --- ρ=m/v=/50(30 – 10) --- ρ=2,5g/cm3
10- figura 1 --- sendo o mesmo volume, o corpo de maior massa terá maior densidade --- d4>d1>d3>d2 --- figura 2 --- d=m/V --- como a massa é a mesma para cada bloco, aquele que tiver maior densidade terá menor volume --- V4<V1<V3<V2 --- 4(A); 1(B); 3(C) e 2(D) --- R- C
11- Em cada litro de álcool hidratado têm-se --- 0,96L de álcool (96%) e 0,04L de água (4%) --- massa de álcool --- dálcool=málcool/Válcool --- 800g/L=málcool/0,96L --- málcool=768g --- massa de água --- dágua=mágua/Vágua --- 1.000g/L=mágua/0,04L --- mágua=40g --- dmistura=(málcool +mágua)/Vmistura=(768 + 40)/1 --- dmistura=808g/L --- R- E
12- Quando o corpo estiver na iminência de flutuar, a densidade do corpo é igual à do líquido (mistura) --- dmistura=dcorpo=m/V=90/100 --- d=0,9g/cm3 --- R- A
13- a) O avião decola a partir do instante de t=10 s, pois é a partir deste instante que a força de sustentação supera o peso da aeronave, que é de 3000 N.
b) Pelo gráfico em t = 20s tem-se uma força de sustentação F = 3000 N --- essa força atua sobre uma área de S=50m2 --- Δp = F/S = 3000/50 --- ΔP=60N/m2=60Pa
14- A área de contato é a do cubo inferior --- S=10-1.10-1 --- S=10-2m2 --- P=F/S --- 103=F/10-2 --- F=10N=peso dos 4 cubos ---cada cubo tem p=10/4=2,5N --- m=2,5/10 --- m=0,25kg --- d=m/V =0,25/10-3 --- d=250kg/m3
15- Pint =
0,95.105N/m2
--- Patm =
1,00.105 N/m2
--- A = 0,10 m2
--- P = 40 N --- na placa agem as seguintes forças
--- P- peso da placa --- F- força devida à
diferença entre as pressões externa e interna na câmara ---
N - força vertical de contato entre as paredes da câmara
e a placa --- essas forças são mostradas na figura: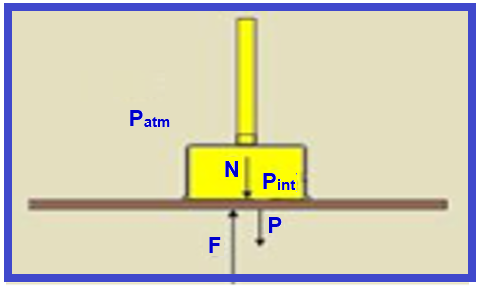
A resultante das forças que agem sobre a placa é nula, pois ela está em equilíbrio --- N + P = F --- N=F – P=(Patm – Pint).A - P --- N=(1,00 – 0,95).105.(0,10) – 40=500 – 40 --- N=460N
16- Sendo a densidade da água dágua=1,00g/mL (quando você tem 0% de etanol) --- 1,00g – 1mL --- mágua g --- 50mL --- mágua =50g --- sendo a densidade do etanol detanol=0,79g/mL(quando você tem 100% de etanol) --- 0,79g – 1mL --- metanol g --- 50mL --- metanol =39,5g --- massa total de água a 20oC --- mtotal= 50g (água) + 39,5g (etanol)=89,5g (água + etanol) --- se você observar no gráfico verá que a densidade da mistura que contém 50% de etanol vale dmistura=0,93g/mL --- dmistura=mmistura/Vmistura --- 0,93 = 89,5/Vmistura --- Vmistura≈ 96 mL --- R- E
17- A pressão no fundo do recipiente varia linearmente com a altura e independe da área de seção reta de cada cilindro --- R- A
18- P1=ρ.g.h --- P2=1,2ρ.g.h’ --- P1/P2=ρ.g.h/1,2ρ.g.h’ --- P1=P2=P --- 1= ρ.g.h/1,2ρ.g.h’ --- h’=1/1,2h10/12h=5/6h --- h – 5/6h=(6h – 5h)/6=h/6 --- h’=h/6 --- R- B
19- Dados --- Z = 100 mL/s = 0,1 L/s --- d = 1 kg/L = 103 kg/m3 --- Pcol.deágua = 103Pa --- g = 10 m/s2 --- pelo teorema de Stevin a pressão da coluna líquida é --- Pcol.deágua =dgh --- 103=103.10.h --- h=0,1m --- caixa cúbica de volume 1m3 tem área da base Ab=1m2 --- cálculo do volume derramado --- V=Ab.h=1.(0,1) --- V=0,1m3=100L --- a vazão (Z) é a razão entre o volume derramado e o tempo --- Z=V/Δt=100/0,1 --- Δt=103s --- R- D
20- Teorema de Stevin --- observe a figura abaixo:
![]() Teorema
de Stevin --- A pressão no ponto B devida apenas à
coluna líquida Plíquido=dlíquido.g.h é
chamada depressão hidrostática e PB=Patm + dlíquido.g.h é
chamada de pressão total, pressão absoluta ou simplesmente pressão.
Teorema
de Stevin --- A pressão no ponto B devida apenas à
coluna líquida Plíquido=dlíquido.g.h é
chamada depressão hidrostática e PB=Patm + dlíquido.g.h é
chamada de pressão total, pressão absoluta ou simplesmente pressão.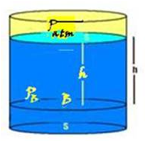
![]() A
pressão exercida por uma coluna líquida não depende das dimensões
do recipiente que a contém, mas apenas da natureza do líquido,
fornecida pela sua densidade (d), do local (g) e da altura da coluna
(h).
A
pressão exercida por uma coluna líquida não depende das dimensões
do recipiente que a contém, mas apenas da natureza do líquido,
fornecida pela sua densidade (d), do local (g) e da altura da coluna
(h).
![]() O
gráfico da pressão total P em função da altura “profundidade”
h, (P=Patm+ d.g.h, que é uma função do primeiro
O
gráfico da pressão total P em função da altura “profundidade”
h, (P=Patm+ d.g.h, que é uma função do primeiro
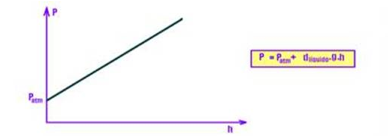
grau)), é uma reta inclinada.
![]() A
pressão devido á coluna líquida é maior quanto maior for a
profundidade, ou seja, a maior a altura da coluna líquida,
A
pressão devido á coluna líquida é maior quanto maior for a
profundidade, ou seja, a maior a altura da coluna líquida,
Observe na teoria acima, que a pressão que a água deve exercer para acionar o sifão depende apenas da altura da coluna líquida, não dependendo das dimensões do recipiente, ou seja, do

volume de água nele armazenada --- assim, mesmo um pequeno volume de água armazenado, mas com altura suficiente pode acionar o sifão --- portanto, a economia deve-se ao volume de água armazenada no tanque --- R- B.
21- A alternativa incorreta é a D, pois com a boca da garrafa totalmente tampada a água não jorrará por nenhum dos dois orifícios, pois a pressão externa é maior que a interna --- R- D
22-
Observe
na figura abaixo que a pressão na superfície da água (ponto Q) é
a mesma que aquela devido à altura da coluna de água (ponto p)
--- PQ=Pp
--- densidade dágua=103kg/m3 e
g=9,8m/s2
--- PQ= Patm
--- Pp==dágua.g.hágua
--- 1,01.105=103.9,8.hágua
--- hágua=10,3m
--- portanto, a pressão atmosférica equilibra uma coluna de
água de altura aproximadamente 10m e, essa pressão não consegue
empurrar qualquer coluna de água a uma altura superior a 10m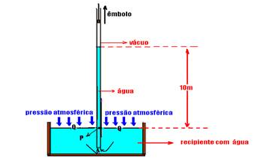
23- a)
A pressão do gás no botijão é a mesma que no ponto A (PA=Pgás),
que por sua vez é a mesma que no ponto M --- Pgás=PM
--- Pgás=Patm + dHg.g.h=105 +
13,6.103.10.1,04
--- Pgás=105 +
14,44.104
--- Pgás=1,0.105 +
1,44.105
--- Pgás=2,44.105 Pa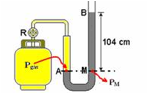
b) Em a --- Pgás=F/S --- 2,44.105=F/2.104 --- F=48,8N
24- a) Na figura II, na extremidade do orifício de altura h1=2,0m a pressão que atua é a pressão atmosférica Po=1,0.105N/m2 --- Po=dgh1 + P1 --- 1,0.105=1,0.103.10.2,0 + P1 --- P1=1,0.105 – 2,0.104 --- P1=8,0.104N/m2
b) Chamando de S a área da base do tanque --- lei geral dos gases perfeitos --- Po.Vo/To=P1.V1/T1 --- 1,0.105.S(6,0 – ho)/300 = 8,0.104.S.(6,0 – 2,0)/360 --- ho=10/3 m=3,3m
25- Princípio enunciado por Pascal, físico e matemático francês (1623 – 1663), conhecido como princípio de Pascal:
“ O acréscimo de pressão exercido num ponto de um líquido ideal em equilíbrio é transmitida integralmente a todos os pontos desse líquido e também às paredes do recipiente onde está contido” --- R- E
26- Força (F1) ampliada pelo sistema de articulações quando no pedal é aplicada a força F=50N
--- colocando o pólo O na articulação central e lembrando que a soma dos momentos das forças em
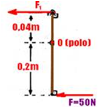
relação ao pólo é nula --- - F.d1 + F1.d2=0 --- 50.0,2 + F1.0,04=0 --- F1=250N --- essa força é transmitida até o êmbolo 1 de área S1=40mm2=4.10-5m2 que está ligado, por meio de vaso comunicante até o êmbolo 2 de área S2=80mm2=8.10-5m2 --- aplicando o teorema de Pascal
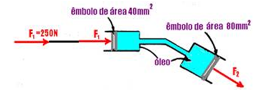
nos êmbolos 1 e 2 --- F1/S1=F2/S2 --- 250/4.10-5=F2/8.10-5 --- F2=500N --- R- E
27- Seja F a força aplicada pelo motorista no pedal --- pelo enunciado a alavanca tem a
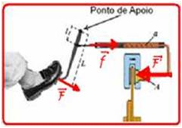
capacidade de ampliação da força aplicada por um fator igual à razão direta de seus braços, que é de 40/10=4 vezes --- f=4F --- a prensa hidráulica amplia a força f na razão direta de suas áreas, ou seja, de 8 vezes --- F’=8f --- F’=8.4F --- F’=32F --- R- A.
28- Sendo o líquido que envolve o recipiente a água e o líquido que o está preenchendo também a água (mesma densidade), para cada unidade preenchida com água, o recipiente desce também uma
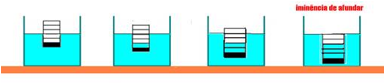
unidade --- Observe atentamente a sequência de figuras abaixo e verifique que a resposta é a C
R- C
29- A maioria dos peixes ósseos apresenta bexiga natatória (atualmente denominada vesícula gasosa), uma bolsa cheia de gases acima do estômago cujo volume é regulado por meio de trocas de gases com o sangue e, pela sua dilação ou contração, determina a posição do peixe na água. Para aumentar a profundidade, os peixes contraem a bexiga natatória e, com isso, aumentam a sua densidade tornando-se mais pesado que a água e descendo. Ao subir, fazem o contrário.
R- A
30- Na figura I, No é a indicação da balança --- No=P
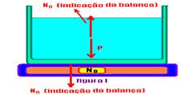
Na figura II, se o corpo imerso recebe do líquido uma força vertical e para cima (Empuxo), pelo princípio da ação e reação o corpo reage sobre o líquido com força de mesma intensidade (Empuxo), mesma direção (vertical) e sentido sentido contrário (para baixo).
A
balança indica apenas as forças que agem no líquido, indicadas na
figura da direita acima, que são: peso P do sistema (recipiente mais
líquido), empuxo sobre o líquido (E) e a reação normal da balança
(indicação da balança N) --- N=P + E ---
da figura I --- No=P
--- N=No +
E --- N
– No=E ---
assim, o
empuxo é fornecido pela diferença entre as indicações da balança
antes e depois de imergir a esfera.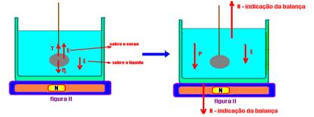
R- (4 + 8)=12
31-
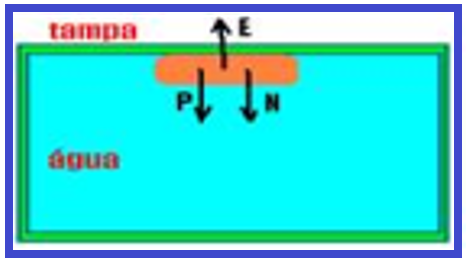
Forças que agem sobre o bloco --- peso P (vertical e para baixo) --- N força que o bloco troca com a tampa (vertical e para baixo) --- empuxo E (vertical e para cima) --- P + N=E --- mg + N=d.V.g --- dbloco.V..g + N=dágua.V.g --- N=dágua.V.g – dbloco.V.g --- N=(1,0.103 – 0,25.103).V.g --- N=0,75.103.V.g --- P= 0,25.103.V..g --- N/P=(0,75.103.V.g)/(0,25.103.V.g) --- N/P=3
32- a) volume de água deslocada --- Vimerso=S.H=8.10-3.5.10-2 --- Vimerso=4.10-4m3 --- estando o recipiente em equilíbrio --- P=E --- mg=dágua.Vimerso.g --- m=1.000.4.10-4 --- m=0,4kg
b) nesse caso, o recipiente está na iminência de afundar, e sua massa será mc (massa dos
chumbinhos) + m (massa do recipiente) --- Vimerso= S.h=8.10-3.8.10-2 --- Vimerso=64.10-5m3 --- peso do recipiente + peso dos chumbinhos=Ps=(m + mc).g --- equilíbrio --- Ps=E --- (m + mc).g=dágua.Vimerso.g --- (0,4 + mc)=1.000.64.10-5 --- mc=0,64 – 0,4 --- mc=0,24kg=240g --- nchumbinhos=240/12 --- nchumbinhos=20
c) não mudariam --- observe na expressão seguinte que a aceleração da gravidade se cancela --- P=E --- dcVc.gmarte=dágua.Vágua.gmarte --- assim , g não interfere na rwesolução.
33- a) A massa do recipiente, da água e do barquinho sobre a balança é a mesma, quer o barquinho esteja flutuando, quer esteja submerso. Portanto, M1 = M2 .
b) Quando o barquinho está flutuando, o empuxo sobre ele é igual a seu peso e, portanto, maior do que o empuxo quando submerso. Sendo maior o empuxo no barquinho flutuando, o volume da água por ele deslocado nesse caso é maior do que o volume da água por ele deslocado quando está submerso. Uma vez que o volume dentro do recipiente sob o nível da superfície livre da água é o volume da água acrescido do volume de água deslocado, concluímos que o volume dentro do recipiente sob o nível da superfície livre é maior com o barquinho flutuando do que com o barquinho submerso. Assim,a altura da superfície livre com o barquinho flutuando é maior do que a altura da superfície livre com o barquinho submerso, ou seja, h1 > h2 .
34- Veja figuras --- a = 4 cm --- dágua = 1 g/cm3 --- Aimersa = 0,7.Atotal --- Δh = 0,50 cm --- a área
imersa é a área do fundo mais uma parte da área das 4 paredes laterais, de altura h --- de acordo com o enunciado --- Aimersa=0,7ªtotal --- a2 + 4ah=0,7.6.a2 ---
4 h = 3,2 a --- h = 0,8 a --- como o cubo é um sólido reto e está em equilíbrio em água, seu peso é equilibrado pelo empuxo:
P
= E --- dcubo.Vtotal.g = dágua.Vimerso.g
--- dcubo/dágua=Vimerso/Vtotal
--- dcubo/1=a2h/a3
--- dcubo=a2.0,8ª/a3
--- dcubo=0,80
g/cm3 ---
o aumento do empuxo equilibra o peso da rã --- Pr=ΔE --- mg=dágua.ΔV.g --- m=dágua.A.Δh --- m=1,0.16.0,5 --- m=8,0g ---
R- E
35- a) Dados --- m=500kg --- Vo=20m/s --- V=0 --- ∆S=20m --- cálculo do módulo da aceleração de retardamento do carro aplicando a equação de Torricelli --- V2=Vo2 + 2.a.∆S --- 02 = 202 + 2.a.20 --- a=-400/40= - 10m/s2 em módulo --- a=10m/s2 --- intensidade da força resultante --- FR=ma --- Fm=500.10=5000N --- cada pistão recebe uma força de F’=5000/4=1250N --- como o disco de freio
é comprimido pela pastilha nos dois lados pela força pedida de intensidade N (força com que a pastilha pressiona o freio de disco) --- F’=2N --- 1250=Fat=μ.2N --- N=1250/2μ --- N=1250/2.08=1250/1,6 --- N=781,25N.
b) Área do pistão --- S=π.R2=3.(2.10-2)2=12.10-4m2 --- P=F/S=781,25/12.10-4 --- P=6,5.105Pa.
36- a) Sim; conhecendo a pressão manométrica (o quanto a pressão interna é maior que a externa) e a área de contato com o solo, é possível conhecer a força resultante exercida pela pressão sobre o solo. No equilíbrio e no plano horizontal, essa força é igual em módulo à força de reação que o solo exerce sobre o pneu. Somando-se as forças de reação do solo sobre todos os pneus, encontramos a força de reação total do solo. Na situação de equilíbrio, e no plano horizontal, essa força de reação total do solo é igual em módulo à força peso do automóvel.
b)A área de contato de cada um dos 4 pneus com o solo vale --- S=110cm2=110.10-4m2 --- força exercida pelos dois pneus dianteiros --- um pneu --- Pd=Fd/S --- 21.104=Fd/110.10-4 --- Fd = 2310N --- como são dois pneus --- Fd=4 620N --- força exercida pelos dois pneus traseiros --- um pneu --- Pd=Fd/S --- 22.104=Fd/110.10-4 --- Fd = 2 240N --- como são dois pneus --- Fd=4 480N --- a soma dessas 4 forças correspondem ao peso do automóvel --- P = 4 620 + 4 480 --- P= 9 460N.