
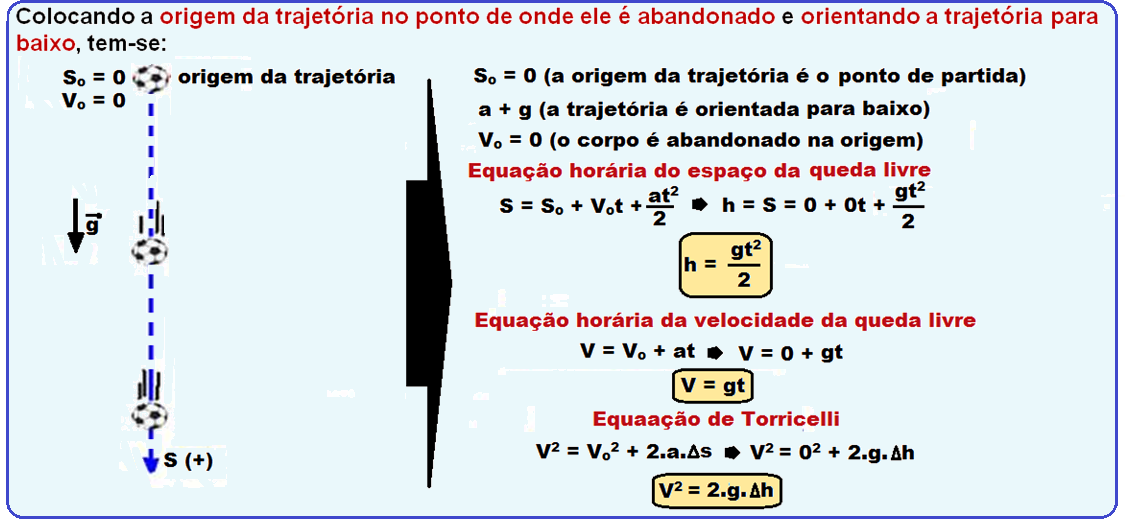
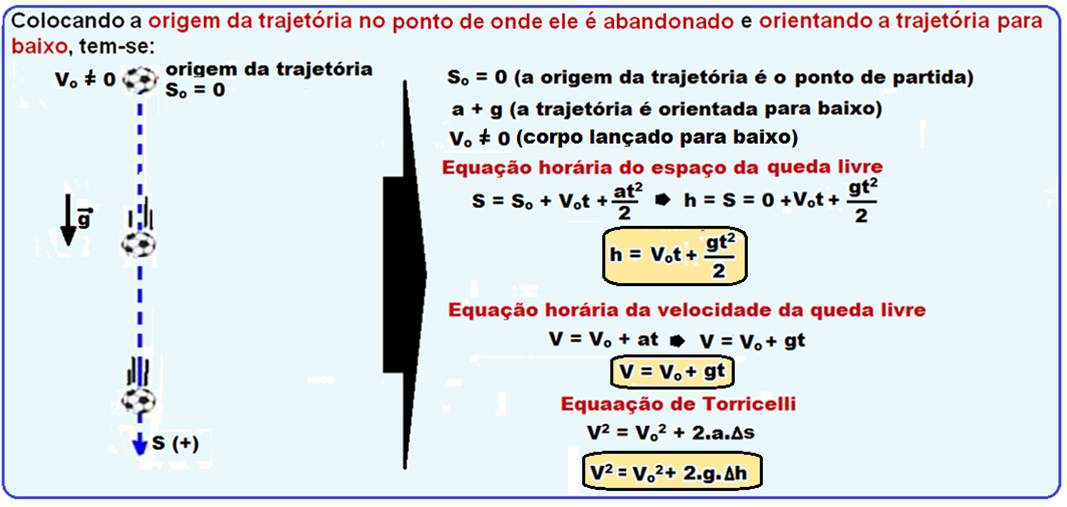
Qualquer corpo abandonado a partir do repouso (Vo = 0), ou lançado verticalmente para baixo com velocidade inicial Vo ≠ 0, descreve um movimento uniformemente acelerado, com aceleração a=g.
![]()
![]()
![]()
![]() A aceleração
da gravidade g
varia com a latitude
e altitude,
mas, próximo
à superfície da Terra,
pode-se considerá-la como constante
e de valor g=10m/s2.
Mas, lembre-se de que medida a uma
A aceleração
da gravidade g
varia com a latitude
e altitude,
mas, próximo
à superfície da Terra,
pode-se considerá-la como constante
e de valor g=10m/s2.
Mas, lembre-se de que medida a uma

latitude de 45o e ao nível do mar chamada de, ela é aceleração normal da gravidade e vale g=9,80655m/s2.
![]() Na resolução
de exercícios de movimentos de corpos sob a ação da gravidade
pode-se desprezar
a resistência do ar desde que os corpos possuam grandes densidades,
pequenas dimensões e caiam de alturas não muito elevadas em relação
ao nível do mar.
Na resolução
de exercícios de movimentos de corpos sob a ação da gravidade
pode-se desprezar
a resistência do ar desde que os corpos possuam grandes densidades,
pequenas dimensões e caiam de alturas não muito elevadas em relação
ao nível do mar.
![]() Se um objeto
é de outro que abandonado do interior está descendo com velocidade
Vo,
deve-se considerar como se o objeto
estivesse sendo lançado verticalmente para baixo com velocidade Vo.
Se um objeto
é de outro que abandonado do interior está descendo com velocidade
Vo,
deve-se considerar como se o objeto
estivesse sendo lançado verticalmente para baixo com velocidade Vo.
Exemplo
![]() Um
helicóptero
desce verticalmente em movimento uniforme com velocidade
constante
Um
helicóptero
desce verticalmente em movimento uniforme com velocidade
constante

de 50km/h, quando um pedra é abandonada de seu interior. Nesse caso, a pedra, ao abandonar o helicóptero tem a velocidade dele, ou seja, Vo=50km/h.
![]() Corpos abandonados
com Vo=0
ou lançados
verticalmente para baixo com Vo≠0
de um mesmo
local
e da mesma altura
(desprezando-se os efeitos do ar) demoram
o mesmo tempo para chegar ao solo, independente de suas massas.
Corpos abandonados
com Vo=0
ou lançados
verticalmente para baixo com Vo≠0
de um mesmo
local
e da mesma altura
(desprezando-se os efeitos do ar) demoram
o mesmo tempo para chegar ao solo, independente de suas massas.

A velocidade com que eles chegam ao solo também é a mesma.
![]() A aceleração da gravidade
g varia conforme o planeta, assim, cada planeta tem seu determinado
g.
A aceleração da gravidade
g varia conforme o planeta, assim, cada planeta tem seu determinado
g.

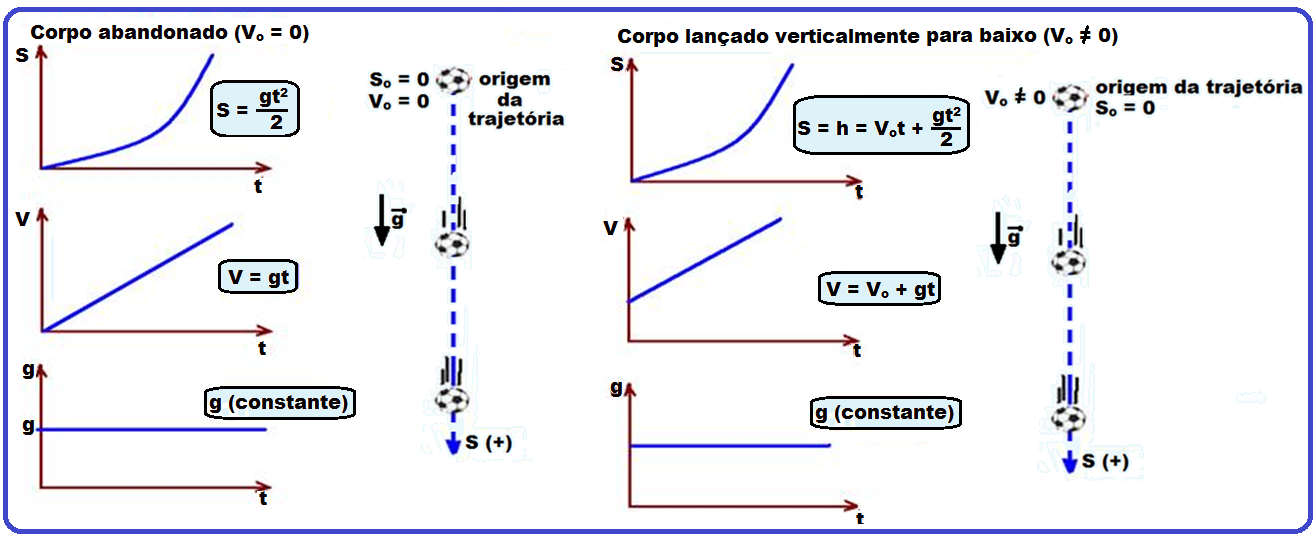
![]() Gráficos da queda livre,
com o corpo partindo da
origem
e a trajetória
orientada
para baixo.
Gráficos da queda livre,
com o corpo partindo da
origem
e a trajetória
orientada
para baixo.
![]() Quando se abre
uma torneira
de forma que saia
apenas um "filete"
de água, a área
da seção
reta
do filete de água abaixo
da boca da torneira é tanto menor quanto mais distante dela,
porque como a velocidade
da
água distante da boca da torneira é maior
devido
Quando se abre
uma torneira
de forma que saia
apenas um "filete"
de água, a área
da seção
reta
do filete de água abaixo
da boca da torneira é tanto menor quanto mais distante dela,
porque como a velocidade
da
água distante da boca da torneira é maior
devido

à ação da gravidade, para que haja conservação da massa, a área da seção reta do filete tem que ser menor.
![]() Proporções
de Galileu para queda livre com Vo=0
e desprezando-se
a resistência do ar:
Proporções
de Galileu para queda livre com Vo=0
e desprezando-se
a resistência do ar:
Para intervalos de tempos iguais e consecutivos, um corpo em queda livre percorre distâncias cada vez maiores, na proporção dos
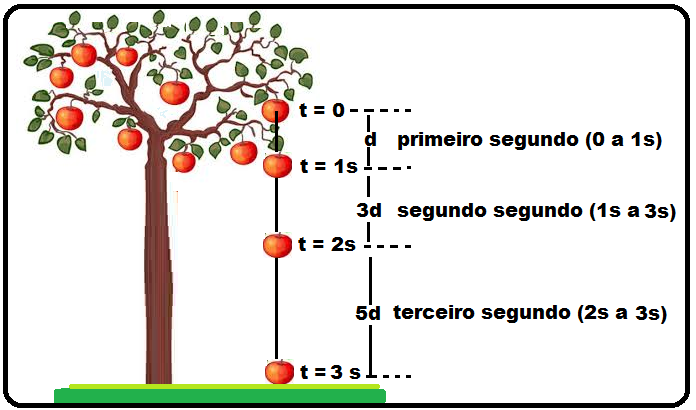
vez maiores, na proporção dos ímpares consecutivos: no primeiro segundo, o móvel cai uma distância d; no segundo seguinte, percorre 3d; no terceiro segundo, 5d, e assim por diante.
Exercícios de vestibulares sobre queda livre
01- (PUC-MG) Dois corpos de pesos diferentes são abandonados no mesmo instante de uma mesma altura.
Desconsiderando-se a resistência do ar, é CORRETO afirmar:
a) Os dois corpos terão a mesma velocidade a cada instante, mas com acelerações diferentes.
b) Os corpos cairão com a mesma aceleração e suas velocidades serão iguais entre si a cada instante.
c) O corpo de menor volume chegará primeiro ao solo.
d) O corpo de maior peso chegará primeiro ao solo.
02-(CESGRANRIO-RJ) O Beach Park, localizado em Fortaleza-CE, é o maior parque aquático da América Latina situado na beira do mar.

Uma de suas principais atrações é um toboágua chamado "Insano". Descendo esse toboágua, uma pessoa atinge sua parte mais baixa com velocidade de 28 m/s. Considerando a aceleração da gravidade g = 9,8 m/s2 e desprezando os atritos, conclui-se que a altura do toboágua, em metros, é de:
![]()
03-(PUC-RJ) Uma pedra, deixada cair de um edifício, leva 4s para atingir o solo.

Desprezando a resistência do ar e considerando g = 10 m/s2, escolha a opção que indica a altura do edifício em metros.
![]()
04-(PUCCAMP-SP) Dois tocos de vela caem da janela de um apartamento bem alto. O intervalo de tempo entre a queda de um e do outro é de 1,0 s. Considere que eles estão em queda livre vertical. que a velocidade inicial é nula e que a aceleração da gravidade é 10 m/s2. Quando o segundo toco de vela completar 1,0 s de queda, a distância entre eles, em metros, será igual a:
![]()
05-(UFSM-RS) Se a resistência do ar for nula e o módulo da aceleração da gravidade for de 10 m/s2, uma gota de chuva, caindo de

uma altura de 500 m, a partir do repouso, atingirá o solo com uma velocidade de módulo, em m/s, de:
![]()
06-(UFPE) Uma esfera de aço de 300 g e uma esfera de plástico de 60 g de mesmo diâmetro são abandonadas, simultaneamente, do alto de uma torre de 60 m de altura. Qual a razão entre os tempos que levarão as esferas até atingirem o solo? (Despreze a resistência do ar).
![]()
07-(UNESP-SP) Um balão se desloca horizontalmente, a 80,0 m do solo, com velocidade constante de 6,0 m/s.

Quando passa exatamente sobre um jovem parado no solo, um saquinho de areia é abandonado do balão. Desprezando qualquer atrito do saquinho com o ar e considerando g = 10,0 m/s2, calcule
a) o tempo gasto pelo saquinho para atingir o solo, considerado plano.
b) a distância entre o jovem e o ponto onde o saquinho atinge o solo.
08-(PUC-PR) Em um planeta, isento de atmosfera e onde a aceleração gravitacional em suas

proximidades pode ser considerada constante igual a 5 m/s2, um pequeno objeto é abandonado em queda livre de determinada altura, atingindo o solo após 8 segundos.
Com essas informações, analise as afirmações:
I. A cada segundo que passa a velocidade do objeto aumenta em 5 m/s durante a queda.
II. A cada segundo que passa, o deslocamento vertical do objeto é igual a 5 metros.
III. A cada segundo que passa, a aceleração do objeto aumenta em 4 m/s2 durante a queda.
IV. A velocidade do objeto ao atingir o solo é igual a 40 m/s.
a) Somente a afirmação I está correta.
b) Somente as afirmações I e II estão corretas.
c) Todas estão corretas.
d) Somente as afirmações I e IV estão corretas.
e) Somente as afirmações II e III estão corretas.
09-(FGV-SP) Freqüentemente, quando estamos por passar sob um viaduto, observamos uma placa orientando o motorista para que comunique à polícia qualquer atitude suspeita em cima do viaduto. O alerta serve para deixar o motorista atento a um tipo de assalto que tem se tornado comum e que segue um procedimento bastante elaborado. Contando que o motorista passe em determinado trecho da estrada com velocidade constante, um assaltante, sobre o viaduto, aguarda a passagem do párabrisa do carro por uma referência previamente marcada na estrada. Nesse momento, abandona em queda livre uma pedra que cai enquanto o carro se move para debaixo do viaduto. A pedra atinge o vidro do carro quebrando-o e forçando o motorista a parar no acostamento mais à frente, onde outro assaltante aguarda para realizar o furto.

Suponha que, em um desses assaltos, a pedra caia por 7,2 m antes de atingir o pára-brisa de um carro. Nessas condições, desprezando-se a resistência do ar e considerando a aceleração da gravidade 10 m/s2, a distância d da marca de referência, relativamente à trajetória vertical que a pedra realizará em sua queda, para um trecho de estrada onde os carros se movem com velocidade constante de 120 km/h, está a
![]()
10-(PUC-RJ) Um objeto em repouso é largado do alto de um prédio de altura H, e leva um intervalo de tempo T para chegar ao

chão (despreze a resistência do ar e considere que g = 10,0 m/s2). O mesmo objeto largado de H/4 chega ao chão em um intervalo de tempo de (T - 3,0 s), ou seja, 3,0 segundos a menos que o objeto largado do alto.
a) Calcule o valor de T.
b) Calcule a altura H.
11- (PUC-MG) Um helicóptero está descendo verticalmente e, quando está a 100 m de altura, um

pequeno objeto se solta dele e cai em direção ao solo, levando 4s para atingi-lo. Considerando-se g = 10m/s2, a velocidade de descida do helicóptero, no momento em que o objeto se soltou, vale em km/h:
![]()
12- (PUC-RJ) Uma pedra é largada do alto de um prédio. Sua altura em relação ao solo t segundos após ser largada é de h=180 -

5t2 metros.
a) Qual a altura do prédio?
b) Quando a pedra atinge o solo?
13-(PUC-SP) Suponha que, ao afundar, o barco, considerado como ponto material, tenha se movido dentro da água, com aceleração

constante de 4,0 m/s2. O tempo decorrido até atingir o fundo, que está a 11m da superfície, foi de, aproximadamente,
![]()
14-(Ufjf-MG) Quando se abre uma torneira de forma que saia apenas um "filete" de água, a área da

seção reta do filete de água abaixo da boca da torneira é tanto menor quanto mais distante dela, porque:
a) como a velocidade da água distante da boca da torneira é maior devido à ação da força gravitacional, para que haja conservação da massa, a área da seção reta do filete tem que ser menor.
b) uma vez que a velocidade da água distante da boca da torneira é menor devido à ação da força gravitacional, para que haja conservação da massa, a área da seção reta do filete tem que ser menor.
c) a velocidade da água caindo não depende da força gravitacional e, portanto, para que haja conservação da massa, a área da seção reta do filete tem que ser menor.
d) as interações entre as moléculas da água tornam-se mais intensas devido à ação da força gravitacional e, assim, a área da seção reta do filete distante da boca da torneira fica menor.
e) devido à velocidade com que a água sai, a boca da torneira é projetada para que a água seja concentrada mais distante da boca.
15- (CFT-CE) Um corpo de pequenas dimensões é abandonado, a partir do repouso, de uma determinada altitude da superfície da Terra. Despreza-se a resistência do ar e considera-se a aceleração da gravidade constante. Sabendo-se que, no primeiro segundo de queda, o corpo percorre uma distância H, no terceiro segundo desse mesmo movimento, percorrerá:
![]()
16-(UNESP-SP) Um corpo é lançado para baixo com velocidade de 15m/s. Sabendo que a altura inicial era de 130m, determine o instante em que o corpo se encontra a 80m do solo.
17-(UNICAMP-SP) Uma atração que está se tornando muito popular nos parques de diversão

consiste
em uma plataforma que despenca, a partir do repouso, em queda livre
de uma altura de 75m. Quando a plataforma se encontra 30m acima do
solo, ela passa a ser freada por uma força constante e atinge o
repouso quando chega ao solo. Dado g = 10m/s2.
a) Qual
é o valor absoluto da aceleração da plataforma durante a queda
livre?
b) Qual é a velocidade da plataforma quando o freio é
acionado?
c) Qual é o módulo da aceleração necessária
para imobilizar a plataforma?
18-(UNESP) Conta-se que Isaac Newton estava sentado embaixo de uma macieira quando uma maçã caiu sobre sua cabeça e ele teve, assim, a intuição que o levou a descrever a lei da Gravitação Universal.

Considerando que a altura da posição da maçã em relação à cabeça de Newton era de 5,0m, que a aceleração da gravidade local era g=10m/s2 e desprezando a resistência do ar, a velocidade da maçã no instante em que tocou a cabeça do cientista, em km/h, era:
![]()
19- (UNESP) Uma torneira, a 0,90 m do solo, apesar de ter sido fechada, continuou pingando água, a uma freqüência constante. Um observador notou que, quando o primeiro pingo de água atingiu o solo, o quarto pingo desprendeu-se da torneira. Considere
que os pingos têm a mesma massa e que, quando deixam a torneira, apresentam velocidade inicial nula. Desprezando-se a resistência do ar, pode-se afirmar corretamente que
a) a velocidade dos pingos é igual à da gravidade.
b) quando o primeiro pingo atingiu o solo, o segundo pingo estava a 0,60 m da torneira.
c) quando o primeiro pingo atingiu o solo, o terceiro pingo estava a 0,30 m do solo.
d) a energia cinética do terceiro pingo é menor do que a energia cinética do quarto pingo
20-(UNICAMP-SP) Uma torneira, situada a uma altura de 1 m acima do solo, pinga lentamente à razão de 3 gotas por minuto.

(a) Com que velocidade uma gota atinge o solo ?
b) Que intervalo de tempo separa as batidas de duas gotas consecutivas no solo ? Considere, para simplificar, g = 10 m/s2.
21-(UNESP-SP) Um objeto é solto do repouso de uma altura de H no instante t = 0. Um segundo objeto é arremessado para baixo com uma velocidade vertical de 80 m/s depois de um intervalo de tempo de 4,0 s, após o primeiro objeto. Sabendo que os dois atingem o solo ao mesmo tempo, calcule H (considere a resistência do ar desprezível e g = 10 m/s2).
![]()
22-(UNESP-SP) Em recente investigação, verificou-se que uma pequena gota de água possui propriedades elásticas, como se fosse uma partícula sólida. Em uma experiência, abandona-se uma gota de uma altura ho, com uma pequena velocidade horizontal. Sua trajetória é apresentada na figura.

Na interação com o solo, a gota não se desmancha e o coeficiente de restituição, definido como f, é dado pela razão entre as componentes verticais das velocidades de saída e de chegada da gota em uma colisão com o solo.
Calcule a altura h atingida pela gota após a sua terceira colisão com o solo, em termos de h³ e do coeficiente f. Considere que a componente horizontal da velocidade permaneça constante e não interfira no resultado.
23-(CFT-SC) Se um objeto cai, a partir do repouso, em um local onde a aceleração da gravidade tem módulo 10 m/s2, desprezando-se a resistência do ar, podemos afirmar que esse objeto:
I. adquire velocidade escalar constante de 10 m/s;
II. cai 10 metros durante o primeiro segundo;
III. tem velocidade escalar de 20 m/s após 2,0 s;
Está(ão) CORRETA(S):
a) apenas as afirmações I e II.
b) apenas a afirmação III.
c) apenas as afirmações II e III.
d) apenas a afirmação I.
e) todas as afirmações.
24-(PUC-RJ) Em um campeonato recente de vôo de precisão, os pilotos de avião deveriam "atirar" um saco de areia dentro de um alvo localizado no solo.

Supondo que o avião voe horizontalmente a 500 m de altitude com uma velocidade de 144 km/h e que o saco é deixado cair do avião, ou seja, no instante do "tiro" a componente vertical do vetor velocidade é zero, podemos afirmar que: Considere a aceleração da gravidade g=10m/s£ e despreze a resistência do ar)
a) o saco deve ser lançado quando o avião se encontra a 100 m do alvo;
b) o saco deve ser lançado quando o avião se encontra a 200 m do alvo;
c) o saco deve ser lançado quando o avião se encontra a 300 m do alvo;
d) o saco deve ser lançado quando o avião se encontra a 400 m do alvo;
e) o saco deve ser lançado quando o avião se encontra a 500 m do alvo.
25-(PUC-SP)

Suponha que, na tirinha anterior, tenha ocorrido o "beijinho", e na falta de outra melancia de 5 kg, o marido ciumento tenha largado uma maçã de 50g.
Comparando as grandezas velocidade e força peso nas duas situações, pode-se afirmar que:
Considere g = 9,8 m/s2 e a altura da queda = 10 m
a) A velocidade seria a mesma, valendo 196 m/s, mas a força peso seria diferente, valendo 10 vezes menos na queda da maçã.
b) A velocidade seria a mesma, valendo 14 m/s, mas a força peso seria diferente, valendo 10 vezes mais na queda da maçã.
c) A velocidade seria a mesma, valendo 14 m/s, mas a força peso seria diferente, valendo 100 vezes menos na queda da maçã.
d) A força peso seria a mesma, valendo 14 N, mas a velocidade de queda seria diferente, valendo 10 vezes mais na queda da maçã.
e) A força peso seria a mesma, valendo 49 N, mas a velocidade de queda seria diferente, valendo 100 vezes menos na queda da maçã.
26-(UEL-PR) Considere um figo desprendendo-se livremente de uma figueira que tem 20 m de altura.

Pode-se afirmar que ele chegará ao solo após __________ segundos, atingindo uma velocidade de _________ metros por segundo.
Dado: Considere g = 10 m /s2.
Assinale a alternativa que completa corretamente os espaços vazios do texto, respectivamente.
![]()
27-(FUVEST-SP) Numa filmagem, no exato instante em que um caminhão passa por uma marca no chão, um dublê se larga de um viaduto para cair dentro de sua caçamba. A velocidade v do caminhão é constante e o dublê inicia sua queda a partir do repouso,

repouso, de uma altura de 5 m da caçamba, que tem 6 m de comprimento. A velocidade ideal do caminhão é aquela em que o dublê cai bem no centro da caçamba, mas a velocidade real v do caminhão poderá ser diferente e ele cairá mais à frente ou mais atrás do centro da caçamba. Para que o dublê caia dentro da caçamba, v pode diferir da velocidade ideal, em módulo, no máximo:
![]()
28-(CESGRANRIO-RJ) A uma altura de 20 m do solo, abandona-se uma pedra. A gravidade local vale 10 m/s2.

Com relação a esse movimento, adotando-se para cima o sentido positivo do movimento, o gráfico da função que associa a altura da pedra ao tempo de queda corresponde a um
a) segmento de uma reta crescente com coeficiente angular igual a 5.
b) segmento de uma reta decrescente com coeficiente angular igual a – 5.
c) segmento de uma reta vertical.
d) trecho de uma parábola cuja concavidade está voltada para baixo.
e) trecho de uma parábola cuja concavidade está voltada para cima.
29-(UFPR-PR) Cecília e Rita querem descobrir a altura de um mirante em relação ao nível do mar.

Para isso, lembram-se de suas aulas de física básica e resolvem soltar uma moeda do alto do mirante e cronometrar o tempo de queda até a água do mar. Cecília solta a moeda e Rita lá embaixo cronometra 6 s. Considerando-se g = 10 m/s2, é correto afirmar que a altura desse mirante será de aproximadamente:
![]()
30-(UEMG-MG) Dois objetos de mesma massa são abandonados, simultaneamente, da mesma altura, na Lua e na Terra, em queda livre. Sobre essa situação, Carolina e Leila chegaram às seguintes conclusões:
Carolina: Como partiram do repouso e de uma mesma altura, ambos atingiram o solo com a mesma energia cinética.
Leila: Como partiram do repouso e da mesma altura, ambos atingiram o solo no mesmo instante.
Sobre tais afirmações, é CORRETO dizer que
a) as duas afirmações são falsas.
b) as duas afirmações são verdadeiras.
c) apenas Carolina fez uma afirmação verdadeira.
d) apenas Leila fez uma afirmação verdadeira.
31-(UERJ-RJ))

Galileu Galilei, estudando a queda dos corpos no vácuo a partir do repouso, observou que as distâncias percorridas a cada segundo de

queda correspondem a uma sequência múltipla dos primeiros números ímpares, como mostra o gráfico abaixo.

Determine a distância total percorrida após 4 segundos de queda de um dado corpo. Em seguida, calcule a velocidade desse corpo em t = 4 s.(considere g=10m/s2).
32-(ENEM-MEC)

Para medir o tempo de reação de uma pessoa, pode-se realizar a seguinte experiência:

I. Mantenha uma régua (com cerca de 30 cm) suspensa verticalmente, segurando-a pela extremidade superior, de modo que o zero da régua esteja situado na extremidade inferior.
II. A pessoa deve colocar os dedos de sua mão, em forma de pinça, próximos do zero da régua, sem tocá-la.
III. Sem aviso prévio, a pessoa que estiver segurando a régua deve soltá-la. A outra pessoa deve procurar segurá-la o mais rapidamente possível e observar a posição onde conseguiu segurar a régua, isto é, a distância que ela percorreu durante a queda.O quadro seguinte mostra a posição em que três pessoas conseguiram segurar a régua e os respectivos tempos de reação.

A distância percorrida pela régua aumenta mais rapidamente que o tempo de reação porque a
A. energia mecânica aumenta, o que a faz cair mais rápido.
B. resistência do ar aumenta, o que faz a régua cair com menor velocidade.
C. aceleração de queda da régua varia, o que provoca um movimento acelerado.
D. força peso da régua tem valor constante, o que gera um movimento acelerado.
E. velocidade da régua é constante, o que provoca uma passagem linear de tempo.
Resolução dos exercícios sobre queda livre vertical
01- Como a resistência do ar é desprezada eles caem com a mesma aceleração que é a da gravidade e consequentemente suas velocidades, em cada instante, serão sempre as mesma, independente das massas e consequentemente dos pesos --- R- B
02- V=28m/s --- Vo=0 --- Torricelli --- V2= Vo2 + 2.g.ΔS --- 282=02 + 2.9,8.ΔS --- ΔS=784/19,6 --- H=40m --- R- A
03- S= gt2/2=5.16 --- S=80m --- R- C
04- Segundo toco B no instante 1s caiu --- SB=gt2/2=5.1=5m --- como o primeiro toco partiu 1s antes, quando t=1s para B, será 2s para A --- SA = 5tA2=5.22=20m --- ΔS=20 – 5=15m --- R- C
05- V2=Vo2 + 2.g.h --- V2 = 02 + 2.10.500 --- V=100ms --- R- C
06- Chegam ao solo com a mesma velocidade --- R- C
07- a) Como o balão se desloca horizontalmente, sua velocidade vertical inicial é nula --- S=gt2/2 --- 80=5t2 --- t=4s
b) Corresponde à distância horizontal que o balão percorre em 4s com velocidade constante de 6m/s --- V=d/t --- 6=d/4 --- d=24m
08- I- Correta – 5m/s2 significa 5(ms)/s, ou seja, variação de velocidade de 5ms em cada 1s
II – Falsa - a cada segundo o deslocamento vai aumentando, pois a velocidade é cada vez maior.
III – Falsa – segundo o enunciado a aceleração é constante e vale 5m/s2
IV – Verdadeira – V=Vo + g.t= 0 + 5.8 --- V=40m/s
R- D
09- Tempo que a pedra demora para cair h=7,2m --- S=gt2/2 --- 7,2=5t2 --- t=1,2s --- nesse tempo o carro com velocidade constante de 120km/h=33,4m/s o carro se deslocou --- V=ΔS/Δt --- 33,4= ΔS/1,2 --- ΔS=40,08m --- R- C
10- a)Corpo que é abandonado da altura H e demora T para chegar ao chão --- H=10T2/2 --- corpo que é abandonado da altura H/4 e que demora (T – 3)s para chegar ao chão --- H/4=10.(T – 3)2/2 --- dividindo membro a membro --- T2/(T – 3)2 =4 --- T/T – 3 =2 --- T=6s
b) H=10T2/2=10.36/2 --- H=180m
11- A velocidade inicial de descida (Vo) do objeto é a mesma que do helicóptero --- S=Vo.t + g.t2/2 --- 100=Vo.4 + 10.16/2 ---
Vo=20/4 --- Vo=5m/sX3,6=18km/h --- R- D
12- a) Nesse caso, pela equação observava-se que a origem da trajetória está no solo e que ela é orientada para cima ---
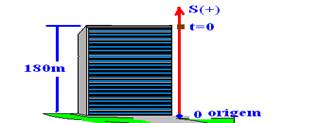
comparando S=So + gt2/2 com S=180 – 5t2 --- So=180m ou, substituindo t=0 na equação --- R- 180m
a) A altura do prédio é dada pela função em t = 0, ou seja, 180 metros.
b) A pedra atinge o solo quando S=0 --- 0= 180 - 5t2, isto é, 5t2 = 180 ==> t2 = 180/5 = 36, de onde vem que t = 6 s.
13- S=gt2/2 --- 11=4t2/2 --- t=√5,5=2,3s --- R- A
14- R- A (veja teoria)
15-

R- C
16-
Colocando a origem no ponto de lançamento e orientando a trajetória para baixo, 1uando ele se encontra a 80m do solo, sua posição é S=130 – 80=50m
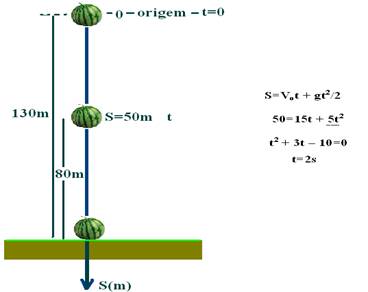
R- t=2s
17- a)
A aceleração de queda da plataforma é a aceleração da gravidade
local fornecida pelo exercício, g=10m/2
b)
Velocidade da plataforma quando se encontra 30m acima do solo, ou
seja, após ter percorrido ΔS=75 – 30=45m ---
Torricelli --- V2=Vo2 +
2.g.ΔS --- V2=02 +
2.10.45 --- V=30m/s
c) Imobilizada
(freando – a<0) --- V=0 --- Torricelli
--- V2=Vo2 +
2.(-a).h --- 02=302 –
2a.30 --- a=900/60 --- a=15m/s2
18- V2=Vo2 +
2.g.h=02 +
2.10.5 --- V=10m/sX3,6=36km/h ---
R- A
19- Proporções de Galileu para queda livre com Vo=0 e desprezando-se a resistência do ar:
Para intervalos de tempos iguais e consecutivos, um corpo em queda livre percorre distâncias cada vez maiores, na proporção dos
ímpares consecutivos: no primeiro segundo, o móvel cai uma distância d; no segundo seguinte, percorre 3d; no terceiro segundo,
5d, e assim por diante.
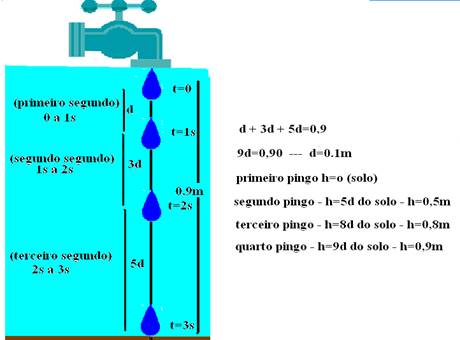
a) falsa – velocidade é diferente de aceleração
b) falsa – estava a 0,50m do solo
c) falsa – estava a 0,80m do solo
d) Verdadeira – Ec=mV2/2 --- quanto maior a velocidade, maior será a energia cinética --- o terceiro pingo tem maior velocidade que o quarto pingo, que, nesse instante está abandonando a torneira.
R- D
20- a) Torricelli --- V2=Vo2 + 2.g.h=02 + 2.10.1 --- V=√20 --- V=4,47m/s
b) Como o tempo de queda é o mesmo, o intervalo de tempo entre as batidas de duas gotas consecutivas é o mesmo intervalo de tempo compreendido entre as saídas de duas gotas consecutivas da torneira. Se saem 3 gotas em cada 60s, tem-se que, entre a 1a e a 2a (20s); entre a 2a e a 3a (20s) e entre a 3a e a 4a (20s) e assim, a partir do instante em que uma bate no solo, depois de 20s chega a outra ao solo --- R- 20s
21- Objeto M, solto do repouso Vo=0 --- SM=H=gtM2/2 --- H=5tM2 --- objeto N arremessado para baixo com velocidade inicial Vo=80m/s --- S=Vo.tN + gtN2/2 --- S=80tN+ 5tN2 --- como M partiu 4s antes --- tM – tN=4 --- tM=tN + 4 --- H=15.(tN + 4)2 --- H=5(tN2 + 8tN + 16) --- H=5tN2 + 40tN + 80 --- se encontram no solo --- H = S --- 5tN2 + 40tN + 80 = 80tN + 5tN2 --- 40tN + 80 = 80tN --- tN=2s --- substituindo tN=2s em S=H=80tN + 5tN2=80.2 + 5.4=160 + 20 --- H=180m --- R- D
22-
Cálculo da velocidade V1 após a 1a colisão --- V12= 02 + 2.g.hO --- V1=√2gho I --- V2 – velocidade logo após a 1a colisão --- f=V2/V1 --- V2=f.√2gho (velocidade de subida que é igual em módulo à velocidade V3 com que ela retorna) --- V2=f.√2gho ---
F=V3/V2 --- V3=f.f.√2gho --- V3=f2.√2gho --- analogamente após a 3a colisão --- V4=f3.√2gho --- assim, após a 3a colisão ela é
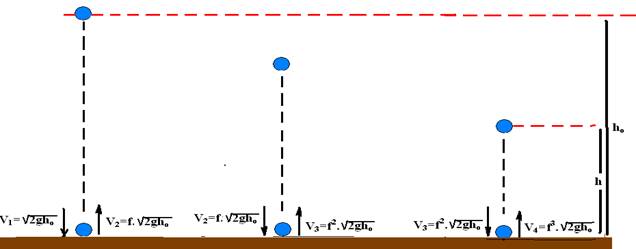
lançada para cima com velocidade V4=f3.√2gho atingindo uma altura h, quando V=0 --- V2= V42 – 2gh --- 0 = (f3.√2gho)2 – 2.g.h --- f6.2gho = 2gh --- h=f6.ho
23- I – Falsa --- a velocidade aumenta de 10ms em cada 1s
II – Falsa --- h=gt2/2 --- h=5.12 --- h=5m
III – Verdadeira --- V=gt=10.2 --- V=20m/s
R- B
24- Tempo de queda do saco --- h=gt2/2 --- 500=5t2 --- t=10s --- Nesse tempo o avião deve se deslocar ΔS com velocidade constante de V=144km/h/3,6=40m/s --- V=ΔS/Δt --- 40= ΔS/10 --- ΔS=400m --- R- D
25- A velocidade é a mesma independente da massa --- Pmelancia=mmelancia.g=5g --- Pmaçã=mmaçã.g=0,05.g --- R- C
26- H=gt2/2 --- 20=5t2 --- t=2s --- V=gt=10.2=20m/s --- R- B
27- Observe a figura abaixo onde L é a distância horizontal entre a mancha e o dublê no instante do salto --- cálculo do tempo de
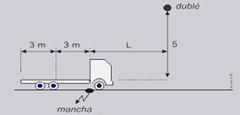
queda do dublê --- h=gt2/2 --- 5=10t2/2 t2=1 --- t=1s --- a velocidade ideal Vi=ΔS/Δt=(L + 3)/1 --- Vi=L + 3 --- velocidade mínima --- Vm= ΔS/Δt=L/1 --- Vmin=L --- velocidade máxima --- Vmax= ΔS/Δt=(L + 6)/1 --- Vmax=L + 6 --- diferenças ---
V1=Vi - Vmin= (L + 3) – L --- V1=3m/s --- V2= Vmax - Vi=(L + 6) – (L + 3) --- V2=3m/s
R- B
28- Dados: ho = 20 m; g = 10 m/s2; vo = 0.
A Figura abaixo ilustra a situação descrita no enunciado --- desprezando a resistência do ar, trata-se de uma queda livre, que é
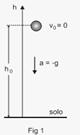
um movimento uniformemente variado --- equação da altura em função do tempo --- h=ho + Vot + gt22 --- h=20 – 5t2 --- o
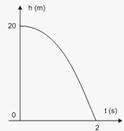
gráfico dessa função é um arco de parábola com concavidade para baixo --- quando h=0 --- 0=20 – 5t2 --- t=√4 --- t=2s
R- D
29- Dados: g = 10 m/s2 ; t = 6 s --- para a queda livre --- h=gt2/2=10.62/2 --- h=180m --- R- A
30- Aplicando a equação de Torricelli --- V2=Vo + 2.g.h --- Vo=0 --- V2=2gh --- Ec=mV2/2 --- EcTerra=m.(2gTerra.h) --- EcLua=m.(2gLua.h) --- como a gravidade na superfície da Terra é maior que a gravidade na superfície da Lua, a energia cinética na superfície da Terra é maior que a energia cinética na superfície da Lua --- em relação à queda livre --- h=gt2/2 --- t=√2h/g --- como gLua<gTerra, o tempo de queda na Lua é maior do que na Terra --- R- A
31-
Cálculo da distância total (∆S) percorrida --- ∆S=5 + 15 + 25 + 35=80m ---∆S=80m --- trata-se de uma queda livre com So=0 e Vo=0 (abandonado) --- V=Vo + gt=0 + 10.4 --- V=40m/s.
32-
A. Falsa --- a energia mecânica diminui se houver atrito com o ar ou permanece a mesma se não houver atrito com o ar.
B. Falsa --- a velocidade da régua aumenta a medida que ela desce.
C. Falsa --- a aceleração da régua é a aceleração da gravidade que permanece constante (mesmo local).
D. Correta --- a força que provoca a queda da régua é a força peso, que a faz descer com aceleração constante que é a da gravidade g, pois P=m.g.
E. Falsa --- veja (B).
R- D.