Potência de uma força

A potência de uma força corresponde à rapidez com que o trabalho é realizado, ou seja, com que a energia é transformada.

Assim, definimos potência média (P_m) como sendo a grandeza escalar fornecida pela relação:

onde W é o trabalho (medido,no SI, em J) realizado no intervalo de tempo ∆t (medido, no SI, em s).

A unidade de potência no sistema internacional de unidades (SI) é o watt (W) em homenagem a James Watt e que é definida como a potência de um sistema capaz de realizar um trabalho de um joule (1 J) em um segundo (1s).

O que você deve saber, informações e dicas

Característica do gráfico da potência em função do tempo

Relação entre potência média (P_m) e velocidade média (V_m)

Considere uma força constante de intensidade F realizando um trabalho W num deslocamento d, de modo que a direção de F forme um ângulo α com a direção do deslocamento.

A potência instantânea P_o é obtida substituindo-se a velocidade média V_m pela instantânea V  --- 

 P_o = F.V

Rendimento de uma máquina

Considere uma determinada máquina realizando certo trabalho. A potência útil (P_u) é a potência que a máquina utiliza na realização de um trabalho externo; a potência dissipada (P_d) corresponde à potência não aproveitada, transformada no interior da máquina em energia térmica (calor).

Para poder realizar o trabalho útil (externo), a máquina deve receber uma potência total (P_t), que deve valer: P_t = P_d + P_u.

Portanto, da potência total fornecida à máquina só uma porcentagem, potência útil é aproveitada, pois parte dela é perdida (potência dissipada). Assim, rendimento ( η - letra grega eta) de uma máquina é sua capacidade de realização de determinado trabalho e é  definido como sendo a razão entre a potência útil (P_u) e a potência total (P_t):

Então, por exemplo, se o motor de um carro estiver bem regulado ele apresentará maior rendimento, percorrendo uma distancia maior com a mesma quantidade de combustível que outro carro de mesmas características, mas com o motor desregulado.

Como o rendimento é uma relação entre duas grandezas de mesmas unidades, elas se cancelam e ele não terá unidade (grandeza adimensional).

Sendo P_u sempre menor que P_t,  η  sempre será menor que 1, que normalmente é multiplicado por 100, sendo assim expresso em porcentagem.

Exercícios de vestibulares com resolução comentada sobre

Potência de uma força

01-(UFSM-RS) Leia a informação a seguir.

A construção de usinas geradoras de eletricidade causa impacto para o meio ambiente, mas pode proporcionar uma melhor qualidade de vida, trazendo conforto em residências.

Observe a figura:

Essa figura representa a potência em W consumida numa residência alimentada por uma tensão de 220V ao longo de um dia. A energia consumida no período de maior consumo, em kWh, é de:

02-(UFPE-PE) Uma caixa d'água de 66 kg precisa ser içada até o telhado de um pequeno edifício de altura igual a 18 m. A caixa é içada com velocidade constante, em 2,0 min. Calcule a potência mecânica mínima necessária para realizar essa tarefa, em watts. Despreze o efeito do atrito e considere g=10m/s².

03-(PUC-RS) Considere a figura a seguir, que representa uma parte dos degraus de uma escada, com suas medidas.

Uma pessoa de 80,0kg sobe 60 degraus dessa escada em 120s num local onde a aceleração da gravidade é de 10,0m/s². Desprezando eventuais perdas por atrito, o trabalho realizado ao subir esses 60 degraus e a potência média durante a subida são, respectivamente,

a) 7,20kJ e 60,0W          

b) 0,720kJ e 6,00W          

c) 14,4kJ e 60,0W         

d) 1,44kJ e 12,0W         

e) 14,4kJ e 120W

04-(FGV-SP) Procurando um parâmetro para assimilar o significado da informação impressa na embalagem de um pão de forma - valor energético de duas fatias (50 g) = 100 kcal - , um rapaz calcula o tempo que uma lâmpada de 60 W permaneceria acesa utilizando essa energia, concluindo que esse tempo seria, aproximadamente,

Dado: 1 cal = 4,2 J

a) 100 minutos.              

b) 110 minutos.                  

c) 120 minutos.               

d) 140 minutos.               

e) 180 minutos.

05-(FUVEST-SP) Em um terminal de cargas, uma esteira rolante é utilizada para transportar caixas iguais, de massa M = 80 kg, com centros igualmente espaçados de 1 m. Quando a velocidade da esteira é 1,5 m/s, a potência dos motores para mantê-la em movimento é P_o. Em um trecho de seu percurso, é necessário planejar uma inclinação para que a esteira eleve a carga a uma altura de 5 m, como indicado. Para acrescentar essa rampa e manter a velocidade da esteira, os motores devem passar a fornecer uma potência adicional aproximada de

06-(FATEC-SP) Em um apartamento, há um chuveiro elétrico que dissipa 6000W de potência quando usado com o seletor de temperatura na posição inverno e 4000W quando usado com o seletor de temperatura na posição verão. O casal que reside nesse apartamento utiliza o chuveiro em média 30 minutos por dia,sempre com o seletor na posição inverno.

 Assustado com o alto valor da conta de luz, o marido informa a sua esposa que, a partir do dia seguinte, o chuveiro passará a ser utilizado apenas com o seletor na posição verão. Com esse procedimento, num mês de 30 dias, a economia de energia elétrica, em quilowatts-hora, será de:

07-(FUVEST-SP) Pedro mantém uma dieta de 3 000 kcal diárias e toda essa energia é consumida por seu organismo a cada dia. Assim, ao final de um mês (30 dias), seu organismo pode ser considerado como equivalente a um aparelho elétrico que, nesse mês, tenha consumido

a) 50 kW.h                     

b) 80 kW.h                    

c) 100 kW.h                   

d) 175 kW.h                    

e) 225 kW.h

Obs: 1 kW.h é a energia consumida em 1 hora por um equipamento que desenvolve uma potência de 1 kW

1 cal = 4 J

08-(ITA-SP) Projetado para subir com velocidade média constante a uma altura de 32 m em 40 s, um elevador consome a potência de 8,5 kW de seu motor. Considere que seja de 370 kg a massa do elevador vazio e a aceleração da gravidade g = 10 m/s². Nessas condições, o número máximo de passageiros, de 70 kg cada um, a ser transportado pelo elevador é

09-(UNESP-SP) Em vários países no mundo, os recursos hídricos são utilizados como fonte de energia elétrica.

O princípio de funcionamento das hidrelétricas está baseado no aproveitamento da energia potencial gravitacional da água, represada por uma barragem, para movimentar turbinas que convertem essa energia em energia elétrica. Considere que 700 m³ de água chegam por segundo a uma turbina situada 120 m abaixo do nível da represa. Se a massa específica da água é 1000 kg/m³ e considerando g = 10 m/s², calcule a potência fornecida pelo fluxo de água.

10-(ENEM) A eficiência de uma usina, do tipo da representada na figura, é da ordem de 0,9, ou seja, 90% da energia da água no início do processo se transforma em energia elétrica.

A usina Ji-Paraná, do Estado de Rondônia, tem potência instalada de 512 milhões de watts, e a barragem tem altura de aproximadamente 120m. A vazão do Rio Ji-Paraná, em litros de água por segundo, deve ser da ordem de: (g=10m/s²)

11-(UNESP-SP) O teste Margaria de corrida em escada é um meio rápido de medida de potência anaeróbica de uma pessoa. Consiste em fazê-la subir uma escada de dois em dois degraus, cada um com 18 cm de altura, partindo com velocidade máxima e constante de uma distância de alguns metros da escada. Quando pisa no 8^o. degrau, a pessoa aciona um cronômetro, que se desliga quando pisa no 12^o degrau. Se o intervalo de tempo registrado para uma pessoa de 70 kg foi de 2,8 s e considerando a aceleração da gravidade igual a 10 m/s², a potência média  avaliada por este método foi de

12-(Uff-RJ) O projeto de transposição do rio São Francisco, ora em discussão, implicará a necessidade de se elevar 280 m³ de água por segundo até uma altura de 160 m. Sabe-se que a massa de um litro d'água é um quilograma.

Determine o valor da potência necessária para esse fim, em watts.

13-(Ufes)

O recalque das águas do rio São Francisco será feito através de quatro estações elevatórias, representadas na figura. Considerando que o fluxo de transposição será de 26 m³ de água por segundo, a potência mínima necessária para a transposição será, aproximadamente, de:

14-(FUVEST-SP) A usina hidrelétrica de Itaipu possui 20 turbinas, cada uma fornecendo uma potência elétrica útil de 680 MW, a partir de um desnível de água de 120 m.

No complexo, construído no Rio Paraná, as águas da represa passam em cada turbina com vazão de 600 m³/s.

(g=10m/s²) e d_água=10³kg/m³)

a) Estime o número de domicílios, N, que deixariam de ser atendidos se, pela queda de um raio, uma dessas turbinas interrompesse sua operação entre 17 h 30 min e 20 h 30 min, considerando que o consumo médio de energia, por domicílio, nesse período, seja de 4 kWh.

b) Estime a massa M, em kg, de água do rio que entra em cada turbina, a cada segundo.

c) Estime a potência mecânica da água P, em MW, em cada turbina.

NOTE E ADOTE:

Densidade da água = 10³ kg/m³.

1 MW = 1 megawatt = 10⁶ W.

1 kWh = 1000 W . 3600 s = 3,6.10⁶ J

Os valores mencionados foram aproximados para facilitar os cálculos.

15-(ITA-SP) Calcule a área útil das placas de energia solar de um sistema de aquecimento de água, para uma residência com quatro moradores, visando manter um acréscimo médio de 30,0° C em relação à temperatura ambiente.

Considere que cada pessoa gasta 30,0 litros de água quente por dia e que, na latitude geográfica da residência, a conversão média mensal de energia é de 60,0 kWh/mês por metro quadrado de superfície coletora. Considere ainda que o reservatório de água quente com capacidade para 200 litros apresente uma perda de energia de 0,30 kWh por mês para cada litro. É dado o calor específico da água c = 4,19 J/g°C e a densidade da água 1kg/L.

Gráfico da potência em função do tempo

16-(FUVEST-SP) A potência de uma máquina em função do tempo variou da maneira indicada pelo gráfico.

Qual o trabalho realizado pela máquina desde zero segundo a 150 segundos?

Relação entre potência média (P_m) e velocidade média (V_m)

17-(UNESP-SP) No sistema da figura, o motor estacionário M, puxa um bloco de massa m=500kg com velocidade constante V_o=0,50m/s sobre uma superfície horizontal, cujo coeficiente de atrito é 0,10. (g=10m/s²).

Qual deve ser a potência do motor?

18- (UNIFESP-SP) Avalia-se que um atleta de 60kg, numa prova de 10000m rasos, desenvolve uma potência média de 300W.

a) Qual o consumo médio de calorias desse atleta, sabendo que o tempo dessa prova é de cerca de 0,50h?

Dado: 1 cal = 4,2 J.

b) Admita que a velocidade do atleta é constante. Qual a intensidade média da força exercida sobre o atleta durante a corrida?

19-(Ufsm-RS) Um caminhão transporta 30 toneladas de soja numa estrada retilínea e plana, em MRU, com velocidade de módulo igual a 72km/h.

Se 200 kW da potência do motor do caminhão estão sendo usados para vencer a força de resistência do ar, o módulo dessa força é, em N,

a) 10000                     

b) 60000                      

c) 480000                       

d) 6000000                       

 e) 14400000

20- (Ufpe-PE) Um automóvel se desloca em uma estrada plana e reta com velocidade constante v = 80 km/h.,

 A potência do motor do automóvel é P = 25 kW. Supondo que todas as forças que atuam no automóvel são constantes, calcule o módulo da força de atrito total, em newtons.

21- (FUVEST-SP) Nos manuais de automóveis, a caracterização dos motores é feita em CV (cavalo-vapor). Essa unidade, proposta no tempo das primeiras máquinas a vapor, correspondia à capacidade de um cavalo típico, que conseguia erguer, na vertical, com auxílio de uma roldana, um bloco de 75 kg, à velocidade de 1 m/s.

Para subir uma ladeira, inclinada como na figura, um carro de 1000 kg, mantendo uma velocidade constante de 15 m/s (54 km/h), desenvolve uma potência útil que, em CV, é, aproximadamente, de: (g=10m/s²)

22- (FUVEST-SP) Um elevador de carga, com massa M = 5 000 kg, é suspenso por um cabo na parte externa de um edifício em construção. Nas condições das questões a seguir, considere que o motor fornece a potência P = 150 kW. (g=10m/s²)

a) Determine a força F₁, em N, que o cabo exerce sobre o elevador, quando ele é puxado com velocidade constante.

b) Determine a força F₂ em N, que o cabo exerce sobre o elevador, no instante em que ele está subindo com uma aceleração para cima de módulo a = 5 m/s².

c) Levando em conta a potência P do motor, determine a velocidade V₂ em m/s, com que o elevador estará subindo, nas condições do item (b) (a = 5 m/s²).

d) Determine a velocidade máxima V_M, em m/s, com que o elevador pode subir quando puxado pelo motor.

NOTE E ADOTE:

A potência P, desenvolvida por uma força F, é igual ao produto da força pela velocidade V do corpo em que atua, quando V tem a direção e o sentido da força.

23-(Fuvest-SP) Um carro de corrida de massa m=800kg, percorre uma pista de prova plana com velocidade constante V_o=60m/s  Nessa situação, observa-se que a potência desenvolvida pelo motor P₁=120kW, é praticamente utilizada para vencer a resistência do ar Situação 1, pista horizontal).

Prosseguindo com os testes, faz-se o carro descer uma ladeira, com o motor desligado, de forma que mantenha a mesma velocidade V_o e que enfrente a mesma resistência do ar (situação 2, inclinação a)

Finalmente, faz-se o carro subir uma ladeira, com a mesma velocidade V_o, sujeito à mesma resistência do ar (situação 3, inclinação q)

a) Estime, para a situação 1, o valor da força de resistência do ar F_R, em newtons, que age sobre o carro no sentido oposto a seu movimento.

b) Estime, para a situação 2, o seno do ângulo de inclinação da ladeira, sem a, para que o carro desça a ladeira com velocidade=60m/s, constante.

c) Estime, para a Situação 3, a potência P₃ do motor, em kW, para que o carro suba uma ladeira de inclinação dada por senq=0,3, mantendo a velocidade V_o=60m/s.

24-(Ufpe) Um elevador de massa m_e = 200 kg tem capacidade máxima para 6 pessoas, cada uma com massa m_p = 70 kg.

Como forma de economizar energia, há um contra-peso de massa m_cp = 220 kg. Calcule a potência mínima que o motor deve desenvolver para fazer com que o elevador possa subir com a carga máxima e velocidade constante v = 0,5 m/s. Expresse o resultado em kW.  Considere g = 10 m/s².

25-(FUVEST-SP) A figura a seguir representa esquematicamente um elevador E com massa de 800kg e um contrapeso B, também de 800kg, acionados por um motor M.

A carga interna do elevador é de 500kg.

a) Qual a potência fornecida pelo motor com o elevador subindo com velocidade constante de 1m/s?

b) Qual a força aplicada pelo motor através do cabo, para acelerar o elevador em ascensão, a razão de 0,5m/s²?

26- (Ufal) Um pedra é arremessada horizontalmente por uma pessoa que lhe aplica uma força de intensidade F que varia com a velocidade v da pedra segundo o gráfico.

A potência instantânea da força F quando a velocidade da pedra é de 20 m/s é, em W,

a) 8,0 × 10²                   

b) 6,0 × 10²                      

c) 4,0 × 10²                      

d) 2,0 × 10²                     

e) 1,0 × 10²

Rendimento

27-(PUC-SP) Um dispositivo consome 1.000W realizando um trabalho de 3.200J em 4s. Seu rendimento vale:

28-(UNESP-SP) Um motor recebe durante 1 minuto a potência de 200W, realizando um trabalho de 8.640J. Calcule o rendimento do motor.

29-(ITA-SP) Uma escada rolante transporta passageiros do andar térreo A ao andar superior B, com velocidade constante.

A escada tem comprimento total igual a 15m, degraus em número de 75 e inclinação igual a 30^o. Dados: sen30^o=0,5 e g=10m/s². Determine:

a) o trabalho da força motora necessário para elevar um passageiro de 80kg de A até B.

b) a potência correspondente ao item anterior empregada pelo motor que aciona o mecanismo efetuando o transporte em 30s.

c) o rendimento do motor, sabendo-se que a potência total é de 400W.

30-(UNESP-SP) Um motor de potência útil igual a 125W, funcionando como elevador, eleva a 10m de altura, com velocidade

 constante, um corpo de peso igual a 50N, no tempo de:

31-(Inatel-MG) Rendimento de uma máquina é a sua:

a) capacidade de realização de trabalho     

b) taxa temporal de realização de trabalho     

c)capacidade de ampliar as forças aplicadas nela     

d) taxa de transformação de trabalho em calor      e) taxa de transformação da energia disponível em trabalho

32-(MACKENZIE-SP) Um automóvel de massa 800kg partiu do repouso em uma estrada retilínea e horizontal, devido à ação de uma força constante de 1.800N, paralela à estrada e aplicada pelo seu motor, de rendimento 45 %. Ao percorrer 400m, sob a ação exclusiva dessa força, o consumo de energia proveniente do combustível foi, no mínimo, igual a:

33- (UNIFESP-SP) Após algumas informações sobre o carro, saímos em direção ao trecho off-road. Na primeira acelerada já deu para perceber a força do modelo.

De acordo com números do fabricante, são 299 cavalos de potência [...] e os 100 km/h iniciais são conquistados em satisfatórios 7,5 segundos, graças à boa relação peso/potência, já que o carro vem com vários componentes de alumínio.

            (http://carsale.uol.com.br/opapoecarro/testes/aval_050404discovery.shtml 5)

O texto descreve um teste de avaliação de um veículo importado, lançado neste ano no mercado brasileiro. Sabendo que a massa desse carro é de 2 400 kg, e admitindo 1 cv = 740 W e 100 km/h = 28 m/s, pode-se afirmar que, para atingir os 100 km/h iniciais, a potência útil média desenvolvida durante o teste, em relação à potência total do carro, foi, aproximadamente de

34- (Ufg) Nas usinas hidroelétricas, a energia potencial gravitacional de um reservatório de água é convertida em energia elétrica através de turbinas. Uma usina de pequeno porte possui vazão de água de 400 m³/s, queda de 9 m, eficiência de 90% e é utilizada

para o abastecimento de energia elétrica de uma comunidade cujo consumo per capita mensal é igual a 360 kWh.(g=10m/s²). Calcule:

a) a potência elétrica gerada pela usina;

b) o número de habitantes que ela pode atender.

35-(FUVEST-SP)  O que consome mais energia ao longo de um mês, uma residência ou um carro?

Suponha que o consumo mensal de energia elétrica residencial de uma família, E_R, seja 300 kWh (300 quilowatts . hora) e que, nesse período, o carro da família tenha consumido uma energia E_C, fornecida por 180 litros de gasolina. Assim, a razão E_C/E_R será, aproximadamente:

Calor de combustão da gasolina ≈ 30 000 kJ/litro  ---  1 kJ = 1 000 J

36-(UNICAMP-SP) A tração animal pode ter sido a primeira fonte externa de energia usada pelo homem e representa um aspecto marcante da sua relação com os animais.

a) O gráfico mostra a força de tração exercida por um cavalo como função do deslocamento de uma carroça. O trabalho realizado

 pela força é dado pela área sob a curva Fxd. Calcule o trabalho realizado pela força de tração do cavalo na região em que ela é constante.

b) No sistema internacional, a unidade de potência é o watt (W) = 1 J/s. O uso de tração animal era tão difundido no passado que James Watt, aprimorador da máquina a vapor, definiu uma unidade de potência tomando os cavalos como referência. O cavalo –

 vapor (CV), definido a partir da idéia de Watt, vale aproximadamente 740 W. Suponha que um cavalo, transportando uma pessoa ao longo do dia, realize um trabalho total de 444.000 J. Sabendo que o motor de uma moto, operando na potência máxima, executa esse mesmo trabalho em 40 s, calcule a potência máxima do motor da moto em CV.

37-(FGV-SP)  Conhecido como parafuso de Arquimedes, este dispositivo foi utilizado pelos egípcios para retirar água do Nilo. Um modelo simples pode ser construído com uma mangueira enrolada em uma haste reta. Quando a haste é girada no sentido conveniente, a extremidade inferior da mangueira entra e sai da água, aprisionando uma porção desta no interior da mangueira. Enquanto o parafuso gira, a água capturada é obrigada a subir até o outro extremo da mangueira, onde é despejada.

Com um desses dispositivos, elevou-se água proveniente de um rio até um reservatório, localizado a 2,0 m de altura em relação ao nível de água desse rio. O parafuso de Arquimedes utilizado tinha 100 voltas completas de uma mangueira de borracha, sendo que cada anel podia transportar 1,0 cm³ de água. Desconsiderando atritos e supondo uma rotação uniforme, admitindo que o tempo necessário para que o parafuso girasse 360º em torno de seu eixo era de 2,0 s, a potência útil da fonte do movimento de rotação, em W, era de: Dado: densidade da água = 1,0 g/cm³; aceleração da gravidade = 10 m/s²

38-(PUC-MG)  Na leitura da placa de identificação de um chuveiro elétrico, constatam-se os seguintes

valores: 127 V - 4800W. É CORRETO afirmar:

a) Esse equipamento consome uma energia de 4800 J a cada segundo de funcionamento. 

b) A corrente elétrica correta para o funcionamento desse chuveiro é de no máximo 127 V. 

c) A tensão adequada para o seu funcionamento não pode ser superior a 4800 W. 

d) Não é possível determinar o valor correto da corrente elétrica com as informações disponíveis. 

39-(UFOP-MG)  Normalmente, para elevar as camas em hospitais, as enfermeiras utilizam o sistema rosca-manivela.

 Considere que o braço de uma manivela é de 0,2 m e que uma enfermeira, ao girá-lo com uma velocidade constante, gasta 20 s para dar 10 voltas completas, elevando, assim, um peso de 450 N a uma altura de 0,5 m. Desprezando as perdas com atrito, calcule:

a) a velocidade angular da manivela;       

b) o trabalho realizado pela enfermeira;      

c) a potência desenvolvida pela enfermeira.

40-(UFG-GO)  Um trabalhador da construção civil usa uma polia e uma corda para transportar telhas

até a cobertura de uma residência, a 3 m de altura. Se o trabalhador transporta 20 telhas por vez durante duas horas, à velocidade média de 0,1 m/s, calcule:

a) a quantidade de calorias a mais que deve ser ingerida pelo trabalhador, sabendo-se que apenas 15% dessa energia será transformada em energia mecânica pelo corpo humano;

b) o número total de telhas transportadas nesse intervalo de duas horas.

41-(UFSC-SC)  Para que o trabalho na agricultura tenha maior produtividade e seja menos penoso, os

 agricultores contam com a possibilidade de uso de instrumentos e maquinários desde os mais simples aos mais sofisticados. Na tarefa de arar a terra pode ser empregada a tração animal e ou a mecânica, como os tratores.  

Para medir o trabalho realizado por uma força, de acordo com o tempo gasto para que ele seja realizado, utiliza-se uma grandeza escalar chamada potência.

Com relação a esse tema, é correto afirmar que:

a) o  tempo necessário para arar uma área de 20.000 m² do mesmo tipo de solo, utilizando um trator de 65 cv, é menor do que se for utilizado um trator de 130 cv. 

b) quanto menor for o tempo empregado por uma máquina para realizar o trabalho de arar 20.000 m² de terra, maior será a sua potência. 

c) quanto maior for a potência de uma máquina, mais lentamente ela realiza o trabalho. 

d) a relação P = trabalho realizado pela força/tempo decorrido na realização implica que a unidade de potência no Sistema

Internacional de Unidades será 1 J/h. 

P_o = W_F/Δt  ---  P_o = W_F/Δt  ---  o tempo de realização de um trabalho é inversamente proporcional à potência empregada  ---  isso significa que quanto menor é o tempo, maior é a potência  ---  R- B

42-(ENEM-MEC) Com o objetivo de se testar a eficiência de fornos de micro-ondas, planejou-se o

aquecimento em 10°C de amostras de diferentes substâncias, cada uma com determinada massa, em cinco fornos de marcas distintas.

Nesse teste, cada forno operou à potência máxima.

O forno mais eficiente foi aquele que

a) forneceu a maior quantidade de energia às amostras.                        b) cedeu energia à amostra de maior massa em mais tempo. 

c) forneceu a maior quantidade de energia em menos tempo.               d) cedeu energia à amostra de menor calor específico mais lentamente. 

e) forneceu a menor quantidade de energia às amostras em menos tempo. 

 (UEG-GO) Texto para as questões de números 43 e 44.

A habilidade de uma pessoa em exercer uma atividade física depende de sua capacidade de consumir oxigênio. A forma física

de uma pessoa é dada pela absorção máxima de oxigênio por períodos relativamente longos.

Considere que uma pessoa, em boa forma física, consiga, por longos períodos, absorver até cerca de 50 mL de O₂ por minuto e por quilograma de sua massa, liberando 4,9 kcal por litro de O₂.

Considere 1 kcal = 4.200 J e g = 10 m/s².

43-(UEG-GO)  A energia liberada por uma pessoa que utiliza 2,5 litros de O₂ em sua respiração seria o suficiente para elevar um bloco de 400 kg a uma altura de, aproximadamente:

44-(UEG-GO)  Qual é a potência (em watts) liberada, por cada kg de massa,  por uma pessoa absorvendo 50 ml de O₂?

45-(EsPCEx)

Uma força constante de intensidade 25 N atua sobre um bloco e faz com que ele sofra um deslocamento horizontal. A direção da força forma um ângulo de 60º com a direção do deslocamento.

Desprezando todos os atritos, a força faz o bloco percorrer uma distância de 20 m em 5 s. A potência desenvolvida pela força é de:

Dados: sen 60° = 0,87 e cos 60º = 0,50

46-(ETEC-SP)

A hidroponia consiste em um método de plantio fora do solo em que as plantas recebem seus nutrientes de uma solução, que flui em canaletas, e é absorvida pelas raízes. Por meio de uma bomba hidráulica, em determinada horta hidropônica, a solução é elevada até uma altura de 80 cm, sendo vertida na canaleta onde estão presas as mudas. Devido a uma ligeira inclinação da

canaleta, a solução se move para o outro extremo, lá sendo recolhida e direcionada ao reservatório do qual a bomba reimpulsiona o líquido, como mostra a figura.

Suponha que nessa horta hidropônica foi empregada uma bomba com potência de 20 W. Se toda a potência dessa bomba

pudesse ser empregada para elevar a água até a canaleta, a cada um segundo (1 s), o volume de água que fluiria seria, em litros,

47-(UFPA-PA)

Um  painel  de  energia  solar  de  área  igual a  1 m² produz cerca de 0,5 kW.h por dia.  Pensando nisso, um consumidor interessado nessa fonte de energia resolveu avaliar sua necessidade de consumo diário, que está listada na tabela abaixo.

A partir desses dados, o número mínimo de painéis solares que esse consumidor precisa adquirir para fazer frente às suas necessidades de consumo diário de energia é

48-(AFA)

O motor de um determinado veículo consome 8,0 litros de combustível em uma hora. Sabendo-se

que o calor de combustão desse combustível é de 10000 cal/g, que sua densidade é 0,675g/cm³ e que o motor desenvolve uma potência de 24 kW, o rendimento desse motor, em porcentagem, é de (considere 1 cal = 4 J)

49-(FUVEST-SP)

A energia que um atleta gasta pode ser determinada pelo volume de oxigênio por ele consumido na respiração. Abaixo está apresentado o gráfico do volume  V de oxigênio, em litros por minuto, consumido por um atleta de massa corporal de 70 kg, em função de sua velocidade, quando ele anda ou corre.

Considerando que para cada litro de oxigênio consumido são gastas 5 kcal e usando as informações do gráfico, determine, para esse atleta,

a) a velocidade a partir da qual ele passa a gastar menos energia correndo do que andando;

b) a quantidade de energia por ele gasta durante 12 horas de repouso (parado);

c) a potência dissipada, em watts, quando ele corre a 15 km/h;

d) quantos minutos ele deve andar, a 7 km/h, para gastar a quantidade de energia armazenada com a ingestão de uma barra de chocolate de 100 g, cujo conteúdo energético é 560 kcal.

50-(FUVEST-SP)

Um pequeno cata-vento do tipo Savonius, como o esquematizado na figura abaixo, acoplado a uma bomba d'água, é utilizado em uma

propriedade rural. A potência útil  P (W) desse sistema para bombeamento de água pode ser obtida  pela expressão P = 0,1xAxv³, em que A (m²) é a área total das pás do cata-vento e v (m/s), a velocidade do vento. Considerando um cata-vento com área total das pás de 2 m², velocidade do vento de 5 m/s e a água sendo elevada de 7,5 m na vertical, calcule

a) a potência útil P do sistema;

b) a energia E necessária para elevar 1l de água;

c) o volume V₁ de água bombeado por segundo;

d) o volume V₂ de água, bombeado por segundo, se a velocidade do vento cair pela metade.

Resolução comentada dos exercícios de vestibulares sobre

Potência de uma força

 01-Maior consumo – P_o=5.10³W  ---  ∆t=2h  --- P_o=W(energia consumida)/∆t --- 5,10³=W/2  ---  W=10.10³W  ---  W=10kW R- B

02- Velocidade constante – a força que está puxando é igual ao peso da caixa d’agua  ---  P=m.g=66.10  ---  P=660N  ---  W=P.h=660.18  ---  W=11.800 J  ---  P_o=W/Dt=11.800/120  --- P_o=99W

03- O trabalho do peso independe da trajetória e vamos calculá-lo pela altura  ---  h=0,150.60  ---  h=9m  ---  W=m.g.h  ---

W=80.10,9=72.10²  ---  W=7,2.10³ J  ---  P_o=W/Dt=7,2.10³/120  --- P_o=60,0W  R- A

04- Regra de três  ---  1cal – 4,2 J  --  100.000cal  --  x J  ---  x=4,2.10⁵ J=W (energia)  ---  P_o=W/∆t  ---  60=4,2.10⁵/∆t  --- ∆t=4,2.10⁵/60  ---  ∆t=0,07.10⁵=7.000s/60=116,7min  ---  R- C

05- Na horizontal e na subida a esteira se move com velocidade constante de 1,5m/s, ou seja, em 1s ela percorre 1,5m e, pela figura,

Observamos que ela transportou, na horizontal e na vertical ela transportou 1,5 caixas por segundo.1 caixa – 80kg  ---  1,5 caixas ---  m=80.1,5  ---  m=120kg, que é a massa que a esteira na parte inclinada deve elevar de 5m em cada 1s com velocidade constante de 1,5m/s.

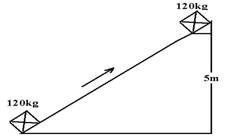
Cálculo do trabalho pela altura  ---  W=m.g.h=120.10.5  ---  W=6.000J – energia consumida para elevar uma massa de 120kg de 5m.  ---  P_o=W/∆t=6.000/1  --- P_o=6.000W - energia consumida para elevar uma massa de 120kg de 5m em 1s.. 

06- com a chave na posição inverno – P_o=W/∆t  ---  6.000=W_i/30.0,5  ---  W_i=90.000W=90kW (energia elétrica consumida) com a chave na posição verão – P_o=W/Dt  ---  4.000=W_v/15  ---  W_v=60.000W=60kW(energia elétrica consumida)

economia – 90kW – 60kW= 30kW R-B

07- Energia consumida em 1 mês (30 dias) – W=30.3.000kcal=9.000.k.(4J)  ---  W=360.000KJ=360.000.000J (energia em Joules, consumida em 1 mês)  ---  regra de três  --- 1kWh – 3.600.000J  ---  x kWh – 360.000.000J  ---  x=100kWh R- C 

08- Potência para elevar o peso do elevador vazio à altura de 32m em 40s  ---  P_oe=W/Dt=m.g.h/Dt=370.10.32/40  ---  P_oe=2.960W

Potência para elevar uma pessoa à altura de 32m em 40s  ---  P_op=W/Dt=m.g.h/Dt=70.10.32/40  ---  P_op=560W

A potência do motor menos a potência para elevar o elevador vazio nos fornece a potência que sobra para elevar o número de pessoas  ---  8.500 – 2.960=5.540W  ---  regra de três  ---  1 pessoa – 560W  ---  n pessoas – 5.540W  ---  n=5.540/560=9,89  --- 

n= 9 pessoas  R- C

09- d=m/V  ---  1.000=m/700  ---  m=700.000kg (massa de água que cai de uma altura de 120m em cada 1s)  --- P_o=m.g.h/Dt  ---  P_o=700.000.10.120/1=840.000.000W  ---  P_o=840.000kW  ---  P_o=8,4.10⁵kW

10- P_o=m.g.h/∆t  ---  512.000.000=m.10.120  ---  m=512.10⁶/12.10²  ---  m=42,7.10⁴=437.000kg  + 0,1 x437.000=480.700kg

Considerando a densidade da água 1kg/L, teremos que uma massa de 1kg ocupa um volume de 1L de água  -- R- E

11- Do 8^o ao 12^o – 4 degraus  ---  h=4.0,18=0,72m  ---  P_o=m.g.h/∆t=70.10.0,72/2,8  --- P_o=180W  R- A

12-V=280m³=280.10³dm³=280.10³L=280.10³kg  --  m=28.10⁴kg  ---  P_o=m.g.h/∆t=28.10⁴.10.160/1=2.816.10⁶  ---   P_o=448.10⁶ P_o=0,448.10⁸ W 

13- Considerando que o volume de 1L de água possui massa de 1kg  ---  V=26m³=26.10³dm³=26.10³ L  ---  m=26.10³kg  ---  a transposição é a elevação da água do rio São Francisco da altura de 315m (elevatória 1) até 475m (elevatória 4) ---  h=475 – 315=160m  ---  P₀=m.g.h/Dt=26.10³.10.160/1  ---  P_o=416.10⁵W=41,6.10⁶W  ---  R- C 

14- a) uma turbina de potência 680.10⁶W foi paralisada durante 3h ---  P_o=W/∆t  ---  680.10⁶=W/3  ---  W=2.040.10⁶=2.040.000kWh (energia elétrica não fornecida por Itaipu durante 3h)  ---  regra de três  ---  1 domicílio – 4kWh  ---  N domicílios – 2.040.000kWh

--- 4N=2.040.000  ---  N=510.000 municípios

b) d=m/V  ---  10³=m/600  ---  m=600.10³  ---  m=600.000kg

c) P=m.g.h=6.10⁵.10.120=720.10⁶W  ---  P=720MW

15- Por dia uma pessoa utiliza 30L  ---  4pessoas  ---  4.30L  ---  120L  ---  em um mês 4 pessoas utilizarão – V=30.120=3600L  -- m=3.600kg  ---  m=3.600.000g  ---   c = 4,19 J/g°C  ---  ∆t=30^oC  ---  equação fundamental da calorimetria – Q=m.c.∆t  ---  Q=3.600.000.4,19.30  ---  Q=W=452.520.000J  ---  lembrando que 1kWh=1.000W.3.600s  ---  1kWh=3.600.000J  --- regra de três  ---  1kWh – 3.600.000W  ---  x kWh – 452.520.000  ---  x=W=452.520.000/3.600.000  ---  W=125,7kWh  ---  Considerando que a água no tanque, de 200 litros, libera 0,30 kWh/litro, a cada mês, tem-se que a perda é de  200x0,30=60 kWh.

Assim os painéis solares terão que fornecer, por mês, 125,7 + 60 = 185,7 kWh  ---  regra de três  ---  se 1m² metro quadrado de painel, no mês, fornece 60 kWh, 187,5kWh serão fornecidos por x m²  ---  60.x=185,7  ---  x=3,1m² de superfície de painéis solares.

16- W=(B + b).h/2 + b.h=(3.10³ + 2.10³).100/2 + 50.3.10³=250.10³ + 150.10³  --- W=400.10³=4.10⁵J

17- Se está com velocidade constante (equilíbrio estático), a intensidade da força  com que o motor puxa o bloco deve ser igual à intensidade da força de atrito .

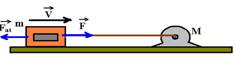
F=F_at=mN=mP=mmg=0,1.500.10  ---     F=500N  ---  P₀=F.V=500.0,5  ---  P_o=250N

18- a) P_o=W/∆t  ---  300=W/1800  ---  W=540.000J (energia “gasta” pelo atleta em joules)  ---  regra de três  ---  1 cal  -  4,2J  ---  X cal  -  540.000J  ---  4,2X=540.000  ---  X=12,9.10⁴=1,29.10⁵ cal.

b) V=∆S/∆t=10.000/1.800  ---  V=50/9m/s  ---  P_o=F.V  ---  300=F/50/9  ---  F=54N

19- V=72km/h/3,6=20m/s  ---  P_o=200.000W  ---  P_o=F.V  ---  200.000=F.20  --- F=10.000N  R- A

20- Como a velocidade é constante a força motora é a força de atrito  ---  F=F_at  ---  P_o=F_at.V  ---  25.000=F_at.80/3,6   ---  F_at=1.125N  ---  R- A

21- Potência utilizada para elevar um bloco de m=75kg a uma altura de 1m   --- P_o=F.V=P.V =m.g.V =75.10.1  ---  P_o=750W

Potência desenvolvida pelo carro  ---  P₀=F.V=P_p.V=mgsenq.V=1.000.10.0,1.15  ---  P₀₌15.000W  ---  regra de três  --- 1 CV – 750W  ---  X CV – 15.000W  ---  X=15.000/750  ---  X=20CV  R- A

22- a) Como ele sobe com velocidade constante (equilíbrio dinâmico – F_R=0), F₁=P=m.g=5.000.10  ---  F₁=5,0.10⁴ N

b) Como tem aceleração  ---  F_R=m.a  ---  F_2­  - P=m.a  ---  F₂ – 50.000=5.000.5  ---  F₂=50.000 + 25.000  ---  F₂=7,5.10⁴N

c) P_o=F₂.V  ---  150.10³=7,5.10⁴.V  ---  V=2,0m/s

d) A velocidade máxima ocorre quando a força motora é o peso (P=50.000N) e a potência é a máxima do motor (P_o=150.000W)

P_o=P.V  ---  150.000=50.000.V  ---  V=3,0m/s.

23- a) Situação 1  ---  V_o=60m/s – constante – equilíbrio dinâmico – força resultante nula – F_R=0

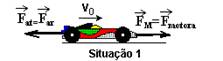
P₁=F_M.V  ---  120.000=F_M.60  ---  F_M=2.000N  ---  como V=constante (equilíbrio dinâmico) – F_M=F_ar=F_R=2.000N 

b) Situação 2  ---  V constante – força resultante nula – motor desligado F_M=0

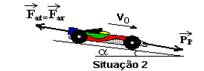
P_P=F_ar=m.g.sena=800.10.sena  ---  ms, F_ar é a mesma da situação 1 (2.000N)  ---  2.000=8.000sena  ---  sena=0,25 

c) Situação 3  ---  V constante – força resultante nula

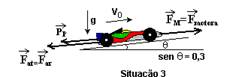
Forças que agem na direção do movimento  ---  P_p=m.g.senq - parcela do peso, paralela à superfície do plano inclinado  ---  P_P=800.10.0,3  ---  P_P=2.400N  ---  F_ar – força de resistência do ar, constante e igual a 2.000N  ---  F_M – força motora  ---

Como a resultante é nula – F_M=P_P + F_ar  ---  F_M=2.400 + 2.000  ---  F_M=4.400N  ---  P_o=F_M.V=4.400.60  ---  P_o=264kW

24- Colocando as forças que agem sobre os sistema:

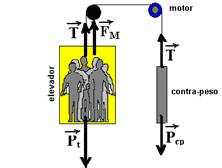
P_t – peso total do elevador  ---  P_t=(200 + 420).10  ---  P_t=6.200N  ---  P_cp=220.10  ---  P_cp=2.200N  ---  Como tanto elevador como contra peso estão com velocidade constante, estão em equilíbrio dinâmico e a força resultante sobre eles é nula  ---  contra peso  ---  P_cp=T  ---  T=2.200N  ---  elevador  ---  P_t=T + F_M  ---  6.200=2.200 + F_M  ---  F_M=4.000N  ---  P_o=F_M.V  ---  P_o=4.000.0,5  --- 

P_o=2.000W=2kW

25- Colocando as forças:

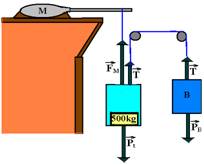
Elevador – peso total - P_t=1.300.10  ---  P_t=13.000N  ---  contra peso B – P_B=m.g=800.10=8.000N  ---  P_B=8.000N 

a) ambos estão em equilíbrio dinâmico com força resultante nula  ---  contra peso – P_B=T  ---  T=8.000N  ---  elevador – Pt=F_M + T  ---  13.000=F_M + 8.000  ---  F_M=5.000N  ---  P_o=F_M.V  ---  P_o=5.000x1  ---  P_o=5kW

b) contra peso B – F_R=m.a  ---  P_B – T=m_B.a  ---  8.000 – T=800.0,5  ---  T=7.600N  ---  elevador - F_R=m_e.a  ---  F_M + T- P_t=1.300.0,5  ---  F_M + 7.600 – 13.000=650  --- F_M=6.050N 

26- Trata-se de uma função de 1^o grau (gráfico é uma reta) de equação F=F_o + k.V, onde k é a constante de proporcionalidade  --- 

F_o=50N (constante)  ---  F=50 + k.V  ---  quando V=30m/s – F=20N  ---  20=50 + k.30  ---  k= -1N.s/m (constante)  ---  a função é F=50 – 1.V  ---  quando V=20m/s  ---  F=50 -1.20 - F=30N  ---  P_o=F.V=30.20  ---  P_o=600W  R-B

27- P_t=1.000W  ---  a potência útil (P_u) é aquela que realiza trabalho – P_u=W_u/∆t=3200/4=800  ---  P_u=800W  ---  h=P_u/P_t=800/1000=0,8  ---  h=80 %  R-D                      

28- P_u=8.640/60=144W  ---  h=144/200=0,72=72 %

29- a) velocidade constante,  a força motora é igual à força peso e o trabalho do peso, que é uma força conservativa independe da trajetória e vamos calcular esse trabalho em função da altura, no deslocamento de C até B.

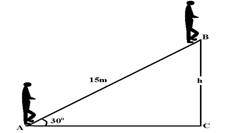
Sen30^o=h/15  ---  h=7,5m  ---  W=m.g.h=80.10.7,5  ---  W=6.000J

b) P_o=W/Dt=6.000/30  ---  P_o=200W                c) h=P_u/P_t=200/400=0,5=50 %  --- h=50 %

30- P_u=P.h/Dt  ---  125=50.10/Dt  ---  Dt=4,0s  R- E

31- R- A – veja teoria

32- Cálculo do trabalho útil  ---  W_u=F.d.cosa=1800.400.1  ---  W_u=7,2.10⁵J  ---h=W_u/W_t  ---  0,45=7,2.10⁵/W_t  ---  W_t=7,2.10⁵/0,45  ---  W_t=1,6MJ  R-E

33- Do enunciado, a potência total P_t é dada por P_t=299cv x 740=221.260W  ---  cálculo da aceleração do carro quando sua velocidade passa de 0 a 28m/s em 7,5s – V=V_o + a.t  ---  28=0 + a.7,5 – a=3,7m/s²  ---  cálculo do deslocamento DS=d=v_o.t + a.t²/2=0 + 3,7.(7,5)²/2  ---  d=104m  ---  cálculo da força motora - F_M=m.a=2.400.3,7  ---  F_M=8.880N  ---  cálculo do trabalho útil realizado pelo motor nesse deslocamento – W_u=F_M.d.cos0^o=8.800.104.1  ---  W_u=915.200J  ---  cálculo da potência útil – P_u=W_u/Dt  --- P_u=915.200/7,5  ---   P_u=122.027W  ---  P_u/P_t=122.027/221.260  ---  P_u/P_t=0,55  R-C

34- a) Considerando a densidade da água 1kg/L - 1m3 = 103L = 103 kg  ---  m=4.105kg ( a usina utiliza essa massa de água por segundo)

Potência elétrica total recebida pela usina em 1s  ---  P_t=m.g.h/Dt=4.10⁵.10.9/1  ---  P_t=36.10⁶W  ---  Potência útil=90 % de P_t=36.10⁶ x 0,9  ---  P_u=32,4.10⁶W=32,4 MW

b) cálculo da energia elétrica útil produzida pela usina hidrelétrica em u mês=720h  ---  P_u=W_u/Dt  ---  32,4.10⁶=W_u/720  --- 

W_u=23.328.10⁶Wh  ---  regra de três  ---  1 habitante – 36.10⁴Wh  ---  N habitantes – 23.328.10⁶Wh  ---  N=23.328.10⁶/36.10⁴  --- 

N=64.800 habitantes

35- E_R = 300 kWh = 300.10³.(J/s).3600 s = 1.080.000x10³ J = 1,08x10⁹ J  ---  E_C = 180x30.000 = 5. 400 .000 kJ = 5,4x10⁹ J  --- 

E_C/E_R=5,4.10⁹/1,08.10⁹=5  ---  R- E

36- a) No trecho em que a força de tração é constante, calculando a área do retângulo (figura), você está calculando o trabalho

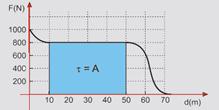
realizado  ---  trabalho = área=base.altura  ---  W=(50 – 10).800  ---  W=32.000J

b) O trabalho realizado foi de 444.000 J no intervalo de tempo de 40 s  ---  como potência é a razão entre o trabalho realizado e o intervalo de tempo  ---  P_o = (Trabalho)/Dt = 444.000/40 = 11.100 W  ---  em  para cavalo-vapor  ---   11.100/740   ---  P_o= 15 CV.

37- Dados  ---  quantidade de anéis  ---  n = 100  ---  volume de água em cada anel  ---  V = 1 cm³= 10^-6 m³  ---  densidade da água  ---   d = 1 g/cm³ = 10³ kg/m³  ---  altura de elevação  ---   h = 2 m  ---  período de rotação do eixo  ---   T = 2 s  ---  volume total de água contido nos 100 anéis  ---  V_T = n V = 100.(10^-6) m³ = 10^-4 m³  ---  esse volume representa uma massa de  ---  M = d V_T=

10³.(10^-4) = 10^-1 kg  ---  tempo de elevação dessa massa de água  ---  Dt = 100.T = 100.(2)  ---    Dt = 200 s.

Potência útil da fonte de rotação  ---  P_o=W/Dt=E_potencial/Dt=Mgh/Dt  ---  P_o=10^-1.10.2/200=2/200=1/100  ---  P_o=1,0.10^-2W  --- 

R- D

38- A potência (em watt) é a razão entre a energia transformada (em joule) e o tempo (em segundo)  ---  1W=1J/1s  --- 4.800W=4.800J/1s  ---  4.800W=4.800J/s  ---  R- A

 39- a) Dados  ---  n = 10 voltas  ---  Dt = 20 s  ---   freqüência  ---  f=n/Δt=10/20  ---  f=0,5Hz  ---  velocidade angular  ---  W=2πf=2π.0,5  ---  W=π rad/s

b) Dado  ---  F = P = 450 N  ---  ∆S = h = 0,5 m  ---  o trabalho (W) realizado pela enfermeira é igual ao trabalho para levantar o peso  ---  W=P.h=450.0,5  ---  W=225J

c) Calculando a potência  ---  P_o=W/Δt=225/20  ---  P_o=11,25W

40- Dados  ---  1 cal  4J  ---  1 telha = 1,5 kg  ---   g = 10 m/s²

a) São dados  ---  n = 20  ---   m = 1,5 kg  ---   g = 10 m/s² ---   h = 3 m  ---   v = 0,1 m/s  ---   r = 20%  ---   ∆t = 2 h = 7.200 s  ---   1 cal = 4 J  ---  como o transporte é feito com velocidade constante, a força exercida pelo trabalhador em cada levantamento tem a mesma intensidade do peso de 20 telhas  ---  a potência (P) é dada pelo produto da intensidade da força (F) pelo módulo da velocidade (v) e o trabalho realizado (W) é igual ao produto da potência pelo tempo (∆t)  ---  P=F.V  ---  W=P_o.Δt  ---  W=F.V.Δt  ---  W=20mgVΔt=20.1,5.10.0,1.7200  ---  W=216.000J  ---  esse trabalho corresponde a 15% da energia (E) a ser ingerida  ---  0,15E=216.000  ---  E=216.000/0,15  ---  E=1.440kJ  ---  em quilocalorias  ---  E=1.440/4  --- E=360kcal

b) Seja N o número de telhas transportadas em 2 h  ---  W = N m g h  ---   N = W/mgh  ---  N=216.000/1,5.10.3  ---  N=4.800 telhas

41- P_o=W_F/Δt  ---  P_o=W_F/Δt  ---  o tempo de realização de um trabalho é inversamente proporcional à potência empregada  ---  isso significa que quanto menor é o tempo, maior é a potência  ---  R- B

42- A potência corresponde à  medida da rapidez com que se transfere energia  ---  P_o=W/Δt  ---  observe nessa expressão que o mais eficiente (maior potência) é aquele que fornece maior quantidade de energia em menos tempo  ---  R- C

43- Dados  ---   m = 400 kg  ---   g = 10 m/s²  ---   1 litro de O₂ libera 4,9 kcal  ---  fazendo a conversão da energia liberada por 2,5 L de O₂  ---   E_liberada = 2,5(4,9)(4.200) = 51.450 J  ---  essa energia corresponde a energia potencial adquirida pelo bloco  ---  E_potencial = E_liberada  ---  mgh = E_liberada  ---  400(10)h = 51.450  ---  h ≈12,9 m. 

R- B

44- Dados  ---  1 L = 1.000 mL de O₂ libera 4,9 kcal = 4,9´4.200 = 20.580 J  ---  Dt = 1 min = 60 s  ---  cálculo da quantidade de energia liberada (E) pela absorção de 50 mL  ---  E=(50mL).(20.580J)/(1.000mL)=1.029J  ---  potência liberada por kg de massa da pessoa  ---  P_o=E/Δt=1.029/60  ---  P_o=17,15W  ---  R- D

45-W=F.d.cos60^o=25.20.0,5  ---  W=250J  ---  P=W/∆T=250/5  ---  P=50W  ---  R- B.

46-  Energia (Trabalho) necessária  para elevar uma massa m de água à altura de h=80cm=0,8m  ---  W=m.g.h=m.10.0,8  ---  W=8.m  ---  massa de água que essa bomba de potência Po=20W consegue elevar com essa energia W=8.m em ∆t=1s  ---  Po=W/∆t  ---  20=8m/1  ---  m=20/8=2,5kg  ---  como o enunciado afirma que 1kg de água equivale ao volume de 1L  ---  V=2,4L  ---  R- B 

47-- Po=W/∆t  ---  W=Po.∆t  ---  lâmpadas  ---  W1=0,1.10=1kWh  ---  televisão  ---  W2=0,1.8=0,8kWh  ---  geladeira  ---  W3=0,3.24=7,2kWh  ---  ventilador  ---  W4=0,125.8=1,0kWh  ---  Wtotal=1,0 + 0,8 + 7,2 + 1,0=10,0kWh  ---  1 painel – 0,5kWh  ---  n painéis – 10,0kWh  ---  N=20 painéis  ---  R-

48-Volume de combustível consumido em 1 hora  ---  V=8L=8dm3=103cm3  ---  massa de combustível consumida em 1 hora  ---  d=m/V  ---  0,675=m/8.103  ---  m=5,4.103g  ---  calor fornecido pela queima dessa massa de combustível  ---  regra de três  ---  1g – 10000cal  ---  5,4.103g – Q cal  ---   Q=5,4.107cal  ---  transformando essa energia em joules  ---  regra de três  ---  1cal – 4J  ---  5,4.107cal  ---  W J  ---  W=4.5,4.107=2,16.108J  ---  potência gerada em 1 hora=3600s  ---  P=W/∆t=2,16.108/3600  ---  P=6.104W  ---  a potência desenvolvida pelo carro é a potência útil=24kW=24.103W  ---  rendimento=potência útil/potência total  ---  η=Pu/Pt=24.103/6.104 =0,4x100=40%  ---R- C 

 49- a) Observe no gráfico que eles vão ter a mesma velocidade no ponto onde a reta (andando) e a curva (correndo) se interceptam que é aproximadamente de V=8,5km/h (eixo horizontal-velocidade)  --- observe também no eixo vertical (volume) que a partir dessa velocidade o consumo de oxigênio do atleta que está correndo é menor do que o do atleta que está andando.

b) Do gráfico, quando ele está parado, velocidade nula eixo horizontal, o volume de oxigênio é de 0,2 ℓ/min  ---  em 12h de repouso ele consumirá  ---  V_r=720.0,2=144ℓ de oxigênio.

c) Pelo gráfico, quando sua velocidade é de 15km/h ele consome 3,6ℓ/min  --- do enunciado, para cada litro de oxigênio consumido são gastas 5 kcal  ---  energia (W) consumida quando V=15km/h  ---  W=3,6.5=18kcal  ---  1 cal= 4 J  ---  W=18.000calx4=72.000J  --- essa energia é consumida em 1min=60s  ---  P=W/∆t=72kJ/60s  ---  P=1,kW=1.200W.

W=72kJ.

d) O gráfico fornece que a cada 7km/h, andando, o consumo de oxigênio é de 1,6 ℓ/min  ---  energia em ∆t minutos  ---  W=1,6.5=8kcal  --- barra de chocolate=560kcal  ---  regra de três  ---  1 min – 8kcal  ---  ∆t min – 560kcal  ---  ∆t=560/8=70 min  ---  ∆t=60min.

50-a) Pelo enunciado, a potência útil  P (W) desse sistema para bombeamento de água pode ser obtida  pela expressão P = 0,1xAxv³  --- 

P=0,1.2.A=2m² e v=5m/s  ---  P=0,1.2.5=25W  ---  P=25W.

b) O trabalho (quantidade de energia) para elevar uma massa m de água a uma altura vertical de h=7,5m é dado por W=m.g.h  ---  d=m/V  ---  1kg/L=1000g/1000cm³=1g/cm³  ---  d=1kg/L  ---  1kg/L=m/1L  ---  m=1kg  ---  W=1.10.7,5  ---  W=75J.

c) P=W/∆t  ---  25=mgh/∆t  ---  25=d.V.g.h/∆t  ===  25=1.V₁.10.7,5/∆t  ---  25/75=V₁/∆t  ---  V₁/∆t=V₁/1=volume de água bombeado em 1s=25/75=1/3  ---  V₁=(1/3) L.

d) Analisando a expressão fornecida pelo enunciado P = 0,1xAxv³ você  observa que a pressão P é diretamente proporcional ao cubo da velocidade v  ---  se v for reduzida à metade a potência P ficará 2³=8 vezes menor, o que implica que a vazão (V₁=(1/3)L também ficará dividida por 8  --- V₂=(1/3.8)L=(1/24) L  ---  V₂=(1/24) L.