sobre
o bloco).
Polias ou Roldanas
São dispositivos que têm por função mudar a direção e o sentido (mas mantendo a intensidade) da força que traciona ou tensiona um fio ou uma corda ou podem ser usadas para aumentar ou diminuir a intensidade de uma força. Podem ser fixas ou móveis:
Polia fixa
Muda a direção e sentido de uma força, mantendo sua intensidade. Está presa a um suporte rígido, fixo e executa apenas movimento de rotação, não de translação.
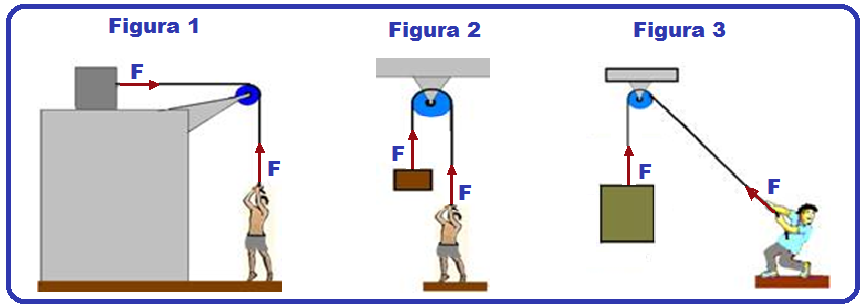
Exemplos de polia fixa
Na figura 1, a força aplicada pelo homem que tem direção vertical e sentido para baixo passa a agir sobre o bloco na direção horizontal e sentido para a direita, mas com a mesma intensidade.
Na figura 2, passa de vertical e para baixo (aplicada pelo homem) para vertical e para cima (agindo
sobre
o bloco).
Na figura 3 a força aplicada pelo homem é transmitida ao bloco como vertical e para cima.
Nas figuras 2 e 3, se os blocos estiverem em equilíbrio, a intensidade da força aplicada é sempre igual ao peso do bloco.
Observe que, se o homem puxar a corda de 1 metro, cada bloco também se deslocará de 1 metro.
Polia móvel
Assim, uma polia móvel consegue aumentar ou diminuir a intensidade de forças, mas tem a inconveniência de diminuir o deslocamento do corpo, ou seja, se sua mão subir de 2 metros, o bloco subirá metade, apenas 1 metro.
Associação de polias
Uma
polia
fixa e outra móvel
Uma
polia
fixa
e várias
polias móveis
(talha exponencial)
O que você deve saber, informações e dicas
Polia
fixa
muda
a direção e sentido de uma força,
mantendo
sua intensidade.
Está presa a um suporte
rígido, fixo e executa apenas movimento
de rotação,
não de translação.
Polia
móvel
aumenta
ou diminui a intensidade de forças,
mas tem a inconveniência
de diminuir o deslocamento do corpo.
Associação
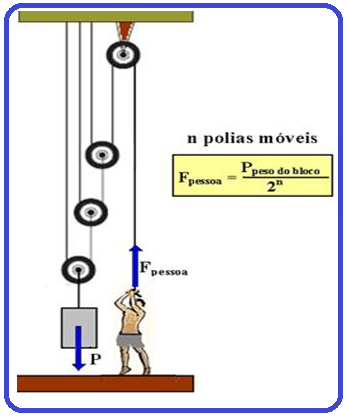
de polias
A
expressão abaixo
é válida para n
polias móveis, com n = 1, 2, 3, ...
Apoio
horizontal móvel (peso
aparente, elevadores)
Observações:
Lembre-se
de que, se o cabo
do elevador quebrar,
tanto ele
como o homem caem
em queda livre,
com a mesma
aceleração g
e consequentemente com a mesma
velocidade em cada instante, e a balança indicará zero (N = 0).
Exercícios de vestibulares com resoluções comentadas sobre
Polias e Roldanas
01-(UFU-MG) Na figura abaixo despreze as forças dissipativas e calcule o valor da carga Q, sabendo que o rapaz exerce uma força de 25N para mantê-la em equilíbrio.
02-(FUVEST-SP) Considere o esquema representado na figura abaixo. As roldanas e a corda são ideais. O corpo suspenso da
roldana móvel tem peso de 550N.
a) Qual o módulo da força vertical (para baixo) que o homem deve exercer sobre a corda, para equilibrar o sistema?
b) Para cada 1 metro de corda que o homem puxa, de quanto se eleva o corpo suspenso?
03-(MACKENZIE-SP) Dispõe-se de um conjunto de fios e polias ideais para um determinado experimento. Quatro dessas polias são associadas conforme a ilustração abaixo, sendo três móveis e uma fixa.
No fio que passa pela polia fixa, suspende-se o corpo de massa m e o conjunto é mantido em repouso por estar preso ao solo, por meio de fios e de um dinamômetro (d) de massa desprezível, que registra 400N.
Qual é o valor da massa do corpo?
04.(UFABC-SP) Um mecânico afirma ao seu assistente que é possível erguer e manter um carro no alto e em equilíbrio estático, usando-se um contrapeso mais leve do que o carro. A figura mostra, fora de escala, o esquema sugerido pelo mecânico para obter o seu intento.
Considerando as polias e os cabos como ideais e, ainda, os cabos convenientemente presos ao carro para que não haja movimento de rotação, determine a massa mínima do contrapeso e o valor da força que o cabo central exerce sobre o carro, com massa de 700 kg, quando esse se encontra suspenso e em equilíbrio estático.
Dado: Adote g = 10 m/s2
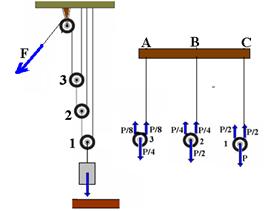
05-(CESGRANRIO-RJ) Um corpo de peso P encontra-se em equilíbrio devido à ação da força de inteensidade F aplicada pelo homem da figura abaixo.
Os pontos A, B e C são os pontos de contato entre os fios e a superfície. A força que a superfíe exerce sobre os fios nos pontos A, B e C são respectivamente.
a) P/8, P/4, P/2
b) P/8, P/2, P/4
c) P/2, P/4, P/8
d) P, P/2, P/4
e) iguais a P
06-(CEFET-SP) Embora abrigue toda uma floresta, o solo amazônico constitui uma fina camada fértil. Após uma temporada de chuvas, um caminhão ficou atolado no solo desmatado. Rapidamente, providenciaram alguns cabos de aço e quatro roldanas.
Aproveitando-se da enorme inércia de uma colheitadeira, montaram a máquina simples da figura.
A solução encontrada permite que uma força resistente FR
seja vencida por uma força potente FP
(A) duas vezes menor.
(B) quatro vezes menor.
(C) seis vezes menor.
(D) oito vezes menor.
(E) dezesseis vezes menor.
07-(FUVEST-SP) As figuras mostram dois arranjos (A e B) de polias construídos para erguer um corpo de massa M=8kg. As polias e os fios são ideais. Calcule as forças FA e FB, em Newton,necessária para manter o corpo suspenso e em repouso nos dois casos. (Considere g=10m/s2).
A B
08-(MACKENZIE-SP) Admita que sua massa seja 60kg e que você esteja sobre uma balança, dentro da cabine de um elevador.
Sendo g=10m/s2 e a balança calibrada em newtons, a indicação por ela fornecida, quando a cabine desce com aceleração constante de 3m/s2, é:
09-(UFB) Um elevador de massa 1.000kg está subindo e acelerando com a=3m/s2. No interior de sua cabine há uma pessoa de massa 70kg que se encontra sobre uma balança calibrada em newtons. Consi dere g=10m/s2 e despreze os atritos:
a) Calcule a indicação da balança
b) Determine a intensidade da força de tração em cada um dos três cabos do elevador da figura acima?
c) Se o elevador cair em queda livre (a=g), então não haverá compressão entre a balança e a pessoa e a mesma terá a impressão de “ter perdido peso”. Normalmente é usada em elevadores especiais ou em aviões em queda livre para acostumar os astronautas com a “ausência da gravidade”.
Pense e responda: O que aconteceria se o elevador cair com aceleração a, tal que a>g?
10-(UFMG-MG) Qual é o peso aparente de um corpo de massa 10kg que está dentro de um elevador que tem uma aceleração de 5m/s2, dirigida para baixo? (g=10m/s2)
11-(UFPA) Um corpo de peso 2,0N pende de um dinamômetro que está fixo no teto de um elevador em movimento. Verifica-se que a leitura do dinamômetro é de 2,5N. Podemos afirmar que o elevador está:
a) em repouso
b) subindo com velocidade constante
c) descendo com velocidade constante
d) subindo com velocidade crescente
e) descendo com velocidade crescente.
12-(PUC-BA) Um cabo de aço utilizado para mover um elevador suporta um peso máximo igual ao peso de um corpo de massa igual a 1200kg. Se ele está sustentando um elevador de massa igual a 1000kg, qual pode ser a máxima aceleração do elevador na subida? (g=10m/s2)
13-(UFB) Num elevador há uma balança graduada em newtons. Uma pessoa de massa 80kg que está sobre a balança lê 960N quando o elevador sobe com certa aceleração e 640N quando o elevador desce com a mesma aceleração. Quais as intensidades das acelerações da gravidade e do elevador? O que estará acontecendo quando a balança registrar 800N? E quando registrar zero?
14-(UNIFESP-SP) Às vezes, as pessoas que estão num elevador em movimento sentem uma sensação de desconforto, em geral na região do estômago. Isso se deve à inércia de nossos órgãos internos localizados nessa região, e pode ocorrer:
a) quando o elevador sobe ou desce em movimento uniforme.
b) apenas quando o elevador sobe em movimento uniforme
c) apenas quando o elevador desce em movimento uniforme.
d) quando o elevador sobe ou desce em movimento variado.
e) apenas quando o elevador sobe em movimento variado.
15-(UFPE) “Uma pessoa comprou uma balança de chão e, ao chegar em casa, ansiosa para controlar o peso, resolve testa-la ainda no elevador. Ela concluiu que a balança estava com defeito ao notar um aumento de seu peso”.
Considerando as informações, identifique a opção correta.
a) O aumento da indicação da balança pode ocorrer se o elevador está subindo com velocidade constante.
b) O aumento da indicação da balança pode ocorrer se o elevador está descendo com velocidade constante
c) O aumento da indicação da balança pode ocorrer se o elevador está subindo com aceleração constante
d) O aumento da indicação da balança pode ocorrer se o elevador está descendo com aceleração constante
e) A balança está necessariamente com defeito e deve ser trocada em respeito aos direitos do consumidor.
16-(MACKENZIE-SP) Uma moça entra em um elevador que está parado no 5o andar de um edifício de 10 andares, carregando uma caixa de 800g, suspensa por um barbante que suporta, no máximo, a tração de 9,6N, como mostra a figura abaixo.
Estando a caixa em repouso em relação ao elevador, o barbante arrebentará somente se o elevador (adote g=10m/s2):
a) descer com aceleração maior que 2,0m/s2
b) descer com aceleração maior que 1,2m/s2
c) subir com aceleração maior que 2,0m/s2
d) subir com aceleração maior que 1,2m/s2
e) subir ou descer com aceleração maior que 2,5m/s2
17-(UFSCAR-SP) O sistema esquematizado compõe-se de um elevador de massa M e um homem de massa m. O elevador está suspenso por uma corda que passa por uma polia fixa e vem às mãos do operador; a corda e a roldana são supostas ideais.
O
operador puxa a corda e sobe com aceleração constante a, juntamente
com o elevador. São supostos conhecidos M, m, a e g. Determine a
intensidade da força 
que
traciona a corda.
18-(UERJ-RJ) Um passageiro está no interior de um elevador que desce verticalmente, com aceleração constante "a".
Se "a" vale 1/5 da aceleração da gravidade, a razão entre a intensidade da força que o piso do elevador exerce sobre o passageiro e o peso do passageiro é igual a:
19-(UFRJ-RJ) Quando o cabo de um elevador se quebra, os freios de emergência são acionados contra trilhos laterais, de modo que esses passam a exercer, sobre o elevador, quatro forças verticais constantes e iguais a f , como indicado na figura.
Considere g = 10m/s2
Suponha que, numa situação como essa, a massa total do elevador seja M = 600kg e que o módulo de cada força f seja | f | = 1350N.
Calcule o módulo da aceleração com que o elevador desce sob a frenagem dessas forças.
20-(UFU-MG) Uma pessoa de massa m está no interior de um elevador de massa M, que desce verticalmente, diminuindo sua velocidade com uma aceleração de módulo a.
Se a aceleração local da gravidade é g, a força feita pelo cabo que sustenta o elevador é
a) (M+m)(g-a)
b) (M+m)(g+a)
c) (M+m)(a-g)
d) (M-m)(g+a)
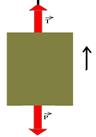
21-(ITA-SP) Uma pilha de seis blocos iguais, de mesma massa m, repousa sobre o piso de um elevador, como mostra a figura.
O elevador está subindo em movimento uniformemente retardado com aceleração de módulo a. O módulo da força que o bloco 3 exerce sobre o bloco 2 é dado por:
(UFT-TO)
Leia o texto para responder às questões 22, 23 e 24.
A fim de conferir realismo à gravação da cena de um filme que envolve um astronauta caindo na superfície lunar, a equipe de
efeitos especiais de um estúdio utilizou uma montagem com polias, um cabo de aço e um contrapeso. A montagem consiste em um cabo de aço com uma extremidade presa ao astronauta, passando por duas polias fixas sobre o teto do estúdio e por uma polia móvel (na qual o contrapeso está preso). A outra extremidade do cabo está fixada ao teto do estúdio, conforme ilustrado na figura abaixo:
Existem forças de atrito que influenciam o movimento do astronauta e do contrapeso. Geralmente estas forças são
desconsideradas em situações envolvendo cabos e polias ideais. Cabos ideais são inextensíveis (comprimento constante) e têm massa nula. Polias ideais não possuem atrito e têm massa nula.
Em uma situação real podemos considerar os cabos e polias como ideais desde que:
1) a massa destes seja muito inferior à dos demais elementos do sistema;
2) o comprimento do cabo seja aproximadamente constante;
3) o atrito na polia seja aproximadamente nulo.
Para calcular a massa do contrapeso, de forma que o astronauta em queda esteja submetido a uma aceleração igual à aceleração gravitacional lunar, a equipe de efeitos especiais considerou o cabo e as polias ideais, a massa total do astronauta (com equipamentos) igual a 220 kg e a aceleração gravitacional lunar (gLua) igual a vinte por cento da aceleração gravitacional terrestre, gTerra = 10 m/s2
22-(UFT-TO)
Assinale a alternativa que mais se aproxima da massa calculada para o contrapeso utilizado pela equipe de efeitos especiais do estúdio.
(A) 320kg (B) 100kg (C) 220kg (D) 151kg (E) 352kg
23-(UFT-TO)
Considere a distância vertical inicial entre os centros de massa do astronauta e do contrapeso d = 9,0m e as velocidades iniciais do astronauta e do contrapeso iguais a zero.
Assinale a alternativa que mais se aproxima do menor intervalo de tempo necessário para que a distância vertical entre os centros de massa do astronauta e do contrapeso seja igual a 4,5m
24-(UFT-TO)
Considere o cabo utilizado no estúdio como ideal e, agora, as polias com coeficiente de atrito diferente de zero, dissipando
energia, e possuindo massa nula. Considere também que exista o movimento.
Assinale a alternativa CORRETA.
(A) O módulo da aceleração do astronauta é nulo enquanto o módulo da aceleração do contrapeso é igual a 0,2gTerra
(B) Os módulos das acelerações do astronauta e do contrapeso são inferiores a 0,2gTerra
(C) Os módulos das acelerações do astronauta e do contrapeso são superiores a 0,2gTerra
(D) O módulo da aceleração do astronauta é igual a 0,2gTerra enquanto o módulo da aceleração do contrapeso é nulo.
(E) Os módulos das acelerações do astronauta e do contrapeso são iguais a 0,2gTerra
Resolução comentada dos exercícios de vestibulares sobre
Polias ou Roldanas
01- Observe que temos duas polias móveis --- n=2 --- F =25/2n --- 25 = Q/22 --- Q = 100N.
02- a) Uma roldana móvel, o homem deve aplicar uma força 2n=21=2 vezes menor, ou seja, de 550/2=275N.
b) Duas vezes menor, ou seja, de 0,5m.
03- O dinamômetro indica a intensidade da força que traciona o fio que está preso ao solo, ou seja, 400N. Observe na figura, que a
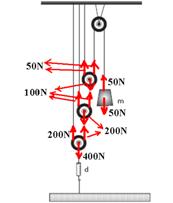
distribuição de forças nos fornece o peso do bloco, 50N. Como P=m.g --- 50=m.10 --- m=5kg
04- Peso do carro --- PC=m.g --- PC=700.10 --- PC=7000N
Chamando de P o peso do contrapeso, de m sua massa, e colocando todas as forças, observamos
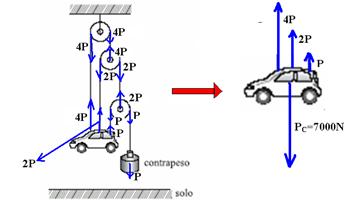
que sobre o carro agem as forças 7P (para cima) o peso do carro PC=7000N (para baixo). Como ele está em equilíbrio --- 7P=PC --- 7P=7000 --- P=1000N e m=100kg.
O cabo central exerce uma força de 2P (veja figura) --- F=2.1000 --- F=2000N
05- Observe a figura abaixo:
R- A
06- Três polias móveis n=3 --- 2n=23=8 vezes menor
07- P=m.g --- P=8.10 --- P=80N --- Observe nas figuras abaixo as distribuições de forças.
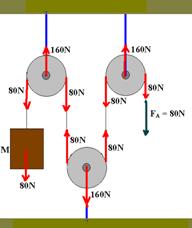
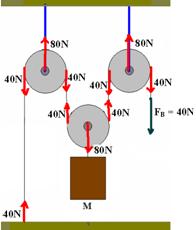
Observe também que no esquema A todas as polias são fixas e o peso do bloco é transmitido integralmente (FA=80N).
No esquema B temos uma polia móvel e o peso do bloco cai pela metade.
08- Forças que agem sobre você --- seu peso de intensidade --- P=m.g --- P=60.10 --- P=600N e a indicação da balança N
Desce acelerando --- P – N = m.a --- 600 – N=60.3 --- -N=180 – 600 --- N=420N --- você se sente “mais leve” (peso aparente).
09- a) Quem está sobre a balança é a pessoa de massa 70kg e sobre ela agem duas forças. Seu peso P para baixo, que ela troca com a Terra, de intensidade P=m.g=70.10 --- P=700N e a força normal N para cima, que ela troca com a balança.
Como ele sobe acelerando, a balança indicará um valor maior que o peso (N>P) --- FR=m.a --- N – P = m.a --- N – 700=70.3
--- N=700 + 210 --- N=910N
b) A força de tração para cima nos cabos está puxando o elevador mais a pessoa (sistema) de peso --- P=(1000 + 70).10 ---
P=10.700N.
Como ele sobe acelerando T>P --- FRm.a --- T – 10.700 = 1.070.3 ---T=10.700 + 3.210 --- T= 13.910N
Como temos três cabos, a força de tração em cada cabo será 13.910/3 --- T=4.636,7N
c) A pessoa bateria com a cabeça no teto e depois cairia com a mesma aceleração e velocidades que o elevador.
10- O peso aparente corresponde à força normal N --- FR=ma --- P – N=m.a --- 100 – N =10.5 --- N=50N.
11- Sobre o corpo agem duas forças. A indicação do dinamômetro para cima (T=2,5N) e o peso para baixo (P=2,0N). Sendo T>P, ele está subindo e acelerando ou descendo e freando. R- D
12- A tração máxima suportada pelo cabo vale T=m.g=1200.10 --- T=12.000N.
O peso do elevador é de P=1000.10 --- P=10.000N. --- sobe acelerando - T>P --- FR=m.a --- T – P =m.a --- 12000 – 10.000=
1.000.a --- a=2m/s2.
13- O peso da pessoa é constante e vale --- P=m.g --- P=80g (g é pedido) --- Quando o elevador sobe com aceleração a, N=960N e
FR=ma --- N – P=ma --- 960 – 80g = 80a I
Quando o elevador desce com aceleração a, N=640N e FR=ma --- P – N=ma --- 80g – 640=80a II
Somando I com II obtemos a=2m/s2, que, substituído em I ou em II nos forneceg=10m/s2.
Então o peso da pessoa é P=mg --- P=80.10 --- P=800N. Quando a balança registrar 800N está registrando o peso da pessoa e nesse caso o elevador estará em repouso ou subindo ou descendo em MRU.
Quando a balança registrar zero o elevador e a pessoa estão em queda livre.
14- Os órgãos internos só se movem ou tendem a se mover, por inércia, quando houver variação de velocidade, ou seja, surgir aceleração. R- D
15- Se indica um peso maior, N>P e o elevador pode estar subindo e acelerando ou descendo e freando. R- C
16- P=m.g --- P=0,8.10 --- P=8,0N --- tração máxima que o fio suporta --- T=9,6N --- FR=m.a --- T – P=ma --- 9,6 – 8,0=0,8.a --- a=1,6/0,8 --- a=2,0m/s2. Como T>P, ele sobe acelerando ou desce freando. R- C
17- Vamos colocar todas as forças que agem sobre o homem e sobre o elevador
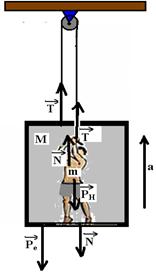
Pe – peso do elevador --- Pe=Mg PH – peso do homem --- PH=mg --- N – força trocada entre o homem e o piso do elevador --- T – força de tração na corda que puxa o homem e o elevador para cima.
Homem --- FR=ma --- T + N - PH=ma --- T + N – mg = ma I
Elevador --- FR=Ma --- T – Pe – N = Ma --- T – Mg – N = Ma II
Somando I com II --- 2T – Mg – mg = Ma + ma --- 2T = (M + m)g + (M + m)a --- T=(M + m).(a + g)/2
18- a=g/5 --- Desce acelerando --- N<P --- FR=m.a --- P – N=m.a --- m.g – N=m.g/5 --- N=(5mg – mg)/5 --- N=4mg/5 I
P=mg II --- Dividindo I por II --- N/P=4mg/5X1/mg --- N/P=4/5 R- D
19- Sobre o elevador temos T=4f=4.1350 --- T=5400N (para cima) e P=mg=600.10 --- P=6000N (para baixo). --- FR=ma ---
P – T=m.a --- 6000 – 5400=600.a --- a=600/600 --- a=1m/s2.
20- Considerando o sistema, elevador mais pessoa de massas (M + m) --- desce freando --- T>P --- FR=m.a --- T – P=(M + m).a --- T – (M + m).g= (M + m).a --- T=(M + m).(a + g) R- B
21- Colocando a força pedida e o peso que interessa:
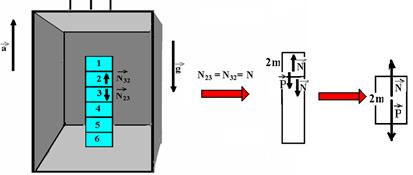
Como o bloco de massa 2m sobe freando com aceleração a, N<P --- FR =m.a --- P – N=2m.a --- 2mg – N=2m.a ---
N=2m(g – a).
22-O astronauta tem que descer com aceleração igual à da gravidade da Lua que é 20% da terrestre
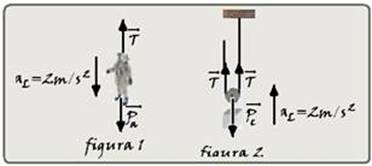
--- al=0,2.10=2m/s2 --- observe a figura 1 onde estão colocadas as forças que agem sobre o astronauta --- FR=m.a --- Pa – T = ma.aL --- 220.10 - T = 220.2 ---
T=2200 – 440 --- T= 1760N --- essa tração é transmitida até o contrapeso --- figura 2 --- o contrapeso deve subir com a mesma aceleração que o astronauta está descendo, ou seja, aL=2m/s2 --- FR=mc.aL --- 2T – Pc = mc.aL --- 2.1760 = mc.10 =
Mc.2 --- mc≈293kg --- como, segundo o enunciado existem forças de atrito, este resultado é aproximado eestá mais próxima da alternativa A --- R- A
23-Para que a distância vertical entre os centros de massa de cada um passe de 9m para 4,5m, o contrapeso deve estar verticalmente mais abaixo que o astronauta e cada um deles deve se deslocar de S=4,5/2=2,25m (veja figura) --- escolhendo um
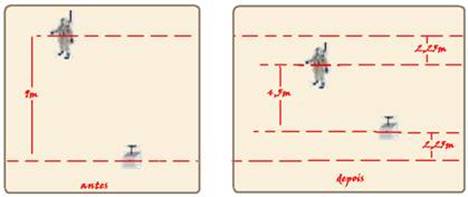
deles, por exemplo, o astronauta --- ele deve subir Sa=2,25m enquanto que no mesmo tempo o contrapeso desce de 2,25m --- equação do astronauta --- Sa=So + Vot + a.t2/2 --- 2,25 = 0 + 0.t + 2.t2/2 --- t2=2,25 --- t=1,5s --- R- D
24-Pelo enunciado eles se movem com acelerações de 0,2gTerra, mas como existe atrito essa aceleração vai diminuir com a dissipação de energia --- R- B