Plano inclinado sem atrito

Cálculo da intensidade de P_P e P_N utilizando o triângulo retângulo da figura abaixo:

Como não existe atrito, o bloco desce com aceleração de intensidade a, tal que F_R = m.a    P_P = m.a    m,g.senα = m.a    a = g.senα (aceleração de descida do bloco de massa m).

Se o bloco estiver em equilíbrio (estático ou dinâmico), a força resultante sobre ele seria nula e, nesse caso haveria ou uma força de atrito (F_at) ou uma força externa (F) anulando P_P.

O que você deve saber, informações e dicas

Num plano inclinado, se não houver atrito e nem força externa, o bloco desce com aceleração de

intensidade a, tal que F_R=m.a    P_P = m.a   m.g.senα = m.a     a = g.senα.

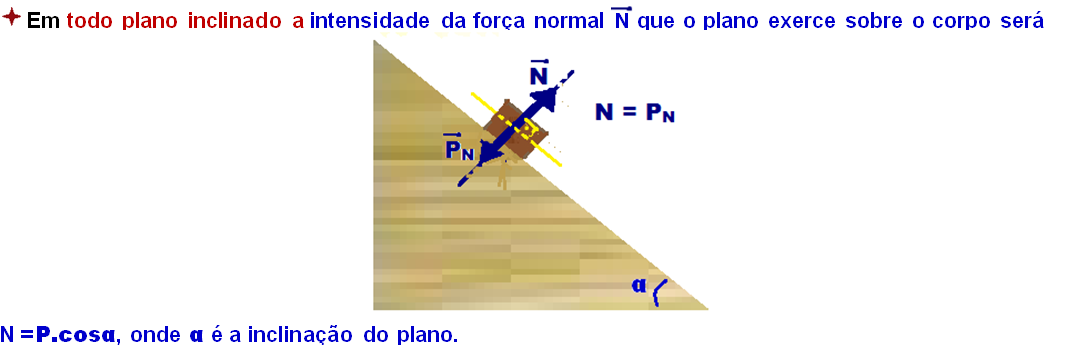
Resolução comentada de exercícios de vestibulares sobre

Plano inclinado sem atrito

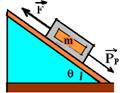
01-(UNESP-SP) A figura mostra um bloco de massa m subindo uma rampa sem atrito, inclinada de um ângulo q, depois de ter sido lançado com uma certa velocidade inicial.

Desprezando a resistência do ar,

a) faça um diagrama vetorial das forças que atuam no bloco e especifique a natureza de cada uma delas.

b) determine o módulo da força resultante no bloco, em termos da massa m, da aceleração g da gravidade e do ângulo q. Dê a direção e o sentido dessa força.

02-(PUC-MG) A figura1 representa um bloco de massa m que, após ser lançado com velocidade v, sobe uma rampa de comprimento L, sem atrito, inclinada de um ângulo q.

Assinale a opção que corresponde às forças que atuam no bloco enquanto ele estiver subindo a rampa. R- C

Assinale a opção que corresponde às forças que atuam no bloco enquanto ele estiver subindo a rampa.

03-(Ufpr-PR) O empregado de uma transportadora precisa descarregar de dentro do seu caminhão um balcão de 200 kg. Para facilitar a tarefa do empregado, esse tipo de caminhão é dotado de uma rampa, pela qual podem-se deslizar os objetos de dentro do caminhão até o solo sem muito esforço.

 Considere que o balcão está completamente sobre a rampa e deslizando para baixo. O empregado aplica nele uma força paralela à superfície da rampa, segurando-o, de modo que o balcão desça até o solo com velocidade constante. Desprezando a força de atrito entre o balcão e a rampa, e supondo que esta forme um ângulo de 30° com o solo, determine o módulo da força paralela ao plano inclinado exercida pelo empregado.(g=10m/s²).

04-(UNIMEP-SP) Um bloco de massa 5kg é arrastado ao longo de um plano inclinado sem atrito, conforme a figura.

Para que o bloco adquira uma aceleração de 3m/s² para cima, a intensidade de  deverá ser: (g=10m/s², senq=0,8 e cosq=0,6).

a) igual ao peso do bloco     

b) menor que o peso do bloco     

c) igual à reação do plano     

d) igual a 55N    

e) igual a 10N

05-(UFGO) Um bloco desliza sobre um plano horizontal sem atrito com velocidade constante .

Em seguida, ele sobe uma rampa de inclinação q, também sem atrito, até parar no ponto C da figura. Calcule a distância percorrida BC ao longo da rampa.

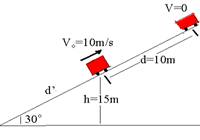
06-(UFBA) Uma garota puxa um carrinho de massa 2,0kg com velocidade V_o=10m/s, por uma rampa de inclinação de 30^o,conforme a figura.

Ao atingir a altura h=15m o barbante se rompe. Sabendo que g=10m/s², calcule o intervalo de tempo entre o instante do rompimento do barbante e a chegada do carrinho até a base da rampa. Despreze o atrito.

07-(UFRJ-RJ) Um plano está inclinado, em relação à horizontal, de um ângulo q cujo seno é igual a 0,6 (o ângulo é menor do que 45°).

Um bloco de massa m sobe nesse plano inclinado sob a ação de uma forca horizontal  , de módulo exatamente igual ao módulo de seu peso, como indica a figura a seguir.

 Supondo que não haja atrito entre o bloco e o plano inclinado, calcule o módulo da aceleração do bloco.

08-(UFRJ-RJ) Deseja-se manter um bloco em repouso sobre um plano inclinado 30° com a horizontal. Para isso, como os atritos entre o bloco e o plano inclinado são desprezíveis, é necessário aplicar sobre o bloco uma força. Numa primeira experiência, mantém-se o bloco em repouso aplicando uma força horizontal , cujo sentido está indicado na figura 1.

Numa segunda experiência, mantém-se o bloco em repouso aplicando uma força  paralela ao plano inclinado, cujo sentido está indicado na figura 2

Calcule a razão /

09-(FUVEST- SP) O mostrador de uma balança, quando um objeto é colocado sobre ela, indica 100 N, como esquematizado em A.

Se tal balança estiver desnivelada, como se observa em B, seu mostrador deverá indicar, para esse mesmo objeto, o valor de

10-(UNESP-SP) Um bloco sobe uma rampa deslizando sem atrito, em movimento uniformemente retardado, exclusivamente sob a ação da gravidade, conforme mostrado na figura 1.

Ele parte do solo no instante t = 0 e chega ao ponto mais alto em 1,2 s. O módulo da velocidade em função do tempo é apresentado no gráfico na figura 2.

Considerando g = 10,0 m/s², a altura em que o bloco se encontrava em t = 0,4 s era

11- (Ufal) Uma rampa AB, inclinada de 37° em relação à horizontal, tem 12 m de comprimento e não oferece atrito para um pequeno corpo de massa 1,0 kg, abandonado, a partir do repouso no ponto A.

Adote g = 10 m/s², cos 37° = 0,80 e sen 37° = 0,60.

Determine:

a) a força resultante sobre o corpo;                                         

b) o tempo necessário para o percurso AB.

12-(FATEC-SP) Um fio, que tem suas extremidades presas aos corpos A e B, passa por uma roldana sem atrito e de massa desprezível. O corpo A, de massa 1,0 kg, está apoiado num plano inclinado de 37° com a horizontal, suposto sem atrito.

Adote g = 10m/s², sen 37° = 0,60 e cos 37° = 0,80.

Para o corpo B descer com aceleração de 2,0 m/s², o seu peso deve ser, em newtons,

13- (PUC-MG) Na montagem mostrada na figura, os corpos A e B estão em repouso e todos os atritos são desprezíveis.

O corpo B tem uma massa de 8,0 kg. Qual é então o peso do corpo A em newtons?

14-(UFU-MG) 

a) Em um plano inclinado de 30° em relação à horizontal, são colocados dois blocos de massas M₁ = 10 kg e M₂ = 10 kg, sustentados por uma única roldana, como mostra a figura 1 a seguir.

A aceleração da gravidade é de 10 m/s², sen 30° = 0,50 e cos 30° = 0,87. Desprezando o peso da corda, bem como os efeitos de atrito, determine o vetor aceleração do bloco de massa M₁.

b) No mesmo sistema, o bloco de massa M₂ é preso agora a uma segunda roldana. A corda em uma das extremidades está fixada no ponto A, conforme figura 2.

Desprezando o peso da corda e da segunda roldana, bem como os efeitos de atrito, determine o vetor aceleração para cada um dos dois blocos.

15-(UFU-MG) Um bloco de massa M = 8 kg encontra-se apoiado em um plano inclinado e conectado a um bloco de massa m por meio de polias, conforme figura a seguir.

Dados: sen 30° = 1/2; cos 30° = Ö3/2

O sistema encontra-se em equilíbrio estático, sendo que o plano inclinado está fixo no solo. As polias são ideais e os fios de massa desprezível. Considerando g = 10 m/s², q = 30° e que não há atrito entre o plano inclinado e o bloco de massa M, marque a alternativa que apresenta o valor correto da massa m, em kg.

16-(UEL-PR) Dois blocos A e B de massas m_A=2kg e m_B=3kg, ligados por um fio, são dispostos conforme o esquema a seguir, num local onde g=10m/s².

Desprezando-se os atritos e considerando ideais a polia e o fio, determine a intensidade da força tensora no fio. Considere sen30^o=0,5 e cos30^o=0,87

17-(UERJ-RJ) Um jovem, utilizando peças de um brinquedo de montar, constrói uma estrutura na qual consegue equilibrar dois corpos, ligados por um fio ideal que passa por uma roldana. Observe o esquema.

Admita as seguintes informações:

• os corpos 1 e 2 têm massas respectivamente iguais a 0,4 kg e 0,6 kg;

• a massa do fio e os atritos entre os corpos e as superfícies e entre o fio e a roldana são desprezíveis.

Nessa situação, determine o valor do ângulo β.

18-(INATEL) Num experimento de mecânica, um carrinho desce um plano inclinado e continua movendo-se por um plano

 horizontal. O carrinho possui um pequeno tanque cheio de tinta, que vaza por um pequeno furo na sua parte inferior, com as gotas caindo em intervalos de tempos iguais. Desprezando-se a resistência do ar, e possíveis forças de atrito no eixo do carrinho, podemos afirmar, a respeito da posição das gotas de tinta deixadas na superfície pela qual o carrinho se move, que elas:

a) estarão igualmente espaçadas durante todo o trajeto.

b) estarão aumentando suas distâncias na descida e permanecerão igualmente espaçadas na horizontal.

c) estarão aumentando suas distâncias tanto na descida quanto na horizontal.

d) estarão diminuindo suas distâncias na descida e aumentando na horizontal.

e) estarão diminuindo suas distâncias tanto na descida quanto na horizontal.

19-(UFSJ-MG) Um bloco de massa 10 kg e abandonado a partir do repouso no topo de uma rampa de

altura igual a 2 m e inclinação igual a 30º. Considerando a aceleração da gravidade igual a 10 m/s² e que o atrito entre o bloco e a rampa é muito pequeno. determine o intervalo de tempo para que o bloco saia do topo da rampa e atinja sua base.

20-(UFLA-MG) Um bloco é abandonado (v_o= 0) do alto de um plano inclinado, totalmente isento de

atrito. No final do 1º segundo de movimento, o bloco desliza uma distância d. Ao final do 3º segundo de movimento, terá percorrido uma distância de:

21-(UFS-SE) Um corpo de massa 2,0 kg é abandonado, a partir do repouso, do topo de um plano inclinado de 30^o com relação à horizontal. A superfície não oferece atrito ao movimento e, ao chegar à base do plano inclinado, o corpo apresenta velocidade de 6,0 m/s. Adote g = 10 m/s² e analise as afirmações seguintes:

a)A aceleração do movimento tem módulo 10m/s²

b) O topo do plano inclinado está a 1,8 m de altura.

c) O tempo gasto na descida do corpo é de 1,2 s.

d) Até chegar à base do plano o corpo recebeu impulso de 12 N.s.

e) O trabalho realizado pelo peso do corpo na descida tem valor 36 J.

22-(UERJ-RJ) A figura abaixo representa o plano inclinado ABFE, inserido em um paralelepípedo retângulo ABCDEFGH de base horizontal, com 6 m de altura CF, 8 m de comprimento BC e 15 m de largura AB, em repouso, apoiado no solo.

Considere o deslocamento em movimento retilíneo de um corpo P₁ de M até N e de um corpo P₂ de A até F.

Admita as seguintes informações:

- P₁ e P₂ são corpos idênticos;

- F₁ e F₂ são, respectivamente, as componentes dos pesos de P₁ e P₂ ao longo das respectivas trajetórias;

- M e N são, respectivamente, os pontos médios das arestas AB e EF.

Considerando esses dados, a razão F₁/F₂ equivale a:

a) 17/6                           

b) 4/3                                  

c) √15/3                               

d) √15/3                             

e) √13/2

23-(UECE-CE)

Em dois experimentos de mecânica, uma massa puntiforme desliza sobre duas rampas de mesmo

comprimento, 5m, e inclinações diferentes. Em um dos experimentos a distância horizontal percorrida pela massa é d_I = 3 m e no outro é d_II = 4 m. Suponha que ambas as massas partam do repouso e estejam sob a ação de um mesmo campo gravitacional uniforme e vertical, e despreze todos os atritos. Ao atingir o ponto final da rampa, a razão entre as velocidades das massas nos dois experimentos, v_II/v_I, é dada por

24-UDESC-SC)

A figura mostra dois blocos de massa  m_A e  m_B conectados por um fio inextensível e de massa  desprezível, que passa por duas polias também de massa desprezível. O bloco de massa  m_A está sobre um plano inclinado que forma um ângulo α com a horizontal e sustenta o bloco de massa m_B

.   

Assinale a alternativa que apresenta o valor de  m_B capaz de fazer com que o sistema permaneça em equilíbrio, desprezando todas as forças de atrito.

a.(   )  m_B = m_A cos(α)         

b.(   )  m_B = m_A sen(α)         

c.(   )  m_B = 2m_A         

d.(   )  m_B = 2m_A sen(α)          

e.(   )  m_B = 2m_Acos(α)

Resolução comentada dos exercícios de vestibulares sobre

Plano inclinado sem atrito

01-

a)

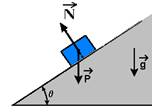
b)

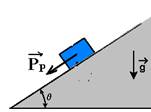
F_R=P_P=Psenq =mgsenq  ---   direção paralela ao plano, no sentido para baixo (oposto ao do lançamento) que retarda o bloco na subida e o acelera na descida.

02- R- C  ---  veja a teoria

03- Forças que agem sobre o balcão na direção do movimento:

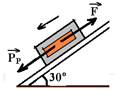
P_P  ---  parcela do peso que tenta fazer o bloco descer o plano inclinado  ---  P_P=m.g.sen30^o  ---  P_P=200.10.0,5  ---  P_P=1.000N

F  --- intensidade da força aplicada pelo empregado sobre o balcão fazendo-o descer com velocidade constante, ou seja, está em equilíbrio estático (F_R=0). Assim, F=P_P=1.000N_.

04- P_P=m.g.senq  ---  P_P=5.10.0,8  ---  P_P=40N

Como ele sobe com aceleração de 3m/s², F_R=m.a  ---  F – P_P=m.a  ---  F – 40=5.3  --- F=55N R- D

05- A força que reduz a velocidade do bloco é P_P=m.g.senq  ---  P_P=F_R=m.a  ---  m.g.senq= m.a  ---  a=g.senq

Como ele pára em C – V=0  ---  Torricelli  ---  V² = V_o² + 2.a.DS  ---  0² = V_o² + 2.(-g.senq).BC  ---  BC = V_o²/2.g.senq

06- Cálculo da aceleração de subida e de descida do carrinho  ---  P_P=F_R=m.a  ---  m.g.sen30^o = m.a  ---  a=g.sen30^o  ---

a=10.0,5  ---  a=5m/s²

1^a etapa  ---  tempo de subida com a velocidade variando de V_o=10m/s a V=0 e com a=-5m/s²

 ---  V=V_o + a.t  ---  0=10 – 5t  --- t=2s (tempo de subida) 

---  distância percorrida na subida  ---  d=V_o.t + a.t²/2  ---  d=10.2 – 5.2²/2  ---  d=10m 

2^a etapa  ---  cálculo de d’  ---  sen30^o=15/d’  ---  d’=15/0,5  ---  d’=30m  ---  tempo que o carrinho demora para ir do topo do plano inclinado (V_o=0) até sua base, percorrendoDS=40m com a=5m/s².

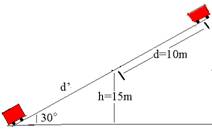
DS= v^o.t + a.t²/2  ---  40=0.t + 5.t²/2  ---  t²=16  ---  t=4s  ---  tempo total de subida e descida = 2 + 4=6s

07- A parcela do peso paralela ao plano inclinado vale  ---  P_P=mgsenq. A parcela de F (F_P), paralela ao plano inclinado vale:

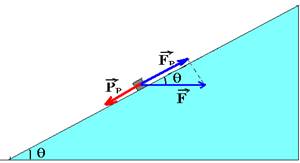
cosq=cateto adjacente/hipotenusa  ---  cosq=F_P/F  ---  F_P=F.cosq  ---  sendo F=P=mg  ---  F_P=mgcosq

Como o bloco sobe com aceleração a  ---  F_R=m.a  ---  F_P – P_P=m.a  ---  mgcosq - mgsenq=m.a  gcosq - gsenq =a  ---  10.0,8 – 10.0,6=a  ---  a=2m/s².

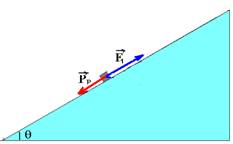
08- Forças que agem sobre o corpo na figura 1 

Como o corpo está em repouso  ---  F_R=0  --- P_P=F_P  ---  P.sen30^o = F.cos30^o  ---  P/2 = F.Ö3/2  ---  P=F.Ö3 I 

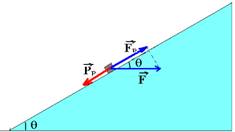
Forças que agem sobre o corpo na figura 2

Como o corpo está em repouso  ---  F_R=0  ---  P_P=F₁  ---  P.sen30^o = F₁  ---  P/2=F₁  --- P=2F₁ II

Igualando I com II  ---  F.Ö3 = 2.F₁  ---  F₁/F=Ö3/2

09- Em A  ---  N=P  ---  N=100N (indicação da balança)

Em B  ---  N=P_N  ---  N=P.cosa  ---  N=100.cateto adjacente/hipotenusa  ---  N=100.40/50  ---  N=100.0,8  ---  N=80N  R- D

10- Da figura 2  ---  V_o=6m/s  ---  V=0  --- t=1,2s  ---  V=V_o + a.t  ---0=6 + a.1,2  ---  a= - 5m/s²  em módulo a=5m/s²

A força que retarda o bloco é P_P tal que  ---  F_R=m.a  ---  P_P=m.a  ---m.g.sena=ma  ---  10.sena=5  ---  sena=1/2  ---  a=30^o

Em todo gráfico VXt o deslocamento do corpo é fornecido pela área  ---  de 0 a 0,4s a área é:

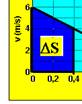
DS=área do trapézio=(B + b).h/2  ---  DS=(6 + 4).0,4/2  ---  DS=2m.

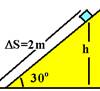
sen30^o=h/2  ---  0,5=h/2  ---  h=1m   R- B

11- a) Como não tem atrito  ---  F_R=P_P=m.g.sen37^o=1.10.0,6  ---  F_R=P_P=6N

b) F_R=m.a  ---  6=1.a  ---  a=6m/s²  ---  DS=V_o.t + a.t²/2  ---  12=0.t + 6.t²/2  ---  t=Ö4  ---  t=2s

12- Colocando as forças:

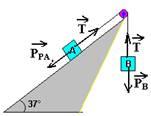
Bloco A  ---  sobe com aceleração de 2m/s² tal que  ---  T – P_PA=m_A.a  ---  T – m.g.sen37^o=1.2  ---  T=1.10.0,6+2  ---  T=8N

Bloco B  ---  desce com a=2m/s²  ---  P_B – T=m_B.a  ---  m_B.10 – 8=m_B.2  --- 8m_B=8  ---  m_B=1kg  ---  P_B=10N  R-D

13- Colocando as forças:

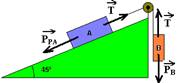
 Repouso  ---  F_R=0  ---  bloco B  ---    P_B=T  ---  T=m_B.g  ---  T=8.10  ---  T=80N     bloco A  ---  P_PA=T  --- P_A.sen45^o=80  ---

P_A.Ö2/2=80  ---  P_A=80.Ö2N

14- a)Figura 1: M₂  ---  P=10.10  ---  P=100N  ---  M₁  ---  P_P=m.g.sen30^o  ---  P_P=10.10.1/2  ---  P_P=50N

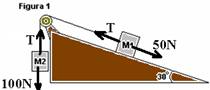
O sistema se move no sentido anti-horário  ---  100 – T=10.a I  ---  T – 50=10.a II  ---  somando I com II  ---  50 =20.a  ---  a=2,5m/s² e é a mesma para os dois blocos.

b) figura 2  ---  observe que a polia de baixo é móvel, então ela transmite apenas metade do peso de M₂ para M₁ sendo que a outra metade é suportada pelo teto em A.

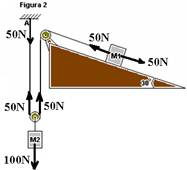
Assim, observe que a força resultante sobre M₁ é nula e a=0.  O mesmo ocorre com M₂.

15-   m  ---  P=10m  ---  M  ---  observe na figura abaixo que q e a são complementares portanto sena=cosq  ---    P_P=mgsena=mgcosq  ---  P_P=8.10.Ö3/2  ---  P_P=40Ö3N

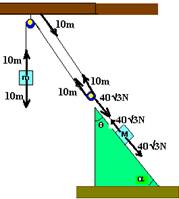
Observe na figura acima que do peso de M apenas 10m é transmitido a m, pois os outros 10m são sustentados pelo teto. Assim,

10m=40Ö3  ---  m=4Ö3kg.  R- B

16- Como não existe atrito o sistema se move no sentido horário. Colocando as forças que atuam na direção do movimento.

P_PB=m_B.g.sen30^o=3.10.0,5  ---  P_PB=15N

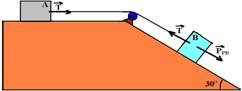
bloco A  ---  F_R=m_A.a  ---  T=2.a I  ---  bloco B  ---  F_R=m_B.a  ---  P_PB – T=3.a   ---   15 – T=3.a II  ---  somando I com II  --- 

15=5.a  ---  a=3m/s²  ---  T=2.3  ---  T=6N.

a.

17- Dados: m₁= 0,4 kg; m₂= 0,6 kg  ---  Analisando a figura:

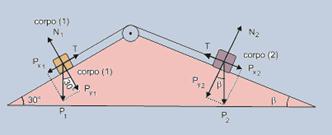
Como os corpos estão em equilíbrio, as forças também se equilibram em todas as direções: Assim:

T = P_x1 T = P_x2  ---  P_x2=P_x1  ---  m₂gsenβ=m₁gsen30^o  ---  senβ=m₁/m₂.sen30^o  ---  senβ=1/3  ---  β=arc sem 1/3

18- Como os atritos são desprezados, o movimento é acelerado no plano inclinado e uniforme no plano horizontal: 

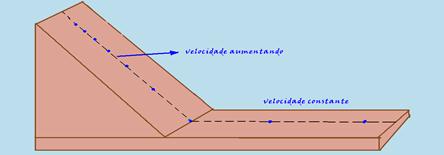
R- B

19- Como não existe atrito, a força resultante sobre o bloco na direção do deslocamento, tem intensidade  ---  F_R=P_p=mgsen30^o  ---  pela lei fundamental da dinâmica F_R=ma  ---  mgsen30^o=ma  ---  a=gsen30^o=10.1/2  ---  a=5m/s²  ---  S=S_o + V_ot + at²/2  ---  4=0 +

0.t + 5t²/2  ---  t²=1,6  ---  t≈1,26s
20- A intensidade da força resultante sobre o bloco na direção do movimento é F_R=P_p=mgsenθ=ma  ---  a=gsenθ  ---  quando t=1s – S=d  ---  d=at²/2  ---  d=gsenθ.1²/2  ---  d=gsenθ/2  ---  quando t=3s  ---  d’=at²/2  ---  d’=gsenθ.9/2  ---  d’/d=(9.gsenθ/2)/gsenθ/2  ---  d’=9d  ---  R- C

21- a) mgsen30^o=ma  ---  a=gsen30^o=10.1/2  ---  a=5m/s²  ---  falsa

b) cálculo do deslocamento ΔS  ---  equação de Torricelli  ---  V²=V_o² + 2.a. ΔS  ---  6²=0²+ 2.5.ΔS  ---  ΔS=3,6m  ---  altura h  ---  sen30^o=h/3,6  ---  h=1,8m  ---  correta

c) V=V_o + at  ---  6=0 + 5t  ---  t=1,2s  ---  correta

d) Na base  ---  I=m.ΔV=2.(6 – 0)  ---  I=12N.s  ---  correta

e) Trabalho na vertical  ---  W=P.h=20.1,8  ---  W=36J  ---  correta

R- (F,C,C,C,C)

22- Os corpos se movimentam nos seguintes planos inclinados:

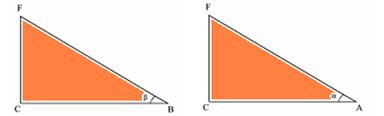
As componentes dos pesos de P₁ e P₂, ao longo das respectivas trajetórias, são dadas por  ---  F₁=Psenβ  ---  F₂=Psenα  --- 

F₁/F₂=senβ/senα  ---  senβ=CF/BF=6/10  ---  AF é a diagonal do paralelepípedo  ---  (AF)²=36 + 64 + 225  ---  AF=5√13  --senα=CF/AF=6/5√13  ---  F₁/F₂=6/10 x 5√13/6  ---  F₁/F₂=√13/2  ---  R- E

23-

  Observe que os dois triângulos são pitagóricos, então a altura de I vale 4m e a de II, 3m  ---  como não existe atrito

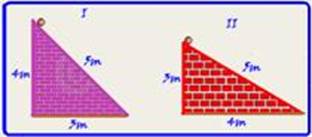
e a força peso é conservativa (independe da trajetória), você pode considerá-las como em queda livre, com a=g e V_o=0, I da altura de 4m e II da altura de 3m  ---  Torricelli  ---  I  ---  V_I² = V_oI² + 2gh_I=0² + 2.10.4  ---  V_I = √80  --- 

II  ---  V_II² = V_oII² + 2gh_II=0² + 2.10.3  ---  V_I = √60  ---  V_II/V_I = √80/√60= (√3.√5)/(2.√5)  ---  V_II/V_I=√3/2  --- 

R- B.

24-

 A parcela do peso responsável pela descida do bloco A é dada por P_pA=P_Asenα=m_A.g.senα  ---  a figura mostra todas as forças

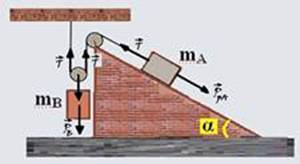
 que agem sobre o bloco  ---  como o sistema está em equilíbrio a força resultante sobre cada bloco é nula  ---  bloco A  ---  P_pA=T  ---  m_A.g.senα =T  ---  bloco B  ---  P_B=2T  ---  m_B.g =2.m_A.g.senα  ---  m_B=2m_A.g.senα  ---  R- D