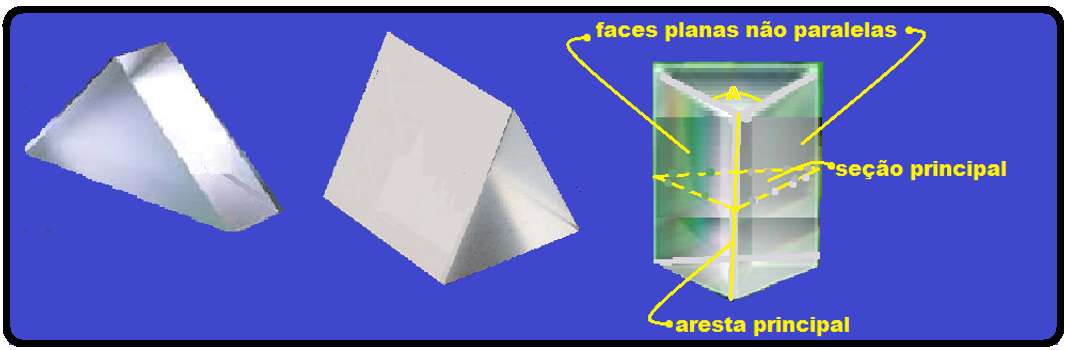
Prismas

Prisma óptico

Um prisma óptico corresponde a um conjunto formado por três meios homogêneos e transparentes

ou por dois dioptros planos, em que as superfícies planas não são paralelas (faces do prisma) que se interceptam em retas que são as arestas.

Tipos de prismas

Prismas dispersivos decompõem (dispersam) a luz policromática branca em suas infinitas

componentes monocromáticas (cores) que compõem o espectro luminoso.

Prismas refletivos (de reflexão total) substituem os espelhos, com melhor rendimento, na

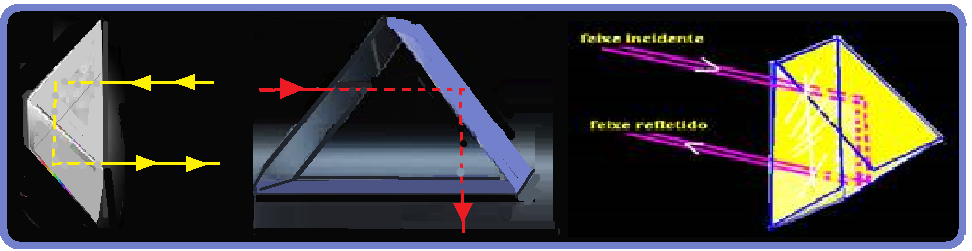
reflexão da luz.

Cálculo do desvio total ou desvio total angular (d)

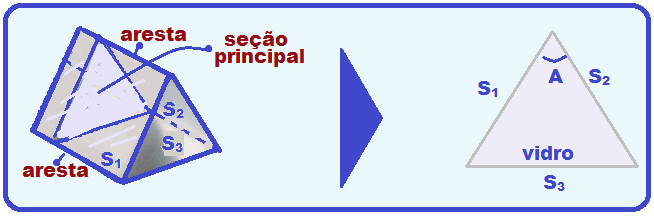
As superfícies S₁, S₂ e S₃ são as faces do prisma. A interseção das faces S₁ e S₂ determinam o ângulo A que é chamado de ângulo de refringência. 

A superfície S₃ que geralmente é opaca é utilizada apenas como apoio.

Considere o prisma da figura feito de material de índice de refração n₂ e imerso num meio de índice de refração n₁.

Um raio de luz monocromático incide na face da esquerda com ângulo de incidência i e se refrata no interior do prisma com ângulo de refração r.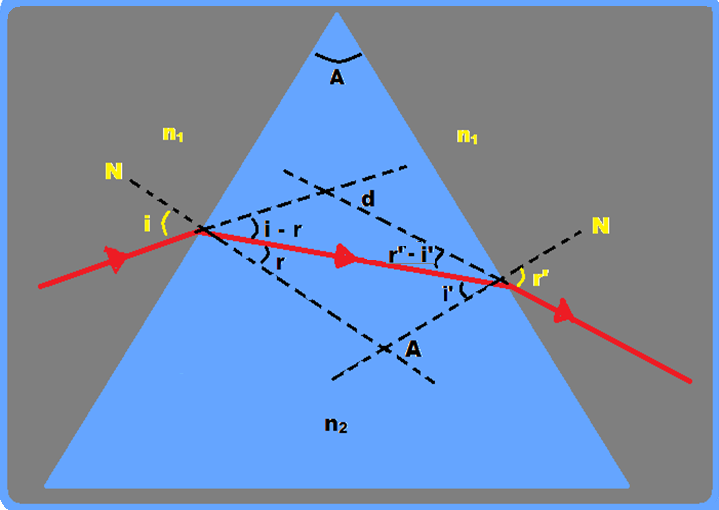

Aplicando a lei de Snell-Descartes na face da esquerda  n₁.sen i = n₂.sen r.

Esse raio incide na outra face com ângulo de incidência i’ e se refrata novamente para o meio 1 com ângulo de refração r’, tal que    n₂.sen i’ = n₁.sen r’.

O desvio total ou desvio angular (d) é definido como sendo o ângulo entre os prolongamentos dos raios incidente na 1^a face e emergente na 2^a face.

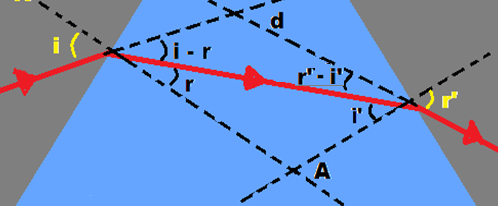
Observe na figura ao lado que o desvio angular na 1^a face (ângulo entre o prolongamento do raio

incidente e o do raio refratado) 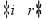, somado ao desvio angular na 2^a face ( ângulo entre o prolongamento do raio emergente e o raio incidente) 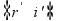nos fornece o desvio total d, ou seja, d = (i - r) + (r’- i’)  (I)

Observe ainda na mesma figura que o ângulo de refringência (A) do prisma é fornecido pela expressão A = r + i’    r = A - i’ (II)

Substituindo II em I obtemos a fórmula do desvio total:

Desvio mínimo

Prismas de reflexão total

 Prismas de reflexão total  Quando a luz incide perpendicularmente à uma das faces de um prisma, ele pode sofrer refração sem sofrer desvio nesta face, reflexão total na segunda face e emergir na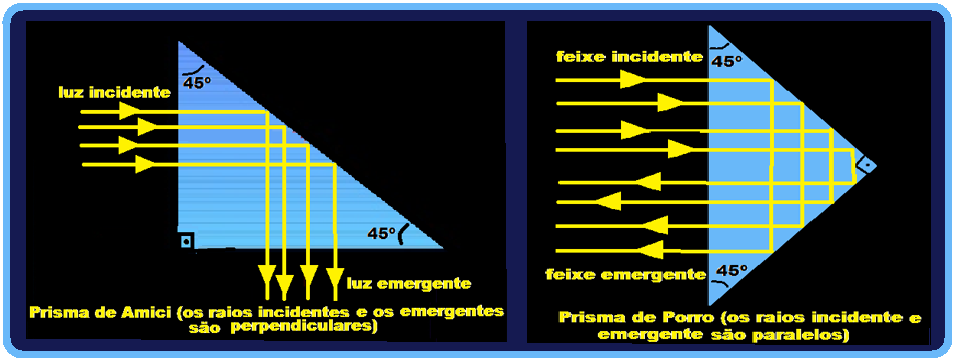

terceira face, também sem sofrer desvio.

Os prismas de reflexão total mais usados são constituídos de um triângulo retângulo isósceles, que recebem a luz em posições diferentes.

Normalmente são de vidro e imersos no ar, substituindo os espelhos planos com melhor rendimento.

O que você deve saber, informações e dicas

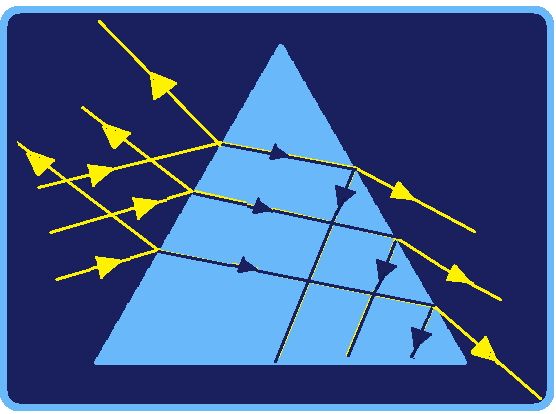
 Embora a refração seja predominante, ocorre também absorção e reflexão em ambas as faces do prisma.

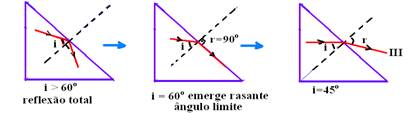
As trajetórias dos raios incidente, do refratado no interior do prisma e do emergente se deslocam como se você estivesse girando um “saca-rolhas” no sentido horário, ou seja, o raio incidente sobe,

e os outros dois descem conforme a sequência das figuras acima.

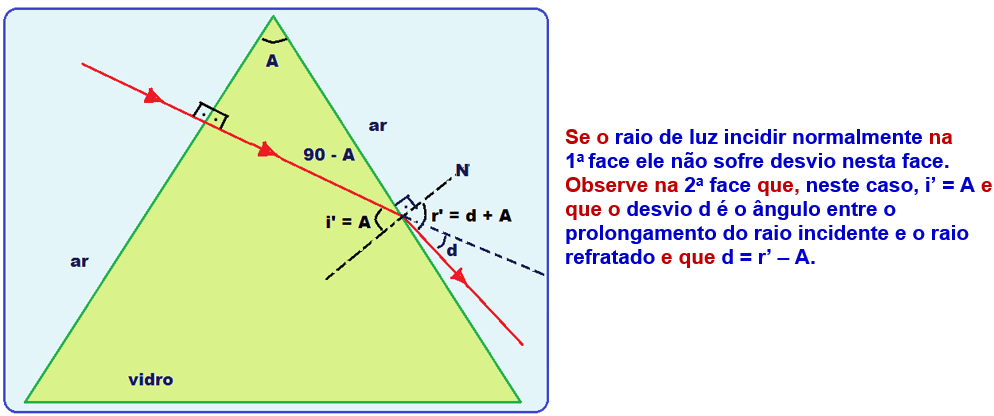
Incidência normal na primeira face do prisma

Ainda neste caso, se o raio emergir rasante, teremos que o ângulo de incidência i’ é igual ao ângulo

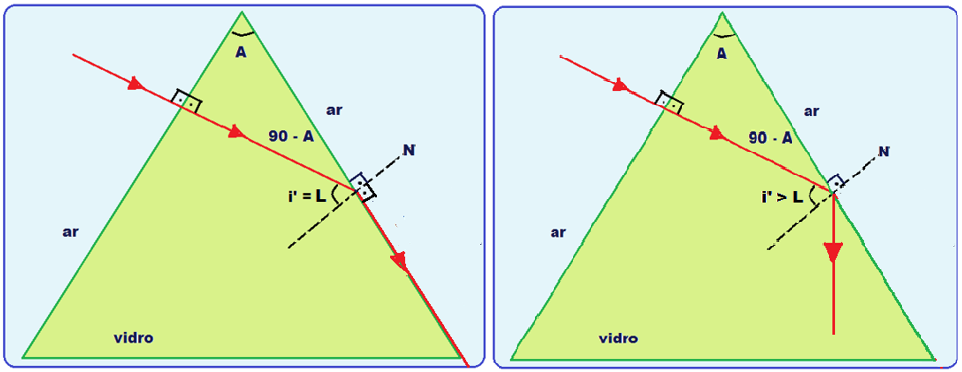
limite L, fornecido pela expressão senL = n_menor /n_maior    senL =n_ar/n   senL = 1/n.

Como i’ = L   sen i’ = sen L   sen i’ = 1/n . 

Portanto se sen i’ for igual a 1/n, o raio de luz emerge rasante e se, i’ for maior que L, o raio de luz sofre reflexão total pois neste caso sen L > 1/n .

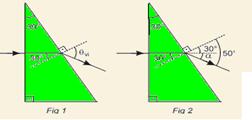
 Se qualquer um dos dois prismas de reflexão total abaixo tiver índice de refração absoluto (n) e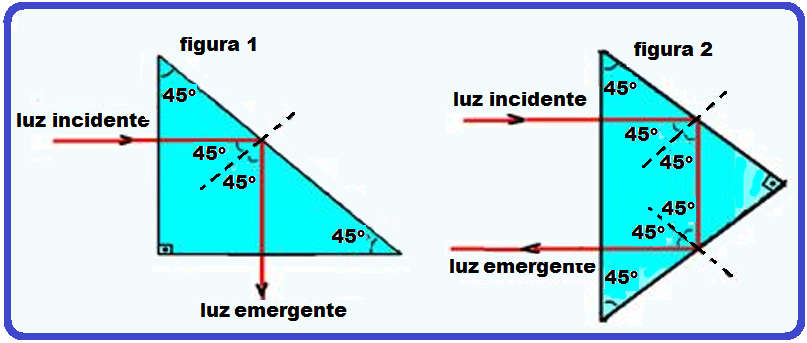

estiver imerso no ar (n_ar = 1), o valor do índice de refração n do prisma para que ocorra reflexão total na face interna (figura 1) ou faces internas (figura 2) deve incidir com ângulo superior ao ângulo limite, ou seja i > L, ou ainda seni > senL    sen 45^o > senL    √2/2 > 1/n   

n > √2 > 1,4.

Experiência de Newton na dispersão da luz policromática branca

Veja como Isaac Newton descreveu a proposta do experimento que lhe permitiu descartar a influência do vidro do prisma como causa da dispersão da luz branca.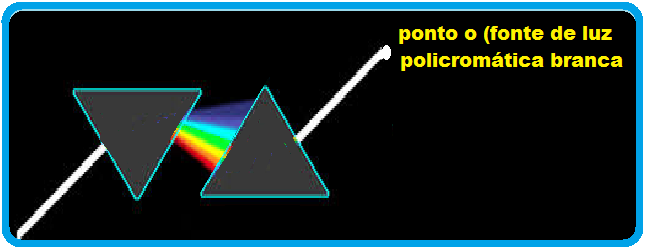

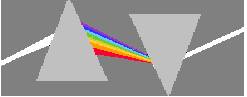
Considerando que a fonte de luz era o orifício O da janela do quarto de Newton, veja a descrição e o desenho da montagem executada por ele experiência:

"Eu peguei outro prisma igual ao primeiro e o coloquei de maneira que a luz fosse refratada de modos opostos ao passar através de ambos e, assim, ao final, voltaria a ser como era antes do primeiro prisma tê-la dispersado."

Exercícios interessantes:

01-

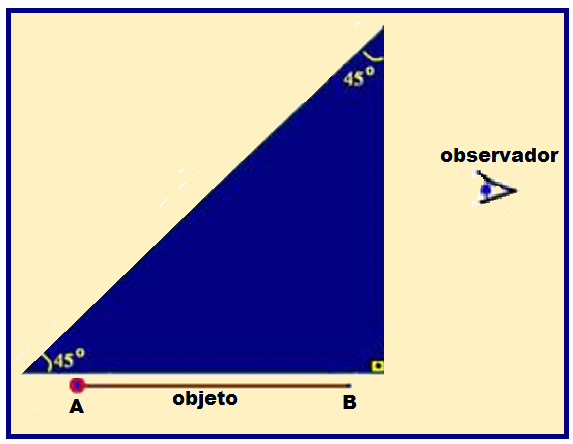
Na figura ao lado, estão representados um prisma retangular, cujos ângulos da base são iguais a 45^o, um objeto AB e o olho de um observador.

Devido ao fenômeno da reflexão total, os raios de luz provenientes do objeto são refletidos na base do prisma, que funciona como um espelho plano.

Esquematize a imagem A’B’ do objeto AB visto pelo observador:

Resolução:

Na figura o raio de luz vertical e para cima que sai de A penetra no prisma sem sofrer desvio, sofre

reflexão total na face interna inclinada e sai horizontalmente do prisma sem sofrer desvio e atinge os olhos do observador que vê a imagem A’ de A.

O mesmo processo é realizado pelo raio de luz que sai de B e atinge os olhos do observador que vê B’.

Unindo A’ com B’ você localiza a imagem A’B’ de AB vista pelo observador. 

02- Um tipo de sinalização utilizado em estradas e avenidas é o chamado olho-de-gato, o qual consiste na justaposição de vários prismas retos feitos de plásticos que refletem a luz incidente dos faróis dos automóveis.

a) Reproduza o prisma ABC representado na figura abaixo e desenhe a trajetória de um raio de luz que incide perpendicularmente sobre a face OG e sofre reflexões totais nas superfícies AC e BC.

Resolução:

a)

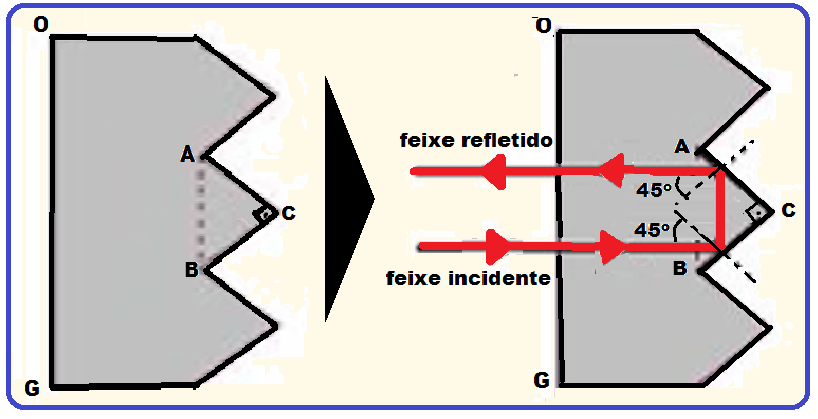
b) Determine o mínimo valor do índice de refração do plástico acima do qual o prisma funciona como um refletor perfeito de luz (toda luz que incide perpendicularmente à superfície OG é refletida). Considere o prisma no ar, onde o índice de refração vale 1,0.

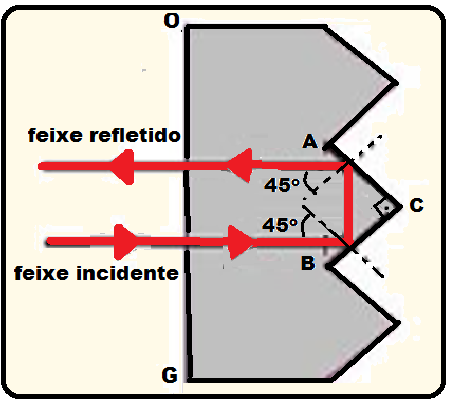
Para que haja reflexão total    i > L   seni > senL    sen45^o > senL    √2/2 > 1/n    n > √2.

03- Um raio monocromático de luz incide no ponto A de uma das faces de um prisma feito de vidro e imerso no ar.

A figura 1 representa apenas o raio incidente i e o raio refratado r num plano normal às faces do prisma, cujas arestas são representadas pelos pontos P, S e T, formando um triângulo eqüilátero.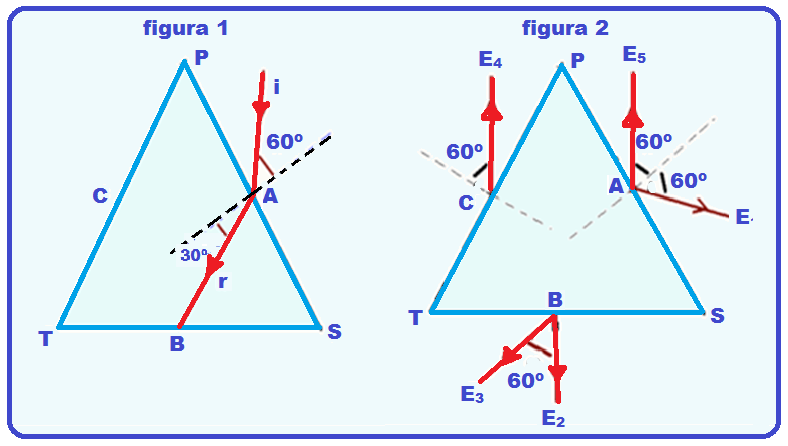

Os pontos A, B e C também formam um triângulo equilátero e são, respectivamente, equidistantes de P e S, S e T, e T e P. Considere os raios E₁, E₂, E₃, E₄ e E₅, que se afastam do prisma, representados na figura 2.

Podemos afirmar que os raios compatíveis com as reflexões e refrações sofridas pelo raio incidente, no prisma, são:

Resolução:

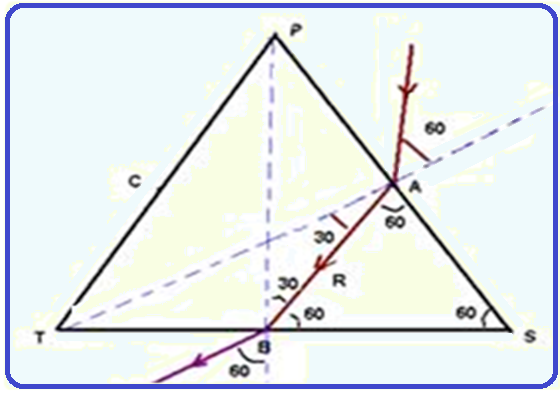
Refração no ponto A    n_ar.sen60^o = n_v.senr    1.√3/2 = n_v.sen30^o    1.√3/2 = n_v.1/2    n_v = √3 (índice de refração do vidro).

Quando atinge o ponto B o raio de luz sofre refração passando para o ar onde n_ar = 1, pois sen30^o = 1/2 e senL = n_menor/n_maior = 1/√3 = √3/3    assim, como seni < senL    i < L    ele não sofre reflexão total em B, sofrendo refração e passando para o ar. 

Aplicando Snell-Descartes no ponto B    n_v.sen30^o = n_ar.senr    √3.1/2 = 1.senr    senr =

√3/2    r = 60^o    R- A

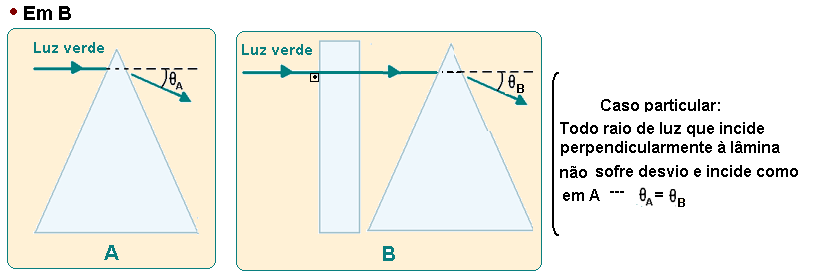
04- Um prisma triangular desvia um feixe de luz verde de um ângulo Ө_A, em relação à direção de incidência, como ilustra a figura A.

Se uma placa plana, do mesmo material do prisma, for colocada entre a fonte de luz e o prisma, nas posições mostradas nas figuras B e C, a luz, ao sair do prisma, será desviada, respectivamente,

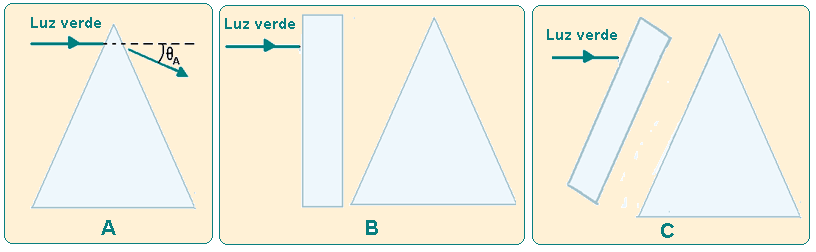de ângulos Ө_B e Ө_C, em relação à direção de incidência indicada pela seta.

Os desvios angulares serão tais que

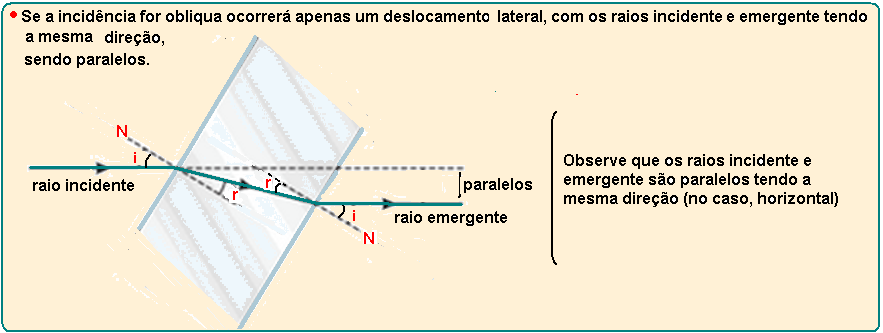
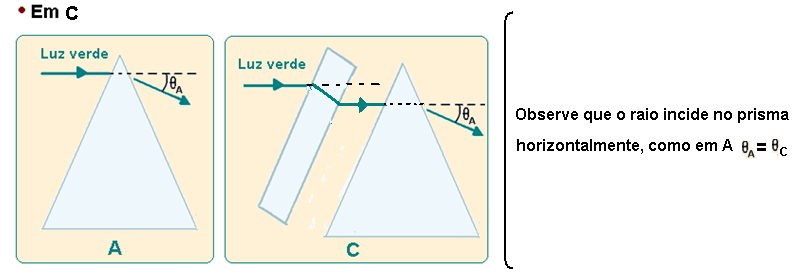
Sempre que um feixe de luz monocromática (uma só cor, no caso, verde) incide sobre uma lâmina de faces paralelas (placa plana do exercício) imersa em um mesmo meio, o raio incidente e o raio emergente são paralelos não sofrendo mudança na direção, no caso horizontal, veja a análise nas figuras abaixo:

R- A

Exercícios de vestibulares com resoluções comentadas sobre

Prismas Ópticos

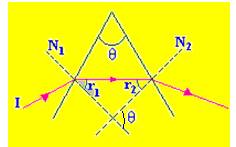
01-(UEL - PR) No esquema adiante considere:

Considerando as indicações do esquema, é correta a relação;

a) r₁ - r₂ = θ       

b) r₁ + r₂ = θ         

c) r₁ + r₂ = 90° - θ      

d) r₁ - r₂= 90° - θ 

e) 2 (r₁ + r₂) = θ 

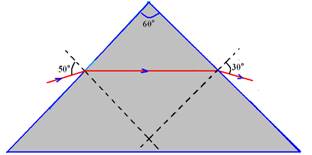
 02-(UEL-PR) A figura abaixo representa um raio de luz que atravessa um prisma. O desvio sofrido por esse raio de luz, em graus, vale:

03-(MACKENZIE-SP) Um raio luminoso incide perpendicularmente a uma das faces de um prisma de vidro (n vidro=), imerso no ar (n ar=1), e emerge rasante à outra face. O ângulo de refringência A desse prisma é:

04-(PUC-SP) Um prisma de vidro, cujo ângulo de refringência é 60°, está imerso no ar. Um raio de luz monocromática incide em uma das faces do prisma sob ângulo de 45° e, em seguida, na segunda face sob ângulo de 30°, como está representado no esquema.

Calcule o índice de refração do vidro em relação ao ar, para essa luz monocromática.

05- (PUC-SP) Um raio de luz monocromática incide perpendicularmente em uma das faces de um prisma equilátero e emerge de forma rasante pela outra face. Considerando  = 1,73 e supondo o prisma imerso no ar, cujo índice de refração é 1, o índice de refração do material que constitui o prisma será, aproximadamente,

06-(ITA-SP) Um prisma de vidro, de índice de refração n=, tem por secção normal um triângulo retângulo isósceles ABC no plano vertical. O volume de secção transversal ABD é mantido cheio de um líquido de índice de refração n'=. Um raio incide normalmente à face transparente da parede vertical BD e atravessa o líquido.

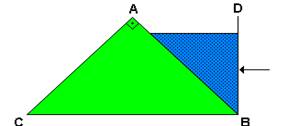
Considere as seguintes afirmações:

I) O raio luminoso não penetrará no prisma.

II) O ângulo de refração na face AB é de 45°.

III) O raio emerge do prisma pela face AC com ângulo de refração de 45°.

IV) O raio emergente definitivo é paralelo ao raio incidente em BD.

Das afirmativas mencionadas, é (são) correta (s):

a) Apenas I   

b) Apenas I e IV    

c) Apenas II e III    

d) Apenas III e IV    

e) II, III e IV

07-(UNIFESP-SP) Um raio de luz monocromático, propagando-se no ar, incide perpendicularmente à face AB de um prisma de vidro, cuja secção reta é apresentada na figura. A face AB é paralela à DC e a face AD é paralela à BC.

Considerando que as faces DC e BC formam um ângulo de 45° e que o ângulo limite de refração para esse raio, quando se propaga do vidro para o ar, é 42°, o percurso que melhor representa a trajetória do raio de luz é

a) 1.             

b) 2.                  

c) 3.               

d) 4.                   

e) 5.

08-(UNESP-SP) Um prisma de vidro imerso em água, com a face AB perpendicular à face BC, e a face AC com uma inclinação de 45° em relação a AB, é utilizado para desviar um feixe de luz monocromático. O feixe penetra perpendicularmente à face AB, incidindo na face AC com ângulo de incidência de 45°. O ângulo limite para a ocorrência de reflexão total na face AC é 60°.

Considerando que o índice de refração do vidro é maior que o da água, a trajetória que melhor representa o raio emergente é

a) I.                 

b) IV.                  

c) II.                    

d) V.                  

e) III

09-(UNIFESP-SP) "Eu peguei outro prisma igual ao primeiro e o coloquei de maneira que a luz fosse refratada de modos opostos ao passar através de ambos e, assim, ao final, voltaria a ser como era antes do primeiro prisma tê-la dispersado."

Assim Newton descreve a proposta do experimento que lhe permitiu descartar a influência do vidro do prisma como causa da dispersão da luz branca. Considerando que a fonte de luz era o orifício O da janela do quarto de Newton, assinale a alternativa que esquematiza corretamente a montagem sugerida por ele para essa experiência.

10-(UFG-GO) Como ilustrado na figura, a luz colimada de uma fonte F incide no espelho E, no ar, e é refletida para a face maior do prisma reto P. A luz emerge da face horizontal do prisma, formando com ela um ângulo reto. O espelho E é perpendicular à face maior do prisma. Sabendo que a luz incide na direção horizontal e que a = 30°, calcule o índice de refração do prisma. Dado: n(ar) =1,0.

11-(UFG) Com a finalidade de obter um efeito visual, através da propagação da luz em meios homogêneos, colocou-se dentro de um aquário um prisma triangular feito de vidro crown, conforme mostra a figura a seguir.

Um feixe de luz violeta, após refratar-se na parede do aquário, incidiu perpendicularmente sobre a face A do prisma, atingindo a face B. Com base nesses dados e conhecidos os índices de refração do prisma e do líquido, respectivamente, 1,52 e 1,33, conclui-se que o efeito obtido foi um feixe de luz emergindo da face

a) B, por causa da refração em B.

b) C, por causa da reflexão total em B.

c) B, por causa da reflexão total em B e C.

d) C, por causa da reflexão em B seguida de refração em C.

e) A, por causa das reflexões em B e C e refração em A.

12-(UNESP-SP) Um prisma de vidro tem os três lados iguais e índice de refração n=Ö2 em relação ao do ar, para um determinado comprimento de onda l. Um raio luminoso de comprimento de onda l incide no prisma formando um ângulo de 45^o com a normal e se refrata paralelo à base do prisma. Calcule o ângulo de desvio do raio que emerge do prisma, em relação ao raio incidente. (n_ar=1).

13-(UNESP-SP) Um raio de luz I, de uma única cor, incide num prisma e descreve o caminho mostrado na figura.

Se o ângulo θ for diminuído, a trajetória do raio R será mais bem descrita por:

14-(FUVEST-SP) Um raio monocromático de luz incide no ponto A de uma das faces de um prisma feito de vidro e imerso no ar. A figura 1 representa apenas o raio incidente e o raio refratado num plano normal às faces do prisma, cujas arestas são representadas pelos pontos P, S e T, formando um triângulo eqüilátero.Os pontos A, B e C também formam um triângulo eqüilátero e são, respectivamente, eqüidistantes de P e S, S e T, e T e P. Considere os raios E₁, E₂, E₃, E₄ e E₅, que se afastam do prisma,, representados na figura 2.

Figura 1                                Figura 2

Podemos afirmar que os raios compatíveis com as reflexões e refrações sofridas pelo raio incidente, no prisma, são:

a) somente E₃          b) somente E₁ e E₂          c) somente E₂ e E₅

d) somente E₁, E₃ e E₄          e) todos

15-(UNIFESP-SP) Dois raios de luz, um vermelho (v) e outro azul (a), incidem perpendicularmente em pontos diferentes da face AB de um prisma transparente imerso no ar. No interior do prisma, o ângulo limite de incidência na face AC é 44° para o raio azul e 46° para o vermelho. A figura que mostra corretamente as trajetórias desses dois raios é:

16-(UNESP-SP) Um feixe de luz composto pelas cores vermelha (V) e azul (A), propagando-se no ar,

incide num prisma de vidro perpendicularmente a uma de suas faces. Após atravessar o prisma, o feixe impressiona um filme colorido, orientado conforme a figura. A direção inicial do feixe incidente é identificada pela posição O no filme.

Sabendo-se que o índice de refração do vidro é maior para a luz azul do que para a vermelha, a figura que melhor representa o filme depois de revelado é:

17-(FUVEST-SP) O esquema representa um bloco de vidro com uma cavidade prismática vazia e a trajetória percorrida por um raio de luz incidente no ponto A (Dados:sen30^o=0,5, sen60^o=√3/2) e n_ar=1).

a) Desenhe a trajetória de um outro raio de luz que entra na cavidade, no ponto B, perpendicularmente à face.

b) Calcule o índice de refração do vidro

18-(ITA-SP) Na ilustração abaixo, qual deve ser o índice de refração do prisma para que o raio

mostrado sofra reflexão total na face S? (n_ar=1,00)

19-(FUVEST-SP) Alguns instrumentos de óptica utilizam “’prismas de reflexão total” como espelhos, como no caso da figura.

O valor do índice de refração do vidro desse prisma deve ser maior que:

20-(UNICAMP-SP) Um tipo de sinalização utilizado em estradas e avenidas é o chamado olho-de-gato, o qual consiste na justaposição de vários prismas retos feitos de plásticos que refletem a luz incidente dos faróis dos automóveis.

a) Reproduza o prisma ABC representado na figura abaixo e desenhe a trejetória de um raio de luz que incide perpendicularmente sobre a face OG e sofre reflexões totais nas superfícies AC e BC.

b) Determine o mínimo valor do índice de refração do plástico acima do qual o prisma funciona como um refletor perfeito de luz (toda luz que incide perpendicularmente à superfície OG é refletida). Considere o prisma no ar , onde o índice de refração vale 1,0.

21-(UFC) Considere um raio de luz monocromático incidindo perpendicularmente em uma das faces (AB) de um prisma de seção reta triangular, cujos lados são do mesmo tamanho.

Suponha que o prisma está mergulhado no ar e possui índice de refração absoluto n. Obtenha a condição sobre n para que haja emergência do raio de luz apenas pela face AC. Considere que o índice de refração absoluto do ar é igual a 1.

22-(UNESP-SP) Na figura abaixo, estão representados um prisma retangular, cujos ângulos da base são iguais a 45^o, um objeto AB e o olho de um observador. Devido ao fenômeno da reflexão total, os raios de luz provenientes do objeto são refletidos na base do prisma, que funciona como um espelho plano.

Assinale a alternativa que melhor representa a imagem A’B’, vista pelo observador:

23-(UECE-CE) 

A figura a seguir mostra um prisma feito de um material, cujo índice de refração é 1,5, localizado na frente de um espelho plano vertical, em um meio onde o índice de refração é igual a 1. Um raio de luz horizontal incide no prisma.

Sabendo que sen(6^o)0,104 e sen(9^o) = 0,157, o ângulo de reflexão no espelho é de

a) 2^o.                                 

b) 3^o.                                          

c) 4^o.                                          

d) 6^o. 

24-(FUVEST-SP)

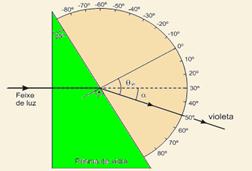
 Luz proveniente de uma lâmpada de vapor de mercúrio incide perpendicularmente em uma das faces de um prisma de vidro de ângulos 30^o, 60^o e 90^o, imerso no ar, como mostra a figura a seguir.

A radiação atravessa o vidro e atinge um anteparo.

Devido ao fenômeno de refração, o prisma separa as diferentes cores que compõem a luz da lâmpada de mercúrio e observam-se, no anteparo, linhas de cor violeta, azul, verde e amarela. Os valores do índice de refração n do vidro para as diferentes cores estão dados adiante.

a) Calcule o desvio angular α, em relação a direção de incidência, do raio de cor violeta que sai do prisma.

b) Desenhe, na figura da página de respostas, o raio de cor violeta que sai do prisma.

c) Indique, na representação do anteparo na folha de respostas, a correspondência entre as posições das linhas L₁, L₂, L₃ e L₄ e as cores do espectro do mercúrio.

b)

c)

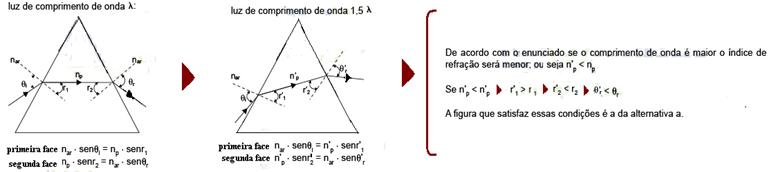
25-(UNESP-SP)

 Considere um raio de luz monocromático de comprimento de onda λ, que incide com ângulo θ_i em uma das

faces de um prisma de vidro que está imerso no ar, atravessando-o como indica a figura.

Sabendo que o índice de refração do vidro em relação ao ar diminui com o aumento do comprimento de onda

do raio de luz que atravessa o prisma, assinale a alternativa que melhor representa a trajetória de outro raio

de luz de comprimento 1,5 λ, que incide sobre esse mesmo prisma de vidro.

26-(UFPE-PE)

Um raio de luz incide na parte curva de um cilindro de plástico de seção semicircular formando um ângulo θ_i com o eixo de simetria. O raio emerge na face plana formando um ângulo θ_r com o mesmo eixo. Um estudante fez medidas do ângulo θ_r em função do ângulo θi e o resultado está mostrado no gráfico θ_r  θ versus_r.

Determine o índice de refração deste plástico.

 27-(UFG-GO)

O arco-íris é um fenômeno ótico em que a luz solar incide nas gotículas de água suspensas na atmosfera, gerando as cores do

espectro eletromagnético. Nesse fenômeno, em que ordem ocorrem os processos físicos envolvidos?

(A) Refração, dispersão, reflexão e refração.                                

(B) Dispersão, refração, reflexão e refração.

(C) Dispersão, reflexão, refração e transmissão.                          

(D) Refração, dispersão, transmissão e refração.

(E) Refração, reflexão, refração e dispersão.

Resolução comentada dos exercícios de vestibulares sobre

Prismas ópticos

01- Veja figura abaixo:

R- B

02- Observe a figura abaixo:

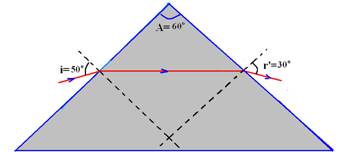
d=i + r’ – A  ---  d=50 + 30 -60  ---  d=20^o  R- A

03- Se o raio emergir rasante, teremos que o ângulo de incidência i’ na segunda face é igual ao

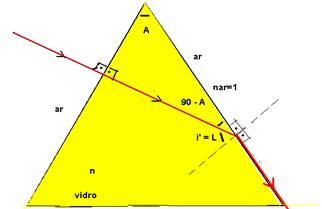
ângulo limite L que é igual ao ângulo de refringência A, fornecido pela expressão – senL=n_menor/n_maior  ® senL=n_ar/n ®senL=1/n

Como i’=L ® sen i’=sen L  ® sen i’=senA=1/n   ---  senA=1/√2  ---  senA=√2/2  ---  A=45^o R- D. 

04- A=60^o  --  i=45^o  --  i’=30^o  ---  A=r + i’  ---  60=r + 30^o  ---  r=30^o  ---  Aplicando Snell-Descartes na face onde o raio incide  ---  n_ar.seni=n_v.senr  ---  1.sen45^o=n_v.sen30^o  ---  1.√2/2=n_v.1/2  ---  n_v=√2

05- Veja a figura abaixo:

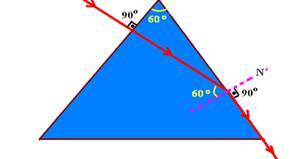
Como o raio de luz incide perpendicularmente na primeira fase, ele não sofre desvio até atingir a segunda face quando emerge rasante, onde, aplicando Snell-Descartes  ---  n_v.sen60^o=n_ar.sen90^o  ---  n_v.1,73/2=1.1  ---  n_v=1,15  ---  R- B

06- I- Como ele incide normalmente no líquido ele não sofre desvio até atingir a interface líquido-

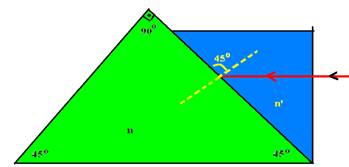
 prisma com ângulo de 45^o (sen45^o=√2/2=0,7) e, nessa interface  ---  cálculo do ângulo limite  ---   senL=n_menor/n_maior=√2/√3=0,8  ---  como seni<senL  ---  i<L  ---  assim, não haverá reflexão total e sim,  refração, penetrando no prisma  ---  Falsa 

II- Aplicando Snell-Descartes na interface líquido-prisma  ---  n’.sen45^o=n.senr  ---  √3. √2/2=√2.senr  ---  senr=√3/2  ---  r=60^o  ---  Falsa

III – Cálculo de i’  ---  A=r + i’  ---  90=60 + i’  ---  i’=30^o  ---  Aplicando Snell-Descartes na face em que o raio emerge para o ar

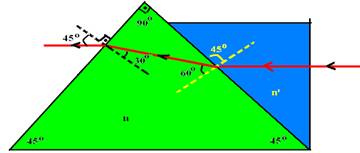
 ---  n.sen30^o=n_ar.senr’  ---  √2. 1/2=1.senr’  ---  senr’=√2/2  ---  r’=45^o  ---  Verdadeira

IV- Verdadeira  ---  veja que os raios incidente e emergente possuem o mesmo ângulo (45^o), portanto possuem direções paralelas.

R- D

07- Visualizando a figura de frente:

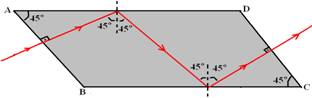
Observe que na face AB e CD ele não sofre desvio, pois incide e emerge perpendicularmente e nas outras duas faces sofre reflexão total, pois incide com 45^o, que é superior ao ângulo limite que é 42^o.  R- D

08- Observe na sequência de figuras abaixo que à medida que i diminui no sentido anti-horário, r

também diminui, mas no sentido horário  R- E

09- R- A – veja figura abaixo

10- Veja a figura abaixo:

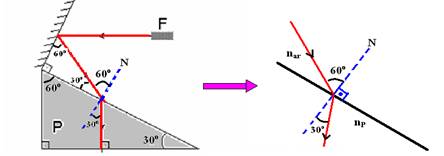
n_ar.sen60^o=n_P.sen30^o  ---  1.√3/2=n_P.1/2  ---  n_P=√3=1,7

11- Como o raio incide perpendicularmente na face A ele não sofre desvio até atingir a face B, onde incide com ângulo i=45^o e sen45^o=  sen45^o = √2/2 = 070  ---     o ângulo limite na interface prisma-água vale senL=n_menor/n_maior  ---  senL=1,33/1,52  ---  senL=8,87  ---  sen45^o<senL  ---   45^o<L  ---  incide na face B com ângulo inferior ao ângulo limite, ou seja, não sofre reflexão total em B, mas sim refração, passando para a água.  R- A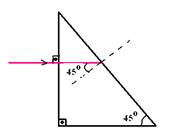

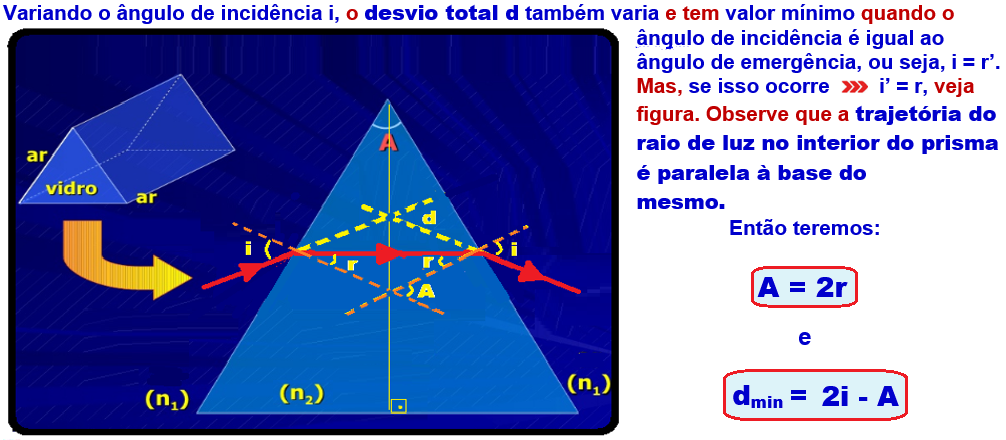
12- Quando o raio de luz se refrata paralelo à base o desvio (d) tem valor mínimo e o ângulo de incidência é igual ao ângulo de emergência, ou seja, i = r’. Mas, se isso ocorre ® i’ = r e i=r, veja figura abaixo.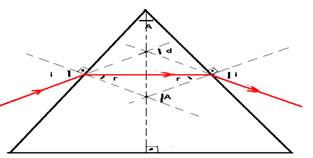

A=2r  ---   aplicando Snell-Descartes na primeira face  ---  n_ar.seni=n_v.senr  ---  1.√2/2=√2.senr  ---  senr=1/2  ---  r=30^o  ---  A=2r=2.30  ---  A=60^o  ---  d_min=d=i + r’ – A=2i – A  d=2.45 – 60  ---  d=90 – 60^o  ---  d=30^o

13- As trajetórias dos raios incidente, no interior do prisma e emergente se deslocam como se você estivesse girando um “saca-rolhas” no sentido horário, ou seja, o raio incidente sobe, e os outros dois descem conforme as figuras abaixo.

R- A    

14- Refração no pontoA  ---  n_ar.sen60^o=n_v.senr  ---  1.√3/2=n_v.sen30^o  ---  1.√3/2=n_v.1/2  ---  n_v=√3  ---  incide no ponto B onde sofre refração, pois sen30^o=1/2 e senL=n_menor/n_maior=1/√3= √3/3  ---  assim, como seni<senL  ---  i<L  ---  ele não sofre reflexão total  --- 

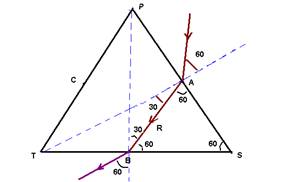
Aplicando Snell-Descartes no ponto B  ---  n_v.sen30^o=n_ar.senr  ---  √3.1/2=1.senr  ---  senr=√3/2  ---  r=60^o  ---  R- A

15- Observe na figura abaixo que os dois raios de luz incidem com ângulo de 45^o  ---  o ângulo limite para o raio azul (a) é de 44^oe, como ele incide com 45^o que é  superior ao ângulo limite, ele sofre reflexão total, retornando ao prisma. O raio vermelho (v) incide também com 45^o, que é inferior ao seu ângulo limite (46^o), sofrendo refração e passando para o ar.  R- E

16- Veja a figura abaixo:

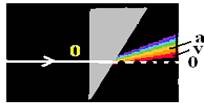
R- D

17- a)

Pelo princípio da reversibilidade dos raios de luz, o caminho na “ida” é o mesmo que na “volta”

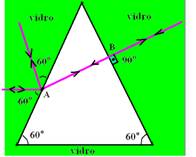
b) No ponto A  ---  n_v.sen30^o=n_ar.sen60^o  ---  n_v.1/2=1.√3/2  ---  n_v=√3

18- Observe que a luz incide na face interna  com ângulo i=45^o  ---  cálculo do ângulo limite  nessa face  ---  senL=n_menor/n_maior=1/n  

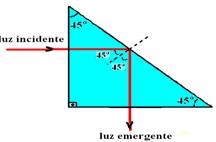
 para que ocorra reflexão total ele deve incidir com ângulo superior ao ângulo limite, ou seja i>L, ou ainda seni > senL  ---  sen45^o > senL  ---  √2/2 > 1/n  ---  n > √2  R- A

19-  R- C  (veja resolução da questão anterior)

20- a)

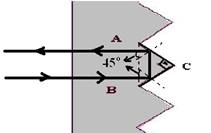
b)  seni > senL  ---  sen45^o > senL  ---  √2/2 > 1/n  ---  n > √2

21- Veja figura abaixo: 

 para que haja reflexão total  ---  i > L  ---  seni > senL  ---  sen60^o > 1/n  ---  √3/2 > 1/n  ---  n > 2√3/3

22- Observe a figura abaixo:

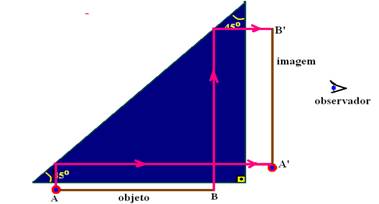
R- D

23- Dados  ---   n_p = 1,5  ---  n_ar = 1  ---  sen 6° = 0,104 e sen 9° = 0,157  ---  afigura a seguir ilustra a situação, mostrando a trajetória do raio até a reflexão no espelho plano  ---  na primeira face, a incidência é normal, portanto não há desvio  ---  a segunda face,

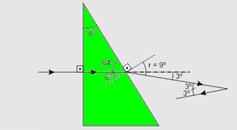
 aplicando a lei de Snell  ---  n_p sen i = n_ar sen r  ---  1,5 sen 6° = 1 sen r  ---  1,5 (0,104) = sen r  ---  sen r = 0,157   ---   r = 9º  ---   partir daí, acompanhando a figura, você conclui que o ângulo de reflexão no espelho plano é 3°  ---  R- B

24-   

a) Dado  ---   n_vi = 1,532  ---  a Fig 1  mostra a refração sofrida pelo raio violeta  ---  lei de Snell  ---  n_vi sen 30° = n_ar sen θ_{vi  ---} 

 1,532 (0,5) = 1 (senq_vi θ_vi )  --- sen θ_vi  = 0,766  ---  da tabela dada, θ_vi   = 50° ---  na Fig 2  ---  a + 30° = 50°  ---  α = 20°.

b)

c) Na refração, o desvio angular cresce do vermelho para o violeta o que pode ser provado aplicando a lei de Snell para as demais radiações envolvidas  ---  o ângulo de incidência é θ_rad = 30° para todas as radiações  ---  n_rad sen 30° = n_ar senθ_ar  --- 

1.senθ_ar = n_rad. (0,5)  ---  .senθ_ar = n_rad.(0,5)  ---  para cada radiação (cor) envolvida  ---  senθ_azul=1,528.0,5=0,764  ---  senθ_verde=1,519.0,5=0,760  ---  senθ_amarelo=1,515.0,5=0,758  ---  no intervalo de 0° a 90°, quanto menor o seno do ângulo, menor é o ângulo o que implica que o raio amarelo é o que sofre menor desvio, depois, nessa ordem, verde, azul e violeta  ---  observe o esquema:

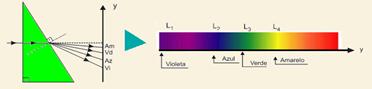
25- 

26- Observe no gráfico que ambos os ângulos vão aumentando até que, a refração acontece quando θr=90o (ângulo critico) e, nesse caso θr=30o  ---  alicando a lei de Snell-Descartes  ---  ni.sen θi = nar.sen θr ---  ni.sen30o=1.sen90o  ---  ni.1/2=1.1  ---  ni=2. 

27- Observe a figura abaixo que mostra a luz entrando e saindo de uma gota de chuva  ---  nesta  figura, em 1 ocorre refração, em

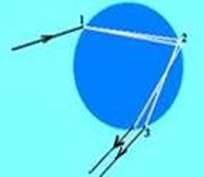
2 reflexão, e em 3 nova refração  ---  entre 1 e 2, ocorre dispersão  ---  R- A