Lâminas de faces paralelas

Comportamento óptico de uma lâmina de faces paralelas

 Considere um raio de luz se propagando num meio 1 de índice de refração n₁ e incidindo numa lâmina de faces paralelas de material de índice de refração n₂.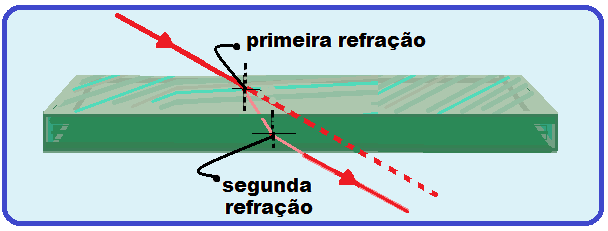

Esse raio de luz sofre duas refrações, uma quando entra na lâmina e outra quando sai dela, fazendo com que a luz seja desviada sem alterar sua direção de propagação (veja que os raios de luz incidente e emergente são paralelos).

Exemplos de lâminas de faces paralelas: vidros de: uma vidraça, uma estufa, uma cobertura, para-

brisa de um carro, moldura de vidro de um quadro, etc.

Equação do desvio lateral de um raio de luz ao atravessar uma lâmina de faces paralelas

Na figura abaixo temos uma lâmina de faces paralelas de índice de refração n₂, imersa num meio

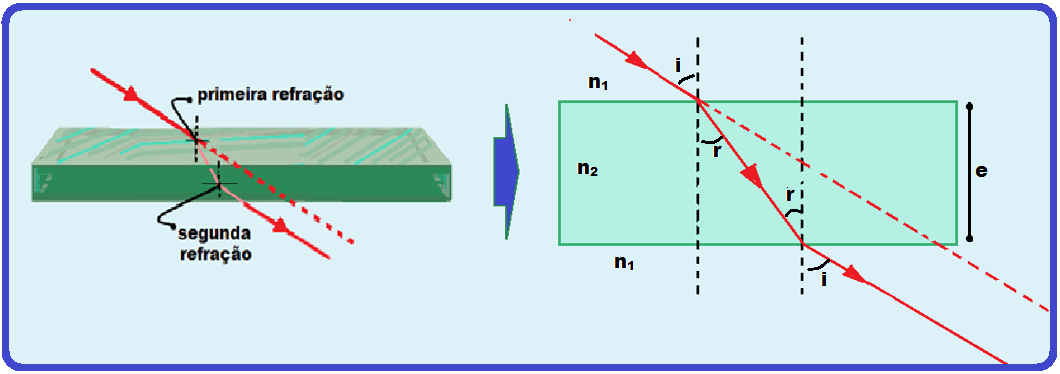
de índice de refração n_1­ e sendo atravessada por um raio de luz monocromático.

Aplicando a lei de Snell Descartes nas duas refrações da figura:

1^a refração entrando na lâmina  n₁.sen i = n₂.sen r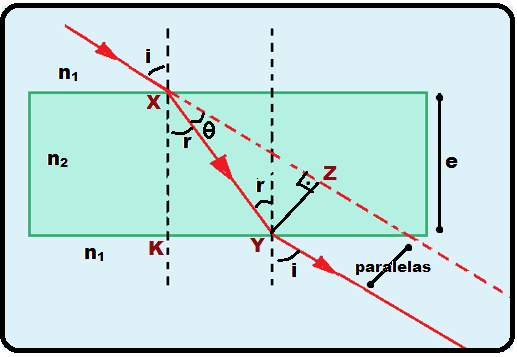

2^a refração saindo da lâmina   n_2.sen r = n₁.sen i

Não existe desvio angular que é nulo, pois os raios incidente e emergente são paralelos, mas sim desvio lateral (d) que corresponde à distância entre as retas que contém os raios incidente (seu prolongamento) e emergente.

Cálculo do desvio (d):

Triângulo XYZ    sen θ = d/XY sen θ = sen (i - r) = d/XY XY = sen (i – r)/d (I).

Triângulo KXY    cos r = e/XY     XY = cos r/e (II).

O que você deve saber, informações e dicas

Observe na expressão do desvio lateral que, quanto maior for a espessura e da lâmina, maior será

o desvio sofrido.

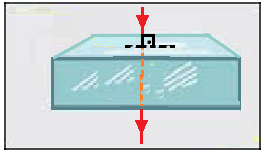
Se o raio incidente na lâmina for perpendicular a uma de suas faces o desvio lateral será nulo. A incidência normal ocorre sem desvio do raio de luz.

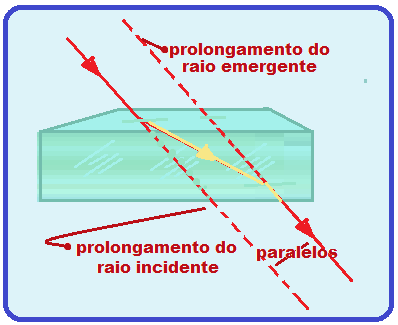
Os prolongamentos dos raios incidente e emergente são sempre retas paralelas.

A imagem de um objeto vista através de uma lâmina de faces paralelas (placa de vidro no ar) é sempre virtual e está sempre mais próxima da lâmina que o objeto, pois ao penetrarem na lâmina os raios de luz se aproximam da normal.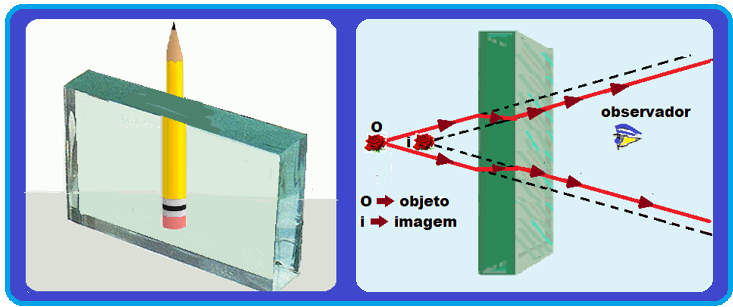

Assim, a imagem é vista pelo observador como sendo maior que o objeto por estar mais próxima (aumenta o campo visual).

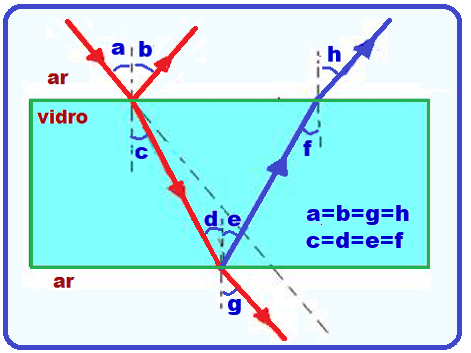
Se o raio de luz sofrer reflexão e refração em ambas as faces e, nelas, retornar ao ar, os seguintes ângulos serão iguais a = b = g = h e c = d = e = f.

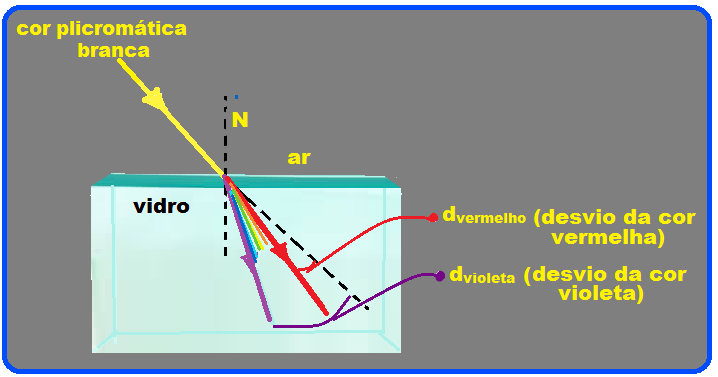
Podemos também decompor uma luz policromática fazendo-a atravessar uma lâmina de vidro de faces paralelas.

No interior da lâmina cada cor se move com velocidades diferentes e ao saírem da mesma sofrerão desvios laterais diferentes, sofrendo assim, dispersão.

A cor que sofre menor desvio ao penetrar no vidro é o vermelho (maior velocidade) e menor desvio é o violeta (maior velocidade).

Associação de lâminas de faces paralelas

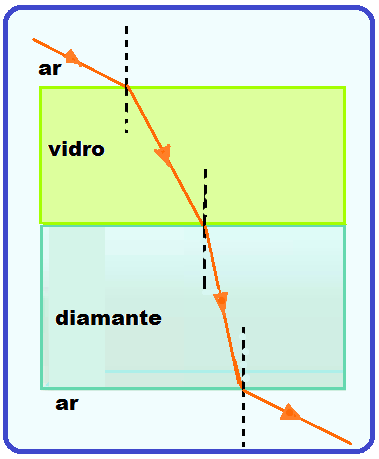
Considere as duas lâminas da figura, imersas no ar, uma de vidro e a outra de diamante

O índice de refração do diamante é maior que o do vidro, que por sua vez é maior que o do ar.

 Observe que, quanto mais refringente for o meio (maior índice de refração), mais o raio de luz se aproxima da normal,

menor será a velocidade da luz nesse meio e maior será o desvio sofrido.

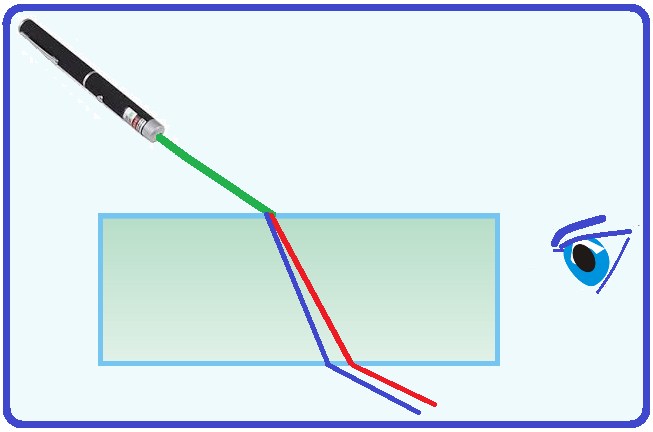
Tem-se um aparelho que emite um feixe colimado, estreito, de luz verde. Mas o feixe é, na verdade,

mistura de luz amarela com azul.

Pode-se descobrir tal fato, fazendo-se incidir o feixe numa lâmina de vidro de faces paralelas e assim uma das cores sofreria um deslocamento paralelo maior que a outra, numa incidência oblíqua. 

Diferentes cores sofrem desvios diferentes e, consequentemente, deslocamentos paralelos diferentes

Veja um exercício de aplicação sobre desvio lateral nas lâminas de faces paralelas:

A espessura de uma lâmina de vidro de faces paralelas é de 2,0 cm.

Um raio monocromático de luz incide numa de suas faces com ângulo de 60^o e se refrata com ângulo de 45^o.

Considerando cos75^o = sen15^o = 0,25, sen60^o = cos30^o = √3/2 = 0,8,  n_ar = 1,0 e sen45^o = cos45^o = √2/2 = 0,7,  pede-se:

a) Esboçar o trajeto do raio de luz ao atravessar a lâmina

b) Determinar o índice de refração do vidro

c) Determinar o desvio lateral (d) e o desvio angular (β)

d) Determinar o valor do ângulo de emergência

a)

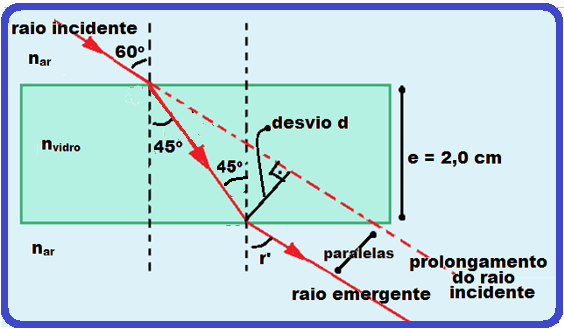
n_vidro = 1,2.

c) d = e.sen(i – r)/cosr    d = 2.sen(60^o – 45^o )/cos45^o  d = 2.sen(15^o)/cos45^o    d = 2.0,25/0,7   d = 0,71cm (desvio lateral)    o desvio angular é nulo, pois o prolongamento do raio incidente e o raio emergente tem a mesma direção, ou seja, são paralelos    β = 0.

d) Aplicando Snell-Descartes na face inferior da lâmina    n_vidro.senr = n_ar.senr’    1,2.sen45^o = 1.senr’  1,2.0,7 = 1.senr’    senr’ = 0,8    r’ = 60^o    observe que i = r’ = 60^o (por essa razão que o raio incidente e o prolongamento do raio incidente são paralelos).

Exercícios de vestibulares com resoluções comentadas sobre

Lâminas de faces paralelas

01- (MACKENZIE-SP)

Sabe-se que uma onda eletromagnética, que se propaga em um meio homogêneo, transparente e isótropo, ao incidir sobre a superfície de outro meio, também transparente, homogêneo e isótropo, continua a se propagar nele, porém, com

algumas alterações. Se o segundo meio citado for um corpo com a forma de paralelepípedo, pode-se ter uma situação como a ilustrada ao lado, conhecida por Lâmina de Faces Paralelas.

Para este exemplo, é válido o modelo utilizado em Óptica Geométrica, em que os raios incidente e emergente indicam a direção orientada de certa radiação eletromagnética na faixa da luz e, nesse caso, é válida a equação:

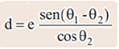
Com base nessa descrição, e considerando θ₁ > θ₂, pode-se afirmar que

a) A velocidade de propagação da luz no meio A é maior que a velocidade   de propagação da luz no meio B.

b) A velocidade de propagação da luz no meio A é menor que a velocidade de propagação da luz no meio B.

c) A velocidade de propagação da luz no meio A é menor que a velocidade de propagação da luz no meio B, se 45º  <  θ₁ <  90º.

d) A velocidade de propagação da luz no meio A é menor que a velocidade de propagação da luz no meio B, se 0º < θ₁

 < 45º.

e) A velocidade de propagação da luz no meio A é igual à velocidade de propagação da luz no meio B.

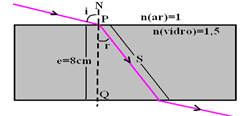
02-(UFG-GO) Observe a lâmina de faces paralelas da figura abaixo,em que:

S₁ e S₂ são superfícies;

e é a espessura da lâmina;

i é o ângulo de incidência em S₁;

r é o ângulo de refração em S_1;

Sendo  o valor do índice de refração da lâmina, i=45^o e 1,4cm a espessura da lâmina, e considerando que o meio 1 é o ar (n_ar=1), determine o valor do desvio lateral. Dados: sen 30^o=0.5; cos 30^o=0,87 e sen 15^o=0,26.

03-(PUCC) Quando se observa um objeto através de uma vidraça comum, vemos:

 a) uma imagem real do objeto;         

b) uma imagem virtual do objeto          

c) o próprio objeto           

d) uma imagem imprópria do objeto;         

e) uma imagem invertida.

04- (UNIRIO) Um cão está diante de uma mesa, observando um peixinho dentro do aquário, conforme  representado na figura. Ao mesmo tempo, o peixinho também observa o cão. Em relação à parede P do aquário e às distâncias reais, podemos afirmar que as imagens observadas por cada um dos animais obedecem às seguintes relações:

a) O cão observa o olho do peixinho mais próximo da parede P, enquanto o peixinho observa o olho do cão mais distante do aquário.

b) O cão observa o olho do peixinho mais distante da parede P, enquanto o peixinho observa o olho do cão mais próximo do aquário.

c) O cão observa o olho do peixinho mais próximo da parede P, enquanto o peixinho observa o olho do cão mais próximo do aquário.

d) O cão observa o olho do peixinho mais distante da parede P, enquanto o peixinho observa o olho do cão também mais distante do aquário.

e) O cão e o peixinho observam o olho um do outro, em relação à parede P, em distâncias iguais às distâncias reais que eles ocupam na figura.

05-(UEL) Um raio de luz r atravessa uma lâmina de vidro de faces paralelas, imersa no ar, sendo parcialmente refletido nas duas faces.

 Considerando os ângulos indicados no esquema, o ângulo q é igual a:

06-(UFRS-RS) Um raio de luz, proveniente da esquerda, incide sobre uma lâmina de vidro de faces paralelas, imersa no ar, com ângulo de incidência i₁ na interface ar-vidro. Depois de atravessar a lâmina, ele emerge do vidro com ângulo r₂. O trajeto do raio luminoso está representado na figura, onde o ângulo r₁ designa o ângulo de refração no vidro, e i₁, o ângulo de incidência na interface vidro-ar.

Nessa situação, pode-se afirmar que

07-(UFRS-RS) Na figura a seguir, um feixe de luz monocromática I, proveniente do ar, incide sobre uma placa de vidro de faces planas e paralelas, sofrendo reflexões e refrações em ambas as faces da placa.

Na figura, θ_i representa o ângulo formado pela direção do feixe incidente com a normal à superfície no ponto A, e θ_r representa o ângulo formado pela direção da parte refratada desse feixe com a normal no mesmo ponto A.

Quais ângulos são iguais a a, b e l?

08-(UFPA) O desvio angular sofrido por um raio de luz que incide segundo o ângulo de 60° com a normal à superfície de uma lâmina de faces paralelas, após atravessá-la é de:

09-(UFBA) Um feixe de luz monocromática, cuja velocidade no vácuo tem módulo igual a 3,0 .10⁸m/s, incide perpendicularmente em uma lâmina transparente e espessa de índice de refração absoluto n = 1,50. Determine a espessura da lâmina, sabendo-se que a luz gasta 1,0 .10^-10s para atravessá-la

10-(FUVEST-SP) Um raio luminoso proveniente do ar atinge uma lâmina de vidro de faces paralelas com 8,0 cm de espessura e 1,5 de índice de refração. Este raio sofre refração e reflexão ao atingir a primeira superfície; refração e reflexão ao atingir a segunda superfície (interna).

a) Trace as trajetórias dos raios: incidente, refratados e refletidos

b) Determine o tempo para o raio refrato atravessar a lâmina, sendo o seno do ângulo de incidência 0,9. Considere: C=3,0.10⁸m/s e n(ar)=1,0.

11-(MED. TAUBATÉ) Tem-se  um aparelho que emite um feixe colimado, estreito, de luz verde. Mas o feixe é, na verdade, mistura de luz amarela com azul. Pode-se descobrir tal fato, fazendo-se incidir o feixe numa lâmina de vidro de faces paralelas?

 a) Não; os dois feixes emergiriam da lâmina coincidentes.

 b) Sim; aumentando-se o ângulo de incidência até o ângulo limite de refração de uma das cores; então só a outra se transmitiria.

 c) Sim; uma das cores sofreria um desvio de direção maior que a outra, numa incidência oblíqua.

 d) Sim; uma das cores sofreria um deslocamento paralelo maior que a outra, numa incidência oblíqua. 

 e) Sim; a cor do feixe emergente seria diferente para diferentes ângulos de incidência.

12-(UEFS) Uma lâmina de faces paralelas, construída de forma que uma das suas faces é espelhada internamente, está imersa no ar. Um raio luminoso, propagando-se no ar, incide, com ângulo i, na face não espelhada e é refratado. Em seguida, o raio é refletido na face espelhada e volta ao ar, depois de ser novamente refratado. O ângulo de refração, no retorno do raio luminoso da lâmina para o ar, é igual a:

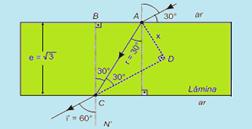
13-(UnB-DF)

Um feixe de luz passa de um meio 1 para um meio 2 e chega novamente ao meio 1, conforme figura.

A linha tracejada representa um prolongamento de feixe incidente. Sendo q=30^o, e=2Ö3cm e X=1cm, calcule o índice de refração do meio 2. Considere o meio 1 como sendo o ar o ar (n_ar=1,0) e sen15⁰=cos75^o=0,26

14-(FUVEST) Um feixe de luz monocromática incide sobre lâminas paralelas de diamante e vidro, como representado na figura. Sendo os índices de refração absolutos 2,42 para o diamante e 1,52 para o vidro, qual das linhas da figura que melhor representa a trajetória do feixe luminoso?

15-(CESGRANRIO)

Dois meios A e C estão separados por uma lâmina de faces paralelas (B). Um raio luminoso I,

propagando-se em A, penetra em B e sofre reflexão total na face que separa B de C, conforme indica a figura anterior.

Sendo n_A, n_B e n_C os índices de refração dos meios A, B e C, qual a relação entre eles?

16-(UFMG) A figura mostra a trajetória de um feixe de luz que vem de um meio I, atravessa um meio II, é totalmente refletido na interface dos meios II e III e retorna ao meio I.

Sabe-se que o índice de refração do ar é menor que o da água e que o da água é menor que o do vidro. Nesse caso é correto afirmar que os meios I, II e III podem ser, respectivamente:

a) ar, água e vidro     

b) vidro, água e ar      

c) água, ar e vidro     

d)  ar, vidro e água

17-(FUVEST-SP) Numa folha de papel num plano horizontal, está desenhado um círculo de centro C. Sobre a folha é colocada uma placa grossa de vidro, cobrindo metade do círculo. A figura a seguir mostra uma pessoa olhando para o círculo, com seu olho no eixo vertical OC.

A alternativa que melhor representa o que a pessoa enxerga é:

18-(UFBA) A figura mostra um raio de luz  monocromático que atravessa uma lâmina de faces paralelas, de índice de refração igual a √3 e espessura 2√3cm.

Sendo o índice de refração do ar igual a 1, sen30^o=cos60^o=1/2 e sen60^o=cos30^o=√3/2, é correto afirmar:

(01) O raio incidente e o raio que emerge da lâmina possuem direções diferentes.

(02) O ângulo de refração, no interior da lâmina, mede 30^o.

(04) O desvio lateral, (d), sofrido pelo raio após atravessar a lâmina, é igual a 2cm.

(08) A velocidade de propagação do raio luminoso, no interior da lâmina, é inversamente proporcional ao índice de refração do material que a constitui.

(16) O raio refratado não sofrerá desvio, se o raio luminoso incidir numa direção normal à lâmina.                   

19-(UFRJ-RJ) Uma lâmina homogênea de faces paralelas é constituída de um material com índice de refração n₂=1,5. De um lado da lâmina, há um meio homogêneo de índice de refração n₁=2,0; do outro lado, há ar, cujo índice de refração n₃ consideramos igual a 1,0. Um raio luminoso proveniente do primeiro meio incide sobre a lâmina com ângulo de incidência θ₁, como indica a figura.

Calcule o valor de θ₁ a partir do qual o raio que atravessa a lâmina sofra reflexão total na interface com o ar.

20-(UFCE)  Um raio de luz propagando-se no ar ( n_ar=1 ) incide com um angulo de incidência igual a 45^o, em uma das faces de uma lamina feita com um material transparente de índice de refração  n, como mostra a figura.

Sabendo-se que a linha AC é o prolongamento do raio incidente e que, d = 4 cm e BC = 1 cm, determine o valor de n.

21-(ITA-SP)

Uma lâmina de faces paralelas de espessura 4√3 cm é constituída de um material de índice de refração √3. Um raio luminoso, propagando-se no ar, encontra a lâmina, formando um ângulo de 60^o com a normal. Determine o desvio sofrido pelo raio luminoso incidente.

22-(CESGRANRIO-RJ)

Um raio de luz monocromática incide sobre a superfície de uma lâmina delgada de vidro, com faces paralelas, fazendo com ela um ângulo de 30º, como ilustra a figura. A lâmina está imersa no ar e sua espessura é cm.

Sabendo-se que os índices de

refração desse vidro e do ar valem, respectivamente, e 1, determine o desvio x, em mm, sofrido pelo raio ao sair da lâmina.

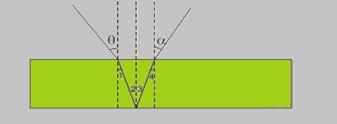
23-(UDESC-SC)

Considere uma lâmina de vidro de faces paralelas imersa no ar. Um raio luminoso propaga-se no ar e incide em uma das faces da lâmina, segundo um ângulo θ em relação à direção normal ao plano da lâmina. O raio é refratado nesta face e refletido na outra

face, que é espelhada. O raio refletido é novamente refratado na face não espelhada, voltando a propagar-se no ar. Sendo n_ar e n_vidro, respectivamente, os índices de refração da luz no ar e no vidro, o ângulo de refração α que o raio refletido forma no vidro, com a direção normal ao plano da lâmina, ao refratar-se pela segunda vez, obedece à equação:

a) n_vidro. sen θ = n_ar. sen θ /2         

b) α = θ          

c) sen α = cos θ         

d) n_vidro. sen α = n_ar.sen θ         

e) n_ar. sen α = n_vidro. sen θ  

24-(UEMG-MG)

Refração é o nome dado ao fenômeno em que uma onda que se propaga num meio passa a se propagar em outro meio. Considere que você veja, por uma janela de vidro, uma árvore. Até atingir os seus olhos, a luz proveniente da árvore veio pelo ar, passou a se propagar no vidro e, finalmente, passou do vidro para o ar novamente, até atingir os seus olhos.

Ao sofrer essas duas refrações - do ar para o vidro e do vidro para o ar -, respectivamente, assinale a alternativa que apresenta CORRETAMENTE as alterações que ocorrem com a luz.

A) Sua frequência aumenta, ao passar do ar para o vidro, e diminui, ao passar do vidro para o ar.

B) Sua frequência diminui, ao passar do ar para o vidro, e aumenta, ao passar do vidro para o ar.

C) Sua velocidade aumenta, ao passar do ar para o vidro, e diminui, ao passar do vidro para o ar.

D) Sua velocidade diminui, ao passar do ar para o vidro, e aumenta, ao passar do vidro para o ar.

25-(PUC-RJ)

Um feixe luminoso se propagando no ar incide em uma superfície de vidro. Calcule o ângulo que o feixe refratado faz com a normal à superfície sabendo que o ângulo de incidência θ_i é de 60º e que os índices de refração do ar e do vidro, η_ar e η_vidro vidro, são respectivamente 1,0 e √3.

(A) 30°                      

(B) 45°                       

(C) 60°                               

(D) 73°                           

(E) 90°

Resolução comentada dos exercícios de vestibulares sobre

Lâminas de faces paralelas

01- Lei de Snell-Descartes - A relação entre o seno do ângulo de incidência e o seno do ângulo de refração é uma grandeza constante denominada índice de refração do segundo meio em relação ao primeiro, ou seja,  seni/senr=n₂/n₁   

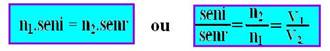
As expressões acima nos mostram que quando a luz passar de um meio menos refringente (menor indice de refração) para um meio mais refringente (maior índice de refração), o ângulo de refração será menor que o ângulo de incidência (ele se aproxima da normal) e menor será a velocidade da luz nele  ---  no caso do exercício, veja na figura fornecida que θ₁ > θ₂, o que implica que n_B > n_A  ---  assim, V_A > V_B  ---  R- A.

02- Aplicando Snell-Descartes  ---  n_ar.seni=n_lâmina.senr  ---  1.√2/2=√2.senr  ---  senr=1/2  ---  r=30^o  ---  aplicando a fórmula do desvio latera  ---  d=e.sen(i – r)/cosr  ---  d=1,4.sen(45 – 30)/cos30^o  ---  d=0,364/0,86  ---  d=0,42cm.

03-  A imagem de um objeto vista através de uma lâmina de faces paralelas (placa de vidro no ar) é sempre virtual e está sempre mais próxima da lâmina que o objeto, pois ao penetrarem na lâmina os raios de luz se aproximam da normal.

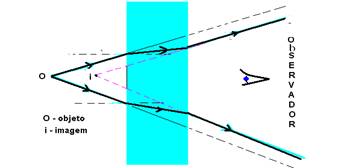
R- B

04- Um observador que vê um peixe dentro de um aquário enxerga-o mais próximo da parede do aquário 

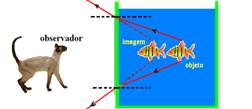
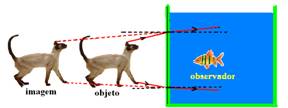
Ao mesmo tempo, o peixe vê o observador mais distante do aquário.  --  R- A

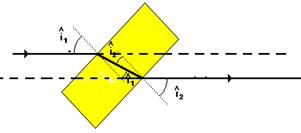
05-   R- D  ---  os raios incidente e emergente são paralelos e, portanto, os ângulos a e g são iguais.  

06- Os ângulos incidente e emergente são iguais porque os prolongamentos dos raios incidente e emergente são paralelos

R- A

07- Veja a figura abaixo:

Se o raio de luz sofrer reflexão e refração em ambas as faces e, nelas, retornar ao ar, os seguintes ângulos serão iguais:

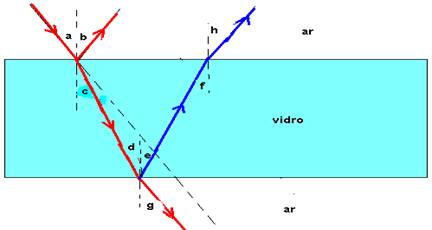
a=b=g=h             c=d=e=f   ---  R- a=qi,  b=q_r  e  l=qi         

08- O desvio angular é nulo, pois não há mudança de direção dos raios incidentes e emergentes  

R- A

09- Como o raio de luz incide perpendicularmente, ele não sofre desvio  ---  cálculo da velocidade do raio de luz no interior do vidro 

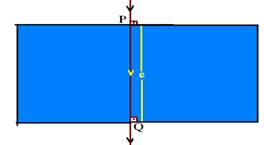
N_vidro=C/V_vidro  ---  1,5=3.10⁸/V_vidro  ---  V_vidro=2.10⁸m/s  ---  para percorrer e=PQ com V=2.10⁸m/s, a luz demora t=10^-10s  ---  V=e/t  ---  2.10⁸=e/10^-10  ---  e=2.10^-2m=2,0cm

10- a)

b)Aplicando Snell-Descartes na face superior  ---  n(ar).seni=n(vidro).senr  ---  1.0,9=1,5.senr  ---  senr=0,6  ---  sen²r + cos²r=1  --

-  (0,6)²+ cos²r=1 ---  cosr=0,8  ---   cosr=cateto adjacente/hipotenusa  ---  0.8=0.08/S  ---  S==0,1m  ---  cálculo da velocidade da luz no vidro  ---  n_vidro=C/V_vidro  ---  1,5=3.10⁸/V_vidro0,5.10^-9  ---  V_vidro=2,0.10⁸m/s  ---  V_vidro=S/t  ---  2.10⁸=10^-1/t  ---  t=10^-1/2.10⁸  ---

t=5,0.10^-10s

11-  R- D – diferentes cores sofrem desvios diferentes e, consequentemente, deslocamentos paralelos diferentes

12- Veja figura abaixo:

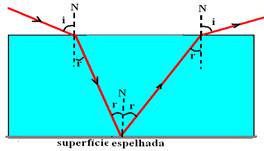
R- B

13- Observe a figura abaixo:

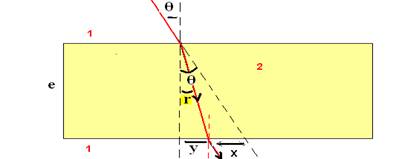
θ=30^o  ---  tg30^o=√3/3  ---  tg30^o=cateto oposto/cateto adjacente  ---  √3/3=(1 + y)/2√3  ---  y=1cm  ---  se X=Y=1cm – 2θ=r  ---  2.30^o=r  ---  r=15^o  --- aplicando Snell-Descartes na face superior  ---  n₁.sen30^o=n₂.sen15^o  ---  1.0,5=n₂.0,26  ---  n₂=1,9

14- Quando a luz se refrata de um meio de menor índice de refração para outro de maior índice de refração, o raio refratado se aproxima da normal  ---  R- B

15- R- n_A< n_B > n_{C ­} - Veja justificativa da questão anterior        

16- R- B -  ---  I vidro/II água -  sofre refração quando passa do meio mais refringente para o menos refringente  ---  II água/III ar – sofre reflexão total quando passa do meio mais refringente para o menos refringente.

17- Como a imagem está acima do observador, ela estará mais próxima do mesmo e, devido ao campo visual maior dará ao observador a impressão de ser maior que o objeto R- D 

18- (01) Falsa – eles possuem a mesma direção, ou seja, são paralelos.

(02) n_ar.sen60^o=n.senr  ---  1.√3/2=√3.senr  ---  senr=1/2  ---  r=30^o – correta.

(04) d=e.sen(i – r)/cosr  ---  d=2√3.sen(60^o – 30^o)/cos30^o  ---  d=(2√3.1/2)/√3/2  ---  d=2cm - correta

(08) Correta  ---  n=C/V  ---  como C é constante, n é inversamente proporcional a V.

(16) Correta – em toda incidência normal, o raio de luz não sofre desvio.

19- Interface n₁ – n₂  ---  n₁.sen θ₁=n₂.senr  ---  2.sen θ₁=1,5.senr  ---  senr=2.sen θ₁/1,5  I

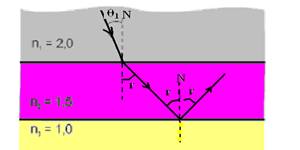
Interface n₂ – ar  ---  cálculo do ângulo limite L  ---  senL=n_menor/n_maior=1/1,5  ---  para que haja reflexão total nessa interface o raio de luz deve incidir nela com um ângulo r tal que r>L, ou seja, senr>senL  ---  senr>1/1,5  II  ---  substituindo I em II  --- 

2.sen θ₁/1,5 > 1/1,5  ---  sen θ₁>1/2  ---  θ₁>30^o  ---  para qualquer valor de θ₁ maior que 30^o, o raio de luz sofrerá reflexão total na interface n₂ – n₁.

20- Observe a figura abaixo:

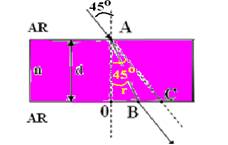
tg45^o=OC/d  ---  1=(1 + OB)/4  ---  4=1 + OB  ---  OB=3cm  ---  (AB)²= d² + (OB)²  ---  (AB)²= (4)² + (3)²   ---  AB=5cm  ---  senr=OB/AB  ---  senr=3/5  ---  aplicando Snell-Descartes na face superior  ---  n_ar.sen45^o=n.senr  ---  1.√2/2=n.3/5  ---  n=5√2/6

21- Lei de Snell  ---  n₁.seni = n₂.senr  ---  (1).(√3/ 2) = (√3).senr  ---  sen r =1/2  ---   r = 30 º  ---  no interior da lâmina você obtém um

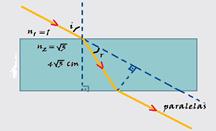
triangulo retângulo  ---  d = cateto oposto  ---  4√3 = cateto adjacente  ---  tg30^o=cateto oposto/cateto adjacente  ---  tg30^o=d / 4 √3 ---  d / 4 √3 = √3 / 3  --- 3d = 4.√3.√3  ---  d = 12/3  ---  d = 4 cm 

22- n_ar=1  ---  n_vidro =  ---   e = cm  ---  como o ângulo entre o raio e a lâmina é de 30°, o ângulo de incidência é: i = 60°  --- 

o raio provem do ar, atravessa a lâmina e volta para o ar, o raio emergente é paralelo ao incidente  ---  i’ = i = 60°  ---  observe a

figura  ---  lei de Snell na primeira face  ---  n_ar sen i = n_vidro sen r  ---   (1) sen 60° = senr  --- √3/2 = √3sen r  ---  sem r = ½  --- 

r = 30^o  ---  no ponto C  ---   os ângulos  e r são alternos-internos  ---  = 30°  ---   os ângulos e i’ são opostos pelo vértice  ---  = 60°  ---  = +  _---  60° = 30° + ---  = 30°  ---  no triângulo ABC  ---  cós 30^o=BC/AC  ---  √3/2 = √3/AC  ---  AC=2cm  ---  no triângulo ACD  ---  sen30^o=AD/AC  ---  1/2=x/2  ---  x=1cm

23- Observe o trajeto feito pelo raio luminoso  --- os ângulos 1 e 2 são iguais (alternos internos)  ---  os ângulos 2 e 3 são iguais

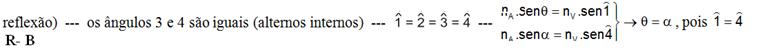
24-(UEMG-MG)

  A frequência é característica da onda (no caso, luz)  ---  quando a luz de determinada frequência se refrata passando de um meio para outro, sua velocidade de propagação e seu comprimento de onda variam, mas sua frequência permanece a mesma, independente do meio em que estiver se propagando  ---  assim, as alternativas A, B e C estão erradas.

A correta é a D, pois, quanto mais refringente é o meio, maior será o valor de seu índice de refração n,  menor a velocidade da luz nesse meio e maior será o desvio sofrido.

25-(PUC-RJ)

Aplicando a lei de Snell  ---  n₁.senθ₁ = n₂.senθ₂  ---  1.sen60^o = √3.sen.θ₂  ---  1.√3/2 = √3.sen θ₂  ---  sen θ₂=1/2  ---  θ₂=30^o  ---

R- A.