Instrumentos Ópticos

Instrumentos de projeção

São aqueles cuja imagem formada é real, pois pode ser projetada sobre um filme, uma tela, um anteparo, etc.                                        

I - Câmera fotográfica ou máquina fotográfica  dispositivo utilizado para capturar imagens. Consiste básicamente de uma caixa com orifício no qual se encontram uma ou mais lentes convergentes (objetiva), por onde entram os raios de luz  provenientes dos objetos que queremos

fotografar ou filmar e que produzem uma imagem real, menor e invertida sobre o filme (câmera comum) ou sobre um censor que armazena as imagens em cartões de memória (câmera digital).

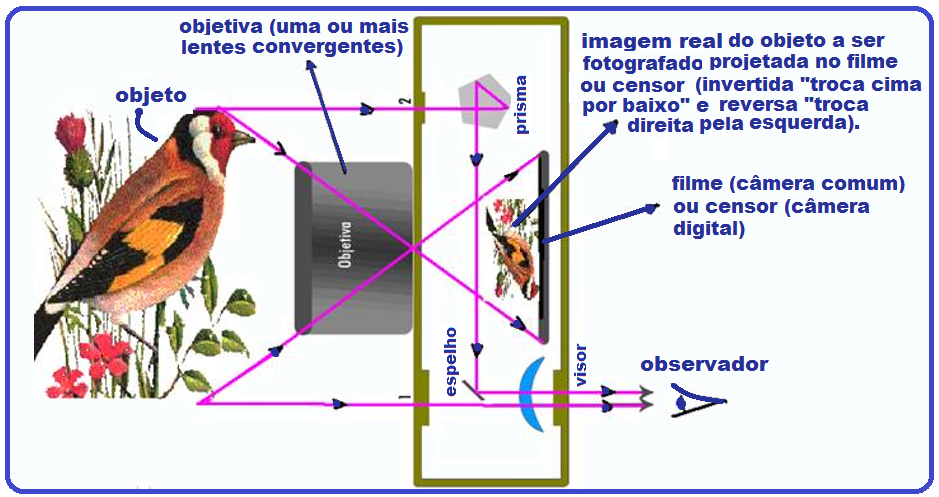 Quando queremos focalizar a imagem devemos variar a distância lente-filme ou seja, variar a imagem P’ pois P e o foco são constantes.

Assim, quando o objeto se aproxima devemos afastar a lente para que a imagem seja projetada novamente sobrfe o filme. 

II- Projetor  consta de uma fonte de luz que, através de uma intensa iluminação e de uma lente convergente (ou um sistema de lentes), projeta a imagem de um objeto (filme, slide, transparência) em uma tela.

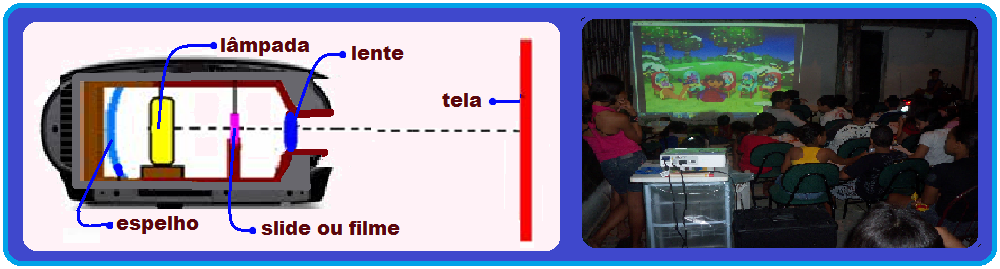
  Essa imagem é real, invertida e maior, desde que o objeto esteja entre o centro de curvatura da lente e o foco objeto.

Instrumentos de observação

 A imagem é observada diretamente pelo observador e é virtual e direita.

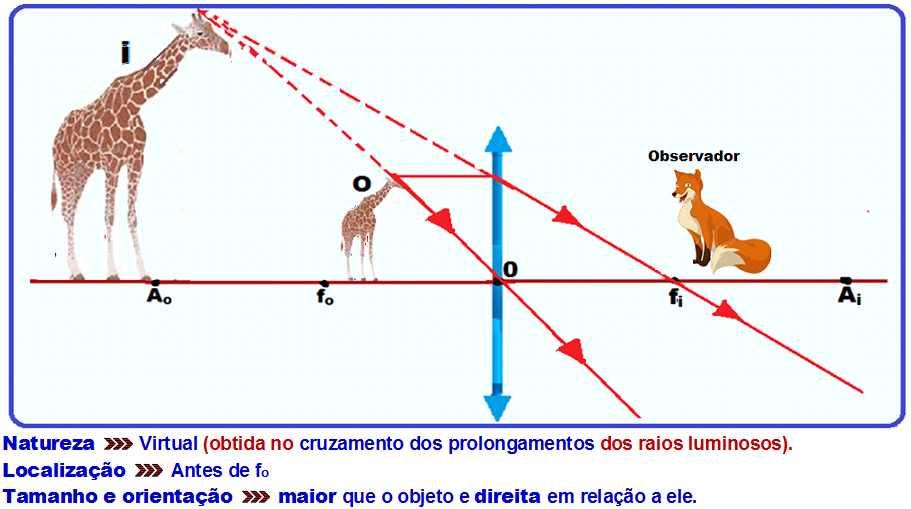
I-Lupa  Também chamada de lente de aumento é uma simples lente convergente que fornece de um objeto colocado entre seu foco F e seu centro óptico O uma imagem virtual, direita e maior que o objeto observado.

 Observe no esquema abaixo a formação da imagem A’B’ de um objeto AB em uma lupa, onde o objeto a ser observado tem que estar entre o foco objeto f_o e a lente.

Sendo a imagem formada virtual, nas equações 1/f = 1/P + 1/P’, i/o = -P’/P e A = i/o = -P’/P, P’ deve e ser substituída com sinal negativo, pois P’< 0.

II- Microscópio composto Utilizado na observação de regiões de dimensões microscópicas que o olho humano não consegue perceber, como por exemplo, na histologia, anatomia, mineralogia, etc.

Consta de duas lentes convergentes (geralmente compostas) de pequenas distâncias focais que são: a objetiva (sistema de lentes bastante sofisticado) que está próxima ao objeto observado e a ocular (com no mínimo duas lentes) com a qual observamos a imagem fornecida pela objetiva.

Veja o esquema simplificado do microscópio composto.

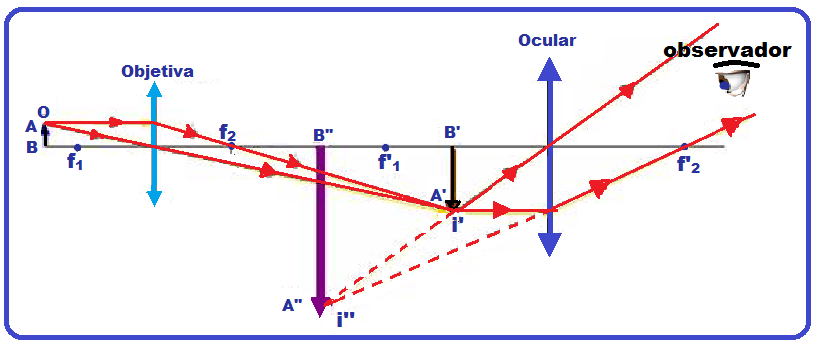
A distância focal da objetiva é muito pequena (milímetros). A objetiva forma do objeto AB uma imagem A’B’ real, invertida e maior que o objeto e essa imagem serve como objeto para a ocular (de distância focal da ordem de centímetros) que fornece uma imagem final A’’B’’, virtual, maior e direita em relação a A’B’.

Observe que A’’B’’ é direita em relação a A’B’ e invertida em relação ao objeto AB.

O aumento linear transversal do microscópio é fornecido pela expressão:

A_microscópio = A_objetiva . A_ocular

O aumento produzido por esse microscópio chega até a 2000 vezes. Atualmente existem microscópios eletrônicos que produzem ampliações de até cem mil vezes.

III- Luneta astronômica  utilizada na observação de astros ou de objetos distantes.

Consta de 2 lentes convergentes, a objetiva e a ocular.  Ao contrário do microscópio composto, a distância focal da objetiva é muito grande (da ordem de metros). A ocular tem pequena distância focal.

Devido ao fato de o objeto estar muito afastado, a imagem (i₁) formada pela objetiva está praticamente sobre seu foco (f_objetiva) e é real e invertida (veja figura).

Essa imagem (i₁) vai servir como objeto para a ocular resultando numa imagem final (i₂), virtual e invertida em relação ao objeto.

Observe que os focos da ocular (f_ocular) e da objetiva (f_objetiva) estão muito próximos, praticamente coincidindo.

O aumento desta luneta é dado por  A =f_obj / f_oc. Observe por essa expressão que, para que o aumento seja bem grande, a distância focal da ocular deve ser bem menor que a da objetiva, ou seja, f_oc < f_ob.             

No caso de uma luneta terrestre, onde a imagem final não é invertida devemos trocar a lente ocular convergente por uma lente divergente que tem distância focal negativa.

Como o aumento é dado por A = f_obj / f_oc, é claro que maior será o aumento quanto maior o módulo da objetiva for maior que o módulo da ocular.

O que você deve saber, informações e dicas

Entender o funcionamento de todos os dispositivos descritos acima.

Se você quiser aprofundar mais, analise as resoluções dos exercícios a seguir:

01- Uma pequena luneta consiste em uma lente objetiva convergente de distância focal f_ob = 35 cm e de uma lente ocular divergente de distância focal f_oc = - 5,0 cm.

As duas lentes estão separadas por uma distância d = 30 cm, como ilustrado na figura 1.

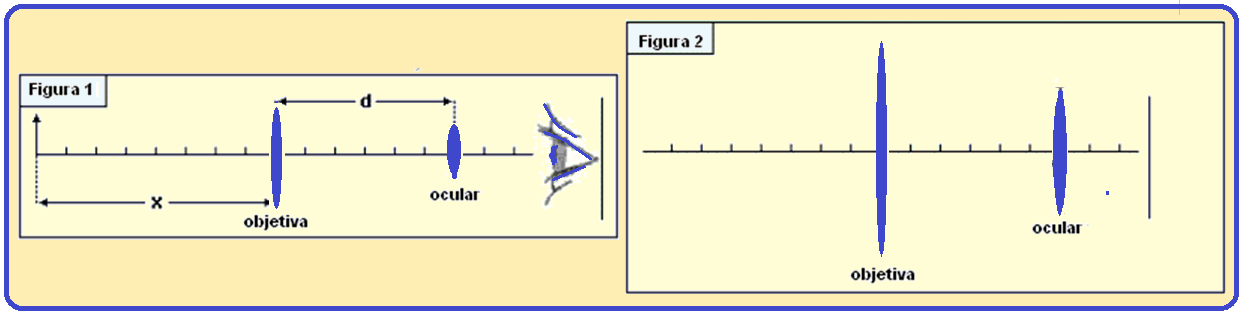
Um objeto é colocado sobre o eixo óptico da luneta, à esquerda da objetiva, distando x da mesma.

a) Calcule a posição da imagem final desse objeto, medida em relação ao centro da lente ocular, quando x = 40 cm.

b) Considere um feixe de raios paralelos de luz incidente na objetiva.

Complete o diagrama de raios, na figura 2, representando suas trajetórias no interior da luneta e indicando claramente a direção em que emergem da ocular (a figura foi ampliada na direção transversal ao eixo óptico da luneta para facilitar seu desenho)

Resolução:

a) Localizando a imagem P’ formada pela objetiva com o objeto P colocado à 40 cm da mesma tal que P = 4 0cm, sendo fornecida a distância focal da objetiva f_objetiva = 35 cm.

Aplicando a equação dos pontos conjugados    P = 40 cm    f = 35 cm  1/f = 1/P + 1/P’  

1/35 = 1/40 + 1/P’    1/35 – 1/40 = 1/P’    1/P’ = (8 – 7)/280    P’ = 280cm (distância da objetiva até i₁ conforme a figura abaixo com i₁ localizada através dos dois raios notáveis traçados).

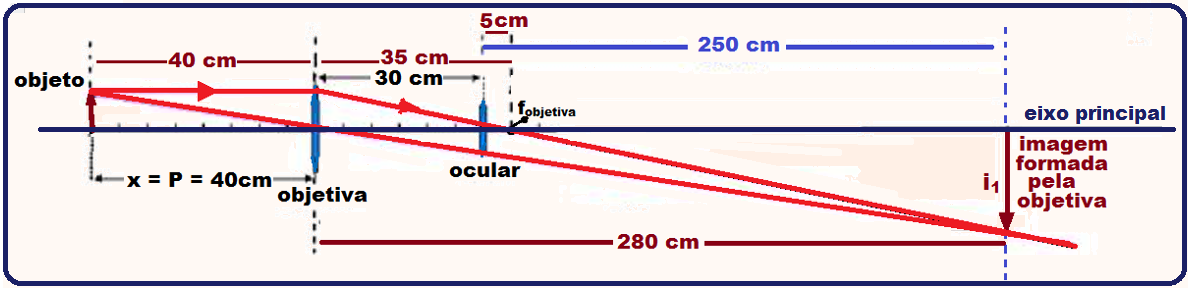
Localização da imagem i₂ de i₁, que funciona como objeto para a ocular sendo dados:

P = 250cm (distância do objeto i₁ até a ocular) f_ocular = - 5cm (divergente)   equação dos pontos conjugados de Gauss 1/f = 1/P + 1/P’ 1/-5 = 1/250 + 1/P’    1/P’ = - 1/5 - 1/250  1/P’ = (- 50 – 1)/250    P’= - 4,9cm (distância pedida de i₂ até a ocular conforme a figura abaixo localizado por dois raios notáveis)

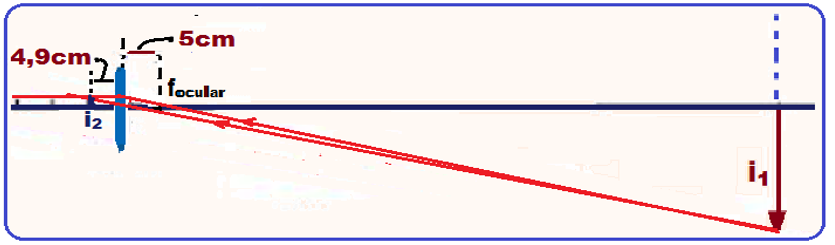
b) os raios que incidem paralelamente ao eixo da lente objetiva, emergem desta, em direção ao foco

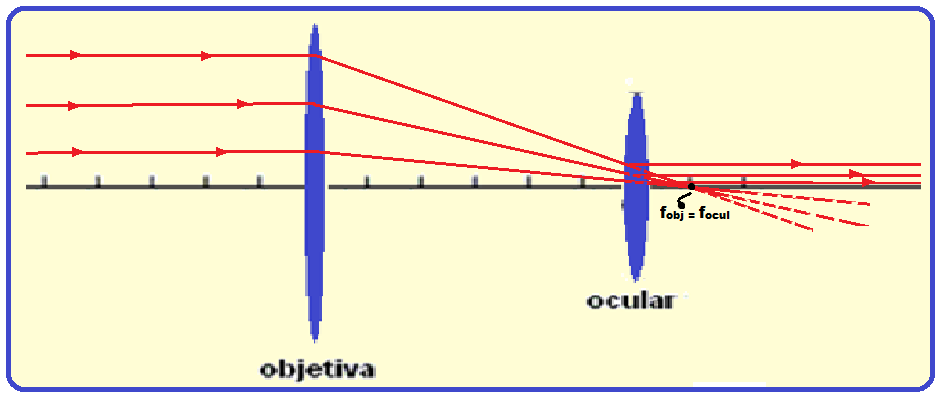
da lente ocular, emergindo da ocular, paralelamente ao eixo principal das lentes.

02- A figura a seguir é a representação esquemática de um sistema óptico formado por duas lentes convergentes, separadas por 50 cm.

As distâncias focais das lentes 1 e 2 são, respectivamente, 10 cm e 15 cm.

Utiliza-se um lápis com 4 cm de comprimento como objeto, o qual é posicionado a 15 cm da lente 1. Com base nesses dados:

a) Determine a posição da imagem formada pelo sistema de lentes.

b) Determine o tamanho da imagem formada pelo sistema. Ela é direita ou invertida, em relação ao objeto? Justifique sua resposta.

c) Empregando a representação de raios, faça um desenho em escala, mostrando a localização e o tamanho da imagem formada pelo sistema. Utilize a escala 10 para 1, ou seja, cada 10 cm no sistema real correspondem a 1 cm no seu desenho. (Cada quadrícula tem 0,5 cm de lado).

Resolução:

a) Dados  distância focal da lente 1 (f₁ = 10 cm)  distância focal da lente 2 (f₂ = 15 cm) distância entre as duas lentes (d = 50 cm)  distância do objeto (lápis) à lente 1 (p₁ = 15 cm).

 Cálculo da distância (P₁’) da primeira imagem à Lente 1 aplicando a equação dos pontos conjugados de Gauss   1/f = 1/P + 1/P’    1/10 = 1/15 + 1/P₁’    P₁’= + 30cm  (a primeira imagem é real e forma-se 30 cm à direita da Lente 1).

 Essa primeira imagem funciona como objeto para a segunda lente    sendo a distância entre as lentes é d = 50 cm, a distância (p₂) da primeira imagem à lente 2 é    p₂ = d – P₁’= 50 – 30    p₂ =20 cm (distância da primeira imagem, agora objeto, para a lente 2).

Cálculo da distância (P₂’) da imagem final à lente 2 de distância focal f₂ = 15 cm    1/f₂ = 1/P₂ + 1/P’₂

1/15 = 1/20 + 1/ P₂’    P₂’= + 60cm (a imagem final é real e se forma 60 cm à direita da lente 2 ou 110 cm à direita da Lente 1).

 b) O aumento fornecido pelo sistema é o produto dos aumentos A = A₁ x A₂    A= P₁’/P₁ x P₂’/P₂  A = 30/15 x 60/20   A= +6 (a imagem final é direita e 6 vezes maior que o objeto).

 Altura h’₂ da imagem final em relação à altura h = 4 cm do objeto A=h’₂/h    6 = h’₂/4    h’₂ = 24cm (a imagem final é real, tem comprimento 24 cm e é direita em relação ao objeto, pois o aumento linear transversal é positivo).

c) Escala dada     [10 cm : 1 cm : 2 quadrículas]   [5 cm : 1 cm : 1 quadrícula]    observe que

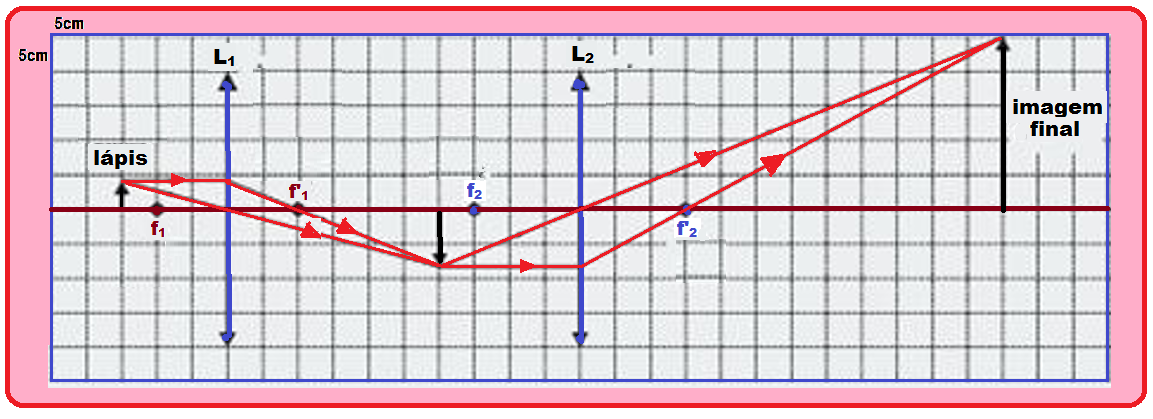
na figura acima, o lado de cada quadrícula representa 5 cm nas medidas dadas no enunciado.

03- Um microscópio composto é formado por duas lentes convergentes. A lente que fica mais próxima do objeto é a objetiva e aquela através da qual se observa a imagem é a ocular.

A imagem I₁, formada pela objetiva, funciona como um objeto para a ocular (figura)

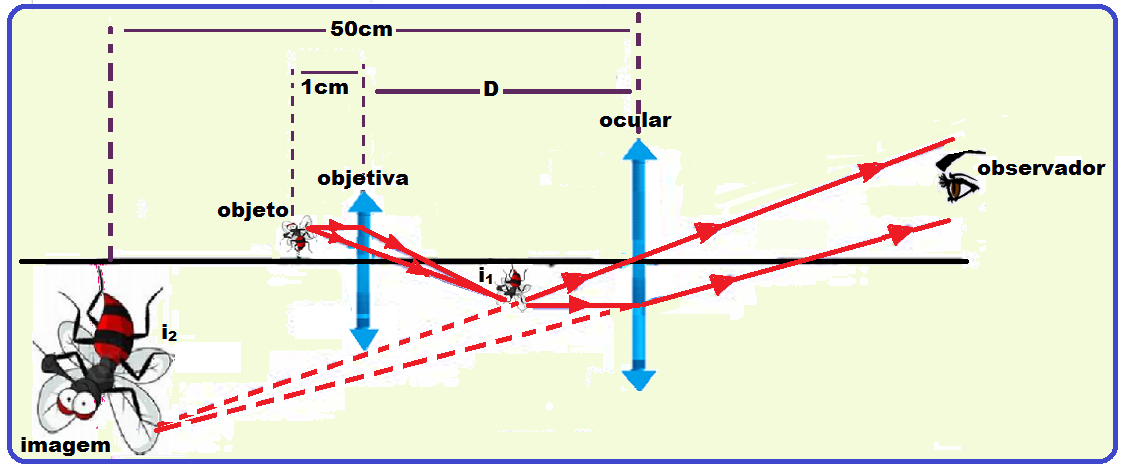
Quando o objeto é colocado a 1cm da objetiva a imagem final que se observa é 100 vezes maior que o objeto e se encontra a 50cm da lente ocular.

Se a ampliação devido à lente objetiva é 20 vezes, determine a distância D, em centímetros.

Resolução:

O aumento fornecido pela objetiva vale   A_objetiva = - 20 (negativo, a imagem é invertida).

Distância do objeto à objetiva P = 1 cm    A_objetiva = - P’/P    -20 = - P’/1    P’ = 20 cm (distância da objetiva até a imagem por ela formada que é i₁).

A_final = A_objetiva.A_ocular    -100 = - 20.A_ocular    A_oc = 5 (aumento fornecido pela ocular, positivo pois i₂ é direita em relação à i₁).

Imagem fornecida pela ocular dista 50cm da mesma e P’ é negativa pois a imagem é virtual) P’ = - 50cm    A_ocular = - P’/P    5 = - (- 50)/P    P = 10cm (distância da ocular até i₁).

A distância D pedida vale   D = 20 + 10    D = 30cm.

Exercícios de vestibulares com resoluções comentadas sobre Instrumentos Ópticos

01-(UNESP-SP) Uma câmara fotográfica rudimentar utiliza uma lente convergente de distância focal f = 50 mm para focalizar e projetar a imagem de um objeto sobre o filme. A distância da lente ao filme é p' = 52 mm. A figura mostra o esboço dessa câmara.

Para se obter uma boa foto, é necessário que a imagem do objeto seja formada exatamente sobre o filme e o seu tamanho não deve exceder a área sensível do filme. Assim:

a) Calcule a posição que o objeto deve ficar em relação à lente.

b) Sabendo-se que a altura máxima da imagem não pode exceder a 36,0 mm, determine a altura máxima do objeto para que ele seja fotografado em toda a sua extensão.

02-(PUC-SP) Uma máquina fotográfica simples é constituída por uma câmara escura. Numa das faces verticais é colocado um filme fotográfico sensível e, na oposta, uma lente adequada que pode se afastar ou se aproximar do filme. Pergunta-se:

a) A lente pode ser divergente? Justifique sua resposta.

b) Em que lugar, relativamente à lente, deve ser colocado o filme, para se obterem imagens nítidas de um objeto infinitamente afastado?

c) Fixando o filme na face vertical acima indicada, como proceder para que a imagem continue nítida no filme quando o objeto  se aproximar da câmara?

03-(UFU-MG) A objetiva de uma máquina fotográfica tem distância focal 100mm e possui um dispositivo que permite seu avanço ou retrocesso. A máquina é utilizada para tirar duas fotos: uma de um objeto no infinito e outra de um objeto distante 30cm da objetiva. O deslocamento da objetiva, de uma foto para outra, em mm, foi de:

04-(UNICAMP-SP) Em uma máquina fotográfica de foco fixo, a imagem de um ponto no infinito é formada antes do filme, conforme figura.

No filme, este ponto está ligeiramente deslocado e sua imagem tem 0,03mm de diâmetro. Mesmo assim, as cópias ampliadas  ainda são nítidas para o olho humano. A abertura para a entrada da luz é de 3,5mm de diâmetro e a distância focal da lente é de 35mm.

a) Calcule a distância d do filme à lente.

b) A que distância da lente um objeto precisa estar para que sua imagem fique exatamente focalizada no filme?

05-(UFV-MG) Uma câmara fotográfica deve produzir, sobre o filme, a imagem de um objeto real situado a 30 cm da lente. Essa imagem deve ser 5 vezes menor que o objeto.

a) Diga o tipo de lente que deve ser usado.

b) Determine a que distância do filme deve estar a lente.

c) Ache a distância focal da lente

06-(ULPE-PE) Uma "câmera tipo caixote" possui uma única lente delgada convergente, de distância focal f = 20 cm.

Qual deve ser a distância da lente ao filme, em cm, para que a imagem de uma pessoa que está de pé a 400 cm da câmera seja focalizada sobre o filme?

07-(UFMG-MG) Usando uma lente convergente, José Geraldo construiu uma câmera fotográfica simplificada, cuja parte óptica está esboçada nesta figura:

Ele deseja instalar um mecanismo para mover a lente ao longo de um intervalo de comprimento x, de modo que possa aproximá-la ou afastá-la do filme e, assim, conseguir formar, sobre este, imagens nítidas.

 a) Sabe-se que a distância focal da lente usada é de 4,0 cm e que essa câmera é capaz de fotografar objetos à frente dela, situados a qualquer distância igual ou superior a 20 cm da lente. Considerando essas informações, DETERMINE o valor de x.

b) Pretendendo fotografar a Lua, José Geraldo posiciona a lente dessa câmera a uma distância D do filme. Em seguida, ele substitui a lente da câmera por outra, de mesmo formato e tamanho, porém feita com outro material, cujo índice de refração é maior. Considerando essas informações, RESPONDA:

Para José Geraldo fotografar a Lua com essa nova montagem, a distância da lente ao filme deve ser menor, igual ou maior que D? JUSTIFIQUE sua resposta.

08-(UNESP-SP) Dispõe-se de uma tela, de um objeto e de uma lente convergente com distância focal de 12cm.

Pretende-se, com auxílio da lente, obter na tela uma imagem desse objeto cujo tamanho seja 4 vezes maior que o do objeto.

a) A que distância da lente deverá ficar a tela?

b) A que distância da lente deverá ficar o objeto?

09-(UNESP-SP) Um projetor rudimentar, confeccionado com uma lente convergente, tem o objetivo de formar uma imagem real e aumentada de um slide. Quando esse slide é colocado bem próximo do foco da lente e fortemente iluminado, produz-se uma imagem real, que pode ser projetada em uma tela, como ilustrado na figura.

A distância focal é de 5 cm e o slide é colocado a 6 cm da lente. A imagem projetada é real e direita. Calcule

a) a posição, em relação à lente, onde se deve colocar a tela, para se ter uma boa imagem.

b) a ampliação lateral (aumento linear transversal).

10-(UFG) Em um arranjo experimental, uma lente convergente, disposta frontalmente entre uma lâmpada acesa de bulbo transparente e uma parede, foi deslocada horizontalmente até se obter uma imagem do filamento aumentada em 3 vezes. Sendo 2,0 m a distância da lâmpada à parede, calcule a distância focal da lente.

11-(UFF-RJ)  A figura representa o esquema simplificado de um projetor de slide, em que S é um slide, i o dispositivo que o ilumina, L uma lente e T a tela de projeção.  Sabe-se que a distância x entre o slide e a tela é x=6,0.10²cm e que a imagem projetada na tela é ampliada 59 vezes.

Nessa situação conclui-se que:

a) A lente é divergente e sua distância focal é, aproximadamente, 5,9.10²cm

b) A lente é convergente e sua distância focal é, aproximadamente, 59cm

c) A lente é convergente e sua distância focal é, aproximadamente, 5,9.10²cm

d) A lente é convergente e sua distância focal é, aproximadamente, 9,8cm

e) A lente é divergente   e sua distância focal é, aproximadamente, 9,8cm

12-(UNESP-SP) Um estudante, utilizando uma lente, projeta a imagem da tela da sua televisão, que mede 0,42m X 0,55 m, na parede oposta da sala.

Ele obtém uma imagem plana e nítida com a lente localizada a 1,8m da tela da televisão e a 3,6m da parede.

a) Quais as dimensões da tela projetada na parede? Qual a distância focal da lente?

b) Como a imagem aparece na tela projetada na parede; sem qualquer inversão?  Invertida apenas na vertical (de cabeça para baixo)?  Invertida na vertical e na horizontal (de cabeça para baixo e trocando o lado esquerdo pelo direito)? Justifique.

13-(PUC-SP) Um projetor de slide deve projetar na tela  uma imagem ampliada 24 vezes.

Se a distância focal da lente objetiva do projetor é de 9,6cm, a que distância do slide deve ser colocada a tela?

a) 250cm         

b) 240cm         

c) 10cm         

d) 230cm         

e) nenhuma das anteriores

14- (ULPE-PE) Um estudante usando uma lupa sob a luz do sol consegue queimar uma folha de papel devido à concentração dos raios do sol em uma pequena região.

 Ele verificou que a maior concentração dos raios solares ocorria quando a distância entre o papel e a lente era de 20 cm. Com a mesma lupa, ele observou letras em seu relógio e constatou que uma imagem nítida delas era obtida quando a lente e o relógio estavam separados por uma distância de 10 cm. A partir dessas informações, considere as seguintes afirmativas:

1. A distância focal da lente vale f = 20 cm.

2. A imagem das letras formada pela lente é invertida e virtual.

3. A lente produz uma imagem cujo tamanho é duas vezes maior que o tamanho das letras impressas no relógio.

Assinale a alternativa correta.

a) Somente a afirmativa 1 é verdadeira.     

b) Somente a afirmativa 2 é verdadeira.     

c) Somente a afirmativa 3 é verdadeira.

d) Somente as afirmativas 1 e 3 são verdadeiras.     

e) Somente as afirmativas 2 e 3 são verdadeiras

15-(UFLA-MG) Um biólogo utiliza uma lente convergente com distância focal de 30cm para observar insetos.

Supondo um inseto de 2cm a uma distância de 20cm da lente, determine o aumento linear transversal.

16-((UFU-MG) Uma lupa, quando produz uma imagem a 30cm da lente, para fornecer um aumento linear transversal de 16 vezes, deve ter sua distância focal de:

17-(UNESP-SP) Uma lupa utilizada para leitura é confeccionada com uma lente delgada convergente, caracterizada por uma distância focal f. Um objeto é colocado a uma distância 0,8 f, medida a partir da lente.

 Se uma letra de um texto tem altura 1,6 mm, determine o tamanho da letra observado pelo leitor.

18-(Ufpr-PR) Uma certa lupa tem uma convergência de 5 di. Observando um pequeno objeto com essa lupa, só veremos uma  imagem ampliada e direita (não invertida) se a lupa for mantida a uma distância d do objeto, tal que:

a) 0 cm < d < 5 cm.     

b) 0 cm < d < 10 cm.     

c) 0 cm < d < 20 cm.      

d) 10 cm < d < 40 cm.     

e) 20 cm < d < 40 cm.

19- (UFPE-PE) Um microscópio composto é formado por duas lentes convergentes. A lente que fica mais próxima do objeto é a objetiva e aquela através da qual se observa a imagem é a ocular. A imagem I₁, formada pela objetiva, funciona como um objeto para a ocular (figura)

Quando o objeto é colocado a 1cm da objetiva a imagem final que se observa é 100 vezes maior que o objeto e se encontra a 50cm da lente ocular. Se a ampliação devido à lente objetiva é 20 vezes, determine a distância D, em centímetros

20-(UFF-RJ) A figura mostra um microscópio artesanal construído por um tubo de plástico PVC e duas lentes convergentes.

As lentes L₁ e L₂ distam 20cm uma da outra e tem distâncias focais f₁=3,0cm e f₂=10,0cm, respectivamente. Um inseto, colocado a 4,0cm da lente L₁, é observado com esse microscópio. Nessa situação, o observador vê o inseto com tamanho N vezes maior, sendo N igual a:

21-(UFPE) Um microscópio é composto de duas lentes convergentes. A lente que fica mais próxima do objeto é chamada objetiva, e aquela através da qual se observa a imagem é a ocular. Considere uma situação na qual a objetiva amplia 50 vezes o objeto e a ampliação total do microscópio é de 600 vezes. Qual é a ampliação devida à lente ocular?

22-(FMTM-MG) Um microscópio composto é um dispositivo que permite visualizar objetos de pequenas dimensões. Seu sistema óptico é constituído de duas lentes: a ocular e a objetiva. Ode-se afirmar que:

a) as duas lentes são divergentes     

b) as duas lentes são convergentes     

c) as duas lentes têm convergências negativas      

d) a ocular é convergente e a objetiva divergente     

e) a ocular é divergente e a objetiva convergente

23-(UERJ-RJ) A imagem que se observa de um microscópio composto é:

a) real e invertida     

b)real e direita     

c) virtual e direita     

d) real e ampliada     

e) virtual e invertida

24-(PUCCAMP-SP) O esquema a seguir mostra a formação da imagem em uma luneta astronômica.

Numa certa luneta, as distâncias focais da objetiva e da ocular são de 60cm e 30cm, respectivamente, e a distância entre elas é de 80cm. Determine, nessa luneta, a distância entre a imagem final formada de um astro distante e a ocular.

25- (UFF-RJ) Uma pequena luneta consiste em uma lente objetiva convergente de distância focal f_ob = 35 cm e de uma lente ocular divergente de distância focal f_oc = - 5,0 cm. As duas lentes estão separadas por uma distância d = 30 cm, como ilustrado na figura 1. Um objeto é colocado sobre o eixo óptico da luneta, à esquerda da objetiva, distando x da mesma.

a) Calcule a posição da imagem final desse objeto, medida em relação ao centro da lente ocular, quando x = 40 cm.

b) Considere um feixe de raios paralelos de luz incidente na objetiva. Complete o diagrama de raios, na figura 2, representando suas trajetórias no interior da luneta e indicando claramente a direção em que emergem da ocular (a figura foi ampliada na direção transversal ao eixo óptico da luneta para facilitar seu desenho

26-(CESGRANRIO-RJ)  Durante o mês de Junho de 1996, foi possível observar Júpiter com seus satélites, próximo da constelação de Escorpião, com o auxílio de uma pequena luneta. Sabendo disso, um estudante resolveu fazer suas próprias observações, montando o seguinte dispositivo:

L₁ e L₂  são lentes, sendo que L₁ é a ocular e L₂ é a objetiva. Sejam f₁ e f₂ as distâncias focais dessas lentes. Assinale a opção que indica o caso no qual foi possível o estudante fazer suas observações:

a) f₁ < 0, f₂ < 0 e módulo de f₁  <  módulo de f₂                      

b)   f₁ <  0, f₂  <  0    módulo de f₁ >  módulo de f₂

c) f₁ > 0, f₂ <  0 e módulo de f₁ <   módulo de f₂                     

d)  f₁>  0, f₂ <  0 e  módulo de f₁ >   módulo de f₂  

e) f₁ > 0, f₂ > 0 e  módulo de f₁ <  módulo de f₂

27-(UFF-RJ) Uma pessoa dispõe de lentes divergentes e convergentes, com distâncias focais (f) de -40cm, -10cm, 10cm e 40cm. A correta associação de lentes para que ela obtenha uma luneta que forneça uma imagem não invertida é:

a) Objetiva f=40cm ; ocular f=10cm       

b) Objetiva f=40cm ; ocular f= -10cm            

c) Objetiva f=10cm ; ocular f=40cm

d) Objetiva f=10cm ; ocular f=-40cm      

e) Objetiva f=40cm ; ocular f=40cm

28-(PUC-SP) Uma luneta improvisada foi construída com duas lentes de óculos cujas distâncias focais são 200cm e 20cm. O aumento visual dessa luneta é de:

a) 4.000 vezes         

b) 220 vezes         

c) 200 vezes         

d) 180 vezes       

e) 10 vezes

29-(PUC-MG) Com relação à luneta astronômica, é correto afirmar que:

a) ambas as lentes são convergentes         

b) a ocular tem grande distância focal         

c) a imagem final é direita

d) a objetiva é convergente e a ocular divergente         

e) apenas a ocular é convergente

30-(UERJ-RJ) O transatlântico dispõe de uma luneta astronômica com aumento visual G igual a 10, composta por duas lentes convergentes. A distância focal da objetiva é igual a 40 cm.

Em relação às lentes da luneta, determine:

a) suas convergências;

b) o tipo de imagem produzida por cada uma delas.

31-(PUC-PR) Nas últimas décadas, a alimentação tem sido motivo de preocupação em todos os países. Um grande desafio é adequar a produção de alimentos à demanda crescente da população mundial, já que existem milhões de indivíduos famintos no planeta.     

Com a globalização, ficaram mais evidentes os problemas relativos à qualidade dos alimentos para consumo humano. A Organização Mundial da Saúde (OMS) tem alertado para a necessidade de se coibir a contaminação de alimentos por agentes biológicos com potencial de causar danos à saúde. Os agentes biológicos podem ser visíveis, como moscas, pulgões, lesmas, parasitas (como lombrigas e tênias) ou não serem visíveis a olho nu, como os microrganismos, que só podem ser vistos através do microscópio.

Microscópio é o instrumento que serve para ampliar, com a finalidade de observação, a imagem de objetos de pequenas dimensões. A lupa, quando fixa em um suporte, recebe o nome de microscópio simples. O microscópio composto é constituído da associação de duas lentes separadas por um tubo e, com ele, é possível observar a maioria das células vivas. A lente que fica próxima do objeto é denominada objetiva e a lente através da qual a pessoa observa a imagem é chamada ocular.

Analise as afirmativas a seguir:

I. As bactérias, quando patogênicas, podem causar doenças como botulismo, salmonelose, gastroenterite entre outras. Se uma bactéria for observada num microscópio composto, a imagem final formada pelo sistema é, além de invertida, virtual e maior que a própria bactéria.

II. Os fungos, em alguns alimentos, são utilizados propositalmente para dar sabor, porém, em casos de contaminação, podem provocar cirrose hepática, necrose, edema, carcinoma e favorecer o aparecimento do cancro hepático. Se um fungo for colocado a 4,0 cm de uma lupa de 6,0 cm de distância focal, o aumento linear será de 1,5 vezes.

III. Os parasitas são transmitidos pela ingestão de alimentos contaminados. Podem causar teníase, ascaridíase, amebíase e outras. Observando um parasita num microscópio composto, verificou-se que a imagem ficou ampliada. As lentes do microscópio são do tipo convergente.

Pode-se AFIRMAR que:

a) Apenas a alternativa III é correta.            b) Apenas a alternativa II é correta.            c) Apenas as alternativas I e II são corretas. 

d) Apenas as alternativas I e III são corretas.            e) Todas as alternativas são incorretas. 

32-(UEM-PR) Os instrumentos ópticos podem ordinariamente ser classificados como instrumentos de observação ou de projeção. Com relação aos instrumentos ópticos e suas imagens conjugadas, assinale o que for correto.

 01. A lupa, ou microscópio simples, conjuga uma imagem real, direita e maior.

02. Em um microscópio composto, a objetiva conjuga uma imagem real, invertida e maior.

04. Em uma luneta astronômica refratora, a ocular conjuga uma imagem final virtual, direita e ampliada.

08. Em um projetor, o conjunto de lentes projetoras conjuga uma imagem real, invertida e maior.

16. Uma máquina fotográfica simplificada, como uma câmera escura, conjuga uma imagem real, invertida e maior.

33-(UFSCAR-SP)

 Neste ano o mundo todo comemora os 400 anos das primeiras observações astronômicas realizadas por Galileu Galilei. Popularizam-se esquemas de montagens caseiras de lunetas utilizando materiais de baixo custo, tais como, por exemplo, tubos de PVC, uma lente convergente (objetiva) e uma lente divergente ou convergente (ocular).

Na escolha das lentes a serem utilizadas na montagem da luneta, geralmente, não são relevantes as suas distâncias focais, f1 e f2 (medidas em metros), mas sim as suas potências de refração (vergência), cuja unidade de medida é a dioptria (“grau”). A vergência V de uma lente convergente ou divergente é dada pelo inverso da distância focal.

Na montagem da luneta, a distância entre as duas lentes é igual à soma das distâncias focais dessas lentes e o aumento no tamanho da imagem observada com a luneta é dado pela razão entre as distâncias focais das lentes objetiva e ocular.

De posse dessas informações e desejando construir uma luneta, um estudante adquiriu tubos de PVC, uma lente objetiva convergente de 1,50 grau e uma lente ocular divergente com distância focal de 3 cm.

a) Calcule a que distância máxima da lente objetiva ele deverá fixar a ocular. A imagem formada será direta ou invertida?

b) Empolgado com essa montagem, o estudante deseja construir uma luneta com o triplo da capacidade de ampliação da imagem. Mantendo-se fixa a objetiva em 1,50 grau, calcule qual será o valor da vergência da ocular e o tamanho máximo da luneta.

34-(UFPR-PR) A figura a seguir é a representação esquemática de um sistema óptico formado por duas lentes convergentes, separadas por 50 cm. As distâncias focais das lentes 1 e 2 são, respectivamente, 10 cm e 15 cm.

Utiliza-se um lápis com 4 cm de comprimento como objeto, o qual é posicionado a 15 cm da lente 1. Com base nesses dados:

a) Determine a posição da imagem formada pelo sistema de lentes.

b) Determine o tamanho da imagem formada pelo sistema. Ela é direita ou invertida, em relação ao objeto? Justifique sua resposta.

c) Empregando a representação de raios, faça um desenho em escala, mostrando a localização e o tamanho da imagem formada pelo sistema. Utilize a escala 10 para 1, ou seja, cada 10 cm no sistema real correspondem a 1 cm no seu desenho. (Cada quadrícula tem 0,5 cm de lado.)

35-(IFNMG-MG)

Em uma antiga máquina fotográfica de foco fixo, a imagem de um ponto muito distante, “no infinito”, é formada antes do filme, conforme ilustra o esquema da figura seguinte.

No filme, esse ponto está ligeiramente “desfocado” e sua imagem tem 0,03 mm de diâmetro (apesar disso, as cópias ampliadas ainda são nítidas para o olho humano). A abertura para a entrada de luz é de 3,5 mm de diâmetro e a distância focal da lente é igual a 35,0 mm. Nessas condições, o valor da distância, expresso em metro, entre a lente e um objeto, para que sua imagem fique exatamente focalizada no filme, está corretamente apresentado na alternativa:

A) 4,1                           

B) 3,3                                  

C) 2,7                                    

D) 5,4

36-(UFF-RJ)

Uma das principais diferenças entre câmeras fotográficas digitais e analógicas é o tamanho do sistema que armazena a luz do objeto

fotografado. Em uma câmera analógica, o sistema utilizado é um filme de 24 mm de altura e 36 mm de largura. Nas câmeras digitais, o sensor possui 16 mm de altura por 24 mm de largura, aproximadamente. Tanto o filme quanto o sensor são colocados no plano onde se forma a imagem.

Possuímos duas câmeras, uma analógica e uma digital. A distância focal da lente da câmera analógica é f_a=50mm. Queremos fotografar um objeto de altura h = 480 mm.

a) Utilizando a câmera analógica, calcule a distância D entre a lente e o filme, e a distância L entre a lente e o objeto a ser fotografado, de forma que a imagem ocupe a altura máxima do filme e esteja em foco.

b) Utilizando agora a câmera digital, calcule a distância D’ entre a lente e o sensor e a distância focal da lente f_d, de forma que o mesmo objeto, situado à mesma distância L do caso analógico, esteja em foco e ocupe a altura máxima do sensor.

37-(UFF-RJ)

A macrofografia é uma técnica utilizada para fotografar pequenos objetos. Uma condição que deve ser obedecida na realização dessa

técnica é que a imagem do objeto no filme deve ter o mesmo tamanho do objeto real, ou seja, imagem e objeto devem estar na razão 1:1. Suponha uma câmera formada por uma lente, uma caixa vedada e um filme, como ilustra esquematicamente a figura.

Considere que a distância focal da lente é 55mm e que D e D_o representam, respectivamente, as distâncias da lente ao filme e do objeto à lente. Nesse caso, para realizar a macrofotografia, os valores de D e D_o devem ser

a) D=110mm e D_o=55mm             

b) D=55mm e D_o=110mm             

c) D=110mm e D_o=110mm               

d) D=55mm e D_o=55mm

e) D=55mm e D_o=220mm

Resolução comentada dos exercícios de vestibulares sobre

Instrumentos Ópticos

 01- a) 1/f=1/P + 1/P’  ---  1/50=1/52 + 1/P’  ---  1/50 – 1/52=1/P’  ---  1/P’=(26 – 25)/1300  ---  P’=1.300mm=1,3m

b) i=-36mm 9negativo, a imagem é projetada e portanto, invertida) ---  i/o= - P’/P  ---  36/o= - (-52)/1.300  ---  o=900mm=90cm

02- a) Não, a imagem é virtual e não pode ser fotografada (projetada no filme)  

     b) No plano focal imagem 

     c) afasta-se a lente do filme, pois a proporção deve ser mantida

03- Com o objeto no infinito, a imagem se forma sobre o foco  ---  d₁=100mm  ---  com o objeto onde P=30cm=300mm  ---  1/f=1/P + 1/P’  ---  1/100 – 1/300=1/P’  ---  1/P’=(3 – 1)/300  ---  P’=150mm  ---  d₂=150mm  ---  d=150 – 100  ---  d=50mm  ---  R- A

04- a) o=35mm  --  i=3.10^-2mm  ---  f=35mm

Pela semelhança entre os triângulos hachurados da figura abaixo:

3,5/3.10^-2=35/c  ---  3,5c=3.35.10^-2  ---  c=0,3mm  ---  d=35 +0,3  ---  d=35,5mm

b) 1/f=1/P + 1/P’  ---  1/35 – 1/35,3=1/P  ---  P=4.118mm

05- a) Lente convergente, pois a imagem deve ser real para poder ser projetada

b) i=-o/5 (negativo, toda imagem projetada é real e portanto, invertida)   ---  o=-5i  ---  i/o= - P’/P  ---  i/-5i=-P’/30  ---  P’=6cm

c) 1/f=1/P + 1/P’  ---  1/f=1/30 + 1/6  ---  1/f=1/30 + 1/6  ---  1/f=(1 + 5)/30  ---  f=5cm

06- 1/f=1/P + 1/P’  ---  1/20-1/400=1/P’  ---  p’=400/19  ---  P’=21cm

07- a) Para o objeto no infinito, o filme deverá estar a uma distância igual à distância focal, ou seja, 4,0 cm.

No ponto próximo, ou seja, p = 20 cm, a distância da imagem deverá ser igual a 4 + x. Então:

1/4 = (1/20) + [1/(4 + x)]

(1/4) - (1/20) = 1/(4 + x)

(5/20) - (1/20) = 1/(4 + x)

(4/20) = 1/(4 + x)

1/5 =  1/(4 + x)

4 + x = 5  ---   x = 1 cm

b) Para fotografar um objeto mais distante, a distância focal deve ser maior que a distância focal anterior, logo, a distância da lente ao filme deverá ser maior.

08- a) i=-4.o (negativo, invertida)  ---  i/o= -P’/P  ---  -4.0/0= -P’/P  ---  P’=4P  ---  1/12 = 1/P + 1/4P  ---  1/12=(4 + 1)/4P  ---  P=15cm  ---  P’=4P  ---  P’=4.15  ---  P’=60cm

b) P=15cm (veja resolução (a)

09- a) A lente é convergente, pois a imagem é projetada (real e invertida) e, na tela ela aprece como direita, pois o slide é colocado invertido  ---  f=5cm  ---  P=6cm  ---  1/f=1/P + 1/P’  ---  1/5=1/6 + 1/P’  ---  1/5 – 1/6=1/P’  ---  1/P’=(6 – 5)/30  ---  P’=30cm

b) A=-P’/P=-30/6  ---  A= -5 (a imagem é ampliada 5 vezes e é invertida)

10- Veja a figura abaixo:

i=-3.0  ---  i/o=-(2 – x)/x  -3.0/0= -(2 – x)/x  ---  3=(2 – x)/x  ---  4x=2  ---  x=P=0,5m  --- P’=2 – 0,5  ---  P’+1,5m  ---  1/f=1/0,5 + 1/1,5  ---  1/f=(3 + 1)/1,5  ---  f=0,375m

11- Como a imagem é projetada na tela, a lente é convergente

I= - 59.o  ---  i/o= -P’/P  ---  -59.o/0= - (600-P)/P  ---  P=600/60  ---  P=10cm  ---  P’=600 – 10  ---  P’=590cm  ---  1/f=1/10 + 1/590  ---  1/f=(59 + 1)/590  ---  f=9,8cm  ---  R- D

12- a) i/o= -P’/P  ---  i/o=-(-3,6)/1,8  ---  i=2.o  ---  i=2.(0,42X0,55)  ---  i=0,84mX0,11m  ---  1/f=1/P + 1/P’  ---  1/f=1/1,8 + 1/3,6  --- f=1,2m

b) b) invertidas na horizontal e na vertical         

13- i= -24.o  ---  -24.o/o= -P’/P  ---  P’=24P  ---  1/f=1/P + 1/P’  ---  1/9,6=1/P + 1/24P  ---  1/9,6 =(24 + 1)/24P  ---  P=10cm  ---  P’=24.10  ---  P’=240cm  ---  d=P + P’=240 + 10  ---  d=250cm  ---  R- A

14- - 1- Correta – os raios de luz paralelos provenientes do Sol, se refratam na lupa (lente convergente) e convergem para um único ponto que é o foco.

2- Falsa – é direita e virtual

3- Correta – f=20cm  ---  P=10cm  ---  1/f=1/P + 1/P’  ---  1/20 – 1/10 =1/P’  ---  P’= -20cm  ---  i/o=-P’/P  ---  i/o=-(-20)/10  --- 

i/o=2  ---  i=2.o 

R- D

15- 1/30=1/20 + 1/P’  ---  1/30 – 1/20=1/P’  ---  1/P’=(2 – 3)/60  ---  P’=-60cm  ---  A=-P’/P=-(-60)/20  ---  A=3

16- A=-P’/P  ---  16=-(-30)/P  ---  P=1,875cm  ---  1/f=1/1,785 – 1/30  ---  1/f=(30 – 1,875)/53,55  ---  f=53,55/28,125=1,9  --- 

R- A

17-  1/f=1/08f + 1/P’  ---  1/f – 1/08f =1/P’  ---  (0,8 – 1,0)/0.8f=1/P’  ---  P’=-4f  ---  i/o=-P’/P  ---  i/1,6=-(-4f)/0,8f  ---  i=8mm

18-  Uma lente convergente funciona como lupa somente se o objeto estiver entre o foco e a lente  ---  C=1/f  ---  5=1/f  ---  f=0,2m  ---  f=20cm  ---  R- C

19- Objetiva  ---  A_ob=-20 (negativa, a imagem é invertida)  ---  P=1cm  ---  A_ob=-P’/P  ---  -20=-P’/1  ---  P’=20cm (distância da objetiva até i₁)  ---  A_final=A_ob.A_oc  ---  -100=-20.A_oc  ---  A_oc=5  ---  ocular  ---  P’=-50cm (invertida em relação a i₁)  ---  A_oc=-P’/P  ---  5=-(-50)/P  ---  P=10cm (distância da ocular até i₁)  ---  D=20 + 10  ---  D=30cm

20- Objetiva (L₂) ---  1/f=1/P + ‘/P’  ---  1/3 – 1/4 =1/P’ ---  P’=12cm (distancia da imagem i₁ até L₂) ---  aumento linear da objetiva  ---  A_ob= -P’/P= -12/4  ---  A_ob= -3  ---  ocular (L₁) ---  i₁, que agora é objeto para L₁ tem P=20 – 12  ---  P=8cm  ---  1/f=1/P + 1/P’  ---  1/10=1/8 + 1/P’  ---  1/10 – 1/8=1/P’  ---  P’= -40cm  ---  aumento final  ---  A_final=A_ob.A_oc=3.5=15  ---  R- E

21- A_total=A_ob.A_oc  ---  600=50.A_oc  ---  A_oc=12  ---  R- D

22- Consta de duas lentes convergentes (geralmente compostas) de pequenas distâncias focais  ---  R- B

23- Observe na figura abaixo que a imagem final observada através de um microscópio composto é virtual (obtida no prolongamento

dos raios luminosos), maior que o objeto e invertida em relação ao mesmo  ---  R- E

24- Objetiva  ---  Como o objeto está distante, sua imagem converge para o foco da objetiva e P’= 60cm (distância da objetiva até i₁)  ---  ocular  ---  i₁ funciona como objeto para a ocular  ---  P=80 – 60  ---  P=20cm  ---  1/f_oc=1/60 + 1/P’  ---  1/30 – 1/20=1/P’  -

 P’= - 60cm (a nova imagem i₂ é virtual e está a 60cm da ocular)

25- a) Objetiva  ---  P=40cm  --  f=35cm  ---  1/35=1/40 + 1/P’  ---  1/35 – 1/40=1/P’  ---  1/P’=(8 – 7)/280  ---  P’=280cm (distância da objetiva até i₁)

Ocular  ---  i₁ funciona como objeto para a ocular  ---  P=250cm  --  f_oc=-5cm (divergente)  ---  1/-5=1/250 + 1/P’  ---  1/P’=-1/5 – 1/250  ---  1/P’=(-50 – 1)/250  ---  P’= -4,9cm (distância de i₂ até a ocular)

R- 4,9cm

b) os raios que incidem paralelamente ao eixo da lente objetiva, emergem desta, em direção ao foco da lente ocular, emergindo

 da ocular, paralelamente ao eixo principal das lentes.

26- Consta de 2 lentes convergentes, a objetiva e a ocular. Observe pela expressão A=f_obj / f_oc  que, para que o aumento seja bem grande, a distância focal da ocular deve ser bem menor que a da objetiva, ou seja, f_oc < f_ob. R- E            

27- Se a imagem final não é invertida, trata-se de uma luneta terrestre, onde devemos trocar a lente ocular convergente por uma lente divergente que tem distância focal negativa  ---  R- B

28- A=f_ob / f_oc=200/20  ---  A=10  ---  R- E  

29- R- A

30- a) A=f_ob/f_oc  ---  10=40/f_oc  ---  f_oc=4cm  ---  C_oc=1/4.10^-2  ---  C_oc=25di  ---  C_ob=1/40.10^-2  ---  C_ob=2,5di

 b) Objetiva – imagem real e ocular – imagem virtual

31- A afirmação I é correta  ---  a afirmação II é falsa  ---  1/f = 1/p + 1/p’  ---  1/6 = 1/4 + 1/p’  ---  1/6 – 1/4 = 1/p’  ---  4/24 – 6/24 = 1/p’  ---  -2/24 = 1/p’  ---  p’ = - 24/2 = - 12 cm  ---   aumento linear  ---  A = -p’/p = 12/4 = 3  ---  a afirmação III é correta  ---R- D

32- 01. Falsa  ---  a lupa conjuga uma imagem virtual, direita e maior e sòmente quando o objeto está entre o foco e a lente (convergente)

02. Correta  ---  veja na figura abaixo que a objetiva conjuga uma imagem real, invertida e maior (i’)

04- Correta  ---  veja esquema abaixo:

08. Correta  ---  se a imagem é projetada ela real e invertida e, como é projetada numa tela, deve ser maior que o objeto (filme)

16, Falsa  ---  a imagem é real, invertida e menor.

R- (02 + 04 + 08)=14

33- a) Dados  ---  C_ob = 1,5 di  ---  f_oc = – 3 cm (lente divergente f < 0)  ---  cálculo da distância focal da objetiva  ---  f_ob=1/C_ob  ---

f_ob=1/1,5  ---  f_ob=0,67cm  ---  do enunciado  ---  D_máx =  f_ob + f_oc  ---  D_máx =  67 – 3 = 64 cm  ---  esse tipo de arranjo das lentes é conhecido como “Luneta de Galileu”  ---  a imagem é direita, conforme mostra figuras abaixo, que estão fora de escala  ---   

na Fig 1, traçamos a imagem fornecida pela objetiva (I1)  ---  como o objeto é um astro (objeto impróprio) a imagem forma-se no foco imagem da objetiva (f’_ob)  ---  na Fig 2 você observa a ocular  ---   imagem da objetiva comporta-se como objeto virtual para a ocular com a distância entre as lentes menor que a distância máxima  ---  a imagem final (I₂) é direita.

b)

Como a lente é divergente, retirando o módulo  ---  d=10^-2m  ---  a vergência C é o inverso da distância focal  ---  C=1/10^-2  ---

C=100 di  ---  máximo tamanho da luneta  ---  D’_máx=f_ob + d=67 – 1  ---  D’_máx= 66cm

34- a) Dados  ---  f₁ = 10 cm  ---  f₂ = 15 cm  ---  d = 50 cm  ---   p₁ = 15 cm  ---  cálculo da distância (P₁’) da primeira imagem à Lente 1  ---  1/f=1/P + 1/P’  ---  1/10=1/15 + 1/P₁’  ---  P₁’= + 30cm  ---  a primeira imagem é real e forma-se 30 cm à direita da Lente 1  ---  essa primeira imagem funciona como objeto para a segunda lente  ---  sendo a distância entre as lentes é d = 50 cm, a distância da primeira imagem à Lente 2 é  ---  p₂ = d – P₁’= 50 – 30  ---  p₂ =20 cm  ---  cálculo da distância (P₂’) da imagem final à Lente 2  ---  1/15=1/20 + 1/ P₂’  ---  P₂’= + 60cm  ---  a imagem final é real e se forma 60 cm à direita da Lente 2 ou 110 cm à direita da Lente 1.

 b) O aumento fornecido pelo sistema é o produto dos aumentos  ---  A=A₁ x A₂  ---  A= P₁’/P₁ x P₂’/P₂  ---  A= +6  ---  A=h’₂/h  ---  6=h’₂/4  ---  h’₂=24cm  ---  a imagem final é real, tem comprimento 24 cm e é direita em relação ao objeto, pois o aumento linear transversal é positivo

c) Escala dada  ---   [10 cm : 1 cm : 2 quadrículas]  ---  [5 cm : 1 cm : 1 quadrícula]  ---  observe que na figura abaixo, o lado de cada quadrícula representa 5 cm nas medidas dadas no enunciado.

35- Com o objeto muito distante “no infinito” a imagem está localizada no foco, ou seja, a 35mm da lente (figura)  --- 

Calculando a distância d’, do foco até onde está o filme  ---  semelhança de triângulos  ---  3,5/35 = 0,03/d’  ---  d’=0,3mm  ---  para que a imagem do objeto que está colocado a uma distância P da lente seja nítida ela deve estar exatamente sobre o filme, ou seja, a uma distância P’=35,03mm da lente de distância focal f=35mm  ---  equação dos pontos conjugados  ---  1/f = 1/P + 1/P’  ---  1/35 = 1/P + 1/35,3  ---  1/P = 1/35 – 1/35,3  ---  1/P=(35,3 – 35)/1235,5  ---  P=4118,3mm≈4,1m  ---  R- A.

36- a) Câmera analógica  ---  distância entre a lente e o filme (imagem) é P’=D  ---  a distância L entre a lente e o objeto é P=L  ---  a altura máxima da imagem deve ser a altura máxima do filme que é de i= - 24mm (negativa porque toda imagem real é invertida) 

---  distância focal da lente f_a=50mm (positiva porque a lente é convergente, pois a imagem deve ser real para poder ser projetada)  ---  a altura do objeto é fornecida e vale o=480mm  ---  i/o= - P’/P  ---  24/480= - D/L  ---  D=L/20  ---  equação dos pontos conjugados  ---  1/f_a = 1/P + 1/P’  ---  1/50 = 1/L + 1/D  ---  1/50 = 1/L + 1/(L/20)  ---

1/50 = 1/L + 20/L  ---  1/50 = 21/L  ---  L = 1050mm  ---  D=L/20=1050/20  ---  D=52,5mm.

b) Agora trata-se de uma câmera fotográfica digital onde a imagem formada no censor tem altura i= -16mm (negativa porque a imagem para ser projetada deve ser real e invertida) e a distância do objeto à lente continua a mesma, ou seja P=L= 1050mm  --- 

observe atentamente na figura todos os dados fornecidos e pedidos  ---  i/o = - P’/P  ---  - 16/480 = - D’/L  ---  D’=L/30=1050/30  ---  D’= 35mm  ---  equação dos pontos conjugados de Gauss  ---  1/f_d = 1/P + 1/P’  ---  1/f_d = 1/L + 1/D’  ---   1/f_d = 1/L + 1/(L/30)  ---   1/f_d = 1/L + 30/L  ---  1/f_d = 31/L  ---  f_d=L/31=1050/31≈33,89mm  ---  f_d≈ 33,9 mm

37- O ponto antiprincipal de qualquer lente é o dobro de sua distância focal  ---  f₀=55mm  ---  A_o=2.55=110mm  ---  veja as características da imagem formada quando o objeto está sobre o ponto antiprincipal:

Objeto P sobre A_o

 Características da imagem P’:

Natureza – real

Localização – sob A_i

Tamanho e orientação – mesmo tamanho que o do objeto e invertida em relação a ele.

Utilidade: Xérox – tamanho normal, macrofotografia.

R- C