
Fórmula (equação) dos Fabricantes de Lentes
Podemos determinar a distância focal f e a vergência C de uma lente conhecendo os raios de curvatura de suas faces e os índices de refração da lente e do meio que a envolve, através da equação dos fabricantes de lentes:

Considerações importantes para a resolução de exercícios
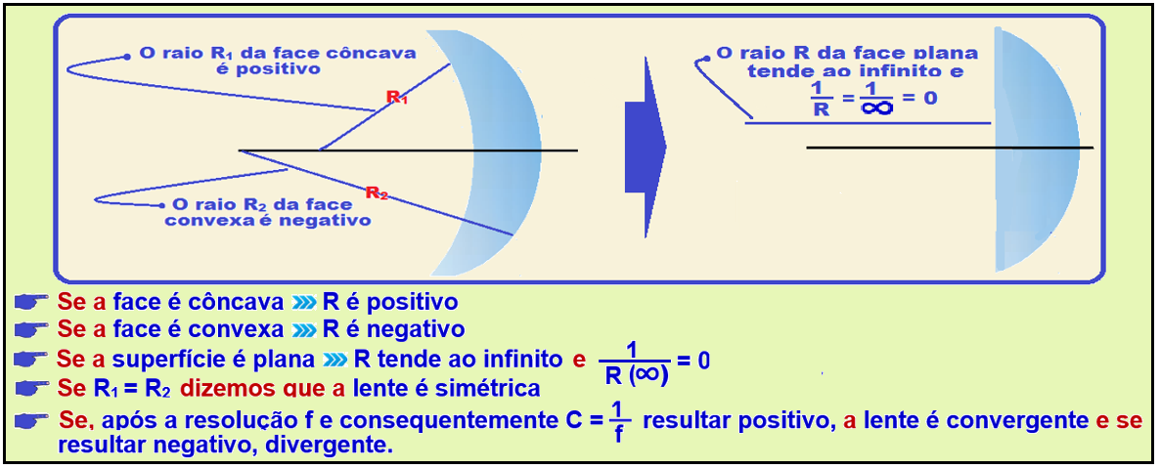
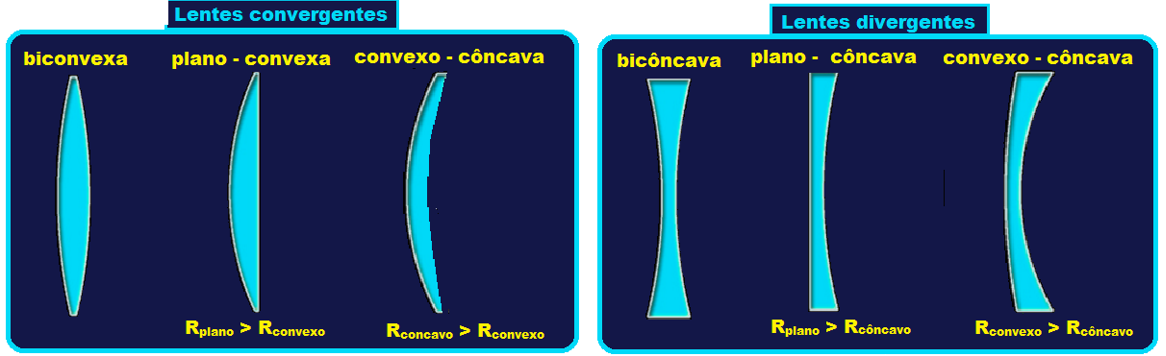
Recordando:
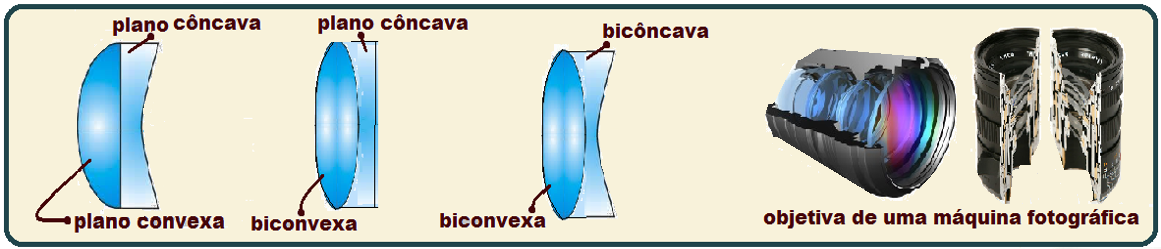
Justaposição de lentes
Quando justapomos duas lentes obtemos uma lente equivalente cuja vergência ou convergência Ceq é a soma algébrica da vergência de cada uma das lentes, ou seja, Ceq = C1+ C2.
Lembre-se que C = 1 / f e que se a lente é divergente f e C são negativos e se a lente é convergente, positivos.
Exemplo numérico:
Uma
lente
convergente de 12di é
justaposta
a uma lente divergente de 20di.
A associação funciona como uma única lente convergente ou divergente? Determine sua vergência.
Resolução:
Lente
convergente
![]() C1
=
+12di.
C1
=
+12di.
Lente
divergente
![]() C2
=
- 20di.
C2
=
- 20di.
Ceq
=
+ 12di – 20di
![]() Ceq
=
- 8di.
Ceq
=
- 8di.
Essa associação funciona como uma única lente divergente, pois Ceq é negativa.
O que você deve saber, informações e dicas
![]() Quando
uma
lente quebra,
a distância
focal e consequentemente a vergência de cada pedaço não se altera,
pois baseado na equação dos fabricantes, as superfícies externas
continuam com os mesmos raios e a lente continua com mesmo índice de
refração
Quando
uma
lente quebra,
a distância
focal e consequentemente a vergência de cada pedaço não se altera,
pois baseado na equação dos fabricantes, as superfícies externas
continuam com os mesmos raios e a lente continua com mesmo índice de
refração
![]() Observe na expressão
C = 1/f = (nl/nm –
1).(1/R1
+ 1/R2)
onde
nl é
o índice de refração da lente e nm o
índice de refração do meio que a envolve, que:
Observe na expressão
C = 1/f = (nl/nm –
1).(1/R1
+ 1/R2)
onde
nl é
o índice de refração da lente e nm o
índice de refração do meio que a envolve, que:
![]() se a lente estiver imersa
no ar (nm
=
1), a
expressão
C =1/f = (nl/nm –
1).(1/R1
+ 1/R2)
fica
C
= 1/f = (nl –
1).(1/R1
+ 1/R2).
se a lente estiver imersa
no ar (nm
=
1), a
expressão
C =1/f = (nl/nm –
1).(1/R1
+ 1/R2)
fica
C
= 1/f = (nl –
1).(1/R1
+ 1/R2).
Assim, se a lente possuir os mesmos raios, f é inversamente proporcional a (nl - 1), ou seja, quanto maior for o índice de refração da lente, menor será sua distância focal.
![]() como (nl/nm –
1) é
inversamente
proporcional a f,
quanto maior
for a razão nl/nm,
menor será a distância focal da lente.
como (nl/nm –
1) é
inversamente
proporcional a f,
quanto maior
for a razão nl/nm,
menor será a distância focal da lente.
![]() Analise as resoluções
dessas questões interessantes:
Analise as resoluções
dessas questões interessantes:
01-(ITA)
Uma
lente
convergente biconvexa tem distância focal de 20cm quando
está mergulhada
em
ar.
A lente é feita de vidro, cujo índice de refração é nv = 1,6. Se a lente é mergulhada em um meio, menos refringente do que o material da lente, cujo índice de refração é nm, considere as seguintes afirmações e analise-as como verdadeiras ou falsas:
I. A distância focal não varia se o índice de refração do meio for igual ao do material da lente.
II. A distância focal torna-se maior se o índice de refração nm for maior que o do ar.
III. Neste exemplo, uma maior diferença entre os índices de refração do material da lente e do meio implica numa menor distância focal.


III- Verdadeira, veja justificativa anterior.
02-(UFC-CE) Uma lente esférica delgada, constituída de material de índice de refração n, está imersa no ar (nar=1,00).
A lente tem distância focal f e suas superfícies esféricas tem raios de curvatura R1 e R2.
Esses parâmetros obedecem a uma relação, conhecida como “equação dos fabricantes”, mostrada abaixo.
1/f=(n-1).(1/R1+1/R2)
Suponha uma lente biconvexa de raios de curvatura iguais (R1 = R2 = R), distância focal f e índice de refração n = 1,8 (figura 1).
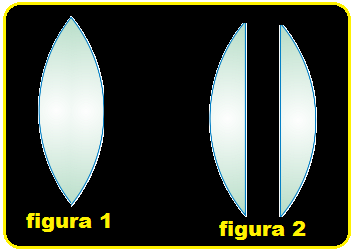
Essa lente é partida dando origem a duas lentes plano-convexas iguais (figura 2).
Calcule o valor da distância focal de cada uma das novas lentes.
Resolução:

Antes
de a lente
ser partida, ela
possui
duas faces convexas de
raio
R tal
que, pela
equação dos fabricantes fornece o valor do raio R em função da
distância focal f
![]() 1/f = (n – 1).(1/R1
+ 1/R2)
1/f = (n – 1).(1/R1
+ 1/R2)
![]() 1/f=(1,8-1).(1/R+1/R)
1/f=(1,8-1).(1/R+1/R)
![]() 1/f=(0,8).2/R
1/f=(0,8).2/R
![]() R=1,6f (I)
R=1,6f (I)

Exercícios de vestibulares com resoluções comentadas sobre
Fórmula (equação) dos Fabricantes de Lentes
01-(UNAERP-SP) Duas lentes convergentes delgadas, de distâncias focais respectivamente iguais a 5,00cm e 15,00cm, são justapostas. Calcule a distância focal (em cm) e a vergência (em dioptrias) do sistema.
02- (UFU-MG) Duas lentes delgadas e convergentes, de distâncias focais f1=10cm e f2=40cm, foram justapostas para se obter uma maior vergência. A convergência obtida com essa associação é, em dioptrias:
a) 2 b) 0,125 c) 8 d) 12,5 e) 50
03-(UFU-MG) Um sistema óptico é formado por duas lentes convergentes delgadas em contato, de distâncias focais f1 e f 2. Para obter um sistema equivalente, pode-se substituir essas lentes por uma que possua a distância focal, f, dada por:
a) f=f1+f2/f1.f2
b) f= f1.f2/ f1+f2
c) f= f1-f2/f1+f2
d) f= f1+f2/ f1-f2
e) f=2f1.f2/f1-f2
04-(UFB) Uma lente convergente de 12di é justaposta a uma lente divergente de 20di. A associação funciona como uma única lente convergente ou divergente? Determine sua vergência.
05- (UNIFESP-SP) Um estudante observa uma gota de água em repouso sobre sua régua de acrílico, como ilustrado na figura
Curioso,
percebe que, ao olhar para o caderno de anotações através dessa
gota, as letras aumentam ou diminuem de tamanho conforme afasta ou
aproxima a régua do caderno. Fazendo alguns testes e algumas
considerações, ele percebe que a gota de água pode ser utilizada
como uma lente e que os efeitos ópticos do acrílico podem ser
desprezados. Se a gota tem raio de curvatura de 2,5 mm e índice de
refração 1,35 em relação ao ar,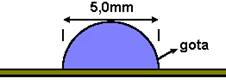
a) calcule a convergência C dessa lente.
b) Suponha que o estudante queira obter um aumento de 50 vezes para uma imagem direita, utilizando essa gota. A que distância d da lente deve-se colocar o objeto?
06- (FGV-SP) Do lado de fora, pelo vitrô do banheiro, um bisbilhoteiro tenta enxergar seu interior
Frustrado,
o xereta só conseguiu ver as múltiplas imagens de um frasco de
xampu, guardado sobre o aparador do boxe, a 36 cm de distância do
vidro. De fato, mal conseguiu identificar que se tratava de um frasco
de xampu, uma vez que cada uma de suas imagens, embora com a mesma
largura, tinha a altura, que no original é de 20 cm, reduzida a
apenas:
(Informações: suponha válidas as condições de estigmatismo de Gauss e que os índices de refração do vidro e do ar sejam, respectivamente, 1,5 e 1,0.)
a) 0,5 cm. b) 1,0 cm. c) 1,5 cm. d) 2,0 cm. e) 2,5 cm.
07-(ITA) Uma lente convergente tem distância focal de 20cm quando está mergulhada em ar. A lente é feita de vidro, cujo índice de refração é nv = 1,6. Se a lente é mergulhada em um meio, menos refringente do que o material da lente, cujo índice de refração é n, considere as seguintes afirmações:
I. A distância focal não varia se o índice de refração do meio for igual ao do material da lente.
II. A distância focal torna-se maior se o índice de refração n for maior que o do ar.
III. Neste exemplo, uma maior diferença entre os índices de refração do material da lente e do meio implica numa menor distância focal.
Então, pode-se afirmar que:
a) apenas a II é correta.
b) apenas a III é correta.
c) apenas II e III são corretas.
d) todas são corretas.
e) todas são incorretas.
08-(UNIFESP-SP)
Tendo-se
em vista que as lentes são, na prática, quase sempre usadas no ar,
a equação dos fabricantes de lentes costuma ser escrita na forma: C
= (n - 1) (1/R1+1/R2)
Nessas
condições, pode-se afirmar que a convergência de uma lente
plano-convexa de índice de refração n = 1,5 e cujo raio da face
convexa é R = 20 cm é:![]()
a) 0,50 di.
b) 1,0 di.
c) 1,5 di.
d) 2,0 di.
e) 2,5 di.
09-(UFC-CE) Uma lente esférica delgada, constituída de material de índice de refração n, está imersa no ar (nar=1,00). A lente tem distância focal f e suas superfícies esféricas tem raios de curvatura R1 e R2. Esses parâmetros obedecem a uma relação, conhecida como “equação dos fabricantes”, mostrada abaixo.
1/f=(n-1).(1/R1+1/R2)

Suponha uma lente biconvexa de raios de curvatura iguais (R1=R2=R), distância focal f e índice de refração n=1,8 (figura 1). Essa lente é partida dando origem a duas lentes plano-convexas iguais (figura 2)
O valor da distância focal de cada uma das novas lentes é:
a) f/2
b) 4f/5
c) f
d) 9f/5
e) 2f
10-(UNESP-SP) Em um laboratório, uma lente plano-convexa de raio de curvatura 0,5m é parcialmente mergulhada em água, de modo que o eixo principal fique no mesmo plano da superfície de separação entre a água e o ar. Um feixe de luz, incidindo paralelamente a esse eixo, após passar pela lente, converge para dois focos distintos. Na região em que a lente está imersa no ar, a convergência é de 1di. Se o índice de refração do ar tem valor 1 e o índice de refração da água, valor 4/3, a convergência da parte da lente mergulhada no líquido é, em di:

![]()
11-(UMTM-MG) Em uma régua de acrílico transparente, pingou-se uma gota d’água. Devido às forças que agem sobre a água, a gota tomou a forma de uma pequena lente plano-convexa de raio de curvatura 3mm.
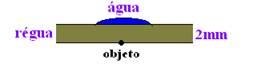
Dados: índice de refração da água=1,3; índice de refração do ar=1,0.
Se a régua tem espessura de 2mm, quando ela é colocada sobre um texto escrito, olhando-se através da gota, essa letra terá suas dimensões aumentadas em:
![]()
12-(FMTM-MG) A face convexa de uma lente de vidro plano-convexa possui um raio de curvatura de 6,0cm.

Sendo o índice de refração do vidro igual a 1,5, determine a distância focal da lente, em cm.(nar=1).
13-(UFG)
Um
indivíduo usa uma lente plano-convexa para concentrar raios solares
sobre grama seca, visando acender uma fogueira.
Para tanto, ele ajusta a lente para sua posição ótima. Sabendo-se que o índice de refração da lente é 1,5, o raio de curvatura do lado convexo é igual a 10 cm e a equação do fabricante de lentes é dada por 1/f=(n-1)[(1/R1)+(1/R2)], a que distância da grama a pessoa posicionou a lente?
a) 6,0 cm
b) 12,0 cm
c) 15,0 cm
d) 20,0 cm
e) 30,0 cm
14-(UFU) Lucas é o único sobrevivente de uma queda de avião e encontra-se sozinho numa região desabitada. Ele busca entre os destroços, objetos que possam ajudá-lo e encontra uma lupa. Lembrando-se de suas aulas de Física sobre lentes convergentes, Lucas decide usá-la para fazer uma fogueira. Acumulando alguns gravetos, ele posiciona sua lupa e observa que os raios solares convergem para um ponto situado a uma distância de 10 cm da lupa, proporcionando-lhe, após algum tempo, a fogueira desejada.


Ele resolve então usar a lupa para se divertir um pouco. Observando os pequenos objetos à sua volta, encanta-se com uma pequenina flor amarela, que, com o uso da lupa aparenta ser três vezes maior que o seu tamanho original.
Com base nessas informações:
a) calcule o centro de curvatura da lente (admitindo que ambas as faces sejam simétricas).
b) determine a que distância, em relação à flor, Lucas posiciona a lupa
15-(UFSCAR-SP) Um livro de ciências ensina a fazer um microscópio simples com uma lente de glicerina. Para isso, com um furador de papel, faz-se um furo circular num pedaço de folha fina de plástico que, em seguida, é apoiada sobre uma lâmina de vidro. Depois, pingam-se uma ou mais gotas de glicerina, que preenchem a cavidade formada pelo furo, que se torna a base de uma lente líquida praticamente semi-esférica. Sabendo que o índice de refração absoluto da glicerina é 1,5 e que o diâmetro do furo é 5,0 mm, pode-se afirmar que a vergência dessa lente é de, aproximadamente,
![]()
16-(UNESP-SP)
Duas
lentes convergentes I e II tem distâncias focais respectivamente
f1=20cm
e f2=10cm.
Colocadas em contato com o mesmo eixo, elas produzem uma lente equivalente:
a) divergente e com f=3,33cm
b) divergente e com f=5,00cm
c) convergente e com f=15,0cm
d) convergente e com f=6,67cm
e) convergente e com f=13,3cm
17-(ITA-SP)
As
duas faces de uma lente delgada biconvexa têm um raio de curvatura
igual a 1,00 m.![]()
O índice de refração da lente para luz vermelha é 1,60 e, para luz violeta, 1,64. Sabendo que a lente está imersa no ar, cujo índice de refração é 1,00, calcule a distância entre os focos de luz vermelha e de luz violeta, em centímetros.
18-(UNESP-SP) Duas lentes delgadas, uma convergente e outra divergente, com distâncias focais iguais a 1m e -2m, encontram-se justapostas. Um objeto é colocado a 3m das lentes. A distância entre a imagem e o sistema de lentes (considerado de espessura desprezível) vale:
![]()
19-(UFCE) Duas lâminas delgadas convergentes 1 e 2, com distâncias focais f1 e f2, estão associadas coaxialmente. As lentes estão separadas por uma distância d.

Para os casos em que a separação d é menor que as distâncias focais, (isto é, d < f1 e d < f2), essa associação equivale a uma lente convergente cuja distância focal satisfaz a relação 1/f= 1/f1 + 1/f2 – d/f1.f2. Considere o caso em que a lente equivalente tem distância focal de 12cm, quando a separação d é igual a 10cm, e distância focal de 60/7cm, quando as lentes 1 e 2 estão justapostas. Determine o valor de f1 e f2.
20-(AFA)

A figura 1 abaixo ilustra o que o observador visualiza quando este coloca uma lente delgada côncavo-convexa a uma distância d
sobre uma folha de papel onde está escrita a palavra LENTE.

Justapondo-se uma outra lente delgada à primeira, mantendo esta associação à mesma distância d da folha, o observador passa a enxergar, da mesma posição, uma nova imagem, duas vezes menor, como mostra a figura 2. Considerando que o observador e as lentes estão imersos em ar, são feitas as seguintes afirmativas.
I. a primeira lente é convergente.
II. a segunda lente pode ser uma lente plano-côncava.
III. quando as duas lentes estão justapostas, a distância focal da lente equivalente é menor do que a distância focal da primeira lente.
São corretas apenas
a) I e II apenas.
b) I e III apenas.
c) II e III apenas.
d) I, II e III.
Resolução dos exercícios de vestibulares sobre
Equação dos Fabricantes de Lentes
01- C1=1/f1=1/5.10-2 --- C1=20di --- C2=1/f2=1/15.10-2 --- C2= 6,7di --- Ceq=C1 + C2=20 + 6,7 --- Ceq=26,7di --- Ceq=1/feq --- 26,7=1/feq --- feq=3,7cm
02- C1=1/f1=1/10.10-2 --- C1=10di --- C2=1/f2=1/40.10-2 --- C2= 2,5di --- Ceq=C1 + C2=10 + 2,5 --- Ceq=12,5di --- R- D
03- Ceq= C1 + C2 --- 1/feq=1/f1 + 1/f2 --- 1/feq=(f2 + f1)/f1.f2 --- feq=f1.f2/(f1 + f2) --- R- B
04- Lente convergente – C1=+12di --- C2= - 20di --- Ceq= +12di – 20di --- Ceq= - 8di --- divergente, pois ceq é negativo.
05- a) Trata-se de uma lente convergente (bordas finas) de índice de refração em relação ao ar – nlente/nar=1,35 --- face convexa – Rc=2,5.10-3 m --- face plana Rp=∞ --- equação dos fabricantes de lentes C=1/f=((nlente/nar – 1).(1/Rc + 1/Rp) --- C=1,35 – 1,00).(1/2,5.10-3 +1/∞) --- C=(0,35).(0,4.103 + 0) --- C=140di
b) Se a imagem é direita --- i=50.O --- i/O=-P’/P --- 50.O/O=-P’/P --- P’=-50P --- 1/f=140m --- 1/f=1/P + 1/P’ --- 140=1/P - 1/50P --- 140=49/50P --- P=0,007m=7mm
06- nv=1,5 --- nar=1,0 --- Rc=2.10-2m --- Rp=∞ --- equação dos fabricantes de lente --- 1/f=C=(nv - nar).(1/Rc + 1/Rp) ---
1/f=(1,5 – 1,0).(1/2.10-2 + 0) --- 1/f=25m --- P’=-36cm=-36.10-2m (negativa-imagem virtual-lente divergente) --- 1/f=1/P + 1/P’ --- 25=1/P – 1/36.10-2 --- 25 + 1/36.10-2=1/P --- P=0,04m --- i=20.10-2 m (positiva – direita) --- i/O=-P’/P ---
20.10-2/O=-(-36.10-2)/4.10-2 --- O=2.10-2m --- O=2cm --- R- D
07- I- 1/f=(nl/nm – 1).(1/R1 + 1/R2) --- (1/R1 + 1/R2) é constante --- 1/f=(nl/nm – 1). (constante) --- observe nesta expressão que, como (nl/nm – 1) é inversamente proporcional a f, quanto maior for a razão nl/nm, menor será a distância focal da lente --- Falsa
II- Se (nl/nm – 1) é inversamente proporcional a f, se nl aumenta, o conjunto (nl/nm – 1) diminui e como ele é inversamente proporcional a f, f aumenta --- Verdadeira
III- Verdadeira, veja justificativa anterior.
R- C
08- C=(1,5
– 1).(1/Rconvexa +
1/Rplana)
--- C=(0,5).(1/20.10-2 +
1/∞) --- C=(0,5).(1/20.10-2 –
0) --- C=2,5di --- R- E
09- Antes de a lente ser partida, duas faces convexas de raio R
![]()
1/f=(n-1).(1/R1+1/R2) --- 1/f=(1,8-1).(1/R+1/R) --- 1/f=(0,8).2/R --- R=1,6f I
Depois de partida, o índice de refração da lente (n=1,8) continua o mesmo --- uma face plana de raio ∞ e outra convexa de raio R
![]()
1/f=(n-1).(1/R1+1/R2) --- 1/f1=(1,8-1).(1/R+1/∞) --- 1/f1=(0,8).(1/R + 0) --- f1=R/0,8 --- R=0,8f1 II
Igualando I com II --- 1,6f=0,8f1 --- f1=2f --- R- E
10- No ar --- Car=(nlente/nar – 1)(1/R + 1/∞) --- 1=(nlente/1 – 1).(1/0,5 + 0) --- 1=(nlente 1).2 --- nlente=1,5
Na água --- Cágua=(nlente/nágua – 1)(1/R + 1/∞) --- Cágua=(1,5/(4/3) – 1)(1/R + 1/∞) --- Cágua=(4,5/4 – 1)(1/0,5 + 0) ---
Cágua=(0,125).2 --- Cágua=0,25 --- R- A
11- Cálculo da convergência da lente --- C=(nágua/nar – 1). (1/Rc + 1/Rp) --- C=(1,3/1 – 1). (1/3.10-3 + 1/∞) --- C=102m ---

f=1/C --- f=10-2m --- P=2.10-3m --- 1/f=1/P + 1/P’ --- 1/10-2=1/2.10-3 + 1/P’ --- 102 – 2.103=1/P’ --- 102 – 20.102=1/P’ ---
P’= - 1/19.10-2m --- A= - P’/P= - (- 1/19.10-2)/2.10-3 --- A=0,26 --- R- A
12- C=(1,5/1 – 1).(1/6.10-2 + 1/∞) --- C=(0,5).102/6 --- C=50/6m --- f=1/C=6/50=0,12m --- f=12,0cm
13- A grama deve estar no foco da lente --- 1/f=(n-1)[(1/R1)+(1/R2)] --- 1/f=(1,5-1)[(1/0,1)+(1/∞)] --- 1/f=5m --- f=1/5=0,2m=20cm --- R- D
14- a) A distância focal, onde ele concentra os raios de luz é de f=10cm=0,1m --- 1/f=(n-1)[(1/R1)+(1/R2)] --- 1/0,1=(n-1)[(1/R)+(1/R)] --- 10=(n – 1).2/R --- R=0,2.(n-1), onde n é o índice de refração da lente
b) i=3.o --- i/o=-P’/P --- 3.0/o= - P’/P --- 3= - P’/P --- P’= - 3P --- 1/f=1/P + 1/P’ --- 1/f=1/P – 1/3P --- 1/10=(3 – 1)/3P --- P=20/3 = 6,7cm
15- C=1/f=(n-1)[(1/R1)+(1/R2)] --- C=(1,5 – 1).(1/2,5.10-3 + 1/∞) --- C=0,5. 400 --- C=200di --- R- E
16-
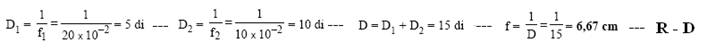
17- Os focos de luz encontram-se no foco de cada lente --- Vermelha --- 1/fv=(1,6 -1).(1/1 + 1/1) --- fv=1/1,2=0,83m --- 1/fvi=(1,64 – 1).(1/1 + 1/1) --- fvi=1/1,28 --- fvi=0,78m --- d=0,83 – 0,78 --- d=0,05m=5cm
18-
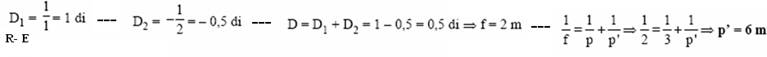
19- Primeiro caso

--- fe=12cm -- d=10cm --- 1/fe= 1/f1 + 1/f2 – d/f1.f2. --- 1/12=1/f1 + 1/f2 – 10/f1.f2 --- f1.f2=12f2 + 12f1 – 120 ---
f1.f2=12(f1 + f2) – 120 I
Segundo caso

--- fe=60/7cm -- d=0 (justapostas) --- 1/fe= 1/f1 + 1/f2 – d/f1.f2 --- 7/60=.1/f1 + 1/f2– 0/f1.f2 --- 7/60=1/f1 + 1/f2 --- 7f1.f2=60f2 + 60f1 --- f1.f2=60.(f1 + f2)/7 II --- igualando I com II --- 12(f1 + f2) – 120 = f1.f2=60.(f1 + f2)/7 --- 84(f1 + f2 – 840=60.(f1+ f2) --- 24.(f1 + f2)=840 --- f1 + f2=35 III --- III em I --- f1.f2=12.35 – 120 --- f1.f2=420 – 120 --- f1.f2=300 VI
Observe o sistema composto por III e IV, cujo produto é 300 e cuja soma é 35 e assim, esses números são --- f1=15cm e f2=20cm ou f2=20cm e f1=15cm
20- I- Correta --- trata-se de uma lente convergente, pois essa lente tem extremidades finas e está imersa no ar, assim é convergente e nesse caso o objeto está entre fo e o centro óptico O da lente --- a imagem tem as seguintes cacterísticas:
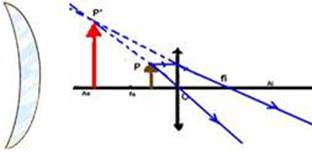
Natureza: Virtual (obtida no cruzamento dos prolongamentos dos raios luminosos.
Localização: Antes de foco
Tamanho e orientação: Maior que o objeto e direita em relação a ele.
Utilidade – Lupa (lente de aumento) e microscópios.
II.Correta --- observe nas figuras que o aumento da figura 1 é maior que o aumento da figura 2 (lente resultante) e que, em ambos os casos a imagem é aumentada --- assim, a lente 1 e a lente equivalente são convergentes --- A1>Aeq --- quando justapomos duas lentes
obtemos uma lente equivalente cuja vergência ou convergência Ceq é a soma algébrica da vergência de cada uma das lentes, ou seja, Ceq=C1+ C2 --- lembre-se de que C=1/f e que se a lente é divergente f e C são negativos e se a lente é convergente, positivos --- no caso do exercício --- Ceq>0 (convergente) --- C1>0 (convergente) --- quanto maior o aumento, maior a vergência --- se C1>Ceq - (A1>Aeq) --- Cx(justaposta a C1) --- Ceq = C1 + Cx --- (Ceq – C1)=Cx --- nessa expressão, Cx deverá ser negativo pois C1>Ceq --- se a vergência é negativa a lente x é divergente o que é o caso da lente plano côncava.
III. Falsa --- do item II --- Ceq<C1 --- 1/feq < 1f1 --- f1 < feq.
R- A