Estudo Analítico das Lentes Esféricas

Introdução

As lentes possuem dois focos, sendo, um ofoco principal objeto (f_o) e o outro ofoco principal imagem (f_i).

Ambos são simétricos e estão localizados sobre o eixo principal.

As posições e as alturas de objetos colocados diante de uma lente esférica são determinadas através das mesmas equações estudadas nos espelhos esféricos.

Seus sinais são fornecidos pelo referencial de Gauss.

Referencial de Gauss – Convenção de sinais

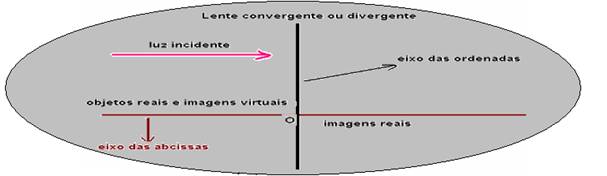
O sistema de eixo ortogonaistem origem no centro óptico da lente.

 A origem do referencial está no centro óptico da lente.

 O eixo das abscissas coincide com o eixo principal e tem sentido contrário ao da luz incidente para os objetos e a favor da luz incidente para as imagens.

Assim, observe na figura acima que imagens reais (à direita da lente) e objetos reais (à esquerda da lente) têm abscissas positivas e que imagens virtuais (à esquerda da lente) tem abscissas negativas.

 O eixo das ordenadas é orientado para cima. Assim, a imagemie oobjeto O tem mesmo sinal se a imagem for direita em relação ao objeto e sinais opostos se a imagem for invertida em relação ao objeto.

Observe que a distância focal  fé positiva para lentes convergentes e negativa para lentes divergentes.

Equação de Gauss

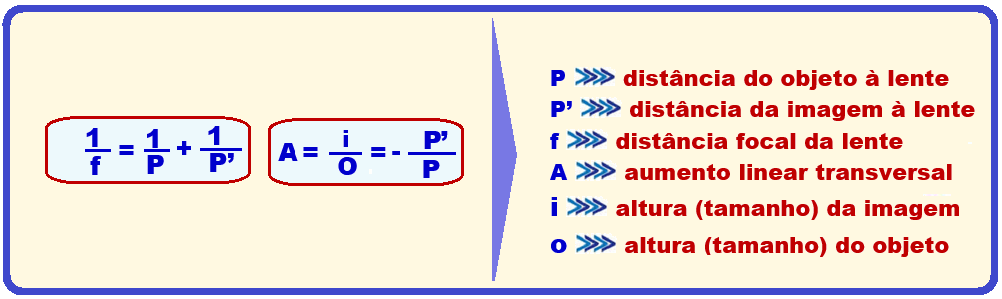
Vergência C de uma lente esférica

O que você deve saber, informações e dicas

  Observe na expressão C=1/f que f e C são inversamente proporcionais, ou seja, lentes de pequenas distâncias focais, que provocam maiores alterações nas imagens dos objetos, têm maior vergência, na linguagem cotidiana “maior grau”.

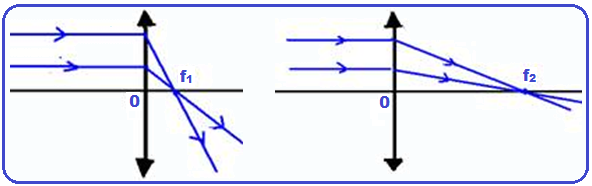
Note nas figuras que a vergência (grau) da lente da esquerda é maior que a da direita.

Questões interessantes nas quais você deve analisar atentamente os processos de resoluções:

01-(ITA-SP) 

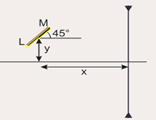
A figura mostra uma barra LM de 10√2cm de comprimento, formando um ângulo de 45° com a horizontal, tendo o seu centro situado a x = 30,0 cm de uma lente divergente, com distância focal igual a 20,0 cm, e a y = 10,0 cm acima do eixo ótico da mesma.

Determine o comprimento da imagem da barra e faça um desenho esquemático para mostrar a orientação da imagem.

Resolução:

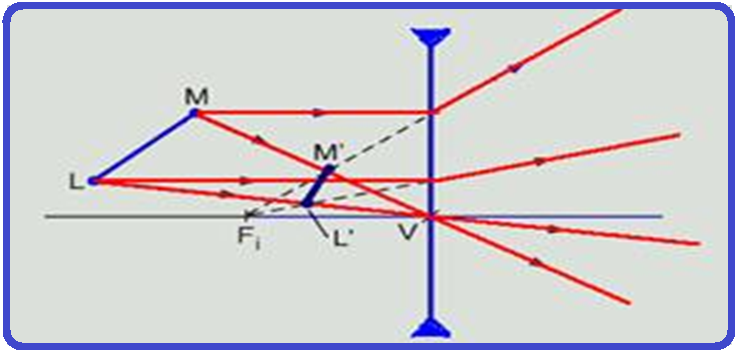
Determinação gráfica da imagem   utilizando os dois raios notáveis da figura localizamos a imagem M’ do ponto M e a imagem L’ do ponto L unindo-os achamos a imagem L’M’ do objeto LM.

A figura mostra as coordenadas X e Y dos pontos M e L    M(25;15)    L(5;35):

Cálculo da coordenada P’ das imagens M’ e L’ pela equação dos pontos conjugados: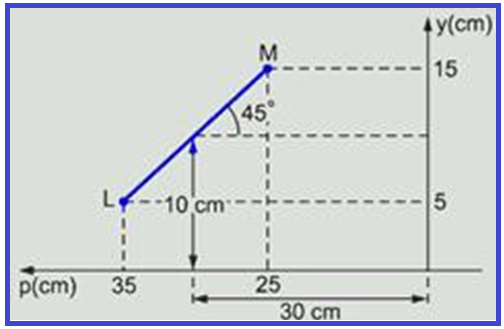

Coordenada da imagem de M    1/f = 1/P_M + 1/ P’_M    1/-20 = 1/25 + 1/P’_M    P’_M = - 100/9 cm = - 11,1 cm (o sinal negativo significa que a imagem é virtual) em módulo P’_M =11,1cm

M’_x = 11,1 cm.

Coordenada da imagem de L   1/f = 1/P_L + 1/ P’_L   1/-20 = 1/35 + 1/P’_L    P’_L= - 140/11 cm = - 12,7 cm   em módulo P’_L = L’_x = 12,7 cm.

  cálculo da coordenada Y’ das imagens M’ e L’ pela equação do aumento linear transversal 

  Y’_L / Y_L= - P’_L / P_L    Y’_L/5= - ( - 140/11)/35    Y’_L = 20/11 cm Y’_L = 1,8 cm.

Y’_M/Y_M= - P’_M/P_M    Y’_M/15 = - ( - 100/9)/25    Y’_M = 20/3 cm = 6,7 cm.

coordenadas M’_x e M’_y do ponto M’(11,1;6,7)

coordenadas L’_x e L’_y do ponto L’(12,7;1,8)

  Comprimento c da imagem da barra    c² = (P’_M – P’_L)² + (Y’_M – Y’_L)²    c² = { - 100/9 – ( - 140/11)}² + (20/3 – 20/11)²    c² ≈ 256.000/9.800    c² ≈ 26    c ≈ 5,1cm.

02- Um objeto luminoso e uma tela de projeção estão separados pela distância D = 80 cm.

Existem duas posições em que uma lente convergente de distância focal f = 15 cm, colocada entre o objeto e a tela, produz uma imagem real na tela.

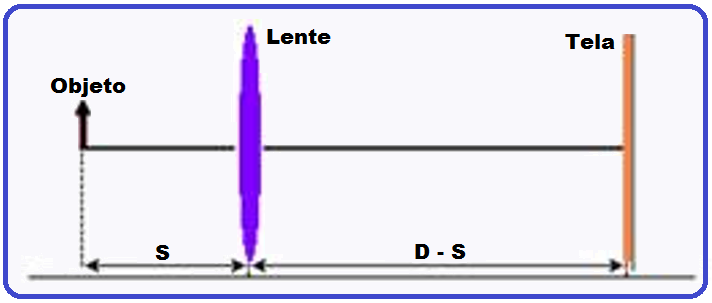
Calcule a distância, em cm, entre estas duas posições.

Resoluções:

Observe a figura abaixo:

1/15 = 1/S + 1/ 80 – S)  1/15 = (80 – S) + S / S.(80 – S)    1200 = 80S – S²    S² – 80S + 1200 = 0    Δ = B²- 4.A.C    Δ = 40   S = - B ±√(Δ)/2.A    S₁ = (80 + 40)/2  S₁ = 60 cm e P₁’= 80 – 60 = 20cm    S₂ = (80 – 40)/2    S₂ = 20cm e P₂’ = 80 – 20 = 60cm.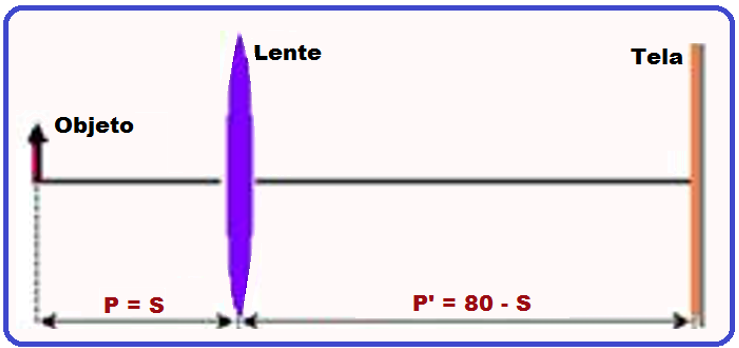

Portanto, para que a imagem seja real e nítida sobre a tela existe duas  posições, uma a 20cm da lente e a outra a 40 cm da lente.

03- O sistema de imagens street view disponível na internet permite a visualização de vários lugares do mundo através de fotografias de alta definição, tomadas em 360 graus, no nível da rua.

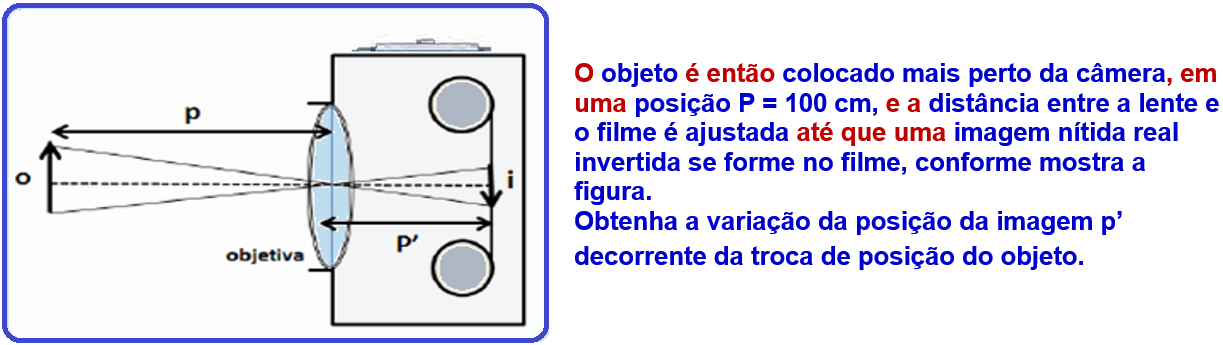
Em uma câmera fotográfica tradicional, a imagem é gravada em um filme fotográfico para posterior revelação.

A posição da lente é ajustada de modo a produzir a imagem no filme colocado na parte posterior da câmera.

Considere uma câmera para a qual um objeto muito distante fornece

uma imagem pontual no filme em uma posição P’ = 5 cm.

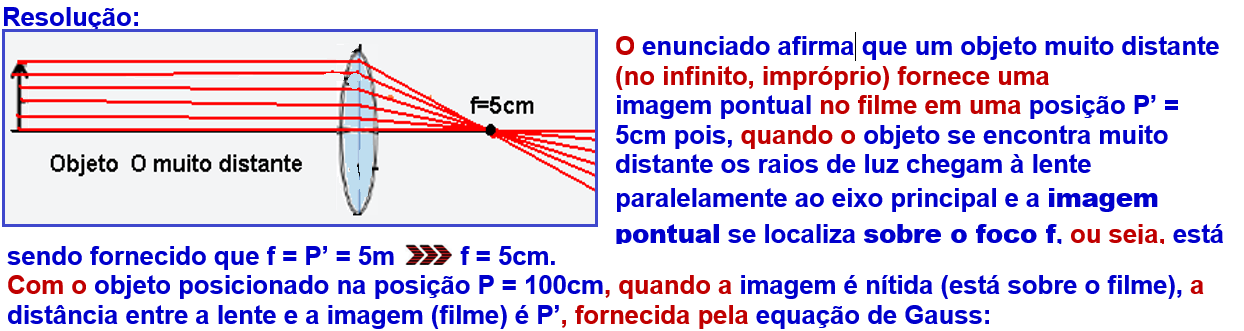
A variação da posição da imagem pedida devido à troca da posição do objeto vale ΔP’ = 5,26 – 5,0 ΔP’= 0,26cm.

Exercícios de vestibulares com resoluções comentadas sobre

Estudo Analítico das Lentes Esféricas

01-(UNESP-SP) Na figura, estão representados, esquematicamente, o perfil de uma lente esférica delgada, de vidro, imersa no ar, e a trajetória de um raio de luz que parte de um ponto O do eixo principal, atravessa a lente e passa novamente pelo eixo principal no ponto I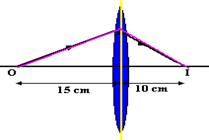

a) A lente da figura é convergente ou divergente? Justifique sua resposta.

b) Admitindo-se válidas as condições de estigmatismo de Gauss, calcule a distância focal dessa lente.

02-(UFF-RJ) Um operador cinematográfico deve saber selecionar a lente de projeção adequada para que a tela fique totalmente preenchida com a imagem do filme. A largura de um quadro na fita de um filme de longa metragem é 35 mm.

Para um cinema em que a tela tem 10,5m de largura e está a 30 m da lente da máquina de projeção, determine:

a) a ampliação necessária para que a tela seja totalmente utilizada;

b) a distância entre a fita e a lente para que a ampliação necessária seja obtida;

c) a distância focal da lente.

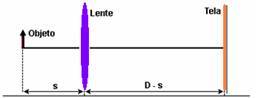
03-(UNESP-SP) Um projetor rudimentar, confeccionado com uma lente convergente, tem o objetivo de formar uma imagem real e aumentada de um slide. Quando esse slide é colocado bem próximo do foco da lente e fortemente iluminado, produz-se uma imagem real, que pode ser projetada em uma tela, como ilustrado na figura.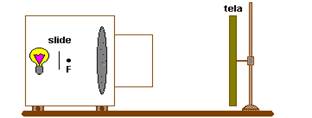

A distância focal é de 5 cm e o slide é colocado a 6 cm da lente. A imagem projetada é real e direita. Calcule

a) a posição, em relação à lente, onde se deve colocar a tela, para se ter uma boa imagem.

b) a ampliação lateral (aumento linear transversal).

04-(UNESP-SP) Uma câmara fotográfica rudimentar utiliza uma lente convergente de distância focal f = 50 mm para focalizar e projetar a imagem de um objeto sobre o filme. A distância da lente ao filme é p' = 52 mm. A figura mostra o esboço dessa câmara.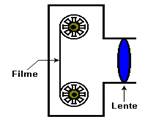

Para se obter uma boa foto, é necessário que a imagem do objeto seja formada exatamente sobre o filme e o seu tamanho não deve exceder a área sensível do filme. Assim:

a) Calcule a posição que o objeto deve ficar em relação à lente.

b) Sabendo-se que a altura máxima da imagem não pode exceder a 36,0 mm, determine a altura máxima do objeto para que ele seja fotografado em toda a sua extensão.

05-(UNIFESP-SP) Uma lente convergente tem uma distância focal f = 20,0 cm quando o meio ambiente onde ela é utilizada é o ar. Ao colocarmos um objeto a uma distância p = 40,0 cm da lente, uma imagem real e de mesmo tamanho que o objeto é formada a uma distância p' = 40,0 cm da lente. Quando essa lente passa a ser utilizada na água, sua distância focal é modificada e passa a ser 65,0 cm. Se mantivermos o mesmo objeto à mesma distância da lente, agora no meio aquoso, é correto afirmar que a imagem será

a) virtual, direita e maior.     

b) virtual, invertida e maior.     

c) real, direita e maior.     

d) real, invertida e menor.

e) real, direita e menor.

06-(UNESP-SP) Dispõem-se de uma tela, de um objeto e de uma lente convergente com distância focal de 12 cm. Pretende-se, com auxílio da lente, obter na tela uma imagem desse objeto cujo tamanho seja 4 vezes maior que o do objeto.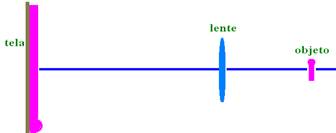

 a) A que distância da lente deverá ficar a tela?

b) A que distância da lente deverá ficar o objeto?

07-(UEM) Um objeto de tamanho  igual a 15 cm está situado a uma distância  igual a 30 cm de uma lente. Verifica-se que a lente forma uma imagem virtual do objeto cujo tamanho é igual a 3 cm. Qual é o módulo da distância (em cm) da imagem à lente?

08-(UFPE) Um objeto luminoso e uma tela de projeção estão separados pela distância D = 80 cm. Existem duas posições em que uma lente convergente de distância focal f = 15 cm, colocada entre o objeto e a tela, produz uma imagem real na tela. Calcule a distância, em cm, entre estas duas posições.

09-(UNESP-SP) Uma pessoa, com certa deficiência visual, utiliza óculos com lentes convergentes. Colocando-se um objeto de 0,6 cm de altura a 25,0 cm da lente, é obtida uma imagem a 100 cm da lente. Considerando que a imagem e o objeto estão localizados do mesmo lado da lente, calcule

a) a convergência da lente, em dioptrias.

b) a altura da imagem do objeto, formada pela lente.

10-(FUVEST-SP) Uma lente L é colocada sob uma lâmpada fluorescente AB cujo comprimento é AB = 120 cm. A imagem é focalizada na superfície de uma mesa a 36 cm da lente. A lente situa-se a 180 cm da lâmpada e o seu eixo principal é perpendicular à face cilíndrica da lâmpada e à superfície plana da mesa. A figura a seguir ilustra a situação.

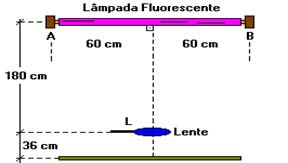
Pede-se:

a) a distância focal da lente.

b) o comprimento da imagem da lâmpada e a sua representação geométrica. Utilize os símbolos A' e B' para indicar as extremidades da imagem da lâmpada.

11-(UFU-MG) Um objeto (O) de 1 cm de altura é colocado a uma distância de 2 cm do centro de uma lente convergente (L₁) de distância focal 1,5 cm, conforme figura a seguir

Deseja-se aumentar a imagem formada por este objeto, de modo que ela atinja 6 vezes a altura do objeto original. Para isso utiliza-se uma segunda lente L₂‚, de características idênticas a L₁.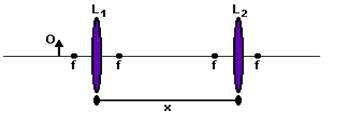

Calcule a que distância x essa segunda lente L₂‚ deve ser colocada da lente L₁ (veja a figura apresentada) para que a imagem formada seja real, direita, e 6 vezes maior que o objeto original.

12-(PUC-SP) Um toco de vela está entre duas lentes delgadas, uma divergente L_X e outra convergente L_Y, a 20cm de cada uma, como está representado no esquema a seguir. As duas lentes têm distâncias focais de mesmo valor absoluto, 10cm.

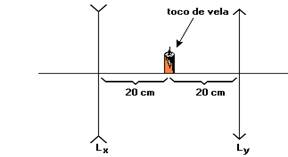
Nessas condições, a distância entre as imagens do toco de vela, conjugadas pelas lentes vale, em cm, aproximadamente,

a) 6,6                       b) 20                        c) 33                        d) 47                        e) 53

13-(UFB) Considere duas lentes convergentes  L₁ e L₂ de mesmo ponto antiprincipal, com eixos principais coincidentes e dispostas de modo que o ponto antiprincipal imagem de L₁ coincida com o ponto antiprincipal objeto de L₂ (figura).

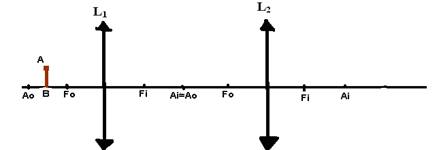
Um objeto AB é colocado antes de L₁ entre Ao e Fo. Determine as características da imagem final formada pelo sistema de lentes.

14-(PUC-SP) Um espelho côncavo de distância focal 30cm e uma lente convergente de distância focal 12cm são dispostos coaxialmente, separados por uma distância de 75cm. Um objeto AB é colocado entre o espelho e a lente e a 15cm da lente, como mostra a figura.

Admitindo que o espelho e a lente estão sendo usados dentro das condições de Gauss, a imagem obtida por reflexão no espelho e refração na lente, é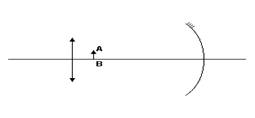

a) real, direita e a 60cm da lente.     

b) virtual, direita e a 60cm da lente.     

c) real, invertida e a 30cm da lente.

d) real, direita e a 30cm da lente.     

e) real, invertida e a 15cm da lente.

15-(UNIFESP-SP) Um estudante observa uma gota de água em repouso sobre sua régua de acrílico, como ilustrado na figura.

Curioso, percebe que, ao olhar para o caderno de anotações através dessa gota, as letras aumentam ou diminuem de tamanho conforme afasta ou aproxima a régua do caderno. Fazendo alguns testes e algumas considerações, ele percebe que a gota de água pode ser utilizada como uma lente e que os efeitos ópticos do acrílico podem ser desprezados. Se a gota tem raio de curvatura de 2,5 mm e índice de refração 1,35 em relação ao ar,

a) calcule a convergência C dessa lente.

b) Suponha que o estudante queira obter um aumento de 50 vezes para uma imagem direita, utilizando essa gota. A que distância d da lente deve-se colocar o objeto?

16-(FUVEST-SP) Uma fonte de luz intensa L, praticamente pontual, é utilizada para projetar sombras em um grande telão T, a 150cm de distância. Para isso, uma lente convergente, de distância focal igual a 20cm, é encaixada em um suporte opaco a 60cm de L, entre a fonte e o telão, como indicado na figura A, em vista lateral. Um objeto, cuja região opaca está representada pela cor escura na figura B, é, então, colocado a 40cm da fonte, para que sua sombra apareça no telão. Para analisar o efeito obtido, indique, no esquema a seguir:

a) a posição da imagem da fonte, representando-a por L'.

b) a região do telão, na ausência do objeto, que NÃO é iluminada pela fonte, escurecendo-a a lápis. (Faça, a lápis, as construções dos raios auxiliares, indicando por A₁ e A₂ os raios que permitem definir os limites de tal região).

c) a região do telão, na presença do objeto, que NÃO é iluminada pela fonte, escurecendo-a a lápis. (Faça, a lápis, as construções dos raios auxiliares necessários para tal determinação).

17-(FGV-SP) Do lado de fora, pelo vitrô do banheiro, um bisbilhoteiro tenta enxergar seu interior.

Frustrado, o xereta só conseguiu ver as múltiplas imagens de um frasco de xampu, guardado sobre o aparador do boxe, a 36 cm de distância do vidro. De fato, mal conseguiu identificar que se tratava de um frasco de xampu, uma vez que cada uma de suas imagens, embora com a mesma largura, tinha a altura, que no original é de 20 cm, reduzida a apenas:

(Informações: suponha válidas as condições de estigmatismo de Gauss e que os índices de refração do vidro e do ar sejam, respectivamente, 1,5 e 1,0.)

18- (UFPR-PR) Um estudante usando uma lupa sob a luz do sol consegue queimar uma folha de papel devido à concentração dos raios do sol em uma pequena região. Ele verificou que a maior concentração dos raios solares ocorria quando a distância entre o papel e a lente era de 20 cm.

   Com a mesma lupa, ele observou letras em seu relógio e constatou que uma imagem nítida delas era obtida quando a lente e o relógio estavam separados por uma distância de 10 cm. A partir dessas informações, considere as seguintes afirmativas: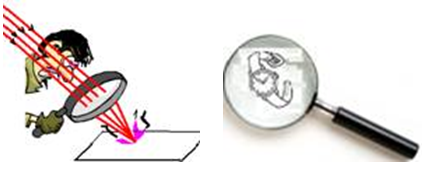

1. A distância focal da lente vale f = 20 cm.

2. A imagem das letras formada pela lente é invertida e virtual.

3. A lente produz uma imagem cujo tamanho é duas vezes maior que o tamanho das letras impressas no relógio.

Assinale a alternativa correta.

a) Somente a afirmativa 1 é verdadeira.     

b) Somente a afirmativa 2 é verdadeira.     

c) Somente a afirmativa 3 é verdadeira.

d) Somente as afirmativas 1 e 3 são verdadeiras.     

e) Somente as afirmativas 2 e 3 são verdadeiras.  

19-(Ufpr-PR) Uma certa lupa tem uma convergência de 5 di. Observando um pequeno objeto com essa lupa, só veremos uma imagem ampliada e direita (não invertida) se a lupa for mantida a uma distância d do objeto, tal que:

a) 0 cm < d < 5 cm.     

b) 0 cm < d < 10 cm.     

c) 0 cm < d < 20 cm.       

d) 10 cm < d < 40 cm.     

e) 20 cm < d < 40 cm.

20-(FATEC-SP) Sobre uma mesa, são colocados alinhados uma vela acesa, uma lente convergente e um alvo de papel.

Inicialmente, a vela é afastada da lente tanto quanto possível, e ajusta-se a posição do alvo para se obter nele a imagem mínima da vela. Mede-se e anota-se a distância f do alvo à lente. Aproximando-se a vela, até que fique à distância (3/2) . f da lente, para captar imagem nítida da vela o alvo deverá ser posicionado à distância da lente igual a

a) 2f/3                       

b) f                     

c) 3f/2                       

d) 2f                    

e) 3f

21-(UNIFESP-SP) A figura representa um banco óptico didático: coloca-se uma lente no suporte e varia-se a sua posição até que se forme no anteparo uma imagem nítida da fonte (em geral uma seta luminosa vertical). As abscissas do anteparo, da lente e do objeto são medidas na escala, que tem uma origem única.

a) Represente graficamente (sem valores numéricos) a situação correspondente ao esquema da figura, em que apareçam: o objeto (seta luminosa da fonte); a lente e seus dois focos; a imagem e pelo menos dois raios de luz que emergem do objeto, atravessem a lente e formem a imagem no anteparo.

b) Nessa condição, determine a distância focal da lente, sendo dadas as posições dos seguintes componentes, medidas na escala do banco óptico: anteparo, na abscissa 15 cm; suporte da lente, na abscissa 35 cm; fonte, na abscissa 95 cm

22-(UNESP-SP) Uma lupa utilizada para leitura é confeccionada com uma lente delgada convergente, caracterizada por uma distância focal f. Um objeto é colocado a uma distância 0,8 f, medida a partir da lente.

 Se uma letra de um texto tem altura 1,6 mm, determine o tamanho da letra observado pelo leitor.

23(UDESC) Uma lente convergente de distância focal d é colocada entre um objeto e uma parede. Para que a imagem do objeto seja projetada na parede com uma ampliação de 20 vezes, a distância entre a lente e a parede deve ser igual a:

24-(UNIFESP-SP) Dentro de um aquário sem água são colocados uma lente delgada convergente e um parafuso, posicionado frontalmente à lente, ambos presos a suportes, conforme a figura.

Nessas condições, a imagem conjugada pela lente é direita e tem o dobro do tamanho do objeto.

a) Calcule a razão f/p, entre a distância focal da lente e a distância do objeto ao centro óptico da lente.

b) Preenchido totalmente o aquário com água, a distância focal da lente aumenta para 2,5 vezes a distância focal na situação anterior, e a lente mantém o comportamento óptico convergente. Para as mesmas posições da lente e do objeto, calcule o aumento linear transversal para a nova imagem conjugada pela lente.

25-(UFRJ-RJ) 

A figura a seguir mostra uma lente convergente de distância focal 10 cm frente a um espelho plano paralelo à lente. O espelho encontra-se a uma distância de 20 cm do vértice V da lente. Do outro lado da lente, uma vela de 6,0 cm de altura encontra-se a uma distância de 30 cm do vértice da lente.

a) Calcule a distância entre a vela e sua imagem formada pelo espelho plano.

b) Calcule a altura da imagem da vela formada pelo espelho plano.

26-(UPE-PE) 

Um anteparo é colocado a 90 cm de um garoto, e uma lente situada entre eles projeta, no anteparo, a imagem do garoto diminuída

 2 vezes. Pode-se afirmar que

(     )  o garoto está posicionado a 60 cm do centro óptico.

(     )  a distância focal da lente é de 20 cm.

(     )  a convergência da lente é de 5 dioptrias.

(     )  a imagem é real, invertida, menor e está posicionada a 20 cm da lente.

(     )  a imagem é virtual, invertida, menor e está posicionada a 20 cm da lente.

27-(UEPG-PR) 

Lente é qualquer meio transparente e isotrópico limitado por dois dioptros esféricos ou cilindricos, podendo um deles ser plano. A luz ao

atravessar uma lente esférica pode sofrer refração. Sobre lentes esféricas, assinale o que for correto.

01) Quando o índice de refração do material que constitui a lente é maior que o índice de refração do meio envolvente, todas as lentes esféricas delgadas são convergentes. 

02) Um sistema de lentes esféricas delgadas justapostas se comporta como se fosse uma única lente, cuja convergência é igual à soma algébrica das convergências das lentes componentes do sistema. 

04) Lentes divergentes têm convergência negativa. 

08) Lentes esféricas podem gerar imagens reais ou virtuais de um objeto. 

16) Um raio luminoso que passa pelo centro ótico de uma lente esférica delgada não sofre nem desvio angular nem desvio linear. 

28-(PUC-PR) 

David Hockney, pintor pop inglês, um dos mais importantes artistas da atualidade, defende a ideia de que alguns grandes mestres da pintura no passado teriam recorrido a dispositivos ópticos para projetar sobre as telas as imagens que pintavam. Hockney

procurou saber que recurso óptico eles poderiam ter usado e descobriu a câmara lúcida, invenção patenteada, em 1807, pelo físico inglês William Hyde Wollaston. A câmara lúcida é um pequeno prisma com quatro ou cinco faces, uma semiespelhada e outra espelhada, que permite ao pintor ver sobre a tela ou papel onde faz o esboço a imagem do objeto que pinta, à sua frente.

Outros recursos ópticos também eram utilizados, tais como: lentes, espelhos côncavos e câmara escura, já com implementos de lentes e espelhos. A câmara escura era usada por artistas no século XVI, como um auxílio para os esboços nas pinturas, conforme ilustrado a seguir:

Sobre lentes, espelhos e câmara escura é CORRETO afirmar:

a) A lente utilizada para projetar a imagem sobre a tela é a mesma que se utiliza para a correção da miopia. 

b) O espelho côncavo utilizado produz uma imagem virtual direita e maior que o objeto. 

c) O espelho côncavo era utilizado para projetar uma imagem real invertida e menor que o objeto. A função da lente convergente era ampliar a imagem. 

d) Na câmara lúcida a imagem vista pelo observador é real invertida e menor que o objeto. 

e) A lente utilizada na câmara escura produz uma imagem com as mesmas características de uma lupa. 

29-(UFG-GO)

 Para realizar a medida do coeficiente de dilatação linear de um objeto, cujo material é desconhecido, montou-se o arranjo experimental ilustrado na figura a seguir, na qual, d = 3,0cm e D = 150,0 cm.

O objeto tem um comprimento inicial de 4,0 cm. Após ser submetido a uma variação de temperatura de 250 ºC, sua imagem projetada na tela aumentou 1,0 cm. Com base no exposto, calcule o valor do coeficiente de dilatação linear do objeto.

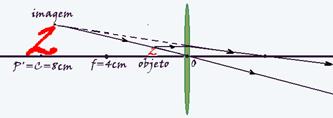
30-(ITA-SP) 

A figura mostra uma barra LM de 10√2cm de comprimento, formando um ângulo de 45° com a horizontal, tendo o seu centro situado a x = 30,0 cm de uma lente divergente, com distância focal igual a 20,0 cm, e a y = 10,0 cm acima do eixo ótico da mesma. Determine o comprimento da imagem da barra e faça um desenho esquemático para mostrar a orientação da imagem.

31-(IFSP-SP) 

Os fenômenos luminosos são estudados há muito tempo. A luz, como qualquer onda eletromagnética, tem grandes aplicações na

 engenharia e na medicina, entre outras áreas. Quando a luz atinge uma superfície, um ou mais fenômenos podem ocorrer, como a reflexão, refração, difusão e absorção.

A seguir são feitas as seguintes afirmativas:

I. Quando olhamos uma moeda dentro de um recipiente com água, sabemos que ela não se encontra na posição vista aparentemente, por causa do fenômeno da reflexão, que desvia os raios luminosos.

II. Para acendermos um palito de fósforo por meio de raios solares, podemos usar lentes do tipo convergentes.

III. Toda onda eletromagnética, como a luz, pode se propagar no vácuo.

IV. Colocando-se um objeto entre dois espelhos planos e paralelos, obtém-se um número infinito de imagens.

São corretas apenas

32-(MACKENZIE-SP) A figura ilustra o esquema, sem escala, de um pequeno objeto real P, situado sobre o eixo principal de uma lente delgada convergente, com os respectivos focos principais, F e F’, e Pontos Antiprincipais, C e C’.

A imagem conjugada de P é ________ , ________ e de altura ________ que a do objeto. A alternativa que preenche, corretamente, na ordem correta de leitura, as lacunas do texto é

a) virtual, direita, igual ao dobro.                    

b) virtual, invertida, igual ao triplo.                        

c) real, direita, igual ao dobro.

d) real, invertida, igual ao triplo.                    

e) real, invertida, igual ao dobro.

 33-(UNIFESP-SP)

Uma lente convergente pode servir para formar uma imagem virtual, direita, maior e mais afastada do que o próprio objeto. Uma lente empregada dessa maneira é chamada lupa, e é utilizada para observar, com mais detalhes, pequenos objetos ou superfícies.

Um perito criminal utiliza uma lupa de distância focal igual a 4,0cm e fator de ampliação da imagem igual a 3,0 para analisar vestígios de adulteração de um dos números de série identificador, de 0,7 cm de altura, tipados em um motor de um automóvel.

a) A que distância do número tipado no motor o perito deve posicionar a lente para proceder sua análise nas condições descritas?

b) Em relação à lente, onde se forma a imagem do número analisado? Qual o tamanho da imagem obtida?

 34-(UFSC-SC)

Pedrinho, em uma aula de Física, apresenta um trabalho sobre ótica para o seu professor e colegas de classe. Para tal, ele montou um aparato, conforme a figura abaixo.

Baseado nos princípios da ótica e no aparato da figura, assinale a(s) proposição(ões) CORRETA(S).

01. I é uma fonte de luz primária do tipo incandescente; II é uma lente côncavo-convexa que, quando colocada em um meio adequado, pode se tornar divergente; III é um prisma de reflexão total; IV é um espelho plano e V é um espelho côncavo.

02. I está no foco da lente II; III é um prisma cujo índice de refração é maior que 1,0; em IV ocorre a reflexão especular e em V os raios incidentes são paralelos ao eixo principal do espelho côncavo.

04. Para que ocorra a reflexão total em III, o índice de refração do prisma deve ser maior que o do meio em que está imerso e a luz deve ir do meio mais refringente para o menos refringente.

08. As leis da reflexão são aplicadas somente em III e IV. 16. As leis da refração são aplicadas somente em II e III.

32. No aparato em questão, podemos afirmar que tanto a frequência como a velocidade da luz variam de acordo com o índice de refração do meio no qual o raio está se propagando.

64. Ao afastar o espelho V da fonte de luz, na direção horizontal, a imagem conjugada por ele será real, invertida e menor.

35-(UFPE-PE)

Um objeto de altura 1,0 cm é colocado perpendicularmente ao eixo principal de uma lente delgada, convergente. A imagem formada pelo objeto tem altura de 0,40 cm e é invertida. A distância entre o objeto e a imagem é de 56 cm.

Determine a distância d entre a lente e o objeto.

Dê sua resposta em centímetros.

36-(UFPR-PR)

Um datiloscopista munido de uma lupa analisa uma impressão digital. Sua lupa é constituída por uma lente convergente com

distância focal de 10 cm. Ao utilizá-la, ele vê a imagem virtual da impressão digital aumentada de 10 vezes em relação ao

tamanho real. Com base nesses dados, assinale a alternativa correta para a distância que separa a lupa da impressão digital.

a) 9,0 cm.                

b) 20,0 cm.                          

c) 10,0 cm.                          

d) 15,0 cm.                                

e) 5,0 cm.

37-(FGV-SP)

Um estudante usou uma lupa para pesquisar a formação de imagens de objetos reais. Ele conseguiu obter um ponto luminoso a partir de um feixe de raios paralelos incidentes na lupa, colocando a lupa a 20 cm dele e paralelamente a ele.

A seguir, aproximando a lupa a 15 cm de seu celular, obteve uma imagem do celular

(A) real, invertida e ampliada.                          

(B) real, invertida e reduzida.                                     

(C) virtual, direita e ampliada.

(D) virtual, direita e reduzida.                         

(E) virtual, invertida e ampliada.

38-(UNESP-SP)

Em um experimento didático de óptica geométrica, o professor apresenta aos seus alunos o diagrama da posição da imagem conjugada

 por uma lente esférica delgada, determinada por sua coordenada p’, em função da posição do objeto, determinada por sua coordenada p, ambas medidas em relação ao centro óptico da lente.

Analise as afirmações.

I. A convergência da lente utilizada é 5 di.

II. A lente utilizada produz imagens reais de objetos colocados entre 0 e 10 cm de seu centro óptico.

III. A imagem conjugada pela lente a um objeto linear colocado a 50 cm de seu centro óptico será invertida e terá 1/4 da altura do objeto. Está correto apenas o contido em

Resolução comentada dos exercícios de vestibulares sobre

Estudo Analítico das Lentes Esféricas

01- a) Lente convergente – lentes de vidro no ar, de bordas finas são convergentes ou, observe que , após se refratarem na lente os raios de luz convergem para o eixo principal.

b) P=15cm  --  P’=10cm  ---  1/f=1/P + 1/P’  ---  1/f=1/15 + 1/10  ---  1/f=(10 + 15)/150   --  f=150/25  ---  f=6cm

02- a) largura do quadro da fita=tamanho do objeto  ---  o=35mm  ---  o=35.10^-3m  ---  largura da tela=tamanho da imagem  ---

 i= - 10,5m ( negativo, pois toda imagem real “projetada” é invertida)  ---  P’=30m  ---  A=i/o= - 10,5/35.10^-3  ---  A= - 300 (a imagem é 300 vezes maior que o objeto e é invertida)

b) A=-P’P/P  ---  -300=-30/P  ---  P=10cm (a fita está a 10cm da lente)

c) 1/f=1/P + 1/P’  ---  1/f=1/10 + 1/30  ---  1/f=(3 + 1)/30  --- f=7,5cm

03- a) A lente é convergente, pois a imagem é projetada (real e invertida) e, na tela ela aprece como direita, pois o slide é colocado invertido  ---  f=5cm  ---  P=6cm  ---  1/f=1/P + 1/P’  ---  1/5=1/6 + 1/P’  ---  1/5 – 1/6=1/P’  ---  1/P’=(6 – 5)/30  ---  P’=30cm

b) A=-P’/P=-30/6  ---  A= -5 (a imagem é ampliada 5 vezes e é invertida)

04- a) 1/50=1/P + 1/52  ---  1/50 – 1/52=1/P  ---  1/P=(52 – 50)/2600  ---  P=1.300mm=1,3m

b) i= -36mm (negativa, pois é invertida)  ---   i/o=-P’/P  ---  -36/o=-52/1.300  ---  o=900mm=90cm

05- Na água  ---  f=65cm  ---  P=40cm  ---  1/65=1/40 + 1/P’  ---  1/P’=(40 – 65)/2.600  ---  P’= - 104cm (negativa, imagem virtual)  ---  i/o=-P’/P  ---  i/0=-(-104)/40  ---  i=2,6.o  (a imagem é direita e 2,6 vezes maior que o objeto)  ---  R- A

06- A e b) A lente é convergente porque a imagem é maior que o objeto e porque é projetada e consequentemente real e invertida  --- 

i= - 4.o  ---  i/o=-P’p/P  ---  - 4.o/o = -P’/P  ---  P’=4P  ---  1/f=1/P + 1/P’  ---  1/12=1/P + 1/4P  ---  1/12=(4 + 1)/4P  ---  4P=60  --- 

P=15cm (distância do objeto à lente) ---  P’=4P  ---  P’=4.15  ---  P’=60cm (distância da imagem à lente)

07- o=15cm  ---  i=+3cm (positiva porque toda imagem virtual é direita)  ---  P=30cm  --- i/o=-P’/P  ---  3/15=- P’/30  ---  P’= - 6cm  ---  módulo P’=6cm

08- Observe a figura abaixo: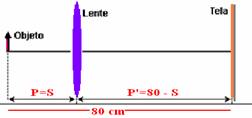

1/15=1/S + 1/(80 – S)  --- 1/15=(80 – S) + S/S.(80 – S)  ---  1200=80S – S²  ---  S² – 80S + 1200=0  ---  Δ=B²-4.A.C  ---  Δ=40  --- 

S= - B ±√ Δ/2.A  ---  S₁=(80 + 40)/2  ---  S₁=60cm e P₁’=80 – 60=20cm  ---  S₂=(80 – 40)/2  ---  S₂=20cm e P₂’=80 – 20=60cm

Observe que, para que a imagem seja real e nítida sobre a tela existem duas  posições entre elas 20cm e 60cm, mas a distância d

entre essas duas posições é a mesma e vale d=60 – 20  ---  d=40cm

09- a) o=0,6cm  ---  P=20cm  ---   se objeto e imagem estão do mesmo lado, a imagem é virtual e  P’=

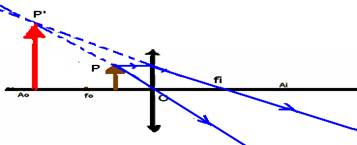
- 100cm   --- 1/f=1/P + 1/P’  ---  1/f=1/25 + 1/-100  ---   1/f=3/100  ---  f=100/3cm, mas a convergência C será em dioptrias se f estiver em metros  ---   C=1/f=1/(1/3)  ---  C=3 di

b) i/o=-P’/P  ---  i/0,6=-(-100)/25  ---  i=2,4cm

10- a) 1/f=1/180 + 1/36  ---  1/f=(1 + 5)/180  ---  f=30cm

b) O comprimento da imagem da lâmpada é de - 24 cm. A representação geométrica está representada na figura adiante.

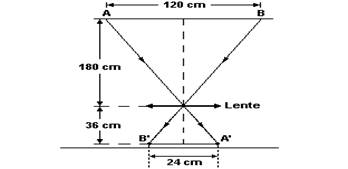
Semelhança de triângulos  ---  120/A’B’=180/36  ---  A’B’=24cm

11- Cálculo da altura da imagem formada pela lente L₁  ---  1/1,5=1/2 + 1/P’  ---  1/1,5 – 1/2= 1/P’  ---  P’=6cm  ---  i/o=-P’/P  ---  i/1=-6/2  ---  i= - 3cm (negativa, pois é invertida)

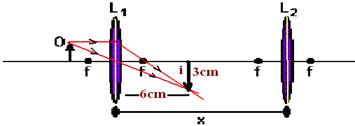
Lente L₂  ---   O=3cm  i=-6cm (deve ser direita em relação ao objeto, portanto invertida em relação a i) ---  i/O=-P’/P  --- - 6/3=

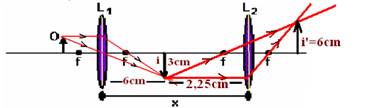
-P’/P  ---  P’=2P  ---  1/1,5=1/P + 1/2P  ---  P=2,25cm  ---  x=6 + 2,25  ---  x=8,25cm 

12- Lente L_x  ---  f=-10cm (divergente)  ---  P=20cm  ---  1/-10=1/20 + 1/P’  ---  -1/10 – 1/20=1/P’  ---  P’=-20/3cm (virtual, atrás da lente)

Lente L_y  ---  f=10cm  ---  P=20cm  ---  1/10=1/20 + 1/P’  ---  1/10 – 1/20=1/P’  ---  1/P’=(2 – 1)/20  ---  P’=20cm

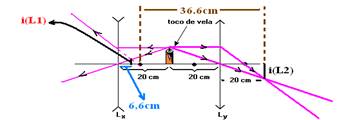
D=60,0 – 6,6  ---  d=53,4cm  ---  R- E

13- Lente L₁  ---  A’B’  ---  lente L₂  ---  A’’B’’

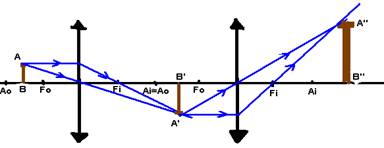
A imagem final é real (intersecção dos próprios raios luminosos), direita e maior em relação ao objeto original.

14- Espelho côncavo  ---  1/30=1/60 + 1/P’  ---  1/30 – 1/60=1/P’  ---  P’=60cm (A’B’)

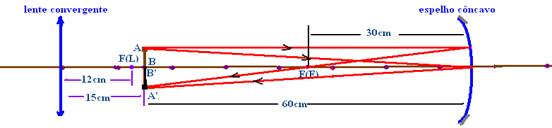
Lente convergente  ---  a imagem i(E) conjugada pelo espelho funciona como objeto para a lente  ---  P=15cm  ---  f=12cm  ---  1/12=1/15 + 1/P’  --- 1/ 12 – 1/15=1/P’  ---  1/P’=(5 – 4)/60  ---  P’=60cm 

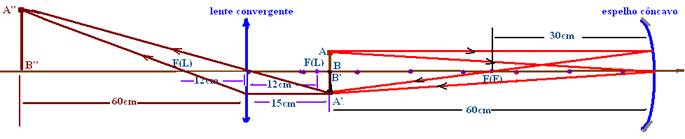
R- A

15- a) Trata-se de uma lente convergente (bordas finas) de índice de refração em relação ao ar – n_lente/n_ar=1,35 --- face convexa – Rc=2,5.10^-3 m  ---   face plana Rp=∞  ---  equação dos fabricantes de lentes C=1/f=((n_lente/n_ar – 1).(1/R_c + 1/R_p)  ---  C=1,35 – 1,00).(1/2,5.10^-3 +1/∞)  ---  C=(0,35).(0,4.10³ + 0)  ---  C=140di

b) Se a imagem é direita  ---  i=50.O  ---  i/O=-P’/P  ---  50.O/O=-P’/P  ---  P’=-50P  ---  1/f=140m  ---  1/f=1/P + 1/P’  ---  140=1/P - 1/50P  ---  140=49/50P  --- P=0,007m=7mm

16- a) f=20cm  ---  P=60cm  ---  1/20=1/60 + 1/P’  ---  1/20 – 1/60 =1/P’  ---  1/P’=(3 – 1)/60  ---  P’=30cm

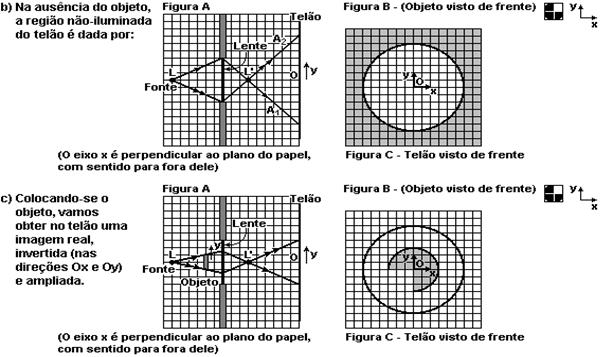
Como a imagem é projetada, ela é invertida (troca cima por baixo) e reversa (troca direita pela esquerda) Figura C)

17- n_v=1,5  ---  n_ar=1,0  ---  R_c=2.10^-2m  ---  R_p=∞  ---  equação dos fabricantes de lente  ---  1/f=C=(n_v - n_ar).(1/R_c + 1/R_p)  --- 

1/f=(1,5 – 1,0).(1/2.10^-2 + 0)  ---  1/f=25m  ---  P’=-36cm=-36.10^-2m (negativa-imagem virtual-lente divergente) ---  1/f=1/P + 1/P’  ---  25=1/P – 1/36.10^-2  ---  25 + 1/36.10^-2=1/P  ---  P=0,04m  ---   i=20.10^-2 m (positiva – direita)  ---  i/O=-P’/P  --- 

20.10^-2/O=-(-36.10^-2)/4.10^-2  ---  O=2.10^-2m  --- O=2cm  ---  R- D

18- 1- Correta – os raios de luz paralelos provenientes do Sol, se refratam na lupa (lente convergente) e convergem para um único ponto que é o foco.

2- Falsa – é direita e virtual

3- Correta – f=20cm  ---  P=10cm  ---  1/f=1/P + 1/P’  ---  1/20 – 1/10 =1/P’  ---  P’= -20cm  ---  i/o=-P’/P  ---  i/o=-(-20)/10  --- 

i/o=2  ---  i=2.o 

R- D

19- Uma lente convergente funciona como lupa somente se o objeto estiver entre o foco e a lente  ---  C=1/f  ---  5=1/f  ---  f=0,2m  ---  f=20cm  ---  R- C

20- Inicialmente o alvo está no foco da lente, pois a imagem é nítida  ---  aproxima-se a vela da lente até  P=3f/2  ---  P’=?  ---  1/f=1/P + 1/P’  ---  1/f=1/1,5f +1/P’  ---  1/f – 1/1,5f=1/P’  ---   0,5/1,5f=1/P’  ---  P’=3f   ---  R- E

21- a) Como a imagem está projetada no anteparo, ela é real. O objeto também é real. Concluímos que se trata de uma lente convergente.

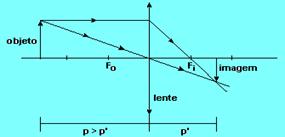
b)

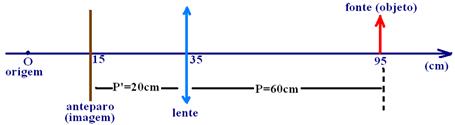
1/f=1/P + 1/P’   ---  1/f=1/60 + 1/20  ---  1/f= (1 + 3)/60  ---  f=15cm 

22- 1/f=1/08f + 1/P’  ---  1/f – 1/08f =1/P’  ---  (0,8 – 1,0)/0.8f=1/P’  ---  P’=-4f  ---  i/o=-P’/P  ---  i/1,6=-(-4f)/0,8f  ---  i=8mm

23- Como a imagem é projetada, ela é invertida  ---  A=-20=-P’/P  ---  P’=20P  ---  1/f=1/P + 1/20P  ---  1/d=1/P + 1/20P  ---  20P=21d   ---  P’=20P=21d  ---  R- D

24- a) i=2.o  ---  i/o=-P’/P  ---  2.o/o=-P’/P  ---  P’=-2P  ---  1/f=1/P – 1/2P  ---  1/f=(2 – 1)/2P  ---  f=2P  ---  f/P=2

b) Com água  ---  f_a=2,5f  ---  P é o mesmo e vale  ---   P=f/2  ---  1/f_a=1/P + 1/P_a’  ---  1/2.5f=1/(f/2) + 1/P_a’  ---   1/2,5f – 2/f=1/P_a’  ---  1/P_a’ =(1 – 5)/2,5f  ---  P_a’ = - 0,625f  ---  A= - P_a’/P  ---  A= - (-0,625f)/f/2  ---  A=1,25 

25- Dados  ---   P = 30 cm  ---  f = 10 cm  ---   o = 6 cm.

a) 1/f=1/P + 1/P’  ---  1/10=1/30 + 1/P’  ---  (3 – 1)/30=1/P’  ---  P’=15cm  ---  essa imagem real (p’ > 0) da vela funciona como objeto real para o espelho plano, que fornece uma segunda imagem, virtual e simétrica conforme você pode observar na figura

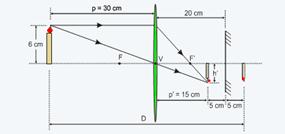
 fornecida onde a distância D da imagem final da vela até a mesma vale  ---   D = 30 + 20 + 5  ---   D = 55 cm.

b) O altura da imagem da vela fornecida pelo espelho plano é igual a altura da imagem fornecida pela lente, pois a imagem formada no espelho plano tem o mesmo tamanho que o objeto  ---  equação do aumento linear transversal  ---  i/o=-P’/P  ---

i/6=-15/30  ---  i= - 3cm  ---  a imagem é invertida e tem altura de 3 cm. 

26- A figura mostra a construção da imagem: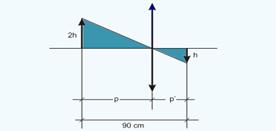

Observe na figura acima que os triângulos sombreados são semelhantes  ---  2h/h=P/P’  ---  P=2P’  ---  P + P’+=90  ---  2P’ + P’+=90  ---  P’=30cm  ---  P=60cm  ---  1/f=1/P + 1/P’  ---  1/f=1/60 + 1/30  ---  f=60/3  ---  f=20cm  ---  C=1/f  ---  C=1/0,2  ---  C=5di

27- Uma lente esférica é delgada quando sua espessura é desprezível, em ralação aos raios de curvatura das faces. Ela pode ser de bordas delgadas (finas) ou de bordas grossas, como representado abaixo.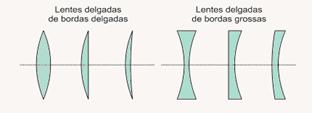

(01) Errada  ---  se o índice de refração do material que constitui a lente é maior que o índice de refração do meio, lentes delgadas de bordas delgadas são convergentes e lentes delgadas de bordas grossas são divergentes.

(02) Correta  ---  trata-se do Teorema da Vergência.

(04) Correta.

(08) Correta.

(16) Correta. 

R- (02 + 04 + 08 + 16) = 30

28- a) Falsa  ---  a lente usada para projeções de imagens (de objetos reais) é convergente, e para correção de miopia utiliza-se lente divergente.

b) Falsa  --- iImagens virtuais não são projetáveis.

c) Correta.

d) Falsa  ---  as faces dos prismas são espelhos planos, fornecendo imagens de mesmo tamanho.

e) Falsa  ---  A lupa fornece imagem virtual, não podendo ser projetada.  

R- C

29- Dados  ---   y = 4 cm  ---   y’ = 1 cm  ---   p = d = 3 cm  ---   p’ = D = 150 cm  ---   T = 250 °C  ---  calculando o aumento linear transversal (em módulo), antes do aquecimento.

Depois do aquecimento, o aumento linear é o mesmo, pois não se alteram as posições do objeto e da imagem  ---  os novos comprimentos da imagem e do objeto são, respectivamente: (y’ + ∆y’) e (y + ∆y)  ---  aplicando novamente a equação do aumento  ---  A=(Y’+ ∆Y)/(Y + ∆Y)  ---  substituindo valores  ---  50=(200 + 1)/(4 + ∆Y)  ---  ∆y=2.10^-2cm  ---  ∆y é a dilatação sofrida pelo objeto  ---   ∆y=Yα ∆T  ---  2.10^-2=4α250  --- α=2,0.10^-5 oC^-1

30-Determinação gráfica da imagem  ---  LM – objeto  ---  L’M’ – imagem:

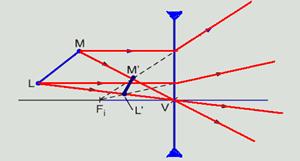
A figura abaixo mostra as coordenadas X e Y dos pontos M e L  ---  M(25;15)  ---  L(5;35):

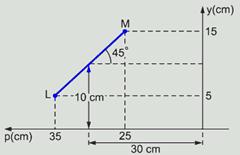
Cálculo da coordenada P’ das imagens M’ e L’ pela equação dos pontos conjugados  ---  1/f=1/P_M + 1/P’_M  ---  1/-20=1/25 + 1/P’_M  ---  P’_M= - 100/9cm  ---  1/f=1/P_L + 1/P’_L ---  1/-20=1/35 + 1/P’_L  ---  P’_L= - 140/11cm  ---  cálculo da coordenada Y’ das imagens M’ e L’ pela equação do aumento linear transversal  ---  Y’_L/Y_L= - P’_L/P_L  ---  Y’_L/5= - ( - 140/11)/35  ---  Y’_L=20/11cm  ---

Y’_M/Y_M= - P’_M/P_M  ---  Y’_M/15= - ( - 100/9)/25  ---  Y’_M=20/3cm  ---  Comprimento da imagem da barra  ---  c²= (P’_M – P’_L)² + (Y’_M – Y’_L)²  ---  c²={ - 100/9 – ( - 140/11)}² + (20/3 – 20/11)²  ---  c²≈256.000/9.800  ---  c²≈26  ---  c≈5,1cm

31- I. Falsa  ---  a moeda não está na posição vista aparentemente devido ao fenômeno da refração, que desvia os raios luminosos.

II. Correta  ---  você pode acender o palito de fósforo colocando a cabeça dele no foco, ponto de encontro dos raios solares refratados pela lente convergente.

III. Correta.

IV. Correta  ---  o número de imagens (n) fornecidas pela associação de dois espelhos planos é dado por:

N=360/θ - 1, sendo θ o ângulo formado entre os espelhos  ---  se os espelhos são colocados paralelamente entre si, θ= 0º  ---  então n tende para infinito. 

R- E

32- Observe na figura abaixo que P=7,5cm  ---  f=+5cm  ---  1/f=1/P + 1/P’  ---  1/5=1/7,5 + 1/P’  ---  P’=37,5/2,5  ---  P’=15cm  --

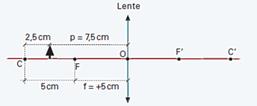
P’ > 0  ---  imagem real  ---  aumento linear transversal  ---  A= - P’/P= - 15/7,5  ---  A= - 2  ---  como A < 0 a imagem é invertida e como │A│=2, a altura da imagem é o dobro da altura do objeto  ---  observe a construção geométrica abaixo:

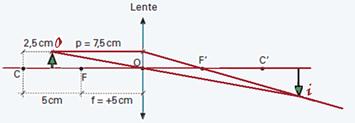
33- Lente convergente  ---  f=+4cm  ---  a imagem é direita (aumento positivo) e de tamanho três vezes maior que o do objeto  --- 

A=+3

a) A= - P’/P  ---  3= - P’/P  ---  P’= - 3P  ---  1/f=1/P + 1/P’  ---   1/4 = 1/P – 1/3P  ---  1/4 = 2/3P  ---  P=8/3 cm (distância do objeto à lente)

b) P’ = - 3P  ---  P’= - 3.(8/3)  ---  P’= - 8 cm  ---  como a imagem é virtual, ela é direita e se encontra a 8cm do centro óptico da lente, e do mesmo lado que o objeto  ---  imagem direita  ---  A > 0  ---  A= i/o  ---  3=i/0,7  ---  i=+2,1cm (tamanho da imagem)

---  observe a construção geométrica da imagem na figura abaixo:

34- R- (01 + 04 + 16)=21  ---  veja teoria

35- Observe na figura abaixo  ---  o=altura do objeto=1cm  ---  i=altura da imagem= - 0,4cm (invertida em relação ao

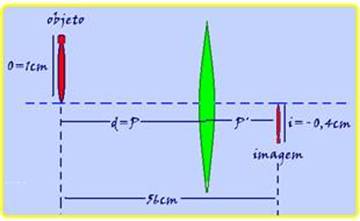
objeto)  ---  distância do objeto à lente=P=d  ---  distância da imagem à lente=P’  ---  P + P’ = 56cm  ---  P=56 – P’  --- i/o = - P’/P  ---   - 0,4/1 = - P’/(56 – P’)  ---  0,4.56 – 0,4P’=P’  ---  1,4P’=22,4  ---  P’=16cm  ---  P + P’=56  --- P + 16=56  ---  P=d=40cm.

36-  Lupa – Também chamada de lente de aumento é uma simples lente convergente que fornece de um objeto colocado entre seu foco F e seu centro óptico O uma imagem virtual, direita e maior que o objeto observado  ---  Observe no esquema abaixo a

formação da imagem A’B’ de um objeto AB em uma lupa  ---   observe  que a imagem é virtual e assim, nas equações  ---   1/f =

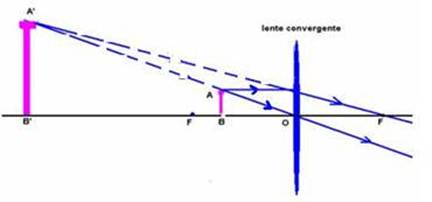
1/P + 1/P’  ---  i/o = -P’/P  ---   A = i/o = -P’/P  ---  P’ deve e ser substituída com sinal negativo,  pois P’< 0 (a imagem é virtual)  --- dados do exercício  ---  f=+10cm (lente convergente)  ---  i=+100 (toda imagem virtual é direita)  ---  i/o = - P’/P  ---  100.o/o = - P’/P  ---  P’ = - 10P  ---  equação dos pontos conjugados de Gauss  ---  1/f=1/P + 1/P’  ---  1/10=1/P + 1/(- 10P)  ---  1/10=1/P – 1/10P  ---

P=10 – 1  ---  P = 9cm  (distância entre a lupa e o objeto que é a impressão digital) ---  R- A 

37- Como os raios de luz incidem paralelamente na superfície da lupa (lente convergente), eles se refratam convergindo para o foco f formando o ponto luminoso  ---  f=20cm  ---  o celular é o objeto que está a 15cm da lupa  ---  P=15cm  ---  1/20 = 1/15 + 1/P’  ---  (3 – 4)/60=1/P’  ---  P’= -60cm (imagem virtual P’<0)  ---  i/o= - P’/P  ---  i/o= - (-60)/15  ---  i/o=4  ---  A=4  ---  imagem direita (A>0) e 4 vezes maior que o objeto  ---  R- C  ---  observação  ---  como o objeto está entre o foco e a lente convergente

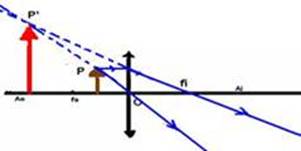
(lupa), você poderia traçar os raios de luz e caracterizar a imagem obtida  --- natureza: virtual (obtida no cruzamento dos prolongamentos dos raios luminosos)  ---  localização: antes do foco  ---  tamanho e orientação: maior que o objeto e direita em relação a ele.

38- Observando o gráfico fornecido você notará que, quando o objeto estiver a 20cm do centro óptico da lente (P=20cm), a imagem estará também a 20cm do centro óptico da lente (P’=20cm)   ---  essas duas posições correspondem aos dois pontos antiprincipais da lente, que correspondem ao dobro da distância focal  ---  2f=20  ---  f=10cm  ---  analisando cada alternativa:

I. Falsa  ---  a vergência C de uma lente corresponde ao inverso de sua distância focal, medida em metros  ---  C=1/f=1/0,1  --- C=10 dioptrias (di)

II. Falsa  ---  quando o objeto estiver entre 0 e 10cm do centro óptico da lente, ele estará entre o foco e a lente e a imagem

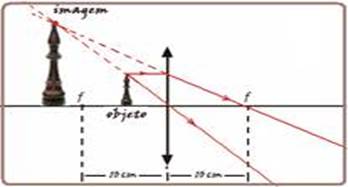
conjugada será virtual, direita e maior em relação ao objeto, como você pode observar na figura acima.

III. Verdadeira  ---  dados  ---  P=50cm  ---  f=10cm  ---  P’=?  ---  equação dos pontos conjugados  ---  1/f = 1/P + 1/P’  ---

1/10 = 1/50 + 1/P’  ---  1/p’ = 4/50  ---  p’ = 12,5cm  ---  aumento linear transversal  ---  A= - P’/P= - 12,5/50  ---  A= - 1/4 ( o

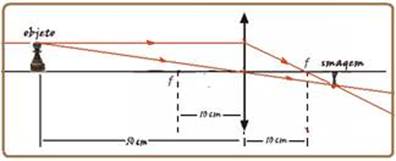
sinal negativo mostra que a imagem é invertida em relação ao objeto  ---  veja figura acima  ---  R- B