Estudo analítico dos espelhos esféricos

Como você já viu no capítulo anterior, é possível determinar graficamente as características da imagem conjugada por um dado espelho esférico.

Mas, existe também uma relação matemática entre a posição (localização) do objeto P, da imagem P’ e a distância focal f para os espelhos esféricos, denominada equação dos pontos conjugados, num referencial conveniente denominado referencial de Gauss, com as seguintes características
O eixo das abscissas coincide com o eixo principal do espelho.
O eixo das ordenadas coincide com o espelho.
A origem coincide com o vértice do espelho.

Equação dos pontos conjugados ou equação de Gauss para espelhos esféricos

Equação do aumento linear transversal

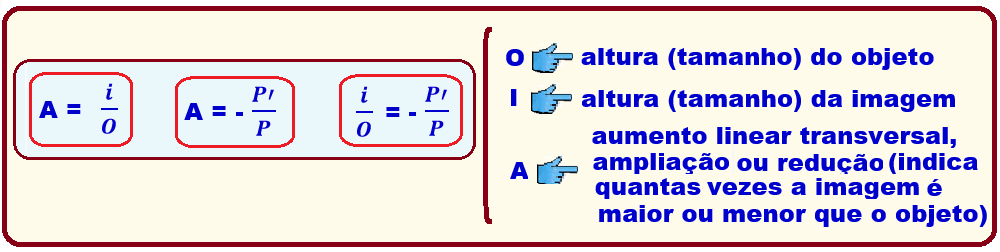
Convenções do referencial de Gauss

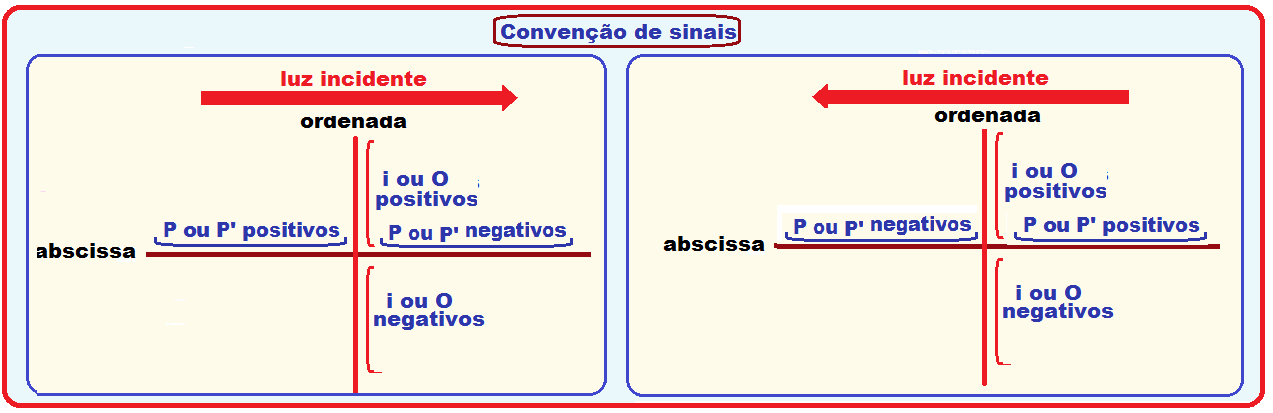
No referencial de Gauss adotado no estudo dessas equações, as posições são transformadas em coordenadas onde:

No vértice V do espelho está localizada a origem das abscissas e das ordenadas.

No lado onde a luz incide as abscissas (P e P’) são positivas e no lado oposto, negativas.

As coordenadas (i e O) são positivas acima do vértice do espelho e negativas abaixo.

Imagem real P’ > 0, (positivo) imagem virtual, P’< 0 (negativo).

Informações importantes

O que você deve saber, informações e dicas

Toda imagem real pode ser projetada e é invertida (i e o tem sinais opostos) P’ é positivo e i é negativo

Toda imagem virtual é direita P’ é negativo e i é positivo

Demonstração da equação dos pontos conjugados ou equação de Gauss

Para a demonstração da equação de Gauss, vamos considerar um objeto de altura O e sua correspondente imagem de altura i conjugada por um espelho esférico côncavo, conforme a figura abaixo.

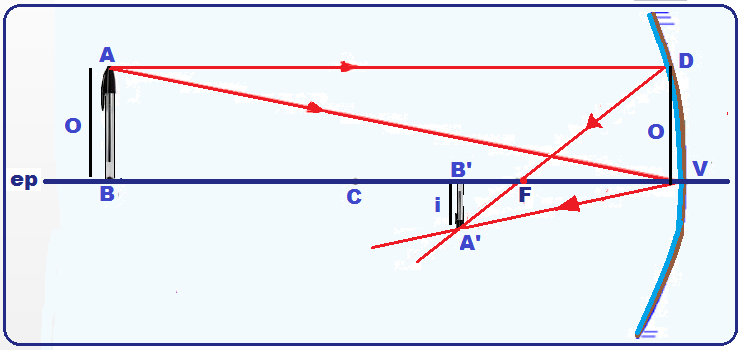
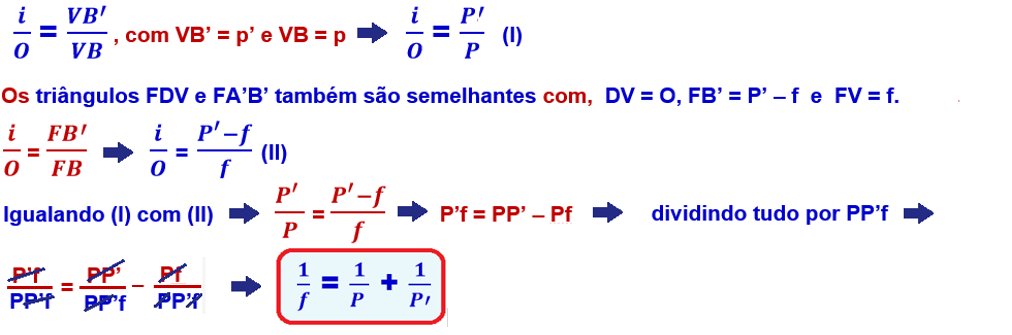
Os triângulos ABV e A’B’V são semelhantes

Algumas vezes você precisa aplicar a equação dos pontos conjugados mais que uma vez como no exemplo a seguir:

Um objeto desloca-se ao longo do eixo principal, em direção ao vértice de um espelho esférico côncavo Gaussiano, com velocidade constante de 4cm/s. A distância focal do espelho é de 10cm.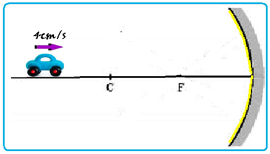

Em um certo instante, o objeto está a 50cm do vértice.

Determine, após 5s, a distância percorrida pela imagem do objeto.

Situação inicial (t = 0) P = 50cm f = 10cm 1/f = 1/P + 1/P’ 1/10 = 1/50 + 1/P’ 1/10 – 1/50 = 1/P’ 4/50 = 1/P’ P’ = 12,5cm (posição inicial da imagem).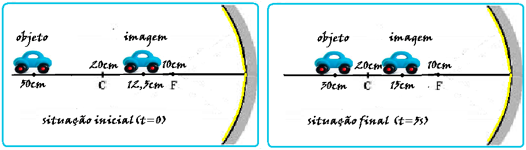

Situação final (t = 5s) V=ΔS/Δt 4= ΔS/5 ΔS=20cm como ele se aproxima do espelho sua nova distância do vértice do espelho será P = 50 – 20 P = 30cm f = 10cm 1/10 = 1/30 + 1/P’ P’= 15cm (nova posição da imagem).

A imagem percorreu ΔS = 15 – 12,5 ΔS = 2,5cm.

Exercício interessante:

A imagem do Sol é formada em um espelho esférico côncavo, de distância focal igual a 1 metro. Considerando a distância do Sol à Terra 250 vezes maior que o diâmetro do Sol, determine o diâmetro da imagem formada.

Sendo a distância do Sol à Terra muito grande, os raios de luz emitidos por ele chegam à Terra como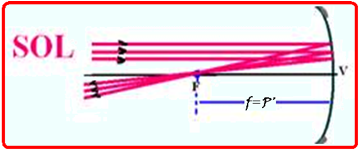

feixes de raios paralelos e a imagem P’ do Sol se forma no foco P’ = f = 1m P=250d O = d i/O = - P’/P i/d = - 1/250d i = -1/250 = 4.10^-3m (i < 0, imagem do Sol invertida e de diâmetro

0,004 m)

Comparando as distâncias aparentes entre um espelho esférico convexo e um espelho plano

Para evitar acidentes de trânsito, foram instalados espelhos convexos em alguns cruzamentos.

A experiência não foi bem sucedida porque, como os espelhos convexos fornecem imagens menores, perde-se completamente a noção de distância.

Para perceber esse efeito, suponha que um objeto linear seja colocado a 30 m de um espelho convexo de 12 m de raio, perpendicularmente a seu eixo principal.

a) A que distância do espelho convexo seria vista a imagem desse objeto?

b) Se substituíssemos o espelho convexo por um espelho plano, a que distância deste espelho seria vista a imagem daquele objeto?

a) Objeto a P=30m do espelho convexo de distância focal f = - 6m 1/f = 1/P + 1/P’ -1/6 = 1/30 + 1/P’ P’ = - 5m (observe que para um objeto a 30m do espelho convexo, a imagem seria vista como se estivesse a 5m do mesmo, aparentando assim, ser menor).

b) No espelho plano a imagem é simétrica (objeto e imagem são equidistantes do espelho) e de mesmo tamanho do objeto. Assim você veria a distância real que é de 30m.

Exercícios de vestibulares com resolução comentada sobre

Estudo Analítico dos Espelhos Esféricos

01-(FUVEST-SP) A imagem de um objeto forma-se a 40 cm de um espelho côncavo com distância focal de 30 cm. A imagem formada situa-se sobre o eixo principal do espelho, é real, invertida e tem 3 cm de altura.

a) Determine a posição do objeto.

b) Construa o esquema referente à questão representando objeto, imagem, espelho e raios utilizados e indicando as distâncias envolvidas.

02- (PUC-SP) O espelho esférico convexo de um retrovisor de automóvel tem raio de curvatura de 80cm.

Esse espelho conjuga, para certo objeto sobre o seu eixo principal, imagem 20 vezes menor. Nessas condições, a distância do objeto ao espelho, em metros, é de

a) 1,9 b) 3,8 c) 7,6 d) 9,5 e) 12

03-(UNICAMP-SP) Uma das primeiras aplicações militares da ótica ocorreu no século III a.C. quando Siracusa estava sitiada pelas forças navais romanas. Na véspera da batalha, Arquimedes ordenou que 60 soldados polissem seus escudos retangulares de bronze, medindo 0,5m de largura por 1,0m de altura. Quando o primeiro navio romano se encontrava a aproximadamente 30m da praia para atacar, à luz do sol nascente, foi dada a ordem para que os soldados se colocassem formando um arco e empunhassem seus escudos, como representado esquematicamente na figura a seguir. Em poucos minutos as velas do navio estavam ardendo em chamas.

Isso foi repetido para cada navio, e assim não foi dessa vez que Siracusa caiu. Uma forma de entendermos o que ocorreu consiste em tratar o conjunto de espelhos como um espelho côncavo. Suponha que os raios do sol cheguem paralelos ao espelho e sejam focalizados na vela do navio.

a) Qual deve ser o raio do espelho côncavo para que a intensidade do sol concentrado seja máxima?

b) Considere a intensidade da radiação solar no momento da batalha como 500W/m2. Considere que a refletividade efetiva do bronze sobre todo o espectro solar é de 0,6, ou seja, 60% da intensidade incidente é refletida. Estime a potência total incidente na região do foco.

04- (ITA-SP) Um objeto linear de altura h está assentado perpendicularmente no eixo principal de um espelho esférico, a 15cm de seu vértice. A imagem produzida é direita e tem altura de h/5. Este espelho é:

a) côncavo, de raio 15 cm.

b) côncavo, de raio 7,5 cm.

c) convexo, de raio 7,5 cm.

d) convexo, de raio 15 cm.

e) convexo, de raio 10 cm.

05- (UFES) Um objeto desloca-se ao longo do eixo principal, em direção ao vértice de um espelho esférico côncavo Gaussiano, com velocidade constante de 4cm/s. A distância focal do espelho é de 10cm. Em um certo instante, o objeto está a 50cm do vértice. Após 5s, a distância percorrida pela imagem do objeto é de:

06-(UERJ) Na entrada do circo existe um espelho convexo. Uma menina de 1,0m de altura vê sua imagem refletida quando se encontra a 1,2m do vértice do espelho.

A relação entre os tamanhos da menina e de sua imagem é igual a 4.

Calcule a distância focal do espelho da entrada do circo.

07- (UERJ) Com o objetivo de obter mais visibilidade da área interna do supermercado, facilitando o controle da movimentação de pessoas, são utilizados espelhos esféricos cuja distância focal em módulo é igual a 25 cm. Um cliente de 1,6 m de altura está a 2,25 m de distância do vértice de um dos espelhos.

a) Indique o tipo de espelho utilizado e a natureza da imagem por ele oferecida.

b) Calcule a altura da imagem do cliente.

08- (MACKENZIE-SP) Dispõe-se de dois espelhos esféricos, um convexo e um côncavo, com raios de curvatura 20,0 cm cada um, e que obedecem às condições de Gauss. Quando um objeto real é colocado perpendicularmente ao eixo principal do espelho convexo, a 6,0 cm de seu vértice, obtém-se uma imagem conjugada de 1,5 cm de altura. Para que seja obtida uma imagem conjugada, também de 1,5 cm de altura, colocando esse objeto perpendicularmente ao eixo principal do espelho côncavo, sua distância até o vértice desse espelho deverá ser

a) 11,0 cm b) 15,0 cm c) 26,0 cm d) 30,0 cm 25,5cm

09-(FATEC-SP) Um espelho esférico côncavo tem distância focal 3,0m. Um objeto de dimensões desprezíveis se encontra sobre o eixo principal do espelho, a 6,0m deste. O objeto desliza sobre o eixo principal, aproximando-se do espelho com velocidade constante de 1,0 m/s. Após 2,0 segundos, sua imagem

a) terá se aproximado 6,0m do espelho.

b) terá se afastado 6,0m do espelho.

c) terá se aproximado 3,0m do espelho.

d) terá se afastado 3,0m do espelho.

e) terá se aproximado 12,0m do espelho.

10-(UFPE-PE)

Um espelho côncavo tem um raio de curvatura R = 2,0 m.

A que distância do centro do espelho, em centímetros, o rosto de uma pessoa deve se posicionar sobre o eixo do espelho para que a ampliação de sua imagem seja A = +2?

11-(Ufrj-RJ) Para evitar acidentes de trânsito, foram instalados espelhos convexos em alguns cruzamentos.

A experiência não foi bem sucedida porque, como os espelhos convexos fornecem imagens menores, perde-se completamente a noção de distância. Para perceber esse efeito, suponha que um objeto linear seja colocado a 30 m de um espelho convexo de 12 m de raio, perpendicularmente a seu eixo principal.

a) A que distância do espelho convexo seria vista a imagem desse objeto?

b) Se substituíssemos o espelho convexo por um espelho plano, a que distância deste espelho seria vista a imagem daquele objeto?

12-(Ueg-GO) Conforme a ilustração a seguir, um objeto de 10 cm de altura move-se no eixo de um espelho esférico côncavo com raio de curvatura R = 20 cm, aproximando-se dele. O objeto parte de uma distância de 50 cm do vértice do espelho, animado com uma velocidade constante de 5 cm/s.

Responda ao que se pede.

a) No instante t = 2 s, quais são as características da imagem formada? Justifique.

b) Em qual instante a imagem do objeto se formará no infinito? Justifique.

c) No instante t = 7 s, qual é a posição e tamanho da imagem formada? Justifique.

13-(UFSCAR-SP) Uma mocinha possuía um grande espelho esférico côncavo que obedecia às condições de estigmatismo de Gauss. Com seu espelho, de raio de curvatura 3,0 m, estava acostumada a observar recentes cravos e espinhas. Certo dia, sem que nada se interpusesse entre ela e seu espelho, observando-o diretamente, a uma distância de 2,0 m da superfície refletora e sobre o eixo principal,

a) não pôde observar a imagem de seu rosto, que é de tamanho menor e em posição invertida.

b) não pôde observar a imagem de seu rosto, que é de tamanho maior e em posição invertida.

c) pôde observar a imagem de seu rosto em tamanho reduzido e disposta em posição direita.

d) pôde observar a imagem de seu rosto em tamanho ampliado e disposta em posição direita.

e) pôde observar a imagem de seu rosto em tamanho ampliado e disposta em posição invertida.

14-(UNICAMP-SP) Para espelhos esféricos nas condições de Gauss, a distância do objeto ao espelho, p, a distância da imagem ao espelho, p', e o raio de curvatura do espelho, R, estão relacionados através da equação (1/p) + (1/p') = 2/R. O aumento linear transversal do espelho esférico é dado por A = - p'/p, onde o sinal de A representa a orientação da imagem, direita quando positivo e invertida, quando negativo. Em particular, espelhos convexos são úteis por permitir o aumento do campo de visão e por essa razão são frequentemente empregados em saídas de garagens e em corredores de supermercados. A figura a seguir mostra um espelho esférico convexo de raio de curvatura R. Quando uma pessoa está a uma distância de 4,0 m da superfície do espelho, sua imagem virtual se forma a 20 cm deste, conforme mostra a figura. Usando as expressões fornecidas acima, calcule o que se pede.

a) O raio de curvatura do espelho.

b) O tamanho h da imagem, se a pessoa tiver H = 1,60 m de altura.

15-(PUC-SP)

A litografia produzida pelo artista gráfico holandês M. C. Escher (1898 - 1972) comporta-se como um espelho convexo, no qual o artista, situado a 90 cm do espelho, observa sua imagem, refletida na superfície da esfera refletora, com um tamanho dez vezes menor.

Nessas condições, o módulo da distância focal do espelho, em centímetros, é igual a

a) 1

b) 3

c) 5

d) 10

e) 20

16-(ITA-SP) Um espelho esférico convexo reflete uma imagem equivalente a 3/4 da altura de um objeto dele situado a uma distância p₁. Então, para que essa imagem seja refletida com apenas 1/4 da sua altura, o objeto deverá se situar a uma distância p₂ do espelho, dada por

17-(UNESP-SP) A imagem do Sol é formada em um espelho esférico côncavo, de distância focal igual a 1 metro. Considerando a distância do Sol à Terra 250 vezes maior que o diâmetro do Sol, o diâmetro da imagem formada será:

18-(ITA-SP) Um espelho plano está colocado na frente de um espelho côncavo, perpendicularmente ao eixo principal. Uma fonte luminosa A, centrada no eixo principal entre os dois espelhos, emite raios que se refletem sucessivamente sobre os dois espelhos e formam, sobre a própria fonte A, uma imagem real da mesma. O raio de curvatura do espelho é 40cm e a distância do centro da fonte A até o centro do espelho esférico é de 30cm.

A distância d do espelho plano até o centro do espelho côncavo é, então:

a) 20cm

b) 30cm

c) 40cm

d) 45cm

e) 50cm

19-(Ufrj-RJ) Um dispositivo para a observação da imagem do Sol é constituído por dois espelhos esféricos concêntricos e uma tela, como ilustra a figura a seguir. O espelho convexo tem raio de curvatura R’ igual a 12 cm e o espelho côncavo tem raio de curvatura R’’ igual a 30 cm.

Calcule o valor da distância (d) entre a tela e o centro de curvatura C, comum aos dois espelhos, quando a imagem do Sol se forma com nitidez sobre a tela.

20-(FGV-SP)

Dois espelhos esféricos côncavos, um de distância focal 2,0 m e outro de distância focal 5,0 m, foram colocados um voltado para o outro, de forma que seus eixos principais coincidissem. Na metade da distância entre os dois espelhos, a 1 m da superfície refletora de cada um deles, foi colocado o objeto AB.

A distância entre as imagens do objeto AB, conjugadas pelos espelhos, isoladamente, em m, é de

a) 21/4

b) 19/4

c) 17/4

d) 15/4

e) 13/4

21-(UNEMAT-MT)

Uma pessoa encontra-se de pé a uma distância de 10 cm de um espelho esférico. Esta pessoa vê, no espelho, sua imagem direita e aumentada em 5 vezes. Com os dados acima, pode-se dizer que a distância focal do espelho vale:

a) 12,5 cm.

b) 10 cm.

c) 20 cm.

d) 30,5 cm.

e) 25,5 cm.

22-(UFAL-AL)

Um palito de fósforo, de 8 cm de comprimento, é colocado a 80 cm de distância de um espelho esférico convexo, perpendicularmente ao eixo principal e sobre o mesmo. A imagem do palito possui comprimento de 1,6 cm e a mesma orientação

deste. Pode-se concluir que o valor absoluto da distância focal do espelho vale:

a) 10 cm

b) 20 cm

c) 30 cm

d) 40 cm

e) 50 cm

23-(FGV-SP)

Ao estacionar seu carro, o motorista percebeu a projeção da imagem da pequena lâmpada acesa de um dos faroletes, ampliada em 5 vezes, sobre a parede vertical adiante do carro. Em princípio, o farolete deveria projetar raios de luz paralelos, já que se tratava

de um farol de longo alcance.

Percebeu, então, que o conjunto lâmpada-soquete tinha se deslocado da posição original, que mantinha a lâmpada a 10,0 cm da superfície espelhada do espelho esférico côncavo existente no farol. Considerando que o foco ocupa uma posição adiante do vértice do espelho, sobre o eixo principal, é possível concluir que, agora, a lâmpada se encontra a

a) 2,0 cm atrás do foco.

b) 1,0 cm atrás do foco

c) 0,5 cm atrás do foco.

d) 0,5 cm adiante do foco.

e) 2,0 cm adiante do foco.

24-(UERJ-RJ) Um raio de luz vindo do ar, denominado meio A, incide no ponto O da superfície de separação entre esse meio e o meio B, com um ângulo de incidência igual a 7º.

No interior do meio B, o raio incide em um espelho côncavo E, passando pelo foco principal F.

O centro de curvatura C do espelho, cuja distância focal é igual a 1,0 m, encontra-se a 1,0 m da superfície de separação dos meios A e B.

Observe o esquema:

Considere sen7^o=0,12 e os seguintes índices de refração, n_A= 1,0 (meio A) e n_B = 1,2 (meio B).

Determine a que distância do ponto O o raio emerge, após a reflexão no espelho.

25-(MACKENZIE-SP)

Um pequeno objeto foi colocado sobre o eixo principal de um espelho esférico côncavo, que obedece às condições de Gauss, conforme

ilustra a figura ao lado. O raio da esfera, da qual foi retirada a calota que constitui o espelho, mede 1,00 m. Nessas condições, a distância entre esse objeto e sua respectiva imagem conjugada é de

a) 240 cm

b) 150 cm

c) 75 cm

d) 60 cm

e) 50 cm

26-(UNESP-SP)

Observe o adesivo plástico apresentado no espelho côncavo de raio de curvatura igual a 1,0 m, na figura 1. Essa informação

indica que o espelho produz imagens nítidas com dimensões até cinco vezes maiores do que as de

um objeto colocado diante dele.

Considerando válidas as condições de nitidez de Gauss para esse espelho, calcule o aumento linear conseguido quando o lápis

estiver a 10 cm do vértice do espelho, perpendicularmente ao seu eixo principal, e a distância em que o lápis deveria estar do vértice do espelho, para que sua imagem fosse direita e ampliada cinco vezes.

Resolução comentada dos exercícios de vestibulares sobre

Estudo Analítico dos Espelhos Esféricos

01- a) P’=+40cm (real) --- f=+30cm (côncavo) i= -3cm (invertida) --- 1/f=1/P + 1/P’ --- 1/30=1/P + 1/40 --- 1/P = 1/30 – 1/40 --- (4 – 3)/120 = 1/P --- P=120cm

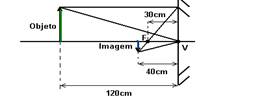
02- f=-40cm espelho convexo) --- espelho convexo a imagem é direita e i e O tem mesmo sinal --- O=20i --- i/O=-P’/P ---

i/20i=-P’/P --- P=-20P’ --- 1/f = 1/P + 1/P’ --- 1/-40 = 1/-20P’ + 1/P’ --- -1/40 = 19/20P’ --- 20P’P=-760 --- P’=-38cm --- P=-20P’ --- P=(-20).(-38)=760cm --- P=7,6m R- C

03- a) O espelho, para obter a maior intensidade de radiação solar possível, deve ter 60m de raio de curvatura, de modo que o navio fique em seu foco quando estiver a 30m da praia.

b) Intensidade de radiação = Potência/área --- I=P/S --- 60% de I=0,6.500 --- I=300W/m² --- cada espelho tem área ---

S=0,5.1,0 --- S=0,5m² --- como são 60 espelhos --- S_t=60.0,5 --- S_t=30m² --- I=P/S_t --- 300=P/30 --- P=9.000W ou P=9kW

04- O=h --- P=15cm --- sendo a imagem direita e menor que o objeto a imagem é virtual e o espelho é convexo e i=h/5 ---

i/O=-P’/P --- (h/5)/h=-P’/15 --- P’=-3cm --- 1/f = 1/P + 1/P’ --- 1/f=1/15 + 1/-3 --- f=-3,75cm --- R=2.(-3,75) ---

R=-7,5cm e o sinal negativo significa que o espelho é convexo R- C

05- Situação inicial (t=0) --- P=50cm --- f=10cm --- 1/f=1/P+1/P’ --- 1/10=1/50+1/P’ --- 1/10 – 1/50=1/P’ --- 4/50=1/P’ --- P’=12,5cm (posição inicial da imagem)

Situação final (t=5s) --- V=ΔS/Δt --- 4= ΔS/5 --- ΔS=20cm --- como ele se aproxima do espelho sua nova distância do vértice do espelho será --- P=50 – 20 --- P=30cm --- f=10cm --- 1/10 = 1/30 + 1/P’ --- P’= 15cm (nova posição da imagem) --- A imagem percorreu ΔS=15 – 12,5 --- ΔS=2,5cm --- R- E

06- O=1m --- espelho convexo – a imagem é virtual, direita e menor que o objeto --- O=4i --- P=1,2m --- i/O=-P’/P --- i/4i=-P’/1,2 --- P’= - 0,3m --- 1/f = 1/P + 1/P’ --- 1/f=1/1,2 + 1/-0,3 --- f= -1,2/3 --- f= - 0,4m (o sinal negativo significa que o espelho é convexo)

07- a) Espelho convexo e a imagem é virtual, direita e menor que o objeto. (tem a vantagem de aumentar o campo visual).

b) f=-0,25m (espelho convexo) --- O=1,6m --- P=2,25m ---1/f=1/P + 1/P’ --- -1/0,25=1/2,25 + 1/P’ --- P’= -0,225m ---

i/O=-P’/P --- i/1,6=-(-0,225)/2,25 --- i=0,16m=16cm

08- Convexo --- f=-10cm --- P=6cm --- 1/-10=1/6 + 1/P’ --- P’= -3,75cm --- i/O=-P’/P --- 1,5/O=-(-3,75)/6 --- O=2,4cm --- côncavo --- f=10cm --- i=-1,5m (imagem invertida) --- O=2,4cm --- i/O=-P’/P --- -1,5/2,4=-P’/P ---

P’=0,625P --- 1/10=1/P + 1/0,625P --- P=16,25/0,625 --- P=26cm R- C

09- Situação inicial (t=0) --- como o objeto está sobre C, a imagem estará sob C e P’=6m (figura abaixo)

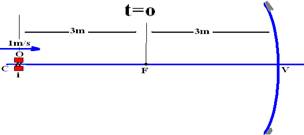
Situação final (t=2s) --- V=d/t --- 1=d/2 --- d=2m – o objeto se deslocou 2m e está a P=6-2=4m do vértice P=4cm ---

1/f=1/P + 1/P’ --- 1/3=1/4 + 1/P’ --- P’=12m (figura abaixo)

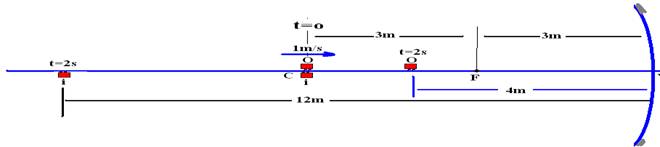
A imagem, que estava a 6m do espelho, se afastou 6m do mesmo R- B

10- A=-P’/P --- 2=-P’/P --- P’=-2P --- 1/1=1/P – 1/2P --- P=0,5m=50cm

11- a) P=30m --- f=-6m (convexo) --- 1/f = 1/P + 1/P’ --- -1/6=1/30 + 1/P’ --- P’=-5m (observe que para um objeto a 30m do espelho convexo, a imagem seria vista como se estivesse a 5m do mesmo, aparentando assim, ser menor).

b) No espelho plano a imagem é simétrica (objeto e imagem são eqüidistantes do espelho) e de mesmo tamanho do objeto – 30m

12- a) V=d/t --- 5=d/2 --- d=10cm

Para t = 2,0 s ë x = 10 cm. --- em t = 2,0 s, o objeto estará a 40 cm do vértice do espelho, ou seja, ele estará antes do centro de curvatura C do espelho.

Para um objeto que se encontra antes do centro de curvatura de um espelho côncavo, as características da imagem formada são: real, invertida e menor.

b) Para que a imagem se forme no infinito (imagem imprópria) o objeto deve se encontrar no foco do espelho. Portanto, ele deverá percorrer d=40 cm --- V=d/t --- 5=40/t --- t=8s.

c) Distância percorrida pelo objeto em 7 s:

V=d/t --- 5=d/7 --- d=35cm --- logo a posição do objeto será: p = 15 cm. --- calculando a posição da imagem formada usando a relação: (1/p) + (1/p') = 1/f --- utilizamos o fato de que f = R/2 ---p' = 30 cm

Em t = 7,0 s o objeto se encontra entre o foco e o Centro de Curvatura e, portanto, sua imagem será real, maior e invertida.

O cálculo do tamanho da imagem formada pode ser realizado utilizando a equação para ampliação da imagem, dada por:

A = i/o = p'/p --- i/10 = - [(30)/15] --- i = - 20 cm

Nesta equação i e o são os tamanhos da imagem e do objeto, respectivamente. O sinal negativo indica que a imagem formada é invertida.

13- Quando observava cravos e espinhas seu rosto estava entre o foco (1,5m) e o espelho, que fornecia uma imagem virtual, direita e maior. Quando colou seu rosto a 2m do espelho, ele ficou entre o foco e o centro de curvatura e, nesse caso, a imagem fica maior e invertida. R- B

14- a) P=4m --- P’=-0,2m (imagem virtual) --- 1/f = 1/P + 1/P’ --- 1/f=1/4 – 1/0,2 --- f=-4/19m --- R=2f=2.(-4/10) ---

R= (8/19) m

b) H=O=1,6m --- i=h --- i/O=-P’/P --- h/1,6=-(-0,2)/4 --- h=0,08m=8cm

15- P=90cm --- O=10i --- i/O=-P’/P --- i/10i=-P’/90 --- P’=-9cm --- 1/f=1/90-1/9 --- f=-10cm --- em módulo f=10cm R- D

16- Antes --- i=3O/4 --- i/O=-P₁’/P₁ --- (3O/4)/O = -P₁’/P₁ --- P₁’= - 3P₁/4 --- 1/f=1/P₁+ 1/P’₁ --- 1/f= 1/P₁ -4/3P₁ ---

f=-3P₁ (I) --- i=O/4 --- i/O= -P₂’/P₂ --- (O/4)/O=-P’₂/P₂ --- p₂’=-P₂/4 --- 1/f=1/P₂+ 1/P₂’ --- 1/f=1/P₂ – 4/P₂ --- f= -P₂/3 (II) --- igualando I com II --- -3P₁=-P₂/3 --- P₂=9P₁ R- A

17- Sendo a distância do Sol à Terra muito grande, os raios de luz emitidos por ele chegam à Terra como feixes de raios paralelos e a imagem P’ se forma no foco --- P’= f =1m --- P=250d --- O=d

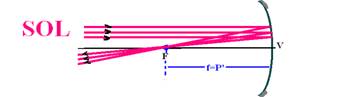
i/O = -P’/P --- i/d = - 1/250d --- i=-1/250=4.10^-3m - R- E

18- Cálculo da imagem A’ de A, conjugada pelo espelho esférico côncavo --- P=30cm --- f=20cm --- 1/f=1/P + 1/P’ --- 1/20 – 1/30=1/P’ --- P’=60cm --- observe na figura abaixo que os raios de luz emitidos por A, sofrem reflexão no espelho

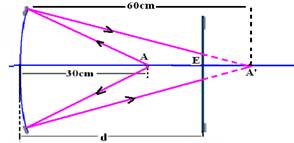
côncavo, incidem no espelho, onde são refletidos mas,a imagem se forma em A’, que se comporta como objeto virtual para o espelho plano. Os raios de luz que atingem o espelho plano devem sofrer reflexão e retornar a A.

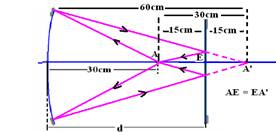
Como no espelho plano objeto e imagem são simétricos ao espelho as distâncias AE e AE’ são iguais e de 15cm cada uma. Assim, a distância pedida d vale30 + 15 --- d=45cm

19- Observe na figura abaixo que, como os raios solares incidem paralelamente ao eixo principal, eles se refletem de modo que o prolongamento dos raios refletidos se encontre no foco F’, onde está a imagem do Sol, que vai servir como objeto virtual para o espelho côncavo E’’.

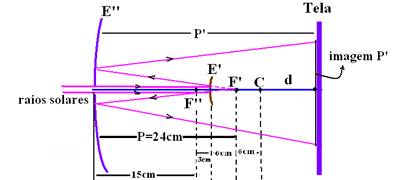
Então, para E’’, temos --- P=24cm --- P’ (distância da imagem do Sol projetada na tela por E’’) --- f=15cm --- 1/f=1/P+1/P’ --- 1/15=1/24 + 1/P’ --- 1/P’=(8 – 5)/120 --- P’=40cm --- d=40 – 30 --- d=10cm

20- Ambos os espelhos são côncavos, possuindo, então, abscissas focais positivas --- equação dos pontos conjugados --- 1/f=1/P + 1/P’ --- P´=P.f/(P – f) --- espelho da esquerda (1) --- f₁=2m --- P₁=1m --- P₁’=1 x 2/(1 – 2) --- P₁’= - 2m (imagem virtual e atrás do espelho) --- espelho da direita (2) --- f₂=5m --- P₂=1m --- P₂’=1 x 5/(1 – 5) --- P₂’= - 5/4 m (imagem virtual e atrás do espelho) --- a figura mostra as localizações objeto e imagens em relação aos espelhos --- observe que a distância D entre a

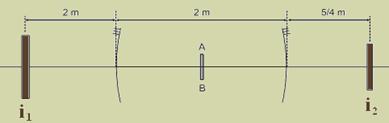
imagem da esquerda (i₁) e a da direita i₂ vale --- D=2 + 2 + 5/4 --- D=21/4 m --- R- A

21- p = 10 cm --- A = 5 --- A= - P’/P --- 5= - P’/10 --- P’=-50cm --- 1/f=1/P + 1/P’ --- 1/f=1/10 + 1/(-50) --- 1/f=(5 – 1)/50 --f=50/4 --- f=12,5cm --- R- A

22- h =o= 8 cm --- p = 80 cm --- h’ = i=1,6 cm --- i/o=-P’/P --- 1,6/8= - P’/80 --- P’= - 16cm --- 1/f=1/P + 1/P’ --- 1/f=1/80 + 1/(-16) --- f= - 20cm --- valor absoluto --- |f| = 20 cm --- R- B

23- Observe que, pelo enunciado, o farolete deve emitir raios de luz paralelos quando a lâmpada estiver localizada a 10cm do espelho esférico côncavo, ou seja, ela deve estar sobre o foco, pois os raios de luz, nessa posição emergem paralelos --- f=+10cm (I) ---

Como a imagem é projetada e ampliada 5 vezes, a imagem é invertida em relação ao objeto e, consequentemente o aumento linear transversal é negativo --- A=-5 --- A=-P’/P --- -5=-P’/P --- P’=5P (II) --- substituindo (I) e (II) na equação dos pontos conjugados --- 1/f=1/p + 1/P’ --- 1/10=1/P + 1/5P --- P=12cm --- portanto a lâmpada encontra-se 2cm adiante do foco ---

R- E

24- Observe a situação descrita ilustrada na figura abaixo --- como o raio refratado incide no

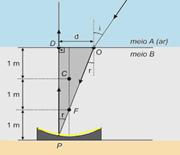
espelho passando pelo foco, ele reflete paralelo ao eixo principal --- quando um ângulo é pequeno (θ < 10°), você pode fazer a aproximação --- sen θ = tg θ = θ (radiano) --- como nesse caso i = 7° e r < i (ângulos pequenos), você pode trocar o seno pela tangente na lei de Snell ---

n_A.tg i = n_B.tg r --- 1.(0,12)=1,2.tg r --- tg r = 0,12/1,2 --- tg r = 0,1 --- observe no triângulo OPD hachurado da figura ---

tg r = d/3 --- 0,1=d/3 --- d=0,3m

25- Dados: f=R/2=1/2=0,5m=50cm --- P=50 + 10=60cm --- equação dos pontos conjugados de

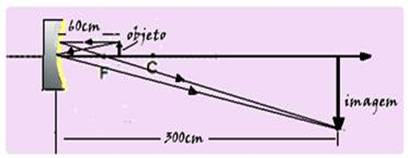
Gauss --- 1/f=1/P + 1/P’ --- 1/50=1/60 + 1/P’ --- 1/50 – 1/60=1/P’ --- (6 – 5)/300=1/P’ --- P’=300cm --- distância entre objeto e imagem --- d=300 – 60=240cm --- R- A

26- A distância focal do espelho é igual à metade de seu raio de curvatura --- f=+1/2m --- f= + 50cm (positiva porque o espelho é côncavo) --- quando o lápis estiver a 10cm do espelho – P=10cm --- equação dos pontos conjugados de Gauss --- 1/f=1/P + 1/P’ --- 1/50 – 1/10=1/P’ --- (1 – 5)/50=1/P’ --- 4P’=-50 --- P’= - 12,5cm (a imagem é virtual e está atrás do espelho e a

12,5cm dele) --- A= -P’/P=-(-12,5)/10 --- A=1,25 (a imagem é direita A>0 e 1,25 vezes maior que o objeto).

Segunda etapa --- distância (P) em que o lápis deveria estar do vértice do espelho, para que sua imagem fosse direita e ampliada cinco vezes --- A=+5 (imagem direita A>0) --- A= - P’/P --- 5= - P’/P --- P’=-5P --- 1/f=1/P + 1/P’ --- 1/50=1/P + 1/(-5P).

1/50=1/P – 1/5P --- 1/50=4/5P --- 5P=200 --- P=40cm