Dioptro Plano
Um dioptro plano é um sistema refrator que apresenta dois meios transparentes e homogêneos separados por uma superfície ou, mais especificamente consiste num conjunto de dois meios opticamente homogêneos e transparentes separados por uma superfície plana como, por exemplo,
o ar em contato com a água parada e transparente de uma piscina (dioptro plano “ar-água”)
Localização das imagens num dioptro plano
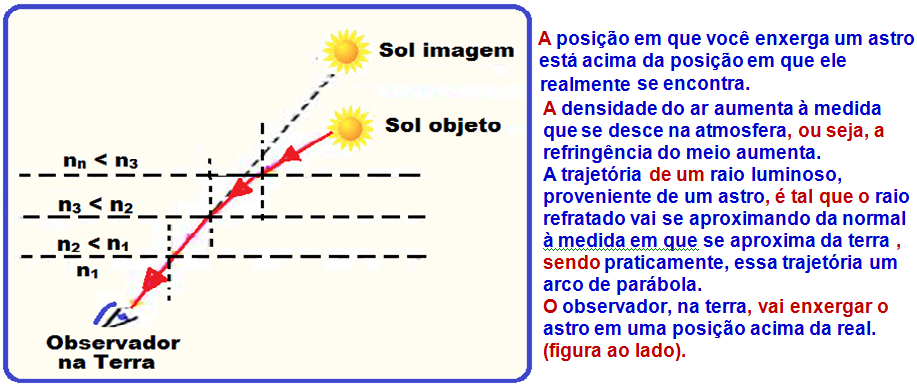
Quando observamos uma pessoa mergulhada numa piscina cheia de água, estamos observando sua imagem virtual, que está acima do objeto.
Da mesma maneira, se estivermos debaixo da água, e olharmos para um corpo fora da piscina, estaremos observando sua imagem virtual, que está acima do objeto.
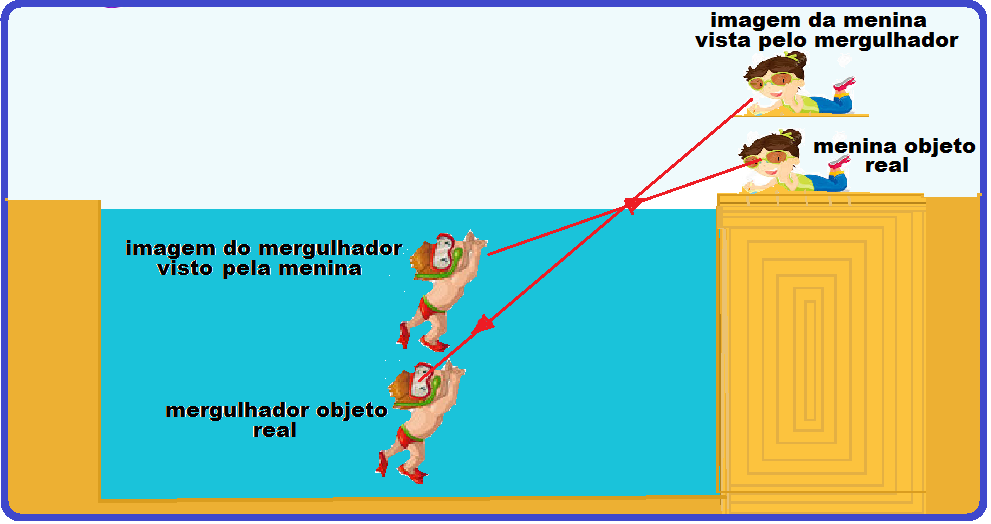
Essa posição, diferente da real, em que enxergamos a imagem virtual, chamamos de posição (ou distância) aparente.
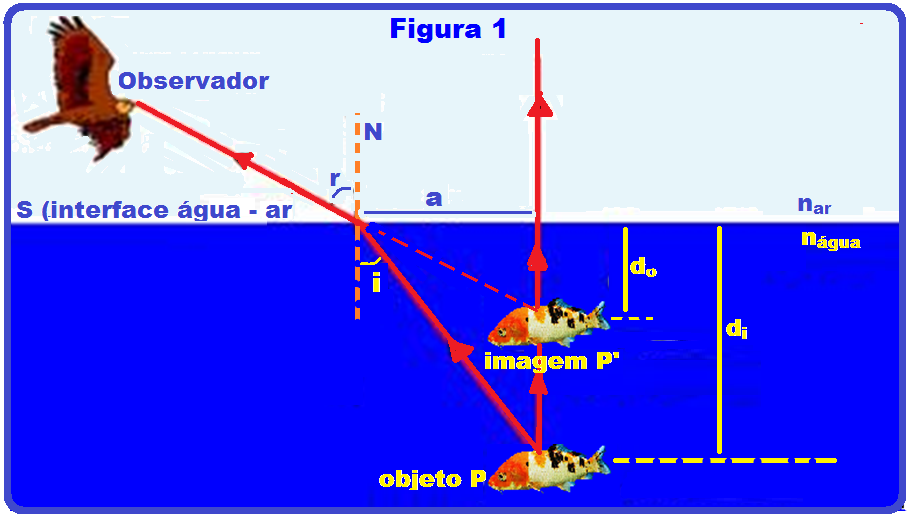
Na figura 1 o ponto objeto real P está dentro da água (mais refringente, maior índice de refração) e emitindo dois raios de luz, um vertical que não sofre desvio e o outro oblíquo que, ao se refratar para o ar, afasta-se da normal atingindo os olhos do observador e determina a imagem virtual (P’), obtida no prolongamento desse raio e onde ele intercepta o raio de luz vertical, fornecendo essa imagem P’, acima do objeto real P.
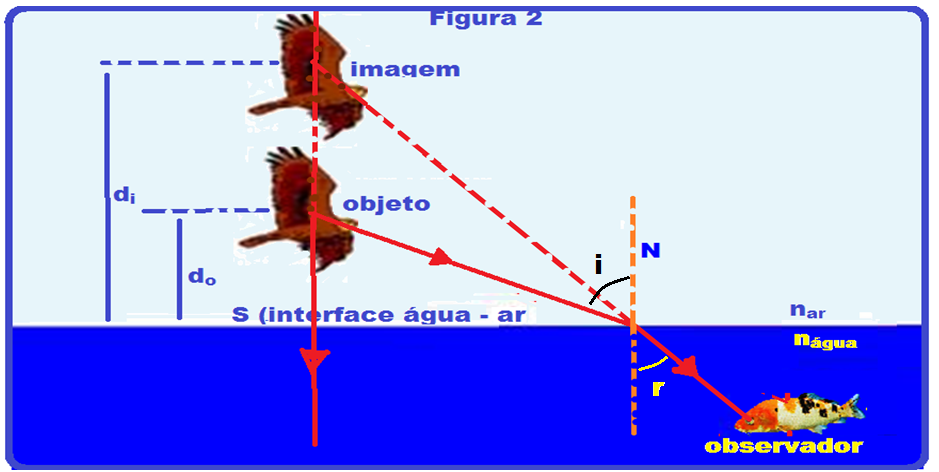
Na figura II o ponto objeto real P está no ar (menos refringente, menor índice de refração) e emitindo dois raios de luz, um vertical que não sofre desvio e o outro oblíquo que, ao refratar-se para a água aproxima-se da normal atingindo os olhos do observador e determina a imagem virtual P’, acima do objeto real P.
Observe que, em ambos os casos a imagem está sempre acima do objeto.
Dedução da equação do dioptro plano
Aplicando a lei de Snell-Descartes, por exemplo, no primeiro caso acima, temos:
n1.seni
= n2senr
(I)
considerando os ângulos
muito pequenos de modo que o observador
esteja
bem próximo da normal de
maneira que o seno
e a tangente de cada ângulo sejam aproximadamente iguais ou
seja, seni ≈ tgi ≈ a/do (II) e senr ≈ tgr ≈
a/di (III).
Substituindo
(II) e (III) em (I) n1.do
=
n2.di.
Como utilizar a equação do dioptro-plano
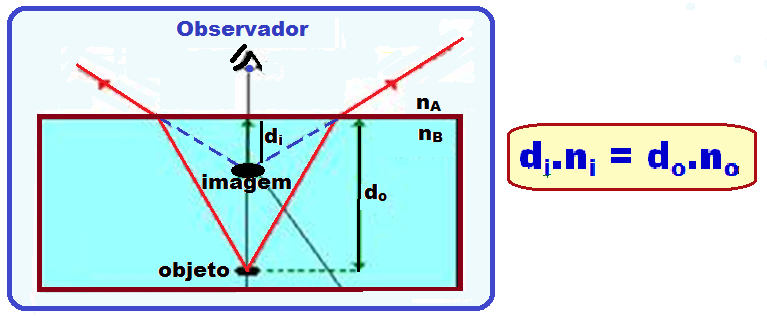
Sendo:
di
distância
vertical da imagem à superfície de separação
dos meios A e B (distância
aparente, em que o observador enxerga a imagem)
do
distância
vertical do objeto, até a superfície de separação dos
meios A e B.
no
índice
de refração do meio onde está o observador (no
caso, meio A)
ni
índice
de refração do meio onde está o objeto e a imagem
(no caso, meio B)
Um exemplo de aplicação:
De acordo com o desenho, onde você tem um peixe e uma andorinha se visualizando mutuamente. Considerando o índice de refração absoluto da água como nágua = 1,3 e o índice de refração absoluto do ar como nar = 1,0, pede-se:
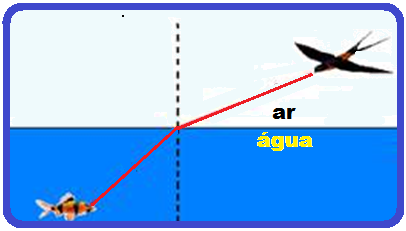
a) Determine a altura aparente com que o peixe verá a andorinha sabendo que ela se encontra a 10m da superfície livre da água.
no
índice
de refração
do meio onde está o observador,
no caso, o peixe
no
=
nágua
=
1,3.
ni
índice
de refração
do meio onde está o
objeto
e a imagem,
no
caso, o ar
ni
=nar
=
1,0.
do
distância
vertical do objeto (andorinha), até a superfície de separação
do
= 10 m.
di
distância vertical da imagem da andorinha até a superfície de
separação
di
= ?
di.ni
= do.no
di.1,0
= 10.1,3
di
= 13 m
(altura aparente da andorinha) altura de sua imagem vista pelo peixe
em relação à superfície da água.
b) Determine a profundidade aparente com que a andorinha verá o peixe sabendo que ele se encontra a uma profundidade de 2,6 m da superfície livre da água.
no
índice
de refração
do meio onde está o observador,
no caso, a andorinha
no
=
nar
=
1,0.
ni
índice
de refração
do meio onde está o
objeto
e a imagem,
no
caso, a água
ni
=
nágua
=
1,3.
do
distância
vertical do objeto (peixe), até a superfície de separação
do
= 2.6 m.
di
distância vertical da imagem do peixe até a superfície de
separação
di
= ?
di.ni
= do.no
di.1,3
= 2,6.1,0
di
= 2,6/1,3
di
= 2,0 m
(profundidade aparente do peixe em
relação à superfície)
altura aparente do peixe visto pela andorinha.
O que você deve saber, informações e dicas
Em qualquer situação a imagem está sempre acima do objeto e ambos na mesma reta vertical.
A posição da imagem depende do ponto de onde o observador estiver olhando.
Se ele estiver numa direção
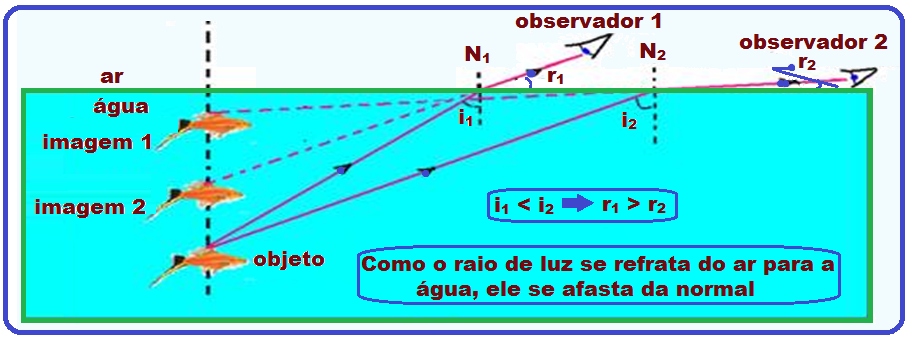
aproximadamente perpendicular à superfície da água, a expressão di.ni = do.no é sempre válida.
À medida que ele se afasta, a imagem vai parecendo cada vez mais elevada.
Um gato que observa um peixe dentro de um aquário enxerga-o mais próximo da parede do aquário (observador no ar).
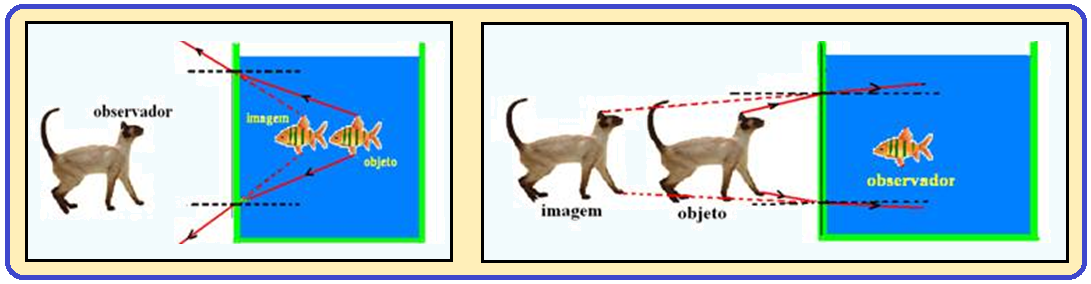
Ao mesmo tempo, o peixe observa o gato mais distante do aquário (observador na água).
Se você quiser pode resolver o exercício de número 10 com a respectiva resolução, que é sobre esse assunto.
Exercício interessante:
Exercícios de vestibulares com resoluções comentadas sobre
Dioptro Plano
01- (Ufg-GO) Um ponto luminoso, encontra-se imerso na água em uma piscina totalmente limpa, quando visto por um observador que esteja fora da piscina (no ar) e que olha com uma inclinação de
45o em relação ao eixo normal da superfície da água, é CORRETO afirmar que
(A) o ponto luminoso parecerá mais afastado da superfície da água do que realmente está.
(B) o ponto luminoso parecerá mais próximo da superfície da água do que realmente está.
(C) o fato de a luz estar mudando de meio não interfere na percepção visual do observador.
(D) a luz não irá conseguir passar da água para o ar.
(E) o ponto luminoso não será percebido pelo observador.
02-.
(UFC-CE)
Uma folha de papel, com um texto impresso, está protegida por uma
espessa placa de vidro.
O
índice de refração do ar é 1,0 e o do vidro 1,5. Se a placa tiver
3 cm de espessura, a distância do topo da placa à imagem de uma
letra do texto, quando observada na vertical, é:
03- (UFMG-MG) Qual a alternativa que melhor explica porque a profundidade aparente de uma piscina é menor do que a real?
a) A luz refletida na superfície da água é perturbada pela luz refletida pelo fundo da piscina
b) A luz refletida pela superfície da água sofre refração no ar.
c) A luz refletida pelo fundo da piscina sofre reflexão total na superfície da água.
d) A luz refletida pelo fundo da piscina sofre refração ao passar da água para o ar.
e) A luz é refratada ao passar do ar para a água.
04- MACKENZIE-SP) De acordo com o desenho a seguir, consideremos para um determinado instante a seguinte situação:
Admitindo-se que:
1) A seja uma andorinha que se encontra a 10m da superfície livre do líquido;
2) P seja um peixe que se encontra a uma profundidade h da superfície S;
3) n = 1,3 seja o índice de refração absoluto da água.
Podemos afirmar que:
a) o peixe verá a andorinha só se estiver a 10m de profundidade;
b) o peixe verá a andorinha a uma altura aparente de 5,0m;
c) o peixe verá a andorinha a uma altura aparente de 13m acima da superfície da água;
d) o peixe não verá a andorinha, pois a luz não se propaga de um meio mais refringente para outro de menor refringência
e) o peixe verá a andorinha a uma altura aparente de 26m
05- (FUVEST-SP) Um pássaro sobrevoa em linha reta e a baixa altitude uma piscina em cujo fundo se encontra uma pedra. Podemos afirmar que:
a) com a piscina cheia o pássaro poderá ver a pedra durante um intervalo de tempo maior do que se a piscina estivesse vazia;
b) com a piscina cheia ou vazia o pássaro poderá ver a pedra durante o mesmo intervalo de tempo;
c) o pássaro somente poderá ver a pedra enquanto estiver voando sobre a superfície da água;
d) o pássaro, ao passar sobre a piscina, verá a pedra numa posição mais profunda do que aquela em que ela realmente se encontra;
e) o pássaro nunca poderá ver a pedra.
06-(UNIFESP-SP) Na figura, P representa um peixinho no interior de um aquário a 13 cm de profundidade em relação à superfície da água. Um garoto vê esse peixinho através da superfície livre do aquário, olhando de duas posições O1 e O2.
Sendo nágua=1,3 o índice de refração da água e dar=1,0 o índice de refração do ar, pode-se afirmar que o garoto vê o peixinho a uma profundidade de:
a) 10 cm, de ambas as posições
b) 17 cm, de ambas as posições
c) 10 cm em O1 e 17 cm em O2
d) 10 cm em O1 e a uma profundidade maior que 10 cm em O2
e) 10cm em O1 e a uma profundidade menor que 10cm em O2
07-(ITA-SP) Um pescador deixa cair uma lanterna acesa em um lago a 10.0m de profundidade.
No fundo do lago, a lanterna emite um feixe luminoso formando um pequeno ângulo q com a vertical. Considere o índice de refração da água como 1,33 e determine a profundidade aparente h vista pelo pescador.
08-(UFU-MG) A profundidade de uma piscina é tal que sua parede, revestida com azulejos quadrados de 12 cm de lado, contém 12 azulejos justapostos verticalmente.
Um banhista, na borda da piscina, cheia de água (nágua=4/3), olhando quase perpendicularmente, verá a parede da piscina formada por:
a) 12 azulejos de 9cm de lado vertical
b) 9 azulejos de 16cm de lado vertical
c) 16 azulejos de 9cm de lado vertical
d) 12 azulejos de 12cm de lado vertical
e) 9 azulejos de 12cm de lado vertical
09-(UFRJ-RJ) Temos dificuldade de enxergar com nitidez debaixo da água porque os índices de refração da córnea e das demais estruturas do olho são muito próximos do índice de refração da água (nágua=4/3). Por isso usamos máscaras de mergulho, o que interpõe uma pequena camada de ar (nar=1) entre a água e o olho.
Um peixe está a uma distância de 2,0m de um mergulhador. Suponha o vidro da máscara plano e de espessura desprezível. Calcule a que distância o mergulhador vê a imagem do peixe.
10- (UFBA-BA) Um objeto pontual P encontra-se na base de um recipiente que contém duas camadas de líquidos, A e B, com espessuras eA=28cm e eB=39cm. Os líquidos são homogêneos, transparentes e imiscíveis. Considere o índice de
refração do ar igual a 1 e os dos líquidos A e B iguais a 1,4 e 1,3, respectivamente. Determine a altura aparente de P, vista por um observador, olhando numa direção aproximadamente perpendicular à base do recipiente.
11-(UFMS) A figura mostra um jacaré, imerso na água, o qual avança lentamente com velocidade constante e horizontal, para abocanhar um pato que flutua em repouso na superfície de um lago. Os olhos do jacaré estão no ponto O atrás do ponto N que corresponde ao nariz dele. Enquanto que os olhos do pato estão no ponto P. Considere todos esses pontos contidos no plano da página. Os três caminhos a, b, e c, mostrados na figura, representam raios de luz que saem do ponto N (nariz do jacaré) e chegam até o ponto P (olhos do pato). Considere a água transparente, parada e mais refringente que o ar. Com relação à propagação retilínea da luz, é correto afirmar:
(01) O caminho (c) pode representar um raio de luz que sai de N e chega até o ponto P.
(02) O pato vê a imagem do ponto N, mais próximo que a distância real que esse ponto se encontra do dele.
(04) Como as patas do pato estão imersas na água, a posição da imagem das patas, vista pelo jacaré, coincide com a posição real das patas na água.
(08) A velocidade da luz na água é maior que a velocidade da luz no ar.
(16) Para acontecer a reflexão total de um raio de luz que sai do ponto N, e esse ponto tornar-se invisível para o pato, o jacaré deverá aproximar-se do pato.
12-(FUVEST-SP) Certa máquina fotográfica é fixada a uma distância Do da superfície de uma mesa, montada de tal forma a fotografar, com nitidez, um desenho em uma folha de papel que está sobre a mesa.
Desejando manter a folha esticada, é colocada uma placa de vidro, com 5 cm de espessura, sobre a mesma.. Nessa nova situação, pode-se fazer com que a fotografia continue igualmente nítida
a) aumentando Do de menos de 5 cm
b) aumentando Do de mais de 5 cm
c) reduzindo Do de menos de 5 cm
d) reduzindo Do de 5 cm
e) reduzindo Do de mais de 5 cm.
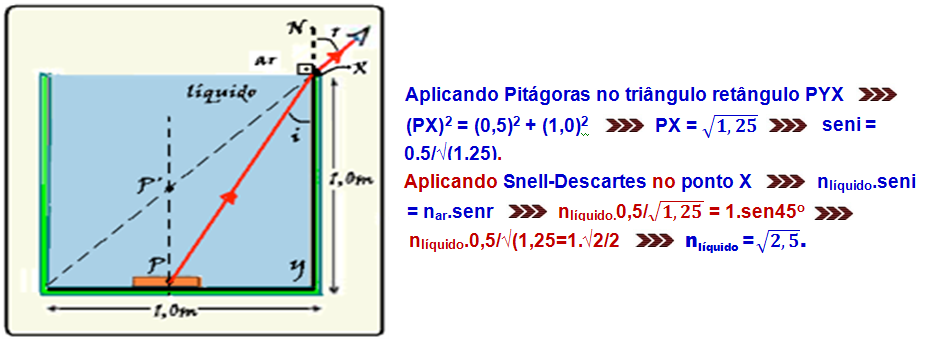
13-(UFRN-RN) Um observador, quando colocado numa posição adequada, pode ver o canto do recipiente como representado na figura abaixo.
Enchendo o recipiente com um líquido, o observador passa a ver a moeda que está colocada no centro. Qual o índice de refração do líquido? Dados: sen45o=√2/2; índice de refração do ar=1,0)
14-(UNIMAR-SP) Um observador deseja saber qual a profundidade em que se encontra um peixe flutuando na água de um tanque. Sabe-se que esse observador está olhando exatamente na posição vertical, que o índice de refração da água é 1,33, e que a distância aparente é de 3 metros. Dentre as alternativas a seguir, assinale a correta:
a) a distância real é menor que a distância aparente e vale 2,25 metros;
b) a distância real é maior e a distância aparente e vale 4,0 metros
c) a distância real é menor que a distância aparente e vale 2,5m;
d) a distância real é maior que a distância aparente e vale 2,5m
e) a distância real é maior que a distância aparente e vale 4,0m
15-(UFSCAR) Um canhão de luz foi montado no fundo de um laguinho artificial. Quando o lago se encontra vazio, o feixe produzido corresponde ao representado na figura.
Quando cheio de água, uma vez que o índice de refração da luz na água é maior que no ar, o esquema que melhor representa o caminho a ser seguido pelo feixe de luz é
16-(UNIRIO-RJ) Um cão está diante de uma mesa, observando um peixinho dentro do aquário, conforme representado na figura. Ao mesmo tempo, o peixinho também observa o cão. Em relação à parede P do aquário e às distâncias reais, podemos afirmar que as imagens observadas por cada um dos animais obedecem às seguintes relações:
a) O cão observa o olho do peixinho mais próximo da parede P, enquanto o peixinho observa o olho do cão mais distante do aquário.
b) O cão observa o olho do peixinho mais distante da parede P, enquanto o peixinho observa o olho do cão mais próximo do aquário.
c) O cão observa o olho do peixinho mais próximo da parede P, enquanto o peixinho observa o olho do cão mais próximo do aquário.
d) O cão observa o olho do peixinho mais distante da parede P, enquanto o peixinho observa o olho do cão também mais distante do aquário.
e) O cão e o peixinho observam o olho um do outro, em relação à parede P, em distâncias iguais às distâncias reais que eles ocupam na figura.
17-(UFSC-SC) A mãe zelosa de um candidato, preocupada com o nervosismo do filho antes do
vestibular, prepara uma receita caseira de "água com açúcar" para acalmá-lo. Sem querer, a mãe faz o filho relembrar alguns conceitos relacionados à luz, quando o mesmo observa a colher no copo com água, como mostrado na figura a seguir.
Sobre o fenômeno apresentado na figura acima, é CORRETO afirmar que:
(01) a luz tem um comportamento somente de partícula.
(02) a velocidade da luz independe do meio em que se propaga.
(04) a colher parece quebrada, pois a direção da propagação da luz muda ao se propagar do ar para a água.
(08) a velocidade da luz na água e no ar é a mesma.
(16) a luz é refratada ao se propagar do ar para a água.
18-(UFMS-MS) Um biólogo, na tentativa de obter o comprimento de um tubarão que está no interior de um grande aquário de vidro, observa-o atentamente do lado externo. Em um dado instante, o tubarão permanece em repouso na posição horizontal, paralelo e a uma distância de 1 m de uma das paredes de vidro transparente do aquário. Nesse momento, o biólogo está a 2 m de distância dessa parede e em frente do ponto A que está na extremidade da barbatana caudal. O biólogo permanece nessa mesma posição e gira a cabeça de um ângulo de 30° para a esquerda, e a nova linha de visada coincide com o ponto B que está na cabeça do tubarão, veja a figura. Considere o índice de refração do ar e da água iguais a 1,0 e 1,33, respectivamente, e despreze a espessura e os efeitos de refração do vidro. Com fundamentos nos fenômenos da propagação da luz em meios diferentes, assinale a(s) proposição(ões) CORRETA(S).
(Dados: sen 22° = 0,37; cos 22° = 0,93; sen 30° = 0,50; cos 30° = 0,87)
(01) A velocidade da luz vermelha é menor que a velocidade da luz violeta na água.
(02) Se o tubarão for nadando lentamente para a esquerda e na horizontal, devido ao fenômeno de reflexão total, a imagem da cabeça dele, vista pelo biólogo, desaparecerá primeiro que a imagem da cauda dele vista pelo biólogo.
(04) O fenômeno de refração da luz não acontece em meio dispersivo.
(08) O índice de refração na água, para a luz violeta, é maior que o índice de refração na água para a luz vermelha.
(16) O comprimento real do tubarão é menor que 1,60 m.
20-(UDESC-SC)
Um bastão é colocado sequencialmente em três recipientes com líquidos diferentes. Olhando-se o bastão através de cada recipiente, observam-se as imagens I, II e III, conforme ilustração a seguir, pois os líquidos são transparentes. Sendo nar, nI, nII e nIII os índices de refração do ar, do líquido em I, do líquido em II e do líquido em III, respectivamente, a relação que está correta é:
a) nar < nI < nII
b) nII < nar < nIII
c) nI > nII > nIII
d) nIII > nII > nI
e) nIII < nI < nII
21-(FUVEST-SP)
Um jovem pesca em uma lagoa de água transparente, utilizando, para isto, uma lança. Ao enxergar um peixe, ele atira sua lança na direção em que o observa. O jovem está fora da água e o peixe está 1 m abaixo da superfície. A lança atinge a água a uma
distância x = 90 cm da direção vertical em que o peixe se encontra, como ilustra a figura abaixo.
Para essas condições, determine:
a) O ângulo α, de incidência na superfície da água, da luz refletida pelo peixe.
b) O ângulo β que a lança faz com a superfície da água.
c) A distância y, da superfície da água, em que o jovem enxerga o peixe.
22-(UFF-RJ-012)
O fenômeno de reflexão interna pode ser usado para medir o índice de refração da água de uma forma simples. A figura representa, esquematicamente, um relógio imerso em água. Com a luz de um laser incidindo perperdicularmente sobre a superfície da água e variando-se o ângulo θc, a partir do qual ocorre reflexão total do raio na interface entre o vidro e o ar.
a) Obtenha o índice de refração da água em função de θc, considerando que o índice de refração do ar é aproximadamente igual a 1.
3.10 b) Calcule a velocidade da luz na água, sabendo que a velocidade da luz no vácuo é c ≈5 km/s e que o ângulo crítico θc= 48,6o.
23- (ENEM-MEC)
Alguns povos indígenas ainda preservam suas tradições realizando a pesca com lanças,
demonstrando uma notável habilidade. Para fisgar um peixe em um lago com águas tranquilas o índio deve mirar abaixo da posição em que enxerga o peixe, Ele deve proceder dessa forma porque os raios de luz:
a) refletidos pelo peixe não descrevem uma trajetória retilínea no interior da água.
b) emitidos pelos olhos do índio desviam sua trajetória quando passam do ar para a água.
c) espalhados pelo peixe são refletidos pela superfície da água.
d) emitidos pelos olhos são espalhados pela superfície da água.
e) refletidos pelo peixe desviam sua trajetória quando passam da água para o ar.
24-(FUVEST-SP)
Numa folha de papel num plano horizontal, está desenhado um círculo de centro C. Sobre a folha é colocada uma placa grossa de vidro, cobrindo metade do círculo. A figura a seguir mostra uma pessoa olhando para o círculo, com seu olho no eixo vertical OC.
A alternativa que melhor representa o que a pessoa enxerga é:
Resolução comentada dos exercícios de vestibulares sobre
Dioptro Plano
01- A imagem está sempre acima do objeto e quanto mais afastado estiver o observador, mais próxima ainda da superfície ela estará. R-B
02- A imagem está sempre acima do objeto e na vertical que os une
do=3cm -- no=1 -- di=? -- ni=1,5 --- di.ni=do.no --- di.1,5=3.1 --- di=2cm (a altura aparente, distância da imagem da letra até o topo da placa de vidro) R- B
03- R- D
04- Observe a figura abaixo e veja que a imagem está sempre acima do objeto e na mesma reta vertical:
do=10m -- di=? -- no=1,3 -- ni=1 --- di.ni=do.no --- di.1=10.1,3 --- di=13m R- C
05- A imagem está sempre acima do objeto R- A
06- di.ni=do.no --- di.1,3=13.1,0 --- di=10cm --- esta expressão só é válida para posições onde o observador esteja bem próximo à vertical que une objeto e imagem (posição O1) e, à medida que o observador for se afastando (posição O2), a imagem vai subindo R- E
07- di.ni=do.no --- di.1,33=10.1 --- di=7,5m R- C
08- Continuará vendo os 12 azulejos mas mais curtos, de altura (lado vertical) menor e valendo --- di.ni=do.no --- do=12.12=144cm
no=1 -- ni=4/3 --- di.ni=do.no --- di.3/3=144.1 --- di=108cm/12=9cm R- A
09- no=1 -- do=2,0m --- ni=4/3 --- di.ni=do.no --- di.4/3=2.1 --- di=1,5m
10- Dioptro A-B --- cálculo de d’, elevação de P para P’ em relação a S --- di.ni=do.no --- d’.1,4=28.1,3 --- d’=26cm
Diopro B-ar --- P’ torna-se objeto fornecendo uma imagem P’’, em relação a S’, que évista pelo observador --- di.ni=do.no ---
1,3=1.(26 + 39) --- d’’=65/1,3 --- d’’=50cm
11- (01) Correta – a luz sai do nariz do jacaré, sofre refração na interface água-ar aproximando-se da normal e atingindo os olhos do pato, que o enxerga na posição N.
(02) Correta – Correta, a imagem está sempre acima do objeto.
(04) Correta, pois é o mesmo meio (água).
(08) Errada – mais refringente o meio implica em maior índice de refração e menor velocidade.
(16) Errada – quanto mais afastado o pato estiver, maior será o ângulo de incidência que, para que ocorra reflexão total, deverá superar o ângulo limite.
Soma=01 + 02 + 04 = 07
12- Do deve ser aumentada, pois a máquina deve fotografar com nitidez a imagem, que está acima do objeto, de menos de 5 cm pois, ela ainda deverá estar no interior da placa de vidro R- A
13- Tomando um ponto P no centro da moeda e, com o recipiente cheio de líquido, o observador deve ver a imagem do ponto P em P’, na posição indicada na figura.
Aplicando Pitágoras no triângulo retângulo PYX --- (PX)2 = (0,5)2 + (1,0)2 --- PX=√(1,25) --- seni=0,5/√(1,25) --- aplicando Snell-Descartes no ponto X --- nlíquido.seni=nar.senr --- . nlíquido.0,5/√(1,25) = 1.sen45o --- nlíquido.0,5/√(1,25=1.√2/2 --- nlíquido=√2,5 R- D
14- di.ni=do.no --- 3.1,33=do.1 --- do=4,0m R- E
15- R- B --- à medida que a luz vai se distanciando da interface água-ar, o raio refratado vai se afastando cada vez mais da normal.
16- R- A (veja teoria)
17- (01) Falsa – a luz comporta-se como onda e partícula
(02) Falsa – a velocidade de propagação da luz depende do meio
(04) Verdadeira – ao se refratar na interface entre dois meios transparentes diferentes, a luz sofre desvio, mudando sua direção de propagação
(16) Verdadeira -
Soma=(04) + (16) = 20
18- (01) – Falsa – quando a luz policromática branca se refrata do ar para a água, quem sofre menor desvio é a cor vermelha, pois sua velocidade é maior na água
(02) Correta – à medida que ele se afasta para a esquerda, o ângulo de incidência da luz emitida pela cabeça torna-se maior que o da cauda, tornando-se maior que o ângulo limite, fazendo com que a cabeça sofra reflexão total primeiro e que desapareça primeiro que a cauda
(04) Falsa – claro que acontece, se ela não se refratasse do ar para a água, ela não se dispersaria.
(08) Correta – maior índice de refração, maior desvio
(16) Correta) – tg30o=3/comprimento do tubarão c) --- √3=3/c --- c=5,3m
Soma=(02 + 08 + 16) = 26
19- A resposta só pode estar entre as alternativas A, D ou C, pois D1 capta a luz emitida na vertical onde não sofre desvio (incidência normal), assim o indicador só pode estar na vertical. Quando se refrata do vidro (água) para o ar a luz sofre desvio, se afastando da normal, até atingir D2. A única alternativa que satisfaz é a C.
20- Lei de Snell --- nsenβ=constante --- se o índice de refração aumenta, o ângulo diminui e vice – versa --- observe nas figuras a seguir que:
R- E
21- Observe a figura abaixo --- α – ângulo de incidência --- (90 – β) – ângulo de refração:
a) Da figura, no triângulo retângulo APC --- tgα=0,9/1=0,9 --- da tabela fornecida --- α = 42o
b) Lei de Snell --- nágua.senα = nar.sen(90 – β) --- (1,3)x(0,67) = (1)xsen(90 – β) --- sen(90 – β) = 0,87 --- da tabela fornecida --- (90 – β) = 60o --- β = 30o
c) Da figura acima, no triângulo ABI --- tgβ = y/x --- tg30o=y/0,9 --- 0,58=y/0.9 --- y=0,52m
22- Dados: sen 48,6o = 0,75, cos 48,6º = 0,66.
a) Observe na figura 1, nos dois triângulos hachurados), que o ângulo de incidência da luz na superfície de separação água-
vidro vale θ --- observe na figura 2 que o ângulo de refração na interface água-vidro é φ e na interface vidro-ar, o ângulo de incidência é φ e o de refração é β --- lei de Snell-Descartes na interface água-vidro --- nágua.senθ = nvidro.senφ --- lei de Snell-Descartes na interface vidro-ar ---nvidro.senφ = nar.senβ --- nvidro.senφ = 1.senβ --- ângulo limite (L) para que ocorra reflexão total na interface vidro-ar --- senL=senφ=nmenor/nmaior=nar/nvidro=1/nvidro --- senφ=1/nvidro --- nvidro.1/nvidro = 1.senβ (II) --- senβ=1 (IV) --- β=45o --- nágua.senθc= nvidro.senφ (I)=nar.senβ=1 --- nágua.senθc=1 --- nágua=1/senθc.
b) nágua = c/Vágua --- 1/sen θc= c/Vágua --- 1/0,75=3.105/Vágua --- Vágua = 2,25.105km/s.
23- Na figura o ponto objeto real P está dentro da água e emitindo dois raios de luz, um vertical que não sofre desvio e
o outro oblíquo que, ao se refratar para o ar, afasta-se da normal atingindo os olhos do observador e determina a imagem, vista pelo observador e que é virtual (P’), e está acima do objeto real P.
R- E.
24- Como a imagem está acima do observador, ela estará mais próxima do mesmo e, devido ao campo visual maior dará ao observador a impressão de ser maior que o objeto --- R- D.