Reflexão e Refração de Ondas
Reflexão de uma onda
Uma onda sofre reflexão quando, propagando-se em um dado meio, atinge a interface de separação com outro meio e, em seguida, volta a se propagar no meio inicial.
Reflexão em meios unidimensionais
A reflexão de uma onda num meio unidimensional, como por exemplo, numa corda, pode ocorrer em duas situações:
![]() Extremidade
fixa
Extremidade
fixa ![]() A
fonte
(A) provoca
uma oscilação
completa e
a onda
se propaga com velocidade V até o ponto B que está fixo, preso,
por exemplo, a uma parede.
A
fonte
(A) provoca
uma oscilação
completa e
a onda
se propaga com velocidade V até o ponto B que está fixo, preso,
por exemplo, a uma parede.

Quando o pulso chega à B (extremidade fixa), cada ponto da corda aplica na parede uma força e, pelo princípio da ação e reação, a parede reagirá sobre cada ponto da corda com uma força de mesma intensidade, mesma direção mas sentido contrário, produzindo um pulso invertido após a reflexão, mas com a mesma velocidade V, pois o meio (corda) é o mesmo.
A amplitude A também será a mesma, supondo não haver perda de energia.
![]()
![]() Extremidade
livre
Extremidade
livre ![]() Neste
caso, quando o pulso
chega em B, cada ponto da corda não trocará forças com a parede,
pois
a argola
de
massa
desprezível e sem atrito, sobe e desce, provocando,
após
a reflexão, um pulso que retornará sem
inversão de fase,
ou
seja, idêntico ao
Neste
caso, quando o pulso
chega em B, cada ponto da corda não trocará forças com a parede,
pois
a argola
de
massa
desprezível e sem atrito, sobe e desce, provocando,
após
a reflexão, um pulso que retornará sem
inversão de fase,
ou
seja, idêntico ao

que chega, mas com a mesma velocidade V, pois o meio (corda) é o mesmo.
![]()
Reflexão em meios bidimensionais
A reflexão de uma onda num meio bidimensional, como por exemplo, na superfície da água de uma cuba, pode ocorrer em duas situações:
![]() Ondas
circulares (esféricas)
Ondas
circulares (esféricas) ![]() Quando
a ponta
de uma régua bate
continua
e periodicamente
na superfície da água origina
perturbações
circulares (ondas circulares) que
se movem
na superfície da água, afastando-se do ponto onde as perturbações
são geradas.
Quando
a ponta
de uma régua bate
continua
e periodicamente
na superfície da água origina
perturbações
circulares (ondas circulares) que
se movem
na superfície da água, afastando-se do ponto onde as perturbações
são geradas.

Como determinar o formato das ondas circulares refletidas num obstáculo
Considere
as ondas
circulares (esféricas) da
figura 1, produzidas
pela fonte F
e que incidem
no obstáculo plano P.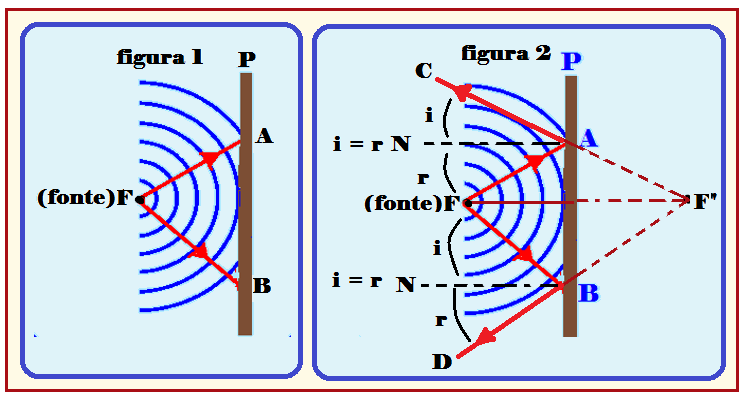
FA e FB são dois raios de onda incidentes, perpendiculares a cada frente de onda e que indicam a direção e sentido de sua propagação.
Ao atingirem o obstáculo P essas ondas sofrem reflexão de modo que cada ponto do obstáculo torna-se fonte de uma onda secundária.
Pelo princípio da reflexão os raios incidentes FA e FB sofrem reflexão e retornam (AC e BD), de modo que os ângulos i e r entre a normal N, e os raios incidente e refletido sejam iguais, ou seja, i = r (figura 2).
Então,
todos
os raios refletidos se encontram em um ponto comum F’,
e as ondas
refletidas se comportam como se fossem originadas por uma fonte F’,
simétrica de F, em relação ao obstáculo refletor P.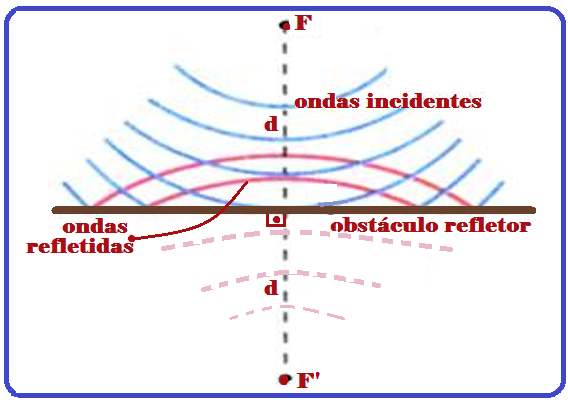
Assim, para você esquematizar as ondas refletidas, basta você localizar a fonte F’, simétrica a F e, a partir dela traçar as ondas refletidas, em vermelho na figura.
Lembre-se de que a velocidade de propagação e o comprimento de onda das ondas incidentes e refletidas são os mesmos, pois o meio é o mesmo.
A frequência também não muda, é a da fonte.
Ondas
planas (retas) ![]() Podem
ser
produzidas tocando-se
leve
e continuamente a
superfície
da água com uma régua (fonte) na posição indicada na figura.
Podem
ser
produzidas tocando-se
leve
e continuamente a
superfície
da água com uma régua (fonte) na posição indicada na figura.
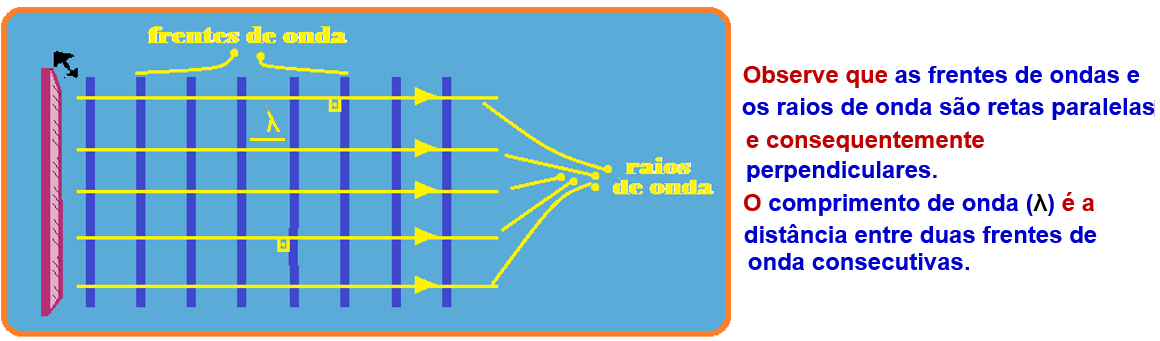
Como determinar o formato das ondas retas (planas) refletidas num obstáculo
Considere as ondas retas da figura 1, produzidas pela fonte F e que incidem no obstáculo plano P.
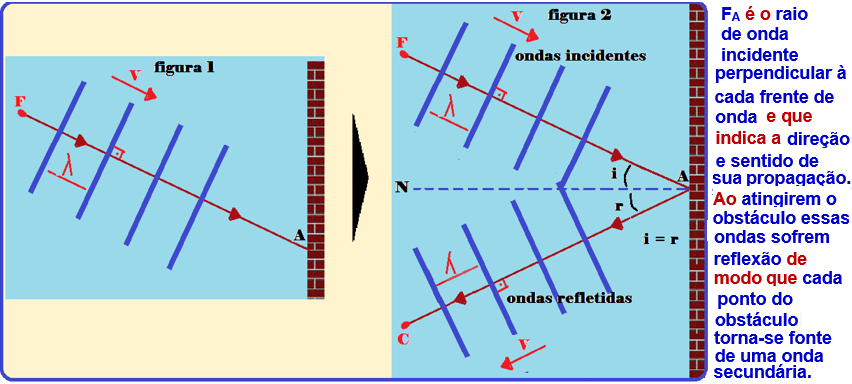
Pelo princípio da reflexão o raio incidente FA sofre reflexão e retorna (AC), de modo que os ângulos i e r entre a normal N, e o raio incidente e refletido sejam iguais, ou seja, i = r (figura 2)
Lembre-se de que a velocidade de propagação e o comprimento de onda das ondas incidentes e refletidas são os mesmos, pois o meio é o mesmo.
A frequência também não muda, é a da fonte.
O que você deve saber, informações e dicas
![]()
Conhecer o comportamento da reflexão de ondas em meios unidimensionais numa corda com extremidades fixas e livres.
![]()
Você deve saber como determinar formato das ondas retas (planas) e circulares (esféricas) refletidas num obstáculo, conforme explicado na teoria.
![]()
Não importa se o meio é uni, bi ou tridimensional, na reflexão das ondas, as ondas incidentes e refletidas tem sempre a mesma velocidade de propagação V (o meio é o mesmo), a mesma freqüência f (a fonte é a mesma) e consequentemente o mesmo comprimento de ondaλ, pois V = λ.f.
![]()
A amplitude A da onda não está relacionada com V, f e λ e sim com a energia transportada pela onda.
Quanto maior a energia, maior a amplitude e vice-versa.
Exemplos de reflexão de ondas planas:
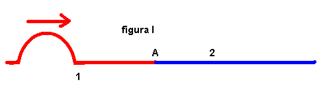
Nas figuras I, II, III e IV, estão representas as frentes de ondas retas (planas) que incidem em anteparos. Os sentidos de propagação estão representados pelas setas.
Esboce, em cada caso, as frentes de onda após a reflexão.
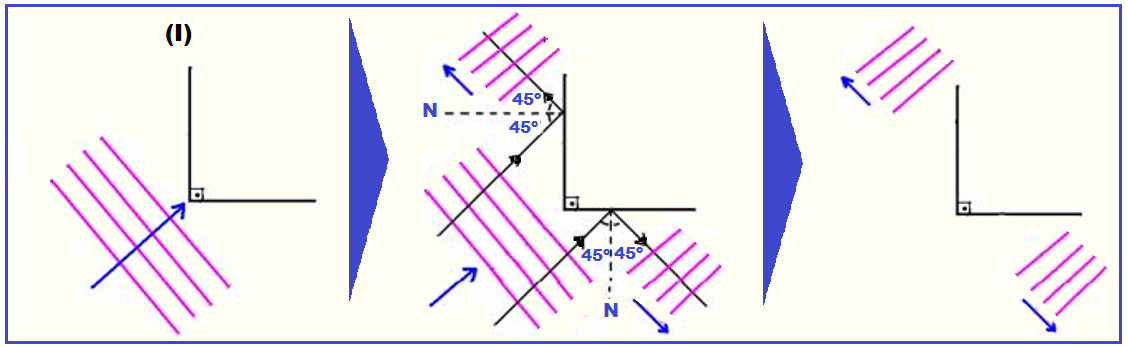
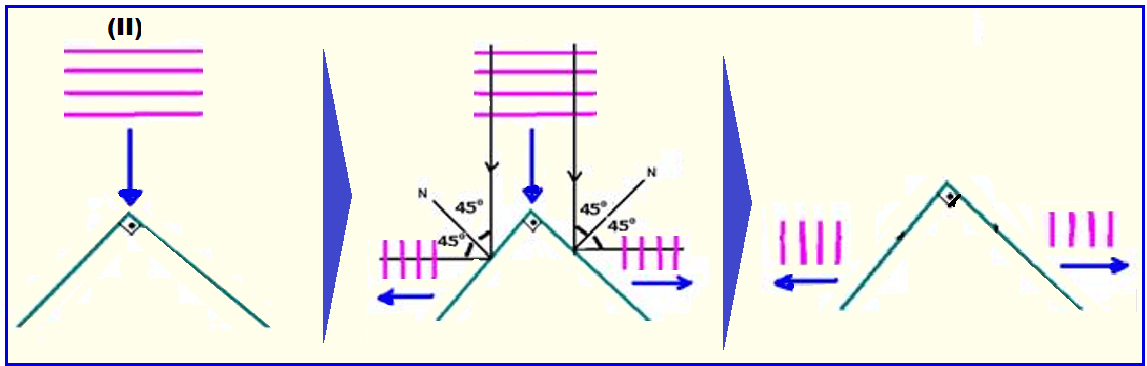
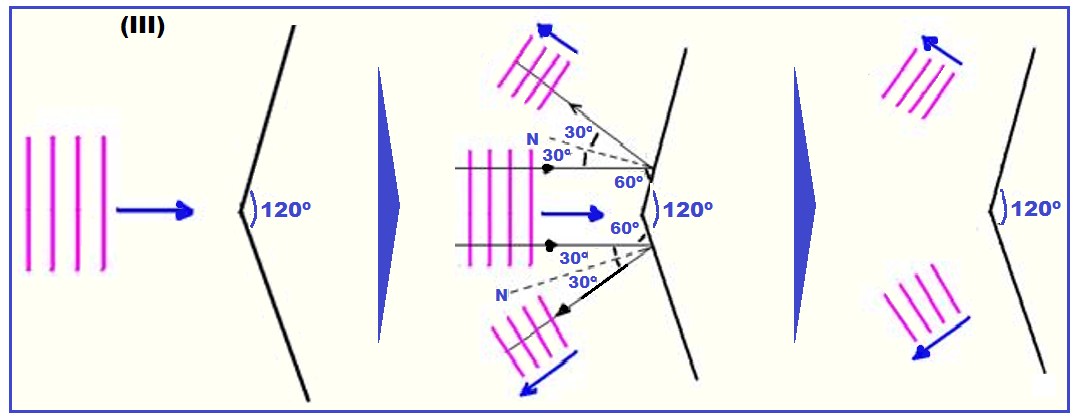
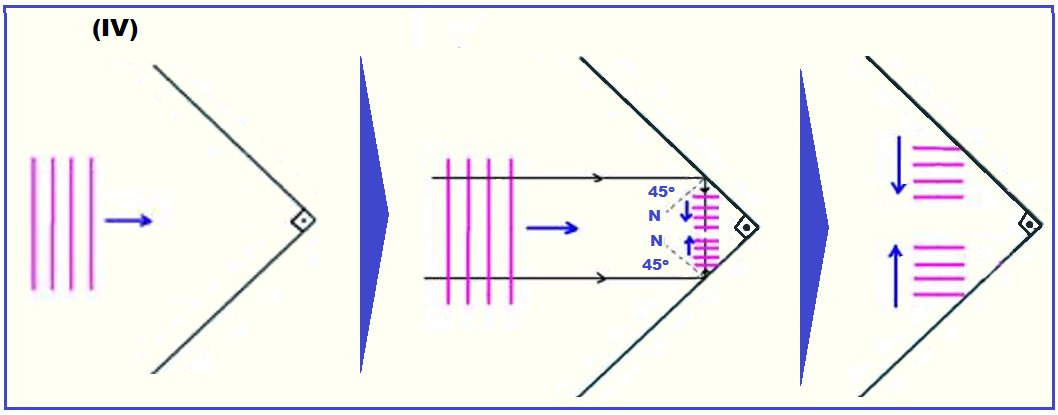
Lembre-se de que as ondas refletidas tem sempre a mesma velocidade de propagação, a mesma freqüência (da fonte) e o mesmo comprimento de onda.
Refração de ondas em meios unidimencionais
Refração de uma onda
A Refração de uma onda é um fenômeno que ocorre quando uma onda, muda seu meio inicial de propagação para outro meio de características diferentes, variando sua direção de propagação.
Considere duas cordas de diferentes densidades lineares de massa (µ = m/L), unidas, e o sistema preso numa parede com uma das extremidades fixas.
Vamos considerar três casos:
![]() 1o
caso
1o
caso
![]() A
densidade
linear (µ) das
cordas é a mesma,
ou seja, µ1
=
µ2.
A
densidade
linear (µ) das
cordas é a mesma,
ou seja, µ1
=
µ2.
Quando o pulso passa de uma corda para a outra, toda energia é transmitida, não ocorrerá reflexão e a onda continua como se estivesse no mesmo meio, mantendo todas suas

características (freqüência, amplitude, velocidade e comprimento de onda).
![]() 2o
caso
2o
caso
![]() A densidade
linear da
primeira
corda (µ1)
é maior
do que a da segunda (µ2),
ou seja, µ1
> µ2.
A densidade
linear da
primeira
corda (µ1)
é maior
do que a da segunda (µ2),
ou seja, µ1
> µ2.
Quando o pulso chega ao ponto de junção das cordas, ocorre ao mesmo tempo refração e reflexão. Esse ponto (junção) funciona como uma extremidade livre e o pulso refletido retorna sem inversão de fase.
O pulso refratado tem sempre a mesma fase do incidente.
Parte da energia do pulso incidente é transmitida ao pulso refratado e parte ao pulso refletido, diminuindo assim a amplitude desses dois pulsos, ou seja, A > A1 e A > A2.

A força de tração (T) nas duas cordas é a mesma e a velocidade em cada corda é fornecida por
![]()
Observe na expressão acima que a velocidade V é inversamente proporcional à densidade linear µ, assim, a velocidade da onda na corda mais densa “mais pesada” é menor do que a velocidade na corda menos densa “mais leve”. Então, V2 > V1.
A freqüência f é a mesma nas duas cordas, pois a fonte é a mesma.
V
= λf
![]() f
= V/λ
f
= V/λ
![]() f = V1/λ1 e
f = V2/λ2
f = V1/λ1 e
f = V2/λ2
![]() V1/λ1=
V2/λ2
(I)
V1/λ1=
V2/λ2
(I)
Observe na expressão (I) que, quanto maior a velocidade V maior o comprimento de onda λ. Portanto o comprimento de onda da corda menos densa é maior que o da corda mais densa.
![]() 3o
caso
3o
caso
![]() A
densidade
linear da
primeira corda (µ1)
é
menor do
que a da segunda (µ2),
ou
seja, µ1
< µ2.
A
densidade
linear da
primeira corda (µ1)
é
menor do
que a da segunda (µ2),
ou
seja, µ1
< µ2.
Quando o pulso chega ao ponto de junção das cordas, ocorre ao mesmo tempo refração e reflexão. Esse ponto (junção) funciona como uma extremidade fixa e o pulso refletido retorna com inversão de fase.
O pulso refratado tem sempre a mesma fase do incidente.
Parte da energia do pulso incidente é transmitida ao pulso refratado e parte ao pulso refletido, diminuindo assim a amplitude desses dois pulsos, ou seja, A > A1 e A > A2.

A freqüência (f) desses dois pulsos é a mesma, pois a fonte é a mesma. V1 > V2 e λ1 > λ2.
Refração de ondas em meios bidimensionais
Na
refração
a freqüência das
ondas
incidentes é
a mesma que
das ondas refratadas (a
fonte é a mesma) e, como V
= λf
![]() f = V/λ
f = V/λ
![]() V
e λ são diretamente proporcionais (maior
V, maior λ e vice versa).
V
e λ são diretamente proporcionais (maior
V, maior λ e vice versa).
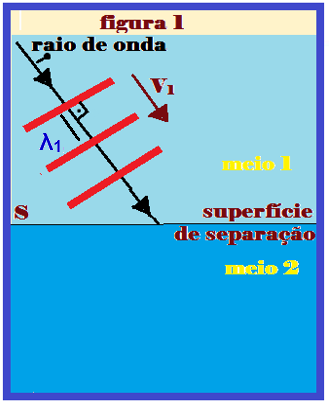
Considere dois meios diferentes 1 e 2 e ondas retas (planas) se propagando no meio 1, com velocidade V1 e comprimento de onda λ1, que vão incidir no meio 2, com velocidade V2 e comprimento de onda λ2 e, com V1 > V2. (figura I).
Sendo a velocidade da onda do meio 1 maior que a velocidade da onda no meio 2, o raio de onda, ao penetrar no meio 2 se aproximará da normal, com i > r e com λ1 > λ2.
As figuras II e III mostram as etapas da refração.
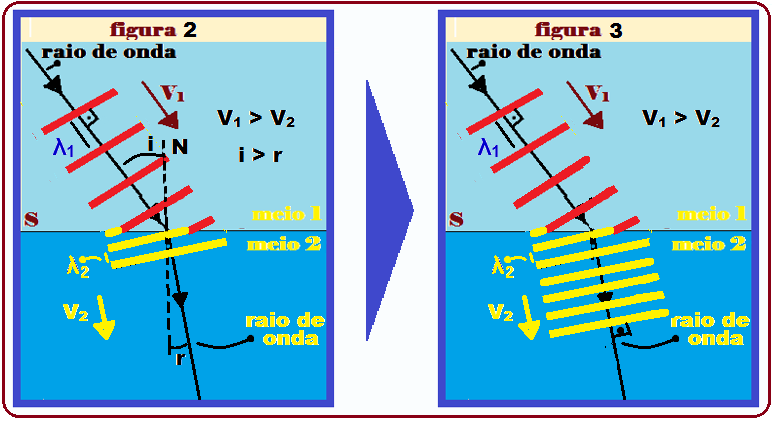
Informações e fórmulas necessárias para a resolução de exercícios sobre refração de ondas planas
Na figura abaixo, AB representa o raio de onda incidente, CD o raio de onda refratado, i o ângulo de incidência e r o ângulo de refração, bem como as relações matemáticas entre os elementos que envolvem o fenômeno da refração de ondas planas.
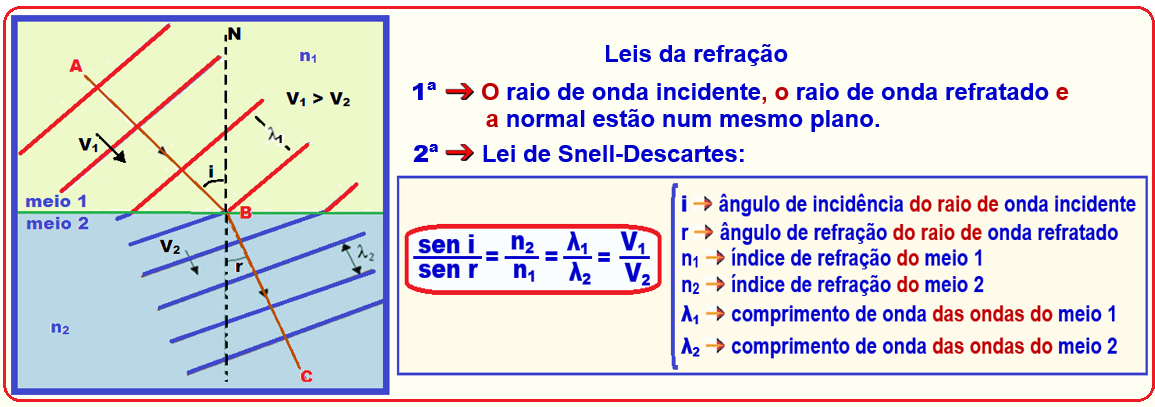

Na
refração
a freqüência das
ondas
incidentes é
a mesma que
das ondas refratadas (a
fonte é a mesma) e, como V
= λf
![]() f = V/λ
f = V/λ
![]() V
e λ são diretamente proporcionais (maior
V, maior λ e vice versa).
V
e λ são diretamente proporcionais (maior
V, maior λ e vice versa).
Baseado nas expressões acima você pode concluir que:

Observação:
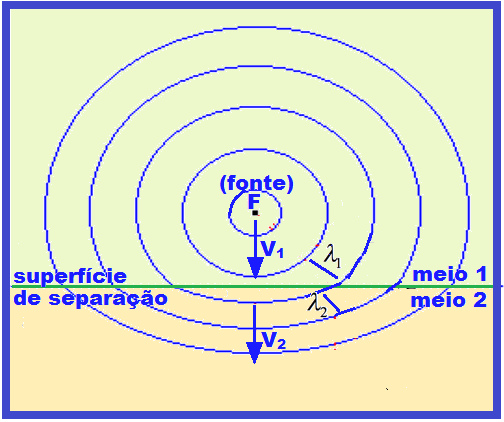
Dentro de certos limites as expressões acima também são válidas para refraação de ondas circulares (esféricas)
O que você deve saber, informações e dicas
![]()
Conhecer o comportamento da refração de ondas em meios unidimensionais numa corda, nos três casos, quando passa se deslocar em meios de diferentes densidades lineares de massa.
![]()
Você deve saber como determinar formato das ondas retas (planas) e circulares (esféricas), refratadas numa determinada superfície de separação, conforme explicado na teoria.
![]()
Informações e fórmulas necessárias para a resolução de exercícios sobre refração de ondas planas


Na
refração
a freqüência das
ondas
incidentes é
a mesma que
das ondas refratadas (a
fonte é a mesma) e, como V
= λf
![]() f = V/λ
f = V/λ
![]() V
e λ são diretamente proporcionais (maior
V, maior λ e vice versa).
V
e λ são diretamente proporcionais (maior
V, maior λ e vice versa).
Baseado na lei de Snell-Descartes n1.seni = n2.senr = constante para o mesmo sistema de meios, você conclui que n.senα = constante e que o índice de refração n de um meio é inversamente proporcional ao seno do ângulo que o raio forma com esse meio.
Consequentemente n é inversamente proporcional a α, portanto maior n, menor α.
Baseado nas expressões acima você pode concluir que:

Observação:

Dentro de certos limites as expressões acima também são válidas para refração de ondas circulares (esféricas)
![]()
Para esboçar as ondas planas refratadas num dado exercício, você deve seguir as etapas, apresentas no exemplo a seguir:
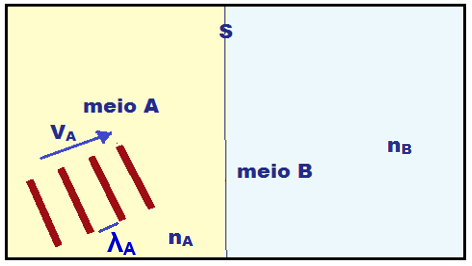
Na figura ao lado, esquematizar as ondas planas refratadas no meio B, a partir das ondas esquematizadas no meio A.
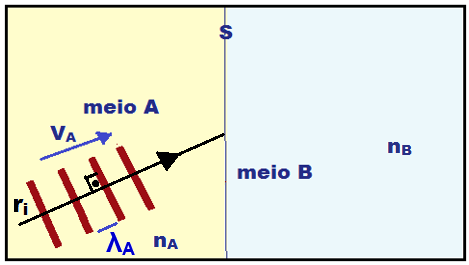
1a
etapa
![]() Traçar
o raio
de onda incidente (ri)
que é sempre perpendicular
às frentes de onda.
Traçar
o raio
de onda incidente (ri)
que é sempre perpendicular
às frentes de onda.
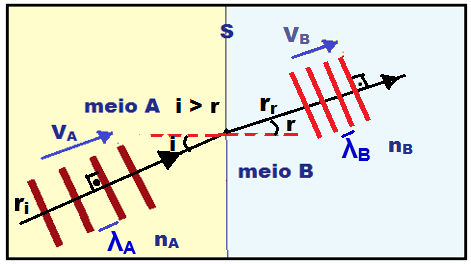
2a
etapa ![]() Traçar
o raio
de onda refratado (rr),
o
ângulo
de incidência (i), a
normal
(N) e
o ângulo
de refração (r).
Supondo
nA
<
nB,
teremos que λA
>
λB,
VA
>
VB
e
r < i (veja
informações na teoria).
Traçar
o raio
de onda refratado (rr),
o
ângulo
de incidência (i), a
normal
(N) e
o ângulo
de refração (r).
Supondo
nA
<
nB,
teremos que λA
>
λB,
VA
>
VB
e
r < i (veja
informações na teoria).
3a
etapa ![]() Utilizar a equação
fundamental da ondulatória V
= λ.f.
Utilizar a equação
fundamental da ondulatória V
= λ.f.
![]()
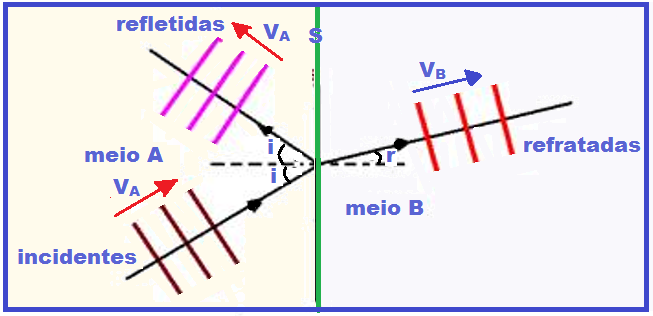
Se houver refração, sempre ocorrerá também reflexão.
![]()
As expressões:

são válidas também para ondas eletromagnéticas, como por exemplo, a luz.

![]()
A freqüência é característica da fonte e independe do meio. Assim, por exemplo, se uma fonte luminosa emitir um feixe de luz azul (freqüência 7.1014 Hz), em qualquer meio que este feixe luminoso estiver se propagando ele sempre será azul, pois terá sempre essa frequência.
O mesmo é válido para ondas.
![]()
Alguns exercícios interessantes resolvidos para que você possa se aprofundar no assunto:
Resolução:
a)
V = λ.f
![]() V = 6.50
V = 6.50
![]() V
= 300m/s.
V
= 300m/s.
b)
intervalo de tempo (Δt1)
que
a onda
demora para
ir de A
até B
![]() V
= ΔS/Δt1
V
= ΔS/Δt1
![]() 300 = 30/Δt1
300 = 30/Δt1
![]() Δt1 =1/10s
Δt1 =1/10s
c)

02-(PUCC-SP) Na superfície da água parada de um tanque quadrado de 30cm de lado, provoca-se
no
centro
do mesmo uma
onda
que se propaga com frentes de onda circulares, com
freqüência
de 5Hz e velocidade de 8cm/s.

a) Represente a configuração da frente de onda, depois de 2s de sua geração.
b) As ondas, ao se refletirem na parede do tanque retornam com, ou sem inversão de fase?
Justifique
Resolução:
a)
Cálculo
da distância
percorrida pela
onda em
2s
![]() V
= ΔS/Δt
V
= ΔS/Δt
![]() 8 = ΔS/2
8 = ΔS/2
![]() ΔS
= 16cm.
ΔS
= 16cm.
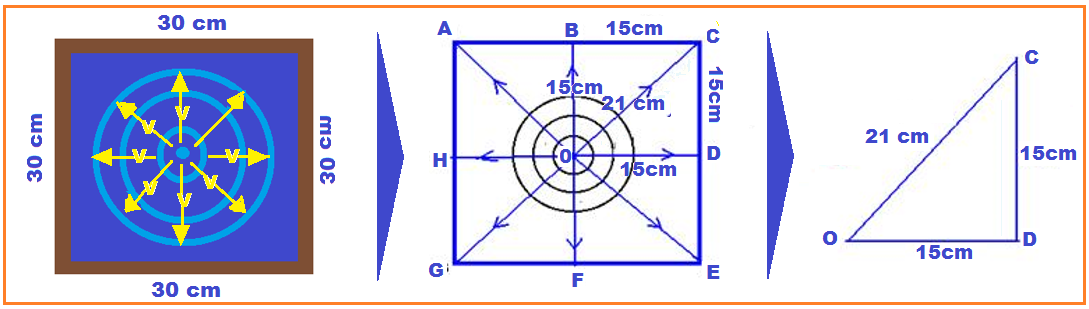
Aplicando
o teorema
de Pitágoras no
triângulo
OCD
![]() d2
= 152
+ 152
=
2.152
d2
= 152
+ 152
=
2.152
![]() d
= 15
d
= 15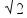 =
15.1,4
=
15.1,4
![]() d = 21 cm.
d = 21 cm.
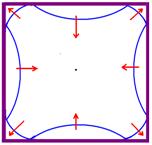
Observe nas figuras acima e na figura ao lado que, em t = 2s, a onda não chegou aos pontos A,C,E e G e que já está voltando dos pontos B, D, F e H.
b) Sem inversão de fase, pois as paredes comportam-se como extremidades livres.
03-(FUVEST-SP)
Um
canal
de navegação de 4,0m de largura tem
suas comportas
semi-abertas, como
está indicado na figura. Ondas
planas propagam-se na superfície da água do canal com
velocidade
igual a 2,0m/s.
Considere uma crista
AB,
na posição
indicada na
figura, no instante
t=0.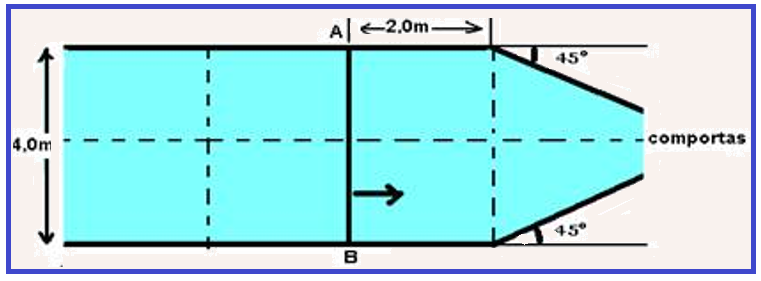
Esboce a configuração dessa crista depois de decorridos 1,5s, indicando a distância, em metros, entre seus extremos A’B’ nessa configuração (despreze efeitos da difração).
Resolução:
Vamos
calcular
a distância
percorrida por
cada
ponto da onda
no instante
t = 1,5 s
![]() V
= ΔS/Δt
V
= ΔS/Δt
![]() 2 = ΔS/1,5
2 = ΔS/1,5
![]() ΔS
= 3,0m.
ΔS
= 3,0m.
Verifique
nas
figuras abaixo que
![]() AA’
= BB’ = ΔS = 3,0m e
que PP’
= QO’ = ΔS = 3,0m.
AA’
= BB’ = ΔS = 3,0m e
que PP’
= QO’ = ΔS = 3,0m.
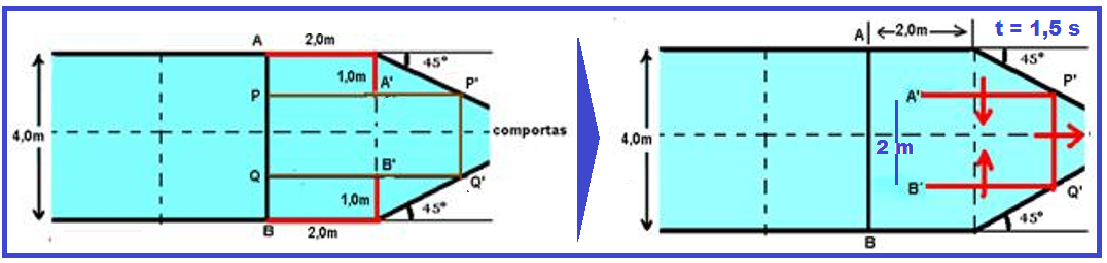
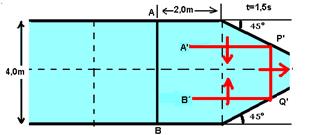
Quando t = 1,5s:
Os pontos da onda entre A’ e P’ já atingiram o anteparo e estão retornando. O mesmo acontece com os pontos da onda entre B’ e Q’.
Os pontos P’ e Q’ estão no anteparo.
Os pontos da onda entre P’ e Q’ ainda não atingiram o anteparo e estão se deslocando para a direita.
![]()
Se você deseja ainda mais se aprofundar no assunto confira as resoluções dos exercícios de números 03, 04, 06, 11, 17, 24, 32, 38 e 43.
Exercícios de vestibulares com resoluções comentadas sobre
Reflexão e Refração de ondas
01-(UNIFESP-SP) A figura representa um pulso se propagando em uma corda.
Pode-se
afirmar que, ao atingir a extremidade dessa corda, o pulso se reflete
a) se a extremidade for fixa e se extingue se a extremidade for livre.
b) se a extremidade for livre e se extingue se a extremidade for fixa.
c) com inversão de fase se a extremidade for livre e com a mesma fase se a extremidade for fixa.
d) com inversão de fase se a extremidade for fixa e com a mesma fase se a extremidade for livre.
e) com mesma fase, seja a extremidade livre ou fixa.
02-FGV-SP) A figura mostra um pulso que se aproxima de uma parede rígida onde está fixada a corda. Supondo que a superfície reflita perfeitamente o pulso, deve-se esperar que no retorno, após uma reflexão, o pulso assuma a configuração indicada em

03-(UFC-CE) A figura mostra duas fotografias de um mesmo pulso que se propaga em uma corda de 15m de comprimento e densidade linear uniforme, tensionada ao longo da direção x. As fotografias foram tiradas em dois instantes de tempo, separados de 1,5s. Durante esse intervalo de tempo o pulso sofreu uma reflexão na extremidade da corda que está fixa na parede P.

Observando as fotografias, verificamos que a velocidade de propagação do pulso na corda, suposta constante é:
![]()
04-(UFOP-MG) A figura mostra, num determinado instante, um pulso simétrico propagando-se para a direita, ao longo de uma corda tensa, comprida e fixa em P. Dois pontos A e B, simétricos em relação ao ponto médio do pulso, são mostrados na figura.

a) Represente os vetores velocidade dos pontos A e B no instante considerado.
b) Desenhe o pulso após sua reflexão considerando a corda fixa em P.
c) Considere outros dois pontos em relação ao ponto médio do pulso refletido e represente, como no item a, seus vetores velocidade.
05-(UFF-RJ) A figura representa a propagação de dois pulsos em cordas idênticas.e homogêneas. A extremidade esquerda da corda, na situação I, está fixa na parede.e, na situação II, está livre para deslizar, com atrito desprezível, ao longo de uma haste.


Identifique a opção em estão mais bem representados os pulsos refletidos nas situações I e II.

06-(UCS-BA) O esquema representa um pulso que se propaga numa mola de extremidade fixa. A seta indica o sentido de propagação.

Dentre os esquemas a seguir, o que corresponde ao pulso refletido é:

07-(FATEC-SP) Um pulso reto P propaga-se na superfície da água em direção a um obstáculo M rígido, onde se reflete. O pulso e o obstáculo estão representados na figura. A seta indica o sentido de propagação de P.

Assinale a alternativa contendo a figura que melhor representa P depois de sua reflexão em M.

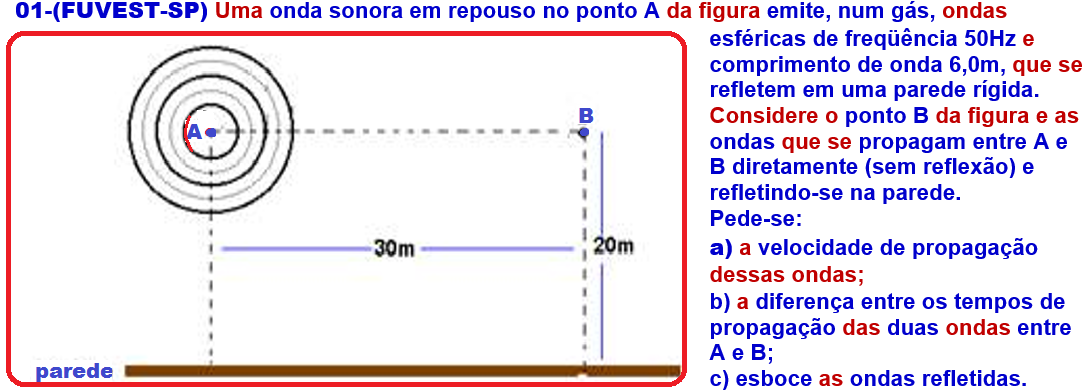
08-(FUVEST-SP) Uma onda sonora em repouso no ponto A da figura emite, num gás, ondas
esféricas
de freqüência 50Hz e comprimento de onda 6,0m, que se refletem em
uma parede rígida. Considere o ponto B da figura e as ondas que se
propagam entre A e B diretamente (sem reflexão) e refletindo-se na
parede.
Pede-se:
a) a velocidade de propagação dessas ondas;
b) a diferença entre os tempos de propagação das duas ondas entre A e B;
c) esboce as ondas refletidas.
09-(FATEC-SP) A figura representa as cristas de uma onda propagando-se na superfície da água em direção a uma barreira.

È correto afirmar que, após a reflexão na barreira,
a) a freqüência das ondas aumenta
b) a velocidade da onda diminui
c) o comprimento da onda aumenta
d) o ângulo de reflexão é igual ao ângulo de incidência
e) o ângulo de reflexão é menor que o ângulo de incidência
10-(UFB) Nas figuras I, II, III e IV, estão representas as frentes de ondas retas (planas) que incidem em anteparos. Os sentidos de propagação estão representados pelas setas. Esboce, em cada caso, as frentes de onda após a reflexão.

11-(UFB)
A
figura representa as cristas de ondas circulares (esféricas) cuja
fonte F que as produz tem freqüência de 30Hz.
Pede-se para essas ondas:
a) A velocidade de propagação das ondas incidentes.
b) A velocidade de propagação das ondas refletidas.
c) A freqüência das ondas refletidas.
d) O comprimento de onda das ondas refletidas.
e) Esboce as ondas refletidas.
12-(PUCC-SP) Na superfície da água parada de um tanque quadrado de 30cm de lado, provoca-se no centro do mesmo uma onda que se propaga com frentes de onda circulares,com freqüência de 5Hz e velocidade de 8cm/s. Represente a configuração da frente de onda, depois de 2s de sua geração.

a) Represente a configuração da frente de onda, depois de 2s de sua geração.
b) As ondas, ao se refletirem na parede do tanque retornam com, ou sem inversão de fase? Justifique
13-(UFB) As frentes de ondas sucessivas emitidas por uma fonte F, possuem velocidade de 10m/s, incidem no anteparo A da figura, onde está representado o raio de onda incidente, e são refletidas.

a) Determine o comprimento de onda das ondas refletidas.
b) Qual é a freqüência das ondas refletidas?
c) Represente numa figura, o raio de onda refletido, os ângulos de incidência e de reflexão e as frentes de ondas refletidas.
14-(FUVEST-SP) Um canal de navegação de 4,0m de largura tem suas comportas semi-abertas, como está indicado na figura. Ondas planas propagam-se na superfície da água do canal com velocidade igual a 2,0m/s. Considere uma crista AB, na posição indicada na figura, no instante t=0.

Esboce a configuração dessa crista depois de decorridos 1,5s, indicando a distância, em metros, entre seus extremos A’B’ nessa configuração (despreze efeitos da difração).
15-(Mackenzie-SP)
A
figura mostra uma onda transversal periódica, que se propaga com
velocidade v1 =
8 m/s em uma corda AB, cuja densidade linear é µ1.
Esta corda está ligada a uma outra BC, cuja densidade é m2,
sendo que a velocidade de propagação da onda nesta segunda corda é
v2 =
10 m/s.
O comprimento de onda quando a onda se propaga na corda BC
é igual a:

a) 7m
b) 6m
c) 5m
d) 4m
e) 3m
16-(UFV-MG) A figura mostra uma onda transversal periódica, que se propaga com velocidade V1=12m/s, numa corda AB de comprimento 1,5m, cuja densidade linear é m1. Essa corda está ligada a uma outra, BC, cuja densidade linear é m2, sendo a velocidade de propagação da onda V2=8m/s. Calcule:
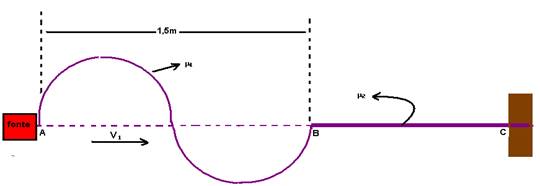
a) O comprimento da onda quando se propaga na corda BC.
b) A freqüência da onda.
17-(UFU-MG)
Sabe-se
que a velocidade V de propagação de uma onda em uma corda é dada
por V= F/µ,
em que F é a tensão na corda e µ, a densidade linear de massa
da corda (massa por unidade de comprimento).
F/µ,
em que F é a tensão na corda e µ, a densidade linear de massa
da corda (massa por unidade de comprimento).
Uma corda grossa tem uma de suas extremidades unidas à extremidade de uma corda fina. A outra extremidade da corda está amarrada a uma árvore. Clara segura a extremidade livre da corda grossa.
Fazendo oscilar a extremidade da corda quatro vezes por segundo, Clara produz uma onda que se propaga em direção à corda fina. Na sua brincadeira, ela mantém constante a tensão na corda. A densidade linear da corda grossa é quatro vezes maior que a da corda fina. Considere que as duas cordas são muito longas.
Com base nessas informações:
a) determine a razão entre as freqüências das ondas nas duas cordas e justifique sua resposta;
b) determine a razão entre os comprimentos de onda das ondas nas duas cordas.
18- (Mackenzie-SP) Com relação ao movimento ondulatório, podemos afirmar que:
a)
a velocidade de propagação da onda não depende do meio de
propagação.
b) a onda mecânica, ao se propagar, carrega consigo
as partículas do meio.
c) o comprimento de onda não se altera
quando a onda muda de meio.
d) a freqüência da onda não se
altera quando a onda muda de meio.
e) as ondas eletromagnéticas
somente se propagam no vácuo.
19-(UFB) Considere as duas cordas 1 e 2 (figura I), de densidades lineares diferentes e ponto A é a junção dessas duas cordas.

Um pulso incidente é gerado em uma delas e, ao atingir A, gera outros dois, cujo perfil das ondas é mostrado na figura II, 2s após o pulso incidente ter atingido A.

Pede-se:
a) Copie a figura I, esboce o pulso e justifique sua resposta.
b) Calcule a intensidade da força de tração T nas duas cordas sabendo que a densidade linear de massa da corda 1 é µ1=0,1g/cm.
c) Calcule a densidade linear de massa da corda 2.
20-
(UFF-RJ)
Uma
onda se propaga no meio 1, não dispersivo, com velocidade v1,
freqüência f1,
e comprimento de onda λ1.
Ao penetrar no meio 2, sua velocidade de propagação v2 é
três vezes maior que v1,
sua freqüência é f2 e
seu comprimento de onda é λ2
Logo,
conclui-se que:
a) ![]() 2 =
2 = ![]() 1/3
e f2 =f1.
1/3
e f2 =f1.
b) ![]() 2 =
2 = ![]() 1 e
f2 =
3f1.
1 e
f2 =
3f1.
c) ![]() 2 =
2 = ![]() 1 e
f2 =
f1
1 e
f2 =
f1
d) ![]() 2 =
3
2 =
3 ![]() 1 e
f2 =
f1.
1 e
f2 =
f1.
e) ![]() 2 =
2 = ![]() 1 e
f2 =
f1/3
1 e
f2 =
f1/3
21-(UNESP-SP) A figura representa uma onda periódica I que atinge a superfície de separação S entre dois meios. Representa também outros dois trens de ondas, X e Y, a serem identificados, e a linha pontilhada representa a normal à superfície de separação S.

Os dois trens de ondas X e Y correspondem, respectivamente, a ondas:
a) refletida e refratada
b) refletida e difratada
c) refratada e refletida
d) difratada e refratada
e) refletida e polarizada
22- (Unirio-RJ) Um vibrador produz ondas planas na superfície de um líquido com freqüência f = 10 Hz e comprimento de onda l= 28 cm. Ao passarem do meio I para o meio II, como mostra a figura, foi verificada uma mudança na direção de propagação das ondas.

Dados:
sen30° = cos60° = 0,5 sen60° = cos30° = ![]() sen60° = cos30° =
sen60° = cos30° = ![]() sen45° = cos45° =
sen45° = cos45° = ![]() e
considere
e
considere ![]() =
1,4
=
1,4
No meio II os valores da freqüência e do comprimento de onda serão, respectivamente, iguais a:
a)10
Hz; 14 cm.
b) 10 Hz; 20 cm.
c) 10 Hz; 25 cm.
d) 15 Hz;
14 cm.
e) 15 Hz; 25 cm.
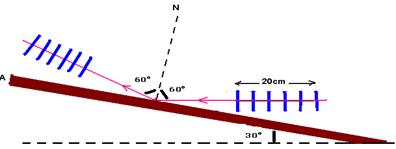
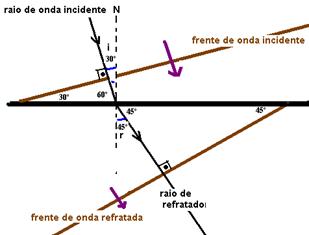
23- (UFG) Um feixe estreito de luz monocromática, propagando-se inicialmente no ar, penetra em um meio transparente, formando ângulos de 60° e 30° com a normal, como ilustrado na figura a seguir.

Dados:
Índice de refração do ar = 1,00
Velocidade da luz no vácuo e no ar = 3 × 108 m/s
Comprimento de onda da luz no ar = 633 nm
Calcule o comprimento de onda da luz no novo meio.
24-(UFC) A figura a seguir mostra frentes de onda passando de um meio 1 para um meio 2. A velocidade da onda no meio 1 é V1= 200,0 m/s, e a distância entre duas frentes de ondas consecutivas é de 4,0 m no meio 1.

Considere senθ1= 0,8 e senθ2 = 0,5 e determine:
a) os valores das freqüências f1, no meio 1, e f2 no meio 2.
b) a velocidade da onda no meio 2.
c) a distância d entre duas frentes de ondas consecutivas no meio 2.
d) o índice de refração n2 do meio 2.
25-(UFF-RJ) Sabe-se que a velocidade de propagação de uma onda eletromagnética depende do meio em que a mesma se propaga. Assim sendo, pode-se afirmar que uma onda eletromagnética na região do visível, ao mudar de um meio para outro:
a) tem a velocidade de propagação alterada, bem como a sua freqüência.
b) tem a sua cor alterada, permanecendo com a mesma freqüência.
c) tem a velocidade de propagação alterada, bem como a freqüência e o comprimento de onda.
d) tem a velocidade de propagação alterada, bem como o seu comprimento de onda.
e) tem a sua cor inalterada, permanecendo com o mesmo comprimento de onda.
26-(UFMG-MG) Quando uma onda sonora incide na superfície de um lago, uma parte dela é refletida e a outra é transmitida para a água. Sejam fi a freqüência da onda incidente, fr a freqüência da onda refletida e ft a freqüência da onda transmitida para a água.
Considerando-se essas informações, é CORRETO afirmar que
a) fr = f i e ft > f i .
b) fr < f i e ft > f i .
c) fr = f i e ft = f i .
d) fr < f i e ft = f i .
27-(PUC-PR) Na figura a seguir é mostrada uma piscina que possui uma metade mais funda que a outra. Um trem de frentes de ondas planas propaga-se da parte rasa (esquerda) para a parte mais funda (direita).
Observe a figura e analise as afirmativas a seguir.

I. A velocidade da onda é maior na metade mais funda da piscina;
II. A freqüência da onda é a mesma nas duas metades da piscina;
III. A figura ilustra o fenômeno ondulatório denominado difração;
IV. A onda sofre uma inversão de fase ao passar para a metade mais profunda;
Marque a alternativa correta:
a) I e II.
b) Apenas I.
c) I, II e III.
d) II e IV.
e) I, II e IV.
28-(UFR-RJ) A figura mostra frentes de uma onda, correspondendo a máximos sucessivos, passando de um certo meio 1 para um certo meio 2. A distância entre os máximos sucessivos no meio 1 é de 2,0 cm. No meio 1, esta distância é percorrida pelas frentes de onda em 0,5 s.

Calcule:
a) A freqüência da onda.
b) A velocidade da onda no meio 2.
29-(UFBA) A figura mostra, esquematicamente, as frentes de ondas planas, geradas em uma cuba de ondas, em que duas regiões, nas quais a água tem profundidades diferentes, são separadas pela superfície imaginária S. As ondas são geradas na região I, com freqüência de 4Hz, e se deslocam em direção à região II. Os valores medidos, no experimento, para distâncias entre duas cristas consecutivas nas regiões I e II valem, respectivamente, 1,25cm e 2,00cm.

Com base nessas informações e na análise da figura, dê a soma dos números das afirmativas corretas:
(01) O experimento ilustra o fenômeno da difração de ondas.
(02) A freqüência da onda na região II vale 4Hz.
(04) O comprimento de onda, nas regiões I e II, valem, respectivamente, 2,30cm e 4,00cm.
(08) A velocidade da onda, na região II, é maior do que na região I.
(16) Seria correto esperar-se que o comprimento de onda fosse menor nas duas regiões, caso a onda gerada tivesse freqüência maior do que 4Hz.
30- (UNB-DF) Considere a situação em que uma onda se propaga do meio I para o meio II, sendo que q velocidade de propagação V1 é maior que a velocidade de propagação V2, no meio II. Representando por fo a freqüência da fonte e por λ1 e λ2 os comprimentos de onda nos meios I e II, respectivamente, julgue os itens abaixo:
(01) Como VI>VII, então λ1 > λII.
(02) A freqüência fo é a mesma para ambos os meios.
(03) Um pulso se propagando do meio I para o meio II é parcialmente refletido na junção dos dois meios.
(04) Ao se propagar do meio II para o meio I, a luz jamais sofrerá reflexão total.
(05) O fato de as ondas quebrarem na praia não está relacionado com a variação da profundidade do mar.
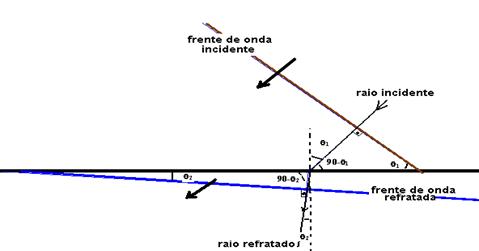
31-(UNESP-SP) Uma onda plana de freqüência f=20Hz, propagando-se com velocidade V1=340m/s no meio 1, refrata-se ao atingir a superfície de separação entre o meio 1 e o meio 2, como indicado na figura.

Sabendo-se que as frentes de onda plana incidente e refratada formam, com a superfície de separação, ângulos de 30o e 45o, respectivamente, determine, utilizando a tabela seguinte:

a) Velocidade V2 da onda refratada no meio 2
b) O comprimento de onda l2 da onda refratada no meio 2.
32-(FUVEST-SP) A curva da figura 1 mostra a dependência do índice de refração n de uma substância transparente com a freqüência F da luz. Três raios de luz, 1, 2 e 3, paralelos, incidem segundo um ângulo de 45osobre a superfície plana de um bloco da substância e são refratados, conforme indicado na figura 2.


Denominando f1, f2 e f3 as freqüências dos raios 1, 2 e 3, respectivamente, se conclui que:
a) f3 < f2 < f1
b) f1 < f2< f3
c) f2 < f1< f3
d) f2 < f3 < f1
e) f2< f3<< f1
33- (PUC-RJ)

Uma
onda eletromagnética se propaga no vácuo e incide sobre uma
superfície de um cristal fazendo um ângulo de θ1 =
60º com a
direção normal a superfície. Considerando a velocidade de propagação da onda no vácuo como c = 3 x 108 m/s e sabendo que a onda refratada faz um ângulo de θ2 = 30º com a direção normal, podemos dizer que a velocidade de propagação da onda no cristal em m/s é: (o índice de refração do vácuo é nv=1)
![]()
34- (UPE-PE)

Próxima
à superfície de um lago, uma fonte emite onda sonora de frequência
500 Hz e sofre refração na água. Admita que a velocidade de
propagação da onda no ar seja igual a 300 m/s, e, ao se propagar na
água, sua velocidade é igual a 1500 m/s. A razão entre os
comprimentos de onda no ar e na água vale aproximadamente
a) 1/3
b) 3/5
c) 3
d) 1/5
e) 1
35-(FAMECA-SP)


Para
diagnosticar uma lesão em determinado tecido humano, é usado um
ultrassonógrafo cujas ondas vibram com frequência de 1015 kHz.
Essas ondas percorrem 1,0 cm de tecido em 0,1 ms. O comprimento
de onda dessas ondas é, em Ǻ, da ordem de (1 angstrom = 1 Ǻ
= 10-10 m)
a) 10-5.
b) 10-3.
c) 10-1.
d) 10.
e) 103.
36-(FMJ-SP)

Um
feixe de luz monocromática vermelha propaga-se pelo ar e incide
sobre a superfície da água de uma piscina. Considerando as
propriedades ondulatórias da luz, pode-se afirmar corretamente que,
quando o feixe passa a propagar-se pela água,
a) tem sua cor alterada devido à variação de sua velocidade de propagação.
b) mantém sua velocidade de propagação e sua frequência inalteradas.
c) sofre aumento em seu comprimento de onda.
d) tem seu comprimento de onda diminuído e sua frequência aumentada.
e) sofre diminuição em sua velocidade e mantém inalterada sua cor.
37-(MACKENZIE-SP)

Um
estudante, ao fazer a experiência em que um feixe de luz
monocromático vai da água, de índice de refração 1,3, para o ar,
de índice de refração 1,0, pode concluir que, para essa onda,
a) o comprimento de onda diminui e a velocidade aumenta.
b) o comprimento de onda e a frequência da luz diminuem.
c) a frequência aumenta, mas o comprimento de onda diminui.
d) a frequência não se altera e o comprimento de onda diminui.
e) a frequência não se altera e o comprimento de onda aumenta.
38-(UFPR-PR) O primeiro forno de micro-ondas foi patenteado no início da década de 1950 nos Estados Unidos pelo engenheiro eletrônico Percy Spence. Fornos de micro-ondas mais práticos e eficientes foram desenvolvidos nos anos 1970 e a partir daí ganharam grande
popularidade,
sendo amplamente utilizados em residências e no comércio. Em geral,
a frequência das ondas eletromagnéticas geradas em um forno de
micro-ondas é de 2.450 MHz. Em relação à Física de um forno de
micro-ondas, considere as seguintes afirmativas:
1. Um forno de micro-ondas transmite calor para assar e esquentar alimentos sólidos e líquidos.
2. O comprimento de onda dessas ondas é de aproximadamente 12,2 cm.
3. As ondas eletromagnéticas geradas ficam confinadas no interior do aparelho, pois sofrem reflexões nas paredes metálicas do forno e na grade metálica que recobre o vidro da porta.
Assinale a alternativa correta.
a) Somente a afirmativa 1 é verdadeira.
b) Somente a afirmativa 2 é verdadeira.
c) Somente a afirmativa 3 é verdadeira.
d) Somente as afirmativas 1 e 2 são verdadeiras.
e) Somente as afirmativas 2 e 3 são verdadeiras.
39-(UFOP-MG)
Uma
criança está brincando com um xilofone ao lado de uma piscina. Num
dado instante, com uma baqueta,ela bate em uma das
varetas metálicas do instrumento musical, produzindo, assim, uma nota musical de frequência 160 Hz. Considerando que a velocidade do som é de 340 m/s no ar e de 1.450 m/s na água, determine:
a) o comprimento de onda desse som no ar;
b) a frequência desse som ao atingir o ouvido do pai da criança, que está totalmente submerso na piscina;
c) o comprimento de onda desse som na água.
40-(UFF-RJ)




As figuras a seguir mostram duas ondas eletromagnéticas que se propagam do ar para dois materiais transparentes distintos, da mesma espessura d, e continuam a se propagar no ar depois de atravessar esses dois materiais. As figuras representam as distribuições espaciais dos campos elétricos em um certo instante de tempo. A velocidade das duas ondas no ar é c= 3.108 m/s.
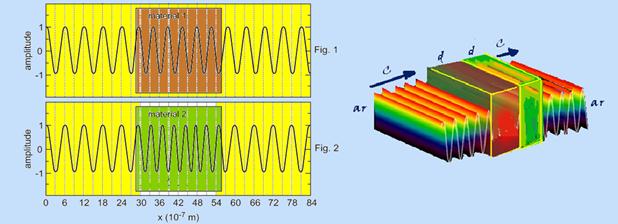
a) Determine o comprimento de onda e a frequência das ondas no ar.
b) Determine os comprimentos de onda, as frequências e as velocidades das ondas nos dois meios transparentes e os respectivos índices de refração dos dois materiais.
41-(FGV-SP)
![]()
Verifica-se que, ao sofrer refração, um trem de ondas mecânicas apresenta um novo perfil de oscilação, onde
a distância entre duas cristas consecutivas de suas ondas, tornou-se maior. Comparativamente ao que possuía o trem de ondas antes da refração, a frequência se________ , a velocidade de propagação se__________ e a amplitude se manteve, já que o novo meio é________ refringente.
Assinale a alternativa que preenche corretamente as lacunas.
a) alterou … alterou … menos
b) alterou … manteve … mais
c) manteve … alterou … mais
d) manteve … alterou … menos
e) manteve … manteve … manteve
42-(UEM-PR)

Três cordas, A, B e C, homogêneas, flexíveis e com densidades lineares µ, 3µ, e 2µ, respectivamente, são conectadas

na sequência ABC. Em uma das extremidades livres do conjunto, a corda C é mantida fixa, enquanto na outra extremidade livre, na corda A, um pulso mecânico é repentinamente aplicado. Considerando que o conjunto é mantido reto na horizontal e desprezando a resistência do ar e a ação da gravidade, assinale o que for correto.
01) Na junção AB, parte do pulso é refratada para B, enquanto outra parte é refletida em A, com inversão de fase.
02) Na corda B, o pulso é transmitido com uma velocidade maior que nas cordas A e C.
04) Na junção BC, o pulso é refratado.
08) Na corda C, o pulso é transmitido com velocidade maior que na corda B.
16) Nas junções AB e BC, o pulso é refratado com inversão de fase.
43-(UFSM-RS)

Uma
sala de concertos deve permitir uma percepção clara dos sons, por
isso deve estar livre de eco e o tempo de reverberação deve ser
pequeno. Assim,
I - na reverberação, trens de onda emitidos simultaneamente pela mesma fonte sonora, percorrendo caminhos diferentes no ar, chegam ao ouvinte em instantes de tempo diferentes, mas não são percebidos como sons separados.
II - o fenômeno de reverberação pode ser explicado considerando-se a interferência dos trens de onda emitidos pela mesma fonte.
III - no eco, trens de onda emitidos simultaneamente pela mesma fonte sonora, percorrendo caminhos diferentes no ar, chegam ao ouvinte em instantes de tempo diferentes e são percebidos como sons separados.
Está(ão) correta(s)
a) apenas I.
b) apenas II.
c) apenas III.
d) apenas I e III.
e) apenas II e III.
44-(UFJF-MG)

A audição humana, normalmente, consegue distinguir sons que vão de uma frequência mínima de 20 Hz até uma frequência máxima de 20 000 Hz , embora o limite superior possa decrescer com a idade. Uma onda sonora,
de
comprimento de onda λ = 2,0 m , emitida no ar, é facilmente
percebida pelo ouvido humano. Se essa onda sonora fosse emitida na
água, o ouvido humano poderia percebê-la? Considere a velocidade do
som na água vágua=1480m/s.
a) Não, pois a frequência desse som na água será de 12 Hz .
b) Sim, pois a frequência desse som na água será de 370 Hz .
c) Sim, pois a frequência desse som na água será de 740 Hz .
d)
Não, pois a frequência desse som na água será de 1480
![]() Hz .
Hz .
e) Sim, pois a frequência desse som na água será de 1480 kHz .
Resolução comentada dos exercícios de vestibulares sobre
Reflexão e Refração de Ondas
O1- D
02- D
03- Observe nas figuras que, antes da reflexão, a parte da frente da onda (que está em x=9), até chegar à parede percorreu S=6m e que, após a reflexão, chegou até x=3, ou seja, percorreu ΔS=12m. Assim,ΔStotal=6 + 12 = 18m.
Δt=1,5s --- V=ΔS/Δt --- V=18/1,5 --- V=12m/s
R- E
04-
a)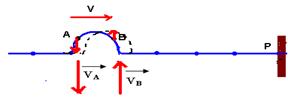
b)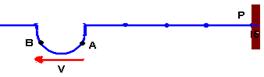
c)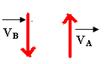
05- B
06- A
07-Traçando os raios de onda incidente (ri) e refletido (rr), a normal N e lembrando que os ângulos i e r são iguais,, no caso, 45o (figura abaixo).
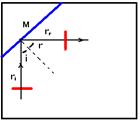
R- A
08- a) V=λ.f --- V=6.50 --- V=300m/s
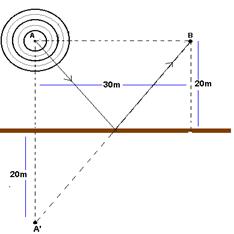
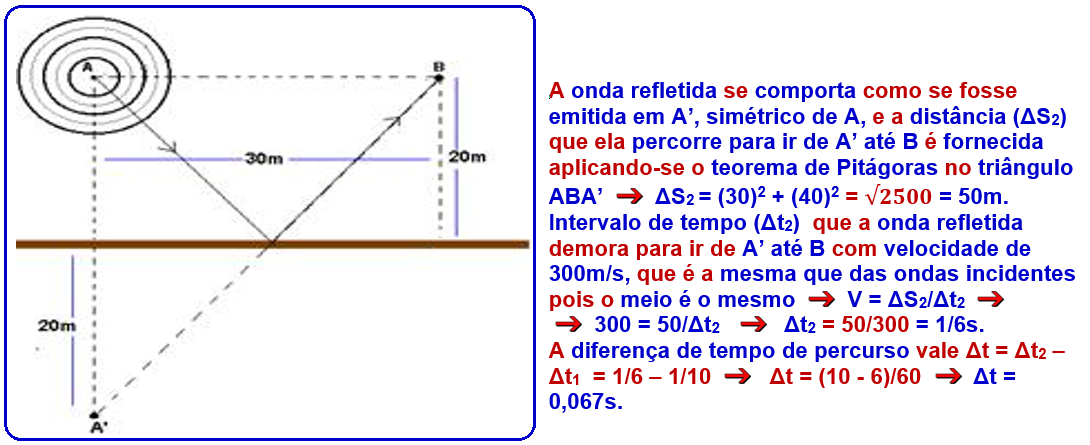
b) tempo (Dt1) que a onda demora para ir de A até B --- V=ΔS/Δt1 --- 300=30/Δt1 --- Dt1 =1/10s a onda refletida se comporta como se fosse emitida em A’, simétrico de A, e a distância (ΔS2) que ela percorre para ir de A’ até B é fornecida aplicando-se o teorema de Pitágoras no triângulo ABA’ --- ΔS2=50m.
tempo (Δt2) que a onda refletida demora para ir de A’ até B com velocidade de 300m/s, que é a mesma que das ondas incidentes pois o meio é o mesmo --- V=ΔS2/Δt2 --- 300=50/Δt2 --- Δt2 = 50/300=1/6s
A diferença de tempo de percurso vale Dt=1/6 – 1/10 --- Dt=(10-6)/60 --- Dt=0,067s
c) As ondas refletidas se comportam como se fossem emitidas pela fonte colocada em A’, simétrico de A.
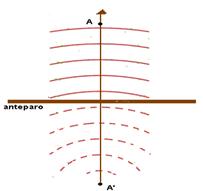
09- R- D A freqüência é a mesma (mesma fonte). A velocidade de propagação é a mesma (mesmo meio). O comprimento de onda é o mesmo. O ângulo de incidência (que o raio de onda forma com a normal no ponto de incidência) é igual ao ângulo de reflexão (que o raio refletido forma com a normal no ponto de incidência)
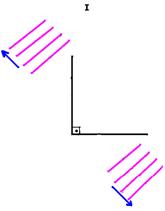
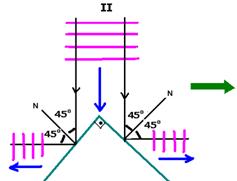
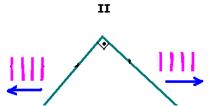
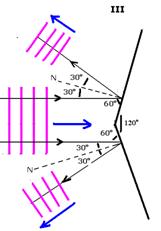
10- Traçando em cada caso, os raios de onda, os ângulos de incidência e de reflexão, teremos:
I-
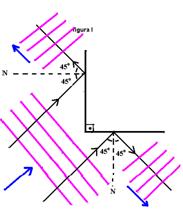
![]()
II-
III-
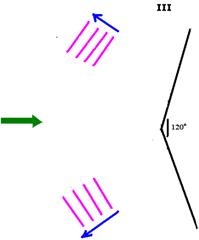
IV-
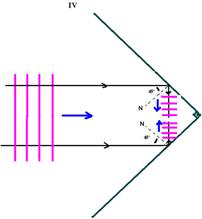
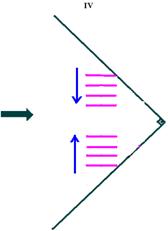
Lembre-se de que as ondas refletidas tem sempre a mesma velocidade de propagação, a mesma freqüência e o mesmo comprimento de onda.
11-a) V=λ.f --- V=1.30 --- V=30m/s
b) V=30m/s (é a mesma pois o meio é o mesmo)
c) f=30Hz (é a mesma pois a fonte é a mesma)
d) λ=1m (é o mesmo, pois V=λ.f e V e f são os mesmos)
e) As ondas refletidas comportam-se como se estivessem emitidas pela fonte F’, simétrica de F.
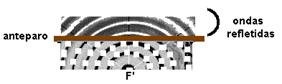
12- a) Cálculo da distância percorrida pela onda em 2s --- V=ΔS/Δt --- 8=ΔS/2 --- ΔS=16cm
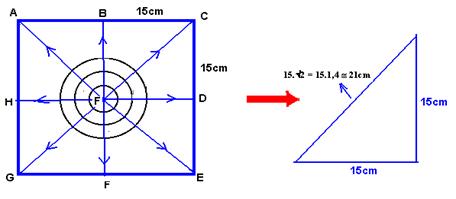
Observe na figura acima que, em t=2s, a onda não chegou aos pontos A,C,E e G e que já está voltando dos pontos B, D, F e H.

b) Sem inversão de fase, pois as paredes comportam-se como extremidades livres.
13- a) É o mesmo que das ondas incidentes --- λ=20/5 --- λ=4cm
b) É a mesma que das ondas incidentes, emitidas pela fonte F --- V=λf --- 10=4f --- f=2,5Hz
c)
14- Vamos calcular a distância percorrida por cada ponto da onda no instante t=1,5s --- V=ΔS/Δt --- 2=ΔS/1,5 --- ΔS=3,0m
Verifique na figura abaixo que --- AA’=BB’=3,0m e que PP’=QO’=3,0m
Quando
t=1,5s: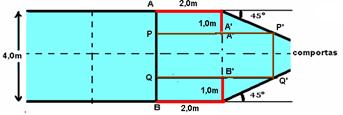
Os pontos da onda entre A’ e P’ já atingiram o anteparo e estão retornando. O mesmo acontece com os pontos da onda entre B’ e Q’.
Os pontos P’ e Q’ estão no anteparo.
Os pontos da onda entre P’ e Q’ ainda não atingiram o anteparo e estão se deslocando para a direita.
15- Meio 1
1,5λ1=6 --- λ1=4m V1=λ1.f --- 8=4f --- f=2Hz
Meio 2
A freqüência f é a mesma, pois a fonte é a mesma --- f=2Hz e V2=10m/s --- V2=λ2f --- 10=λ2.2 --- λ2=5m
16- a) λ1=1,5m --- V1=λ1f --- 12=1,5f --- f=8Hz (constante) --- V2=λ2f --- 8=λ28 --- λ2=1m
b) f=8Hz para as duas cordas.
17- a) A razão é 1, pois a freqüência é a mesma em cada corda (mesma fonte)
b) f=4Hz (para as duas cordas) --- µ1=4µ2 --- T (é a mesma para as duas cordas)
V1=λ1f
--- f=V1/λ1 V2=λ2f
--- f=V2/λ2
--- V1/λ1=V2/λ2
---  T/4µ2/λ1)=
T/4µ2/λ1)= T/µ2/λ2)
--- λ1/λ2=1/2
T/µ2/λ2)
--- λ1/λ2=1/2
18- D
19- a)
Velocidade do pulso em cada corda V1=18/2=9cm/s --- V1=0,09m/s V2=6/2=3cm/s --- V2=0,03m/s
Como V1>V2 --- µ1 < µ2 e a corda 1 é menos densa “mais leve” que a corda 2. Se o pulso incidente tivesse vindo pela corda 2, mais densa “mais pesada”, o pulso na corda 1 seria sem inversão de fase. Outra explicação: O pulso está na 1 (menos densa), pois ao atingir A (que funciona como extremidade fixa), ele retorna com inversão de fase.
b)
Corda 1 --- V1= T/m1
--- 0,09=
T/m1
--- 0,09= T/0,01
--- (0,09)2=(
T/0,01
--- (0,09)2=( T/0,01)2
--- 0,0081=T/0,01 --- T =
T/0,01)2
--- 0,0081=T/0,01 --- T =
0,000081N (nas duas cordas)
c)
V2= T/m2
--- (0,03)2=(
T/m2
--- (0,03)2=( 0,000081 /m2)2 ---
0,0009=0,81//m2
--- m2=0,09kg/m
0,000081 /m2)2 ---
0,0009=0,81//m2
--- m2=0,09kg/m
20- D
21- A
22-R: B
Observe na figura abaixo que i=45o e que r=30o
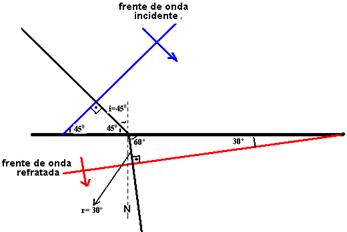
A frequência é a mesma (mesma fonte) --- f=10Hz
sen
i/sen r = λ1/λ2 ---
sen 45o /
sen 30o =
28/λ2 ---  2/2/1/2
= 28/λ2 --- λ2 =
20m
2/2/1/2
= 28/λ2 --- λ2 =
20m
23- Freqüência da luz no ar --- V=λf --- 3.108=633.10-9.f --- f ≈ 5.1014Hz
Cálculo
do índice de refração do meio ---
nar.sen60o=nt.sen30o
--- 1. 3
/2=nt.1/2
--- nt=
3
/2=nt.1/2
--- nt= 3
3
Velocidade
da luz no meio --- nt =
C/V ---  3
= 3.108/V
--- V =
3
= 3.108/V
--- V =  3.108m/s
--- V=λf ---
3.108m/s
--- V=λf ---  3.108 = l.5.1014
--- λ ≈ 0,347.10-6 =
347.10-9 = 347
nm
3.108 = l.5.1014
--- λ ≈ 0,347.10-6 =
347.10-9 = 347
nm
24- a) freqüência no meio 1 -- V=lf --- 200=4.f --- f=50Hz – é a mesma nos dois meios
b) Observe na figura abaixo que i=q1 e que r=q2
seni/senr = V1/V2 --- 0,8/0,5=200/V2 --- V2=125m/s
c) V1/V2 = λ1/λ2 --- 200/125=4/λ2 --- λ2 = 2,5m
d) n2/n1=V1/V2 --- n2/n1=200/125 --- n2/n1=1,6 --- n2=1,6n1
25- D
26- C
27- R – A
I e II- verdadeiras --- como a freqüência é a mesma (mesma fonte) --- f=V/λ=constante --- V e λ são diretamente proporcionais
28- a) A distância entre os máximos sucessivos no meio 1 é o comprimento de onda ΔS = 2,0 cm. Se a onda percorre esta distância em 0,5 s, sua velocidade neste meio será v1= 2,0 / 0,5 = 4,0 cm/s. A freqüência será, portanto, f = V/λ = 4/2=2Hz.
b) Pela Lei de Snell-Descartes, temos
sen30o/sen45o=V1/V2
--- 1/2/ 2/2
= 4/V2
--- V2=4
2/2
= 4/V2
--- V2=4 2cm/s
2cm/s
29-
(01) Falsa. O experimento ilustra o fenômeno da refração.
(02) Correta. A freqüência é a mesma nas duas regiões (mesma fonte).
(04) Falsa. Valem, respectivamente, 2,30cm e 4,00cm (distância entre duas cristas consecutivas)
(08) Verdadeira. Maior comprimento de onda (l), maior velocidade (V).
(16) Verdadeira. V=lf --- Como V é a mesma (mesmo meio), l e f são inversamente proporcionais, ou seja, se f aumentar, l tem que diminuir.
Soma (02 + 08 + 16) = 26
30-
(01) Verdadeira. V é diretamente proporcional a l.
(02) Verdadeira. A freqüência é mesma, pois a fonte é a mesma.
(03) Verdadeira. Sempre que ocorre refração, ocorre reflexão.
(04) Falsa. A onda está passando de um meio mais refringente (maior índice de refração) para outro menos refringente (menor índice de refração) e pode haver reflexão total.
(05) Falsa. A velocidade das ondas na superfície dos líquidos depende da profundidade e, para profundidades inferiores a 10m é dada por V=Ögh.
31- a)Observe na figura abaixo que i=30o e r=45o
seni/senr
= V2/V1
--- sen30o/sen45o=340/V2
--- 1/2 / 2
/2 = 340/V2
--- V2 =
340
2
/2 = 340/V2
--- V2 =
340 2
m/s
2
m/s
b)
Como f é a mesma --- V=λf --- 340 2
= λ2.20
--- λ2 =
172 m
2
= λ2.20
--- λ2 =
172 m
32- R: E
Figura 1 --- quanto maior o índice de refração n,. maior a freqüência f
Figura 2 --- r1 > r3 > r2
Lei --- maior n, menor r
Conclusão --- maior f, menor
33- nv.senθ1 = nc.senθ2 --- 1.√3/2 = nc.1/2 --- nc=√3 --- nc=c/√3 --- nc=c/Vc --- √3=3.108/Vc --- Vc=√3.108m/s --- R- C
34- A frequência f=500Hz é a mesma nos dois meios --- Var/λar=Vágua/λágua --- λar/λágua = Vágua/Var = 1.500/300=1/5 --- R- D
35- ∆S=1cm=10-3m --- ∆t=0,1μs=10-1.10-6=10-7s --- V=∆S/∆t=10-3/10-7 --- V=105m/s --- f = 1015.103 = 1018m --- V=λ.f --- 105=λ.1018 --- λ=10-13=10-3.10-10 --- λ=10-3 Ǻ --- R- B
36- Cada cor possui sua frequência que independe do meio na qual ela está se propagando e, quando a luz passa de um meio
menos refringente para outro mais refringente sua velocidade de propagação diminui --- R- E
37- V=λf --- f=constante=V/λ --- quando a luz passa de um meio mais refringente para um meio menos refringente sua velocidade aumenta e consequentemente seu comprimento de onda também irá aumentar, pois a frequência é a mesma nos dois meios --- R-E
38- 1. Falsa --- o aquecimento ocorre devido à fricção entre as moléculas de água contidas no alimento, que tendem sempre a se orientar na direção de um campo elétrico de direção variável aplicado pelo magneto.
2.
Verdadeira --- dados --- f = 2.450 MHz =
2,45 109 Hz
--- considerando a velocidade de propagação das micro-ondas
no interior do forno, v = c =
3.108 m/s,
da equação fundamental da ondulatória --- V=λf
--- λ=V/f=3.108/2,45.109
--- λ=12,2cm
3. Verdadeira --- as micro-ondas são refletidas nas paredes para evitar vazamentos, aumentando a segurança do aparelho e a sua eficiência, além de propiciar o aquecimento homogêneo dos alimentos, também favorecido pela rotação do prato.
R- E
39- a) Equação fundamental da ondulatória --- Var=λar.f --- λar=Var/f=340/160 --- λar=2,1m
b) Quando uma onda sofre refração, sua frequência não se altera --- far = f = 160 Hz.
c) λágua=Vágua/f=1.450/160 --- λágua = 9,1m
40- a)
Observe as figuras abaixo --- da figura 1
--- λar=(18
– 12).10-7m=6.10-7m
--- equação fundamental da ondulatória --- V=λf
--- c=λar.f
--- 3.108
=
6.10-7.f
--- f=5,0.1014Hz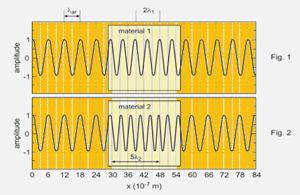
b) Na Fig 1, você observa que, no material 1 --- 2λ1 = (48 – 39).10-7 m --- λ1=4,5.10-7m --- material 2, na figura 2 --- 5λ2 = (48 – 30).10-7 m --- λ2 =18.10-7/5 --- λ2 = 3,6.10-7m --- frequência permanece constante nos dois meios, e é também a mesma que a frequência de propagação no ar --- f1 = f2 = f = 5.1014 Hz --- cálculo da velocidade de propagação da onda em cada meio --- v1 = λ1.f = (4,5.10-7)x(5.1014) = 2,25.1088 m/s --- v2 = λ2.f = (3,6.10-7)x(5.1014) = 1,8.108 m/s --- da definição de índice de refração --- n1=c/V1=3.108/2,25.108 --- n1=1,3 --- n2=c/V2=3.108/1,8.108 --- n2=1,7
41- A frequência é característica da onda, sendo sempre a mesma independente do meio --- quando a onda sofre refração passando a se mover em meios diferentes, sua velocidade varia e, consequentemente o comprimento de onda também varia --- se f1=f2 ---
V1/λ1= V2/λ2 --- como o comprimento de onda aumentou λ2/λ1>1 --- V2/V1>1 --- V2>V1 --- assi, o meio 2 é menos refringente que o meio 1 --- R- D
42-(UEM-PR)
Todas as respostas estão baseadas nas informações abaixo --- leia-as atentamente e responda.

 Corretas:
01, 04 e 08 --- Soma=13.
Corretas:
01, 04 e 08 --- Soma=13.
43-
I. Correta --- reverberação é um fenômeno de prolongamento de um som após o fim de emissão por parte de uma mesma fonte sonora --- quando o obstáculo refletor do som está um pouco mais afastado, de modo que a som emitido e o som refletido têm um intervalo de tempo menor que 0,1s ocorre o fenômeno da reverberação --- nesse caso ao receber dois estímulos do mesmo tipo em menos de 0,1s o ouvinte tem a sensação que o som ainda não foi extinto.
II. Falsa --- veja justificativa da I.
III. Correta --- eco é uma reflexão de som que chega ao ouvinte pouco tempo depois do som direto --- um eco verdadeiro é uma única reflexão do som emitido pela fonte, que você ouve instantes após ouvir o som idêntico inicial.
R- D
44- Equação fundamental da ondulatória --- v=λ.f --- na água --- 1480=2.f --- f=740Hz --- R- C