Ondas Estacionárias
Formação de ondas estacionárias
Obtemos ondas estacionárias pela superposição de duas ondas idênticas, de mesma amplitude, mesma frequência, mesmo comprimento de onda e que se movem na mesma direção e sentidos opostos.
Considere uma corda fixa em uma das extremidades e na outra uma fonte produz ondas periódicas
que, ao atingirem a extremidade fixa, sofrem reflexão e retornam.
Assim, as ondas incidentes e as refletidas se superpõem, originando as ondas estacionárias.
Para
entender
como surgem
as ondas estacionárias,
observe atentamente as sequências das figuras
abaixo,
onde, em
todas,
temos, no
mesmo instante,
nas duas
figuras da esquerda,
as ondas
se
movendo
em sentidos contrários
e, na figura
da direita, a superposição das mesmas, nesse mesmo instante.
O intervalo de tempo entre uma figura e outra é de um quarto de período (T/4), ou seja, entre cada intervalo a onda percorreu um quarto de comprimento de onda.
No instante t = 0, as duas ondas estão exatamente superpostas e a onda resultante dessa superposição tem amplitude 2A. (interferência construtiva).
No instante t = T/4, cada uma delas se moveu λ/4 e suas configurações estão nas duas figuras da esquerda. Observe, na figura da direita, que todos os pontos dessas ondas se anulam. (interferência destrutiva).
No instante t = T/2, a onda resultante tem amplitude 2A.
No instante t = 3T/2 essas ondas novamente se anulam.
No
instante
t=T,
essas ondas voltaram
à situação inicial
e a partir daí
começa a repetição.
Observe que, em todos os instantes, os pontos P, Q e R, da onda resultante não se moveram. Esses pontos, sempre fixos são chamados de nodos ou nós e estão em interferência destrutiva.
Observe também que, em todos os instantes, todos os pontos compreendidos entre P e Q e entre Q e
Cada uma dessas amplitudes é o dobro das amplitudes das ondas constituintes.
Como os nós estão em repouso, não pode haver passagem de energia por eles, não havendo, então, em uma corda estacionária o transporte de energia.
Assim, ondas estacionárias não são ondas de propagação, mas sim, as diferentes maneiras de vibração de uma corda, membrana, etc.
Interferência sonora
Ocorre quando duas ou mais ondas sonoras se superpõem num mesmo ponto.
Vamos supor duas ondas sonoras de freqüências ligeiramente diferentes, uma de fA = 100 Hz e outra de fB = 110 Hz.
Então, você ouvirá um som forte (interferência construtiva) e depois um som fraco (interferência destrutiva) e assim sucessivamente. Este fenômeno recebe o nome de batimento (figura).
Observe que a onda resultante apresenta pontos onde a amplitude é máxima (sons fortes, interferência construtiva) como nos pontos A, C e E, vai diminuindo e praticamente desaparece ou se anula (interferência destrutiva) como nos pontos B, D e F.
A freqüência do batimento é definida como sendo fbatimento = fmaior – fmenor.
O fenômeno do batimento é muitas vezes utilizado na afinação de instrumentos musicais.
Se as freqüências da fonte afiadora e do instrumento forem diferentes, ouve-se o batimento.
A freqüência do batimento vai diminuindo à medida que o instrumento vai sendo afinado e, quando desaparecer, o instrumento estará afinado.
O que você deve saber, informações e dicas
Cada uma das amplitudes da onda estacionária é o dobro das amplitudes das ondas constituintes.
Como os nós estão em repouso, não pode haver passagem de energia por eles, não havendo, então, em uma onda estacionária o transporte de energia.
Assim, ondas estacionárias não são ondas de propagação, mas sim, as diferentes maneiras de vibração de uma corda, membrana, etc.
|
|
A freqüência do batimento é definida como sendo fbatimento = fmaior – fmenor.
O fenômeno do batimento é muitas vezes utilizado na afinação de instrumentos musicais.
Se as freqüências da fonte afiadora e do instrumento forem diferentes, ouve-se o batimento.
A freqüência do batimento vai diminuindo à medida que o instrumento vai sendo afinado e, quando desaparecer, o instrumento estará afinado.
Fórmulas
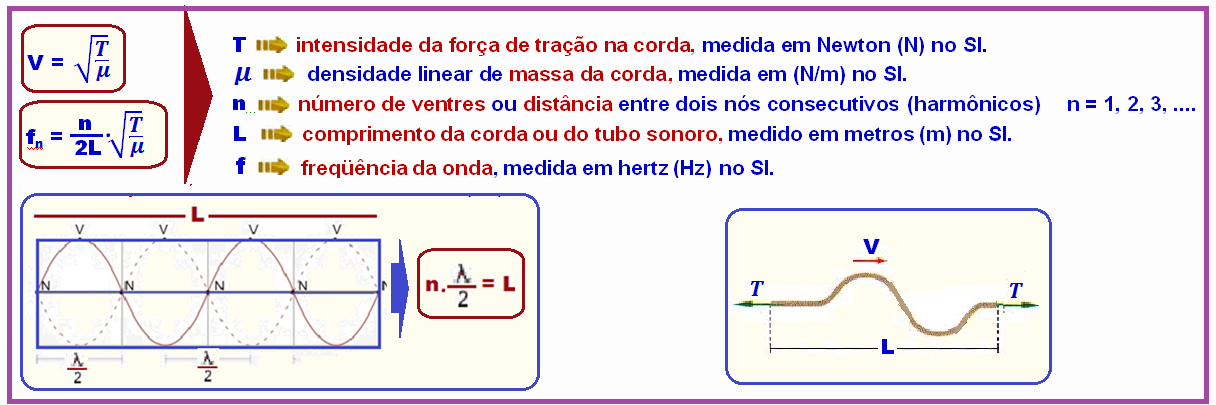
Alguns exercícios interessantes nos quais seria conveniente você analisar as resoluções:
02- (UFMS) A figura mostra ondas estacionárias em uma corda de comprimento 45cm, de densidade linear de massa μ = 6,2 g/m, com as duas extremidades fixas, e que está vibrando a 450Hz.
Dê como resposta a soma dos números correspondentes às afirmações corretas.
É correto afirmar que:
(01) todos os pontos da corda vibram com a mesma amplitude.
(02) todos os pontos da corda vibram com a mesma freqüência.
(04)
o comprimento
de onda
na corda é de 90
cm.
(08) a velocidade de propagação da onda na corda é de 135m/s.
(16) a força tensora na corda é de 113N, aproximadamente.
Resolução:
(01) Errada. O movimento de cada ponto da onda estacionária é somente na vertical e verifique na figura abaixo que os pontos A, A1 e A2 tem amplitudes diferentes no seu “sobe e desce” completo.
(02) Correta. Esta freqüência de 450Hz é a freqüência das ondas que se superpõe e é a mesma para todos os pontos da corda que vibram.
(04)
Errada.
3λ/2
= 45
λ
= 30 cm.
(08)
Correta.
V
= λf
V
=
30.450 = 13.500
cm/s = 135m/s.
(16)
Correta.
V=√(F/μ)
135 = √(F/6,2.10-3)
(135)2
=
(F/6,2.10-3)2
18.225 = F/0,0062
F = 112,995 N.
Soma = (02 + 08 +16) = 26
Resolução:
Aplicando a equação fundamental da ondulatória para a:
Rádio
da cidade
V
= λc.fc.
Rádio
pirata
V
= λp.fp.
Como a velocidade (V) de propagação da onda é a mesma, pois se trata do mesmo meio de propagação (ar), e as frequências (f), pelo enunciado, são iguais, os comprimentos onda (λ) também o serão.
R- E
Resolução:
O ponto 2 da corda é um nó (ou nodo) da onda estacionária e permanece fixo .
Os pontos 1 e 3 possuem velocidade nula nas extremidades superiores e inferiores e velocidades máximas quando passam pela centro (onde estão esses pontos), apenas que eles possuem velocidades de sentidos contrários, ou seja, enquanto um está subindo o outro estará descendo .
R- D.
Resolução:
Observe nas figuras abaixo as ondas estacionárias formadas em cada caso :
Primeira
figura
λ1/2
= L
γ 1=
2L
V1
=
γ1.f1
V1
=
2L.f1
(I).
Segunda
figura
γ2/2
= L/2
γ2
=
L
V2
=
γ2.f2
V2
=
L.f2 (II).
Como
a velocidade
de propagação em cada caso é a mesma
(mesmo meio, ar)
V1
=
V2
I
= II
2Lf1
=
Lf2
--- 2.220 = f2
f2
=
440 Hz.
R- A
Exercícios de vestibulares com resoluções comentadas sobre
Ondas Estacionárias
03-(MACKENZIE-SP) Um fio de aço de 60cm de comprimento é mantido tracionado pelas suas extremidades fixas. Nesse fio, quando excitado por uma fonte de onda de 60Hz, origina-se uma fonte de onda estacionária, conforme a figura abaixo.
Determine a velocidade de propagação da onda no fio.
.
04- (UFMS) A figura mostra ondas estacionárias em uma corda de comprimento 45cm, de densidade linear de massa μ=6,2g/m, com as duas extremidades fixas, e que está vibrando a 450Hz.
Dê como resposta a soma dos números correspondentes às afirmações corretas.
É correto afirmar que:
(01) todos os pontos da corda vibram com a mesma amplitude.
(02) todos os pontos da corda vibram com a mesma freqüência..
(04) o comprimento de onda na corda é de 90cm.
(08) a velocidade de propagação da onda na corda é de 135m/s.
(16) a força tensora na corda é de 113N, aproximadamente.
05-(UFSCAR-SP) A figura representa uma configuração de ondas estacionárias em uma corda.
A extremidade A está presa a um oscilador que vibra com pequena amplitude. A extremidade B é fixa
e a tração na corda é constante. Na situação da figura, onde aparecem três ventres (V) e quatro nós (N), a freqüência do oscilador é 360Hz.Aumentando-se gradativamente a freqüência do oscilador, observa-se que essa configuração se desfaz até aparecer, em seguida, uma nova configuração de ondas estacionárias, formadas por:
a) quatro nós e quatro ventres, quando a freqüência atingir 400Hz
b) quatro nós e cinco ventres, quando a freqüência atingir 440Hz
c) cinco nós e quatro ventres, quando a freqüência atingir 480Hz
d) cinco nós e quatro ventres, quando a freqüência atingir 540Hz
e) seis nós e oito ventres, quando a freqüência atingir 720Hz
06- (UNIFESP-SP) A figura representa uma configuração de ondas estacionárias produzida num laboratório didático com uma fonte oscilante.
a) Sendo d = 12 cm a distância entre dois nós sucessivos, qual o comprimento de onda da onda que se propaga no fio?
b) O conjunto P de cargas que traciona o fio tem massa m = 180 g. Sabe-se que a densidade linear do fio é μ = 5,0 × 10-4 kg/m. Determine a freqüência de oscilação da fonte.
Dados:
velocidade de propagação de uma onda numa corda: v = 
;
g = 10m/s2.
07-(UFF-RJ) Numa corda homogênea, com suas extremidades fixas no laboratório, se estabelece uma onda estacionária.
Nesta situação, a corda vibra entre as duas posições extremas, indicadas pelas linhas contínua e tracejadas na figura a seguir.
Sabendo que a corda se alterna entre essas duas posições a cada 0,50s, é correto afirmar que a velocidade de propagação das ondas ao longo da corda vale:
08-(MACKENZIE-SP) Uma corda feita de um material cuja densidade linear é 10g/m está sob tensão provocada por uma fora de 900N. Os suportes fixos distam 90cm. Faz-se vibrar a corda transversalmente e esta produz ondas estacionárias, representadas na figura a seguir.
Determine a freqüência das ondas componentes, cuja superposição causa esta vibração.
09-(FEI-SP) Com dois diapasões obtêm-se batimentos se ambos vibrarem com:
a) mesma amplitude
b) amplitudes pouco diferentes entre si
c) freqüências bem distintas
d) freqüências iguais
e) freqüências pouco diferentes entre si.
10-(PUC-MG) Para que um ser humano normal perceba o fenômeno “batimento”, gerado por duas ondas, é necessário, entre outras coisas, que tais ondas sejam:
a) eletromagnéticas, de comprimentos de onda bem diferentes, e audíveis.
b) eletromagnéticas, de freqüências bem afastadas, e visíveis
c) mecânicas, de comprimentos de onda idênticos, e audíveis.
d) mecânicas, de freqüências bem próximas, e estejam na faixa audível
e) de amplitudes ligeiramente diferentes, podendo ser de qualquer natureza.
11-(MACKENZIE-SP) Para que duas ondas sonoras produzam batimento, é necessário que tenham:
a) mesma freqüência
b) mesma amplitude
c) o mesmo número de harmônicos
d) freqüências ligeiramente diferentes
e) amplitudes ligeiramente diferentes
12-(ENEM-MEC)
Um garoto que passeia de carro com seu pai pela cidade, ao ouvir o rádio, percebe que a sua estação de rádio preferida, a 94,9 FM, que opera na banda de frequência de megahertz, tem seu sinal de
transmissão superposto pela transmissão de uma rádio pirata de mesma frequência que interfere no sinal da emissora do centro em algumas regiões da cidade.
Considerando a situação apresentada, a rádio pirata interfere no sinal da rádio pirata interfere no sinal da rádio do centro devido à
a) atenuação promovida pelo ar nas radiações emitidas.
b) maior amplitude da radiação emitida pela estação do centro.
c) diferença de intensidade entre as fontes emissoras de ondas.
d) menor potência de transmissão das ondas da emissora pirata.
e) semelhança dos comprimentos de onda das radiações emitidas.
13-(UFU-MG) Após uma competição de natação, forma-se um padrão de ondas estacionárias na piscina olímpica. Uma piscina olímpica oficial mede 50 metros.
Se a distância entre os ventres do padrão de ondas é de 50 centímetros, o número de ventres que aparecem na piscina e o comprimento das ondas propagantes é de:
a) 98 ventres e comprimento de onda de 1 metro
b) 50 ventres e comprimento de onda de 50 centímetros
c) 200 ventres e comprimento de onda de 2 metros
d) 100 ventres e comprimento de onda de 1 metro
14- (UFPE-PE)
Uma onda estacionária se forma em um fio fixado por seus extremos entre duas paredes, como mostrado na figura.
Calcule o comprimento de onda desta onda estacionária, em metros.
15-(UFF-RJ)
A figura abaixo representa um dos modos de vibração de uma corda presa nas suas extremidades.
Marque a alternativa que quantifica corretamente as velocidades dos pontos 1.2 e 3 da corda no instante em que ela passa pela configuração horizontal.
(a) V1 = V2 = V3 = 0
b) V1 = V2 = V3 ≠ 0
c) V1 = - V2 = V3 = 0
d) V1 = - V3 ≠ 0; V2 = 0
e) V1 = V2 ≠; 0; V3 = 0
16-(AFA)
A figura 1 abaixo apresenta a configuração de uma onda estacionária que se forma em uma corda inextensível de comprimento L e densidade linear μ quando esta é submetida a oscilações de frequência constante fo, através de uma fonte presa em uma de suas extremidades. A corda é tencionada por um corpo homogêneo e maciço de densidade ρ, preso na outra extremidade, que se encontra dentro de um recipiente inicialmente vazio.
Considere que o recipiente seja lentamente preenchido com um líquido homogêneo de densidade δ e que, no equilíbrio, o corpo M fique completamente submerso nesse líquido. Dessa forma, a nova configuração de onda estacionária, que se estabelece na corda é mostrada na figura 2.
Nessas
condições, a razão (ρ/δ) entre as densidades do corpo e do
líquido, é
17-(FGV-SP)
A nota lá da escala cromática musical é tida como referência na afinação dos instrumentos. No violão comum de 6 cordas, a quinta corda (segunda de cima para baixo), devidamente afinada, emite a nota lá vibrando com frequência de 220 Hz. Se o instrumentista colocar seu dedo num traste localizado a meia distância dos extremos desta corda e percuti-la, ele ouvirá a nota lá vibrando com frequência de
(A) 440 Hz, mantida a velocidade de propagação da onda formada.
(B) 110 Hz, mantida a velocidade de propagação da onda formada.
(C) 440 Hz, com velocidade de propagação da onda dobrada.
(D) 110 Hz, com velocidade de propagação da onda dobrada.
(E) 440 Hz, com velocidade de propagação da onda reduzida à metade.
Resolução comentada dos exercícios de vestibulares sobre
Ondas Estacionárias
01- 4λ/2=1 --- λ=1/2m --- V=λf --- V=1/2.1000 --- V=500m/s.
02- Formam-se ondas estacionárias com os pedacinhos de papel jogados pelos ventres formados
nos pontos D, F e H. figura acima
03- 4λ/2=60 --- λ=30cm --- V=λf --- V=30.60 --- V=1800cm/s=18m/s
04-
(01) Errada. O movimento de cada ponto da onda estacionária é somente na vertical e verifique na figura abaixo que os pontos A, A1 e A2 tem amplitudes diferentes no seu “sobe e desce” completo.
(02) Correta. Esta freqüência de 450Hz é a freqüência das ondas que se superpõe e é a mesma para todos os pontos da corda.
(04) Errada. 3λ/2=45 --- λ=30cm
(08) Correta. V=λf --- V=30.450=13.500cm/s=135m/s.
(16)
Correta. V=
--- 135=√(F/6,2.10-3)
--- (135)2=(√(F/6,2.10-3)2
--- 18.225=F/0,0062 --- F= 112,995N
Soma=(02 + 08 +16)=26
05- Na configuração da figura abaixo, onde L é o comprimento da corda, a frequência é de 360Hz.
Sendo l1 o comprimento de onda dessa onda estacionária, temos que 3l1/2=L --- l1=2L/3 --- V1=l1.f1 --- V1=2L/3.360 --- V1=240L
Como a velocidade V na corda é a mesma (mesmo meio) e V=λf, λ e f são inversamente proporcionais. Assim, sendo L o mesmo, se aumentarmos f, λ irá diminuir e teremos um ventre a mais na corda.
4λ2/2=L --- λ2=L/2 --- V2=λ2.f --- V1=V2 (mesmo meio) --- 240L=L/2f2 --- f2=480Hz
R- C
06- a) λ/2=12 --- λ=24cm = 0,24m
b) F=P=mg --- F=0,18.10 --- F=1,8N --- m=5.10‑4‑kg/m
V=√(F/μ) --- V=√(1,8/5.10-4) --- V=√(36.102) = 60m/sm --- V=λf --- 60=0,24f --- f=250Hz
07- 3λ/2=15 --- λ=10m --- esse intervalo de tempo 0,50s é metade do período de cada uma das ondas que geraram a onda estacionária --- T/2=0,50 --- T=1s --- f=1/T --- f=1/1 --- f=1Hz --- V=λf --- V= 10.1 --- V=10m/s
O8- 3λ/2=0,9 --- λ=0,6m
μ=m/L --- m=0,01kg/m --- V=√(F/μ) --- V=√(900/0,01) --- V=300m/s --- V=λf --- 300=0,6.f --- f=500Hz
09- E
10- D
11- D
12- Da equação fundamental da ondulatória --- rádio da cidade --- V=λc.fc --- rádio pirata --- V=λp.fp --- como a velocidade de propagação da onda é a mesma, pois se trata do mesmo meio (ar), se as frequências são iguais, os comprimentos onde também o serão --- R- E
13- Observe a figura abaixo:
Ventres --- 50/0,5=100 --- comprimento de onda --- λ=1m --- R- D
14- Ondas estacionárias são ondas formadas pela superposição de duas ondas idênticas, de mesma amplitude, mesma freqüência, mesmo comprimento de onda e que se movem na mesma direção e sentidos opostos
* Os pontos A, C, E, G e I são nós ou nodos e não se movem, são fixos.
Todos os pontos que estão entre AC, CE, EG e GI são ventres (fusos) e estão sempre em movimento vibratório.
A distância entre dois nós consecutivos é sempre λ/2.
Observe na figura do exercício que λ/2=6m --- λ/2=6 --- λ=12m.
15- O ponto 2 da corda é um nó (ou nodo) da onda estacionária e permanece fixo --- os pontos 1 e 3 possuem velocidade nula nas extremidades superiores e inferiores e velocidades máximas quando passam pela centro (onde estão esses pontos), apenas que eles possuem velocidades de sentidos contrários, ou seja, enquanto um está subindo o outro estará descendo --- R- D.
Se você quer entender como se originam ondas estacionárias leia atentamente a teoria abaixo:
Obtemos ondas estacionárias pela superposição de duas ondas idênticas, de mesma amplitude, mesma frequência, mesmo comprimento de onda e que se movem na mesma direção e sentidos opostos.
Considere uma corda fixa em uma das extremidades e na outra uma fonte produz ondas periódicas que, ao atingirem a extremidade fixa, sofrem reflexão e retornam. Assim, as ondas incidentes e as refletidas se superpõem, originando as ondas estacionárias.
Para
entender como surgem as ondas estacionárias, observe as figuras
abaixo, onde, em todas, temos, no mesmo instante, nas duas figuras da
esquerda, as ondas se movendo em sentidos contrários e, na figura da
direita, a superposição das mesmas, nesse mesmo instante.
O intervalo de tempo entre uma figura e outra é de um quarto de período (T/4), ou seja, entre cada intervalo a onda percorreu um quarto de comprimento de onda.
No instante t=0, as duas ondas estão exatamente superpostas e a onda resultante dessa superposição tem amplitude 2A.(interferência construtiva).
No instante t=T/4, cada uma delas se moveu λ/4 e suas configurações estão nas duas figuras da esquerda. Observe, na figura da direita, que todos os pontos dessas ondas se anulam.(interferência destrutiva)
No instante t=T/2, a onda resultante tem amplitude 2A.
No instante t=3T/2 essas ondas novamente se anulam.
No instante t=T, essas ondas voltaram à situação inicial e a partir daí começa a repetição.
Observe que, em todos os instantes, os pontos P, Q e R, da onda resultante não se moveram. Esses pontos, sempre fixos são chamados de nodos ou nós e estão em interferência destrutiva --- suas velocidades verticais são nulas.
Observe também que, em todos os instantes, todos os pontos compreendidos entre P e Q e entre Q e R, estão em constante movimento, subindo e descendo, em interferência construtiva, e sua amplitude será a soma das amplitudes das ondas constituintes. Esses pontos são chamados de ventres..
Observe na figura abaixo, que os pontos A, C, E, G e I são nós e que os pontos B, D, F e H são ventres.
Se o comprimento de onda de cada onda que originou a estacionária é l, a distância entre dois nós consecutivos (fuso) vale l/2.
Entre os nós, os pontos dos ventres vibram na vertical com a mesma freqüência que é a mesma de cada onda que se superpõe, mas com amplitudes diferentes (figura abaixo)
. 
Como a freqüência de cada ponto é a mesma, o período (tempo que cada ponto demora para efetuar um “sobe e desce” completo) também será. Assim, a velocidade vertical do ponto A é maior que a do ponto A1, que por sua vez, é maior que a do ponto A2.
Cada uma dessas amplitudes é o dobro das amplitudes das ondas constituintes.
Como os nós estão em repouso, não pode haver passagem de energia por eles, não havendo, então, em uma corda estacionária o transporte de energia.
Assim, ondas estacionárias não são ondas de propagação, mas sim, as diferentes maneiras de vibração de uma corda, membrana, etc.
16- Equações das ondas estacionárias em uma corda de extremidades fixas --- fn=n.V/2.L --- V=√(T/μ) --- f – frequência do harmônico (que é sempre a mesma que a da fonte) --- n – ordem do harmônico --- V – velocidade de propagação da onda na corda --- L – comprimento da corda --- T – força que traciona a corda --- μ – densidade linear da corda --- na situação da
figura
1 --- as forças que agem sobre o corpo são seu peso 
e
a força de tração no fio 
---
no equilíbrio P e T se anulam --- P=T ---
P=mg=ρVg --- T= ρVg --- observe pela figura
1 que a configuração fornecida corresponde ao 2o harmônico
(n=2) --- f2=2.V/2L=2.√(T/μ)/2L
--- f2=1/L.√
(ρVg/μ) --- na situação da figura 2 surge sobre o
corpo também um empuxo 
,
vertical e
para cima e no equilíbrio --- P= T’ + E --- T’= P – E --- T’ = ρVg – δVg --- T’=Vg(ρ – δ) --- observe pela figura 2 que a configuração fornecida corresponde ao 4o harmônico (n=4) ---
f4=4V’/2L --- V’=√(T’/μ)= √( Vg(ρ – δ)/μ) --- f4=4.√( Vg(ρ – δ)/μ)/2L --- f4=(2/L).√( Vg(ρ – δ)/μ) --- observe que nos dois casos a frequência de oscilação é a mesma, que é a da fonte --- f2=f4 --- 1/L.√ (ρVg/μ) = (2/L).√( Vg(ρ – δ)/μ) --- 1/L.√ (ρVg/μ) = 1/L.√(4 Vg(ρ – δ)/μ) --- ρ = 4(ρ – δ) --- ρ = 4ρ – 4 δ --- 3ρ = 4 δ --- ρ/δ = 4/3 --- R- B
17- Observe nas figuras abaixo as ondas estacionárias formadas em cada caso --- γ1/2=L --- γ1=2L --- V1= γ1.f1 --- V1=2L.f1
(I) ---γ2/2=L/2 --- γ2=L --- V2= γ2.f2 --- V2=L.f2 (II) --- como a velocidade de propagação em cada caso é a mesma --- V1=V2 --- I=II --- 2Lf1=Lf2 --- 2.220=f2 --- f2=440Hz --- R- A