Interferência de Ondas

Interferência de ondas em meios unidimensionais

Considere dois pulsos propagando-se numa mesma corda em sentidos opostos.

Ao se encontrarem ocorre a interferência e no encontro ocorre o fenômeno da superposição e nele, cada ponto da corda corresponde à soma das perturbações que seriam causadas por cada onda separadamente.

Após a interferência (cruzamento), cada pulso continua seu caminho como se nada tivesse acontecido.

Se os pulsos tiverem a mesma amplitude e a mesma fase teremos interferência construtiva.

Se os pulsos tiverem a mesma amplitude e em oposição de fase teremos interferência destrutiva.

Se as amplitudes forem diferentes e tiverem mesma fase teremos interferência construtiva:

Se as amplitudes forem diferentes e estiverem em oposição de fase teremos uma interferência destrutiva.

Interferência em meios bi e tri dimensionais

O que você deve saber, informações e dicas

Procure entender e memorizar os casos de interferências fornecidos na teoria acima.

Quando duas ou mais ondas sofrem superposição temos o fenômeno da interferência, que ocorre tanto para ondas transversais como para ondas longitudinais.

Durante a superposição, a amplitude da onda resultante é a soma algébrica das amplitudes de cada onda.

Quando os pulsos tiverem a mesma amplitude e em oposição de fase teremosinterferência destrutiva e durante a interferência, quando a corda estiver na horizontal, cada ponto da

mesma terá velocidade vertical e horizontal nulas.

Nos presídios, a necessidade de se impossibilitar qualquer tipo de comunicação, no caso de organizações criminosas, tornou-se patente.

Embora existam muitos sistemas de comunicação móvel, o foco centrou-se em celulares, em virtude de suas pequenas dimensões físicas e da facilidade de aquisição e uso.

Uma das propostas é utilizar um aparelho que origine ondas eletromagnéticas na mesma faixa de freqüência utilizada pelas operadoras de telefonia móvel.

Essas ondas serão espalhadas por meio de antenas, normalmente instaladas nos muros do presídio.

Essas ondas seriam emitidas nas mesmas freqüências utilizadas pelas operadoras de telefonia móvel.

Com isso, através de interferências destrutivas, compromete-se a comunicação entre a ERB (torre celular ou estação de rádio) e o telefone. (Ueg).

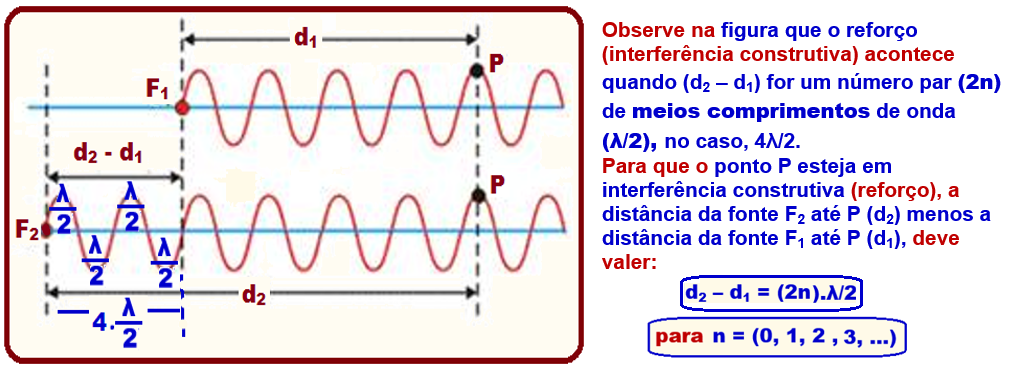
Determinando o tipo de interferência num ponto P sob influência de duas fontes de ondas

Condições para que um ponto P de um meio, devido à interferência de duas ondas esteja em interferência construtiva (reforço) ou interferência destrutiva (aniquilação).

 I Meio unidimensional

Considere duas fontes F₁ e F₂ produzindo no mesmo meio, ondas de mesma freqüência (f), mesmo comprimento de onda (λ), mesma amplitude A, em fase e se interferindo.

O ponto P é distante d₁ de F₁ e d₂ de F₂.

Devido à interferência das ondas geradas por essas duas fontes, podem ocorrer duas situações particulares:

1^a  O ponto P fica em repouso (interferência destrutiva), o que ocorre quando, no mesmo instante, uma crista e um vale estão se superpondo.

2^a  O ponto P fica em reforço (interferência construtiva), o que ocorre quando, no mesmo instante, duas cristas ou dois vales estão se superpondo.

II Meio bi e tridimensional

Considere a figura abaixo onde as fontes F₁ e F₂ estão interferindo.

O que você deve saber, informações e dicas

Procure entender e memorizar as informações e relações acima para ondas sofrendo interferência em meios uni, bi ou tridimensionais.

A interferência entre duas ondas não atrapalha a propagação de ambas pois, a interferência é um fenômeno que descreve a soma das amplitudes das onda e, após a mesma, elas continuam seu movimento como se nada tivesse acontecido.

E também, na interferência entre duas ondas não ocorre perda de energia pois, a energia de uma onda está relacionada à potência do gerador que a fez oscilar.

Alguns exercícios resolvidos, interessantes, que podem ajudá-lo a se aprofundar no assunto e melhorar seu desempenho:

01-(UFC) Duas ondas ocupam a mesma região no espaço e têm amplitudes que variam com o tempo, conforme o gráfico a seguir.

Assinale a alternativa que contém o gráfico resultante da soma dessas duas ondas.

Resolução:

Observe atentamente as figuras e as explicações abaixo:

R- C

 02-(FUVEST-SP) A figura representa, no instante t = 0 s, a forma de uma corda esticada e presa entre duas paredes fixas, na qual dois pulsos (I e II) se propagam, sem mudar de forma, com velocidade de módulo V = 4 m/s nos sentidos indicados.

Não há dissipação de energia na corda. Considere 4 pontos da corda definidos por suas coordenadas X: A (X_A = 7,0 m), B (X_B = 9,0 m, C (X_C = 11,0 m) e D (X_D = 13,0 m).

a) Indique na figura dada, por meio de setas verticais, os sentidos das velocidades na direção do eixo Y, dos pontos A e B, no instante t = 0 s. Se alguma dessas velocidades for nula, escreva “nula”, identificando-a.

b) Determine o valor do módulo da velocidade na direção do eixo Y, do ponto A, no instante t = 0 s.

c) Desenhe a forma da corda no instante t = 1s.

Indique por meio de setas, os sentidos das velocidades na direção do eixo Y, dos pontos C e D.

Se alguma dessas velocidades for nula, escreva “nula”, identificando-a.

Resolução:

a) Os pontos A (7m) e B (9m) estão no pulso I que se move para a direita e localizados conforme a

figura e suas velocidades verticais indicadas na mesma, redesenhando o pulso um pouco para a direita, num instante imediatamente posterior t (linha pontilhada).

b) Observe na figura que cada deslocamento horizontal de 2 m corresponde a um deslocamento vertical de 3 cm.

Assim, enquanto os pontos do pulso I se deslocam de 2m na direção X com velocidade de 4 m/s, eles se deslocam-se de 3 cm na direção Y, no mesmo intervalo de tempo Δt.   

Pulso I    V_I = ΔX/Δt    Δt = ΔX/V_I    Δt = 2/4   Δt = 0,5 s.

Nesse mesmo intervalo de tempo Δt = 0.5s, o ponto A, com velocidade V_A, percorreu ΔY= 3 cm = 0,03 m na direção vertical   V_A=ΔY/Δt    V_A = 0,03/0,5    V_A = 0,06 m/s ou 6 cm/s. 

c) Tanto o pulso I como o II, com velocidade de 4m/s, em 1s, deslocam-se, na direção X de V =

ΔX/Δt    4 = ΔX/1    ΔX = 4m.

Como cada pulso desloca-se 4m em sentidos contrários, no instante t = 1 s eles estarão exatamente superpostos e ocorrerá interferência destrutiva, com a corda exatamente na horizontal e com todos seus pontos tendo velocidade nula, inclusive C e D.

03-(UNESP-SP) Duas fontes, F₁ e F₂, estão emitindo sons de mesma freqüência.

Elas estão posicionadas conforme ilustrado na figura, onde se apresenta um reticulado cuja unidade de comprimento é dada por u = 6,0 m.

No ponto P ocorre interferência construtiva entre as ondas e é um ponto onde ocorre um máximo de intensidade.

Considerando que a velocidade do som no ar é 340 m/s e que as ondas são emitidas sempre em fase pelas fontes F₁ e F₂ , calcule

a) o maior comprimento de onda dentre os que interferem construtivamente em P.

b) as duas menores freqüências para as quais ocorre interferência construtiva em P.

Resolução:

d₁ = 6x6 = 36 m cálculo de d₂ aplicando pitágoras no triângulo hachurado d₂² = 24² + 18² = 576

+ 324 = 900 d₂ = 30 m.

a) Observe, na expressão da interferência construtiva da onda, onde, d_1­ – d₂ = 2n.λ/2    λ = (d₁ -d₂)/n    que λ  e n são inversamente proporcionais. Assim, o maior comprimento de onda λ ocorre quando n = 1 d_1­ – d₂ = 2n.λ/2    36 - 30=2.1.λ/2  λ = 6 m. 

b) Verifique na expressão V=λf que, como a velociade V de propagação da onda é constante (mesmo meio), a freqüência (f) e o comprimento de onda (λ) são inversamente proporcionais. Assim:

1^a menor freqüência    V = λf  340 = 6f    f = 56,7Hz.

2^a menor freqüência    d₁ - d₂ = 2n.(λ/2)    36 – 30 = 2.2. (λ/2)    λ = 3m    V = λf    340 = 3f    f = 113,3 Hz.

Se você deseja se aprofundar ainda mais no assunto, selecionei alguns exercícios cujas resoluções seria interessante você conferir. São as de números 02, 06, 07, 10, 12, 14, 17, 20 e 24.

Exercícios de vestibulares com resoluções comentadas sobre

Interferência de Ondas

01-(UFSCAR-SP) Dois pulsos, A e B, são produzidos em uma corda esticada, que tem uma extremidade fixada em uma parede, conforme mostra a figura.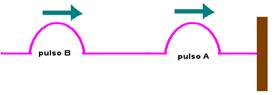

Quando os dois pulsos se superpuserem, após o pulso A ter sofrido reflexão na parede, ocorrerá interferência:

a) construtiva e, em seguida, cada pulso seguirá se caminho mantendo suas características originais.

b) construtiva e, em seguida, os dois pulsos seguirão juntos no sentido do pulso de maior energia.

c) destrutiva e, em seguida os pulsos deixarão de existir, devido a absorção de energia durante a interação.

d) destrutiva e, em seguida, os dois pulsos seguirão juntos no sentido do pulso de maior energia.

e) destrutiva e, em seguida, cada pulso seguirá se caminho mantendo suas características originais.

02-(UFRJ-RJ) A figura 1 retrata, em um dado instante, uma corda na qual se propagam, em sentidos opostos, dois pulsos transversais de mesma forma, um invertido em relação ao outro.

A figura 2 mostra a mesma corda no instante em que a superposição dos pulsos faz com que a corda esteja na horizontal. Estão marcados dois pontos da corda: A e B.

Tendo em conta o eixo transversal orientado representado na figura, cujo sentido positivo é de baixo para cima, verifique se as velocidades escalares dos pontos A e B são positivas, negativas ou nulas. Justifique sua resposta

03-(PUC-PR) O fenômeno da interferência não pode ocorrer com o som, porque, ao contrário da luz, o som consiste de ondas longitudinais. Esta afirmação é:

a) verdadeira, pelos motivos expostos.

b) falsa, pois a interferência se dá nos dois casos.

c) verdadeira, mas não pelos motivos expostos.

d) falsa, pois somente com ondas longitudinais é possível obter interferência.

e) verdadeira, pois em nenhum dos casos, é possível obter interferência.

04-(UFSC) A figura representa dois pulsos de onda, inicialmente separados por  6,0 cm,  propagando-se em um meio com velocidades iguais a 2,0 cm/s, em sentidos opostos.

Considerando a situação descrita, assinale a(s) proposição(ões) CORRETA(S):

(01) Inicialmente as amplitudes dos pulsos são idênticas e iguais a 2,0 cm.

(02) Decorridos 8,0 segundos, os pulsos continuarão com a mesma velocidade e forma de onda, independentemente um do outro.

(04) Decorridos 2,0 segundos, haverá sobreposição dos pulsos e a amplitude será nula nesse instante.

(08) Decorridos 2,0 segundos, haverá sobreposição dos pulsos e a amplitude será máxima nesse instante e igual a 2,0 cm.

(16) Quando os pulsos se encontrarem, haverá interferência de um sobre o outro e não mais haverá propagação dos mesmos.

05-(UFC) Duas ondas ocupam a mesma região no espaço e têm amplitudes que variam com o tempo, conforme o gráfico a seguir.

Assinale a alternativa que contém o gráfico resultante da soma dessas duas ondas.

06-(UFSCAR-SP) A figura mostra dois pulsos numa corda  tensionada no instante t=0 s, propagando-se com velocidade de 2m/s em sentidos opostos.

A configuração da corda no instante t=20ms é:

07- (UFG-GO) Considere duas ondas que se propagam numa mesma corda homogênea, segundo o esquema abaixo, onde a extremidade da direita é fixa.

As ondas se movem no sentido indicado, a uma velocidade de 2m/s.

a) Qual é a amplitude, o comprimento de onda e a freqüência dessas ondas.

b) Faça o desenho da corda após 4s do instante representado no esquema. Qual é a amplitude da onda resultante?

08- (UNIFENAS-MG) No desenho a seguir, vemos duas ondas se propagarem em uma mesma corda, em sentidos opostos

(figura A).

Quando elas estiverem totalmente superpostas (figura B), a forma da corda será:

09-(FUVEST-SP) A figura representa, no instante t=0 s, a forma de uma corda esticada e presa entre duas paredes fixas, na qual dois pulsos (I e II) se propagam, sem mudar de forma, com velocidade de módulo V=4m/s nos sentidos indicados. Não há dissipação de energia na corda. Considere 4 pontos da corda definidos por suas coordenadas X: A (X_A=7,0m), B (X_B=9,0m, C (X_C=11,0m) e D (X_D=13,0m).

a) Indique na figura dada, por meio de setas verticais, os sentidos das velocidades na direção do eixo Y, dos pontos A e B, no instante t=0 s. Se alguma dessas velocidades for nula, escreva “nula”, identificando-a.

b) Determine o valor do módulo da velocidade na direção do eixo Y, do ponto A, no instante t=0 s.

c) Desenhe a forma da corda no instante t=1s. Indique por meio de setas, os sentidos das velocidades na direção do eixo Y, dos pontos C e D. Se alguma dessas velocidades for nula, escreva “nula”, identificando-a.

10-(UEL-PR) Dois pulsos praticamente iguais estão se propagando numa corda elástica AB, com velocidade de propagação de 2cm/s. A extremidade A é livre e nela se originam os pulsos, enquanto a extremidade B é fixa. Considere que a posição dos pulsos no esquema 1 corresponde ao instante t=0.

O esquema 2 também representa a corda elástica AB em outro instante diferente de t=0. Determine o menor intervalo de tempo entre a primeira e a segunda configuração

11-(UFV-MG) Um aparelho de rádio R recebe simultaneamente os sinais direto e refletido em uma camada atmosférica, provenientes de uma emissora E. Quando a camada está a uma altura H, o sinal é forte; à medida que a camada se desloca verticalmente a partir dessa posição, o sinal enfraquece gradualmente, passa por um mínimo e recupera gradativamente o valor inicial.                                                     

Esse fenômeno se deve à:

a) difração, pois a facilidade para o sinal contornar a camada é função da altura.

b) variação do índice de refração da camada, que depende de sua altura em relação ao nível da Terra.

c) interferência entre os sinais direto e refletido, construtiva, quando o sinal for máximo, e destrutiva, quando o sinal for mínimo.

d) absorção do sinal pela camada, que depende de sua altura em relação à Terra.

e) variação do índice de reflexão da camada, o qual é uma função da altura.

12-(UFRJ-RJ)  Duas fontes, F₁ e F₂, em fase, produzem ondas periódicas de comprimento de onda λ. A distância entre as fontes vale 5λ. Alinhado com as fontes temos o ponto P, no qual as ondas tem a mesma amplitude A.

Calcule a amplitude da onda resultante no ponto P

13-(UEL-PR) Dois geradores de ondas periódicas situados em pontos P e Q emitem ondas de mesma amplitude e mesmo comprimento de onda. Se as ondas se anulam num ponto M, devido à interferência, a distância MP – MQ, em módulo, pode ser igual a:

 14-(UFMG-MG) Em uma loja de instrumentos musicais, dois alto-falantes estão ligados a um mesmo amplificador e este, a um microfone. Inicialmente, esses alto-falantes estão um ao lado do outro, como representado, esquematicamente, nesta figura, vistos de cima

Ana produz, ao microfone, um som com freqüência de 680 Hz e José Guilherme escuta o som produzido pelos alto-falantes. Em seguida, um dos alto-falantes é deslocado, lentamente, de uma distância d, em direção a José Guilherme. Este percebe, então, que a intensidade do som diminui à medida que esse alto-falante é deslocado. Dado que a velocidade do som é de 340m/s.

a) EXPLIQUE por que, na situação descrita, a intensidade do som diminui.

b) DETERMINE o deslocamento d necessário para que José Guilherme ouça o som produzido pelos alto-falantes com intensidade mínima.

15-(UFPE-PE) Duas fontes sonoras pontuais F₁ e F₂, separadas entre si de 4,0 m, emitem em fase e na mesma freqüência.

Um observador, se afastando lentamente da fonte F₁, ao longo do eixo x, detecta o primeiro mínimo de intensidade sonora, devido à interferência das ondas geradas por F₁ e F₂, na posição x = 3,0 m. Sabendo-se que a velocidade do som é 340 m/s, qual a freqüência das ondas sonoras emitidas, em Hz?

16-(UNIFESP-SP) Duas fontes, F_A e F_B, separadas por uma distância de 3,0 m, emitem, continuamente e em fase, ondas sonoras com comprimentos de onda iguais. Um detector de som é colocado em um ponto P, a uma distância de 4,0 m da fonte F_A, como ilustrado na figura.

Embora o aparelho detector esteja funcionando bem, o sinal sonoro captado por ele em P, é muito mais fraco do que aquele emitido por uma única fonte. Pode-se dizer que

a) há interferência construtiva no ponto P e o comprimento de onda do som emitido pelas fontes é de 5,0 m.

b) há interferência destrutiva no ponto P e o comprimento de onda do som emitido pelas fontes é de 3,0 m.

c) há interferência construtiva no ponto P e o comprimento de onda do som emitido pelas fontes é de 4,0 m.

d) há interferência construtiva no ponto P e o comprimento de onda do som emitido pelas fontes é de 2,0 m.

e) há interferência destrutiva no ponto P e o comprimento de onda do som emitido pelas fontes é de 2m.

17- (FUVEST-SP) Duas hastes, A e B, movendo-se verticalmente, produzem ondas em fase, que se propagam na superfície da água, com mesma freqüência f e período T, conforme a figura 1. No ponto P, ponto médio do segmento AB, uma bóia sente o efeito das duas ondas e se movimenta para cima e para baixo.

O gráfico que poderia representar o deslocamento vertical y da bóia, em relação ao nível médio da água, em função do tempo t, é

18-(UNESP-SP) Duas fontes, F₁ e F₂, estão emitindo sons de mesma freqüência. Elas estão posicionadas conforme ilustrado na figura, onde se apresenta um reticulado cuja unidade de comprimento é dada por u = 6,0 m.

No ponto P ocorre interferência construtiva entre as ondas e é um ponto onde ocorre um máximo de intensidade. Considerando que a velocidade do som no ar é 340 m/s e que as ondas são emitidas sempre em fase pelas fontes F₁ e F₂ , calcule

a) o maior comprimento de onda dentre os que interferem construtivamente em P.

b) as duas menores freqüências para as quais ocorre interferência construtiva em P.

19-(UECE-CE) A figura mostra dois alto-falantes A e B separados por uma distância de 2m. Os alto-falantes estão emitindo ondas sonoras em fase e de freqüência 0,68kHz. O ponto P mostrado na figura está a uma distância de 1,5m do alto-falante A.

Supondo que a velocidade de propagação do som no ar seja 340m/s, a distância X mínima do alto-falante B ao ponto P para que este ponto seja um ponto nodal (ponto onde a interferência é destrutiva) é:

a) 1,50m         

b) 1,75m         

c) 2,00m         

d) 2,50m         

e) 3,00m

20-(FUVEST-SP) Duas  fontes sonoras F₁ e F₂ estão separadas de 2,5m. Dois observadores A e B estão distantes 10m da fonte F₁, sendo que o observador A está no eixo X e o observador B, no eixo Y, conforme figura.

As duas fontes estão em fase e emitem som numa freqüência fixa f=170Hz. Num dado instante a fonte F₂ começa a deslocar-se lentamente ao longo do eixo X, afastando-se da fonte F₁. Com esse deslocamento, os observadores detectam uma variação periódica na intensidade do som resultante das duas fontes, passando por máximos e mínimos consecutivos de intensidade. Sabe-se que a velocidade do som é de 340m/s nas condições do experimento.Levando em conta a posição inicial das fontes, determine:

a) A separação L_a entre as fontes para a qual o observador A detecta o primeiro mínimo de intensidade.

b) A separação L_b entre as fontes para a qual o observador B detecta o primeiro máximo de intensidade.

21-(UFMG-MG)

Na Figura I, estão representados os pulsos P e Q, que estão se propagando em uma corda e se aproximam um do outro com velocidades de mesmo módulo.

Na Figura II, está representado o pulso P, em um instante t, posterior, caso ele estivesse se propagando sozinho.

A partir da análise dessas informações, assinale a alternativa em que a forma da corda no instante t está CORRETAMENTE representada.

22-(UEG-GO)

23-(FGV-SP) A figura mostra dois pulsos que se movimentam em sentidos contrários, um em direção ao outro sobre a mesma corda, que pode ser considerada ideal.

No momento em que houver sobreposição total, a disposição esperada para os pontos da corda estará melhor indicada por:

24-(UFMG-MG)

Dois alto-falantes idênticos, bem pequenos, estão ligados ao mesmo amplificador e emitem ondas sonoras em fase, em uma só frequência, com a mesma intensidade, como mostrado nessa figura.

Igor está posicionado no ponto O, equidistante dos dois alto-falantes, e escuta o som com grande intensidade. Ele começa a andar ao longo da linha paralela aos alto-falantes e percebe que o som vai diminuindo de intensidade, passa por um mínimo e, depois, aumenta novamente.

Quando Igor chega ao ponto M, a 1,0 m do ponto O, a intensidade do som alcança, de novo, o valor máximo.

Em seguida, Igor mede a distância entre o ponto M e cada um dos alto-falantes e encontra 8,0 m e 10,0m como indicado na figura.

01- Explique por que, ao longo da linha OM, a intensidade do som varia da forma descrita e CALCULE o comprimento de onda do som emitido pelos alto-falantes.

02- Assinalando com um X a quadrícula apropriada, responda:

Se a frequência emitida pelos alto-falantes aumentar, o ponto M estará mais distante ou mais próximo do ponto O?

Justifique sua resposta.

Resolução comentada dos exercícios de vestibulares sobre

Interferência de Ondas

 01- R: E.  Como o pulso A retornará invertido (extremidade fixa) ao se superpuserem os dois pulsos sofrerão interferência destrutiva e em seguida, cada pulso seguirá se caminho mantendo suas características originais

02- Nulas; pois no instante da interferência destrutiva não há movimento dos pontos participantes.

03- B    

04- (01+02+04) = 07

05- R- C

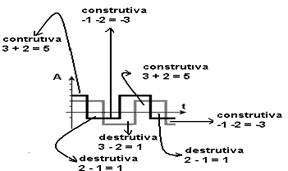
06- R - D

V=ΔS/Δt  ---  200=ΔS/0,02  ---  ΔS=4cm

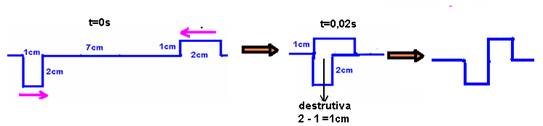
07-  

a) A=2m; l=4m e f=0,5Hz  ---  V=lf  ---  2=4f  ---  f=0,5Hz

b) Após 4s as ondas se deslocaram de V=ΔS/Δt  ---  2=ΔS/4  ---  ΔS=8m. Assim, a primeira onda que está voltando invertida e a segunda que está chegando, no instante 4s, se interferem construtivamente e a amplitude da onda resultante será de 2+2=4m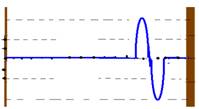

08- Todos os pontos estão em interferência construtiva cuja soma será a altura do retângulo. R: E

09- a) Os pontos A (7m) e B (9m) estão no pulso I que se move para a direita e localizados conforme a figura e suas velocidades verticais indicadas na mesma.

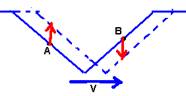
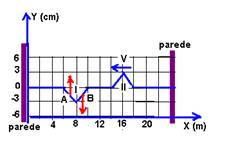
b) Enquanto o pulso I se desloca de 2m na direção X com velocidade de 4m/s, os pontos da corda deslocam-se de 3cm na direção Y, no mesmo intervalo de tempo Δt.   

Pulso I  ---  V_I=ΔX/Δt  ---  Δt=ΔX/V_I  ---  Δt=2/4  --- Δt=0,5s

Nesse mesmo intervalo de tempo Δt=0.5s, o ponto A, com velocidade V_A, percorreu ΔY=0,03m na direção vertical  ---  V_A=ΔY/Δt  ---  V_A=0,03/0,5  ---  V_A=0,06m/s ou 6cm/s. 

c) Tanto o pulso I como o II, com velocidade de 4m/s, em 1s, deslocam-se, na direção Xde:  V=ΔX/Δt  ---  4=ΔX/1  ---  ΔX=4m

Como cada pulso desloca-se 4m em sentidos contrários, no instante t=1s eles estarão exatamente

superpostos e ocorrerá interferência destrutiva, com a corda exatamente na horizontal e com todos seus pontos tendo velocidade nula, inclusive C e D.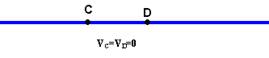

10- A parte da frente de onda da direita (esquema1) percorreu 2cm até atingir o anteparo e mais 3cm de retorno (esquema 2) no intervalo de tempo Δt. A mesma distância percorreu a outra onda.

V=ΔS/Δt  ---  2=5/Δt  ---  Δt = 2,5s

11- C

12- Veja a figura abaixo:

d₁ – d₂ = (5λ + X) – X = 5λ = 10.λ/2  --- portanto n é par  ---  interferência construtiva de amplitude 2 A

13- B

14- a) Como as duas fontes emitem ondas de mesma freqüência e estão lado a lado, estas ondas estão em fase e José Guilherme ouve esses sons com reforço (interferência construtiva). Mas, com o deslocamento de uma delas a interferência vai ficando destrutiva.

b) V=λf  ---  340=l680  ---  λ=0,5m.

A primeira interferência destrutiva ocorre quando n=0. Assim, d=(2n+1).λ/2 ---  d=(2.0 +1).0,5/2  ----d=0,25m=25cm

15- Como é mínimo, trata-se de interferência destrutiva e é válida a relação d₂ – d₁ = (2n+1).λ/2, com n=0 (primeiro mínimo).

Observe na figura abaixo que d₁=3m e d₂=5m

Cálculo do comprimento de onda λ  ---  d₂ – d₁=5-3=2m  ---  d₂ – d₁ = (2n+1).λ/2  ---  2=(2.0 + 1).λ/2  ---  λ=4m.

V=λf  ---  340=4f  ---  f=85Hz

16- E

A interferência é destrutiva, pois o sinal captado é mais fraco.  d(F_AP)=4m  ---  d(F_BP)=5m  ---  d(F_BP) -  d(F_AP)= (2n+1).λ/2    5-4=(2.0 +1).λ/2  ---  1=λ/2  ---  λ=2m

17-  E

Observe que o ponto P está exatamente no meio das duas fontes de onda e, então como elas se movem com a mesma velocidade (mesmo meio), haverá sempre uma interferência construtiva, pois as ondas estão em fase.

Assim, duas cristas e dois vales sempre chegarão juntas ao ponto P e a bóia sobe e desce com amplitude que é o dobro da amplitude de cada fonte, mas com o mesmo período T das fontes originais.

18- Observe na figura abaixo que d₁=36m e d₂=30m

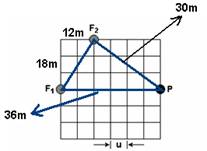
a) Verifique, na expressão da interferência construtiva da onda, onde, d_1­ – d₂ = 2n.λ/2  --- λ=d₁-d₂/n  ---  que λ n são inversamente proporcionais. Assim, o maior comprimento de onda (λ) ocorre quando n=1.

D_1­ – d₂ = 2n.λ/2  ---  36-30=2.1.λ/2  ---  λ=6m 

b) Verifique na expressão V=λf  ---  f=V/lλ ---  que a freqüência (f) e o comprimento de onda (λ) são inversamente proporcionais. Assim:

1^a menor freqüência  ---  V=λf  ---340=6f  ---  f=56,7Hz

2^a menor freqüência  ---  d₁-d₂=2n. λ/2  ---  36-30=2.2. λ/2  ---  λ=3m    ----     V=λf  ---  340=3f  ---  f=113,3Hz

19- R – B

V=λf  ---  340=λ680  ---  λ=0,5m          Interferência destrutiva – X-1,5=(2n+1). λ/2  ---  mínima (n=0)  ---  X=1,5+ (2.0+1). λ/2 --- X=1,75m.

20- O comprimento de onda de cada uma das fontes vale  ---  V=λf  ---  340=λ.170  ---  λ=2m

a) Ao atingirem A, as ondas provenientes de F₁ e F₂ devem sofrer aí, interferência destrutiva (mínimos de intensidade).

Na situação inicial  ---  d(F₁A)=10m e d(F₂A)=12,5m  ---  d(F₂A)- d(F₁A)=12,5 -10=2,5m =ΔX_i

Na situação de interferência destrutiva com a fonte F₂ mais afastada, a distância entre as mesmas será ΔX_d

A equação da interferência destrutiva é ΔX_d=(2n+1).λ/2. Quando n=0, a solução não satisfaz, pois nesse caso, ΔX_d=1m e como F₂ deve ser afastada, ΔX_d que é a distância entre as fontes, deve ser maior que 2,5m.

Para n=1  ---  ΔX_d=(2n+1).l/2.  ---    ΔX_d = (2.1+1).l/2  ---  ΔX_d = (2.1+1).2/2  --- ΔX_d=3m (L_a)

b) Ao atingirem B, as ondas provenientes de F₁ e F₂ devem sofrer aí, interferência construtiva (máximos de intensidade) e, nesse caso, ΔX_d=2n.λ/2. A condição n=0 não satisfaz, pois, nesse caso DX_d=0 e as fontes estaria coincidentes e sabemos que elas estão distanciadas de mais de 2,5m.

d(F₁B)=10m  ---  d(F₂B)=?

Para n=1  ---  ΔX_d=2n.l/2  ---  ΔX_d=2.1.2/2  ---  ΔX_d=2m

ΔX_d= d(F₂B) - d(F₁B)  ---  2= d(F₂B) – 10  ---  d(F₂B)=12m

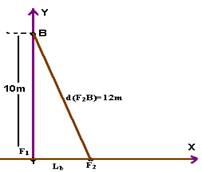
Pitágoras  ---  (10)² + L_b²=(12)²  ---  L_b=6,6m

21- R- D  ---  veja teoria

22- a) Não  ---  a interferência é um fenômeno que descreve a soma das amplitudes das onda e, após a mesma, elas continuam seu movimento como se nada tivesse acontecido..

b) Não  ---  a energia de uma onda está relacionada à potência do gerador que a fez oscilar.

23- 

Observe a figura abaixo onde está representado o instante  em que as ondas estão totalmente sobrepostas  ---  haverá interferência construtiva na metade esquerda do intervalo e destrutiva na metade direita do mesmo intervalo  ---  R- C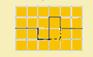

24-

01- Como as ondas emitidas pelos dois alto-falantes estão em fase elas possuem a mesma freqüência (f), o mesmo comprimento de onda (λ), e mesma amplitude (A) e em fase (ambas para cima ou ambas para baixo)  ---  nos pontos O e M as ondas estão em concordância de fase (som de intensidade máxima, reforço)  ---  para o ponto M, onde as ondas estão em concordância de fase (interferência construtiva),  a distância de uma fonte até M (d₂=10m) menos a distância da outra  fonte até M (d₁=8m), deve valer um comprimento de onda 1λ  ---  d₂ – d₁=1λ  ---  10 – 8=1λ  ---  λ=2,0m.

02- Mais próxima  ---  como V=λ.f e como V é constante, o comprimento de onda λ e a frequência f são inversamente proporcionais  ---  assim, como entre O e M existe um λ, se a frequência aumenta, esse λ diminui e o ponto M ficará mais perto do ponto O.