
Cordas vibrantes - Harmônicos
No estudo da acústica, uma harmônica de uma onda sonora corresponde à uma frequência específica de vibração que tem a propriedade de causar o fenômeno de ressonância.
Essas
frequências
são denominadas frequências
de ressonância.
Assim, o conjunto de todos os modos de oscilação possíveis é chamado de série harmônica.
Para que você estude detalhadamente os harmônicos deve dividi-los em duas partes, cordas vibrantes e tubos sonoros.
Cordas vibrantes
As cordas vibrantes correspondem à fios flexíveis e tracionados (tensionados) em seus extremos,
utilizados
em instrumentos
musicais como,
violão,
guitarra, violino, cavaquinho, banjo, etc.
Harmônicos de uma corda vibrante
Os harmônicos de uma corda vibrante são as várias possíveis freqüências naturais das ondas estacionárias que surgem em cordas tensas (sob ação de forças tensoras de intensidade T), com massa m e comprimento L e densidade linear de massa µ.



Velocidade V de propagação da onda na corda
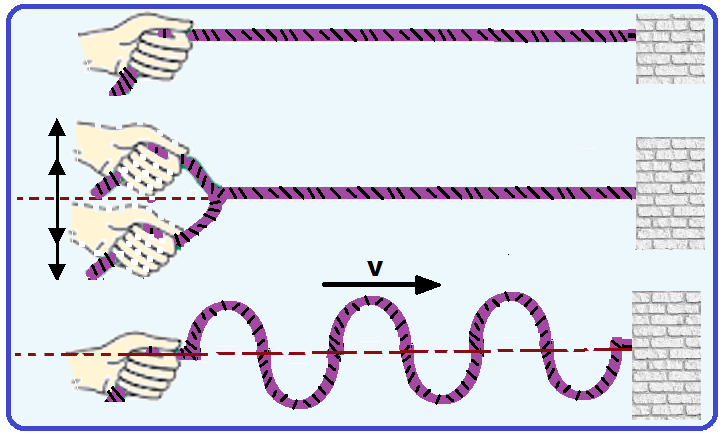
As ondas periódicas são originadas por fontes que executam oscilações periódicas (são repetidas em intervalos de tempos iguais).
Sendo assim, podemos dizer que a propagação de uma onda periódica em um meio homogêneo e isótropo é um movimento uniforme, com a onda se propagando com velocidade constante V, tal que V = ΔS/Δt.
Equação fundamental da ondulatória
Observe
na figura
as características
de uma onda
transversal se
propagando numa corda,
com com
velocidade V: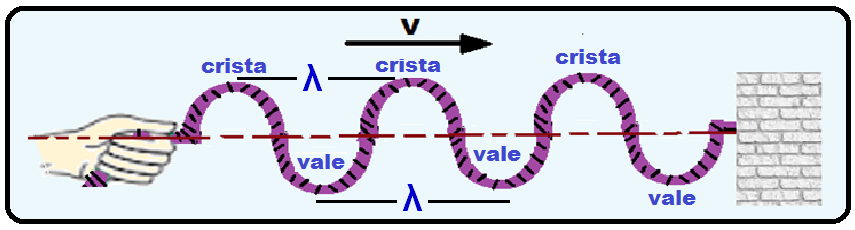
![]() Comprimento
de onda (λ)
Comprimento
de onda (λ)
![]() distância entre
duas cristas
ou
dois vales
consecutivos.
distância entre
duas cristas
ou
dois vales
consecutivos.
![]() Período
(T)
Período
(T)
![]() que
é o intervalo
de tempo para
que cada
ponto homogêneo da onda execute
uma oscilação completa, ou percorra
um comprimento de onda λ.
que
é o intervalo
de tempo para
que cada
ponto homogêneo da onda execute
uma oscilação completa, ou percorra
um comprimento de onda λ.
![]() Frequência
(f)
Frequência
(f)
![]() número
de oscilações
completas que cada ponto homogêneo da onda executa na unidade de
tempo.
número
de oscilações
completas que cada ponto homogêneo da onda executa na unidade de
tempo.
Observe nas informações acima que, num intervalo de tempo Δt que corresponde a um período T (Δt = T), a onda percorre uma distância ΔS que corresponde a um comprimento de onda λ (ΔS = λ).
V
= ΔS/Δt
![]() V = λ/T
V = λ/T
![]() T = 1/f
T = 1/f
![]() V = λ/(1/f)
V = λ/(1/f)
![]() V
= λ.f (equação fundamental da ondulatória)
V
= λ.f (equação fundamental da ondulatória)

Fórmula de Taylor para cordas vibrantes
Pode-se provar que, para a propagação de um pulso transversal ou de uma onda periódica transversal numa corda, a velocidade (V) com que uma onda periódica se propaga depende da densidade linear de massa (µ) da corda e da intensidade da força tensora (T) a que ela está sujeita.
A relação entre essas grandezas foi provada matematicamente pelo britânico Brook Taylor (1685-1731), onde você pode determinar a velocidade de propagação de uma onda numa corda utilizando a equação conhecida como Fórmula de Taylor, expressa a seguir:

Modos de vibração (harmônicos) em cordas vibrantes
Considere uma corda de comprimento L fixa em seus extremos.
Produzindo-se uma perturbação em qualquer ponto entre os extremos fixos, esta perturbação propaga-se até cada uma das extremidades, refletem-se e retornam em sentido contrário, formando
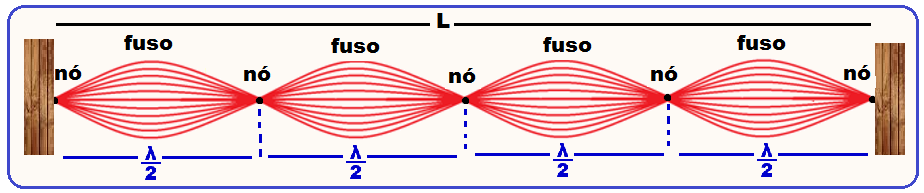
ondas estacionárias com nós (pontos que não vibram) e ventres (distância entre dois nós, que chamamos de fuso, onde todos os pontos estão em movimento vibratório).
As figuras abaixo mostram os diversos modos de vibração numa mesma corda (mesmo meio, mesma velocidade).
A onda estacionária de freqüência mais baixa é chamada freqüência fundamental. Ela corresponde a uma onda estacionaria com um único ventre, o harmônico fundamental ou primeiro harmônico.
As demais freqüências naturais são chamadas sobretons ou harmônicos superiores, pois as freqüências subsequentes são múltiplos inteiros da freqüência fundamental.
![]()

![]()
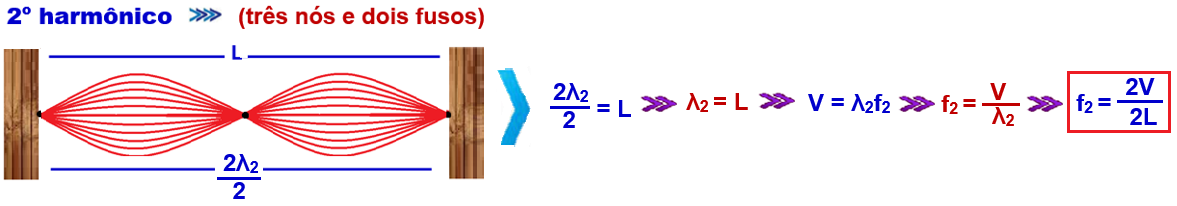
![]()

![]()
Enésimo
harmônico ![]() (“n
+ 1” nós e n
fusos)
(“n
+ 1” nós e n
fusos)
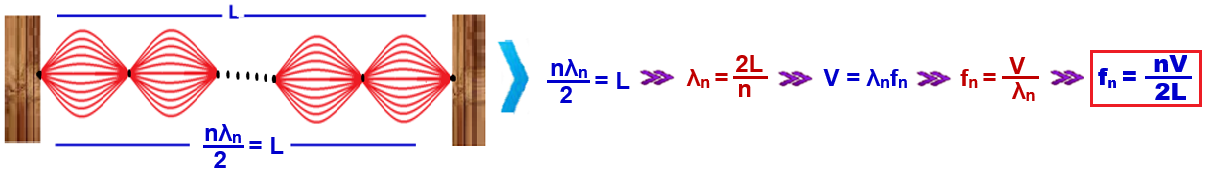
Lembrando
que f1
=
V/2L
![]() fn
= nf1
fn
= nf1
Generalizando:

Observe que existe uma relação simples entre o comprimento L da corda e o comprimento de onda λ da onda estacionária de frequência fn que nela se estabelece.
Generalizando,
para o enésimo
harmônico
![]() n
= 1, 2, 3, 4, 5, ...
n
= 1, 2, 3, 4, 5, ...
O número inteiro n corresponde ao número do harmônico: n = 1, para o harmônico fundamental; n = 2, para o segundo harmônico; n = 3, para o terceiro harmônico; e assim por diante.
Da
equação
de Taylor, para o enésimo harmônico,
teremos
![]() V
=
V
= ,
que,
substituída
em fn
=
n
,
que,
substituída
em fn
=
n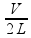 ,
nos fornece:
,
nos fornece:

Observe na expressão acima que temos três variáveis, comprimento da corda L, densidade linear de
massa (corda mais grossa ou mais fina) µ e força de tração T.
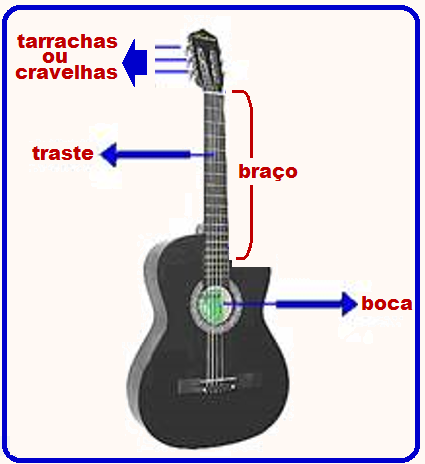
As cordas de um violão, por exemplo, são dedilhadas com o polegar, indicador, médio e anular da mão direita e, para variar o comprimento da corda L, o músico coloca os dedos da mão esquerda fazendo pressão no espaço entre os trastes, produzindo assim as diversas notas musicais.
Para variar a densidade linear µ, o músico muda de uma corda para a outra e, para afinar o instrumento ele varia a força de tração girando as cravelhas ou tarraxas ( roscas para essa finalidade).
Variando dessa maneira essas três grandezas o músico obtém as várias notas musicais (harmônios, freqüências).
O que você deve saber, informações e dicas
 A
frequência
de uma onda é sempre a mesma frequência da fonte produtora da onda.
A
frequência
de uma onda é sempre a mesma frequência da fonte produtora da onda.
Dessa forma, independentemente do meio em que a onda se propaga, sua frequência não vai ser modificada.
![]() A velocidade
de propagação de uma onda mecânica em um determinado meio só
depende das propriedades elásticas do meio.
A velocidade
de propagação de uma onda mecânica em um determinado meio só
depende das propriedades elásticas do meio.
![]() Procure
entender e
memorizar as informações
e as expressões matemáticas fornecidas acima.
Procure
entender e
memorizar as informações
e as expressões matemáticas fornecidas acima.
 Analise
atentamente as
resoluções desses exercícios interessantes:
Analise
atentamente as
resoluções desses exercícios interessantes:
![]() 01-
(UNICAMP-SP) Para
a afinação
de um piano usa-se
um diapasão
com frequência fundamental igual a 440Hz, que é a frequência
da nota Lá.
01-
(UNICAMP-SP) Para
a afinação
de um piano usa-se
um diapasão
com frequência fundamental igual a 440Hz, que é a frequência
da nota Lá.
a)
A
nota
Lá de
certo piano
está desafinada e
o
seu harmônico
fundamental
está representado na curva tracejada do gráfico.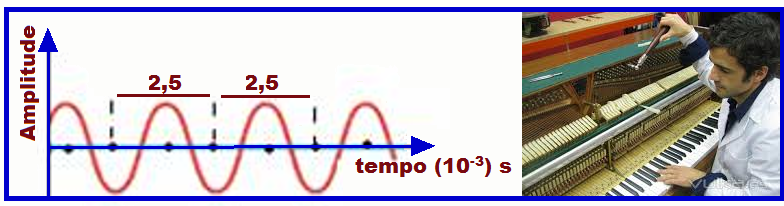
a) Obtenha a freqüência da nota Lá desafinada.
b) O comprimento dessa corda do piano é igual a 1m e sua densidade linear é igual a 5,0.10-2g/cm. Calcule o aumento de tensão na corda necessário para que a nota Lá seja afinada.
Resolução:
a)
Observe no gráfico
que
representa o harmônico
fundamental da
nota
Lá desafinda que o período (tempo
decorrido entre duas cristas ou vales consecutivos) vale
T
= 2,5.10-3s
![]() f
= 1/T
f
= 1/T
![]() f = 1/2,5.10-3
f = 1/2,5.10-3
![]() f
= 400Hz (frequência do harmônico funfamental da nota Lá
desafinada).
f
= 400Hz (frequência do harmônico funfamental da nota Lá
desafinada).
b) Tração (tensão) T1 da nota Lá desafinada de frequência f=400Hz, densidade linear µ = 5,0.10-3kg/m.
![]()
Tração (tensão) T2 da nota Lá afinada (frequência do diapasão) f = 440H z, densidade linear µ = 5,0.
10-3kg/m.
![]()
O aumento pedido de tensão na corda necessário para que a nota lá seja afinada será ΔT =T2 – T1 = 3.872 – 3.200 = 672N.
![]() 02-
(UFMG-MG)
Bruna afina a corda mi de seu violino,
para que ela
vibre com uma freqüência mínima de 680 Hz.
02-
(UFMG-MG)
Bruna afina a corda mi de seu violino,
para que ela
vibre com uma freqüência mínima de 680 Hz.
A
parte
vibrante das cordas do violino de Bruna mede 35 cm de comprimento,
como mostrado nesta figura: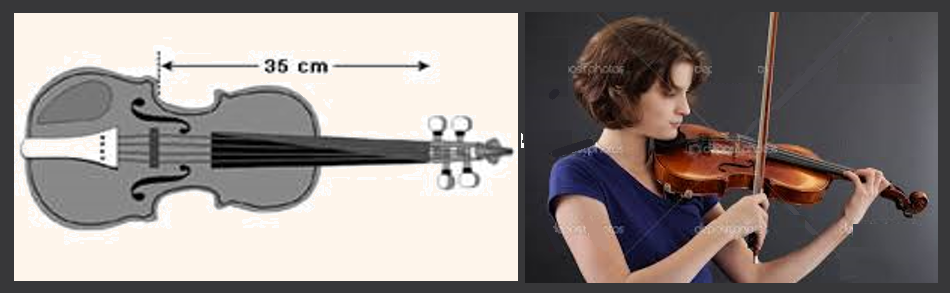
Considerando essas informações,
a) Calcule a velocidade de propagação de uma onda na corda mi desse violino.
b) Considere que a corda mi esteja vibrando com uma freqüência de 680 Hz.
Determine o comprimento de onda, no ar, da onda sonora produzida por essa corda.
Velocidade do som no ar = 340 m/s
Resolução:
a)
Pelo
enunciado a frequência
mínima de vibração que
ele fornece é a
frequência fundamental f1
=
680 Hz ![]() comprimento da corda L = 35cm
comprimento da corda L = 35cm
![]() comprimento
de onda do
primeiro
harmônico λn
= 2L/n
comprimento
de onda do
primeiro
harmônico λn
= 2L/n
![]() n=
1
n=
1
![]() λ1
= 2.35/1
λ1
= 2.35/1
![]() λ1
= 70 cm
λ1
= 70 cm
V
=λ.f
![]() V = 0,7.680
V = 0,7.680
![]() V
= 476 m/s (velocidade da onda na corda mi, constante).
V
= 476 m/s (velocidade da onda na corda mi, constante).
b) Dados: frequência de vibração da corda mi f = 680 Hz que é a mesma que no ar, pois a frequência independe do meio de propagação e velocidade de propagação do som no ar V = 340 m/s.
Equação
fundamental da ondulatória
![]() v = λ.f
v = λ.f
![]() 340 = λ.680
340 = λ.680
![]() λ =
340/680
=
0,5 m = 50
cm
λ =
340/680
=
0,5 m = 50
cm
 03-(UFG)
Na
experiência
de ressonância em cordas
representada na figura, dois
fios de
densidades
diferentes estão tensionados,
através de roldanas
ideais, por
um
bloco que pende deles dois.
03-(UFG)
Na
experiência
de ressonância em cordas
representada na figura, dois
fios de
densidades
diferentes estão tensionados,
através de roldanas
ideais, por
um
bloco que pende deles dois.
As
extremidades
esquerdas de ambos estão ligadas a uma fonte que
produz pequenas
vibrações com
freqüência
conhecida. 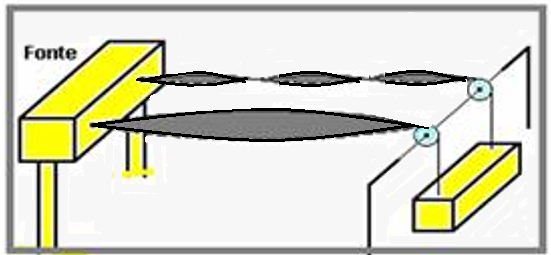
A
distância
entre a fonte e as roldanas é L. Verifica-se que,
quando a freqüência
da fonte atinge o
valor
f, ambos os fios entram em ressonância, o
mais
denso no terceiro harmônico
e o outro, na
freqüência fundamental.
Dados:
v
=
 (velocidade da onda na corda).
(velocidade da onda na corda).
Conhecendo a densidade linear de massa µ do fio mais denso, determine a densidade linear de massa do outro fio;
Resolução:
Cada
fio possui
possui a mesma
frequência f de oscilação que
é a da
fonte,
f1
= f2
= f
![]() a força de tração também é a mesma para cada fio, pois(suportam
o mesmo peso (P/2), T1
= T2
= T.
a força de tração também é a mesma para cada fio, pois(suportam
o mesmo peso (P/2), T1
= T2
= T.
O comprimento L de cada fio é o mesmo (distância entre fonte e roldanas iguais).
O
fio
com três fusos é a mais denso (µ1),
pois
como T
é a mesma (v
=
 )
V
e µ são inversamente proporcionais
e V
é menor na mais densa.
)
V
e µ são inversamente proporcionais
e V
é menor na mais densa.
Da equação V = λf, como f é a mesma, menor V implica em menor λ, que é o da corda com três fusos (µ1).

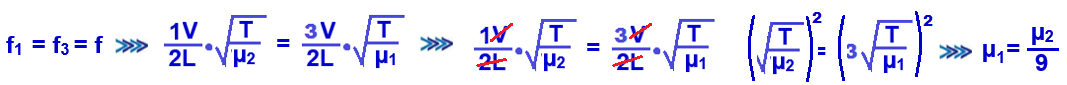
Exercícios de vestibulares com resolução comentada sobre
cordas vibrantes - Harmônicos
01-(UFSCAR-SP)
Com
o carro parado no congestionamento sobre o centro de um viaduto, um
motorista pôde constatar que a estrutura deste estava oscilando
intensa e uniformemente. Curioso, pôs-se a contar o número de
oscilações que estavam ocorrendo. Conseguiu contar 75 sobes e
desces da estrutura no tempo de meio minuto, quando teve que
abandonar a contagem devido ao reinício lento do fluxo de carros.
Mesmo em movimento, observou que conforme percorria lentamente a outra metade a ser transposta do viaduto, a amplitude das oscilações que havia inicialmente percebido gradativamente diminuía, embora mantida a mesma relação com o tempo, até finalmente cessar na chegada em solo firme. Levando em conta essa medição, pode-se concluir que a próxima forma estacionária de oscilação desse viaduto deve ocorrer para a freqüência, em Hz, de
![]()
02-(PUC-PR)
Numa
certa guitarra, o comprimento das cordas (entre suas extremidades
fixas) é de 0,6 m. Ao ser dedilhada, uma das cordas emite um som de
freqüência fundamental igual a 220 Hz.
Marque a proposição verdadeira:
a) Se somente a tensão aplicada na corda for alterada, a freqüência fundamental não se altera.
b) A distância entre dois nós consecutivos é igual ao comprimento de onda.
c) O comprimento de onda do primeiro harmônico é de 0,6 m.
d) A velocidade das ondas transversais na corda é de 264 m/s.
e) As ondas que se formam na corda não são ondas estacionárias.
03- (UNIFESP-SP) A figura representa uma configuração de ondas estacionárias produzida num laboratório didático com uma fonte oscilante.
a)
Sendo d = 12 cm a distância entre dois nós sucessivos, qual o
comprimento de onda da onda que se propaga no fio?
b) O conjunto P de cargas que traciona o fio tem massa m = 180 g. Sabe-se que a densidade linear do fio é m = 5,0.10-4kg/m. Determine a freqüência de oscilação da fonte.
Dados:
velocidade de propagação de uma onda numa corda: v
=
 ;
g =10m/s2.
;
g =10m/s2.
04-(UECE)
Uma
corda de 90 cm é presa por suas extremidades, em suportes fixos,
como mostra a figura.
Assinale a alternativa que contém os três comprimentos de onda mais longos possíveis para as ondas estacionárias nesta corda, em centímetros.
a) 90, 60 e 30
b) 180, 90 e 60
c) 120, 90 e 60
d) 120, 60 e 30
05-(UFPB) A figura a seguir mostra uma corda de densidade linear igual a 1 g/m, que passa por uma roldana. A sua extremidade esquerda está presa a um vibrador e, na extremidade direita, pendura-se um corpo de massa M
Nessa
situação, quando a distância L, entre o vibrador e a roldana, for
0,5 m e a vibração estiver na freqüência de 200 Hz, a corda
vibrará no modo fundamental. Com base nesses dados, o valor de M
deve ser igual a: ( g=10m/s2)
a) 3 kg
b) 4 kg
c) 5 kg
d) 6 kg
e) 7 kg
06-(UFPB) Uma das cordas de uma harpa tem comprimento igual a 50 cm.

O maior comprimento de onda estacionária que um músico pode estabelecer nessa corda, em cm, é:
a) 12,5
b) 25
c) 50
d) 100
e) 200
07- (UFMG-MG) Bruna afina a corda mi de seu violino, para que ela vibre com uma freqüência mínima de 680 Hz.
A
parte vibrante das cordas do violino de Bruna mede 35 cm de
comprimento, como mostrado nesta figura:Considerando essas
informações,
a) CALCULE a velocidade de propagação de uma onda na corda mi desse violino.
b) Considere que a corda mi esteja vibrando com uma freqüência de 680 Hz. DETERMINE o comprimento de onda, no ar, da onda sonora produzida por essa corda.
Velocidade do som no ar = 340 m/s
08-(UFPA) No trabalho de restauração de um antigo piano, um músico observa que se faz necessário substituir uma de suas cordas.
Ao
efetuar a troca, fixando rigidamente a corda pelas duas extremidades
ao piano, ele verifica que as freqüências de 840 Hz, 1050 Hz e 1260
Hz são três freqüências de ressonâncias sucessivas dos
harmônicos gerados na corda. Se a velocidade de propagação de uma
onda transversal na corda for 210 m/s, pode-se afirmar que o
comprimento da corda, colocada no piano, em cm, é
a) 100
b) 90
c) 30
d) 50
e) 30
09-(UFU-MG) Uma corda de um violão emite uma freqüência fundamental de 440,0 Hz ao vibrar livremente, quando tocada na região da boca, como mostra Figura 1.
Pressiona-se então a corda a L/3 de distância da pestana, como mostra Figura 2

A freqüência fundamental emitida pela corda pressionada, quando tocada na região da boca, será de:
a) 660,0 Hz.
b) 146,6 Hz.
c) 880,0 Hz.
d) 293,3 Hz.
10-(ITA-SP)
São
de 100 Hz e 125 Hz, respectivamente, as freqüências de duas
harmônicas adjacentes de uma onda estacionária no trecho horizontal
de um cabo esticado, de comprimento L = 2 m e densidade linear de
massa igual a 10 g/m (veja figura).
Considerando a aceleração da gravidade g = 10 m/s2, a massa do bloco suspenso deve ser de
a) 10 kg
b) 16 kg
c) 60 kg
d) 102 kg
e) 104 kg
11-(UFRN) Afinar a corda de um instrumento musical é ajustar a tensão dessa corda até que a freqüência de seu modo fundamental de vibração coincida com uma freqüência predeterminada. Uma forma usual de se afinar um violão consiste em afinar uma das últimas cordas (valendo-se de memória musical ou da comparação com algum som padrão, obtido por meio de um diapasão, piano, flauta, etc.) e usar tal corda para afinar as outras que ficam abaixo dela. (A figura seguinte ilustra em detalhe o braço de um violão).
Flavita,
acostumada a afinar seu violão, afina inicialmente a corda número
5. Assim, para afinar a corda número 4, ela pressiona a corda 5
entre o quarto e o quinto traste, percute-a, observa se a corda 4
vibra e o quão intensamente vibra em conseqüência desse
procedimento. Flavita vai ajustando a tensão na corda 4 e repetindo
tal procedimento até que ela vibre com a maior amplitude possível.
Quando isso ocorre, essa corda está afinada.
Com base no que foi exposto no enunciado, atenda às solicitações seguintes.
a) Dê o nome do fenômeno físico que fundamenta esse processo de afinação do violão.
b) Com base em seus conhecimentos de acústica, explique como esse fenômeno ocorre no processo de afinação do violão.
12-(UFG)
Na
experiência de ressonância em cordas representada na figura, dois
fios de densidades diferentes estão tensionados, através de
roldanas ideais, por um bloco que pende deles dois. As extremidades
esquerdas de ambos estão ligadas a uma fonte que produz pequenas
vibrações com freqüência conhecida. A distância entre a fonte e
as roldanas é L. Verifica-se que, quando a freqüência da fonte
atinge o valor f, ambos os fios entram em ressonância, o mais denso
no terceiro harmônico e o outro, na freqüência fundamental. Dados:
v = ÖT/m - velocidade da onda na corda.
Conhecendo a densidade linear de massa m do fio mais denso, determine a densidade linear de massa do outro fio;
13-(UECE) Na figura as cordas A e B, de mesmo comprimento, têm densidades mA e mB, respectivamente, (mA < mB) e estão presas a um bloco como mostra a figura.

As duas cordas são perturbadas de tal modo que cada uma vibra em sua respectiva freqüência fundamental. Em relação às velocidades e freqüências nas cordas (v é a velocidade de propagação da onda e f é a freqüência fundamental), podemos afirmar, corretamente:
a) VA> VB e fA< fB
b) VA < VB e fA<fB
c) VA >VB e fA > fB
d) VA < VB e fA>fB
e) VA =VB e fA = fB
14- (UNIFEI-MG) Uma corda de violão de 64cm de comprimento emite uma nota Sol (f=392Hz) quando tocada.. Que comprimento deve ter essa mesma corda para que emita uma nota Lá(f=440Hz)?
15-(UFPE) Uma corda de violão de 1,0m de comprimento tem massa de 20g.
Considerando
que a velocidade (V) de uma onda na corda, a tensão (T) e a
densidade linear de massa da corda (m) estão relacionadas por v
=
 ,
calcule a tensão, em unidades de 102N,
que deve ser aplicada na corda, para afina-la em dó médio(260Hz),
de modo que o comprimento da corda seja igual a meio comprimento de
onda.
,
calcule a tensão, em unidades de 102N,
que deve ser aplicada na corda, para afina-la em dó médio(260Hz),
de modo que o comprimento da corda seja igual a meio comprimento de
onda.
16-(CESGRANRIO-RJ) Pitágoras já havia observado que duas cordas cujos comprimentos estivessem na razão de 1 para 2
Soariam
em uníssono. Hoje sabemos que a razão das freqüências dos sons
emitidos por essas cordas é igual à razão inversa dos seus
comprimentos. A freqüência da nota lá-padrão (o lá central do
piano) é 440Hz., e a freqüência do lá seguinte, mais agudo é
880Hz. A escala cromática (ou bem temperada), usada na música
ocidental de J. S. Bach (século XVIII) para cá, divide esse
intervalo (dito de oitava) em doze semitons iguais, isto é,
tais que a razão das freqüências de notas consecutivas é
constante. Essas notas e suas respectivas freqüências (em Hz e
aproximadas para inteiros) estão na tabela a seguir.

A corda mi de um violino usado em um conjunto de música renascentista está afinada para a freqüência de 660Hz.
Para tocar a nota lá, de freqüência 880Hz, prende-se a corda com um dedo, de modo a utilizar apenas uma fração da corda.
Que fração é essa?
17-(UNICAMP-SP) Para a afinação de um piano usa-se um diapasão com frequência fundamental igual a 440Hz, que é a frequência da nota Lá.
a)
A nota Lá de certo piano está desafinada e o seu harmônico
fundamental está representado na curva tracejada do gráfico.
Obtenha a freqüência da nota Lá desafinada.
b) O comprimento dessa corda do piano é igual a 1m e sua densidade linear é igual a 5,0.10-2g/cm. Calcule o aumento de tensão na corda necessário para que a nota Lá seja afinada.
18-(FUVEST-SP) Considere uma corda de violão com 50cm de comprimento que está afinada para vibrar com frequência de 500Hz.

a) Qual a velocidade de propagação da onda nessa corda?
b) Se o comprimento da corda for reduzido à metade, qual a nova freqüência do som emitido?
19-(UFPE) Ondas estacionárias se formam numa corda de comprimento L, cujas extremidades estão fixas. Determine a razão fn+1/fn, entre as freqüências de vibração de dois harmônicos consecutivos.
20-(CESGRANRIO-RJ) Uma corda de violão é mantida tensionada quando presa entre dois suportes fixos no laboratório. Posta a vibrar, verifica-se que a mais baixa freqüência em que se consegue estabelecer uma onda estacionária na corda é fo=100Hz. Assim, qual das opções a seguir apresenta a sucessão completa das quatro próximas freqüências possíveis para ondas estacionárias na mesma corda, em Hz?
a) 150, 200, 250, 300
b) 150, 250, 350, 450
c) 200, 300, 400, 500
d) 200, 400, 600, 800
e) 300, 500,700, 900
21-(UFC-CE)

Duas cordas de diâmetros iguais foram construídas de um mesmo material, uma de comprimento L1=60cm e outra de comprimento L2=40cm. A primeira é submetida a uma tensão T1=40N e a segunda, a uma tensão T2=90N. Quando postas em

oscilação, verifica-se que a de comprimento L1 tem frequência fundamental de 36Hz. A partir desses dados, determine, em Hz, para a corda L2 a sua frequência fundamental.
22-(UNIFAL-MG)





Em uma corda vibrante de 50,0 cm de comprimento com densidade igual a 2,4.10-4 kg/m, presa em suas
extremidades, e formada uma onda estacionaria apresentando um único ventre, quando excitada por uma fonte de 1000 Hz. Assinale a alternativa correta.
a) A velocidade de propagação da onda na corda e de 1000 m/s quando a corda está sob uma tensão de 240 N.
b) A frequência de vibração é diretamente proporcional ao comprimento de onda.
c) A frequência fundamental da corda é de 2000 Hz.
d) A velocidade de propagação da onda na corda é de 1000 m/s e é inversamente proporcional a tensão na corda.
e) O segundo harmônico possui uma frequência de 500 Hz.
23-(UPE-PE)

Um pulso ondulatório senoidal é produzido em uma extremidade de uma corda longa e se propaga por toda a sua extensão. A onda possui uma frequência de 50 Hz e comprimento de onda 0,5 m. O tempo que a onda leva para percorrer uma distância de 10m na corda vale em segundos:
![]()
24-(FGV-SP)

A
nota lá da escala cromática musical é tida como referência na
afinação dos instrumentos. No violão comum de 6 cordas, a quinta
corda (segunda de cima para baixo), devidamente afinada, emite a nota lá vibrando com frequência de 220 Hz. Se o instrumentista colocar seu dedo num traste localizado a meia distância dos extremos desta corda e percuti-la, ele ouvirá a nota lá vibrando com frequência de
(A) 440 Hz, mantida a velocidade de propagação da onda formada.
(B) 110 Hz, mantida a velocidade de propagação da onda formada.
(C) 440 Hz, com velocidade de propagação da onda dobrada.
(D) 110 Hz, com velocidade de propagação da onda dobrada.
(E) 440 Hz, com velocidade de propagação da onda reduzida à metade.
25-(PUC-SP)
Um
homem mantém em equilíbrio estático um bloco preso a uma corda de
densidade linear igual a 0,01kg/m, conforme a figura. Determine a
massa M do bloco, sabendo que as frequências de duas harmônicas
consecutivas de uma onda estacionária no trecho
vertical de 2m da corda correspondem a 150Hz e 175Hz.
a) 102 g
b) 103 g
c) 104 g
d) 105 g
e) 106 g
Resolução comentada dos exercícios de vestibulares sobre
Cordas vibrantes - Harmônicos
01- 75 oscilações – 30s --- 1 oscilação --- T=30/75s --- f=1/T --- f=75/30 --- f=2,5Hz --- fn=nf1 --- supondo n=1 --- f1=2,5Hz --- a próxima ocorre quando n=2 --- f2=2f1 --- f2=2.2,5 --- f2=5Hz R- D
02- L=0,6m --- som fundamental (1 fuso) --- n=1 --- fn=nV/2L --- f1=V/2L --- 220=V/2.0,6 --- V=264m/s R- D
03- a) λ/2=12 --- λ=24cm=0,24m
b)
P=mg --- P=0,18.10 --- P=1,8N ---
v
=
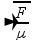 --- v
=
--- v
=
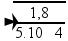 --- V=
--- V=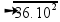 --- V=60m/s
--- V=60m/s
V= λf --- 60=0,24f --- f=250Hz
04- Os três maiores comprimentos de onda são os 3 primeiros
1o - λ1/2=90 --- λ1=180cm 20 -2λ2/2=90 --- λ2=90cm 3o - 3λ3/2=90 --- λ3=60cm
05-
Som fundamental --- n=1 --- f1=1/2.0,5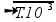 --- 200=1/2.0,5
--- 200=1/2.0,5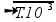 --- 4.104=T/10-3
--- T=40N=P
--- 4.104=T/10-3
--- T=40N=P
P=mg --- 40=m10 --- m=4kg R- B
06-λ1/2=50 --- λ1=100cm R- D
07- a) λ = 2.35 = 70 cm
f = 680 Hz
v = λ.f = 0,7.680 = 476 m/s
b) v = λ.f
340 = l680
λ = 340/680 = 0,5 m = 50 cm
08- fn=840Hz --- fn+1=1260Hz --- fn+1-fn=1260-840=nV/2L --- 210=1.210/2L --- L=0,5m=50cm
09-
Quando
tocada na região da boca, comprimento é L e f=440Hz ---
V=λ1f1
--- freqüência fundamental – 1o harmônico
–
λ1/2=L --- λ1=2L --- V=2L.440 --- V=880L
Quando tocada na região da boca, quando o comprimento for L/3 a freqüência fundamental será --- λx/2=2L/3 --- λx=4L/3
V=λx.fx --- V=4L/3.fx --- 880L=4L/3. fx --- fx=660Hz
10- µ=10g/m=0,01kg/m
Adjacentes --- uma é n e a seguinte n+1
fn=n/2L. --- fn+1=(n+1)/2L.
--- fn+1=(n+1)/2L. --- fn –
fn+1=1/2L.
--- fn –
fn+1=1/2L. --- (125-100)=1/2.2
--- (125-100)=1/2.2 (125-100)=1/2.2
(125-100)=1/2.2
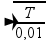 --- (100)2=(T/0,01)2
--- 104=T/10-2
--- T=100N=P --- P=mg --- 100=m10
--- m=10kg
R- A
--- (100)2=(T/0,01)2
--- 104=T/10-2
--- T=100N=P --- P=mg --- 100=m10
--- m=10kg
R- A
11- a) RESSONÂNCIA
b) I - Todo corpo tem suas freqüências naturais de vibração (modos de vibração).
II - Quando o corpo é submetido a estímulos externos periódicos com freqüência igual a uma de suas freqüências naturais, o corpo oscilará com maior amplitude, quando se diz que o mesmo está em ressonância.
III - No caso, Flavita ajustava a tensão na corda 4 para deixá-la com as mesmas freqüências naturais das da corda 5, pressionada entre o 4o e o 5o traste.
12- A fonte é a mesma (mesma f)---A tração é a mesma (mesmo peso – P/2) --- L é o mesmo (distância entre fonte e roldanas iguais)
A
corda com três fusos é a mais densa (m1),
pois como T é a mesma (v = )
V e m são inversamente proporcionais e V é menor na mais
densa. Da equação V=λf, como f é a mesma, menor V implica em
menor l, que é o da corda com três fusos (m1).
)
V e m são inversamente proporcionais e V é menor na mais
densa. Da equação V=λf, como f é a mesma, menor V implica em
menor l, que é o da corda com três fusos (m1).
Fio
1 --- 3o harmônico
--- n=3 --- fn=nV/2L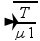 --- f3=3V/2L
--- f3=3V/2L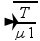
Fio
2 --- 1o haemônico
--- n=1 --- f1=1V/2L
f1=f3=f
--- 1V/2L. =
3V/2L
=
3V/2L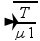 ---
---  =
3
=
3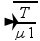 --- (
--- ( )2 =
(3
)2 =
(3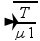 )2
--- µ1=µ/9
)2
--- µ1=µ/9
13- Sendo V inversamente proporcional a m --- VA>VB. Como o comprimento de onda é o mesmo, de V=λf, concluímos que V é diretamente proporcional a f, ou seja, fA > fB. R- C
14- O Sol considerado é a frequência fundamental --- λSol/2=0,64 --- λSol=1,28m --- V=λSolfSol=392.1,28=501,76m/s
Como a corda é a mesma (mesmo meio), a velocidade V é a mesma para a freqüência Lá, também fundamental ---
V=λLá.fLá --- 501,76=λLá.440 --- λLá=1,14m --- som fundamental --- λLá/2=L --- 1,14/2=L --- L=0,57m
15- Se o comprimento da corda é igual a meio comprimento de onda, trata-se da freqüência fundamental e λ/2=1 --- λ/=2m
V= λ.f
--- V=2.260 --- V=520m/s --- V= ,
--- 520=
,
--- 520=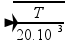 --- T=5.408N
--- T=5.408N
16- Mesma corda (mesmo meio), a V é a mesma. ---- considerando a freqüência fundamental (λ=2L) --- λMifMi=λLáfLá --- 2L1.660=2L2.880 --- L2/L1=3/4
17- a) T=2,5.10-3s --- f=1/T --- f=1/2,5.10-3 --- f=400Hz
b)
Nota desafinada – T1 –
f=400Hz - µ=5,0.10-3kg/m
– som fundamental n=1 --- fn=n/2L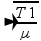 --- 400=1/2.1
--- 400=1/2.1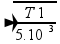 --- T1=3.200N
--- T1=3.200N
Nota
afinada – T2 –
f=440Hz - m=5,0.10-3kg/m
– som fundamental n=1 --- fn=n/2L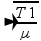 --- 440=1/2.1
--- 440=1/2.1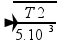 --- T2=3.872N
--- T2=3.872N
O aumento de tensão na corda será ΔT=T2 – T1=3.872 – 3.200=672N
18- a) som fundamental --- λ1/2=50 --- λ1=1m --- V=λ1f1=1.500 --- V=500m/s
b) V=λf --- 500=0,5f --- f=1000Hz
19- V e L são constantes (mesma corda).
fn+1=(n + 1)V/2L --- fn=nV/2L --- fn+1/fn = (n+1)V/2LX2L/nV --- fn+1/fn+ = (n+1)/n
20- fn=nf1 --- fn=n.100 (n=2,3,4,5) R- C
21- Relação entre as equações da frequência e da velocidade --- fn=n.V/2L --- V=√(T/μ) --- fn=1/2L. √(T/μ) --- para a corda 1 --- f1=1/2L. √(T/μ) --- 36=1/2.(0,60).√(40/μ1) --- (72.0,60)2=(√40/μ1)2 --- μ1=0,021 --- frequência fundamental da corda 2 ---
f’1=1/2L. √(T2/μ) --- f’1=1/2.(0,40).√(90/0,021) --- f’1=81 Hz
22- V=√T/μ=√(240/2,4.10-4) --- V=√(100.104) --- V=10.102 --- V=103=1.000m/s --- R- A
23- Velocidade de propagação da onda --- V=λ.f --- V=50.0,5 --- V=25m/s --- V=∆S/∆t --- 25=10/∆t --- ∆t=0,4s R- B
24- Observe nas figuras abaixo as ondas estacionárias formadas em cada caso --- γ1/2=L --- γ1=2L --- V1= γ1.f1 --- V1=2L.f1
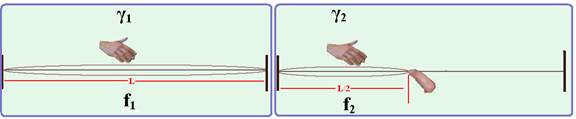
(I) ---γ2/2=L/2 --- γ2=L --- V2= γ2.f2 --- V2=L.f2 (II) --- como a velocidade de propagação em cada caso é a mesma --- V1=V2 --- I=II --- 2Lf1=Lf2 --- 2.220=f2 --- f2=440Hz --- R- A
25- Observe abaixo a expressão genérica para n harmônicos:
enésimo harmônico --- (“n + 1” nós e n fusos)
n.γn/2=L
--- .γn =2L/n
--- V=.γn.fn
--- fn=V/γn
--- fn=nV/2L
Lembrando que f1=V/2L --- fn=nf1
Se você tiver dois harmônicos consecutivos --- fn=n.V/2L e f(n + 1)=(n + 1).V/2L --- ∆f=(n + 1).V/2L – n.V/2L --- ∆f=nV/2L +
V/2L – nV/2L --- ∆f=V/2L --- 175 – 150=V/2.2 --- V=100m/s --- R- A