Aplicações das Leis de Newton em blocos apoiados ou suspensos

Leis de Newton aplicadas em movimentos uniformemente variados (a ≠0 e F_R≠ 0),

sem atrito

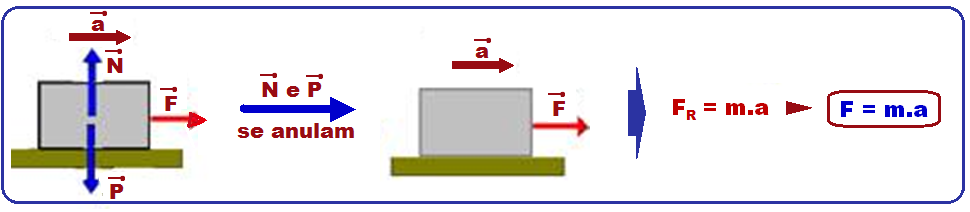
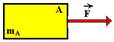
Corpos apoiados

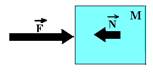
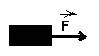
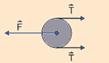
Bloco de massa m apoiado num plano horizontal sem atrito sujeito à uma força externa , paralela ao plano, que lhe imprime uma aceleração

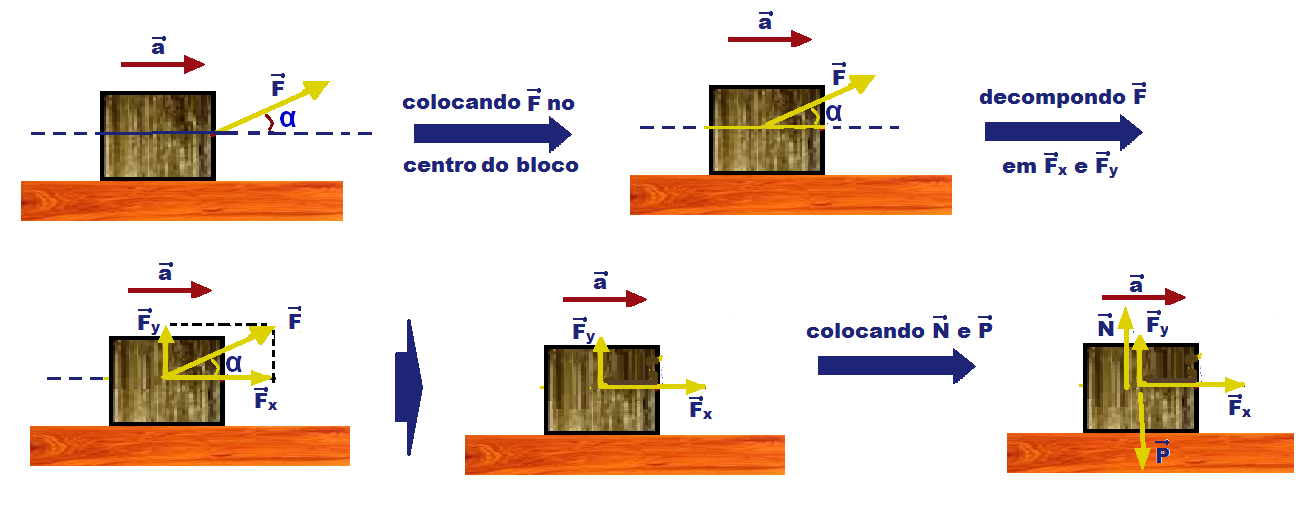
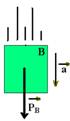
Bloco de massa m apoiado num plano horizontal sem atrito com aceleração originada por uma força externa , que forma um ângulo α com a horizontal.

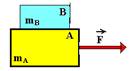
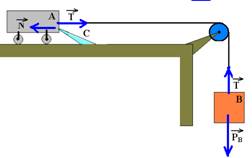
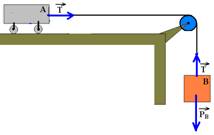
Observe atentamente a sequência de figuras abaixo:

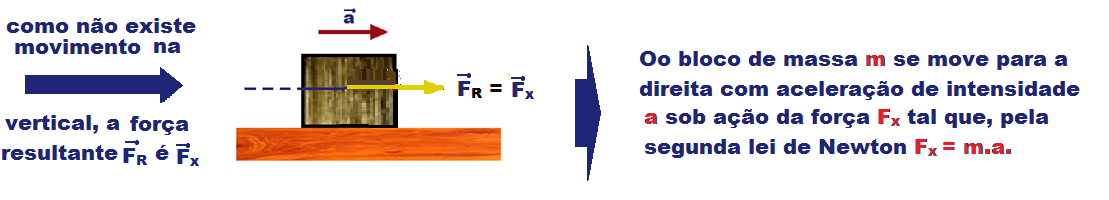
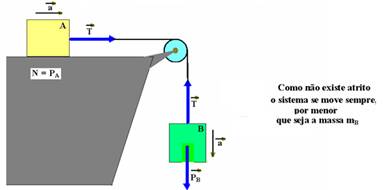
Como não existe atrito o sistema se move sempre no sentido horário, por menor que seja a massa m_B.

Isolando os corpos:

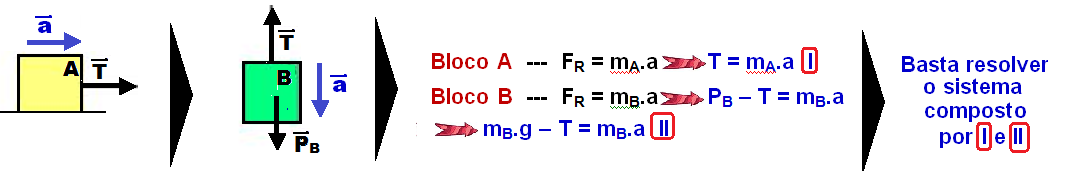
OBSERVAÇÃO:

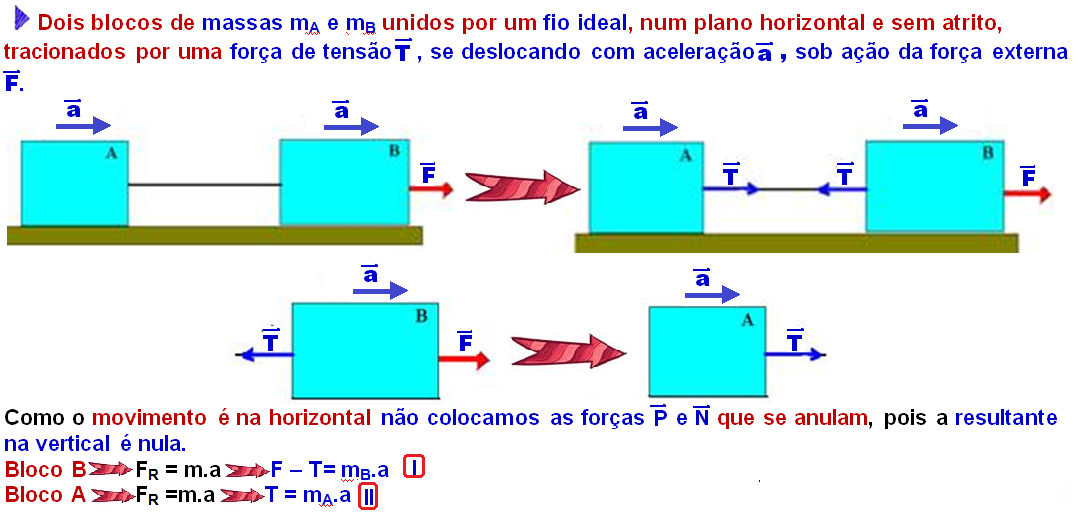
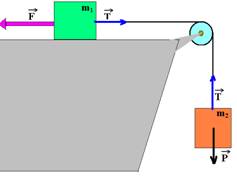
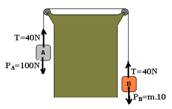
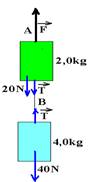
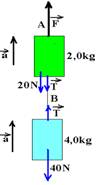
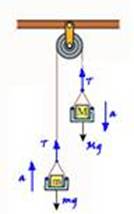
Corpos suspensos

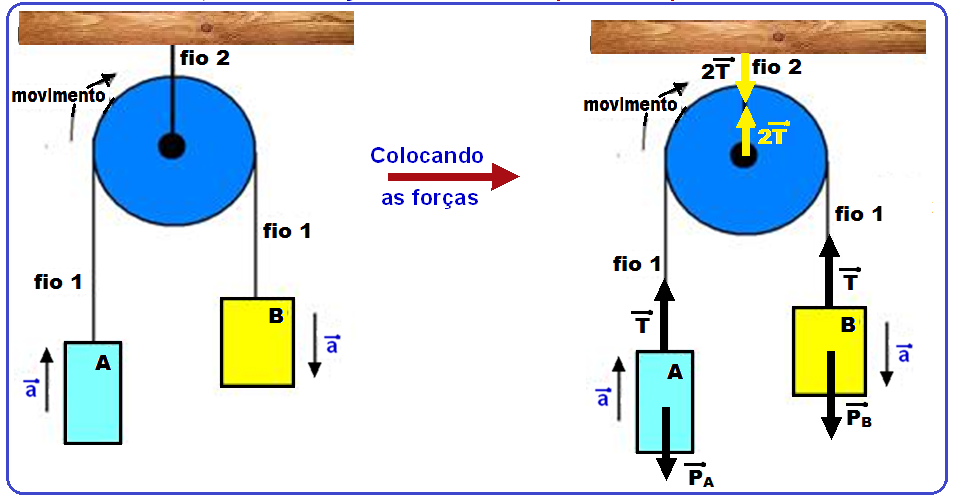
No esquema abaixo, não há atrito, os fios e as polias são ideais e como m_B> m_A o sistema se move no sentido horário, com aceleração a. A massa da polia é desprezível.

Bloco A F_R = m_A.a T – P_A = m_A.a I

Bloco B F_R = m_B.a P_B – T = m_B.a m_B.g – T = m_B.a II

Basta resolver o sistema composto por I e II

O que você deve saber

Procure entender todas as informações acima

Coloque as forças sempre na direção do movimento (que influem no movimento) e as outras, apenas se for pedido e, em seguida utilize para cada bloco a equação da lei fundamental da dinâmica F_R = m.a.

Exercícios de vestibulares com resolução comentada sobre Aplicações das Leis de Newton em blocos apoiados ou suspensos

01-(UCS-RS) Uma força de intensidade 20N atua sobre os blocos A e B, de massas m_A=3kg e m_B=1kg, como mostra a figura.

A superfície sobre a qual desliza o conjunto é horizontal e sem atrito. Considere g=10m/s² e determine:

a) a intensidade da força que A aplica em B

b) a intensidade da força que B aplica em A

c) a intensidade da força resultante sobre cada bloco.

02-(UFB) Os três blocos P, Q e R da figura abaixo encontram-se em repouso sobre uma superfície plana, horizontal e perfeitamente lisa.

Suas massas são m_P=6kg, m_Q=4kg e m_R=2kg. Uma força de intensidade F=48N é aplicada sobre o bloco P. Considere g=10m/s² e determine a intensidade, direção e sentido da força que o bloco R aplica no bloco Q.

03-(FCC-BA) Quatro blocos M, N, P e Q deslizam sobre uma superfície horizontal, empurrados por uma força , conforme o esquema abaixo.

A força de atrito entre os blocos e a superfície é desprezível e a massa de cada bloco vale 3,0kg. Sabendo-se que a aceleração escalar dos blocos vale 2,0m/s², a força do bloco M sobre o bloco N é, em newtons, igual a:

04-(FATEC-SP) Dois blocos A e B de massas 10 kg e 20 kg, respectivamente, unidos por um fio de massa desprezível, estão em repouso sobre um plano horizontal sem atrito. Uma força, também horizontal, de intensidade F = 60N é aplicada no bloco B, conforme mostra a figura.

O módulo da força de tração no fio que une os dois blocos, em newtons, vale

05-(F.M.Itajubá-MG) Três blocos são atados por fios ideais e puxados no espaço interestelar, onde inexiste gravidade, com uma aceleração de módulo 10m/s².

Quais as intensidades T₁, T₂ e T₃ das forças tensoras nos fios?

06-FUVEST-SP) Dois corpos A e B de massas m_A=3kg e m_B=1kg estão ligados por um fio flexível, como mostra a figura,a mover-se sob a ação da gravidade, sem atrito. (considere g=10m/s²).

a) Determine a aceleração do conjunto e a intensidade da força de tração no fio.

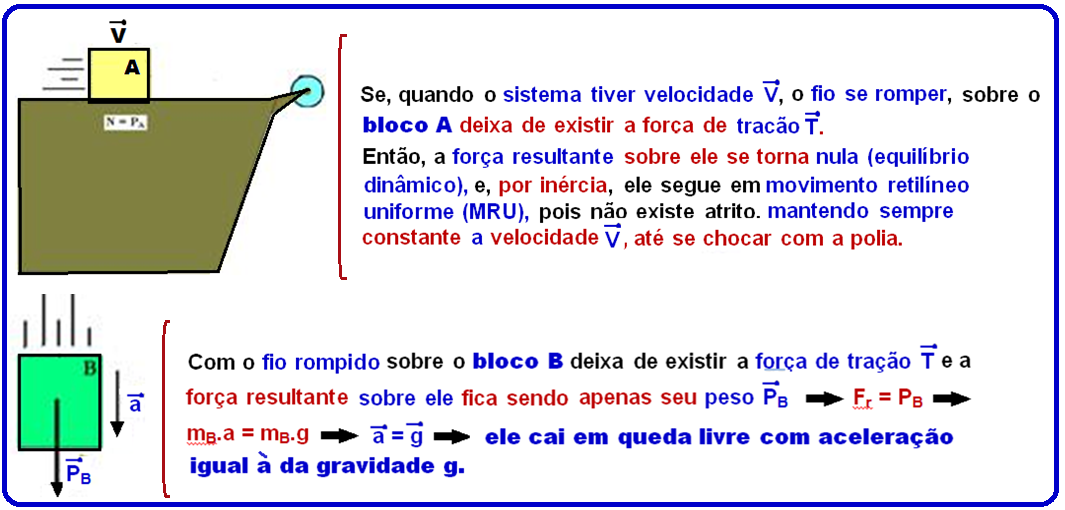
b) Supondo que num certo instante, após iniciado o movimento, o fio de ligação se rompa, o que acontecerá com os movimentos dos corpos A e B

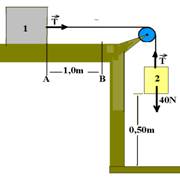
07-(UFMG-MG) Na montagem abaixo, sabendo-se que F=40N, m₁=m₂=1,0kg e que g=10m/s², qual é o valor de T? Despreze qualquer atrito.

08-(UFB) Na figura abaixo os blocos 1, 2 e 3 tem massas m₁=40kg, m₂=20kg e m₃=60kg. Considere os fios A e B e a polia ideais, despreze todos os atritos e calcule:

a) a aceleração do sistema

b) a intensidade da força de tração no fio B

09-(ITA-SP) O arranjo experimental esquematizado na figura consiste de uma roldana por onde passa um fio perfeitamente flexível e sem peso. Este fio sustenta em uma de suas extremidades a massa de 10kg e na outra, um dinamômetro no qual está pendurada uma massa de 6kg. A roldana pode girar sem atrito e sua massa, bem como a do dinamômetro, é desprezível em relação àquela do sistema.

O sistema, a partir do repouso, vai se movimentar pela ação da gravidade. Sendo g=10m/s², determine:

a) o módulo da aceleração de cada bloco

b) a intensidade da força, em newtons, indicada pelo dinamômetro.

10- (UNIFESP-SP) Na representação da figura, o bloco A desce verticalmente e traciona o bloco B, que se movimenta em um plano horizontal por meio de um fio inextensível. Considere desprezíveis as massas do fio e da roldana e todas as forças de resistência ao movimento.

Suponha que, no instante representado na figura, o fio se quebre. Pode-se afirmar que, a partir desse instante,

a) o bloco A adquire aceleração igual à da gravidade; o bloco B pára.

b) o bloco A adquire aceleração igual à da gravidade; o bloco B passa a se mover com velocidade constante.

c) o bloco A adquire aceleração igual à da gravidade; o bloco B reduz sua velocidade e tende a parar.

d) os dois blocos passam a se mover com velocidade constante.

e) os dois blocos passam a se mover com a mesma aceleração.

11- (FGV-SP) Dois carrinhos de supermercado podem ser acoplados um ao outro por meio de uma pequena corrente, de modo que uma única pessoa, ao invés de empurrar dois carrinhos separadamente, possa puxar o conjunto pelo interior do supermercado. Um cliente aplica uma força horizontal de intensidade F, sobre o carrinho da frente, dando ao conjunto uma aceleração de intensidade 0,5 m/s².

Sendo o piso plano e as forças de atrito desprezíveis, o módulo da força F e o da força de tração na corrente são, em N, respectivamente:

a) 70 e 20.

b) 70 e 40.

c) 70 e 50.

d) 60 e 20.

e) 60 e 50.

12-(UFRJ-RJ) Um bloco de massa m é abaixado e levantado por meio de um fio ideal. Inicialmente, o bloco é abaixado com aceleração constante vertical, para baixo, de módulo a (por hipótese, menor do que o módulo g da aceleração da gravidade), como mostra a figura 1.

Em seguida, o bloco é levantado com aceleração constante vertical, para cima, também de módulo a, como mostra a figura 2. Sejam T a tensão do fio na descida e T' a tensão do fio na subida.

Determine a razão T'/T em função de a e g.

13- (UNESP-SP) Dois blocos, A e B, de massas m e 2m, respectivamente, ligados por um fio inextensível e de massa desprezível, estão inicialmente em repouso sobre um plano horizontal sem atrito. Quando o conjunto é puxado para a direita pela força horizontal aplicada em B, como mostra a figura, o fio fica sujeito à tração T₁. Quando puxado para a esquerda por uma força de mesma intensidade que a anterior, mas agindo em sentido contrário, o fio fica sujeito à tração T₂.

Nessas condições, pode-se afirmar que T₂‚ é igual a

14-(UNESP-SP) Uma barra AC homogênea de massa m e comprimento L, colocada numa mesa lisa e horizontal, desliza sem girar sob ação de uma força , também horizontal, aplicada na sua extremidade esquerda.

Mostre que a força com que a fração BC de comprimento 2L/3, atua sobre a fração AB é igual a - 2/3.

15- (UFRJ-RJ) O sistema representado na figura é abandonado sem velocidade inicial. Os três blocos têm massas iguais. Os fios e a roldana são ideais e são desprezíveis os atritos no eixo da roldana. São também desprezíveis os atritos entre os blocos (2) e (3) e a superfície horizontal na qual estão apoiados.

O sistema parte do repouso e o bloco (1) adquire uma aceleração de módulo igual a a. Após alguns instantes, rompe-se o fio que liga os blocos (2) e (3). A partir de então, a aceleração do bloco (1) passa a ter um módulo igual a a'.

Calcule a razão a' / a.

16-(UFRJ-RJ) Analise as figuras a seguir e leia com atenção o texto.

Dois blocos de massas m e M, sendo M>m estão em repouso e em contato um ao lado do outro, sobre uma superfície plana. Se empurrarmos um dos blocos com uma força F, paralela à superfície, o conjunto irá mover-se com uma dada aceleração.

Determine se faria diferença para as magnitudes da aceleração do conjunto e das forças de contato entre os blocos, se tivéssemos empurrado o outro bloco.

17- (Ufrrj) Em uma obra, realizada na cobertura de um prédio, há um sistema para subir e descer material entre o térreo e o último andar através de baldes e cordas. Um dos operários, interessado em Física, colocou um dinamômetro na extremidade de uma corda. Durante o transporte de um dos baldes, ele percebeu que o dinamômetro marcava 100 N com o balde em repouso e 120 N quando o balde passava por um ponto A no meio do trajeto.(considere g=10m/s²)

a) Determine a aceleração do balde nesse instante em que ele passa pelo ponto A.

b) É possível concluir se, nesse instante, o balde está subindo ou descendo? Justifique.

18- (Ufpb) Uma locomotiva desenvolvendo uma aceleração de 2m/², puxa três vagões ao longo de uma ferrovia retilínea, conforme a figura. (g=10m/s²).

Se o vagão 3 pesa 2 × 10³ N, determine a intensidade da força a força exercida sobre ele pelo vagão 2.

19-(UFRJ-RJ) Um sistema é constituído por um barco de 100 kg, uma pessoa de 58 kg e um pacote de 2,0 kg que ela carrega consigo. O barco é puxado por uma corda de modo que a força resultante sobre o sistema seja constante, horizontal e de módulo 240 newtons.

Supondo que não haja movimento relativo entre as partes do sistema, calcule o módulo da força horizontal que a pessoa exerce sobre o pacote.

20-(UERJ-RJ) Os corpos A e B, ligados ao dinamômetro D por fios inextensíveis, deslocam-se em movimento uniformemente acelerado. Observe a representação desse sistema, posicionado sobre a bancada de um laboratório.

A massa de A é igual a 10 kg e a indicação no dinamômetro é igual a 40 N.

Desprezando qualquer atrito e as massas das roldanas e dos fios, estime a massa de B.(g=10m/s²).

21-(UNESP-SP) Um bloco de massa m_Adeslisa no solo horizontal, sem atrito, sob ação de uma força constante, quando um bloco de massa m_B é depositado sobre ele.

Após a união, a força aplicada continua sendo a mesma, porém a aceleração dos dois blocos fica reduzida à quarta parte da aceleração que o bloco A possuía. Pode-se afirmar que a razão entre as massas, m_A/m_B, é

22-(MACKENZIE-SP) O conjunto abaixo, constituído de fios e polias ideais, é abandonado do repouso no instante t=0 e a velocidade do corpo A varia em função do tempo segundo o diagrama dado.

Desprezando o atrito e admitindo g=10m/s², calculea relação entre as massas de A (m_A) e de B (m_B).

23-(PUC-SP) Uma caminhonete de 2.000kg tenta resgatar um caixote a partir de um precipício, usando um cabo inextensível que liga o veículo ao objeto, de massa 80kg. Considere a polia ideal. Se o caixote sobe com aceleração de 1m/s², responda: (g=10m/s²)

a) Qual a força que movimenta a caminhonete?

b) O cabo suporta no máximo uma tração de 2.000N. Será possível o resgate com essa aceleração sem que ele arrebente?

24-(FUVEST-SP) Uma esfera de massa m_o está pendurada por um fio, ligado em sua outra extremidade a um caixote, de massa M=3 m_o, sobre uma mesa horizontal. Quando o fio entre eles permanece não esticado e a esfera é largada, após percorrer uma distância H_o, ela atingirá uma velocidade V_o, sem que o caixote se mova. Na situação em que o fio entre eles estiver esticado, a esfera, puxando o caixote, após percorrer a mesma distância H_o, atingirá uma velocidade V. Determine V em função de V_o.

25-(UNESP-SP) Dois blocos estão suspensos em um campo gravitacional de aceleração g, por duas cordas A e B de massas desprezíveis, como indica a figura.

Determine as tensões em cada corda nos seguintes casos:

a) os corpos são mantidos suspensos em repouso pela força .

b) os corpos são submetidos a uma força tal que os acelera a 2,0m/s², para cima.

26-(FUVEST-SP) Um carrinho A de 20kg de massa é unido a um bloco B de 5kg por meio de um fio leve e inextensível, conforme a figura.

Inicialmente o sistema está em repouso, devido à presença do anteparo C que bloqueia o carrinho A. (g=10m/s²).

a) Qual o valor da força que o anteparo C exerce sobre o carrinho A

b) Retirando C, com que aceleração o carrinho A se movimenta?

27-(MACKENZIE-SP) O sistema abaixo é constituído por fios e polias ideais, num local onde g=10m/s².

Desprezando-se qualquer tipo de resistência e abandonando-se o conjunto quando o corpo A se encontra na posição X, a sua velocidade, ao passar por Y, é, em m/s:

28-(MACKENZIE-SP) No sistema abaixo, o corpo 1, de massa 6,0kg, está preso na posição A. O corpo 2, tem massa de 4kg. Despreze os atritos e adote g=10m/s².

Abandonando o corpo 1, a sua velocidade, em m/s, ao passar pela posição B será de:

29-(Ceub-DF) Na figura a seguir temos dois blocos, A e B, de massas respectivamente iguais a m_A=4,0kg e m_B=6,0kg, que deslizam, sem atrito, em uma superfície plana e horizontal, sob ação de uma força horizontal e constante e de intensidade F. Os blocos estão ligados por fios ideais a um dinamômetro também ideal (massa desprezível), calibrado em newtons.

Não considere o efeito do ar e admita que os blocos tem uma aceleração horizontal, para a direita, constante e de módulo igual a 2,0m/s².

Julgue os itens a seguir.

(1) a força tensora no fio (1) tem intensidade igual a 12N.

(2) O valor de F é 20N.

(3) como o dinamômetro tem massa desprezível, as forças que tracionam os fios (1) e (2) tem intensidades iguais.

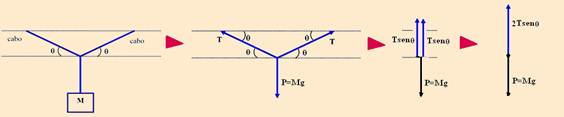
(4) o dinamômetro indica 12N.

30-(FUVEST-SP) Um sistema mecânico é formado por duas polias ideais que suportam três corpos A, B e C de mesma massa m, suspensos por fios ideais como representado na figura.

O corpo B está suspenso simultaneamente por dois fios, um ligado a A e outro a C. Podemos afirmar que a aceleração do corpo B será:

a) zero

b) (g/3) para baixo

c) (g/3) para cima

d) (2g/3) para baixo

e) (2g/3) para cima

31-(Aman-RJ) No sistema apresentado na figura, não há forças de atrito e o fio tem massa desprezível. (g=10m/s²).

São dados F=500N; m_A=15kg e m_B=10kg.

Determine a intensidade da força de tração no fio e a aceleração do sistema.

32-(UFMG) A figura mostra uma corrente formada por três elos. A massa de cada elo é de 100g e uma força vertical puxa essa corrente para cima. A corrente sobe com uma aceleração de 3,0m/s².

Considerando essas informações calcule:

a) o módulo da força que puxa a corrente.

b) o módulo da força resultante que atua sobre o elo do meio.

c) o módulo da força que o elo do meio faz sobre o elo de baixo.

33-(UFRJ) O sistema ilustrado na figura abaixo é uma máquina de Atwood. A roldana tem massa desprezível e gira livremente em torno de um eixo fixo perpendicular ao plano da figura, passando pelo centro geométrico da roldana. Uma das massas vale m e a outra 2m. O sistema encontra-se inicialmente na situação ilustrada pela figura a, isto é, com as duas massas no mesmo nível. O sistema é então abandonado a partir do repouso e, após um certo intervalo de tempo, a distância vertical entre as massas é h (figura b).

Calcule o módulo da velocidade de cada uma das massas na situação mostrada na figura (b).

34-(UFRN) Uma corrente constituída de sete anéis, cada um com massa de 200g, está sendo puxada verticalmente para cima, com aceleração constante de 2,0m/s². A força para cima no anel do meio é: (g=10m/s²).

35-(UNESP-SP) Em uma circular técnica da Embrapa, depois da figura,

Encontramos uma recomendação que, em resumo, diz:

“No caso do arraste com a carga junto ao solo (se por algum motivo não pode ou não deve e ser erguida . . .) o ideal é arrastá-la. . . reduzindo a porca necessária para movimentá-la, causando menos dano ao solo . . . e facilitando as manobras. Mas neste caso o peso da tora aumenta. (www.cpafac.embrapa.br/pdficirtec39.pdf.Modificado.)

Pode-se afirmar que a frase destacada é conceitualmente

A) inadequada, pois o peso da tora diminui, já que se distribui sobre uma área maior.

B) inadequada, pois o peso da tora é sempre o mesmo, mas é correto afirmar que em II a força exercida pela tora sobre o solo aumenta;

C) inadequada: o peso da tora é sempre o mesmo e, além disso, a força a força exercida pela tora sobre o solo em II diminui, pois se distribui por uma área maior.

D) adequada, pois nessa situação a tora está integralmente apoiada sobre o solo.

E) adequada, pois nessa situação a área sobre a qual a tora está apoiada sobre o solo também aumenta

36-(UNESP-SP) Um rebocador puxa duas barcaças pela águas de um lago tranqüilo. A primeira delas tem massa de 30 toneladas e a segunda, 20 toneladas. Por uma questão de economia, o cabo de aço I que conecta o rebocador à primeira barcaça suporta, no máximo, 6.10⁵N, e o cabo II, 8.10⁴N.

Desprezando o efeito de forças resistivas, calcule a aceleração máxima do conjunto, a fim de evitar o rompimento de um dos cabos.

37-(UFSC-SP) Em repouso, o sistema de vasos comunicantes apresentado está em equilíbrio, de acordo com a figura.

Quando o sistema é submetido a um movimento uniformemente variado devido à ação de uma força horizontal voltada para direita, o líquido deverá permanecer em uma posição tal qual o esquematizado em

38-(UEL-PR) Considere o sistema constituído por três blocos de massas m₁, m₂ e m₃, apoiados um sobre o outro, em repouso sobre uma superfície horizontal, como mostra a figura a seguir.

Observe que uma força F é aplicada ao bloco de massa m₂, conforme a representação. Entretanto, esta força é incapaz de vencer as forças de f_ij entre os blocos m_i e m_j, onde i e j variam de 1 a 3.

Desprezando a resistência do ar, assinale a alternativa que representa todas as forças que atuam no bloco de massa m₂, onde os N_i, representam as normais que atuam nos blocos e P_i, correspondem aos pesos dos respectivos blocos com i variando de 1 a 3.

39-(UFCG-PB) Durante uma viagem, Lucinha observou as enormes curvas que os cabos das linhas de transmissão de energia

elétrica apresentavam (figura). Ao comentar a observação, disse que os engenheiros poderiam economizar o material dos cabos se os esticassem entre as torres de sustentação até que estivessem dispostos horizontalmente.

Proponha um modelo, fundamentado nas Leis de Newton, para a situação observada e discuta o comentário feito por Lucinha.

40-(PUC-RJ) Alberto (A) desafiou seu colega Cabral (C) para uma competição de cabo de guerra, de uma maneira especial, mostrada na figura. Alberto segurou no pedaço de corda que passava ao redor da polia enquanto que Cabral segurou no pedaço atado ao centro da polia. Apesar de mais forte, Cabral não conseguiu puxar Alberto, que lentamente foi arrastando o seu adversário até ganhar o jogo. Sabendo que a força com que Alberto puxa a corda é de 200 N e que a polia não tem massa nem

atritos:

a) especifique a tensão na corda que Alberto está segurando;

b) desenhe as forças que agem sobre a polia, fazendo um diagrama de corpo livre;

c) calcule a força exercida pelo Cabral sobre a corda que ele puxava;

d) considerando que Cabral foi puxado por 2,0 m para frente, indique quanto Alberto andou para trás.

41-(UFT-TO) Uma pequena esfera de chumbo com massa igual a 50 g é amarrada por um fio, de comprimento igual a 10 cm e massa desprezível, e fixada no interior de um automóvel conforme figura. O carro se move horizontalmente com aceleração constante. Considerando-se hipoteticamente o ângulo que o fio faz com a vertical igual a 45 graus, qual seria o melhor valor para representar o módulo da aceleração do carro?

Desconsidere o atrito com o ar, e considere o módulo da aceleração da gravidade igual a 9,8 m/s².

a) 5,3 m/s²

b) 8,2 m/s²

c) 9,8 m/s²

d) 7,4 m/s²

e) 6,8 m/s²

42-(UFLA-MG) Um corpo, ao se deslocar em um meio fluido (líquido ou gasoso) fica sujeito a uma

força de resistência que é expressa por: F_R = kv², em que k é uma constante de proporcionalidade e v a velocidade do corpo no meio. Considerando o Sistema Internacional de Unidades (SI), é CORRETO afirmar que a constante k é dada pelas unidades:

43-(UFRN-RN) É muito comum observarmos nas fachadas de edifícios em construção andaimes constituídos por uma tábua horizontal sustentada por cordas que passam por roldanas presas no topo da edificação. O fato de um dos operários se deslocar sobre o andaime em direção ao outro, por exemplo, quando vai entregar alguma ferramenta ao companheiro, afeta a distribuição de forças sobre as cordas. Nesse sentido, considere a situação mostrada na Figura abaixo. Nela, um dos operários se encontra na

extremidade esquerda do andaime, enquanto o outro, após ter caminhado em direção a ele, conduzindo uma marreta, encontra-se parado no meio do andaime.

Considerando a situação mostrada na Figura, pode-se afirmar que a

A) força resultante sobre o andaime é diferente de zero e a tensão na corda Y é maior que na corda X.

B) força resultante sobre o andaime é igual a zero e a tensão na corda Y é maior que na corda X.

C) força resultante sobre o andaime é diferente de zero e a tensão na corda X é maior que na corda Y.

D) força resultante sobre o andaime é igual a zero e a tensão na corda X é maior que na corda

44-(UFV-MG) Nas extremidades de um fio inextensível e de massa desprezível, que passa por uma polia, estão pendurados dois blocos maciços A e B, feitos de um mesmo material de densidade de massa ρ. O bloco B se encontra suspenso no ar, enquanto que o bloco A esta com a metade de seu volume imerso em um liquido, conforme a figura.

Sabe-se que o volume do bloco A é três vezes maior que o do bloco B. Desprezando qualquer tipo de atrito e qualquer influencia do ar sobre os blocos, e CORRETO afirmar que a densidade de massa do liquido é:

45-(UEPG-PR)

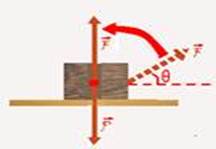
O corpo abaixo ilustrado está sob a ação de um sistema de forças, onde a força F poderá desequilibrar esse sistema.

Analise as assertivas e assinale a alternativa correta.

I – Para que o corpo se desloque é necessário que a força F seja maior que (FsenӨ).

II – O corpo estará pronto a romper o repouso quando a força F_atrito for igual ao valor FcosӨ.

III – Se a força F for maior que P quando Ө for igual a 90^o o corpo, primeiramente, rotacionará até que a linha de ação de F coincida com a linha de ação da força de P, para então se elevar.

IV – Se a força N for maior que o peso ocorrerá a elevação do corpo.

a) As assertivas I e II são corretas.

b) As assertivas I e III são corretas.

c) As assertivas II e IV são corretas.

d) As assertivas II e III são corretas.

e) As assertivas II, III e IV são corretas.

46-(UNESP-SP)

Em uma obra, para permitir o transporte de objetos para cima, foi montada uma máquina constituída por uma polia, fios e duas plataformas A e B horizontais, todos de massas desprezíveis, como mostra a figura.

Um objeto de massa m = 225 kg, colocado na plataforma A, inicialmente em repouso no solo, deve ser levado verticalmente para cima e atingir um ponto a 4,5 m de altura, em movimento uniformemente acelerado, num intervalo de tempo de 3 s.

A partir daí, um sistema de freios passa a atuar, fazendo a plataforma A parar na posição onde o objeto será descarregado.

Considerando g = 10 m/s², desprezando os efeitos do ar sobre o sistema e os atritos durante o movimento acelerado, a massa M,em kg, do corpo que deve ser colocado na plataforma B para acelerar para cima a massa m no intervalo de 3 s é igual a

47-(UNICAMP-SP)

O tempo de viagem de qualquer entrada da Unicamp até a região central do campus é de apenas

alguns minutos. Assim, a

economia de tempo obtida, desrespeitando-se o limite de velocidade, é muito pequena, enquanto o risco de acidentes aumenta significativamente.

a) Considere que um ônibus de massa M = 9000 kg , viajando a 80 km/h, colide na traseira de um carro de massa m_a=1000 kg

que se encontrava parado. A colisão é inelástica, ou seja, carro e ônibus seguem grudados após a batida. Calcule a velocidade do

conjunto logo após a colisão.

b) Além do excesso de velocidade, a falta de manutenção do veículo pode causar acidentes. Por exemplo, o desalinhamento das rodas faz com que o carro sofra a ação de uma força lateral. Considere um carro com um pneu dianteiro desalinhado de 3°, conforme a figura abaixo, gerando uma componente lateral da força de atrito em uma das rodas.

Para um carro de massa m_b=1600 kg, calcule o módulo da aceleração lateral do carro, sabendo que o módulo da força de atrito em cada roda vale F_at= 8000 N . Dados:sen 3° = 0,05 e cos 3° = 0,99.

Resolução comentada dos exercícios de vestibulares sobre Aplicações das Leis de Newton em blocos apoiados ou suspensos

01- a) Como não existe atrito, por menor que seja a massa do sistema e a força aplicada o sistema sempre se moverá no caso, para a direita. Colocando as forças que agem sobre cada bloco apenas na direção do movimento (forças horizontais).

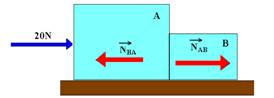
N_AB – intensidade da força que A aplica em B. N_BA – intensidade da força com que B reage em A. Como N_AB e N_BA constituem par ação e reação elas tem a mesma intensidade que chamaremos de N.

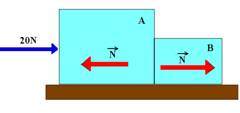
Bloco A --- F_R=m_A.a --- 20 – N=3.a I Bloco B --- F_R=m_B.a --- N=1.a II

Somando I com II, obtemos --- 20=4a --- a=5m/s² (é a mesma para cada bloco, pois se movem juntos).

b) Substituindo a=5m/s² em I ou em II obtemos --- N=5N.

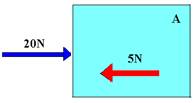
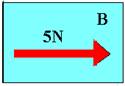
Observe nas figuras acima que F_RA=20 – 5=15N e que F_RB=5N.

02- Colocando as forças que influem no movimento:

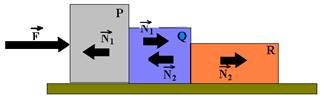
Bloco P --- F_R=m_P.a --- F – N₁=6.a I --- bloco Q --- F_R=m_Q.a --- N₁ – N₂=4.a II --- bloco R --- N₂ = m_R.a ---

N₂ = 2.a III --- somando I com II com III, obtemos 48=12ª --- a=4m/s². A força pedida tem intensidade N₂=2.a ---

N₂=2.4 --- N₂=8N

03- Vamos achar a intensidade de , considerando os 4 blocos como um só, de massa M=12kg e aplicar a lei fundamental --- F_R=m.a --- F=12.2 --- F=24N

Colocando as forças apenas sobre o bloco M que são F=24N e a reação a entre N e M que é N:

Bloco M --- F_R=m_M.a --- 24 – N = 3.2 --- N =18N

04- Em fios a força é de tração :

Bloco A --- F_R=m_A.a --- T=10.a I bloco B --- F_R=m_B.a --- F – T=m_B.a --- 60 – T=20.a II --- Somando I com II ---

60 = 30.a --- a=2m/s², que, substituído em I ou II, fornecerá --- T=20N R- E

05- Bloco A --- F_R=m.a --- T₁ – T₂=1.10 --- T₁ - T₂=10 Bloco B --- FR=m.a --- T₂ – T₃=2.10 --- T₂ – T₃=20

Bloco C --- F_R=m.a --- T₃=3.10 --- T₃=30N, que substituído em T₂ – T₃=20 --- T₂-30=20 --- T₂=50N

T₁ – T₂=10 --- T₁ – 50=10 --- T₁=60N

06- (a) Colocando as forças que influem no movimento:

Bloco A --- F_R=m_A.a --- T=3.a I --- Bloco B --- F_R=m_B.a --- P_B – T=m_B.a --- m_B.g – T=m_B.a --- 1.10 – T=1.a

10 – T=a II --- somando I com II --- 10=4.a --- a=2,5m/s²

T=3.a --- T=3.2,5 --- T=7,5N

b) Sobre o bloco A deixa de existir a força de tração , a força resultante sobre ele torna-se nula, ele fica em equilíbrio dinâmico

e segue em MRU com velocidade constante , até se chocar com a polia.

Sobre o bloco B deixa de existir a força de tração e a força resultante sobre ele fica sendo apenas seu peso --- F_r =P_B ---

m_B.a = m_B.g --- a = g --- ele cai em queda livre com aceleração da gravidade.

07- Colocando o peso do bloco m₂ --- P=1.10 ---P=10N

O sistema se move no sentido anti-horário, pois F>P, ou seja, m₂ sobe e m₁ se desloca para a esquerda.

Bloco m₁ --- F_R=m.a --- F – T=m₁.a --- 40 – T=1.a --- 40 – T=a I Bloco m₂ --- T – P=m.a --- T – 10=1.a ---

T – 10=a II --- somando I com II --- 40 – 10=2.a --- a=15m/s² --- T – 10=1.a --- T=10 + 15 --- T=25N

08- a)Colocando as forças:

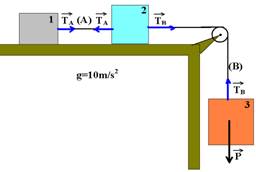
bloco 1 --- F_R=m₁.a --- T_A=40.a I bloco 2 --- F_R=m₂.a --- T_B - T_A=20.a II bloco 3 --- F_R=m₃.a ---

T_B – P=m₃.a --- T_B – 600=60.a III --- somando I com II com III --- 600=120.a --- a=5m/s², que, substituído em III nos fornece --- T_B=600 + 60.5 --- T_B=900N

09- a) P_A=m_A.g --- P_A=6.10 --- P_A=60N P_B=m_B.g --- P_B=10.10 --- P_B=100N

Colocando as forças que agem sobre cada bloco e tirando o dinamômetro, pois sua massa é desprezível.

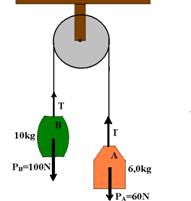
Observe que, como P_B>P_A, o sistema se move no sentido anti-horário (A sobe e B desce).

bloco A --- F_R=m_A.a --- T – 60=6.a I bloco B --- F_R=m_B.a --- 100 – T=10.a II somando I com II ---

100 – 60=16.a --- a=40/16 --- a=2,5m/s²

b) o dinamômetro indica a intensidade da força de tração no fio no qual ele está inserido, ou seja, indica T --- T – 60=6.a ---

T=60 + 6.2,5 --- T=75N

10- R- B (veja teoria

11- primeiro carrinho --- F – T=40.0,5 --- F – T=20 segundo carrinho --- T=100.0,5 --- T=50N --- F – 50=20 --- F=70N R- C

12- Considerando o princípio fundamental da Dinâmica, F(resultante) = massa x aceleração temos: --- Na descida: mg - T = ma

Na subida: T' - mg = ma --- Isolando as trações --- T = mg - ma = m(g - a) --- T' = mg + ma = m(g + a)

Então --- T'/T = (g + a)/(g - a)

13- A aceleração de cada bloco em cada caso é a mesma, pois F é a mesma e a massa do sistema (3m) é a mesma.

Primeira situação --- bloco m --- T₁=m.a I segunda situação --- bloco2 m --- T₂=2m.a II

comparando I com II --- T₂ = 2T₁ --- R- A

14- A proporção de comprimento é válida também para massa. Separando as frações:

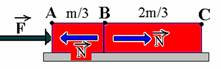
Considerando o sistema todo --- F_R=(m/3 + 2m/3).a --- F=(3m/3).a --- F=m.a I

Sobre a massa m/3 --- F_R=m/3.a --- F – N=m/3.a --- 3F – 3N=m.a --- veja em I que F=m.a --- 3F – 3N=F --- 3N=2F ---

N=2F/3

15- Colocando as forças:

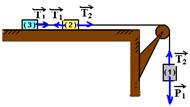
bloco3 --- T₁=ma I bloco 2 --- T₂ – T₁=ma II bloco 1 --- P₁ – T₂=ma III somando I, II e III ---

P₁=3ma --- mg=3ma --- a=g/3

Quando o fio que une 2 e 3 se rompe, teremos:

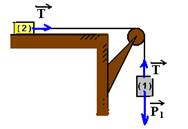
bloco 2 --- T=ma’ I bloco 1 --- P₁ – T=ma’ II somando I com II --- P₁=2ma’ --- mg=2ma’ --- a’=2g

dividindo membro a membro a=g/3 por a’=2g, obtemos --- a’/a=3/2

16- A aceleração é a mesma nas duas situações, pois as massas e a força aplicada são as mesmas.. A força de contato será maior na situação do conjunto 1, pois o bloco da esquerda terá que empurrar uma massa maior.

17- a) As forças que atuam no balde são a tração do fio, T, e o peso P. Quando o balde está em repouso, temos T = P = 100 N. Como P = mg --- 100=m.10 --- m=10kg. . Já quando o dinamômetro acusa T = 120 N, temos, F_R=ma --- T - P = ma, ou seja, a = (120 - 100)/10 = 2 m/s².

b) Não é possível concluir, pois só conhecemos a aceleração, e não a velocidade. Apenas sabemos que T>P, ou seja, ele pode estar subindo acelerado ou descendo retardado.

18-

F_R=ma --- T=2.10².2 --- T=4.10²N

19- Vamos calcular a aceleração do sistema (barco + pessoa + pacote) --- Pela segunda lei de Newton, F_R = m.a --- 240 = (100 + 58 + 2).a --- 240 = 160.a ==> a = 240/160 = 1,5 m/s².

Apenas sobre o pacote de 2 kg

F = m.a = 2.1,5 = 3,0 N

20- O dinamômetro indica a tração no fio que é de 40N e as forças sobre o sistema estão indicadas na figura.

Observe no bloco A que, como P_A>T, ele deve descer e consequentemente B deve subir.

Assim, considerando que A desça acelerado, pelo princípio fundamental da dinâmica temos, para o corpo A, que: --- F_R=m_A.a ---

100 - 40 = 10.a ==> a = 60/10 = 6 m/s².

Para o corpo B: --- F_R=m_B.a --- 40 - m.10 = m.6 --- 40 = 16.m --- m = 40/16 = 2,5 kg

21- Bloco A

F_R=m_A.a --- F=m_A.a I

Bloco B sobre o bloco A

F_R=(m_A + m_B).a/4 ---- F==(m_A + m_B).a/4 --- 4F=m_Aa + m_Ba --- 4F=F + m_Ba --- 3F=m_Ba II

Dividindo membro a membro II por I --- 3m_A=m_B --- m_A/m_B=1/3

22- Calculando a aceleração do sistema pelo gráfico --- a=DV/Dt --- a=24/6 --- a=4m/s²

Bloco A --- P_A – T=m_Aa --- 10m_A – T=4m_A --- T=6m_AI blobo B --- T=m_Ba --- T=m_B.4 II --- igualando I com II -- 6m_A=4m_B --- m_A/m_B=2/3

23- a) caminhonete --- F_R=m_c.a --- F – T=2.000X1 --- F – T=2.000 I caixote --- T – 800=80X1 --- T=880N II

substituindo II em I --- F – 880=2.000 --- F=2.880N

b) Sim, será possível, pois a tração máxima que o cabo suporta é 2000N e a tração aplicada é de 880N

24-1^a etapa --- queda livre da esfera m_o, com a=g e a velocidade variando de 0 a V_o, numa queda de altura H_o.

Torricelli --- V_o² = 0² + 2.g.H_o --- V_o² =2gH_o 2^a etapa --- as duas esferas se movem juntas com aceleração a que vale:

M=3m_o, se desloca para a direita puxada por T --- F_R=ma --- T=3m_oa I m_o, desce de modo que P – T=m_oa ---

M_o.g - T=m_o.a II --- substituindo I em II --- m_og – 3m_oa=m_oa --- g=4.a --- a=g/4

Queda de m_o com aceleração a=g/4 e velocidade variando de V_o a V, numa queda de altura H_o

Torricelli --- V²=V_o² +2.a.DS --- V²= V_o² + 2.g/4.H_o --- V²=2gH_o + (2gH_o)/4 --- V²=V_o² + (V_o²)/4 --- V²=(5V_o²)/4 --- V=Ö5V_o/2 --- V=2,2.V_o

25- a) equilíbrio estático (força resultante nula)

corda B bloco de baixo --- F_R=0 --- T=40N bloco de cima --- F_R=0 --- F = 20 + T --- F = 20 + 40 --- F=60N

b) os dois blocos sobem com a=2m/s² e F_R¹0

Bloco de baixo --- F_R=ma --- T-40=4.2 --- T=48N (tração na corda B) bloco de cima --- F_R=ma --- F – T – 20=2.2 ---

F – 48 – 20=4 --- F=72N (tração na corda A)

26- a) sistema em repouso --- força que o anteparo exerce sobre A, impedindo-o de ir para a direita.

bloco B --- P_B=T --- T=50N bloco A --- N=T --- N=50N

b) retirando-se o anteparo C, N deixa de agir sobre A e o sistema se move no sentido horário com aceleração a

bloco A --- F_R=ma --- T=20.a I bloco B --- F_R=ma --- P_B– T =ma --- 50 – T =5.a II substituindo I em II ---

50 – 20.a = 5.a --- a=2m/s².

27- Colocando as forças sobre cada bloco:

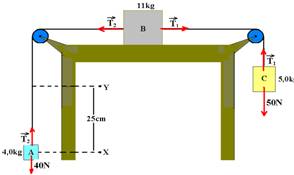
bloco A – sobe --- F_R=ma --- T₂ - 40= 4.a I bloco B – direita --- F_R=ma --- T₁ – T₂=11.a II bloco C – desce ---

F_R=ma --- 50 – T₁=ma --- 50 – T₁=5.a III Somando I, II e III --- 10=20.a --- a= 0,5m/s²

Bloco A que sobe com aceleração de 0,5m/s², percorrendo DS=25cm=0,25m e tendo V_o=0 em X e V em Y.

Torricelli --- V² = V_o² + 2.a.DS --- V² = 0² + 2.0,5.0,25 --- V=Ö0,25 --- V=0,5m/s

28- Colocando as forças e calculando a aceleração do sistema:

bloco 1 --- F_R=m.a --- T=6.a I bloco 2 --- F_R=m.a --- 40 – T=4.a II substituindo I em II --- 40 – 6.a=4.a ---

a=4m/s². Observe na figura que os dois blocos se movem juntos enquanto percorrem apenas 0,5m, com aceleração a=4m/s² e, no instante em que 2 chega ao solo,eles tem velocidade:

Torricelli --- V² = V_o² + 2.a.DS --- V²= 0² + 2.4.0,5 --- V=2m/s. A partir daí, 2 não puxa mais 1 e ele segue em MRU com velocidade constante de 2m/s, com que chega em B.

29- (1) bloco A --- F – T=m.a --- F – T=4.2 --- F – T=8 I bloco B --- T=6.2 --- T=12N II substituindo II em I ---

F – 12=8 --- F=20N --- está correta

(2) está correta – vide (1)

(3) está correta, pois o dinamômetro é ideal (como se não existisse).

(4) está correta, o dinamômetro indica a tração no fio.

Todas corretas

30- colocando as forças e, como as massas são iguais, a tração (T) em cada fio é a mesma.

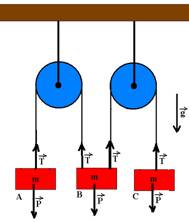
Observe na figura acima que o bloco B sobe, pois nele temos 2T para cima. Bloco A --- desce --- P-T=ma --- mg-T=ma I --- bloco B --- sobe --- 2T-P-ma --- 2T-mg=ma II --- bloco C --- desce --- P-T=ma --- mg-T=ma III --- somando I, II e III --- mg=3ma --- a=g/3 R- C

31- Colocando as forças:

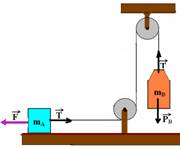
Bloco B --- sobe --- T – P_B = m_B.a --- T – 100 = 10.a I bloco A --- para a esquerda --- F – T=m_A.a ---

500 – T=15.a II --- somando I com II --- a=16m/s² --- T – 100=10.16 --- T=260N

32- a) m=100g=0,1kg --- F-P=m.a --- F – 3=0,3.3 --- F=3,9N.

b) só sobre o elo do meio --- F_R=m.a --- F_R=0,1.3 --- F_r=0,3N

c) elo de baixo --- T-P=ma --- T-1=0,1.3 --- T=1,3N

33- Cálculo da aceleração do sistema:

Bloco da esquerda --- 2mg – T=2ma bloco da direita --- T – mg=ma resolvendo o sistema --- mg=3ma --- a=g/3

Torricelli --- V²= V_o² + 2.a.DS --- V²= 0² + 2.g/3.h --- V=Ö2.g.h/3

34- Quem está subindo é o anel do meio mais os três anéis de baixo, portanto 4 anéis de peso P=(4X0,2).10 --- P=8N

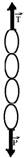
T – P=m.a --- T – 8=0,8.2 --- T=9,6N R- B

35-Decompondo, na figura I a força de tração T₁, observamos que:

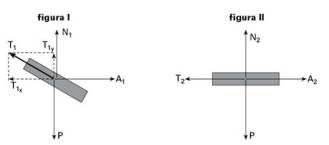
figura I --- T_1X + N₁=P --- N₁=P – T_1X figura II --- N₂=P --- portanto N₂>N₁ --- R-B

36-Colocando as forças nas barcaças:

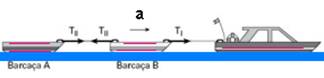
Barcaça A --- F_R=m_A.a --- T_II =30.10³.a --- T_II=20.10³.a --- 8.10⁴=20.10³.a_A --- a_A=4m/s² qualquer aceleração acima desse valor arrebenta o cabo II

O cabo I puxa as duas barcaças de massa m_A+B=50.10³kg --- F_R=m_A+B.a_B --- T_I= m_A+B.a_B --- 6.10⁵=50.10³.a_B --- a_B=12m/s² --- qualquer aceleração acima desse valor arrebenta o cabo I.

Como a aceleração das duas barcaças deve ser a mesma, para que os dois cabos não arrebentem temos que pegar o menor valor de a, ou seja, a=4m/s².

37- De uma maneira bem simples e prática --- quando o recipiente é acelerado para a direita, o líquido, por inércia, tende a permanecer em repouso, ou seja, fica contrário ao deslocamento dos recipientes --- R- B

38- O bloco m₂ está sujeito a 6 forças. Seu próprio peso e a força de ação F são duas delas --- as outras quatro são devidas aos contatos com os outros dois corpos, sendo duas delas para cada corpo --- a ação na direção da gravidade em função do peso destes corpos e ações na direção do movimento, mas no sentido oposto, por resistência a ação de F --- R- B

39- Considere o sistema abaixo em repouso em relação a um referencial inercial em que o bloco de massa M representa o peso do cabo (aplicado em seu centro de gravidade) e as cordas representam o cabo, e q o ângulo que o cabo faz com a horizontal do lugar.

Observe na seqüência das figuras acima que, como o sistema está em equilíbrio, F_R=0 --- 2Tsenθ=Mg --- senq = Mg/2T ---

assim, se q = 0 --- sen(q) = 0 o que significa que as forças exercidas pela corda sobre o bloco devem ser infinitas --- ou, deve existir uma força de módulo infinito para que, somada ao peso do bloco (aqui modelando a massa do cabo), resulte zero --- como isso não é possível, não há como se ter q = 0, isto é, deverá sempre existir, num campo gravitacional, a “curva” observada por Lucinha.

40- a) A tensão (ou tração, que é o termo mais adequado) na corda corresponde à intensidade da força aplicada por Alberto ---

T = 200 N.

b) : força de tração no centro da polia, aplicada por Cabral --- : forças aplicadas pela corda que passa pela polia ---

c) Como a polia não tem massa (ou seja, sua massa é desprezível) e, além disso, ela está sendo arrastada quase que estaticamente (ou seja, com velocidade constante --- a = 0) --- princípio fundamental --- F_R=ma --- F – 2 T = m a --- F – 2 T = 0 ---

F = 2 T = 2 (200) --- F = 400 N.

d) A figura a seguir mostra que quando a ponta da corda desloca D (do ponto P até o ponto P’ ), o centro da polia desloca D/2.

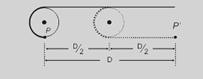
Se corda que Alberto puxa enrola D, essa distância é distribuída nos dois braços da polia, fazendo com o seu centro desloque D/2 --- portanto, se Carlos avança 2 m, Alberto recua 4 m.

41- As forças que agem sobre a esfera são seu peso (), vertical e para baixo e a força de tração no fio (), conforme figura ---

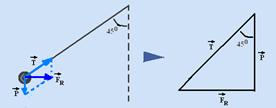
somando vetorialmente com você obtém a força resultante --- tg45^o = cateto oposto/cateto adjacente --- tg45^o=F_R/P --- 1=ma/mg --- a=g=9,8m/s² --- R- C

42- F_R=KV² --- K=F_RV²=m.aV²=(m.V/t)/V² --- K=(m/t)/V --- K=(kg/s)/(m/s) --- K=kg/s x s/m --- K=kg/m --- R- D

43- Como o andaime se encontra parado (equilíbrio estático) a resultante das forças que agem sobre ele ê nula --- observe que os pesos sobre o andaime encontram-se no meio (peso de um operário + peso do andaime, supondo-o homogêneo) e na extremidade esquerda (peso do outro operário) --- assim, a tensão na corda X é maior que a na corda Y --- R- D

44- Colocando as forças que agem sobre cada bloco (pesos de A e de B, P_A e P_B, verticais e para baixo; tração T em cada bloco,

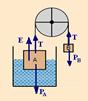
verticais e para cima e o empuxo E sobre o bloco A devido ao líquido, vertical e para cima) --- E=ρ_liq.V_liq.g --- E= ρ_liq.3(V/2).g --- P_B=m.g --- P_B= ρ_bloco.V_bloco.g --- P_B= ρ_bloco.Vg --- P_A=3mg=3.ρ_bloco.V.g --- o sistema está em equilíbrio (F_R=0) --- bloco B --- T=P_B --- T= ρ_bloco.Vg --- bloco A --- V_liq=V_bloco/2 --- V=2V --- E + T = P_A --- ρ_liq.3(V/2).g + ρ_bloco.Vg = 3.ρ_bloco.V.g --- ρ_liq.3(V/2).g = ρ_bloco.2.(2V).g --- 3ρ_liq/2 = 2.ρ_bloco.2 --- ρ_liq=4 ρ_bloco/3 --- R- D

45-

I. Falsa --- para que o corpo se desloque é necessário que a projeção de F na horizontal (Fcosθ) seja maior que a força de atrito --- Fcosθ > F_atrito.

II. Correta --- o corpo estará na iminência de se mover quando Fcosθ = F_atrito.

III. Correta --- se F > P e θ=90^o, o bloco girará no sentido anti-horário até que a direção de F seja a mesma que de P e, a partir daí,

como F>P a força resultante será vertical e para cima, e o corpo subirá.

IV- Falsa --- o corpo só será elevado se N + Fsenθ > P, pois, nesse caso sobrará uma força resultante vertical e para cima.

R- D

46-

Aceleração de subida da plataforma A que sobe ∆S=4,5m em ∆t=3,0s, a partir do repouso V_o=0 --- ∆S=V_o.t + a.t²/2 --- 4,5 =

0.3 + a.3²/2 --- a=4,4/4,5 --- a=1,0m/s² --- esta é a aceleração de subida da massa m e de descida da massa M --- a figura

mostra as forças que agem sobre o sistema --- equações --- massa m --- F_R=m.a --- T – mg = m.a --- T – 225.10 = 225.1 ---

T=2 475N --- massa M --- M.g – T = M.a --- M.10 – 2 475 = M.1 --- 9M=2 475 --- M=275kg --- R- A

47-

a) Se você considerar o sistema carro-ônibus como um sistema isolado, você pode utilizar o teorema da conservação da

quantidade de movimento --- Q_antes=M.V_o + m_a.V_a=9000.80 +1000.0 --- Q_antes=720000kg.m/s --- Q_depois=(M + m_a).V=10.000.V

Q_depois=10000V --- Q_antes = Q_depois --- 720000=10000V --- V=72km/h.

b) Pela figura fornecida você pode determinar a intensidade da força lateral --- sen3^o=F_L/F_at --- 0,05=F_L/8000 --- F_L=400N

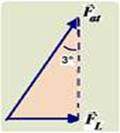
A aceleração lateral do carro tem intensidade --- F_L=m.a_L --- 400=1600.a_L --- a_L=0,25m/s².