Características de um MUV

 Observe a figura abaixo, que representas as posições de um móvel (beija flor), bem como suas velocidades. Ele efetua deslocamentos diferentes em intervalos de tempo iguais.

Considere agora a velocidade e veja que ela sofre, a cada 0,5s, um aumento constante de 50m/s. Nessas condições ele efetua movimento uniformemente variado.

Movimento uniformemente variado (MUV) é aquele em que a velocidade varia de maneira uniforme com o tempo e a aceleração escalar é constante e não nula.

Função (equação) horária da velocidade do MUV

 O móvel da figura abaixo tem velocidade V_o no instante t_o e velocidade V num instante posterior t.

Admitindo t_o=0 como a origem dos tempos   a=(V – V_o)/(t – t_o)  a=(V – V_o)/t V – V_o=a.t  

V = V_o + a.t

Diagrama velocidade X tempo de um móvel em MUV 

Como a função V= V_o + a.t é uma função do primeiro grau, seu gráfico é uma reta de inclinação não nula.

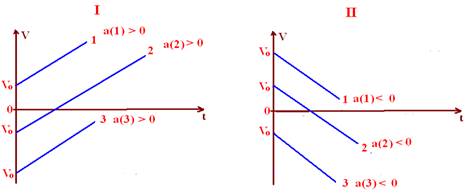
Observe nos gráficos acima que:

se V=f(t) é uma função crescente (reta representativa forma um ângulo agudo com a horizontal), a aceleração é positiva (Figura I). 

se V=f(t) é uma função decrescente (reta representativa forma um ângulo obtuso com a horizontal), a aceleração é negativa Figura II).

O que você deve saber

Equação horária da velocidade do MUV.

 Se o movimento é acelerado (acelerando), a>0, o gráfico VXt é uma reta inclinada para cima e se é retardado (freando), a<0, o gráfico VXt é uma reta inclinada para baixo.

Em todo MUV a aceleração é constante e seu gráfico é uma reta paralela ao eixo t (I) e, nesse 

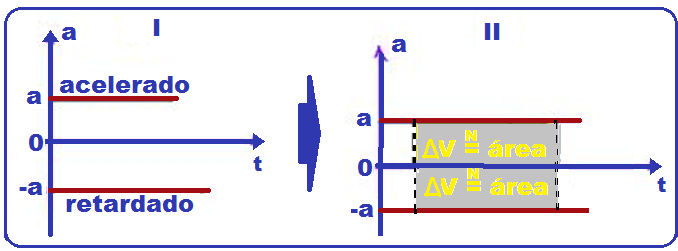
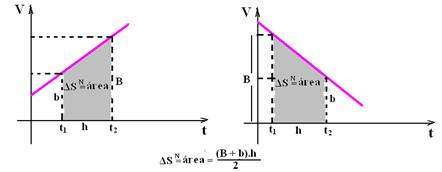
gráfico, entre dois instantes quaisquer t₁ e t₂, a variação de velocidade ΔV é numericamente igual à área (II)

 Em todo gráfico VXt a área entre a reta representativa e o eixo dos tempos é numericamente igual à variação de espaço ΔS, entre dois instantes quaisquer t₁ e t₂

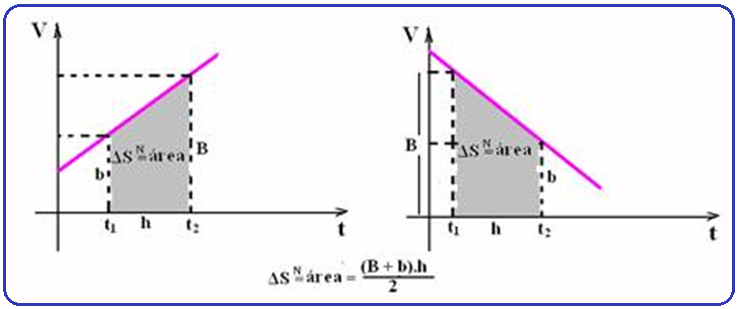
 Análise do gráfico V X t de um MUV:(leia com atenção as informações abaixo)

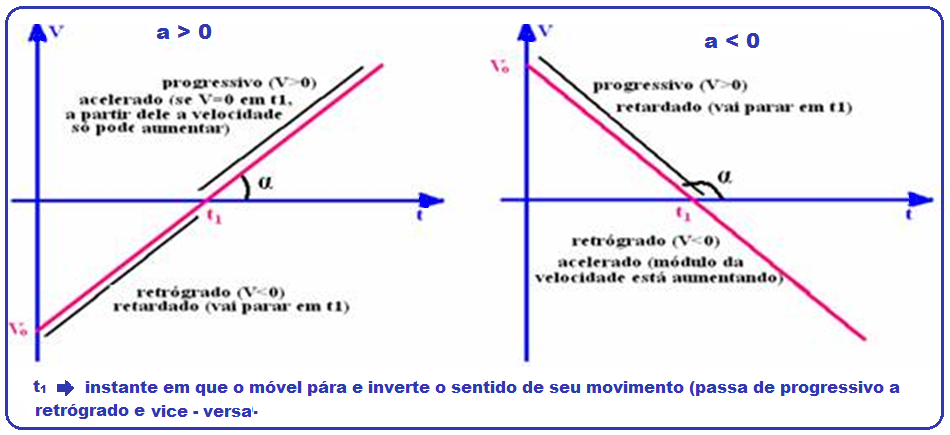
O ângulo α que a reta representativa da velocidade forma com um eixo horizontal é tal que tgα =

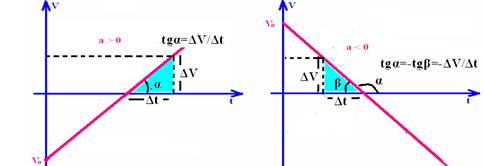
ΔV/Δt corresponde à aceleração do móvel, pois a= ΔV/Δt e é denominada coeficiente angular da reta ou declividade da reta. Observe que, se α é agudo, f(t) é crescente e a > 0 e se α é obtuso , f(t) é decrescente e a < 0.

Exercícios sobre:

Equação da velocidade de um MUV

Gráfico horário da velocidade de um MUV

01-(UFB) Um gato realiza um MUV em trajetória retilínea e horizontal que obedece à função horária da velocidade V= - 20 + 5t em unidades do SI. Pede-se:

a) a velocidade inicial e a aceleração

b) o instante em que ele muda o sentido de seu movimento

c) classificar o movimento em progressivo ou retrógrado, acelerado ou retardado, orientando a trajetória para a direita.

Qual o tipo de movimento do gato nos instantes 2s e 10s

02-(UFB) No gráfico abaixo, da velocidade de um móvel em MUV em função do tempo, pede-se determinar:

a) a velocidade inicial V_o e a aceleração a

b) o instante em que o móvel inverte o sentido de seu movimento

c) classificar o movimento

d) o deslocamento sofrido no intervalo de tempo compreendido entre 0 e 4s

03-(PUC-RJ) Considere o movimento de um caminhante em linha reta. Este caminhante percorre os 20,0 s iniciais à velocidade constante v₁ = 2,0 m/s.

Em seguida, ele percorre os próximos 8,0 s com aceleração constante a = 1 m/s² (a velocidade inicial é 2,0 m/s). Calcule a velocidade final do caminhante.

04- (UFSM-RS) Ao preparar um corredor para uma prova rápida, o treinador observa que o desempenho dele pode ser descrito, de forma aproximada, pelo seguinte gráfico:

A velocidade média desse corredor, em m/s, é de

a) 8,5                  

b) 10,0                 

c) 12,5                  

d) 15,0                  

e) 17,5

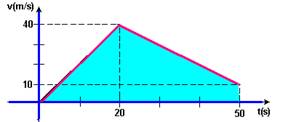
05-(FUVEST-SP) Na figura a seguir estão representadas as velocidades, em função do tempo, desenvolvidas por um atleta, em dois treinos A e B, para uma corrida de 100m rasos.

Com relação aos tempos gastos pelo atleta para percorrer os 100m, podemos afirmar que, aproximadamente:

a) no B levou 0,4s a menos que no A     

b) a) no A levou 0,4s a menos que no B     

c) a) no B levou 1,0s a menos que no A

d)  no A levou 0,4s a menos que no B     

e) no A e no B levou o mesmo tempo

06-(CFT-CE) Observe o movimento da moto a seguir, supostamente tomada como partícula.

a) O instante em que sua velocidade será de 20m/s.

b) O deslocamento efetuado até este instante.

07-(UNIFESP-SP) A velocidade em função do tempo de um ponto material em movimento retilíneo uniformemente variado, expressa em unidades do SI, é v = 50 - 10t. Pode-se afirmar que, no instante t = 5,0 s, esse ponto material tem

a) velocidade e aceleração nulas.                          

B) velocidade nula e daí em diante não se movimenta mais.

c) velocidade nula e aceleração a = - 10 m/s².     

d) velocidade nula e a sua aceleração muda de sentido.

e) aceleração nula e a sua velocidade muda de sentido.

08-(UFRS-RS) Um automóvel que trafega com velocidade constante de 10 m/s, em uma pista reta e horizontal, passa a acelerar uniformemente à razão de 60 m/s em cada minuto, mantendo essa aceleração durante meio minuto. A velocidade instantânea do automóvel, ao final desse intervalo de tempo, e sua velocidade média, no mesmo intervalo de tempo, são, respectivamente:

a) 30 m/s e 15 m/s.          b) 30 m/s e 20 m/s.           c) 20 m/s e 15 m/s.          d) 40 m/s e 20 m/s.          –e) 40 m/s e 25 m/s.

09-(PUC-PR) Um automóvel trafega em uma estrada retilínea. No instante t = 0 s, os freios são acionados, causando uma aceleração constante até anular a velocidade, como mostra a figura.

A tabela mostra a velocidade em determinados instantes

Com base nestas informações, são feitas algumas afirmativas a respeito do movimento:

I. O automóvel apresenta uma aceleração no sentido do deslocamento.

II. O deslocamento do veículo nos primeiros 2 s é 34 m.

III. A aceleração do veículo é -1,5 m/s².

IV. A velocidade varia de modo inversamente proporcional ao tempo decorrido.

V. A velocidade do veículo se anula no instante 7,5 s.

Está correta ou estão corretas:

a) somente I.              

b) I e II.                

c) somente III.                  

d) IV e V.                  

e) II e V.

10-(MACKENZIE-SP) A aceleração de um móvel, que parte do repouso, varia com o tempo de acordo com o gráfico abaixo.

O instante, contado a partir do início do movimento, no qual o móvel pára, é:

a) 5s                     

b) 6s                    

c) 8s                     

d) 13s                     

e) 18s

11-(UFPE) O gráfico da velocidade em função do tempo de um ciclista, que se move ao longo de uma pista retilínea, é mostrado a seguir.

 Considerando que ele mantém a mesma aceleração entre os instantes t = 0 e t = 7 segundos, determine a distância percorrida neste intervalo de tempo. Expresse sua resposta em metros.

12-(UFB) Considerando um diagrama v x t, onde v é a velocidade instantânea de uma partícula no instante t, o que representa:

a) a declividade ou inclinação da reta representativa do gráfico?

b) o que representa a área sob a reta?

13- (FUVEST-SP) O gráfico na figura descreve o movimento de um caminhão de coleta de lixo em uma rua reta e plana, durante 15s de trabalho

a) Calcule a distância total percorrida neste intervalo de tempo.

b) Calcule a velocidade média do veículo.

14-(Ufpe) Uma partícula, que se move em linha reta, está sujeita à aceleração a(t), cuja variação com o tempo é mostrada no gráfico a seguir.

 Sabendo-se que no instante t = 0 a partícula está em repouso, calcule a sua velocidade no instante t = 8,0 s, em m/s.

15- (UNESP-SP) O motorista de um veículo A é obrigado a frear bruscamente quando avista um veículo B à sua frente, locomovendo-se no mesmo sentido, com uma velocidade constante menor que a do veículo A. Ao final da desaceleração, o veículo A atinge a mesma velocidade que B, e passa também a se locomover com velocidade constante. O movimento, a partir do início da frenagem, é descrito pelo gráfico da figura.

Considerando que a distância que separava ambos os veículos no início da frenagem era de 32 m, ao final dela a distância entre ambos é de

a) 1,0 m.                     b) 2,0 m.                     c) 3,0 m.                      d) 4,0 m.                       e) 5,0 m.

16-(CFT-MG) Três carros A, B, e C, trafegando numa avenida reta, estão lado a lado, quando o semáforo a 55 metros à frente fecha. Sabendo-se que o gráfico a seguir mostra a variação da velocidade dos veículos a partir desse momento, é correto afirmar que irá(ão) ultrapassar o sinal somente o(s) carro(s)

a) A.                     

b) B.                     

c) A e B.                          

d) A e C.

17-(UFU-MG) O gráfico a seguir representa a velocidade em função do tempo de um automóvel que parte do repouso. A velocidade máxima permitida é de 72 km/h. No instante t, quando o motorista atinge essa velocidade limite, ele deixa de acelerar o automóvel e passa a se deslocar com velocidade constante.

Sabendo-se que o automóvel percorreu 1,2 km em 90 segundos, o valor do instante t é

a) 80 s.                 

b) 30 s.                 

c) 60 s.                

d) 50 s.

18-(UnB-DF) A tabela abaixo indica a velocidade instantânea  de um objeto, em intervalos de um segundo.

As velocidades instantâneas do objeto nos instantes 3,60s e 5,80s são, respectivamente:

a) 17,5m/s e 20,5m/s          b) 13,8m/s e 22,6m/s          c) 14,5m/s e 19,5m/s          d) 15,5m/s e 22,2m/s          e) 8,20m/s e 12,2m/s

19-(Olimpíada Brasileira de Física) Uma partícula executa um movimento retilíneo uniformemente variado. Num dado instante a partícula tem velocidade 50m/s e aceleração negativa de módulo 0,2m/s². Quanto tempo decorre até a partícula alcançar a mesma velocidade em sentido contrário?

a) 500s                   

b) 250s                      

c) 125s                        

d) 100s                       

e) 10s

20-(CFT-MG) O movimento retilíneo de um corpo é descrito pela equação v = 10 - 2t em que v é a velocidade, em m/s, e t é o tempo, em segundos.

Durante os primeiros 5,0 s, a distância percorrida por ele, em metros, é:

a) 10.                    

b) 15.                      

c) 20.                       

d) 25.

21-(PUC-RJ) O movimento de um objeto pode ser descrito pelo gráfico velocidade versus tempo, apresentado na figura a seguir.

Podemos afirmar que:

a) a aceleração do objeto é 2,0 m/s², e a distância percorrida em 5,0 s é 10,0 m.

b) a aceleração do objeto é 4,0 m/s², e a distância percorrida em 5,0 s é 20,0 m.

c) a aceleração do objeto é 2,0 m/s², e a distância percorrida em 5,0 s é 25,0 m.

d) a aceleração do objeto é 2,0 m/s², e a distância percorrida em 5,0 s é 10,0 m.

e) a aceleração do objeto é 2,0 m/s², e a distância percorrida em 5,0 s é 20,0 m.

22-(PUC-RJ) É CORRETO afirmar que a distância percorrida pelo objeto entre t = 0 e t = 1,4s foi aproximadamente de:

a) 0,7 m                       b) 1,8 m                       c) 0,1 m                       d) 1,6 m

 23-(UERJ-RJ) A velocidade de um corpo que se desloca ao longo de uma reta, em função do tempo, é representada pelo seguinte gráfico:

Calcule a velocidade média desse corpo no intervalo entre 0 e 30 segundos.

24-(Ufrj-RJ) Um móvel parte do repouso e descreve uma trajetória retilínea durante um intervalo de tempo de 50s, com a aceleração indicada no gráfico a seguir.

a) Faça um gráfico da velocidade do móvel no intervalo de 0 até 50s.

b) Calcule a distância percorrida pelo móvel nesse intervalo.

25-(UNIFESP-SP) A função da velocidade em relação ao tempo de um ponto material em trajetória retilínea, no SI, é v = 5,0 - 2,0 t. Por meio dela pode-se afirmar que, no instante t = 4,0 s, a velocidade desse ponto material tem módulo

a) 13 m/s e o mesmo sentido da velocidade inicial.                          

b) 3,0 m/s e o mesmo sentido da velocidade inicial.

c) zero, pois o ponto material já parou e não se movimenta mais.     

d) 3,0 m/s e sentido oposto ao da velocidade inicial.

e) 13 m/s e sentido oposto ao da velocidade inicial.

26-(UFPE-PE)  Um motorista dirige um carro com velocidade constante de 80 km/h, em linha reta, quando percebe uma “lombada” eletrônica indicando a velocidade máxima permitida de 40 km/h. O motorista aciona os freios, imprimindo uma

 desaceleração constante, para obedecer à sinalização e passar pela “lombada” com a velocidade máxima permitida. Observando-se a velocidade do carro em função do tempo, desde o instante em que os freios foram acionados até o instante de passagem pela “lombada”, podemos traçar o gráfico abaixo.

Determine a distância percorrida entre o instante t = 0, em que os freios foram acionados, e o instante t = 3,0 s, em que o carro ultrapassa a “lombada”. Dê sua resposta em metros.

27-(UNCISAL-AL) João Gabriel, vestibulando da UNCISAL, preparando-se para as provas de acesso à

universidade, vai conhecer o local das provas. Sai de casa de carro e, partindo do repouso, trafega por uma avenida retilínea que o conduz diretamente ao local desejado. A avenida é dotada de cruzamentos com semáforos e impõe limite de velocidade, aos quais João Gabriel obedece. O gráfico que melhor esboça o comportamento da velocidade do carro dele, em função do tempo, desde que ele sai de casa até a chegada ao local da prova, onde estaciona no instante t’, é:

28-(UNEMAT-MT) O gráfico em função do tempo mostra dois carros A e B em movimento retilíneo.

Em t = 0 seg. os carros estão na mesma posição.

Com base na análise do gráfico, é correto afirmar.

a) Os carros vão estar na mesma posição nos instantes t = 0 seg. e t = 4,0 seg.

b) Os carros não vão se encontrar após t = 0, porque a velocidade de A é maior que a do carro B

c) Os carros vão se encontrar novamente na posição S = 10 m

d) Os carros não vão se encontrar, porque estão em sentidos contrários.

e) Os instantes em que os carros vão estar na mesma posição é t = 0 seg. e t = 8,0 seg.

29-(MACKENZIE-SP)  Dois automóveis A e B se movimentam sobre uma mesma trajetória retilínea,

com suas velocidades variando com o tempo de acordo com o gráfico a seguir. Sabe-se que esses móveis se encontram no instante 10 s. A distância entre eles, no instante inicial (t = 0 s), era de

a) 575 m                       

b) 425 m                         

c) 375 m                         

d) 275 m                         

e) 200 m 

30-(CFT-SC) O gráfico abaixo representa a variação da velocidade em função do tempo de uma

partícula em movimento uniformemente variado. Em relação à área abaixo da reta do gráfico, é correto afirmar que ela representa a:

a) aceleração média.           

b) velocidade média.            

c) variação da velocidade.           

d) distância percorrida pela partícula.                              

e) velocidade instantânea. 

31-(FUVEST-SP)  Na Cidade Universitária (USP), um jovem, em um carrinho de rolimã, desce a  rua do

Matão, cujo perfil está representado na figura a seguir, em um sistema de coordenadas em que o eixo O_x tem a direção horizontal.

No instante t = 0, o carrinho passa em movimento pela posição o_y = y_o e x = 0.

Dentre os gráficos das figuras a seguir, os que melhor poderiam descrever a posição x e a velocidade v do carrinho em função do tempo t são, respectivamente,

a) I e II.                             

b) I e III.                                

c) II e IV.                                

d) III e II.                             

e) IV e III. 

32-(UFRJ-RJ) Um avião vai decolar em uma pista retilínea. Ele inicia seu movimento na cabeceira da

pista com velocidade nula e corre por ela com aceleração média de 2,0 m/s² até o instante em que levanta vôo, com uma velocidade de 80 m/s, antes de terminar a pista.

a) Calcule quanto tempo o avião permanece na pista desde o início do movimento até o instante em que levanta vôo.

b) Determine o menor comprimento possível dessa pista.

33-(UNICAMP-SP) O radar é um dos dispositivos mais usados para coibir o excesso de velocidade nas vias de trânsito. O seu princípio de funcionamento é baseado no efeito Doppler das ondas eletromagnéticas refletidas pelo carro em movimento.

Considere que a velocidade medida por um radar foi V = 72 km/h para um carro que se aproximava do aparelho.

Quando um carro não se move diretamente na direção do radar, é preciso fazer uma correção da velocidade medida pelo aparelho  V_m para obter a velocidade real do veículo Vr. Essa correção pode ser calculada a partir da fórmula V_m=V_r.cosα, em que α é o ângulo formado entre a direção de tráfego da rua e o segmento de reta que liga o radar ao ponto da via que ele mira. Suponha que o radar tenha sido instalado a uma distância de 50 m do centro da faixa na qual o carro trafegava, e tenha detectado a velocidade do carro quando este estava a 130 m de distância, como mostra a figura abaixo

Se o radar detectou que o carro trafegava a 72 km/h, sua velocidade real era igual a

a) 66,5 km/h                     

b) 36 3 km/h.                                  

c) 78 km/h.                                   

d) 144 / 3 km/h

34-(UFPE-PE)

Dois veículos partem simultaneamente do repouso e se movem ao longo da mesma rodovia reta, um

ao encontro do outro, em sentidos opostos. O veículo A parte com aceleração constante igual a a_A = 2,0 m/s². O veículo B, distando d = 19,2 km do veículo A, parte com aceleração constante igual a a_B = 4,0 m/s². Calcule o intervalo de tempo até o encontro dos veículos, em segundos.

35-(UERJ-RJ)

Dois carros, A e B, em movimento retilíneo acelerado, cruzam um mesmo ponto em t = 0 s. Nesse

instante, a velocidade v_o de A é igual

à metade da de B, e sua aceleração a corresponde ao dobro da de B. Determine o instante em que os dois carros se reencontrarão, em função de v_o e a.

36-(UEPA-PA)

No Pará, o perigo relacionado às altas velocidades no trânsito tem aumentado os  riscos de acidentes, principalmente em Belém.

Considerando que a "distância de freagem" é a distância que o carro percorre desde o momento que os freios são acionados até parar e que o modelo matemático que expressa essa relação é dado por  D = K . V², onde  D representa a distância de freagem em metros, K é uma constante e  V  é a velocidade em Km/h. Assim, um automóvel que tem seus freios acionados estando a uma velocidade de 80 Km/h ainda percorre 44 metros até parar. A distância de  freagem de um automóvel que tem seus freios acionados, estando a uma velocidade de 160 Km/h é:

a) 2 vezes a distância de freagem se estivesse a 80 Km/h.                  

b) 3 vezes a distância de freagem se estivesse a 80 Km/h.

c) 4 vezes a distância de freagem se estivesse a 80 Km/h.              

d) 5 vezes a distância de freagem se estivesse a 80 Km/h.

e) 6 vezes a distância de freagem se estivesse a 80 Km/h.

37-(AFA)

 Considere um móvel deslocando–se numa trajetória horizontal e descrevendo um movimento retilíneo uniformemente acelerado e

retrógrado. A alternativa que contém o gráfico que melhor representam movimento descrito pelo móvel é

38-(AFA)

 Um bloco se movimenta retilineamente, do ponto A até o ponto C, conforme figura abaixo

Sua velocidade v em função do tempo t, ao longo da trajetória, é descrita pelo diagrama v×t mostrado a seguir.

Considerando que o bloco passa pelos pontos A e B nos instantes 0 e t₁, respectivamente, e para noponto C no instante t₂, a razão entre

as distâncias percorridas pelo bloco nos trechos BC e AB , vale

a) (t₂ + t₁)/t₁                              

b) (t₂ – t₁)/t₂²        

c) (t₂ – t₁)/2t₁                                 

d) (t₂ + t₁)/2t₂

39-(ACAFE-SC)

Para garantir a segurança no trânsito, deve-se reduzir a velocidade de um veículo em dias de chuva,

senão vejamos: um veículo em uma pista reta, asfaltada e seca, movendo-se com velocidade de módulo 36 km/h (10 m/s) é freado e desloca-se 5,0 m até parar. Nas mesmas circunstâncias, só que com a pista molhada sob chuva, necessita de 1,0 m a mais para parar. 

Considerando a mesma situação (pista seca e molhada) e agora a velocidade do veículo de módulo 108 km/h (30 m/s), a alternativa correta que indica a distância a mais para parar, em metros, com a pista molhada em relação a pista seca é:

A) 6         

B) 2         

C)1,5         

D) 9

Resolução dos exercícios sobre:

Equação horária da velocidade de um MUV

Gráfico da velocidade de um MUV

01- a)

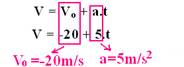
b) Quando ele muda o sentido se seu movimento ele pára (V=0) e, a partir desse instante, o movimento que era progressivo se torna retrógrado  ---  V=-20 + 5t  ---  0=-20 + 5t  ---  t=4s (instante em que ele pára para inverter o sentido do movimento)

c)

d) 2s – retrógrado retardado  ---  10s - progressivo acelerado  ---  Veja esquema acima)

02- a) V_o=-8m/s  ---  a=(8 – (-8))/(4 – 0)  ---  a=16/4  ---  a=4m/s²  

b) V= V_o + at  ---  V=-8 + 4t  ---  inverte o sentido (pára) – V=0  ---  0=-8 + 4t  ---  t=2sou pelo gráfico que corresponde ao ponto onde a reta intercepta o eixo t.

c) entre 0 e 2s  ---  retrógrado (V<0) e retardado (módulo de V está diminuindo)  ---  após 2s  ---  progressivo (V>0) e acelerado (módulo de V está aumentando)

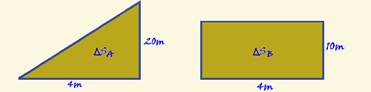
d) ΔS=área entre 0 e 4s, que corresponde à soma das áreas hachuradas da figura abaixo

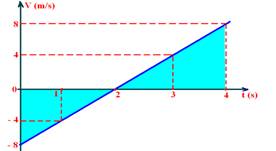
ΔS=b.h/ + b.h/2=2.(-8)/2 + 8.2/2  ---  ΔS=0

03- V_o=2m/s  ---  a=1ms²  ---  V=V_o + at  ---  V=2 + 1.8  ---  V=10m/s

04- ΔS=área=(10 + 6).12,5/2  ---  ΔS=100m  ---  V_m=ΔS/Δt  ---  V_m=10m/s  ---  R- B

05- A – ΔS_A=área do trapézio=100m

ΔS_A=(t_A + (t_A – 4)).11/2  ---  100=2t_A – 4).11/2  ---  t_A=244/22  ---  t_A=11,1s (treino A)

B – ΔS_B=área do trapézio=100m

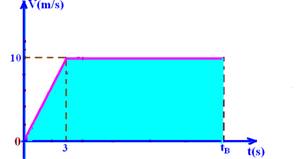
ΔS_B=(t_B + (t_B – 3)).10/2  ---  100=10t_B – 15  ---  t_B=115/10  ---  t_B=11,5s (treino B)

Δt=t_B – t_A=0,4s  ---  R- B

06- a) V_o=0  ---  a=(V – V_o)/(t – t_o)=10/5  ---  a=2m/s²  ---  V = V_o + a.t  ---  20=0 + 2t  ---  t=10s

b) o deslocamento é fornecido pela área

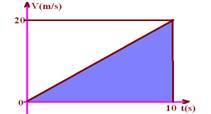
ΔS=b.h/2=10.20/2  ---  ΔS=100m

07- T=5s  ---  V=50 – 10.5  ---  V=0  ---  a=-10m/s² (constante)  ---  R- C

08- V_o=10m/s  ---  a=ΔV/Δt=(60m/s)/60s  ---  a=1m/s²  ---  V=V_o + at=10 + 1.30  --- V=40m/s

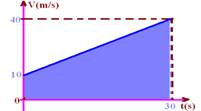
ΔS=(B + b).h/2=(40 + 10).30/2  ---  ΔS=750m  ---  V_m= ΔS/Δt=750/30  ---  V_m=25m/s

09- I – Falsa – é no sentido contrário ao do movimento – a velocidade está diminuindo

II –

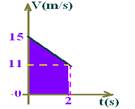
ΔS=(15 + 11).2/2=26m  ---  Falsa

III – a=(9 - 15)/3=-2m/s²  ---  Falsa

iV – Correta – observe que à medida que a velocidade diminui o tempo aumenta

V – V= V_o + at  ---  0=15 – 2t  ---  t=7,5s  ---  Correta

R- D

10- entre 0 e 5s  ---  V= V_o + at=0 + 4.5  ---  V₅=20m/s  ---  de 5s a 8s V vale 20m/s  ---  a partir de 8s – a=-2m/s² até ele parar V=0  -- V=V_o + at  ---  0=20 -2t  ---  t=10s (de 8s até ele parar)  ---  desde o inicio do movimento  --- t=8 + 10=18s  ---  R- E

11- ΔS=área hachurada da figura abaixo

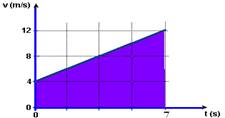
ΔS=(12 + 4).7/2 = 56m

12- a) O ângulo α que a reta representativa da velocidade forma com um eixo horizontal é tal que tgα=ΔV/Δt corresponde à aceleração do

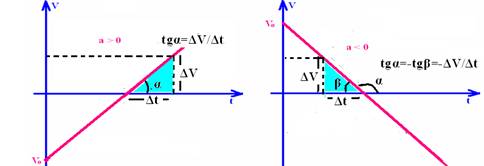
móvel, pois a= ΔV/ Δt e é denominada coeficiente angular da reta ou declividade da reta. Observe que, se α é agudo, f(t) é crescente e a>0 e se α é obtuso , f(t) é decrescente e a<0.

b) Em todo gráfico VXt a área entre a reta representativa e o eixo dos tempos é numericamente igual à variação de espaço ΔS, entre dois instantes quaisquer t₁ e t₂

13- a) ΔS=área total=b.h/2 + (B + b).h/2 + b.h/2=3.8/2 + (4 + 2).12/2 + 2.12/2=1260  ---  12 + 36 + 12=60m  ---  ΔS=60m

b) V_m=60/16=3,75  ---  V_m=3,75m

14- Entre 0 e 4s  ---  a=4m/s²  ---  V=V_o + at=0 + 4.4  ---  V=16m/s  ---  entre 4s e 8s  ---  V= V_o + at  ---  V=16 + (-2).4  ---  V=8m/s

15- Quando t=0 a distância entre eles é de 32m  ---  quando t=4s  ---  ΔS_A=área do trapézio=(30 + 15).4/2   ---  ΔS_A=90m  ---  ΔS_B=área do retângulo=4.15=60m  ---  antes – ΔS_a=32m  ---  depois – ΔS_d=(90 – 60)=30m  ---  a distância entre eles no final da frenagem será de d=32 – 30=2m  ---  R- B 

16- ΔS_A=b.h/2=6.20/2=60m  ---  ΔS_B=B + b).h/2=(8 + 2).10/2=50m  --- ΔS_C=b.h/2=4.20/2=40m  ---  R- A

17- ΔS=1.200=área do trapézio=(B + b).h/2=(90 + (90 - t)).20/2  ---  1.200=(180 – t).10  ---  1200=1800 -10t  ---  t=60s  ---  R- C  

18- Trata-se de um MUV em que a velocidade aumenta de 2,3m/s em cada 1s e, assim, sua aceleração vale a=2,3m/s²  ---  V_o=6,20m/s  ---  V= V_o + at  ---  V=6,20 + 2,3t  ---  t=3,60s – V=6,20 + 2,3.3,60  ---  V=14,48m/s  ---  t=5,80s – V=6,20 + 2,3.5,80  --- V=19,54m/s

R- C

19- Se, na ida ela tem velocidade de 50m/s, na volta deverá ter velocidade de -50m/s  ---  na ida, até parar (V=0) ela demorou  --- 

V=V_o + at  ---  0=50 – 0,2t  ---  t=250s (na ida)  ---  na volta  ---  V₀=0 e V=-50m/s  ---  V=V_o + at  ---  -50=0 -0,2t  ---  t=250s (na volta)  ---  t_pedido=t_ida + t_volta  ---  t_pedido=250 + 250=500s  ---   t=500s  ---  R- A

20- Colocando no gráfico  ---  t=0 – V_o=10m/s  ---  V=0  ---   0=10 -2t  ---  t=5s

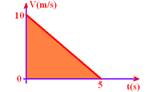
ΔS=área=b.h/2=5.10/2  ---  ΔS=25m  ---  R- D

21- a=(20 – 0)/(10 – 0)  ---  a=2m/s²  ---  d=área=5.10/2  ---  d=25m  ---  R- C

22- Considerando a área como sendo de um triângulo

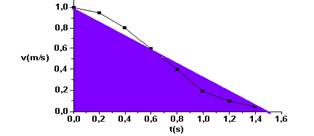
ΔS=b.h/=1,5.1,0/2  ---  ΔS=0,75m  ---  R- A

23- ΔS=área total=b.h + (B + b).h/2 + b.h=10.5 + (15 + 5).10/2 + 10.15=300m  ---  ΔS=300m  ---  V_m= ΔS/ Δt=300/30  ---  V_m=10m/s

24- a) entre 0 e 20s  ---  a=2m/s²  ---  V_o=0  ---  V₁= V_o + at=0 + 2.20  ---  V₁=40m/s  ---  entre 20s e 50s  ---  V_o=40m/s  ---  a=-1m/s²  ---V₂=V_o + at=40 – 1.30  ---  V₂=10m/s  ---  gráfico abaixo

 b) ΔS=área=b.h/2 + (B _ b).h/2=20.40/2 + (40 + 10).30/2  ---  A distância percorrida é 1150m.

25- T=4s  ---  V=5 – 2.4  ---  V=-3m/s  ---  velocidade inicial – movimento progressivo, velocidade de -3m/s – movimento retrógrado  ---  R- D

26- A distância percorrida corresponde à área compreendida entre a reta representativa  e o eixo do tempo, entre 0 e 3s, ou seja, à área de um trapézio  ---  ΔS=área=(B + b).h/2=(80/3,6 + 40/3,6).3/2= (22,2 + 11,1).1,5  ---  ΔS=49,95≈50m 

27- Observe atentamente que o único gráfico coerente com o enunciado é o da alternativa E  ---  R- E

28- Quando t=0 eles estão na mesma posição (dado do exercício) ---  quando t=4s, o deslocamento de cada carro é fornecido pela área

 entre 0 e 4s  ---  carro A, a área é de um triângulo  ---  ΔS_A=b.h/2=4.20/2  ---  ΔS_A=40m  ---  carro B, a área é de um retângulo  ---  ΔS_B=b.h=4.10  ---  ΔS_B=40m  ---  R- A 

29-  Calculando o espaço percorrido pela área  ---  ΔS_A=(B + b).h/2=(45 + 30).10/2  ---  ΔS_A=375m  ---  ΔS_B=(-10 – 30).10/2  --- 

ΔS_B=-200m  ---  d=375 + 200  ---  d=575m  ---  ou aceleração escalar de cada móvel, lembrando que  ---  a_A=(45 – 30)/(10 – 0)  ---  a_A=1,5m/s²  ---  a_B=(-30 – (-10)/(10 – 0)  --- 

a_B= -2m/s²  --- S_A=S_oA + 30t + 0,75t²  ---  S_B=S_oB – 10t – t²  ---  supondo S_oA=0 e fazendo t=10s no encontro onde você iguala as equações  ---  30(10) + 0,75(10)² = S_oB – 10(10) – (10)²  ---  375 = S_oB – 200  ---  S_oB = 575 m, que é a distância inicial entre os móveis, pois supusemos o móvel A partindo da origem.

R- A

30- Propriedade do gráfico v = f(t)  ---   a área entre a linha do gráfico e o eixo t representa o espaço percorrido pelo móvel (DS)  ---  como não há mudança de sentido, o espaço percorrido é igual à distância percorrida  ---  R- D   

31-

R- A

32- a) V=V_o + at  ---  80=0 + 2.t  ---  t=40s

b) Na situação em que a pista tem o comprimento mínimo (d_m), o avião perde o contato com a pista exatamente em seu final  ---    equação de Torricelli  ---  v² – v_o² + 2.a.d_m  ---  80²=0² + 2.2.d_m  ---  6.400=4d_m  ---  d_m=1.600m

33- Observe a figura abaixo  ---  determinando a distância d por Pitágoras  ---  (130)²=d² + (50)²  ---  16.900=d² + 2.500  ---  d=120m 

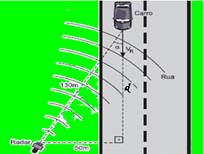
---  V_m=V_r.cosα  ---  72=V_r.120/130  ---  V_r=78km/h  ---  R- C

34- Observe na figura abaixo onde a origem da trajetória foi colocada no ponto de partida do móvel A S_oA=0  ---  a

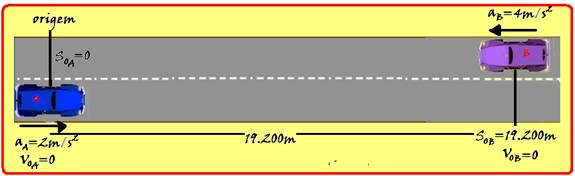
trajetória foi orientada para a direita S_oB=19200m  ---  ambos os móveis partiram do repouso, V_oA=V_oB=0  ---  como o móvel B está em movimento retrógrado e acelerado sua velocidade e sua aceleração são negativas (veja fisicaevestibular.com.br – mecânica – cinemática – gráficos do MUV)  ---  dedução da função horária de cada móvel  ---  S_A=S_oA + V_oAt + a_A.t²/2=0 + 0.t + 2t²/2  ---  S_A=t²  ---  S_B=S_oB + V_oBt + a_B.t²/2=19200 – 0.t – 4.t²/2  ---  S_B=19200 – 2t²  ---  no encontro AS=S_B  ---  t²=19200 – 2t²  ---  t²=6400  ---  t=80s.

35-Colocando a origem das posições no instante inicial (t=0 e S_o=0) e deduzindo a equação de cada carro  ---  S_A=V_ot + at²/2  ---  S_B=2V_ot +(a/2).t²/2  ---  S_B=2V_ot + at²/4  ---  no encontro  ---   S_A=S_B  ---  V_ot + at²/2 = 2V_ot + at²/4  ---  V_ot – 2V_ot + at²/2 – at²/4 = 0   --- 

-4V_ot + at² = 0  ---  t(at – 4V_o)=0  ---  at – 4V_o=0  ---  t=4V_o/a.

36-Observe na expressão D=K.V², onde K é constante e, nela você observa que a velocidade V é diretamente proporcional ao quadrado da velocidade  ---  assim, se a velocidade dobra passando de 80kmh para 160kmh, a distância percorrida pelo carro até parar fica 2²=4 vezes maior  ---  R- C

37- a) Falsa  ---  a aceleração é positiva (concavidade para cima)  ---  Entre 0 e t – o espaço decresce (movimento retrógrado, V<0)

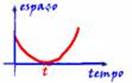
e o movimento é retardado, pois a e V tem sinais contrários (a>0 e V<0)  ---  após t – o espaço cresce (movimento progressivo, V>0) e o movimento é acelerado, pois a e V tem mesmo sinal (a>0 e V>0)

b) Correta  ---  como o movimento é retrógrado, a velocidade é negativa e, para que o movimento seja acelerado, a aceleração também tem que ser negativa, o que é o caso.

c) Falsa  ---  o movimento é acelerado mas é progressivo (V>0).

d)  Falsa  ---  se existe aceleração, o gráfico Sxt tem que ser uma parábola (equação do segundo grau).

R- B

38-  A área compreendida entre a reta representativa e o eixo dos tempos corresponde ao deslocamento ∆S do móvel no intervalo de tempo considerado  ---  A e B (0 e t+Em todo gráfico da velocidade em função do tempo₁)  ---  ∆S_AB=área do retângulo=b.h  ---  ∆S_AB=V_ot₁  ---  B e C (t₁ e t₂)  ---  ∆S_BC=área do triângulo=b.h/2  --- ∆S_BC=(t₂ – t₁).(V_o – 0)/2  ---  ∆S_BC=V_o.(t₂ – t₁)/2  ---  ∆S_BC/∆S_AB= [V_o.(t₂ – t₁)/2]/ V_ot₁  ---  ∆S_BC/∆S_AB=(t₂ – t₁)/2t₁  ---  R- C

39- Primeira situação  ---  cálculo da aceleração do carro com a pista seca  ---  V²=V_o² + 2.a.∆S  ---  0² = 10² + 2.a.5  ---  a=-10ms²  ---  cálculo da aceleração do carro com a pista molhada  ---  V²=V_o² + 2.a.∆S  ---  0² = 10² + 2.a.6  ---  a=-100/12=-25/3 ms²  ---  Segunda situação  ---  cálculo da distância percorrida com a pista seca  ---  V²=V_o² + 2.a.∆S  ---  0² = 30² + 2.(-10). ∆S  ---  ∆S =45m  ---  cálculo da distância percorrida com a pista molhada  ---  V²=V_o²+ 2.a.∆S  ---  0² = 30² + 2.(-25/3).∆S  ---  ∆S=54m  ---  distância a mais  ---  d=54 – 45=9m  ---  R- D