
Estrutura Atômica – Átomo de Bohr
Breve histórico da descoberta do átomo
A partir dos anos 1600 do século atual, a busca do átomo se tornou um exercício experimental para

diversos cientistas notáveis entre eles estão Robert Boyle, John Dalton, JJ Thomson, Ernest Rutherford e Niels Bohr.
Boyle
realizou experimentos com raios catódicos (final
do século XIX) cuja
consequência foi
a descoberta
do elétron carregado negativamente e as origens das primeiras noções
da estrutura destes átomos indivisíveis.
Thomson
propôs um modelo,
sugerindo
que o átomo tivesse uma estrutura semelhante a um pudim de ameixa, ou seja, um fluído com carga positiva (homogêneo e quase esférico) no qual as passas dispersas sobre o pudim de ameixa são comparados aos elétrons carregados negativamente imerso em uma geléia de carga positiva.
Em
1911,
depois de Thomson,
Ernest Rutherford apresentou seu modelo atômico com um núcleo
densamente composto de carga positiva e rodeado por elétrons
carregados negativamente,
semelhante
ao nosso sistema planetário, com o Sol sendo o
núcleo.
Experimentalmente,
Rutherford
concluiu que o átomo era constituído de uma parte central positiva
muito pequena, mas
de grande
massa que denominou de núcleo e
uma parte
envolvente negativa
e relativamente
enorme, a eletrosfera.
A dimensão do núcleo era anormalmente pequena em comparação com o real tamanho do átomo.
Em
1913,
Neils
Bohr aperfeiçoou o modelo nuclear de Rutherford, concluindo
que os elétrons
estavam presentes em órbitas fora do núcleo e que essas órbitas
eram específicas de raio fixo, cada uma caracterizada por níveis
energéticos bem definidos. Segundo Bohr,
existem
estados
estacionários nos quais os elétrons possuem órbitas estáveis, ou
seja, podem
permanecer nelas indefinidamente, sem perder energia. Essa
é
tanto maior quanto mais longe o elétron estiver do núcleo, ou
seja, quanto
mais afastada for sua órbita. 
A
presença
dessas órbitas energéticas, permitiu a Bohr a
construção
de um novo modelo atômico com as seguintes características:
Características do modelo atômico de Bohr
![]()

Cada elétron só pode ocupar determinada órbita circular sempre com a mesma energia, que permanece indefinidamente, sem irradiá-la.
Essas órbitas correspondem a situações estáveis, denominadas de estados estacionários.
A
quantidade
constante de energia de cada órbita é tanto maior quanto mais longe
o elétron estiver do núcleo, ou seja, quanto mais afastada for sua
órbita.
![]()
Um átomo armazena energia quando seus elétrons saltam de uma órbita mais interna (de menor potencial de energia) para uma órbita mais externa (de maior potencial de energia).
Assim,
sempre
que um átomo absorve energia, um ou mais de seus elétrons “saltam”
para uma órbita mais externa.
Quando
o fornecimento
de energia
cessa, os
elétrons
que foram deslocados para as órbitas mais distantes tendem a
restaurar o equilíbrio
retornando à sua órbita original.
Porém, toda ação que acumula energia, se for revertida, terá que liberar essa mesma energia.
Então, quando o elétron retorna à órbita original ele deve liberar a mesma quantidade de energia recebida e o faz sob forma de energia luminosa, ou seja, emitindo um fóton.
A
seqüência
de figuras abaixo ilustra
essa situação, para
um átomo de hidrogênio.
Na
figura
I você
vê um átomo
em repouso, com
um elétron girando em torno de seu núcleo.
Na figura II você vê que um fóton, proveniente do meio exterior, colidir com esse elétron, transferindo-lhe energia, o que faz com que ele salte para uma órbita mais externa, conforme mostra a figura III.
Porém, em sua nova órbita, o elétron está fora de sua posição de equilíbrio. E como a natureza busca incessantemente o equilíbrio, o elétron salta novamente para sua órbita original, o que faz com que a energia seja liberada através da emissão de um fóton luminoso.
![]()
Como a energia dos fótons só se encontra na natureza em forma de pacotes quantizados e de valores determinados, fornecidos por E = h.f, o elétron só pode transferir energia para órbitas determinadas.
Se o elétron mudar de um estado estacionário para outro, de energia diferente haverá a emissão de um fóton, e sua frequência será dada por f = (Einicial - Efinal)/h ou (Einicial – Efinal) = h.f.

![]()
As órbitas do elétron são restritas, isto é, nem todas as órbitas são permitidas em qualquer situação. A restrição é que o momento angular do elétron é necessariamente quantizado, ou seja, é um múltiplo de um valor fundamental.
![]()
Para saber as frequências permitidas, na equação de Bohr será necessário conhecer as energias dos diversos estados estacionários em que um átomo de hidrogênio pode existir.
Esse cálculo foi efetuado, pela primeira vez, por Bohr baseando-se em um modelo específico do átomo de hidrogênio por ele imaginado.
O modelo de Bohr teve sucesso apenas no caso do átomo de hidrogênio, mas mesmo assim influenciou muito o desenvolvimento posterior na Física Quântica.
Para o átomo de hidrogênio(um único elétron girando em órbita circular em torno de um único próton que se encontra no núcleo), a equação de Bohr, que permite calcular o nível energético de cada órbita n, é expressa por:

![]()
Como cada transição eletrônica (salto quântico, pulo entre dois níveis de energia) é quantizada, a energia do fóton emitido ou absorvido também é quantizada e consequentemente o comprimento de onda e a freqüência também o são. Assim, cada frequência de cada fóton emitido ou absorvido tem uma freqüência determinada e fixa para aquele átomo e para aquele salto quântico. Cada transição eletrônica entre átomo contribui para a produção de uma linha individual no espectro daquele elemento.

![]()
Observe na figura I acima que os intervalos entre os níveis de energia não são constantes, pois à medida que aumenta o valor de n, se afastando do núcleo, diminui a variação de energia entre dois níveis energéticos consecutivos.
A energia de cada transição genérica de nível ninicial (ni) a nfinal (nf) é fornecida por:

![]()
Para
calcular
o comprimento de onda λ (Einicial
– Efinal)=ΔE=h.f
![]() c=velocidade da Luz = λ.f
c=velocidade da Luz = λ.f ![]()
F
= c/λ
![]() ΔE
= h.(c/λ)
ΔE
= h.(c/λ)
![]() λ
λ
![]() comprimento
de onda do fóton emitido ou absorvido.
comprimento
de onda do fóton emitido ou absorvido.
![]()
Outra
relação matemática ![]() ΔE
= h(c/λ)
ΔE
= h(c/λ)
![]() ΔE
= mc2
ΔE
= mc2
![]() mc2
=
(hc/λ)
mc2
=
(hc/λ)
![]() mc
= Q = h/λ
mc
= Q = h/λ
![]() quantidade de movimento.
quantidade de movimento.
![]()

Um átomo emite um fóton luminoso quando o elétron salta novamente para sua órbita original, de níveis de energia mais baixos, o que faz com que a energia seja liberada através da emissão de um fóton luminoso.
![]()
Fissão Nuclear

A fissão nuclear consiste numa reação que se inicia com o choque de um nêutron com um núcleo instável que proporciona a quebra deste último e, por este motivo, é chamado de fissão nuclear (divisão do núcleo).
![]()
Fusão Nuclear
A Fusão Nuclear é o processo no qual dois ou mais núcleos atômicos se juntam e formam um outro núcleo de maior número
Atômico.
O principal tipo de fusão que ocorre no interior das estrelas é o de Hidrogênio em Hélio, onde dois

prótons se fundem em uma partícula alfa (um núcleo de hélio), liberando dois pósitrons, dois neutrinos e energia.
![]()
Buraco Negro
Um buraco negro é o que sobra quando morre uma gigantesca estrela, no mínimo 10 vezes maior que o nosso Sol.
Uma estrela é um imenso e incrível reator de fusão. As reações de fusão, que ocorrem no núcleo,

funcionam como gigantescas bombas, cujas explosões impedem que a massa da estrela se concentre numa região pequena.
O equilíbrio entre as forças oriundas das explosões e as de origem gravitacional define o tamanho da estrela.
Quando o combustível para as reações se esgota, a fusão nuclear é interrompida.
Ao mesmo tempo, a gravidade atrai a matéria para o interior da estrela, havendo compressão do núcleo, que se aquece muito.
O núcleo termina por explodir, arremessando para o espaço matéria e radiação.
O que fica é o núcleo altamente comprimido e extremamente maciço. A gravidade em torno dele é tão forte que nem a luz consegue escapar. Esse objeto literalmente desaparece da visão.
![]()
Corpo negro

O nome "corpo negro" foi introduzido por Gustav Kirchhoff em 1860 e, em Física, é um corpo que absorve toda a radiação que nele incide não refletindo a luz e nem se deixando atravessar por ela.
É um absorvedor ideal, sua absorvidade é a = 1 e sua refletividade é nula r = 0. Como todo bom absorvedor é bom emissor, ele é também emissor ideal e sua emissividade é e = 1.
![]()
TEMPERATURAS DE COR NA ESCALA KELVIN
O nome acima foi criado por um físico escocês no século 19, Lord Kelvin com a finalidade de medir os desvios de proporção na composição da luz branca.
Para isso, ele imaginou um hipotético objeto totalmente negro chamado por ele de 'corpo negro’, porque absorveria 100% de qualquer luz que incidisse sobre ele que, ao ser aquecido, passaria a emitir luz, pois todo bom absorvedor é também bom emissor.
E, além disso, a luz emitida por esse “corpo negro” iria mudando gradualmente de cor.
A analogia foi feita com um pedaço de metal (teórico corpo negro) que ao ser aquecido mudava de

cor começando com o vermelho e passando pelo amarelo, pelo branco e pelo branco azulado, conforme você pode observar na escala de temperatura de cor acima.,A à qual deu seu nome e
Quando
um corpo
negro é aquecido, ele
se torna uma fonte
ideal de radiação térmica e de radiação eletromagnética.
Um
corpo
negro a
uma temperatura
T emite exatamente
os mesmos
comprimentos de onda e intensidades que estariam presentes num
ambiente em equilíbrio térmico em T.
Como a radiação em tal ambiente possuiria um espectro dependente apenas de sua temperatura, a temperatura do objeto está diretamente associada aos comprimentos de onda que emite.
Em
temperatura
ambiente,
corpos negros emitem infravermelho,
mas
à
medida que a temperatura aumenta algumas centenas de graus Celsius,
corpos negros começam a emitir radiação em comprimentos de onda
visíveis: começando no vermelho, passando por amarelo, branco e
finalmente acabando no azul, após o qual a emissão passa a incluir
crescentes quantidades de ultravioleta.
A
radiação
emitida por um corpo negro mostrou
uma falha na teoria
clássica, que
explicava
as emissões
satisfatoriamente apenas em baixas temperaturas.
O estudo das leis de corpos negros levou ao surgimento da mecânica quântica.
stabeleceu que à temperatura de 1.200 K (graus Kelvin) o corpo negro tornaria vermelho. E q
![]() quanto
mais aquecido, mais sua tonalidade se alterava, correspondendo a
temperaturas intee
quanto
mais aquecido, mais sua tonalidade se alterava, correspondendo a
temperaturas intee
Variação a intensidade da radiação emitida por um corpo negro em função do comprimento de onda para algumas temperaturas.
e temperatura. A escala Kelvin, Assalém de utilizada na representação de cores, é uma das escalas utilizadas para medir quaisquer temperaturas. Nesta escala, o valor zero é associado à
A
figura
abaixo mostra
como
varia a intensidade da radiação emitida por um corpo negro em
funçãodo comprimento de onda para algumas temperaturas
temperaturas. correspondente
ao c hamado
"zero absoluto". Esta temperatura corresponde a -273,3
graus na escala Celsius de tO que você deve saber, O
que você deve saber, informações e dicas
hamado
"zero absoluto". Esta temperatura corresponde a -273,3
graus na escala Celsius de tO que você deve saber, O
que você deve saber, informações e dicas
 r
O
modelo atômico de Bohr tem as seguintes características:
r
O
modelo atômico de Bohr tem as seguintes características:
 Cada
elétron só pode
ocupar determinada
órbita circular sempre
com a mesma
energia, que
permanece
indefinidamente, sem irradiá-la.
Cada
elétron só pode
ocupar determinada
órbita circular sempre
com a mesma
energia, que
permanece
indefinidamente, sem irradiá-la.
Essas órbitas correspondem a situações estáveis, denominadas de estados estacionários.
A quantidade constante de energia de cada órbita é tanto maior quanto mais longe o elétron estiver do núcleo, ou seja, quanto mais afastada for sua órbita.
 Um
átomo
armazena energia fazendo
seus
elétrons saltarem de uma órbita mais interna (de
menor potencial de energia) para
uma órbita mais externa (de
maior potencial de energia).
Um
átomo
armazena energia fazendo
seus
elétrons saltarem de uma órbita mais interna (de
menor potencial de energia) para
uma órbita mais externa (de
maior potencial de energia).
Assim,
sempre
que um átomo absorve energia, um ou mais de seus elétrons “saltam”
para uma órbita mais externa.
Quando
o fornecimento
de energia cessa,
os elétrons
que foram deslocados para as órbitas mais distantes
tendem a restaurar
o equilíbrio retornando à sua órbita original.
Porém, toda ação que acumula energia, se for revertida, terá que liberar essa mesma energia.
Então, quando o elétron retorna à órbita original ele deve liberar a mesma quantidade de energia recebida e o faz sob forma de energia luminosa, ou seja, emitindo um fóton.
![]()

![]() A
energia de cada transição genérica de nível ninicial (ni)
a nfinal (nf)
é fornecida por:
A
energia de cada transição genérica de nível ninicial (ni)
a nfinal (nf)
é fornecida por:

![]() (Einicial
– Efinal)
= ΔE = h.f
(Einicial
– Efinal)
= ΔE = h.f
![]() c = velocidade da luz=λ.f
c = velocidade da luz=λ.f
![]() f = c/λ
f = c/λ
![]() ΔE
= h.(c/λ)
ΔE
= h.(c/λ)
![]() λ (comprimento de onda do fóton emitido ou absorvido).
λ (comprimento de onda do fóton emitido ou absorvido).
![]() Outra
relação matemática
Outra
relação matemática
![]() ΔE=h.(c/λ)
ΔE=h.(c/λ)
![]() ΔE=mc2
ΔE=mc2
![]() mc2=hc/λ
mc2=hc/λ
![]() mc
= h/λ = Q ( quantidade de movimento).
mc
= h/λ = Q ( quantidade de movimento).



Radiografias
Os
raios
X, descobertos
em 1895 pelo físico alemão
Wilhelm Rontgen,
são produzidos quando elétrons
são desacelerados ao atingirem um alvo metálico de alto ponto de
fusão como, por exemplo, o Tungstênio. Essa
desaceleração
produz ondas eletromagnéticas de alta freqüência denominadas de
Raios X, que atravessam a maioria dos materiais conhecidos e
impressionam chapas fotográficas.

A imagem do corpo de uma pessoa em uma chapa de Raios X representa um processo em que parte da radiação é absorvida pelo corpo, e os claros e escuros da imagem representam, respectivamente, os tecidos mais e menos absorvedores de radiação.
Assim,
nas radiografias
os ossos saem brancos
e tecidos
em volta negros
![]() isso ocorre porque o
osso, cuja estrutura é mais densa que a do tecido mole, absorve mais
radiação ficando com aparência clara enquanto
que o tecido
mole, menos denso, é atravessado pelos raios X, ficando com
aparência mais escura.
isso ocorre porque o
osso, cuja estrutura é mais densa que a do tecido mole, absorve mais
radiação ficando com aparência clara enquanto
que o tecido
mole, menos denso, é atravessado pelos raios X, ficando com
aparência mais escura.
![]() Você deve conhecer
e entender os
conceitos
de corpo
negro, buraco negro, fusão e fissão nuclear fornecidos acima.
Você deve conhecer
e entender os
conceitos
de corpo
negro, buraco negro, fusão e fissão nuclear fornecidos acima.
![]()
Alguns exercícios interessantes que seria conveniente para você conferir as resoluções:
01-(UFJF-MG)

Resolução:
Observe
que para
saltar do nível 1 (n1)
para o nível zero (n∞),
onde
o elétron
se ioniza, foram
gastos
(E1 -
E∞)
= │-13,6 - 0│= 13,6 eV
![]() como recebeu
20 eV e gastou 16,3 eV,
vão sobrar
como recebeu
20 eV e gastou 16,3 eV,
vão sobrar
![]() 20,0 – 13,6 = 6,4
eV
20,0 – 13,6 = 6,4
eV
R- C

Resolução:
Lembre-se
de que a velocidade
de todas as cores e de todas as radiações eletromagnéticas é
sempre a mesma no vácuo e,
aproximadamente no ar (3,0.108m/s)
![]() cada
cor tem velocidades diferentes em
outros
meios homogêneos e transparentes (vidro, água, etc.).
cada
cor tem velocidades diferentes em
outros
meios homogêneos e transparentes (vidro, água, etc.).
A
energia
de cada cor é diretamente proporcional à freqüência (f) e
inversamente
proporcional ao comprimento de onda (λ), pois ΔE = h.(c/λ) =
h.f ![]() da tabela,
o menor λ, a mais energética é a violeta.
da tabela,
o menor λ, a mais energética é a violeta.
R- C
03-(UFC-CE) Na figura, as flechas numeradas de 1 até 9 representam transições possíveis de ocorrer entre alguns níveis de energia do átomo de hidrogênio de acordo com o modelo de Bohr.
Para
ocorrer
a transição, o
átomo
emite (ou
absorve) um
fóton cuja energia │ΔE│= h(c/λ), onde (h é a constante de
Planck, λ é o comprimento de onda do fóton e ΔE é a diferença
de energia entre os dois níveis envolvidos na transição).
Suponha que o átomo emite os fótons X e Y, cujos comprimentos de onda são, respectivamente, λx = 1,03.10-7 m e λy = 4,85.
10-7m.
As transições corretamente associadas às emissões desses dois fótons são (use h = 4,13.10-15 eV.s e c = 3,0.108 m/s).
a) 4 e 8
b) 2 e 6
c) 3 e 9
d) 5 e 7
e) 1 e 7
Resolução:
│ΔE│x
=
h(c/λ) =
4,13.10-15.(3.108/1,03.10-7)
![]() │ΔE│x
=
12,03 eV.
│ΔE│x
=
12,03 eV.
│ΔE│y=
h(c/λ) =
4,13.10-15.
(3.108/4,85.10-7)
![]() │ΔE│y
=
2,55 eV.
│ΔE│y
=
2,55 eV.
Os
valores
mais próximos são de 2 e 6
![]() │ΔE2│
=
13,6 – 1,51 =
12,09 eV
│ΔE2│
=
13,6 – 1,51 =
12,09 eV
![]() │ΔE6│
=
3,40 – 0,85 =
2,55 eV.
│ΔE6│
=
3,40 – 0,85 =
2,55 eV.
R- B

Se você quiser se aprofundar e dominar melhor o assunto eu separei algunas exercícios para que você possa analisar as resoluções. São os exercícios de números 02, 04, 08, 09, 11, 12, 14, 16, 18, 20, 25, 29 e 39.
Exercícios de vestibulares com resoluções comentadas sobre
Estrutura Atômica – Átomo de Bohr
01-(PUC-RS) Um átomo excitado emite energia, muitas vezes em forma de luz visível, porque:
a)
um de seus elétrons foi arrancado do átomo.
b) um dos elétrons desloca-se para níveis de energia mais baixos, aproximando-se do núcleo.
c) um dos elétrons desloca-se para níveis de energia mais altos, afastando-se do núcleo.
d) os elétrons permanecem estacionários em seus níveis de energia.
e) os elétrons se transformam em luz, segundo Einstein.
02-(UFMG-MG)

No modelo de Bohr para o átomo de hidrogênio, a energia do átomo:
a) pode ter qualquer valor.
b) tem um único valor fixo.
c) independe da órbita do elétron.
d) tem alguns valores possíveis.
03-(UFRGS-RS)
No
início do século XX, as teorias clássicas da Física– como o
eletromagnetismo, de Maxwell, e a mecânica, de Newton – não
conduziam a uma explicação satisfatória para a dinâmica do átomo.
Nessa época, duas descobertas históricas tiveram lugar: o
experimento de Rutherford demonstrou a existência do núcleo atômico
e a interpretação de Einstein para o efeito
fotoelétrico revelou a natureza corpuscular da interação da luz com a matéria. Em 1913, incorporando o resultado dessas descobertas, Bohr propôs um modelo atômico que obteve grande sucesso, embora não respeitasse as leis da física clássica.
Considere as seguintes afirmações sobre a dinâmica do átomo.
I. No átomo, os raios das órbitas dos elétrons podem assumir um conjunto contínuo de valores, tal como os raios das órbitas dos planetas em torno do Sol.
II. O átomo pode existir, sem emitir radiação, em estados estacionários cujas energias só podem assumir um conjunto discreto de valores.
III. O átomo absorve ou emite radiação somente ao passar de um estado estacionário para outro.
Quais dessas afirmações foram adotadas por Bohr como postulados para o seu modelo atômico?
a) Apenas I.
b) Apenas II.
c) Apenas III.
d) Apenas II e III.
e) I, II e III.
04-(UNIUBE-MG)
Considere
dois níveis de energia de um átomo de sódio, representados no
diagrama abaixo.A diferença de energia entre os níveis (inicial e
final) é igual a 3,4.10-19J,
e a energia do fóton é igual a h.f, em que h é a constante de
Planck (6,6.10-34 J.s)
e f é a freqüência do fóton emitido.
Considerando
os dados apresentados e utilizando a tabela acima como
referência, marque a alternativa que representa a cor da luz emitida
nessa transição eletrônica.
a) vermelha
b) amarela
c) violeta
d) azul
e) verde
05-(UFJF-MG)

06-(PUC- MG)

Escolha, entre os modelos atômicos citados nas opções, aquele (aqueles) que, na sua descrição, incluiu (incluíram) o conceito de fóton:
a) Modelo atômico de Thomson.
b) Modelo atômico de Rutherford.
c) Modelo atômico de Bohr.
d) Modelos atômicos de Rutherford e de Bohr.
e) Modelos atômicos de Thomson e de Rutherford
07-(UFMG-MG)
A
luz emitida por uma lâmpada fluorescente é produzida por átomos de
mercúrio excitados, que, ao perderem energia, emitem luz. Alguns dos
comprimentos de onda de luz visível emitida pelo mercúrio, nesse
processo, estão mostradas nesta tabela: Considere que, nesse caso, a
luz emitida se propaga no ar. Considerando-se essas informações, é
CORRETO afirmar que, em comparação com os de luz violeta, os fótons
de luz amarela têm:

a) menor energia e menor velocidade.
b) maior energia e maior velocidade.
c) menor energia e mesma velocidade.
d) maior energia e mesma velocidade.
08-(OLIMPÍADA PAULISTA DE FÍSICA) Um elétron de um átomo de hidrogênio, ao passar de um estado quântico para outro, emite ou absorve fóton. Na figura abaixo, representamos os três primeiros níveis de energia do átomo de hidrogênio.

Considere três fótons f1, f2 e f3 com energias 12,1 eV, 10,2 eV e 8,5 eV, respectivamente. O átomo de hidrogênio está no estado fundamental. Quais fótons (f1, f2 ou f3) poderá o átomo de hidrogênio absorver?
09-(ITA-SP) O diagrama ao lado mostra os níveis de energia (n) de um elétron em certo átomo.

Qual das transições mostradas na figura representa a emissão de um fóton com o menor comprimento de onda?
a) I
b) II
c) III
d) IV
e) V
10-(UFC-CE) Na figura, as flechas numeradas de 1 até 9 representam transições possíveis de ocorrer entre alguns níveis de energia do átomo de hidrogênio de acordo com o modelo de Bohr.
Para
ocorrer a transição, o átomo emite (ou absorve) um fóton cuja
energia │ΔE│= hc/λ (h é a constante de Planck, λ é o
comprimento de onda do fóton e ΔE é a diferença de energia entre
os dois níveis envolvidos na transição).
Suponha que o átomo emite os fótons X e Y, cujos comprimentos de onda são, respectivamente, λx=1,03.10-7 m e λy=4,85.10-7m.
As transições corretamente associadas às emissões desses dois fótons são (use h=4,13.10-15eV.s e c=3,0.108m/s).
a) 4 e 8
b) 2 e 6
c) 3 e 9
d) 5 e 7
e) 1 e 7
11-(UFPI) Um átomo de hidrogênio está em um estado excitado com n = 2, com uma energia E2 = –3,4 eV. Ocorre uma transição para o estado n = 1, com energia E1 = –13,6 eV, e um fóton é emitido. A frequência da radiação emitida, em Hz, vale aproximadamente:
(Dados: 1 eV = 1,6 .10-19 J; h = 6,63 .10-34 Js.)
![]()
12-(UNICAMP-SP) Todos os corpos trocam energia com seu ambiente por meio da emissão e da absorção de ondas eletromagnéticas em todas as frequências.
Um
corpo negro é um corpo que absorve toda onda eletromagnética nele
incidente e também apresenta a máxima eficiência de emissão. A
intensidade das ondas emitidas por um corpo negro só depende da
temperatura desse corpo. O corpo humano à temperatura normal de 37
°C pode ser considerado um corpo negro. Considere que a velocidade
das ondas eletromagnéticas é igual a 3,0.108m/s.
a)
A f igura abaixo mostra a intensidade das ondas eletromagnéticas
emitidas por um corpo negro a 37 °C em função da gz\frequência.
Qual é o comprimento de onda correspondente à frequência para qual
a intensidade é máxima?
b) Se um corpo negro cuja temperatura absoluta é T se encontra em um ambiente cuja temperatura absoluta é Ta, a potência líquida que ele perde por emissão e absorção de ondas eletromagnéticas é dada por P = σA(T4 – T4a) em que A é a área da superfície do corpo e σ=6.10-8W/(m2K4).

Usando como referência uma pessoa com 1,70 m de altura e 70 kg de massa, faça uma
estimativa da área da superfície do corpo humano. A partir da área estimada, calcule a perda total diária de energia por emissão e absorção de ondas eletromagnéticas por essa pessoa se ela se encontra num ambiente a 27 °C. Aproxime a duração de 1 dia por 9,0 · 104 s.
13-(UFJF-MG) A presença de um elemento atômico em um gás pode ser determinada verificando-se as energias dos fótons que são emitidos pelo gás, quando este é aquecido. No modelo de Bohr para o átomo de hidrogênio, as energias dos dois níveis de menor
energia são: E1 = - 13,6 eV e E2 = - 3,40 eV. Considerando-se essas informações, um valor possível para a energia dos fótons emitidos pelo hidrogênio aquecido é:
![]()
14-(UFMG-MG)
Nos
diodos emissores de luz, conhecidos como LEDs, a emissão de luz
ocorre quando elétrons passam de um nível de maior energia para um
outro de menor energia. Dois tipos comuns de LEDs são o que emite
luz vermelha e o que emite luz verde. Sabe-se que a freqüência da
luz vermelha é menor que a da luz verde.
Sejam λverde o comprimento de onda da luz emitida pelo LED verde e Everde a diferença de energia entre os níveis desse mesmo LED. Para o LED vermelho, essas grandezas são, respectivamente, λvermelho e Evermelho .
Considerando-se essas informações, é CORRETO afirmar que
a) Everde > Evermelho e λverde > λvermelho .
b) Everde > Evermelho e λverde < λvermelho .
c) Everde < Evermelho e λverde> λvermelho .
d) Everde < Evermelho e λverde < λvermelho .
15-(ITA-SP)

Suponha que o átomo de hidrogênio emita energia quando seu elétron sofre uma transição entre os estados inicialn=4, e final n=1. Qual é a energia do fóton emitido? Qual é a freqüência da radiação emitida (Constante de Planck = 6,63 .10-34J.s)
16-(UNIRIO-RJ)
Os
raios X, descobertos em 1895 pelo físico alemão Wilhelm Rontgen,
são produzidos quando elétrons são desacelerados ao atingirem um
alvo metálico de alto ponto de fusão como, por exemplo, o
Tungstênio. Essa desaceleração produz ondas eletromagnéticas de
alta freqüência denominadas de Raios X, que atravessam a maioria
dos materiais conhecidos e impressionam chapas fotográficas. A
imagem do corpo de uma pessoa em uma chapa de Raios X representa um
processo em que parte da radiação é:
a) refletida, e a imagem mostra apenas a radiação que atravessou o corpo, e os claros e escuros da imagem devem-se aos tecidos que refletem, respectivamente, menos ou mais os raios X.
b) absorvida pelo corpo, e os tecidos menos e mais absorvedores de radiação representam, respectivamente, os claros e escuros da imagem.
c) absorvida pelo corpo, e os claros e escuros da imagem representam, respectivamente, os tecidos mais e menos absorvedores de radiação.
d) absorvida pelo corpo, e os claros e escuros na imagem são devidos à interferência dos Raios X oriundos de diversos pontos do paciente sob exame.
17-(UFMG-MG)
Para
se produzirem fogos de artifício de diferentes cores, misturam-se
diferentes
compostos químicos à pólvora. Os compostos à base de sódio produzem luz amarela e os à base de bário, luz verde. Sabe-se que a freqüência da luz amarela é menor que a da verde. Sejam ENa e EBa as diferenças de energia entre os níveis de energia envolvidos na emissão de luz pelos átomos de sódio e de bário, respectivamente, e
vNa e vBa as velocidades dos fótons emitidos, também respectivamente. Assim sendo, é
CORRETO afirmar que:
a) ENa < EBa e vNa = vBa.
b) ENa < EBa e vNa ≠ vBa.
c) ENa > EBa e vNa = vBa.
d) ENa > EBa e vNa ≠ vBa.
18-(UNIMONTES-MG)
Um
buraco negro é o que sobra quando morre uma gigantesca estrela, no
mínimo 10 vezes maior que o nosso Sol. Uma estrela é um imenso e
incrível reator de fusão. As reações de fusão, que ocorrem no
núcleo, funcionam como gigantescas bombas, cujas explosões impedem
que a massa da estrela se concentre numa região pequena. O
equilíbrio entre as forças oriundas das explosões e as de origem
gravitacional define o tamanho da estrela. Quando o combustível para
as reações se esgota, a fusão nuclear é interrompida.
Ao mesmo tempo, a gravidade atrai a matéria para o interior da estrela, havendo compressão do núcleo, que se aquece muito. O núcleo finda por explodir, arremessando para o espaço matéria e radiação. O que fica é o núcleo altamente comprimido e extremamente maciço. A gravidade em torno dele é tão forte que nem a luz consegue escapar. Esse objeto literalmente desaparece da visão. O diâmetro da região esférica, dentro da qual toda a massa de uma estrela deveria ser concentrada, para que ela começasse a se comportar como um buraco negro, pode ser calculado utilizando-se a equação para a velocidade de escape, que permite encontrar a velocidade mínima, v, para que um corpo maciço escape do campo gravitacional de uma estrela ou planeta. A equação é v2 = 2GM/R , em que G = 6,67.10-11(m3/s2·kg) é a constante gravitacional, M é a massa e R o raio do planeta. Nesse caso, a velocidade de escape deveria ser igual à da luz, ou seja, 3.108 m/s. Considerando ser possível a
Terra transformar-se num buraco negro, o diâmetro da região esférica, dentro da qual toda a sua massa, igual a
5,98.10224kg, deveria ser concentrada, seria, aproximadamente,
![]()
19-(UFRS-RS) Assinale a alternativa que preenche corretamente a lacuna do parágrafo abaixo.
O Sol é a grande fonte de energia para toda a vida na Terra. Durante muito tempo, a origem da energia irradiada pelo Sol foi um mistério para a humanidade. Hoje, as modernas teorias de evolução das estrelas nos dizem que a energia irradiada pelo Sol provém de processos de .......... que ocorrem no seu interior, envolvendo núcleos de elementos leves.
a) espalhamento
b) fusão nuclear
c) fissão nuclear
d) fotossíntese
e) combustão
20-(FUVEST-SP) Um aparelho de Raios X industrial produz um feixe paralelo, com intensidade Io. O operador dispõe de diversas placas de Pb, cada uma com 2 cm de espessura, para serem utilizadas como blindagem, quando colocadas perpendicularmente ao feixe.

Em certa situação, os índices de segurança determinam que a intensidade máxima I dos raios que atravessam a blindagem seja inferior a 0,15 Io. Nesse caso, o operador deverá utilizar um número mínimo de placas igual a:
a) 2 b) 3 c) 4 d) 5 e) 6
21-(PUC-MG)
No
modelo atômico de BOHR para o átomo de hidrogênio, o elétron gira
em órbita circular em volta do prótoncentral. Supõe-se que o
próton esteja em repouso em um referencial inercial. Essa hipótese
da imobilidade do próton pode ser justificada porque o próton tem:
a) carga elétrica de sinal oposto à do elétron.
b) carga elétrica infinitamente maior que a do elétron.
c) massa igual à do elétron.
d) massa muito maior que a do elétron.
22-(UFRS-RS) Um átomo de hidrogênio tem sua energia quantizada em níveis de energia (EŠ), cujo valor genérico é dado pela expressão En = -Eo/n2, sendo n igual a 1, 2, 3, ... e Eoigual à energia do estado fundamental (que corresponde a n = 1).
Supondo-se que o átomo passe do estado fundamental para o terceiro nível excitado (n = 4), a energia do fóton necessário para provocar essa transição é
![]()
23-(FUVEST-SP)
Uma
unidade industrial de raios-X consiste em uma fonte X e um detector
R, posicionados de forma a examinar cilindros com regiões
cilíndricas ocas (representadas pelos círculos brancos), dispostas
em uma esteira, como vistos de cima na figura. A informação é
obtida pela intensidade I da radiação X que atinge o detector, à
medida que a esteira se move com velocidade constante. O Gráfico 1
representa a intensidade detectada em R para um cilindro teste
homogêneo.
Quando no detector R for obtido o Gráfico 2, é possível concluir que o objeto em exame tem uma forma semelhante a
a) A b) B c) C d) D e) E
24-(UFPR-PR) Segundo o modelo atômico de Niels Bohr, proposto em 1913, é correto afirmar:
a) No átomo, somente é permitido ao elétron estar em certos estados estacionários, e cada um desses estados possui uma energia fixa e definida.
b) Quando um elétron passa de um estado estacionário de baixa energia para um de alta energia, há a emissão de radiação (energia).
c) O elétron pode assumir qualquer estado estacionário permitido sem absorver ou emitir radiação.
d) No átomo, a separação energética entre dois estados estacionários consecutivos é sempre a mesma.
e) No átomo, o elétron pode assumir qualquer valor de energia.
25-(UEL-PR) O LHC ("Large Hadron Collider"), maior acelerador de partículas do mundo, foi

inaugurado em setembro de 2008, após 20 anos de intenso trabalho. Sua função é acelerar feixes de partículas, de tal forma que estes atinjam uma velocidadeestimada em cerca de 99,99% da velocidade da luz. A colisão entre prótons será tão violenta que a expectativa é de se obterem condições próximas àquelas que existiram logo após o Big Bang.
"A
primeira missão desse novo acelerador é estudar partículas
indivisíveis (elementares) e as forças (interações) que agem
sobre elas. Quanto às forças, há quatro delas no universo: I) a
__________, responsável por manter o núcleo atômico coeso; II) a
__________, que age quando uma partícula se transforma em outra;
III) a __________, que atua quando cargas elétricas estão
envolvidas. A quarta força é a _______ (a primeira conhecida pelo
ser humano)".
(Adaptado: BEDIAGA, I. LHC: o colosso criador e esmagador de matéria. "Ciência Hoje". n. 247, v. 42. Abr. 2008. p. 40.)
No texto, foram omitidas as expressões correspondentes às nomenclaturas das quatro forças fundamentais da natureza, em acordo com a teoria mais aceita no meio científico hoje.
Assinale a alternativa que apresenta, correta e respectivamente, os nomes dessas forças.
a) força gravitacional, força nuclear fraca, força eletromagnética, força nuclear forte.
b) força nuclear forte, força eletromagnética, força nuclear fraca,força gravitacional.
c) força nuclear forte, força nuclear fraca, força eletromagnética, força gravitacional.
d) força gravitacional, força nuclear forte, força eletromagnética, força nuclear fraca.
e) força nuclear fraca, força gravitacional, força nuclear forte, força eletromagnética.
26-(UDESC-SC)
A
Figura 1 mostra um diagrama com cinco níveis de energia do átomo de
hidrogênio. A Figura 2 mostra o espectro de emissão do átomo de
hidrogênio na faixa do visível e do ultravioleta próximo.
A linha Hα (comprimento de onda de 656,3 x 10-9 m) do espectro de emissão do átomo de hidrogênio (Figura 2) corresponde a uma transição entre os níveis:
a) n2 e n1
b) n4 e n2
c) nα e n3
d) n3 e n2
e) n3 e n1
27-(UFU-MG) Um átomo excitado emite energia, muitas vezes em forma de luz visível, porque:
a) um dos elétrons decai para níveis de energia mais baixos, aproximando-se do núcleo.
b) um dos elétrons foi arrancado do átomo.
c) um dos elétrons desloca-se para níveis de energia mais altos, afastando-se do núcleo.
d) os elétrons permanecem estacionários em seus níveis de energia.
28-(UDESC-SC)
A
Figura 1 mostra o gráfico da intensidade de radiação por
comprimento de onda emitida por um corpo negro para diferentes
temperaturas. Com base nas informações do gráfico, analise as
afirmativas abaixo.
I – A temperatura T1 é maior que a temperatura T3.
II – A intensidade total de radiação emitida é maior para temperatura T3.
III – O comprimento de onda para o qual a radiação é máxima é maior para temperatura T3.
IV – As temperaturas T1, T2 e T3 são iguais.
V – As intensidades totais de radiação emitida são iguais para T1, T2 e T3.
Assinale a alternativa correta.
a) Somente as afirmativas I, II e V são verdadeiras.
b) Somente as afirmativas II e IV são verdadeiras.
c) Somente a afirmativa I é verdadeira.
d) Somente as afirmativas III e IV são verdadeiras.
e) Somente a afirmativa II é verdadeira.
29-(UFRGS-RS)
Na
passagem do século XIX para o século XX, várias questões e
fenômenos que eram temas de discussão e pesquisa começaram a ser
esclarecidos graças a idéias que, mais tarde, viriam a
constituir a área da física hoje conhecida como Mecânica Quântica.
Na primeira coluna da tabela a seguir, estão listados três desses
temas; na segunda, equações fundamentais relacionadas às soluções
encontradas.

Assinale a alternativa que associa corretamente os temas apontados na primeira coluna às respectivas equações, listadas na segunda coluna.
a) 1(a) – 2(b) – 3(c)
b) 1(a) – 2(c) – 3(b)
c) 1(b) – 2(c) – 3(a)
d) 1(b) – 2(a) – 3(c)
e) 1(c) – 2(b) – 3(a)
30-(UFRN-RN) Sobre um átomo de hidrogênio no estado fundamental, incidem três fótons, cujas energias, em eletrovolt (eV), são, respectivamente, 13,20; 12,09 e 10,20. Uma vez num estado excitado, o átomo de hidrogênio decairá, emitindo energia na forma de fótons.
Na
figura abaixo, estão representadas as energias dos quatro primeiros
níveis de energia do átomo de hidrogênio.
A partir dessas informações:
a) determine quais desses fótons incidentes podem ser absorvidos pelo átomo de hidrogênio no estado fundamental e explicite qual o estado final do átomo em cada caso;
b) represente, na figura localizada no Espaço destinado à Resposta, as possíveis transições dos elétrons que se encontram nos níveis excitados, após a emissão dos respectivos fótons;
c) determine as energias dos fótons emitidos.
31-(UFMG-MG)
O
espectro de emissão de luz do átomo de hidrogênio é discreto, ou
seja, são emitidas apenas ondas eletromagnéticas de determinadas
frequências, que, por sua vez, fornecem informações sobre os
níveis de energia desse átomo.
Na figura abaixo, está representado o diagrama de níveis de energia do átomo de hidrogênio.
1. No século XIX, já se sabia que cada frequência do espectro de emissão do hidrogênio é igual à soma ou à diferença de duas outras frequências desse espectro.
Explique por que isso ocorre.
2. Sabe-se que o espectro do átomo de hidrogênio contém as frequências 2,7.1014 Hz e 4,6.1014 Hz.
A partir desses dados, DETERMINE outra frequência desse espectro que corresponde a uma luz emitida na região do visível.
32--(UFU-MG) Um átomo excitado emite energia, muitas vezes em forma de luz visível, porque
a)
um dos elétrons decai para níveis de energia mais baixos,
aproximando-se do núcleo.
b) um dos elétrons foi arrancado do átomo.
c) um dos elétrons desloca-se para níveis de energia mais altos, afastando-se do núcleo.
d) os elétrons permanecem estacionários em seus níveis de energia.
33-(UNIR-RO) No início do século XX, Niels Bohr apresentou um modelo atômico cujos postulados fundamentais descrevem que os elétrons de um átomo situam-se
a) sobre órbitas elípticas com o núcleo atômico ocupando um dos focos e emitindo energia ao completar cada órbita.
b) sobre órbitas estacionárias, emitindo radiação somente quando passam de uma órbita para outra de menor energia.
c) sobre órbitas estacionárias, mantendo-se sempre em níveis energéticos nulos.
d) em orbitais tipo s, p, d e f e emitem energia quando ascendem do orbital s para o p, do p para o d e do d para o f.
e) em cascas esféricas concêntricas de raios iguais a nl, em que l é o raio atômico e n é um número inteiro ou semi-inteiro.
34-(UFJF-MG)
Fótons
de raios X, com energias da ordem de 1,98.10-15 J,
são utilizados em experimentos de difração comcristais. Nesses
experimentos, o espaçamento entre os átomos do cristal é da ordem
do comprimento de onda dos raios X. Em 1924, Louis de Broglie
apresentou a teoria de que a matéria possuía tanto características
corpusculares como ondulatórias. A teoria de Louis de Broglie foi
comprovada por um experimento de difração com cristais,
utilizando-se um feixe de elétrons no lugar de um feixe de raios X.
Considere: a constante de Planck h = 6,60.10-34 J
. s; a velocidade da luz no vácuo c = 3,00.108 m/s;
massa do elétron m = 9,1.10-31 kg e
1 eV = 1,60.10-19 J.
a) Calcule o valor do espaçamento entre os átomos do cristal, supondo que o valor do espaçamento é igual ao comprimento de onda dos raios X com energia de 1,98.10-15 J;
b) Calcule o valor da quantidade de movimento dos elétrons utilizados no experimento de difração com o cristal, cujo espaçamento entre os átomos foi determinado no item anterior. Despreze os efeitos relativísticos no movimento dos elétrons.
35-(UFRN-RN) As usinas nucleares funcionam a partir da grande quantidade de calor liberada pelas reações nucleares. O calor é absorvido por um circuito de água primário, do tipo ciclo fechado. Esse circuito fica em contato com outro, o circuito secundário, que, por sua vez, produz vapor de água a alta pressão, para fazer girar uma turbina capaz de acionar um gerador elétrico, conforme mostra, esquematicamente, a figura abaixo.

Com base nas informações acima, a seqüência correta das principais formas de energia envolvidas nesse processo é:
a) energia nuclear, energia mecânica, energia potencial e energia elétrica.
b) energia nuclear, energia mecânica, energia térmica e energia elétrica.
c) energia nuclear, energia potencial, energia mecânica e energia elétrica.
d) energia nuclear, energia térmica, energia mecânica e energia elétrica.
36-(FUVEST-SP) A partícula neutra conhecida como méson K0 é instável e decai, emitindo duas partículas, com massas iguais, uma positiva e outra negativa, chamadas respectivamente, méson π+ e méson π -. Em um experimento, foi observado o decaimento de um K0, em repouso, com emissão do par π+ e π -. Das figuras abaixo, qual poderia representar as direções e sentidos das velocidades das partículas π+ e π – no sistema de referência em que K0 estava em repouso?

37-(UNESP-SP)
Em
desintegrações radioativas, várias grandezas físicas são
conservadas. Na situação representada na figura,
temos um núcleo de Tório (228Th), inicialmente em repouso, decaindo em núcleo de Radio (224Ra) e emitindo uma partícula α. Na desintegração, a partícula α e emitida com uma energia cinética de aproximadamente 8,4.10-13 J.
Qual é a energia cinética aproximada do núcleo do Radio?
a) 15,0.10-15 J.
b) 8,4.10-15 J.
c) 9,0.10-15 J.
d) 9,0.10-13 J.
e) 15,0.10-13 J.
38-(ITA-SP)
No
processo de fotossíntese, as moléculas de clorofila do tipo a nas
plantas verdes apresentam um pico de absorção da radiação
eletromagnética no comprimento de onda l =6,80.10-7m.
Considere que a
formação de glicose (C6H12O6) por este processo de fotossíntese é descrita, de forma simplificada, pela reação:
![]()
Sabendo-se que a energia total necessária para que uma molécula de CO2 reaja é de 2,34.10-18J, o número de fótons que deve ser absolvido para formar 1mol de glicose é (velocidade da luz – c=3,0.108m/s e constante de Planck – h=6,6.10-34 J.s):
![]()
39-(PUC-SP) O Solenóide de Múon Compacto (do inglês CMS – Compact Muon Solenoid) é um dos detectores de partículas construídos no Grande Colisor de Hádrons, que irá colidir prótons no CERN, na suíça. O CMS é um detector de uso geral, capaz de estudar múltiplos aspectos das colisões de prótons a 14 TeV, a energia média do LHC. Contém sistemas para medir a energia e a quantidade de movimento de fótons, elétrons, múons e outras partículas resultantes das colisões. A camada

detectora interior é um semicondutor de silício. Ao seu redor, um calorímetro eletromagnético de cristais centelhadores é rodeado por um calorímetro de amostragem de hádrons. O rastreador e o calorímetro são suficientemente compactados para que possam ficar entre o imã e solenoidal do CMS, que gera um campo magnético de 4 teslas.
No exterior do imã situam-se os detectores de múons. Considerando que o campo magnético terrestre sobre a maior parte da América do Sul é da ordem de 30 microteslas (0,3 gauss), o campo magnético gerado pelo CMS é maior do que dessa região da Terra, aproximadamente, (Dado: 1 microtesla = 1,T = 1.10-6T)
a) 133.333 vezes
b) 1.333 vezes
c) 10.000 vezes
d) 0,01 vezes
e) 100 vezes
40-(UFJF-MG)

De
acordo com o modelo de Bohr, as energias possíveis dos estados que o
elétron pode ocupar no átomo de hidrogênio são, aproximadamente,
dadas por Em= - Eo/n2 ,
em que Eo=
13,6eV e n =1,2,3,4,........ O elétron faz uma transição do estado
excitado n = 2 para o estado fundamental n = 1. Admitindo que a massa
do átomo de hidrogênio é igual à massa do próton MP =
1,6.
10-27 kg , faça o que se pede nos itens seguintes.
a) Calcule a energia E, em elétron – volts, do fóton emitido.
b) Sabendo que a quantidade de movimento (momento linear) do fóton emitido é dada por Q=E/c considerando que a quantidade de movimento do sistema se conserva, qual é a velocidade v de recuo do átomo?
41-(UNICAMP-SP)

A
radiação Cerenkov ocorre quando uma partícula carregada atravessa
um meio isolante com uma velocidade maior do que a velocidade da luz
nesse meio. O estudo desse efeito rendeu a Pavel A. Cerenkov e
colaboradores o prêmio Nobel de Física de 1958. Um exemplo desse
fenômeno pode ser observado na água usada para refrigerar reatores
nucleares, em que ocorre a emissão de luz azul devido às partículas
de alta energia que atravessam a água.
a) Sabendo-se que o índice de refração da água é n = 1,3, calcule a velocidade máxima das partículas na água para que não ocorra a radiação Cerenkov. A velocidade da luz no vácuo é c = 3,0.108m/s.

b) A radiação Cerenkov emitida por uma partícula tem a forma de um cone, como ilustrado na figura abaixo, pois a sua
velocidade, vp , é maior do que a velocidade da luz no meio, vl . Sabendo que o cone formado tem um ângulo θ= 50º e que a radiação emitida percorreu uma distância d = 1,6m em t = 12ns, calcule vp.
Dados: cos50º = 0,64 e sen50º = 0,76.
42-(ITA-SP)

Obtenha uma expressão para as energias das órbitas do modelo de Bohr do átomo de Hidrogênio usando a condição de que o comprimento da circunferência de uma órbita do elétron ao redor do próton seja igual um número inteiro de comprimentos de onda de Broglie do elétron.
43-(UERJ-RJ)


Considere as seguintes informações do Modelo Padrão da Física de Partículas:
- prótons e nêutrons são constituídos por três quarks dos tipos u e d;
- o quark u tem carga elétrica positiva igual a 2/3 do módulo da carga do elétron;
- um próton p é constituído por dois quarks u e um quark d, ou seja, p = uud.
Determine o número de quarks u e o número de quarks d que constituem um nêutron n.
44-(UEPB-PB)

A energia nuclear resulta de processos de transformação de núcleos atômicos. Alguns isótopos de certos elementos apresentam a capacidade de se transformar em outros isótopos ou elementos através de reações nucleares. Baseia-se no princípio da equivalência de energia e massa, observado por Albert Einstein. e foi descoberta por Hahn, Frita e Meitner com a observação de uma fissão nuclear depois da irradiação de urânio com nêutrons.
(Adaptado de http:/pt.wikipcdiaorg!wiki’Ttz_Stra’3%9Fmann)
Com base cm seus conhecimentos relacionados à energia nuclear, é correto afirmar que:
a) Nas reações de fissão nuclear, como acontece nas usinas, há um aumento de massa do núcleo que é transformada em energia
b) A energia irradiada pelo sol, quando os átomos de hidrogênio e de outros elementos leves se combinam, se dá pelo processo da fusão nuclear e não pela fissão nuclear.
c) Nas reações de fusão nuclear, devido à quebra de átomos mais pesados, há um aumento de massa do núcleo que é transformada em energia.
d) A energia irradiada pelas estrelas, quando os átomos de hidrogênio e de outros elementos leves se combinam, se dá pelo processo de fissão nuclear.
e) A luz e calor irradiados pelo Sol, quando os átomos de hidrogênio e de outros elementos leves se combinam, se dão pelo processo de fissão nuclear.
45-(UFBA-BA)

O
tsunami que atingiu o Japão em 11 de março de 2011 também
comprometeu a segurança da estação nuclear em Fukushima. A planta
inteira foi inundada, os sistemas de resfriamento foram desativados,
e os reatores começaram a
superaquecer, ocasionando explosões e incêndios, provocando o vazamento de radionuclídeos.
A fissão nuclear consiste na quebra de um núcleo atômico resultando em novos núcleos e nêutrons. A reação tem início pela absorção de um nêutron e produz grande energia, porque a massa total dos novos elementos é menor que a do núcleo original, e a diferença de massa é transformada em energia. Essa energia é distribuída principalmente em forma de energia cinética dos núcleos e nêutrons produzidos e em energia de radiação λ.
A fissão nuclear do urânio produz vários isótopos em múltiplas possibilidades de reação. A maioria dos fragmentos de fissão são altamente instáveis (radioativos).
Alguns deles, como o 137Cs e 90Sr são muito perigosos, quando lançados ao ambiente.
Um
exemplo de reação cujos produtos são o ![]()
![]()
Com
base nas informações e nos conhecimentos de Física, 1
uma×c2 ≈ 930 MeV, e os dados apresentados na tabela•
calcule a energia liberada na reação, utilizando a equação de
Einstein de equivalência entre a massa e a energia, ≈
• cite os principais tipos de decaimento nuclear.
46-(PUC-SP)

Questões interdisciplinares:


A população mundial hoje gira em torno de 7 bilhões de pessoas e até meados do século XXI deverá atingir 10 bilhões. De acordo com os cenários escolhidos para a procura energética, o consumo da energia primária mundial poderá atingir duas a três vezes o consumo atual.
Em 1990, o consumo de energia primária por habitante e por ano era de 5,1 TEP nos países industrializados e apenas 10% nos países em vias de desenvolvimento.
1TEP (Tonelada Equivalente de Petróleo) é a unidade de medição de consumo de energia e equivale a 10x109 cal.
1BEP (Barril Equivalente de Petróleo), variação da TEP, equivalente a 1,45x109 cal.
Ou ainda que:

Uma fonte de energia capaz de corresponder de forma substancial a esta procura é a energia nuclear, através da FISSÃO e da FUSÃO nuclear. Vejamos:
Esse fenômeno da repulsão elétrica constitui um dos Princípios da Eletrostática, cujo módulo da força pode ser determinado pela Lei de Coulomb F=k.|Q1|. |Q2|./d2. .
O quanto esta força atua está relacionado à carga, ao meio e à distância entre os centros dos núcleos das partículas que estão interagindo. Caso os núcleos conseguissem se aproximar o suficiente, prevalecendo a interação forte, ocorreria o fenômeno da fusão nuclear.
O controle dessa fusão nuclear continua sendo objeto de pesquisa. Essa fusão é o processo no qual dois núcleos de átomos leves (por exemplo, o hidrogênio – cujo núcleo é constituído por 1 próton com carga elétrica elementar é 1,6.10-19 C) se combinam, ou se fundem, constituindo um elemento mais pesado. Os núcleos, então, carregados positivamente, devem se aproximar suficientemente um do outro, ou seja, vencer a força de repulsão eletrostática entre eles.
Para que as reações de fusão possam ser produzidas a uma taxa conveniente, são necessárias temperaturas altíssimas, da ordem de 100 milhões de graus Celsius e a pressão faz com que os átomos de hidrogênio sejam comprimidos.

Os centros de seus núcleos devem estar a 1.10-15 metros um do outro para que ocorra a fusão. Nesse estágio, eles se transformam em plasma. Uma característica especial desse estado é que, nele, a matéria reage a influências elétricas e magnéticas.

Por modestas que sejam as esperanças de chegar à fusão, estima-se que ainda demorará 30 anos para termos um reator comercial e, por mais caras que sejam as pesquisas, as vantagens da fusão são sedutoras.
Segundo todos os cálculos, as futuras usinas de fusão nuclear poderão extrair de 1 metro cúbico de água uma quantidade de energia igual à de 2 mil barris de petróleo.
a) Segundo as expectativas, após a instalação de um reator comercial com capacidade diária de 100 metros cúbicos de água para a fusão nuclear, qual seria a sua produção, diária, correspondente a Barris Equivalentes de Petróleo? (admita que 1 barril [159L] de petróleo de composição média contenha 1,5x106 kcal)
b) Determine o valor da força elétrica repulsiva entre dois núcleos de hidrogênio quando colocados no vácuo e separados à
distância necessária para a ocorrência da fusão nuclear.
![]()
47-(FUVEST-SP)

Em um laboratório de física, estudantes fazem um experimento em que radiação eletromagnética de comprimento de onda γ =300 nm incide em uma placa de sódio, provocando a emissão de elétrons.
Os
elétrons escapam da placa de sódio com energia cinética máxima
EC =
E – W, sendo E a energia de um fóton da radiação e W a energia
mínima necessária para extrair um elétron da placa. A energia de
cada fóton é E = h f, sendo h a constante de Planck e f a
frequência da radiação. Determine
a) a frequência f da radiação incidente na placa de sódio;
b) a energia E de um fóton dessa radiação;
c) a energia cinética máxima EC de um elétron que escapa da placa de sódio;
d) a frequência fo da radiação eletromagnética, abaixo da qual é impossível haver emissão de elétrons da placa de sódio.
Resolução comentada dos exercícios de física sobre
Estrutura Atômica – Átomo de Bohr
01- Quando o elétron salta novamente para sua órbita original, de níveis de energia mais baixos, o que faz com que a energia seja liberada através da emissão de um fóton luminoso. --- R- B
02- R- D --- veja teoria
03- I. Falsa --- não é contínua, só pode ter valores determinados.
II. Correta.
III. Correta.
R- D
04- ΔE=h.f=h.c/λ --- 3,4.10-19=6,6.10-34.3.108/λ --- λ=5.824.10-10 m --- R- B
05- Observe que para saltar do nível 1 (n1) para o nível zero (n∞), onde o elétron se ioniza, foram gastos (E1 - E∞)=│-13,6 - 0│= 13,6 eV --- como recebeu 20 eV e gastou 16,3 eV, vão sobrar --- 20,0 – 13,6=6,4 eV --- R- C
06- R- C --- veja teoria
07- Lembre-se de que a velocidade de todas as cores e de todas as radiações eletromagnéticas é sempre a mesma no vácuo e, aproximadamente no ar (3,0.108m/s) --- cada cor tem velocidades diferentes em outros meios homogêneos e transparentes (vidro, água, etc.) --- a energia de cada cor é diretamente proporcional à freqüência (f) e inversamente proporcional ao comprimento de onda (λ) --- da tabela, o menor λ, a mais energética é a violeta --- R- C
08- Na transição de 2 para 1 --- ΔE=(-3,4) – (-13,6) --- ΔE=10,2 eV --- compatível com f2, que será absorvido --- De 3 para 1 --- ΔE=(-1,5) – (-13,6) --- ΔE=12,1 eV --- compatível com f1, que será absorvido --- de 3 para 2 --- ΔE=(-1,5) – (3,4) --- ΔE=1,9 eV --- incompatível com f3, que não será absorvido --- R- f1 e f2.
09- Quando a transição ocorrer de um nível mais alto de energia para um nível mais baixo (órbita mais externa para órbita mais interna), ocorre a emissão de um fóton --- como ao menor comprimento de onda corresponde a maior freqüência e consequentemente maior nível energético você deve escolher a alternativa em que ocorre maior variação de energia --- R- C
10- │ΔE│x= hc/λ=4,13.10-15.3.108/1,03.10-7 --- │ΔE│x=12.03 eV --- │ΔE│y= hc/λ= 4,13.10-15.3.108/4,85.10-7 --- │ΔE│y=
2,55 eV --- os valores mais próximos são de 2 e 6 --- │ΔE│2= 13,6 – 1,51=12,09 --- │ΔE│6=3,40 – 0,85=2,55 --- R- B
11- ΔE=E2 – E1=(-3,4) – (-13,6) --- ΔE=10,2 eV=10,2.1,6.10-19 --- ΔE= 16,3.10-19J --- ΔE=h.f --- f=16,3.10-19/6,63.10-34 --- f=2,5.1015Hz
12- a) Pelo gráfico, a intensidade é máxima quando f=1,8.1013 Hz --- c=λf --- 3.108=λ.1,8.1013 --- λ=1,7.10-5m
b) Estimando a área, considere a pessoa como um cilindro de 0,3m de diâmetro e altura 1,7m --- A=2πRh + 2πR2=2.3.0,15.1,7 + 2.3.(0,15)2 --- A≈1,7m2 --- Po=E/Δt --- σA(T4 – T4a) = E/9.104 --- 6.10-8.1,7.((37 + 273)4 - (27 + 273)4)=E/9.104 ---
10,2.10-8.(3104 - 3004)=E/9.104 --- E=10,2.10-8.9.104.(9.235.210.000 – 8.100.000.000) --- E≈1,04.107 J
13- Se os fótons foram emitidos, o elétron pulou da órbita 2 para a 1 --- E2 – E1= -3,40 – ( -13,6) --- ΔE= + 10,2 eV --- R- D
14- O exercício está afirmando que a freqüência do vermelho é menor que a do verde --- a freqüência é diretamente proporcional ao nível energético --- Evermelho < Everde --- a freqüência é inversamente proporcional ao comprimento de onda λ e consequentemente ao nível energético E --- λvermelho > λverde --- R- B
15- Para o átomo de hidrogênio --- (E4 – E1)=- 13,6(1/(n4)2 - (n1)2) --- ΔE= - 13,6.(1/16 – 1/1) --- ΔE= - 13,6.(-15/16) ---
ΔE= +12,75 eV --- ou --- ΔE=12,75.1,6.10-19=20,4.10-19J --- ΔE=h.f --- 20,4.10-19=6,63.10-34.f --- f=3,07.1015 Hz
16- Nas radiografias os ossos saem brancos e tecidos em volta negros --- isso ocorre porque o osso, cuja estrutura é mais densa que a do tecido mole, absorve mais radiação ficando com aparência clara enquanto que o tecido mole, menos denso, é atravessado pelos raios X, ficando com aparência mais escura --- R- C
17- Lembre-se de que a energia dos fótons de luz é diretamente proporcional à frequência da luz f --- como a freqüência da luz amarela, do sódio, é menor, então sua energia também é menor --- a velocidade de propagação de todas as cores e de todas as radiações eletromagnéticas é sempre a mesma no ar e no vácuo (c=3,0.108m/s) --- R- A
18- Basta substituir na equação, que é fornecida, lembrando que a velocidade v é c (velocidade da luz) --- V2=2GM/R --- R=2GM/c2 --- R=2.6,67.10-11.5,98.1024(3.108)2 --- R≈9.10-3m --- diâmetro d=2R=2.9.10-3=18.10-3=0,018m=1,8cm
19- Fissão
Nuclear --- reação que se inicia com o choque de um
nêutron com um núcleo instável que proporciona a quebra deste
último e, por este motivo, é chamado de fissão nuclear (divisão
do núcleo) --- Fusão Nuclear - é o processo no qual
dois ou mais núcleos atômicos se juntam e formam um outro núcleo
de maior número atômico.

O principal tipo de fusão que ocorre no interior das estrelas é o de Hidrogênio em Hélio, onde dois prótons se fundem em uma partícula alfa (um núcleo de hélio), liberando dois pósitrons, dois neutrinos e energia.
20- 
R- B
21- R- D --- veja teoria
22- E1=Eo --- n=1 --- E1=-Eo/12 --- E1=-Eo --- n=4 --- E4=-Eo/42 --- E4=Eo/16 --- E1 – E4=(-Eo) – (-Eo/16) --- ΔE1,4=(-15/16).Eo --- R- D
23- Observe no gráfico 1 a queda de intensidade de radiação quando os raios X atravessam a parte maciça do cilindro em teste --- no gráfico 2 você observa que a metade esquerda do cilindro, em comparação com o gráfico 1, deve ser maciça e a metade direita oca --- R- E
24- R- A --- veja teoria
25- A força nuclear forte é a responsável pela atração mútua entre os nêutrons e prótons do núcleo atômico --- a força nuclear fraca participa das transmutações atômicas --- a força elétrica está associada aos campos elétricos criados em torno das cargas elétricas
--- a força gravitacional é uma das mais presentes em nosso cotidiano, haja vista que nosso peso é uma manifestação gravitacional --- R- C
26- Velocidade da luz no vácuo --- c = 3.108 m/s --- constante de Planck --- h = 6,6.10-34 J·s = 4,1.10-15 eV·s --- combinando a equação fundamental da ondulatória com a equação de Planck --- E=h.c/λ --- para a linha Hα --- λ=656,3.10-9 --- E=4,1.10-15.
3.108/653,6.10-9 --- E≈1,88 eV --- R- D
27- De acordo com o postulado de Bohr, o elétron excitado passa para um nível mais energético --- Ao sofrer decaimento para o nível estacionário, ele emite um fóton, que dependendo da frequência, poderá ser ou não na forma de luz visível --- R- A
28- (I) Incorreta --- intensidade de radiação emitida aumenta com a temperatura --- I=σ.T4 --- portanto, T3 > T1.
(II) Correta --- pelo gráfico
(III) Incorreta --- pelo gráfico, vemos que o comprimento de onda para o qual a radiação é máxima é menor para T3.
(IV) Incorreta. Já justificado em (I).
(V) Incorreta. Já justificado em (I).
R- E
29- A lei de Stefan-Boltzmann afirma que a potência total irradiada pelo corpo negro é diretamente proporcional à área (S) da superfície emissora e diretamente proporcional à quarta potência da temperatura absoluta (T): P = sST4 --- a equação do efeito fotoelétrico dada por Einstein afirma que quando uma onda eletromagnética de alta frequência atinge uma chapa metálica, cada fóton pode arrancar um único elétron que é ejetado com energia cinética máxima (K) dada pela expressão --- K = h f – W, sendo h a constante de Planck, f a frequência da onda incidente e W o trabalho para arrancar o elétron do metal --- a equação de Louis de Broglie concilia as características ondulatórias e corpusculares dos fenômenos relacionados à luz, através da equação --- λ=h/Q, sendo l o comprimento de onda associado ao movimento da partícula que se desloca com quantidade de movimento (momento linear) Q --- R- C
30- a) Os fótons incidentes que podem ser absorvidos são determinados a partir das diferenças de energia entre os estados inicial (nível fundamental) e final (1º, 2º ou 3º nível) --- aqueles fótons cujas energias coincidem com uma das diferenças de energia entre os níveis mostrados na figura poderão ser absorvidos --- as diferenças de energia entre os estados inicial e final são dadas por --- DEf3 = - 0,85 - ( -13,60) = 12,75eV (nível fundamental e 3o nível) --- DEf2 = - 1,51 - ( -13,60) = 12,09eV (nível fundamental e 2onível) --- DEf1 = - 3,40 - ( -13,60) = 10,20eV (nível fundamental e 1o nível) --- logo, os fótons que podem ser absorvidos pelo átomo de hidrogênio no estado fundamental são aqueles cujas energias são respectivamente iguais a: 12,09 eV, quando o átomo é excitado do estado fundamental para o 2º nível, e 10,20 eV, quando o átomo é excitado do estado fundamental para o 1º nível.
b)
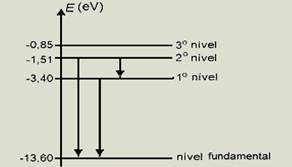
c) As energias dos fótons emitidos são determinadas a partir da diferença de energia entre o nível inicial e o nível final --- portanto, os fótons emitidos terão as seguintes energias --- DE2f = -1,51 - ( -13,60) = 12,09eV --- DE1f = -3,40 - ( -13,60) = 10,20eV --- DE21 = -1,51 - ( - 3,40) = 1,89eV
31- 1. Tomando os níveis 0, 1 e 2 de energias Eo, E1 e E2, tal que Eo < E1 < E2 (ver representação na figura acima) para transições do nível 2 para o 0, temos duas hipótese --- 1ª hipótese --- emissão de 1 fóton de energia E = h . f – E2 – Eo --- 2ª hipótese --- emissão de 2 fótons de energias E’ = h . f’ = E2 – E1 e E” = h . f” = E1 – Eo --- por conservação da energia --- (E2 – Eo) = (E2 – E1) + E1 – Eo) --- E = E’ + E’ e assim, h . f = h . f’ + h . f” --- f = f’ + f” --- portanto, cada frequência pode ser a soma ou a diferença entre outras.
2. Os comprimentos de onda que limitam a região do visível são l = 4,0.10-7 m e l’ = 7,0.10-7m (tabela de constantes), que correspondem, respectivamente, às frequências f=3.108/4.10-7 --- f=7,5.1014 Hz --- f’=3.108/7.10-7 --- f’=4,3.1014 Hz
32- R- A --- veja teoria
33- R- B --- veja teoria
34- a) E=h.c/ λ --- 1,98.10-15=6,6.10-34.3.108/λ --- λ=19,8.10-26/1,98.10-15 --- λ=10-10m --- λ=1 A
b) Q – quantidade de movimento --- λ=h/mv --- λ=h/Q --- Q=h/λ=6,6.10-34/10-10 --- Q=6,6.10-24 kg.m/s
35- R- D
36-

R- A
37-

R- A
38- Observe que na reação para a formação de uma molécula de glicose surgem seis moléculas de CO2 --- energia necessária --- E=6.2,34.10-18J --- E=1,404.10-17J --- freqüência f da radiação eletromagnética --- c=λf --- 3.108=6,80.10-7f --- f=4,4.1014Hz --- equação de Planck --- E=n.h.f --- n – número de fótons absorvidos --- 1,404.10-7=n.6,62.10-34.4,4.1014 --- n≈48 --- R- C
39- Observe que o pedido é a razão R entre a intensidade do campo magnético no CMS (BCMS) e do campo magnético da Terra (BTerra) --- n=BCMS/BTerra=4/30.10-6 --- n≈133.333 vezes --- R- A
40- a) Dado --- Eo = 13,6 eV --- pela conservação da energia, a energia (E) do fóton emitido é em módulo, igual à variação da energia do elétron --- E=│Eo/22 – Eo/12│=│13,6/4 – 13,6│ --- E=10,2 e
b) Dados --- E = 10,2 eV; 1 eV = 1,6.10-19 J --- MP = 1,6.10-27 kg --- c = 3.108 m/s --- Q=E/c --- conversão de elétron-volt para joule --- E = 10,2 (1,6.10-19) J --- pela conservação da quantidade de movimento, o próton adquire quantidade de movimento de mesma intensidade que o fóton, em sentido oposto --- assim, sendo v a velocidade adquirida pelo próton ---
│Qfóton│= │Qpróton│ --- E/c=Mp.V --- V=E/(MP.c) --- V=10,2.1,6.10-19/1,6.10-27.3.108 --- V=3,4m/s
41- a) nágua=c/vágua --- 1,3=3.108/Vágua --- Vágua≈ 2,3.108m/s
b)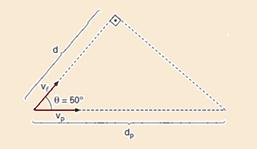
Observe na figura --- cos50o=d/dp --- 0,64=1,6/dp --- dp=2,5m --- sendo a velocidade da radiação Cerenkov constante --- Vp=ΔS/Δt --- Vp=dp/Δt --- a radiação Cerenkov percorre a distância dp no mesmo intervalo de tempo em que a luz percorre a distância d nesse meio --- Vp=2,5/12.10-9 --- Vp≈2,1.108m/s
42- Observe
a figura, que mostra o elétron movendo-se em uma de suas órbitas,
sendo --- m – massa do elétron --- e –
carga elementar – módulo da carga do próton que é igual ao
módulo da carga do elétron=e --- e – raio da órbita
do elétron --- k – constante eletrostática ---
a força eletrostática (![]() )
trocada entre o próton e o elétron age como resultante centrípeta
(
)
trocada entre o próton e o elétron age como resultante centrípeta
(![]() )
--- Fe=FC
--- mV2/r=k.e.e/r2
--- mV2=ke2/r
--- multiplicando ambos os membros por ½ --- mV2/2
= ke2/2r
(I) --- a energia (E) do elétron é a soma da sua
energia cinética (Ec)
com a sua energia potencial (Ep)
--- E=Ec +
Ep (II)
--- com o referencial no infinito --- Ep=
- ke2/r
(III) --- substituindo (I) e (III) em (II) ---
E=ke2/2r
– ke2/r
--- E= - ke2/2r
(IV) --- de acordo com o enunciado,
)
--- Fe=FC
--- mV2/r=k.e.e/r2
--- mV2=ke2/r
--- multiplicando ambos os membros por ½ --- mV2/2
= ke2/2r
(I) --- a energia (E) do elétron é a soma da sua
energia cinética (Ec)
com a sua energia potencial (Ep)
--- E=Ec +
Ep (II)
--- com o referencial no infinito --- Ep=
- ke2/r
(III) --- substituindo (I) e (III) em (II) ---
E=ke2/2r
– ke2/r
--- E= - ke2/2r
(IV) --- de acordo com o enunciado,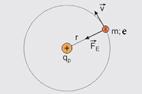
o comprimento (C) da órbita é igual a um número inteiro (n) de comprimentos de onda (λ) do elétron --- C=nλ --- 2πr=nλ --- r=nλ/2π (V) --- substituindo (V) em (IV) --- E= - ke2/2(nλ/2π) --- E= - kπe2/nλ
43-
Dados
--- carga do próton --- qp=e
--- carga do quark u --- qu=2/3e
--- calculando a carga do quark down --- do
enunciado --- p=u + u + d --- qp=2qu +
qd ---
e=2.(2/3)e + qd
--- e=(4/3)e + qd
--- qd=
- (1/3)e --- considere que o nêutron seja formado de x
quarks up e y quarks down --- como sua carga é nula
--- x + y = 3 --- x(2/3)e + y(-1/3)e = 0 ---
2x – y = 0 --- y=2x --- X + 2x=3 ---
x=1 --- y=2 --- conclui-se que um
nêutron é formado de 1 quark up e 2 quarks down (n=udd)
44- a) Falsa --- A fissão nuclear — divisão de um núcleo atômico pesado em dois núcleos mais leves.
b) Correta --- Durante a fusão nuclear ocorre grande liberação de energia, já que as massas dos núcleos produzidos são inferiores as dos núcleos iniciais. Parte da massa perdida durante a fusão nuclear é convertida em energia, de acordo com a Equação de Einstein E=MC2. Estas fusões nucleares explicam o calor e a luz do Sol, percebidos por nós, aqui na Terra.
c) Falsa --- veja b.
d) Falsa --- veja b.
e) Falsa --- veja b.
R- B.
45-
Veja
no esquema abaixo a soma das massas dos reagentes e a soma das massas
dos produtos da reação --- diferença entre a soma
dessas massas --- ∆m=236,05 – 235,88=0,17 uma
--- equação de Einstein de equivalência entre massa e
energia --- E= ∆m.c2
--- E=0,17uma=0,17.930MeV --- E=158,1 MeV.
(essa energia é liberada principalmente sob forma de energia
cinética).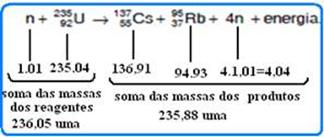
• Decaimento alfa (α) – emissão de partículas α (núcleo de 4He) --- decaimento beta (β) – emissão, pelo núcleo, de partículas β (cargas negativas, elétrons) --- decaimento gama (γ) – emissão de raios gama (fótons de alta energia).
46- a) Do texto --- “Segundo todos os cálculos, as futuras usinas de fusão nuclear poderão extrair de 1 metro cúbico de água uma quantidade de energia igual à de 2 mil barris de petróleo” --- regra de três --- 1 m3 – 2.103 barris --- 100 m3 – n barris ---
n=2.103.102 --- n=2.105 barris de petróleo --- como cada barril contém 1,5.106 kcal, 2.105 barris conterão --- W=2.105 barris x
1,5.106kcal/barril --- W=3,0.1011 kcal=3,0.1014cal --- do enunciado --- 1 BEP (Barril Equivalente de Petróleo), equivale a 1,45.109 cal --- regra de três --- 1 BEP – 1,45.109 cal --- n’ BEP – 3.1014 cal --- n’=3.1014 cal/1,45.109 cal ---
n’≈2,07.105 BEP.
b) Do texto: “Os centros dos núcleos dos átomos de hidrogênio devem estar a 1.10-15 metros um do outro para que ocorra a fusão” --- ainda do texto --- “essa fusão é o processo no qual dois núcleos de átomos leves (por exemplo, o hidrogênio – cujo núcleo é constituído por 1 próton com carga elétrica elementar é 1,6.10-19C) se combinam, ou se fundem, constituindo um elemento mais pesado. Os núcleos, então, carregados positivamente, devem se aproximar suficientemente um do outro, ou seja, vencer a força de repulsão eletrostática entre eles” --- portanto, são dados --- d=1.10-15m --- .|Q1|= |Q2|=1,6.10-19C --- k=9.109N.m2/C2 --- Lei de Coulomb --- F=k.|Q1|. |Q2|./d2 = 9.109.1,6.10-19.1,6.10-19/(1.10-15)2 --- F=23,04.101 --- F=230,4 N.
47-
As
duas leis estabelecidas por Phillip Lenard para o efeito fotoelétrico
são:
1ª Lei: para determinada frequência, o número de elétrons emitidos (conhecidos como fotoelétrons) pela placa iluminada (emissora) é proporcional à intensidade da luz nela incidente.
2ª Lei: a energia cinética dos fotoelétrons depende da frequência da radiação incidente na placa emissora, não dependendo da intensidade dessa radiação.
Como, na situação b, a intensidade da luz incidente na placa emissora é o dobro em relação à situação a, de acordo com a 1ª lei, o número de elétrons liberados também é o dobro, provocando corrente elétrica também duas vezes maior --- ib = 2 ia --- como se trata da mesma radiação nas duas situações (mesma frequência), a 2ª lei garante que energia cinética dos fotoelétrons também é a mesma, exigindo o mesmo potencial elétrico de frenamento (-Vo) --- R- C