MHS – SISTEMA MASSA-MOLA

Sistema massa-mola Um corpo de massa m realiza MHS quando, sobre uma trajetória retilínea, oscila periodicamente em torno de uma posição de equilíbrio O, sob ação de uma força denominada força restauradora  (F_el) que sempre é dirigida para O. Essa força é a força elástica fornecida pela expressão F_el = - kx (lei de Hooke)

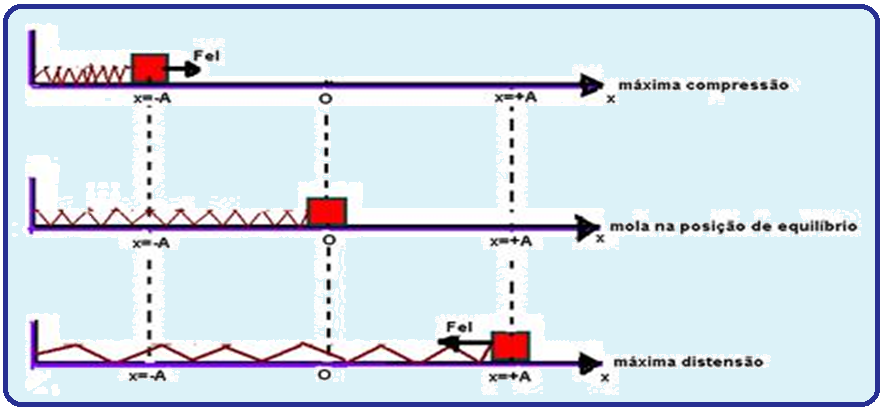
 À medida que afastamos o bloco de massa m para a direita a partir da posição de equilíbrio O ( origem da abscissa x orientada para a direita), a força restauradora vai aumentando  até atingir um valor máximo no ponto x = +A (abscissa máxima, a partir da qual, retornará)).

Analogamente, se empurramos o bloco de massa m para a esquerda a partir da posição 0, uma  força de sentido contrário e proporcional ao deslocamento X surgirá tentando manter o bloco na posição de equilíbrio 0, e esta força terá módulo máximo no ponto de abscissa x = -A, a partir de onde, retornará.

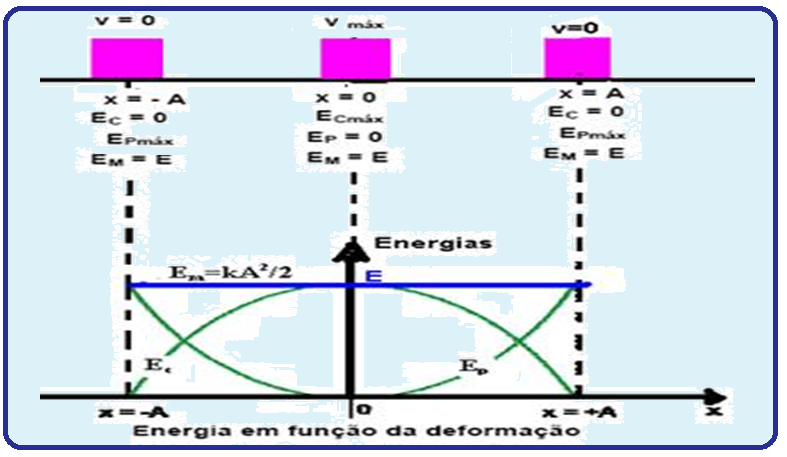
A distância do ponto O até os extremos x= +A e x= -A é chamada de amplitude A desse MHS. Observe que nesses extremos +A e –A, ocorre inversão de sentido do movimento e a velocidade se anula.

Observe também que na passagem pela posição de equilíbrio (ponto O), a velocidade é máxima em módulo.

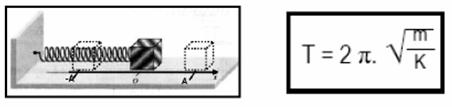
O período T desse MHS é fornecido pela expressão:

T período tempo que a massa m demora para efetuar um “vai e vem” completo

m massa que executa o MHS

k constante elástica da mola

Da lei de Hooke F= -kx e da segunda lei de Newton F=m.a, obtemos   -k.x = m.a  

a = - k/m.x.

Igualando  a = -k/m.x. com a = -w².x, obtemos    - k/m.x = - w².x    w=√(k/m).

Lembrando que w=2π/T e igualando essa expressão com a anterior    √(k/m) = 2π/T isolando T, obtemos a expressão   T=2π√(m/k).

Observe na expressão acima que o período T da massa oscilante não depende da amplitude e nem da aceleração da gravidade local, independente do fato da oscilação ser na vertical.

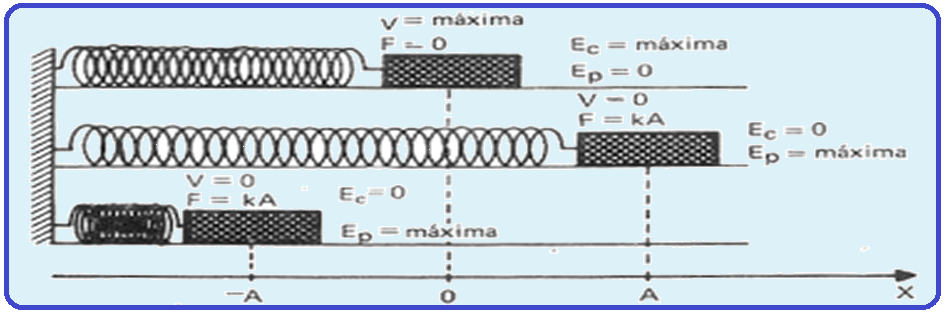
Energia no MHS no plano horizontal

A energia potencial é a elástica    E_p = k.x²/2.

Observe na equação acima que a energia potencial é nula no ponto médio 0 da trajetória onde x = 0 e é máxima nos extremos onde x = +A e X = -A, onde x² é máximo e vale A² E_p=kA²/2.

A energia cinética vale E_c=m.v²/2.

Essa energia é máxima no ponto médio 0, onde o módulo de v é máximo e nula nos extremos onde

v = 0.

A energia mecânica é sempre constante no MHS e vale E_m= kA²/2  ou  E_m=E_c + E_p  ou 

E_m = kx²/2 + m.v²/2.

Nos extremos onde v=0 e o módulo de x é A, temos que  E_m=E_c + E_p  E_m= 0 + k.A²/2    

E_m = k.A²/2 = constante.

No ponto médio 0, onde o módulo de v é máximo e x = 0, temos que  E_m=E_c + E_p    E_m=mv²/2 + 0    E_m= mv²_max/2 = constante.

Gráficos

Se a massa estiver oscilando na vertical

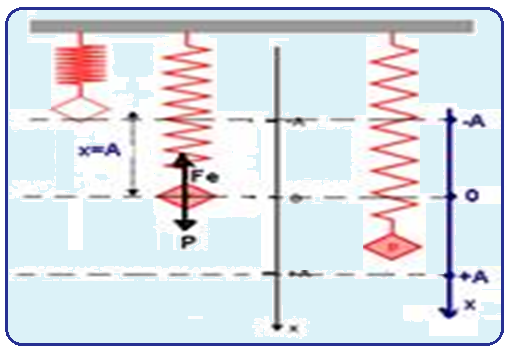
Na primeira situação, sem a massa m, a mola está em sua situação natural.

Na segunda situação, já com a massa m e em equilíbrio e distendida de x, temos    F_e= P    k.x = m.g    x = m.g/k e x = A. 

Observe que nesta situação, quanto maior for a constante elástica k, menor será a amplitude A, desde que a massa m seja a mesma.                                      

Na terceira situação, a massa m oscila em MHS de amplitude A,  em torno de 0. Neste caso, a energia mecânica é a soma das energias cinética, potencial elástica e potencial gravitacional

O que você deve saber, informações e dicas

Na expressão T=2π√(m/k) você observa que o período (e consequentemente a freqüência) do MHS do sistema massa-mola depende da massa m do corpo e da constante elástica k da mola, mas não depende da amplitude A da oscilação e nem da aceleração da gravidade local, mesmo que o movimento seja na vertical, desde que seja a mesma mola e a mesma massa.

 Energia no MHS no plano horizontal

A energia potencial é a elástica    E_p = k.x²/2.

Observe na equação acima que a energia potencial é nula no ponto médio 0 da trajetória onde x = 0 e é máxima nos extremos onde x = +A e X = -A, onde x² é máximo e vale A² E_p=kA²/2.

A energia cinética vale E_c=m.v²/2.

Essa energia é máxima no ponto médio 0, onde o módulo de v é máximo e nula nos extremos onde

v = 0.

A energia mecânica é sempre constante no MHS e vale E_m= kA²/2  ou  E_m=E_c + E_p  ou 

E_m = kx²/2 + m.v²/2.

Nos extremos onde v=0 e o módulo de x é A, temos que  E_m=E_c + E_p  E_m= 0 + k.A²/2    

E_m = k.A²/2 = constante.

No ponto médio 0, onde o módulo de v é máximo e x = 0, temos que  E_m=E_c + E_p    E_m=mv²/2 + 0    E_m= mv²_max/2 = constante.

Se a massa estiver oscilando na vertical

Na primeira situação, sem a massa m, a mola está em sua situação natural.

Na segunda situação, já com a massa m e em equilíbrio e distendida de x, temos    F_e= P    k.x = m.g    x = m.g/k e x = A. 

Observe que nesta situação, quanto maior for a constante elástica k, menor será a amplitude A, desde que a massa m seja a mesma.                                      

Na terceira situação, a massa m oscila em MHS de amplitude A,  em torno de 0. Neste caso, a energia mecânica é a soma das energias cinética, potencial elástica e potencial gravitacional

Exercícios de vestibulares com resolução comentada sobre

MHS – Sistema massa-mola

01-(UFC) Uma partícula de massa m move-se sobre o eixo x, de modo que as equações horárias para sua velocidade e sua aceleração são, respectivamente, v(t) = - wAsen (wt + j) e a(t) = w²Acos(wt + j), com w, A e j constantes.

a) Determine a força resultante em função do tempo, F(t) , que atua na partícula.

b) Considere que a força resultante também pode ser escrita como F(t) = - kx(t), onde k = mw². Determine a equação horária para a posição da partícula, x(t), ao longo do eixo x.

c) Usando as expressões para as energias cinética, Ec(t) = 1/2 mv²(t), e potencial, Ep(t) = 1/2 kx²(t), mostre que a energia mecânica da partícula é constante.

2-(UFPB) Um Professor de Física utiliza uma mola, de constante elástica k e comprimento L (quando não distendida), para demonstrar em sala de aula o movimento harmônico simples (MHS). A mola, presa ao teto da sala, pende verticalmente. Um corpo de massa m é preso à extremidade livre da mola e subitamente largado.

Desprezando todas as forças dissipativas, admitindo que a mola tem massa desprezível e que a gravidade terrestre é g, analise as afirmações a seguir:

(g = 10 m/s²)

I. O período do MHS obtido é T = 2pÖ(L/g).

II. O corpo não realiza MHS devido à gravidade.

III. A nova posição de equilíbrio está deslocada de DL = mg/k.

IV. A energia mecânica total do corpo, no movimento vertical, é igual à soma das suas energias cinética, potencial elástica e potencial gravitacional.

Estão corretas apenas:

a) I e II

b) I e III

c) I e IV

d) II e III

e) III e IV

3-(UECE) Um sistema oscilante massa-mola possui uma energia mecânica igual a 1,0 J, uma amplitude de oscilação 0,5 m e uma velocidade máxima igual a 2 m/s. Portanto, a constante da mola, a massa e a freqüência são, respectivamente, iguais a:

a) 8,0 N/m, 1,0 kg e 4/π Hz

b) 4,0 N/m, 0,5 kg e 4/π Hz

c) 8,0 N/m, 0,5 kg e 2/π Hz

d) 4,0 N/m, 1,0 kg e 2/π Hz

4-(UFMS) O Bungee Jump é um esporte radical que consiste na queda de grandes altitudes de uma pessoa amarrada numa corda elástica. Considerando desprezível a resistência do ar, é correto afirmar que

(01) a velocidade da pessoa é máxima quando a força elástica da corda é igual à força peso que atua na pessoa.

(02) a velocidade da pessoa é máxima quando o deslocamento da pessoa, em relação ao ponto que saltou, é igual ao comprimento da corda sob tensão nula.

(04) o tempo de movimento de queda independe da massa da pessoa.

(08) a altura mínima que a pessoa atinge em relação ao solo depende da massa dessa pessoa.

(16) a aceleração resultante da pessoa é nula quando ela atinge a posição mais baixa.

5-(ITA-SP) Duas molas ideais, sem massa e de constantes de elasticidade k₁ e k₂, sendo k₁<.k₂, acham-se dependuradas no teto de uma sala. Em suas extremidades livres penduram-se massas idênticas.

Observa-se que, quando os sistemas oscilam verticalmente, as massas atingem a mesma velocidade máxima. Indicando por A₁ e A₃, as amplitudes dos movimentos e por  E₁ e E₂ as energias mecânicas dos sistemas (1) e (2), respectivamente, podemos dizer que:

a) A₁ > A₂ e E₁ = E₂     

b) A₁ > A₂ e E₁ = E₂        

c) A₁ > A₂ e E₁ > E₂     

d) A₁ > A₂ e E₁ > E₂     

e) A₁ = A₂ e E₁ > E₂     

06-(PUC-MG) Uma partícula de massa 0,5kg move-se sob ação de apenas uma força, à qual está associada uma energia potencial E_p cujo gráfico em função de x está representado na figura abaixo.

Esse gráfico consiste em uma parábola passando pela origem. A partícula inicia o movimento a partir do repouso, em

x= -2,0m. Pede-se:

a) Sua energia mecânica

b) A velocidade da partícula ao passar por x=0

c) A energia cinética da partícula ao passar por x=1m.

07-(MACKENZIE-SP) Um corpo de 250g de massa encontra-se em equilíbrio, preso a uma mola helicoidal de massa desprezível e constante elástica k igual a 100N/m, como mostra a figura abaixo.

O atrito entre as superfícies em contato é desprezível. Estica-se a mola, com o corpo até o ponto A, e abandona-se o conjunto nesse ponto, com velocidade zero. Em um intervalo de 1,0s, medido a partir desse instante, o corpo retornará ao ponto A

a) um vez     

b) duas vezes     

c) três vezes     

d) quatro vezes     

e) seis vezes

08-(UNESP-SP) Em um sistema massa-mola, conforme mostra a figura (superfície horizontal sem atrito), onde k é a constante elástica da mola, a massa é deslocada de uma distância x_o, passando a oscilar.

a) em que ponto, ou pontos, a energia cinética da massa é igual a 7/9 da energia potencial do sistema?
b) a energia cinética pode ser superior à potencial em algum ponto? Explique sua resposta.

09-(UEM-PR) Um corpo de massa igual a 2,0kg oscila sobre uma mesa horizontal lisa, preso a uma mola também horizontal, cuja constante elástica é k = 200N/m. A amplitude da oscilação é A = 10cm. Nessas condições, dê como resposta a soma dos números correspondentes às afirmações corretas. Considere g = 10m/s².

(01)  A força que a mola exerce sobre o corpo é constante e vale 20N

(02) Se nenhuma força externa agir sobre o sistema, o mesmo oscilará indefinidamente.

(04) A frequência angular de oscilação é de 10rad/s

(08) O módulo da velocidade máxima do corpo é de 1,0m/s e ocorre no ponto  de máximo deslocamento, em relação à posição de equilíbrio.

(16) O período de oscilação é igual a p/5 s.

10-(UFU-MG) Uma massa m executa um MHS. Sua energia potencial U, em função de sua posição x, está no gráfico abaixo.

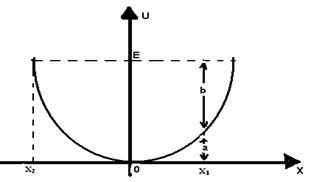
Se E for sua energia total, teremos:

a) em x₁, sua energia cinética será a

b) em x₁, sua energia potencial será b

c) em x₁, sua energia cinética será +b

d) na posição x₂ sua energia cinética será máxima

e) na posição x₂ sua energia potencial será nula.

11-(PUC-SP)  Na figura abaixo, está representada a situação de equilíbrio de uma mola ideal quando livre e depois de ser presa a um corpo de massa 400g.

 Considere g=10m/s² e determine:

a) a constante elástica da mola

b) o tipo e o período do movimento que o corpo descreveria, caso fosse suspenso 1,cm de sua posição de equilíbrio. Despreze a ação do ar sobre o movimento.

12-(UNICAMP-SP) Os átomos de carbono têm a propriedade de se ligarem formando materiais muito distintos entre si, como o diamante, o grafite e os diversos polímeros. Há alguns anos foi descoberto um novo arranjo para esses átomos: os nanotubos, cujas paredes são malhas de átomos de carbono. O diâmetro desses tubos é de apenas alguns nanômetros (1nm=10^-9m). No ano passado, foi possível montar um sistema no qual um “nanotubo de carbono” fechado nas pontas oscila no interior de um outro nanotubo de diâmetro maior e aberto nas extremidades. As interações entre os dois tubos dão origem a uma força restauradora representada no gráfico. (1nN=10^-9N)

a) Encontre, por meio do gráfico, a constante da mola desse oscilador.

b) O tubo oscilante é constituído de 90 átomos de carbono. Qual  é a velocidade máxima desse tubo, sabendo-se que um átomo de carbono equivale a uma massa de 2.10^-26kg.

13-(ITA-SP) 

Um cubo de 81,0 kg e 1,00 m de lado flutua na água cuja massa específica é ρ= 1000 kg/m³. O cubo é então calcado ligeiramente

para baixo e, quando liberado, oscila em um movimento harmônico simples com uma certa frequência angular. Desprezando-se as forças de atrito e tomando g = 10 m/s², essa frequência angular é igual a:

a) 100/9 rad/s.                 

b) 1.000/81 rad/s                   

c) 1/9 rad/s.                    

d) 9/100 rad/s.                    

e) 81/1.000 rad/s

14-(PUC-MG)

A figura a seguir mostra um corpo de massa m = 0,05 kg, preso a uma mola de constante elástica k = 20 N/m.

 O objeto é deslocado 20 cm para a direita, a partir da posição de equilíbrio sobre uma superfície sem atrito, passando a oscilar entre x = A e x = - A.

Assinale a afirmativa CORRETA. 

a) Na posição x = -20 cm, a mola tem uma energia cinética de 0,4 J e a energia potencial elástica do corpo é nula.  

b) Na posição x = -20 cm, toda a energia do sistema vale 0,4 J e está no objeto sob a forma de energia cinética.  

c) Na posição x = 0, toda a energia do sistema está no corpo na forma de energia cinética e sua velocidade vale 4 m/s.  

d) Na posição x = 20 cm, toda a energia do sistema vale 0,8 J sendo 0,6 J na mola e o restante no objeto. 

15-(UNICAMP-SP) 

A piezeletricidade também é importante nos relógios modernos que usam as vibrações de um cristal

de quartzo como padrão de tempo e apresentam grande estabilidade com respeito a variações de temperatura.

a) Pode-se utilizar uma analogia entre as vibrações de um cristal de massa m e aquelas de um corpo de mesma massa preso a uma mola. Por exemplo: a frequência de vibração do cristal e a sua energia potencial elástica também são dadas por f = (1/2π).√(k/m) e

E_p=(1/2).k.∆x², respectivamente, onde k é a propriedade do cristal análoga à constante elástica da mola e ∆x é o análogo da sua deformação. Um cristal de massa m = 5,0 g oscila com uma frequência de 30 kHz. Usando essa analogia, calcule a energia potencial elástica do cristal para ∆x = 0,020 μm.

b) Em 1582, Galileu mostrou a utilidade do movimento pendular na construção de relógios. O período de um pêndulo simples depende do seu comprimento L. Este varia com a temperatura, o que produz pequenas alterações no período.

 No verão, um pêndulo com L = 90 cm executa um certo número de oscilações durante um tempo t = 1800 s. Calcule em quanto tempo esse pêndulo executará o mesmo número de oscilações no inverno, se com a diminuição da temperatura seu comprimento variar 0,20 cm, em módulo. Para uma pequena variação de comprimento ∆L, a variação correspondente no tempo das oscilações ∆t é dada

(∆t/t)=(1/2).(∆L/L), assim ∆t pode ser positivo ou negativo, dependendo do sinal de ∆L.

16-(ITA-SP-010) 

Considere um oscilador harmônico simples composto por uma mola de constante elástica k, tendo uma extremidade fixada e a outra acoplada a uma partícula de massa m. O oscilador gira num plano horizontal com velocidade angular constante ω em torno da extremidade fixa, mantendo-se apenas na direção radial, conforme mostra a figura. Considerando R_o a posição de equilíbrio do

oscilador para ω = 0, pode-se afirmar que

a) o movimento é harmônico simples para qualquer que seja velocidade angular ω. 

b) o ponto de equilíbrio é deslocado para R < R_o.  

c) a frequência do MHS cresce em relação ao caso de ω = 0. 

d) o quadrado da frequência do MHS depende linearmente do quadrado da velocidade angular. 

e) se a partícula tiver carga, um campo magnético na direção do eixo de rotação só poderá aumentar a frequência do MHS. 

17-(MACKENZIE-SP)

Um corpo de 0,50kg oscila, periodicamente, sobre uma reta em torno de um ponto, com sua posição x

em função do tempo, na reta, dada em relação a esse ponto, pela função x = 0,30cosπt. A posição x é medida

em rad/s e t em segundos. Dentre as alternativas, o valor mais próximo da força resultante queem metros, π

age sobre esse corpo, no instante t=1/3s s, é

a) 0,74N                                      

b) 0,82N                                

c) 0,96N                           

d) 1,20N                             

e) 1,48N

18-(UNICAMP-SP)

Várias leis da Física são facilmente verificadas em brinquedos encontrados em parques de diversões. Suponha que em certo

parque de diversões uma criança está brincando em uma roda gigante e outra em um carrossel.

a) A roda gigante de raio R = 20m gira com velocidade angular constante e executa uma volta completa em T = 240s. No gráfico abaixo (ver resolução), marque claramente com um ponto a altura h da criança em relação à base da roda gigante nos instantes t = 60s, t = 120 s, t = 180 s e t = 240s, e, em seguida, esboce o comportamento de h em função tempo. Considere que, para t = 0, a criança se encontra na base da roda gigante, onde h = 0.

b) No carrossel, a criança se mantém a uma distância r = 4m do centro do carrossel e gira com velocidade angular constante ω_o. Baseado em sua experiência cotidiana, estime o valor de ω_o para o carrossel e, a partir dele, calcule o módulo da aceleração centrípeta a_cda criança nos instantes t = 10s, t = 20 s, t = 30 s e t = 40 s.

Em seguida, esboce o comportamento de a_c em função do tempo no gráfico abaixo (ver resolução), marcando claramente com um ponto os valores de a_c para cada um dos instantes acima. Considere que, para t = 0, o carrossel já se encontra em movimento.

19-(EsPCEx)

Um objeto preso por uma mola de constante elástica igual a 20 N/m executa um movimento harmônico simples em

torno da posição de equilíbrio. A energia mecânica do sistema é de 0,4 J e as forças dissipativas são desprezíveis. A amplitude de oscilação do objeto é de:

Resolução comentada dos exercícios de vestibulares sobre

MHS Sistema massa-mola

01.a) F(t) = ma  ---  F(t) = mw²Acos(wt + j)

b) mw²Acos(wt = j) = mw²x  ---  x(t) = A cos(wt + j)

c) Usando as equações para a energia cinética e potencial, juntamente com as equações horárias da posição e velocidade, temos que                                                                  k

Ec(t) = 1/2mv2(t) = 1/2 m(wAsen(wt + j))² =  1/2mw²A²sen²(wt +j)  ---  E_c = 1/2 kA² sen²(wt + j)                                                 Ep(t) = 1/2kx²(t) = 1/2 k(Acos(wt + j) )²  --- E_p(t)=1/2kA²cos²(wt + j)                                                

A energia mecânica é a soma da energia cinética com a energia potencial. Logo,

Emec = 1/2 kA² sen²(wt + j) + 1/2kA²cos²(wt + j)  ---  E_m=1/2kA²(sen²(wt + j) + cos²(wt + j))  ---  E_m=1/2kA²(1)

E_m=1/2kA2, que é uma constante

02- E

03-

 E_m-1J      A=0,5m        V_máxima=2m/s

E_m=1/2.kA²  ---  1=1/2.k.(0,5)²  ---  k=8N/m      E_m=1/2.mV²_máxima  ---  1=1/2.m.(2)²  ---  m=0,5kg

T=2pÖm/k  ---  T=2pÖ0,5/8  ---  T=2p.1/4  ---  T=p/2 s  ---  f=1/T  ---  f=1/p/2  --- f=2/pHz

04-

01- Verdadera – a força elástica iguala a força peso no ponto médio onde a velocidade é máxima e a aceleração nula

02- Falsa – a velocidade da pessoa aumenta até o ponto médio e a partir daí começa a diminuir.

04- Falsa – pois, T=2pÖm/k

08- Verdadeira—veja equação acima

16- Falsa- a aceleração é nula no ponto médio, a partir do qual ela inverte seu sentido, retardando a pessoa.

05-

E_m=kA²/2 (constante) e E_m=m.v²_máxima/2  ---k.A²/2 = m.V²_máxima/2  ---  k.A² = m.V²_máxima = constante, ou seja, k é inversamente proporcional a A, e E_m é sempre constante  ---  alternativa a

 06-

a)  Como ela está sujeita a apenas uma força, o movimento é horizontal e essa força é a força elástica.Quando x=1m  ---  E_p=1J  ---  E_p=k.x²/2  ---  1=k.1²/2  ---  k=2N/m. A amplitude A vale 2m, pois é aí que v=0.

E_m=k.A²/2  --- E_m=2.2²/2  ---  E_m=4J

b) Quando x=0  ---  E_p=0  --- E_m=E_c + E_{p  ---}   4=mV²/2 + 0  ---  4=0,5V²/2  ---  V=Ö16  ---  V=4m/s

c) E_m=E_c + Ep  ---  4=E_c + k.x²/2  ---  4=E_c + 2.1²/2  ---  E_c=3J

07-

Vamos calcular o período T, que é o tempo que ele demora para efetuar um vai e vem completo.

T=2pÖm/k  ---  T=2.3.Ö0,35/100  ---  T=6.5.10^-2  ---  T@0,3s

0,3s ------ 1 vai e vem completo

1,0s ------    n

n@3,3     -----  alternativa C

08- 
a) E_m=k.A²/2   ---  E_p=k.x²/2  ---  E_c=7/9.k.x²/2
E_m= E­_c + E_o  ---  k.A²/2 = 7/9.k.x²/2 + k.x²/2  ---  k.A²/2 = (7.k.x² + 9.k.x²)/18  ---  9.k.A² = 16.k.x²  ---  x = Ö9/16.A²

X = ± 3/4.A  --- Nas posições x = + 3/4.A e X = - 3/4.A 

b) Sim. Por exemplo, no ponto O quando toda a energia mecânica estará na forma de energia cinética.

09-

(01) Falsa. A força elástica não é constante, pois varia de acordo com a deformação.

(02) Correta. Desprezando-se as forças externas dissipativas o sistema oscilará sempre.

(04) Correta  ---  w =Ök/m  ---  w = Ö200/2  ---  w = 10rad/s

(08) Falsa. A velocidade máxima do corpo vale  ---  V_máxima = w.A = 10.0,1 = 1,0m/s, mas não é no ponto de máximo deslocamento, mas sim na posição central 0.

(16) Correta. O período T é dado por T = 2pÖm/k  ---  T = 2pÖ2/200  ---  T = 2p.1/10  ---  T = p/5 s.

Soma=(02 + 04 + 16) = 22

 10-

Em X₂  ---  E_p é máxima e E_c é nula. Em X₁  ---  E_p = a  ---   E = E_c + E_p  ---  E = a + b  ---  E_c + a = a + b  ---  E_c = +b

R: C

11-

a) No equilíbrio  ---  F_e = P  ---  k.x = m.g  ---  k = m.g/x  ---  k = 0,4.10/0,05  ---  k=4/0,05  ---  k =80N/m

b) O movimento é um MHS e o seu período não depende da amplitude A e é fornecido pela expressão  ---  T = 2.pÖm/k                                                            

T = 2pÖ0,4/80  ---  T = 2p.2,24  ---  T = 4,48p s

12-

a) Escolhendo qualquer ponto por exemplo, quando E  ---  F = 0,75nN, x=-15nm. F =- k.x  ---  0,75.10^-9 = -(-15).10^-9.k  --- 

k = 0,75/15---  k = 0,05N/m.

b) T = 2pÖm/k  ---  T = 2pÖ180.10^-26/0,05  ---  T = 12p10^-12 s  ---  w =2p/T  ---  w = 2p/12p10^-12  ---  w = 1/6.10¹²rad/s

V_máaima = w.A  ---  V_máxima = 1/6.10¹².30.10^-9  ---  V_máxima = 5.10³ m/s

13- Com o cubo em equilíbrio, a força resultante sobre ele é nula  ---  empuxo = peso  ---  ρ.g.v = m.g  ---  1.000v=81  --- 

V=0,081m³  ---  como a área da base é 1 m², isto significa que o ponto de equilíbrio fica a 0,081 m ou 8,1 cm abaixo da linha da superfície, pois V=s.h  ---  0, 081=1.h  ---  h=0,081m  ---  o cubo é forçado para baixo, digamos uma profundidade x além de 0,081 m  ---  a força resultante sobre o cubo funcionará como a força restauradora do MHS  ---  F_resultante = Empuxo – Peso  --- 

F_resultante = ρ.g.(0,081 + x) – m.g  ---  F_resultante = ρ.g.0,081 + ρ.g.x – m.g = ρ.g.x  ---  se esta força é a restauradora do MHS então ρ.g.x = k.x  ---   k = ρ.g  --- frequência angular de um sistema oscilante  --- w=√(k/m)=√ (ρ.g/m)=√(1.000x10/81)  ---  w=√(10.000/81)  ---  w=100/9 rad/s  ---  R- A

14- No MHS (movimento harmônico simples) o sistema apresenta energia potencial elástica máxima nas extremidades (A e –A) e energia cinética máxima no centro (0). Desta forma a velocidade da partícula no centro do sistema é dada por  ---  mv²/2=kx²/2  --- 

0,05v²=20.(0,2)²  ---  v²=0,8/0,05  ---  v=√16  ---  v=4m/s  ---  R- C

15- a) Expressão da frequência  ---  f = (1/2π).√(k/m)  ---  30.10³ = (1/2.3,14).√(k/5.10^-3)  ---  30.6,28.10³ = √(k/5.10^-3)  ---  (188,4.10³)² = k/5.10^-3  ---  k=35.495.10⁶.5.10^-3  ---  k=1,77.10⁸ N/m  ---  energia potencial elástica  ---  E_p=(1/2).k.∆x²  --- E_p=0,5.1,77.10⁸.(0,02.10^-6)²  ---  E_p= 3.54.10^-8 J    

b) Expressão fornecida  ---  (∆t/t)=(1/2).(∆L/L)  ---  (∆t/1.800)=(1/2).(- 0,2)/90)  ---  ∆t/1.800= - 1/900  ---  ∆t=-1.800/900  --- 

∆t= - 2s  ---  novo intervalo de tempo  ---  ∆t’= 1800 – 2 = 1798 s

16- Nas figuras abaixo  ---  R_o: distância da extremidade fixa da mola até o centro de oscilação para o sistema não em rotação  --- 

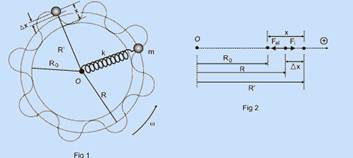
R: distância da extremidade fixa da mola até o centro de oscilação para o sistema em rotação  ---  R’: distância da extremidade fixa da mola até um ponto qualquer da trajetória  ---  x: deformação da mola  ---  ∆x: variação da deformação entre o centro de oscilação em rotação e um ponto qualquer da trajetória  ---  se o sistema apenas girasse sem oscilar, o movimento circular uniforme teria raio R  ---  a força resultante sobre a partícula seria apenas a força elástica agindo como resultante centrípeta  ---    

F_R=F_c=F_elétrica=mw²R=kx  ---  mw²R=k(R – R_o) (I)  ---  para o sistema girando e oscilando vamos considerar um referencial fixo ao oscilador (referencial não-inercial)  ---  para esse referencial há um movimento oscilatório, com uma deformação aparente da mola igual a ∆x, quando a partícula está numa posição de raio R’R  ---  para esse referencial, temos que introduzir a “força de inércia” ou força centrífuga (F_i), dirigida para fora, oposta à força elástica, como mostrado na Fig 2  ---  nesse referencial, obedecendo ao sentido de orientação, a força resultante vale  --- F_R= - F_elétrica + F_i  ---  m.a = -k.x + m∆2R’ (II)  ---  figura 2  ---  x= (R’ – R_o)  --- 

R’=∆x + R  --- substituindo-os em (II)  ---   ma = -k(∆x + R – R_o) + m∆2(∆x + R)  ---  ma = -k∆x – k(R – R_o) + m∆2∆x + m∆2R (IV)  ---  substituindo (I) em (IV)  ---  ma = -k∆x – k(R – R_o) + 2∆x + k(R – R_o)  ---  fazendo os cancelamentos e isolando a  ---  a= ( - k/m + w²).∆x  ---  a= - (k/m –w²).∆x (V)  ---  a propriedade fundamental de um MHS diz que a aceleração é diretamente proporcional à elongação (∆x)  ---  a constante de proporcionalidade é o oposto do quadrado da pulsação do movimento oscilatório (∆_osc)  ---  a= - w²_osc.∆x  ---  a= - 2(∆f)².∆x (VI)  ---  igualando (V) com (VI)  ---  4∆2f²=k/m – w²  ---  f²=k/4π²m – 1/4π².w²  ---  assim, o quadrado da frequência do MHS depende linearmente do quadrado da velocidade angular  ---  R- D

17- Relação fundamental do MHS  ---  a= - w².x  ---  quando t=1/3s  ---  x=0,3cosπt=0,3cosπ.1/3  ---  x=0,3cosπ/3=0,3.1/2  ---  x=0,15m  ---  x=0,3c0swt  ---  w=π  ---  a=-w².x= - π².0,15  ---  π²=10  ---  a=1,5m/s²  ---  lei fundamental da dinâmica  ---  F_R=ma  ---  F_R=0,5.1,5  ---  F_R=0,75N  ---  R- A

18- a) Observe na figura abaixo, as posições ocupadas  pela criança na roda gigante nos instantes t=0, t=60s, t=120s, t=180s e t=240s,

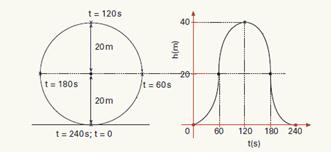
 e o gráfico da altura da criança em função do tempo equivale a um MHS de amplitude a=20m, com a origem no ponto h=20m..

b) Supondo que o carrossel efetue uma volta completa em 20s, ou seja, T=20s  ---  velocidade escalar  ---  v=2πr/T=2.(3).4/20  ---

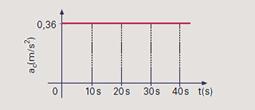
v=1,2m/s  ---  a_c=V²/R=1,44/4=0,36ms²  ---  a_c=0,36m/s² ---  o gráfico pedido está representado abaixo:

19-

 Como as forças dissipativas são desprezíveis, a energia mecânica é sempre constante no MHS e vale E_m= kA²/2  ou  E_m=E_c + E_p  ou  E_m=kx²/2 + m.v²/2  ---  E_m=k.A²/2  ---  0,4=20.A²/2  ---  A²=8,8/20  ---  A=√(4.10^-2)=2.10^-1m  --- A=0,2m  ---  R- B.