Movimento Harmônico Simples (MHS) – Função horária da elongação

Movimento periódico   todo movimento que se repete em intervalos de tempo iguais.

Movimento oscilatório (vibratório) harmônico  o móvel se desloca sobre a mesma trajetória, indo e vindo, em relação a uma posição média de equilíbrio (ponto O, onde a resultante das forças que agem sobre ele é nula)

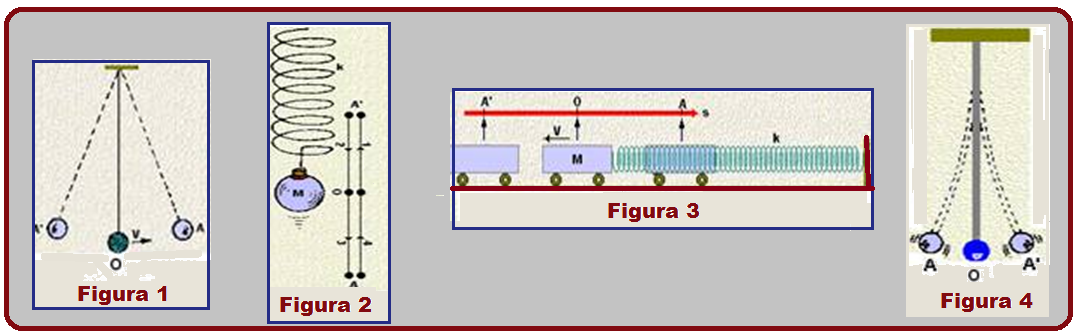
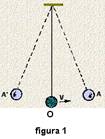
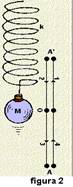
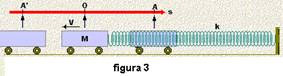
O período T é o tempo em que o corpo em cada uma das figuras (figura 1 – pêndulo simples; figura 2 – pêndulo de mola; figura 3 – sistema massa-mola e figura 4 – lâmina vibrante) demora  para ir de A até A’ e depois retornar a A, ou seja,.é o tempo decorrido entre  duas passagens consecutivas do corpo por um mesmo ponto da trajetória.

A freqüência f representa o número de vezes que o móvel passa pelo mesmo ponto da trajetória, na unidade de tempo, ou seja, é o número de vezes que o fenômeno se repete, na unidade de tempo.

Quando o período T é medido em segundos (s), a freqüência f é medida em hertz (Hz), sendo

1 Hz = 1oscilação por segundo.

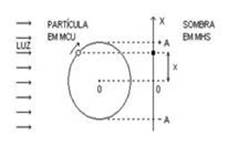
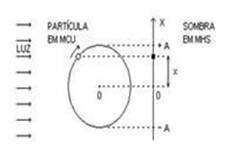
Movimento Harmônico Simples (MHS)    Podemos generalizar um MHS como a projeção ortogonal de um movimento circular uniforme (MCU) sobre uma reta.

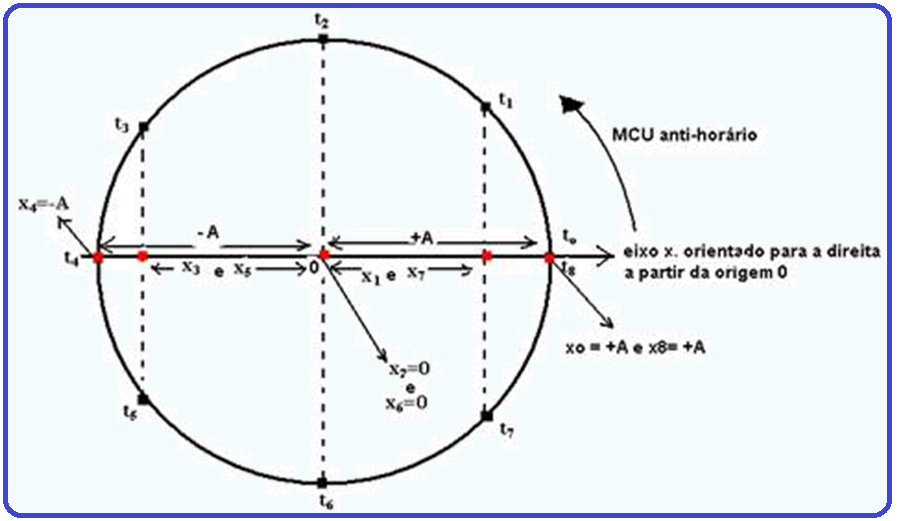
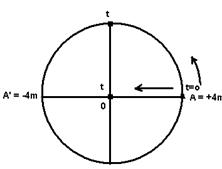
Observe na figura acima que, enquanto o corpo descreve um MCU anti-horário entre os instantes t_o e t₄, sua projeção sobre o eixo x, em MHS, se desloca para a esquerda em movimento retrógrado de +A até –A e quando o corpo em MCU se move do instante t₄ até o instante t₈, sua projeção sobre o eixo x se move para a direita, em movimento progressivo, de –A até +A, completando um período em t₈. A partir daí, tudo se repete.

O mesmo será válido se o eixo x estiver na vertical e for orientado para cima (figura abaixo).

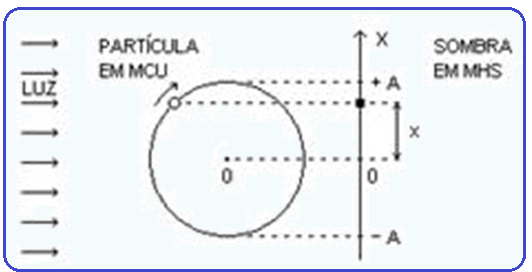
Definições

Elongação (x)  posição (localização) da partícula em MHS sobre o eixo x em relação à origem 0, ou seja, mostra a que distância de 0 a partícula se encontra em determinado instante.

Amplitude (A)  em módulo é a elongação máxima do MHS e corresponde ao raio da circunferência do MCU (R = A).

Período (T)  corresponde ao tempo que o MCU demora  para efetuar uma volta completa ou ao tempo que o MHS demora para efetuar um “vai e vem” completo sobre a reta x.

Freqüência (f)  número de voltas completas (MCU) ou número de idas e voltas completas (MHS), na unidade de tempo.

Ângulo de fase (φ)  posição (localização) angular no MCU, ou seja, localiza angularmente o corpo em MCU, num dado instante t.

Fase inicial (φ_o)  indica, no instante t=0, o ângulo de fase inicial do MCU.

O ângulo de fase (φ) e a fase inicial (φ_o) são medidos em radianos (rad).

Velocidade angular ou pulsação (w)   mede no MCU o ângulo “varrido” na unidade de tempo e fornece o período ou a freqüência do MCU através das expressões w=2π/T ou w=2πf.

Funções

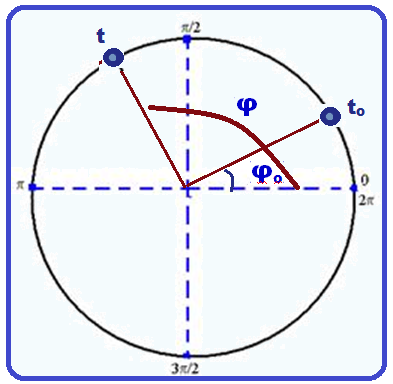
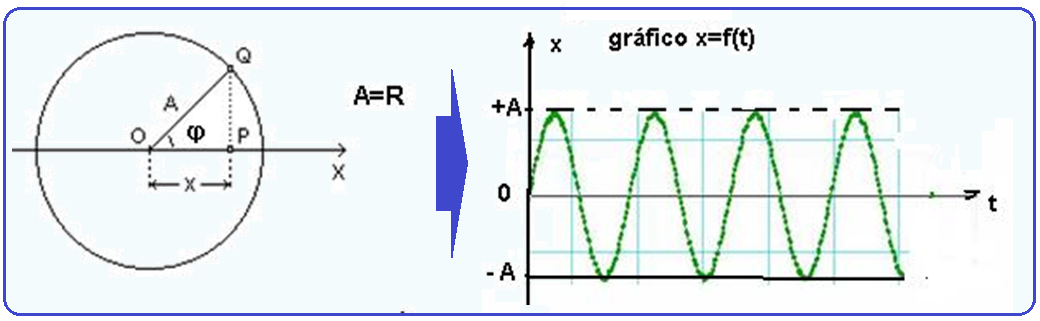
Função horária da elongação x  Na figura abaixo, considere o ponto P em MHS e o ponto Q em MCU num instante qualquer t.

 No triângulo OPQ da figura acima cosφ = 0P/0Q cosφ = x/A   x = Acosφ (1)

Lembrando que, no MCU, a posição angular φ varia com o tempo conforme a função φ = φ_o + wt, teremos, substituindo-a em 1    x = A.cos(φ_o + wt)   que é a função horária da elongação e onde  x é a elongação; w, a pulsação ou freqüência angular ou ainda velocidade angular;  A, a amplitude (elongação máxima) e φ_o a fase inicial  da partícula em MHS.

O mesmo será válido se o eixo x estiver na vertical

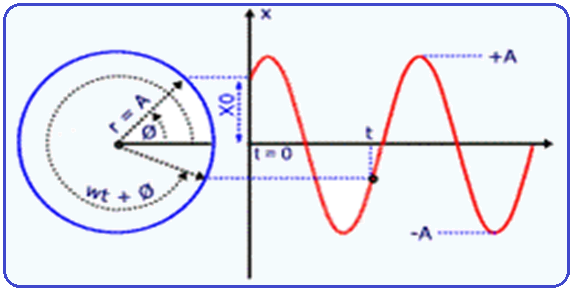
Os ângulos são medidos em radianos (rad) e a pulsação w em radianos por segundo (rad/s)

O que você deve saber

Função horária da elongação

Exercícios de vestibulares com resolução comentada sobre Função horária da elongação do MHS

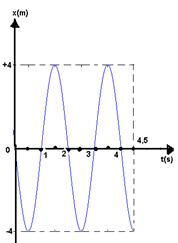
01-(UFB) Uma partícula realiza um MHS em torno do ponto O com período de 2s (figura).

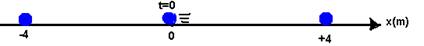
Os pontos M e N são os extremos da oscilação e no instante t=0 a partícula está passando sobre o ponto 0, deslocando-se para a esquerda.

Pede-se para esse MHS:

a) a freqüência f

b) a pulsação w (velocidade angular)

c) a amplitude

d) a fase inicial

e) a função horária da elongação

f) a elongação nos instantes  t=0; t=0,5s; t=1s; t=1,5s, t=2s e t=4,5s.

g) Esboce o gráfico da elongação x em função do tempo t, desde t=0 até t=4,5s.

02- (Unicamp-SP) Enquanto o ponto P se move sobre uma circunferência, em movimento circular uniforme com velocidade angular ω=2rad/s, o ponto M (projeção de P sobre o eixo x) executa um movimento harmônico simples entre os pontos A e A'.

Nota:
B e C são os pontos médios de AD e DA', respectivamente.

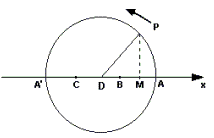
a) qual é a freqüência do MHS executado por M?
b) determine o tempo necessário para o ponto M deslocar-se do ponto B ao ponto C.

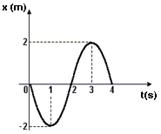
03-(UFG-GO) O gráfico mostra a posição em função do tempo de uma partícula em movimento harmônico simples (MHS) no intervalo de tempo entre 0 e 4 s. A equação da posição em função do tempo para este movimento é dada por x=A cos(ω t+ w_o). A partir do gráfico, encontre os valores das constantes A, ω e w_o.

04- (UFV-MG) Duas partículas descrevem movimentos harmônicos simples representados nos gráficos (I) e (II) a seguir.

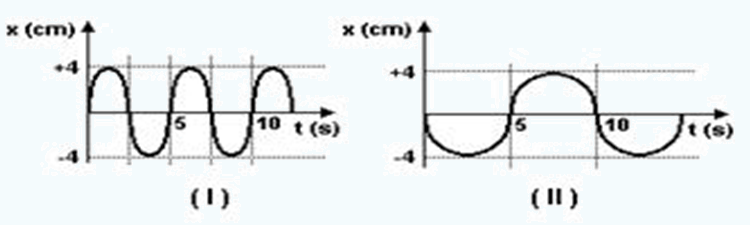
É CORRETO afirmar que os dois movimentos têm:

a) mesma freqüência, amplitudes iguais e fases diferentes.

b) freqüências diferentes, amplitudes iguais e fases diferentes.

c) mesma freqüência, amplitudes diferentes e mesma fase.

d) mesma freqüência, amplitudes iguais e mesma fase.

e) freqüências diferentes, amplitudes iguais e mesma fase.

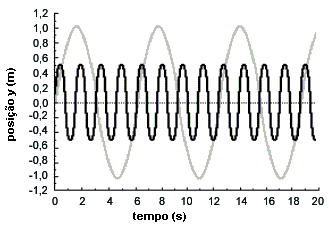
05-. (UFPE) Dois corpos descrevem movimentos de oscilação periódicos ao longo do eixo y, conforme indicado na figura. Qual a razão entre as freqüências de oscilação dos corpos?

06-(UFL-MG) Um corpo executa um movimento harmônico simples descrito pela equação x=4.cos(4πt) (SI)

a) Identifique a amplitude, a freqüência e o período do movimento.

b) Em que instante, após o início do movimento, o corpo passará pela posição x=0?

07-(MACKENZIE-SP) Uma partícula realiza um MHS (movimento Harmônico simples), segundo a equação x=0,2.cos(π/2 + π/2t), no SI. A partir da posição de elongação máxima, o menor tempo que essa partícula gastará para passar pela posição de equilíbrio é:

a) 0,5s         

b) 1s         

c) 2s         

d) 4s         

e) 8s

08-(UFPI) O gráfico da elongação x=Acos(wt+q) de uma partícula que executa um movimento harmônico simples está representado na figura.

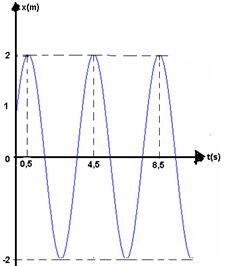
Determine a fase inicial, a pulsação ou freqüência angular e a função horária da elongação  desse movimento.

09-(FUVEST-SP) Enquanto uma folha de papel é puxada com velocidade constante sobre uma mesa, uma caneta executa movimento de vaivém perpendicularmente à direção de deslocamento do papel, deixando registrado na folha um traço em forma de senóide. A figura abaixo representa um trecho AB do traço, bem como as posições de alguns de seus pontos e os respectivos instantes.

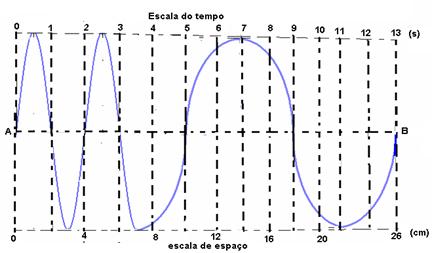
Pede-se:

a) a velocidade de deslocamento da folha

b) a razão das freqüências do movimento de vaivém da caneta entre os instantes 0 a 3s e 5s a 13s.

10-(PUC-SP) O gráfico abaixo representa as posições ocupadas, em função do tempo, por uma partícula que oscila em MHS.

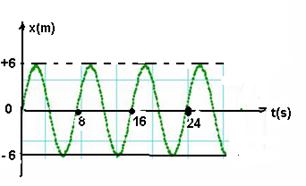
Determine a função horária da elongação

11-(ITA-SP) 

Uma partícula P₁ de dimensões desprezíveis oscila em movimento harmônico simples ao longo de uma reta com período de 8/3 s e amplitude a. Uma segunda partícula, P₂ , semelhante a P₁ , oscila de modo idêntico numa reta muito próxima e paralela à primeira, porém com atraso de π/12 rad em relação a P₁ . Qual a distância que separa P₁ de P₂, 8/9 s depois de P₂ passar por um ponto de máximo deslocamento?

a) 1,00 a                          

b) 0,29 a                            

c) 1,21 a                             

d) 0,21 a                                      

e) 1,71 a 

12-(ITA-SP) 

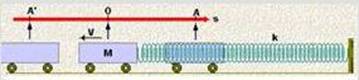
Uma partícula de massa m move-se sobre uma linha reta horizontal num Movimento Harmônico Simples (MHS) com centro O. Inicialmente, a partícula encontra-se na máxima distância x_o de O e, a seguir, percorre uma distância a no primeiro segundo e uma distânciab no segundo seguinte, na mesma direção e sentido. Quanto vale a amplitude x_o desse movimento?

a) 2.a³ / (3.a² – b²)             

b) 2.b² / (4a – b)              

c) 2.a² / (3a – b)          

d) 2.a².b / (3.a² – b²)                    

e) 4.a² / (3a – 2b)

13-(UPE-PE)

Dada a equação horária da elongação de um MHS x(t) = 4.cos[(π/2)t + π], onde x(t) é dado em metros e t em

segundos, analise as seguintes afirmativas:

I. A amplitude é 4 m.

II. O período é 4 s.

III. A frequência do movimento oscilatório é 0,25 Hz.

Está CORRETO o que se afirma em

A) I, apenas.        

B) I e II, apenas.         

C) I e III, apenas.            

D) II e III, apenas.            

E) I, II e III.

14-(UCPEL-RS)

Considere as afirmativas abaixo e as analise como VERDADEIRAS (V) ou FALSAS (F).

I. Deslocamento ou elongação de uma partícula em movimento oscilatório é a distância entre os extremos da trajetória.

II. Amplitude de um movimento oscilatório é o tempo que a partícula vai da posição de equilíbrio a um extremo da trajetória.

III. Movimento harmônico simples é qualquer movimento periódico.

IV. A aceleração de um movimento harmônico simples é constante e diferente de zero.

V. O período de um movimento harmônico simples independe da amplitude.

A sequência correta é

(A) V – F – V – V – F

(B) F – F – F – F – F

(C) V – V – V – V – V

(D) V – V – V – V – F

(E) F – F – F – F – V

Resolução comentada dos exercícios de vestibulares sobre

função horária da elongação do MHS

 1-

a)  T=2s ---  f =1/T --- f= 1/2Hz  (percorre meia volta em cada 1s)

b)  w=2p/T --- w=2p/2 --- w=prad/s (varre um ângulo de prad em cada 1s)

c) A=4m

d) na posição (elongação) x=0 existem duas fases.

Como ela está se deslocando em 0, para a esquerda, teremos quej_o=p/2 rad                       

e) j = j_o + w.t  ---  j = p/2 + p.t

x = A.cosj  ---  x = 4.cos (p/2 + p.t)

f) 

t=0  ---  x=4cos(p/2 + p.t)  --- x=4cos (p/2 + p.0) --- x=4cos (p/2)  ---  x=4.0  ---  x=0

t=0,5s  --- x=4cos (p/2 + p.t)  --- x=4cos (p/2 + p.0,5) --- x=4cos (p)  ---  x=4.(-1)  ---  x= -4m

t=1s  --- x=4cos (p/2 + p.t)  --- x=4cos (p/2 + p.1) --- x=4cos (3p/2)  ---  x=4.0  ---  x=0

t=1,5s  --- x=4cos (p/2 + p.t) --- x=4cos (p/2 + p.1,5) --- x=4cos (2p)  ---  x=4.(+1)  ---  x= +4m

t=2s  --- x=4cos (p/2 + p.t) --- x=4cos (p/2 + p.2) --- x=4cos (5p/2)  ---  x=4.0  ---  x=0

t=4,5s  --- x=4cos (p/2 + p.t) --- x=4cos (p/2 + p.4,5) --- x=4cos (5p)  ---  x=4.(-1)  ---  x= -4m   

g)

02-

 a)     w=2p/T = 2pf   ---   2p = 2pf   ---   f = 1Hz
b) Para que DB e CD sejam pontos médios de AD e A’D, os ângulos estão indicados na figura abaixo

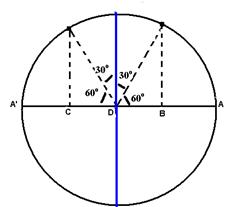
Para se deslocar de B a C o ponto P deve varrer um ângulo de 30^o + 30^o = 60^o = p/3 rad.

Dj= p/3rad               w=Dj/Dt   ---   2p =  p/3/Dt   ---   Dt = 1/6s 

w= 2prad/s

03-

A = 2m

T = 4s   ---   w=2p/T   ---   w=2p/4   ---   w = p/2 rad/s

 Quando x=0, W_o pode ser p/2 rad ou 3p/2. Observando o gráfico verificamos que é p/2, pois, quando t=1s  ---  A = -2m 

04- B

05-

T₁ = 1,5s   ---   f₁ = 1/1,5Hz                   T₂ = 6s   ---   f₂ = 1/6 Hz

F₁ / f₂ = 1/1,5 X1/6   ---   f₁/f₂ = 4

06-

a) A=4m      ----     w=2p/T      ----    4p = 2p/T     ----    T = 1/2s       ---    f=1/T       ---- f=2Hz

b) Como j_o=0, ele partiu do ponto A=+4m

Até chegar a 0, ele demorou um tempo t que é igual a um quarto do período T=0,5s   ---   t=0,5/4  ---   t = 0,125s

07-

:Cálculo do período T   ---   w=2p/T    ---   p/2 = 2p/T   ---   T = 4s

Para ir de +A até 0 ela andou durante um quarto do período, ou seja, durante t=4/4   ---   t=1s

08-

 O período é T=4s       -----    w=2p/T    ----    w= 2p/4       ----    w=p/2rad/s    e A=2m

Quando x=1m --- t=0     ---    x=Acos(wt+q)   ---     1=2cos(w.0 +q)    ----    1=2cosq    ----    cosq=1/2    ----    q=60^o=p/3

x=Acos(wt+q)   ----    x=2cos(p/2+p/3)

09-

a) V=DS/Dt    ----    V=26/13    ----    V=2cm/s

b) f₁=1/2Hz     ----    f₂=1/8Hz    ----    f₁/f₂=1/2X8/1    ----    f₁/f₂=4

10-

A=6m    ----    T=8s    ----    w=2p/T    ----    w=2p/8    ----    w=p/4rad/s

Quando x=0, a partícula está na posição angular inicial p/2 rad ou 3p/2 rad. Se o MCU for no sentido anti-horário, observando o gráfico verificamos que j_o=3p/2 rad.

X = A.cos(j_o+ wt)    ----    x=6.cos(3p/2 + p/4.t)

11- Função horária para o MHS   ---  x = a.cos(Φ_o+ω.t)  ---   ω =2π/T   ---  T (período)  ---  x₁=a.cos {(π/12) + (3π/4).t}  --- 

X₂=a.cos {(3π/4).t}  ---   como oscilam de modo idêntico a amplitude e o período são os mesmos para as duas partículas  --- 

Quando t=8/9s  ---  x₁=a.cos {(π/12) + (3π/4).(8/9)} ---  x₁=a.cos(3π/4)  ---  x₁=a.√2/2  ---  X₂=a.cos {(3π/4).(8/9)}  ---  x₂=a.cos(2π/3)  ---  x₂=a/2  ---  x₁ – x₂=a√2/2 – a/2  ---  √2≈1,41  ---  x₁ – x₂=0,21.a  ---  R- D

12- Função horária da elongação x de um MHS de amplitude x_o e pulsação w  ---  x=x_o.cos(wt + ф_o)  ---  veja o esquema abaixo  --- 

No caso em estudo, em t = 0 a partícula está no ponto de elongação máxima, portanto ф_o= 0  ---  quando t=1s  ---  x_o – a=x_ocos(w.1 + 0)  ---  cosw=(x_o – a)/x_o (I)  ---  quando t=2s  ---  x_o – (a + b)=x_ocos(w.2)  ---  x_o – a – b = x_o.cos2w  --- 

cos2w=(x_o –a – b)/x_o II)  ---  cos2w=2.(cos²w) – 1 (III)  ---  (I) e (III) em (II)  ---  2{(x_o– a)/x_o}² – 1 = (x_o – a – b)/x_o  --- 

2{(x_o² – 2.a.x_o + a²)/x_o²} = (x_o – a – b)/x_o + 1  ---  2x_o² – ax_o – bx_o = 2x_o² – 4ax_o + 2.a²  ---  (4ª – a – b).x_o = 2.a²  ---

 x_o=2.a²/(3.a – b)  ---  R- C

13-

  Num MHS a posição angular x varia com o tempo conforme a função  x = A.cos(φ_o + wt)   que é a função horária da elongação e onde  x é a elongação; w, a pulsação ou freqüência angular ou ainda velocidade angular;  A, a amplitude (elongação máxima) e φ_o a fase inicial  da partícula em MHS.

I. Correta  ---  compare x(t) = 4.cos[(π/2)t + π] com  x = A.cos(φ_o + wt) e verifique que a amplitude A=4m.

II. Correta  --- observe que W=π/2rad/s  ---  W=2π/T  ---  π/2=2π/T  ---  T=4s.

III. Correta  ---  f=1/T=1/4=0,25Hz.

R- E.

14-

  I. Falsa  ---  Elongação (x) – posição (localização) da partícula em MHS sobre o eixo x em relação à origem 0, ou seja,

mostra a que distância de 0 a partícula se encontra em determinado instante.

II. Falsa  ---  Amplitude (A) – em módulo é a elongação máxima do MHS e corresponde ao raio da circunferência do

 MCU (R=A).

III. Falsa  ---   O MHS não é qualquer movimento vibratório ---   nele o móvel se desloca sobre a mesma trajetória, indo

 e vindo, em relação a uma posição média de equilíbrio (ponto O, onde a resultante das forças que agem sobre ele é nula)

IV. Falsa  --- ela varia de acordo com a função  ---  a= -w².A.cos(φ_o + w.t)    função horária da aceleração do MHS

Observe que:

* quando x=0  ---   a=0

* quando x= +A  ---   a= -w²A  --- valor mínimo de a, pois φ=π rad e cos π= -1 --- a_mínimo= - w².A

* quando x= -A  ---   a= w²A    --- valor máximo de a, pois φ=2π  rad  e cos 2π= 1  --- a_máximo = w².A

V. Correta  ---  Período (T) – corresponde ao tempo que o MCU demora  para efetuar uma volta completa ou ao tempo que o MHS demora para efetuar um “vai e vem” completo sobre a reta x  ---  observe, pela definição, que ele independe da amplitude A do MHS.

R- E.