LANÇAMENTO HORIZONTAL

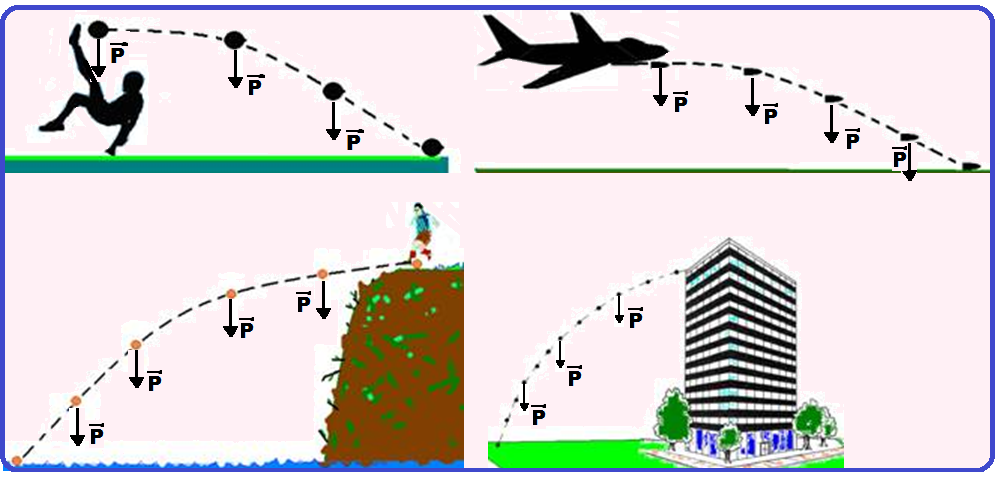
Todo corpo lançado horizontalmente com velocidade V_o de um ponto L, próximo da superfície da Terra, desprezados os atritos do ar, fica sujeito unicamente à força peso, (sempre de direção vertical e sentido para baixo) e que obedece à trajetória da figura abaixo, que é um arco de parábola.

 Colocando-se a origem do sistema de referência no ponto de lançamento, orienta-se, por exemplo, o eixo X para a direita e o eixo Y para baixo.

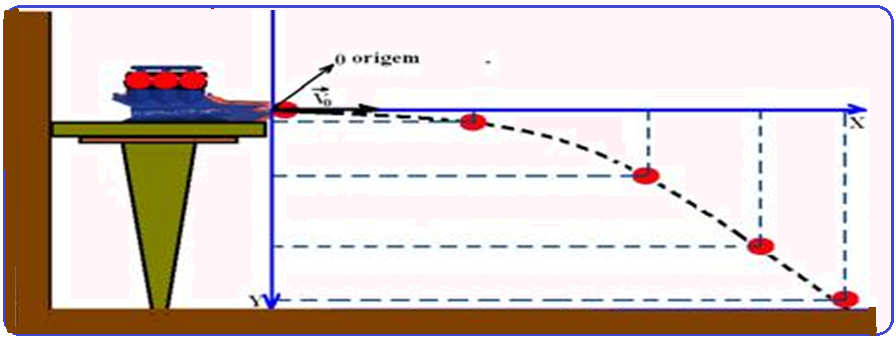
Decompõe-se o movimento em duas parcelas: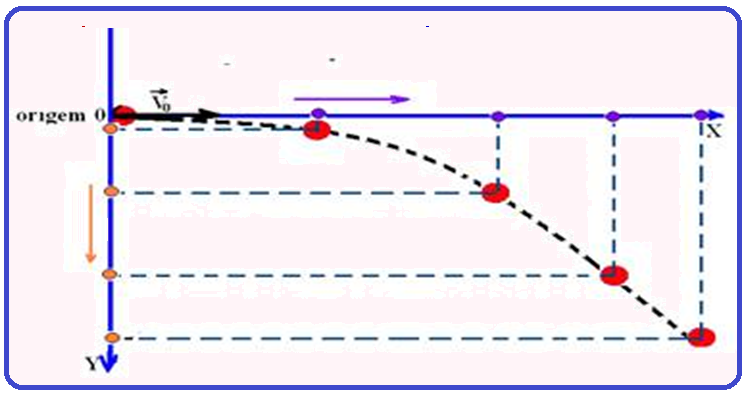

Segundo o eixo X   trata-se de um movimento horizontal uniforme com velocidade constante de intensidade V_o, que é a velocidade de lançamento  S = S_o + V.t  X= 0 + V_o.t   X=V_o.t

Segundo o eixo Y   trata-se de um movimento uniformemente variado com velocidade inicial V_o=0, ou seja, é uma queda livre com o corpo abandonado da origem, sujeito apenas à aceleração da gravidade, de intensidade g, direção vertical e sentido para baixo. 

Equações:

S = S_o + V_o.t + at²/2   Y= 0 + 0.t + gt²/2  Y=g.t²/2

V_y = V_oy + a.t   V_y= 0 + g.t   V_y=g.t

V²=V_o² + 2.a.ΔS   V_y² = V_oy² + 2.g.Δh   V_y² = 0² + 2.g.Δh  V_y² = 2.g.Δh

O que você deve saber (informações, dicas)

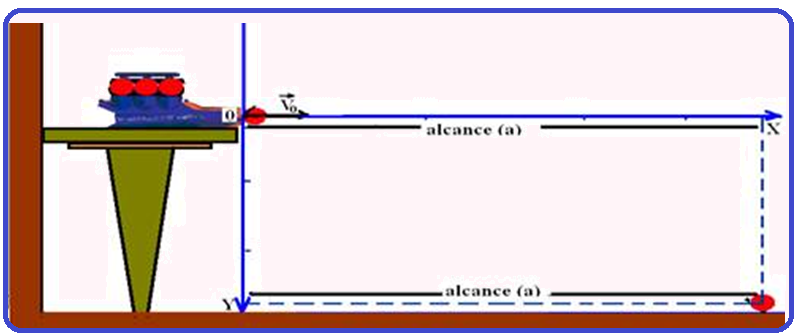
A máxima distância horizontal por ele atingida é chamada de alcance a (veja figura abaixo)

Em cada ponto da trajetória, a velocidade resultante  é dada por:

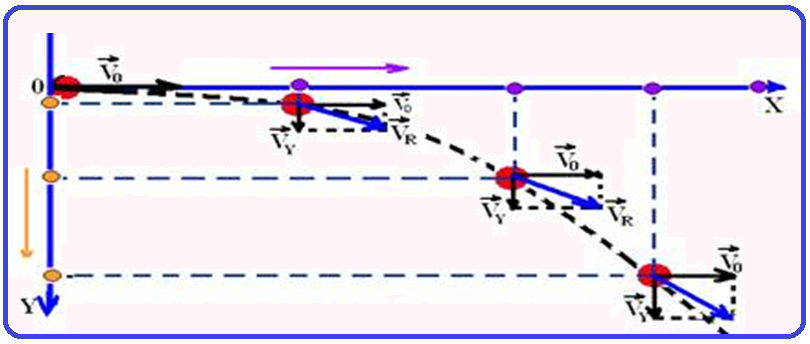
V_x=V_o=constante   V_y=g.t   V_r=V  V² = V_o² + V_y²

Observe na figura abaixo que, à medida que o abacaxi vai caindo, a flecha também, na mesma proporção, pois ambos caem sujeitos apenas à ação da aceleração da gravidade g.

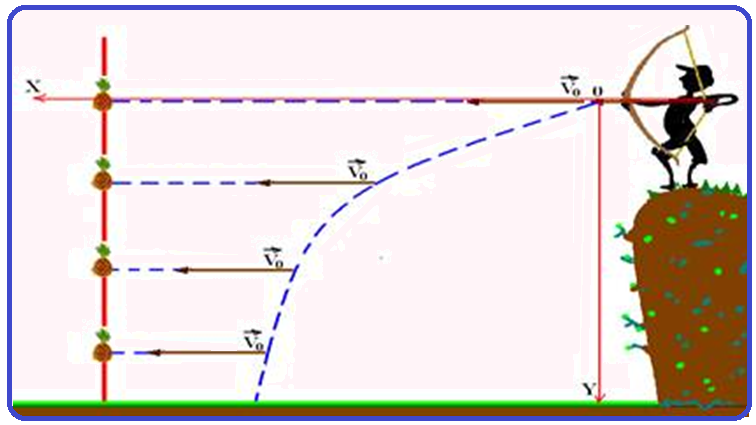
Então, se o garoto fizesse mira sobre o abacaxi e ele não caísse, o garoto erraria o alvo, pois a flecha, à medida que avança na horizontal com velocidade constante V_o, também está caindo com velocidade V_y.

Se o instante da queda do abacaxi e do lançamento da flecha for simultâneo, os dois possuirão em cada instante, as mesmas velocidades horizontais e verticais e, para se determinar o instante do encontro, você deve isolar o tempo na equação X=V_ot   t=X/V_o e substituí-lo na equação da altura Y=gt²/2.

Lançamento horizontal – Exercícios de vestibulares com resolução comentada

01-(Uff-RJ) Recentemente, o PAM (Programa Alimentar Mundial) efetuou lançamentos aéreos de 87 t de alimentos (sem uso de pára-quedas) na localidade de Luvemba, em Angola. Os produtos foram ensacados e amarrados sobre placas de madeira para resistirem ao impacto da queda.

www.angola.org.

A figura ilustra o instante em que um desses pacotes é abandonado do avião. Para um observador em repouso na Terra, o diagrama que melhor representa a trajetória do pacote depois de abandonado, é :

02-(CEFET-MG) Três pedras são atiradas horizontalmente, do alto de um edifício, tendo suas trajetórias representadas a seguir.

Admitindo-se a resistência do ar desprezível, é correto afirmar que, durante a queda, as pedras possuem

a) acelerações diferentes.  

b) tempos de queda diferentes.  

c) componentes horizontais das velocidades constantes.

d) componentes verticais das velocidades diferentes, a uma mesma altura.

03-(PUCCAMP-SP) Um avião, em võo horizontal, está bombardeando. De uma altura de 8km, um destróier parado.

A velocidade do avião é de 504km/h. De quanto tempo dispõe o destróier para mudar seu curso depois de uma bomba ter sido lançada?(g=10m/s²)

04-(CEFET-PR) Um menino posicionado na borda de uma piscina atira uma pedra horizontalmente de uma altura de 1m da superfície da água.

A pedra atinge a água a 3m da borda. Qual a velocidade, em m/s, com que o menino lançou a pedra? (g=10m/s²)

05-(PUC-RS) Uma bola rolou para fora de uma mesa de 80cm de altura e avançou horizontalmente, desde o instante em que abandonou a mesa até o instante em que atingiu o chão, 80cm. Considerando g = 10m/s², a velocidade da bola, ao abandonar a mesa, era de

06-(PUC-SP) O esquema apresenta uma correia que transporta minério, lançando-o no recipiente R.

A velocidade da correia é constante. Para que todo o minério caia dentro do recipiente, a velocidade v da correia, dada em m/s, deve satisfazer a desigualdade:

07-(PUC-SP)No exercício anterior,se for aumentado o desnível entre a correia transportadora e o recipiente R, o intervalo de variação  das velocidades-limite, para que todo minério caia em R:

a) permanece o mesmo, assim como os valores das velocidades-limite.     

b) permanece o mesmo, mas os valores das velocidades-limite aumentam.    

c) permanece o mesmo, mas os valores das velocidades-limite diminuem.    

d) aumenta    

e) diminui

08-(UNIFESP-SP) Uma pequena esfera maciça é lançada de uma altura de 0,6 m na direção horizontal, com velocidade inicial de 2,0 m/s.

Ao chegar ao chão, somente pela ação da gravidade, colide elasticamente com o piso e é lançada novamente para o alto. Considerando g = 10,0 m/s², o módulo da velocidade e o ângulo de lançamento do solo, em relação à direção horizontal, imediatamente após a colisão, são respectivamente dados por

a) 4,0 m/s e 30°.                     

b) 3,0 m/s e 30°.                   

c) 4,0 m/s e 60°.                    

d) 6,0 m/s e 45°.

e) 6,0 m/s e 60°.

09-(Ufg) Os quatro blocos, representados na figura com suas respectivas massas, são abandonados em um plano inclinado que não apresenta atrito e termina voltado para a direção horizontal.

Os blocos, ao deixarem a plataforma, descrevem trajetórias parabólicas em queda livre e alcançam o solo, formando, da esquerda para a direita, a seqüência:

a) m; 5m; 2m; 3m           

b) m; 2m; 3m; 5m           

c) 3m; 2m; 5m; m         

d) 3m; 5m; m; 2m        

e) 5m; 3m; 2m; m

10-(UNESP-SP) Para determinar a velocidade de um projétil, um perito, devidamente autorizado, toma um pequeno bloco de madeira, com massa de 480 g e o coloca em repouso na borda de um balcão horizontal de altura h = 1,25 m. A seguir, dispara o projétil, de massa 20 g, paralelamente ao balcão. O projétil penetra no bloco, lançando-o ao solo, a uma distância d = 5,0 m da borda do balcão, como ilustrado na figura.

Considerando g = 10 m/s² e desprezando os efeitos de atrito com o ar e o movimento de rotação do projétil e do bloco, calcule

a) a velocidade com que o bloco deixa o balcão.           b) a velocidade do projétil obtida pelo perito.

11-(UFB) Se, numa competição de tiro, um dos concorrentes mirar diretamente o centro do alvo. Ele o atingirá?

Justifique.

12-(FEI-SP) Em uma competição de tiro, o atirador posiciona seu rifle na horizontal e faz mira

exatamente no centro do alvo. Se a distância entre o alvo e a saída do cano é de 30m, a velocidade de disparo do rifle é 600m/s, qual a distância do centro do alvo que o projétil atingirá? Considere g=10m/s² e despreze a resistência do ar)

a) 0,25cm                  b) 0,5cm                  c) 0,75cm                  d) 1,00cm                 e) 1,25cm

13-(ITA-SP) Uma bola é lançada horizontalmente do alto de um edifício, tocando o solo decorrido

aproximadamente 2s. Sendo 2,5m a altura de cada andar, o número de andares do edifício é:

a) 5     

b) 6     

c) 7     

d) 8     

e) indeterminado, pois a velocidade horizontal de arremesso da bola não foi fornecida

14-(FUVEST-SP) Um motociclista de MotoCross, move-se com velocidade V=10m/s, sobre uma superfície plana, até atingir uma rampa (em A), inclinada de 45^o com a horizontal, como indicado na figura.

A trajetória do motociclista deverá atingir novamente a rampa a uma distância horizontal D (D=H), do ponto A, aproximadamente igual a: (g=10m/s²)

15-(PUC-RJ) Em um campeonato recente de vôo de precisão, os pilotos de avião deveriam "atirar" um saco de areia dentro de um alvo localizado no solo.

Supondo que o avião voe horizontalmente a 500 m de altitude com uma velocidade de 144 km/h e que o saco é deixado cair do avião, ou seja, no instante do "tiro" a componente vertical do vetor velocidade é zero, podemos afirmar que: Considere a aceleração da gravidade g=10m/s² e despreze a resistência do ar)

a) o saco deve ser lançado quando o avião se encontra a 100 m do alvo;

b) o saco deve ser lançado quando o avião se encontra a 200 m do alvo;

c) o saco deve ser lançado quando o avião se encontra a 300 m do alvo;

d) o saco deve ser lançado quando o avião se encontra a 400 m do alvo;

e) o saco deve ser lançado quando o avião se encontra a 500 m do alvo.

16-(PUC-SP) Em um experimento escolar, um aluno deseja saber o valor da velocidade com que uma esfera é lançada horizontalmente, a partir de uma mesa. Para isso, mediu a altura da mesa e o alcance horizontal atingido pela esfera, encontrando os valores mostrados na figura.

A partir dessas informações e desprezando as influências do ar, o aluno concluiu corretamente que a velocidade de lançamento da esfera, em m/s, era de

17-(PUC-RJ) Um pacote do correio é deixado cair de um avião que voa horizontalmente com velocidade constante. Podemos afirmar que (desprezando a resistência do ar):

a) um observador no avião e um observador em repouso no solo vêem apenas o movimento vertical do objeto.

b) um observador no avião e um observador em repouso no solo vêem apenas o movimento horizontal do objeto.

c) um observador no solo vê apenas um movimento vertical do objeto, enquanto um observador no avião vê o movimento horizontal e vertical.

d) um observador no solo vê apenas um movimento horizontal do objeto, enquanto um observador no avião vê apenas um movimento vertical.

e) um observador no solo vê um movimento horizontal e vertical do objeto, enquanto um observador no avião vê apenas um movimento vertical.

18-(Uerj-RJ) Um avião, em trajetória retilínea paralela à superfície horizontal do solo, sobrevoa uma região com velocidade constante igual a 360 km/h.

Três pequenas caixas são largadas, com velocidade inicial nula, de um compartimento na base do avião, uma a uma, a intervalos regulares iguais a 1 segundo.

Desprezando-se os efeitos do ar no movimento de queda das caixas, determine as distâncias entre os respectivos pontos de impacto das caixas no solo.

19-(UERJ-RJ)  Um avião, em trajetória retilínea paralela à superfície horizontal do solo, sobrevoa uma região com velocidade

constante igual a 360 km/h.

Três pequenas caixas são largadas, com velocidade inicial nula, de um compartimento na base do avião, uma a uma, a intervalos regulares iguais a 1 segundo.

Desprezando-se os efeitos do ar no movimento de queda das caixas, determine as distâncias entre os respectivos pontos de impacto das caixas no solo.

20-(UFMS-MS) Uma bola de bilhar de massa m é lançada horizontalmente com velocidade V_o da borda de uma mesa que está a uma altura H do solo também horizontal. A aceleração da gravidade no local é g e é uniforme, veja a figura.

Considerando que o ar exerce uma força F_a de arrasto na bola dada pelo formalismo vetorial F_a = -bV, onde b é uma constante de proporcionalidade, e V é o vetor velocidade da bola vista de um referencial inercial, assinale a(s) proposição(ões) correta(s).

01) A trajetória da bola não será uma parábola. 

02) A componente da velocidade da bola na direção horizontal permanece constante durante a queda. 

04) A força de arrasto é sempre vertical para cima. 

08) O alcance A na horizontal é igual a V_o(2H/g)1/2. 

16) A intensidade do vetor aceleração da bola vai diminuindo durante a queda. 

21-(UFLA-MG) Uma plataforma horizontal, posicionada a uma altura h em relação ao solo, contém uma mola de constante elástica k que sofreu uma compressão de uma distância x e encostado a ela uma bola de massa m em repouso, conforme figura abaixo.

Disparando-se a mola, a bola é projetada ao longo da plataforma e atinge o solo na posição P. Considerando g a aceleração da gravidade e todo o sistema isento de atrito, é CORRETO afirmar que a velocidade da bola ao atingir o solo é dada pela expressão:

22-(FUVEST-SP) Uma menina, segurando uma bola de tênis, corre com velocidade constante, de

módulo igual a 10,8 km/h, em trajetória retilínea, numa quadra plana e horizontal. Num certo instante, a menina, com o braço esticado horizontalmente ao lado do corpo, sem alterar o seu estado de movimento, solta a bola, que leva 0,5 s para atingir o solo. As distâncias s­_m e s_b percorridas, respectivamente, pela menina e pela bola, na direção horizontal, entre o instante em que a menina soltou a

bola (t = 0 s) e o instante t = 0,5 s, valem:

a) s_m = 1,25 m e s_b = 0 m.                            

b) s_m = 1,25 m e s _b = 1,50 m.                               

c) s_m = 1,50 m e s _b = 0 m.

d) s_m = 1,50 m e s _b = 1,25 m.                       

e) s_m = 1,50 m e s _b = 1,50 m.

Utilize as informações a seguir para responder às questões de números 23 e 24

Três bolas − X, Y e Z − são lançadas da borda de uma mesa, com velocidades iniciais paralelas ao solo e mesma direção e sentido.

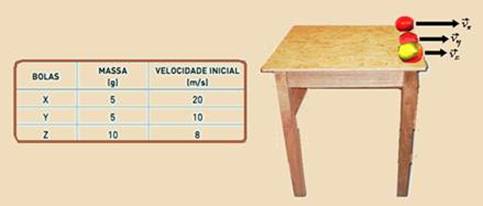
A tabela acima mostra as magnitudes das massas e das velocidades iniciais das bolas.

23-(UERJ-RJ)

As relações entre os respectivos tempos de queda  t_x, t_y e t_z das bolas x, y e z com relação à borda da mesa, estão apresentadas em:

a) t_x  <  t_y  < t_z                         

b) t_y  < t_z < t_x                                   

c) t_z < t_y <  t_x                                    

d) t_x =  t_y  =  t_z

24-(UERJ-RJ)

As relações entre os respectivos alcances horizontais A_x, A_y e A_z das bolas x, y e z, com relação à borda da mesa , estão apresentadas em:

(A) A_x < A_y < A_z                           

(B) A_y = A_yx = A_z                                         

(C) A_z < A_y < A_x                             

(D) A_y < A_z < A_x

25-(PUC-GO)

Um morteiro, fazendo um ângulo de 30º com a horizontal, dispara um projétil com uma velocidade de

30 m/s num terreno plano. Após transcorrido 1,0 segundo do disparo, o projétil estará a uma determinada altura em relação ao plano do terreno. Calcule-a e marque a alternativa que contenha a resposta correta:

Dados: sen(30º) = 0,5; cos(30º) ≈ 0,9; aceleração de gravidade = 10 m/s²

A (     ) 10 metros               

B (     ) 22 metros                          

C (     ) 30 metros                        

D (     ) 15 metros

Resolução comentada dos exercícios sobre  LANÇAMENTO HORIZONTAL

 01- R- E – veja teoria

02- R- C – em todo lançamento horizontal, a componente V_0x=V_o=V_x=constante.

03- O tempo que o destróier dispõe é o tempo que a bomba demora para cair e percorrer a distância vertical de 8km  ---  Y=8.000m  ---  Y=gt²/2  ---  8.000=10t²/2  ---  t=√1.600  ---  t=40s

04- Tempo que a pedra demora para atingir a superfície da água, ou seja, percorrer verticalmente Y=1m  ---  Y=gt²/2  --- 

1=5t²  ---  t=√0,2s  ---  em t=√0,2=0,45s ela percorre na horizontal X=3m  ---  X=V_o.t  ---  3=V_o.0,45  ---  V_o=6,7m/s

05- Y=gt²/2  ---  0,8=5t²  ---  t=0,4s  ---  X=V_ot  ---  0,8=V_o.0,4  ---  V_o=2,0m/s  ---  R- D

06- tempo de queda  ---  Y=gt2/2  ---  5=5t2  ---  t=1s (é sempre o mesmo, depende apenas da altura vertical)  ---  velocidade mínima (limite inferior de R)  ---  X=V.t  ---  1=V.1  ---  V=1ms  ---  limite posterior (velocidade máxima)  ---  X=V’.t  ---  4=V’.1  ---  V’=4ms  ---  R- D

07- O tempo t de queda aumenta, pois a altura aumenta  --- como X1=1m e X2=4m permanecem constantes, V1 e V2 devem diminuir para manter a igualdade X=V.t  ---  R- E

08- Velocidade vertical com que ela chega ao solo  ---  V_y²=2.g.h=2.10.0,6  ---  V_y²=12  ---  velocidade horizontal com que ela chega ao solo  ---  é a mesma de lançamento  ---  V_x=2m/s  ---  velocidade resultante V com que ela chega ao solo

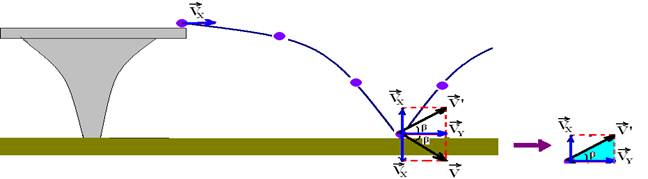
A intensidade da velocidade resultante com que ela chega ao solo vale V²=V_y² + V_X²=12 + 4  ---  V=√16  ---  V=4m/s  ---  mas, como o choque é perfeitamente elástico, ela retorna com velocidade resultante de mesma intensidade, ou seja, V’=V=4m/s  ---  no triângulo hachurado da figura acima  ---  senβ=V_y/V’=√12/4=2√3/4=√3/2  ---  β=60^o  ---  R- C

09- A ordem de chegada ao solo, independente das massas , depende da altura de queda  ---  menor altura, menos tempo de queda  ---  R- C

10- a) Lançamento horizontal do sistema (bloco + projétil) que independe da massa  ---  tempo que demora para chegar ao solo na vertical percorrendo a altura Y=1,25m  ---  Y=gt²/2  ---  1,25=5t²  ---  t=0,5s  ---  nesse tempo ele percorre na horizontal X=5m com velocidade V_o  ---  X=V_ot  ---  5=V_o.0,5  ---  V_o=10m/s

b) choque inelástico  ---  movem-se juntos após o mesmo  ---  princípio da conservação da

quantidade de movimento  -- quantidade de movimento  --Q_antes=m_pV_p + m_bV_b=0,02.V_p + 0,480.0  ---  Q_antes=0,02.V_p  ---  Q_depois=(m_p + m_b).V=(0,02 + 0,480).10  ---  Q_depois=5kg.m/s  ---  Q_antes=Q_depois  ---  0.02V_p=5  --- V_p=250m/s

11- Não, pois enquanto o alvo permanece imóvel, o projétil, durante todo seu movimento estará caindo, sujeito à aceleração da gravidade e chegará ao alvo numa posição abaixo daquela em que ele mirou.

12- Como o alvo permanece imóvel, o projétil, durante todo seu movimento estará caindo, sujeito à aceleração da gravidade e chegará ao alvo numa posição abaixo daquela em que ele mirou  ---  tempo que o projétil demora para percorrer a distância horizontal de X=30m com V_o=600m/s (constante)  ---  X=V_ot  ---  30=600t  ---  t=0,05s  ---  nesse tempo ele desce uma altura Y de  ---  Y=gt²2=5.(0,05)²  ---  Y=5.(0,0025)=0,0125m=1,25cm  ---  R- E

13- Distância vertical (altura do prédio) percorrida em 2s  ---  Y=gt²/2=5.4=20m  ---  número de andares  ---  n=altura do prédio/altura de cada andar=20/2,5  ---  n=8 andares  ---  R- D

14- tg45^o=D/H  ---  1=D/H  ---  D=H  --- na vertical  ---   H=gt²/2  ---  H=5t²  ---  na horizontal  ---  X=Vt  ---  D=H=10t  ---

10t=5t²  ---  t=2s  ---  D=H=10.2=20m  ---  R- A

15- V_o=144km/h=144/3,6  ---  V_o=40m/s  --- tempo que o saco demora para chegar ao solo na direção vertical  ---  Y=gt²/2  ---  500=5t²  ---  t=10s  ---  nesse instante o alvo deve estar a uma distância horizontal de X=V_ot=40.10  ---  X=400m  ---  R- D

16- tempo que demora para percorrer Y=0,80m na vertical  ---  Y=gt²/2  ---  0,80=5t²  ---  t=0,4s  ---  nesse tempo ele percorre na horizontal X=2,8m com velocidade V_o  ---  X=V_ot  ---  2,8=V_o.0,4  ---  V_o=7,0m/s  ---  R- D

17- R- E  ---  (veja teoria)

18- V_o=360/3,6=100m/s  ---  t=0  ---  X_o=0  ---  t=1s  ---  X₁=V_ot=100.1=100m  ---  t=2s  ---  X=V_ot=100.2=200m  ---  a distância entre os pontos de impacto será de 100 m.

19- Por inércia as três caixas continuaram em movimento com a mesma velocidade horizontal do avião de 360 km/h  ---  desta forma os impactos no solo ocorrerão sobre a mesma linha reta, separadas pela distância percorrida pelo avião durante aquele 1 s entre os lançamentos das caixas  ---   velocidade de 360 km/h corresponde a 100 m/s e desta forma a distância entre os pontos de impacto será de 100 m.

20- (01) Correta  ---  a trajetória somente é parabólica quando a resistência do ar é nula.

(02) Errada  ---  a componente horizontal da velocidade só se mantém constante se a resistência do ar é nula.

(04) Errada  ---  a força de arrasto tem sentido oposto ao da velocidade em cada ponto, sempre tangente à trajetória.

(08) Errada  ---  mesma justificativa de (01) e (02).

(16) Correta  ---   componente horizontal da força de resistência do ar faz diminuir a componente horizontal da velocidade, que tende para zero, enquanto a componente vertical da resistência do ar tende a equilibrar o peso. Assim o movimento tende a se tornar retilíneo e uniforme, na direção vertical. 

R- (01+ 16) = 17

21- Com a mola comprimida de X a energia potencial elástica armazenada na mesma vale  ---  E_p=kX²/2  ---ao deixar o contato com a mola toda a energia potencial elástica é transformada em energia cinética de valor E_c=mV²/2  ---  considerando o sistema conservativo (sem atrito) essas energias se igualam  ---  KX²/2 = mV²/2  ---  V²=KX²/m  ---  utilizando agora a conservação da energia mecânica  ---  no topo do plano  ---  E_MA=mV²/2 + mgh  --- no solo chega com velocidade V’  ---  E_MB = mV’²/2 + mg.0  ---  E_MA = E_MB  ---  mV²/2 + mgh=mV^’2/2  ---   V’=√(2gh + KX²/m)  ---  R- A

22-Quando a menina abandona a bola, a menina continua em movimento retilíneo e a bola executa um lançamento horizontal  ---  as velocidades horizontais da bola e da menina são as mesmas e valem V_m=V_s=10,8/3,6=3m/s  ---  então, a distância horizontal percorrida pela menina e pela bola é a mesma  ---  S_b=S_m=V.Δt=3.0,5  ---  S_b=S_m=1,5m  ---  R- E

Utilize as informações a seguir para responder às questões de números 23 e 24

Três bolas − X, Y e Z − são lançadas da borda de uma mesa, com velocidades iniciais paralelas ao solo e mesma direção e sentido.

A tabela acima mostra as magnitudes das massas e das velocidades iniciais das bolas.

23-

 Trata-se de um lançamento horizontal que segundo o eixo y é uma queda livre com V_oy=0 e sob aceleração da gravidade g  ---  h=V_oyt + gt²/2=0 + gt²/2  ---  h=gt²/2  ---  observe que, como h e g são os mesmos, o tempo de queda também será o mesmo  ---  R- D

24-

  Em todo lançamento horizontal a velocidade horizontal é constante, igual à velocidade de lançamento, independente da massa do corpo  ---  assim, a esfera que é lançada com maior velocidade consegue o maior alcance  ---  R- C

25-

Como o exercício pede a altura você deve utilizar apenas o movimento parcial na direção vertical (eixo Y)

A projeção da aceleração da gravidade () é o próprio .  Assim, na direção vertical tem-se um movimento uniformemente variado (MUV), ou seja, um lançamento vertical para cima, com aceleração igual à aceleração da gravidade  e velocidade inicial de lançamento  Voy, tal que Voy=Vo.senα, onde α é o ângulo de lançamento..   

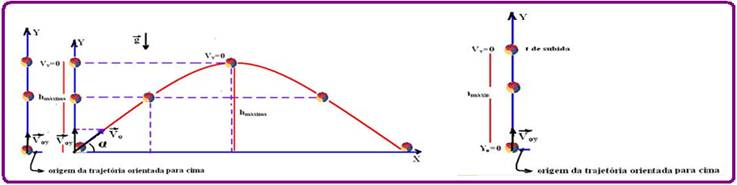
V_oy=V_o.senα - componente vertical de V_o  ---  Y - altura num instante qualquer t  ---  Y_o  ---  altura inicial  ---  g - aceleração da gravidade  ---  orientando o eixo Y para cima tem-se um lançamento vertical de equações  ---  S=Y  ---  S_o=Y_o=0  ---  V_o=V_oy=V_o.senα  ---  a=-g  ---  equação da posição (dos espaços) ou da altura Y  ---  S=S_o + V_o.t + a.t²/2  ---  Y=Y_o + V_oy.t – gt²/2  ---  Y=0 + V_oy.t – gt²/2  ---  Y= V_oy.t – gt²/2, com V_oy=Vo.senα. 

V_oy=V_o.senθ=30.0,5  ---  V_oy=15m/s  ---  Y=15.1 – 10.1²/2  ---  Y=10m  ---  R- A