Notação Científica, Ordem de Grandeza e Algarismos Significativos
Conceito de Notação Científica
A Notação Científicas serve para facilitar a representação de números muito pequenos ou muito grandes, expressando-os através de uma forma mais fácil de se trabalhar, diminuindo seu tamanho através de uma multiplicação por uma potência de 10 (notação em forma exponencial).
Vantagens em se escrever um número na notação exponencial (notação científica) :
Podem fazer com que
números muito grandes ou muito pequenos possam
ser escritos
de forma mais abreviada.
Tornam os cálculos muito mais rápidos e fáceis.
Exemplos numéricos:
Quantidade
de espécies
de formigas
catalogadas
mais de 10.000
em
notação científica 104.
Em áreas referentes a Química e Física costuma-se muito grandes ou muito pequenos, como por exemplo:
A
massa
do próton é
cerca de
0,00000000000000000000000001673
kg
em
notação científica 1,673.10-27
kg
.
A
distância
média de
Netuno
ao Sol
é de 4.500.000.000
km
em
notação científica 5,5.109
km
.
Representação matemática de um número sob a forma de notação científica
Para que um determinado número N seja escrito sob forma de notação científica ele deve obedecer ao seguinte modelo que indica a representação de um número através de uma multiplicação por uma potência de 10:
Como escrever números sob forma de Notação Científica
Exemplos:
Você coloca
o número,
por exemplo, (19450)
e,
em seguida
obtém a mantissa colocando
a vírgula
depois do primeiro algarismo significativo desse
número (1,9450).
Se você deslocar a vírgula 4 casas para a esquerda, a ordem de grandeza b terá o mesmo número de posições deslocadas (4), será positiva e a notação científica do número 19450 será 1,9450.104.
Você coloca
o número, por
exemplo, (-
0,00194) e,
em seguida
obtém a mantissa colocando
a vírgula
depois do primeiro algarismo significativo desse número (- 1,9450).
Como a vírgula foi deslocada 3 casas para a direita, a ordem de grandeza b terá o mesmo número de posições deslocadas (3), será negativa e a notação científica do número - 0,0019450 será - 1,9450.10-3 .
A ordem
de grandeza do número 1 escrito sob forma de notação cientifica é
0
1 = 1.100,
pois a vírgula
não sofru deslocamento.
Lembre-se de que o módulo da mantissa a deve ser igual ou maior que 1 e menor que 10 e que a ordem de grandeza b deve ser um número inteiro.
Assim, a notação científica do número 24,2,10-4 não está escrito sob notação científica correta, pois a mantissa é maior que 10 e o número 3,3.107,5 também não está escrito sob notação científica correta, pois a ordem de grandeza 7,5 não é um número inteiro.
Alguns números escritos sob forma de notação científica:
a) 620.000 = 6,2.105 b) 12.500 = 1,25,104 c) - 600.000.00 0 = - 6,0.108
d) 5,55 = 5,55.10o e) - 60 = - 6,0.101
Ordem de Grandeza
Ordem de grandeza (OG) é uma estimativa do valor de algo em termos de potência de 10.
Trata-se de uma "noção" do valor daquela grandeza e, assim é a potência de 10 mais próxima do valor que se deseja encontrar.
Antes de determinar a ordem de grandeza (OG) de um número X você precisa transformá-lo em notação científica na forma X = a.10n.
Como a mantissa deve desaparecer você deve arredondá-la para a potência de 10 mais próxima.
Assim,
a ordem
de grandeza do número 24 é 101
já que 24 está mais próximo de 101
= 10 do que 102
= 100.
A
ordem
de grandeza do número 78 é 102
já que 78 está mais próximo de 102
= 100 do que 103
= 1000.
Então,
a mantissa
(parte
numérica do número que precede a potência de 10)
deve ser arredondada de acordo com a potência de 10 média que deve
estar está compreendida entre o
ponto
médio do
intervalo
[1 (10o)
e 10 (101)],
ou seja, entre 10(0
+ 1)/2
= 101/2
=
3,1622.
Se
a mantissa
a
(parte numérica do número que precede a potência de 10) for menor
que
3,1622, esse número deve ser aproximado para 1º = 1, ficando 1.10n
com (n = 0,1,2,3,...).
Se
a
mantissa (parte
numérica do número que precede a potência de 10) for
maior que
3,1622, esse número deve ser aproximado para 101
= 10, ficando 10.10n
= 10(n
)
com (n = 0,1,2,3,...).
Exemplos
01-
O número de habitantes no Brasil é aproximadamente de 205.000.000. A OG desse número é
2,05.108
2,05 < 3,126
arredondado para 1
OG = 1.108
OG
= 108.
02-
O mol é uma quantidade bastante usada em Química e Física e vale, aproximadamente, 6,02 x1023.
A
OG
desse
número
é
6,02 > 3,126
arredondado para 10
10.1023
= 1024
OG
= 1024.
03-
Qual é a ordem de grandeza da altura de uma pessoa adulta normal? Resposta: Está compreendida entre 1m e 2m e terá OG = (1 ou 2).100.
04-
Ordem
de grandeza da quantidade
de água nos oceanos da Terra
1.350.000.
000.000.000.000.000 L
1,35.1021
1.1021
OG = 1021
L.
05-
Ordem
de grandeza da massa
de um átomo
0,000.000.000.000.000.000.000.000.1992
kg
1,992.10-27
kg
OG = 10-27
kg.
Algarismos significativos
Algarismos significativos e incerteza
Excetuando-se
quando todos
os números envolvidos são inteiros,
como por exemplo, o número
de pessoas numa sala de
aula
(45), é
impossível
determinar o valor exato de
determinada quantidade, como por exemplo, o número
de pessoas gordas e magras, greandes e pequenas que enchem totalmente
uma perua. 
Então, é importante indicar a margem de erro numa medição indicando os algarismos significativos, sendo estes os dígitos com significado numa quantidade ou medição.
Qualquer medida que você fizer experimentalmente fornece informação limitada e nenhum processo de medição é totalmente confiável.
Assim, ao efetuar qualquer medida é necessário deixar indicado o ponto até o qual se pode confiar no resultado obtido.
Veja,
no exemplo
a seguir como você determinar as incertezas de uma medição,
medindo
o comprimento
de uma caneta usando uma régua cuja menor divisão de escala é o
milímetro. 
Observe na figura que o comprimento da caneta está aproximadamente entre 14,6 cm e 14,7 cm
Vamos supor que você afirme essa caneta possua possua 14,63 cm.
Assim,você
pode afirmar, com
certeza, que o comprimento da caneta está entre 14,6 cm e 14,7 cm e
que, na
medida 14,63 cm o algarismo 3 é incerto, que foi estimado por
você.
Algarismos
significativos são todos os que expressam o valor medido até o
primeiro incerto,
inclusive
este último. Então
o número
de nosso exemplo (14,63) possui 4 algarismos significativos.
Regras para algarismos significativos
Zeros
consecutivos à esquerda não são algarismos significativos
significativos. Exemplos:
0,
0000012 (tem
2 algarismos significativos).
0,0004567
(tem
4 algarismos significativos).
00,000005
(tem
1 algarismo significativo).
Zeros
à direita são considerados e não podem ser desprezados no caso de
medições.
Exemplos:
3,24000
(tem
6 algarismos significativos).
0,0000500
(tem
três algarismos significativos).
Se
a incerteza
não
for especificada,
é usual que ela seja subentendida
como uma
unidade
decimal
da casa correspondente ao último algarismo. Exemplo:
47,07 m equivale a 47,07 ± 0,01 m e,
se
a incerteza
é conhecida, ela deve ser especificada como, por
exemplo, 52,35
± 0,02 km.
Observe
que os
resultados
de todas
as medidas devem
sempre ser expressas com a mesma quantidade de casas decimais que
suas respectivas incertezas. Assim,
você não
pode escrever 35,7 ±
0,01.
Quando
um número
é expresso em termos de ordem de grandeza,
a potência
de dez
deve
ser
desprezada no cálculo dos números de algarismos significativos.
Exemplo
os
dois
membros da igualdade 3675,8 = 3,6758.103
possuem
5
algarismos significativos. A
potência
de dez não influi,
ela
apenas
desloca a vírgula, o
que não
afeta a quantidade de algarismos significativos.
A posição da vírgula não influi no número de algarismos significativos.
Assim, o comprimento de 0,00450 m possui três algarismos significativos e pode ter a posição da vírgula alterado de várias formas usando uma potência de dez adequada, e sem alterar o seu número de algarismos significativos.
0,00450 m = 4,50 .10-3 m = 0,0450 dm = 0,450 cm = 4,50 mm
Observe que o número de algarismos significativos é sempre três, independentemente da forma que o número foi escrito e da posição de sua vírgula.
Observe também que o valor da medida é sempre a mesma, já que: 0,00450 m = 0,0450 dm = 0,450 cm = 4,50 mm
O que você deve saber, informações e dicas
Conhecer
o conceito
de Notação Científica
Saber
escrever
números sob
forma de notação
científica e, posteriormente
sob forma
de ordem de grandeza.
Conhecer
os conceitos
de algarismos significativos.
Saber
as regras
para se escrever algarismos significativos
Exercícios de vestibulares com resoluções comentadas sobre
Notação Científica, Ordem de Grandeza e Algarismos Significativos
01-(Unioeste-PR) Com base na teoria dos algarismos significativos, com a utilização da régua
centimetrada (figura), é correto afirmar que o comprimento da barra acima da régua é:
a) 7,30 cm. b) 7,35 cm. c) 7,3 cm d) 73,0 mm. e) 7, 40 cm.
02-(Cefet-PE) A medição do comprimento de um lápis foi realizada por um aluno usando uma régua graduada em mm. Das alternativas apresentadas, aquela que expressa corretamente a medida obtida é:
03-(PUC-SP) O número de algarismo significativos de 0,00000000008065 cm é:
a) 3 b) 4 c) 11 d) 14 e) 15
04- (UNIFESP-SP) Na medida de temperatura de uma pessoa por meio de um termômetro clínico, observou-se que o nível de mercúrio estacionou na região entre 38 ºC e 39 ºC da escala, como está ilustrado na figura.
Após
a leitura
da temperatura, o
médico necessita
do valor
transformado para
uma nova
escala, definida
por tx =
2tc/3
e
em unidades
ºX, onde
tc é
a temperatura na escala Celsius. 
Lembrando de seus conhecimentos sobre algarismos significativos, ele conclui que o valor mais apropriado para a temperatura tx é:
a) 25,7 ºX. b) 25,7667 ºX. c) 25,766 ºX. d) 25,77 ºX. e) 26 ºX.
05-(FUVEST-SP)
Qual
é a ordem
de grandeza do número de voltas dadas pela roda de um automóvel ao
percorrer uma estrada de 200km?
a) 102
b) 103
c) 105
d) 107
e) 109
06-(CEFET-MG) Nos trabalhos científicos, números muito grandes ou próximos de zero, são escritos em notação científica, que consiste em um número x, tal que 1 < x < 10 multiplicado por uma potência de base 10.
Assim sendo, 0,00000045 deve ser escrito da seguinte forma:
a) 0,45.10-7 b) 4,5.10-7 c) 45.10-6 d) 4,5.10-8 e) 4,5.10-5
07-(UFRGS) Considere que o corpo de uma determina pessoa contém 5,5 litros de sangue e 5 milhões
de
glóbulos vermelhos por milímetro cúbico de sangue.
Com
base nesses
dados, é
correto
afirmar que o número de glóbulos vermelhos no corpo dessa pessoa
é:
A) 2,75.1019
B)
5,5.1010
C)
5.1011
D)
5,5.1012
E)
2,75.1013
08-(UFRGS)
Durante
os jogos
Pan-Americanos de Santo Domingo,
os brasileiros perderam
o ouro
para
os cubanos por 37
centésimos de segundo nas provas de remo. Dentre as alternativas, o
valor mais próximo
desse tempo, medido
em horas,
é:
a)
1,03.10-4
b)
1,3
.10-4
c)
1,03.10-3
d)
1,3
.10-3
e)
1,03.10-2 
09-(UFRGS) Dadas as informações:
I. Velocidade da luz no vácuo: 300000000 m/s
II. Distância da Terra ao Sol: 149000000 km
III. Raio do átomo de hidrogênio: 0,000000005 cm
IV. Idade das rochas mais antigas: 100000000000000000 s
Escreva cada um desses númerossob forma de notação científica.
10-(UFRGS)
Em
texto
publicado na Folha de S. Paulo, o físico Marcelo
Gleiser escreveu
que “átomos
têm diâmetros de aproximadamente um décimo de bilionésimo de
metro”. Escrito
em potência
de 10,
um décimo de bilionésimo é
(A) 10-8
(B) 10-9
(C) 10-10
(D) 10-11
(E) 10-12
11-(UFRRJ)
Uma
determinada
marca de automóvel possui
um tanque
de gasolina
com volume
igual a
54
litros.
O
manual de apresentação do veiculo informa que ele pode
percorrer 12 km com 1 litro. Supondo
que a informações do fabricante sejam verdadeiras, a ordem
de grandeza da distancia, medida em metros, que o automóvel pode
percorrer, após ter o tanque completamente cheio, sem precisar
reabastecer,
é de:
a)
100
b)
102
c)
103
d)
105
e)
106
12-(UFCE-CE)
A
escala
de volume dos organismos vivos varia, entre
uma bactéria
e uma baleia,
de 21
ordens de
grandeza. Se
o volume
de uma baleia é 102
m3,
o volume
de
uma bactéria
é:
a)
1011
m3
b) 10-19 m3
c) 101/21 m3
d) 1019 m3
e) 10-11 m3
13- (UFPE-PE) Em um hotel com 200 apartamentos o consumo médio de água por apartamento é de
100
litros por dia. Qual
a ordem
de grandeza do
volume
que deve
ter o reservatório do hotel,
em metros
cúbicos,
para abastecer
todos os apartamentos durante um dia?
a) 101
b) 102
c) 103
d) 104
e) 105
14-(UFF-RJ)
A
luz
proveniente do Sol demora, aproximadamente,
8
minutos para chegar à Terra.
A ordem de grandeza da distancia entre estes dois astros celestes, em km, é:
a) 103
b) 106
c) 108
d) 1010
e) 1023
15-(CEFET-SP) Uma pessoa percebeu que, durante 10 anos, para acender o seu aquecedor, consumiu
uma
caixa de palitos de fósforo a cada mês. Cada caixa apresenta,
em média, 40
palitos. 
A ordem de grandeza do número de palitos consumidos ao final dos 10 anos é:
a) 10
b) 102
c) 103
d) 104
e) 105
16-(UFRRJ)
Uma
determinada
marca de automóvel possui
um tanque
de gasolina
com volume
igual a
54
litros.
O
manual de apresentação do veiculo informa que ele pode
percorrer 12 km com 1 litro. Supondo
que a informações do fabricante sejam verdadeiras, a ordem
de grandeza da distancia, medida em metros, que o automóvel pode
percorrer, após ter o tanque completamente cheio, sem precisar
reabastecer,
é de:
a)
100
b)
102
c)
103
d)
105
e)
106
17-(UFRRJ)
Leia
atentamente o
quadrinho a seguir. Com base
no relatório do gari, calcule
a ordem
de
grandeza do somatório do número de folhas de árvores e de pontas
de cigarros que ele recolheu.
a) 102
b) 104
c) 105
d) 107
e) 108
18-(UFPE-PE)
O
fluxo
total de sangue na grande circulação,
também chamado de débito
cardíaco, faz
com que o coração
de
um homem
adulto seja
responsável pelo bombeamento,
em média, de 20 litros por minuto. 
Qual a ordem de grandeza do volume de sangue, em litros, bombeados pelo coração em um dia?
a) 102
b) 103
c) 104
d) 105
e) 106
19-(UFJF- MG) Supondo-se que um grão de feijão ocupe o espaço equivalente a um paralelepípedo
de
arestas
0,5cm, 0,5cm e 1,0cm, qual
das alternativas
abaixo melhor
estima à ordem
de grandeza do número de feijões contido no volume de um litro?
a) 10
b) 102
c) 103
d) 104
e) 105
20-(ENEM-MEC) A cor de uma estrela tem relação com a temperatura em sua superfície.
Estrelas não muito quentes (cerca de 3 000 K) nos parecem avermelhadas. Já as estrelas amarelas, como o Sol, possuem temperatura em torno dos 6 000 K; as mais quentes são brancas ou azuis porque sua temperatura fica acima dos 10 000 K.
A tabela apresenta uma classificação espectral e outros dados para as estrelas dessas classes.
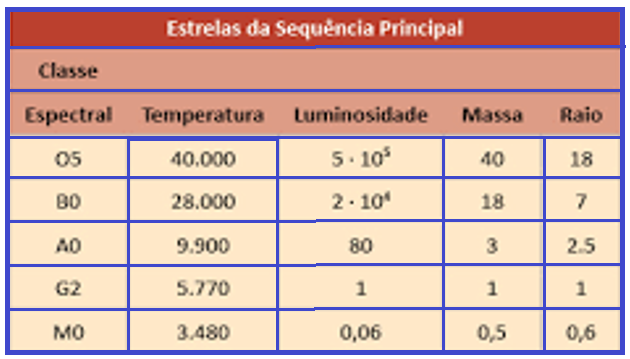
Se tomarmos uma estrela que tenha temperatura 5 vezes maior que a temperatura do Sol, qual será a ordem de grandeza de sua luminosidade?
A- 20 000 vezes a luminosidade do Sol.
B- 28 000 vezes a luminosidade do Sol.
C- 28 850 vezes a luminosidade do Sol.
D- 30 000 vezes a luminosidade do Sol.
E- 50 000 vezes a luminosidade do Sol.
Resolução comentada dos exercícios de vestibulares sobre
Notação Científica, Ordem de Grandeza e Algarismos Significativos
01- Como a a régua é centimetrada podemos dizer que o comprimento da barra está
compreendido entre 7 cm e 8 cm, estando mais próximo de 7 cm.
O algarismo que representa a primeira casa depois da vírgula não pode ser determinado com precisão, devendo ser estimado (é o duvidoso).
Assim, estimamos a medida do comprimento L da barra em 7,3 cm. O algarismo 7 é correto, mas o
algarismo 3 é duvidoso.
R- C
02- Com a utilização da régua milimetrada podemos dizer que o comprimento do lápis está
compreendido entre 150 mm e 160 mm, estando mais próximo do 150 mm.
O algarismo que representa a primeira casa depois da vírgula não pode ser determinado com precisão, devendo ser estimado (duvidoso) . Assim, estimamos a medida do comprimento do lápis em 150,0 mm = 15,00.
R- C
03- Zeros consecutivos à esquerda não são algarismos significativos significativos.
R- B
04- Como o erro da leitura corresponde à metade da menor divisão, ou seja, 0,05 oC, a medida mais confiável na escala Celsius é 38,6 + 0,05 = 38,65 oC.
Substituindo esse valor em tx = 2tc/3 tx = 2.(38,65)/3 = 25,77 oX
R- C
05-
Diâmetro
estimado da
roda = 60cm =
0,6m
raio
da roda R = 30
cm =
0,3 m.
Deslocamento
de cada volta da roda
s = 2
R
s
= 2.3,14.0,3 =
1,88m.
Número
de voltas para
percorrer 200km
= 2.105
m
n
= 2.105
m/1,88 m =
1,06.105
OG = 105.
R- C
06- 0,00000045 = 4,5.10-7
R- B
07-
Como
1000 L = 1 m3
5,5
L =
0,0055 m3
= 5.500.000 mL3
=
5,5.106
mL3.
O
número
de glóbulos
vermelhos no corpo será
5
milhõesx 5,5.106
=
5.106
x
5,5.106
= 27,5.1012
=
2,75.1013.
R- E
08- Transformando 37 centésinos de segundos em horas = 0,37/3600 = 0,000102777... ≈ 0,000103 = 1,03.10-4 h.
R
- A
09- I. 300.000.000 m/s = 3,0.108 m/s
II. 149.000.000 km = 1,49.108 km
III. 0,000.000.005 cm = 5,0.10-9 cm
IV. 100.000.000.000.000.000 s = 1,0.1017 s
10- (1/10)x(1/1.000.000.000) = 10-1x10-9 = 10-10 m
R- C
11-
54
Lx12 km = 648
kmx103
m
= 648.103m
=
6,48.105
m
6,48
> 3,162
OG
=
10.105
=
106
m.
R- E
12-
Vbactéria
= 10-21
Vbaleia
Vbactéria
= 102m3x10-21
= 10-19
m3.
R- B
13-
V
= 200x100 = 2.104
L/dia
1dm3
= 1 L = 103
dm3
1
L = 10-3
m3
V
= 2.104x10-3
=
101
m3.
R- A
14-
Velocidade
da luz no vácuo V = 3.108
m/s
Δt
=
8 min = 8.60 =
480 s
V
= ΔS/Δt
3.108
= ΔS/480
ΔS
=
3.108.480
= 1440.108
= 1,44x103.108
=
1,44.1011
m = 1,44.108
km
ΔS = 108
km.
R- C
15-
10anosx12meses
= 120 meses
20 mesesx1 caixa (40 palitos) = 4800 palitos.
4800
= 4,8.103
4,8 > 3,162
OG
=
10.103
=
104.
R- D
16- 54 Lx12 km = 648 kmx103 m = 648.103m = 6,48.105 m 6,48 > 3,162 OG = 10.105 = 106 m.
R- E
17-
35.000
folhas
+ 85.000
pontas
de cigarros = 120.000
materiais recolhidos entre folhas de árvores e
pontas
de cigarros
120.000 = 1,2.105
1,2
< 3,162
OG = 1.105
OG
= 105.
R- C
18-
1
dia = 24
hx60 min =
1440 min
V = 20Lx1440 min = 28.800 = 2,8.104
2,8
< 3,126
OG = 1.104
OG
= 104.
R- C
19-
Volume
ocupado por um grão
V1
=0,5 cmx0,5 cmx1,0 cm = 0,25 cm3
= 0,25.103.10-3
dm3
= 0,25 dm3.
1
L ocupa um volume de 1 dm3
V2
= 1 dm3
1 L contém V2/V1
= 1 dm3/0,25
dm3
= 4
4 > 3,126
OG = 10.
R- A
20-
Se
Te
é
a temperatura da estrela
Te
= 5.TSol
=5x5770
=
28850
pela
tabela essa
estrela pertence à classe
espectral BO cuja luminosidade vale 2.104
vezes a luminosidade do Sol, ou seja,
20000.
R- A