Força elástica – Lei de Hooke

Considere uma mola (ou um corpo elástico qualquer, corda de borracha, elástico etc.) sujeita a uma deformação x, devido à aplicação de uma força externa .

F  ---  intensidade da força externa deformadora (que comprime ou distende a mola)

F_e  ---  intensidade da força elástica que tende a fazer com que a mola retorne à posição normal

x ---  deformação da mola em relação à posição normal

K  ---  constante elástica da mola medida no SI em N/m, que é característica de cada mola e que depende do material de que a mesma é feita, do número de espiras, das dimensões, etc.

Hooke determinou experimentalmente que “em regime de deformação elástica, a intensidade da força elástica F_e é diretamente proporcional à deformação x”, ou seja,

Representando graficamente a expressão acima:

O que você deve saber, informações e dicas

Significado físico de K se a constante elástica de uma mola for, por exemplo, K = 20N/cm, isto significa que uma força de 20N provoca nessa mola uma deformação de 1 cm.

Uma deformação é elástica quando ela obedece à lei de Hooke, ou seja, retorna à posição normal (natural,relaxada) quando a força deformadora é retirada, pois existe um limite, acima do qual a mola é deformada e não retorna mais à posição normal com a deformação ficando permanente.

Um dinamômetro (dispositivo que mede intensidade de forças) é baseado na deformação de um corpo elástico (mola, corda de borracha, elástico, etc.) e que quando tracionado por duas forças

iguais, como por exemplo, de 15N, indica a força de apenas uma delas, ou seja de 15N. Observe que a força resultante sobre o dinamômetro é nula.

  Um sistema pode ser elástico e não cumprir a Lei de Hooke; ou seja, ele pode sofrer deformações não permanentes e a força elástica NÃO ser proporcional à deformação.

Muitas vezes na prática, nem sempre é desejável que um sistema elástico obedeça a Lei de Hooke.

Um exemplo são as molas de suspensão de carros, caminhões, motos etc, onde o desejável é que o constante elástica aumente com a deformação da mola.  

Um exemplo são as molas mostradas nas figuras acima.

Associação de molas

Duas molas 1 e 2 tem constantes elásticas k₁ e k₂, respectivamente. Podemos associá-las em série ou em paralelo. Em cada uma dessas associações podemos substituir as duas molas por uma única, que produza o mesmo efeito e que chamamos de mola equivalente de constante elástica k_e.

Associação em paralelo

Nesse caso a deformação x sofrida por cada uma das molas é a mesma.

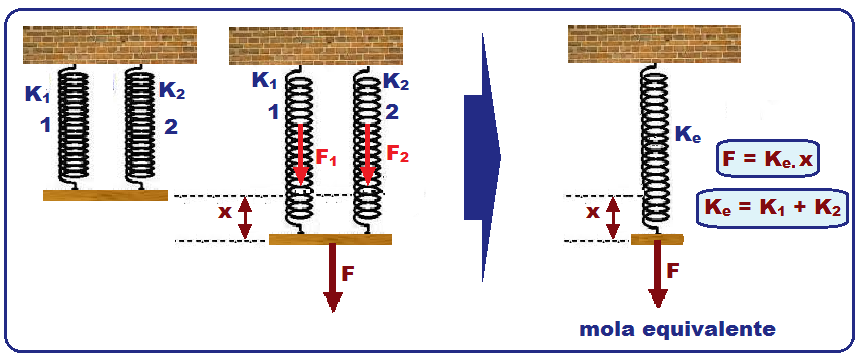
Quando deformadas de x, a mola 1 fica sujeita a uma força F₁ = k₁.x e a mola 2 a uma força F₂ = k₂.x.

A mola equivalente, quando submetida à mesma força F, sofre a mesma deformação x de modo que F = k_e.x.

Observe que F = F₁ + F₂   k_e.x = k₁.x + k₂.x k_e = k₁ + k₂.

Se você tiver n molas   K_e = K₁ + K₂ + K₃ + .... K_n.

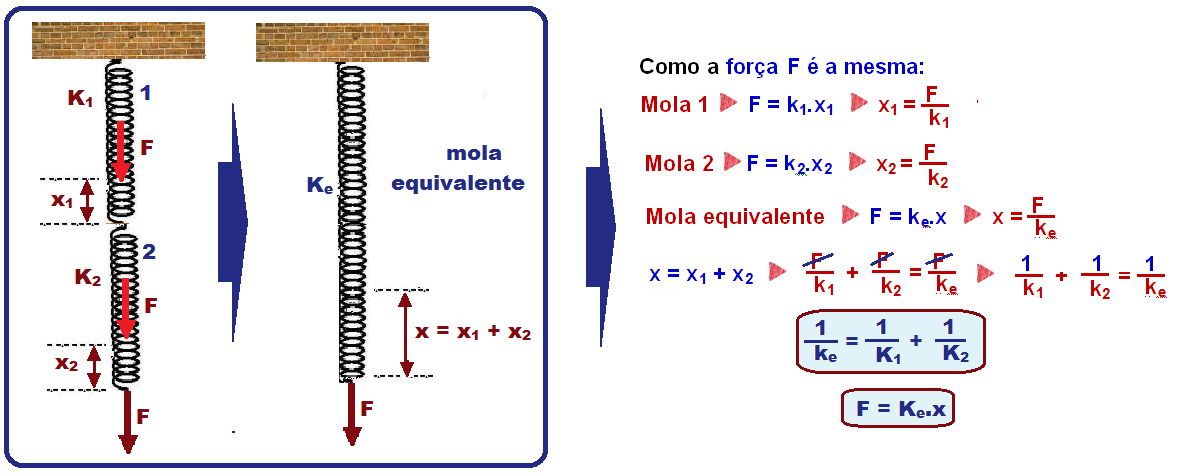
Associação em série

Nesse caso as molas 1 e 2 estão sujeitas à mesma força F e sofrem deformações diferentes x₁ e x_2.

Se você tiver n molas 1/K_e = 1/K₁ + 1/K₂ + 1/K₃ + .... 1/K_n.

O que você deve saber, informações e dicas

A constante elástica é algo que define a mola, isto é, suas características físicas (maleabilidade, maciez), constantes elásticas maiores tendem a ter uma rigidez maior.

Associação em série

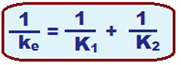
Associação em paralelo

Na associação de molas em série onde 1/k_e = 1/k₁ + 1/k₂, o valor de k_e fica bastante reduzido, sendo que a mola equivalente é menos rígida, mais deformável.

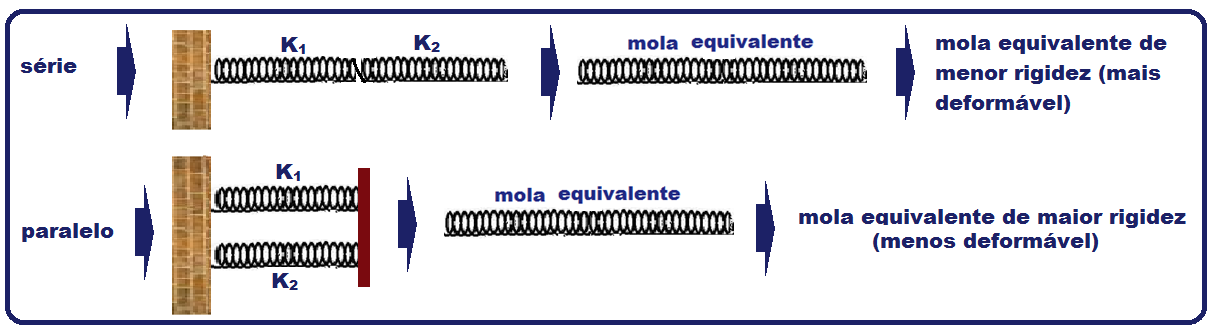
Se quisermos aumentar a rigidez da mola equivalente, torna-a menos deformável, devemos associar as molas em paralelo, onde k_e = k₁  + k₂. É mais eficaz e ocupa menos espaço.

 Você parte uma mola de constante elástica K em duas partes iguais, de modo a obter duas molas idênticas.

Cálculo da constante elástica K’ de cada pedaço que é diferente de K, pois apesar do material ser o mesmo, o número de espiras diminui:

A mola original de constante elástica K é composta das duas metades de constantes elásticas K’, associadas em série.

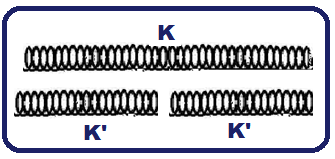
Na associação em série 1/K = 1/K’ + 1/K’ 1/K = 2/K’ K’ = 2K (a rigidez de cada metade fica o dobro da constante da mola original, tornando-as menos deformáveis).

Se você associar cada uma dessas metades de (K’ = 2K) em paralelo você obterá uma mola de

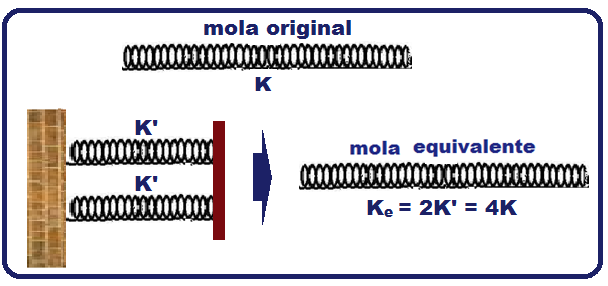
constante elástica equivalente K_e, tal que K_e = K’ + K’ = 2K + 2K K_e = 4K (a rigidez da mola equivalente da associação paralelo dessas duas metades fica quatro vezes maior que o da constante da mola original, tornando a mola equivalente menos deformável).

Exercícios de vestibulares com resolução comentada sobre

Lei de Hooke e Associação de molas

01-(MACKENZIE-SP) A mola da figura varia seu comprimento de 10cm para 22cm quando penduramos em sua extremidade um corpo de 4N.

Determine o comprimento total dessa mola quando penduramos nela um corpo de 6N.

02- (UNIRIO) O dinamômetro, ou balança de mola, é um instrumento para medir força. Se graduado em newtons, ele indica o par de forças que é exercido sobre ele, distendendo a mola. Com a graduação em quilogramas é que ele se tornou conhecido no tempo do império como "balança de peixeiro", pois o peixe era carregado em cestas sobre burros e comercializado pelas ruas. A figura a seguir mostra um dinamômetro de peso desprezível, em cujas extremidades estão aplicadas as forças indicadas.

Assinale a alternativa correta.

a) A indicação do dinamômetro no primeiro caso é zero.

b) A leitura do dinamômetro no segundo caso é 300 N.

c) A resultante sobre o dinamômetro no primeiro caso é 100 N.

d) A indicação do dinamômetro no primeiro caso é 100 N.

e) A leitura do dinamômetro no segundo caso é 50 N.

03-(UFSM) Durante os exercícios de força realizados por um corredor, é usada uma tira de borracha presa ao seu abdome. Nos arranques, o atleta obtém os seguintes resultados:

O máximo de força atingido pelo atleta, sabendo-se que a constante elástica da tira é de 300 N/m e que obedece à lei de Hooke, é, em N,

04-(Ufrrj-RJ) Um bloco de massa 5 kg está parado sobre um plano inclinado de um ângulo de 30° com a horizontal, preso a uma mola, de constante elástica k = 100 N/m, como mostra a figura. O atrito entre o bloco e o plano pode ser desprezado.

a) Represente as forças que atuam na caixa e escreva quem exerce cada uma das forças.

b) Calcule a deformação da mola nessa situação.

05-(UFB) A mola da figura está:

- em (1) no seu tamanho natural

- em (2) tracionada por uma força de 10N

- em (3) tracionada por uma força de 25N

Verifique, justificando, se ela obedece à lei de Hooke

06-(UFB) Entre dois blocos 1 e 2 de massas m₁=12kg e m₂=8kg existe uma mola ideal A. Os dois blocos estão apoiados sobre

um plano horizontal sem atrito. O bloco 1 é puxado por uma força , constante, horizontal e paralela ao plano por meio de outra mola ideal B, idêntica à mola A. Calcule a relação x_A/x_B entre as deformações das molas A e B, depois que o sistema entrou em movimento com aceleração constante .

07-(UFRJ-RJ) Uma mola de constante elástica k e comprimento natural L está presa, por uma de suas extremidades, ao teto de um elevador e, pela outra extremidade, a um balde vazio de massa M que pende na vertical. Suponha que a mola seja ideal, isto é, que tenha massa desprezível e satisfaça à lei de Hooke.

a) Calcule a elongação x_o da mola supondo que tanto o elevador quanto o balde estejam em repouso, situação ilustrada na figura 1, em função de M, k e do módulo g da aceleração da gravidade.

b) Considere, agora, uma situação na qual o elevador se mova com aceleração constante para cima e o balde esteja em repouso relativamente ao elevador. Verifica-se que a elongação da mola é maior do que a anterior por um valor d, como ilustra a figura 2. Calcule o módulo da aceleração do balde em termos de k, M e d.

08-(UFG) No sistema representado na figura abaixo, as duas molas são iguais, têm 1 m de comprimento e estão relaxadas. Quando o fio é cortado, a esfera de massa 5,1 kg desce 1 m até parar momentaneamente.

Dados:

√2 = 1,41

g = 10 m/s²

Calcule o valor da constante elástica k das molas.

09-(UNICAMP-SP) Sensores de dimensões muito pequenas têm sido acoplados a circuitos microeletrônicos. Um exemplo é um medidor de aceleração que consiste de uma massa m presa a uma micromola de constante elástica k. Quando o conjunto é submetido a uma aceleração a, a micromola se deforma, aplicando uma força F na massa (ver diagrama a seguir). O gráfico a seguir do diagrama mostra o módulo da força aplicada versus a deformação de uma micromola utilizada num medidor de aceleração.

a) Qual é a constante elástica k da micromola?

b) O medidor de aceleração foi dimensionado de forma que essa micromola sofra uma deformação de 0,50 mm quando a massa tem uma aceleração de módulo igual a 25 vezes o da aceleração da gravidade. Qual é o valor da massa m ligada à micromola?

10-(UNICAMP-SP) Nas cenas dos filmes e nas ilustrações gráficas do Homem-aranha, a espessura do cabo de teia de aranha que seria necessário para sustentá- lo é normalmente exagerada.

De fato, os fios de seda da teia de aranha são materiais extremamente resistentes e elásticos. Para deformações ΔL relativamente pequenas, um cabo feito de teia de aranha pode ser aproximado por uma mola de constante elástica k dada pela fórmula (K=10¹⁰ A/L),  onde L é o comprimento inicial e A a área da seção transversal do cabo. Para os cálculos abaixo, considere a massa do Homem-aranha M = 70 kg.

Calcule a área A da seção transversal do cabo de teia de aranha que suportaria o peso do Homem-aranha com uma deformação de 1,0 % do comprimento inicial do cabo. (g=10m/s²)

11-(UFRJ-RJ) O sistema representado na figura (carrinhos de mesma massa ligados a molas idênticas) está inicialmente em repouso, podendo mover-se com atrito desprezível sobre trilhos horizontais:

Aplica-se à extremidade livre da mola 3, uma força constante, paralela aos trilhos e orientada para a direita. Depois de as oscilações iniciais terem sido amortecidas, o conjunto desloca-se em bloco para a direita. Nessa situação, sendo l₁, l₂ e l₃ os comprimentos respectivos das molas 1, 2 e 3, assinale a alternativa correta:

Associação de molas

12-(MACKENZIE-SP) Uma mola helicoidal de massa desprezível está presa pela extremidade A, a uma parede rígida e, na extremidade B, encontra-se preso um corpo de massa m, conforme mostra a figura 1. Quando o conjunto oscila livremente na direção da reta horizontal AB, perpendicular à parede, constitui-se um oscilador harmônico de período T. Se dispusermos de duas molas idênticas à anterior e as fixarmos conforme a figura 2, ao constituirmos um oscilador harmônico, com a oscilação do mesmo corpo de massa m, segundo a mesma direção AB, seu respectivo período será:

                               Figura 1                                                                          figura 2

13-(UFB) Uma massa M=(20/9)kg, encontra-se suspensa ao conjunto de molas ilustrado na figura abaixo,

Suas constantes elásticas são k₁ = k₂=30N/m.

Calcule a constante elástica total equivalente do conjunto.

14-(ITA-SP) Um sistema massa-molas é constituído por molas de constantes k₁ e k₂, respectivamente, barras de massas desprezíveis e um corpo de massa m, como mostrado na figura.

Determine a freqüência desse sistema.

15-(UFB) A mola helicoidal (figura 1), de constante elástica k=12N/m, foi partida em 3 partes iguais. Em seguida, essas 3 partes foram associadas em paralelo (figura 2) e em série (figura 3).   

As massas das figuras 2 e 3 são iguais e valem 100g. Adote g=10m/s² e determine:

a) a constante elástica de cada parte.

b) o período de oscilação do conjunto quando as três molas estão associadas em paralelo.

c) o período de oscilação do conjunto quando as três molas estão associadas em série.

16-(PUC-SP) Na figura abaixo, as três molas ideais 1, 2 e 3 são idênticas  e possuem a mesma constante elástica de valor 0,1N/cm e as massas também são idênticas e de mesmo valor (10g).

Inicialmente, o conjunto está em equilíbrio e as molas estão em seu comprimento natural (20cm cada uma). Em seguida, retira-se o suporte S e cada mola se distende até que o conjunto adquira novamente o equilíbrio.

Após o novo equilíbrio, determine: (g=10m/s²)

a) deformação de cada mola.

b) o comprimento de cada mola

c) a deformação total do conjunto

17- (UFMS) Considere um sistema constituído de duas molas de constantes elásticas K₁ e K₂. É correto afirmar que

(01) a constante elástica do sistema é maior quando as molas são associadas em série.

(02) a constante elástica do sistema é menor quando as molas são associadas em paralelo.

(04) a elongação das molas é a mesma quando elas são associadas em paralelo.

(08) a constante elástica do sistema é K₁ + K₂ quando elas são associadas em paralelo.

(16) a força de elongação das molas é a mesma quando elas são associadas em paralelo.

18-(UFMS-MS)  A figura a seguir mostra duas massas iguais a m, presas nas extremidades de uma mola de constante elástica K e que obedece à lei de Hooke. Um fio mantém esse sistema suspenso em um teto. Todo o sistema está em equilíbrio, até que uma tesoura corta o fio que mantém o sistema suspenso. Considere a massa da mola desprezível, a aceleração da gravidade uniforme e igual a g no local e assinale a(s) proposição(ões) CORRETA(S).

 01) Imediatamente após cortar o fio, a força resultante na massa superior será de 2 mg. 

02) Imediatamente após cortar o fio, as duas massas cairão com aceleração da gravidade. 

04) Enquanto o sistema estiver em equilíbrio e suspenso pelo fio ao teto, a força aplicada pela mola será igual a 2 mg. 

08) Imediatamente após cortar o fio, a aceleração resultante na massa superior será maior que a aceleração resultante da massa inferior. 

16) Depois de cortar o fio e enquanto o sistema cai, o centro de massa do sistema oscilará enquanto cai em queda livre. 

19-(PUC-SP) O corpo A da figura, de peso 10N e volume 400cm³, é erguido 10cm, com velocidade

constante, por meio de um fio ideal no qual é aplicada uma força de tração.Considerando que o corpo permanece o tempo todo completamente imerso na água (d=10³kg/m³), o trabalho, em joules, realizado pela força de tração indicada no dinamômetro D é de (considere g=10m/s²).

20-(PUC-SP)  A violência urbana, tanto contra a pessoa quanto aquela realizada contra o patrimônio, tem feito com que a população procure as mais variadas formas de proteção. Carros blindados, contratação de empresas privadas de segurança e eletrificação de muros e cercas estão entre as mais comuns.

O Arame Espetante é um produto que oferece uma boa proteção para o seu patrimônio, contra vandalismo e roubo. Ele pode ser utilizado em empresas, residências, edifícios e condomínios.

O que é o Arame Espetante? É um arame de aço, com dois tratamentos contra ferrugem, encapado por uma lâmina de aço, com pontas perfurantes e inflexíveis. Ele pode ser facilmente instalado sobre: muro de alvenaria, alambrado, grade, marquise ou direto no solo.

Em formato de hélice cilíndrica (ou helicoidal), travado em dois cabos de aço, forma uma barreira contra invasão por vândalos e ladrões.

A idéia de um construtor é instalar, nos 20 m de comprimento de um muro frontal de uma residência, arame espetante de bitola (diâmetro do fio) 8 mm. Para isso, ele utilizará arame com formato helicoidal, cuja secção transversal apresenta diâmetro de 40 cm, e com anéis separados por 10 cm de distância.

Instruções:

Nas respostas, lembre-se de deixar os processos de resolução claramente expostos. Não basta escrever apenas o resultado final. É necessário registrar os cálculos e/ou o raciocínio utilizado.

a) Admitindo que esse produto seja vendido em caixas cúbicas de 40 cm de arestas, desprezando as eventuais folgas entre os anéis e supondo que eles fiquem justos na caixa, calcule o número mínimo de caixas que deverão ser compradas para montar uma cerca nesse muro. Considere em sua resolução que as extremidades do arame estão fixadas no topo do muro, em seu início e final, não ocorrendo sobreposição nas emendas.

b) Antes de sua fixação no topo do muro, que força deve ser feita sobre o arame espetante de cada caixa para esticá-lo, separando os anéis conforme o planejado? Considere que ele se comporta como uma mola helicoidal, de constante elástica 5 N/m, que obedece à lei de Hooke.

21-(UFG-GO) A saltadora brasileira Fabiana Murer terminou as olimpíadas de Pequim em décimo lugar, após descobrir, no meio da competição, que o Comitê Organizador dos Jogos havia perdido uma de suas varas, a de flexibilidade 21. 

Considerando que este tipo de vara se comporta com uma mola ideal, qual é a constante em N/m da mola ideal equivalente a uma vara de flexibilidade 21?

Dado: g = 10 m/s²

a) 9,25.10^-6                 

b) 9,25.10^-4                 

c) 1,081.10¹                        

d) 1,081.10²                    

e) 1,081.10³ 

22-(UFU-MG) O tiro com arco é um esporte olímpico desde a realização da segunda olimpíada em Paris, no ano de 1900. O arco é um dispositivo que converte energia potencial elástica, armazenada quando a corda do arco é tensionada, em energia cinética, que é transferida para a flecha.

Num experimento, medimos a força F necessária para tensionar o arco até uma certa distância x, obtendo os seguintes valores:

O valor e unidades da constante elástica, k, do arco são:

23-(ITA-SP) Sobre uma mesa sem atrito, uma bola de massa M é presa por duas molas alinhadas, de constante de mola k e comprimento natural ℓ_o, fixadas nas extremidades da mesa. Então, a bola é deslocada a uma distância x na direção perpendicular à linha inicial das molas, como mostra a figura, sendo solta a seguir.

 Obtenha a aceleração da bola, usando a aproximação (1 + a)^α_= 1 + a.α

a) a = - kx/M         

b) a = - kx²/2M ℓ_o         

c) a = - kx³/M ℓ_o         

d) a = - kx³/2M ℓ_o         

e) a = - kx³/M ℓ_o²

24-(UPE-PE)

Um corpo de massa m está suspenso por duas molas ideais, paralelas, com constantes elásticas k e deformadas de d.

Sabendo que o sistema se encontra em equilíbrio, assinale a alternativa que expressa k.

Dado: Considere a aceleração da gravidade g.

A) 2mg/d             

B) mg/d                    

C) mg/2d                         

D) 2d/mg                     

E) mg

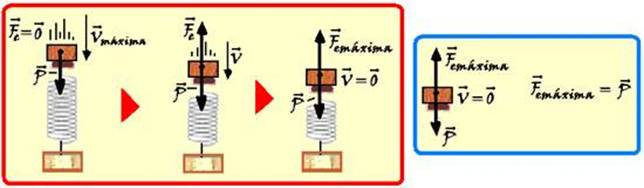
25-(UFES-ES)

Um bloco de massa 0,10 kg é abandonado, a partir do repouso, de uma altura h de 1,2 m em relação a uma mola ideal de constante elástica 0,10 N/cm. Como é mostrado na figura rotulada como “Depois”,

ao lado, o bloco adere à mola após o choque. No desenho, A é o ponto de abandono do bloco, B é o ponto de equilíbrio da mola, e C é o ponto onde há maior compressão da mola. Despreze perdas de energia por atrito.

A) Identifique, em um diagrama, as forças que atuam no corpo, quando a deformação da mola é máxima.

B) Determine a velocidade do bloco imediatamente antes de se chocar com a mola.

C) Determine o trabalho realizado sobre o bloco pela força gravitacional entre os pontos A e B.

D) Determine a deformação máxima sofrida pela mola.

26-(UPE-PE)

27-(UFG-GO)

Para proteção e conforto, os tênis modernos são equipados com amortecedores constituídos de molas. Um determinado modelo,

molas. Um determinado modelo, que possui três molas idênticas, sofre uma deformação de 4 mm ao ser calçado por uma pessoa de 84 kg. Considerando-se que essa pessoa permaneça parada, a constante elástica de uma das molas será, em kN/m, de

Resolução comentada dos exercícios de vestibulares sobre

Lei de Hooke e Associação de molas

 01- A mola fica deformada de x=(22 – 10)=12cm  ---  x=12cm 

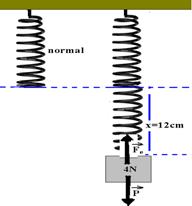
Numa deformação de 12cm  ---  F_e = P = 4N  ---  F_e = K.x  ---  4 =K.12  ---  K=1/3 N/cm

K é constante para qualquer deformação (lei de Hooke)  ---  para F_e=P=6N  ---  F_e=K.x  ---  6=1/3.x  ---  x=18cm  ---  fica deformada de 18cm e seu comprimento será L=18 + 10 = 28cm

02- R- D – vide teoria

03- K=300N/m e é constante (obedece à lei de Hooke). A máxima deformação da tira de borracha é de 28cm (Dx=28cm=0,28m)  --- 

F=K.Dx  ---  F=300.0,28  ---  F=84N  R-E

04- a) As forças que atuam sobre a caixa são o peso,  vertical e para baixo, a força normal, exercida pelo plano e perpendicular a ele, e a força elástica, exercida pela mola.

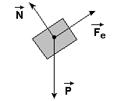
b) Como a caixa está em repouso, temos: F_R=0  ---  P_P = F_e

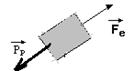
m.g.sen30^o = K.x  ---  5.10.1/2 = 100.x  ---  x=25/100  ---  x=0,25m

05- Em 2  ---  F=Kx  ---  10=K.5  ---  K=2N/cm  ---  em 3  ---  F=Kx  ---  25=K.12,5  ---  K=2N/cm  ---  Sim, obedece, pois K é constante

 06- Após o sistema entrar em movimento com aceleração , as molas já se encontram deformadas de x_A e x_B e a mola A sujeita à força de tração   ---  

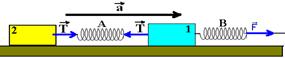
   bloco 2   ---  F_R=m₂.a  ---  T=8a I  ---  bloco 1  ---  F_R=m₁a  ---  F – T =12a  II  ---  resolvendo I com II  ---   F=20a e T=8a   ---  sendo as molas idênticas, elas possuem a mesma constante elástica K  --- F=Kx_B  ---  x_B=20a/K  ---  T=Kx_A  ---  8a = Kx_A  --- 

x_A=8a/K  ---  x_A/x_B=8a/K/K/20a  ---  x_A/x_B=2/5 

07- a) balde e elevador em repouso  ---  F_R=0  ---  P=F_e  ---  mg=Kx_o  ---  x_o=mg/K

b) balde e elevador subindo com aceleração a  ---  F_R=ma  --- F_e – P=ma  ---  K.(x_o + d) – mg=ma  ---  a=(K.(x_o + d) – mg)/m

08- Quando o fio é cortado, a esfera desce 1m e pára momentaneamente e, nesse instante temos o esquema abaixo:

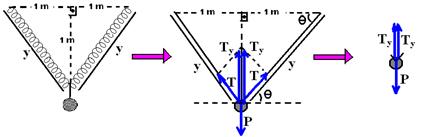
T – força de tração em cada uma das molas e o peso da esfera - P=mg=5,1.10  ---  P=51N  --- aplicando Pitágoras num dos triângulos retângulos  ---  y²=1²+ 1²  ---  y=√2=1,41m  ---  observe que y é o comprimento da mola na posição normal (1m) e que Δx é sua deformação e que y=1 + Δx  ---  1,41=1 + Δx  ---  Δx=0,41m  ---  observe também que senӨ=1/y=1/√2  ---  senӨ=√2/2=1,41/2  ---  senӨ=0,7  ---  T_y=TsenӨ=0,7T  ---  como a esfera está em equilíbrio, P=2T_y  ---  51=2.0,7T  ---  T≈36N  ---  T=F_e=K.Δx  ---  36=K.0,41  ---  K=87,8N/m

09- a) F_e=Kx  ---  0,40.10^-6=K.0,40.10^-6  ---  K=1,0N/m

b) F_e=ma  ---  a=25.10=250m/s²  ---  Kx=m.250  ---  1.0,5.10^-6=m.250  ---  m=5.10^-7/250=0,02.10^-7  ---  m=9,0.10‑9‑kg

10- Deformação da teia quando em equilíbrio Δx=0,01L  ---  Δx=10^-2L  ---  no equilíbrio P=F_e  ---  mg=KΔx  ---  70.10=10¹⁰.A/L.10^-2L  ---  A=10^-6m²

11- Depois das oscilações iniciais terem sido amortecidas, as molas não se deformam mais e o conjunto se desloca coma aceleração constante a;

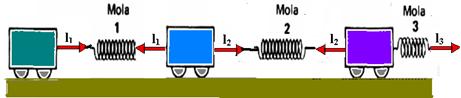
Bloco 3  ---  l₃ – l₂=ma I  ---   bloco 2  ---  l₂ - l₁=ma II   ---   bloco 1  ---  l₁=ma III  ---  III em II  ---  l₂ – ma = ma  ---  l₂=2ma  

Somando I, com II com III  ---  I₃=3ma       R- C

Associação de molas

12- Período T da mola da figura 1  ---  T = 2p√m/k

Como as molas estão associadas em paralelo, a constante elástica da mola equivalente, que, substituindo as duas produz o mesmo efeito será k_e = k + k  ---  k_e =2k e seu período será T’ = 2pm/2k  ---  T’ = 2p√m/k.1/√2.

T/T’ = √2  ---  T’ = T/√2  --- racionalizando  ---  T’= T√2/2  Resposta C

13-  Como as duas molas de constantes k₂ estão em para, a mola equivalente terá constante k_e1 =30 + 30 = 60N/m. Então teremos:

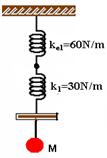
As duas molas acima estão em série, então a mola equivalente terá constante k_e, dada por: 1/k_e = 1/60 + 1/30  ---  k_e = 20N/m,

que é a constante elástica total  equivalente do conjunto.

14- As 3 molas de constantes k₂ estão em paralelo e serão substituídas por uma única mola de constante k_e1=3k₂.

As duas molas de constantes k₁ também estão em paralelo e serão substituídas por um única mola de constante k_e2=2k₁

Então, teremos:

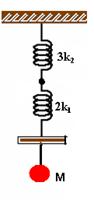
A mola resultante das duas acima, que estão em série, terá k_e, tal que: 1/k_e = 1/3k₂ + 1/2k₁  ---  1/k_e = 2k₁ + 3k₂ / 6k₁.

K_e = 6k₁.k₂ / 2k₁ + 3k₂

O período desse sistema vale  ---  T = 2p√m/6k₁.k₂ / 2k₁ + 3k₂  ---  T = 2p√m(2k₁ + 3k₂)/6k₁.k₂

F = 1/T = 1/2p√6k₁.k₂ / m(2k₁ + 3k₂)

15- a) A mola inteira (mola equivalente) tem constante elástica k’=10N/m sendo que 1/k’= 1/k + 1/k +1/k, onde k é a constante elástica de cada parte.

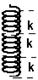
1/k’=3/k  ---  1/12 = 3/k  ---  k =36N/m

b) Paralelo  ---  k­e=36 + 36 +36  ---  k_e=108N/m  ---  T=2p√m/k_e  ---  T=2p√0,1/108  --- T @ 6..10^-2.p s

c) Série  ---  k_e=12N/m  ---  T=2p√m/k_e  ---  T=2p√0,1/12  ---  T@ 18.10^-2.p s

16- a) Peso de cada massa  ---  P=mg  ---  P=0,01.10  ---  P=0,1N. Como as molas são ideais, suas massas são desprezíveis.

Observe que a mola 1 está sujeita à força F=0,3N (são as 3 massas que estão deformando-a)

F₁=k₁.x₁  ---  0,3=0,1.x₁  ---  x₁ = 3cm

A mola 2 está sujeita à F=0,2N (apenas duas massas estão deformando-a)

F₂=k₂.x₂  ---  0,2=0,1.x₂  ---  x₂= 2cm

Mola 3  ---  F₃=k₃.x₃  ---  0,1=0,1.x₃  ---  x₃= 1cm

b) mola 1 – L₁= 23cm

    mola 2 – L₂= 22cm

    mola 3 – L₃= 21cm

c) 6 cm

17- Soma (04 + 08) =12  Vide teoria

18- No momento em que o fio é cortado a massa mais próxima do teto ficará, neste instante, sujeita a uma força resultante de intensidade  igual a 2P= 2mg e, portanto, a uma aceleração descendente de 2g  ---  o outro corpo neste instante estará sujeito ao seu próprio peso P=mg e logo a uma aceleração igual a g.

R- (01 + 08) = 09

19- A força de tração, o empuxo da água e o peso do corpo estão relacionados: E + T = P  ---  d.g.V + T = P  ---  T = P - d.g.V  ---  T = 10 - 1000.10.0,0004 = 10 - 4 = 6 N  ---  o trabalho é o produto da força pelo deslocamento  ---  W=6.0,1 = 0,6 J  --- 

  R- C

20- a) Para instalar os 20 m de comprimento (L), o número n de passos de mola necessário é dado por  ---  L = n × a + (n + 1) e  ---  a = separação entre os anéis  ---  e = diâmetro do fio (bitola)  ---  L = comprimento do muro  ---  20 = n 0,1 + (n + 1) 0,008  ---  20 = 0,1n + 0,008n + 0,008  ---  20 = 0,108n + 0,008  ---  n ≈ 20 / 0,108  ---  n ≈ 185  ---  número de voltas N  ---  N = n + 1 = 186  ---  com as voltas compactadas e superpostas, a altura total é dada por  ---  H = N e = 186 × 0,008 m ≈ 1,5 m  ---  quantidade C de caixas necessárias  ---  C ≥ 1,5/0,4 = 3,75  ---  como o número de caixas deve ser inteiro  ---  C_mínimo = 4

b) O comprimento inicial da mola vale L_o = 1,5 m e o comprimento final deverá ser L = 20 m  ---  Lei de Hooke  ---  F = k (L – L_o)  ---  F = 5 (20 - 1,5) N = 92,5N  ---  F = 92,5N 

21- Dados  ---  x = 21 cm = 0,21 m  ---  F = P = m g = 22,7(10) = 227 N  ---  da lei de Hooke: F = k x  ---  K=F/x=227/0,21  --- 

K=1.080,95  ---  K=1,081.10³N/m  ---  R- E N/m 

R- E

22- Pela tabela  ---  K=F_e/X=160/10=320/20=480/30=16N/cm  ---  K=1.600N/m=1,6kN/m  ---  R- B

23- As forças que agem sobre a bola e sua soma vetorial estão indicadas na figura  ---  F_R=2F_ecosθ  ---  cosθ=x/ℓ  ---  F_e=-K(ℓ -

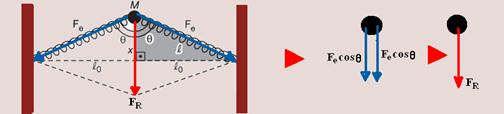
ℓ_o)  ---  F_R=-2.K. (ℓ - ℓ_o).x/ℓ  ---  F_R=-2K.(x -  (ℓ_o.x)/ℓ)  ---  F_R=-2Kx(1 - ℓ_o/ℓ)  ---  F_R=-2Kx(ℓ_o/√ (ℓ_o² + x²))  ---  para chegar na aproximação do enunciado  ---  ℓ_o/√ (ℓ_o² + x²) = ℓ_o/√ (ℓ_o² + x²)= ℓ_o/ℓ_o x  ℓ_o/√ (ℓ_o² + x²)=1/√(1 + x²/ ℓ_o²)  ---  F_R=1/√(1 + x²/ ℓ_o²) ℓ_o/√ (ℓ_o² + x²)= (1 +  x²)=(1 + x²/ ℓ_o²)^-1/2=1 + (-1/2.x²/ ℓ_o²)  ---  F_R=1 + (-1/2.x²/ ℓ_o²)=Ma  ---  Ma= -2Kx{1 – (-1/2.x²/ℓ_o²) 1 + (-1/2.x²/ ℓ_o²)}  ---  a= -Kx³)/Mℓ_o²  ---  R- E

24-

  Como o sistema está em equilíbrio as intensidades da força P=mg e das forças elásticas F_e=k.d devem se igualar  ---

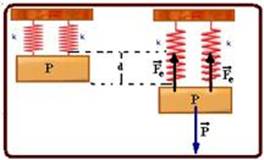
P=2F_e  ---  m.g=2.k.d  ---  k=mg/2d  ---  R- C.

25-

26-

 I- Falsa  ---  quando a esfera atinge a mola, sua velocidade vai aumentando, enquanto houver resultante para baixo (P>F_e)  --- a partir do instante em que as forças peso e elástica se anulam, a força elástica continua aumentando ficando maior que a força peso, a resultante agora é para cima, diminuindo a velocidade da esfera.

II. Falsa  ---  a mola atinge sua máxima deformação quando a velocidade da esfera é nula (ela inverte o sentido de seu movimento e fica em repouso, para começar a voltar)  ---  chamando esse ponto de C e colocando nele o nível zero de

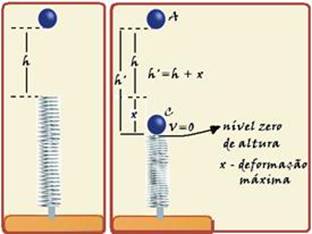
altura, a energia mecânica nele será  ---  E_mC=mV²/2 + m.g.h + kx²/2=m.0²/2 m.g.0 + kx²/2  ---  E_mC=kx²/2  ---  E_mC=50x² (I)  ---  no ponto mais alto (A) de onde a esfera e´abandonada (V=0), sua energia mecânica vale  ---  E_mA=mV²/2 + m.g.h’=m.0²/2 + m.g.h=1.10.(6 + x)  ---  E_mA=60 + 10x (II)  ---  igualando (I) com (II)  ---  50x² = 60 + 10x  ---  5x² – x - 6=0  ---  resolvendo essa equação  ---  x=1,2m.

III. Correta  ---  a velocidade é máxima quando F_e=P (veja I)  ---  kx=mg  ---  100.x=1.10  ---  x=0,1m=10cm.

IV. Correta  --- a velocidade é máxima quando x=0,1m (veja III)  ---  chamando esse ponto de D e colocando nele o

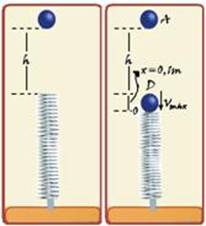
 nível zero de altura  ---  E_mD=m(V_máx)²/2 + k.x²/2 + m.g.0=1.(V_máx)²/2 + 100.(0,1)²/2 + 0  ---  E_mD=0,5 + 0,5(V_máx)² (I)  ---  em A  ---  E_mA=m.g.(h + x) + mV²/2=1.10.(6 + 0,1) + 0  ---  E_mA=61J (II)  ---  igualando (I) com (II)  ---  61=0,5 + 0,5(V_máx)²  ---  V_máx=√121  ---  V_máx=11m/s.

V- Correta  ---  como o sistema é conservativo, os atritos são desprezados e as forças são conservativas, a velocidade com que a esfera atinge a mola é a mesma com que ela deve retornar para atingir a mesma altura de h=6m  ---  conservação da energia mecânica  ---  A  ---  E_mA=m.g.h=1.10.6=60J  ---  quando atinge a mola (ponto B)  sua energia mecânica será  ---  E_mB=mV²/2=1.V²/2  ---  E_mA = bem  ---  60 = V²/2  ---  V=√(120)=2.(30)^0,5m/s.

R- D.

27- Como cada um dos tênis tem 3 molas, a pessoa em pé está apoiada sobre dois tênis, então você terá 6 molas associadas em paralelo  ---  assim, cada mola suportará uma força de  ---  P=m.g=84.10=840N/6  ---  F=140N (força suportada por cada mola, que é a força elástica Fe)  ---  Fe=k.x  ---  140=k.4.10-3  ---  k=140/4.10-3  ---  k=35.103N/m  ---  k=35kN/m  ---  R- A