Experiência de Torricelli e Vasos comunicantes com líquidos imiscíveis em equilíbrio

Pressão atmosférica

 A atmosfera terrestre é uma imensa camada de ar e outros gases, com dezenas de quilômetros de altura, que são atraídos pela gravidade da Terra e por isso, sua densidade é maior em pontos mais próximos da superfície.

Ela atua como uma zona intermediária entre o espaço sideral e a Terra e acompanha todos os movimentos da Terra.

Essa camada gasosa exerce uma pressão sobre os corpos nela mergulhados, devida ao peso da coluna de ar que se encontra sobre esses corpos, e que é chamada de pressão atmosférica, sendo tanto maior quanto mais o corpo estiver mais perto da superfície da Terra.

  O físico italiano  Evangelista Torricelli (1608-1647), demonstrou que a pressão atmosférica ao nível do mar equivale à pressão exercida por uma coluna de 76cm de altura.

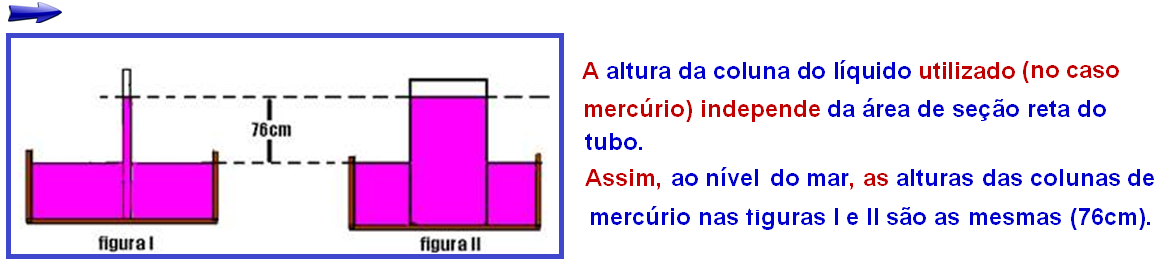
Ao nível do mar, Torricelli tomou um tubo de vidro, fechado em uma das extremidades, e encheu-o até a borda com mercúrio (Hg).

Em seguida, tampou a ponta aberta e, invertendo o tubo, mergulhou essa ponta em uma bacia com mercúrio.Soltando a ponta aberta notou que a coluna de mercúrio descia até certo nível.

Lembrando que g=9,8m/s² e que d_Hg=13.600kg/m³, tem-se    P_Q=P_P    P_atm=d_Hg.g.h  P_atm=13.600.9,8.0,76   P_atm=1,01N/m² (Pa).

Torricelli fixou uma escala vertical graduadano tubo de mercúrio utilizado nesta experiência,

obtendo desta forma oaparelho de medição da pressão atmosférica, o barômetro de mercúrio.

 Se o líquido fosse a água, de densidade d_água=10³kg/m³  P_atm=d_água.g.h_água  1,01.10⁵=10³.9,8.h_água   h_água=10,3m.

O que você deve saber, informações e dicas

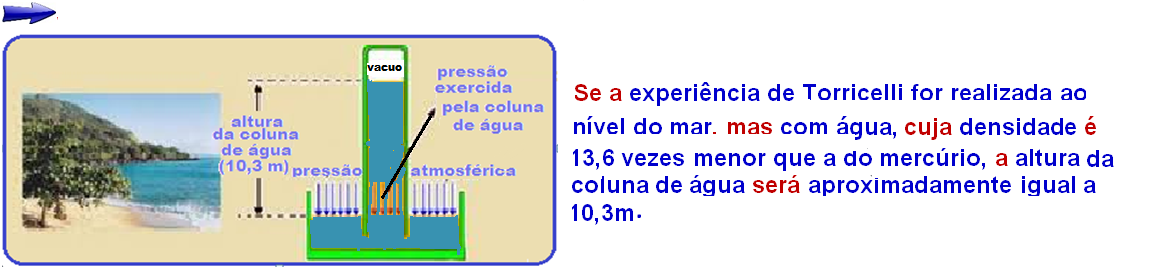
 Se a experiência de Torricelli fosse realizada no cume de uma montanha muito alta, a altura da

coluna de mercúrio será menor que ao nível do mar, pois a pressão atmosférica diminui com a altitude.

 A pressão atmosférica depende da altitude (P_atm = d_ar.g.h), conforme indica o gráfico abaixo

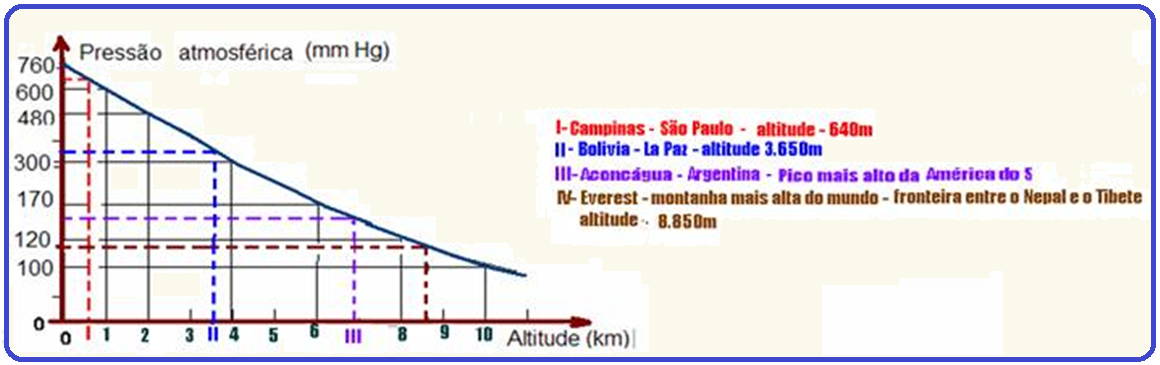
  à medida que a altitude aumenta, a pressão diminui e o ar vai ficando cada vez mais rarefeito    em La Paz, de altitude 3.650m, a pressão cai para cerca de 507mmHg, o ar fica rarefeito e a quantidade de oxigênio fica cerca de 40% menor que ao nível do mar, dificultando a respiração.

A água ferve a 90^oC.   O ar  menos denso e faz com que os corpos em movimento (por exemplo, bolas de futebol) enfrentem menor atrito aerodinâmico e se tornem mais velozes que ao nível do mar. Por, isso os atletas não gostam de jogar na Bolívia.  

 A pressão atmosférica depende, além da altitude, da temperatura do ar (maior temperatura, ar menos denso, menor pressão atmosférica) e da umidade do ar (as moléculas de vapor d’água, são mais leves que as de oxigênio e nitrogênio que compõem a maior parte do ar atmosférico, portanto, mais úmido o ar, menor a pressão atmosférica).

Uma bexiga sobe porque o gás em seu interior é menos denso que o ar ao redor e, à medida que sobe seu volume vai aumentando porque a diferença entre a pressão do gás dentro da bexiga e a

pressão cada vez mais reduzida fora dela gera uma força resultante que empurra o plástico da bexiga para fora.

 Os barômetros aneróides baseiam-se na deformação que variações da pressão atmosférica provocam em cápsulas metálicas de paredes onduladas e flexíveis, em cujo interior se faz o vácuo.

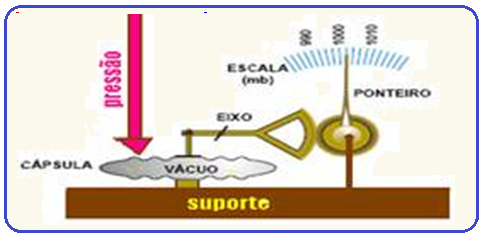
Quando a pressão atmosférica aumenta provoca uma compressão na câmara (cápsula) do barômetro

e quando a pressão diminui verifica-se uma expansão da câmara (cápsula).

Estas oscilações são transmitidas pelo eixo ao ponteiro que se encontra associado a um mostrador que indica essa variação de pressão.

Este instrumento pode ser usado no âmbito do estudo das alterações metereológicas.

 Considere uma lata de óleo totalmente vedada. Se você fizer apenas um furo na lata de óleo, o óleo não escoará, pois a pressão externa (atmosférica) é maior que a pressão interna exercida pela coluna de óleo dentro da lata.

Para que o óleo escoe com facilidade da lata, você deve fazer dois furos na mesma, um para que a pressão atmosférica compense a pressão de um dos furos, e o outro, adicional, para que o óleo saia da mesma.

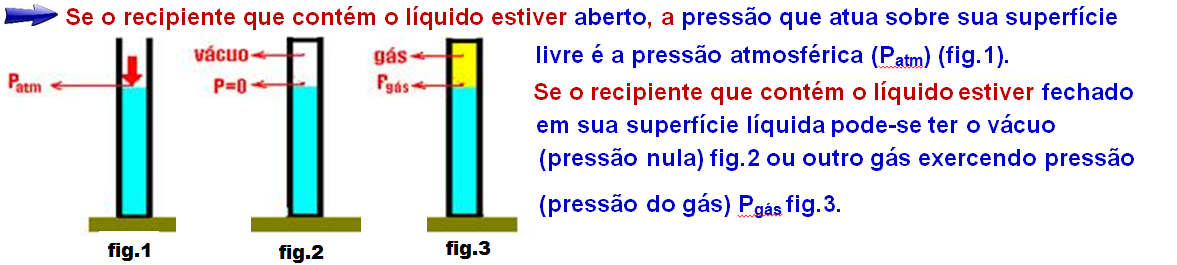
Observações:

se você fizer um pequeno furo na garrafa fechada, acima da superfície líquida, ela se comportará como se fosse aberta, e a água vazará.

o alcance da água que jorra da garrafa aberta será máximo quando o orifício estiver a uma altura h = h’/2 (veja figura)

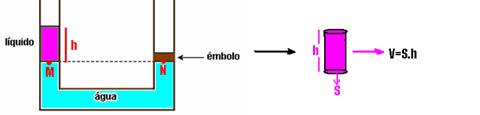
Vasos comunicantes com líquidos imiscíveis

 Vasos comunicantes Pelo teorema de Stevin, se os pontos da figura abaixo estiverem na

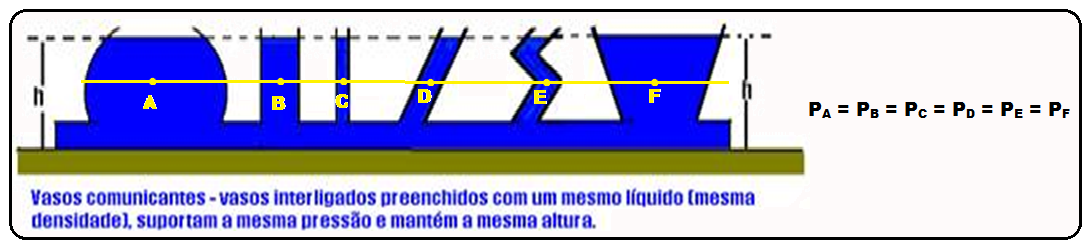
mesma profundidade (mesma horizontal, mesmo nível de altura) no interior de um mesmo líquido em equilíbrio, eles suportam a mesma pressão.

Por esse motivo a superfície livre de um líquido em equilíbrio é sempre plana e horizontal e está no mesmo nível.

  Como resolver exercícios com líquidos imiscíveis:

Se você tiver, por exemplo, três líquidos imiscíveis em um vaso comunicante, para estabelecer a

relação entre eles você deve proceder da seguinte maneira: 

Escolher convenientemente dois pontos P e Q, com mesmo nível horizontal, que separe as superfíes de contatos dos líquidos (figura).

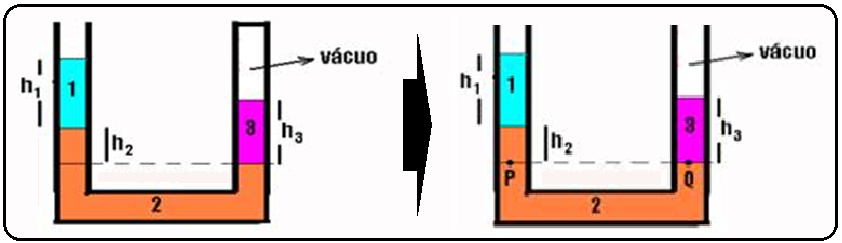
Esses pontos,como você sabe, possuem a mesma pressão    P_P = P_Q    P_p = P_atm + d₁.g.h₁ + d₂.g.h₂  P_Q = 0 + d₃.g.h₃  P_P = P_Q    P_atm + d₁.g.h₁ + d₂.g.h₂ = d₃.g.h₃, em seguida, achar o que é pedido.

Exercício exemplo:

Exercícios de vestibulares sobre

Experiência de Torricelli e Vasos comunicantes com líquidos imiscíveis em equilíbrio

01-(FGV) As figuras a seguir mostram um conta-gotas sendo abastecido:

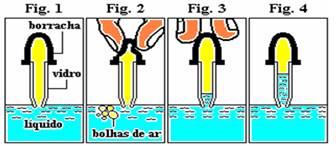
a) Por que aparecem bolhas como mostra a figura 2?

b) Por que a água entra no conta-gotas como mostram as figuras 3 e 4?

02-(UFSCAR-SP) Na garrafa térmica representada pela figura, uma pequena sanfona de borracha (fole), ao ser pressionada suavemente, empurra o ar contido em seu interior, sem impedimentos, para dentro do bulbo de vidro, onde um tubo vertical ligando o fundo do recipiente à base da tampa permite a retirada do líquido contido na garrafa.

Considere que o fole está pressionado em uma posição fixa e o líquido está estacionado no interior do tubo vertical próximo à saída. Pode-se dizer que, nessas condições, as pressões nos pontos 1, 2, 3 e 4 relacionam-se por

03-(UFRS-RS) A atmosfera terrestre é uma imensa camada de ar, com dezenas de quilômetros de altura, que exerce uma pressão sobre os corpos nela mergulhados: a pressão atmosférica.

O físico italiano Evangelista Torricelli (1608-1647), usando um tubo de vidro com cerca de 1 m de comprimento completamente cheio de mercúrio, demonstrou que a pressão atmosférica ao nível do mar equivale à pressão exercida por uma coluna de mercúrio de 76 cm de altura. O dispositivo utilizado por Torricelli era, portanto, um tipo de barômetro, isto é, um aparelho capaz de medir a pressão atmosférica.

A esse respeito, considere as seguintes afirmações.

I - Se a experiência de Torricelli for realizada no cume de uma montanha muito alta, a altura da coluna de mercúrio será maior que ao nível do mar.

II - Se a experiência de Torricelli for realizada ao nível do mar, porém com água, cuja densidade é cerca de 13,6 vezes menor que a do mercúrio, a altura da coluna de água será aproximadamente igual a 10,3 m.

III - Barômetros como o de Torricelli permitem, através da medida da pressão atmosférica, determinar a altitude de um lugar.

Quais estão corretas?

a) Apenas I.              

b) Apenas II.                  

c) Apenas I e II.                 

d) Apenas II e III.                

e) I, II e III.

04-(UEG-GO) Uma maneira de observar a pressão exercida por uma "coluna de líquido" é efetuar orifícios numa garrafa plástica de dois litros (como as de refrigerante) e enchê-las de água. A seguir, são apresentadas três situações experimentais bem simples.

Tendo em vista as informações apresentadas, é INCORRETO afirmar:

a) Na situação (I), com a garrafa tampada, a água não escoará, enquanto com a garrafa aberta a água jorrará pelo orifício.

b) Na situação (II), com a boca da garrafa totalmente tampada, a água não escoará pelos orifícios, porém, retirando-se a tampa, a água jorrará pelos dois orifícios.

c) Na situação (III), com a garrafa aberta, a água jorrará com menor velocidade pelo orifício superior do que pelo orifício inferior.

d) Na situação (III), tampando-se a boca da garrafa, a água jorrará apenas pelo orifício superior.

05-(PUC-PR) Algumas pessoas que pretendem fazer um piquenique param no armazém no pé de uma montanha e compram comida, incluindo sacos de salgadinhos.

Elas sobem a montanha até o local do piquenique. Quando descarregam o alimento, observam que os sacos de salgadinhos estão inflados como balões. Por que isso ocorre?

a) Porque, quando os sacos são levados para cima da montanha, a pressão atmosférica nos sacos é aumentada.

b) Porque a diferença entre a pressão do ar dentro dos sacos e a pressão reduzida fora deles gera uma força resultante que empurra o plástico do saco para fora.

c) Porque a pressão atmosférica no pé da montanha é menor que no alto da montanha.

d) Porque quanto maior a altitude maior a pressão.

e) Porque a diferença entre a pressão do ar dentro dos sacos e a pressão aumentada fora deles gera uma força resultante que empurra o plástico para dentro.

06-(UnB-DF) Ao nível do mar, o experimento de Torricelli para medir a pressão atmosférica usando o mercúrio metálico, cuja densidade é igual a 13,6g/cm³, apresenta uma coluna de mercúrio de 76cm.

Em um local de Brasília, situado 1.000m acima do nível do mar, o mesmo experimento apresenta uma coluna de mercúrio igual a 67cm. Calcule, em decímetros, a altura da coluna nesse local de Brasília se, em vez do mercúrio metálico, fosse usado o mercurocromo, cuja densidade é igual a 0,99g/cm³. Despreze a parte fracionária de seu resultado, caso exista. (considere g=9,8m/s²).

07- (Acafe-Se) Em Camboriú, a pressão atmosférica equivale a 76 cmHg e a água ferve a 100°C. Em,

 relação a Camboriú,no Pico da Neblina, ponto culminante do Brasil, a pressão atmosférica e o ponto de ebulição da água são, respectivamente:

a) menor e menor.        

b) maior e maior         

c) maior e menor.         

d) menor e maior.             

e) igual e igual. 

08-(UECE) Determine, aproximadamente, a altura da atmosfera terrestre se a densidade do ar fosse

 constante e igual a 1,3 kg/m³. Considere g = 10,0 m/s² e a pressão atmosférica ao nível do mar igual a 1,0 × 10⁵ N/m².

09-(PUCCAMP-SP) O cientista John Dalton é bastante conhecido elas suas contribuições para a Química e a Física. Descreveu a forma e o uso de vários instrumentos de meteorologia, fazendo

considerações sobre a variação da altura  barométrica. Além disso, Dalton descreveu uma doença hereditária que o impossibilitava de distinguir a cor verde da vermelha. Essa doença hereditária, causada por um alelo recessivo ligado ao cromossomo X, recebeu o nome de daltonismo.

Para medir pequenos valores de altitudes pode-se utilizar um barômetro fazendo a seguinte correspondência: para cada 100 m de altitude acima do nível do mar, 1,0 cm de mercúrio a menos na leitura do barômetro. Suponha um barômetro no qual se substitua o mercúrio por outro líquido com 1/4 da densidade do mercúrio, e que se leve esse barômetro a uma cidade a 900 m acima do nível do mar. Nessas condições, a leitura desse barômetro seria, em metros  desse outro líquido, igual a

Dado: pressão atmosférica ao nível do mar = 76 cm Hg

10-(UEL-PR) Uma sala tem as seguintes dimensões: 4,0m x 5,0m x 3,0m. A densidade do ar é de

 1,2kg/m³ e a aceleração da gravidade vale 10m/s². O peso do ar na sala, em newtons, é de:

11-(UFRJ-RJ) Aristóteles acreditava que a natureza tinha horror ao vácuo. Assim, segundo Aristóteles,  num tubo como o da figura, onde se produzisse o vácuo pela elevação de um êmbolo, a água subiria até preencher totalmente o espaço vazio. Séculos mais tarde, ao construir os chafarizes

 de Florença,os florentinos descobriram que a água recusava-se a subir, por sucção mais do que 10 metros. Perplexos, os construtores pediram a Galileu que explicasse esse fenômeno. Após brincar dizendo que talvez a Natureza não abominasse mais o vácuo acima de 10 metros, Galileu sugeriu que Torricelli e Viviani, então seus alunos, obtivessem a explicação.; como sabemos, eles conseguiram.

Com os conhecimentos de hoje, explique porque a água recusou-se a subir mais que 10 metros.

12-(UNESP) Para realizar a experiência que leva seu nome, Torricelli tomou um tubo de vidro, com cerca de 1m de comprimento, fechou uma das extremidades e encheu-o completamente de mercúrio (figura 1). Tampando a extremidade livre e invertendo o tubo, mergulhou essa extremidade em um recipiente  que também continha mercúrio.

Ao destapar o tubo, Torricelli verificou que o nível da coluna líquida descia, até estacionar a uma altura de cerca de 76cm acima do nível do mercúrio no recipiente (figura 2)

Concluiu, então, que a pressão atmosférica, P_atm, atuando na superfície do líquido no recipiente, equilibrava a coluna de mercúrio e, portanto, que a pressão atmosférica equivalia à pressão exercida pelo peso da coluna de mercúrio de 76cm.

a) Se essa experiência fosse realizada na Lua, em condições tais que o mercúrio não se solidificasse, toda coluna líquida desceria para o recipiente. Explique por quê.

b) Determine a altura da coluna de mercúrio, imaginando essa experiência realizada num planeta onde a pressão atmosférica fosse 10 vezes menor que a pressão atmosférica na Terra e a aceleração da gravidade na superfície 2,5 vezes, menor que a aceleração da gravidade na Terra.  (Suponha: desprezível a variação da massa específica do mercúrio com a gravidade e com a temperatura, d_Hg=13,6.10³kg/m³ e g_Terra=10m/s²).

13-(UFRJ-RJ) Para a alegria dos habitantes de Ruão, na França, em 1648 Pascal realizou, em público, várias experiências espetaculares, com o intuito de investigar a pressão atmosférica. No decorrer das experiências verificou-se que a mesma pressão atmosférica que equilibra uma coluna de água de 10m de altura é capaz de equilibrar uma coluna de vinho tinto de 15m de altura.

a) Calcule a razão d_água/d_vinho entre as densidades da água (d_água) e do vinho (d_vinho).

b) Se o vinho tivesse sido fornecido por um comerciante desonesto, que lhe acrescentara água, o resultado seria uma coluna de vinho misturado, maior, menor ou igual a 15m? Justifique sua resposta.

14-(PUC-SP) A figura representa um bule transparente de café ao ser tombado para que a bebida seja servida. O bule pode ser considerado como um sistema de vasos comunicantes em que o bico do recipiente comunica-se com o corpo principal.

A respeito da situação, são feitas as afirmativas:

I. Ao tombarmos o bule para servir o café, a superfície livre da bebida fica à mesma altura h em relação à linha de referência do sistema, tanto no bico como no corpo principal do bule, pois a pressão sobre a superfície livre do café é a mesma em ambos os ramos deste sistema de vasos comunicantes.

II. Se o café fosse substituído por óleo, a superfície livre do líquido não ficaria a uma mesma altura h em relação à linha de referência do sistema nos dois ramos do bule (bico e corpo principal) pois o óleo é mais denso do que o café.

III. Embora a superfície livre do café fique a uma mesma altura h nos dois ramos do bule, a pressão é maior na superfície do líquido contido no bico, pois este é mais estreito que o corpo principal do bule.

Dessas afirmativas, está correto apenas o que se lê em

15-(PUC-PR) A figura mostra um tubo em U, aberto nas duas extremidades. Esse tubo contém dois líquidos que não se misturam e que têm densidades diferentes. Sejam p_M e p_Nas pressões nos pontos M e N, respectivamente. Esses pontos estão no mesmo nível, como indicado pela linha tracejada, e as densidades dos dois líquidos são tais que d_M = 2d_N.

Nessas condições, é correto afirmar que:

a) p_M = 2p_N                       

b) p_M = p_N                     

c) p_M > p_N                          

d) p_M < p_N                  

e) Nada se pode afirmar a respeito das pressões.

16-(UNIFESP-SP) A figura representa um tubo em U contendo um líquido L e fechado em uma das extremidades, onde está confinado um gás G; A e B são dois pontos no mesmo nível.

Sendo p_o a pressão atmosférica local, p_g a pressão do gás confinado, p_A e p_B a pressão total nos pontos A e B (pressão devida à coluna líquida somada à pressão que atua na sua superfície), pode-se afirmar que:

17-(UFU-MG) Dois líquidos imiscíveis, de densidades ‚, são colocados em um tubo comunicante. Tendo por base essas informações, marque a alternativa que corresponde à situação correta de equilíbrio dos líquidos no tubo.

18-(UNIFESP-SP) O sistema de vasos comunicantes da figura contém água em repouso e simula uma situação que costuma ocorrer em cavernas: o tubo A representa a abertura para o meio ambiente exterior e os tubos B e C representam ambientes fechados, onde o ar está aprisionado.

Sendo P_A a pressão atmosférica ambiente, P_B e P_C as pressões do ar confinado nos ambientes B e C, pode-se afirmar que é válida a relação

a) P_A=P_B  > P_C              

b) P_A > P_B=P_C              

c) P_A > P_B > P_C                    

d) P_B > P_A > P_C                

e) P_B > P_C > P_A

19-(PUC-MG) No diagrama mostrado a seguir, x e y representam dois líquidos não miscíveis e homogêneos, contidos num sistema de vasos comunicantes em equilíbrio hidrostático.

Assinale o valor que mais se aproxima da razão entre as densidades do líquido y em relação ao líquido x.

20-(UNESP-SP) Uma pessoa, com o objetivo de medir a pressão interna de um botijão de gás contendo butano, conecta à válvula do botijão um manômetro em forma de U, contendo mercúrio. Ao abrir o registro R, a pressão do gás provoca um desnível de mercúrio no tubo, como ilustrado na figura.

Considere a pressão atmosférica dada por 10⁵ Pa, o desnível h = 104 cm de Hg e a secção do tubo 2 cm².

Adotando a massa específica do mercúrio igual a 13,6 g/cm³ e g = 10 m/s², calcule

a) a pressão do gás, em pascal.

b) a força que o gás aplica na superfície do mercúrio em A.

(Advertência: este experimento é perigoso. Não tente realizá-lo.)

21- (UNESP-SP) O tubo aberto em forma de U da figura contém dois líquidos não miscíveis, A e B, em equilíbrio. As alturas das colunas de A e B, medidas em relação à linha de separação dos dois líquidos, valem 50 cm e 80 cm, respectivamente.

a) Sabendo que a massa específica de A é 2,0 x 10³ kg/m³, determine a massa específica do líquido B.

b) Considerando g = 10 m/s² e a pressão atmosférica igual a 1,0 x 10⁵ N/m², determine a pressão no interior do tubo na altura da linha de separação dos dois líquidos.

22-(UFSM-RS) A figura representa um tubo em forma de U com água e petróleo, cujas densidades são, respectivamente, 1.000 kg/m³ e 800 kg/m³. Sabendo que h = 4 cm e que a aceleração da gravidade tem módulo 10 m/s², a pressão causada pelo petróleo, na interface A, vale, em Pa,

23-(UNIFESP-SP) Um fluido A, de massa específica ρ_A é colocado em um tubo curvo aberto, onde já existe um fluido B, de massa específica ρ_B. Os fluidos não se misturam e, quando em equilíbrio, B preenche uma parte de altura h do tubo. Neste caso, o desnível entre as superfícies dos fluidos, que se encontram à pressão atmosférica. É de 0,25h. A figura ilustra a situação descrita.

Considerando que as interações entre os fluidos e o tubo sejam desprezíveis, pode-se afirmar que a razão ρ_B/ρ_A é

 A

24-(UFPE-PE) Um tubo em U, aberto em ambas as extremidades e de seção reta uniforme, contém uma certa quantidade de água. Adiciona-se 500 mL de um líquido imiscível, de densidade d= = 0,8 g/cm3, no ramo da esquerda.

 Qual o peso do êmbolo, em newtons, que deve ser colocado no ramo da direita, para que os níveis de água nos dois ramos sejam iguais? Despreze o atrito do êmbolo com as paredes do tubo.

25-(UNIFESP-SP) A figura reproduz o esquema da montagem feita por Robert Boyle para estabelecer a lei dos gases para transformações isotérmicas. Boyle colocou no tubo certa quantidade de mercúrio, até aprisionar um determinado volume de ar no ramo fechado, e igualou os níveis dos dois ramos. Em seguida, passou a acrescentar mais mercúrio no ramo aberto e a medir, no outro ramo, o volume do ar aprisionado (em unidades arbitrárias) e a correspondente pressão pelo desnível da coluna de mercúrio, em polegadas de mercúrio. Na tabela, estão alguns dos dados por ele obtidos, de acordo com a sua publicação "New Experiments Physico-Mechanicall, Touching the Spring of Air, and its Effects", de 1662.(http://chemed.chem.purdue.edu/gench m/history/)

a) Todos os resultados obtidos por Boyle, com uma pequena aproximação, confirmaram a sua lei. Que resultados foram esses? Justifique.

b) De acordo com os dados da tabela, qual a pressão, em pascal, do ar aprisionado no tubo para o volume de 24 unidades arbitrárias?

Utilize para este cálculo: pressão atmosférica p_o = 1,0 × 10⁵ pascal; densidade do mercúrio d(Hg) = 14 × 10³ kg/m³; g=10m/s²

26-(UFPE) Um tubo em forma de U com seção reta circular igual a 1,0cm² contém dois líquidos miscíveis A e B, separados por um diafragma preso a um pino, que impede a mistura dos líquidos, como mostra a figura.

As densidades dos dois líquidos são d_A=5,0g/cm³ e d_B=0,5g/cm³. Qual o módulo da força resultante sobre o diafragma, em unidades de 10^-4N, devida apenas às forças exercidas pelos dois líquidos?

27-(ITA-SP) Um vaso comunicante  em forma de U possui duas colunas de mesma altura  h=42,0 cm, preenchidas com água (d_água=1,0g/cm³) até a metade. Em seguida, adiciona-se óleo  de massa específica igual a 0,80g/cm³ a uma das colunas até a coluna estar totalmente preenchida conforme a figura B.

A coluna de óleo terá comprimento de:

a) 14,0cm                          

b) 16,8cm                          

c) 28,0cm                           

d) 35,0cm                         

e) 37,8cm

28-(FUVEST) Um tubo em forma de U, graduado em centímetros, de pequeno diâmetro, secção constante, aberto nas extremidades, contém dois líquidos I e II, incompressíveis, em equilíbrio, e que não se misturam. A densidade do líquido I é d_I = 1.800 kg/m3 e as alturas h_I = 20 cm e h_II = 60 cm, dos respectivos líquidos, estão representadas na figura.

A pressão atmosférica local vale P_o = 10⁵ N/m².

a) Determine o valor da densidade d_II do líquido II.

b) Faça um gráfico quantitativo da pressão P nos líquidos, em função da posição ao longo do tubo, utilizando os eixos desenhados acima. Considere zero (0) o ponto médio da base do tubo; considere valores positivos as marcas no tubo à direita do zero e negativos, à esquerda.

c) Faça um gráfico quantitativo da pressão P’ nos líquidos, em função da posição ao longo do tubo, na situação em que, através de um êmbolo, empurra-se o líquido II até que os níveis dos líquidos nas colunas se igualem, ficando novamente em equilíbrio. Utilize os mesmos eixos do item b.

29-(FUVEST-SP) Um tanque industrial, cilíndrico, com altura total H_o=6,0m, contém em seu interior água até uma altura h_o, a uma temperatura de 27°C (300 K).

O tanque possui um pequeno orifício A e, portanto, está à pressão atmosférica P_o, como esquematizado em I. No procedimento seguinte, o orifício é fechado, sendo o tanque invertido e aquecido até 87°C (360 K).

Quando o orifício é reaberto, e mantida a temperatura do tanque, parte da água escoa, até que as pressões no orifício se equilibrem, restando no interior do tanque uma altura h₁=2,0m de água, como em II.

Determine

a) a pressão P₁, em N/m², no interior do tanque, na situação II.

b) a altura inicial h_o da água no tanque, em metros, na situação I.

30-(CFT-MG) O desenho a seguir representa um manômetro de mercúrio de tubo aberto, ligado a um recipiente contendo gás. O mercúrio fica 30 cm mais alto no ramo da direita do que no da esquerda. Quando a pressão atmosférica é 76 cmHg, a pressão absoluta do gás, em cmHg, é

31-(UNIFESP-SP) Um fluido A, de massa específica ρ_A, é colocado em um tubo curvo aberto, onde já existe um fluido B, de massa específica ρ_B. Os fluidos não se misturam e, quando em equilíbrio, B preenche uma parte de altura h do tubo. Neste caso, o desnível entre as superfícies dos fluidos, que se encontram à pressão atmosférica, é de 0,25 h. A figura ilustra a situação descrita.

Considerando que as interações entre os fluidos e o tubo sejam desprezíveis, pode-se afirmar que a razão ρ_B /ρ_A é

32-(UFF-RJ) Um recipiente transparente é preenchido com água até uma certa altura antes de ser hermeticamente tampado. Uma certa quantidade de ar fica, assim, presa no interior do recipiente e exerce sobre a superfície livre do líquido uma pressão igual à pressão atmosférica p_o. A figura 1 ilustra a situação descrita.

Em seguida, uma torneira, localizada no fundo do recipiente e com canal de escoamento fino o suficiente para evitar a entrada de

ar, é aberta, deixando que o líquido escoe. Esse escoamento se interrompe espontaneamente quando a superfície livre da água no interior do recipiente está a uma altura H relativa ao nível da torneira, como mostra a figura 2.

a) Determine a pressão exercida pela massa de ar acima da superfície livre da água na situação final de equilíbrio hidrostático, em função da pressão atmosférica local p_o, da altura H, da densidade da água ρ_o e da aceleração da gravidade local g.

b) O resultado obtido no item anterior sugere uma experiência simples, capaz de obter a pressão atmosférica local p_o, através da medida das quantidades H, V e ΔV. O gráfico abaixo mostra os

resultados obtidos nessas experiências quando feitas em duas cidades A e B, localizadas em diferentes altitudes em relação ao nível do mar. Qual das duas cidades está localizada a uma maior altitude? Justifique sua resposta.

33-(UFSM-RS)

Dentro de uma mina de carvão, existe acumulo de água. Para retirar essa água, uma bomba de

sucção e instalada na boca da mina, ao nível do solo. Assim,

a) quanto maior a profundidade da água, maior deve ser a potencia do motor que aciona a bomba.

b) se a profundidade da água é maior  do que 11 m, a bomba não retira água da mina.

c) se a profundidade da água é grande, duas ou mais bombas devem ser instaladas em série ao nível do solo.

d) a mesma bomba pode retirar a água em qualquer profundidade, mas, com profundidades maiores, diminui a vazão nas tubulações.

e) a bomba de sucção não pode retirar água da mina, porque só funciona no vácuo.

34-(UFF-RJ)

Um recipiente transparente é preenchido com água até uma certa altura antes de ser hermeticamente tampado. Uma certa quantidade de ar fica, assim, presa no interior do recipiente e exerce sobre a superfície livre do líquido uma pressão igual à pressão atmosférica p_o. A figura 1 ilustra a situação descrita. Em seguida, uma torneira, localizada no fundo do recipiente e com canal de escoamento fino o suficiente para evitar a entrada de ar, é aberta, deixando que o líquido escoe. Esse escoamento se interrompe espontaneamente quando a superfície livre da água no interior do recipiente está a uma altura H relativa ao nível da torneira, como mostra a figura 2.

a) Determine a pressão exercida pela massa de ar acima da superfície livre da água na situação final de equilíbrio hidrostático, em função da pressão atmosférica local p_o, da altura H, da densidade da água ρ_e e da aceleração da gravidade local g.

b) Considere isotérmica a expansão sofrida pela massa de ar interna ao recipiente, durante o processo descrito. Use essa hipótese para determinar outra vez a pressão exercida por essa massa de ar ao final desse processo, agora em função de sua pressão inicial, que era a pressão atmosférica p_o, do volume V que ocupava inicialmente, e do volume ∆V de líquido escoado.

c) Os resultados obtidos nos itens a) e b) sugerem uma experiência simples, capaz de obter a pressão atmosférica local p_o, através da medida das quantidades H, V e ∆V. O gráfico abaixo mostra os resultados obtidos nessas experiências quando feitas em duas cidades A

e B, localizadas em diferentes altitudes em relação ao nível domar. Qual das duas cidades está localizada a uma maior altitude? Justifique sua resposta.

 Resolução comentada dos exercícios de vestibulares sobre

Experiência de Torricelli e Vasos comunicantes com líquidos imiscíveis em equilíbrio

01- a) São bolhas de ar que é expulso do interior do vidro do conta-gotas.

b) Com o ar expulso, a pressão interna diminui e a maior pressão externa empurra o líquido para dentro.

02- O ar no interior da sanfona e no interior do bulbo de vidro e em contato com a superfície do líquido está igualmente concentrado (igualmente denso) e suportam a mesma pressão (P₁=P₂)  ---   como 2 (no bulbo de vidro) e 3 (no tubo) estão no mesmo nível, suportam também a mesma pressão (P₁=P₂=P₃)  ---  no tubo , P₃>P₄, pois 3 suporta maior altura de coluna líquida que 4  ---  R- C

03- I- Falsa, será menor, pois no alto da montanha a pressão é menor.

II- Correta – veja teoria

III- Correta – veja teoria

04- A alternativa incorreta é a D, pois com a boca da garrafa totalmente tampada a água não jorrará por nenhum dos dois orifícios, pois a pressão externa é maior que a interna  ---  R- D

05- À medida que os sacos sobem sobe seu volume vai aumentando porque a diferença entre a pressão do ar dentro dos sacos e a pressão cada vez mais reduzida fora dela gera uma força resultante que empurra o plástico da bexiga para fora  ---  R- B.

06- Cálculo do valor da pressão atmosférica em Brasília  ---  P=d_Hg.g.h=13,6.10³.9,8.0,67 

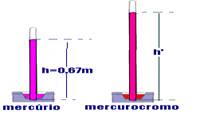
---  P=8,9.10⁴N/m² (Pa)  --- Essa pressão, em Brasília (P=8,9.10⁴N/m²), quando medida com mercurocromo de densidade d_mc=0,99.10³kg/m³) equivalerá à uma altura de  ---  P=d_mc.g.h’  ---  8,9.10⁴=0,99.10³.9,8.h’  ---  h’=8,9.10⁴/9,702.10³  ---  h’=0,92.10¹  ---  h’=9,2m=92dm

07- Quanto maior a altitude, menor é a pressão e quanto menor a pressão menor é a temperatura de ebulição da água  ---

R- A

08- A pressão ao nível do mar corresponde à pressão devida a altura da coluna de ar  ---  P_atm=d_ar.g.h  ---  1,0.10⁵=1,3.10³.10.h  ---  h=78.10²m=7,8.10³m=7,8km  ---  R- C

09- Ao nível do mar o barômetro de mercúrio equilibra uma coluna de 76cm de Hg  ---  como a pressão diminui de 1cm de Hg a cada 100m, na altura de 900m a coluna de mercúrio diminuirá de 9cm e, terá uma altura de P=76-9=67cmHg  ---  sendo a densidade do líquido 4 vezes menor que a do mercúrio, ela equilibrará uma altura 4 vezes maior de líquido  --- 

P=67 x 4=268cm de líquido  ---  P=2,68m de líquido  ---  R- C

10- V=4m.5m.3m=60m³  ---  d=m/V  ---  1,2=m/60  ---  m=72kg  ---  P=mg=72.10  ---  P=720N  ---  R- A

11- Observe na figura abaixo que a pressão na superfície da água (ponto Q) é a mesma que aquela devido à altura da coluna

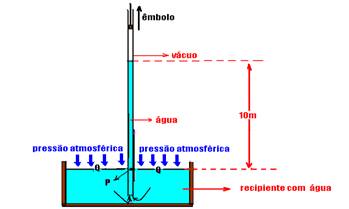
 de água (ponto p)  ---  P_Q=P_p  ---  densidade d_água=10³kg/m³ e g=9,8m/s²  --- P_Q= P_atm  ---  P_p==d_água.g.h_água  ---  1,01.10⁵=10³.9,8.h_água  ---  h_água=10,3m  ---  portanto, a pressão atmosférica equilibra uma coluna de água de altura aproximadamente 10m e, essa pressão não consegue empurrar qualquer coluna de água a uma altura superior a 10m

12- a) Na Lua não existiria atmosfera que exerceria pressão sobre a coluna de mercúrio, de modo que a coluna não subiria.

b) P_planeta=d_Hg.1g/2,5.h  ---  1,0.10⁵/10=13,6.10³.10/2,5.h  ---  h=1,0.10⁴/54,4.10⁴  ---  h=0,0184m  ---  h=184mm     

13- a) d_água.g.10=d_vinho.g.15 ---  d_água/d_vinho=1,5

b) menor que 15m  ---  valor compreendido entre 10m e 15m, dependendo da quantidade de água acrescentada ao vinho

14- Todos os pontos da superfície livre do café estão submetidos à mesma pressão e consequentemente possuem o mesmo nível horizontal em relação à linha de referência do sistema  ---  R- C

15- Todos os pontos que se encontram na mesma linha horizontal (altura, profundidade)estão submetidos à mesma pressão   ---  R- B

16- p_A=p_B (mesmo nível)  ---  o gás pressiona mais o líquido que a pressão atmosférica pó  ---  p_g > p_o  ---  R- C

17- O líquido 2 é mais denso e deve ficar na parte inferior dos vasos  ---  R- A

18- Observe que P_B é maior que P_A (pressiona mais a coluna de água) e P_C é menor que P_A(pressiona menos a coluna de água)  ---  R- D

19- A pressão nos pontos M e N é a mesma  ---  P_M=P_N  ---  P_atm  + d_X.g_..18=P_atm + d_X.g.10 + d_y.g.10 

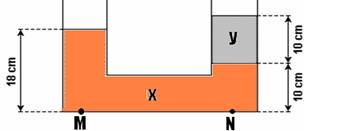
---  18.d_X=10.d_Y +10.d_X  ---  8d_X=10d_y  ---  d_Y/d_X=8/10=0,8  ---  R- A  

20- a) A pressão do gás no botijão é a mesma que no ponto A (P_A=P_gás), que por sua vez é a mesma

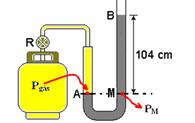
que no ponto M  ---P_gás=P_M­  ---  P_gás=P_atm + d_Hg.g.h=10⁵ + 13,6.10³.10.1,04  ---  P_gás=10⁵ + 14,44.10⁴  ---  P_gás=1,0.10⁵ + 1,44.10⁵  ---  P_gás=2,44.10⁵ Pa

b) Em a  ---  P_gás=F/S  ---  2,44.10⁵=F/2.10^-4  ---  F=48,8N

21- a) A pressão nos pontos M e N da figura é a mesma  ---  P_M=P_N  ---  P_atm + d_B.g.0,8 = P_atm  +

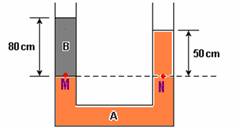
d_A.g.0,5  ---  0,8.d_B =0,5_.d_A  ---  0,8.d_B=0,5.2.10³  ---  d_B=10³/0,8  ---  d_B=1,25.10³kig/m³

b) P_M= P_atm + d_B.g.0,8=1,0.10⁵ + 1,25.10³.10.0,8  ---  P_M=P_N=1,0.10⁵ + 10.10³=1,0.10⁵+ 0,1.10⁵ ---  P_M=P_N=1,1.10⁵Pa

22- Pressão causada pelo petróleo, P_atm não participa  ---  P_A=P_B  ---  P_B=d_B.g.h=  1,0.10³.10.4.10^-2= 40.10  ---  P_A=P_B=400Pa  ---

 R- B

23- P_M=P_N  ---  P_atm + ρ_B.g.h = P_atm + ρ_A.g.0,75h  

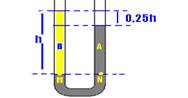
ρ_B=0,75ρ_A  ---  ρ_B/ρ_A=0,75  ---  R- A

24- V_l=500mL=500.10^-3L=500.10^-3dm³=500.10^-3.10^-3m³  ---  V_l=5.10^-4m³  ---  V_l=S.h  ---  5.10^-4=S.h 

 ---  h=5.10^-4/S  --- d_l=0,8.10³  ---  d_l=8.10²kg/m³  ---  P_M=P_atm + d_l.g.h= P_atm + 8.10².10.5.10^-4/S  --- P_M=P_atm + 4/S  ---  P_N=P_atm + P_êmbolo  ---  P_N=P_atm + F/S=P_atm + p/S  ---  P_N=P_atm + p/S  ---  P_M=P_N  ---  P_atm + 4/S=P_atm + p/S  ---  p=4N

25- a) Observe na última coluna que o produto  PxV é praticamente constante (Lei de Boyle para transformações isotérmicas)

b) Supondo que cada 8 unidades tenha 0,5cm  ---  regra de três  ---  8u - 0,5m  ---  24u – h  ---  h=1,5m  ---  P=P_o + dgh=1,0.10⁵ + 14.10³.10.1,5  ---  P=3,1.10⁵N/m²(Pa)

26- Sendo a seção reta circular (S=1,0.10^-4m²) no diafragma a mesma, e como a densidade do líquido A é maior que a do líquido B, a intensidade da força resultante sobre o diafragma vale  ---  F_R=F_A – F_B  ---  P_A=F_A/S  ---  F_A=P_A.S  ---  F_B=P_B.S  ---  F_R=P_A.S - P_B.S=S(P_A – P_B)  ---  F_R=S.(d_A.g.h – d_B.g.h)=1,0.10^-4.(5.10³.10.0,1 – 0,5.10³.10.0,1)=

1,0.10^-4.4,5.10³  ---  F_R=4.500.10^-4 N

27- Observe a figura abaixo, onde os pontos R e S estão no mesmo nível e suportam a mesma

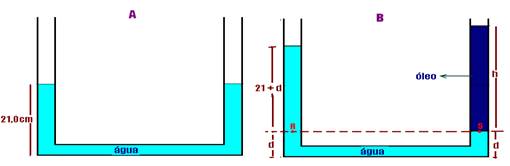
pressão  ---  P_R=P_S     ---    P_R=P_atm + d_água.g.(21 + d)  ---  P_S =P_atm + d_óleo.g.h  ---  P_R=OS  ---  P_atm + d_água.g.(21 + d)= P_atm + d_óleo.g.h  ---  d_água.(21 + d)=  d_óleo.h  ---   observe que h + d=42  ---  d=42 - h  ---  d_água.(21 + 42 - h)=d_óleo.h  ---  1.63 – 1.h=0,8h  ---  1,8h=63  ---  h=63/1,8  ---  h=35cm  ---  R- D

28- a) As pressões exercidas pelos líquidos I e II no fundo do tubo (pontos M e N) são iguais ---  P_M=P_N   ---  P_o + d_I . g . h_I = P_o + d_II . g . h_II  ---  1800 . g . 0,20 = d_II . g . 0,60  ---    d_II = 600 kg/m³

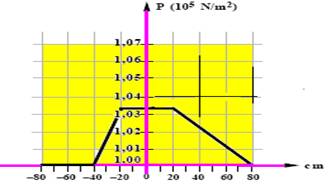
b) Nos pontos compreendidos entre -80cm até -40cm a pressão é constante e é a atmosférica de valor P_o=10⁵N/m²  ---  np ponto 80cm a pressão também é a atmosférica de valor P_o=10⁵N/m²  ---  nos pontos de abscissas -20cm até + 20cm a pressão é constante e vale  ---  P_-20=P_atm  + d_I.g.h_I= 10⁵ + 1800.10.0,20=1,036.10⁵ N/m²   ---  de -20cm até + 20cm – P=1,036.10⁵N/m²  ---  entre esses valores a variação é linear (reta inclinada)  ---  veja gráfico abaixo

c) Para que os níveis dos líquidos se igualem, a superfície livre do líquido I deve subir 20cm, estacionando na abscissa

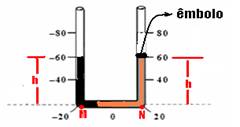
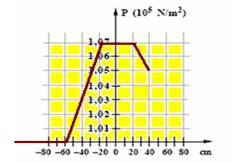
-60cm e a do líquido II descer 20cm, estacionando na abscissa +60cm  --- nos pontos M e N a pressão é a mesma e, no ponto M vale  ---  P_M=P_atm + d_I.g.h=10⁵ + 1.800.10.0,40=10⁵ + 0,072.10⁵  ---  P_M=P_N= 1,072.10⁵N/m²  ---   pressão no ponto de abscissa +60cm  ---  P_N=P_+60cm + d_II.g.h  ---  1,072.10⁵=P_+60cm + 600.10.0,40  ---  P_+60cm=1,072.10⁵ – 0,024.10⁵  ---  P_+60cm=1,048.10⁵N/m²  ---  gráfico abaixo

29- a) Na figura II, na extremidade do orifício de altura h₁=2,0m a pressão que atua é a pressão atmosférica P_o=1,0.10⁵N/m²  ---  P_o=dgh₁ + P₁  ---  1,0.10⁵=1,0.10³.10.2,0 + P₁  ---  P₁=1,0.10⁵ – 2,0.10⁴  ---  P₁=8,0.10⁴N/m²

b) Chamando de S a área da base do tanque  ---  lei geral dos gases perfeitos  ---  P_o.V_o/T_o=P₁.V₁/T₁  ---  1,0.10⁵.S(6,0 – h_o)/300 = 8,0.10⁴.S.(6,0 – 2,0)/360  ---  h_o=10/3 m=3,3m

30- P_M=P_gás=P_N ---  P_N=P_atm + dgh=76cmHg + 30cmHg  --- 

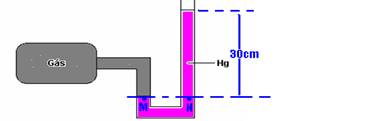
P_gás=106cmHg  ---  R- D

31- P_M=P_atm + ρ_A.g.h  ---  P_N=P_atm + ρ_B.g (h – 0,25h)  ---  P_M=P_N  ---  P_atm + ρ_A.g.h=P_atm+ ρ_B.g.(h-0,25)  ---  ρ_A.h= ρ_B.(h-0,25h)  ---  ρ_A.h= ρ_B.0,75h  ---  ρ_B/ρ_A0,75  ---  R- A

 Para que o óleo escoe com facilidade da lata, você deve fazer dois furos na mesma, um para que a pressão atmosférica empurre o óleo para fora da lata e o outro para que o óleo saia da mesma.

32- a) O escoamento do líquido se interrompe quando a pressão no fundo do recipiente se iguala à pressão no bico da torneira, que é a pressão atmosférica p_o  ---  chamando de p a pressão exercida sobre a superfície livre do líquido nesta situação  ---  pelo teorema de Stevin  ---  p_o = p + ρg H  ---  P_o – P=ρgH  ---  ΔP=ρgH

c) Como a pressão atmosférica diminui com a altitude, a cidade localizada à maior altitude é aquela na qual é menor a pressão atmosférica  ---  a cidade B

33- a) Falsa  ---  uma bomba de sucção é uma bomba que retira o ar de sua extremidade superior, produzindo o vácuo  ---  com ar  expulso,a pressão interna diminui e a maior pressão externa empurra o líquido para cima  ---  isso ocorre independente da espessura dos canos e da potência do motor que produz a sucção (vácuo).

b) Correta  --- Se a experiência de Torricelli for realizada ao nível do mar, mas com água, cuja densidade é 13,6 vezes menor que a do mercúrio, a altura da coluna de água será aproximadamente igual a 10,3m.

c) Falsa  ---  veja justificativa a.

d) Falsa  ---  veja justificativa b.

e) Falsa.

R- B   

34- a) O líquido só vai parar de escoar pela torneira quando a pressão (P_o) em todos os pontos do fundo do recipiente for igual à

pressão na ponta da torneira que está aberta e essa pressão é a pressão atmosférica (P_o)  ---  isso ocorre porque todos os pontos de mesmo nível de altura (mesma horizontal) suportam a mesma pressão (teorema de Stevin)  ---  chamando de P a pressão na interface ar-líquido e de P_o(pressão atmosférica) a pressão na parte inferior do líquido, pelo teorema de Stevin  ---  P_o = P + ρ.g.H  ---  P= P_o - ρ.g.H.

b) Veja a figura abaixo que mostra a pressão e o volume do ar contido no recipiente antes e depois do volume ∆V de água ser

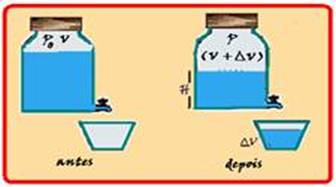
transferido  ---  numa evolução isotérmica a temperatura é constante (T_o = T)  ---  P_o.V_o/T_o = P.V/T  ---  P_o.V = P.(V + ∆V)  ---  P=P_o.V/(V + ∆V).

c) Observe no gráfico que a menor pressão atmosférica (P_o=ρ.g.H) é a da cidade B  ---  como a pressão atmosférica diminui com a

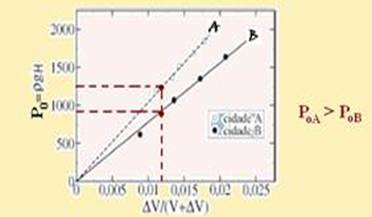
altitude,quanto menor a pressão atmosférica maior é a altitude da cidade  ---  a cidade B está numa altitude maior.