Teorema de Stevin – Pressão Hidrostática – Vasos Comunicantes

Teorema de Stevin - Pressão no interior de um líquido em repouso

Considere um fluido (líquidos que fluem para as regiões inferiores de um recipiente até preenchê-los totalmente e gases que se expandem para encher os recipientes) em equilíbrio (vertical e horizontal) no interior de um recipiente.

Observe a figura abaixo onde, quem varia é apenas a pressão vertical, e que o líquido que é homogêneo e incompressível está em equilíbrio.

Na superfície livre superior (A) desse líquido age a pressão atmosférica (P_atm)_, exercida pela coluna de ar que está sobre ele. Num ponto qualquer B do interior do líquido, a pressão (P_B) que age é a soma da pressão atmosférica com a pressão exercida pela coluna líquida h acima dele, devido à seu peso.

O que você deve saber, informações e dicas

 A pressão no ponto B devida apenas à coluna líquida P_líquido= d_líquido.g.h é chamada de pressão

hidrostática e P_B= P_atm + d_líquido.g.h é chamada de pressão total, pressão absoluta ou simplesmente pressão.

 A pressão exercida por uma coluna líquida não depende das dimensões do recipiente que a contém, mas apenas da natureza do líquido, fornecida pela sua densidade (d), do local (g) e da altura da coluna (h).

 Uma das conseqüências do teorema de Stevin é de que todos os pontos de uma superfície horizontal (a uma mesma altura h) suportam a mesma pressão, desde que o líquido seja o mesmo.

Uma das utilidades práticas dessa conseqüência são os vasos comunicantes onde um mesmo

líquido que está em recipientes de formatos e volumes diferentes, interligados entre si, ficam sempre na mesma altura, pois suportam a mesma pressão.

Os reservatórios de água de uma cidade, interligados aos de uma residência, funcionam como um sistema de vasos comunicantes, onde, devido à tendência de nivelarem suas alturas, os

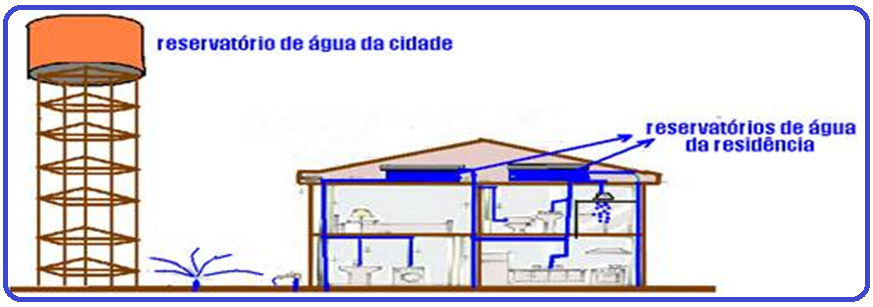
reservatórios de água da cidade devem estar numa altura superior aos das residências e estes, numa altura superior às das torneiras, chuveiros, descargas, etc.

No (SI) a unidade de pressão é o pascal (Pa), onde a força é medida em newton (N) e a área em metro quadrado (m²) sendo 1Pa = 1N/m².

Ao nível do mar a pressão atmosférica é de aproximadamente 1atm sendo 1 atm =1,0.10⁵ N/m² (Pa).

Questões com características de “dicas” 05, 07, 08, 10, 20 e 34. Vejam os exercícios e as resoluções.

Exercícios de vestibulares sobre

Teorema de Stevin – Pressão Hidrostática – Vasos Comunicantes

01-(UERJ-RJ) Algumas cafeteiras industriais possuem um tubo de vidro transparente para facilitar a verificação da quantidade de café no reservatório, como mostra a figura. Observe que os pontos A e B correspondem a aberturas na máquina.

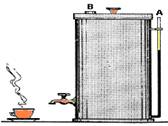
(Adaptado de MÁXIMO, Antônio & ALVARENGA, Beatriz. Curso de Física. São Paulo: Harbra, 1992.)

Admita que a área da seção reta horizontal do reservatório seja 20 vezes maior do que a do tubo de vidro.

Quando a altura alcançada pelo café no tubo é x, a altura do café no interior do reservatório corresponde a:

02-(UERJ-RJ) Para um mergulhador, cada 5 m de profundidade atingida corresponde a um acréscimo de 0,5 atm na pressão exercida sobre ele. Admita que esse mergulhador não consiga respirar quando sua caixa toráxica está submetida a uma pressão acima de 1,02 atm.

Para respirar ar atmosférico por um tubo, a profundidade máxima, em centímetros, que pode ser

 atingida pela caixa torácica desse mergulhador é igual a: (d_água=10³kg/m³ e g=10ms²)

03-(UFPE-PE) É impossível para uma pessoa respirar se a diferença de pressão entre o meio externo e o ar dentro dos pulmões for maior do que 0,05 atm. Calcule a profundidade máxima, h, dentro d'água, em cm, na qual um

 mergulhador pode respirar por meio de um tubo, cuja extremidade superior é mantida fora da água. (d_água=10³kg/m³ e g=10m/s²)

04-(CPS-SP) Quando você está na lanchonete tomando um refrigerante num copo com canudo, o

líquido sobe em direção à sua boca, em virtude de

a) a pressão no interior da sua boca ser maior do que a pressão atmosférica.

b) a pressão atmosférica e da sua boca serem iguais.

c) a pressão atmosférica ser variável em função do volume do refrigerante.

d) a pressão atmosférica ser maior que a pressão na boca e "empurrar" o líquido no canudo.

e) a pressão atmosférica da sua boca não interferir ao tomar o refrigerante.

05-(UFMG-MG) Um reservatório de água é constituído de duas partes cilíndricas, interligadas, como mostrado na figura.

A área da seção reta do cilindro inferior é maior que a do cilindro superior.

Inicialmente, esse reservatório está vazio. Em certo instante, começa-se a enchê-lo com água, mantendo-se uma vazão constante.

Assinale a alternativa cujo gráfico MELHOR representa a pressão, no fundo do reservatório, em função do tempo, desde o instante em que se começa a enchê-lo até o instante em que ele começa a transbordar.

06-(CFT-CE) Na figura a seguir, temos três recipientes, 1, 2 e 3, de pesos desprezíveis e de bases de mesma área. Os recipientes são preenchidos com água até uma mesma altura e colocados sobre três balanças. Comparando os valores das forças exercidas pela água nas bases dos recipientes  e comparando os valores das forças exercidas pelas balanças sobre as mesmas bases, , é correto afirmar que:

07-(PUC-MG) A figura representa duas caixas d'água, abertas para o ar, interligadas por um cano com uma válvula de passagem. A caixa da esquerda está cheia. Quando a válvula é aberta, a caixa da direita começa a encher até que o nível da água nas duas caixas seja o mesmo.

É CORRETO afirmar:

a) Ao final do processo, a pressão no fundo da caixa à esquerda será menor que no início.

b) Durante o processo, a velocidade de escoamento da água é constante.

c) Ao final do processo, a pressão no fundo da caixa à direita será maior que a pressão no fundo da caixa à esquerda.

d) Durante o processo, a velocidade de escoamento da água aumenta.

08-(FGV) A figura ao lado representa uma talha contendo água.

 A pressão da água exercida sobre a torneira, fechada, depende:

a) do volume de água contido no recipiente.     

b) da massa de água contida no recipiente.     

c) do diâmetro do orifício em que está ligada a torneira.     

d) da altura da superfície da água em relação ao fundo do recipiente.     

e) da altura da superfície da água em relação à torneira.

09-(UERJ-RJ) Uma moeda é encontrada por um mergulhador no fundo plano de um lago, a 4 m de profundidade, com uma das faces, cuja área mede 12 cm², voltada para cima.

A força, em newtons, exercida sobre a face superior da moeda em repouso no fundo do lago equivale a:

10-(FUVEST-SP) Um vaso cilíndrico I contém água à altura de 1,0m e está ligado, por um tubo fino, a outro vaso cilíndrico II, inicialmente vazio, com diâmetro duas vezes maior que o de I. O tubo de comunicação está a 0,5m de altura e fechado, no início, por uma torneira T, como mostra a figura.

Considere: d_água=10³kg/m³, P_atm=10⁵N/m² e g=10m/s²

a) Abrindo-se a torneira T, que altura atinge a água no vaso II?

b) Antes de abrir a torneira, qual era a pressão da água no fundo do vaso I?

11-(UFRJ-RJ)

No terceiro quadrinho, a irritação da mulher foi descrita, simbolicamente, por uma pressão de 1000 atm.

Suponha a densidade da água igual a 1000kg/m³, 1 atm = 10⁵ N/m² e a aceleração da gravidade g = 10m/s².

Calcule a que profundidade, na água, o mergulhador sofreria essa pressão de 1000 atm.

12-(FUVEST-SP) O organismo humano pode ser submetido, sem conseqüências danosas, a uma pressão de no máximo 4.10⁵N/m² e a taxa de variação de pressão de no máximo 10⁴N/m² por segundo.

Nessas condições:

a) qual a máxima profundidade recomendada a um mergulhador?

b) qual a máxima velocidade de movimentação na vertical recomendada para um mergulhador?

13-(UFRJ-RJ) Um líquido de densidade 1,25 g/cm³ está em repouso dentro de um recipiente.

No fundo do recipiente existe uma conexão com um tubo cilíndrico de 2,0 cm de diâmetro. O tubo possui um êmbolo cuja parte exterior está sob a ação da atmosfera e em contato com uma mola. Considere que não haja atrito entre o êmbolo e o tubo cilíndrico.

Num determinado experimento, a força da mola sobre o êmbolo tem módulo igual a 6,28 N.

Calcule a altura h do líquido indicada na figura. Use π = 3,14.

14-(Covest-Pe) Se o fluxo sanguíneo não fosse ajustado pela expansão de artérias, para uma pessoa em pé a diferença de pressão arterial entre o coração e a cabeça seria de natureza puramente hidrostática.

Nesse caso, para uma pessoa em que a distância entre a cabeça e o coração vale 50 cm, qual o valor em mmHg dessa diferença de pressão ? ( Considere a densidade do sangue igual a 10³Kg/m³ e a densidade do mercúrio igual a 13,6.10³ Kg/m³.)

15-(UEPB) É do conhecimento dos técnicos de enfermagem que, para o soro penetrar na veia de um paciente, o nível do soro deve ficar acima do nível da via, conforme a figura, devido à pressão sanguínea sempre superior à pressão atmosférica.

Considerando a aceleração da gravidade g=10m/s², a densidade do soro d=1,0g/cm³, a pressão exercida, exclusivamente, pela coluna de soro na veia do paciente P=9,0.10³Pa, a altura em que se encontra o nível do soro do braço do paciente, para que o sangue não saia em vez do soro entrar, em metros, é de:

16-(UFRJ-RJ) Dois fugitivos devem atravessar um lago sem serem notados. Para tal, emborcam um pequeno barco, que afunda com o auxílio de pesos adicionais. O barco emborcado mantém, aprisionada em seu interior, uma certa quantidade de ar, como mostra a figura.

No instante retratado, tanto o barco quanto os fugitivos estão em repouso e a água está em equilíbrio hidrostático. Considere a densidade da água do lago igual a 1,00 × 10³ kg/m³ e a aceleração da gravidade igual a 10,0 m/s².

Usando os dados indicados na figura, calcule a diferença entre a pressão do ar aprisionado pelo barco e a pressão do ar atmosférico.

17-(UNIFOR-CE) Afundando 10,0m na água, fica-se sob o efeito de uma pressão, devida ao líquido, de 1,00 atmosfera.

 Em um líquido com 80% da densidade da água, para ficar também sob o efeito de 1,00 atmosfera de pressão devida a esse líquido, precisa-se afundar, em metros,

18-(UFG-GO) A instalação de uma torneira num edifício segue o esquema ilustrado na figura a seguir

Considerando que a caixa d'água está cheia e destampada, a pressão no ponto P, em N/m², onde será instalada a torneira, é

19-(UNESP-SP) Para que se administre medicamento via endovenosa, o frasco deve ser colocado a uma certa altura acima do ponto de aplicação no paciente. O frasco fica suspenso em um suporte vertical com pontos de fixação de altura variável e se conecta ao paciente por um cateter, por onde desce o medicamento.

 A pressão na superfície livre é a pressão atmosférica; no ponto de aplicação no paciente, a pressão deve ter um valor maior do que a atmosférica. Considere que dois medicamentos diferentes precisam ser administrados. O frasco do primeiro foi colocado em uma posição tal que a superfície livre do líquido encontra-se a uma altura h do ponto de aplicação.

Para aplicação do segundo medicamento, de massa específica 1,2 vezes maior que a do anterior, a altura de fixação do frasco deve ser outra. Tomando h como referência, para a aplicação do segundo medicamento deve - se

a) diminuir a altura de h/5.           

 b) diminuir a altura de h/6.             

c) aumentar a altura de h/5.             

d) aumentar a altura de 2h/5.            

e) aumentar a altura de h/6.

20-(UEL-PR) O sifão é usado normalmente nas pias e vasos sanitários para evitar a passagem de gases e pequenos animais dentro de casa.

 Além do sifão, usa-se um "respiro", isto é, uma abertura, conectada à atmosfera externa através de um cano, que:

a) Mantém iguais as pressões nos dois lados dos sifões, ajudando a manter os níveis de água equilibrados.

b) Serve para manter a ventilação no sistema de descarga.

c) Serve para escoar o excesso de água quando de uma descarga no vaso sanitário.

d) Serve para retirar o som muito alto de descargas.

e) Aumenta a fluidez da água, ajudando em seu escoamento.

21-(UDESC-SC) O gráfico a seguir ilustra a variação da pressão em função da profundidade, para um líquido contido em um reservatório aberto.

No local onde se encontra o reservatório, calcule os valores da pressão atmosférica e da densidade do líquido (g=10m/s²).

22-(PUC-MG) A figura representa duas caixas d'água, abertas para o ar, interligadas por um cano com uma válvula de passagem. A caixa da esquerda está cheia. Quando a válvula é aberta, a caixa da direita começa a encher até que o nível da água nas duas caixas seja o mesmo. É CORRETO afirmar:

 a) Ao final do processo, a pressão no fundo da caixa à esquerda será menor que no início. 

b) Durante o processo, a velocidade de escoamento da água é constante. 

c) Ao final do processo, a pressão no fundo da caixa à direita será maior que a pressão no fundo da caixa à esquerda. 

d) Durante o processo, a velocidade de escoamento da água aumenta. 

23-(UFPR-PR) A pressão atmosférica normal é de 1,0 atm (1 atmosfera). Em Curitiba, no entanto, é

comum a pressão atmosférica estabilizar-se no valor de 0,90 atm. A característica da cidade responsável por isso é:

a) o clima frio.       

b) a alta umidade do ar.        

c) a altitude.         

d) a longitude.         

e) a latitude. 

24-(UFPR-PR)  Um reservatório cilíndrico de 2 m de altura e base com área 2,4 m², como mostra a figura, foi escolhido para guardar um produto líquido de massa específica igual a 1,2 g/cm³. Durante o enchimento, quando o líquido atingiu a altura de 1,8 m em relação ao fundo do reservatório, este não suportou a pressão do líquido e se rompeu. Com base nesses dados, assinale a alternativa correta para o módulo da força máxima suportada pelo fundo do reservatório.

a) É maior que 58.000 N.            

b) É menor que 49.000 N.            

c) É igual a 50.000 N.            

d) Está entre 50.100 N e 52.000 N. 

e) Está entre 49.100 N e 49.800 N. 

25-(UFAL-AL)  Uma torneira aberta derrama água à vazão constante de 100 mL por segundo numa

caixa d’água cúbica de volume 1 m³, inicialmente vazia. Após algum tempo, a torneira é fechada, e a pressão medida no fundo da caixa, devido à água derramada, é igual a 10³ Pa. Considere a densidade da água e a aceleração da gravidade respectivamente iguais a 1 kg/L e 10 m/s².

Durante quanto tempo, em segundos, a torneira permaneceu aberta?

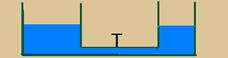
26-(UDESC-SC)  Certa quantidade de água é colocada em um tubo em forma de U, aberto nas extremidades. Em um dos ramos do tubo, adiciona-se um líquido de densidade maior que a da água e ambos não se misturam.

Assinale a alternativa que representa corretamente a posição dos dois líquidos no tubo após o equilíbrio.

27-(PUC-RS)  Um recipiente aberto na parte superior contém glicerina até a altura de 1,00m e, sobre

ela, mais 10,0cm de água, conforme representado na figura. Considere a massa específica da água 1,00 g/cm3 e da glicerina 1,30 g/cm3. Use a aceleração da gravidade igual a 10,0 m/s2 e a pressão atmosférica igual a 1,01 x 105 Pa. Neste caso, a pressão, em pascals, na interface água-glicerina e no fundo do recipiente é, respectivamente,

_________ e _________.

a) 1,02 x 105   1,34 x 105                      

b) 1,21 x 105          1,34 x 105                       

c) 1,02 x 105          1,25 x 105 

d) 1,01 x 105 1,21 x 105                      

e) 1,02 x 105           1,15 x 105 

28-(UECE-CE) No elevador mostrado na figura a seguir, o carro no cilindro à esquerda, na posição E, tem uma massa de 900 kg, e a área da secção transversal do cilindro é 2500 cm². Considere a massa do pistão desprezível e a aceleração da gravidade igual a 10 m/s². A área da secção transversal do cilindro, na posição D, é 25 cm², e o pistão tem massa desprezível.

Se o elevador for preenchido com óleo de densidade 900 kg/m3, a força mínima F, em Newton, necessária para manter o sistema em equilíbrio será

29-(UDESC-SC) A pressão atmosférica é 76 cmHg em um local onde há uma piscina cheia de água,

 que tem uma profundidade de 5,0 m. Assinale a alternativa correta quanto à pressão total no fundo da piscina.

30-(UFF-RJ)  O sifão é um instrumento usado para a retirada de água de lugares de difícil acesso.

 Como mostra a figura a seguir, seu funcionamento se baseia no fato de que, quando o tubo que liga os recipientes A e B está cheio, há uma diferença de pressão hidrostática entre os pontos P e Q, o que provoca um fluxo de água de A para B.

Essa diferença de pressão depende da seguinte característica do nosso planeta:

a) pressão atmosférica.        

b) aceleração da gravidade local.        

c) temperatura da superfície.        

d) densidade da atmosfera. 

e) velocidade de rotação do planeta. 

31-(UNICAMP-SP) TEXTO PARA A PRÓXIMA QUESTÃO:

O vazamento de petróleo no Golfo do México, em abril de 2010, foi considerado o pior da história dos EUA. O vazamento causou o aparecimento de uma extensa mancha de óleo na superfície do oceano, ameaçando a fauna e a flora da região. Estima-se que

o vazamento foi da ordem de 800 milhões de litros de petróleo em cerca de 100 dias.

Quando uma reserva submarina de petróleo é atingida por uma broca de perfuração, o petróleo tende

a escoar para cima na tubulação como consequência da diferença de pressão, ΔP, entre a reserva e a superfície. Para uma reserva de petróleo que está a uma profundidade de 2000 m e dado g = 10 m/s², o menor valor de ΔP para que o petróleo de densidade ρ = 0,90 g/cm³ forme uma coluna que alcance a superfície é de

a) 1,8×10² Pa.                                

b) 1,8×10⁷ Pa.                                     

c) 2,2×10⁵ Pa.                                  

d) 2,2×10² Pa. 

32-(FGV-SP)

A figura seguinte mostra o esquema de um reservatório de água e o encanamento que conduz a água até uma torneira fechada. A água

exerce sobre a torneira uma força de intensidade 80 N. A área da seção transversal do cano mede 4 cm² e a pressão atmosférica local sobre a superfície livre da água é de 1,0 · 10⁵ Pa. A densidade da água é de 1,0 · 10³ kg ∕ m³ e a aceleração da gravidade local é de

10 m ∕s². Nessas condições, a coluna de água mede, em metros,

 33-(ACAFE-SC)

O instrumento utilizado para medir a pressão arterial é o esfigmomanômetro (um tipo de manômetro), e os tipos mais usados são os de

coluna de mercúrio e o ponteiro (aneróide), possuindo ambos um manguito inflável que é colocada em torno do braço do paciente. Esta medição é feita no braço, na altura do coração, pois pontos situados no mesmo nível de um líquido (no caso o sangue) estão na mesma pressão. Essa aplicação está ligada ao princípio de:

34-(ENEM-MEC)

Um tipo de vaso sanitário que vem substituindo as válvulas de descarga está esquematizado na figura. Ao acionar a alavanca, toda a água do tanque é escoada e aumenta o nível no vaso, até cobrir o sifão. De acordo com o Teorema de Stevin, quanto maior a profundidade, maior a pressão. Assim, a água desce levando os rejeitos até o sistema de esgoto.

A válvula da caixa da descarga se fecha e ocorre o seu enchimento. Em relação às válvulas de descarga, esse tipo de sistema proporciona maior economia de água.

A característica  de funcionamento que garante essa economia é devida

A) à altura do sifão de água.

B) ao volume do tanque de água.

C) à altura do nível de água no vaso.

D) ao diâmetro do distribuidor de água.

E) à eficiência da válvula de enchimento do tanque.

35-(EsPCEx)

A pressão (P) no interior de um líquido homogêneo, incompressível e em equilíbrio, varia com a profundidade (X) de acordo com o gráfico abaixo.

Considerando a aceleração da gravidade igual a 10 m/s², podemos afirmar que a densidade

do líquido é de:

36-(UFRN-RN)

O mergulho autônomo é uma atividade esportiva praticada na s cidades litorâneas do Brasil. Na sua prática, mergulhadores, que levam   cilindros de ar, conseguem atingir profundidades da ordem de dezenas de metros.

A maior parte do corpo do mergulhador suporta bem as pressões em tais profundidades, mas os pulmões são muito comprimidos e, portanto, ficam sujeitos a fortes estresses.

Assim, existe um limite máximo de profundidade a partir do qual é possível ao mergulhador voltar rapidamente à superfície sem que o processo compressão-descompressão do seu pulmão leve ao colapso dos alvéolos pulmonares e até a hemorragias fatais.

DADOS:

Lei fundamental da hidrostática P = P_o + µgh.

Lei de Boyle, P_oV­_o = P₁V₁. 

Aceleração da gravidade, g = 10,0 m/s².

Considere a densidade da água do mar, µ_água = 1,0.10³kg/m³.

Pressão atmosférica ao nível do mar, P_o = 1,0 atm = 1,0.10⁵Nm².

Considerando V_o o volume do pulmão ao nível do mar, onde a pressão atmosférica é P_o, e supondo que os pulmões do mergulhador obedecem à lei geral dos gases  a temperatura constante,

A) determine o valor da pressão sobre o mergulhador, quando ele se encontra a uma profundidade de 30m.

B) verifique se o mergulhador poderá ultrapassar a profundidade de 30 m, sabendo que o limite máximo de contração do pulmão, sem que  este sofra danos, é  25% do volume do pulmão na superfície. Justifique sua resposta.

 Resolução comentada das questões de vestibulares sobre

Teorema de Stevin – Pressão Hidrostática – Vasos Comunicantes

01- A pressão hidrostática é fornecida por P_h=d_café.g.h e observe que ela não depende das dimensões do tubo e da cafeteira e, como os pontos A e B estão abertos, a pressão nos dois é a mesma e ficam na mesma altura  ---  R- A

02- ΔP=P_máx – P_atm=1,02 – 1,00  ---  ΔP=0,2atm=0,2.10⁵N/m²  ---  ΔP=dgh  ---  2.10⁴=10³.10.h  ---  h=2m  ---  regra de três  ---  5m – 0,5atm  ---  2m - xatm  ---  5x=2.0,5  ---  x=1/5=0,2m=20cm  ---  R- C

03- P=d.g.h  ---  0,05.10⁵N/m²=10³kg/m³.10m/s².h  ---  h=0,5m  --- h=50cm

04- R- D  (veja teoria)

05- A pressão no fundo do recipiente varia linearmente com a altura e independe da área de seção reta de cada cilindro  ---  R- A

06- Como as bases tem a mesma área (S), o líquido é o mesmo (água) e a as alturas das colunas líquidas são as mesmas, a pressão (P) no fundo dos recipientes é a mesma  ---  P=F/S  ---  portanto os valores das forças exercidas pela água nas bases dos recipientes é a mesma ()  ---  as forças exercidas pelas balanças sobre as bases correspondem ao peso dos volumes dos líquidos contidos em cada recipiente  ---  maior volume, maior peso ()  ---  R- E

07- Quando você abre a válvula,a água flui da caixa da esquerda para a da direita até que elas tenham a mesma altura  ---  a altura da caixa da esquerda diminui e consequentemente a pressão na base da mesma também diminui  ---  R- A

08- R- E  (veja teoria)

09- P=dgh  ---  P=10³.10.4  ---  P=4.10⁴N/m²  ---  P=F/S  ---  4.10⁴=F/12  ---  F=4.10⁴/12.10^-4  ---  F=48N  ---  R- B

10- a) Com a torneira aberta, o volume de água que preencheu o recipiente II é o mesmo que escoou do recipiente I  --- 

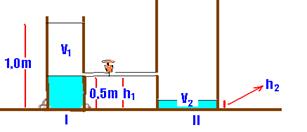
V₁=V₂  ---  S₁.h₁= S₂.h₂  ---  πR₁².h₁= πR₂².h₂  ---  R₁².0,5= (2R₁)².h₂   ---  h₂=0,125m

b) P=P_atm + d.g.h  ---  P= 10⁵ + 10³.10.1  ---  P=1,1.10⁵N/m²

11- A cada 10m de profundidade que você desce sob a superfície da água sua pressão devido à coluna líquida aumenta de 1 atm  --- P_Valdirene= 1.000atm - P_atm(1atm)  ---  P_Valdirene=999atm  ---  regra de três  ---  1atm – 10m  ---  999atm - x  ---

 x=999 x 10  ---  x=h=9.990m

12- a) P= P_atm + dgh  ---  4.10⁵ = 10⁵ + 10³.10.h  ---  h=3.10⁵/10⁴  ---  h=30m

b) Para sofrer na subida vertical uma variação de pressão ΔP=10⁴N/m², em Δt=1s, ele deve se deslocar  ---  ΔP=d.g.h  ---  10⁴=10³.10.h  ---  h=1m  ---  V= Δh/Δt  ---  V=1/1  ---  V=1m/s

13- Pressão exercida pelo êmbolo na profundidade h  ---  P=P_atm + F/S  ---  P=P_atm + 6,28/π.(R)²=P_{atm +} 6,28/3,14.2/2.10^-4  ---  P= P_atm +2.10⁴  ---  Pressão exercida pelo líquido na profundidade h  ---  P_líq=P_atm + dgh=P_atm + 1,25.10³.10.h  ---  P_líq=P_atm + 1,25.10⁴.h  ---  P=P_líq  ---  P_atm + 2.10⁴=P_atm + 1,25.10⁴.h  ---  h=2/1,25  ---  h=1,6m

14- P_sanguínea=P_{hidrostática}  ---  d_s.g.h_s=d_Hg.g.h_Hg  ---  10³.0,5=13,6.10³.h_Hg  ---  h_Hg=0,0367mHg  ---  h_Hg=36,7mmHg

15- P=d.g.h  ---  9.10³=10³.10.h  ---  h=0,9m  ---  R- E

16- A   pressão do ar aprisionado no barco à profundidade h=(2,20 – 1,70)=0,5m é dada por P= P_atm + d.g.h  ---  P -P_atm=d.g.h=10³.10.0,5  ---  P – P_atm=5,0.10³N/m²

17- P=1atm=10⁵N/m²  ---  h=10m  ---  P=dgh  ---  10⁵=d.10.10  ---  d=1,0.10³k/m³  ---  d’=0,8d  ---  P’=10⁵N/m²  ---  P’=d’.g.h’  ---  10⁵=0,8.10³.10.h’  ---  h’=10⁵/8.10³  ---  h’=12,5m  ---  R- D

18- P=P_atm + dgh=1,01.10⁵ + 1,00.10³.10.(1,0 + 2,0)  ---  P=1,01.10⁵ + 3,00.10⁴  ---  P=1,01.10⁵ + 0,30.10⁵  ---  P=1,31.10⁵N/m²  ---  R- D

19- P₁=ρ.g.h  ---  P₂=1,2ρ.g.h’  ---  P₁/P₂=ρ.g.h/1,2ρ.g.h’  ---  P₁=P₂=P  ---  1= ρ.g.h/1,2ρ.g.h’  ---  h’=1/1,2h10/12h=5/6h  ---  h – 5/6h=(6h – 5h)/6=h/6  ---  h’=h/6  ---  R- B

20- R- A  (veja teoria)

21- Do gráfico  ---  P_atm=0,5.10⁵=5,0.10⁴N/m²  ---  quando h=15m – P=5,0.10⁵N/m²  ---  P=d.g.h  ---  5.10⁵=d.10.15  ---  d=0,033.10⁵=3,3.10³kg/m³

22- Como haverá redução na altura do nível de líquido na caixa da esquerda, pela lei de Stevin, p =

 d.g.h, haverá menor pressão no fundo da caixa  ---  R- A

23- Aumentando-se a altitude, diminui a espessura da camada atmosférica sobre a superfície, diminuindo a pressão  ---  Curitiba encontra-se na altitude de 945m  ---  R- C

24- Dados  ---  A = 2,4 m²  ---   h = 1,8 m  ---  d = 1,2 g/cm³ = 1.200 kg/m³  ---   g = 10 m/s²  ---  a força máxima suportada correspode ao peso do líquido  ---  F = P = m.g = d.V.g = d.A.h.g = 1.200.(2,4).(1,8).(10)  ---  F = 51.840 N  ---  50.100 N < F < 52.000 N  -- R- D    

25- Dados  ---  Z = 100 mL/s = 0,1 L/s  ---   d = 1 kg/L = 10³ kg/m³  ---  P_col.deágua = 10³Pa  ---   g = 10 m/s²  ---   pelo teorema de Stevin a pressão da coluna líquida é  ---  P_col.deágua=dgh  ---  10³=10³.10.h  ---  h=0,1m  ---  caixa cúbica de volume 1m³ tem área da base A_b=1m²  ---  cálculo do volume derramado  ---  V=A_b.h=1.(0,1)  ---  V=0,1m³=100L  ---  a vazão (Z) é a razão entre o volume derramado e o tempo  ---  Z=V/Δt=100/0,1  ---  Δt=10³s  ---  R- D

26- De acordo com Teorema de Stevin, pontos de mesmo líquido em repouso que estão na mesma horizontal estão sob mesma pressão --- então, no ponto A da horizontal que passa pela interface entre a água e o líquido mais denso, a pressão deve ser a

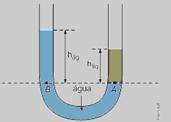
mesma que no ponto B situado na água, na mesma horizontal  ---  p_A = p_B  ---   ---  como d_liq > d_{ág  ---}   

h_líq < h_ág  ---  R- D

27- Dados  ---  d_ag = 1 g/cm³ = 10³ kg/m³;  ---  d_glic = 1,3 g/cm³ = 1,3.10³ kg/m³  ---   h_ág= 10 cm = 10^-1 m; h_glic = 1 m  ---   g = 10 m/s²  ---  p_atm = 1,01.10⁵ Pa  ---  pressão da coluna de água  ---  P_ág=d_ággh_ág=(10³).10.(10^-1)  ---  P_ág=1,0.10³Pa=0,01.10⁵Pa  ---  pressão da coluna de glicerina  ---  P_glic=d_glicgh_glic=(1,3.10³).(10).(1)  ---  P_glic=1,3.10⁴Pa=0,13.10⁵Pa  ---  na superfície que separa água-glicerina a pressão a pressão é P₁=P_atm + P_ág=1,01.10⁵ + 0,01.10⁵  ---  P₁=1,02.10⁵Pa  ---  no fundo do recipiente, a pressão (p₂) é vale  ---  P₂=P_{atm + P}água + P_glic  ---  P₂=1,01.10⁵ + 0,01.10⁵ + 0,13.10⁵   ---  P₂=1,15.10⁵ Pa.  ---  R- E

Obs: segundo o Sistema Internacional de Unidades o plural das unidades é feito apenas acrescentando a letra s no final, quando não terminada em s. Caso seja terminada em s, não sofre flexão, e quando grafadas por extenso, deve ser em letras minúsculas. Exemplos: pascal - pascals; decibel - decibels; newton - newtons.

28- Dados: m = 900 kg; A₁ = 2.500 cm² = 25.10^-2 m² ; A₂= 25 cm² = 25.10^-4 m²; d_óleo = 900 kg/m³; h = 4m  ---  de acordo com o teorema de Stevin, pontos de um mesmo líquido em repouso que estão na mesma horizontal suportam a mesma pressão  --- a

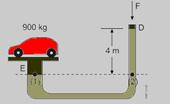
pressão no ponto (1) provocada pelo peso do carro é igual à pressão no ponto (2) provocada pela força , somada à da coluna líquida  ---  P₁=P₂  ---  mg/A₁=F/A₂ + d_óleogh  ---  9000/25.10^-2=F/25.10^-4 + 900.10.4  ---  36.000 – 36.000=F/25.10^-4  ---  F=0  ---

R- A

29-  76cm Hg -------------- 10m de H2O-----------------1,0atm----------------- 10⁵N/m²

      X Hg-------------------  5 m de H2O --------------Yatm--------------------Z N/m²

X=76x5/10  ---  X=38cmHg  ---  Y=5x1/10  ---  Y=0,5atm  ---  Z=0,5x10⁵/1  ---  Z=0,5.10⁵N/m²  ---  apressão no fundo é a soma da pressão atmosférica com a pressão da coluna de água  ---  P=1,0 + 0,5  ---  1,5atm  ---  P=76 + 38  ---  P=114cmHg  --- 

P=10⁵ + 0,5.10⁵  ---  P=1,5.10⁵Nm²  ---  R- B

30- A diferença de pressão hidrostática (ΔP) entre dois pontos de desnível h, para um líquido de densidade d_liq, é dada pelo teorema de Stevin  ---  ΔP = d_liq.g.h  ---  assim,, essa diferença só depende da densidade do líquido, do desnível e da gravidade local  ---   R- B

31- h = 2.000 m  ---  g = 10 m/s²; r = 0,9 g/cm³ = 9 ´10² kg/m³  ---  teorema de Stevin  ---  DP = r g h = 9 ´10² ´ 10 ´ 2 ´ 10³ = 180 ´ 10⁵  ---   DP = 1,8 ´ 10⁷ Pa  ---  R- B

32- P_torneira = P_água + P_atm  ---  F/S = dgh + P_atm  ---  80/4.10^-4 = 1.10³.10.h + 1.10⁵  ---  2.10⁵=10⁴h + 1.10⁵  ---  h=10⁵/10⁴  ---  h=10m

R- E

33- Observe na figura abaixo que a pressão no ponto B no interior do líquido é fornecida por P_B =

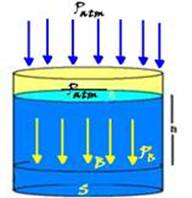
P_atm + d_líquido.g.h  ---   essa expressão é chamada de Teorema Fundamental da Hidrostática ou de Teorema de Stevin  ---  uma das conseqüências do teorema de Stevin é de que todos os pontos de uma superfície horizontal (a uma mesma altura h) suportam a mesma pressão, desde que o líquido seja o mesmo.

R- D

34- Teorema de Stevin  --- observe a figura abaixo:

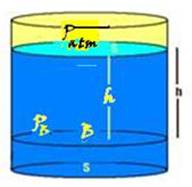
 Teorema de Stevin  ---  A pressão no ponto B devida apenas à coluna líquida P_líquido=d_líquido.g.h é chamada depressão hidrostática e P_B=P_atm + d_líquido.g.h é chamada de pressão total, pressão absoluta ou simplesmente pressão.

 A pressão exercida por uma coluna líquida não depende das dimensões do recipiente que a contém, mas apenas da natureza do líquido, fornecida pela sua densidade (d), do local (g) e da altura da coluna (h).

 O gráfico da pressão total P em função da altura “profundidade” h, (P=Patm+ d.g.h, que é uma função do primeiro

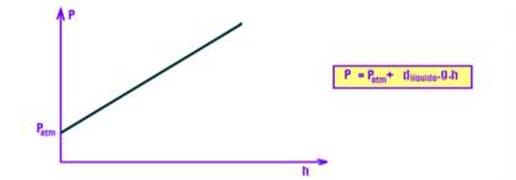
 grau)), é uma reta inclinada.

 A pressão devido á coluna líquida é maior quanto maior for a profundidade, ou seja, a maior a altura da coluna líquida,

Observe na teoria acima, que a pressão que a água deve exercer para acionar o sifão depende apenas da altura da coluna líquida, não dependendo das dimensões do recipiente, ou seja, do volume de água nele armazenada  ---  assim, mesmo

um pequeno volume de água armazenado, mas com altura suficiente pode acionar o sifão  ---  portanto, a economia deve-se ao volume de água armazenada no tanque  ---  R- B.35-(EsPCEx-012)

Teorema de Stevin  ---  P = P_o + d.g.h  ---  2,2.10⁵ = 1,0.10⁵ + d.10.5  ---  d=1,2.10⁵/50  ---  d=0,024.10⁵=2,4.10³kg/m³

R- E.

36- A) Pressão sobre o mergulhador que se encontra a uma profundidade de 30 m é determinada a partir da expressão  ---  P = P_o + μgh  - (Teorema Fundamental da Hidrostática ou de Teorema de Stevin), onde P_o é a pressão atmosférica ao nível do mar, μ é a

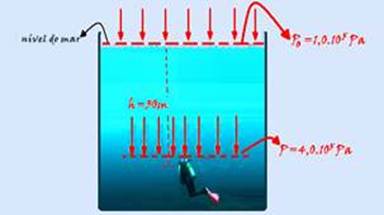
densidade da água do mar 1,0.10³kg/m³, h é a profundidade em que se encontra o mergulhador e g é a aceleração da gravidade 10 m/s²   ---  P=1.10⁵+10³x10x30  ---  P=1.10⁵+3.10⁵  ---  P=4.10⁵ N/m² ou P=4 atm  ---  a pressão hidrostática (devida somente à coluna de água) é P=3,0.10⁵N/m² (Pa) ou P=3,0 atm e a pressão (absoluta, total) é P=4,0.10⁵N/m² (Pa)ou P=4,0 atm.  ---  Observação:  à cada 10m de profundidade na água, a pressão devido à coluna líquida aumenta de 10⁵Pa ou de 1 atm  ---  Exemplo: Se um peixe está a 20m de profundidade da superfície líquida da água, ele suporta uma pressão  

hidrostática de P_h=2,0.10⁵Pa ou 2atm. A pressão total deve ser acrescida da pressão atmosférica na superfície  ---  P_t=10⁵Pa + 2.10⁵Pa=3.10⁵Pa ou de 3 atm.

B) Trata-se de uma transformação isotérmica (temperatura constante)  ---  P_o.V_o/T_o = P.V/T  ---  T= T_o  ---  P_o.V_o = P.V=constante (Lei de Boyle)  ---  pressão na superfície  ---  P_o=1 atm  ---  volume na superfície  ---  V_o  ---  à uma profundidade onde a pressão é P, o volume é V=25% de V_o=0,25V_o  ---  P_o.V_o = P.V  ---  1.V_o=0,25V_o.P  ---  P=4 atm  ---  observe que essa pressão é exatamente igual à pressão sobre o mergulhador a 30m de profundidade, então ele não poderá ultrapassar essa profundidade sem que o seu pulmão possa vir a sofrer danos