Equação da Continuidade – Equação de Bernoulli

Hidrodinâmica

 Hidrodinâmica estuda o comportamento de fluidos (líquidos e gases) em movimento. Esse movimento pode ocorrer de modo que a velocidade do fluido varie, como nas corredeiras ou

cachoeiras, ou permaneça constante, ou seja, em cada ponto cada partícula do fluido tem a mesma velocidade (regime estacionário ou permanente).

 Em termos de nível médio considera-se o fluido ideal (incompressível, ou seja, em todos os pontos tem sempre a mesma densidade) e não viscoso (atrito interno nulo).

Equação da continuidade

Considere três pedaços de tubos com diâmetros diversos e áreas de seção transversal S₁, S₂ e S₃ conectados, e com água escoando através deles no sentido de A para B, com velocidades de intensidades V₁, V₂ e V₃, respectivamente.

Essa equação Z = S.v, denominada equação da continuidade afirma que a velocidade com que o líquido escoa no interior do tubo é inversamente proporcional à área de seção transversal (S) do mesmo, ou seja, diminuindo a área, a velocidade (v) com que o líquido flui aumenta na mesma proporção.

Equação de Bernoulli

Considere dois pedaços de tubos com diâmetros diversos e áreas de seção transversal S₁ e  S₂  conectados, e com água escoando através deles no sentido de A para B, com velocidades de intensidades V₁ e V₂, respectivamente.

Equação deduzida por Bernoulli:

Se os tubos estiverem na horizontal, as alturas h₁ e h₂ serão iguais e a equação fica  P₁ + d(v₁)²/2 = P₂ + d.(v₂)²/2.

 Observe na equação P + d.v²/2 = constante que a pressão P é inversamente proporcional à velocidade v, ou seja, quanto menor a área, maior a velocidade e menor a pressão.

 Equação de Torricelli  A figura ilustra um reservatório contendo um fluido de densidade d.

O que você deve saber, informações e dicas

  Viscosidade é definida como a resistência que um fluido oferece ao seu próprio movimento. Quanto maior for a

 viscosidade do fluido, menor será a sua capacidade de escoar (fluir) e maior será a força de atrito entre o fluido e as paredes do recipiente onde ele está escoando, pois o fluido diretamente em contato como cada placa fica preso à superfície de contato, devido a existência de uma força coesiva entre as moléculas do líquido e da placa.

Assim, na figura acima o líquido B é mais viscoso que o líquido A.  

Aplicações da equação de Bernoulli

Exercícios de vestibulares com resolução comentada sobre

Equação da Continuidade e Teorema de Bernoulli

01-(UFMS) Água escoa em uma tubulação, onde a região 2 situa-se a uma altura h acima da região 1, conforme figura a seguir. É correto afirmar que:

a) a pressão cinética é maior na região 1.     

b) a vazão é a mesma nas duas regiões.        

c) a pressão estática é maior na região 2.         

d) a velocidade de escoamento é maior na região 1.       

e) a pressão em 1 é menor do que a pressão em 2.

02-(UFSM-RS) Em uma cultura irrigada por um cano que tem área de secção reta de 100 cm², passa água com uma vazão de 7200 litros por hora.

 A velocidade de escoamento da água nesse cano, em m/s, é

O3-(UNAMA-PA) Uma piscina, cujas dimensões são 18m.10m.2m, está vazia. O tempo necessário

para enchê-la é 10 h, através de um conduto de seção A = 25 cm². A velocidade da água, admitida constante, ao sair do conduto, terá módulo igual a:

04-(UFSM-RS) Observe a figura que representa um vaporizador simples.

Sabendo que, normalmente, o herbicida líquido é vaporizado sobre a plantação, um jato de ar, passando por A, ocasiona, nesse ponto, um __________ na pressão quando comparado com B, onde o ar está __________. Então, o líquido sobe pelo conduto porque sempre se desloca da __________ pressão.

Assinale a alternativa que completa corretamente as lacunas.

a) acréscimo - em movimento - menor para a maior         

b) abaixamento - em movimento - maior para a menor

c) acréscimo - praticamente parado - menor para a maior 

d) acréscimo - em movimento - maior para a menor

e) abaixamento - praticamente parado - maior para a menor

05-(UFSM-RS) Vaporizadores semelhantes ao da figura são usados em nebulização.

 Ao pressionar a bexiga do vaporizador, o ar no seu interior é projetado com velocidade de módulo V_B > 0, enquanto o líquido permanece em repouso em A. A relação entre as pressões em A e B é

a) P_A = P_B                

b) P_A + P_B = 0                  

c) P_A > P_B                      

d) P_A < P_B              

e) P_A = P_B + 1 atmosfera

06-(UFPE) O sistema de abastecimento de água de uma rua, que possui 10 casas, está ilustrado na figura abaixo. A vazão do tubo principal é de 0,01 m³/s. Supondo que cada casa possui uma caixa d'água de 1500 litros de capacidade e que estão todas inicialmente vazias, em quantos minutos todas as caixas-d'água estarão cheias?  Suponha que durante o período de abastecimento nenhuma caixa estará fornecendo água para as suas respectivas casas.

07-(ITA-SP) Durante uma tempestade, Maria fecha a janela de seu apartamento e ouve zumbido do vento lá fora.

 Subitamente o vidro de uma janela se quebra. Considerando que o vento tenha soprado  tangencialmente à janela, o acidente pode ser melhor explicado pelo(a):

a) princípio da conservação da massa     

b) equação de Bernoulli     

c) princípio de Arquimedes     

d) princípio de Pascal     

e) princípio de Stevin

08-(UFSM) Um fluido ideal percorre um cano cilíndrico em regime permanente. Em um estrangulamento onde o diâmetro do cano fica reduzido à metade, a velocidade do fluido fica:

a) reduzida a 1/4.           

b) reduzida à metade.            

c) a mesma.            

d) duplicada.           

e) quadruplicada.

09-(UFPE) Um funil tem área de saída quatro vezes menor que a área de entrada, como indica a figura.

Se esse funil diminui de uma altura h=9,0cm, num intervalo de tempo de 3s, determine, em cm/s, a velocidade com que o fluido abandona o funil na saída.

10-(UFSM-RS) A figura representa uma tubulação horizontal em que escoa um fluido ideal.

A velocidade de escoamento do fluido no ponto 1, em relação à velocidade verificada no ponto 2, e a pressão no ponto 1, em relação à pressão no ponto 2, são:

a) maior, maior              

b) maior, menor               

c) menor, maior                 

d) menor, maior             

e) menor, menor

11-(UFMS-MS) Um dos métodos utilizados pelos jardineiros, durante a irrigação de plantas, é diminuir a secção transversal da mangueira por onde sai a água para que o jato de água tenha um maior alcance. Geralmente isso é feito através de esguichos. A figura a seguir mostra a extremidade de uma mangueira de secção transversal uniforme e na horizontal, conectada a um esguicho de forma cônica. A mangueira está sendo alimentada por um reservatório de água com nível constante e aberto. O jato de água sai na extremidade do esguicho com velocidade horizontal. Considere que as superfícies internas da mangueira e do esguicho não ofereçam resistência ao escoamento e que a água seja um fluido ideal. Com relação ao escoamento da água nessa extremidade da mangueira e no esguicho, é correto afirmar:

(01) Se, de alguma maneira, for impedida a saída de água pelo esguicho (tampar a saída), a pressão aumentará em todos os pontos.

(02) O alcance do jato de água é maior quando se usa o esguicho, porque a menor secção transversal na saída do esguicho faz aumentar a vazão do jato de água.

(04) A pressão, no ponto P₂ (onde a secção transversal é menor), é maior que a pressão no ponto P₁ (onde a secção transversal é maior).

(08) A pressão, na saída do esguicho, é igual à pressão no nível superior do reservatório.

(16) A trajetória das partículas de água que saem do esguicho é parabólica quando se despreza a resistência do ar.

12-(UFMS-MS) A figura a seguir mostra um vaso com água, em cuja boca é soldado um tubo fino, aberto nas duas extremidades, e que não atinge o fundo do vaso. Esse sistema também é chamado de Vaso de Mariote. Inicialmente o vaso se encontra com água até o nível H acima da extremidade inferior do tubo que está no ponto O. Um registro no fundo do vaso, quando aberto, permite que a água escoe para fora lentamente. Sejam os pontos A e B, localizados inicialmente no mesmo nível H, nas superfícies da água que estão no interior do vaso e no interior do tubo, respectivamente, e os pontos C e D localizados no interior do vaso e do tubo, respectivamente, e ambos no mesmo nível de O, veja a figura. Considere a pressão atmosférica igual a Po, e despreze os efeitos de pressão cinética devido ao escoamento. Com fundamentos na hidrostática, assinale a(s) proposição(ões) CORRETA(S).

(01) Abrindo o registro para permitir a saída de água do interior do vaso, as pressões, nos pontos C e D, diminuem.

(02) Abrindo o registro para permitir a saída de água do interior do vaso, as pressões, nos pontos A e B, diminuem.

(04) Abrindo o registro para permitir a saída de água do interior do vaso, o nível do ponto B desce mais rapidamente que o nível do ponto A.

(08) Abrindo o registro para permitir a saída de água do interior do vaso, a diferença de pressão entre os pontos D e B é sempre maior que a diferença de pressão entre os pontos C e A.

(16) Antes de abrir o registro, a pressão no ponto A é igual no ponto B, mas a pressão no ponto C é maior que no ponto D.

13-(UFRRJ) Um jardineiro dispõe de mangueiras de dois tipos, porém com a mesma vazão. Na

 primeira, a água sai com velocidade de módulo V e, na segunda, sai com velocidade de módulo 2V. A primeira mangueira apresenta:

a) a metade da área transversal da segunda.           

b) o dobro da área transversal da segunda.
c) um quarto da área transversal da segunda.         

d) o quádruplo da área transversal da segunda.
e) dois quintos da área transversal da segunda.

14- (UFJF-MG) A figura representa uma caixa de água ligada a duas torneiras t₁ e T₂. A superfície livre da água na caixa tem área A=0,8m² e as vazões nas torneiras são 5 litros/minutos e 3 litros/ minutos, respectivamente.

Pode-se afirmar que o módulo da velocidade V, com que a superfície da água desce, vale:

15-(Unirio-RJ) Um menino deve regar o jardim de sua mãe e pretende fazer isso da varanda de sua residência, segurando uma mangueira na posição horizontal, conforme a figura. Durante toda a tarefa, a altura da mangueira, em relação ao jardim, permanecerá constante. Inicialmente a vazão de água, que pode ser definida como o volume de água que atravessa a área transversal da mangueira na unidade de tempo, é Z_o. Para que a água da mangueira atinja a planta mais distante no jardim, ele percebe que o alcance inicial deve ser quadruplicado. A mangueira tem em sua extremidade um dispositivo com orifício circular de raio variável. Para que consiga molhar todas as plantas do jardim sem molhar o resto do terreno, ele deve:

a) reduzir o raio do orifício em 50% e quadruplicar a vazão de água.
b) manter a vazão constante e diminuir a área do orifício em 50%.
c) manter a vazão constante e diminuir o raio do orifício em 50%.
d) manter constante a área do orifício e dobrar a vazão da água.
e) reduzir o raio do orifício em 50% e dobrar a vazão de água.

16-(FUVEST-SP) A artéria aorta de um adulto tem um raio de cerca de 1cm, e o sangue nela flui com

 velocidade de 33cm/s.

a) Quantos litros de sangue são transportados pela aorta?

b) Sendo de 5 litros o volume de sangue no organismo, use o resultado anterior para estimar o tempo médio que o sangue demora a retornar ao coração.

17-(Mackenzie-SP) Um fazendeiro, para estimar a vazão de água em um canal de irrigação, cuja seção transversal é aproximadamente semicircular (como na figura), procede do seguinte modo: faz

duas marcas numa das margens do canal, separadas por quatro passadas (cada passada vale aproximadamente um metro); coloca na água um ramo seco e mede um minuto para o mesmo ir de uma marca à outra. Finalmente, verifica que a largura do canal equivale a uma sua passada. O fazendeiro faz cálculos e conclui que a vazão procurada vale aproximadamente:

18-(UEL-PR) Observe as figuras a seguir.

Com base nos esquemas físicos apresentados nas figuras, considere as afirmativas a seguir.

I - A figura I mostra dois copos contendo suco de laranja à mesma altura. Independentemente do formato dos copos, a pressão no ponto A é igual à pressão no ponto B.

II - A figura II mostra um tubo em forma de "U" contendo dois líquidos que não se misturam. No ramo da esquerda, tem-se óleo de soja e, no da direita, água. A pressão no ponto A é igual à pressão no ponto B.

III - A figura III mostra dois líquidos de viscosidades diferentes escorrendo através de um capilar: o suco de laranja, menos viscoso, escorre em A, ao passo que o xarope de milho, mais viscoso, escorre em B.

IV - A figura IV mostra um liquido em escoamento no sentido do ponto A para o ponto B. Apesar de a velocidade de escoamento no ponto A ser maior do que a velocidade de escoamento no ponto B, a pressão no ponto A é menor que a pressão no ponto B.

Assinale a alternativa CORRETA.

a) Somente as afirmativas I e II são corretas.         

b) Somente as afirmativas I e III são corretas.

c) Somente as afirmativas II e IV são corretas.       

d) Somente as afirmativas I, III e IV são corretas.

e) Somente as afirmativas II, III e IV são corretas.

19-(UFPA) Considere duas regiões distintas do leito de um rio: uma larga A, com 200 m² de área de

 secção transversal, onde a velocidade escalar média da água é de 1,0 m/s e outra estreita B, com 40 m² de área de secção transversal.
Calcule:

a) a vazão volumétrica do rio.
b) a velocidade escalar média da água do rio na região estreita B.

20-(UNICAMP-SP) Uma caixa-d'água com volume de 150 litros coleta água da chuva à razão de 10 litros por hora.

a) por quanto tempo deverá chover para encher completamente essa caixa-d'água?
b) admitindo-se que a área da base da caixa é 0,50 m², com que velocidade subirá o nível da água na caixa, enquanto durar a chuva?

21-(UFPE-PE) A velocidade do sangue na artéria aorta de um adulto, que possui em média 5,4 litros

de sangue, tem módulo igual a aproximadamente 30 cm/s. A área transversal da artéria é de aproximadamente 2,5 cm². Qual o intervalo de tempo, em segundos, necessário para a aorta transportar o volume de sangue de um adulto?

22-Mackenzie-SP) A figura ilustra um reservatório contendo água. A 5 m abaixo da superfície livre

existe um pequeno orifício de área igual a 3 cm². Admitindo g = 10 m/s², podemos afirmar que a vazão instantânea através desse orifício é:

23-(AFA-SP) Através de uma tubulação horizontal de seção reta variável, escoa água, cuja densidade é 1,0.10³kg/m³. Numa seção da tubulação, a pressão estática e o módulo da velocidade valem, respectivamente, 1,5.10⁵N/m² e 2,0m/s. A pressão estática em outra seção da tubulação, onde o módulo da velocidade vale 8,0m/s, é, em N/m²;

24-(ITA-SP) Álcool, cuja densidade de massa é de 0,80 g/cm³ está passando através de um tubo como mostra a figura.

A secção reta do tubo em A é 2 vezes maior do que em B. Em A a velocidade é de v_A = 5,0 m/s, a altura h_A= 10,0m e a

pressão P_A= 7,0 x 10³ N/m². Se a altura em B é h_B= 1,0m, calcule a velocidade e a pressão em B.

25-(UNICAMP) “Tornado destrói telhado  do ginásio da Unicamp”. Um tornado com ventos de 180km/h destruiu o telhado do ginásio de esportes da Unicamp ...

Segundo engenheiros da Unicamp, a estrutura destruída pesa aproximadamente 250 toneladas. “Folha de São Paulo, 29/11/95”

Uma possível explicação para o fenômeno seria considerar uma diminuição da pressão atmosférica , devida ao vento, na parte superior do telhado. Para um escoamento de ar ideal, essa redução de pressão é dada por ρv²/2, em que ρ=1,2kg/m³ é a densidade do ar e v a velocidade do vento. Considere que o telhado do ginásio tem 5.400m² de área e que estava apoiado nas paredes. (dado g=10m/s²).

a) Calcule a variação da pressão externa devido ao vento.

b) Quantas toneladas poderiam ser levantadas pela força devida a esse vento?

c) Qual a menor velocidade do vento(em km/h) que levantaria o telhado?

26-(UFSM-RS) Um líquido ideal preenche um recipiente até certa altura. A 5 metros abaixo da

superfície livre, esse recipiente apresenta um orifício com 2.10^-4‑m² de área, por onde o líquido escoa. Considerando g=10m/s² e não alterando o nível da superfície livre, a vazão através do orifício, em m³/s, vale:

27-(CMJF-MG) A água entra em uma casa através de um tubo com diâmetro interno de 2,0 cm, com uma pressão absoluta igual a 4,0 x 10⁵ Pa (cerca de 4 atm). Um tubo com diâmetro interno de 1,0 cm se liga ao banheiro do segundo andar a 5,0 m de altura conforme a figura abaixo.

Sabendo que no tubo de entrada a velocidade é igual a 1,5 m/s, calcule: (densidade da água d=1,0.10³kg/m³)

a) a velocidade do escoamento

b) a pressão no banheiro

c) a vazão volumétrica no banheiro

28-(UnB-DF) Animais como coelhos e toupeiras constroem suas tocas com mais de uma abertura, cada abertura localizada a uma altura diferente, conforme ilustrado na figura I abaixo.

 Nas proximidades do solo, o módulo da velocidade do vento aumenta com a altitude,conforme ilustra a figura II a seguir.

A análise do principio de Bernoulli permite afirmar que, em regiões onde a velocidade do ar é alta, a pressão é baixa, e onde a velocidade é baixa, a pressão é alta.

Com base nas afirmações acima, julgue os itens a seguir.

a) Uma toca com duas aberturas no mesmo nível terá melhor ventilação que a apresentada na figura I, sob as mesmas condições de vento.

b) Se um arbusto crescer nas proximidades da abertura 1, de forma a dificultar a passagem do vento, sem bloquear a abertura, então a ventilação na toca será melhorada.

c) ΔP = P₁ – P₂ é diretamente proporcional à diferença dos módulos das velocidades v₁ e v₂.

d) A circulação de ar no interior da toca mostrada na figura I ocorre da abertura 1 para a abertura 2.

29-(UERJ-RJ) Num edifício, deseja-se instalar uma bomba hidráulica capaz de elevar 500L de água até uma caixa de água vazia situada a 20m de altura acima desta bomba, em 1 minuto e 40 segundos.

 Essa caixa de água tem a forma de um paralelepípedo cuja base mede 2m^2. O rendimento de um sistema hidráulico é definido pela razão entre o trabalho fornecido a ele e o trabalho por ele realizado. Espera-se que o rendimento mínimo desse sistema seja de 50%. Calcule:

a) a potência mínima que deverá ter o motor dessa bomba.

b) a pressão, em N/m², que os 500L de água exercerão sobre o fundo da caixa de água.

30-(Mackenzie-SP) Na tubulação horizontal indicada na figura, o líquido escoa com vazão de 400 cm³.s^-1 e atinge a altura de 0,5 m no tubo vertical. A massa específica do líquido (suposto ideal) é 1 g.cm^-3. Adotar g = 10 m .s^-2 e supor o escoamento permanente e irrotacional. A pressão efetiva no ponto 1, em N.m^-2, é:

31-(UFPE-PE) Diversos edifícios de nossa cidade usam água potável obtida mediante poços profundos. Um dos processos consiste em colocar a bomba no lençol profundo (150m). Noutro, um compressor bombeia ar no lençol para aumentar a pressão e possibilitar a chegada da água no nível do piso onde, então, uma bomba “recalca” a água até a caixa de água superior (100m).

Considerando a densidade da água de 1.000kg/m³ e uma vazão de 0,03m³/s, em relação a esses dois processos de bombeamento, o que podemos estabelecer, sabendo-se que 1 hp=750 W?

Assinale V ou F:

0) Usando um compressor, a potência da bomba que deverá ser de 75 hp com um rendimento de 80%.

1) A potência da bomba instalada no lençol será de 100 hp se o rendimento for 100%.

2) A potência do motor deverá ser de 75 hp com um rendimento de 80%.

3) É teoricamente possível bombear até a caixa d’agua superior, usando apenas o compressor. Nesse caso, a potência será de 125 hp com um rendimento de 80%.

4) Usando o compressor, a potência da bomba deverá ser de 50 hp com um rendimento de 80%.

32-(MACKENZIE-SP) Com uma bomba hidráulica de potência útil 0,5cv, retira-se água de um poço de 15m de profundidade e preenche-se um reservatório de 500L, localizado no solo. Desprezando-se as perdas, adotando g=10m/s², a densidade da água igual a 1 g/cm³ e 1cv=750W, o tempo gasto para encher o reservatório é de:

33-(UEL-PR)  Observe as figuras a seguir.

Com base nos esquemas físicos apresentados nas figuras, considere as afirmativas a seguir.

I - A figura I mostra dois copos contendo suco de laranja à mesma altura. Independentemente do formato dos copos, a pressão no ponto A é igual à pressão no ponto B.

II - A figura II mostra um tubo em forma de "U" contendo dois líquidos que não se misturam. No ramo da esquerda, tem-se óleo de soja e, no da direita, água. A pressão no ponto A é igual à pressão no ponto B.

III - A figura III mostra dois líquidos de viscosidades diferentes escorrendo através de um capilar: o suco de laranja, menos viscoso, escorre em A, ao passo que o xarope de milho, mais viscoso, escorre em B.

IV - A figura IV mostra um liquido em escoamento no sentido do ponto A para o ponto B. Apesar de a velocidade de escoamento no ponto A ser maior do que a velocidade de escoamento no ponto B, a pressão no ponto A é menor que a pressão no ponto B.

Assinale a alternativa CORRETA.

a) Somente as afirmativas I e II são corretas.                                   

b) Somente as afirmativas I e III são corretas. 

c) Somente as afirmativas II e IV são corretas.                                

d) Somente as afirmativas I, III e IV são corretas. 

e) Somente as afirmativas II, III e IV são corretas. 

 34-(PUC-PR)  O coração bombeia o sangue para os demais órgãos do corpo por meio de tubos chamados artérias.

Quando o sangue é bombeado, ele é "empurrado" contra a parede dos vasos sanguíneos. Essa tensão gerada na parede das artérias é denominada pressão arterial.

A hipertensão arterial ou "pressão alta" é a elevação da pressão arterial para números acima dos valores considerados normais (120/80 mmHg). Essa elevação anormal pode causar lesões em diferentes órgãos do corpo humano, tais como cérebro, coração, rins e olhos.

Quando a pressão arterial é medida, dois números são registrados, tais como 120/80. O maior número, chamado pressão arterial sistólica, é a pressão do sangue nos vasos, quando o coração se contrai, ou bombeia, para impulsionar o sangue para o resto do corpo. O menor número, chamado pressão diastólica, é a pressão do sangue nos vasos quando o coração encontra-se na fase de relaxamento (diástole).

Considere o texto para assinalar a alternativa correta:

a) Pode-se afirmar que, no processo de sístole e diástole, a pressão arterial e o volume de sangue no coração são diretamente proporcionais. 

b) O sangue exerce uma força sobre as artérias e as artérias sobre o sangue; portanto, essas forças se anulam. 

c) A diferença de pressão entre dois pontos distantes 10 cm da aorta vale 2,5 Pa, o que significa dizer que é exercida uma força de 2,5 N em 1 cm². 

d) Quando o calibre da artéria fica reduzido, aumenta-se a resistência à passagem do sangue e, consequentemente, eleva-se a pressão diastólica (mínima). 

e) O valor da pressão sistólica no SI é 1,6. 10⁵ Pa. 

35-(ENEM-MEC) O uso da água do subsolo requer o bombeamento para um reservatório elevado. A capacidade de bombeamento (litros/hora) de uma bomba hidráulica depende da pressão máxima de bombeio, conhecida como altura manométrica H (em metros), do comprimento L da tubulação que se estende da bomba até o reservatório (em metros), da altura de bombeio h (em metros) e do desempenho da bomba (exemplificado no gráfico).

De acordo com os dados a seguir, obtidos de um fabricante de bombas, para se determinar a quantidade de litros bombeados por hora para o reservatório com uma determinada bomba, deve-se:

1 — Escolher a linha apropriada na tabela correspondente à altura (h), em metros, da entrada da água na bomba até o reservatório.

2 — Escolher a coluna apropriada, correspondente ao comprimento total da tubulação (L), em metros, da bomba até o reservatório.

3 — Ler a altura manométrica (H) correspondente ao cruzamento das respectivas linha e coluna na tabela.

4 — Usar a altura manométrica no gráfico de desempenho para ler a vazão correspondente.

Considere que se deseja usar uma bomba, cujo desempenho é descrito pelos dados acima, para encher um reservatório de 1.200 L que se encontra 30 m acima da entrada da bomba. Para fazer a tubulação entre a bomba e o reservatório seriam usados 200 m de cano. Nessa situação, é de se esperar que a bomba consiga encher o reservatório

a) entre 30 e 40 minutos.        

b) em menos de 30 minutos.        

c) em mais de 1 h e 40 minutos.        

d) entre 40 minutos e 1 h e 10 minutos.        

e) entre 1 h e 10 minutos e 1 h e 40 minutos. 

36-(CPS) Preocupado com as notícias sobre a escassez da água potável no planeta devido ao mau gerenciamento desse

importante recurso natural, Marcelo, tentando fazer a sua parte para reverter esse processo, tem procurado adotar atitudes ecopráticas, por isso resolveu verificar quanto gasta de água em um banho.

Ele, com a ajuda de seu irmão que cronometrou o tempo e anotou os resultados, procedeu da seguinte forma:

• ligou o chuveiro apenas quando já estava despido e pronto para o início do banho;

• para se molhar, Marcelo deu um quarto de volta no registro do chuveiro que ficou aberto por 1 min 18 s;

• ensaboou-se, com o chuveiro fechado, por 3 min 36 s;

• para se enxaguar, abriu totalmente o registro do chuveiro;

• finalmente, fechou o registro do chuveiro, encerrando o banho que durou 6 min 54 s.

Mais tarde, consultando o site da Sabesp, Marcelo obteve os seguintes dados:

Analisando a situação apresentada, conclui-se que a quantidade total de água que Marcelo utilizou nesse banho foi, em litros,

37-(CPS) Preocupado com as notícias sobre a escassez da água potável no planeta devido ao mau gerenciamento desse importante recurso natural, Marcelo, tentando fazer a sua parte para reverter

esse processo, tem procurado adotar atitudes ecopráticas, por isso resolveu verificar quanto gasta de água em um banho.

Ele, com a ajuda de seu irmão que cronometrou o tempo e anotou os resultados, procedeu da seguinte forma:

• ligou o chuveiro apenas quando já estava despido e pronto para o início do banho;

• para se molhar, Marcelo deu um quarto de volta no registro do chuveiro que ficou aberto por 1 min 18 s;

• ensaboou-se, com o chuveiro fechado, por 3 min 36 s;

• para se enxaguar, abriu totalmente o registro do chuveiro;

• finalmente, fechou o registro do chuveiro, encerrando o banho que durou 6 min 54 s.

Mais tarde, consultando o site da Sabesp, Marcelo obteve os seguintes dados:

Assinale a alternativa que melhor representa o gráfico da quantidade de água consumida, em litros, em função do tempo, em minutos, durante o banho de Marcelo.   

38-(UFG-GO)

No sistema circulatório humano, o sangue é levado do coração aos demais órgãos do corpo por vasos sanguíneos de diferentes

características. Na tabela a seguir estão relacionados dois vasos, I e II, com valores médios de algumas de suas características.

O sangue, que pode ser tratado como um fluido ideal e incompressível possui velocidade média de 30 cm/s no vaso I. O nome do vaso I e a velocidade média do sangue em cm/s no vaso II são, respectivamente,

(A) cava e 3,0.            

(B) aorta e 3,0.              

(C) aorta e 0,03.                    

(D) arteríola e 0,03.                  

(E) arteríola e 300,0.

Resolução comentada dos exercícios de vestibulares sobre

Equação da Continuidade – Teorema de Bernoulli

01- A vazão é a mesma – regime estacionário  ---  R- B

02- S=100cm²=10².10^-4  ---  S=10^-2m³  ---  Z=7.200L/h=7.200/3.600L/s=2.L/s  ---  Z=2.10^-3m³/s  ---  Z=S.v  ---  2.10^-3= 10^-2v  ---  v=2.10^-3/10^-2  ---  v=0,2m/s  ---  R- C

03- ΔV=18.10.2=360m³  ---  Δt=10h  ---  S=25.10^-4m²  ---  Z=ΔV/Δt=360/10  ---  Z=36m³/h  ---  Z=S.v  ---  36=25.10^-4.v  ---  v=36/25.10⁴  ---  v=14.400m/h  ---  v=14.400/3.600=4m/s  ---  R- D

04- O jato de ar que se move com velocidade v, paralelamente ao extremo (A) de um tubo que está imerso em um líquido, faz com que a pressão aí diminua em relação ao extremo inferior (ponto B) do tubo.

A diferença de pressão entre os pontos A e B empurra o fluido para cima. O ar rápido também divide o fluido em pequenas gotas, que são empurradas e se espalham para a frente  ---  R- E

05- R- C  ---  veja exercício anterior

06- Vazão  ---  Z=0,01m³/s=10^-2m³/s  ---  volume total  ---  ΔV=10x1.500=15.000L=15.10³.10^-3  ---  ΔV=15m³  ---  Z= ΔV/ Δt  ---  10^-2=15/ Δt  ---  Δt=1.500s=25min  ---  R- C 

07- R- B  ---  veja teoria

08- Veja a figura abaixo:

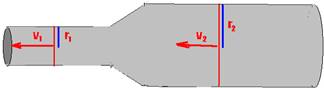
d₂=2d₁  ---  r₂=2r₁  ---  S₁v₁=S₂v₂  ---  π(r₁)².v₁=π(r₂)².v₂  --- (r₁)².v₁=(2r₁)².v₂  ---  (r₁)².v₁=4(r₁)².v₂  ---  v₁=4v₂  ---  R- E

09-

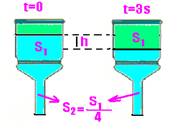
v₁=Δh/Δt=9/3  ---  v₁=3cm/s  ---  S₁=4S₂  ---  S₁.v₁=S₂.v₂  ---  4S₂v₁=S₂.v₂  ---  4.3=v₂  --- v₂=12cm/s

10- Maior área de seção transversal (1), menor velocidade, maior pressão  ---  R- C

11-  (01) correta – “os acréscimos de pressão sofridos por um ponto de um líquido em equilíbrio são transmitidos integralmente a todos os pontos do líquido e das paredes do recipiente que o contém”  ---  Princípio de Pascal.

(02) Falsa, a vazão é a mesma, quem aumenta é a velocidade de saída da água.

(04)  Falsa  --- Observe na equação P + d.v²/2=constante que a pressão P é inversamente proporcional à velocidade v, ou seja, quanto menor a área, maior a velocidade e menor a pressão.

(08) Correta – é a pressão atmosférica – Veja (01)

(16) Correta – a partir da saída, as partículas de água ficam sujeitas à força peso, desprezando-se a resistência do ar, e descrevem um arco de parábola.

 ( 01 + 08 + 16) = 25

12- (01) Correta – P=dgh (teorema de Stevin)  ---  como h diminui, com d e g constantes, a pressão P também diminui.

(02) Falsa, é a pressão atmosférica.

(04) Correta – a pressão no ponto B (pressão atmosférica) é maior que a pressão no ponto A.

(08) Correta – veja (04)

(16) Falsa  ---  P_A=P_B e P_C=P_D  ---  mesmo nível horizontal – teorema de Stevin

(01 + 04 + 08) = 13

13- Z_constante=S_A.v_A = S_B.v_B  ---  S_A.v=S_B.2v  ---  S_A=2S_B  ---  R- B

14- A vazão total das duas torneiras é Z=5L/min + 3L/min=8L/min  ---  Z=8.10^-3m³/min  ---  Z=S.v  ---  8.10^-3=0,8.v  --- 

v=10^-2m/min  ---  v=1cm/min  ---  R- C

15- A vazão é sempre a mesma independente da espessura da mangueira  ---  no lançamento horizontal a velocidade v é a mesma e trata-se de um movimento uniforme de equação  ---  S=S_o + vt   ---  S=v.t  ---  se o alcance S é quadruplicado, a velocidade v também é quadruplicada   ---  S₁.v₁=S₂.v₂  ---  π.(R₁)².v=π.(R₂)².4v  ---  (R₂)²/(R₁)²=1/4  ---  R₂=R₁/2  --- 

R- C

16- a) Z=S.v=πR².v=3,14.1².33  ---  Z=104cm³/s  ---  Z=0,104L/s (transporta 0,104 litros em cada 1 segundo)

b) Z=ΔV/Δt  ---  0,104=5/Δt  ---  Δt=48s

17- Comprimento da canal  ---  s=4m  ---  tempo de percurso  ---  t=1min=60s  ---  velocidade da água 

---  v=s/t=4/60  ---V=1/15m/s  ---  área de seção transversal do canal  ---  R=1m  ---  S=πR²/2=π.(1/2)²/2  ---  S=π/8  ---  vazão  ---  Z=S.v=(π/8).(1/15)  ---  Z=π/120m³/s (m³.s^-1)  ---  R- E

18- I- Correta – Teorema de Stevin (P=d.g.h) – todos os pontos de um mesmo líquido (mesma densidade) localizados num mesmo nível horizontal (no caso,mesma altura), suportam a mesma pressão.

II- Falso – estão em alturas diferentes  ---  P_B<P_A

III- Correta - viscosidade é definida como a resistência que um fluido oferece ao seu próprio movimento. Quanto maior for a sua viscosidade, menor será a sua capacidade de escoar (fluir) e maior será a força de atrito entre o fluido e as paredes do recipiente onde ele está escoando  

IV- Correta – correta – veja teoria

R- D

19- a) Z=S.v=200.1  ---  Z=200m³/s

b) Z=S.v  ---  200=40.v  ---  v=5,0m/s

20- a) 10L -1h  ---  150L – t h  ---  t=15h

b) Z=ΔV/Δt=10.10^-3m³/1h  ---  Z=10^-2m³/h  ---  Z=S.v  ---  10^-2=5.10^-1.v  ---  v=2,0.10^-2m/h  

21- Vazão  ---  Z=S.v=2,5.30  ---  Z=75cm³/s  ---  Z=ΔV/Δt  ---  75=5,4.10³/Δt  ---  Δt=5,4.10³/75=0,072.10³  ---  Δt=72s

22- Z=v.S=√(2gh).S=√(2.10.5).3.10^-4=10.3.10^-4=3.10^-3m³s  ---  Z=3L/s  ---  R- B

23- Equação de Bernoulli  ---  tubulação horizontal – h=0  ---  só tem energia cinética  ---  P₁+ dv₁²/2=P₂ + dv₂²/2  --- 

1,5.10⁵ + 10³.(2)²/2=P₂ + 10³.(8)²/2  --- 152.10³=P₂ + 32.10³  ---  P₂=152.10³ – 32.10³  ---  P₂=120.10³=1,2.10⁵N/m²  ---

R- A

24- S_A=2S_B  ---  S_A.V_A=S_B.V_B  ---  2S_B.5=S_B.V_B  ---  V_B=10m/s  ---  teorema de Bernoulli  ---  P_A + d.g.h_A + d.(V_A)²/2 =

P_B + d.g.h_B + d.(V_B)²/2  ---  7.10³ + 8.10².10.10 + 8.10².(5)²/2=P_B + 8.10².10.1 + 8.10².(10)²/2  ---  7.10³ + 80.10³ + 10.10³=P_B + 8.10³ + 40.10³  ---  97.10³=P_B + 48.10³  --- P_B=49.10³=4,9.10⁴N/m²

25- a) v=180km/h/3,6=50  ---  v=50m/s  ---  redução da pressão  ---  ΔP=ρv²/2=1,2.(50)²/2  ---  ΔP=1,5.10³N/m²

b) variação de pressão=força/área  ---  ΔP=peso/S  ---  1,5.10³=m.10/5.400  ---  m=81.10⁴kg  ---  m=8,1.10²t

c) ρv²/2=ΔP=peso/área  ---  1,2.v²/2=m.g/5.400  ---   1,2.v²/2=250.10³.10/5.400  ---  v=√771,6  ---  v=27,77m/sx3,6  ---  v=100km/h

26- Z=v.S=√(2gh).S=√(2.10.5).2.10^-4  ---  Z=√100.2.10^-4  ---  Z=2.10^-3m³/s

27- a) entrada  ---  P_A=4.10⁵N/m²  ---  R_A=2/1=1cm=10^-2m  ---  h_A=0  ---  v_A=1,5m/s  ---  segundo andar  ---  P_B  ---  R_B=1/2=0,5.10^-2=5.10^-3m  ---  h_B=5m  ---  S_A.v_A=S_B.v_B  ---   π.(R_A)².v_A=π.(R_B)².v_B  ---  (10^-2)².1,5=(5.10^-3)².v_B  ---

1,5.10^-4=25.10^-6.v_B  ---  v_B=1,5.10^-4/25.10^-6  ---  v_B=0,06.10²  ---  v_B=6m/s

b) Bernoulli  ---  P_A + d(v_A)²/2 + d.g.h_B = P_B + d(v_B)²/2 + d.g.h_B  ---  4.10⁵ + 10³.(1,5)²/2 + 10.10.0 = P_B + 10³(6)²/2 + 10³.10.5  ---  40.10⁴ + 0,1125.10⁴ + 0 = P_B + 1,8.10⁴ + 5.10⁴  ---  P_B=40,1125.10⁴ – 6,8.10⁴  ---  P_B=33,3.10⁴=3,3.10⁵Pa

c) vazão  ---  Z=S_B.v_B=π.(R_B)².6=3,14.(5.10^-3)².6  ---  Z=471.10^-6=4,71.10^-4  --- Z=4,71.10^-4m³/s  ou  Z=0,471L/s

28- a) Falsa  - se as alturas estivessem no mesmo nível, as velocidades do vento em cada uma delas seriam iguais e, assim não haveria diferença de pressão para empurrar o ar, não havendo ventilação dentro da toca.

b) Correta – o arbusto diminui a velocidade do vento na abertura 1 aumentando, nela, a pressão. Assim, a diferença de pressão entre as aberturas será aumentada, favorecendo a ventilação.

c) Como as alturas são constantes, a diferença de energia potencial gravitacional também é constante   ---   P₁ + dv₁²/2= P₂ + dv₂²/2  --- ΔP= P₁ – P₂=d/2(v₂² – v₁²)  --- ΔP é diretamente proporcional à diferença do módulo do quadrado das velocidades  ---  Falsa.

d) Correta – ocorre da abertura de menor velocidade do vento, maior pressão (abertura 1) para a abertura de maior velocidade do vento, menor pressão (abertura 2) 

29- a) Δt=1min e 40s=60 + 40  ---  Δt=100s  ---  ΔS=20m  ---  v=ΔS/Δt=100/20  ---  v=5m/s  ---  vazão  ---  Z=ΔV/Δt

=500.10^-3/100  ---  Z=5.10^-3m³/s  ---  energia utilizada para elevar a água a uma altura h=20m num local onde g=10m/s²  ---  ΔW=dgh=10³.10.20  ---  ΔW=2.10⁵J  ---  P_oútil=ΔW.Z=2.10⁵.5.10^-3  ---  P_oútil=1.000W (J/s)  ---  rendimento (η=P_oútil/P_ototal)  ---  0.5=1.000/P_ototal  ---  P_ototal=2.000W

b) V=S.h  ---  5.10^-1=2.h  ---  h=0,25m  ---  P=dgh=10³.10.0,25  ---  P=2,5.10³N/m²

30- Z=400cm³s=4.10².10^-6  ---  Z=4.10^-4m³s  ---  S₁=2.10^-4m²  ---  S₂=10^-4m²  ---  Z  ---  constante  ---  Z=S₁.v₁  --- 

4.10^-4=2.10^-4.v₁  ---  v₁=2m/s  ---  Z=S₂.v₂  ---  4.10^-4=10^-4v₂  ---  v₂=4m/s  ---  Stevin em 2  ---  P₂=d.g.h=10³.10.0,5  --- 

P₂=5.10³N/m²  ---  h=o  ---  dgh=0  ---  Bernoulli  ---  P₁ + d(v₁)²/2=P₂+ d(v₂)²/2  ---  P₁ + 10³.4/2=5.10³ + 10³.16/2  --- 

P₁=13.10³ – 2.10³  ---  P₁=11.10³N/m² (N.m^-2)  ---  R- A

31- Veja a figura abaixo  ---  B_L  ---  bomba no lençol  ---  B_S  ---  bomba no solo  ---  trabalho (energia)

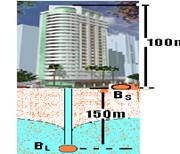
 para elevar a água a uma altura h  ---  W=d.g.h  ---  potência útil  ---  P_u=W.Z  ---  P_u=d.g.h.Z  ---  BS – P_uS=10³.10.100.0,03 =3.10⁴= =3.10⁴.1/750  ---  P_uS=40 hp  ---  rendimento de 80%  ---  η=P_u/P_t  ---  0,8=40/P_t  ---  P_tS=50 hp  ---  B_L  ---  bomba no lençol  ---  P_uL=d.g.h.Z=10³.10.250.0,03  ---    P_uL=100 hp  ---  η=  P_uL/P_tL  ---  0,8=100/P_tL  ---    P_tL=125 hp  ---  utilizando o compressor  ---  h_compressor=1,5h_BS  ---  P_ucompressor=1,5.P_uBS  --- P_ucompressor=1,5.40  ---  P_ucompressor=65 hp  --- 

η=P_ucompressor/P_tcompressor  ---  P_tcompressor=75 hp  ---  0) Falsa  ---  deverá ser de 125 hp  ---  1) verdadeira  ---  2) verdadeira  ---  3) verdadeira  ---  4) verdadeira

32- P=d.g.h.Z=d.g.h.ΔV/Δt  --- P=0,5cv=0,5.750  ---  P=375W  ---   375=10³.10.15.500.10^-3/Δt  ---  Δt=75.000/375=200s  ---  R- B

33- Apenas a afirmação II é incorreta, pois os pontos A e B estão no mesmo líquido, mas em alturas distintas e logo pela Lei de Stevin estão sob pressões diferentes.

R- D  ---  veja teoria 

34- Você pode chegar à opção correta sem apelar para equações ou leis da Física, mas apenas se baseando em fatos do cotidiano  ---  quando você joga água no jardim ou lava o carro com uma mangueira convencional, você coloca o polegar na extremidade de saída da água para diminuirmos a área de fluxo  ---  isso, consequentemente, provoca um aumento de pressão e um aumento na velocidade, lançando a água à maior distância  ---  fisicamente você pode usar a equação da continuidade e a equação de Bernoulli  ---  sendo Q a vazão, v a velocidade do fluxo e A a área da secção transversal, a equação da continuidade  ---  Q = v A. (I)  ---  a equação de Bernoulli relaciona o acréscimo de pressão (p) com a altura de bombeamento (h) e com a velocidade de fluxo (v)  --- 

considerando o sangue um fluido incompressível de densidade d e que seja bombeado a partir do repouso, desprezando perdas nas paredes  ---  p=mV²/2 + mgh (II)  ---  observando a equação (I) você conclui que, se a vazão é constante, diminuindo-se a área de fluxo a velocidade aumenta  ---  na equação (II), se a velocidade aumenta, a pressão também aumenta.

Analisando as opções:

a) Falsa  ---  pelo exposto acima.

b) Falsa  ---  as forças mencionadas formam um par ação-reação.Essas forças nunca se anulam, pois agem em corpos diferentes.

c) Falsa  ---  a pressão de 2,5 Pa significa que é exercida uma força de 2,5 N em 1 m².

d) Correta.

e) Falsa  ---  considerando a densidade do mercúrio, d_Hg = 13,6 g/cm³ = 13,6.10³ kg/m³ (não fornecida no enunciado), a pressão sistólica de 120 mmHg = 0,12 mHg, pode ser calculada no Sistema Internacional pelo teorema de Stevin:

p = d_Hg g h = 13,6.10³.10.0,12  ---  p = 1,6.10³ Pa  ---  R- D

35- Dados: V = 1.200 L; h = 30 m; L = 200 m  ---  seguindo as instruções do fabricante, entremos com os dados na tabela para obtermos o valor de H.

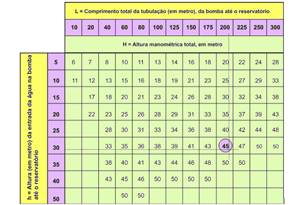
Como mostrado, obtemos H = 45 m  ---  analisando o gráfico dado, temos os valores mostrados: H  = 45 m  ---   Q = 900 L/h.

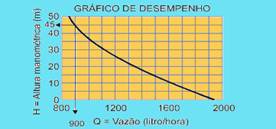
Calculando o tempo para encher o reservatório  ---  Q=V/t  ---  900=1.200/t  ---  t=1.200/900  ---  t=4/3h  ---  t=80min  --- 

t=1h e 20min  ---  R- E

36- Tempo total do banho  ---  Δt_t = 6 min e 54 s = 414 s = 6,9 min  ---  tempo com um quarto de volta  ---  Δt₁ = 1 min e 18 s = 78 s = 1,3 min  ---  tempo com o registro fechado  ---  Δt₂ = 3 min e 36 s = 216 s = 3,6 min  ---  tempo com vazão total  ---  Δt₃ = ?  --- 

soma dos tempos  ---  Δt_t = Δt_t + Δt₂ + Δt₃  ---  6,9 = 1,3 + 3,6 + Δt₃  ---  Δt₃=2 min  ---  cálculo do consumo de água, usando os dados da tabela  ---  C_água = 1,3x1,5 + 2x10,8 = 1,95 + 21,6  ---  C_água = 23,55 L  ---  R- B

37- Cálculos feitos na questão anterior  ---  o chuveiro ficou ligado durante um curto intervalo de 78 s, despejando 1,95 L  ---   a seguir, ficou fechado durante 216 s e, finalmente, com vazão total durante 120 s, despejando 21,6 L  ---  fazendo essas comparações  ---  R- C

38- Artérias: são vasos de maior calibre que os demais, de parede espessa que saem do coração levando sangue para os órgãos e

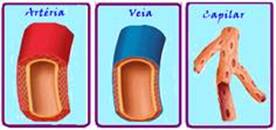
tecidos do corpo  ---  capilares sangüíneos: são vasos de pequeno calibre que ligam as extremidades das  artérias às veias  ---  as veias levam o sangue vindo do corpo, ao coração e suas paredes são mais finas que as das artérias  ---  a artéria Aorta é a maior do corpo humano, pois além de ser a maior em extensão, ela é a de maior (espessura, diâmetro) calibre  ---  observe que o vaso I possui maior área (espessura, diâmetro) que o de cada vaso II, então ele só pode ser a artéria aorta  ---  o fluxo de sangue no corpo humano é constante, ou seja, em cada vaso, o volume que circula no mesmo intervalo de tempo é o mesmo  ---   φ_I = φ_II  --- 

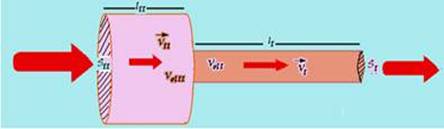
V_olI/∆t = V_olII/∆t  --- (S₁.l_I)/ ∆t = S_II.l_II/∆t  (1)_­  ---  a velocidade do sangue no interior de cada vaso é diferente e vale  ---  V₁=l_I/∆t (2)  ---  V_1I=l_II/∆t (3)  ---  comparando (1) com (2) e com (3)  ---  S_I.V_I = S_II.V_II  ---  240.30 = 240000V₂  ---  V₂=2700/240000  ---

V₂=0,03cm/s  ---  R- C