Gráficos do Movimento Uniformemente Variado (MUV)

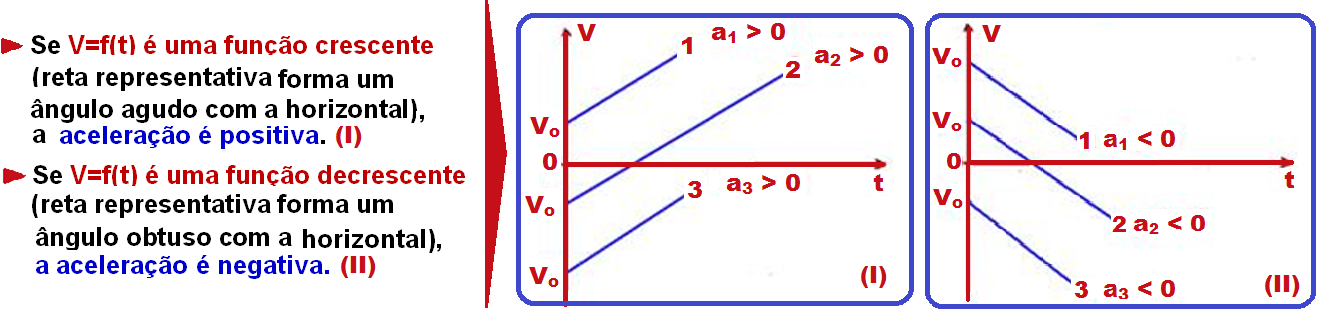
Diagrama da velocidade em função do tempo

Como a função horária da velocidade de um MUV é V= Vo + a.t, que é uma função do primeiro grau e, portanto sua representação gráfica é uma reta de inclinação não nula.

Relação entre o deslocamento ∆S e o gráfico da velocidade x tempo de um MUV.

Em todo gráfico VXt a área entre a reta representativa e o eixo dos tempos é numericamente igual à

variação de espaço ΔS, entre dois instantes quaisquer t₁ e t₂.

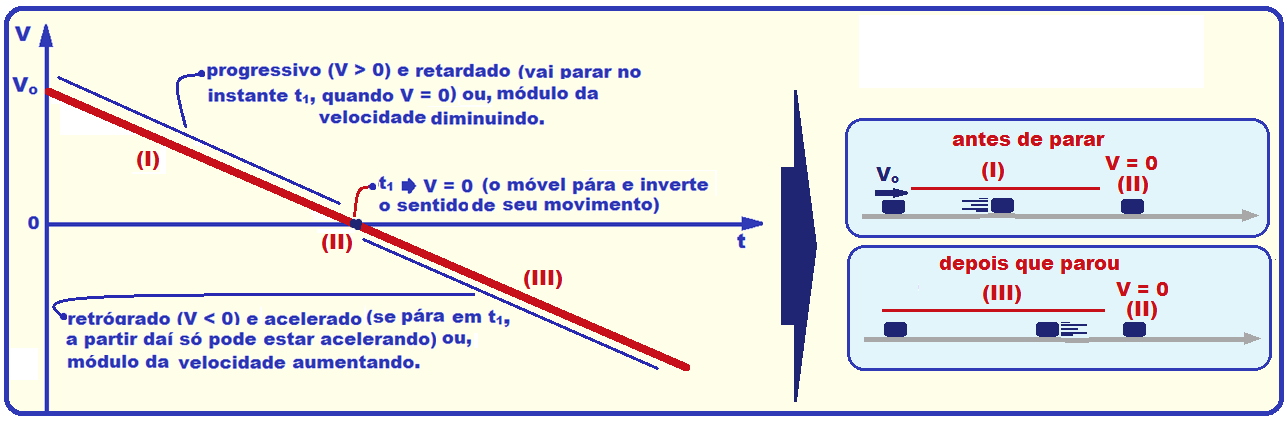
Análise detalhada do gráfico velocidade x tempo do MUV

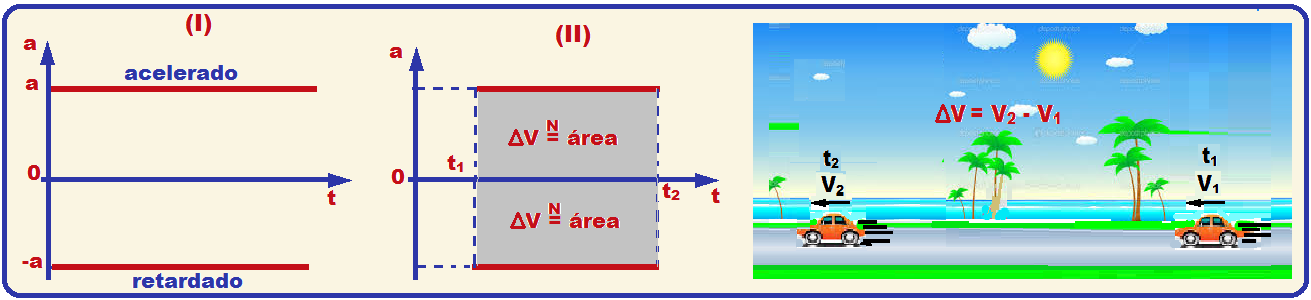
Análise do gráfico aceleração x tempo de um MUV

Em todo MUV a aceleração é constante e seu gráfico é uma reta paralela ao eixo t (I) e entre dois

instantes quaisquer t₁ e t₂, a variação de velocidade ΔV = V₂ – V₁ é numericamente igual à área (II)

 Análise detalhada do gráfico do espaço (S) em função do tempo de um MUV 

Como a função horária de um MUV é uma função do segundo grau (S = S_o + V_o.t + a.t²/2), sua representação gráfica é uma parábola cuja concavidade fornece o sinal da aceleração (a).

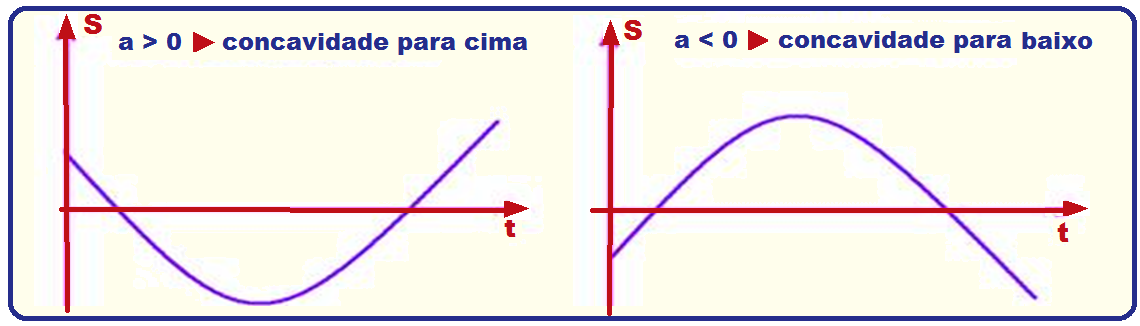
Análise do gráfico S x t de um MUV onde a aceleração é positiva (a concavidade da parábola é para cima)

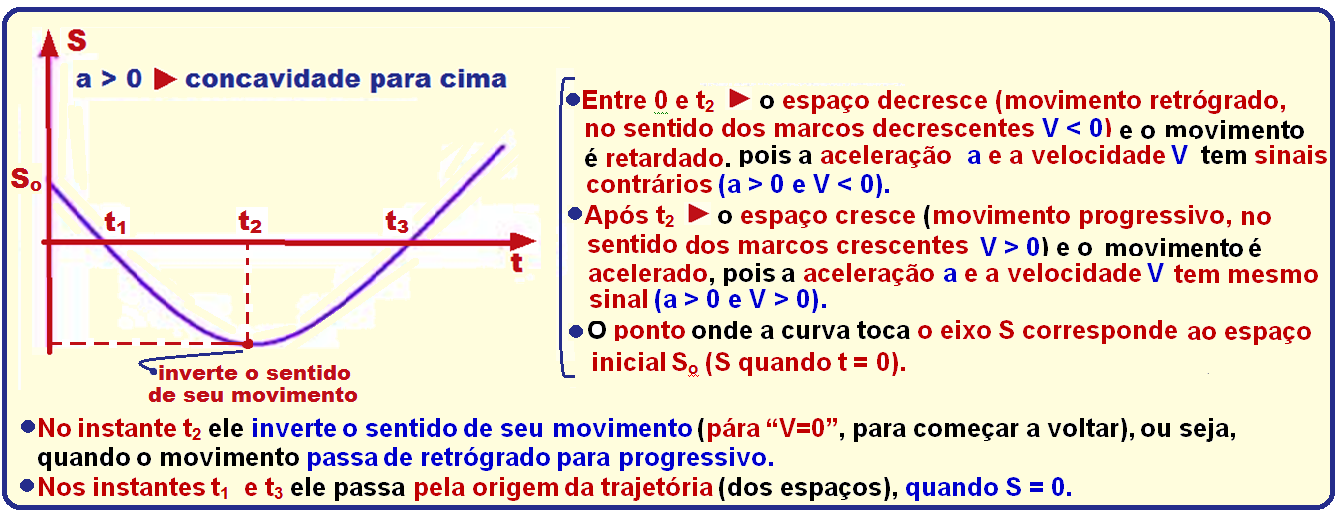
Análise do gráfico S x t de um MUV onde a aceleração é negativa (a concavidade da parábola é para baixo)

O que você deve saber

Resumo de todos os gráficos do MUV

Resumo dos gráficos do espaço, velocidade e aceleração do MUV, com a > 0 e com

a < 0.

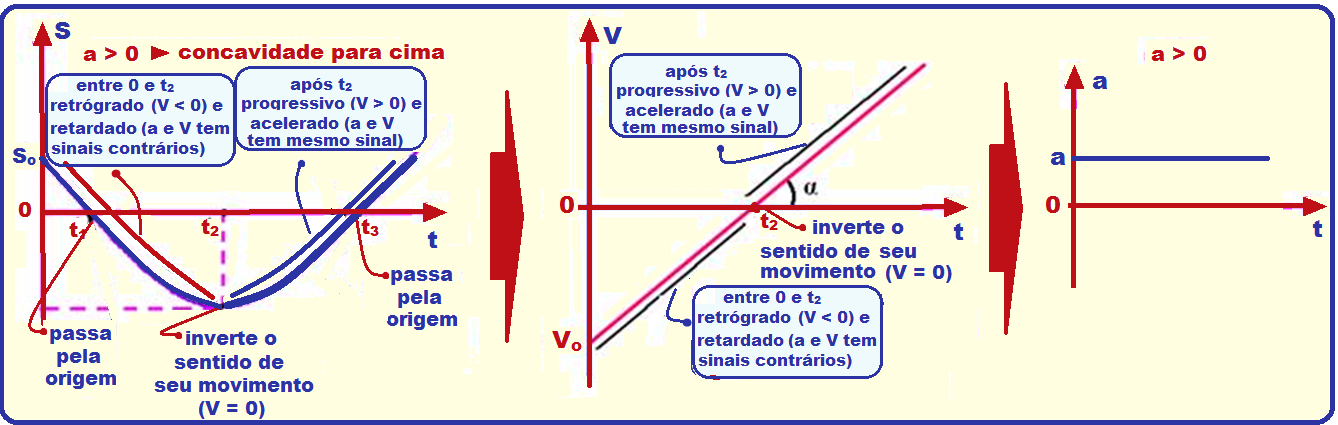
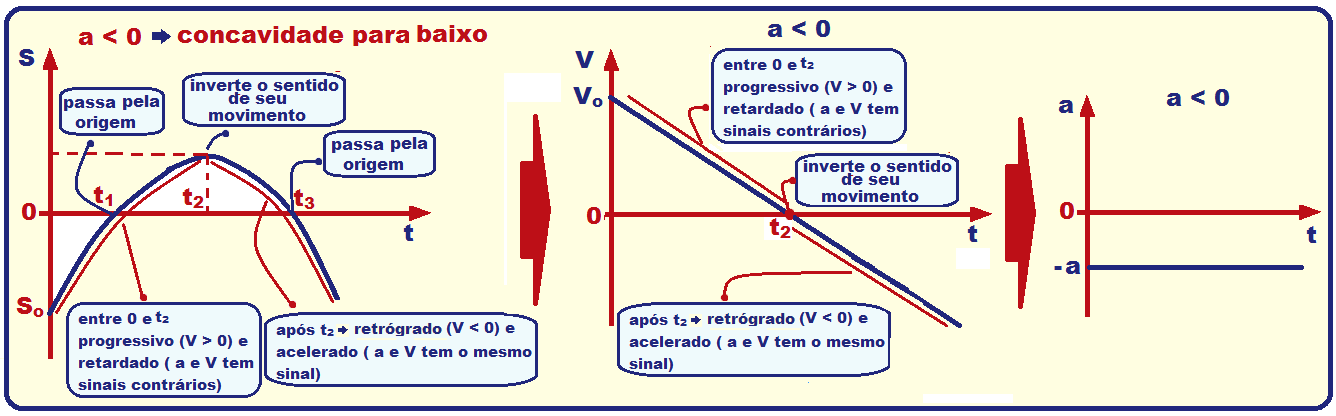
 Lembre-se que os gráficos não mostram as trajetórias dos móveis. Eles apenas representam as equações (funções) do movimento.

Exercícios de vestibulares sobre gráficos do MUV

01-(UFB) O espaço (posição) de um móvel varia com o tempo conforme o gráfico abaixo.

Pede-se determinar:

a) O espaço (posição) inicial S_o, o instante t_i em que o móvel inverte o sentido de seu movimento e o(s) instante(s) em que passa pela origem dos espaços (posições, marco zero).

b) O intervalo de tempo em que o movimento é progressivo e o intervalo de tempo em que o movimento é retrógrado.

c) O intervalo de tempo em que o movimento é acelerado e em que é retardado.

d) A função horária do espaço

e) A função horária da velocidade e sua representação gráfica

f) A função oraria da aceleração e sua representação gráfica.

02-(UFB) O gráfico abaixo mostra a variação do espaço de um móvel em função do tempo.

Classifique o movimento em cada trecho

03-(ENEM) Em uma prova de 100 m rasos, o desempenho típico de um corredor padrão é representado pelo gráfico a seguir:

Em que intervalo de tempo o corredor apresenta ACELERAÇÃO máxima?

a) Entre 0 e 1 segundo.         

b) Entre 1 e 5 segundos.         

c) Entre 5 e 8 segundos.        

d) Entre 8 e 11 segundos.         

e) Entre 9 e 15 segundos.

04-(UFPE) O gráfico da velocidade em função do tempo de um ciclista, que se move ao longo de uma pista retilínea, é mostrado a seguir.

 Considerando que ele mantém a mesma aceleração entre os instantes t = 0 e t = 7 segundos, determine a distância percorrida neste intervalo de tempo. Expresse sua resposta em metros.

05-(UNIFESP-SP)

Em um teste, um automóvel é colocado em movimento retilíneo uniformemente acelerado a partir do repouso até atingir a velocidade máxima. Um técnico constrói o gráfico onde se registra a posição x do veículo em função de sua velocidade v. Através desse gráfico, pode-se afirmar que a aceleração do veículo é

06- (UNICAMP-SP) O famoso salto duplo twistcarpado de Daiane dos Santos foi analisado durante um dia de treinamento no Centro Olímpico em Curitiba, através de sensores e filmagens que permitiram reproduzir a trajetória do centro de gravidade de Daiane na direção vertical (em metros), assim como o tempo de duração do salto.

De acordo com o gráfico, determine:

a) A altura máxima atingida pelo centro de gravidade de Daiane.

b) A velocidade média horizontal do salto, sabendo-se que a distância percorrida nessa direção é de 1,3m.

c) A velocidade vertical de saída do solo.

07-(UFMG-MG) Um carro está andando ao longo de uma estrada reta e plana. Sua posição em função do tempo está representada neste gráfico:

Sejam v_A, v_B e v_C os módulos das velocidades do carro, respectivamente, nos pontos A, B e C, indicados nesse gráfico.

Com base nessas informações, é CORRETO afirmar que

a) v_A < v_B < v_C .                     

b) v_B < v_C < v_A .                     

c) v_A < v_C < v_B.                    

d) v_B < v_A < v_C .

08-(UFRJ-RJ) A posição de um automóvel em viagem entre duas cidades foi registrada em função do tempo.

O gráfico a seguir resume as observações realizadas do início ao fim da viagem.

a) Indique durante quanto tempo o carro permaneceu parado.

b) Calcule a velocidade escalar média do carro nessa viagem.

09-(UFRRJ) Um professor, após passar a um aluno uma questão que apresentava o gráfico "aceleração x tempo" do movimento de um objeto, e pediu a este que construísse o gráfico "posição x tempo" desse movimento.

A resposta dada pelo aluno foi o gráfico apresentado.

A resposta do aluno está correta? Justifique sua resposta.

10-(UNESP-SP) Um veículo A passa por um posto policial a uma velocidade constante acima do permitido no local. Pouco tempo depois, um policial em um veículo B parte em perseguição do veículo A. Os movimentos dos veículos são descritos nos gráficos da figura.

Tomando o posto policial como referência para estabelecer as posições dos veículos e utilizando as informações do gráfico, calcule:

a) a distância que separa o veículo B de A no instante t = 15,0 s.

b) o instante em que o veículo B alcança A.

11-(UNESP-SP) O gráfico na figura descreve o movimento de um caminhão de coleta de lixo em uma rua reta e plana, durante 15s de trabalho.

a) Calcule a distância total percorrida neste intervalo de tempo.

b) Calcule a velocidade média do veículo.

12-(PUC-SP) O gráfico representa a velocidade em função do tempo de uma pequena esfera em movimento retilíneo. Em t = 0, a esfera se encontra na origem da trajetória.

Qual das alternativas seguintes apresenta corretamente os gráficos da aceleração (a) em função do tempo e do espaço (s) em função do tempo (t)?

13-(UFG) O Visconde de Sabugosa vê uma jaca cair da árvore na cabeça da Emília e filosofa:

 "Este movimento poderia ser representado, qualitativamente, pelos gráficos de posição e velocidade, em função do tempo..."

14-(Ufpe-PE) Uma partícula, que se move em linha reta, está sujeita à aceleração a(t), cuja variação com o tempo é mostrada no gráfico a seguir.

Sabendo-se que no instante t = 0 a partícula está em repouso, calcule a sua velocidade no instante t = 8,0 s, em m/s.

15-(UFC) No instante t = 0 , o motorista de um carro que percorre uma estrada retilínea, com velocidade constante de 20 m/s, avista um obstáculo 100 m a sua frente.

 O motorista tem um tempo de reação t = 1 s, após o qual aciona os freios do veículo, parando junto ao obstáculo. Supondo-se que o automóvel tenha uma desaceleração constante, determine qual dos gráficos abaixo melhor representa a velocidade do automóvel desde o instante em que o motorista avista o obstáculo até o instante em que o automóvel pára.

16-(Ufpe) Em t = 0, um objeto parte do repouso a partir da posição x = 1,0 m, executando um movimento retilíneo, com aceleração em função do tempo mostrada no gráfico abaixo. Dos gráficos apresentados em seguida, indique qual representa corretamente a dependência da velocidade com o tempo.

17-(UFC) Um trem, após parar em uma estação, sofre uma aceleração, de acordo com o gráfico da figura a seguir, até parar novamente na próxima estação.

 Assinale a alternativa que apresenta os valores corretos de t_f, o tempo de viagem entre as duas estações, e da distância entre as estações.

a) 80 s, 1600 m         

b) 65 s, 1600 m         

c) 80 s, 1500 m         

d) 65 s, 1500 m         

e) 90 s, 1500 m

18-(UFSCAR-SP) Um pequeno objeto, quando lançado verticalmente para cima, retorna ao local de partida após ter decorrido o tempo 2t. Dos conjuntos de gráficos apresentados, aquele que se pode adequar perfeitamente à situação descrita, supondo desprezível a ação resistiva do ar, é

19-. (PUCCAMP-SP) Considere os gráficos a seguir:
I. Espaço em função do tempo.         

II. Velocidade em função do tempo.         

III. Aceleração em função do tempo. 
                                            

A respeito desses gráficos é correto afirmar que:

a) somente I e II podem representar o mesmo movimento.          b) somente I e III podem representar o mesmo movimento.
c) somente II e III podem representar o mesmo movimento.        d) os três gráficos podem representar o mesmo movimento.
e) cada gráfico representa um movimento distinto.

20-(UFRRJ) O gráfico a seguir representa os movimentos de dois móveis A e B.

Observando o gráfico, pode-se afirmar que:

a) em t = 2s e t = 9 s a velocidade do móvel A é igual a velocidade do móvel B.          -b) a aceleração do móvel A é sempre maior que a do móvel B.                c) a velocidade do móvel B em t = 2 s é nula.              d) a velocidade do móvel A em t = 9 s é 7 m/s.
e) em t = 0 s a aceleração do móvel A é 16 m/s2.

21-(UFMS) O gráfico do espaço (S) em função do tempo (t) de uma partícula está registrado a seguir. Com relação ao movimento da partícula, é correto afirmar que:

a) a trajetória foi retilínea.          b) a velocidade foi sempre positiva.          c) a aceleração foi sempre positiva.          d) a velocidade foi nula em três instantes.          e) o movimento foi uniforme.

22-(UFRGS) O gráfico que segue representa os movimentos unidimensionais de duas partículas, 1 e 2, observadas no intervalo de tempo (0, t_f). A partícula 1 segue uma trajetória partindo do ponto A, e a partícula 2, partindo do ponto B. Essas partículas se cruzam no instante t_C.

Responda às questões de números 22 e 23

22-(UFGRS) As velocidades escalares das partículas 1 e 2 no instante t_C e suas acelerações escalares  são, respectivamente,

23-(UFGRS)

Quando as velocidades escalares das partículas 1 e 2, no intervalo observado, serão iguais?

a) Em t = 0.                

b) Em t_C.                

c) Entre 0 e t_C.                

d) Entre t_C e t_f.               

e) Em nenhum instante de tempo nesse intervalo.

24-(UNESP) Os movimentos de dois veículos, I e II, estão registrados nos gráficos da figura.

Sendo os movimentos retilíneos, a velocidade do veículo II no instante em que alcança I é

a) 15 m/s.                     

b) 20 m/s.                       

c) 25 m/s.                      

d) 30 m/s.                       

e) 35 m/s.

25-(UFF-RJ) Um motorista avista um detector de velocidade e, nesse mesmo instante, pisa no freio.

O gráfico 1 mostra como varia a velocidade de seu automóvel em função do tempo, desde o instante em que o motorista pisa no freio até passar pelo detector. Assinale, dentre as alternativas apresentadas, a que melhor representa a aceleração do automóvel em função do tempo, ao longo desse percurso.

26-(PUC-RJ) O movimento de um objeto pode ser descrito pelo gráfico velocidade versus tempo, apresentado na figura a seguir.

Podemos afirmar que:

a) a aceleração do objeto é 2,0 m/s², e a distância percorrida em 5,0 s é 10,0 m.

b) a aceleração do objeto é 4,0 m/s², e a distância percorrida em 5,0 s é 20,0 m.

c) a aceleração do objeto é 2,0 m/s², e a distância percorrida em 5,0 s é 25,0 m.

d) a aceleração do objeto é 2,0 m/s², e a distância percorrida em 5,0 s é 10,0 m.

e) a aceleração do objeto é 2,0 m/s², e a distância percorrida em 5,0 s é 20,0 m.

27-(UDESC-SC) O movimento de uma bola sobre uma trajetória retilínea é descrito de acordo com a seguinte equação: x = 5 + 16t - 2t², em que x é medido em metros e t em segundos.

a) Faça o esboço do gráfico da posição em função do tempo.

b) Calcule a velocidade da bola em t = 4,0 s.

c) Calcule a distância percorrida pela bola e o seu deslocamento em t = 5,0 s.

28- (UFRJ-RJ) Um móvel parte do repouso e descreve uma trajetória retilínea durante um intervalo de tempo de 50s, com a aceleração indicada no gráfico a seguir.

a) Faça um gráfico da velocidade do móvel no intervalo de 0 até 50s.

b) Calcule a distância percorrida pelo móvel nesse intervalo.

29-(UFG-GO) Ao abrir uma garrafa de refrigerante com gás, muitas bolhas de gás carbônico ali formadas sobem desde o

fundo da garrafa com um movimento acelerado. Supondo-se que as bolhas têm o mesmo tamanho e a mesma quantidade de gás durante toda subida e desprezando-se quaisquer perdas de energia por resistência ao movimento. Dos gráficos a seguir

aqueles que representam, respectivamente, a posição e a velocidade das bolhas são:

a) I  e  IV                    

b) I  e  VI                    

c) II  e  V                       

d) II  e  VI                    

e) III  e  V

30-(UERJ-RJ) Um trem de brinquedo, com velocidade inicial de 2 cm/s, é acelerado durante 16 s.

O comportamento da aceleração nesse intervalo de tempo é mostrado no gráfico a seguir.

Calcule, em cm/s, a velocidade do corpo imediatamente após esses 16 s.

31-(UFSC-SC)  Os diagramas de posição versus tempo, X x t, mostrados a seguir, representam os movimentos retilíneos de

quatro corpos. Em relação ao intervalo de tempo entre os instantes 0 e t’, é CORRETO afirmar que:

01) a velocidade média entre os instantes 0 e t’, das curvas representadas nos gráficos, é numericamente igual ao coeficiente angular da reta que passa pelos pontos que indicam as posições nestes dois instantes. 

02) o movimento do corpo representado no diagrama D, no intervalo entre 0 e t’, ι retilíneo uniformemente retardado. 

04) no instante t_o=0, o corpo, cujo movimento é representado no diagrama C, está na origem do referencial.  

08) no movimento representado no diagrama B, no intervalo de tempo entre 0 e t’, o corpo vai se aproximando da origem do referencial. 

16) no movimento representado no diagrama A, a velocidade inicial do corpo é nula. 

32) o movimento do corpo representado no diagrama B, no intervalo de tempo entre 0 e t’, é retilíneo uniformemente acelerado.  

64) o movimento representado no diagrama B poderia ser o de um corpo lançado verticalmente para cima. 

32-(PUC-PR)  A figura fornece a aceleração em função do tempo, a(t), de um pequeno cachorro Chihuahua enquanto ele

persegue um pastor alemão ao longo de uma linha reta.

Marque a alternativa CORRETA.

a) No intervalo de tempo E, o Chihuahua move-se com velocidade constante. 

b) Nos intervalos de tempo C, E e G, o Chihuahua move-se com velocidade constante. 

c) O Chihuahua está parado no intervalo de tempo E. 

d) Nos intervalos de tempo B e D, a velocidade e o deslocamento do Chihuahua são necessariamente positivos. 

e) Entre os intervalos A e B, o Chihuahua inverte o sentido em que está correndo. 

33-(UFRGS-RS)  Observe o gráfico a seguir, que mostra a velocidade instantânea V em função do tempo t de um móvel que se desloca em uma trajetória retilínea. Neste gráfico, I, II e III identificam, respectivamente, os intervalos de tempo de 0s a 4s, de

4s a 6s e de 6s a 14s. Nos intervalos de tempo indicados, as acelerações do móvel valem, em m/s², respectivamente,

a) 20, 40, e 20.                

b) 10, 20 e 5.                 

c) 10, 0 e -5.                       

d) -10, 0 e 5.                      

e) -10, 0 e -5.

34-(UFC-CE)  O gráfico da velocidade em função do tempo (em unidades arbitrárias), associado ao movimento de um ponto material ao longo do eixo x, é mostrado na figura abaixo.

Analise o que ocorre com a aceleração do ponto material em cada intervalo de tempo.

35-(PUC-PR)  Um motociclista dirige uma motocicleta ao longo de uma estrada reta como mostrado no diagrama velocidade

x tempo. A respeito dessa situação, assinale a alternativa correta:

a) Entre os instantes t = 3 s e t = 5 s o movimento é acelerado.  

b) A aceleração no intervalo de tempo entre t = 5 s e t = 7 s vale – 4 m/s².  

c) O deslocamento do motociclista entre os instantes t = 3 s e t = 5 s foi de 20 m.  

d) A aceleração no intervalo de tempo entre t = 5 s e t = 7 s vale 2 m/s².  

e) A aceleração no intervalo de tempo entre t = 0 e t = 3 s é nula.   

36-(UNESP-SP) No gráfico a seguir são apresentados os valores da velocidade V, em m/s, alcançada por um dos pilotos em uma corrida em um circuito horizontal e fechado, nos primeiros 14 segundos do seu movimento.

Sabe-se que de 8 a 10 segundos a trajetória era retilínea. Considere g = 10 m/s² e que para completar uma volta o piloto deve percorrer uma distância igual a 400 m.

A partir da análise do gráfico, são feitas as afirmações:

I. O piloto completou uma volta nos primeiros 8 segundos de movimento.

II. O piloto demorou 9 segundos para completar uma volta.

III. A força resultante que agiu sobre o piloto, entre os instantes 8 e 10 segundos, tem módulo igual a zero.

IV. Entre os instantes 10 e 12 segundos, agiu sobre o piloto uma força resultante, cuja componente na direção do movimento

é equivalente a três vezes o seu peso.

São verdadeiras apenas as afirmações

(A) I e III.                   

(B) II e IV.                     

(C) III e IV.                  

(D) I, III e IV.                    

(E) II, III e IV.

 37- (UFLA-MG)  O diagrama ao lado, velocidade versus tempo, representa o movimento de um corpo ao longo de uma

trajetória retilínea. Considerando que o corpo parte da posição S_o = 10 m no instante t_o = 0 s, é CORRETO afirmar que o diagrama que representa esse movimento é:

38-(UFPR-PR)

Num teste de esforço físico, o movimento de um indivíduo caminhando em uma esteira foi registrado por um computador. A partir dos dados coletados, foi gerado o gráfico da distância percorrida, em metros, em função do tempo, em minutos, (figura).

De acordo com esse gráfico, considere as seguintes afirmativas:

1. A velocidade média nos primeiros 4 minutos foi de 6 km/h.

2. Durante o teste, a esteira permaneceu parada durante 2 minutos.

3. Durante o teste, a distância total percorrida foi de 1200 m.

Assinale a alternativa correta.

a) Somente as afirmativas 1 e 3 são verdadeiras.                                    b) Somente as afirmativas 2 e 3 são verdadeiras.

c) Somente as afirmativas 1 e 2 são verdadeiras.                                    d) Somente a afirmativa 3 é verdadeira.

e) As afirmativas 1, 2 e 3 são verdadeiras

39-(UFGV-SP)

Um pára-quedista salta de uma altura de 325 m. Durante os primeiros 5,0 s, ele cai em queda livre, praticamente sem interferência do

ar; em seguida, ele abre o pára-quedas e seu movimento passa a ser uniforme, após brusca diminuição de velocidade, como indica o

gráfico da velocidade, em função do tempo. Considere o movimento de queda vertical e retilíneo e a aceleração da gravidade de 10 m ∕s². O tempo total de movimento, até a chegada do pára-quedista ao solo, será de

(A) 20,0 s.                           (B) 25,0 s.                              (C) 28,0 s.                           (D) 30,0 s.                                      (E) 35,0 s.

40-(UFF-RJ)

Policiais rodoviários são avisados de que um carro B vem trafegando em alta velocidade numa estrada. No instante t_o em que o carro B

passa, os policiais saem em sua perseguição. A figura ilustra as velocidades do carro B e do carro dos policiais (P) em função do tempo.

Assinale a alternativa que especifica o restante do tempo em que o carro P alcança o carro B

a) t₁                         b) t₂                           c) t₃                                d) t₄                                   e) t₅

Resoluções dos exercícios sobre gráficos do MUV

01-

a) S_o=8m (ponto em que a parábola encosta na ordenada “eixo S”, ou seja, ponto quando t=0). Inverte o sentido de seu movimento no instante t_i=3s (vértice da parábola, onde V=0, onde o movimento passa de retrógrado para progressivo). Passa pela origem dos espaços quando S=0, ou seja, nos instantes t=2s e t=4s.

b) O movimento é progressivo quando o móvel se desloca no sentido dos marcos crescentes (V>0) o que ocorre após t=3s e retrógrado  quando o móvel se desloca no sentido dos marcos decrescentes (V<0) o que ocorre entre 0 e 3s.

c) O movimento é acelerado após 3s, pois a e V tem mesmo sinal (a é positiva “a concavidade da parábola é para cima” e V é positiva “se desloca no sentido dos marcos crescentes”).

O movimento é retardado entre 0 e 3s 3s, pois a e V tem sinais contrários (a é positiva “a concavidade da parábola é para cima” e V é negativa “se desloca no sentido dos marcos decrescentes”).

d) S_o=8m  ---  quando t=2s  ---  S=0  ---  S=S_o + V_o.t + a.t²/2  ---  0=8 + V_o.2 + a.2²/2  ---  2.a + 2.V_o = -8  I  ---   quando t=4s  ---  S=0  ---  S=S_o + V_o.t + a.t²/2  ---  0=8 + V_o.4 + a.4²/2  ---  8.a + 4.V_o = -8  II  ---  Resolvendo o sistema composto por I e II  ---  a=2m/s² e V_o=-6m/s  --- S=S_o + V_o.t + a.t²/2  ---  S= 8 - 6.t + t²

e) V=V_o + a.t  ---  V= -6 + 2.t  --- gráfico VXt ---  V=0  ---  0= -6 + 2.t  ---  t=3s  ---  V_o=-6m/s  ---  como é uma função do primeiro grau seu gráfico é uma reta que pode ser definida por apenas dois pontos. 

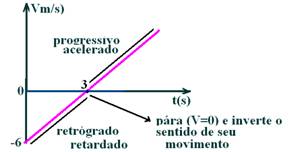
f) A aceleração é constante e vale a=2m/s² e seu gráfico é uma reta paralela ao eixo dos tempos

02- Trecho I – MUV (ramo de parábola) com aceleração positiva “a>0” (concavidade para cima) e velocidade positiva “V>0” (se desloca no sentido dos marcos crescentes,movimento progressivo)  ---  o movimento é acelerado, pois a e V tem mesmo sinal.

Trecho II – MUV (ramo de parábola) com aceleração negativa “a<0” (concavidade para baixo) e velocidade positiva “V>0” (se desloca no sentido dos marcos crescentes,movimento progressivo)  ---  o movimento é retardado, pois a e V sinais contrários.

Trecho III – MU (reta oblíqua) com V constante e negativa (se desloca no sentido dos marcos decrescentes, movimento retrógrado).

Trecho IV – MUV (ramo de parábola) com aceleração positiva “a>0” (concavidade para cima) e velocidade negativa “V<0” (se desloca no sentido dos marcos decrescentes, movimento retrógrado)  ---  o movimento é retardado, pois a e V sinais contrários.

Trecho IV – MUV (ramo de parábola) com aceleração positiva “a>0” (concavidade para cima) e velocidade negativa “V<0” (se desloca no sentido dos marcos decrescentes, movimento retrógrado)  ---  o movimento é retardado, pois a e V sinais contrários.

Trecho V – MUV (ramo de parábola) com aceleração positiva “a>0” (concavidade para cima) e velocidade positiva “V>0” (se desloca no sentido dos marcos crescentes, movimento progressivo)  ---  o movimento é acelerado, pois a e V sinais contrários.

03- A aceleração é máxima onde a curva tem maior inclinação em relação à horizontal  --- R- A

04- V_o=4m/s  ---  a=(V – V_o)/(t – t_o)=(12 – 4)/(4 – 0)  ---  a=2m/s²  ---  V= V_o + a.t  ---  V=4 + 2.7  ---  V=18m/s (velocidade no instante t=7s)  ---  a distância percorrida corresponde à área hachurada do gráfico abaixo

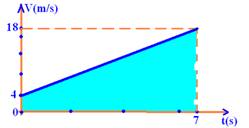
ΔS=(B + b).h/2=(18 + 4).7/2  ---  ΔS=77m

05- ΔS=S – S_o=9 – 0=9m  ---  V_o=0  ---  V=6m/s  ---  Torricelli  ---  V² = V_o² + 2.a.ΔS  ---  36=0 + 2.a.9  ---  a=2m/s²  ---  R- B

06- a) Na vertical  ---   S_o=0  ---  t=0,3s  ---  S=1,2m  ---  S=S_o + V_o.t + a.t²/2   ---  1,2=0 + V_o.0,3 + a,(0,3)²/2  ---  0,3.V_o + 0,045.a=1,2  ---  V_o + 0,15.a=4  I  ---  t=1,1s  ---  S=0  ---  S=S_o + V_o.t + a.t²/2  ---  0=0 + V_o.1,1 + a.(1,1)²/2  ---  1,1V_o + a.0,605=0  II  ---  resolvendo o sistema composto por I e II  ---  a=-10m/s²  ---  V_o=5,5m/s  ---  a altura máxima ocorre quando V=0 (ela pára para começar a descer) que vale 0,55s pelo gráfico  --- S=S_o + V_o.t + a.t²/2  ===  S_máx=0 + 5,5.(0,55) – 10.(0,55)²/2  ---  S_máx=3,025 – 1,5125  ---  S_máx=1,5125m

b) Na horizontal a velocidade é constante e vale V_m=ΔS/Δt=1,3/1,1  ---  V_m=1,18m/s

c) V_o=5,5m/s (veja item a)

07- V_B=0 (vértice da parábola “pára para começar a inverter o sentido de seu movimento”)  ---  quanto mais inclinada a curva em relação à horizontal, maior será a velocidade, ou seja, V_A>V_C  ---  R- B

08- a) Ficou parado entre 1h e 1,8h, ou seja, 48minutos, no km100 (veja gráfico)

b) V_m=ΔS/Δt=(120 – 0)/(3 – 0)  ---  V_m=40km/h (lembre-se de que o tempo de parada está sempre incluído)

09- Os gráficos não podem se referir ao mesmo movimento; se a aceleração é uma constante negativa, a velocidade é uma reta com inclinação negativa, ou seja, está diminuindo. Logo, a função posição x(t) só pode ser representada por uma parábola com concavidade para baixo, ao contrário do que está mostrado.

10- a)Os deslocamentos de cada carro são fornecidos pelas áreas hachuradas nos gráficos abaixo:

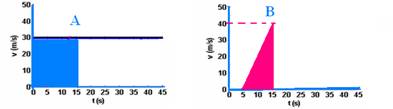
ΔS_A=b.h=15.30=450m  ---  ΔS_B=b.h/2=10.40/2=200m  ---  d=450 – 200  ---  d=250m

b) Se encontram no instante t em que efetuaram o mesmo deslocamento, ou seja, a área em cada gráfico deve ser a mesma:

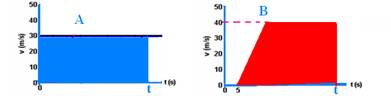
ΔS_A=b.h=t.30=30.t  ---  ΔS_B=(B + b).h/2=(t – 5 + t – 15).40/2=40t – 400  ---  no encontro, percorreram a mesma distância  ---  ΔS_A=ΔS_B  ---  30t=40t – 400  ---  t=40s

11- a) ΔS=soma das áreas=3.8/2 + (4 + 2).12/2 + 2.12/2  ---  ΔS=60m

b) V_m= ΔS/ Δt=60/15  ---  V_m=4m/s

12- Entre 0 e t₁  ---  velocidade aumentando, aceleração positiva e concavidade da parábola para cima  ---  entre t₁ e t₂  ---  velocidade constante, aceleração nula, movimento uniforme com reta ascendente e movimento progressivo  ---  entre t₂ e t₃  ---  velocidade diminuindo, aceleração negativa e parábola com concavidade para baixo  ---  R- D

13- Trata-se de uma queda livre com a=-g (aceleração da gravidade) com concavidade para baixo  e a velocidade a partir de zero e aumentando em módulo (movimento retrógrado acelerado)  ---  R- B

14- Entre 0 e 4s  ---  a=4m/s²  ---  V=V_o + at  ---  V=0 =4.4  ---  V=16m/s  ---  entre 4s (onde V_o=16m/s) e 8s  ---  V=V_o + at  ---  V=16 -2.4  ---  V=8ms

15- Durante 1s ele se move com velocidade constante de 20m/s e depois, sua velocidade diminui até zero segundo uma reta, pois se trata de um MUV com desaceleração constante  ---  R- D

16- Parte do repouso  ---  V_o=0  ---  entre 0 e 2s a aceleração é positiva e vale 0,5m/s²  ---  V=V_o + at=0 + 0,5.2=1m/s e sua velocidade variade 0 a 1m/s  --- ntre 2s e 4s, a aceleração é nula e ele segue em movimento uniforme com velocidade constante de 1m/s  --- 

R- E

17- entre 0 e 10s  ---  V_o=0  ---  V=V_o + at=0 + 1.10=10m/s  ---  entre 10s e 20s  ---  V_o=10m/s  ---  V=V_o + at=10 + 2.10=30m/s  ---  entre 20s e 50s  ---  a aceleração é nula e a velocidade constante de 30m/s  ---  entre 50s e t ele freia e pára com sua velocidade variando de 30m/s para 0  ---  V=V_o + at  ---  0=30 -1.t ---  t=30s  ---  t_f=50 + 30=80s

 Construindo o gráfico Vxt

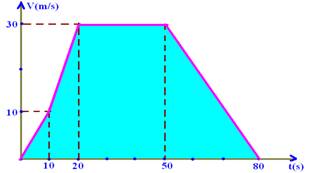
ΔS_total=soma das áreas=10.10/2 + (30 + 10).10/2 + 30.30 + 30.30/2  --- ΔS_total=1.600m  ---  R- A

18- Colocando a origem da trajetória vertical no ponto de lançamento e orientando-a para baixo, na subida o movimento é retrógrado retardado e na descida progressivo acelerado (observe atentamente figuras abaixo)

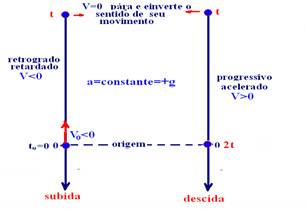
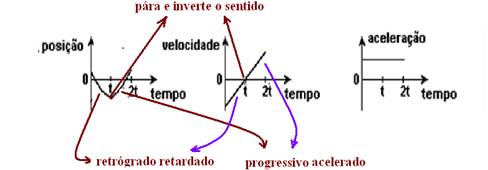
R- D

19- Veja explicação baseada nos gráficos abaixo:

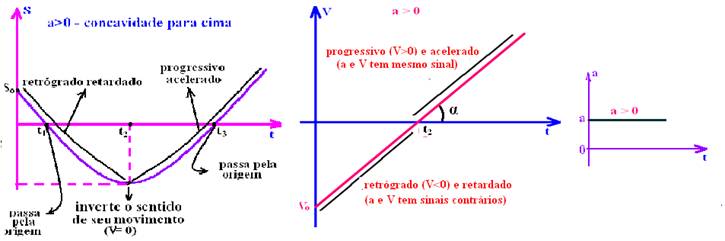
R- D

20- R- B  ---  a aceleração do móvel A é positiva e diferente de zero e o móvel B está em movimento uniforme com velocidade constante e aceleração nula.

21- O vértice da parábola é o ponto onde ocorre a inversão do sentido do movimento. Observe que no gráfico existem três vértices  --- 

R- D

22- 1 – V₁>0  ---  movimento progressivo (se move no sentido dos marcos crescentes) e a₁<0 (parábola com concavidade para baixo)

2 – V₂<0  ---  movimento retrógrado (se move no sentido dos marcos decrescentes) e a₁<0 (parábola com concavidade para baixo)

R- D

23- Veja pela resolução anterior que, nesse intervalo de tempo, V₁ é sempre positiva e V₂sempre negativa e, assim, elas não se igualam  ---  R- E

24- S_oII=0 e supondo V_oII=0 a equação do móvel II, que é um MUV é S=S_o + V_o.t + at²/2  ---  t=15s  ---  S=225m  ---  225=0 + 0 + a.15²/2  ---  a=2m/s²  ---  V=V_o + at=0 +2.15  --- V=30m/s  ---  R- D

25- Entre 0 e 2s  ---  a=(V – V_o)/(t – t_o)=(14 – 26)/(2 – 0)  ---  a=-6m/s²  ---  após 2s, V é constante e assim, a=0  ---  R- A

26- V=V_o + at  ---  20=0 + a.10  ---  a=2,0m/s²  ---  ΔS=area=b.h/2=5.10/2=25m  ---  R- C

27-

a) O gráfico solicitado entre t = 0 e t = 10 s.

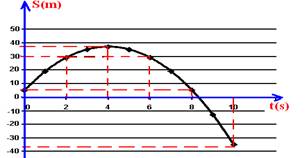
b) Se x = 5 + 16.t - 2.t²  ---   v = 16 - 4.t  ---  v = 16 - 4.4 = 16 - 16 = 0 m/s

c) t=o  ---  S_o=5m  ---  t=5s  ---  S=5 + 16.5 -2.25  ---  S=35m  ---  deslocamento  ---  ΔS=S – S_o=35 – 5=30m  ---  distância percorrida d  ---  até parar ele demora  --- V=Vo +a.t  ---  0=16 – 4t  ---  t=4s e percorre se desloca até o marco  ---  S=5 +16.4 -2.16=37m  ---  entre 4s e 5s ele retorna ao marco S=35m

d ida=(37 – 5)=32m + 2 (volta)  ---  d=34m

28- a) Parte do repouso  ---  V_o=0  ---  entre 0 e 20s  ---  V=V_o + at  ---  V=0 + 2.20  ---  V=40m/s  ---  entre 20s e 50s  ---  V=V_o + at=40 – 1.30  ---  V=10m/s  ---  veja gráfico abaixo

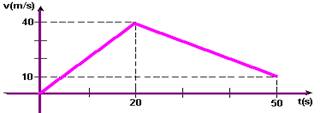
b) A distância percorrida é fornecida pela área hachurada da figura abaixo

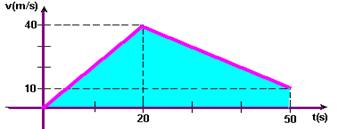
d=b.h/2 + (B + b).h/2=20.40/2 + (40 + 10).30/2  ---  d=1.150m

29- Sendo o movimento acelerado o gráfico posição x tempo é um arco de parábola com concavidade para cima e a velocidade aumenta de modo uniforme, assim o gráfico velocidade x tempo é uma reta com inclinação ascendente  ---  R- D

30- Entre 0 e 6s  ---  V_I=V_o + a_It_I=2 + 4.6  ---  V_i=26 cm/s  ---  entre 6s e 10s  ---  V_I=V_o=26cm/s  ---  V_II=V_o + a_IIt_II=26 + (-3).4  --- 

V_II=14 cm/s  ---  V_II=V_o=14 cm/s  ---  V_III=V_o + a_III.t_III=14 + 4.6  ---  V_III=38 cm/s

31- 01) Correta  ---  no gráfico representado a seguir, seja k o coeficiente angular (declividade) da reta secante à curva entre os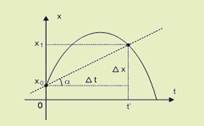 

instantes 0 e t’  ---  k=tgα=(X₁ – X_o)/(t’ – 0)=V_m=ΔX/Δt.  
02) Falsa  ---  no diagrama D, no intervalo considerado, a declividade da reta tangente à curva dada está aumentando (em módulo) logo o módulo da velocidade está aumentando  ---  portanto, o movimento é acelerado.

04) Falsa  ---  no instante considerado, o móvel está numa posição negativa (antes da origem).

08) Falsa  ---  no intervalo considerado, o corpo está se deslocando para posições cada vez mais negativas, portanto afastando-se da origem (em movimento retrógrado retardado).

16) Correta  ---  nesse instante, a reta tangente à curva é horizontal, tendo declividade (coeficiente anular) nula.

32) Falsa  ---  nesse intervalo, em módulo, o coeficiente angular da reta tangente está diminuindo, logo o movimento é uniformemente retardado.

64) Correta  ---  pode corresponder a um lançamento vertical para cima com trajetória orientada para baixo (v_o < 0), sendo o ponto de lançamento acima do plano de referência (x_o < 0), como indicado no esquema a seguir.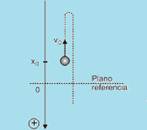

  R- (01 + 16 + 64) = 81

32- Trata-se de um gráfico de aceleração ´ tempo  ---  analisando-o você pode afirmar que a aceleração é constante e não nula nos intervalos C e G e nula no intervalo E, onde a velocidade é constante  ---  R- A

33- Sendo a trajetória é retilínea, a aceleração restringe-se à componente tangencial (), que, em módulo, é igual a aceleração escalar (a), dada pela taxa de variação da velocidade (Dv) em relação ao tempo (Dt)  ---  a=ΔV/Δt:

I. a_I =    Þ   a_I = 10 m/s².

II. a_II = 0 (não houve variaçمo da velocidade)

III. a_III =   Þ  a_III = – 5 m/s².  

 R- C

34- Nos intervalos de tempo em que a velocidade escalar é constante (1 s a 2 s; 3 s a 4 s e 5 s a 6 s) a aceleração escalar é nula  ---  nos intervalos 0 a 1 s; 2 s a 3 s; 4 s a 5 s e 6 s a 7 s, a velocidade varia linearmente com o tempo, sendo, então, a aceleração escalar é constante.

De 0 a 1 s: a =   ---  de 2 s a 3 s: a = m/s²;  ---  de 4 s a 5 s: a = m/s²;  ---  De 6 s a 7 s:

 a = m/s².

R- A

35- Analisando cada intervalo:

– De 0 a 3 s: o movimento é uniformemente acelerado; a aceleração escalar é  ---  a₁ = ΔV₁/Δt₁=8/3=2,7m/s²  ---  o espaço percorrido é calculado pela “área” de 0 a 3 s  ---  ΔS₁=3.8/2  --- ΔS₁=12m.

– De 3 s a 5 s: o movimento é uniforme, com velocidade escalar v₂ = 8 m/s  ---  o espaço percorrido é  ---   DS₂ = v₂ Dt₂=8 ´ 2

DS₂=16 m.

– De 5 s s 7 s: o movimento é uniformemente retardado; a aceleração escalar é  ---  a₃=(0 – 8)/(7 – 5)  ---  a₃=-4m/s²  ---  ΔS₃=2.8/2  --- ΔS₃=8m

R- B

36- I. Cálculo do deslocamento entre 0 e 8s pela área do triângulo  ---  ΔS₁=b.h/2=8.80/2  ---  ΔS₁=320m  ---  não completou a volta, pois ΔS₁ < 400m  ---  Falsa.

II. Cálculo do deslocamento entre 0 e 9s pela soma das áreas do triângulo com a do retângulo  ---  ΔS₂=320 + b.h=320 + 1.80  --- 

ΔS₂=400m  ---  em 9s o piloto completou uma volta  ---  Correta.

III. Entre 8s e 10s, o movimento é retilíneo e uniforme com velocidade constante de 80m/s e consequentemente a força resultante é nula  ---  Correta.

IV. A componente da força resultante na direção do movimento é a tangencial de intensidade  ---  FR=ma=mΔV/Δt  ---  F_R=m.60/2  ---  F_R=30m  ---  P=mg=m10  ---  P=10m  ---  F_R/P=30m/10m  ---  F_R=3p  ---  Correta.

R- E

37- a=(V - V_o)/(t – t_o)=(-20 – 20)/(2 – 0)  ---  a=-20m/s²  ---  R- A

38-

 -1. Correta  ---  V_m=∆S/∆t=(600 – 200)/4  ---  V_m=400/4=100m/min=0,1km/(1/60)h  ---  V_m=0,1x60=6km/h.

2. Correta  ---  a distância não variou entre 6min e 8min, ou seja, durante 2 minutos.

3. Correta  ---  no eixo da distância (vertical)  ---  d=(1400 – 200)= 1200m

R- E

39-Primeira etapa  ---  queda livre no vácuo (durante 5,0s) com velocidade variando de V_o até V , com a=g=10m/s²  ---  V=V_o + a.t  ---  V=0 + 10.5  ---  V=50m/s  ---  durante esse tempo ele caiu uma altura h=V_ot + at²/2=0 + 10.25/2  ---  h=125m  ---  observe no gráfico que no instante t=5,0s o pára-quedas abriu sua velocidade caiu instantaneamente de 50m/s para 10m/s  ---  no intervalo de tempo (t – 5)s ele percorreu, com velocidade constante de V=10m/s a a altura h’=325 – 125=200m  ---  V=h´/(t – 5)  ---  10= 200/(t – 5)  ---  10t – 50=200  ---  t=250/10  ---  t=25s  ---  R- B  ---  você poderia também resolver pela área  ---  h_total=325=área do triângulo + área do retângulo=5.50/2 +

(t – 5).10  ---  t=25s.

40-  Como partem juntos (instante t_o), eles se encontrarão após sofrerem o mesmo deslocamento ∆S  ---  em todo gráfico Vxt o deslocamento é numericamente igual à área entre a reta representativa e o tempo   ---  observe que quando o tempo é t₄ as áreas

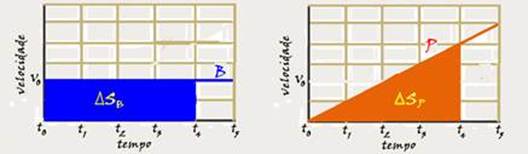
são iguais  ---  carro B  ---  área=∆S_B=b.h=4.2=8 unidades  ---  carro P  ---  área=∆S_P=b.h/2=4.4/2=8 unidades  ---  R- D