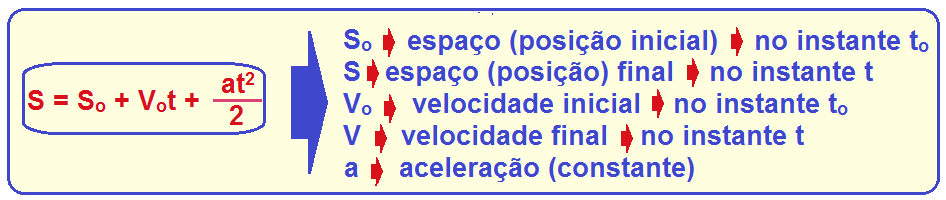
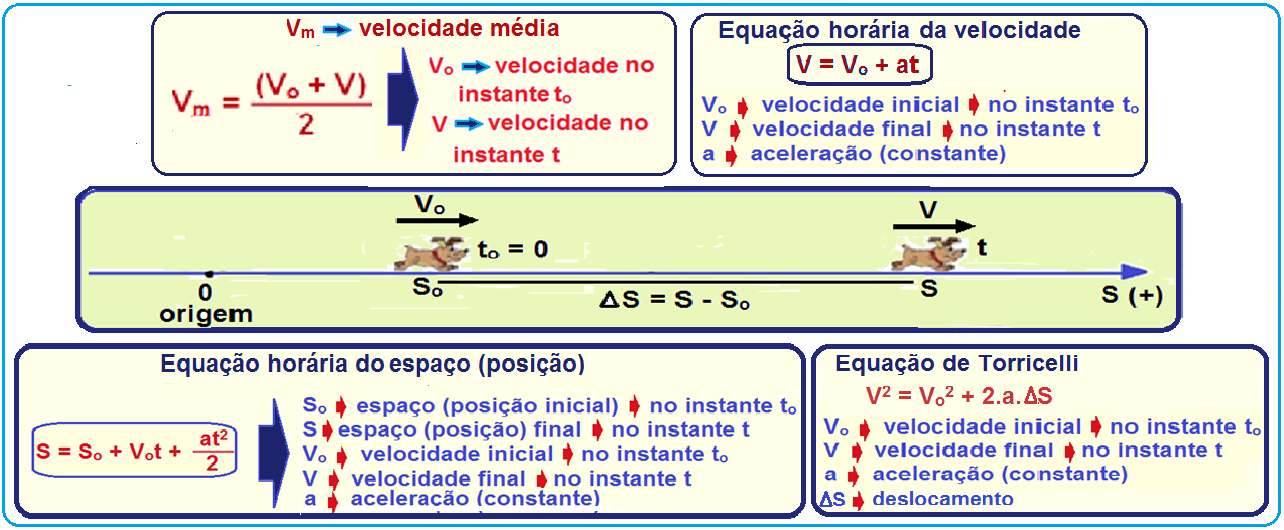
Função (equação) horária do espaço de um MUV

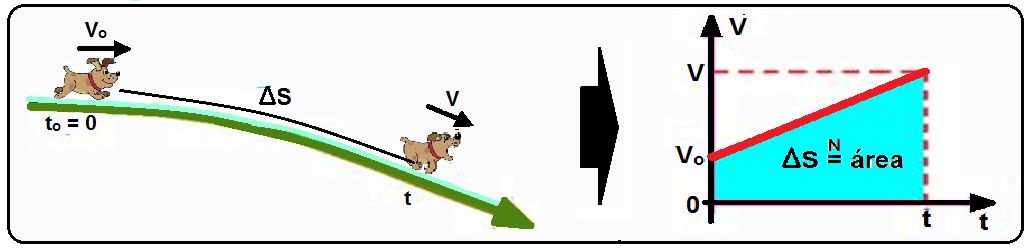
Observe o gráfico V X t de um MUV qualquer, da figura abaixo, onde no instante t_o= 0 o móvel tem velocidade V_o e, num instante posterior t, tem velocidade V.

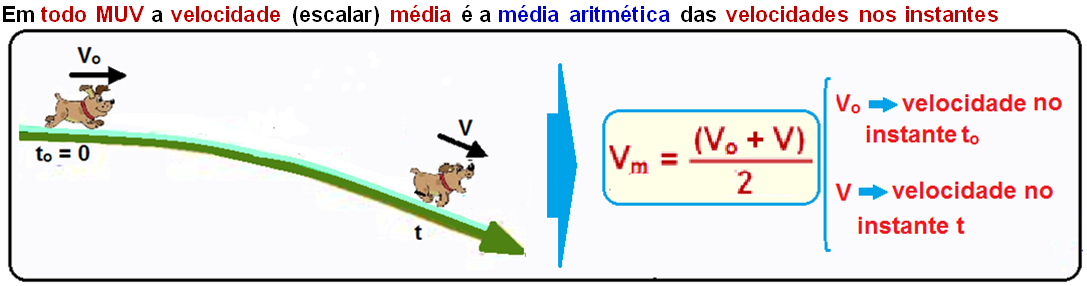
Velocidade média num MUV

extremos de dois intervalos de tempo quaisquer.

Dedução da função (equação) horária do espaço de um móvel em MUV

Casos particulares para a aplicação da equação horária do espaço do MUV

1^o cronômetro acionado (t_o=0) no instante em que o móvel passa pela origem (S_o = 0) das posições (espaços) com velocidade inicial V_o.

2^o O móvel parte do repouso de uma posição S_o qualquer.

3^o O móvel parte do repouso e da origem dos espaços

Relação entre a equação horária do espaço e a da velocidade no MUV

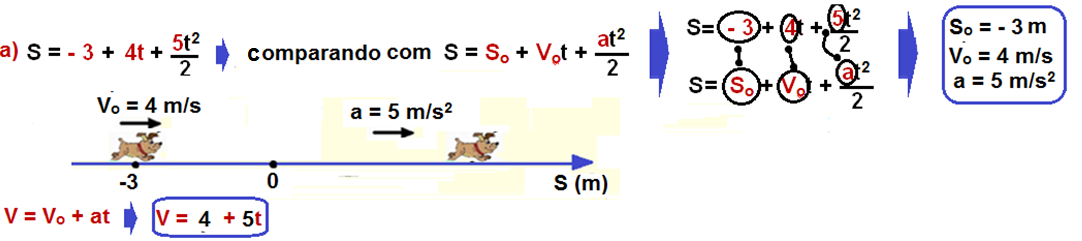
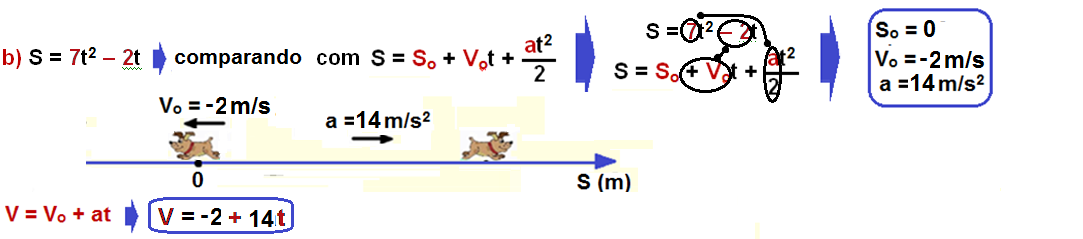
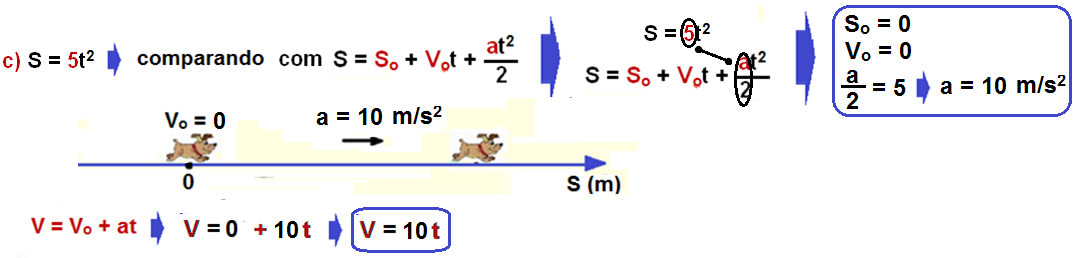
Exemplos: Determine os valores de S_o e V_o e escreva a e a função da velocidade das equações do espaço (posição) abaixo, que estão expressas em unidades do SI:

Equação de Torricelli

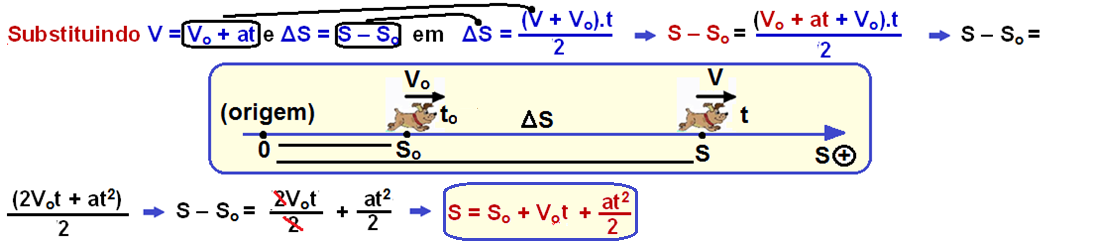
Seja um móvel efetuando um MUV, com velocidade inicial V_o no espaço inicial S_o, e aceleração constante a.

Esse móvel, num instante posterior t terá velocidade V e ocupará o espaço (posição) S e se deslocará de ∆S = S – S_o (figura acima).

Agora você vai utilizar a equação da velocidade V = V_o + at e elevá-la ao quadrado (V = V_o + at)²

O que você deve saber

FORMULÁRIO DAS EQUAÇÕES DO MUV

Exercícios resolvidos sobre MUV

1-(UFB) Um gato realiza um MUV em trajetória retilínea e horizontal que obedece à função horária da velocidade V= - 20 + 5t em unidades do SI. Pede-se:

a) a velocidade inicial e a aceleração

b) o instante em que ele muda o sentido de seu movimento

c) classificar o movimento em progressivo ou retrógrado, acelerado ou retardado, orientando a trajetória para a direita.

Qual o tipo de movimento do gato nos instantes 2s e 10s

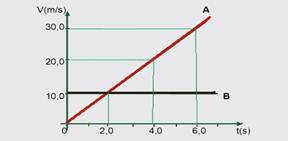
02-(UFB) No gráfico abaixo, da velocidade de um móvel em MUV em função do tempo, pede-se determinar:

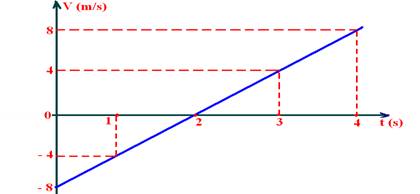
a) a velocidade inicial V_o e a aceleração a

b) o instante em que o móvel inverte o sentido de seu movimento

c) classificar o movimento

d) o deslocamento sofrido no intervalo de tempo compreendido entre 0 e 4s

03-(PUC-RJ) Considere o movimento de um caminhante em linha reta. Este caminhante percorre os 20,0 s iniciais à velocidade constante v₁ = 2,0 m/s.

Em seguida, ele percorre os próximos 8,0 s com aceleração constante a = 1 m/s² (a velocidade inicial é 2,0 m/s). Calcule a velocidade final do caminhante.

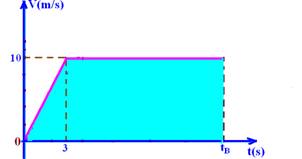
04- (UFSM-RS) Ao preparar um corredor para uma prova rápida, o treinador observa que o desempenho dele pode ser descrito, de forma aproximada, pelo seguinte gráfico:

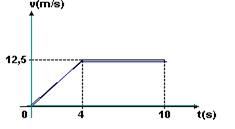
A velocidade média desse corredor, em m/s, é de

05-(FUVEST-SP) Na figura a seguir estão representadas as velocidades, em função do tempo, desenvolvidas por um atleta, em dois treinos A e B, para uma corrida de 100m rasos.

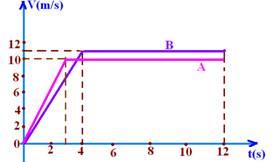
Com relação aos tempos gastos pelo atleta para percorrer os 100m, podemos afirmar que, aproximadamente:

a) no B levou 0,4s a menos que no A

b) a) no A levou 0,4s a menos que no B

c) a) no B levou 1,0s a menos que no A

d) no A levou 0,4s a menos que no B

e) no A e no B levou o mesmo tempo

06-(CFT-CE) Observe o movimento da moto a seguir, supostamente tomada como partícula.

a) O instante em que sua velocidade será de 20m/s.

b) O deslocamento efetuado até este instante.

07-(UNIFESP-SP) A velocidade em função do tempo de um ponto material em movimento retilíneo uniformemente variado, expressa em unidades do SI, é v = 50 - 10t. Pode-se afirmar que, no instante t = 5,0 s, esse ponto material tem

a) velocidade e aceleração nulas.

B) velocidade nula e daí em diante não se movimenta mais.

c) velocidade nula e aceleração a = - 10 m/s².

d) velocidade nula e a sua aceleração muda de sentido.

e) aceleração nula e a sua velocidade muda de sentido.

08-(UFRS-RS) Um automóvel que trafega com velocidade constante de 10 m/s, em uma pista reta e horizontal, passa a acelerar uniformemente à razão de 60 m/s em cada minuto, mantendo essa aceleração durante meio minuto. A velocidade instantânea do automóvel, ao final desse intervalo de tempo, e sua velocidade média, no mesmo intervalo de tempo, são, respectivamente:

a) 30 m/s e 15 m/s.

b) 30 m/s e 20 m/s.

c) 20 m/s e 15 m/s.

d) 40 m/s e 20 m/s.

e) 40 m/s e 25 m/s.

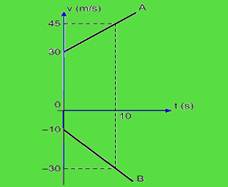
09-(PUC-PR) Um automóvel trafega em uma estrada retilínea. No instante t = 0 s, os freios são acionados, causando uma aceleração constante até anular a velocidade, como mostra a figura.

A tabela mostra a velocidade em determinados instantes

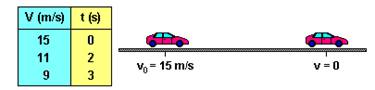
Com base nestas informações, são feitas algumas afirmativas a respeito do movimento:

I. O automóvel apresenta uma aceleração no sentido do deslocamento.

II. O deslocamento do veículo nos primeiros 2 s é 34 m.

III. A aceleração do veículo é -1,5 m/s².

IV. A velocidade varia de modo inversamente proporcional ao tempo decorrido.

V. A velocidade do veículo se anula no instante 7,5 s.

Está correta ou estão corretas:

a) somente I. b) I e II. c) somente III. d) IV e V. e) II e V.

10-(MACKENZIE-SP) A aceleração de um móvel, que parte do repouso, varia com o tempo de acordo com o gráfico abaixo.

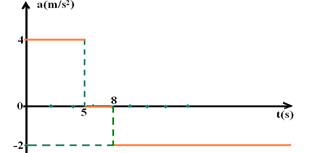
O instante, contado a partir do início do movimento, no qual o móvel pára, é:

a) 5s

b) 6s

c) 8s

d) 13s

e) 18s

11-(UFPE) O gráfico da velocidade em função do tempo de um ciclista, que se move ao longo de uma pista retilínea, é mostrado a seguir.

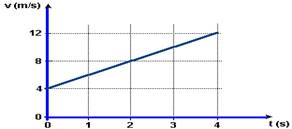
Considerando que ele mantém a mesma aceleração entre os instantes t = 0 e t = 7 segundos, determine a distância percorrida neste intervalo de tempo. Expresse sua resposta em metros.

12-(UFB) Considerando um diagrama v x t, onde v é a velocidade instantânea de uma partícula no instante t, o que representa:

a) a declividade ou inclinação da reta representativa do gráfico?

b) o que representa a área sob a reta?

13- (FUVEST-SP) O gráfico na figura descreve o movimento de um caminhão de coleta de lixo em uma rua reta e plana, durante 15s de trabalho

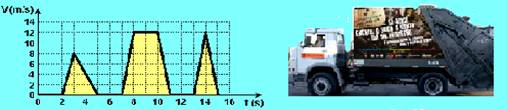
a) Calcule a distância total percorrida neste intervalo de tempo.

b) Calcule a velocidade média do veículo.

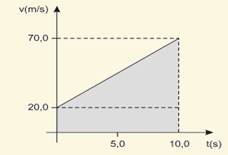
14-(Ufpe) Uma partícula, que se move em linha reta, está sujeita à aceleração a(t), cuja variação com o tempo é mostrada no gráfico a seguir.

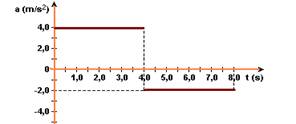
Sabendo-se que no instante t = 0 a partícula está em repouso, calcule a sua velocidade no instante t = 8,0 s, em m/s.

15- (UNESP-SP) O motorista de um veículo A é obrigado a frear bruscamente quando avista um veículo B à sua frente, locomovendo-se no mesmo sentido, com uma velocidade constante menor que a do veículo A. Ao final da desaceleração, o veículo A atinge a mesma velocidade que B, e passa também a se locomover com velocidade constante. O movimento, a partir do início da frenagem, é descrito pelo gráfico da figura.

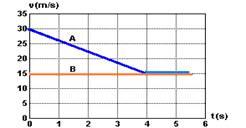
Considerando que a distância que separava ambos os veículos no início da frenagem era de 32 m, ao final dela a distância entre ambos é de

16-(CFT-MG) Três carros A, B, e C, trafegando numa avenida reta, estão lado a lado, quando o semáforo a 55 metros à frente fecha. Sabendo-se que o gráfico a seguir mostra a variação da velocidade dos veículos a partir desse momento, é correto afirmar que irá(ão) ultrapassar o sinal somente o(s) carro(s)

17-(UFU-MG) O gráfico a seguir representa a velocidade em função do tempo de um automóvel que parte do repouso. A velocidade máxima permitida é de 72 km/h. No instante t, quando o motorista atinge essa velocidade limite, ele deixa de acelerar o automóvel e passa a se deslocar com velocidade constante.

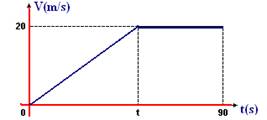
Sabendo-se que o automóvel percorreu 1,2 km em 90 segundos, o valor do instante t é

a) 80 s.

b) 30 s.

c) 60 s.

d) 50 s.

18-(UnB-DF) A tabela abaixo indica a velocidade instantânea de um objeto, em intervalos de um segundo.

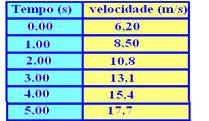
As velocidades instantâneas do objeto nos instantes 3,60s e 5,80s são, respectivamente:

a) 17,5m/s e 20,5m/s

b) 13,8m/s e 22,6m/s

c) 14,5m/s e 19,5m/s

d) 15,5m/s e 22,2m/s

e) 8,20m/s e 12,2m/s

19-(Olimpíada Brasileira de Física) Uma partícula executa um movimento retilíneo uniformemente variado. Num dado instante a partícula tem velocidade 50m/s e aceleração negativa de módulo 0,2m/s². Quanto tempo decorre até a partícula alcançar a mesma velocidade em sentido contrário?

20-(CFT-MG) O movimento retilíneo de um corpo é descrito pela equação v = 10 - 2t em que v é a velocidade, em m/s, e t é o tempo, em segundos.

Durante os primeiros 5,0 s, a distância percorrida por ele, em metros, é:

a) 10.

b) 15.

c) 20.

d) 25.

21-(PUC-RJ) O movimento de um objeto pode ser descrito pelo gráfico velocidade versus tempo, apresentado na figura a seguir.

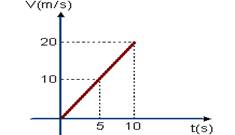
Podemos afirmar que:

a) a aceleração do objeto é 2,0 m/s², e a distância percorrida em 5,0 s é 10,0 m.

b) a aceleração do objeto é 4,0 m/s², e a distância percorrida em 5,0 s é 20,0 m.

c) a aceleração do objeto é 2,0 m/s², e a distância percorrida em 5,0 s é 25,0 m.

d) a aceleração do objeto é 2,0 m/s², e a distância percorrida em 5,0 s é 10,0 m.

e) a aceleração do objeto é 2,0 m/s², e a distância percorrida em 5,0 s é 20,0 m.

22-(PUC-RJ) É CORRETO afirmar que a distância percorrida pelo objeto entre t = 0 e t = 1,4s foi aproximadamente de:

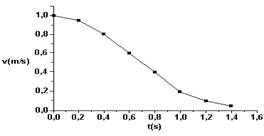
a) 0,7 m

b) 1,8 m

c) 0,1 m

d) 1,6 m

23-(UERJ-RJ) A velocidade de um corpo que se desloca ao longo de uma reta, em função do tempo, é representada pelo seguinte gráfico:

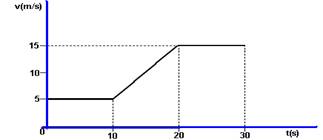
Calcule a velocidade média desse corpo no intervalo entre 0 e 30 segundos.

24-(Ufrj-RJ) Um móvel parte do repouso e descreve uma trajetória retilínea durante um intervalo de tempo de 50s, com a aceleração indicada no gráfico a seguir.

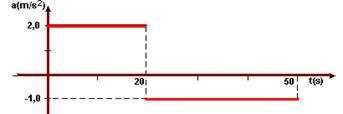
a) Faça um gráfico da velocidade do móvel no intervalo de 0 até 50s.

b) Calcule a distância percorrida pelo móvel nesse intervalo.

25-(UNIFESP-SP) A função da velocidade em relação ao tempo de um ponto material em trajetória retilínea, no SI, é v = 5,0 - 2,0 t. Por meio dela pode-se afirmar que, no instante t = 4,0 s, a velocidade desse ponto material tem módulo

a) 13 m/s e o mesmo sentido da velocidade inicial.

b) 3,0 m/s e o mesmo sentido da velocidade inicial.

c) zero, pois o ponto material já parou e não se movimenta mais.

d) 3,0 m/s e sentido oposto ao da velocidade inicial.

e) 13 m/s e sentido oposto ao da velocidade inicial.

26-(UFPE-PE) Um motorista dirige um carro com velocidade constante de 80 km/h, em linha reta, quando percebe uma “lombada” eletrônica indicando a velocidade máxima permitida de 40 km/h. O motorista aciona os freios,

imprimindo uma desaceleração constante, para obedecer à sinalização e passar pela “lombada” com a velocidade máxima permitida. Observando-se a velocidade do carro em função do tempo, desde o instante em que os freios foram acionados até o instante de passagem pela “lombada”, podemos traçar o gráfico abaixo.

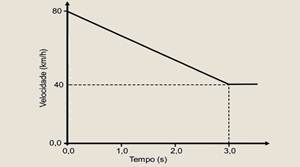
Determine a distância percorrida entre o instante t = 0, em que os freios foram acionados, e o instante t = 3,0 s, em que o carro ultrapassa a “lombada”. Dê sua resposta em metros.

27-(UNCISAL-AL) João Gabriel, vestibulando da UNCISAL, preparando-se para as provas de acesso à universidade, vai

conhecer o local das provas. Sai de casa de carro e, partindo do repouso, trafega por uma avenida retilínea que o conduz diretamente ao local desejado. A avenida é dotada de cruzamentos com semáforos e impõe limite de velocidade, aos quais João Gabriel obedece. O gráfico que melhor esboça o comportamento da velocidade do carro dele, em função do tempo, desde que ele sai de casa até a chegada ao local da prova, onde estaciona no instante t’, é:

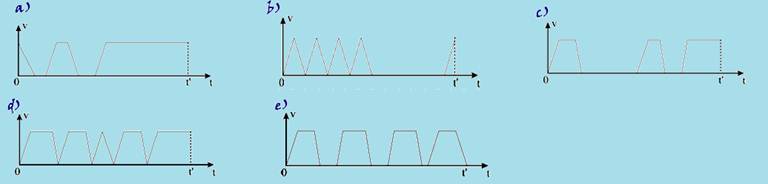
28-(UNEMAT-MT) O gráfico em função do tempo mostra dois carros A e B em movimento retilíneo. Em t = 0 seg. os

carros estão na mesma posição.

Com base na análise do gráfico, é correto afirmar.

a) Os carros vão estar na mesma posição nos instantes t = 0 seg. e t = 4,0 seg.

b) Os carros não vão se encontrar após t = 0, porque a velocidade de A é maior que a do carro B

c) Os carros vão se encontrar novamente na posição S = 10 m

d) Os carros não vão se encontrar, porque estão em sentidos contrários.

e) Os instantes em que os carros vão estar na mesma posição é t = 0 seg. e t = 8,0 seg.

29-(MACKENZIE-SP) Dois automóveis A e B se movimentam sobre uma mesma trajetória retilínea, com suas

velocidades variando com o tempo de acordo com o gráfico a seguir. Sabe-se que esses móveis se encontram no instante 10 s. A distância entre eles, no instante inicial (t = 0 s), era de

a) 575 m

b) 425 m

c) 375 m

d) 275 m

e) 200 m

30-(CFT-SC) O gráfico abaixo representa a variação da velocidade em função do tempo de uma partícula em

movimento uniformemente variado. Em relação à área abaixo da reta do gráfico, é correto afirmar que ela representa a:

a) aceleração média.

b) velocidade média.

c) variação da velocidade.

d) distância percorrida pela partícula.

e) velocidade instantânea.

31-(FUVEST-SP) Na Cidade Universitária (USP), um jovem, em um carrinho de rolimã, desce a rua do Matão, cujo

perfil está representado na figura a seguir, em um sistema de coordenadas em que o eixo O_x tem a direção horizontal.

No instante t = 0, o carrinho passa em movimento pela posição o_y = y_o e x = 0.

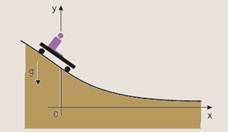
Dentre os gráficos das figuras a seguir, os que melhor poderiam descrever a posição x e a velocidade v do carrinho em função do tempo t são, respectivamente,

32-(UFRJ-RJ)Um avião vai decolar em uma pista retilínea. Ele inicia seu movimento na cabeceira da pista com

velocidade nula e corre por ela com aceleração média de 2,0 m/s² até o instante em que levanta vôo, com uma velocidade de 80 m/s, antes de terminar a pista.

a) Calcule quanto tempo o avião permanece na pista desde o início do movimento até o instante em que levanta vôo.

b) Determine o menor comprimento possível dessa pista.

33-(UNICAMP-SP) O radar é um dos dispositivos mais usados para coibir o excesso de velocidade nas vias de trânsito. O seu princípio de funcionamento é baseado no efeito Doppler das ondas eletromagnéticas refletidas pelo carro em movimento.

Considere que a velocidade medida por um radar foi V = 72 km/h para um carro que se aproximava do aparelho.

Quando um carro não se move diretamente na direção do radar, é preciso fazer uma correção da velocidade medida pelo aparelho V_m para obter a velocidade real do veículo Vr. Essa correção pode ser calculada a partir da fórmula V_m=V_r.cosα, em que α é o ângulo formado entre a direção de tráfego da rua e o segmento de reta que liga o radar ao ponto da via que ele mira. Suponha que o radar tenha sido instalado a uma distância de 50 m do centro da faixa na qual o carro trafegava, e tenha detectado a velocidade do carro quando este estava a 130 m de distância, como mostra a figura abaixo

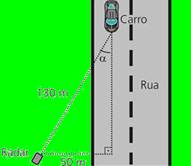
Se o radar detectou que o carro trafegava a 72 km/h, sua velocidade real era igual a

a) 66,5 km/h

b) 36 3 km/h.

c) 78 km/h.

d) 144 / 3 km/h

34-(UFPE-PE)

Dois veículos partem simultaneamente do repouso e se movem ao longo da mesma rodovia reta, um ao encontro do

outro, em sentidos opostos. O veículo A parte com aceleração constante igual a a_A = 2,0 m/s². O veículo B, distando d = 19,2 km do veículo A, parte com aceleração constante igual a a_B = 4,0 m/s². Calcule o intervalo de tempo até o encontro dos veículos, em segundos.

35-(UERJ-RJ)

Dois carros, A e B, em movimento retilíneo acelerado, cruzam um mesmo ponto em t = 0 s. Nesse instante, a

velocidade v_o de A é igual à metade da de B, e sua aceleração a corresponde ao dobro da de B. Determine o instante em que os dois carros se reencontrarão, em função de v_oe a.

36-(UEPA-PA)

No Pará, o perigo relacionado às altas velocidades no trânsito tem aumentado os riscos de acidentes, principalmente em Belém.

Considerando que a "distância de freagem" é a distância que o carro percorre desde o momento que os freios são acionados até parar e que o modelo matemático que expressa essa relação é dado por D = K . V², onde Drepresenta a distância de freagem em metros, K é uma constante e V é a velocidade em Km/h. Assim, um automóvel que tem seus freios acionados estando a uma velocidade de 80 Km/h ainda percorre 44 metros até parar. A distância de freagem de um automóvel que tem seus freios acionados, estando a uma velocidade de 160 Km/h é:

a) 2 vezes a distância de freagem se estivesse a 80 Km/h.

b) 3 vezes a distância de freagem se estivesse a 80 Km/h.

c) 4 vezes a distância de freagem se estivesse a 80 Km/h.

d) 5 vezes a distância de freagem se estivesse a 80 Km/h.

e) 6 vezes a distância de freagem se estivesse a 80 Km/h.

37-(AFA)

Considere um móvel deslocando–se numa trajetória horizontal e descrevendo um movimento retilíneo uniformemente acelerado e

retrógrado. A alternativa que contém o gráfico que melhor representam movimento descrito pelo móvel é

38-(AFA)

Um bloco se movimenta retilineamente, do ponto A até o ponto C, conforme figura abaixo

Sua velocidade v em função do tempo t, ao longo da trajetória, é descrita pelo diagrama v×t mostrado a seguir.

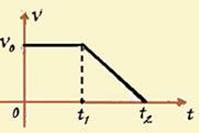
Considerando que o bloco passa pelos pontos A e B nos instantes 0 e t₁, respectivamente, e para no ponto C no instante t₂, a razão entre as distâncias percorridas pelo bloco nos trechos BC e AB , vale

a) (t₂ + t₁)/t₁

b) (t₂ – t₁)/t₂²

c) (t₂ – t₁)/2t₁

d) (t₂ + t₁)/2t₂

39-(ACAFE-SC)

Para garantir a segurança no trânsito, deve-se reduzir a velocidade de um veículo em dias de chuva, senão vejamos:

um veículo em uma pista reta, asfaltada e seca, movendo-se com velocidade de módulo 36 km/h (10 m/s) é freado e desloca-se 5,0 m até parar. Nas mesmas circunstâncias, só que com a pista molhada sob chuva, necessita de 1,0 m a mais para parar.

Considerando a mesma situação (pista seca e molhada) e agora a velocidade do veículo de módulo 108 km/h (30 m/s), a alternativa correta

que indica a distância a mais para parar, em metros, com a pista molhada em relação a pista seca é:

A) 6

B) 2

C)1,5

D) 9

Resolução comentada dos exercícios sobre MUV

01- a)

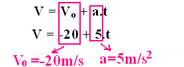
b) Quando ele muda o sentido se seu movimento ele pára (V=0) e, a partir desse instante, o movimento que era progressivo se torna retrógrado --- V=-20 + 5t --- 0=-20 + 5t --- t=4s (instante em que ele pára para inverter o sentido do movimento)

d) 2s – retrógrado retardado --- 10s - progressivo acelerado --- Veja esquema acima)

02- a) V_o=-8m/s --- a=(8 – (-8))/(4 – 0) --- a=16/4 --- a=4m/s²

b) V= V_o + at --- V=-8 + 4t --- inverte o sentido (pára) – V=0 --- 0=-8 + 4t --- t=2sou pelo gráfico que corresponde ao ponto onde a reta intercepta o eixo t.

c) entre 0 e 2s --- retrógrado (V<0) e retardado (módulo de V está diminuindo) --- após 2s --- progressivo (V>0) e acelerado (módulo de V está aumentando)

d) ΔS=área entre 0 e 4s, que corresponde à soma das áreas hachuradas da figura abaixo

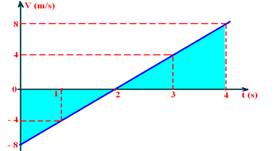
ΔS=b.h/ + b.h/2=2.(-8)/2 + 8.2/2 --- ΔS=0

03- V_o=2m/s --- a=1ms² --- V=V_o + at --- V=2 + 1.8 --- V=10m/s

04- ΔS=área=(10 + 6).12,5/2 --- ΔS=100m --- V_m=ΔS/Δt --- V_m=10m/s --- R- B

05- A – ΔS_A=área do trapézio=100m

ΔS_A=(t_A + (t_A – 4)).11/2 --- 100=2t_A – 4).11/2 --- t_A=244/22 --- t_A=11,1s (treino A)

B – ΔS_B=área do trapézio=100m

ΔS_B=(t_B + (t_B – 3)).10/2 --- 100=10t_B – 15 --- t_B=115/10 --- t_B=11,5s (treino B)

Δt=t_B – t_A=0,4s --- R- B

06- a) V_o=0 --- a=(V – V_o)/(t – t_o)=10/5 --- a=2m/s² --- V = V_o + a.t --- 20=0 + 2t --- t=10s

b) o deslocamento é fornecido pela área

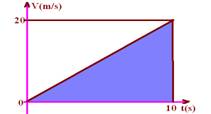
ΔS=b.h/2=10.20/2 --- ΔS=100m

07- T=5s --- V=50 – 10.5 --- V=0 --- a=-10m/s² (constante) --- R- C

08- V_o=10m/s --- a=ΔV/Δt=(60m/s)/60s --- a=1m/s² --- V=V_o + at=10 + 1.30 --- V=40m/s

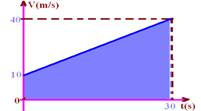
ΔS=(B + b).h/2=(40 + 10).30/2 --- ΔS=750m --- V_m= ΔS/Δt=750/30 --- V_m=25m/s

09- I – Falsa – é no sentido contrário ao do movimento – a velocidade está diminuindo

II –

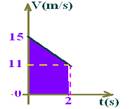
ΔS=(15 + 11).2/2=26m --- Falsa

III – a=(9 - 15)/3=-2m/s² --- Falsa

iV – Correta – observe que à medida que a velocidade diminui o tempo aumenta

V – V= V_o + at --- 0=15 – 2t --- t=7,5s --- Correta

R- D

10- entre 0 e 5s --- V= V_o + at=0 + 4.5 --- V₅=20m/s --- de 5s a 8s V vale 20m/s --- a partir de 8s – a=-2m/s²até ele parar V=0 -- V=V_o + at --- 0=20 -2t --- t=10s (de 8s até ele parar) --- desde o inicio do movimento --- t=8 + 10=18s --- R- E

11- ΔS=área hachurada da figura abaixo

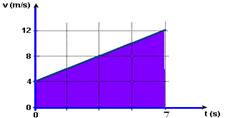
ΔS=(12 + 4).7/2 = 56m

12- a) O ângulo α que a reta representativa da velocidade forma com um eixo horizontal é tal que tgα=ΔV/Δt corresponde à aceleração do

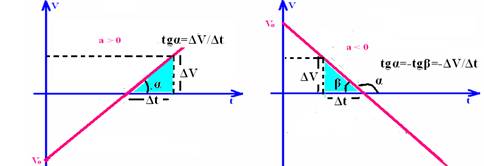
móvel, pois a= ΔV/ Δt e é denominada coeficiente angular da reta ou declividade da reta. Observe que, se α é agudo, f(t) é crescente e a>0 e se α é obtuso , f(t) é decrescente e a<0.

b) Em todo gráfico VXt a área entre a reta representativa e o eixo dos tempos é numericamente igual à variação de espaço ΔS, entre dois instantes quaisquer t₁ e t₂

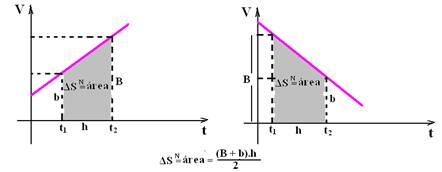
13- a) ΔS=área total=b.h/2 + (B + b).h/2 + b.h/2=3.8/2 + (4 + 2).12/2 + 2.12/2=1260 --- 12 + 36 + 12=60m --- ΔS=60m

b) V_m=60/16=3,75 --- V_m=3,75m

14- Entre 0 e 4s --- a=4m/s² --- V=V_o + at=0 + 4.4 --- V=16m/s --- entre 4s e 8s --- V= V_o + at --- V=16 + (-2).4 --- V=8m/s

15- Quando t=0 a distância entre eles é de 32m --- quando t=4s --- ΔS_A=área do trapézio=(30 + 15).4/2 --- ΔS_A=90m --- ΔS_B=área do retângulo=4.15=60m --- antes – ΔS_a=32m --- depois – ΔS_d=(90 – 60)=30m --- a distância entre eles no final da frenagem será de d=32 – 30=2m --- R- B

16- ΔS_A=b.h/2=6.20/2=60m --- ΔS_B=B + b).h/2=(8 + 2).10/2=50m --- ΔS_C=b.h/2=4.20/2=40m --- R- A

17- ΔS=1.200=área do trapézio=(B + b).h/2=(90 + (90 - t)).20/2 --- 1.200=(180 – t).10 --- 1200=1800 -10t --- t=60s --- R- C

18- Trata-se de um MUV em que a velocidade aumenta de 2,3m/s em cada 1s e, assim, sua aceleração vale a=2,3m/s² --- V_o=6,20m/s --- V= V_o + at --- V=6,20 + 2,3t --- t=3,60s – V=6,20 + 2,3.3,60 --- V=14,48m/s --- t=5,80s – V=6,20 + 2,3.5,80 --- V=19,54m/s

R- C

19- Se, na ida ela tem velocidade de 50m/s, na volta deverá ter velocidade de -50m/s --- na ida, até parar (V=0) ela demorou ---

V=V_o + at --- 0=50 – 0,2t --- t=250s (na ida) --- na volta --- V₀=0 e V=-50m/s --- V=V_o + at --- -50=0 -0,2t --- t=250s (na volta) --- t_pedido=t_ida + t_volta --- t_pedido=250 + 250=500s --- t=500s --- R- A

20- Colocando no gráfico --- t=0 – V_o=10m/s --- V=0 --- 0=10 -2t --- t=5s

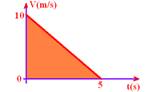
ΔS=área=b.h/2=5.10/2 --- ΔS=25m --- R- D

21- a=(20 – 0)/(10 – 0) --- a=2m/s² --- d=área=5.10/2 --- d=25m --- R- C

22- Considerando a área como sendo de um triângulo

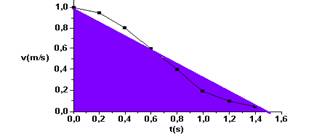
ΔS=b.h/=1,5.1,0/2 --- ΔS=0,75m --- R- A

23- ΔS=área total=b.h + (B + b).h/2 + b.h=10.5 + (15 + 5).10/2 + 10.15=300m --- ΔS=300m --- V_m= ΔS/ Δt=300/30 --- V_m=10m/s

24- a) entre 0 e 20s --- a=2m/s² --- V_o=0 --- V₁= V_o + at=0 + 2.20 --- V₁=40m/s --- entre 20s e 50s --- V_o=40m/s --- a=-1m/s² ---V₂=V_o + at=40 – 1.30 --- V₂=10m/s --- gráfico abaixo

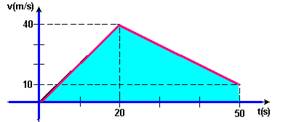
b) ΔS=área=b.h/2 + (B _ b).h/2=20.40/2 + (40 + 10).30/2 --- A distância percorrida é 1150m.

25- T=4s --- V=5 – 2.4 --- V=-3m/s --- velocidade inicial – movimento progressivo, velocidade de -3m/s – movimento retrógrado --- R- D

26- A distância percorrida corresponde à área compreendida entre a reta representativa e o eixo do tempo, entre 0 e 3s, ou seja, à área de um trapézio --- ΔS=área=(B + b).h/2=(80/3,6 + 40/3,6).3/2= (22,2 + 11,1).1,5 --- ΔS=49,95≈50m

27- Observe atentamente que o único gráfico coerente com o enunciado é o da alternativa E --- R- E

28- Quando t=0 eles estão na mesma posição (dado do exercício) --- quando t=4s, o deslocamento de cada carro é fornecido pela área

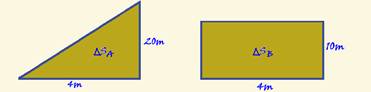
entre 0 e 4s --- carro A, a área é de um triângulo --- ΔS_A=b.h/2=4.20/2 --- ΔS_A=40m --- carro B, a área é de um retângulo --- ΔS_B=b.h=4.10 --- ΔS_B=40m --- R- A

29- Calculando o espaço percorrido pela área --- ΔS_A=(B + b).h/2=(45 + 30).10/2 --- ΔS_A=375m --- ΔS_B=(-10 – 30).10/2 ---

ΔS_B=-200m --- d=375 + 200 --- d=575m --- ou aceleração escalar de cada móvel, lembrando que --- a_A=(45 – 30)/(10 – 0) --- a_A=1,5m/s² --- a_B=(-30 – (-10)/(10 – 0) ---

a_B= -2m/s² --- S_A=S_oA + 30t + 0,75t² --- S_B=S_oB – 10t – t² --- supondo S_oA=0 e fazendo t=10s no encontro onde você iguala as equações --- 30(10) + 0,75(10)² = S_oB – 10(10) – (10)² --- 375 = S_oB – 200 --- S_oB = 575 m, que é a distância inicial entre os móveis, pois supusemos o móvel A partindo da origem.

R- A

30- Propriedade do gráfico v = f(t) --- a área entre a linha do gráfico e o eixo t representa o espaço percorrido pelo móvel (DS) --- como não há mudança de sentido, o espaço percorrido é igual à distância percorrida --- R- D

31-

R- A

32- a) V=V_o + at --- 80=0 + 2.t --- t=40s

b) Na situação em que a pista tem o comprimento mínimo (d_m), o avião perde o contato com a pista exatamente em seu final --- equação de Torricelli --- v² – v_o² + 2.a.d_m --- 80²=0² + 2.2.d_m --- 6.400=4d_m --- d_m=1.600m

33- Observe a figura abaixo --- determinando a distância d por Pitágoras --- (130)²=d² + (50)² --- 16.900=d² + 2.500 --- d=120m

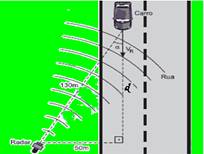
--- V_m=V_r.cosα --- 72=V_r.120/130 --- V_r=78km/h --- R- C

34- Observe na figura abaixo onde a origem da trajetória foi colocada no ponto de partida do móvel A S_oA=0 --- a

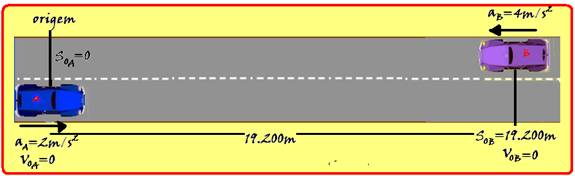
trajetória foi orientada para a direita S_oB=19200m --- ambos os móveis partiram do repouso, V_oA=V_oB=0 --- como o móvel B está em movimento retrógrado e acelerado sua velocidade e sua aceleração são negativas (veja fisicaevestibular.com.br – mecânica – cinemática – gráficos do MUV) --- dedução da função horária de cada móvel --- S_A=S_oA + V_oAt + a_A.t²/2=0 + 0.t + 2t²/2 --- S_A=t² --- S_B=S_oB + V_oBt + a_B.t²/2=19200 – 0.t – 4.t²/2 --- S_B=19200 – 2t² --- no encontro AS=S_B --- t²=19200 – 2t² --- t²=6400 --- t=80s.

35-Colocando a origem das posições no instante inicial (t=0 e S_o=0) e deduzindo a equação de cada carro --- S_A=V_ot + at²/2 --- S_B=2V_ot +(a/2).t²/2 --- S_B=2V_ot + at²/4 --- no encontro --- S_A=S_B --- V_ot + at²/2 = 2V_ot + at²/4 --- V_ot – 2V_ot + at²/2 – at²/4 = 0 ---

-4V_ot + at² = 0 --- t(at – 4V_o)=0 --- at – 4V_o=0 --- t=4V_o/a.

36-Observe na expressão D=K.V², onde K é constante e, nela você observa que a velocidade V é diretamente proporcional ao quadrado da velocidade --- assim, se a velocidade dobra passando de 80kmh para 160kmh, a distância percorrida pelo carro até parar fica 2²=4 vezes maior --- R- C

37- a) Falsa --- a aceleração é positiva (concavidade para cima) --- Entre 0 e t – o espaço decresce (movimento retrógrado, V<0)

e o movimento é retardado, pois a e V tem sinais contrários (a>0 e V<0) --- após t – o espaço cresce (movimento progressivo, V>0) e o movimento é acelerado, pois a e V tem mesmo sinal (a>0 e V>0)

b) Correta --- como o movimento é retrógrado, a velocidade é negativa e, para que o movimento seja acelerado, a aceleração também tem que ser negativa, o que é o caso.

c) Falsa --- o movimento é acelerado mas é progressivo (V>0).

d) Falsa --- se existe aceleração, o gráfico Sxt tem que ser uma parábola (equação do segundo grau).

R- B

38- A área compreendida entre a reta representativa e o eixo dos tempos corresponde ao deslocamento ∆S do móvel no intervalo de tempo considerado --- A e B (0 e t+Em todo gráfico da velocidade em função do tempo1) --- ∆SAB=área do retângulo=b.h --- ∆SAB=Vot1 --- B e C (t1 e t2) --- ∆SBC=área do triângulo=b.h/2 --- ∆SBC=(t2 – t1).(Vo – 0)/2 --- ∆SBC=Vo.(t2 – t1)/2 --- ∆SBC/∆SAB= [Vo.(t2 – t1)/2]/ Vot1 --- ∆SBC/∆SAB=(t2 – t1)/2t1 --- R- C

39- Primeira situação --- cálculo da aceleração do carro com a pista seca --- V2=Vo2 + 2.a.∆S --- 02 = 102 + 2.a.5 --- a=-10ms2 --- cálculo da aceleração do carro com a pista molhada --- V2=Vo2 + 2.a.∆S --- 02 = 102 + 2.a.6 --- a=-100/12=-25/3 ms2 --- Segunda situação --- cálculo da distância percorrida com a pista seca --- V2=Vo2 + 2.a.∆S --- 02 = 302 + 2.(-10). ∆S --- ∆S =45m --- cálculo da distância percorrida com a pista molhada --- V2=Vo2+ 2.a.∆S --- 02 = 302 + 2.(-25/3).∆S --- ∆S=54m --- distância a mais --- d=54 – 45=9m --- R- D