Estática de um Ponto Material

 Estática  parte da mecânica que estuda as condições de equilíbrio de um ponto material (corpo de dimensões desprezíveis) ou de um corpo extenso (o tamanho influi no estudo do fenômeno).    

Todas as figuras acima determinam um sistema estático, ou seja, todos seus pontos encontram-se em equilíbrio estático (repouso).

Equilíbrio de um ponto material

Um corpo está em equilíbrio se sua velocidade vetorial permanecer constante (aceleração nula) no decorrer do tempo, em relação a um determinado referencial.

Para que isso ocorra (o ponto material ou corpo extenso) esteja em equilíbrio, temos dois casos:

Primeiro caso a velocidade vetorial é constante e nula no decorrer do tempo: nesse caso,

o corpo está em repouso em relação a um determinado referencial.

No estado de repouso, dizemos que o corpo se encontra em Equilíbrio Estático.

Segundo caso a velocidade vetorial é constante e não nula no decorrer do tempo: o

corpo descreve um movimento retilíneo e uniforme (MRU), sendo sua velocidade constante em módulo, direção e sentido.

Se ele estiver em movimento retilíneo e uniforme, dizemos que o corpo se encontra em Equilíbrio Dinâmico.

Condição de equilíbrio de um ponto material (corpo de dimensões desprezíveis)

Métodos de resolução de exercícios sobre equilíbrio de um Ponto Material

 Utiliza-se com mais freqüência o método das projeções das forças sobre os eixos horizontal (x) e vertical (y), perpendiculares entre si.

A soma das projeções das forças sobre cada eixo deve ser nula. Exemplo:

A intensidade dessas projeções vale    F_1x = F₁.cos θ    F_2x = F₂.cos β    no equilibro, a soma dessas projeções sobre o eixo horizontal X, deve ser nula, ou seja    F_1x = F_2x    F₁.cos θ = F₂.cos β (I)

Decompondo as forças inclinadas na vertical, projetando-as sobre o eixo Y:

As intensidades dessas projeções sobre o eixo y valem    F_1y=F₁.senθ    F_2y=F₂.senβ    no equilíbrio a soma vetorial dessas projeções deve ser nula    F_1y + F_2y = F₃    F₁.senθ + F₂.senβ = F₃ (II)

Através das expressões (I) e (II) pode-se encontrar a solução do exercício proposto.

Veja um exercício exemplo:

(UNESP-SP) Um semáforo pesando 100 N está pendurado por três cabos conforme ilustra a figura. Os cabos 1 e 2 fazem um ângulo α e β com a horizontal, respectivamente.

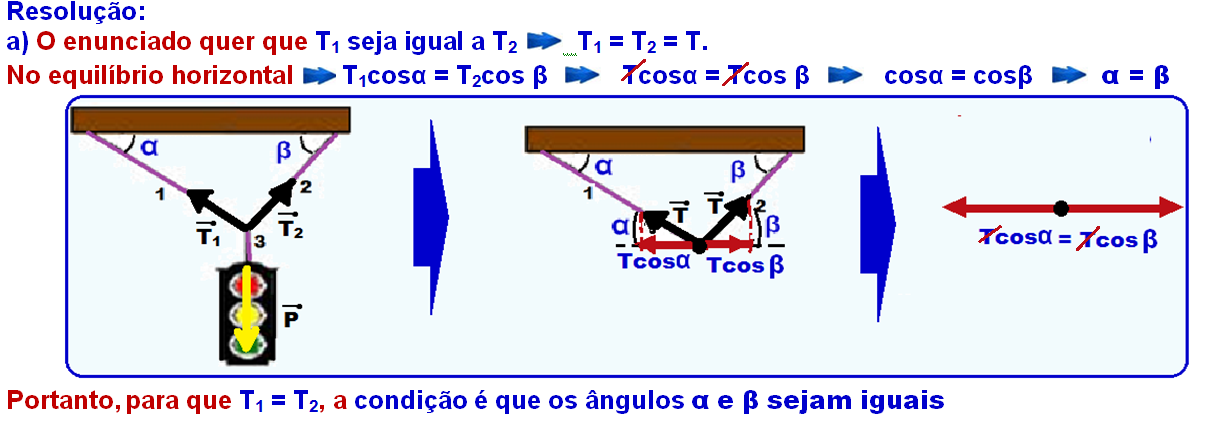
a) Em qual situação as tensões nos fios 1 e 2 serão iguais?

b) Considerando o caso em que α = 30° e β = 60°, determine as tensões nos cabos 1, 2 e 3.

Dados: sen 30° = 1/2 e sen 60° = √3/2

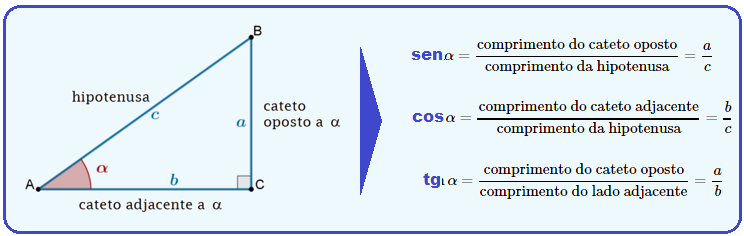
b) Colocando as forças e decompondo-as:

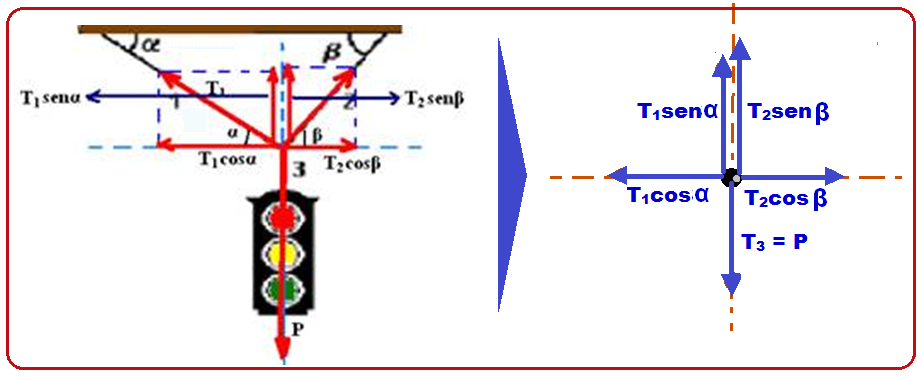
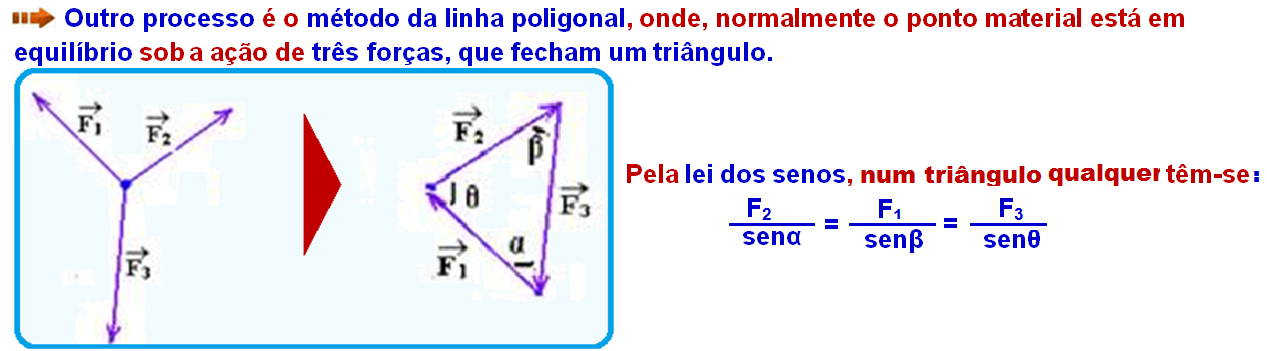
Se o triângulo for retângulo são válidas as relações:

Veja um exercício exemplo:

 (UNESP-SP)  Um professor de física pendurou uma pequena esfera, pelo seu centro de gravidade, ao teto da sala de aula,

 teto da sala de aula,conforme a figura:

Em um dos fios que sustentava a esfera ele acoplou um dinamômetro e verificou que, com o sistema em equilíbrio, ele marcava 10 N.

Calcule o peso, em newtons, da esfera pendurada.

Nas figuras abaixo estão colocadas as forças que  agem sobre a esfera    como a esfera está em

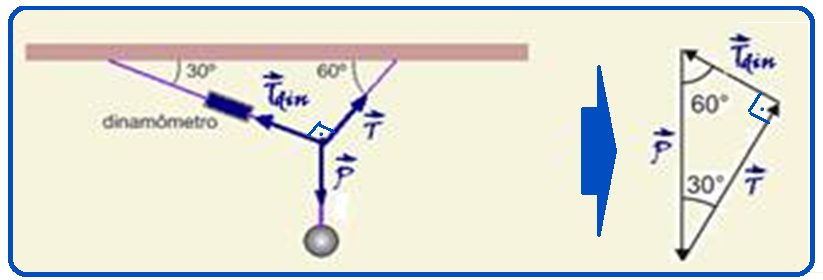
equilíbrio, a resultante das forças é nula e, somando vetorialmente essas forças pelo método da linha poligonal você obterá o triângulo retângulo da figura acima.

O que você deve saber, informações e dicas

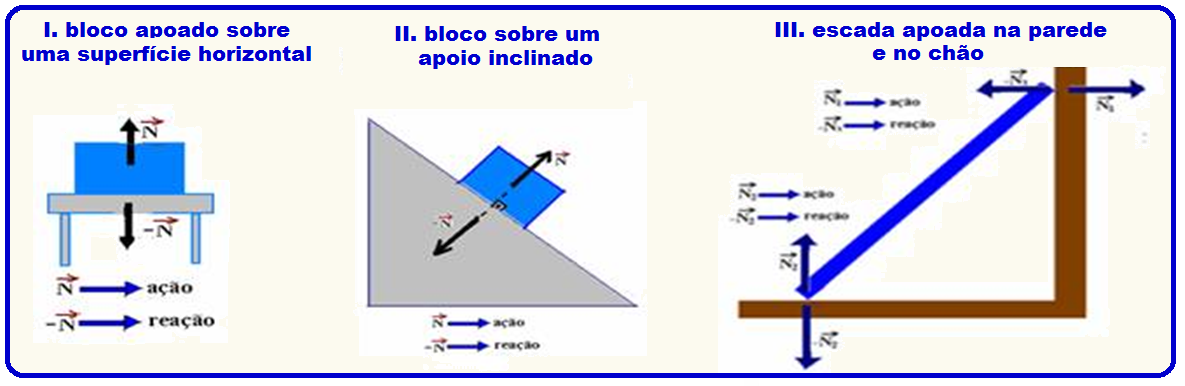
contato. Obedecem ao princípio da ação e reação e não se anulam, pois são aplicadas em corpos diferentes.

  Força de tração ou de tensão (T)  Força que é transmitida sempre por fios cordas ou cabos ideais (inextensíveis e de massas desprezíveis) distendendo-os (tracionando-os, esticando-os).

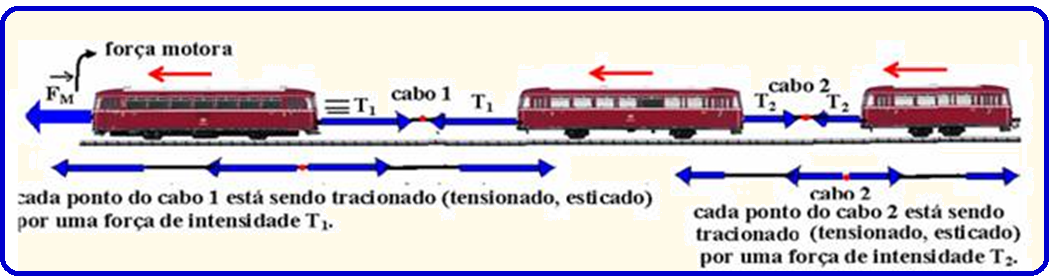
Exemplo: Locomotiva puxando dois vagões através de dois cabos ideais 1 e 2.

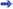 Se você pendurar um quadro na parede por meio de dois fios, quanto menor for o ângulo formado com o teto, ou o suporte, maior será a força de tração (tensão) no fio.

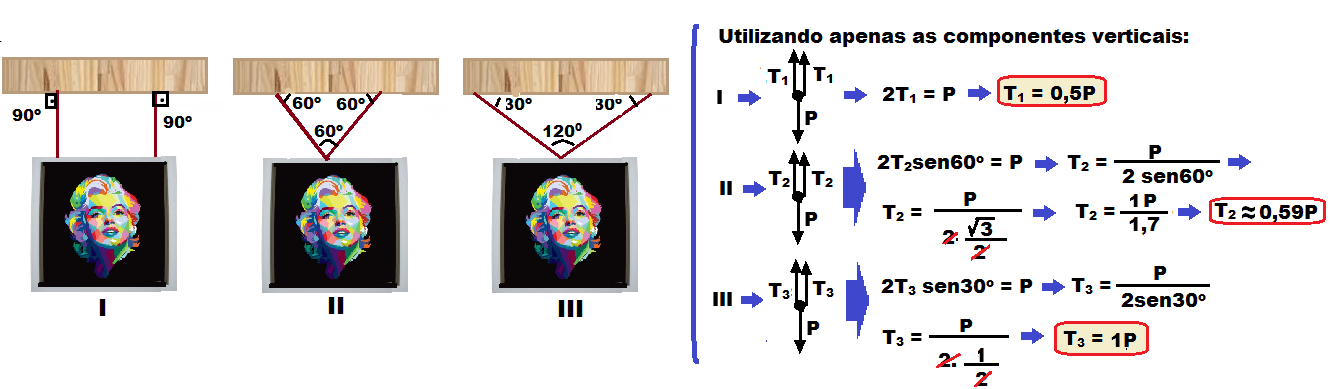
Observe também que, quanto maior for o ângulo entre os dois fios, maior será a força de tração nos fios, como você pode notar nas figuras abaixo, onde um mesmo pacote pode ser carregado com cordas amarradas  de várias maneiras.

A situação, dentre as apresentadas, em que as cordas estão sujeitas à maior tensão é a alternativa (a), onde o ângulo entre os fios é maior.

Exercícios de vestibulares com resolução comentada sobre

Estática de um Ponto Material

01-(Ufrrj-RJ) A figura a seguir mostra um atleta de ginástica olímpica no aparelho de argolas. O ginasta encontra-se parado na posição mostrada.

Assinale qual dentre as alternativas a seguir a que melhor representa as forças que atuam sobre ele, desprezando-se as forças do ar.

02- (PUC-PR) Duas esferas rígidas 1 e 2, de mesmo diâmetro, estão em equilíbrio dentro de uma caixa, como mostra a figura a seguir.

Considerando nulo o atrito entre todas as superfícies, assinale o diagrama que representa corretamente as forças de contato que agem sobre a esfera 2 nos pontos A, B e C.

03-(CFT-MG) As figuras 1 e 2 a seguir representam, respectivamente, todas as forças, constantes e coplanares, que atuam sobre uma partícula e o diagrama da soma vetorial destas forças.

Com base nestas informações, pode-se afirmar que a partícula certamente estará em

a) repouso.     

b) movimento retilíneo uniforme.      

c) equilíbrio.     

d) movimento circular uniforme.

04-(PUC-SP) Um corpo está sujeito a um sistema de três forças concorrentes. As intensidades de duas delas são 5N e 20N. Quanto a intensidade da terceira força f, para que haja equilíbrio deve satisfazer à desigualdade:

05-(Cesgranrio) Um corpo de peso P encontra-se em equilíbrio, devido à ação da força F, como indica a figura a seguir

:

Os pontos A, B e C são os pontos de contato entre os fios e a superfície. A força que a superfície exerce sobre os fios nos pontos A, B e C são, respectivamente:

06-(UFMG) Dois ímãs, presos nas extremidades de dois fios finos, estão em equilíbrio, alinhados verticalmente, como mostrado nesta figura:

Nessas condições, o módulo da tensão no fio que está preso no ímã de cima é

a) igual ao módulo da tensão no fio de baixo.         

b) igual ao módulo do peso desse ímã.

c) maior que o módulo do peso desse ímã.           

d) menor que o módulo da tensão no fio de baixo.

e) nada se pode afirmar.

07- UNIFOR-CE) Com 6 pedaços iguais de corda e três corpos de mesma massa e mesmo formato, um estudante fez as montagens representadas abaixo.

Nos pedaços de corda a intensidade da força de tração é

 (A) a mesma nas montagens 1, 2 e 3.      

(B) maior na montagem 3 que na 2.     

(C) maior na montagem 2 que na 3.

(D) a mesma nas montagens 2 e 3 e menor que na 1.     

(E) a mesma nas montagens 2 e 3 e maior que na 1.

08-(AFA) Na figura abaixo, o ângulo θ vale 30^o, e a relação entre as massas m₂/m₁ tem valor 3/2.

Qual deve ser o valor do coeficiente de atrito entre o bloco 2 e o plano, para que o sistema permaneça em equilíbrio?

09-(CFT-CE) Um quadro de massa m = 6,0 kg se encontra em equilíbrio pendurado ao teto pelos fios 1 e 2, que fazem com a horizontal os ângulos  θ₁ = 60° e  θ₂ = 30°, conforme a figura.

Adotando g=10m/s², calcule as trações nos fios 1 e 2.

Dados: sen30° = cos60° = 1/2  ---  cos30° = sen60° =  (√3)/2

10-(FUVEST-SP) Um bloco de peso P é suspenso por dois fios de massa desprezível, presos a paredes em A e B, como mostra a figura adiante.

 Pode-se afirmar que o módulo da força que tenciona o fio preso em B, vale:

11-(MACKENZIE-SP) Os garotos A e B da figura puxam, por meio de cordas, uma caixa de 40kg, que repousa sobre uma superfície horizontal, aplicando forças paralelas a essa superfície e perpendiculares entre si, de intensidades, 160N e 120N, respectivamente.   

O garoto C, para impedir que a caixa se desloque,aplica outra força horizontal, em determinada direção e sentido. Desprezando o atrito entre a caixa e a superfície de apoio, a força aplicada pelo garoto C tem intensidade de:

12-(UNICAMP-SP) Uma das modalidades de ginástica olímpica é a das argolas. Nessa modalidade, os músculos mais solicitados são os dos braços, que suportam as cargas horizontais, e os da região dorsal, que suportam os esforços verticais. Considerando um atleta cuja massa é de 60 kg e sendo os comprimentos indicados na figura H = 3,0 m; L = 1,5 m e d = 0,5 m, responda:

a) Qual a tensão em cada corda quando o atleta se encontra pendurado no início do exercício com os braços na vertical?

b) Quando o atleta abre os braços na horizontal, qual a componente horizontal da tensão em cada corda?

13-(UEL-PR) As placas I, II, III, IV e V estão submetidas a forças cujas direções estão indicadas no esquema e suas respectivas intensidades devem ser ajustadas para que a resultante seja nula e as placas fiquem em equilíbrio estático.

Em uma das placas, o acerto das intensidades das forças para obter o equilíbrio estático é impossível. Essa placa é a

14-(FUVEST-SP) Para vencer o atrito e deslocar um grande contêiner C, na direção indicada, é necessária uma força F = 500N. Na tentativa de movê-lo, blocos de massa m = 15kg são pendurados em um fio, que é esticado entre o contêiner e o ponto P na parede, como na figura.

 Para movimentar o contêiner, é preciso pendurar no fio, no mínimo,

15-(UNESP-SP) Um semáforo pesando 100 N está pendurado por três cabos conforme ilustra a figura. Os cabos 1 e 2 fazem um ângulo α e β com a horizontal, respectivamente.

a) Em qual situação as tensões nos fios 1 e 2 serão iguais?

b) Considerando o caso em que α = 30° e β = 60°, determine as tensões nos cabos 1, 2 e 3.

Dados: sen 30° = 1/2 e sen 60° = √3/2

16-(Uerj-RJ) Em uma sessão de fisioterapia, a perna de um paciente acidentado é submetida a uma força de tração que depende do ângulo α, como indica a figura a seguir.

O ângulo α varia deslocando-se a roldana R sobre a horizontal. Se, para um mesmo peso P, o fisioterapeuta muda α de 60° para 45°, o valor da tração na perna fica multiplicado por:

17- (UNICAMP-SP) Quando um homem está deitado numa rede (de massa desprezível), as forças que esta aplica na parede formam um ângulo de 30° com a horizontal, e a intensidade de cada uma é de 60 kgf (ver figura adiante)

.

a) Qual é o peso do homem?

b) O gancho da parede foi mal instalado e resiste apenas até 130 kgf. Quantas crianças de 30 kgf a rede suporta? (suponha que o ângulo não mude).

18-(ACAFE-SC) No sistema representado na figura abaixo, as massas dos blocos são, respectivamente, m_A=5,0kg, m_B=10kg e m_P=15kg. Suponha que o bloco P esteja em equilíbrio e que não haja atrito entre ele e a superfície. Pode-se afirmar então, que o valor da força normal, em newtons, que atua sobre o bloco P é:

19-(UFPE-PE) Um bloco de massa m = 20 kg é escorado contra o teto de uma edificação, através da aplicação de uma força oblíqua F, como indicado na figura adiante.

 Sabendo-se que este escoramento deve suportar o peso p = 8,8 x 10³N, devido ao teto, calcule o valor mínimo de F, em unidades de 10³N.

20-(Ufpel-RS) Para garantir o sono tranqüilo de Chico Bento, Rosinha segura a rede, exercendo sobre ela uma força inclinada de 37º em relação à horizontal, como mostra a figura abaixo.

Desprezando o peso da rede e sabendo que Chico Bento pesa 280 N, observamos que Rosinha terá grande dificuldade para permanecer segurando a rede, pois precisa exercer sobre ela uma força de:

21-(UFPB-PB) Conforme a figura a seguir, um barco, puxado por dois tratores, navega contra a corrente de um trecho retilíneo de um rio.

 Os tratores exercem, sobre o barco, forças de mesmo módulo (F₁ = F₂), enquanto a corrente atua com uma força , cujo módulo é 1,92 . 10⁴ N. Sabendo que o barco e os tratores movem-se com velocidades constantes, que sen θ = 0,80 e cos θ = 0,60, então o valor de F₁ é: 

a) 1,20 . 10⁴ N.                   

b) 1,60 . 10⁴ N.                   

c) 1,92 . 10⁴ N.                      

d) 2,40 . 10⁴ N.

e) 3,84 . 10⁴ N.  

22-(UFPE) Uma barra horizontal de massa desprezível possui uma de suas extremidades articulada em uma parede vertical. A outra extremidade está presa à parede por um fio que faz um ângulo de 45° com a horizontal e possui um corpo de 55 N pendurado.

Qual o módulo da força normal à parede, em newtons, que a articulação exerce sobre a barra?

23-(UFRJ-RJ) Sejam três cartazes idênticos em tamanho e massa, pendurados, como mostra a figura. Os cabos têm massas desprezíveis. As tensões nas cordas são, respectivamente, T₁, T₂ e T₃.

Compare as intensidades das tensões T₁, T₂ e T₃ e ordene-as de maneira crescente. Justifique sua resposta.

24-(FUVEST-SP) Um mesmo pacote pode ser carregado com cordas amarradas  de várias maneiras. A situação, dentre as apresentadas, em que as cordas estão sujeitas à maior tensão é:

25-(PUC-SP) Para tentar desencalhar um carro, seu motorista prende a extremidade de uma corda inextensível e de

peso desprezível ao pára choque e a outra extremidade a uma árvore, de modo que a corda fique disposta horizontalmente com um comprimento livre de 10m. No meio da corda é suspenso um corpo de 20N de peso. Nessas condições, observa-se que o ponto médio da corda desce de 0,2m. A intensidade da força transmitida ao carro é, aproximadamente de:

26-(MACKENZIE-SP) Um quadro, pesando 36,0 N, é suspenso por um fio ideal preso às suas extremidades. Esse fio se apoia em um prego fixo à parede, como mostra a figura. Desprezados os atritos, a força de tração no fio tem intensidade de:

27-(UNESP-SP)  Um professor de física pendurou uma pequena esfera, pelo seu centro de gravidade, ao teto da sala de aula, conforme a figura:

Em um dos fios que sustentava a esfera ele acoplou um dinamômetro e verificou que, com o sistema em equilíbrio, ele marcava 10 N. O peso, em newtons, da esfera pendurada é de

28-(UFPR-PR) Uma corrente composta por cinco elos está presa ao teto por meio de um barbante, conforme mostra a figura.  

A massa de cada elo é de 200 g.

a) Faça um diagrama de forças para o terceiro elo, identificando cada uma das forças que atuam sobre ele.

b) Calcule o módulo de todas as forças que estão atuando nesse terceiro elo.

29-(PUC-RS)  Dois operários suspendem um balde por meio de cordas, conforme mostra o esquema a seguir.

cos30º =√3/2. 1/2 e  sen60º =  =São dados: sen30º = cos60º

Sabe-se que o balde, com seu conteúdo, tem peso 50N, e que o ângulo formado entre as partes da corda no ponto de suspensão é 60^o. A corda pode ser considerada como ideal (inextensível e de massa desprezível).

Quando o balde está suspenso no ar, em equilíbrio, a força exercida por um operário, medida em newtons, vale:

30-(UFLA-MG)  Um corpo de massa 10 kg é preso a uma mola, produzindo, assim, um alongamento de 5 cm (Figura A). Coloca-se, agora, esse conjunto mola-corpo sobre um plano inclinado θ isento de atrito (Figura B). Considere a aceleração da gravidade g = 10 m/s², cos θ = 0,8 e sen θ = 0,6.

É CORRETO afirmar que no plano inclinado a mola sofre um alongamento de

a) 0,6 cm.                                   

b) 0,8 cm.                                             

c) 4 cm.                                                    

d) 3 cm. 

31-(UECE-CE)  Na figura a seguir, o peso P₁ é de 500 N e a corda RS é horizontal.

Os valores das tensões T₁, T₂ e T₃ e o peso P₂, em Newton, são, respectivamente,

32-(UPE-PE)

A figura abaixo ilustra uma roda de raio R e massa m. Qual é o módulo da força horizontal , necessária para erguer

a roda sobre um degrau de altura h = R/2, quando aplicada no seu eixo?

Considere a aceleração da gravidade g.

As questões 33 e 34 devem ser respondidas com base na situação física descrita a seguir.

No esquema apresentado na figura abaixo, uma partícula de poeira cósmica, cuja massa é igual a 2,0 g, move-se livremente de norte para o sul, com velocidade de módulo igual a 1,2 km/s. No instante visualizado nesse esquema (t = 0), passam a atuar sobre essa partícula as forças A, B e C nele representadas, sendo todas elas constantes.

Considere também que os valores numéricos associados aos eixos “norte” e “leste” referem-se à unidade de força do Sistema Internacional: newton (N).

33-(IFNMG-MG)

O módulo da velocidade da partícula no instante t = 1,0 s, expresso em km/s, está corretamente apresentado na alternativa:

34-(IFNMG-MG)

No instante t = 1,0 s, as forças A, B e C deixam de atuar na partícula. Nessas condições, a forma da trajetória da partícula, desde t = 0, está corretamente descrita na alternativa:

A) Retilínea, desde t = 0, e ainda retilínea, após t = 1,0 s.            

B) Inicialmente circular e, após 1,0 s, retilínea.

C) Inicialmente circular e, após 1,0 s, parabólica.                          

D) Inicialmente parabólica e, após t = 1,0 s, retilínea.

 35-(UFPR-PR)

Três blocos de massas m₁, m₂ e m₃, respectivamente, estão unidos por cordas de massa desprezível, conforme mostrado na

figura. O sistema encontra-se em equilíbrio estático. Considere que não há atrito no movimento da roldana e que o bloco de

massa m1 está sobre uma superfície horizontal. Assinale a alternativa que apresenta corretamente (em função de m₁ e m₃)   

o coeficiente de atrito estático entre o bloco de massa₁ e a superfície em que ele está apoiado.

36-(UFF-RJ)

Ímãs são frequentemente utilizados para prender pequenos objetos  em superfícies metálicas planas e verticais, como quadros de avisos e portas de geladeiras.

Considere que um ímã, colado a um grampo, esteja em contato com a porta de uma geladeira . Suponha que a força magnética que o ímã faz sobre a superfície da geladeira é perpendicular a ela e tem módulo F_M.

. O conjunto imã/grampo tem massa m_o

.O coeficiente de atrito estático entre a superfície da geladeira e a do ímã é  μ_e

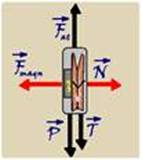
.Uma massa M está pendurada no grampo por um fio de massa desprezível, como mostra a figura.

a) Desenhe no diagrama as forças que agem sobre o conjunto ímã/grampo (representado pelo ponto preto no

cruzamento dos eixos x e y na figura), identificando cada uma dessas forças.

b) Qual o maior valor da massa  M  que pode ser pendurada no grampo sem que o conjunto caia?

37-(MACKENZIE-SP)

Certo corpo de massa 10,0 kg está suspenso por uma pequena argola, que pode deslizar, sem atrito, por um fio, supostamente ideal. Em

uma primeira situação, o corpo encontra-se na posição ilustrada na figura 1 e, depois de certo tempo, encontra-se na posição ilustrada na

figura 2. O trabalho realizado pela força peso, entre a posição 1 e a posição 2, foi           

a)  2,40. 10^-1J                     

b) 2,45.10^-1J                         

c) 5,00.10^-1J                          

d) 2,40J                        

e) 2,45J

Resolução comentada dos exercícios de vestibulares sobre

Estática de um Ponto Material

01- Sobre o homem atuam três forças, seu peso (vertical e para baixo) e as duas forças de tração aplicadas pelo teto através dos fios, agindo sobre suas mãos  ---  R- A

02- A parede da direita aplica em B, sobre a esfera 2 uma força horizontal e para a esquerda, analogamente,  parede da esquerda aplica em A, sobre a esfera 2 uma força horizontal e para a direita e a esfera 1 comprime-a em A  ---  R- A

03-

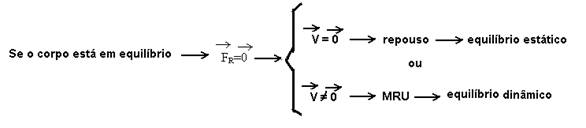
R- C

04- Quando elas tiverem mesma direção e mesmo sentido  ---  valor máximo da terceira força que deve anula-las F_máx=20 + 5=25N  ---  quando elas tiverem mesma direção e sentidos opostos  ---  valor mínimo da terceira que deve anula-las F_mín=20 - 5=15N  ---  R- D

05- Observe atentamente a figura abaixo onde todas as forças foram colocadas

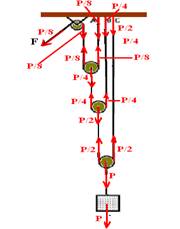
R- A

06- Colocando as forças que agem nos imãs  ---  F_m – força magnética que deve ser de atração, caso contrário não haveria equilíbrio  ---  peso P  ---  T₁ – força de tração no fio de cima  ---  T=2 – força de tração no fio de baixo

R- C

07- (1)  ---  2T₁=P  ---  T₁=P/2  ---  (2) 2T₂sen60^o=P  ---  T₂=P/2sen60^o  ---  T₂=0,58P  ---  (3) 2T₃sen30^o=P  ---  T₃=P/2sen30^o  ---  T₃=P  ---  R- B

08- m₂/m₁=3/2  ---  m₂=3/2m₁  ---  F_at=μN=μP₂=μm₂g  ---  F_at=3/2μm₁g  ---  P₁=m₁g  ---  colocando as forces:

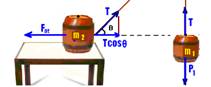
O bloco m₁ está em equilíbrio  ---  T=P₁  ---  T=m₁g  ---  o bloco m₁ também está em equilíbrio  ---  equilíbrio horizontal  ---  F_at=Tcosθ  --- 3/2μm₁g =Tcos30^o  ---  3/2μm₁g=m₁g.√3/2  ---  μ=√3/3

09- Colocando as forças

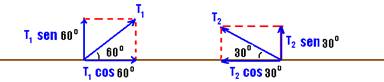
Equilíbrio na horizontal  ---  T₁cos60^o=T₂cos30^o  ---  T₁.1/2=T₂.√3/2  ---  T₁=√3.T₂  ---  equilíbrio na vertical  ---  T₁sen60^o + T₂sen30^o=P  ---  T₁.√3/2 + T₂.1/2=6.10  ---  (√3.T₂.√3)/2 + T₂/2=60  ---  3T₂ + T₂=120  ---  T₂=30N  ---  T₁=√3.T₂  ---  T₁=√3.30  ---  T₁=30√3N

10- colocando as forças

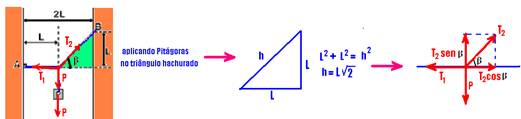
senβ=L/(L√2)  ---  senβ=√2/2  ---  cosβ= L/(L√2)  ---  cosβ=√2/2  ---  equilíbrio vertical  ---  P=(√2/2)T₂  ---  T₂=P√2  ---  R- D

11- Observe a figura abaixo:

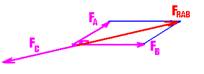
F_RAB=F_A²  F_B²=(160)² + (120)²  ---  F_RAB=200N=F_C­  ---  R- E

12- a) Observe na figura abaixo que 2T=P=mg=60.10  ---  T=600/2  ---  T=300N

b) Prolongando as duas cordas obtemos os dois triângulos da figura abaixo

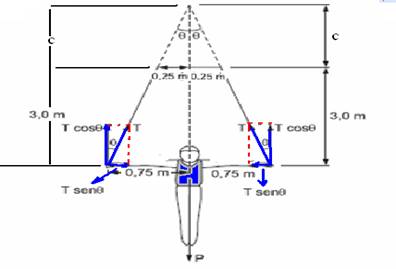
Pela semelhança entre os triângulos de alturas c e (3 + c)  ---  0,25/c=0,75/(3 + c)  ---  c=1,5m  ---  equilíbrio na vertical  ---  2Tcosθ=P  ---  Tcosθ=300   ---  T=300/cosθ (I)  ---  na horizontal, a componente horizontal de T é  ---  T_x=Tsenθ  ---  T=T_x/senθ (II)  ---  igualando (I) com (II)  ---  300/cosθ=T_x/senθ  ---  senθ/cosθ=T_x/300  ---  tgθ=T_x/300  ---  0,75/4,5=T_x/300  ---  T_x=50N

13- Para que as placas fiquem em equilíbrio estático, resultante das força que agem sobre elas devem ter componentes na horizontal e na vertical para que possam se anular  ---  observe que a única alternativa que não tem componentes que possam se anular na horizontal é a V  ---  R- E

14- Para movê-lo, a força de tração deve valer T=500N, conforme a figura abaixo:

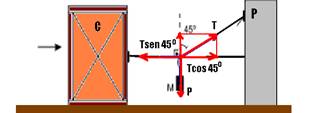
Equilíbrio na horizontal  ---  Tcos45^o=500  ---  T√2/2=500  ---  T=500√2N  ---  equilíbrio na vertical  ---  Tsen45^o= P  ---  500√2.(√2/2)=P  ---  P=500N  ---  para movê-lo é necessário um peso de 500N, ou seja, 500/150=3,3 blocos  ---  R- D

15- a) Somente quando α=β

b) Colocando as forças:

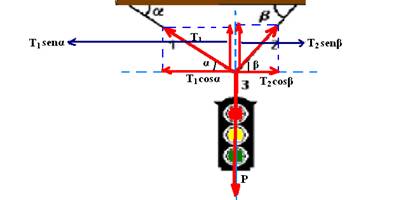
Equilíbrio na horizontal  ---  T₁cosα=T₂cosβ  ---  T₁√3/2=T₂.1/2  ---  T₂=√3.T₁  ---  equilíbrio na vertical  ---  T₃=P=100N  ---  100=T₁sen30^o + T₂sen60^o  ---  100=T₁.1/2 + (√3T₁).√3/2  ---  100=T₁/2 + 3T₁/2  ---  T₁=50N  ---  T₂=√350  ---  T₂=50√3N

16- Ângulo de 60^o  ---  F₁=2Tcos60^o=2T1/2=T  ---  ângulo de 45^o  ---  F₂=2Tcos45^o=2T√2/2=√2T  ---  F₁=√2F₂  ---  R- B

17- a)

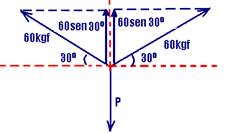
equilíbrio na vertical  ---  2.60.sen30^o=P  ---  2.60.1/2=P  ---  P=60kgf

b) analogamente  ---  2.130.sen30^o=P  ---  P=130kgf  ---  130/30=4,33  ---  4 crianças

18- Colocando as forças:

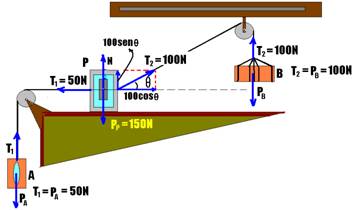
Equilíbrio vertical no bloco P  ---  150=N + 100senθ  ---  150=N + 100.0,87  ---  N=63N  ---  R- E

19-

Equilíbrio na vertical  ---  Fcos60^o=P + 8,8.10³  ---  F.1/2=8,8.10³  + 200 ---  F=(8.800 + 200).2  ---  F=18.000  ---  F=18.10³N

20- Observe a figura abaixo:

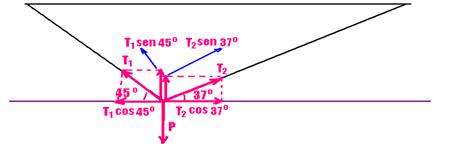
Equilíbrio na horizontal  ---  T₁cos45^o=T₂cos37⁰  ---  T₁.0,7=T₂.0,8  ---  T₁=8T₂/7  ---  equilíbrio na vertical  ---  T₁sen45^o + T₂sen37^o=P  ---  T₁.0,7 + T₂.0,6=280  ---  (8T₂/7).0,7 + 0,6T₂=280  ---  0,8T₂ + 0,6T₂=280  ---  T₂=280/1,4  ---  T₂=200N  ---  R- C

21- Se os tratores e o barco se movem em trajetória retilínea com velocidade constante eles estão em equilíbrio dinâmico e a resultante das forças que agem sobre eles é nula  ---  F₁=F₂=F  --- 

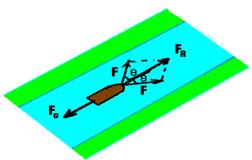
F_R=2Fsenθ=2F.0,8  ---  F_R=1,6F  ---  F_R=F_c  ---1,6F=1,92.10⁴  ---  F=1,20.10⁴N  ---  R- A

22- Equilíbrio na vertical ---  Tsen45^o=P  ---  T√2/2=55  ---  T=55√2N  ---equilíbrio na horizontal  ---  

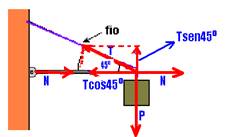
N=Tcos45^o  ---N=55√2.√2/2  ---  N=55N  

23- Se você pendurar um quadro na parede por meio de dois fios, quanto menor for o ângulo formado com o teto, ou o suporte, maior será a força de tração (tensão) no fio.Exemplo:

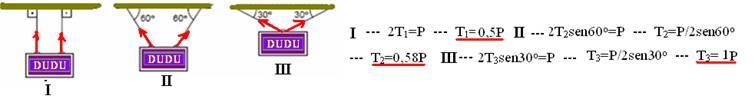
R-  T1 > T2 > T3

24- R- A  (veja resolução do exercício anterior)

25- Observe a figura abaixo:

senθ=0,2/5  ---  senθ=0,04  ---  T_y=Tsenθ=0,04T   ---  2T_y=P  ---  2.0,04T=20  ---  T=2540N  ---  R- D 

26- senβ=30/50  ---  senβ=0,6  ---  P=2Tsenβ  ---  36=2T.0,6  ---  T=36/1,2  ---  T=30N  ---  R- E

27- Nas figuras abaixo estão colocadas as forças que  agem sobre a esfera  ---  como a esfera está em equilíbrio, a resultante das

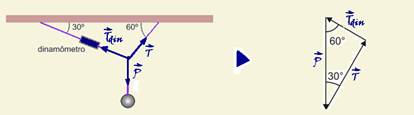
forças é nula  ---  sen30^o=T_din/P  ---  1/2=10/P  ---  P=20N  ---  R- D

28- a) Observe o diagrama abaixo que mostra as forças atuantes no terceiro elo:

b) Dados  ---   m = 200 g = 0,2 kg  ---   g = 10 m/s²  ---  P = m g = 0,2(10)  ---  P = 2 N  --- F₄₃ = 2 P = 4 N  ---  F₂₃ = 3 P = 6 N

29- Observe nas figuras abaixo onde cada força de tração é decomposta na vertical (T_V=Tsen60^o) e na horizontal (T_H=Tcos60^o)  -- 

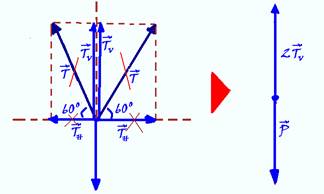
Como o sistema está em equilíbrio, as componentes horizontais se anulam e na vertical você terá  ---  2T­_V=P  ---  2Tsen60^o=P  ---  2T.√3/2=50  ---  T=50/√3N  ---  R- C

30- m = 10 kg  ---   x_A = 5 cm  ---   sen θ = 0,6  ---   cos θ = 0,8  ---  g=10m/s²  ---  observe as figuras a seguir onde o corpo está em equilíbrio nas duas situações e a resultante das forças deve ser nula em

 cada caso  ---  figura A  ---  F_A=P  ---  kx_A=mg  ---k.5=10.10  ---  k=20N/cm  ---  figura B  ---   e  se anulam  ---  F_B=P_t  ---  kx_B=mgsenθ  ---  20.x_B=10.10.0,6  ---  x_B=3cm  --- 

R- D 

31- Dado: P₁ = 500 N.

Como é uma situação de equilíbrio, a resultante em cada um dos nós R e S é nula  ---  aplicando, então, a regra da poligonal em

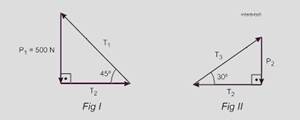
cada um dos nós  ---  figura I  ---  sen45^o=P₁T₁  ---  √2/2=500/T₁  ---  T₁=500√2N  ---  tg45^o=P₁/T₂  ---  1=500/T₂  ---  T₂=500N  --- 

Figura II  ---  cos30⁰=T₂/T₃  ---  √3/2=500/T₃  ---  T₃=1000/√3N  ---  tg30^o=P₂/T₂  ---  √3/3=P₂/500  ---  P₂=500/√3N  ---  R- A

32- Observe na figura 1 abaixo no triângulo hachurado a determinação do ângulo θ entre a horizontal e a direção da força normal,  de contato entre a quina do degrau e a roda  ---  senθ=(R/2)/R  ---  senθ=1/2  ---  θ=30^o  ---  n a figura 2, todas as forças que agem sobre a roda, normal  de contato entre o piso e a roda, peso ,  e , foram colocadas no centro (eixo) da roda  ---    na figura 3,  foi decomposta em sua componente horizontal N₁.cos30^o=N₁√3/2 e vertical N₁sen30^o=N₁/2  ---  à medida que  for aumentando de intensidade para erguer a roda, a intensidade da força normal  vai diminuindo, até que, quando a roda perder contato com o piso (N=0), ela começa a subir (figura 4)  --- no instante em que ela perde contato com o piso ela está em equilíbrio e a resultante das forças que agem sobre ela é nula  ---  equilíbrio na horizontal  ---  F=N1√3/2  ---  equilíbrio na vertical  ---  N₁/2=P  ---  N₁=2P  ---   F=N₁√3/2=2P.√3/2  ---  F=mg√3  ---  R-C.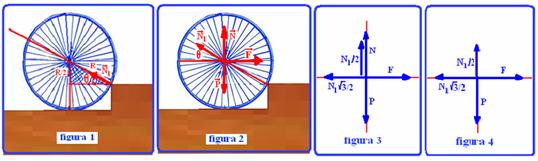

 33- Para calcular a intensidade da força resultante que age sobre a partícula cósmica você pode decompor as forças nas direções norte e leste  ---  observe na sequência abaixo que a intensidade da

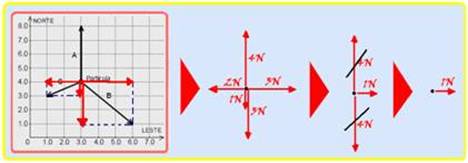
força resultante é de 1N no sentido leste.

Como a velocidade inicial da partícula tem intensidade V_o=1200m/s do norte para o sul e a força resultante sobre ela tem intensidade 1N do oeste para leste, o movimento da partícula tem as características de composição de dois movimentos, um no sentido leste e outro no sentido sul (veja figura)  ---  no sentido leste, a projeção da velocidade inicial é nula V_oL=0 e ela se desloca sob ação de uma força resultante de valor F_R=1N e com aceleração  ---  F_R=m.a  ---  1=2.10^-3.a  ---  a= 500m/s²  ---  sua velocidade nessa direção após t=1s terá intensidade  ---  V_L=V_oL + a_L.t=0 + 500.1  ---  V_L=500m/s  ---  no sentido sul ela será lançada para baixo com V_oS=1200m/s, acelerando com aceleração da gravidade g=10m/s²  ---  após t=1s, sua velocidade nessa direção será  ---  V_S=V_oS + g.t=1200 + 10.1=1210m/s  ---

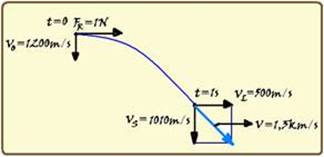
 observe na figura que essas duas velocidades são perpendiculares e, aplicando Pitágoras você obterá V² = V_L² + V_S²=(500)² + (1210)²  ---  V=√(1714100)  ---  V=1309m/s=1,3km/s  ---  R- A.

34- Pelo princípio da inércia, se as forças deixarem de atura, a força resultante sobre ela será nula e, após esse innstante, por inércia, ela seguirá em MRU com velocidade constante de 1,3km/s  ---  observe na resolução do exercício anterior (08) que, antes de 1s a trajetória era parabólica  ---  R- D.

35- Colocando as forças  ---  bloco 1  ---  F_at=μN=μP₁=μm₁g  ---  bloco2  ---  P₂=m₂g  ---  P₃=m₃g  --- 

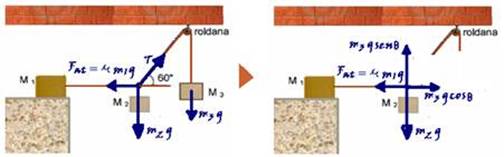
decompondo a tração T  ---T_horizontal=mgcosθ  ---  T_vertical=mgsenθ  ---  equilíbrio na horizontal  ---  μm₁g=m₃gcos60^o  ---   μm₁g=m₃g.(1/2)  ---  μ=m₃/2m₁  ---

R- A

36- a) As forças que agem sobre o conjunto imã-grampo são  ---   – força peso, vertical e para baixo, aplicada sobre o conjunto

pela Terra  ---   - força de tração no fio, vertical e para baixo, aplicada sobre o conjunto pela massa M pendurada  ---  - força de atrito, trocada entre o conjunto  e a parede da geladeira, vertical e para cima, contrária ao movimento ou à sua tendência  ---   -  força magnética, horizontal e que atrai o conjunto para a esquerda, é de atração magnética entre o imã e a parede da geladeira  ---   – força normal, horizontal e para a direita, reação da parede da geladeira sobre o conjunto.

b) Se o conjunto não deve cair a força resultante sobre ele tanto na vertical como na horizontal deve ser nula  ---  equilíbrio na vertical  ---  F_at=P + T  ---  P=m_og  ---  T=Mg  ---  F_at=μ_eN  ---  μ_eN = m_og + Mg (I)  ---  equilíbrio na horizontal  ---  F_M=N (II)  ---  (II0 em (I)  ---  μ_eF_M = m_og + Mg  ---  Mg = μ_eF_M – m_og  ---  M= (μ_eF_M – m_og)/g ou M= μ_eF_M/g - m_o ---  para esse valor de M o conjunto está na iminência de cair  ---  para qualquer valor de M menor que esse, o conjunto não cai.

37- Cálculo de d na figura 1 ---  triângulo retângulo – Pitágoras  ---  d² = 30² + 40²  ---  d=50cm  ---  cálculo de h₁  ---  triângulo amarelo

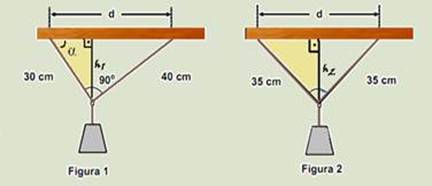
da figura 1  ---  senα=h₁/30  ---  triângulo inteiro  ---  senα=40/d  ---  h₁/30=40/50  ---  h₁=24cm  ---  aplicando Pitágoras no triângulo amarelo da figura 2  ---  35² = (d/2)² + h₂²  ---  1225 = 25² + h²  ---  h=√(600)  ---  h≈24,5cm  ---  o trabalho da força peso é fornecido pela expressão  ---  W_peso=m.g.∆h=10.10.(0,245 – 0,24)  ---  W_peso=0,5J  ---  R- C