 Centro
de massa (CM) de
um corpo
extenso
(dimensões não desprezíveis), rígido
(não
deformável)
e homogêneo
(massa uniformemente distribuída)
Centro
de massa (CM) de
um corpo
extenso
(dimensões não desprezíveis), rígido
(não
deformável)
e homogêneo
(massa uniformemente distribuída)
Estática de um corpo extenso – Centro de massa – Tipos de equilíbrio
Centro de massa
 Centro
de massa (CM) de
um corpo
extenso
(dimensões não desprezíveis), rígido
(não
deformável)
e homogêneo
(massa uniformemente distribuída)
Centro
de massa (CM) de
um corpo
extenso
(dimensões não desprezíveis), rígido
(não
deformável)
e homogêneo
(massa uniformemente distribuída)
![]() Esse corpo extenso
possui
infinitos
pontos materiais de mesma massa
e pode-se representá-lo por meio de um
único ponto
material, o
centro
de massa (CM) do
sistema,
ou
seja, representa o ponto
onde podemos supor que
Esse corpo extenso
possui
infinitos
pontos materiais de mesma massa
e pode-se representá-lo por meio de um
único ponto
material, o
centro
de massa (CM) do
sistema,
ou
seja, representa o ponto
onde podemos supor que

toda a massa de um corpo esteja concentrada e que todas as forcas externas atuem nesse ponto.
Centro de gravidade
 Centro
de gravidade (CG) ou baricentro
Centro
de gravidade (CG) ou baricentro
![]() definido
como sendo o ponto
onde se concentra todo o peso do corpo, ou
seja,
é ponto
de aplicação da força peso de um corpo.
definido
como sendo o ponto
onde se concentra todo o peso do corpo, ou
seja,
é ponto
de aplicação da força peso de um corpo.
Assim, se o corpo for homogêneo, o centro de gravidade (CG) coincide com o centro de massa (CM) do corpo e, estão sobre o eixo (ou plano) de simetria.
Localização do centro de massa (CM)
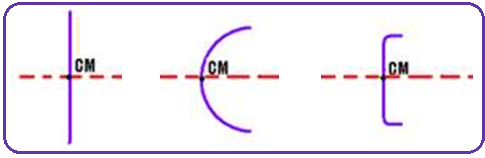
![]() Corpos
lineares
(um eixo de simetria)
Corpos
lineares
(um eixo de simetria) ![]() o centro
de massa
está sobre
o eixo de simetria.
o centro
de massa
está sobre
o eixo de simetria.
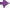 Corpos
planos
(mais
de um eixo de simetria)
Corpos
planos
(mais
de um eixo de simetria)
![]() o
centro
de massa
está no encontro
desses eixos de simetria.
o
centro
de massa
está no encontro
desses eixos de simetria.

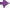 Corpos
sólidos
(mais
de um eixo de simetria)
Corpos
sólidos
(mais
de um eixo de simetria)
![]() o
centro
de massa
está no encontro
desses eixos de simetria.
o
centro
de massa
está no encontro
desses eixos de simetria.
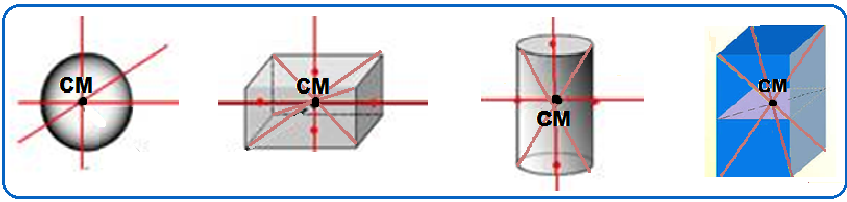
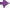 O
centro
de massa
de um corpo
rígido
não
se localiza obrigatoriamente dentro da
O
centro
de massa
de um corpo
rígido
não
se localiza obrigatoriamente dentro da

parte sólida do mesmo, como por exemplo nas figuras acima.
Cálculo do centro de massa de um corpo ou de um sistema de pontos materiais
Considere três pontos materiais A, B e C de massas mA, mB e mC e de coordenadas cartesianas A (XA,YA,ZA), B (XB,YB,ZAB) e C (XC,YC,ZC).
O cálculo da posição das coordenadas de seu centro de massa é dado por:
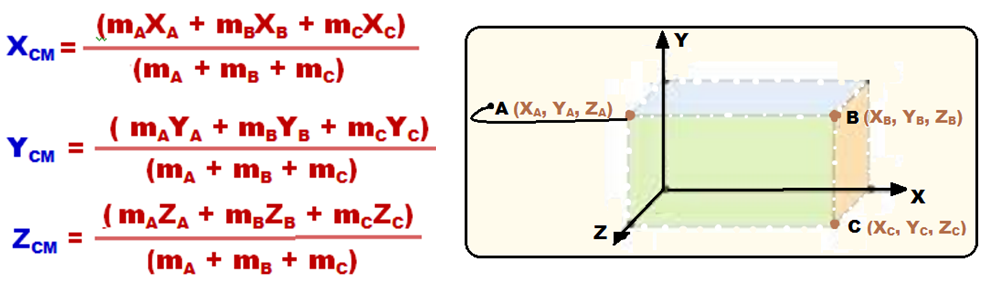
Leia com bastante atenção esse exercício exemplo:
Determine as coordenadas do centro de massa do sistema constituído por duas partículas de massas mp1 = 100g e mp2 = 200g, localizadas conforme a figura abaixo.

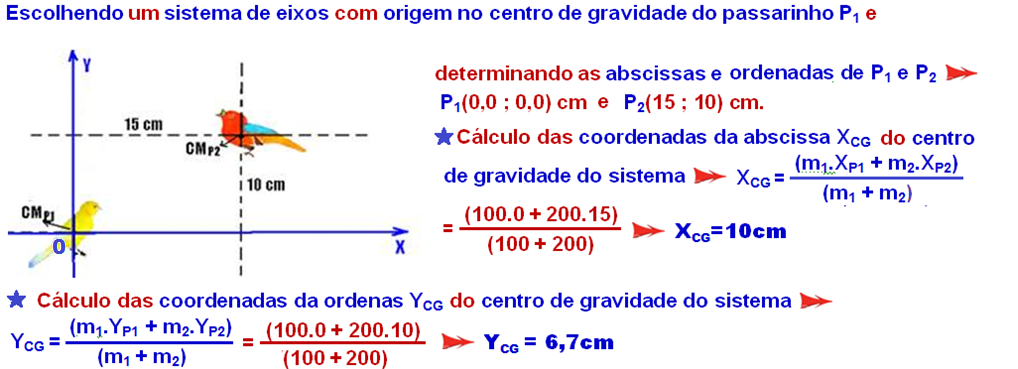
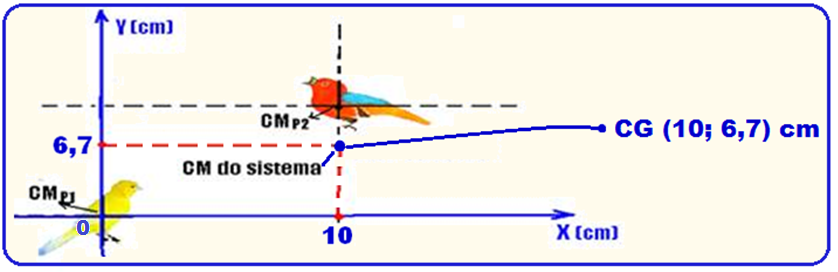
Localizando o centro de massa do sistema constituído de P1 e P2:
![]()
![]() O cálculo
da posição das coordenadas de seu centro de massa é dado
por:
O cálculo
da posição das coordenadas de seu centro de massa é dado
por:

 Numa
competição
olímpica,
quando um atleta pula, num salto, ele movimenta
seus braços,
Numa
competição
olímpica,
quando um atleta pula, num salto, ele movimenta
seus braços,

pernas e cabeça, alterando a posição do centro de massa de seu corpo, mas o mesmo (centro de massa) descreve uma trajetória parabólica em relação à Terra, sujeito ao campo gravitacional.
 Quando
um corpo
se encontra no espaço
sideral,
longe
da atração
gravitacional
de qualquer
Quando
um corpo
se encontra no espaço
sideral,
longe
da atração
gravitacional
de qualquer


planeta, ele possui centro de massa, mas não centro gravitacional (centro de gravidade CG).
 Observe
na figura
abaixo
que a carga
do caminhão
está em desequilíbrio,
concentrada no lado
Observe
na figura
abaixo
que a carga
do caminhão
está em desequilíbrio,
concentrada no lado

direito da carroceria, onde ficará localizado o centro de massa da carga e o caminhão poderá tombar, principalmente se fizer uma curva à esquerda.
Assim, quando a carga estiver deslocada para uma das laterais, haverá um esforço maior sobre a suspensão e os pneus daquele lado, podendo ocasionar derrapagens em razão das condições desiguais de frenagem ou até tombamentos devido a desníveis da pista.
![]() Tipos
de equilíbrio
Tipos
de equilíbrio
Para se determinar se um corpo extenso está em equilíbrio, basta tirá-lo ligeiramente da posição de equilíbrio e, em seguida abandoná-lo.
O equilíbrio será estável se ele retornar à posição inicial, se ele tender a se afastar da posição de
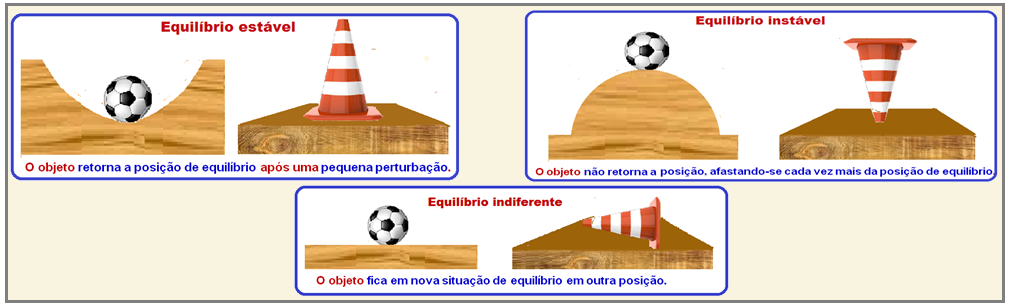 equilíbrio,
o mesmo será instável e,
se ele permanecer
na nova posição,
será indiferente.
equilíbrio,
o mesmo será instável e,
se ele permanecer
na nova posição,
será indiferente.
 Corpos
apoiados
ficam sob ação de duas
forças verticais,
seu peso,
vertical e para baixo
e a reação
normal do apoio, vertical e para cima.
Corpos
apoiados
ficam sob ação de duas
forças verticais,
seu peso,
vertical e para baixo
e a reação
normal do apoio, vertical e para cima.
Essas duas forças devem ser colineares e, assim a reta vertical que contém o centro de

gravidade do corpo deve passar por sua base para que ele não caia.
 Aplicações
práticas do fenômeno acima:
Aplicações
práticas do fenômeno acima:
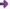 Os
carros
de corrida
são
baixos,
para que seu centro
de gravidade
fique o mais perto
possível do
Os
carros
de corrida
são
baixos,
para que seu centro
de gravidade
fique o mais perto
possível do

solo, adquirindo, assim, grande estabilidade.
 Nas
figuras
abaixo
o equilíbrio
obtido é denominado de estável,
pois o centro
de gravidade (CG)
Nas
figuras
abaixo
o equilíbrio
obtido é denominado de estável,
pois o centro
de gravidade (CG)
encontra-se abaixo do ponto de sustentação ou do apoio.
 Se
você afastar
o
“João
teimoso”
da posição
de equilíbrio (estável),
o contrapeso
(que desloca
Se
você afastar
o
“João
teimoso”
da posição
de equilíbrio (estável),
o contrapeso
(que desloca

seu centro de gravidade para baixo), localizado na posição indicada na figura, tende a fazê-lo retornar à posição inicial, oscilando.
![]() O
prédio
da figura é o Capital
Gate,
em construção em Abu Dhabi, nos Emirados Árabes e sua
O
prédio
da figura é o Capital
Gate,
em construção em Abu Dhabi, nos Emirados Árabes e sua

inclinação é intencional e de 18o para o oeste, sendo o mais inclinado do mundo, com 35 andares.
Ele terá uma estrutura extra com malha extremamente densa de aço, para compensar e sustentar essa inclinação, deslocando seu centro de gravidade para baixo.

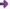 Como
determinar o centro
de gravidade CG
de um corpo,
como por exemplo, de uma placa
metálica.
Como
determinar o centro
de gravidade CG
de um corpo,
como por exemplo, de uma placa
metálica.

![]() Exercício
interessante:
Exercício
interessante:
(Unicamp-SP) Um cigarro sem filtro, de 80 mm, foi aceso e apoiado num cinzeiro, como mostra a

figura. Durante quanto tempo o cigarro ficará sobre o cinzeiro? Considere que a queima se dá à razão de 5 mm por minuto e que a cinza sempre se desprende do cigarro.
Resolução: Como o centro de gravidade CG está sempre no ponto médio e à medida que o cigarro vai queimando ele se desloca para a esquerda e, quando o cigarro estiver na iminência de cair, você
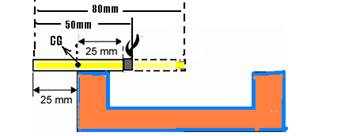
terá
a situação da figura,
onde você deve observar que o cigarro
queimou d = 80 – 50 = 30mm
com velocidade
de 5mm/min
![]() V=d/t
V=d/t
![]() 5=30/t
5=30/t
![]() t
= 6 min.
t
= 6 min.
Exercícios de vestibulares com resolução comentada sobre
Estática de um corpo extenso – Centro de massa – Tipos de equilíbrio.
01- (CESGRANRIO) Seis peças de um jogo de dominó estão dispostas como na figura. Dos pontos indicados (F, G, H, I, J) o que melhor localiza o centro de massa desse conjunto é:

![]()
02- (UnB-DF) Admitindo-se, no sistema de coordenadas da figura abaixo, que cada quadradinho tenha 10cm de lado, determine as coordenadas do centro de massa do sistema constituído de duas placas homogêneas, uma circular e outra triangular, cujas massas são iguais.

Calcule, em centímetros, o valor da soma das coordenadas obtidas e despreze a parte fracionária de seu resultado, caso exista.
03- (CESESP) Num circo, um equilibrista deseja levantar, apoiada em uma vareta, uma bandeja circular contendo um prato, um copo e uma garrafa cujas massas valem respectivamente 0,50kg, 0,10kg e 1,0kg. Escolhendo-se um sistema de eixos com origem no centro de gravidade da bandeja, as posições do prato, do copo e da garrafa são dadas respectivamente pelos pontos A, B e C da figura. Se a massa da bandeja for igual a 400g, em que posição (x, y) sob ela deve o equilibrista apoiar a vareta?

![]()
04- (UNESP-SP) Duas esferas homogêneas, de raios R1 e R2 e massas m1 e m2, foram fixadas uma à outra de modo a formar um sistema rígido, indicado na figura a seguir.
Sendo R1=2R2 e m1=m2/2, o centro do sistema assim constituído encontra-se:

a) no centro da esfera maior.
b) no centro da esfera menor.
c) no ponto de fixação das esferas.
d) a meia distância entre o centro O1 e o ponto
e) a meia distância entre o centro O2e o ponto de fixação.
05- UFC-CE) Cada um dos quadrados mostrados na figura a seguir tem lado b e massa uniformemente distribuída.
Determine as coordenadas (x , y) do centro de massa do sistema formado pelos quadrados.

06- UFPE-PE) A figura mostra uma estrutura vertical que consiste de oito blocos cúbicos idênticos, com densidade de massa uniforme. Os pontos A, B, C, D, E e F, são localizados nos centros de cinco cubos. Podemos afirmar que o centro de massa da estrutura está localizado ao longo do segmento de reta:

![]()
07- (ITA – SP) É dado um pedaço de cartolina com a forma de um sapinho, cujo centro de gravidade situa-se no seu próprio corpo. A seguir, com o auxilio de massa de modelagem, fixamos uma moeda de 10 centavos em cada uma das
patas dianteiras do sapinho. Apoiando-se o nariz do sapinho na extremidade de um lápis, ele permanece em equilíbrio.

Nessas condições, pode-se afirmar que o sapinho com as moedas permanece em equilíbrio estável porque o centro de gravidade do sistema:
a) Continua no corpo do sapinho.
b) Situa-se no ponto médio entre seus olhos.
c) Situa-se no nariz do sapinho.
d) Situa-se abaixo do ponto de apoio.
e) Situa-se no ponto médio entre as patas traseiras
08- UNESP-SP) Justifique por que uma pessoa, sentada conforme a figura, mantendo o tronco e

tíbias na vertical e os pés no piso, não consegue se levantar por esforço próprio. Se julgar necessário, faça um esquema para auxiliar sua explicação.
09- (ITA-SP) Três blocos cúbicos, idênticos de aresta a, estão empilhados conforme mostra a figura.

Qual é a máxima distância x para que ainda se tenha equilíbrio?
10- (ITA-SP) Considere um bloco de base d a altura h em repouso sobre um plano inclinado de ângulo α. Suponha que o coeficiente de atrito estático seja suficientemente para que o bloco não deslize pelo plano.

O valor máximo da altura h do bloco para que a base d permaneça em contato com o plano é:
a) d/α
b) d/sen α
c) d/sen2 α
d) d.cotgα
e) d.cotg α/sen α
11- (UNESP-SP) Num passarinho de madeira cujo centro de gravidade situa-se no seu próprio

corpo, fixamos um arame com duas bolas de madeira (figura acima). Apoiando-se a base do sapinho num suporte de madeira, ele permanece em equilíbrio estável, porque o centro de gravidade do sistema (passarinho e fio com bolas) situa-se:
a) no pescoço do passarinho, por onde passa o fio
b) na barriga do passarinho
c) no bico do passarinho
d) entre os olhos do passarinho
e) abaixo do ponto de apoio do passarinho, no suporte.
12- (Unicamp-SP) Um cigarro sem filtro, de 80 mm, foi aceso e apoiado num cinzeiro, como mostra a

figura. Durante quanto tempo o cigarro ficará sobre o cinzeiro? Considere que a queima se dá à razão de 5 mm por minuto e que a cinza sempre se desprende do cigarro.
13- (CESGRANRIO-RJ) Três hastes homogêneas e idênticas podem ser ligadas conforme mostram as figuras I, II e III. Em cada caso, elas formam um sistema, rígido e plano, capaz de girar livremente, na vertical, em torno de um eixo horizontal que, passa pelo ponto de união das barras. Qual das opções a seguir caracteriza corretamente o tipo de equilíbrio observado em cada uma das situações ilustradas? (Em cada figura, a linha tracejada, dá ma direção da vertical).

14- (UFB) Três placas metálicas com centro de gravidade CG indicado nas figuras podem girar livremente em torno dos pontos P, Q e R, nas figuras I, II e III, respectivamente.

Classifique o tipo de equilíbrio em cada caso.
15- (FCC-BA) O coeficiente de atrito estático entre um bloco homogêneo e um plano inclinado vale 0,80. O bloco é colocado em repouso sobre o plano, cuja inclinação vai sendo aumentada a partir de 10o com a horizontal.

A inclinação máxima do plano, sem que o bloco deslize ou tombe, é tal que a razão h/L vale:
![]()
16- (FUVEST-SP) Duas barras isolantes, A e B, iguais, colocadas sobre uma mesa, têm em suas extremidades, esferas com cargas elétricas de módulos iguais e sinais opostos.

A
barra A é fixa, mas a barra B pode girar livremente em torno de seu
centro O, que permanece fixo. Nas situações I e II, a barra B foi
colocada em equilíbrio, em posições opostas. Para cada uma dessas
duas situações, o equilíbrio da barra B pode ser considerado como
sendo, respectivamente,
SITUAÇÕES DE EQUILÍBRIO
(após
o sistema ser levemente deslocado de sua posição inicial)
Estável
= tende a retornar ao equilíbrio inicial
Instável = tende a
afastar-se do equilíbrio inicial
Indiferente = permanece em
equilíbrio na nova posição
a) indiferente e instável.
b) instável e instável.
c) estável e indiferente.
d) estável e estável.
e) estável e instável
17- (UFPR-PR) Quatro blocos homogêneos e idênticos de massa m, comprimento L = 20 cm e espessura E = 8 cm estão empilhados conforme mostra a figura a seguir. Considere que o eixo y coincide com a parede localizada à esquerda dos blocos,

que o eixo x coincide com a superfície horizontal sobre a qual os blocos se encontram e que a intersecção desses eixos define a origem O. Com base nos dados da figura e do enunciado, calcule as coordenadas X e Y da posição do centro de massa do conjunto de blocos.
18- (PUC-RJ-012)

Um bloco de massa M = 1,0 kg está preso a uma polia de raio R = 0,2 m através de um fio inextensível e sem massa como mostra a figura. Sabendo que o bloco desce com uma aceleração de 3,0 m/s2, calcule o torque em N. m realizado pelo fio na extremidade da polia.

Dado: g = 10,0 m/s2
![]()
19- (UERJ-RJ)

Considere uma balança de dois pratos, na qual são pesados dois recipientes idênticos, A e B.

Os dois recipientes contêm água até a borda. Em B, no entanto, há um pedaço de madeira flutuando na água.
Nessa situação, indique se a balança permanece ou não em equilíbrio, justificando sua resposta.
20- (FUVEST-SP)

O gráfico abaixo representa a força F exercida pela musculatura eretora sobre a coluna vertebral, ao se levantar um peso, em função

do ângulo φ, entre a direção da coluna e a horizontal. Ao se levantar pesos com postura incorreta, essa força pode se tornar muito grande, causando dores lombares e problemas na coluna.
Com base nas informações dadas e no gráfico acima, foram feitas as seguintes afirmações:
I. Quanto menor o valor de φ, maior o peso que se consegue levantar.
II. Para evitar problemas na coluna, um halterofilista deve procurar levantar pesos adotando postura corporal cujo ângulo φ seja grande.
III. Quanto maior o valor de φ, menor a tensão na musculatura eretora ao se levantar um peso.
Está correto apenas o que se afirma em
![]()
Resolução comentada das questões de vestibulares sobre
Estática de um corpo extenso –Centro de Massa – Tipos de Equilíbrio
01- Localizando o centro de massa de cada bloco e colocando a origem do referencial no centro de massa do bloco 1:
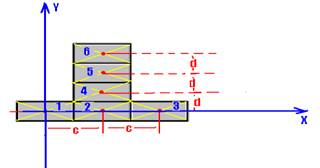
XCM=(mX1 + mX2 + mX3 + mX4 + mX5 + mX6)/6m = (m.0 + m.c + m.2c + m.c + m.c + m.c)/6m --- XCM=6mc/6m -XCM=c --- YCM=(m.0 + m.0 + m.0 + m.d + m.2d + m.3d)/6m --- YCM=6md/6m --- YCM=d --- localizando CM.
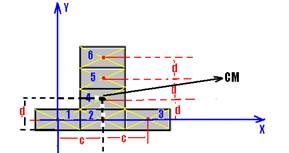
R- D
02- Localizando o centro de massa de cada placa e suas respectivas coordenadas --- circular –
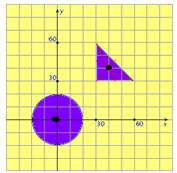
C(0,0) --- triangular T (40,40) --- XCG=(mXC + mXT)/(m + m)=(m.0 + m.40)/2m --- XCG=20cm --- YCG=(mYC + mYT)/2m=(m.40 + m.40)/2m --- YCM=20cm --- XCM + YCM=20 + 20 = 40 cm
03- bandeja – b mb=0,4kg --- prato -A - – mA=0,5kg --- copo – B – mB=0,1kg --- garrafa – C – mC=1,0kg ---XCG=(mb.Xb + mA.XA + mBXB + mCXC)/(mb + mA + mB + mC)= (0,4..0 + 0,5.(-2). + 0,1.(-10) + 1.(+4+)/(0,4 + 0,5 + 0,1 + 1,0)=2/2 --- XCG=1cm --- YCG=(mb.Yb + mA.YA + mBYB + mCYC)/(mb + mA + mB + mC)=(0,4.0 + 0,5.(-5) + 0,1.5 + 1.4)/2 --- YCM=2/2 --- YCM=1cm --- R- E
04- Colocando a origem do sistema de coordenadas no centro de massa da esfera 1 em O1.
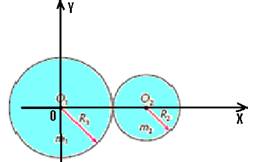
R1=2R2 --- m2=2m1 --- XCM=(m1X1 + m2X2)/(m1 + m2)=(m1.0 + 2m1.(R1 + 2R1)/3m1 --- XCM=6m1R1/3m1 --- XCM=2R1 --- YCM=(m1Y1 + m2Y2)/(m1 + m2)=(m1.0 + m2.0)/3m1 --- YCM=0 --- CM(2R1,0) --- R- C
05- Colocando o centro de massa em cada bloco e os valores de suas respectivas abscissas e
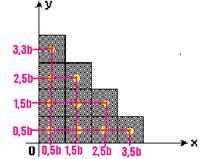
ordenadas --- XCM=(4m.0,5b + 3m.1,5b + 2m.2,5b + m.3,5b)/10m=15mb/10m --- XCM=1,5b --- YCM=(4m.0,5b + 3m.1,5b + 2m.2,5b + m.3,5b)/10m=15mb/10m --- YCM=1,5b --- CM (1,5b;1,5b)
06- O centro de massa dos três blocos da esquerda está em B e o dos quatro blocos da direita está em E. Assim, o centro de massa do sistema está sobre a reta que une B e E --- R- B
07-

R- D
08- Ao se levantar ela perde contato com a cadeira, pois a reta vertical que passa pelo seu centro de
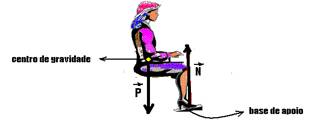
gravidade (onde está o peso) não coincide com a base de apoio (onde está a normal) que estão em seus pés. Assim, ela retorna à cadeira, sem levantar.
09- Colocando os centros de gravidade em cada bloco e analisando os blocos A e B (figura abaixo)
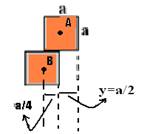
--- para que o bloco A esteja na iminência de cair, y deve valer y=a/2 --- para que A e B estejam na
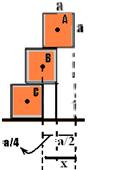
iminência de cair, o bloco C deve ser colocado como na figura acima --- x=a/4 + a/2 --- x=(2a + 4a)/8 --- x=3a/4
10- Para que ele não tombe, a reta vertical que passa pelo centro de gravidade deve passar pela
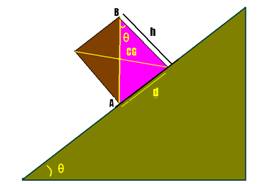
extremidade A da base de apoio --- no triângulo hachurado --- tgθ=d/h --- h=d/tgθ --- h=d.cotgθ --- R- D
11- R- E
12- Como o centro de gravidade CG está sempre no ponto médio e à medida que o cigarro vai queimando ele se desloca para a esquerda, quando o cigarro estiver na iminência de cair, você terá a

situação da figura abaixo, onde você deve observar que o cigarro queimou d=80 – 50=30mm com velocidade de 5mm/min --- V=d/t --- 5=30/t --- t=6 min
13- Corpo apoiado --- I - CG está na junção – indiferente --- II – CG está acima da junção – instável --- III – CG está abaixo da junção – estável --- R- E
14- Corpo suspenso --- I – CG abaixo do ponto de suspensão – estável --- II – CG acima do ponto de suspensão – instável --- III – CG coincide com o ponto de suspensão - indiferente
15- Condição para que o bloco não deslize (iminência de escorregar)
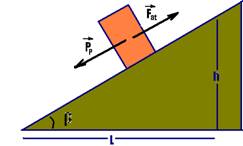
--- PP=Fat --- psenβ=μPcosβ --- μ=tgβ=h/L (I)
Condição para que o bloco não tombe --- a reta vertical que passa pelo centro de gravidade deve passar pela extremidade A da base.
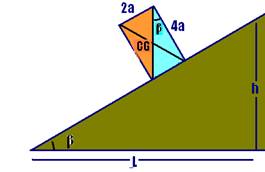
tgβ=2a/4ª --- tgβ=1/2 (II) --- igualando I com II --- h/L=1/2 --- R- d
16- Situação I --- cargas de mesmo sinal se repelem --- se você girar levemente a carga negativa de B para baixo a força de repulsão entre ela e a negativa de A diminui, mas a de repulsão entre as positivas de A e de B aumenta, fazendo com que a barra retorne à situação inicial – equilíbrio estável --- situação II --- cargas de sinais opostos se atraem --- se você girar levemente a negativa de B para cima a força de atração entre ela e a negativa de A aumenta,enquanto que a força de atração entre a positiva de A e a negativa de B diminui, fazendo com que a barra B continue girando --- equilíbrio instável --- R- E
17-A figura mostra as abscissas x1; x2; x3 e x4 e as ordenadas y1; y2; y3 e y4 dos quatro corpos --- abscissa X do centro de massa -
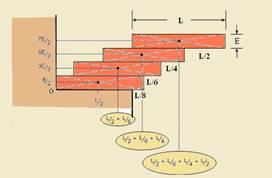
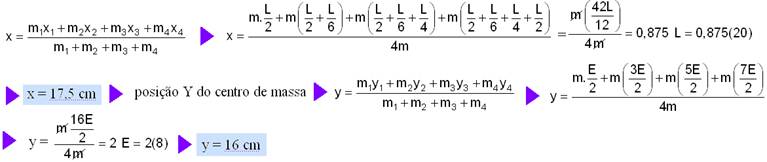
18- O torque a(momento) realizado pelo fio corresponde ao momento da força de tração de
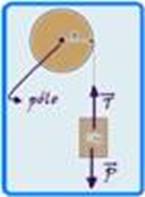
intensidade --- FR= P – T=m.a ---P – T=m.a --- m.g – T = m.a --- 1.10 – T = 1.3 --- T=7N --- o torque da força de tração no fio é fornecido por --- M= F.d --- M =T.R=7.0,2 --- M=1,4N.m --- R- B
19- O peso dos dois recipientes é o mesmo --- se os dois tivessem apenas água até a borda a balança estaria em equilíbrio --- mas, com a madeira flutuando no recipiente B e com água até a borda, a balança continuará em equilíbrio, pois quando você colocou a madeira ela deslocou um volume de líquido que possui o mesmo peso que a parte imersa da madeira “Princípio de Arquimedes”.
20- I. Falsa --- observe pelo gráfico fornecido que a medida que o ângulo φ vai diminuindo a força exercida pelos músculos sobre a coluna vai aumentando e a coluna fica muito solicitada diminuindo a possibilidade de levantar pesos maiores.
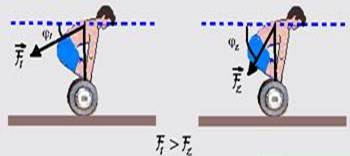
II. Correta --- a medida que o ângulo φ aumenta a força exercida pelos músculos sobre a coluna diminui e a coluna fica menos solicitada o que possibilita ao atleta elevar pesos maiores.
III. Correta --- a medida que o ângulo φ aumenta a força exercida pelos músculos sobre a coluna diminui e a coluna fica menos solicitada, diminuindo a tensão na musculatura eretora.
R- E
|
|