ENEM8

Aplicações das leis de Newton com atrito

Exercícios com características de ENEM

01-(FUVEST-SP) 

O gráfico a seguir descreve o deslocamento vertical y, para baixo, de um surfista aéreo de massa igual a 75 kg, em função do tempo t.

 A origem y = 0, em t = 0, é tomada na altura do salto. Nesse movimento, a força R de resistência do ar é proporcional ao quadrado da velocidade v do surfista (R = kv²), onde k é uma constante que depende principalmente da densidade do ar e da geometria do surfista).

A velocidade inicial do surfista é nula; cresce com o tempo, por aproximadamente 10 s, e tende para uma velocidade constante denominada velocidade limite (V_L).
Os valores da velocidade limite V_L e da constante k são, no SI, respectivamente:

a) 50 m/s e 0,3 N.s²/m²     

b) 60 m/s e 3 N.s²/m²     

c) 5 m/s e 0,6 N.s²/m²     

d) 40 m/s e 0,5 N.s²/m²     

e) 50 m/s e 0,6 N.s²/m²

02-(UEG-GO) 

Entre os poucos animais que desenvolveram o “pára-quedismo” está o sapo voador de Bornéu – Rhacophorus dulitensis, apresentado na figura a seguir.

Na ilustração,  e   são, respectivamente, a força de resistência do ar e a força peso.  

Considerando que esse animal tenha se atirado do alto de uma árvore em direção ao solo, o seu pára-quedas será utilizado e, durante sua queda,

a) as suas membranas interdigitais nas patas favorecem o aumento da força de resistência do ar, haja vista que elas aumentam a área de contato com o ar. 

b) a resultante das forças que atuam sobre ele tenderá a se tornar nula, levando-o, necessariamente, ao repouso no ar. 

c) a sua velocidade tenderá a um valor limite, chamada de velocidade terminal, independentemente da resistência do ar. 

d) a sua aceleração será nula em todo o percurso, independentemente da resistência do ar. 

e) durante sua queda, a força de resistência do ar (vertical e para cima) vai aumentando até superar a força peso (vertical e para baixo), após então, ele começa a subir.

03-(UNESP-SP) 

Um bloco de massa 5,0kg está apoiado sobre um plano inclinado de 30° em relação a um plano horizontal.

Se uma força constante, de intensidade F, paralela ao plano inclinado e dirigida para cima, é aplicada ao bloco, este adquire uma aceleração para baixo e sua velocidade escalar é dada por v = 2,0t (SI), (fig.1).

Se uma força constante, de mesma intensidade F, paralela ao plano inclinado e dirigida para baixo for aplicada ao bloco, este adquire uma aceleração para baixo e sua velocidade escalar é dada por v' = 3,0t (SI), (fig. 2).

Os valores de F e do coeficiente de atrito de deslizamento são, respectivamente: (adote g=10m/s²)

04-(UFJF-MG) 

Um caminhão é carregado com duas caixas  de madeira, de massas iguais a 500kg, conforme mostra a figura.

O caminhão é então posto em movimento numa estrada reta e plana, acelerando até adquirir uma velocidade de 108 km/h e depois é freado até parar, conforme mostra o gráfico. (g=10m/s²).

O coeficiente de atrito estático entre as caixas e a carroceria do caminhão é m=0,1. Qual das figuras abaixo melhor representa a disposição das caixas sobre a carroceria no final do movimento?

05-(UFRRJ-RJ)

Dois carros de corrida são projetados de forma a aumentar o atrito entre os pneus e a pista. Os

projetos são idênticos, exceto que num deles os pneus são mais largos e no outro há um aerofólio. Nessas condições podemos dizer que

a) em ambos os projetos, o atrito será aumentado em relação ao projeto original.

b) em ambos os projetos, o atrito será diminuído em relação ao projeto original.

c) o atrito será maior no carro com aerofólio.

d) o atrito será maior no carro com pneus mais largos.

e) nenhum dos projetos alterará o atrito.

06-(UFAL-AL) 

O bloco da figura possui peso P e se encontra na iminência de movimento sob a ação de uma força de módulo constante F e direção perpendicular à parede vertical. Se o coeficiente de atrito estático entre a parede e o bloco é menor que 1, assinale a relação correta entre P e F.

a) 0 < P < F               b) F < P < 2F               c) 0 < F < P/2               d) P/2 < F < P              e) 0 < F < P

07-(UERJ-RJ) 

Uma pessoa de massa igual a 80 kg encontra-se em repouso, em pé sobre o solo, pressionando perpendicularmente uma parede com uma força de magnitude igual a 120 N, como mostra a ilustração a seguir.

A melhor representação gráfica para as distintas forças externas que atuam sobre a pessoa está indicada em:

 08-(UERJ-RJ) 

Uma caixa está sendo puxada por um trabalhador, conforme mostra a figura.  Para diminuir a força

de atrito entre a caixa e o chão, aplica-se, no ponto X, uma força f. O segmento orientado que pode representar esta força está indicado na alternativa:

09-(UFSCAR-SP) 

Um menino deseja deslocar um bloco de madeira sobre o chão horizontal puxando uma corda amarrada ao bloco.

 Sabendo-se que o coeficiente de atrito estático entre a madeira e o chão vale 0,4, que a massa do bloco é 42 kg e que a aceleração da gravidade é igual a 10 m/s², e considerando √3 = 1,7, qual a

menor intensidade da força que o menino deve puxar a corda para deslocar o bloco, se a direção da corda forma com o chão um ângulo de 60°?

10-(UFF-RJ) 

Um pano de prato retangular, com 60cm de comprimento e constituição homogênea, está em repouso sobre uma mesa, parte sobre sua superfície, horizontal e fina, e parte pendente, como mostra a figura.

Sabendo-se que o coeficiente de atrito estático entre a superfície da mesa  e o pano é igual a 0,5 e que o pano está na iminência de deslizar, pode-se afirmar que o comprimento L da parte sobre a mesa é:

11-(UERJ-RJ) 

Considere um carro de tração dianteira que acelera no sentido indicado na figura em destaque. O motor é capaz de impor às rodas

de tração um determinado sentido de rotação. Só há movimento quando há atrito estático, pois, na sua ausência, as rodas de tração patinam sobre o solo, como acontece em um terreno enlameado. O diagrama que representa corretamente as forças de atrito estático que o solo exerce sobre as rodas é:

12-(UFG-GO) 

A força muscular origina-se nas fibras musculares, conforme figura (a), como resultado das interações entre certas proteínas que experimentam mudanças de configuração e proporcionam a contração rápida e voluntária do músculo.

A força máxima que um músculo pode exercer depende da sua área da seção reta e vale cerca de 30 N/cm². Considere um operário que movimenta com uma velocidade constante uma caixa de 120 kg sobre uma superfície rugosa, de coeficiente de atrito 0,8, usando os dois braços, conforme ilustrado na figura (b).

Dessa forma, a menor seção reta dos músculos de um dos braços do operário, em cm², e uma das proteínas responsáveis pela contração das miofibrilas são:

Dados: g =10,0 m/s²

a) 16 e actina.                      

b) 16 e mielina.                       

c) 20 e miosina.                     

d) 32 e actina.                    

e) 32 e miosina.  

13-(UNICAMP-SP)

Acidentes de trânsito causam milhares de mortes todos os anos nas estradas do país.

Pneus desgastados (“carecas”), freios em péssimas condições e excesso de velocidade são fatores que contribuem para elevar o número de acidentes de trânsito.

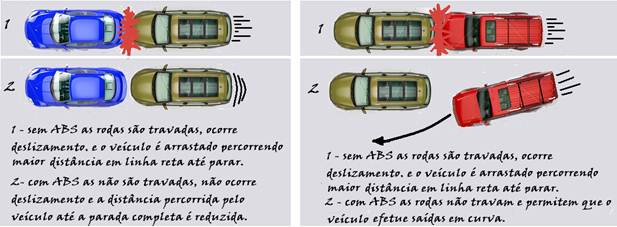
O sistema de freios ABS (do alemão “Antiblockier-Bremssystem”) impede o travamento das rodas do veículo, de forma que elas

não deslizem no chão, o que leva a um menor desgaste do pneu.

Não havendo deslizamento, a distância percorrida pelo veículo até a parada completa é reduzida, pois a força de atrito aplicada pelo chão nas rodas é estática, e seu valor máximo é sempre maior que a força de atrito cinético. O coeficiente de atrito estático entre os pneus e a pista é μ_e= 0,80 e o cinético vale μ_c = 0,60.

Sendo g = 10 m/s² e a massa do carro m = 1200 kg, o módulo da força de atrito estático máxima e a da força de atrito cinético são, respectivamente, iguais a

a) 1200 N e 12000 N.                    

b) 12000 N e 120 N.                      

c) 20000 N e 15000 N.               

d) 9600 N e 7200 N.  

14-(UFABC-SP) 

Quem diria que uma brincadeira de criança já valeu medalha de ouro. Esse esporte esteve presente em todas as Olimpíadas disputadas entre 1900 e 1920, quando ainda era considerado uma modalidade de atletismo. Em 1908, em Londres, o resultado foi um pódio caseiro e fardado. A polícia de Londres ficou em primeiro, seguida por policiais de Liverpool e da polícia metropolitana, respectivamente. (Revista Galileu, Ed. N^o204, julho(2008)

Considere duas equipes A e B, formadas por três garotas cada uma, numa disputa de cabo-de-guerra sobre uma superfície plana e horizontal, como mostra a figura.

A alternativa que mostra corretamente a força de tração aplicada pela corda nas mãos e a força de atrito aplicada pelo solo nos pés, respectivamente, de uma integrante da equipe B, durante a disputa, é

Resolução Comentada

Aplicações das leis de Newton com atrito

01- A velocidade do surfista se torna constante a partir de t=10s quando y≈330m (do enunciado e do gráfico)  ---  a partir daí, ele percorre ∆S≈535- 330=205m, num intervalo de tempo ∆t=14 – 10=4s  ---  nesse intervalo de tempo, sua velocidade é constante e

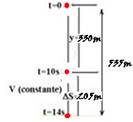
vale  ---  V= ∆S/∆t =205/4  ---  V ≈ 51,25 m/s  (velocidade com que ele chega ao solo, que é a velocidade limite)  ---  do enunciado a força de resistência do ar é fornecida pela expressão  ---  R=K.V²  ---  quando ele atinge a velocidade limite, ele deixa de acelerar e, nesse instante, sua velocidade se torna constante sendo que a condição para que isso ocorra é que as intensidades da força de resistência do ar (vertical e para cima) se iguale à intensidade da força peso (vertical e para baixo)  ---R=P=m.g=75.10=750N  ---  750=K.(50)²  ---  K=0,3Ns²/m²  ---  R- A

02- As membranas interdigitais das patas funcionam como pára-quedas aumentando a força de resistência do ar (devido ao aumento da área de contato com o ar)  ---   chega um momento em que a intensidade da força de resistência do ar  fica igual à intensidade da força peso  e ele entra em equilíbrio dinâmico (força resultante nula ) e sua velocidade vertical, nesse instante, é chamada velocidade terminal ou velocidade limite  ---  essa velocidade permanece constante até ele chegar ao solo  ---  R- A

03- Nas figuras abaixo P_p é a intensidade da parcela do peso que é responsável pela tendência de descida do bloco e F_at é a intensidade da força de atrito  ---  como P_p=Psen30^o e F_at=μPcos30^o eles são os mesmos nas duas situações (fig.1 e fig. 2). 

Figura 1  ---  P_p=mgsen30^o=5.10.0,5  ---  P_p=25N  ---  comparando V=V_o + a.t com V=2,0.t, você conclui que V_o=0 e a=2m/s²

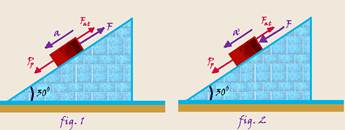
Aplicando a lei fundamental da dinâmica com a aceleração para baixo  ---  F_R=m.a  ---  (P_p –F – F_at)=ma  ---  25 – F – F_at=5.2  ---  F + F_at=15 (I)  ---  figura 2  ---  P_p=25N  ---  comparando V=V_o + a’t com V=3,0.t você conclui que V_o=0 e a’=3m/s². 

Aplicando a segunda lei da dinâmica com a aceleração para baixo  ---  F_R=ma’  ---  (25 + F – F_at)=5.3  ---  F = F_at – 10 (II)  ---  substituindo (II) em (I)  ---  F_at – 10 + F_at =15  ---  2F_at=25  ---  F_at=12,5N  ---  F + F_at=15  ---  F + 12,5=15  ---  F= 2,5N  ---  F_at=μmgcos30^o  ---  12,5=.μ5.10.√3/2  ---  μ=12,5/25√3  ---  μ=1/2√3  ---  μ≈0,29  ---  R- C

04- A intensidade da força de atrito estático entre as caixa e a carroceria vale F_ate=μN  ---  F_ate=μP  ---  F_ate=μmg  ---  F_ate=0,1.500.10  ---  F_ate=500N (acima desse valor as caixas se movem).

  No movimento acelerado  ---  V=Vo + a.t  ---  30=0 + a.20  ---  a=1,5m/s²   ---  F_R=m.a  ---  F_R=500.1,5  ---  F_R=750N ( como F_R>F_ate, as caixas se movem para trás e ficam juntas na parte traseira do caminhão).

No movimento uniforme, elas estão em equilíbrio dinâmico e F_R=0. Assim, elas não se movem e ficam juntas na parte traseira.

No movimento retardado  ---  V=Vo + a.t  ---  0=30 – a.40  ---  a=3/4m/s²  ---  F_R=m.a  ---  F_R=500.3/4  ---  F_R=375N (menor que 500N, portanto elas não se movem e ficam na parte traseira do caminhão)  --- R- A

05- A força de atrito devido aos pneus independe da largura (área de contato dos mesmos com o solo)  ---  o aerofólio, que funciona como uma asa de avião invertida, comprime o carro contra o solo aumentando a intensidade da força normal  que o carro troca com o solo, aumentando assim a intensidade da força de atrito, pois F_at=μN  ---  R- C

Observação: Além do aerofólio, o formato do carro também influi na compressão do carro contra o solo (veja figura), aumentando

ainda mais a força de atrito fazendo com que o carro efetue curvas com velocidades maiores.

06- No equilíbrio estático o corpo está na iminência de movimento  ---  a força de atrito estático é

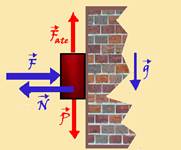
dada por F_ate=μ_eN, e se equilibra com o peso P, ou seja, F_ate=P  ---  na situação do exercício, a força normal N é tal que N = F  ---  assim, μ_eN = P  ---  μ_eF=P  ---  μ_e = P/F  ---  o fato de μ_e < 1 implica que  P/F<1  ---  0 < P < F  ---  R- A

07- Colocando todas as forças que se relacionam com a pessoa, a parede e o solo.

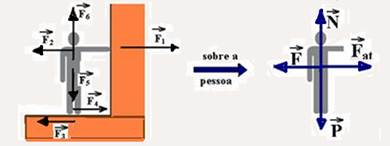
 F₁ e F₂  ---  forças trocadas entre a pessoa e a parede de intensidade 120N  ---   F₃ e F₄  ---   forças de atrito trocadas entre os pés da pessoa e o solo  ---  F₅  ---  peso da pessoa trocada com o centro da Terra  ---  F₆, força normal que a pessoa troca com o solo. 

Como a pessoa está em repouso, a força resultante sobre ela é nula e as forças verticais e horizontais se anulam  ---  R- D

08- Como F_at=μN, e como μ é constante, a força de atrito é diretamente proporcional à intensidade da força normal (trocada entre a caixa e o solo)  ---  quanto menor N, menor será as força que a caixa troca com o solo, tornando-a mais “leve” e consequentemente menor a força de atrito --- das alternativas, a única força capaz de diminuir a  força de compressão N da caixa com o chão é a C  --- R- C

09- Colocando as forças e decompondo em  e 

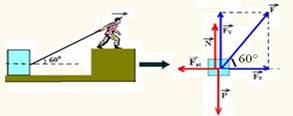
 P=mg=42.10  ---  P=420N  ---  F_X=Fcos60^o=F.0,5  ---  F_X=0,5F  ---  F_Y=Fsen60^o=F.√3/2  ---  F_Y=0,85F.

 No equilíbrio estático temos, na horizontal F_at=F_X e na vertical, P=N + F_Y  ---  N=P - F_Y  ---  F_at=F_X  ---  μN=0,5F  ---  μ(P - F_Y)=0,5F  ---  0,4(420 - 0,85F)=0,5F  ---  168 - 0,34F=0,5F  ---  0,84F=168  ---  F=200N (qualquer valor acima de 200N desloca o bloco)  ---   R- C

10- Vamos chamar de L’, comprimento total do pano e de L’ – L o comprimento da parte pendente  ---  como o pano é de constituição homogênea, sua densidade é a mesma.

d=m_t/V_t  ---  d (densidade) – m_t (massa total) – V_t (volume total)  ---  m_t=d.V_t  ---  m_t=d.(A.L’), sendo A (área se seção transversal, espessura do pano) e L’ (comprimento total do pano)  ---  massa apoiada 

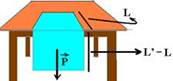
– m_a=d.A.L e massa pendente – m_p=d.A.(L’ – L)  --- 

- peso da parte pendente  ---  P=m_pg (m_p, massa da parte pendente)  ---  a força de atrito entre o pano de comprimento L e a mesa está segurando o peso da parte pendente de comprimento (L’ – L), ou seja, F_at=P  ---  μm_ag= m_pg  ---  μ.d.A.L.g=d.A.(L’ – L).g  ---   0,5.L=(60 – L)  ---  1,5L=60  ---  L=40cm  ---   R- A

11- A força de atrito pode servir como força motora no deslocamento de um veículo  ---  observe a

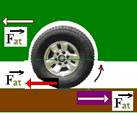
figura  ---  se você quiser acelerar o carro para a esquerda, o motor do mesmo deve fazer o eixo e consequentemente a roda girar no sentido anti-horário  ---  o pneu empurra o solo para trás () e o solo reage sobre o pneu e consequentemente sobre o carro (), movendo-o para a esquerda  ---

em rodas com tração a força de atrito sobre o móvel é a favor do movimento e, em rodas sem tração, é contrária ao movimento  -- R- B

12-  Dados: m = 120 kg; g = 10 m/s²; m = 0,8; F/A= 30 N/cm²; N = P = 1.200 N  ---  para colocar a caixa em movimento o operador tem que vencer a força de atrito  ---  F_operário = F_at = μN=0,8 (1.200) = 960 N  ---  como ele está usando os dois braços, cada braço aplica então  ---   F = F_operário/2=480 N  ---  F/A=30  ---  480/A=30  ---  A=16cm²  ---  uma das proteínas responsáveis pela contração das miofibrilas é a actina  ---  R- A

13- Dados  ---  g = 10 m/s²  ---   μ_e = 0,60  ---   μ_c = 0,80  ---   m = 1.200 kg  ---   força que a pista exerce no veículo tem duas componentes  ---  normal   e  atrito    ---  supondo que a frenagem ocorra em pista horizontal, a componente normal  da força que a pista aplica no veículo tem intensidade igual à do seu peso   ---  N = P = m g = 12.000 N  ---   componente de atrito estático máxima  ---   F_atmax= μ_eN = 0,8 (12.000)  ---    F_atmax = 9.600 N  ---  a componente de atrito cinético: F_atc  = μ_c N = 0,6. (12.000)  ---   F_atc = 7.200 N  ---  R- D       

Observações: As figuras abaixo ilustram algumas das utilidades dos freios ABS

14- A força de tração que a corda aplica nas mãos da garota é a força que está puxando-as para a esquerda  ---  a força de atrito é paralela ao apoio horizontal e para a direita, pois é sempre contrário ao movimento ou à sua tendência  ---  R- E