
ENEM4
Movimento Circular (MC)
01-(ENEM-MEC)

Com relação ao funcionamento de uma bicicleta de marchas, onde cada marcha é uma combinação

de
uma das coroas dianteiras com uma das coroas traseiras, são
formuladas as seguintes afirmativas:
I. numa bicicleta que tenha
duas coroas dianteiras e cinco traseiras, temos um total de dez
marchas possíveis onde cada marcha representa a associação de uma
das coroas dianteiras com uma das traseiras.
II. em alta
velocidade, convém acionar a coroa dianteira de maior raio com a
coroa traseira de maior raio também.
III. em uma subida íngreme,
convém acionar a coroa dianteira de menor raio e a coroa traseira de
maior raio.
Entre as afirmações anteriores, estão corretas:
a)
I e III apenas.
b) I, II e III apenas.
c) I e II apenas.
d) II apenas.
e) III apenas.
02-(ENEM-MEC)

Quando
se dá uma pedalada na bicicleta da figura (isto é, quando
a coroa acionada pelos pedais dá

uma volta completa), qual é a distância aproximada percorrida pela bicicleta, sabendo-se que o comprimento de um círculo de raio R é igual a 2πR, onde π ≈ 3?
![]()
03-(ENEM-MEC)

As bicicletas possuem uma corrente que liga uma coroa dentada dianteira, movimentada pelos pedais, a uma coroa localizada no eixo da roda traseira, como mostra a figura.

O
número de voltas dadas pela roda traseira a cada pedalada depende do
tamanho relativo destas coroas.
Em que opção a seguir a roda
traseira dá o maior número de voltas por pedalada?
04-(ENEM-MEC)


05-(ENEM-MEC)

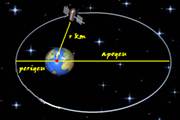
Um satélite de telecomunicações, t minutos após ter atingido sua órbita, está a r quilômetros de distância do centro da Terra.

Quando r assume seus valores máximo e mínimo, diz-se que o satélite atingiu o apogeu e o perigeu, respectivamente. Suponha que, para esse satélite, o valor de r em função de t seja dado por

Um cientista monitora o movimento desse satélite para controlar o seu afastamento do centro da Terra. Para isso, ele precisa calcular a soma dos valores de r, no apogeu e no perigeu, representada por S.
O cientista deveria concluir que, periodicamente, S atinge o valor de
a) 12765 km.
b) 12000 km.
c) 11730 km.
d) 10965 km.
e) 5865 km.
Exercícios com características de ENEM
06-(UNESP-SP)

Quem está na Terra vê sempre a mesma face da lua. Isto ocorre porque:

a) a Lua não efetua rotação e nem translação.
b)
a Lua não efetua rotação, apenas translação.
c) os períodos
de rotação e translação da Lua são iguais.
d)
as oportunidades para se observar a face oculta coincidem com o
período diurno da Terra.
e) enquanto a Lua dá uma volta em torno
da Terra, esta dá uma volta em torno do seu eixo.
07-(PUCCAMP-SP)

Em uma bicicleta que se movimenta com velocidade constante, considere um ponto A na periferia da catraca e um ponto B na periferia da roda.

Analise as afirmações:
I. A velocidade escalar de A é igual à de B.
II. A velocidade angular de A é igual à de B.
III. O período de A é igual ao de B.
Está correto SOMENTE o que se afirma em:
![]()
08-(UNIFESP-SP)

Pai e filho passeiam de bicicleta e andam lado a lado com a mesma velocidade.

Sabe-se que o diâmetro das rodas da bicicleta do pai é o dobro do diâmetro das rodas da bicicleta do filho. Pode-se afirmar que as rodas da bicicleta do pai giram com
a) a metade da frequência e da velocidade angular com que giram as rodas da bicicleta do filho.
b) a mesma frequência e velocidade angular com que giram as rodas da bicicleta do filho.
c) o dobro da frequência e da velocidade angular com que giram as rodas da bicicleta do filho.
d) a mesma frequência das rodas da bicicleta do filho, mas com metade da velocidade angular.
e) a mesma frequência das rodas da bicicleta do filho, mas com o dobro da velocidade angular.
09-(UEJF-MG)

Um velocímetro comum de carro mede, na realidade, a velocidade angular do eixo da roda, e indica um valor que corresponde à velocidade do carro. O velocímetro para um determinado carro sai da

fábrica calibrado para uma roda de 20 polegadas de diâmetro (isso inclui o pneu). Um motorista resolve trocar as rodas do carro para 22 polegadas de diâmetro. Assim, quando o velocímetro indica 100km/h, a velocidade real do carro é:
![]()
10-(UNIFESP-SP)

Três corpos estão em repouso em relação ao solo, situados em três cidades: Macapá, localizada na linha do Equador, São Paulo, no trópico de Capricórnio, e Selekhard, na Rússia, localizada no círculo Pólar Ártico. Pode-se afirmar que esses três corpos giram

em torno do eixo da Terra descrevendo movimentos circulares uniformes, com
A) as mesmas frequência e velocidade angular, mas o corpo localizado em Macapá tem a maior velocidade tangencial.
B) as mesmas frequência e velocidade angular, mas o corpo localizado em São Paulo tem a maior velocidade tangencial.
C) as mesmas frequência e velocidade angular, mas o corpo localizado em Selekhard tem a maior velocidade tangencial.
D) as mesmas frequência, velocidade angular e velocidade tangencial, em qualquer cidade.
E) frequência, velocidade angular e velocidade tangencial diferentes entre si, em cada cidade.
11-(UFRJ-RJ)

O olho humano retém durante 1/24 de segundo as imagens que se formam na retina. Essa memória visual permitiu a invenção do cinema. A filmadora bate 24 fotografias (fotogramas) por segundo.
Uma vez revelado, o filme é projetado à razão de 24 fotogramas por segundo. Assim, o fotograma seguinte é projetado no exato instante em que o fotograma anterior está desaparecendo de nossa memória visual, o que nos dá a sensação de continuidade.

Filma-se um ventilador cujas pás estão girando no sentido horário. Este ventilador possui quatro pás simetricamente dispostas, uma das quais pintadas de cor diferente. Ao projetarmos o filme, os fotogramas aparecem na tela numa sequência que nos dá a sensação de que as pás estão girando em sentido anti- horário.

Desta forma, o número mínimo de rotações por segundo que as pás devem estar efetuando, para que isto ocorra, é de:
![]()
Resolução Comentada
Movimento Circular (MC)
01- I- Correta --- 2 coroas dianteiras x 5 coroas traseiras=10 marchas

II- Falsa --- elas estão ligadas por uma corrente cuja velocidade é a mesma que as velocidades da coroa (no pedal) e da catraca (na roda) --- quanto maior a coroa (no pedal) e menor a catraca (na roda), a corrente se move com velocidade maior fazendo a
roda efetuar mais voltas, a bicicleta anda mais depressa e você efetua mais força no pedal.
III- Correta --- quanto menor a coroa (no pedal) e maior a catraca (na roda), a corrente se move com velocidade menor fazendo a roda efetuar menos voltas, a bicicleta anda mais devagar e você efetua menos força no pedal.
R- A
02- A velocidade tangencial de qualquer ponto da periferia da engrenagem da roda é a mesma que a de qualquer ponto da periferia da engrenagem dos pedais que por sua vez ´a mesma que de qualquer ponto da corrente --- Vepedais=Veroda --- 2πRepedais.fepedais=2πReroda.feroda --- (30/2).1=(10/2).feroda --- feroda=3 voltas --- ao efetuar uma volta completa a roda de raio 80cm percorre --- ∆S’=2πR=2.3.40 --- ∆S’=240cm --- como ela efetua 3 voltas --- ∆S=3.240=720cm=7,2m --- R- C
03-
Para
que a roda traseira efetue o maior número de voltas por cada
pedalada, a diferença entre os diâmetros das coroas dianteira e
traseira tem que ser o maior possível --- R-
A
04- Nos pontos de contato entre a prancha e os pontos da periferia de cada polia, a velocidade
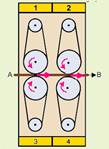
tangencial é a mesma tendo, em cada polia, o sentido em que a prancha está se movendo --- R- C
05- Lembre-se que cos(0,06t) varia entre -1 e 1 --- observe na expressão r(t)=5.865/[1 + 0,15.cos(0,06t)] que, terá valor máximo para um denominador menor e mínimo para um denominador maior --- o valor máximo de r(t) ocorre quando cós(0,6t) for mínimo, ou seja, valer -1 --- r(t)máximo=5.865/[1 + 0,15.cos(0,06t)]=5.865/[1 + 0,15.(-1)] --- r(t)máximo=5.865/(1 – 0,15)=5.865/0,85 --- r(t)máximo=6.900km (mais afastado da Terra) --- o valor mínimo de r(t) ocorre
quando cos(0,6t) for máximo,ou seja, valer 1 --- r(t)mínimo=5.865/[1 + 0,15.cos(0,06t)]=5.865/[1 + 0,15.(1)] --- r(t)mínimo=5.865/(1 + 0,15)=5.865/1,15 --- r(t)mínimo=5.100m (mais próximo da Terra) --- o enunciado afirma que ele quer calcular a soma desses valores --- S=rperigeu + rapogeu=5.100 + 6.900 --- S=12.000km --- R- B
06- O tempo em que a Lua demora para dar uma volta em torno da Terra (período de translação da Lua em torno da Terra), é o mesmo que ela demora para sofrer rotação em torno de si mesma (período de rotação da Lua) --- R- C
07- Observe a figura abaixo:
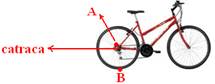
I- falsa --- o ponto B está mais afastado do centro e VB > VA
II- correta --- descrevem o mesmo ângulo no mesmo tempo
III- correta --- demoram o mesmo tempo para efetuar uma volta completa
R-E
08- As velocidades escalares das periferias das rodas das bicicletas do pai e do filho são as mesmas --- Vp=Vf --- fpRp=ffRf --- Rp=2Rf --- fp.2Rf =ffRf --- fp=ff/2 --- R- A
09- Veja na expressão W=V/R, que W é constante (o eixo do carro gira com a mesma velocidade angular) e, assim, V é diretamente proporcional a R --- como o diâmetro e consequentemente o raio teve um aumento de 10%, a velocidade também deverá ter o mesmo aumento, passando de 100km/h para 110km/h --- R- C
10- Em um corpo em rotação todos os pontos apresentam mesmo período (T), frequência (f) e
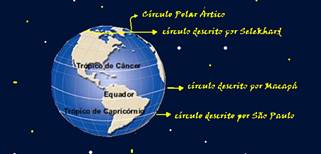
velocidade angular (ω), que são os mesmos que da Terra --- TMacapá = TSão Paulo = T Selekhard --- f Macapá = fSão Paulo = fSelekhard --- W Macapá =WSão Paulo=W Selekhard --- a velocidade escalar de um ponto é dado pela expressão v = W.r --- como a velocidade angular é a mesma para todos os pontos, a velocidade escalar (intensidade da tangencial) será maior quanto maior for o raio (r) em relação ao eixo de rotação --- VMacapá > VSão Paulo > VSelekhard --- R- A
11- Observe que entre o primeiro e o segundo pentagrama a pá de cor diferente girou 3π/2 rad em t=1/24s --- num período T ela gira 2π rad --- regra de três --- 3π/2 rad - t=1/24 s --- 2π rad – T s --- 3πT/2=2π/24 --- T=4/72 --- T=1/18s --- f=1/T --- f=18Hz --- R- B