ENEM19

Estático de um corpo extenso

1-(ENEM-MEC)

Um portão está fixo em um muro por duas dobradiças A e B, conforme mostra a figura, sendo P o peso do portão.

Caso um garoto se dependure no portão pela extremidade livre, e supondo que as reações máximas suportadas pelas dobradiças sejam iguais,

a) é mais provável que a dobradiça A arrebente primeiro que a B.

b) é mais provável que a dobradiça B arrebente primeiro que a A

c) seguramente as dobradiças A e B arrebentarão simultaneamente.

d) nenhuma delas sofrerá qualquer esforço.

e) o portão quebraria ao meio, ou nada sofreria.

Exercícios com características de ENEM

02-(COVEST)

Num circo, uma equilibrista deseja levantar, apoiada em uma vareta, uma bandeja circular contendo

um prato, um copo e uma garrafa cujas massas valem respectivamente 0,50kg, 0,10kg e 1,0kg. Escolhendo-se um sistema de eixos com origem no centro de gravidade da bandeja, as posições do prato, do copo e da garrafa são dadas respectivamente pelos pontos A, B e C da figura. Se a massa da bandeja for igual a 400g, em que posição (x, y) sob ela deve a equilibrista apoiar a vareta?

03-(UFPR-PR) 

Quatro blocos homogêneos e idênticos de massa m, comprimento L = 20 cm e espessura E = 8 cm estão empilhados conforme mostra a figura a seguir. Considere que o eixo y coincide com a parede

localizada à esquerda dos blocos, que o eixo x coincide com a superfície horizontal sobre a qual os blocos se encontram e que a intersecção desses eixos define a origem O. Com base nos dados da figura e do enunciado, as coordenadas X e Y da posição do centro de massa do conjunto de blocos são:

a) (18,0; 14,04)                 

b) (27,5; 16,5)                     

c) (17,5; 16,0)                      

d) (20,2; 18,0)                  

e) c) (24,5; 26,3)       

 04-(ITA-SP)

É dado um pedaço de cartolina com a forma de um sapinho, cujo centro de gravidade situa-se no seu próprio corpo. A seguir, com o auxilio de massa de modelagem, fixamos uma moeda de 10 centavos em cada uma das patas dianteiras do sapinho. Apoiando-se o nariz do sapinho na extremidade de um lápis, ele permanece em equilíbrio.

Nessas condições, pode-se afirmar que o sapinho com as moedas permanece em equilíbrio estável porque o centro de gravidade do sistema:

a) Continua no corpo do sapinho.            

b) Situa-se no ponto médio entre seus olhos.                   

c) Situa-se no nariz do sapinho.

d) Situa-se abaixo do ponto de apoio.     

e) Situa-se no ponto médio entre as patas traseiras

05-UNICAMP-SP)

Um cigarro sem filtro, de 80 mm, foi aceso e apoiado num cinzeiro, como mostra a figura. Durante

quanto tempo o cigarro ficará sobre o cinzeiro? Considere que a queima se dá à razão de 5 mm por minuto e que a cinza sempre se desprende do cigarro.

a) 2 minutos                   

b) 4 minutos                    

c) 6 minutos                   

d) 8 minutos                     

e) 10 minutos

06-(CESGRANRIO-RJ)

Três hastes homogêneas e idênticas podem ser ligadas conforme mostram as figuras I, II e III. Em cada caso, elas formam um sistema, rígido e plano, capaz de girar livremente, na vertical, em torno

de um eixo horizontal que, passa pelo ponto de união das barras. Qual das opções a seguir caracteriza corretamente  o tipo de equilíbrio observado em cada uma das situações ilustradas? (Em cada figura, a linha tracejada, está na direção da vertical).

07-(UFRRJ-RJ)

Na figura abaixo, suponha que o menino esteja empurrando a porta com uma força F_m = 5 N, atuando

a uma distância 2 m das dobradiças (eixo de rotação), e que o homem exerça uma força F_h = 80 N, a uma distância de 10 cm do eixo de rotação.

Nestas condições, pode-se afirmar que:

a) a porta estaria girando no sentido de ser fechada.         

b) a porta estaria girando no sentido de ser aberta.

c) a porta não gira em nenhum sentido.                            

d) o valor do momento aplicado à porta pelo homem é maior que o valor do momento aplicado pelo menino.                                   

e) a porta estaria girando no sentido de ser fechada, pois a massa do homem é maior que a massa do menino.

08-(UFRJ-RJ)

Um jovem e sua namorada passeiam de carro por uma estrada e são surpreendidos por um furo num dos pneus.

O jovem, que pesa 75kgf, pisa a extremidade de uma chave de roda, inclinada em relação à horizontal, como mostra a figura 1, mas só consegue soltar o parafuso quando exerce sobre a chave uma força igual a seu peso.

A namorada do jovem, que pesa 51kgf, encaixa a mesma chave, mas na horizontal, em outro parafuso, e pisa a extremidade da chave, exercendo sobre ela uma força igual a seu peso, como mostra a figura 2.

Supondo que este segundo parafuso esteja tão apertado quanto o primeiro, e levando em conta as distancias indicadas nas figuras, verifique se a moça consegue soltar esse segundo parafuso. Justifique sua resposta.(1kgf=10N)

09- (UFMG-MG) 

Para pintar uma parede, Miguel está sobre um andaime suspenso por duas cordas. Em certo instante, ele está mais próximo da extremidade direita do andaime, como mostrado nesta figura:

Sejam T_E e T_D os módulos das tensões nas cordas, respectivamente, da esquerda e da direita e P o módulo da soma do peso do andaime com o peso de Miguel.

Analisando-se essas informações, é CORRETO afirmar que

a) T_E = T_D  e  T_E  + T_D = P.        

b) T_E = T_D  e  T_E + T_D > P.        

c) T_E < T_D  e  T_E + T_D = P.       

d) T_E < T_D  e  T_E + T_D > P. 

10-(UNICAMP-SP) 

A figura a seguir mostra uma árvore que sofreu uma poda drástica e perdeu a parte esquerda da sua copa. Após a poda, o centro de massa (CM) da árvore passou a ser à direita do eixo do tronco. Uma forte rajada de vento exerce uma força horizontal    sobre a árvore, atuando ao longo de uma linha que fica a uma altura h da raiz.

Para que a árvore permaneça em equilíbrio estático é necessário que tanto a força quanto o torque resultante na árvore sejam nulos. O torque de uma força com relação a um ponto O é dado pelo produto do módulo da força pelo seu braço, que é a distância do ponto O à linha de ação da força.

Assim, qual é o conjunto de forças agindo nas raízes dessa árvore que poderia garantir seu equilíbrio estático?

11-(FGV-SP)

Em um poste, uma trave horizontal feita de madeira serve de suporte para os três isoladores de alta tensão, responsáveis, também, por manter os fios sobrelevados.

Os pesos da trave e dos isoladores podem ser considerados desprezíveis. Cada fio exerce sobre seu isolador uma força vertical de intensidade 400 N e, por essa razão, além da trave ser presa diretamente ao poste, uma haste inclinada exerce um esforço adicional para cima, em newtons, de intensidade

12-(UFF-RJ)

Uma escada homogênea, apoiada sobre um piso áspero, está encostada numa parede lisa. Para que a escada fique em equilíbrio, as linhas de ação das forças que agem sobre a escada devem convergir para um mesmo ponto Q. Assinale a opção que ilustra a situação descrita e apresenta o ponto Q mais bem localizado.

13-(UFRJ-RJ)

Num posto fiscal de pesagem, um caminhão está em repouso sobre duas balanças, uma embaixo de suas rodas dianteiras e a outra sob suas rodas traseiras. Ao fazer as leituras das balanças, o fiscal verifica que a primeira marca 1,0 x 10⁵N, mas percebe que a segunda está quebrada.

Profundo conhecedor de caminhões, o fiscal sabe que as distâncias entre o centro de massa C do caminhão e os planos verticais que contêm os eixos dianteiro e traseiro das rodas valem, respectivamente, d₁ = 2,0 m e d₂ = 4,0 m, como ilustra a figura.

A intensidade da força que o caminhão exerce sobre a segunda balança é de: 

a) N₂=5,0.10⁴N               

b) N₂=6,5.10²N                 

c) N₂=1,0.10⁶N                     

d) N₂=7,0.10³N                        

e) N₂=5,0.10²N

14-(MACKENZIE-SP)

Um "designer" projeta um móbile usando três hastes rígidas de pesos desprezíveis, interligadas por fios ideais, e quatro bonequinhos, conforme a figura.

 Cada haste tem 15cm de comprimento. Para que o conjunto permaneça em equilíbrio, com as hastes na horizontal, a massa do bonequinho X deverá ser:

15-(FGV-SP)

Usado no antigo Egito para retirar água do rio Nilo, o "shaduf" pode ser visto como um ancestral do guindaste. Consistia de uma haste de madeira onde em uma das extremidades era amarrado um balde, enquanto que na outra, uma grande pedra fazia o papel de contra-peso. A haste horizontal apoiava-se em outra verticalmente disposta e o operador, com suas mãos entre o extremo contendo o balde e o apoio (ponto P), exercia uma pequena força adicional para dar ao mecanismo sua mobilidade.

Dados:

Peso do balde e sua corda .................... 200 N

Peso da pedra e sua corda .................... 350 N

Para o esquema apresentado, a força vertical que uma pessoa deve exercer sobre o ponto P, para que o "shaduf" fique horizontalmente em equilíbrio, tem sentido

a) para baixo e intensidade de 100 N.     

b) para baixo e intensidade de 50 N.     

c) para cima e intensidade de 150 N.

d) para cima e intensidade de 100 N.  

e) para cima e intensidade de 50 N.

16-(UEL-PR)

Uma tesoura é uma ferramenta construída para ampliar a força exercida pela mão  que a utiliza para cortar objetos.

A essa ampliação da força dá-se o nome de “vantagem mecânica”, dada por F₂/F₁=d₁/d₂, onde o índice 1 é relativo ao cabo, e o índice 2 está relacionado à lâmina de corte. Sobre a vantagem mecânica da tesoura, é correto afirmar:

a) Se d₁ for menor que d₂, F₂ é maior que F₁          

b) Se d₁ for menor que d₂, F₂ é igual a F₁           

c) Se d₁ for maior que d₂, F₂ é maior que F₁         

d) Se d₁ for menor que d₂, F₂ é menor que F₁         

e) Se d₁ for igual ad₂, F₂ é menor que F₁

Resolução Comentada 

Estático de um corpo extenso

01- Observe na figura abaixo que a força  peso  do portão colocada em seu centro de gravidade (vertical e para baixo) e a força  , aplicada pelo garoto na extremidade livre da direita (também

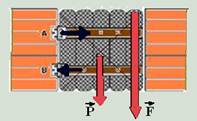
vertical e para baixo) tendem a fazer o portão girar no sentido horário, fazendo-o puxar a dobradiça em A (tentando arrancá-la) e comprimi-la em B  ---  R- A 

02- bandeja – b  m_b=0,4kg  ---  prato -A - – m_A=0,5kg  ---  copo – B – m_B=0,1kg  ---  garrafa – C – m_C=1,0kg  --- cálculo da abscissa do centro de massa  ---  X_CG=(m_b.X_b + m_A.XA_A + m_BX_B + m_CX_C)/(m_b + m_A + m_B + m_C)= (0,4..0 + 0,5.(-2). + 0,1.(-10) + 1.(+4+)/(0,4 + 0,5 + 0,1 + 1,0)=2/2  ---  X_CG=1cm  ---  cálculo do centro de massa da ordenada  ---  Y_CG=(m_b.Y_b + m_A.Y_A +

m_BY_B + m_cY_c)/(m_b + m_A + m_B + m_C)=(0,4.0 + 0,5.(-5) + 0,1.5 + 1.4)/2  ---  Y_CM=2/2  ---  Y_CM=1cm  ---  CG (1,1)  ---   R- E

03-  A figura mostra as abscissas x₁; x₂; x₃ e x₄ e as ordenadas y₁; y₂; y₃ e y₄ dos quatro corpos; a abscissa X e a ordenada Y do centro de massa:

 R - C

04- Sem as moedas o centro de gravidade do sapinho está em seu próprio corpo  ---  quando você

coloca as moedas em suas patas dianteiras e o apoia no lápis, essas duas moedas deslocam seu centro de gravidade para baixo de seu corpo e ele fica em equilíbrio estável  ---  R- D

Observação: No boneco  “João Bobo”, existe uma grande massa (contrapeso, normalmente chumbo), na parte inferior  do brinquedo, fazendo com que seu centro de gravidade esteja bem

embaixo e ele fique em equilíbrio estável  ---  quando você o retira da posição de equilíbrio estável, a tendência do contrapeso é retornar novamente ao equilíbrio, oscilando até que o contrapeso fique novamente em sua parte inferior.

05- Como o centro de gravidade CG está sempre no ponto médio e à medida que o cigarro vai queimando ele se desloca para a esquerda, quando o cigarro estiver na iminência de cair, você terá a situação da figura abaixo, onde você deve

 observar que o cigarro queimou d=80 – 50=30mm com velocidade de 5mm/min ---  V=d/t  ---  5=30/t  --- t=6 min

R- C

06- Trata-se de corpos apoiados  ---  situação I  ---  como os três ângulos são de 120^o o centro de gravidade CG está na junção – indiferente  ---  situação II  ---  o centro de gravidade CG está acima da

 junção – instável  ---  situação III  --- o CG centro de gravidade  está abaixo da junção – estável  --- 

R- E

07- A porta gira no sentido daquele que aplicar o maior momento na mesma  ---  momento da força aplicada pelo homem  --- M_h=+F_h.d  =80.10  ---  M_h=800N.cm  ---  momento da força aplicada pelo menino  ---  M_m=-F_m.d= -5.200  ---  M_m= - 1.000N.cm  ---  ganha o menino  ---  R- B

08-  O jovem consegue soltar o parafuso, fazendo a chave girar quando o momento da  força por ele

aplicada (F_j=75.10=750N)valer ---  M_Fj=F.d=750.20  ---  M_Fj=15.000N.cm  ---  momento da força (F=51.10=510N) aplicada pela namorada  ---  M_Fn=F.d=510.30  ---  M_Fn=15.300N  ---  observe que o momento (torque) da força aplicada pela namorada é maior que o momento da força aplicada pelo jovem  ---  sim, ela consegue soltar o parafuso.

09- Observe a figura abaixo  ---  equilíbrio de translação do andaime (corpo extenso)  ---  a resultante

das forças na vertical deve ser nula,e, para que isso ocorra  ---  T_E + T_D=P  ---  equilíbrio de rotação ( o andaime não deve girar)  ---  a soma dos momentos de cada força deve ser nula  ---  pólo em P  ---  +T_E.(x) – T_D.(y)=0  ---   T_E.(x)=T_D.(y)  ---  observe que, como x>y, T_E deve ser menor que T­_D  ---  T_E<T_D  ---  R- C

10- Como é uma situação de equilíbrio de um corpo extenso, temos que considerar equilíbrio de translação (a resultante das forças deve ser nula) e equilíbrio de rotação (o momento resultante deve ser nulo). Analisando cada uma das opções:

a) Falsa  ---  a resultante das forças na direção horizontal é não nula, não havendo, portanto, equilíbrio.

b) Falsa  ---  a resultante das forças na direção vertical é não nula.

c) Correta  ---  a força resultante pode ser nula bem como o momento resultante  ---  trata-se de uma situação de possível equilíbrio

d) Falsa  ---  o momento resultante é não nulo, provocando rotação no sentido horário.  

R- C

11- Colocando as forças que agem sobre a trave  ---  equilíbrio de rotação  ---  a somatória dos

momentos de todas as forças deve ser nula  ---  pólo em C  ---  - F₁.d₁  + F.d – F₂.d₂ + F₃.d₃ = 0  ---  - 400.(0,2 + 0,1 + 0,3)  + F.(0,1 + 0,3) – 400.(0,3) + 400.(0,3) = 0  ---- 400.0,6 + F.0,4 – 400.0,3 + 400.0,3 = 0  ---  F=240/0,4  ---  F= 600N  ---  R- E

12- Para que a escada não escorregue e caia, no apoio inferior tem que ter atrito, o que não precisa ocorrer no apoio superior  ---  como a parede é lisa, ou seja, no ponto M não existe atrito  ---  a figura abaixo mostra as três forças que agem sobre a escada  que

está em equilíbrio  ---  - força de contato com a parede  ---  - força que a escada troca com o chão  ---  - força peso (ponto médio da escada)  ---  essas três forças obedecem ao teorema das três forças de enunciado: “ Se três forças agem sobre um corpo de modo a mantê-lo em equilíbrio, elas devem ser coplanares (mesmo plano) e concorrentes (seus prolongamentos devem se encontrar) num mesmo ponto, no caso Q”  ---  R- C

13- Observe a figura abaixo  ---  colocando o polo em N₂  ---  a soma dos momentos em relação ao

polo deve ser nula  ---  M_N2=--- M_P=+P.4  ---  M_N1=-N₁.6  --- M_N1=-6.10⁵N.m  ---  +4P – 6.10⁵=0  ---  P=6.10⁴/4  ---  P=1,5.10⁵N  ---  a resultante das forças verticais deve ser nula  ---  N₁ + N₂=1,5.10⁵  ---  1,0.10⁵ + N₂=1,5.10⁵  ---  N₂=0,5.10⁵  ---  N₂=5,0.10⁴N  ---  R- A

14- Observe o comprimento das hastes em relação ao ponto de apoio e verifique que o lado de comprimento 5cm deve equilibrar o dobro da massa que o lado de comprimento 10cm (figura abaixo)

R- C

15- Colocando o polo em N e calculando, calculando o momento de cada força, somando-os e

igualando-os a zero  --- -200.2 + F.0,5 + 350.1=0  ---  -400 + 0,5F + 350=0  ---  F=100N  ---  R- D

16- Observe a relação F₂/F₁=d₁/d₂  ---  se d₁ > d₂   ---  F₂ > F₁  ---  R- C