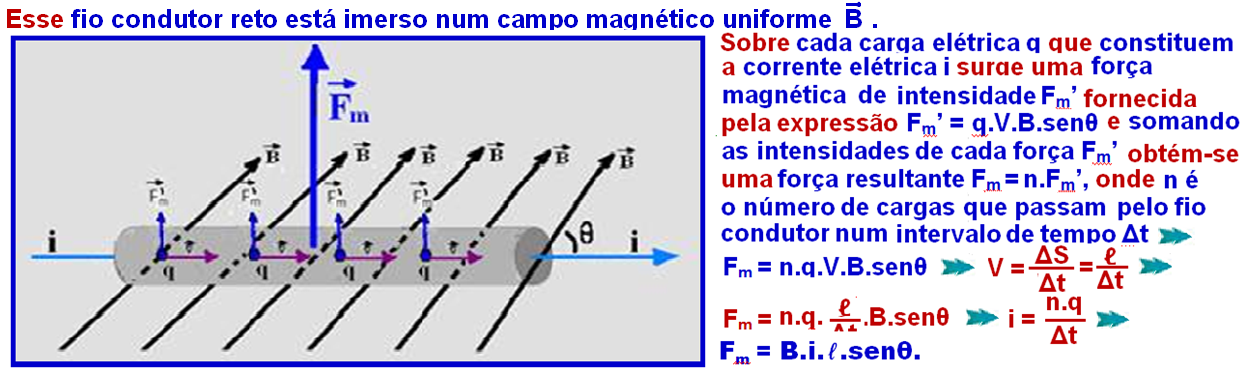
Força Magnética sobre um condutor retilíneo imerso num campo magnético uniforme

 Considere um condutor retilíneo de comprimento ℓ percorrido por uma corrente elétrica (elétrons livres com carga q, movendo-se com velocidade V no interior do condutor, pela sua seção transversal).

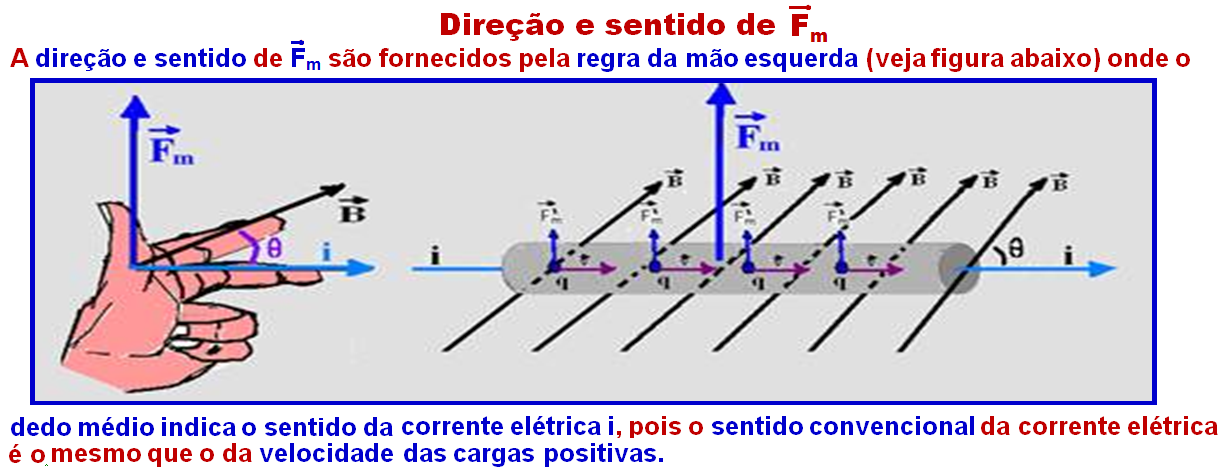
O que você deve saber, informações e dicas

Exercícios com resolução comentada sobre

Força Magnética sobre um condutor retilíneo

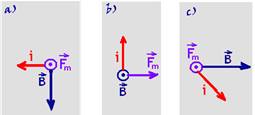
01-(UFB) Represente a força magnética que age sobre cada condutor retilíneo, percorrido por corrente elétrica e imerso no interior de um campo magnético uniforme, nos casos:

02-(UFMS-MS) Um fio condutor, de comprimento L, percorrido por uma corrente de intensidade i, está imerso num campo magnético uniforme B. A figura a seguir mostra três posições diferentes do fio (a), (b) e (c), em relação à direção do campo magnético. Sendo F(a), F(b) e F(c) as intensidades das forças magnéticas produzidas no fio, nas respectivas posições, é correto afirmar que:

a) F(a) > F(b) > F(c).       

b) F(b) > F(a) > F(c).       

c) F(a) > F(c) > F(b).      

d) F(c) > F(b) > F(a).     

e) F(a) = F(b) = F(c).

03-(UFB) Um fio condutor é dobrado formando um retângulo ABCD (espira retangular), que pode girar livremente em torno do eixo e. Seja i a intensidade de corrente constante que percorre a espira no sentido indicado pela figura.

Represente as forças magnéticas que agem em cada lado da espira e determine suas intensidades considerando: L_AD=L_BC=0,1m; L_AB=L_CD=0,2m; i=10 A, B=2,0.10^-3T e o ângulo entre B e i como sendo θ=90^o para os lados AB e CD e θ=0^o para os lados BC e AD.

04-(UFRGS) Na figura a seguir, um fio condutor flexível encontra-se na presença de um campo magnético constante e uniforme perpendicular ao plano da página. Na ausência de corrente elétrica, o fio permanece na posição B. Quando o fio é percorrido por certa corrente elétrica estacionária, ele assume a posição A.

Para que o fio assuma a posição C, é necessário

a) inverter o sentido da corrente e do campo aplicado.                

b) inverter o sentido da corrente ou inverter o sentido do campo.

c) desligar lentamente o campo.                                                   

d) desligar lentamente a corrente.

e) desligar lentamente o campo e a corrente.

05-(UFB) A barra metálica condutora PQ está em equilíbrio e é percorrida pela corrente i indicada na figura. Identifique os pólos

norte e sul do imã.

06-(UE-PB) Um professor de física resolve fazer um experimento de eletromagnetismo que objetiva determinar o valor do campo magnético entre os pólos do imã. Para isso, ele utiliza um imã, uma bateria que fornece 4,8V a um condutor cilíndrico AC com massa 5g, comprimento de 10cm e resistência elétrica igual a 0,10Ω. Ao ligar a bateria ao circuito, mostrado na figura, o condutor cilíndrico fica suspenso em equilíbrio.

Considerando-se que as linhas de campo são perpendiculares ao condutor, que a resistência elétrica dos fios é 0,02Ω, que a massa dos fios é desprezível e adotando g=10m/s², o professor concluiu que o campo magnético, em tesla, tem valor igual a:

07-(UFPE-PE) Um fio MN, de 40cm de comprimento e massa igual a 30g, está suspenso horizontalmente por uma mola ideal de constante elástica k=10N/m. O conjunto encontra-se em uma região de campo magnético uniforme B=0,1Wb/m2, como mostra a figura.

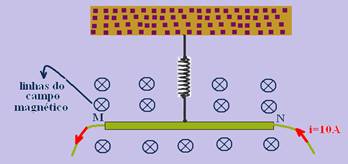
Quando a corrente no fio for 10 A, dirigida de N para M, atuará sobre o fio uma força magnética verticalmente para baixo. Determine a elongação total, devido à força magnética e à força gravitacional, sofrida pela mola, em cm.

08-(UNICAMP-SP) Um fio condutor rígido de 200 g e 20 cm de comprimento é ligado ao restante do circuito por meio de contatos deslizantes sem atrito, como mostra a figura .

 O plano da figura é vertical. Inicialmente a chave está aberta. O fio condutor é preso a um dinamômetro e se encontra numa região com campo magnético de 1,0T, entrando perpendicularmente no plano da figura: (considere g=10m/s²)

a) calcule a força medida pelo dinamômetro com a chave aberta, estando o fio em equilíbrio.
b) determine a direção e a intensidade da corrente elétrica no circuito após o fechamento da chave, sabendo-se que o dinamômetro passa a indicar leitura zero.
c) calcule a tensão da bateria sabendo-se que a resistência total do circuito é de 6,0Ω.

09-(UFG–GO) Para medir a intensidade de um campo magnético uniforme, utiliza-se o aparato ilustrado na figura. O fio condutor tem comprimento 2,5 cm; as molas, condutoras de eletricidade, têm constante elástica 5,0N/m. Quando a tensão elétrica está desligada as molas apresentam deformação de 2,0 mm. Com a tensão ajustada para produzir uma corrente de 1,0A as molas retornam ao estado natural. Dado que o campo magnético é perpendicular ao plano da figura, determine a sua magnitude e o seu sentido. Despreze os efeitos da corrente e do campo sobre as molas.

10-(UEL-PR) "Trem magnético japonês bate seu próprio recorde de velocidade (da Agência Lusa) - Um trem japonês que levita magneticamente, conhecido por "Maglev", bateu hoje o seu próprio recorde de velocidade ao atingir 560 km/h durante um teste de

via. O comboio de cinco vagões MLX01, cujo recorde anterior de 552 km/h fora alcançado em abril de 1999 com 13 pessoas a bordo, alcançou sua nova marca sem levar passageiros. O trem japonês fica ligeiramente suspenso da via pela ação de magnetos, o que elimina a redução da velocidade causada pelo atrito com os trilhos". (Disponível:http:www1.folha.uol.com.br/folha/ciencia    Acesso em: 13 set. 2004).

É possível deixar suspenso um corpo condutor criando uma força magnética contrária à força gravitacional que atua sobre ele. Para isso, o corpo deve estar imerso em um campo magnético e por ele deve passar uma corrente elétrica. Considerando um fio condutor retilíneo como uma linha horizontal nesta folha de papel que você lê, que deve ser considerada como estando posicionada com seu plano paralelo à superfície terrestre e à frente do leitor. Quais devem ser as orientações do campo magnético e da corrente elétrica, de modo que a força magnética resultante esteja na mesma direção e no sentido contrário à força gravitacional que atua sobre o fio? Ignore as ligações do fio com a fonte de corrente elétrica.

a) A corrente deve apontar para esquerda ao longo do fio, e o campo magnético deve estar perpendicular ao fio, apontando para o leitor

b) A corrente deve apontar para a esquerda ao longo do fio, e o campo magnético deve estar paralelo ao fio, apontando para a direita.

c) A corrente deve apontar para a direita ao longo do fio, e o campo magnético deve estar perpendicular ao fio, apontando para fora do plano da folha.

d) A corrente deve apontar para a direita ao longo do fio, e o campo magnético deve estar paralelo ao fio, apontando para a direita.

e) A corrente deve apontar para a esquerda ao longo do fio, e o campo magnético deve estar perpendicular ao fio, apontando para dentro do plano da folha.

11-(UNIFESP-SP) Na região quadriculada da figura existe um campo magnético uniforme, perpendicular ao plano do reticulado e penetrando no plano da figura. Parte de um circuito rígido também passa por ela, como ilustrado na figura.

A aresta de cada célula quadrada do quadrilátero tem comprimento u, e pelo fio passa uma corrente elétrica de intensidade i. Analisando a força magnética que age sobre cada elemento de comprimento u do fio do circuito, coincidente com a aresta das células quadradas, a intensidade da força magnética resultante sobre a parte do circuito exposta ao campo B é:

12-(FUVEST-SP) Para estimar a intensidade de um campo magnético B_o, uniforme e horizontal, é utilizado um fio condutor rígido, dobrado com a forma e dimensões indicadas na figura, apoiado sobre suportes fixos, podendo girar livremente em torno do eixo OO'. Esse arranjo funciona como uma "balança para forças eletromagnéticas". O fio é ligado a um gerador, ajustado para que a corrente contínua fornecida seja sempre i = 2,0 A, sendo que duas pequenas chaves, A e C, quando acionadas, estabelecem diferentes percursos para a corrente. Inicialmente, com o gerador desligado, o fio permanece em equilíbrio na posição horizontal. Quando o gerador é ligado, com a chave A, aberta e C, fechada, é necessário pendurar uma pequena massa M₁ = 0,008 kg, no meio do segmento P₃ – P₄, para restabelecer o equilíbrio e manter o fio na posição horizontal.

a) Determine a intensidade da força eletromagnética F₁, em newtons, que age sobre o segmento P₃P₄ do fio, quando o gerador é ligado com a chave A, aberta e C, fechada.

b) Estime a intensidade do campo magnético B_o, em teslas.

c) Estime a massa M₂, em kg, necessária para equilibrar novamente o fio na horizontal, quando a chave A está fechada e C, aberta. Indique onde deve ser colocada essa massa, levando em conta que a massa M₁ foi retirada.

As extremidades P₁, P₂, P₃ e P₄ estão sempre no mesmo plano.

13-(UFC-CE)  Na figura a seguir, o circuito principal é formado por uma bateria (resistência interna nula e força eletromotriz E), duas molas condutoras (cada uma com constante elástica k = 2 N/m e resistência elétrica R = 0,05 Ω), uma barra condutora de comprimento L = 30 cm e resistência elétrica desprezível. As molas estão em seus comprimentos naturais (sem deformação). Um campo magnético de módulo B=0,01 T, perpendicular ao plano da figura e apontando para dentro da página, está presente na região da barra.

Existe ainda outra barra isolante, conectada a uma ponta condutora, fixa ao ramo superior do circuito principal. A massa da barra isolante é desprezível. Uma lâmpada de resistência r e uma bateria de força eletromotriz E' compõem o circuito anexo (veja a figura a seguir). A altura entre a ponta condutora e o ramo superior do circuito anexo é h = 3 cm.

Assinale a alternativa que contém o valor mínimo da força eletromotriz ε no circuito principal, de modo que a lâmpada no circuito anexo seja percorrida por uma corrente elétrica (desconsidere quaisquer efeitos gravitacionais).

14-(PUC-RS)  Resolver a questão com base nas informações a seguir.

O músculo cardíaco sofre contrações periódicas, as quais geram pequenas diferenças de potencial, ou tensões elétricas, entre determinados pontos do corpo.

A medida dessas tensões fornece importantes informações sobre o funcionamento do coração. Uma forma de realizar essas medidas é através de um instrumento denominado eletrocardiógrafo de fio.

Esse instrumento é constituído de um ímã que produz um campo magnético intenso por onde passa um fio delgado e flexível. Durante o exame, eletrodos são posicionados em pontos específicos do corpo e conectados ao fio. Quando o músculo cardíaco se contrai, uma tensão surge entre esses eletrodos e uma corrente elétrica percorre o fio. Utilizando um modelo simplificado, o posicionamento do fio retilíneo no campo magnético uniforme do ímã do eletrocardiógrafo pode ser representado como indica a figura a seguir, perpendicularmente ao plano da página, e com o sentido da corrente saindo do plano da página.

Com base nessas informações, pode-se dizer que, quando o músculo cardíaco se contrai, o fio sofre uma deflexão

a) lateral e diretamente proporcional à corrente que o percorreu. 

b) lateral e inversamente proporcional à intensidade do campo magnético em que está colocado. 

c) vertical e inversamente proporcional à tensão entre os eletrodos. 

d) lateral e diretamente proporcional à resistência elétrica do fio. 

e) vertical e diretamente proporcional ao comprimento do fio. 

(IFET-MG) O enunciado a seguir refere-se às questões 15 e 16

A figura abaixo mostra uma região onde existe um campo magnético uniforme , de módulo igual a 5,0.10^-1T, localizado entre os pólos de um imã. Nessa região, há uma mola ideal , de constante elástica k igual a 2,0.10²N/m, presa ao teto, que sustenta em sua

extremidade um fio cilíndrico, condutor e retilíneo, de comprimento L igual a 2,0m e massa M igual a 6,0.10²g. O fio é percorrido por uma corrente contínua i, cujo sentido está indicado pelo símbolo .

15-(IFET-MG)

Observando a figura acima, podemos concluir que a força magnética que atua sobre o fio apontará

a) verticalmente para baixo     

b) verticalmente para cima         

c) perpendicularmente ao plano do papel, afastando-se do leitor         

d) perpendicularmente ao plano do papel, aproximando-se do leitor         

e) horizontalmente para a direita

16-(IFET-MG)

Admitindo que o sistema esteja em equilíbrio e adotando a aceleração da gravidade  g igual a 10m/s², o valor da deformação x sofrida pela mola quando a corrente i for igual a 4,0.10^-1 A é, em módulo, igual a

17-(UNIFESP-SP)

Uma mola de massa desprezível presa ao teto de uma sala, tem sua outra extremidade atada ao centro de uma barra metálica homogênea e na horizontal, com 50 cm de comprimento e 500 g de massa. A barra metálica, que pode movimentar-se num plano vertical, apresenta resistência ôhmica de 5 Ω e está ligada por fios condutores de massas desprezíveis a um gerador G de corrente contínua, de resistência ôhmica interna de 5 Ω, apoiado sobre uma mesa horizontal. O sistema barra-mola está em um plano perpendicular a um campo magnético B horizontal, cujas linhas de campo penetram nesse plano, conforme mostra a figura.

Determine:

a) a força eletromotriz, em volts, produzida pelo gerador e a potência elétrica dissipada pela barra metálica, em watts.

b) a deformação, em metros, sofrida pela mola para manter o sistema barra-mola em equilíbrio mecânico. Suponha que os fios elétricos não fiquem sujeitos a tensão mecânica, isto é, esticados.

Resolução comentada dos exercícios de vestibulares sobre

Força magnética sobre um condutor retilíneo

01-

02- Caso(a)  ---  F(a)=B.i.L.sen45⁰=(√2/2).BiL  ---  caso (b)  ---  F(b)=BiL.sen90⁰=BiL  ---  caso (c)  ---  F(c)=BiLsen0^o=0  ---   R- B

03- O campo magnético  é dirigido do pólo norte para o pólo sul  ---  nos trechos BC e AD a força magnética é nula (B e i são paralelos)  ---  usando a regra da mão esquerda as forças nos trechos AB (F_AB) e CD (F_CD) estão indicadas na figura

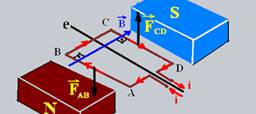
A intensidade das forças que agem sobre BC e AD é zero (B e i são paralelos, θ=0^o)  ---  Intensidade de F_AB  ---  F_AB=F_CD=BiLsenθ=2.10^-3.10.0,2  ---  F_AB=F_CD=4,0.10^-3T  

04- Para a inversão no sentido da força que atua sobre o fio deve-se inverter o sentido da corrente OU o sentido do campo magnético  ---  R- B

05- Para que a barra metálica condutora PQ esteja em equilíbrio, seu peso (vertical e para baixo)

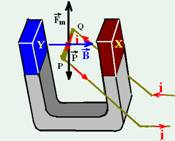
deve ser anulado pela força magnética que deve ser vertical e para cima  ---  usando a regra da mão esquerda,  está indicado na figura acima, saindo do pólo norte e indo para o pólo sul  ---  X é um pólo norte e Y é um pólo sul.

06-  Cálculo da intensidade da corrente elétrica no nos fios e no condutor cilíndrico  ---  R_eq=0,10 + 0,02  ---  R_eq=0,12Ω  ---  R_eq=U/i  ---  0,12=4,8/i  ---  i=4,8/0,12  ---  i=40 A  ---  como o condutor cilíndrico fica em equilíbrio, a força magnética F_m deve ser vertical e para cima para equilibrar o peso que é vertical e para baixo  --- F_m=P  ---  BiLsenθ=mg  ---  B.40.0,10.1=0,005.10  ---  B=0,05/4  ---  B=0,0125T  ---  R- A  

07- Força magnética vertical e para baixo  ---  F_m=BiLsen90^o=0,1.10.0,4.1  ---  F_m=0,4N  ---  força gravitacional vertical e para baixo  ---  P=mg=0,03.10  ---  P=0,3N  ---  força elástica vertical e para cima  ---  F_e=k.x  ---  F_e=10x  ---  F_m + P = F_e  --- 

0,4 + 0,3=10x  ---  x=0,7/10=0,07m  ---  x=7,0cm

08- a) Se a chave está aberta não passa corrente pelo fio e a força magnética sobre ele é nula e assim, a força de tração no fio condutor rígido (indicação do dinamômetro) é igual ao peso do fio  ---  P=m.g=0,2.10  ---  o dinamômetro indica T=2,0N

b) Com a chave fechada, circula no fio condutor rígido uma corrente elétrica i e surge sobre o fio uma força magnética para cima, que deve anular o peso do fio, pois o dinamômetro indica zero  --- F_m=P  ---  i e B são perpendiculares – θ=90^o  ---  B.i.ℓ.sen90^o=2  ---  1.i.0,2=2  ---  i=10A  ---  regra da mão esquerda F_m para cima, B entrando, i deve ter direção horizontal e sentido para a direita.

c) R=U/i  ---  6=U/10  ---  U=60V

09- Com a tensão elétrica desligada a força elástica aplicada por cada mola deve equilibrar o peso do fio  ---  2F_e=P  ---  2.k.x=P  ---  2.5.2.10^-3=P  ---  P=20.10^-3  ---  P=0,02N

10- Veja o esquema abaixo onde foi usada a regra da mão esquerda

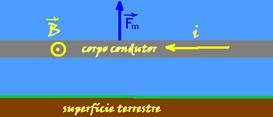
R- A

11- Como as intensidades de B e de i são constantes, então quem varia é o comprimento L de cada trecho do fio, tracionados  por forças diferentes, as quais, em cada trecho tem a direção e sentido fornecidos pela regra da mão esquerda e esquematizados na

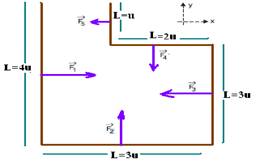
figura  ---  F₁=Bi4u  ---  F₂=Bi3u  ---  F₃=Bi3u  ---  F₄=Bi2u  ---  F₅=Biu  ---  na direção X  ---  F_RX=F₁ – F₃ –F₅=4Biu – 3Biu – Biu  ---  F_RX=0  ---  na direção Y  ---  F_RY=F₂ – F₄=3Biu – 2Biu  ---  F_RY=Biu  ---  R- C

12- a) Quando o gerador é ligado, com a chave A aberta e a chave C fechada, a corrente elétrica circula apenas no trecho OO’P₃P₄  ---  quando a massa M=0,008kg é pendurada no ponto K, meio do segmento P₃P₄, para o sistema permanecer em equilíbrio , a força magnética F_m deve equilibrar o peso da massa M=0,008kg. ou seja, deverá ser vertical e para cima (veja figura) com

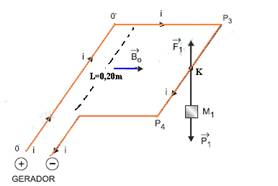
direção e sentido fornecidos pela regra da mão esquerda ---  F₁=P₁=m₁.g  ---  F₁=0,008.10  ---  F₁=0,08N

b) Ainda nas condições anteriores  ---  F₁=BiL  ---  0,08=B.2.0,20  ---  B=0,2T

c) Fechando a chave A e abrindo a chave C a corrente elétrica circulará nos trechos P₁P₂P₃P₄, com as forças  e  - colocadas nos pontos médios K (de P₃P₄) e N (de P₁P₂) e que foram obtidas pela regra da mão esquerda  ---  nessas condições a espira tenderá a girar em torno de OO’  ---   como nos trechos P₁P₂ e P₃P₄ B, L e i são os mesmos, as intensidades de  , - e  são

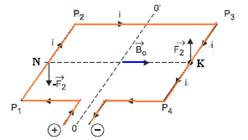
iguais e valem F=0,08N  ---  para que se equilibre o binário ( e  -) você deve provocar um torque no sentido oposto, ou seja,

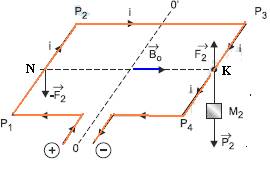
 deve pendurar no ponto K uma massa M₂  que seja o dobro de M1  ---  M₂=0,16kg  ---  (veja figura)

13- A corrente i no circuito principal (no sentido anti-horário) faz surgir na barra condutora uma força magnética de intensidade F, vertical e para baixo (fornecida pela regra da mão esquerda) que comprime para baixo as molas, estabelecendo contato com o circuito secundário anexo, fechando o circuito e acendendo a lâmpada  ---  a força eletromotriz mínima E faz com que as forças elásticas das molas e a força magnética se equilibrem  ---  força magnética  ---  F_m=BiLsenθ=BiLsen90^o  ---  F_m=BiL  ---  força elástica de uma mola  ---  F’_e=kx  ---  como são duas molas F_e= 2F’_e=2kx  ---  F_e=2kx  ---  F_m=F_e  ---  BiL=2kh (I)  ---  R_eq=U/i  ---   

2R=E/i  ---  i=E/2R (II)  ---  (II) em (I)  ---  B(E/2R)L=2kh  ---  0,01.E.2.0,05.0,3=2.2.0,03  ---  E=4,0V  ---  R- E

14- Quando o músculo cardíaco se contrai surge uma corrente elétrica no fio  ---  no caso, i saindo do plano da página  --- o campo magnético  é vertical e para baixo  ---  regra da mão esquerda  ---  a força magnética  será horizontal e para a direita  ---  F_m=BiL (direta mente proporcional a i)  ---  R- A

15- Utilizando a regra da mão esquerda  ---  indicador – indica o campo magnético , horizontal para a direita (do pólo norte para

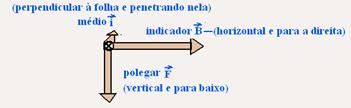
 o pólo sul)  ---  médio – indica a corrente elétrica i (entrando na folha de papel)  ---  polegar – indica a força magnética   --- 

observe na figura que o polegar está indicando que  é vertical e para baixo

R- A

16- Observe no exercício anterior que a força magnética  que age sobre o fio é vertical e para baixo, juntamente com o peso   ---a força elástica  age sobre o fio puxando-o para cima  ---  intensidade de   ---  F_m=B.i.ℓ.senθ=5.10^-1.4.10^-1.2.sen90^o  --- 

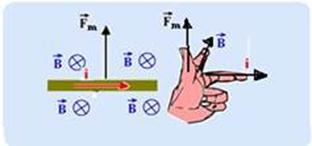
F_m=40.10^-2.1  ---  F_m=0,4N  ---  intensidade do peso   ---  P=mg=6.10².10^-3.10  ---  P=6N  ---  a intensidade da força resultante sobre o fio, vertical e para baixo vale  ---  F_R=6.0 + 0,4  ---  F’_R=6,4N  ---  a força elástica , vertical e para cima vale  ---  F_e=kx  ---  F_e=2.10².x  ---  como o sistema está em equilíbrio a intensidade da força resultante é nula, ou seja  ---  F_e=F’_R  ---  2.10²x=6,4  ---  x=6,4/2.10²  ---  x=3,2.10^-2m  ---  R- D

17- a) Como a barra metálica possui resistência ôhmica R=5Ω e o gerador resistência ôhmica interna r=5Ω e eles estão associados em série, a resistência equivalente  vale R_eq=5 + 5=10Ω  ---  R_eq=U/i  ---  10 = U/5  ---  U=ε=50V  ---  potência elétrica dissipada pela barra metálica  ---  P_d=R_barra.i² = 5.5²  ---  P_d=125W.

b) Conhecendo a direção e sentido do campo magnético (perpendicular à folha de papel e penetrando nela) e da corrente

elétrica i (horizontal e para a direita), utilizando a regra da mão esquerda você localiza a força magnética (vertical e para cima – veja figura acima)  ---  a intensidade dessa força magnética vale  ---  F_m=B.i.ℓ.senθ=0,4.5.0,5.sen90^o=1.1  ---  F_m=1N  ---  sobre a barra agem as forças  ---  força magnética  (vertical e para cima), força elástica  aplicada pela mola (vertical e para cima) e a força peso  (vertical e para baixo)  ---  como o enunciado afirma que o sistema está em equilíbrio, a intensidade da força resultante  sobre a barra deve ser nula  ---  assim, F_e + F_m = P  ---   k.x + 1 = m.g  ---  80.x + 1 = 5  ---  x=4/80  ---  x=0,05m ou x=5.10^-2m.