Força magnética sobre uma carga móvel imersa num campo magnético

 Quando uma carga elétrica que se move com velocidade  no interior de um campo magnético  

sobre ela surge uma força de origem magnética  ( denominada força de Lorentz), com as seguintes características:

 Direção e sentido de  fornecidos pela regra da mão esquerda conforme mostrado na

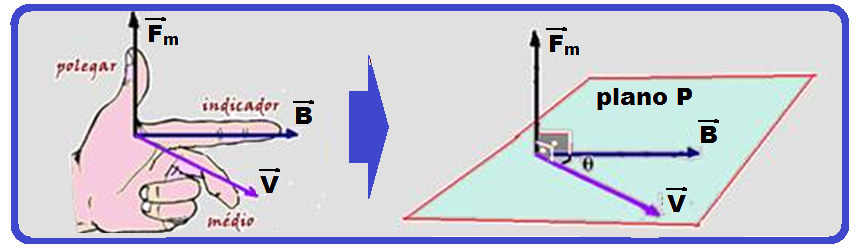
figura acima.

Observe na figura da direita que  é perpendicular a  e a , o que impõe a condição de que  e devem pertencer a um mesmo plano.

Observe também que θ é o ângulo entre  e .

Conhecendo a direção e o sentido de  e de  você pode, pela regra da mão esquerda, determinar a direção e o sentido da força magnética  como você pode observar no esquema abaixo, onde uma carga positiva move-se com velocidade  no interior de um campo magnético uniforme . 

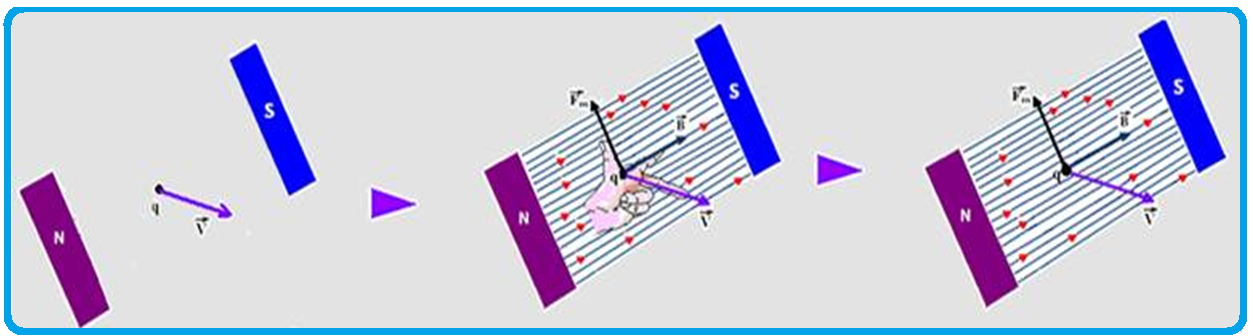
Observe que a direção e sentido das linhas de indução magnética e consequentemente de  é do polo norte para o polo sul.

Adaptando o indicador e o médio nas direções de  e de  você determina a direção e sentido de.

Observação: Se q for negativa você deve inverter o sentido da força magnética .

O que você deve saber, informações e dicas

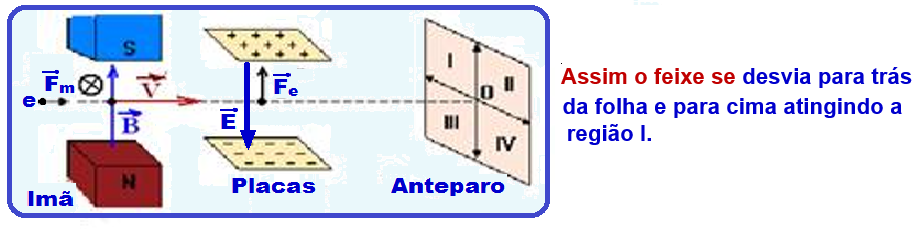
Como a força magnética tem sempre direção perpendicular ao vetor velocidade e como a potência de uma força é fornecida por P_o = F_m.V.cosθ, então θ = 90^o e cos 90^o = 0  P_o = F_m.V.0    P_o = 0   se a potência é nula o trabalho também será, pois P_o = W/∆t 0 = W/∆t

W = 0. 

O trabalho realizado pela força magnética é sempre nulo ou, a força magnética nunca realiza trabalho.

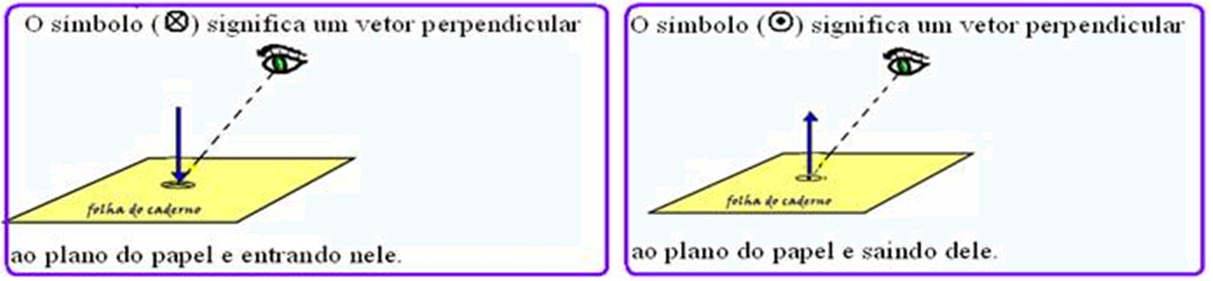
 Convenção

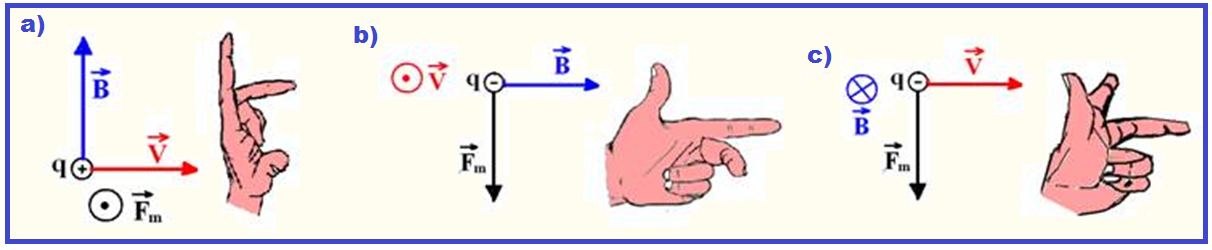
Alguns exemplos:

Nas figuras abaixo estão representadas as forças magnéticas e a disposição final da mão esquerda. Observe que nos casos b e c a força magnética tem sentido oposto ao dado pela regra da mão esquerda, pois a carga elétrica é negativa.

Força magnética sobre carga elétrica - casos particulares

 Você já viu que as principais características da força magnética que atua sobre uma carga elétrica imersa num campo magnético tem as seguintes características:

 Direção e sentido de   fornecidos pela regra da mão esquerda conforme mostrado na figura abaixo.

Observe na figura da direita que  é perpendicular a  e a , o que impõe a condição de que  edevem pertencer a um mesmo plano. Observe também que θ é o ângulo entre  e .

 Intensidade de  é proporcional a q, V, B e ao senθ, obedecendo à equação:

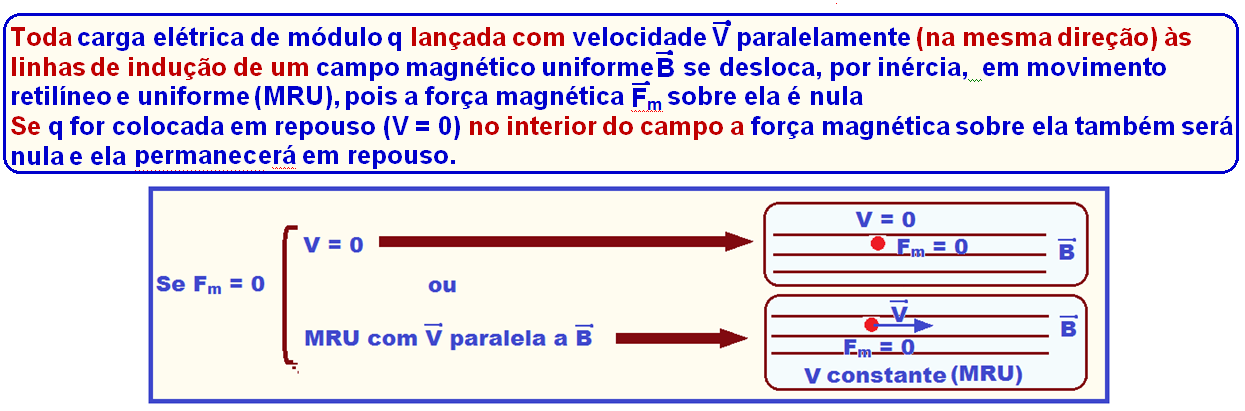
Carga em repouso (V = 0) ou lançada com velocidade  paralelamente às linhas de indução de um campo magnético uniforme

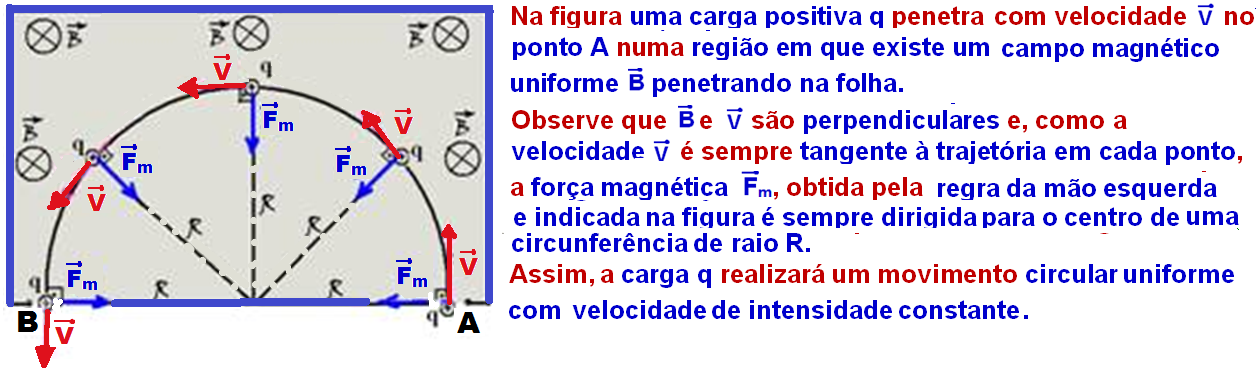
Carga elétrica q lançada com velocidade  lançada perpendicularmente às linhas de indução de um campo magnético uniforme

Observe que, neste caso o ângulo entre  e  é 90^o (são perpendiculares) e que sen90^o = 1.

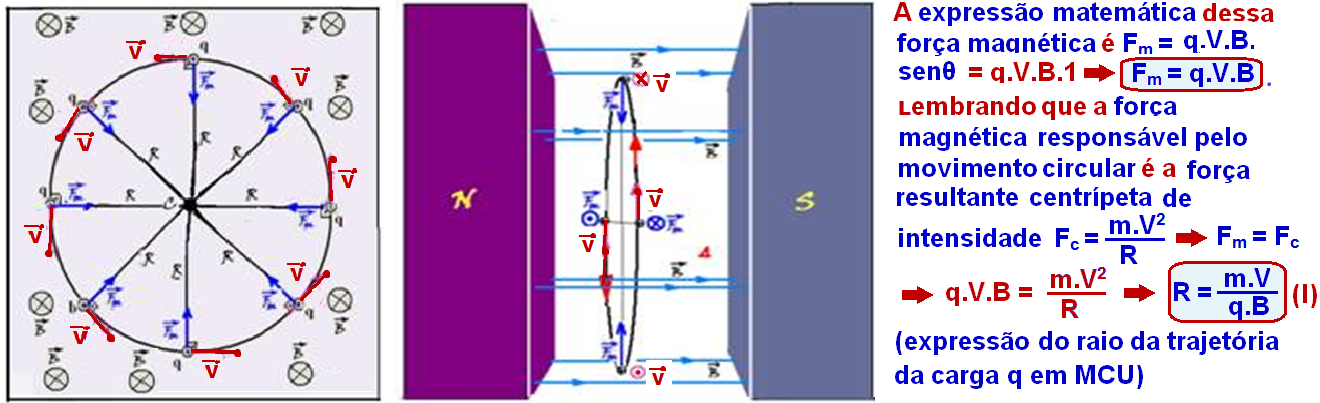
O período T (tempo que a carga q demora para efetuar uma volta completa) é fornecido por    V = ΔS / Δt    numa volta completa    ΔS = 2πR e Δt = T    V = 2πR / T (II).

Substituindo II em I    R = m. (2πR/T)/q.B    T = 2πm/q.B  (período do MCU).

Observe que o período (T) do movimento circular não depende da velocidade com que a partícula q penetra no campo magnético e nem do raio da circunferência.

O que você deve saber, informações e dicas

Observe na expressão do período (T) que ele não depende da velocidade da partícula, nem do raio da circunferência.

O trabalho realizado por sobre q é nulo, pois é perpendicular ao plano formado por e e W = F_m.d.cos90⁰ = F_m.d.0 = 0.

Campos magnético e elétrico agindo sobre uma partícula ou feixe de partículas eletrizadas com carga q

Exercícios de vestibulares com resolução comentada sobre

Força magnética sobre uma carga q imersa num campo magnético uniforme

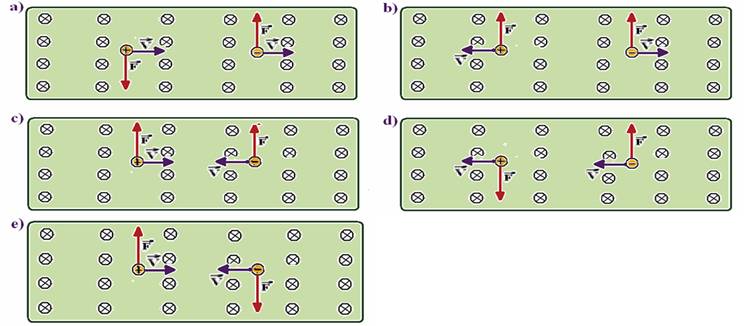
01-(PUC-PR) Uma carga positiva q se movimenta em um campo magnético uniforme  com velocidade . Levando em conta a convenção a seguir, foram representadas três hipóteses com respeito à orientação da força atuante sobre a carga q, devido à sua interação com o campo magnético.

Está correta ou estão corretas:

a) somente I e III.              

b) somente I e II.                 

c) somente II.                     

d) I, II e III.                  

e) somente II e III.

02-(UFU-MG) Um objeto de massa M, carregado com uma carga positiva +Q, cai devido à ação da gravidade e passa por uma região próxima do pólo norte (N) de um ímã, conforme mostra figura a seguir.

De acordo com o sistema de eixos representado acima, assinale a alternativa que contém a afirmativa correta.

a) O objeto sofrerá um desvio no sentido positivo do eixo y, devido à presença do campo magnético na região.

b) O objeto cairá verticalmente, não sofrendo desvio algum até atingir o solo, pois campos gravitacionais e magnéticos não interagem.

c) O objeto sofrerá um desvio no sentido positivo do eixo x, devido à presença do campo magnético na região.

d) O objeto sofrerá um desvio no sentido negativo do eixo x, devido à presença do campo magnético na região.

03-(FUVEST-SP) Assim como ocorre em tubos de TV, um feixe de elétrons move-se em direção ao ponto central O de uma tela, com velocidade constante. A trajetória dos elétrons é modificada por um campo magnético vertical B, na direção perpendicular à trajetória do feixe, cuja intensidade varia em função do tempo t como indicado no gráfico.

Devido a esse campo, os elétrons incidem na tela, deixando um traço representado por uma das figuras a seguir. A figura que pode representar o padrão visível na tela é: 

04-(UFMG-MG) O tubo de imagem de um televisor está representado, esquematicamente, na Figura I.

Elétrons são acelerados da parte de trás desse tubo em direção ao centro da tela. Quatro bobinas - K, L, M e N - produzem campos magnéticos variáveis, que modificam a direção dos elétrons, fazendo com que estes atinjam a tela em diferentes posições, formando uma imagem, como ilustrado na Figura II. As bobinas K e L produzem um campo magnético na direção vertical e as bobinas M e N, na horizontal.

Em um certo instante, um defeito no televisor interrompe a corrente elétrica nas bobinas K e L e apenas as bobinas M e N continuam funcionando.

Assinale a alternativa em que melhor se representa a imagem que esse televisor passa a produzir nessa situação.

05-(UFU-MG) Uma carga q movendo-se com velocidade v imersa em um campo magnético B está sujeita a uma força magnética F_mag. Se v não é paralelo a B, marque a alternativa que apresenta as características corretas da força magnética F_mag.

a) O trabalho realizado por F_mag sobre q é nulo, pois F_mag é perpendicular ao plano formado por v e B .

b) O trabalho realizado por F_mag sobre q é  proporcional a v e B, pois F_mag é perpendicular a v.

c) O valor de F_mag não depende de v, somente de B; portanto F_mag não realiza trabalho algum sobre q.

d) O valor de F_mag é proporcional a v e B, sendo paralela a v; portanto o trabalho realizado por F_mag sobre q é proporcional a v.

06-(UNESP-SP) Uma mistura de substâncias radiativas encontra-se confinada em um recipiente de chumbo, com uma pequena abertura por onde pode sair um feixe paralelo de partículas emitidas. Ao saírem, três tipos de partícula, 1, 2 e 3, adentram uma região de campo magnético uniforme B com velocidades perpendiculares às linhas de campo magnético e descrevem trajetórias conforme ilustradas na figura.

Considerando a ação de forças magnéticas sobre cargas elétricas em movimento uniforme, e as trajetórias de cada partícula ilustradas na figura, pode-se concluir com certeza que

a) as partículas 1 e 2, independentemente de suas massas e velocidades, possuem necessariamente cargas com sinais contrários e a partícula 3 é eletricamente neutra (carga zero).

b) as partículas 1 e 2, independentemente de suas massas e velocidades, possuem necessariamente cargas com sinais contrários e a partícula 3 tem massa zero.

c) as partículas 1 e 2, independentemente de suas massas e velocidades, possuem necessariamente cargas de mesmo sinal e a partícula 3 tem carga e massa zero.

d) as partículas 1 e 2 saíram do recipiente com a mesma velocidade.

e) as partículas 1 e 2 possuem massas iguais, e a partícula 3 não possui massa.

07-(PUC-MG) Uma partícula de carga q, com velocidadee massa m dentro de um campo magnético, fica sujeita a uma força  pela ação  desse campo. Sobre a situação, foram feitas três afirmações.

I. A intensidade da força  depende do valor de q.

II. O sentido da força  depende do sinal de q.

III. A intensidade da força depende da velocidade v e da massa m da partícula.

A afirmativa está CORRETA em:

08-(UNESP-SP) A figura representa as trajetórias de duas partículas, 1 e 2, deixadas numa câmara de bolhas de um acelerador de partículas, imersa num campo magnético uniforme. Concluiu-se que, para que essas trajetórias fossem possíveis, deveria existir uma outra partícula, 3, que interagiu com as duas primeiras. Sabe-se que essas trajetórias estão num mesmo plano, coincidente com o plano da figura, perpendicular à direção do campo magnético.

a) Sabendo-se que a carga elétrica da partícula 1 é positiva, qual a carga das outras duas partículas? Justifique.

b) Qual o sentido do campo magnético? Justifique.

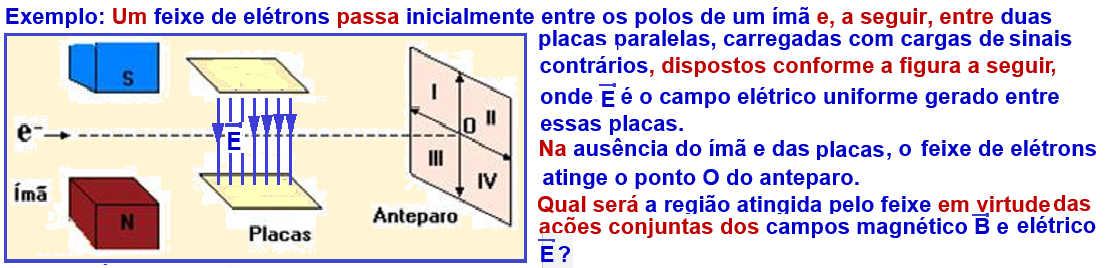
09-(UFMG-MG) Um feixe de elétrons passa inicialmente entre os pólos de um ímã e, a seguir, entre duas placas paralelas, carregadas com cargas de sinais contrários, dispostos conforme a figura a seguir. Na ausência do ímã e das placas, o feixe de elétrons atinge o ponto O do anteparo.

Em virtude das opções dos campos magnético e elétrico, pode-se concluir que o feixe

a) passará a atingir a região I do anteparo.              

b) passará a atingir a região II do anteparo.

c) passará a atingir a região III do anteparo.                

d) passará a atingir a região IV do anteparo.

e) continuará a atingir o ponto O do anteparo.

10-(UNESP-SP) Sabe-se que no ponto P da figura existe um campo magnético na direção da reta RS e apontando de R para S. Quando um próton (partícula de carga positiva) passa por esse ponto com a velocidade  mostrada na figura, atua sobre ele uma força, devida a esse campo magnético,

a) perpendicular ao plano da figura e "penetrando" nele.             

b) na mesma direção e sentido do campo magnético.

c) na direção do campo magnético, mas em sentido contrário a ele.

d) na mesma direção e sentido da velocidade.

e) na direção da velocidade, mas em sentido contrário a ela.

11-(ITA-SP) Qual dos esquemas abaixo ilustra o movimento de uma partícula carregada em um campo magnético uniforme?

Convenções:

12-(UFU-MG) A figura mostra a tela de um osciloscópio onde um feixe de elétrons, que provém perpendicularmente da página para seus olhos, incide no centro da tela. Aproximando-se lateralmente da tela dois imãs iguais com seus respectivos pólos mostrados, verificar-se-á que o feixe:

a) será desviado para cima     

b) será desviado para baixo     

c) será desviado para a esquerda     

d) será desviado para a direita

e) não será desviado

13-(UFSM-RS) As imagens, captadas por um aparelho de ultra–som, são visualizadas na tela de um monitor. O ponto imagem

na tela é obtido pela deflexão de elétrons por bobinas, nas quais circulam correntes elétricas variáveis, conforme mostra a figura.

O ponto P, à direita da tela, acontece somente na situação em que os campos magnéticos, gerados pelas bobinas, estão orientadas de acordo com a figura da alternativa.

14-(UFRS) No interior de um acelerador de partículas existe um campo magnético muito mais i

intenso que o campo magnético terrestre, orientado de tal maneira que um elétron lançado horizontalmente do sul para o norte, através do acelerador é desviado para o oeste. O campo magnético do acelerador aponta:

a) do norte para o sul        

b) do leste para o oeste      

c) do oeste para o leste       

d) de cima para baixo     

e) de baixo para cima

15-(UFSCAR-SP) Uma pequena esfera carregada eletricamente com carga positiva e em queda livre penetra em uma região onde um campo magnético horizontal atua uniformemente.

O esboço que melhor representa a trajetória da esfera no interior dessa região é

16-(UNESP-SP) Uma partícula com carga elétrica positiva desloca-se no plano Z - X na direção d - b, que é diagonal do quadrado a, b, c, d indicado na figura (1). É possível aplicar na região do movimento da carga um campo magnético uniforme nas direções dos eixos (um de cada vez), como é mostrado nas figuras (2), (3) e (4).

  Em quais casos a força sobre a partícula será no sentido negativo do eixo Y?

a) Somente no caso 2.         

b) Nos casos 2 e 4.         

c) Somente no caso 3.         

d) Nos casos 3 e 4.         

e) Somente no caso 4.

17-(FGV-SP) Em 2008, o maior acelerador de partículas já construído foi colocado em funcionamento. Em seu primeiro teste, um feixe de prótons foi mantido em movimento circular dentro do grande anel, sendo gradativamente acelerado até a velocidade desejada.

A figura mostra uma secção reta desse anel. Admita que um feixe de prótons esteja sendo conduzido de modo acelerado no sentido do eixo y. De acordo com as leis do eletromagnetismo, os campos elétrico e magnético, nessa ordem, na origem do sistema de eixos indicado, têm sentidos que apontam para o:

a) positivo de y e negativo de z.         

b) positivo de y e positivo de z.          

c) positivo de y e positivo de x.

d) negativo de y e positivo de z.             

e) negativo de y e negativo de x.              

 18-(FATEC-SP) Ao vídeo de um televisor encostam-se as faces polares de um imã, conforme o esquema abaixo (face norte em cima, face sul para baixo). A imagem se distorce com desvio:

a) para a esquerda           

b) para a direita         

c) para cima          

d) para baixo         

e) a imagem não se distorce                         

19-(PUC-RS) Um feixe de elétrons incide horizontalmente no centro do anteparo. Estabelecendo-se um campo magnético vertical para cima, o feixe de elétrons passa a atingir o anteparo em que região?

a) região 1                      

b) região 2                        

c) segmento 0A                           

d) segmento CD                          

e) região 3

20-(UFRRJ-RJ) Uma partícula de carga q entra com velocidade V_o numa região onde existe um campo magnético uniforme B.

No caso em que V_o e B possuem a mesma direção, podemos afirmar que a partícula

a) sofrerá um desvio para sua direita.              

b) sofrerá um desvio para sua esquerda.                  

c) será acelerada na direção do campo magnético uniforme B.                   

d) não sentirá a ação do campo magnético uniforme B.                 

e) será desacelerada na direção do campo magnético uniforme B.

21-(PUC–SP) Na figura pode-se ver a representação de um ímã. As letras N e S identificam os pólos do ímã, respectivamente, Norte e Sul. Uma carga positiva passa com uma velocidade pela região entre os pólos desse ímã e não sofre nenhum desvio em sua direção. Nessas condições, é correto afirmar que a direção e o sentido de , cujo módulo é diferente de zero, podem ser, respectivamente:

a) perpendicular ao plano desta folha, entrando nele.                  

b) perpendicular ao plano desta folha, saindo dele.
c) paralela ao plano desta folha, da esquerda para a direita.        

d) paralela ao plano desta folha, de cima para baixo.
e) paralela ao plano desta folha, de baixo para cima.

22-(UFMG-MG) Em algumas moléculas, há uma assimetria na distribuição de cargas positivas e negativas, como representado, esquematicamente, na figura a seguir.

Considere que uma molécula desse tipo é colocada em uma região onde existem um campo elétrico  e um campo magnético

, uniformes, constantes e mutuamente perpendiculares.

Nas alternativas a seguir, estão indicados as direções e os sentidos desses campos.

Assinale a alternativa em que está representada CORRETAMENTE a orientação de equilíbrio dessa molécula na presença dos dois campos.

23-(UESC-SC) Um feixe de elétrons penetra na região de um campo magnético uniforme de módulo igual a B. O ângulo formado entre a direção da velocidade do feixe e as linhas de indução do campo mede 60°.

Nessas condições, a trajetória descrita pelo feixe é

24-(UFJF-MG) Um filtro de velocidades é um dispositivo que utiliza campo elétrico uniformeperpendicular ao campo magnético uniforme  (campos cruzados), para selecionar partículas carregadas com determinadas velocidades. A figura a seguir mostra uma região do espaço em vácuo entre as placas planas e paralelas de um capacitor. Perpendicular ao campo produzido pelas placas, está o campo magnético uniforme. Uma partícula positiva de carga q move-se na direção z com velocidade constante (conforme a figura 1).

a) na figura 2, represente os vetores força elétrica, , e força magnética,, que atuam na partícula assim que entra na região de campos cruzados, indicando suas magnitudes.

b) Determine a velocidade que a partícula deve ter, para não ser desviada.

25-(UFRRJ-RJ) Uma partícula de carga positiva q e inicialmente com velocidade V_o no sentido positivo do eixo Y penetra em uma região onde existe um campo elétrico E_o constante, no sentido positivo do eixo X, e um campo magnético B_o, também constante.

Sabendo-se que a velocidade da partícula não se altera, mesmo depois que ela passa a sofrer a ação dos campos, determine em função de V_o e E_o:

(Desconsidere qualquer efeito gravitacional)

a) a componente X do campo magnético;

b) a componente Z do campo magnético;

26-(PUC-SP) Um elétron num tubo de raios catódicos está se movendo paralelamente ao eixo do tubo com velocidade de 10⁷m/s.

Aplicando-se um campo de indução magnética de 2T, paralelo ao eixo do tubo, qual o valor da força magnética que atua sobre o elétron? Considere a carga de um elétron q=1,6.10^-19C.

27-(UFRS-RS) A figura a seguir representa uma região do espaço no interior de um laboratório, onde existe um campo magnético estático e uniforme. As linhas do campo apontam perpendicularmente para dentro da folha, conforme indicado.

Uma partícula carregada negativamente é lançada a partir do ponto P com velocidade inicial v_o em relação ao laboratório.

Assinale com V (verdadeiro) ou F (falso) as afirmações abaixo, referentes ao movimento subseqüente da partícula, com respeito ao laboratório.

I. Se v_o for perpendicular ao plano da página, a partícula seguirá uma linha reta, mantendo sua velocidade inicial.

II. Se v_o apontar para a direita, a partícula se desviará para o pé da página.

III. Se v_o apontar para o alto da página, a partícula se desviará para a direita.

A seqüência correta, de cima para baixo, é

28-(UNIFESP-SP) Uma partícula eletricamente carregada, inicialmente em movimento retilíneo uniforme, adentra uma região de campo magnético uniforme , perpendicular à trajetória da partícula. O plano da figura ilustra a trajetória da partícula, assim como a região de campo magnético uniforme, delimitada pela área sombreada.

Se nenhum outro campo estiver presente, pode-se afirmar corretamente que, durante a passagem da partícula pela região de campo uniforme, sua aceleração é

a) tangente à trajetória, há realização de trabalho e a sua energia cinética aumenta.

b) tangente à trajetória, há realização de trabalho e a sua energia cinética diminui.

c) normal à trajetória, não há realização de trabalho e a sua energia cinética permanece constante.

d) normal à trajetória, há realização de trabalho e a sua energia cinética aumenta.

e) normal à trajetória, não há realização de trabalho e a sua energia cinética diminui.

29-(UFSCAR-SP) O professor de Física decidiu ditar um problema "para casa", faltando apenas um minuto para terminar a aula. Copiando apressadamente, um de seus alunos obteve a seguinte anotação incompleta:

Um elétron ejetado de um acelerador de partículas entra em uma câmara com velocidade de 8.10⁵ m/s, onde atua um campo magnético uniforme de intensidade 2,0.10^-3-----.

Determine a intensidade da força magnética que atua sobre o elétron ejetado, sendo a carga de um elétron -1,6.10^-19 C .

Sabendo que todas as unidades referidas no texto estavam no Sistema Internacional,

a) quais as unidades que acompanham os valores 2,0.10^-3 e -1,6.10^-19, nesta ordem?

b) resolva a "lição de casa' para o aluno, considerando que as direções da velocidade e do campo magnético são perpendiculares entre si”.

30- (UFG-GO) Uma partícula de carga elétrica q e massa m, é ejetada numa região onde existe campo elétrico e magnético, ambos não nulos, mas cuja força resultante sobre a partícula é nula. Desprezando o campo gravitacional, o que você pode dizer quanto a direção dos campos elétrico e magnético? Explique a sua resposta.

31-(UECE-CE) A maior força de origem magnética (medida em newton) que pode atuar sobre um elétron (carga e = 1,6.10^-19 C)

em um tubo de TV, onde existe um campo magnético de módulo B = 83,0 mT, quando sua velocidade é de 7,0.10⁶ m/s, vale aproximadamente

32-(ITA-SP) A figura mostra uma partícula de massa m e carga q > 0 , numa região com campo magnético  constante e uniforme, orientado positivamente no eixo x. A partícula é então lançada com velocidade inicial  no plano xy, formando o

ângulo θ indicado, e passa pelo ponto P, no eixo x, a uma distância d do ponto de lançamento.

Assinale a alternativa correta.

a) O produto d q B deve ser múltiplo de 2πmvcosθ .

b) A energia cinética da partícula é aumentada ao atingir o ponto P.

c) Para θ=0 , a partícula desloca-se com movimento uniformemente acelerado.

d) A partícula passa pelo eixo x a cada intervalo de tempo igual a m/qB.

e) O campo magnético não produz aceleração na partícula.

33-(CFT-CE) Uma partícula, de massa m e carregada positivamente, é lançada com velocidade v do ponto P, centro da face de um paralelepípedo formado por 4 cubos de arestas iguais, numa região onde existe um campo magnético uniforme B, orientado conforme a figura a seguir.

Desprezando ações gravitacionais, podemos afirmar CORRETAMENTE que a partícula seguirá uma trajetória:

a) retilínea, passando pelo ponto L             

b) circular, no plano vertical LIEP                

c) circular, no plano horizontal LKCP

d) parabólica, no plano vertical GFEP       

e) retilínea, passando pelo ponto K

34- (UEPB) Uma maneira de se obter informações sobre a carga e a massa de uma partícula é fazê-la passar, através de um campo magnético uniforme. A partir da sua trajetória circular pode-se, conhecendo-se o campo, a velocidade da partícula e o raio da trajetória, determinar o sinal da carga elétrica e o valor da massa. A figura mostra parte das trajetórias 1 e 2 deixadas por duas partículas P₁ e P₂, respectivamente. Os pontos indicam um campo magnético B constante que sai perpendicular à folha da prova. Considere que as duas partículas, P₁ e P₂, possuem cargas de mesmo módulo e sinais contrários e penetram perpendicularmente, com a mesma velocidade constante V_o, na região do campo B. Analisando as trajetórias e tomando como base o campo magnético mostrado, conclui-se que:

a) a partícula P₁ possui carga negativa e o valor é maior que o da partícula P₂.
b) a partícula P₁ possui carga positiva e o valor é maior que o da partícula P₂.
c) a partícula P₁ possui carga positiva e o valor é menor que o da partícula P₂.
d) a partícula P₁ possui carga negativa e o valor é menor que o da partícula P₂.
e) a partícula P₁ possui carga positiva e o valor é igual ao da partícula P₂.

35-(UFSC) A figura representa um espectrômetro de massa, dispositivo usado para a determinação da massa de íons. Na fonte F, são produzidos íons, praticamente em repouso. Os íons são acelerados por uma diferença de potencial V_AB, adquirindo uma velocidade  sendo lançados em uma região onde existe um campo magnético uniforme . Cada íon descreve uma trajetória semicircular, atingindo uma chapa fotográfica em um ponto que fica registrado, podendo ser determinado o raio R da trajetória.

Considerando a situação descrita, assinale a(s) proposição(ões) CORRETA(S):

(01) A carga dos íons, cujas trajetórias são representadas na figura, é positiva.

(02) A energia cinética E_C que o íon adquire, ao ser acelerado pela diferença de potencial elétrico V_AB, é igual ao trabalho realizado sobre ele e pode ser expressa por  E_C = qV_AB, onde q é a carga do íon.

(04) A carga dos íons, cujas trajetórias são representadas na figura, tanto pode ser positiva como negativa.

(08) O raio da trajetória depende da massa do íon, e é exatamente por isso que é possível distinguir íons de mesma carga elétrica e massas diferentes.

(16) Mesmo que o íon não apresente carga elétrica, sofrerá a ação do campo magnético que atuará com uma força de direção perpendicular à sua velocidade .

 36-(UNICAMP-SP) A utilização de campos elétrico e magnético cruzados é importante para viabilizar o uso da técnica híbrida de tomografia de ressonância magnética e de raios X. A figura a seguir mostra parte de um tubo de raios X, onde um elétron, movendo-se com velocidade v = 5,0.10⁵ m/s ao longo da direção x, penetra na região entre as placas onde há um campo magnético uniforme, , dirigido perpendicularmente para dentro do plano do papel. A massa do elétron é m_e= 9.10^-31 kg e a sua carga elétrica é q = - 1,6.10^-19C. O módulo da força magnética que age sobre o elétron é dado por F = qvB senθ, onde θ é o ângulo entre a velocidade e o campo magnético.

a) Sendo o módulo do campo magnético B = 0,010T, qual é o módulo do campo elétrico que deve ser aplicado na região entre as placas para que o elétron se mantenha em movimento retilíneo uniforme?

b) Numa outra situação, na ausência de campo elétrico, qual é o máximo valor de B para que o elétron ainda atinja o alvo? O comprimento das placas é de 10 cm.

37-(FUVEST-SP) Um próton de massa M=1,26.10^-7kg, com carga elétrica Q=1,6.10^-19C, é lançada em A, com velocidade v_o, em uma região onde atua um campo magnético uniforme B, na direção x. A velocidade v_o, que forma um ângulo θ com o eixo x, tem componentes v_ox=4,0.10⁶m/s e v_oy=3,0.10⁶m/s. O próton descreve um movimento em forma de hélice, voltando a cruzar o eixo x, em P, com a mesma velocidade inicial, a uma distância L_o=12m do ponto A.

Desconsiderando a ação do campo gravitacional e utilizando π=3, determine:

a) o intervalo de tempo Δt, em segundos, que o próton demora para ir de A a P.

b) o raio R, em metros, do cilindro que contém a trajetória em hélice do próton.

c) a intensidade do campo magnético B, em tesla, que provoca esse movimento.

38-(UFBA) A figura esquematiza o experimento realizado por JJ. Thomson para determinar a razão carga/massa do elétron. Nesse experimento, os elétrons, de massa m e carga q, são emitidos pela fonte F, a partir do repouso, e acelerados pela ddp U da fonte, penetrando na região do campo de indução magnética uniforme, através do orifício O existente na placa e incidindo no ponto P.

Desprezando-se as ações gravitacionais, é correto afirmar:

01. As linhas de indução magnética são perpendiculares ao plano da figura, orientadas para fora desse plano.

02. A força magnética que atua nos elétrons  tem sentido da esquerda para a direita.

04. Na região de , a variação da energia cinética é zero.

08. A medida do segmento OP é m.v/qB

16. O tempo de permanência dos elétrons na região de  é πm/qB

Dê como resposta a soma dos números correspondentes às afirmações corretas.

39-(IME–RJ) Considere um elétron de massa m e carga -e, que se move com velocidade  conforme indicado na figura. No instante t = 0 é ligado um campo magnético  uniforme em todo o espaço. Desprezando a ação da gravidade, determine:

a) o trabalho realizado pela força magnética após um intervalo de tempo Δt.
b) o período do movimento no plano perpendicular a .
c) a trajetória seguida pelo elétron, graficamente.

40-(UFRJ-RJ) Uma partícula de massa m e carga elétrica positiva q entra em uma região na qual existem um campo elétrico e um campo magnético, ambos uniformes, constantes, perpendiculares entre si e de módulos respectivos E e B. O peso da partícula é totalmente desprezível comparado à força elétrica, de modo que podemos supor somente as forças elétrica e magnética agindo sobre a partícula na região.

A partícula entra na região com velocidade inicial , de módulo v_o = 2E/B e direção perpendicular aos campos elétrico e magnético, e desvia-se até atingir, com velocidade nula, uma distância máxima d da reta suporte da velocidade inicial . A partícula volta a aproximar-se dessa reta, de modo que sua trajetória é uma curva plana como ilustra a figura a seguir.

Considerando como dados E, B, q e m, calcule a distância d.

41-(UNESP-SP) Uma tecnologia capaz de fornecer altas energias para partículas elementares pode ser encontrada nos aceleradores de partículas, como, por exemplo, nos cíclotrons. O princípio básico dessa tecnologia consiste no movimento de partículas eletricamente carregadas submetidas a um campo magnético perpendicular à sua trajetória.

Um cíclotron foi construído de maneira a utilizar um campo magnético uniforme, , de módulo constante igual a 1,6 T, capaz de gerar uma força magnética, , sempre perpendicular à velocidade da partícula. Considere que esse campo magnético, ao atuar sobre uma partícula positiva de massa igual a 1,7 x 10^–27 kg e carga igual a 1,6 x 10^–19 C, faça com que a partícula se movimente em uma trajetória que, a cada volta, pode ser considerada circular e uniforme, com velocidade igual a 3,0 x 10⁴ m/s. Nessas condições, o raio dessa trajetória circular seria aproximadamente

1. 1 x 10^–4 m.                 

2.  b) 2 x 10^–4 m.                   

3. c) 3 x 10^–4 m.                    

4. d) 4 x 10^–4 m.                    

5. e) 5 x 10^–4 m.  

42-(UFMG-MG) Reações nucleares que ocorrem no Sol produzem partículas – algumas eletricamente carregadas –, que são lançadas no espaço. Muitas dessas partículas vêm em direção à Terra e podem interagir com o campo magnético desse planeta.

Nesta figura, as linhas indicam, aproximadamente, a direção e o sentido do campo magnético em torno da Terra:

Nessa figura, K e L representam duas partículas eletricamente carregadas e as setas indicam suas velocidades em certo instante.

Com base nessas informações, Alice e Clara chegam a estas conclusões:

• Alice - “Independentemente do sinal da sua carga, a partícula L terá a direção de sua velocidade alterada pelo campo magnético da Terra.”

• Clara - “Se a partícula K tiver carga elétrica negativa, sua velocidade será reduzida pelo campo magnético da Terra e poderá não atingi-la.”

Considerando-se a situação descrita, é CORRETO afirmar que

a) apenas a conclusão de Alice está certa.        

b) apenas a conclusão de Clara está certa.        

c) ambas as conclusões estão certas. 

d) nenhuma das duas conclusões está certa. 

43-(ITA-SP)  Um elétron e acelerado do repouso através de uma diferença de potencial V e entra numa região na qual atua um campo magnético, onde ele inicia um movimento ciclotrônico, movendo-se num círculo de raio RE com período TE. Se um próton fosse acelerado do repouso através de uma diferença de potencial de mesma magnitude e entrasse na mesma região em que atua o campo magnético, poderíamos afirmar sobre seu raio RP e período TP que

a) RP = RE e TP = TE.              

b) RP > RE e TP > TE.             

c) RP > RE e TP = TE.             

d) RP < RE e TP = TE.  

e) RP = RE e TP < TE.  

44-(UFMS-MS) O acelerador LHC colidiu dois prótons, girando em trajetórias circulares com sentidos opostos, sendo um no sentido horário e o outro no sentido anti-horário, veja a figura. Considere que as trajetórias dos prótons antes da colisão eram mantidas circulares devido unicamente à interação de campos magnéticos perpendiculares ao plano das órbitas dos prótons. Com fundamentos no eletromagnetismo, é correto afirmar:

01) A finalidade do campo magnético é apenas mudar a direção da velocidade dos prótons.  

02) A finalidade do campo magnético é aumentar a energia cinética dos prótons.  

04) O próton que está girando no sentido anti-horário está submetido a um campo magnético que possui um sentido que está entrando no plano da página.  

08) A força magnética aplicada em cada próton possui direção tangente à trajetória.  

16) A força magnética aplicada em cada próton não realiza trabalho.  

45-(UNIRG-TO)  

Essa configuração de campos elétrico e magnético funciona como um seletor de velocidade para partículas carregadas. Desprezando-se a força gravitacional, a velocidade em que a partícula não sofre desvio, ou seja, a força elétrica anula a força magnética, é dada por

46-(UFG-GO)

Uma cavidade em um bloco de chumbo contém uma amostra radioativa do elemento químico bário. A figura (a) ilustra as trajetórias das partículas a, b e g emitidas após o decaimento radioativo.

Aplica-se um campo magnético uniforme entrando no plano da folha, conforme ilustrado na figura (b). O comportamento representado pelas trajetórias ocorre porque

a) a partícula b tem carga positiva e quantidade de movimento maior que a de a.

b) as partículas a e b têm cargas opostas e mesma quantidade de movimento.

c) a partícula a tem carga positiva e quantidade de movimento maior que a de b.

d) a partícula a tem carga maior e quantidade de movimento menor que a de b.

e) a partícula g tem carga positiva e quantidade de movimento menor que a de b.

47-(FUVEST-SP) 

A figura a seguir mostra o esquema de um instrumento (espectrômetro de massa), constituído de duas partes. Na primeira parte, há um campo elétrico , paralelo a esta folha de papel, apontando para baixo, e também um campo magnético , perpendicular a esta folha, entrando nela. Na segunda, há um campo magnético,  de mesma direção que, mas em sentido oposto. Íons positivos, provenientes de uma fonte, penetram na primeira parte e, devido ao par de fendas F₁ e F₂ , apenas partículas com velocidade , na direção perpendicular aos vetores  e , atingem a segunda parte do equipamento, onde os íons de massa m e carga q tem uma trajetória circular com raio R.

a) Obtenha a expressão do módulo da velocidade em função de  e de .

b) Determine a razão m/q dos íons em função dos parâmetros E, B₁, B₂ e R.

c) Determine, em função de R, o raio R’ da trajetória circular dos íons, quando o campo magnético, na segunda parte do equipamento, dobra de intensidade, mantidas as demais condições.

48-(UFOP-MG)

O cíclotron é um acelerador em que partículas carregadas executam movimento circular em um

plano perpendicular a um campo magnético uniforme de módulo B. Se o campo magnético for o único campo aplicado, a velocidade angular do movimento circular resultante depende somente da razão carga/massa e de B. Em um acelerador típico, o valor de B é de 1 tesla e as partículas percorrem uma trajetória de raio de 50 cm.

Qual a ordem de grandeza da velocidade da partícula (dados: carga igual a 1,6.10^-19C e massa igual 1,67.10^-27 kg)?

49-(UEPG-PR) 

Cargas elétricas em movimento originam campo magnético. Quando uma carga elétrica encontra-se em movimento, em um campo magnético, há uma interação entre esse campo e o campo originado pela carga. Essa interação é manifestada por uma força que age na carga elétrica, a qual é denominada força magnética.

Sobre força magnética, assinale o que for correto.

01) O sentido da força magnética depende do sinal da carga em movimento. 

02) A direção da força magnética, sobre uma carga em movimento, é perpendicular ao plano formado pelo vetor velocidade da carga e pelo vetor indução magnética. 

04) Quando uma carga elétrica é lançada perpendicularmente em direção de um campo magnético uniforme, a carga descreverá uma trajetória circular. 

08) A força magnética sobre uma carga elétrica movendo-se, em uma direção paralela à direção do campo magnético uniforme, é nula. 

50-(UFTM-MG)

Um elétron penetra numa região entre duas placas planas e paralelas pela fenda F₁ e a atravessa segundo a direção tracejada mostrada na figura, saindo pela fenda F₂, sem sofrer desvio.

Durante a travessia, o elétron fica sujeito a um campo de indução magnética  e a um campo elétrico , ambos uniformes. Considerando o sistema de referência xyz, e sabendo que as placas são paralelas ao plano xz, isso será possível se

a)  tiver a mesma direção e o mesmo sentido do eixo x, e  tiver a mesma direção e o mesmo sentido do eixo z.  

b)  tiver a mesma direção e o mesmo sentido do eixo z, e  tiver a mesma direção e o mesmo sentido do eixo y.  

c)  tiver a mesma direção e o mesmo sentido do eixo y, e  tiver a mesma direção e o sentido oposto ao do eixo z.  

d)  e tiverem a mesma direção e o mesmo sentido do eixo z.  

e)  e tiverem a mesma direção e o mesmo sentido do eixo x.  

51-(ITA-SP)

Prótons (carga e e massa m_p), deuterons (carga e e massa m_d = 2m_p) e partículas alfas (carga 2e e massa m_a = 4m_p) entram em um campo magnético uniforme  perpendicular a suas velocidades, onde se movimentam em órbitas circulares de períodos T_p, T_d e T_a, respectivamente. Pode-se afirmar que as razões dos períodos T_d/T_p e T_a/T_p são, respectivamente,

52-(UNIMONTES-MG) 

Uma partícula carregada é injetada em uma região onde atua apenas um campo magnético de módulo B, perpendicular ao movimento inicial da partícula (veja a figura abaixo). Esse campo é

suficiente para fazer com que a partícula descreva um movimento circular. A carga da partícula é o triplo da carga do elétron, o módulo do campo é 2 T, e o módulo da velocidade da partícula é V = 10^-4.c, em que c é a velocidade da luz no vácuo. Se a massa da partícula é M = 3.10^-25 kg, o raio R, descrito pela partícula, será, aproximadamente,

Dados: e = 1,6.10^-19 C e c=3.10⁸ m/s

53-(UFRJ-RJ) 

Uma partícula de massa m e carga q positiva, em movimento retilíneo uniforme, penetra em uma região na qual há um campo magnético uniforme, vertical e de módulo B. Ao sair da região, ela retoma um movimento retilíneo uniforme.

Todo o movimento se processa em um plano horizontal e a direção do movimento retilíneo final faz um ângulo θ com a direção do movimento retilíneo inicial. A velocidade da partícula é grande o bastante para desprezarmos a força gravitacional, de modo a considerarmos apenas a força magnética sobre ela.

a) Determine a razão v’ / v entre o módulo v’ da velocidade do movimento retilíneo final e o módulo v da velocidade do

movimento retilíneo inicial.

b) Calcule quanto tempo a partícula demora para atravessar a região em que há campo magnético em função de q, m, B e .

54-(UFPR-PR)

Uma experiência interessante, que permite determinar a velocidade  com em que partículas elementares se movem, consiste em utilizar um campo magnético em combinação com um campo elétrico . Uma partícula elementar com carga Q negativa move-se com velocidade paralelamente ao plano do papel (referencial inercial) e entra em uma região onde há um campo magnético  uniforme, constante e orientado para dentro do plano do papel, como mostra a figura. Ao se deslocar na região do campo magnético, a partícula fica sujeita a uma força magnética .

a) Obtenha uma expressão literal para o módulo de  e represente na figura o vetor  para a posição indicada da partícula.

b) Dispõe-se de um sistema que pode gerar um campo elétrico  uniforme, constante e paralelo ao plano do papel, que produz uma força elétrica  sobre a partícula. Represente na figura o vetor  necessário para que a partícula de carga Q mova-se em movimento retilíneo uniforme. Em seguida, obtenha uma expressão literal para o módulo da velocidadeda partícula quando ela executa esse movimento, em função das grandezas apresentadas no enunciado.

55-(UCPEL-RS)

Considere as afirmativas abaixo e as analise como VERDADEIRAS (V) ou FALSAS (F).

I. Uma carga elétrica colocada num campo magnético sempre fica sujeita a uma força.

II. Em cada ponto, as linhas do campo magnético são perpendiculares ao vetor campo magnético.

III. Um elétron move-se no vácuo com velocidade constante, quando penetra num campo magnético uniforme de direção perpendicular a sua velocidade, passa a mover-se em movimento retilíneo uniformemente acelerado.

IV. Se vários resistores estiverem ligados em paralelo, o que tiver maior resistência dissipa maior potência elétrica devido ao efeito Joule.

V. A resistividade de um condutor é diretamente proporcional ao comprimento que possui.

A sequência correta é

(A) V – V – F – F – F                              

(B) V – V – V – V – V                                      

(C) V – V – F – V – V

(D) F – V – F – F – V                               

(E) F – F – F – F – F

56-(PUC-RJ)

Em uma experiência de física, observa-se que uma carga elétrica puntiforme com carga elétrica q = 2 x 10^-3C se movimenta com velocidade constante v = 4 m/s, paralela ao eixo y, como ilustra a trajetória tracejada da figura.

Sabendo que a região do espaço por onde a carga se movimenta possui campo elétrico E = 2 N/C ao longo do eixo z e campo magnético B ao longo do eixo x, ambos uniformes, também representados na figura, determine:

a)  módulo, direção e sentido da força feita pelo campo elétrico sobre a carga q;

b)  módulo do campo magnético em N.s/m.C) atuando na carga

57-(UEM-PR)

Uma partícula, de massa M e carga elétrica Q positiva, é lançada horizontalmente com velocidade , da direita  para a esquerda, em uma região do espaço onde existem vácuo e um campo elétrico uniforme , que está direcionado de cima

para baixo. Nessa região do espaço, também existem um campo magnético uniforme  , orientado perpendicularmente para dentro do plano da página. De posse dessas informações, desconsiderando ação da gravidade, assinale o que for correto.

01) O módulo da força resultante que atua sobre a partícula é Q(vH + E).

02) Para que a trajetória da partícula se mantenha retilínea, é necessário que o módulo da sua velocidade de lançamento seja V_o=E/H.

04) Na situação descrita no enunciado, a trajetória da partícula é sempre desviada para baixo.

08) As linhas de força do campo magnético formam superfícies fechadas.

16) A passagem da partícula carregada na região dos campos elétrico e magnético altera as características físicas desses campos.

58-(UFES-ES)

Um bloco rígido e isolante de massa 400 g possui uma carga elétrica embutida positiva de 10,0 C e encontra-se em repouso em uma superfície definida pelo plano zy no ponto A, como é representado na figura ao lado.

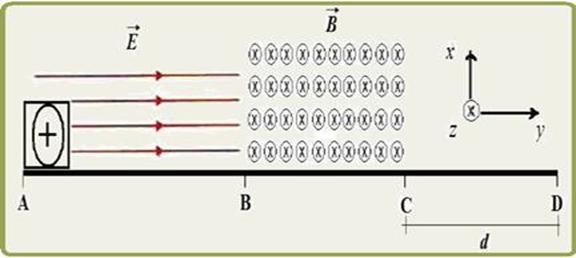
 Um campo elétrico uniforme e constante , de intensidade 1,00.10² N/C, é mantido ligado acelerando linearmente o bloco, até este atingir o ponto B. No trecho entre os pontos B e C, um campo magnético uniforme e constante é aplicado perpendicularmente ao plano xy representado por esta folha de papel e com sentido para dentro do papel. Considere que o bloco pode deslizar livremente, sem atrito, entre os pontos A e C; porém, existe atrito entre os pontos C e D.

A) Determine a velocidade escalar do bloco no momento imediatamente antes de atingir o ponto B. Considere que o bloco é um ponto material e que a distância entre A e B é de 50,0 cm.

B) Identifique e desenhe, num diagrama, as forças que atuam no bloco, quando ele se encontra entre os pontos B e C.

C) Encontre a intensidade do campo magnético para que a força de contato entre o bloco e a superfície definida pelo plano zy seja nula no trecho de B a C.

D) Determine o coeficiente de atrito cinético entre o bloco e a superfície definida pelo plano zy em função de v, g e d, considerando que o bloco chega ao ponto C com uma velocidade horizontal v e para no ponto D, percorrendo uma distância d.

59-(UDESC-SC)

A figura representa uma região do espaço onde existe um campo magnético uniforme  orientado perpendicularmente para dentro do plano desta figura. Uma partícula de massa  m e carga positiva  q penetra nessa região de campo magnético, perpendicularmente às linhas de

campo, com velocidade constante.

Considerando a situação descrita acima, assinale a alternativa incorreta.

a.  (   )  O período do movimento executado pela partícula na  região de campo magnético não depende de sua velocidade .

b.  (   )  O trabalho realizado pela força magnética sobre a partícula é diferente de zero.

c.  (   )  A frequência do movimento é inversamente proporcional à massa m da partícula.

d.  (   )  O módulo da força magnética que atua sobre a partícula é determinado pelo produto qVB.

e.  (   )  O raio da trajetória executada pela partícula na região de campo magnético é proporcional à quantidade de movimento da partícula.   

60-(EsPCEx)

Sob a ação exclusiva de um campo magnético uniforme de intensidade 0,4 T, um próton descreve um

movimento circular uniforme de raio 10 mm em um plano perpendicular à direção deste campo. A razão entre a sua massa e a sua carga é de 10^-8 kg/C. A velocidade com que o próton descreve este movimento é de:

Resolução comentada dos exercícios de vestibulares sobre

Força magnética sobre uma carga q imersa num campo magnético uniforme

01- R- A  ---  regra da mão esquerda

02- O campo magnéticose afasta do pólo norte do imã  ---  aplicando a regra da mão esquerda no

esquema abaixo você verificará que a força magnética desviará a carga na direção de x em seu sentido positivo  ---  R- C   

03- Utilizando a regra da mão esquerda a força  estaria saindo da folha, mas como a carga é negativa (elétrons) ela estará desviando os elétrons para dentro da folha, na direção horizontal da tela  ---  R- E

04- Observe na figura abaixo onde os pólos norte e sul foram aleatoriamente nomeados que a força

magnética tem direção vertical e sentido para baixo, e assim, os feixes são desviados na direção vertical da tela  ---  R- A

05- R- A  ---  veja teoria

06- As forças que desviam cada carga têm sentidos contrários, pois uma carga é positiva (1) e a outra negativa (2) e a carga 3 não sofre desvio, ou seja, é neutra  ---  R- A

07-

R- B

08- a) A partícula 2 desviada para a direita tem carga negativa. A partícula 3 é neutra porque não foi desviada.

b) O campo de indução tem vetor entrando no papel, pela regra da mão esquerda.

09- Entre os pólos do imã a força magnética estaria saindo da folha, mas como a carga é negativa está penetrando e desviando a carga para trás da folha  ---  quando a carga negativa passa entre as placas ela é desviada para cima (atraída pela placa positiva e repelida

 pela negativa)  ---  assim ela se desvia para trás da folha e para cima atingindo a região I  ---  R- A

10- Pela regra da mão esquerda a força magnética sobre a carga estará penetrando na folha  ---  veja a figura

R- A

11- R- D  ---  regra da mão esquerda

12- Pela regra da mão esquerda a força magnética estará para cima, mas como são eletros estará para baixo  ---  R- B    

13- O campo magnético vertical faz surgir sobre o feixe de elétrons uma força horizontal para a

 direita e o campo magnético horizontal faz surgir sobre o feixe de elétrons uma força vertical para cima  --- assim o feixe de elétrons é desviado para a direita e para cima  ---  R- A

14- Observe na figura abaixo que utilizando a regra da mão esquerda o vetor campo magnético

estaria entrando na folha, mas como se  trata de elétron (carga negativa), estará saindo  ---  R- E

15- Como, ao penetrar no campo magnético é vertical e para baixo e está penetrando na folha, a força magnética será horizontal e para a direita, fazendo com que a carga q se mova simultaneamente para baixo e para a direita  ---  R- D

16- Utilizando a regra da mão esquerda  ---  R- B

17- Sendo prótons cargas positivas e como são aceleradas no sentido do eixo positivo do eixo Y, a força elétrica é nesse sentido e consequentemente o campo elétrico também  ---  a força magnética aponta no sentido do eixo x, pois as cargas são desviadas nesse sentido (veja a curva do anel)  e usando a regra da mão esquerda, o sentido deserá o mesmo que o sentido negativo do eixo z  -- 

 R- A

18-  saindo da tela, para baixo (do norte para o sul)  ---  usando a mão esquerda a força magnética estará para a direita, mas como são elétrons o deslocamento será para a esquerda  ---  

R- A

19- R- C   ---  regra da mão esquerda

20- Sendo V_o e B vetores que tem a mesma direção, a força magnética sobre a partícula será nula e ela se moverá em movimento retilíneo e uniforme  ---  R- D

21- A velocidade deve ser paralela a que é do pólo norte para o pólo sul  ---  R- C

22- Como as moléculas estão em repouso a força magnética sobre elas é nula  ---  a força elétrica tem o mesmo sentido quepara a

carga positiva e sentido contrário para a carga negativa  ---  o único caso em que a molécula permanece em equilíbrio é a alternativa b  ---  R- B

23- R- E  ---  veja teoria

24- a)

b) Para a partícula não ser desviada a força resultante sobre ela deve ser nula  ---  F_e=F_m  ---  q.E=q.V.B  ---  V=E/B

25- a) Como a velocidade da carga permanece constante, então as forças elétrica e magnética que atuam sobre ela se cancelam, ou seja, a força magnética deve estar dirigida ao longo de X, no sentido negativo, pois a força elétrica está no sentido de x, positivo (q>0). Se houvesse uma componente X para o campo magnético, a força magnética teria uma componente Z, o que está excluído pela consideração anterior. Assim sendo, temos B_X = 0.

b) A intensidade da força elétrica (Fe=q.Eo) e da força magnética (F_m=q.Vo.B_Z) devem ser iguais  ---  B_Z=Eo/Vo  ---  para que o sentido da força magnética seja contrário ao da força elétrica, a componente B_Z deve ser negativa.

26- Como  e são paralelos, não surgirá força magnética sobre o elétron e ele não sofrerá desvio  ---  F_m=0

27- I. Verdadeira ---    e são paralelos

II. Verdadeira --- aplicando a regra da mão esquerda, a força magnética estará para cima, mas como a carga é negativa ela indicará para baixo.

III. Verdadeira  ---  aplicando a regra da mão esquerda, a força magnética estará para a esquerda, mas como a carga é negativa ela indicará para a direita.   

R- E

28- Dentro do campo magnético  é perpendicular a ela efetua um arco de circunferência em movimento circular uniforme com velocidade constante em intensidade  ---  a força magnética sobre a partícula é a força resultante centrípeta e consequentemente sobre ela surgirá também uma aceleração centrípeta (normal à trajetória)  ---  a força magnética é perpendicular ao deslocamento e consequentemente à velocidade e então o trabalho da força magnética é nulo (W=F.d.cos90^o=F.d.0=0)  ---  como a intensidade da velocidade é constante, a energia cinética também será constante  ---  R- C

29- a) tesla (T) e coulomb (C)

b) F_m=q.V.B.sen90^o=1,6.10^-19.8,0.10⁵.2,0.10³.1  ---  F_m=2,56.10^-16N

30- Para que a força resultante seja nula, as forças elétrica e magnética devem se anular o que só

pode ocorrer quando o vetor campo elétrico for perpendicular ao plano formado pelos vetores  e .

31- F_m=q.V.B.senθ  ---  a maior força magnética ocorre quando θ=90^o e sen90^o=1  ---  F_m=1,6.10^-19.7.10⁶.0,83=7,296.10^-13  ---   R- A

32-

33- Pela regra da mão esquerda a força magnética terá direção horizontal e sentido para a direita e será perpendicular ao plano que contém e , desviando o feixe nessa direção e sentido  ---  R- C

34- As partículas possuem cargas de sinais contrários já que a força magnética as desvia em sentidos opostos  ---  Partículas com a mesma velocidade e a mesma carga elétrica ao penetrarem num campo magnético uniforme com  perpendicular adescrevem trajetórias circulares de raios diferentes, pois na expressão R=m.V/q.B apenas R e m são variáveis, sendo os outros parâmetros constantes.Observe na expressão que R e m são diretamente proporcionais. Maior massa, maior o raio da curva.  ---  maior massa, menor valor q/m, pois q é a mesma para as duas cargas  ---  R-C 

35- (01) Correta  ---  pela regra da mão esquerda a força magnética é para a esquerda o que só acontece se a carga for positiva

(02) Correta  ---  o trabalho realizado para acelerar uma carga elétrica q, a partir do repouso, é igual à variação de sua energia cinética e vale W=ΔE_C=q.V_AB.

(04) Falsa  ---  veja (01)

(08) Correta  ---  massas diferentes sofrem desvios de raios diferente  ---  R=m.V/q.B

(16) Falsa  ---  só surge força se tiver carga elétrica q

R- (01+02+08)=11

36- a) Se o movimento é retilíneo e uniforme a força resultante deve ser nula e consequentemente as forças elétrica e magnética devem se anular  ---  F_e=F_m  ---  qE=qVBsenθ  ---  E=VBsen90^o=5.10⁵.0,010.1  ---  E=5,0.10³V/m ou E=5,0.10³N/C

b) Se não houver campo elétrico e se o campo magnético for nulo, o elétron atingirá o centro do alvo, mas se o valor de B for aumentando, a força magnética também irá aumentando e o elétron atingirá uma posição cada vez mais afastada do centro do alvo  ---  quando a incidência sobre o alvo for tangente, B terá o maior valor possível, pedido no exercício e, nesse caso, o raio da

trajetória circular é R=0,1m e a força magnética é a força resultante centrípeta  ---  F_m=F_C  ---  q.V.B.sen90^o=m.V²/R  ---  B=m.V/q.R  ---  B= 9.10^-31.5.10⁵/1,6.10^-19.10^-1  --- B≈3,0.10^-5T

37- a) Como não existe força magnética agindo sobre o próton, na direção horizontal (eixo x), seu movimento será uniforme de equação  ---  v_x=ΔS/Δt=L/Δt  ---  Δt=12/4.10⁶  ---  Δt=3.10^-6s

b) Esse tempo (que ele demora para ir de A a P), Δt=3.10^-6s é o período do movimento circular (tempo que a carga demora para efetuar uma volta completa)  ---  T=3.10^-6s  ---  no MCU  ---  v_y=ΔS/Δt  ---  uma volta completa  ---  ΔS=2πR  ---  v_y=2πR/T  ---  3.10⁶=2.3.R/3.10-6  ---  R=1,5m

c) R=m.v_y/q.B  ---  1,5=1,26.10^-7.3.10⁶/1,6.10^-19.B  ---  B=2.10^-2T

38- 01. Falsa  ---  pela regra da mão esquerda a força magnética indica para a esquerda, (inverte-se o sentido de F, pois q é negativa) e os eletros se desviariam para a esquerda. Assim as linhas de indução estão penetrando no plano da figura.

02. Falsa  ---  ela só é da esquerda para a direita no ponto onde os elétrons estão entrando no campo magnético e nos outros pontos ela é radial e com sentido para o centro da circunferência.

04. Correta  ---  Como se trata de um MCU com velocidade de módulo constante não há variação de energia cinética.

08- Falsa  ---  é o raio R que vale R=mv/qB  ---  o segmento OP vale 2mv/qB

16- Verdadeira  ---  o período do MCU vale T=2πm/qB  ---  como ele efetua apenas meia circunferência  ---  T=πm/qB

R- (04 + 16)=20

39- a) Este movimento é decomposto em dois, um MRU e um MCU, ambos com velocidade de intensidade constante e, portanto não ocorre em nenhum deles variação de energia cinética e conseqüentemente o trabalho realizado é nulo.

b) No plano perpendicular a , o eletron realiza um MCU onde  a expressão matemática da força magnética é   ---  F_m=q.V.B.senθ=q.V.B.1  ---  F_m=q.V.B  ---  lembrando que a força magnética F_m é responsável pelo movimento circular é a força resultante centrípeta de intensidade F_c=m.V²/R  ---  F_m=F_c  ---  q.V.B=m.V²/R  --- R=m.V/q.B (I)  ---  o período T (tempo que a carga q demora para efetuar uma volta completa) é fornecido por  ---  V=ΔS/Δt  ---  numa volta completa  ---  ΔS=2πR e Δt=T  ---  V=2πR/T (II)  ---  substituindo II em I  ---  R=m. (2πR/T)/q.B  ---  T=2πm/q.B  ---  ou T=2πm/eB  

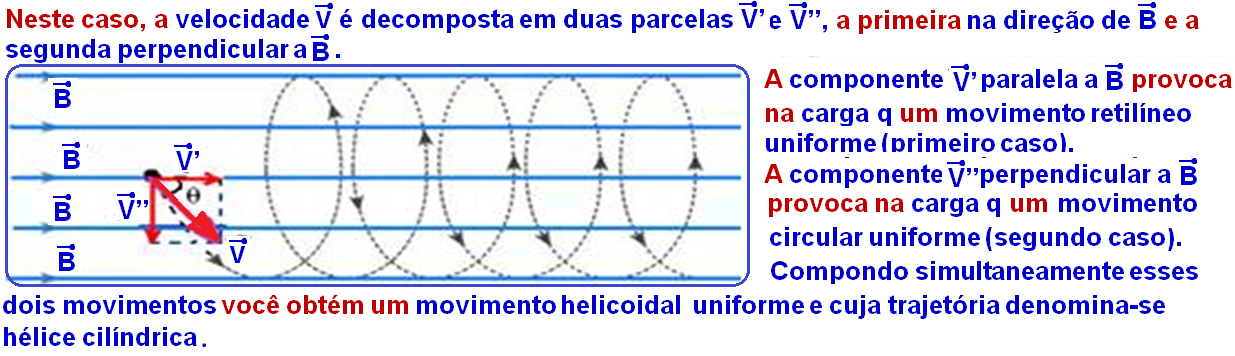
c) A velocidade  é decomposta em duas parcelas e , a primeira na direção de e a segunda perpendicular a .

* A componente paralela a provoca na carga q um movimento retilíneo uniforme (primeiro caso).

* A componente perpendicular a provoca na carga q um movimento circular uniforme (segundo caso).

Compondo simultaneamente esses dois movimentos você obtém um movimento helicoidal uniforme e cuja trajetória denomina-se hélice cilíndrica

40- Pelo teorema da energia cinética os trabalhos realizados pelas forças dos campos elétrico e magnético produziram a variação da energia cinética  ---   assim W_E + WB = mv_f²/2 – m.v_o²/2=0 – mv_o²/2  ---   W_E + W_B = - m.v_o²/2  ---   como os vetores força magnética e velocidade são perpendiculares, o campo magnético produz um MCU e como nele a intensidade da velocidade não varia, ele não provoca variação de energia cinética e o trabalho por ele realizado é nulo  ---   W_B = 0  ---   W_E + 0 = - m.v_o²/2  --- 

W_E = - m.v_o²/2  ---   como o campo elétrico é uniforme tem-se que W_E = - q.U=-qE.d   ---  – q.E.d = - m.v_o²/2 ---   q.E.d = m.(2E/B)²/2  ---   d = 2.m.E/(q.B²)

41- Sendo o movimento é circular uniforme, a força magnética age como resultante centrípeta   F_mag=F_C=  ---  R- B

42-  A força magnética sobre partícula em campo magnético tem intensidade dada por: F_mag= |q| v B senq, onde q é o ângulo entre os vetores .

Para a partícula K, q = 0° Þ senq = 0 Þ F_mag = 0 Þ essa partícula não sofre desvio, pois incide paralelamente a .

Para a partícula L, q = 90° Þ senq = 1 Þ F_mag = |q| v B  ---   a direção e o sentido dessa força são dados pela regra da mão esquerda  ---  a direção é perpendicular ao plano da figura, saindo se a carga é positiva; entrando se a carga é negativa, como ilustra as figuras.

R- A

43- A carga do elétron e a carga do próton têm mesmo módulo  ---   Assim: |q| = e  ---  aplicando o teorema da energia cinética no campo elétrico

. (equação 1)  ---  no campo magnético, a força magnética age como resultante centrípeta.

. (equação 2)  ---  Substituindo (1) em (2)  ---     ---  introduzindono radical  --- 

  ---   R =   ---  com a massa do próton e maior que a massa do elétron. Então: Rp > RE  --- 

Calculo do período (T), lembrando que ele é igual ao tempo gasto em uma volta  ---  T =   ---  como a massa do próton é maior que a do elétron  ---   TP > TE  --- R- B

44- (01) Correta. A força magnética sobre uma partícula eletrizada tem direção simultaneamente perpendicular ao campo e à velocidade. Assim sendo, Essa força exerce a função apenas de força centrípeta, alterando somente a direção do movimento, não alterando a velocidade. Logo, ela não transfere energia cinética às partículas, não realizando trabalho.

(02) Errada. Já justificado em (01).

(04) Correta. Basta aplicar a “regra da mão esquerda, lembrando que o vetor velocidade é tangente em cada ponto da trajetória”.

(08) Errada. Já justificado em (01).

(16) Correta. Já justificado em (01).  

01+ 04 + 16 = 21

45- Do enunciado F­_e = F_m  ---  q.E=q.v.b.sen90^o  ---  E=v.B  ---  v=E/B  ---  R- B

46- Quando as partículas penetram no campo magnético, todas tem velocidade vertical e para cima  ---  o campo magnético penetra no papel  ---  pela regra da mão esquerda a força que age sobre a carga positiva é horizontal e para a esquerda (é a α)  ---  a carga

positiva é desviada para a esquerda  ---  na carga negativa o sentido dessa força é invertido  ---  ela sofre desvio para a direita (é a β)  ---  a neutra não sofre desvio  ---  a neutra não sofre desvio (é a γ)  ---  observe que o desvio da α é menor, ou seja, ela possui maior inércia e consequentemente maior quantidade de movimento  ---  R- C

47- a) Observe a figura abaixo que mostra as forças que agem sobre um íon: a força elétrica no,

mesmo sentido do campo elétrico,pois os íons são positivos; pela regra da mão esquerda encontramos a força magnética, oposta à força elétrica  ---  para o íons que passam pela fenda F₂ essas forças se equilibram, força resultante nula  ---  F_magnética = F_elétrica  ---  q .v .B₁ = q E  ---  v=E/B₁

b) A força magnética  devida a  exerce o papel de resultante centrípeta  ---  F_c = F’_magnética  ---  mv²/R=qvB₂  ---  m/q=B₂R/v  ---  substituindo v em v=E/B₁  ---  m/q=B₂R/(E/B₁)  ---  m/q=(B₁.B₂)/R/E

c) B’₂=2B₂  ---  isolando R na expressão acima  ---  R=mE/qB₁.B₂  ---  novo raio R’  ---  R’=mE/qB₁.2B₂  ---  razão entre esses raios  ---  R’/R=mE/2qB₁.B₂xqB₁.B₂/mE  ---  R’/R=1/2  ---  R’=R/2

48-

R- C

49- Todas as afirmativas estão corretas

R- (01 + 02 + 04 + 08) = 15

50- Para que o elétron não seja desviado, a resultante das forças atuantes sobre ele deve ser nula  ---  como a partícula possui carga negativa, a força elétrica tem sentido oposto ao do campo  ---  se  tem o mesmo sentido do eixo z, a força elétrica está sobre esse mesmo eixo orientada para baixo  ---  se  tem o mesmo sentido do eixo x, pela regra da mão esquerda, o a força magnética está sobre o eixo z, orientada para cima. Podemos ainda relacionar as intensidades desses campos  --- sendo v e q os módulos da velocidade e da carga do elétron  ---  F_elétrica=F_magnética  ---  qE=qvB  ---  v=E/B  ---  R- A

51- Dados  ---  m_p  ---  q_p = e  ---  q_d = e  ---  m_d = 2 mp  ---  q_a = 2 e  ---   m_a = 4 m_p  ---  para uma partícula de massa m e carga de módulo q lançada perpendicularmente às linhas de indução de um campo magnético uniforme, , com velocidade, a força magnética,, age como resultante centrípeta, , provocando movimento circular uniforme de raio r  ---  F_c=F  ---  mv²/R=qvB  ---  r=mv/qB (I)  --- expressão da velocidade para o movimento uniforme  ---  V=∆S/∆t  ---  numa volta completa  ---  ∆S=2πR  ---

∆t=T (período)  ---  v=2πr/T  ---  T=2πr/v (II)  ---  (II) em (I)  ---  T=2π/v.(mv/qB)  ---  T=2πm/qB  ---  substituindo  ---  T_p=2πm_p/eB  ---  T_d=2π2m_p/eB  ---  T_a=2π4m_p/2eB  ---  T_a=4πm_p/eB  ---  razões pedidas  ---  T_d/T_p= 4πm_p/eB x eB/2πmn_p  ---  T_p/T_d=2  ---  T_a/T_p= T=4πm_p/eB x eB/2πm_p  ---  T_a/T_p=2  ---  R- E

52- F_magn=F_cent  ---  qvBsen90^o=mv²/R  ---  R=mv/qB  ---  R=(3.10^-25.10^-4.3.10⁸)/(3.1,6.10^-19.2)  ---  R=0,009m≈10mm≈1cm  ---  R- A

53- a) Como a força magnética age como resultante centrípeta, ela altera apenas a direção da velocidade da partícula, pois trata-se de um movimento circular uniforme (MCU) onde o módulo da partícula permanece constante  ---  V’=V  ---  V’/V=1

b) No MCU, a força magnética (F_m) é a própria resultante centrípeta (F_c)  --- cálculo do raio R da trajetória do MCU  ---  F_m=F_c   ---  qvB=mv²/R  ---  R=mv/qB (I)  ---  o espaço percorrido (∆S) pela partícula no campo magnético é igual ao arco por ela descrito  -

--  da definição de ângulo em radiano  ---  θ_rad=∆S/R (II)  ---  (I) em (II)  ---  ∆S=(mv/qB).θ_rad (III)  ---  v=∆S/∆t  ---  ∆t=∆S/v (IV) 

---  (III) em (IV)  ---  ∆t={(mv/qB).θ_rad}/v  ---  ∆t=(m/qB).θ_rad

54- a) Intensidade da força magnética  ---  F_M=Q.v.B.senθ  ---  θ é o ângulo entre os vetores e   ---  nesse exercício esses vetores são perpendiculares entre si  ---  θ = 90^o  ---  senθ = 1  ---  F_M=Q.v.B  --- a direção e o sentido dessa força são dados pela regra da

mão esquerda, invertendo o sentido de , pois a carga Q é negativa, como indicado na figura acima.

b) Como se trata de movimento retilíneo e uniforme, a força elétrica deve equilibrar a força magnética, anulando a resultante entre elas  ---  assim, a força elétrica deve ser vertical e para cima  ---  como a carga é negativa, a força elétrica tem sentido oposto ao do campo elétrico   ---  então, esse campo elétrico deve ser vertical, orientado para baixo, como indica a figura  ---  F_M=F_E  ---

Q.v.B = Q.E  ---  v=E/B

55- I. Falsa  ---  ela fica sujeita a uma força somente se estiver em movimento com velocidadee desde quenão seja paralela ao campo magnético.

II. Falsa  ---  são tangentes em cada ponto.

III. Falsa  ---  Toda carga elétrica lançada com velocidade  perpendicularmente às linhas de indução de um campo magnético realiza um movimento circular uniforme numa circunferência que está num plano perpendicular à direção de .

IV. Falsa  ---  em paralelo todos os resistores estão sob a mesma ddp U  ---  P=U²/R  ---  observe que P é inversamente proporcional a R  ---  o que tiver menor resistência dissipa maior potência elétrica devido ao efeito Joule.

V. Falsa  ---  segunda lei de Ohm  ---  R=ρ.ℓ/S  ---  ρ=R.S/ℓ  ---  observe que ρ é inversamente proporcional a ℓ.

R- E.

56-(PUC-RJ)

a) Sobre uma carga q colocada numa região onde existe um campo elétrico (esteja a carga em movimento ou não) surge um campo elétrico  com as seguintes características:

No caso do exercício, como q é positiva, a força elétrica sobre a carga  tem a mesma direção e sentido que o campo ou

seja, vertical e para cima e de intensidade  ---  E=F/q  ---  2=F/2.10^-3  ---  F=4.10^-3 N.

b) Observe que o campo magnético  tem direção perpendicular à velocidade   ---  a intensidade da força magnética que age sobre a carga q é fornecida pela expressão F_m=q.v.B.senθ=q.v.B.sen90^o  ---  F_m=q.v.B.1  ---  F_m=q.v.B  --- 

F_m=2.10^-3.B.4  ---  F_m=8.10^-3B  ---  a direção e sentido dessa força magnética é fornecida pela regra da mão esquerda de características:

Direção e sentido de  - fornecidos pela regra da mão esquerda conforme mostrado na figura abaixo. Observe na figura da

direita que  é perpendicular a  e a , o que impõe a condição de que e devem pertencer a um mesmo plano. Observe também que θ é o ângulo entre e .

---  observe na figura do exercício que a força magnética, utilizando a regra da mão esquerda, tem direção vertical e

sentido para baixo (figura I )  ---  assim, a situação fica conforme o esquema da figura II  ---  como o enunciado afirma que a velocidade da carga q é constante, ela está em equilíbrio dinâmico e a resultante das forças que agem sobre ela é nula, o que significa que as forças elétrica e magnética devem se anular (como a massa não foi mencionada você pode desprezar o peso da carga)  ---  F_e=F_m  ---  4.10^-3=8.10^-3.B  ---  B=0,5 T  ---  unidades do Tesla T  ---  F_m=q.v.B  ---   B=F_m/q.v  ---  T=N/C.(m/s)  ---  T=N.s/m.C.

57- 01. Correta  ---  quando a carga elétrica é positiva, a força elétrica  que surge sobre ela tem a mesma direção e sentido do campo elétrico , no caso vertical e para baixo  ---  intensidade de   ---  F_e=Q.E  ---  a força magnética  sobre a carga Q é fornecida pela regra da mão esquerda  ---  indicador () penetrando na folha, médio () para a esquerda e o

polegar indicará () para baixo  ---  intensidade de   ---  F_m=Q.V.H.sen90^o  ---  F_m=Q.V.H  ---  como  e  indicam para baixo, a intensidade da força resultante também será para baixo e de valor F_R= Q.E + Q.V.H  ---  F_R=Q.(E + V.H).

02. Falsa  ---  para que a trajetória da partícula Q seja retilínea, a força resultante sobre ela deve ser nula, o que, no caso, é impossível, pois as forças elétrica e magnética têm a mesma direção (vertical) e mesmo sentido (para baixo), portanto não podem se anular.

04. Correta  ---  observe que a força resultante sobre Q indica para baixo e, assim, a carga Q será desviada para baixo.

08. Correta  ---  São sempre linhas fechadas e por isso nunca se cruzam  ---  fora do ímã, as linhas saem do pólo norte e se dirigem para o pólo sul;

Dentro do ímã, as linhas são orientadas do pólo sul para o pólo norte.

16- Falsa  ---  a carga elétrica no interior dos campos magnético e elétrico não altera as características dos mesmos.

Corretas: 01, 04 e 08  ---  Soma=13.

58- a) Sendo a carga q positiva, o campo elétrico  e a força elétrica  tem a mesma direção e o

mesmo sentido  --- não havendo atrito aq intensidade da força elétrica F_e=q.E tem a mesma intensidade da força resultante F_R=m.a  ---

q.E = m.a  ---  a=q.E/m=10.10²/4.10^-1  ---  a=2,5.10³m/s²  ---  com essa aceleração a carga q parte do repouso V_o=0 e percorre ∆S=5.10^-1m onde chega com velocidade V fornecida pela equação de Torricelli  ---  V² = V_o² + 2.a.∆S  ---

V² = 0² + 2.2,5.10³.5.10^-1  ---  V=√(25.10²)  ---  V=50m/s.

b) Para determinar a direção e sentido da força magnética  sobre o bloco você pode utilizar a regra da mão esquerda

 ---  indicador na direção e sentido de  (entrando na folha e perpendicular a ela), médio na direção e sentido de

 (horizontal e para a direita)   ---  observe que o polegar, que indica  terá direção vertical e sentido para cima  --- 

além de existem também a força normal  que o bloco troca com a superfície de apoio (vertical e para cima) e  a força peso , vertical e para baixo.

c) Para que a força de contato  seja nula, você terá, na vertical, que  ---   +  =   ---como, pelo enunciado, a força  deve ser nula  ---  F_m = P  ---  F_m=q.v.B  ---  P=m.g   ---  q.v.B=m.g  ---  B=m.g/q.v=0,4.10/10.50  ---  B=8.10^-3T.

d) Trabalho da força de atrito  W_Fat=F_at.d.cos180⁰  ---  W_Fat = - F_at.d  --- F_at=μN=μm.g  ---  W_Fat=μ.m.g.d  ---   trabalho

da força de atrito como variação de energia cinética  ---  W_Fat=E_cD – E_cC = m.V_D²/2 – m.V_C²/2=0 – mV_C²/2  ---  W_Fat = - m.V_C²/2  ---  μ.m.g.d = m.V_C²/2  ---  μ = V_C²/2.μ.g.d.

59-  Na figura abaixo uma carga positiva q penetra com velocidade no ponto A numa região em que existe um campo magnético uniforme  penetrando na folha. Observe que e são perpendiculares e, como a velocidade  é sempre tangente à trajetória em cada ponto, a força magnética , obtida pela regra da mão esquerda e indicada na figura é sempre dirigida para o centro de

 uma circunferência de raio R. Assim, a carga q realizará um movimento circular uniforme com velocidade de intensidade constante  ---  expressão matemática dessa força magnética é Fm=q.V.B.senθ=q.V.B.1  ---  Fm=q.V.B  ---  o trabalho realizado pela força resultante centrípeta (no caso, coincide com a força magnética) é sempre nulo, pois ela é sempre perpendicular à velocidade  que   

é sempre tangente em cada ponto da circunferência) e consequentemente ao deslocamento  (vide figura acima)  ---  isso ocorre pois W=F.d.cos90^o=F.d.0=0  ---  R- B

60- Se você não domina essa teoria, leia atentamente as informações a seguir:

Carga elétrica q lançada com velocidade  lançada perpendicularmente às linhas de indução de um campo magnético uniforme   ---  observe que, neste caso o ângulo entre e  é 90^o e que sen90^o=1  ---  na figura abaixo uma carga positiva q penetra com velocidade no ponto A numa região em que existe um campo magnético uniforme  penetrando na folha. Observe que e são perpendiculares e, como a velocidade  é sempre tangente à trajetória em cada ponto, a força magnética , obtida pela regra da mão esquerda e indicada na figura é sempre dirigida para o

centro de uma circunferência de raio R. Assim, a carga q realizará um movimento circular uniforme com velocidade de intensidade constante .

A expressão matemática dessa força magnética é F_m=q.V.B.senθ=q.V.B.1  ---  F_m=q.V.B  ---  lembrando que a força magnética F_m é responsável pelo movimento circular é a força resultante centrípeta de intensidade F_c=m.V²/R  ---  F_m=F_c  ---  q.V.B=m.V²/R  ---

 R=m.V/q.B (I)  ---  o período T (tempo que a carga q demora para efetuar uma volta completa) é fornecido por  ---  V=ΔS/Δt  ---  numa volta completa  ---  ΔS=2πR e Δt=T  ---  V=2πR/T (II)  ---  substituindo II em I  ---  R=m. (2πR/T)/q.B  ---  T=2πm/q.B  ---  observe que o período (T) do movimento circular não depende da velocidade com que a partícula q penetra no campo magnético.

Dados do exercício  ---  B=0,4T  ---  m/q=10^-8kg/C  ---  R=10mm10.10^-3m=10^-2m  ---  da teoria acima  ---  R=mV/q.B  ---  R.B/V=m/q  ---  10^-2.4.10^-1/V = 10^-8  ---  V=4.10^-3/10^-8  ---  V=4.10⁵ m/s  ---  R- A.