Resistor equivalente

Resistor equivalente (R_eq)  Muitas vezes você deve substituir um resistor de determinado valor nominal, num circuito elétrico, mas não o possui.

No entanto você pode substituí-lo por uma associação de resistores que possua o mesmo valor nominal. Essa associação recebe o nome de resistor equivalente (R_eq) da associação, que é aquele que, submetido à mesma diferença de potencial da associação, é percorrido pela mesma corrente, não alterando as características do circuito.

Resistor equivalente na associação série

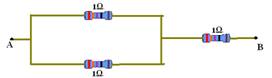
Uma  associação série é aquela em que os resistores estão associados um em seguida do outro de modo que a corrente em cada um seja a mesma.

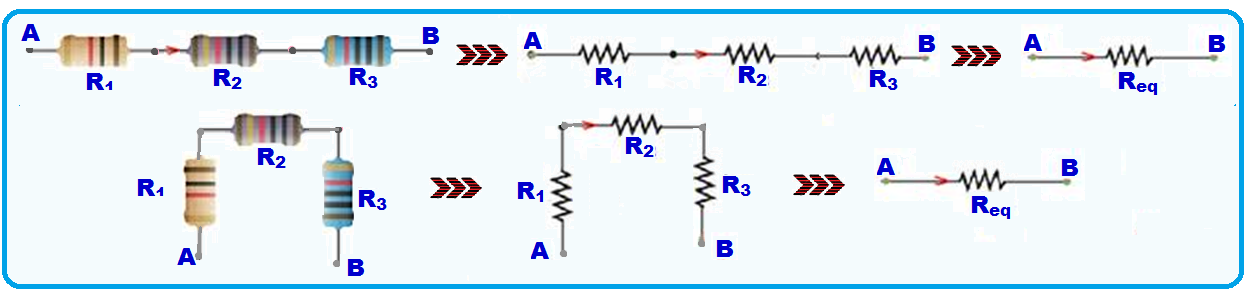
Cálculo da resistência (R_eq) do resistor equivalente na associação série a  resistência do resistor equivalente entre A e B é fornecida pela soma das resistências de cada resistor.

Exemplos numéricos:

Resistor equivalente na associação paralelo

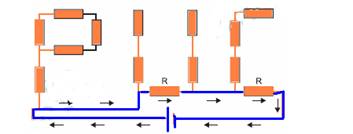
A associação paralelo é aquela em que  os resistores são associados pelos seus terminais, ou seja, todos saem do mesmo ponto (A) e todos chegam ao mesmo ponto (B).

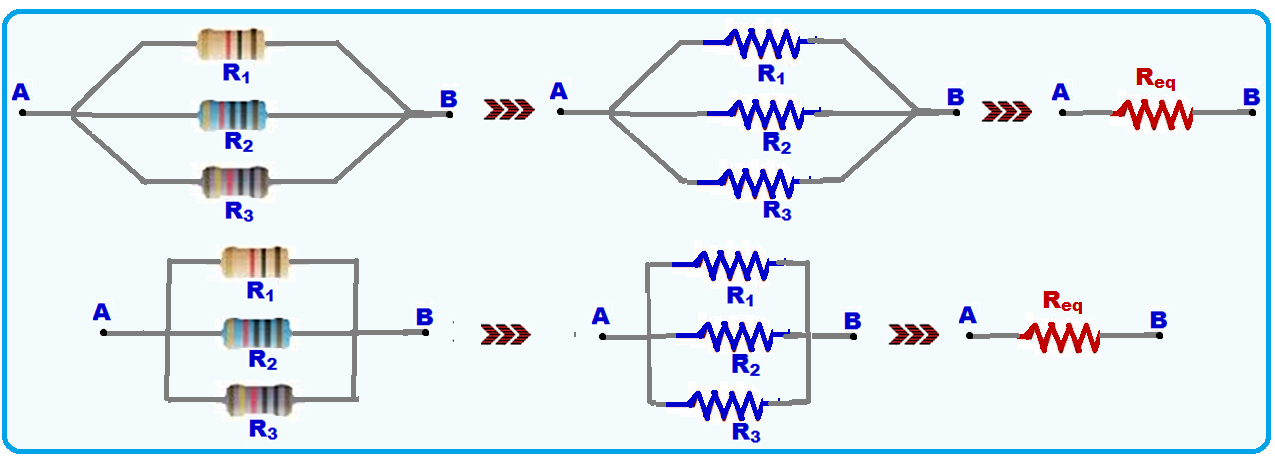
Cálculo da resistência (R_eq) do resistor equivalente na associação paralelo:

Três processos:

3^o – Regra prática:

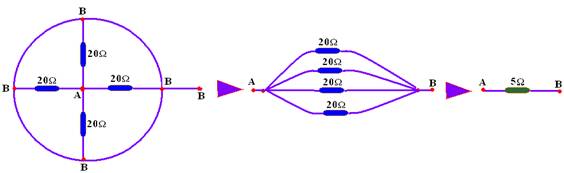
 quando um é o dobro do outro, você pega o maior e divide por três;

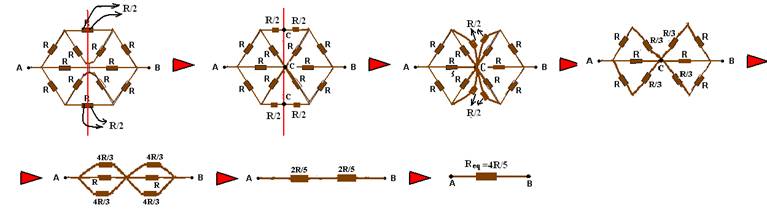
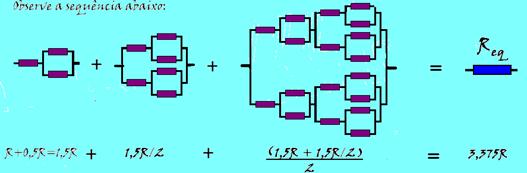
  quando um é o triplo do outro, você pega o maior e divide por quatro, e assim por diante.

 dois resistores iguais, você divide o valor de um deles por dois;

   três resistores iguais, você divide o valor de um deles por três, e assim por diante. 

Em alguns casos essa regra prática, quando o número não der exato, pode ser substituída por uma das duas acima.

Exemplo numérico:

1^o processo:

Se você invertesse a ordem, o resultado seria o mesmo:

Resistor equivalente na associação mista

 Associação Mista  consta de uma combinação das associações série e paralelo, cujo cálculo você deve fazer por partes até chegar a um único resistor equivalente R_eq.

Para isso deve-se ir substituindo cada associação parcial, série ou paralelo, por um único resistor e ir diminuindo aos poucos o esquema da associação.

Analise detalhadamente esses exemplos:

Em cada caso abaixo, calcule a resistência equivalente entre os pontos P e Q.

01-

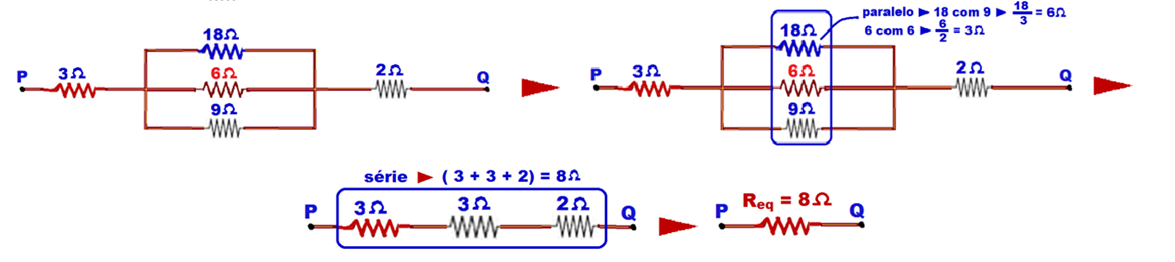
02-

03- Veja bem, os três últimos estão em série, comece por eles:

 Quer se aprofundar mais? Veja, com as respectivas resoluções os exercícios 01 (d, e, i, j e l); 06; 13 e 33.

O que você deve saber, informações e dicas

Cálculo da resistência (R_eq) do resistor equivalente na associação paralelo:

Três processos:

3^o – Regra prática:

 quando um é o dobro do outro, você pega o maior e divide por três;

  quando um é o triplo do outro, você pega o maior e divide por quatro, e assim por diante.

 dois resistores iguais, você divide o valor de um deles por dois;

   três resistores iguais, você divide o valor de um deles por três, e assim por diante. 

Em alguns casos essa regra prática, quando o número não der exato, pode ser substituída por uma das duas acima.

 Quanto menor for a resistência equivalente de uma associação de resistores, maior será a potência dissipada por ela de modo que sua eficiência seja maior   justificativa  P_o=U²/R_eq    observe que a potência é inversamente proporcional à resistência equivalente.

Disjuntores

 Disjuntores  A função do disjuntor é interromper automaticamente a passagem da corrente elétrica por um dos pontos (cômodos) da residência, quando sua intensidade excede determinado valor (a chave desliga).

Se a chave do disjuntor, com o excesso de corrente elétrica não desligasse, os fios do circuito seriam muito aquecidos podendo fundir, causando incêndios.

Junto aos disjuntores, na caixa de luz, existe um quadro identificador dos cômodos ou pontos atendidos por cada disjuntor, como por exemplo, iluminação, tomadas, chuveiros, etc..

Reostatos

 Reostatos são resistores variáveis cuja finalidade é adaptar a intensidade da corrente elétrica a valores desejados.

Tipos de reostatos:

Os principais tipos de reostatos são    reostato de cursor  variando o cursor você está

variando a resistência (figura 1)    reostato de pontos em cada posição da chave aresistência elétrica tem um determinado valor (figura 2).

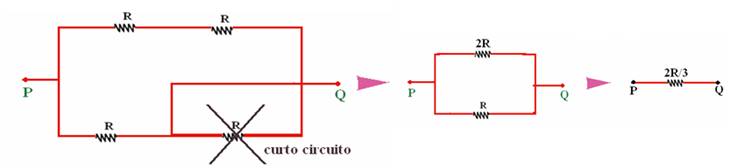
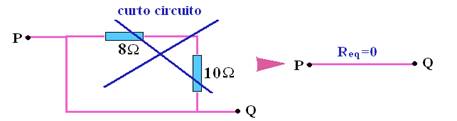
Curto circuito (CC)

 Quando se liga (une) dois pontos de um circuito elétrico por um condutor (fio) de resistência desprezível (fio ideal, fio sem resistência), diz-se que esses dois pontos ficam em curto circuito (CC).

Considere um resistor R sendo percorrido por uma corrente elétrica i e submetido a uma diferença de potencial U_AB = V_A - V_B.

Ligando-se, em paralelo, entre os pontos A e B desse resistor, um condutor de resistência desprezível (fio ideal), provoca-se um curto circuito entre A e B e verifica-se que toda a corrente elétrica se desviará, passando pelo fio ideal, no qual, aplicando-se a lei de Ohm ter-se-á    V_A – V_B = U_AB = R.i    como R = 0 (fio ideal), tem-se    V_A – V_B = R.i    V_A – V_B = 0.i    V_A – V_B = 0    V_A = V_B.

Assim, o circuito se comporta como se o resistor não existisse e pode-se redesenhar o circuito, tornando os pontos A e B coincidentes.

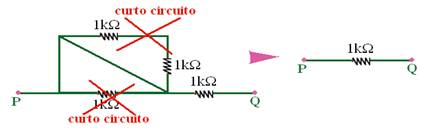
Exemplos de cálculo do valor da resistência (R_eq) do resistor equivalente, com curto-circuito (CC)

Calcule, em cada caso, a resistência do resistor equivalente entre os pontos A e B:

a)

b)

c)

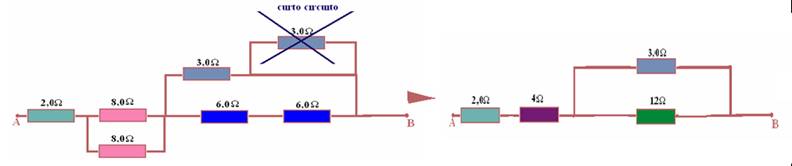
Cálculo do resistor equivalente em casos mais complexos de curto-circuito

 Em alguns casos de curto circuito mais complexos, não é possível visualizar a situação (os pontos em curto-circuito) e é preciso refazer o circuito, procedendo da seguinte maneira prática:

1^o  Marcar todos os nós da associação (nó – ponto de cruzamento de 3 ou mais fios ).

2^o  Colocar letras em cada nó, lembrando que os pontos unidos por fio ideal (nós) estão em curto circuito e devem ser nomeados a mesma letra, pois possuem o mesmo potencial.

3^o  Refazer o circuito

Exemplos de cálculo do valor da resistência (R_eq) do resistor equivalente, com curto-circuito (CC), refazendo o circuito

Determine, em cada caso, entre os pontos P e Q, a resistência equivalente de cada associação:

a)

Etapas: Preste muita atenção nas etapas da resolução.

 Refazendo o circuito

Os resistores entre os pontos P e P, unidos pela mesma letra, estão em curto circuito não colocar os resistores de 5Ω e 30 Ω    entre P e B tem um de 30 Ω e um de 8 Ω    entre B e Q tem

um de 10Ω    veja esquema e seqüência acima.

c)

Observação: Se você quiser aprofundar mais, analise os exercícios 26; 28(c); 29; 30; 34(c) e 35, com as respectivas resoluções.

Exercícios de vestibulares com resolução comentada sobre

Resistor equivalente

 01- (UFB) Em cada uma das associações abaixo, calcule a resistência do resistor equivalente entre os pontos especificados:

a) 

b) 

c) 

d) 

e) 

f) 

g) 

h) 

i) 

j) 

l) 

02-(UFMS-MS) No circuito elétrico abaixo, determine o valor da resistência equivalente entre os pontos A e B.

03-(UEL-PR) Considere o circuito representado no esquema abaixo, onde cada resistência vale 10Ω.

A resistência equivalente entre os terminais X e Y, em ohms, é igual a:

a) 10                             

b) 15                            

c) 30                                      

d) 40                                 

e) 90

04-(UFRJ-RJ) A menor resistência equivalente dos circuitos a seguir é (considere que as resistências são todas iguais):

05-(FGV-SP) Pensando em como utilizar o imenso estoque de resistores de 20Ω e 5Ω que estavam “encalhados” no depósito de uma fábrica, o engenheiro responsável  determina que se faça uma associação de valor equivalente (entre os pontos A e B) ao resistor de que precisariam para a montagem de um determinado aparelho.

O funcionário que fazia a soldagem do circuito alternativo, distraidamente, trocou a ordem dos resistores e um lote intenso de associações teve que ser descartado.

As resistências corretas em cada associação deveriam ser: R₁=20Ω, R₂=20Ω e R₃=5Ω.

As resistências montadas erradamente  em cada associação foram: R₁=5Ω, R₂=20Ω e R₃=20Ω.

A troca dos resistores acarretou uma diminuição da resistência desejada, em cada associação, de:

 a) 5 Ω                            

b) 9 Ω                              

c) 15 Ω                                         

d) 24 Ω                                         

e) 25 Ω

06-(MACKENZIE-SP) Uma caixa contém resistores conectados a três terminais, como mostra a figura abaixo.

A relação entre as resistências equivalentes entre os pontos A e B e entre os pontos B e C (R_AB/R_BC) é:

a) 4/3                                  

b) 1                                

c) 1/2                                        

d) 2/3                                   

e) 2

07-(UNICAMP-SP) Dispõe-se de vários resistores iguais de resistência R=1Ω..

a) Faça um esquema mostrando o número mínimo de resistores necessários e a maneira como eles devem ser associados para se obter uma resistência equivalente de 1,5Ω.

b) Mostre o esquema de outra associação de resistores disponíveis que também tenha uma resistência equivalente de 1,5Ω

08-(UFF-RJ) Em meados da primeira metade do século XIX, Georg Simon Ohm formulou uma lei que relaciona três grandezas importantes no estudo da eletricidade: tensão (V), intensidade de corrente (i) e resistência (R). Baseado nessa lei, a fim de

verificar se um determinado resistor era ôhmico, um estudante reproduziu a experiência de Ohm, obtendo o seguinte gráfico:

A) Informe se o resistor utilizado na experiência do estudante é ôhmico e, em caso afirmativo, calcule o valor de sua resistência.

B) Considere esse resistor submetido a uma tensão de 9,0 volts, durante um intervalo de tempo de 5,0 minutos, e determine, em joule, a energia dissipada.

C) Repetindo a experiência com diversos resistores, o estudante encontrou um conjunto de três resistores ôhmicos idênticos e os associou de duas maneiras distintas, conforme representado na figura 1. O estudante, então, imergiu cada associação em iguais quantidades de água e submeteu seus terminais (X e Y) a uma mesma diferença de potencial, mantendo-a constante.

Identifique, nesse caso, a associação capaz de aquecer, mais rapidamente, a água. Justifique sua resposta.

09-(CESGRANRIO-RJ) No circuito abaixo, sabe-se que a resistência equivalente entre os pontos A e B vale 3Ω.

Então, o valor da resistência R, em ohms, deve ser igual a:

10-(PUC-RJ) Quando as resistências R₁ e R₂ são colocadas em série, elas possuem uma resistência equivalente de 6 Ω. Quando R₁ e R₂ são colocadas em paralelo, a resistência equivalente cai para 4/3 Ω. Os valores das resistências R₁ e R₂ , respectivamente, são:

a) 5 Ω e 1 Ω                             

b) 3 Ω e 3 Ω                          

c) 4 Ω  e 2 Ω                       

d) 6 Ω e 0 Ω                   

e)  0 Ω e 6 Ω

11-(PUC-MG) No circuito da figura a seguir, é CORRETO afirmar que os resistores:

a) R1, R2 e R5 estão em série.              

b) R1 e R2 estão em série.                     

c) R4 e R5 não estão em paralelo.

d) R1 e R3 estão em paralelo.

12-(PUC-RJ) Três resistores idênticos de R = 30 Ω estão ligados em paralelo com uma bateria de 12 V. Pode-se afirmar que a resistência equivalente do circuito é de

a) Req = 10 Ω             

b) Req = 20 Ω                

c) Req = 30 Ω              

d) Req = 40 Ω                   

e) Req = 60 Ω

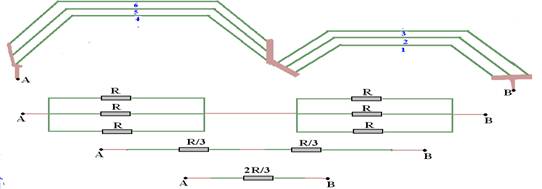
13-(UNESP-SP) Os carros atuais são equipados com um vidro térmico traseiro para eliminar o embaçamento em dias úmidos ou chuvosos. Para isso, tiras resistivas instaladas na face interna do vidro são conectadas ao sistema elétrico do veículo, de modo que possa transformar energia elétrica em energia térmica. Num dos veículos fabricados no país, por exemplo, essas tiras (resistores) são arranjadas de forma semelhante à representada na figura.

Considerando as resistências das tiras 1,2,....,6 respectivamente como R₁=R₂=......,=R₆=R, faça um esquema da associação que corresponde ao arranjo das tiras da figura e calcule a resistência do resistor equivalente.

14-(UFRN-RN) Um anel feito a partir de um fio condutor homogêneo possui, entre pontos diametralmente opostos, uma resistência R.

Se cortarmos esse anel em 4 partes iguais, duas a duas, tendo os pedaços maiores o dobro do comprimento dos pedaços menores, e os ligarmos como mostra a figura acima, podemos afirmar que, entre os pontos A e B, a resistência valerá:

15-(UFRRJ-RJ) A figura a seguir mostra um circuito simples que alimenta um chuveiro elétrico C.

Dentre os sistemas de resistências a seguir, o que aquecerá mais rapidamente a água é:

16-(UFRJ-RJ) Um circuito é formado por uma bateria ideal, que mantém em seus terminais uma diferença de potencial V, um amperímetro ideal A, uma chave e três resistores idênticos, de resistência R cada um, dispostos como indica a figura. Com a chave fechada, o amperímetro registra a corrente I. Com a chave aberta, o amperímetro registra a corrente I':

a) Calcule a razão I'/ I.

b) Se esses três resistores fossem usados para aquecimento da água de um chuveiro elétrico, indique se teríamos água mais quente com a chave aberta ou fechada. Justifique sua resposta.

17-(UERJ-RJ) Considere a associação de três resistores: A, B, e C. Suas respectivas resistências são R_A, R_B, e R_C, e R_A > R_B > R_C.

O esquema que apresenta a maior resistência entre os pontos P e M está indicado em:

18-(UNESP-SP) Um indivíduo deseja fazer com que o aquecedor elétrico central de sua residência aqueça a água do reservatório no menor tempo possível. O aquecedor possui um resistor com resistência R. Contudo, ele possui mais dois resistores exatamente iguais ao instalado no aquecedor e que podem ser utilizados para esse fim. Para que consiga seu objetivo, tomando todas as precauções para evitar acidentes, e considerando que as resistências não variem com a temperatura, ele deve utilizar o circuito

19-(UNESP-SP) Como conseqüência do rápido desenvolvimento da tecnologia eletrônica, hoje é possível realizar experimentos nas diversas áreas da ciência utilizando amostras com dimensões da ordem de nm (1 nm = 10^-9 m). Novas perspectivas foram introduzidas e vêm sendo exploradas, como as investigações sobre propriedades elétricas de macromoléculas e cadeias poliméricas, como as proteínas.

 Diante dessa possibilidade, um pesquisador verificou com sucesso a sua hipótese de que uma determinada proteína, esticada, satisfazia à lei de Ohm. Depois de medidas sistemáticas da resistência elétrica, ele concluiu que o seu valor é R. Prosseguindo na investigação, partiu essa cadeia em dois pedaços, ligando-os em paralelo, e a medida da resistência efetiva foi de 3R/16. Considerando que o pedaço de menor comprimento tenha resistência R₁ e o de comprimento maior, resistência R₂, calcule esses valores expressos em termos de R.

 20-(PUC-RJ) Dois resistores R₁ = 1 Ω e R₂ = 2 Ω são ligados a uma bateria de 2 V. De que maneira esses dois resistores devem ser combinados para que a potência dissipada no circuito seja a menor possível?

a) Os resistores devem ser colocados em série, e a potência dissipada será de 4/3 W.

b) Os resistores devem ser colocados em série, e a potência dissipada será de 3/4 W.

c) Os resistores podem ser igualmente colocados em série ou em paralelo, e a potência dissipada será de 1 W.

d) Os resistores devem ser colocados em paralelo, e a potência dissipada será de 4/3 W.

e) Os resistores devem ser colocados em paralelo, e a potência dissipada será de 3/4 W.

21-(CFT-MG) A FIG. 1 representa uma associação de resistências idênticas e a FIG. 2, uma bateria e fios de ligação.

Para se obter o maior valor de corrente elétrica, os fios devem ser ligados nos pontos

a) A e B.                         

b) A e D.                              

c) B e C.                             

d) C e D.

22-(PUC-RJ) Duas resistências elétricas, uma de 2Ω e outra de 6Ω, devem ser ligadas a uma bateria ideal de 12 V em um circuito elétrico.

a) Determine de que maneira as resistências devem ser ligadas para que a potência dissipada pelo circuito seja a menor possível.

b) Desenhe o circuito correspondente à resposta do item a.

c) Determine o valor de tensão para o qual a bateria deveria ser ajustada de forma que a potência no circuito elétrico aumente em 300%.

23-(ITA-SP) No circuito elétrico da figura, os vários elementos têm resistências R₁, R₂ e R₃conforme indicado.

Sabendo que R₃ = R₁/2, para que a resistência equivalente entre os pontos A e B da associação da figura seja igual a 2 R₂ a razão r = R₂/R₁ deve ser

24-(ITA-SP) Um circuito elétrico é constituído por um número infinito de resistores idênticos, conforme a figura.

 A resistência de cada elemento é igual a R. A resistência equivalente entre os pontos A e B vale:

a) infinita              

b) R.(√3 – 1)               

c) R√3               

d) R.(1 - √3/3)                  

e) R(1 + √3)

25-(UECE-CE) Um longo cabo subterrâneo de 10km se estende de leste para oeste e consiste de dois fios paralelos de 13Ω/km. Um contato indevido se forma a uma distância x, medida a partir da extremidade oeste, quando um caminho condutor de resistência R faz a ligação entre os fios, como mostra a figura.

A resistência é R=60Ω, quando medida a partir das extremidades do oeste e 216Ω, quando medida a partir  das extremidades do leste. O valor de x, em quilômetros é:

26-(UECE-CE)

A resistência equivalente R, entre os pontos P e Q, em ohms, da combinação de resistores mostrada na figura é:

a) 0,15                            

b) 6,67                            

c) 9,33                              

d) 15,00                              

e) 22,5

27-(PUC-PR) O setor agropecuário, nos últimos anos, vem passando por grandes transformações. Atualmente, as propriedades rurais são dotadas de um bom nível de conforto, o que anteriormente era privilégio somente dos habitantes urbanos. Sem dúvida, a energia elétrica é a principal responsável por essa modernização.

 Ela permite desde a implantação de motores elétricos, que aumentam a capacidade produtiva da fazenda, até uma iluminação eficiente bem como a utilização de aparelhos de comunicação, como rádio, telefone, TV e vários outros, proporcionando melhor qualidade de vida e reduzindo o êxodo rural.

Dessa maneira, a construção de usinas de pequeno porte pode ser uma alternativa para o fornecimento de energia elétrica para pequenas propriedades rurais.

Em granjas, por exemplo, é comum a utilização de chocadeiras de ovos. Uma chocadeira de ovos comum necessita de quatro lâmpadas de 40 W - 120 V para aquecer o ambiente interno.

Essas lâmpadas devem ficar ligadas 24 horas.

De acordo com o texto, assinale a alternativa CORRETA.

a) Utilizando-se a usina hidroelétrica e supondo que as lâmpadas da chocadeira estão associadas em paralelo, é possível fornecer energia elétrica para 150 chocadeiras por dia.

b) Na tabela acima a capacidade de geração está relacionada à potência elétrica gerada em cada tipo de usina.

c) Na usina eólica, a energia é do tipo não renovável.

d) Supondo que a tensão permaneça constante na associação das lâmpadas da chocadeira, a potência total será a mesma independente de a ligação ser em série ou em paralelo.

e) Supondo que a tensão elétrica obtida gerada a partir de painéis fotovoltaicos seja contínua e igual a 220 V, se ligarmos as lâmpadas da chocadeira em série, nesta tensão elas funcionarão normalmente.

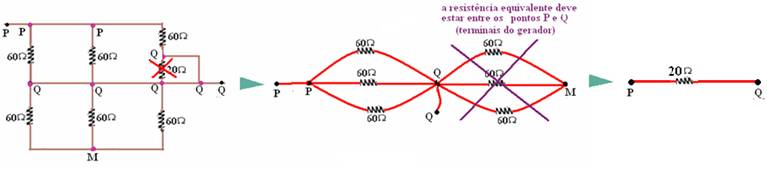
28-(UFB) Calcule em cada caso a resistência do resistor equivalente entre os pontos P e Q:

a)

b)

c)

29-(UFV-MG) Um circuito com três resistores é representado na figura a seguir.

Um circuito com três resistores é representado na figura a seguir.

A resistência medida entre os pontos A e B é:

a) 6,0 Ω                             

b) 5,0 Ω                           

c) 2,2 Ω                           

d) 1,8 Ω                                

e) 1,2 Ω

30-(FUVEST-SP) Um material condutor especial se torna luminoso quando é percorrido por uma corrente elétrica. Com esse material foram escritas palavras, e nos terminais 1 e 2 foram ligadas fontes de tensão, numa sala escura. A palavra legível é:

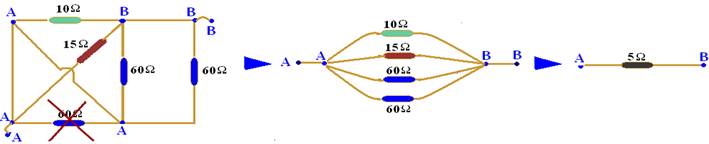
31-(PUC-SP) Determine o valor da resistência equivalente na associação de resistores esquematizada:

32-(FUVEST-SP) Considere um circuito formado por 4 resistores iguais, interligados por fios perfeitamente condutores. Cada resistor tem resistência R e ocupa uma das arestas de um cubo, como mostra a figura.

Aplicando entre os pontos A e B uma diferença de potencial U, a corrente que circulará entre A e B valerá:

a) 4U/R                         

b) 2U/R                                

c) U/R                                    

d) U/2R                                   

e) U/4R

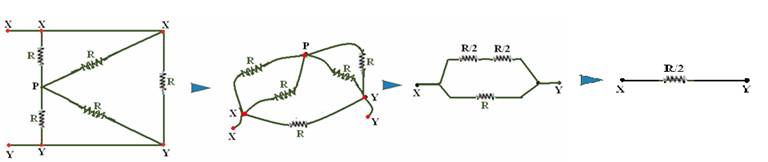
33-(MACKENZIE-SP) A resistência do resistor equivalente à associação abaixo, entre os terminais A e B, é:

34-(UFB) Determine a resistência equivalente em cada uma das associações abaixo, entre os pontos especificados:

a) 

b) 

c) 

35-(FGV-SP) Determine a resistência do resistor equivalente da associação abaixo, entre os pontos x e y:

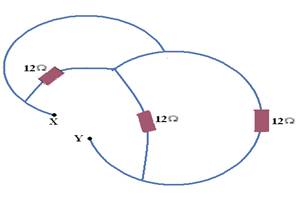
36-(UEL-PR) No circuito elétrico, representado abaixo, os cinco resistores  apresentam a mesma resistência elétrica R. Calcule a resistência do resistor equivalente.

37-(MACKENZIE-SP) A resistência elétrica do resistor equivalente à associação abaixo, entre os pontos A e B, é:

a) zero                             

b) 5,0 Ω                               

c) 10 Ω                             

d) 60 Ω                     

e) 135 Ω

38-(UF-PE) No circuito, qual a resistência equivalente entre os pontos A e B?

39-(UECE-CE) Considere a figura a seguir. Ela é formada de um conjunto de resistores todos de resistência R.

A resistência equivalente entre os pontos A e B é:

40-(PUC-SP) Para o circuito abaixo, considere que todos os resistores são ôhmicos e de resistência elétrica R.

Calcule o valor da resistência elétrica equivalente da associação.

41-(FGV-SP) Após ter lido um artigo sobre a geometria e a formação de fractais, um técnico de rádio e TV decidiu aplicar a teoria a associações com resistores de mesmo valor R. Para iniciar seu fractal, determinou que a primeira célula seria a desenhada a seguir: Em seguida, fez evoluir seu fractal, substituindo cada resistor por uma célula idêntica à original. Prosseguiu a evolução até atingir a configuração dada:

O resistor equivalente a esse arranjo tem valor:

a) 3,375R                        

b) 3,250R                              

c) 3,125R                           

d) 3,000R                                      

e) 2,875R

42-(UERJ-RJ)  Observe a representação do trecho de um circuito elétrico entre os pontos X e Y, contendo três resistores cujas resistências medem, em ohms, a, b e c.

Admita que a sequência (a, b, c) é uma progressão geométrica de razão 1/2  e que a resistência equivalente entre X e Y mede

2,0 W.

O valor, em ohms, de (a + b + c) é igual a:

a) 21,0                                            

b) 22,5                                         

c) 24,0                                                   

d) 24,5

43-(PUC-RJ) Calcule a resistência do circuito formado por 10 resistores de 10 kW, colocados todos em paralelo entre si, e em série com 2 resistores de 2 kW, colocados em paralelo.

a) 1 kW                                  

b) 2 kW                                    

c) 5 kW                             

d) 7 kW                                          

e) 9 kW

44 - (IME-RJ) 

Sabendo que todos os resistores da malha infinita da figura têm resistência R, a resistência equivalente entre A e B é:

a) R(1 + √2)/2                     

b) R(1 + √3)/2                          

c) 3R/2                        

d) R(1 + √5)/2           

e) R(1 + √6)/2

45-(UESPI-PI)  

A resistência equivalente entre os terminais A e B da bateria ideal no circuito elétrico a seguir é igual a:

46-(MACKENZIE-SP) A resistência elétrica do resistor equivalente da

associação abaixo, entre os pontos A e B, é:

a) 2 R                       

b) R                             

c) R/ 2                             

d) R/ 3                                         

e) R/ 4

47-(UFMS-MS)

Resistências elétricas iguais (cada uma de valor 12 Ω) ligam os vértices A,B e C de um triângulo, conforme a figura.

Sobre a resistência elétrica equivalente, é correto afirmar que,

a) entre os vértices A e B, é de 12 Ω                                                 

b) entre os vértices B e C, é de 8Ω

c) entre os vértices A e C, é de 36 Ω                                                 

d) entre os vértices A e B, é de 24 Ω

e) entre os vértices A e B, é de 36 Ω

48-(CEFET-MG) Dois resistores de 2,0 Ω e 4,0 Ω são ligados em série e, em seguida, o conjunto é conectado em paralelo a um resistor de 12 Ω. A resistência equivalente dessa associação, em Ω, é

a) 2,0.                             

b) 4,0.                               

c) 8,0.                                   

d) 12.                                     

e) 16.

Resolução comentada dos exercícios de vestibulares sobre

Resistor equivalente

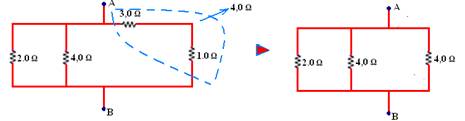
 01- a) Veja figura abaixo, onde os resistores de 2 Ω, 4 Ω e 4 Ω estão associados em paralelo  ---  4 com 4=4/2=2 Ω  ---  2 com

2=2/2=1 Ω  ---  R_eq=1 Ω

b)

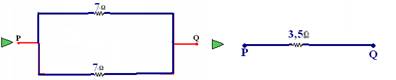
c)

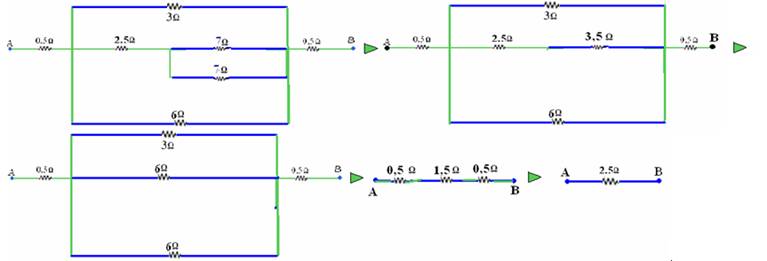
d)

e)

f)

g)

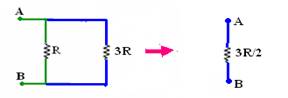
h)

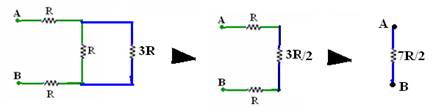
i)

j)

l)

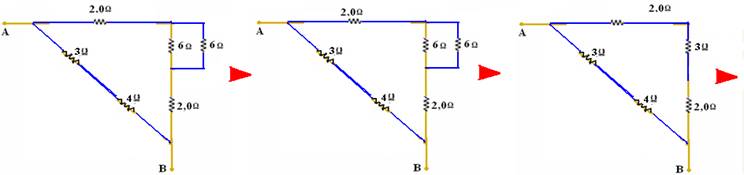
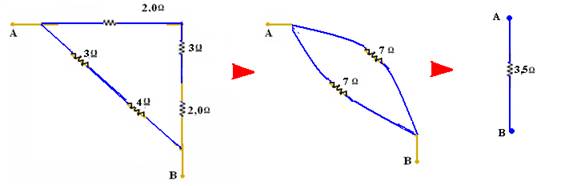
02-

03-

R- B

04- R- A  ---  R/5

05- Correta  ---  R₂ paralelo com R₃  --- R’=20/5=4Ω  ---  R’ série com R₁  ---  R_eq1=20 + 4=24Ω  ---  errada  ---  R₂ paralelo com R₃ =20/2=10Ω ---  10Ω em série com R₁  ---  R_eq2=10 + 5=15Ω  ---  diferença  ---  R=24 – 15=9Ω  ---  R-B

06- Observe as resoluções nas figuras abaixo:

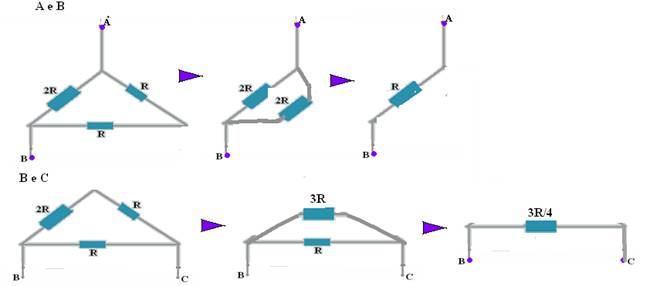
 R_AB/R_BC=R/1 x 4/3R=4/3  ---  R- A

07- a)

b) Como o número de resistores não foi especificado, existem várias associações cuja resistência equivalente é 1,5Ω  ---  uma delas está no esquema abaixo

08- A) Sim, é ôhmico, pois o gráfico Uxi é uma reta inclinada a partir da origem, ou seja , U é  proporcional a i de modo que R seja constante  ---  R=U/i=0,6/0,2=1.2/0,4=3,0/1,0=3Ω

B) R=U/i  ---  3=9/i  ---  i=3A   ---  P_o=i.U=3.9=27W  ---  W=P_o..Δt=27.300  --- W=8.100J=8,1kJ

C) È a associação I onde a resistência equivalente é menor (R/2), dissipando assim, maior potência.

09- (5 + R) paralelo com 4Ω  ---  R_eq=produto pela soma  ---  3=(5 + R).4/5 + R + 4  ---  3=(20 + 4R)/9 + R  ---  27 + 3R=20 + 4R  ---  R=7Ω  ---  R- E

10- série  ---  R_eq=R₁ + R₂  ---  6=R₁ + R₂  ---  R₁=6 – R₂ (I)  ---  paralelo  ---  R_eq=R₁.R₂/(R₁ + R₂)  ---  4/3=R₁.R₂/(R₁ + R₂)  ---  3R₁R₂=4R₁ + 4R₂ (II)  --- (I) em (II)  ---  3.(6 – R₂).R₂=4(6 – R₂) + 4R₂  ---  3R₂² – 18R₂ + 24=0  ---  resolvendo essa equação, obtém-se 2Ω e 4Ω  ---  R- C

11- R- B  ---  veja teoria

12- R_eq=30/3=10 Ω  ---  R- A

13-

14- Observe nas figuras abaixo a seqüência de operações:

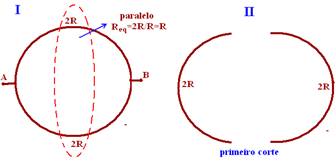
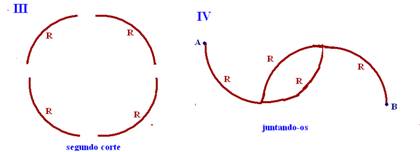
Os dois que estão em paralelo  ---  R’=R/2  ---  R’ fica em série com R e R  ---  R_eq=R + R/2 + R  ---  R_eq=5R/2  ---  R- E

15- O sistema que aquece mais rapidamente a água é aquele que possui menor resistência equivalente  ---  R_eq=0,5Ω  ---  R- B

16- a) chave fechada  ---  todos os resistores são percorridos por corrente e participam do circuito  ---  R paralelo com R – R/2  ---  R/2 em série com R  ---  R_eq=3R/2=1,5R  --- R_eq=U/i  ---  1,5R=U/i  ---  i=U/1,5R  ---  chave aberta  ---  passa corrente apenas pelos dois resistores que estão em série  ---  R’_eq=2R  ---  R’_eq=U/i’  ---  2R=U/i’  ---  i’=U/2R  ---  i’/i=U/2R x 1,5R/U=1,5/2  ---  i’/i=0,75.

b) Com a chave fechada onde a resistência equivalente é menor, dissipando maior potência e aquecendo mais a água.

17- Como o resistor maior é o A e ele vai ser somado com o R_eq dos outros dois, a alternativa correta é a D  ---  R- D

18- R- C  ---  R_eq=R/3

19- R₂ é a menor resistência, tem o maior   ---  série  ---  R₁ + R₂=R (I)  ---  paralelo  ---  R₁.R₂/(R₁ + R₂)=3R/16  ---   R₁.R₂/R=3R/16  ---  R₁.R₂=3R²/16 (II)  ---  resolvendo o sistema composto por (I) e (II)  ---  R₁=R/4 e R₂=3R/4

20- Para que a potência dissipada seja a menor possível, a resistência equivalente deve ser a maior possível, o que ocorrerá quando eles forem ligados em série  ---  R_eq=1 + 2=3  ---  R_eq=3 Ω  ---  P_o=U²/R_eq=4/3W  ---  R- A

21- Maior corrente implica em maior potência e consequentemente em menor resistência  --- R- D

22- a) menor potência implica em maior resistência equivalente, no caso, em série  ---  R_eq=2 + 6=8Ω  ---  potência dissipada  ---  P_o=U²/R_eq=144/8  ---  P_o=18W

b)

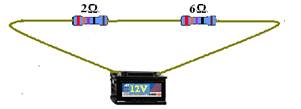
c) Sendo P_o=U²/R_eq  ---  U² é diretamente proporcional a P_o  ---  para que a potência fique 4 vezes maior, a tensão U deve ser dobrada  ---  U=2.12  ---  U=24V

23- Refazendo o circuito e chamando de P e Q na figura abaixo os pontos de interseção de fios:

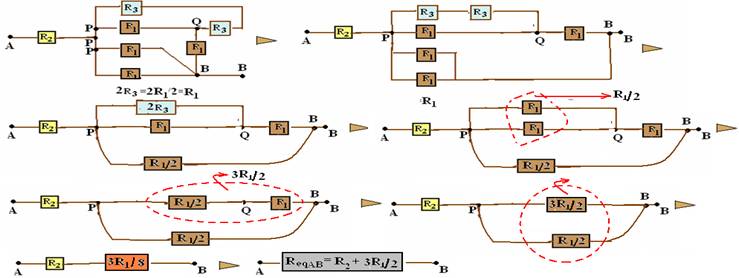
Como R_eqAB=2R₂  ---  2R₂=R₂ + 3R₁/9  ---  R₂=3R₁/8  ---  R₂/R₁=3/8  ---  R- A

24- Chamando de r a resistência equivalente dos infinitos resistores que estão a direita dos pontos P e Q (região delimitada em

vermelho)  ---  lembre-se que,se a seqüência é infinita, a resistência da seqüência situada à direita dos pontos P e Q também é r, e então pode-se fazer ---  r = r paralelo com R (r’) + r’ em série com 2R  ---  r= r.R/(r + R) + 2R  ---  r(r + R) = rR + (r + R).2R  ---  r² + rR = rR + 2Rr + 2R²  ---  r² – 2Rr – 2R²=0  ---  Δ=B² – 4.A.C=4R² – 4.1.(-2R²)  --- 

Δ=4R² + 8R²=12R²  ---  √Δ=2√3R  ---  r₁= (2R  + 2√3R)/2  ---  r₁=R(1 + √3) e r₂=R(1 - √3)  ---  r₂ não satisfaz por ser negativa  ---

R- E

25- lado oeste  ---   cada km tem 13Ω de resistência  ---  13x + R + 13x=60  ---  26x + R=60  ---  R=60 – 26x (I)  ---  lado leste  --- 

13.(10 – x) + R + 13.(10 – x)=216  ---  130 – 13x + R + 130 – 13x=216  ---  -26x + R=-44 (II)  ---  (I) em (II)  ---  -26x + (60 – 26x)=-44  ---  -52x=-104  ---  x=2km  ---  R- A

26- Observe que os dois resistores estão entre os pontos P e Q  ---  paralelos  ---  R_eq=20/3=6,66Ω  ---  R- B

27- Cálculo da resistência de cada lâmpada  ---  P_o=U²/R  ---  40=(120)²/R  ---  R=360Ω  ---  cálculo do valor da resistência equivalente das 4 lâmpadas associadas em paralelo  ---  R_eq=360/4  ---  R_eq=90Ω  ---  cálculo da potência total fornecida por essas 4 lâmpadas em paralelo (uma chocadeira)  ---  P_ot=U²/R_eq=(120)²/90  ---  P_ot=160W  ---  cálculo da energia consumida por essa chocadeira em um dia  ---  W=P_ot.Δt=160W.1dia  ---  W=160W por dia ou W=0,16kW por dia  ---  hidrelétrica fornece 24kW por dia  ---  chocadeira consome 0,16kW por dia  ---  número de chocadeiras  ---  n=24/0,16  ---  n=150 chocadeiras por dia  ---  R- A

28- a)

b)

c)

29-

R- C

30- Só são iluminados os trechos percorridos por corrente  ---  os trechos que estão em curo circuito foram eliminados nas figuras abaixo

R- E

31-

32- Observe na figura abaixo que todos os pontos B estão em curto circuito, ou seja, são coincidentes e o mesmo ocorre com todos

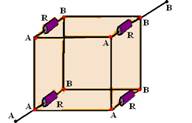
os pontos A  ---  então os 4 resistores estão em paralelo  ---  R_eq=R/4  ---  R_eq=U/i  ---  R/4=U/i  ---  i=4U/R  ---  R- A

33- Marcando os nós e colocando letras:

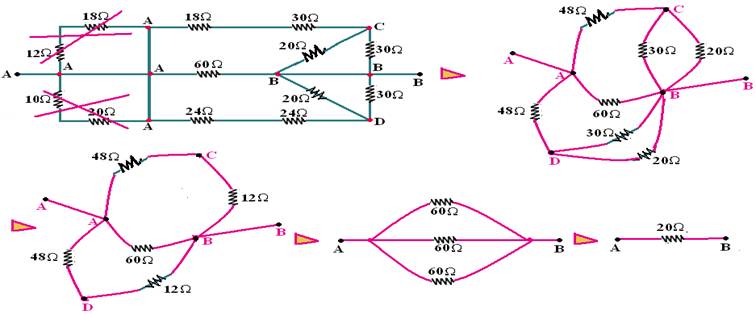
R- B

34- a)

b)

c)

35-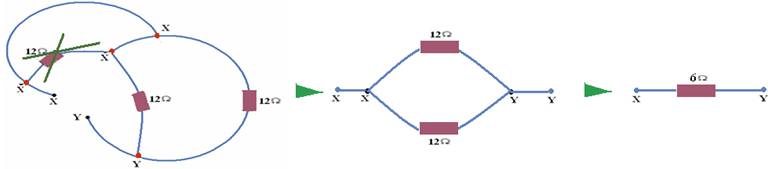 

36-

37-

R- B

38-

39- Observe que, por simetria, os três pontos da reta vertical tem o mesmo potencial  --- 

40- Observe que existe um curto circuito e que a corrente passará somente pelos dois resistores de baixo  ---  R_eq=R + R=2R

R_eq=2R

41-

R- A

42- Resistência equivalente R dos três resistores de resistências a, b e c, associados em paralelo  ---  1/R=1/a + 1/b + 1/c  ---  esses valores estão em progressão geométrica  ---  b/a=c/b=1/2  ---  a=2b  ---  c=b/2  --- do enunciado  ---  R=2Ω  ---  ½=1/2b + 1/b +1/(b/2)  ---  1/2=1/b(1/2 + 1 + 2)=7/2b  ---  b=7Ω  ---  a=2b=2.7=14Ω  ---  c=b/2=7/2=3,5Ω  ---  (a + b + c)=(7 + 14 + 3,5)=24,5Ω
R- D

43- Veja a seqüência abaixo:

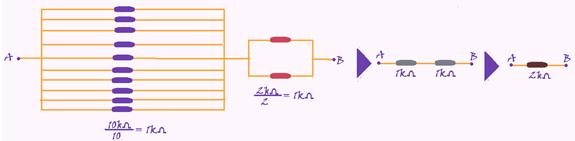
R- B

44- A resistência entre A e B corresponde à soma de R com a associação em paralelo entre R e R_eq (restante do circuito)  ---

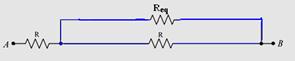
R_AB= R + R,R_eq/(R + R_eq)  ---  R_AB=R_eq já que o padrão do circuito se repete ao infinito e os dois são tão grandes que podem ser igualados  ---  R_AB= R + R. R_AB/(R + R_AB)  --- 

R²_AB – R. R_AB – R²=0  ---  R_AB=(R + R√5)/2  ---  R_AB=(R - R√5)/2 (excluído, pois R_AB deve ser positivo)  ---  R_AB=R( 1 + √5)/2  ---

R- D

45- Refazendo o circuito:

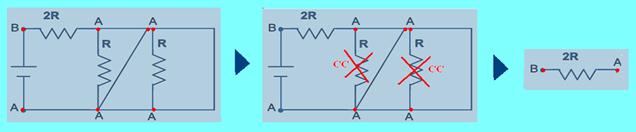
R- B

46- Observe a sequência abaixo:

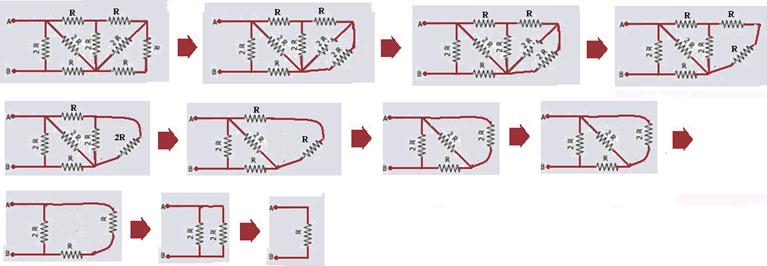
R- B

47- Observe a  sequência de figuras abaixo:

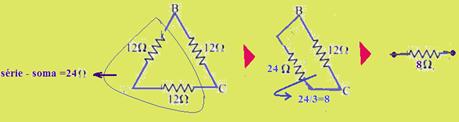
R- B

48- Observe a seqüência abaixo:

R- B