Receptores – Associação de geradores com receptores – Lei de Pouillet

Receptor elétrico

Dispositivo que converte energia elétrica em outra forma de energia, não exclusivamente térmica. Exemplos: motores elétricos, ventiladores, liquidificadores, geladeiras, aparelhos de sons, vídeos, celulares, computadores, etc.

Um ventilador, por exemplo, converte energia térmica em energia mecânica; essa conversão, entretanto, não é integral, pois uma parte da energia  converte-se, inevitavelmente, em energia térmica.

Grandezas características de um receptor elétrico

São duas: a primeira é a força contra-eletromotriz (E’), grandeza (medida em volts “1V=1J/C”) definida como a razão entre o trabalho (W) e a quantidade de carga (Q) que efetua esse trabalho no interior do receptor e que é a diferença de potencial realmente aproveitada para produzir a energia não térmica; a segunda é sua resistência interna r’.

Representação esquemática de um receptor

Circuito elétrico com um gerador alimentando um receptor

 No circuito da figura, um gerador (bateria) alimenta um receptor (motor), estabelecendo nele uma diferença de potencial.

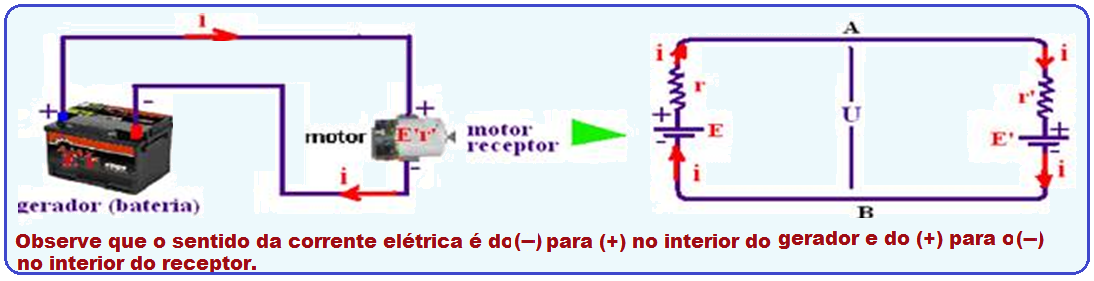
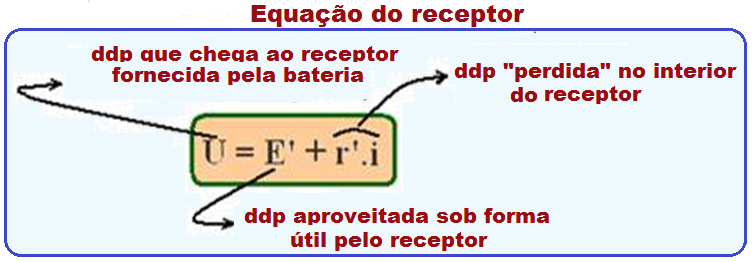
Equação do receptor

Considere um receptor elétrico (ventiladorzinho elétrico, por exemplo), recebendo U =2 V de uma pilha (significa que o motor recebe da pilha 2J de energia elétrica para cada 1C de carga que passa por ele).

Suponha que U’ = r’.i = 0,5V (significa que uma parcela de energia elétrica igual a 0,5J recebida pelo ventilador, para cada 1C de carga que passa por ele, é convertida em energia térmica, aquecendo inutilmente o motor (energia dissipada, perdida, desperdiçada).

Para o motor (receptor) produzir energia mecânica, resta    E’ =U – r’.i =2 – 0,5  E’ = 1,5V, o que significa que uma energia elétrica de 1,5J é convertida utilmente em energia não térmica (mecânica, no caso), para cada 1C de carga que passa pelo motor (receptor).

Assim:

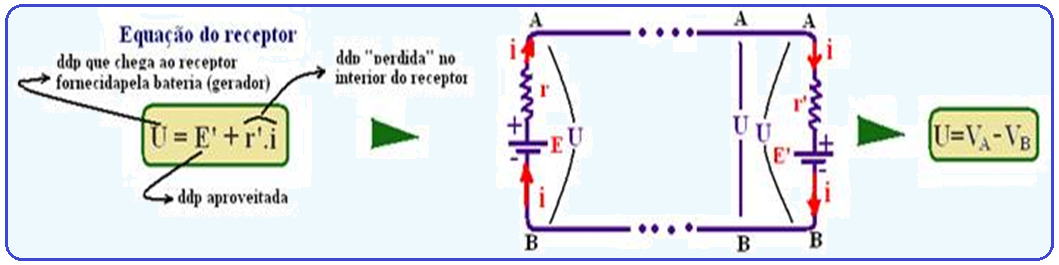
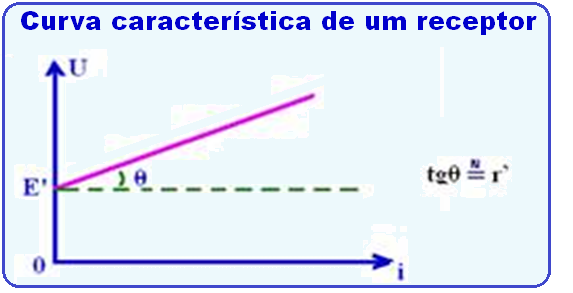
Curva característica do receptor

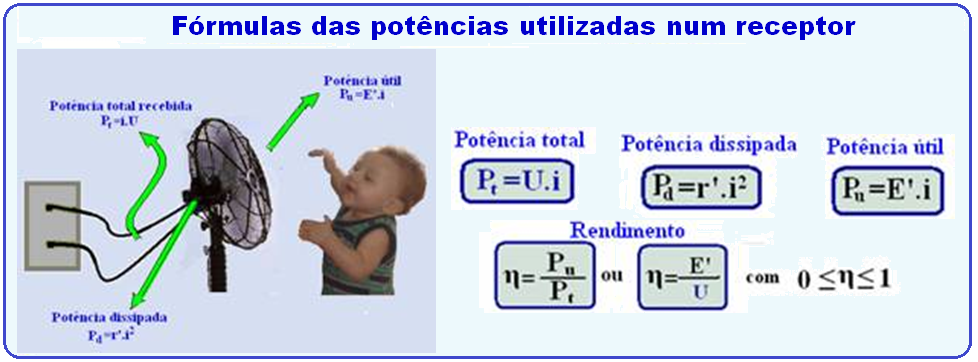
Potências de um receptor (equações)

  Potência total (P_t) corresponde à energia total recebida pelo receptor da fonte externa (gerador) por unidade de tempo:

  Potência dissipada (P_d) refere-se à potência consumida (“perdida”, dissipada, sob forma térmica) pela resistência interna r’ do receptor e fornecida por:

 Potência útil (P_u) potência aproveitada pelo receptor para seu funcionamento normal, sob forma não térmica.

Exemplo: num ventilador é a parcela da energia total que é transformada em energia exclusivamente mecânica, para girar as pás do mesmo.

Rendimento (η) de um receptor 

 O rendimento (η) de um receptor é definido como sendo a razão entre sua potência útil (P_u) e sua potência total P_t):

O que você deve saber, informações e dicas

 Se você paralisar o eixo de um motor elétrico, ele funcionará como um resistor, com toda sua energia elétrica se transformando em energia térmica, podendo queimá-lo.

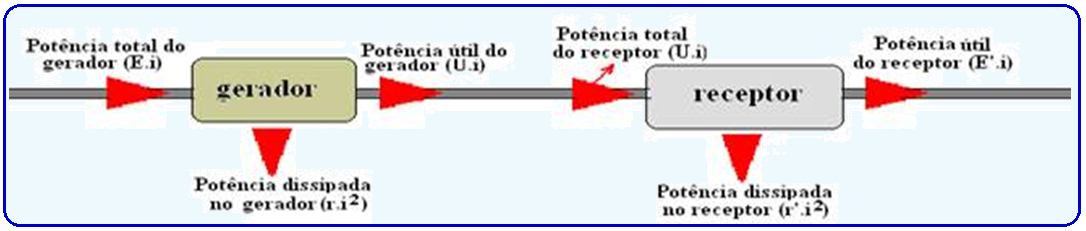
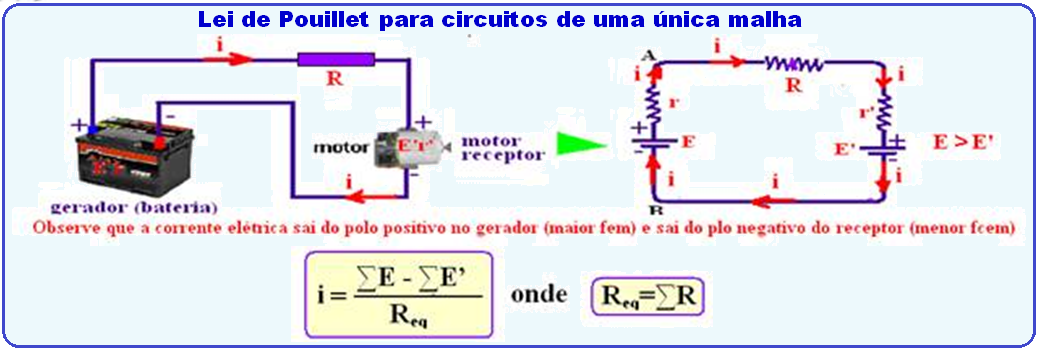
 A potência elétrica que o gerador entrega ao receptor é a potência útil do gerador (U.i).

Para o receptor, essa mesma potência representa a potência total. Desse total, uma parcela é útil (E’.i) e a outra dissipada (r’.i²). Observe atentamente o esquema abaixo.

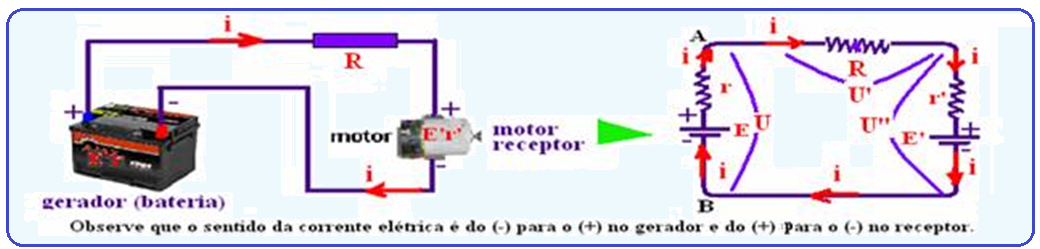
Lei de Pouillet - Circuito elétrico de malha única com geradores e receptores

Seja um gerador de força eletromotriz (fem) e resistência interna r, um receptor de força contra- eletromotriz (fcem) E’ e resistência interna r’ e um resistor de resistência R, associados em série conforme a figura, constituindo um circuito elétrico de malha única.

Como estão em série a intensidade da corrente elétrica i é a mesma em cada dispositivo.

O gerador origina em seus terminais A e B uma ddp (tensão) U que provoca uma elevação de potencial e que deve ser igual à soma das quedas de potenciais provocadas pelo resistor U’ e pelo receptor U’’, ou seja, U = U’ + U’’    U = E – r.i    U’ = R.i    U’ = E’ + r’.i    E - r.i = R.i + E’ + r’.i    E – E’=(r + r’ + R).i    i=(E – E’)/(r + r’ + R)    generalizando    em circuitos de uma única malha:

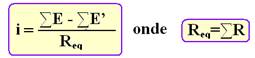
Analise com atenção esse exemplo: No circuito esquematizado abaixo, determine:

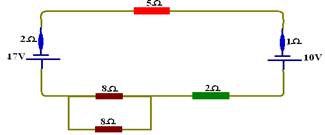
a) a intensidade da corrente elétrica no gerador, no receptor e na resistência de 5Ω.

b) A diferença de potencial nos terminais do gerador, do receptor e do resistor de 5Ω.

a) Como o sentido da corrente elétrica não é especificado, ela obedece ao de maior fem, que é a do gerador, onde a corrente sai pelo pólo positivo.

No caso, o de fem 17V é o gerador e a corrente no circuito é no sentido anti-horário, pois a corrente sai do pólo positivo do mesmo. Deve-se transformar o circuito num de malha única e, assim, deve-se resolver a associação paralelo (8/2 = 4Ω).

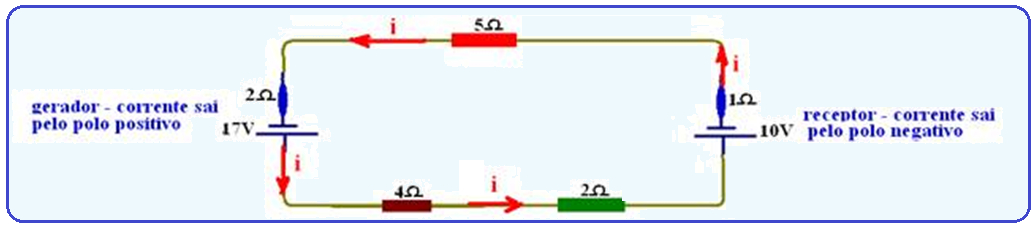
Aplicando a lei de Pouillet    i = (∑E - ∑E’)/∑R = (17 – 10)/(4 + 2 + 1 + 5 + 2)    i = 7/14    i = 0,5A, que é a mesma através de todos os elementos do circuito, pois estão em série.

b) Gerador    U_g = E – r.i = 17 – 2.0,5    U_g = 16V    receptor    U_r = E’ + r’.i = 10 + 1.0,5    U_r = 9,5V    U_5Ω = R.i = 5.0,5    U_5Ω = 2,5V.

O que você deve saber, informações e dicas

Exercícios de vestibulares com resolução comentada sobre lei de Receptores – Associação de geradores com receptores – Lei de Pouillet

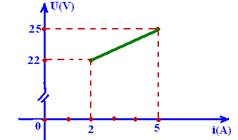
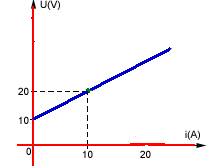
01-(MACKENZIE-SP) A diferença de potencial nos terminais de um receptor varia com a corrente conforme o gráfico abaixo.

a) 25Ve 50 Ω                    

b) 22V e 2,0 Ω                    

c) 20V e 1,0 Ω                    

d) 12,5V e 2,5 Ω                    

e) 11V e 1,0 Ω

02-(ESAL-MG) Um motor elétrico (receptor), de resistência interna 10Ω, está ligado a uma tomada

de 200V, recebendo uma potência de 1.600W. Calcule:

a) A potência elétrica dissipada internamente

b) a força contra-eletromotriz do motor

c) o rendimento do motor

03-(UFB) Aplica-se uma ddp de 50V a um motor de resistência interna 1Ω, o qual é percorrido por

uma corrente elétrica de intensidade 2,5A. Determine:

a) a força contra-eletromotriz do motor

b) a indicação de um voltímetro ligado aos terminais do motor

04-(AFA) Um gerador fornece a um motor uma ddp de 440V. O motor tem resistência interna de

25W e é percorrido por uma corrente elétrica de 400mA. A força contra-eletromotriz do motor, em volts, é igual a:

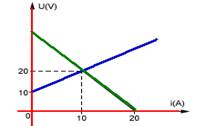
05-(UEL-PR) No gráfico a seguir estão representadas as curvas características de um gerador e de um receptor. A f.e.m. do gerador e a resistência interna do receptor valem, respectivamente:

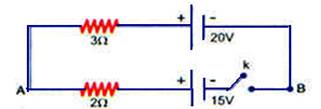
06- (PUC - SP) No circuito da figura abaixo, a diferença de potencial V_A – V_B, com a chave K aberta, e posteriormente fechada, tem valores, aproximadamente iguais a:  

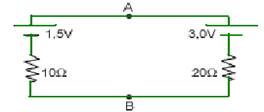
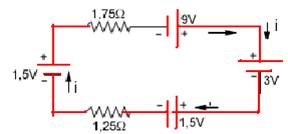
07-(UNESP-SP) O esquema a seguir representa duas pilhas ligadas em paralelo, com as resistências internas indicadas:

a) Qual o valor da corrente que circula pelas pilhas?
b) Qual é o valor da diferença de potencial entre os pontos A e B?
c) Qual das duas pilhas está se "descarregando"?

08-(UFPA) A figura representa um circuito elétrico:

Calcule a intensidade da corrente elétrica que passa pelo resistor R₁ e a diferença de potencial nos terminais de R_2.

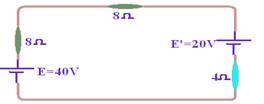
09-(UFRS-RS) Calcule o valor de R para que a corrente fornecida pela associação de geradores em oposição seja 2 A.

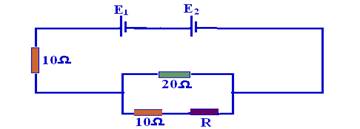
 Dados: E₁=55V e E₂=5V

10-(UFCE-CE) No circuito abaixo, determine a diferença de potencial nos terminais do resistor de 2Ω

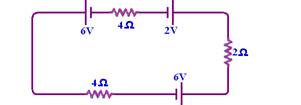
11-(UFPE-PE) Calcule o potencial elétrico no ponto A, em volts, considerando que as baterias têm resistências internas

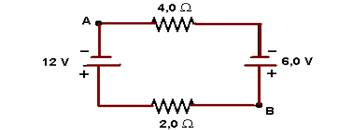
desprezíveis e que o potencial no ponto B é igual a 15 volts.

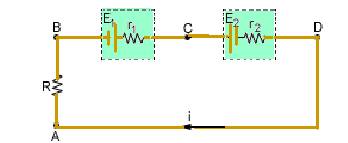
12-(UFPA) No circuito a seguir, i = 2A,  R = 2Ω,  E₁ = 10V, r₁ = 0,5Ω, E₂ = 3,0V e r₂ = 1,0Ω. Sabendo que o potencial no ponto A é de 4V, podemos afirmar que os potenciais, em volts, nos pontos B, C e D são, respectivamente:

13-(UFLA-MG) No circuito apresentado na figura a seguir, estão representadas diversas fontes de força eletromotriz de resistência interna desprezível que alimentam os resistores R₁ = 1,75Ω e R₂ = 1,25Ω. A corrente i no circuito é de:

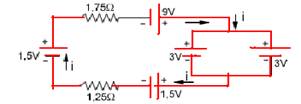
a) 6,0 A                              

b) 5,0 A                                 

c) 4,5 A                                 

d) 2,0 A                                 

e) 3,0 A

 14-(UFRS-RS) O circuito a seguir representa três pilhas ideais de 1, 5 V cada uma, um resistor R de resistência elétrica 1, 0 Ω e um motor, todos ligados em série.

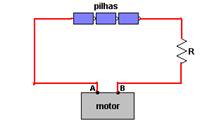
(Considere desprezível a resistência elétrica dos fios de ligação do circuito.)

A tensão entre os terminais A e B do motor é 4, 0 V. Qual é a potência elétrica consumida pelo motor?

15-(UFRJ-RJ) Os gráficos característicos de um motor elétrico (receptor) e de uma bateria (gerador) são mostrados nas figuras (1) e (2), respectivamente.

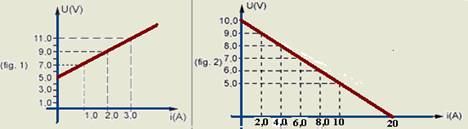
Sendo o motor ligado a essa bateria, é correto afirmar que a intensidade da corrente elétrica que o percorrerá, em ampères, será de:

(PUCCAMP-SP) Este enunciado refere-se às questões de números 16 e 17.  São dadas as curvas características de três elementos de um circuito elétrico:

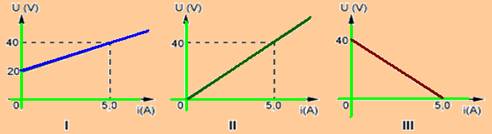
16-(PUCCAMP-SP) Associando os três elementos em série, fechando um circuito, a intensidade da corrente que os percorre, em ampère, vale:

17-(PUCCAMP-SP) Considere as retas suportes das curvas que aparecem nos gráficos I e III. Se ambas estivessem representadas em um mesmo sistema de eixos, elas se interceptariam no ponto:

 18-(ITA-SP-09) Considere um circuito constituído por um gerador de tensão E = 122,4 V, pelo qual passa uma corrente I = 12 A, ligado a uma linha de transmissão com condutores de resistência r = 0,1Ω. Nessa linha encontram-se um motor e uma carga de 5 lâmpadas idênticas, cada qual com resistência R = 99Ω, ligadas em paralelo, de acordo com a figura.

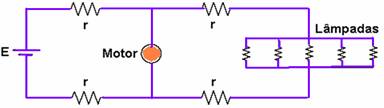
Determinar a potência absorvida pelo motor, P_M, pelas lâmpadas, P_L, e a dissipada na rede, P_R.

19-(ITA-SP) No gráfico a seguir estão representadas as características de um gerador, de força eletromotriz igual a E e resistência interna r, e um receptor ativo de força contra eletromotriz E’ e resistência interna r’.

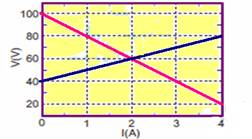
Sabendo que os dois estão interligados, determine a resistência interna e o rendimento para o gerador e para o receptor.

20-(UFRJ-RJ) Um estudante dispunha de duas baterias comerciais de mesma resistência interna de 0,10 W, mas verificou, por meio de um voltímetro ideal, que uma delas tinha força eletromotriz de 12 Volts e a outra, de 11Volts. A fim de avaliar se deveria conectar em paralelo as baterias para montar uma fonte de tensão, ele desenhou o circuito indicado na figura a seguir e calculou a corrente i que passaria pelas baterias desse circuito.

a) Calcule o valor encontrado pelo estudante para a corrente i.

b) Calcule a diferença de potencial V_A − V_B entre os pontos A e B indicados no circuito.

21-(UFG-GO)

Dois geradores ideais, de tensões iguais a V, foram ligados a dois resistores iguais, de resistência R, conforme ilustram os

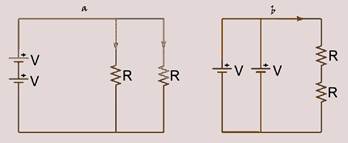
circuitos a seguir. Considerando o exposto, a razão da corrente em um dos resistores do circuito (a) pela de um resistor de (b) é:

22-(UFPA-PA)  

Na Figura 1 estão representados três objetos que utilizam eletricidade.

Os gráficos da Figura 2 mostram o comportamento desses objetos por meio de suas características tensão (U) versus intensidade de corrente (I).

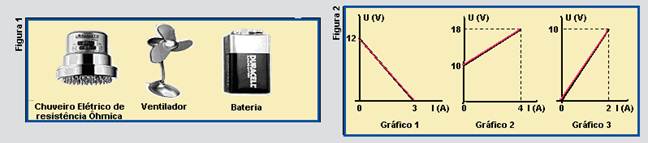
a) Levando-se em conta o comportamento elétrico desses objetos, associe cada um deles com o gráfico correspondente que o caracteriza.

b) Para uma corrente de 2A, calcule o rendimento do objeto que se comporta como receptor.

23-(UEPB-PB)

Em 1820, o cientista dinamarquês Hans Christian Oersted (1777-1851) não imaginava que, com uma singela experiência, descobriria um princípio físico fundamental para o funcionamento do motor elétrico, que possibilitou o surgimento e o desenvolvimento de um grande número de aparelhos elétricos, tais como: bateria, ventilador, furadeira, liquidificador, aspirador de pó, enceradeira, espremedor de frutas, lixadeira, além de inúmeros brinquedos movidos a pilha e/ou tomada, como robôs,

carrinhos, etc, utilizados em todo o mundo.

Acerca do assunto tratado no texto acima, resolva a seguinte situação-problema:

Um motor elétrico tem resistência interna de 2,0W e está ligado a uma ddp de 100 V. Verifica-se que ele é percorrido por uma corrente elétrica de intensidade igual a 5,0 A. A força contra-eletromotriz do motor e a potência total recebida pelo motor, respectivamente, são

a) 80 V; 350 W                 

b) 90 V; 450 W             

c) 90 V; 500 W           

d) 70 V; 300 W             

e) 100 V; 400 W

24-(UEPB-PB) Em 1820, o cientista dinamarquês Hans Christian Oersted (1777-1851) não imaginava que, com uma singela experiência, descobriria um princípio físico fundamental para o funcionamento do motor elétrico, que possibilitou o surgimento e o desenvolvimento de um grande número de aparelhos elétricos, tais como: bateria, ventilador, furadeira, liquidificador, aspirador de pó, enceradeira, espremedor de frutas, lixadeira, além de inúmeros brinquedos movidos a pilha e/ou tomada, como robôs, carrinhos, etc, utilizados em todo o mundo.

  Acerca do assunto tratado no texto, em relação ao motor elétrico, analise as proposições a seguir, escrevendo V ou F conforme sejam verdadeiras ou falsas, respectivamente:

(  ) O motor elétrico é um elemento de trabalho que converte energia elétrica em energia mecânica de rotação.

(  ) O motor elétrico é uma máquina que converte energia mecânica de rotação em energia elétrica.

(  ) Um motor elétrico é uma aplicação do princípio fundamental do eletromagnetismo que afirma que uma força magnética vai atuar sobre um condutor elétrico se esse condutor estiver convenientemente colocado num campo magnético e for percorrido por uma corrente elétrica.

Após a análise feita, assinale a alternativa que corresponde à seqüência correta:

25-(UEPG-PR)  Dispositivos que transformam outras formas de energia em energia elétrica são conhecidos como geradores elétricos. Dispositivos capazes de receber energia elétrica e transformá-la em outras formas de energia que não a térmica são denominados receptores elétricos. Sobre geradores elétricos e receptores elétricos, assinale o que for correto.

01. Quando um gerador encontra-se em circuito aberto, a diferença entre seus terminais é igual a sua força eletromotriz.

02. A potência útil fornecida por um gerador a um circuito onde só existem resistores será máxima se a resistência equivalente do circuito for igual à resistência interna do gerador.

04.Geradores elétricos podem ser associados somente em paralelo.

08. O rendimento elétrico de um receptor corresponde ao produto entre a potência elétrica útil e a potência elétrica fornecida ao receptor.

16.       A força contra-eletromotriz pode, em termos práticos, ser pensada como uma força eletromotriz que se opõe à passagem da corrente elétrica.

26-(ITA-SP)  Considere um circuito constituído por um gerador de tensão E = 122,4 V, pelo qual passa uma corrente I = 12 A, ligado a uma linha de transmissão com condutores de resistência r = 0,1Ω. Nessa linha encontram-se um motor e uma carga de 5 lâmpadas idênticas, cada qual com resistência R = 99 Ω, ligadas em paralelo, de acordo com a figura.

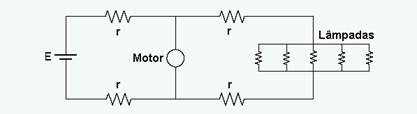
 Determinar a potência absorvida pelo motor, P_M, pelas lâmpadas, P_L, e a dissipada na rede, P_R.

27-(UFSC-SC) Considere o circuito abaixo.

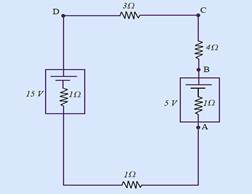
Assinale a(s) proposição(ões) CORRETA(S).

01. A corrente no circuito é 2,0 A.

02. O potencial elétrico no ponto D é menor do que no ponto C.

04. A potência fornecida ao circuito externo pela fonte de 15 V é 14 W.

08. A potência dissipada no resistor de 4Ω é 16 W. 16. A diferença de potencial entre os pontos A e B (VB – VA) é 6 V.

28-(UPE-PE)

Um motor elétrico sob tensão 220 V é alimentado por uma corrente elétrica de 10 A. A potência elétrica útil do motor é

de 2000 W. Assinale a alternativa que corresponde à força contra eletromotriz, em volts, à resistência interna do motor, em ohms, e ao rendimento elétrico do motor, respectivamente.

A) 200; 2; 0,80      

B) 200; 2; 0,91      

C) 400; 4; 1      

D) 400; 4; 0,80      

E) 400; 4; 1,5

29-(UPE-PE)

Um circuito com duas malhas contém duas fontes de tensão constante E₁ = E₂ = 14 V e três resistores R₁ = 1,0 ohm, R₂ = 3,0 ohms e R = 1,0 ohm, conforme mostrado na figura a seguir:

Analise as seguintes proposições:

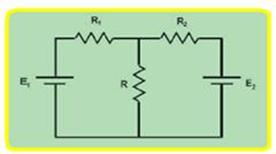
I. A corrente que passa pelo resistor R₁ vale 6 A.

II. O sentido da corrente que passa pelo resistor R₂ é da esquerda para a direita.

III. A potência dissipada no resistor R₂ vale 12 W.

IV. O sentido da corrente que passa pelo resistor R é de cima para baixo.

Estão CORRETAS

Resolução comentada dos exercícios de vestibulares sobre

Receptores – Associação de geradores com receptores – Lei de Pouillet

01- j Quando i=2A  ---  U=22V  ---  U=E’ + r’.i  ---  22=E’ + r’.2 (I)  ---  quando i=5 A  ---  U=25V  ---  U=E’ + r’.i  ---  25=E’ + r’.5 (II)  ---  resolvendo o sistema composto por (I) e (II)  ---  R- C

02- a) Cálculo da corrente elétrica no receptor  ---  P_t=i.U  ---  1.600=i.200  ---  i=8A  ---  P_d=r’.i²=10.(8)²  ---  P_d=640W

b) Potência útil  ---  P_t=P_d + P_u  ---  1.600=640 + P_u  ---  P_u=960W  ---  P_u=E’.i  ---  960=E’.8  ---  E’=120V

c) η=E’/U=120/200=0,6  ---   η=60%

03- a) Equação do receptor  ---  U=E’ + r’.i  ---  50=E’+1.2,5  --- E’=47,5V

b) O voltímetro indica o valor da força contra-eletromotriz do receptor  ---  U=50V

04- Equação do receptor  ---  U=E’ + r’.i  ---  440=E’ + 25.0,4  ---  E’=440 – 10  ---  E’=430V  ---  R- D 

05- O gráfico do gerador é o da reta descendente  ---  icc=20A --- icc=E/r  ---  20=E/r  ---  E=20r  --- 

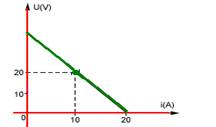
Equação do gerador   ---  quando i=10A – U=20V  ---  U=E – r.i  ---  20=E – r.10  ---  20=20r – 10r  ---  r=2Ω  ---  E=20r=20.2  ---  E=40V

O gráfico do receptor é o da reta ascendente  ---  observe que E’=10V  ---  quando 1=10A – U=20V  ---  equação do receptor  --- 

U=E’ + r’.i  ---  20=10 +r’.10  ---  r’=10/10  ---  r’=1Ω  ---  R- D

06- Chave aberta  ---  se você ligar um voltímetro ideal (resistência interna infinita) nos terminais de um gerador ele indicará sua força eletromotriz (no caso E=20V), pois ele funciona como se estivesse em circuito aberto  ---   se você ligar um voltímetro nos terminais de um receptor desligado (chave k aberta) como por exemplo de um liquidificador, ferro elétrico, etc., ele indicará zero  Chave fechada  --- circulará corrente de valor  ---  i=(∑E - ∑E’)/∑R=(20 – 15)//(3 + 2)  ---  i=1A  ---   cálculo de U_AB pelo gerador  ---  U_AB=E – r.i=20 – 3.1  ---  U_AB=17V   ---  U_AB=E’ + r’.i=15 + 2.1  ---  U_AB=17V   ---  R- B

07- a) i=(3 – 1,5)/((10 + 20)  ---  i=0.05A 

b) pelo gerador  ---  U=E – r.i=3 – 20.0,05  ---  U=2V  ---  ou, pelo receptor  ---  U=E’ + r’+.i=1,5 + 1=.0,05  ---  U=2V

c) Haverá desgaste da pilha de maior fem, que é a de 3V  ---  Observação  ---  esse tipo de ligação é inconveniente, pois sempre haverá corrente entre elas com a de 3V funcionando como gerador e fornecendo corrente para a de 1,5V que funciona como receptor. Então, o desgaste é inevitável.

08- Resolvendo R₂ paralelo com R₃ paralelo com R₄ para chegar à uma malha única  --- R’=2Ω  ---  i=(4 – 2)/(2 + 0,5 + 0,5 + 2)  ---  i=2/5  ---  i=0,4 A  ---   U=R’.i=2.0,4  --- U=0,8V

09- Deixando uma malha única  ---  20 Ω paralelo com (10 Ω + R)  ---  R’=20.(10 + R)/20 + 10 + R  ---  R’=(200 + 20R)/(30 + R)  ---  i=(55 – 5)/(200 + 20R)/(30 + R) + 10  ---  2=50/(500 + 30R)/(30 + R)  ---  1.000 + 60R=1.500 + 50R  ---  R=50Ω

10- Observe que o sentido da corrente é no horário  ---  i=(+6 +6 -2)/(4 + 2 +4)  ---  i=10/10  ---  i=1A  ---  R=U/i  ---  2=U/1  ---  U=2V

11- i=(12 – 6)/(4 + 2)  ---  i=1A  ---  pelo gerador (E=12V e r=2Ω)  ---  U_AB=E – r.i=12 – 2.1  ---  U=10V  ---  ou, pelo receptor (E’=6V e r’=4Ω)  ---  U=E’ + r’.i=6 + 4.1  ---  U=10V  ---  observe que V_B é maior que V_A  ---  V_B – V_A=10  ---  15  - V_A=10  ---  V_A=5V

12- entre A e B  ---  U_AB=V_A­ – V_B  ---  U_AB=R.i=2.2  ---  U_AB=4V  ---  V_A – V_B=4  ---  4 – V_B= 4  ---  V_B=0  ---  gerador  ---  V_C > V_B  ---  U_CB=E₁ – r₁.i=10 – 0,5.2  ---  U_CB=9V  ---  V_C – V_B=9  ---  V_C – 0 = 9  ---  V_C=9V  ---  receptor  ---  V_C > V_D  ---  U_CD=V_C – V_D  ---  U_CD=E₂ + r₂.i=3 + 1.2  ---  U_CD=5V  ---  U_CD= V_C – V_D  ---  5=9 – V_D  ---  V_D=4V  ---  R- A  ---  Observe que V_A=V_D (unidos por fio ideal)

13- Substituindo os dois geradores de 3V que estão em paralelo, o circuito fica com malha única e

conforme a figura abaixo  ---i=((1,5+9) – (3+1,5))/(1,75 + 1,25)= 6/3  ---  i=2 A  ---  R- D

14- Como eles estão associados em série, a tensão nos terminais das pilhas (U_g=4,5V) é igual à soma das tensões nos terminais da resistência R (U’) e do motor (U_m=4V)  ---  4,5=U’ + 4  ---  U’=0,5V  ---  R=U’/i  ---  1=0,5/i  ---  i=0,5 A  ---  P_motor=i.U=0,5.4  --- R- D

15- Receptor  ---  figura 1  ---  reta ascendente  ---  E’=5V  ---  i=2 A – U=9V  ---  U=E’ + r’.i  ---  9=5 + r’.2  --- r’=2Ω  ---  gerador  ---  reta descendente  ---  figura 2  ---  E=10V  ---  i_cc=E/r  ---  20=10/r  ---  r=0,5Ω  --- i=(10 – 5)/((0,5 + 2)  ---  i=5/2,5  ---  i=2 A 

R- A

16- I  ---  receptor  ---  E’=20V  ---  i=5A – U=40V  ---  U=E’ + r’.i  ---  40=20 + r’.5  ---  r’=4Ω  ---  II  ---  resistor  ---  R=U/i=40/5  ---  R=8Ω  ---  III  ---  gerador  ---  E=40V  ---  i=5A   ---  i_cc=E/r  ---  5=40/r  --- 

r=8Ω  ---  montando o circuito  --- i=(40 – 20)/(8 + 8 + 4)  ---i=20/20  ---  i=1A  ---  R- A

17- Equação do gerador  ---  U=E – r.i  ---  U_g=40 – 8i (I)  ---  equação do receptor  ---  U_r=E’ + r’.i  --- 

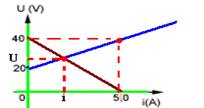
U=20 + 4.i (II)  ---  na intersecção  ---  U_g=U_r  ---  substituindo (I) em (II)  ---  40 – 8i=20 + 4i  ---  20=12i  ---  i=20/12  ---  i=5/3 A  ---  U=20 + 4.5/3  ---  U=80/3V  ---  R- C  

18-

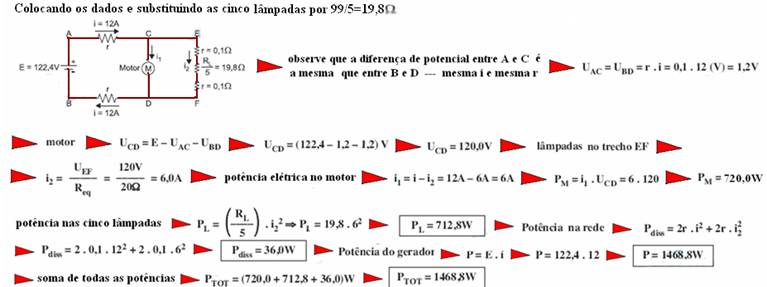
19- Gerador  ---  reta descendente  ---  E=100V  ---  i=4 A  ---  U=20V  ---  equação do gerador  ---  U=E – r.i  ---  20=100 – r.4  ---  r=20Ω  ---  receptor  ---  E’=40V  ---  i=2 A  ---  U=60V  ---  equação do receptor  ---  U=E’ + r’.i  ---  60=40 + r’.2  ---  r’=10Ω  --- cálculo da corrente i pela lei de Pouillet  ---  i=(100 – 40)/(20 + 10)  ---  i=2 A  ---  observe que para essa corrente U é comum ao gerador e ao receptor  ---  rendimento do gerador  ---  η=U/E=60/100  ---  η_gerador=0,6=60%  ---  η_receptor=E’/U=40/60  --- η_receptor=0,67=67%

20- a) O circuito está esquematizado abaixo onde estão indicados os sentidos de percurso e da

corrente  ---  + 11 + 0,1i + 0,1i –  12=0 ---  i=1/0,2  ---  i=5 A

b) Pela parte superior  ---  V_A – V_B=+ 12 – 0,10.5  ---  V_A - V_B=11,5V  ---  ou pela parte inferior  ---  V_A – V_B=+ 11 + 0,10.5  ---  V_A - V_B=11,5V

21- Observe o esquema abaixo  ---  figura a  ---  U=2V  ---  R_eq=R/2  ---  i’=i/2  ---  i=2i’ ---  R_eq=U/i  ---  R/2=2V/i  ---  i=4V/R  ---  2i’=4V/R  ---  i’=2V/R  ---  figura b  ---  U=V  ---  R_eq=2R  ---  R_eq=U/i’’  ---  2R=V/i’’  ---  i’’=V/2R  ---  i’/i’’=2V/R x 2R/V  ---  I’/i’’=4  --- R- E

22- a) O gráfico 1 refere-se a um gerador e, portanto, representa a bateria  ---  o  gráfico 2 representa um receptor e, portanto, é o ventilador  ---   gráfico 3 representa um resistor e, portanto, é o chuveiro.

b) O rendimento do receptor, ou seja, do ventilador  ---   U = 10 + 2i  ---  para i = 2 A  ---  U = 14 V  ---  rendimento  ---  η = 10/14   ---  η = 71,4% 

23- Equação do receptor  ---  U=E’ + r’.i  ---  100=E’ + 2.5  ---  E’=90V  ---  P=U.i=100.5  ---  P=500W  ---  R- C

24- R- E  ---  veja teoria

25- 01. Correta  ---  se i=0, ou seja, se o gerador estiver em circuito aberto, tem-se:

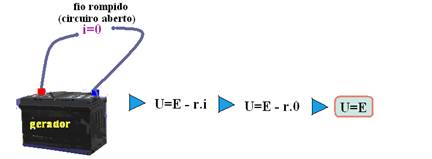
02. Correta  ---  se o gerador estiver ligado a uma associação de resistores de resistência equivalente R_eq a potência máxima fornecida à essa

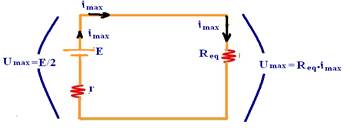
associação será  ---  U_máx=Req.i_máx  ---  E/2=R_eq.(E/2r)  ---  r=R_eq

04. Falsa  ---  veja teoria

08. Falsa  ---  o rendimento elétrico de um receptor é definido pela razão entre sua potência útil e sua potência consumida  ---  η=P_u/P_c  ---  η=E.i/U.i  ---  η=E/U
16- Correta  ---  veja teoria 
R- (01 + 02 + 16)=19

26-

27- 01. Percorrendo i circuito no sentido horário e supondo a corrente também no sentido horário  ---  i – 15 + 3i + 4i + 5 + i + i=0  ---  i=1 A  ---  Falsa

02- V_D – V_C=3.1=3V  ---  V_D – V_C=3V  ---  V_D > V_C  ---  Falsa

04. U=E – ri=15 – 1.1  ---  U=14V  ---  P=i.u=1.14  ---  P=14W  ---  Verdadeira

08. P=R.i²=4.1²  ---  P=4W  ---  Falsa

R- 4

28- Potências de um receptor:

 Potência total (Pt) – corresponde à energia total recebida pelo receptor da fonte externa (gerador) por unidade de tempo:

 Potência dissipada (Pd) – refere-se à potência consumida (perdida, dissipada, sob forma térmica) pela resistência interna r’ do receptor e fornecida por:

 Potência útil (Pu) –potência aproveitada pelo receptor para seu funcionamento normal, sob forma não térmica.Exemplo: num ventilador é a parcela da energia total que é transformada em energia exclusivamente mecânica.

 Rendimento (η) de um receptor – definido como sendo a razão entre sua potência útil (Pu) e sua potência total Pt):

P_u=E’.i  ---  2000=E’.10  ---  E’= 200V  ---  P_t=U.i=220.10=2200W  ---  P_t=P_u + P_d  ---  2200=2000 + r’.i²  ---  200=r’.100  ---  r’=2Ω  ---  η=P_u/P_t=2000/2200  ---  0,909  ---  R- B.

29- O processo de resolução está explicado em fisicaevestibular.com.br (eletricidade-eletrodinâmica-circuitos compostos)

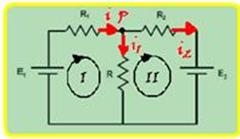
(I) partindo de P e percorrendo a malha no sentido horário  ---  1.i₁ – 14 + 1i=0  ---  i₁ + i = 14 (a)  ---  (II) partindo de P e percorrendo a malha no sentido horário  ---  3i₂ + 14 – i₁=0  ---  3i₂ – i₁ = -14 (b)  ---  i=i₁ + i₂ (c)  ---  resolvendo o sistema formado por (a), (b) e (c)  ---  i₂=-2 A (sentido correto-anti-horário)  ---  i₁=8 A sentido correto-horário)  --- 

i=6 A (sentido correto-horário)  ---  P_R2=R₂.i₂²=3.4=12W  ---  R- E.