Galvanômetro como Amperímetro e como Voltímetro – Ponte de Wheatstone

Galvanômetro

 O galvanômetro é um dispositivo que mede correntes de pequenas intensidades e que é composto, de uma maneira bem simples, por muitos condutores retilíneos sendo percorrido por uma corrente elétrica, mesmo princípio utilizado na construção de motores elétricos.

Símbolo de um galvanômetro

Galvanômetro adaptado para amperímetro

 Quando você quer que o galvanômetro meça correntes maiores que as de seu fundo de escala (funcionando como amperímetro) você deve associar, em paralelo a ele, um resistor (R_S) denominado shunt (em inglês, desvio).
O conjunto todo, galvanômetro com resistência R_G e a resistência shunt paralela a ele constitui o amperímetro, que se transforma num galvanômetro de escala ampliada.

i corrente total de fundo de escala que você quer medir

i_G  corrente de fundo de escala do galvanômetro

i_S  corrente que é desviada para a resistência shunt (R_S)    

R_G  resistência interna do galvanômetro

Analise com atenção esse exemplo numérico:

Você possui um galvanômetro de resistência interna R_G = 100 Ω e corrente de fundo de escala i_G = 10 mA.

Para você medir correntes de até i = 1 A (quando a corrente de fundo de escala do galvanômetro estiver marcando 10 mA, na realidade deverá estar marcando 1 A), você deve transformá-lo num amperímetro, colocando em paralelo uma resistência de (100/99) Ω.

Assim, a corrente que faz o ponteiro do galvanômetro ir até o fundo de escala é i = 1A quando no galvanômetro está passando 0,01 A e a parte que desvia para o shunt é i_S = 0,99 A.

Assim, se o galvanômetro estivesse marcando 5mA (metade da escala), na realidade a corrente medida seria de 0,5 A (metade de 1 A).

Observe que o fator de multiplicação é n = (1 + R_G/R_S)=1 + 100/(100/99) =100    n = 100 (quando deveria marcar 0,01 A estará marcando 100x0,01 = 1 A).

Galvanômetro adaptado para voltímetro

Quando você quer que o galvanômetro meça tensões (voltagens ou ddps) maiores que as de seu fundo de escala você deve associar, em série a ele, um resistência (R_M) denominada resistência multiplicadora.

O conjunto todo, galvanômetro com resistência R_G e a resistência multiplicadora em série com ele constitui o voltímetro, que se transforma num galvanômetro de escala ampliada.

Observe que a corrente i é a mesma tanto no galvanômetro como na resistência multiplicadora R_M e que a tensão total (U) que é a tensão de fundo de escala indicada pelo voltímetro é a soma da tensão de fundo de escala no galvanômetro (U_G) com a tensão na resistência multiplicadora (U_M).

U = U_G + U_M    U_M = R_M.i    U_G = R_G.i    i = U_G/R_G    U = U_G + R_M.U_G/R_G    U = U_G( 1 + R_M/R_G)    U = m.U_G    a expressão m = (1 + R_M/R_G) é chamada fator de multiplicação.

Analise com atenção esse exemplo numérico:

Você possui um galvanômetro de resistência interna R_G=100Ω e corrente de fundo de escala i_G = 10mA.

Para você medir tensões de até 3V (quando a corrente de fundo de escala do galvanômetro estiver marcando 10mA, na realidade estará marcando 3V), você deve associar em série uma resistência multiplicadora de 200Ω de modo que ele se transforme num voltímetro que indique entre 0 e 3V  ---  provando  U=R_G.i + R_M.i=100.0,01 + 200.0,01    U=3V.

Ponte de Wheatstone

Trata-se de uma associação de três resistores fixos e um variável (reostato), como representado na figura.

Serve, dentre outras coisas, para determinar a resistência de um resistor. Conhecendo, por exemplo, R₁, R₂ e R₄, pode-se determinar R₃, da seguinte maneira:

 Liga-se entre B e D um amperímetro muito sensível (galvanômetro).

Varia-se o reostato (resistência variável) R_X até que a intensidade i_A de corrente no amperímetro se torne nula (i_A = 0).

Nessa situação, diz-se que a ponte está em equilíbrio. Sendo nula a corrente no amperímetro, não existe diferença de potencial entre os pontos B e D.

Ponte de fio

O que você deve saber, informações e dicas

 Se a ponte está em equilíbrio, ou seja, se R₁.R_X = R₂.R₃, você pode tocar os pontos B e D com as mãos e não leva choque e também qualquer aparelho elétrico colocado entre B e D não funcionará, pois V_B = V_D e nesse trecho não passa corrente elétrica.

Exercícios de vestibulares com resolução comentada sobre

Galvanômetro como Amperímetro e como Voltímetro – Ponte de Wheatstone

 01-(FUVEST-SP) Um galvanômetro permite a passagem de corrente máxima i_G.

A finalidade de se colocar uma resistência em paralelo com ele é:

 a) fazer passar uma corrente mais intensa que i_G pelo galvanômetro sem danificá-lo;

b) permitir a medida de corrente (I) mais intensa que i_G;

c) permitir a medida de tensões elevadas;

d) as três resoluções anteriores;

e) fazer passar uma corrente menos intensa que i_G

02-(MACKENZIE-SP) É dado um galvanômetro de resistência 10W e fundo de escala 1,0V. Qual deve ser o valor da resistência série para medir 10V? Qual deve ser o fator de multiplicação?

 a) 90 W e 10                      

b) 9 W e 10                  

c) 100 W e 10                     

d) 10 W e 100                     

e) 1000 W e 10

03. (MACKENZIE) Usando um voltímetro de fundo de escala 20V e resistência interna de 2000W, desejamos medir uma ddp de 100V. A resistência do resistor adicional que devemos associar a esse voltímetro é:

04-(UFG-GO) Um laboratório possui um galvanômetro de resistência interna 100 Ω e corrente de fundo de escala 2,0 mA. Calcule a resistência necessária para utilizá-lo como:

A) um amperímetro para medir uma corrente máxima de 50 mA;

B) um voltímetro para medir uma tensão máxima de 20 V.

05-(UFRS-RS) Selecione a alternativa que preenche corretamente as lacunas do texto abaixo, na ordem em que elas aparecem.

Um "galvanômetro" é um aparelho delicado e sensível capaz de medir uma corrente elétrica contínua, I, muito pequena, da ordem de alguns microampères ou, quando muito, miliampères. Para medir correntes elétricas maiores do que essas, usa-se um "amperímetro", que é um galvanômetro modificado da maneira representada na figura adiante.

Constrói-se um amperímetro a partir de um galvanômetro, ligando-se a resistência interna R_G do galvanômetro em paralelo com uma resistência R_S, chamada de 'shunt' (palavra inglesa que significa desvio). Assim, para se obter um amperímetro cuja "corrente de fundo de escala" seja 10 vezes maior do que a do galvanômetro usado, ........ da corrente elétrica I deverá passar pelo galvanômetro, e o valor de R_S deverá ser ........ do que o valor de R_G.

(Dado: A "corrente de fundo de escala" é o valor máximo de corrente elétrica que o amperímetro ou o galvanômetro podem medir.)

a) 1/9 - 9 vezes menor         

b) 1/10 - 9 vezes menor         

c) 1/10 - 10 vezes maior         

d) 9/10 – 9 vezes maior

e) 9/10 – 10 vezes maior

06- (UNESP-SP) A corrente que corresponde à deflexão máxima do ponteiro de um galvanômetro é de 1,0mA e sua resistência é de 0,5Ω. Qual deve ser o valor da resistência de um resistor que precisa ser colocado nesse aparelho para que ele se transforme num voltímetro apto a medir até 10V? Como deve ser colocado esse resistor, em série ou em paralelo com o galvanômetro?

07-(UERJ-RJ) O galvanômetro abaixo tem resistência interna de 100Ω e sofre a máxima deflexão com a passagem de uma corrente de 1,0.10^-4 A. O instrumento é acoplado a um voltímetro de escala múltipla, como indicam os valores que representam as leituras máximas de cada escala no esquema que se segue.

Os valores das resistências R₁, R₂ e R₃, em ohms, devem ser de, respectivamente:

a) 9,9.10²; 9,9.10³ e 9,9.10⁴    

b) 9,0.10³; 9,0.10⁴ e 9,0.10⁵     

c) 9,9.10³; 9,0.10⁴ e 9,0.10⁵     

d) 9,9.10³; 9,9.10⁴ e 9,9.10⁵

e) 9,0.10⁴; 9,0.10⁵ e 9,0.10⁶

08-(UNESP-SP) Pretende-se medir a corrente no circuito abaixo intercalando-se entre os pontos A e B um amperímetro que tem resistência interna de 1,5Ω.

Acontece que o máximo valor que o instrumento mede (fundo de escala) é 3,0A, e a corrente no circuito é maior que isso. Aumentando-se o fundo de escala para 4,5 A, o instrumento pode ser utilizado. São fornecidos resistores ( r )  que devem ser ligados ao amperímetro , na forma indicada, de modo que sua escala seja ampliada para 4,5 A. Que valor de resistência ( r )  satisfaz o requisito?

a) 4,0 Ω                                 

b) 3,0 Ω                                 

c) 2,0 Ω                                 

d) 1,0 Ω                             

e) 0,5 Ω

09-(UFB) Na parede de uma loja de produtos elétricos estão expostos cinco ventiladores idênticos (A,B,C,D e E) e desligados, Os pontos M e N estão ligados à uma rede de tensão elétrica constante de 117V, conforme o esquema da figura.

Ligando-se o interruptor I, qual dos ventiladores não funcionará? Justifique.

10-(UEL-PR) Abaixo está esquematizado um trecho de circuito em que todos os resistores são iguais.
Entre os pontos A e F existe uma diferença de potencial de 500V.

Entretanto, pode-se tocar simultaneamente em dois pontos desse circuito sem tomar um "choque". Esses pontos são:

11-(UFLA-MG) A ponte de Wheatstone mostrada abaixo estará em equilíbrio quando o galvanômetro G indicar zero volt. Para que isso ocorra, R₁ deve ter valor igual a:

a) R/3                          

b) R                          

c) 2R                      

d) R²/2                               

e)R²                            

12-(UEL-PR) No circuito esquematizado, R₁=210Ω, R₂=30Ω, AB é um fio homogêneo de seção reta transversal constante e resistência 50Ω e comprimento 500mm. Obteve-se o equilíbrio do galvanômetro para L=150mm. O valor de X é, em ohms:

13-(UNICAMP-SP) A variação de uma resistência elétrica com a temperatura pode ser utilizada para medir a temperatura de um corpo. Considere uma resistência R que varia com a temperatura θ de acordo com a expressão R=R_o(1 + αθ) onde R_o=100Ω, α=4.10^-3oC^-1 e θ é dada em graus celsius. Esta resistência está em equilíbrio térmico com o corpo, cuja temperatura θ se deseja conhecer. Para medir o valor de R, ajusta-se a resistência R₂, indicada no circuito abaixo, até que a corrente medida pelo amperímetro no trecho AB seja nula.

a) Qual a temperatura θ do corpo quando a resistência R₂ for igual a 108Ω?

b) A corrente através da resistência R é igual a 5,0.10^-3A. Qual a diferença de potencial entre os pontos C e D indicados na figura?

14-(UFRN-RN) No circuito da figura abaixo, o galvanômetro indica uma corrente nula.

Neste caso, pode-se afirmar que:

a) i₁R₄ + i₂R₃=0         

b) i₁R₁ – i₂R₃=0         

c) i₁R₄ – i₂R₃=0          

d) i₁R₄ + i₂R₂=0         

e) i₁R₁ + i₂R₂=0

15-(UNICAMP-SP) No circuito abaixo a corrente na resistência de 5Ω é nula.

a) Determine o valor da resistência X

b) Qual a corrente fornecida pela bateria?

16-(UFSC) O circuito fechado é o de uma “ponte de fio” e serve para determinação de uma resistência desconhecida R_X.

Sabendo que a ponte da figura está equilibrada , isto é, o galvanômetro G não acusa nenhuma passagem de corrente elétrica, determine o valor numérico de R (em ohms), na situação de equilíbrio, considerando que L₁=20cm e L₂=50cm.

17-(FUVEST) Considere o circuito da figura, onde E=10V e R=1.000Ω.

a) Qual a leitura do amperímetro A?

b) Qual a leitura do voltímetro V?

18-(UNESP-SP) Um circuito contendo quatro resistores é alimentado por uma fonte de tensão, conforme figura.

Calcule o valor da resistência R, sabendo-se que o potencial eletrostático em A é igual ao potencial em B.

19-(UFPE) O circuito da figura é formado por resistores idênticos, de resistência igual a 42 ohms cada. Se, quando uma diferença de potencial de 100V é aplicada entre os pontos A e B, a diferença de potencial entre A e C é igual a 50V.

Determine a diferença de potencial em volts entre os pontos D e B.

20-(UnB-DF) Quatro resistores iguais são ligados, formando um quadrilátero, cujos vértices são identificados pelas letras A, B, C e D. Entre os vértices A e C, diagonalmente opostos, é ligada uma fonte de 6 volts. Se o potencial do vértice D vale 6 volts, calcule o potencial do vértice B, diametralmente oposto a D.

21- (Mackenzie-SP) No circuito a seguir, a ddp entre os terminais A e B é de 60V e o galvanômetro G acusa uma intensidade de corrente elétrica zero. Se a ddp entre os terminais A e B for duplicada e o galvanômetro continuar acusando zero, poderemos afirmar que:

a) a resistência R permanecerá constante e igual a 25 Ω.          

b) a resistência R permanecerá constante e igual a 15 Ω. 
c) a resistência R permanecerá constante e igual a 10 Ω.          

d) a resistência R, que era de 25 Ω, será alterada para 50 Ω. 
e) a resistência R, que era de 50 Ω, será alterada para 12,5 Ω.

22- (Mackenzie-SP) No circuito abaixo, para que ambos os amperímetros ideais, A₁ e A₂, indiquem zero, é necessário que as resistências R₁ e R₂ valham, respectivamente, em ohms:

a) 10 e 120                         

b) 40 e 90                          

c) 90 e 40                        

d) 40 e 10                         

e) 10 e 40

23-(AFA)

A figura abaixo mostra quatro passarinhos pousados em um circuito elétrico ligado a uma fonte de tensão, composto de fios ideais

e cinco lâmpadas idênticas L.

Ao ligar a chave Ch, o(s) passarinho(s) pelo(s) qual(ais) certamente não passará(ão) corrente elétrica é(são) o(s) indicado(s)

pelo(s) número(s)

Resolução comentada dos exercícios de vestibulares sobre  

Galvanômetro como Amperímetro e como Voltímetro – Ponte de Wheatstone

01- A corrente de fundo de escala (i_G) do galvanômetro continua a mesma  ---  quem muda é a corrente de fundo de escala (I) do sistema (galvanômetro + resistência shunt em paralelo com ele), que funciona como amperímetro, indicando uma corrente maior que i_G  ---  R- B

02- Observe a figura abaixo  ---  U=U_G( 1 + R_M/R_G)  ---  10=1(1 + R_M/10)  ---  R_M=90Ω

É claro que o fator de multiplicação é 10 (uma tensão de fundo de escala de 1V deve indicar 10V)  ---  R- A

03-  U=U_G(1 + R_M/R_G)  ---  100=20(1 + R_M/2.000)  ---  R_M=8.000Ω=8kΩ  ---  R- D

04- a) i=i_G(1 + R_g/R_S)  ---  50.10^-3=2.10^-3(1 + 100/R_S)  ---  24=100/R_s  ---  R_S=4,2Ω (associado em paralelo com o galvanômetro)

b) Veja figura abaixo  ---   U=U_G + U_M  ---  20=R_G.i_G + R_M.i_M  ---  20=100.0,002 + R_M.0,002  ---  20=0,2 + 0,002R_M  --- 

R_M=9.900Ω  ---  (associado em série com o galvanômetro)

05- o fator de multiplicação é n=10  ---  I=n.i_G  ---  I=10.I_G  ---  i_G=I/10  ---  n=1 + R_G/R_S  ---  10=1 + R_G/R_S  ---  R_S=R_G/9  --- 

R- B

06- U=R_G.i + R_M.i  ---  10=0,5.10^-3 + R_M.10^-3 (/10^-3)  ---   10⁴=0,5 + R_M  ---  R_M≈10⁴Ω em série com o galvanômetro

07- U=U_G + U_M1  ---  1=100.10^-4 + R₁.10^-4 (/10^-4) --- 10⁴= 100 + R₁  ---  R₁=10.000 – 100  ---  R₁=9.900Ω  ---  R₁=9,9.10³Ω  --- 

U_R2=10 – 1=9V  ---  R₂=U_R2/i=9/10^-4  ---  R₂=9.10⁴Ω  ---  U_R3=100 – 10=90V  ---  R₃=U_R3/i=90/10^-4  ---  R₃=9.10⁵Ω  ---

 R- C

08- I=i_G(1 + R_g/R_S)  ---  4,5=3(1 + R_G/R_S)  ---  4,5=3 + 4,5/R_S  ---  r=R_S=3,0Ω  ---  R- B

09- O ventilador C, pois trata-se de uma ponte de Wheatstone, não passando corrente elétrica entre os pontos P e Q que estão sob mesma diferença de potencial, ou seja V_P=V_Q

10- Trata-se de uma ponte de Wheatstone, não passando corrente elétrica entre os pontos C e D que estão sob mesma diferença de potencial, ou seja C_C=V_D  ---  R- C

11- Quando o galvanômetro indica zero, a ponte está em equilíbrio  ---  150.R=300.(R.R₁)/(R + R₁)  ---  150R² + 150.R.R₁=300R.R₁  ---  150R=150R₁  ---  R₁=R  ---  R- B

12- Relação comprimento-resistência  ---  50Ω - 500mm  ---  PΩ - 350mm  ---  500P=50.350  ---  P=35Ω  ---  Q=50 – 35  ---  Q=15Ω

(R₂ + P).R₁=Q.X  ---  (30 + 15).210=35.X  ---  X=270Ω  ---  R- E

13- a) R=R_o(1 + αθ)  ---  108=100(1 + 4.10^-3θ)  --- 1,08 – 1=4.10^-3θ  ---  θ=8.10^-2/4.10^-3  ---  θ=20^oC

b) R.R₁=R₁.R₂  ---  R=R₂=108Ω  ---  R=U/i  ---  108=U/5.10^-3  ---  U=1.080.10^-3  --- U=1,08V

14- Se a corrente no galvanômetro é nula, a corrente i₁ que passa por R₄ é a mesma que passa por R₁ e a corrente i₂ é a mesma em R₃ e R₄  ---  U_CA=U_CB  ---  R₄i₁=R₃i₂  ---  U_AD=U_BD  ---  R₁i₁=R₂i₂  ---  R- C 

15- a) 3.2=1.X  ---  X=6Ω

b) Observe a seqüência abaixo

R_eq=8/3Ω  ---  R_eq=U/i  ---  8/3=12/i  ---  i=36/8  ---  i=4,5A

16- L₁.(200 paralelo com 200)=L₂.R_X  ---  20.100=50.R_X  ---  R_X=40Ω

17- a) Supondo o amperímetro e o voltímetro ideais  ---  tirando o voltímetro e curto-circuitando o amperímetro  ---  figura abaixo  --- 

O amperímetro indica i=5,0.10^-3A

b) Tensão que o gerador fornece ao circuito  ---  U=E – r.i=10 – 500.0,005  ---  U=7,5V  ---  observe o esquema abaixo  --- 

U_AB=V_A – V_B=1.000x0,0025  ---  V_A – V_B=2,5V  ---  V_B=V_A – 2,5  ---  U_AD=V_A – V_D=2.000x0,0025  ---  V_A – V_D=5V  --- 

V_D=V_A - 5  ---  como o voltímetro está inserido entre os pontos B e D, interessa U_BD  ---  U_BD=V_B – V_D=(V_A – 2,5) – (V_A – 5)  --- 

U_BD=V_A – 2,5 – V_A + 5  ---  U_BD=2,5V  ---  o voltímetro indica 2,5V

18- Se V_A=V_B a ddp entre os ponto A e B do circuito é nula e a ponte de Wheatstone está em equilíbrio  ---  120.R=90.60  ---  R=45Ω

19- Observe que não passa corrente entre C e D  ---  ponte está em equilíbrio   ---  se U_AB=100V e U_AC=50V, U_DB=50V  ---  veja

esquema abaixo

R- 50V

20- Observe que se trata de uma ponte de Wheatstone que está em equilíbrio (resistores iguais)  ---  os pontos B e D possuem o mesmo potencial  ---  R- V_B=6V

21- Se o galvanômetro indica zero, a ponte está em equilíbrio e a relação a seguir é sempre válida, independente da tensão   --- 

15.(10 + 5)=5.(20 + R)  ---  225=100 + 5R  ---  R=125/5  ---  R=25Ω  ---  R- A

22- São duas pontes em equilíbrio  ---  ponte onde está o amperímetro A₁  ---  20.20=10.R₁  ---  R₁=40Ω  ---  o circuito, então, fica  --- 

R- B

23-(AFA)

 Com a chave Ch fechada, observe que como os fios são ideais e as lâmpadas idênticas (mesma resistência), o pássaro III está

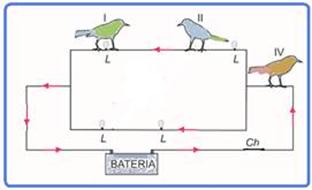
num fio onde não passa corrente elétrica (ponte de Wheatstone equilibrada)  ---  assim, sobre os pássaros II e IV não passará corrente, pois os fios são ideais e não haverá diferença de potencial entre suas patas  ---  entre as patas do pássaro I existe diferença de potencial e, por ele passará corrente elétrica  ---  R- C